Résumés
Résumé
Cet article a pour objectif l’estimation indirecte de la transmissivité (T, m2/s) de l’aquifère du Haouz (6 000 km2) au Maroc, à partir de la résistance transversale (R, Ωm2). L’aquifère du Haouz est constitué par une succession complexe de séries lenticulaires, argilo-marneuses ou formées d’éléments grossiers, d’âge plio-quaternaire reposant sur un substratum marneux d’âge miocène. Une importante base de données des valeurs de transmissivité (≈500) et de résistance transversale (≈2 500) a été compilée. Une recherche a ensuite été effectuée pour retenir les couples (Ti, Ri) caractérisant le même volume d’aquifère. Deux cas de résistance transversale sont considérés : 1) résistance transversale de l’ensemble mio-plio-quaternaire (RA); 2) résistance transversale des lentilles perméables uniquement (RB). La meilleure régression, de forme géométrique, est obtenue entre la transmissivité et la résistance transversale des lentilles grossières perméables. Cette régression est sensiblement améliorée lorsque les valeurs (T, RB) d’un même couple sont ramenées à un même état piézométrique de la nappe, après correction de la transmissivité en fonction des variations piézométriques de la nappe. On procède ensuite à l’estimation indirecte du champ de transmissivité de l’aquifère à l’échelle régionale à l’aide de l’équation de régression précédemment établie. Le champ de transmissivité ainsi estimé est validé par comparaison de ses propriétés statistiques (tendance centrale, dispersion, loi de distribution) à celles de l’échantillon des valeurs de transmissivité mesurées par pompages d’essais.
Mots Clés:
- transmissivité,
- résistance transversale,
- aquifère hétérogène,
- prospection électrique,
- distribution lognormale,
- régressions statistiques,
- Haouz de Marrakech
Abstract
This article aims at the indirect estimation of the transmissivity (T, m2/s) of the aquifer of Haouz (6,000 km2) in Morocco, using the transverse resistance (R, Ωm2). This aquifer consists of a complex succession of lenticular layers, argilo-marly or formed of coarse elements, of plio-quaternary age, lying on a marly substratum of miocene age. A significant database of the values of transmissivity (≈500) and transverse resistance (≈2,500) was compiled. A research was then carried out to select the pairs (Ti, Ri) characterizing the same volume of aquifer. Two cases of transverse resistance are considered: 1) transverse resistance of the mio-plio-quaternary unit (RA); 2) transverse resistance of the permeable coarse lenses only (RB). The best regression, of geometrical form, is obtained between the transmissivity and the transverse resistance of the permeable coarse lenses. This regression is significantly improved when the values (T; RB) of a given pair are brought back to the same level of the water table, after correction of the transmissivity according to the variations of the water table. The indirect estimate of the field of transmissivity of the aquifer is then carried out at a regional scale using the regression equation previously established. The estimated field of transmissivity is validated through the comparison of its statistical properties (central tendency, dispersion, distribution law) to those of the sample of the values of transmissivity measured by pumping tests.
Key-words:
- transmissivity,
- transverse resistance,
- heterogeneous aquifer,
- lognormal distribution,
- statistical relationships,
- Haouz of Marrakech
Corps de l’article
1. Introduction
L’optimisation des résultats et des coûts des travaux de prospection hydrogéologique demeure conditionnée par le degré de connaissance des paramètres hydrodynamiques des aquifères. La mesure la plus fiable de ces paramètres est faite par la réalisation d’un forage d’essai et son test hydraulique par un pompage de longue durée. Les coûts de réalisation s’élèvent, au Maroc, à environ 300 000 à 400 000 DH (Dirhams) pour un forage de profondeur moyenne de 100 m, soit environ 30 000 à 40 000 Euros. La nature souvent hétérogène des aquifères alluvionnaires exige en plus un nombre important d’essais, ce qui rend la prospection encore plus coûteuse (le nombre d’essais dépend bien entendu du degré d’hétérogénéité du milieu).
L’évaluation des paramètres hydrodynamiques des aquifères hétérogènes à l’aide des seuls pompages d’essai représente ainsi un coût prohibitif, d’où l’intérêt de recourir à des estimations indirectes, avec des moyens plus économiques tels que la prospection électrique. En effet, le coût moyen d’un sondage électrique de longueur de ligne AB = 1 000 m est d’environ 2 000 DH (environ 200 Euros), soit 150 à 200 fois moins cher que le coût de foration d’un forage de profondeur moyenne de 100 m et de réalisation d’un test par pompage d’essai.
Le besoin de recourir à des estimations indirectes des propriétés hydrodynamiques des réservoirs, moins coûteuses que les essais hydrauliques in situ, à l’aide notamment de la prospection géoélectrique, est assez largement partagé dans la littérature (Troisiet al., 2000).
Les relations proposées dans la littérature entre les paramètres hydrodynamiques et géoélectriques des aquifères reposent sur les travaux d’Archie (1942) qui, pour des terrains dépourvus d’argile, a proposé les expressions suivantes :
où F est le facteur de formation du terrain; ρ, la résistivité du terrain en Ω.m; ρw, la résistivité de l’eau de formation en Ω.m; Ø, la porosité totale de la formation; et m, le coefficient de cimentation de la formation. Le facteur de formation F dépend de la porosité totale du terrain (Ø), et donc de sa perméabilité K (ms-1). De ce fait, la résistivité du terrain (ρ, Ωm) et la perméabilité (K, ms-1) sont également liées. La perméabilité intervient dans la loi de Darcy (Équation 3), qui décrit l’écoulement de l’eau dans le terrain et la résistivité dans la loi d’Ohm (Équation 4), qui régit la propagation du courant électrique :
où Q est le flux (m3s-1); H, le potentiel hydraulique (m); Σ, la section (m2); L, la longueur (m); J, l’intensité de courant électrique (ampères); σ, la conductivité électrique (= 1/ρ); et E, le potentiel électrique (volts).
Ces deux lois ont une expression analogue et les deux paramètres K et σ y jouent un rôle similaire. Mettant à profit cette similarité, de nombreux auteurs ont proposé des relations empiriques permettant d’estimer K en fonction de ρ ou de F (Jones et Buford, 1951; Croft, 1971; Kelly, 1977; Urish, 1981; Schimschal, 1981; Kosinski et Kelly, 1981; Kelly et Reiter, 1984; Kwader, 1985; Mazacet al., 1985; Huntley, 1986; Yadav, 1995; Frohlichet al., 1996).
L’interprétation des sondages électriques en terrain multicouche se heurte au principe de non-unicité des solutions. Ce principe stipule que plusieurs solutions (résistivité ρi, épaisseur, bi) peuvent être déduites d’un même sondage électrique (Frohlich et Kelly, 1985). Ce problème a été quantitativement formulé par Maillet (1947) qui, à cet effet, a introduit les paramètres de Dar Zarrouk. Ces paramètres sont la conductance longitudinale C et la résistance transversale R :
où C est la conductance longitudinale (mΩ‑1); R, la résistance transversale (Ωm2); T, la transmissivité (m2s‑1); b, l’épaisseur saturée d’aquifère (m); et ρ, la résistivité (Ωm).
La loi de Darcy (Équation 3) peut également s’écrire en décomposant la section d’écoulement Σ :
où b est l’épaisseur saturée d’aquifère (m); et l, la largeur du front d’écoulement (m).
Dans l’expression (8), le produit K b définit la transmissivité de l’aquifère :
Compte tenu de l’analogie entre la transmissivité T(m2s‑1) et la résistance transversale R(Ωm2) (Expressions 6 et 8), quelques travaux ont également été développés pour rechercher des relations empiriques T = f(R) entre ces deux paramètres (Ungemachet al., 1969; Heigoldet al., 1979; Niwas et Singhal, 1981; Ponziniet al., 1984; Frohlich et Kelly, 1985; Yadav et Abolfazli, 1998). L’intérêt d’une telle relation est évident, puisque la transmissivité est déduite directement des essais hydrauliques in situ (Kruseman et de Ridder, 1973). De plus, ce paramètre quantifie au mieux les possibilités aquifères des réservoirs.
Des estimations géostatistiques des propriétés hydrodynamiques basées sur les paramètres géoélectriques ont également été proposées par certains auteurs (Ahmed et de Marsily, 1987; Ahmed et al., 1988; Cassiani et Medina, 1997; Kupfersberger et Blöschl, 1995; Troisiet al., 2000). L’estimation géostatistique a l’avantage d’incorporer la corrélation spatiale entre les valeurs des paramètres (Isaak et Srivastava, 1989).
Notons que des estimations indirectes de la transmissivité ont également été proposées à l’aide de paramètres autres que géoélectriques. Bracq et Delay (1984) proposent une estimation de la transmissivité de l’aquifère crayeux du Nord de la France basée sur les traits morphologiques. Coptyet al. (1993) utilisent les vitesses de propagation d’ondes sismiques pour estimer la perméabilité.
L’objectif de l’étude présentée dans cet article concerne l’estimation indirecte de la transmissivité de l’aquifère du Haouz (Maroc) d’extension régionale (6 000 km2), à l’aide de la résistance transversale. Une relation statistique suffisamment précise est d’abord recherchée entre ces deux paramètres. Compte tenu ensuite du très grand nombre de sondages électriques réalisés sur cet aquifère (≈2 500), cette relation est utilisée pour estimer la transmissivité sur l’ensemble de l’aquifère. Le champ de transmissivité, ainsi estimé, est caractérisé par ses propriétés statistiques. La démarche adoptée dans ce travail est strictement empirique. Les deux paramètres T (transmissivité) et R (résistance transversale) sont considérés comme aléatoires.
2. Le bassin du Haouz de Marrakech
Le Haouz de Marrakech (Figure 1) est une vaste plaine d’environ 6 000 km2, constituée par un bassin de subsidence d’origine tectonique, à remplissage détritique mio-plio-quaternaire. Le principal réservoir est localisé au sein des dépôts alluvionnaires du Plio-Quaternaire, constitués par une alternance de lentilles perméables (composées de galets, graviers et sables) et de formations argilo-marneuses quasi-imperméables. L’ensemble repose sur un substratum imperméable de faciès essentiellement argileux et marneux du Miocène (SINAN, 2000). Cette configuration géologique du bassin confère principalement aux lentilles perméables la propriété de conduite de l’eau souterraine dans cet aquifère (Castany, 1980).
Figure 1
Situation géographique et lithologie de l’aquifère du Haouz. 1 : Alluvions grossières (galets, graviers et sables); 2 : Alluvions grossières alternant avec des lentilles imperméables ou calcaires; 3 : Alluvions hétérogènes (galets, graviers, sable, argiles, marnes, etc.); 4 : Alluvions avec des passages calcaires ou marno-calcaires; 5 : Conglomérat, conglomérat alternant avec des niveaux imperméables, calcaires ou marno-calcaires.
Geographical situation and lithology of the Haouz basin. 1: Coarse alluvia (gravels and sands); 2: Coarse alluvia alternating with impermeable or calcareous lenses; 3: Heterogeneous alluvia (rollers, gravels, sand, clay, marls, etc.); 4: Alluvia with calcareous or marly-calcareous beds; 5: Conglomerate, conglomerate alternating with impermeable, calcareous or marly-calcareous beds.
Le rôle économique déterminant que joue la nappe du Haouz a incité les responsables des ressources en eau de ce bassin à mener de très nombreux travaux de reconnaissance géophysique et hydrogéologique, et ce depuis les années 40. Cette richesse en données a permis d’envisager la recherche de corrélations statistiques entre les paramètres hydrodynamiques et les paramètres géophysiques de cet important aquifère.
3. Données disponibles et caractéristiques statistiques.
Les données actuellement disponibles sont en nombre relativement important (DGH, 1989a et b). Les valeurs de transmissivité ont été déterminées à partir de l’interprétation des résultats des pompages d’essai en régime transitoire, selon la méthode semi-logarithmique de Jacob (Kruseman et DE Ridder, 1973). Seuls les pompages d’essai d’une durée au moins égale à 24 heures ont été retenus, pour que l’essai mette en jeu un volume d’aquifère suffisamment grand. Les puits et forages captent l’aquifère sur toute leur hauteur sans distinguer les lentilles perméables des autres formations quasi-imperméables (marnes et argiles). Dans ces conditions, la valeur de transmissivité déduite d’un essai par pompage représente une valeur moyenne caractérisant la tranche saturée d’aquifère en ce point.
Les sondages électriques et leur interprétation ont été réalisés par des géophysiciens professionnels. Les résultats mis à notre disposition par la DGH (résistivité ρ (Ωm), épaisseur b (m) des couches, résistance transversale R(Ωm2)) n’ont pas été revus dans le cadre de ce travail. Notons que pour s’affranchir du principe de non-unicité, les géophysiciens se sont appuyés sur les informations géologiques disponibles (notamment les nombreuses coupes de forages), pour l’interprétation des sondages électriques, comme cela est préconisé dans la littérature (Astier, 1971; Koefoed, 1979). À partir des résultats d’interprétation des sondages électriques (ρi , bi), la résistance transversale d’une couche i a été déterminée par l’expression suivante :
La résistance transversale du Mio-Plio-Quaternaire (RA) et des lentilles perméables (RB) a ensuite été obtenue comme suit :
où Ri et Rj représentent les résistances transversales des couches considérées dans chaque cas.
La figure 2 montre la localisation des ouvrages testés par un pompage d’essai de durée minimale de 24 heures environ. Le nombre de ces ouvrages est d’environ 500 et ils sont relativement bien répartis sur le territoire. Ces ouvrages sont constitués par 160 forages et 343 puits. Les puits sont des ouvrages de grand diamètre (Ø > 1 m). La profondeur moyenne des forages testés est d’environ 80 m et celle des puits est d’environ 35 m. La figure 3 montre la localisation des sondages électriques (SE) effectués en dix campagnes différentes s’étalant entre 1969 et 1991. On dénombre environ 2 500 SE, dont la longueur de ligne AB est généralement comprise entre 500 et 5 000 m.
Figure 2
Localisation des ouvrages testés par pompages d’essai. 1 : Forage; 2 : Puits à grand diamètre.
Location of the tested wells using pumping tests. 1: Borehole; 2: Large diameter well.
Figure 3
Localisation des sondages électriques. 1 : Position des sondages électriques.
Location of the electric surveys. 1: Position of electric sounding.
Les paramètres statistiques (moyenne, écart‑type, coefficient de variation, valeurs extrêmes) de la transmissivité mesurée à partir de pompages d’essais (Tmes) et de la résistance transversale des lentilles perméables RB sont reportés dans le tableau 1. Les valeurs de transmissivité sont incluses dans la fourchette [10‑5 - 9 10‑2 m2/s], avec une moyenne de 6,7 10‑3 m2/s, un écart‑type de 9,7 10‑3 m2/s et un coefficient de variation de 144 %. Les valeurs de résistance transversale des lentilles perméables RB varient entre 1 et 69 000 Ωm2, avec une moyenne de 3 240 Ωm2 , un écart‑type de 5 250 Ωm2 et un coefficient de variation de 162 %. Le coefficient de variation des deux paramètres (Tmes et RB) est élevé. L’importance de la dispersion statistique des échantillons des valeurs des deux paramètres est associée à la forte hétérogénéité de l’aquifère.
Tableau 1
Paramètres statistiques de la résistance transversale des lentilles perméables (RB), de la transmissivité mesurée par pompages d’essai (Tmes) et de la transmissivité estimée par régression (Test). N : effectif; m : moyenne arithmétique; s : écart-type; CV : coefficient de variation; Min : valeur minimum; Max : valeur maximum.
Statistical parameters of the transverse resistance (RB) of the pervious layers, measured transmissivity (Tmes) and estimated transmissivity (Test). N: size; m: arithmetic mean; S: standard deviation; CV: coefficient of variation; Min: minimum value; Max: maximum value.
Les distributions de fréquences des deux paramètres sont reportées sur un diagramme fonctionnel lognormal (Figures 4 et 5). Les fréquences cumulées s’alignent suivant une droite sur ce diagramme dans les deux cas. On peut noter cependant que les plus faibles valeurs de transmissivité s’écartent de la droite théorique. Cet écart peut être imputé à une sous-estimation de ces valeurs au niveau des puits et des forages imparfaits (ne captant généralement que la tranche supérieure de l’aquifère). Le caractère lognormal des deux paramètres peut être accepté. Un test du Chi-deux (Spiegel, 1961) portant sur les fréquences absolues s’est révélé positif au seuil d’acceptation de 5 %, attestant la distribution lognormale des deux paramètres.
Figure 4
Distribution de fréquences de la transmissivité mesurée par pompages d’essai. Ajustement à une loi lognormale.
Frequency distribution of the measured transmissivity values using pumping tests. Adjustment with a lognormal law.
Figure 5
Distribution de fréquences de la résistance transversale des lentilles perméables. Ajustement à une loi lognormale.
Frequency distribution of the transverse resistance of the pervious layers. Adjustment with a lognormal law.
4. Recherche de corrélations statistiques entre T et R
Parmi l’ensemble des données hydrogéologiques et géophysiques disponibles, une sélection s’est avérée nécessaire de façon à ne retenir que les couples (Ti, Ri) se rapportant au même volume d’aquifère investigué à la fois par le pompage d’essai et par le sondage électrique. La détermination du volume de terrain investigué par les sondages électriques fait l’objet de controverse dans la littérature (Evjen, 1938; Roy et Apparao, 1971; Koefoed, 1972; Apparao et Gangadhara, 1974; Bhattacharya et Sen, 1981; Apparaoet al., 1997). En revanche, en hydrogéologie, le volume d’aquifère influencé par un pompage d’essai en régime transitoire est représenté par un cylindre de rayon r égal au rayon d’influence de l’essai, et de hauteur égale à la tranche saturée. L’expression du rayon d’influence r (m) des pompages d’essai s’écrit (Kruseman et de Ridder, 1973) :
où T est la transmissivité (m2/s); t, la durée de pompage (sec); et S, le coefficient d’emmagasinement de la nappe (sans dimension).
Le procédé suivant a finalement été adopté pour la sélection des couples (Ti, Ri). Lorsque la ligne d’un sondage électrique est incluse (totalement ou partiellement) dans le cercle de rayon r autour d’un forage, la valeur de résistance transversale Ri déduite de ce sondage a été couplée avec la valeur de transmissivité Ti déduite sur le forage.
Dans un précédent travail (Sinan, 1986; Razack et Sinan, 1988), l’application de cette méthode avait permis de retenir des échantillons de couples (Ti, Ri) d’effectif supérieur à 30 en considérant plusieurs cas (Figure 6) :
corrélation entre la transmissivité mesurée (Tmes) et la résistance transversale de l’ensemble mio-plio-quaternaire (RA);
corrélation entre la transmissivité mesurée (Tmes) et la résistance transversale uniquement des lentilles perméables (RB);
corrélation entre la transmissivité corrigée en fonction du niveau piézométrique de la nappe (Tcorr) et la résistance transversale uniquement des lentilles perméables (RB).
Figure 6
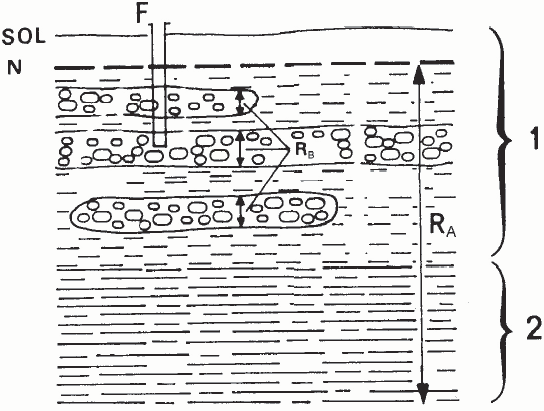
Coupe schématique à travers l’aquifère du Haouz montrant les différents cas de résistance transversale envisagés dans l’étude. 1 : Plio-Quaternaire; 2 : Miocène; F : forage; N : niveau piézométrique; RA : résistance transversale de l’ensemble mio-plio-quaternaire; RB : résistance transversale des lentilles perméables.
Simplified cross-section of the Haouz aquifer showing the different transverse resistances assumed in this study. 1: Plio-Quaternary; 2: Miocene; F: well; N: water table; RA: transverse resistance of the whole Mio-Plio-Quaternary; RB: transverse resistance of the pervious layers.
Compte tenu de la nature lognormale des deux paramètres, les régressions ont été effectuées après transformation logarithmique des valeurs. Les résultats sont résumés dans le tableau 2.
Tableau 2
Régression géométrique entre les valeurs de transmissivité mesurées par pompage d’essai et les résistances transversales (les calculs sont effectués après transformation logarithmique des variables). t(exp) = paramètre expérimental de Student obtenu par transformation du coefficient de corrélation; t(théo) = paramètre t théorique de Student au seuil de signification de 1 % et pour un nombre de degrés de libertés = N-2 (la régression est d’autant plus significative que t(exp) est supérieur à t(théo)); RA = résistance transversale de l’ensemble mio-plio-quaternaire; RB = résistance transversale des lentilles perméables; Tmes = transmissivité mesurée; Tcor = transmissivité corrigée de l’effet des variations piézométriques.
Geometrical regression between measured transmissivities and transverse resistances (calculations are carried out after logarithmic transformation of the variables). t(exp) = Student experimental parameter obtained by transformation of the correlation coefficient; t(théo) = Student theoretical parameter at a significance level of 1% and for a number of degrees of freedom = N-2 (the greater the difference between t(exp) and t(théo), the more significant the regression); RA = transverse resistance of the whole Mio-Plio-Quaternary formation; RB = transverse resistance of the pervious lenses; Tmes = measured transmissivity; Tcor = corrected transmissivity for the effect of the piezometric variations.
Les différentes régressions effectuées ont été soumises au test t de Student et leurs coefficients de détermination Q (rapport entre la variance de T expliquée par la régression et la variance totale de T) ont été comparés. Ces différents tests ont montré que la plus forte liaison est obtenue entre Tmes et RB. En effet, le coefficient de corrélation est de 0,63 avec un intervalle de confiance de [0,38; 0,72] au seuil de 95 %, le test de Student est le plus significatif (texp > tthéo ) et le coefficient de détermination est de 40 %.
La régression est sensiblement améliorée lorsque les valeurs de transmissivité sont corrigées en fonction du niveau piézométrique. En effet, la réalisation des ouvrages d’eau souterraine (puits et forages) et l’exécution des sondages électriques se sont échelonnées sur plusieurs décennies pendant lesquelles le niveau de la nappe a subi de grandes variations, notamment dans sa partie centrale. Les baisses de niveaux (dépassant 10 mètres par endroits) sont dues à l’impact du déficit d’alimentation de la nappe pendant les années de sécheresse (notamment depuis le début des années 80) et de sa surexploitation dans certains secteurs, particulièrement dans le Haouz central. Les remontées des niveaux (atteignant parfois 20 m) sont dues à un excès de recharge, par le retour des eaux d’irrigation au niveau des périmètres irrigués, alimentés essentiellement à partir des eaux superficielles régularisées par des barrages.
La nappe du Haouz étant libre, les variations de son niveau piézométrique (N) se répercutent sur son épaisseur saturée, et donc sur les valeurs de transmissivité et de résistance transversale. La correction de l’effet de cette variation des niveaux a consisté à ramener le niveau piézométrique de la nappe (et donc son épaisseur saturée) à la même côte pour chaque couple (Tmes; RB) pris en compte dans le calcul de la régression. La correction de la transmissivité mesurée (Tmes) a été effectuée comme suit :
où Nsondage électrique est le niveau piézométrique de la nappe au moment de la réalisation du sondage électrique; Npompage d’essai, le niveau piézométrique de la nappe au moment de la réalisation du pompage d’essai.
On constate une amélioration significative du coefficient de corrélation qui s’élève à 0,71 avec un intervalle de confiance [0,53; 0,82] au seuil de 95 %. Le test de Student est largement positif et le coefficient de détermination (51 %) a augmenté de 11 % par rapport à la régression obtenue entre les données brutes. L’équation de régression finale s’écrit :
avec RB en Ω.m2 et Tcorr en m2/s.
La droite de régression est reportée sur la figure 7, ainsi que les intervalles de confiance au seuil de 99 %. La fiabilité de cette régression permet d’envisager l’identification indirecte et à moindre coût du champ de transmissivité de l’aquifère du Haouz, à partir des valeurs de résistance transversale des lentilles perméables saturées.
Figure 7
Diagramme de régression Log-Log entre les transmissivités (Tmes) et les résistances transversales des lentilles perméables saturées (RB).
Log-Log regression diagram between measured transmissivities (Tmes) and transverse resistances of the pervious layers (RB).
5. Estimation du champ de transmissivité
L’équation 13 ci-dessus a été appliquée à l’échantillon de 2 523 valeurs de résistance transversale des lentilles perméables saturées. Le champ de transmissivité estimé à l’aide de cette équation est reporté sur la figure 8. Afin de valider le champ de transmissivité estimé, celui-ci est statistiquement comparé à l’échantillon de valeurs mesurées.
Figure 8
Distribution spatiale de la transmissivité estimée de l’aquifère. 1 : Test ≥ 10‑2 m2/s; 2 : 610‑3 ≤ Test < 10‑2 m2/s; 3: 310‑3 ≤ Test < 610‑3 m2/s; 4: Test < 310‑3 m2/s.
Spatial distribution of estimated transmissivity in the aquifer. 1: Test > = 10‑2 m2/s; 2: 610‑3 ≤ Test < 10‑2 m2/s; 3: 310‑3 ≤ Test < 610‑3 m2/s; 4: Test < 310‑3 m2/s.
Les paramètres statistiques de la transmissivité estimée sont reportés dans le tableau 1 (ligne 3). Statistiquement, le champ estimé est comparable à l’échantillon des valeurs mesurées de la transmissivité. Les deux moyennes sont très proches (![]() mes = 6,7 10‑3m2s‑1 ;
mes = 6,7 10‑3m2s‑1 ; ![]() est = 5,7 10‑3m2s‑1). La dispersion des valeurs mesurées et estimées est également du même ordre de grandeur (σmes = 9,7 10‑3 m2s‑1 ; σmes = 6,9 10‑3 m2s‑1). Cette dispersion statistique est assez élevée ainsi que l’attestent les coefficients de variation respectifs (CVmes = 144 % et CVest = 120 % ).
est = 5,7 10‑3m2s‑1). La dispersion des valeurs mesurées et estimées est également du même ordre de grandeur (σmes = 9,7 10‑3 m2s‑1 ; σmes = 6,9 10‑3 m2s‑1). Cette dispersion statistique est assez élevée ainsi que l’attestent les coefficients de variation respectifs (CVmes = 144 % et CVest = 120 % ).
La distribution de fréquences des valeurs estimées de transmissivité est reportée sur un diagramme fonctionnel lognormal (Figure 9). Les valeurs de transmissivité estimées s’alignent bien sur une droite, ce qui démontre que ces valeurs sont distribuées suivant une loi lognormale. Un test d’ajustement du Chi-2 a été réalisé (Spiegel, 1961) au seuil d’acceptation de 5 % et s’est révélé positif.
Figure 9
Distribution de fréquences de la transmissivité estimée. Ajustement à une loi lognormale.
Frequency distribution of estimated transmissivity. Adjustment with a lognormal law.
En conséquence, le champ de transmissivité estimée, conserve les propriétés statistiques caractérisant l’échantillon des valeurs mesurées de transmissivité.
6. Commentaires
L’examen du champ de transmissivité estimée à partir de la résistance transversale (Figure 8) met bien en évidence la variabilité spatiale importante de ce paramètre, due à la forte hétérogénéité des alluvions aquifères.
Les zones les plus transmissives sont situées dans l’axe central de l’aquifère de direction SW – NE, le long de la faille d’Assoufid qui s’étend entre le nord de l’affleurement primaire de Guemassa et le Haouz oriental. La zone d’Aït Ourir et la partie sud du Haouz oriental présentent également une transmissivité élevée.
Les zones de faible transmissivité sont situées généralement au nord de la nappe, en raison de la réduction de l’épaisseur de celle-ci. La nappe affleure en effet au niveau de l’oued Tensift qui la draine dans son parcours de direction Est‑Ouest. Le Haouz occidental est généralement caractérisé par une faible transmissivité (de l’ordre de 10‑4 m2/s ) en raison de la réduction de l’épaisseur et du caractère argileux de ses alluvions.
7. Conclusion
Les principaux résultats acquis à l’issue de ce travail sont rappelés ci-dessous.
Ce travail a permis de rassembler une importante base de données concernant les paramètres hydrauliques et géoélectriques de l’aquifère du Haouz.
La transmissivité de l’aquifère mesurée à l’aide de pompages d’essai (Tmes) et la résistance transversale des lentilles perméables (RB) déduite des sondages électriques s’apparentent à des variables distribuées selon une loi lognormale. Les valeurs de Tmes et RB s’étendent sur plusieurs ordres de grandeurs. Cette forte dispersion des valeurs des deux paramètres est liée à l’hétérogénéité marquée de l’aquifère.
Une régression statistique significative a été établie entre la transmissivité (Tmes) et la résistance transversale des lentilles perméables (RB). La régression est sensiblement meilleure lorsque chaque couple (Tmes, RB) est associé à un même état piézométrique de la nappe.
Un champ de transmissivité a été estimé sur l’ensemble de l’aquifère à l’aide de l’équation de régression précédemment établie.
Ce champ de transmissivité estimé a été validé en comparant ses propriétés statistiques à celles de l’échantillon de valeurs mesurées de transmissivité.
On propose en définitive une solution statistique suffisamment précise au problème d’estimation de la transmissivité des nappes alluviales fortement hétérogènes à partir de leurs paramètres géoélectriques. La portée pratique et économique d’une telle estimation indirecte par régression est évidente, puisqu’elle permet d’estimer la transmissivité de la nappe (et donc sa productivité) rapidement et à moindre coût, sans avoir recours à la réalisation d’un forage et d’un pompage d’essai, travaux généralement coûteux et de longue durée.
Il convient de souligner également que par rapport à d’autres méthodes d’estimation plus sophistiquées, telles que les méthodes numériques de modélisation inverse (Rubinet al., 1990), l’estimation indirecte du champ de transmissivité développée ici demeure proche de la « réalité du terrain » car elle prend en considération les caractéristiques physiques propres du réservoir aquifère.
Dans une prochaine étape, nous comptons développer l’estimation géostatistique du champ de transmissivité de cet aquifère à l’aide de méthodes telles que le krigeage et le cokrigeage (Isaak et Srivastava, 1989). Le champ de transmissivité sera en définitive validé dans le cadre de la réactualisation du modèle mathématique de l’aquifère du Haouz.
Parties annexes
Remerciements
Les auteurs remercient sincèrement la Direction Générale de l’Hydraulique du Maroc pour la mise à disposition des données de pompage d’essai et de la prospection géophysique, ainsi que les réviseurs anonymes pour la pertinence de leurs remarques et de leurs suggestions.
Références bibliographiques
- Ahmed S. et G. De Marsily, 1987. Comparison of geostatistical methods for estimating transmissivity using data on transmissivity and specific capacty. Water Resour. Res., 23, 1717-1737.
- Ahmed S., de Marsily G. et A. Talbot, 1988. Combined use of hydraulic and electrical properties of an aquifer in a geostatistical estimation of transmissivity. Ground Water, 26, 78-86.
- Apparao A. et R. Gangadhara, 1974. Depth of investigation in resistivity methods using linear electrodes. Geophys. Prospect., 22, 211-223.
- Apparao A., Sivaroma Sastry R. et V. Subrahmanya, 1997. Depth of detection of burried resistive targets with some electrode arrays in electrical prospecting. Geophys. Prospect., 45, 365-375.
- Archie G., 1942. The electrical resistivity log as an aid in determining some reservoir caracteristics. Am. Inst. Min. Metall. Petr. Eng. Tech. Publ., 146, 54-62.
- Astier J., 1971. Géophysique appliquée à l’hydrogéologie, Masson (éditeur), Paris, 227 p.
- Bhattacharya B.B. et M.K. Sen, 1981. Depth of investigation of collinear electrode arrays over homogeneous anisotropic half-space in direct current methods. Geophys., 46, 768-780.
- Bracq P. et F. Delay, 1984. Transmissivity and morphological features in a chalk aquifer: a geostatistical approach of their relationship. J. Hydrol., 199, 139-160.
- Cassiani G. et M. Medina, 1997. Incorporating auxiliairy geophysical data into groundwater flow parameter estimation. Ground Water, 35, 79-91.
- Castany G., 1980. Hydrogéologie. Principes et méthodes. Dunod (éditeur), Paris, 220 p.
- Copty N., Rubin Y. et G. Mavco, 1993. Geophysical-hydrological identification of field permeabilities through bayesian updating. Water Resour. Res., 19, 2813-2825.
- Croft M.G.,1971. A method for calculating permeability from electric logs. USGSPP, 750-B, 265-269.
- DGH (Direction Générale de l’Hydraulique), 1989a. Étude du plan directeur intégré d’aménagement des eaux des bassins de Sebou, Bou Regreg, Oun Er Rbiaa et Tensift. Sous mission IA : Analyse critique de la situation existante – Hydrogéologie. Rapport inédit, 75 p.
- DGH (Direction Générale de l’Hydraulique), 1989b. Étude du plan directeur intégré d’aménagement des eaux des bassins de Sebou, Bou Regreg, Oun Er Rbiaa et Tensift. Sous mission ID : Bilan : Ressources-Besoins. Sélection des Schémas. Rapport inédit, 197 p.
- Evjen H.M., 1938. Depth factor and resolving power in electrical measurements. Geophys., 3, 78-95.
- Frohlich R.K. et W.E. Kelly, 1985. The relation between hydraulic transmissivity and transverse resistance in a complicated aquifer of glacial outwash deposits. J. Hydrol., 79, 215-229.
- Frohlich R.K., Fisher J. et E. Summarly, 1996. Electric - hydraulic conductivity correlation in fractured crystalline rock: Central landfill, Rhodes Island, USA. J. Appl. Geophys., 35, 249-259.
- Heigold P.C., Gilkeson R.H., Cartwright K. et P. Reed, 1979. Aquifer transmissivity from surficial electrical methods. Ground Water, 17, 338-345.
- Huntley D., 1986. Relations between permeability and electrical resistivity in granular aquifers. Ground Water, 24, 466-474.
- Isaak E. et R. Srivastava, 1989. An introduction to applied Geostatistics. Oxford Univ. Press, New York, États-Unis.
- Jones P.H. et T.B. Buford, 1951. Electric loging applied to groundwater exploration. Geophys., 16, 115-139.
- Kelly W., 1977. Electrical resistivity for estimating aquifer hydraulic conductivity. Ground Water, 15, 420-424.
- Kelly W. et P. Reiter, 1984. Influence of anisotropy on relations between aquifer hydraulic and electrical properties. J. Hydrol., 74, 311-321.
- Koefoed O., 1972. Discussion on «Depth of investigation in direct current methods» by Roy and Apparao. Geophys., 37, 703-704.
- Koefoed O., 1979. Geosounding principles. Resistivity sounding measurements. Elsevier Scientific Publ. Co. (éditeurs), N.Y., États-Unis, 276 p.
- Kosinski W.K. et W. Kelly, 1981. Geoelectrical soundings for predicting aquifer properties. Ground Water, 19, 163‑ 171.
- Kruseman G. et N. de Ridder, 1973. Interprétation et discussion des pompages d’essai. Int. Land Reclam. And Improv., Wageningen, 11, 230 p.
- Kupfersberger H. et G. Blöschl, 1995. Estimating aquifer transmissivities on the value of auxiliary data. J. Hydrol., 165, 85-99.
- Kwader T., 1985. Estimating aquifer permeability from formation resistivity factors. Ground Water, 36, 762-766.
- Maillet R., 1947. The fundamental equations of electrical prospecting. Geophys., 12, 529-556.
- Mazac J., Kelly W. et I. Landa, 1985. A hydrogeophysical model for relations between electrical and hydraulic properties of aquifers. J. Hydrol., 79, 1-19.
- Niwas S. et D. Singhal, 1981. Estimation of aquifer transmissivity from Dar-Zarouk parameters in porous media. J. Hydrol., 50, 393-399.
- Ponzini G., Ostroman A. et M. Molinari, 1984. Empirical relation between electrical transverse resistance and hydraulic transmissivity. Geoexplor., 22, 1-15.
- Razack M. et M. Sinan, 1988. Possibilités statistiques de prédiction des propriétés aquifères à l’aide des paramètres géoélectriques en milieu sédimentaire fortement hétérogène. Plaine du Haouz, Maroc. J. Hydrol., 97, 323-340.
- Roy A. et A. Apparao, 1971. Depth of investigation in direct current methods. Geophys., 39, 190-204.
- Rubin Y., Lobo Ferreira J.P., Rodrigues J.D. et G. Dagan, 1990. Estimation of the hydraulic parameters of the Rio-Maior aquifer in Portugal by using stochastic inverse modeling. J. Hydrol., 118, 257-279.
- Schimschal U., 1981. The relation of geophysical measurements to hydraulic conductivity at the Brantley Dam site, New Mexico. Geoexplor., 19, 115-126.
- SINAN M., 2000. Méthodologie d’identification, d’évaluation et de protection des ressources en eau des aquifères régionaux par la combinaison des SIG, de la géophysique et de la géostatistique. Application à l’aquifère de Haouz de Marrakech (Maroc). Thèse de Doctorat d’État, Université Mohammed V, École Mohammadia d’Ingénieurs, Rabat, Maroc, 372 p.
- Sinan M., 1986. Paramètres hydrogéologiques et géoélectriques en milieu alluvial fortement hétérogène : relations statistiques et approche géostatistique comparative (exemple de la nappe du Haouz-Maroc). Thèse de 3e cycle, Université Montpellier II, France, 397 p.
- Spiegel M., 1961. Theory and problems of statistics. McGraw Hill, New York, États-Unis. 359 p.
- Troisi S., Fallico C., Straface S. et E. Migliari, 2000. Application of kriging with external drift to estimate hydraulic conductivity from electrical resisitivity data in uncosilated deposits near Montalto Uffugo, Italy. Hydrogeol. J., 8, 356-367.
- Ungemach P., Mostaghimi F. et A. Duprat, 1969. Essai de détermination du coefficient d’emmagasinement en nappe libre. Bull. Ass. Int. Hydrol. Scient., XIV, 169‑190.
- Urish D., 1981. Electrical resistivity - hydraulic conductivity relationships in glacial outwash aquifers. Water Resour. Res., 17, 1401-1407.
- Yadav G.S., 1995. Relating hydraulic and geoelectric parameters of the Jayant aquifer, India. J. Hydrol., 167, 23‑38.
- Yadav G. S. et Abolfazli H., 1998. Geoelectrical soundings and their relationship to hydraulic parameters in semiarid regions of Jalore, Northwestern India. J. Appl. Geophys., 39, 35-51.
Liste des figures
Figure 1
Situation géographique et lithologie de l’aquifère du Haouz. 1 : Alluvions grossières (galets, graviers et sables); 2 : Alluvions grossières alternant avec des lentilles imperméables ou calcaires; 3 : Alluvions hétérogènes (galets, graviers, sable, argiles, marnes, etc.); 4 : Alluvions avec des passages calcaires ou marno-calcaires; 5 : Conglomérat, conglomérat alternant avec des niveaux imperméables, calcaires ou marno-calcaires.
Geographical situation and lithology of the Haouz basin. 1: Coarse alluvia (gravels and sands); 2: Coarse alluvia alternating with impermeable or calcareous lenses; 3: Heterogeneous alluvia (rollers, gravels, sand, clay, marls, etc.); 4: Alluvia with calcareous or marly-calcareous beds; 5: Conglomerate, conglomerate alternating with impermeable, calcareous or marly-calcareous beds.
Figure 2
Localisation des ouvrages testés par pompages d’essai. 1 : Forage; 2 : Puits à grand diamètre.
Location of the tested wells using pumping tests. 1: Borehole; 2: Large diameter well.
Figure 3
Localisation des sondages électriques. 1 : Position des sondages électriques.
Location of the electric surveys. 1: Position of electric sounding.
Figure 4
Distribution de fréquences de la transmissivité mesurée par pompages d’essai. Ajustement à une loi lognormale.
Frequency distribution of the measured transmissivity values using pumping tests. Adjustment with a lognormal law.
Figure 5
Distribution de fréquences de la résistance transversale des lentilles perméables. Ajustement à une loi lognormale.
Frequency distribution of the transverse resistance of the pervious layers. Adjustment with a lognormal law.
Figure 6
Coupe schématique à travers l’aquifère du Haouz montrant les différents cas de résistance transversale envisagés dans l’étude. 1 : Plio-Quaternaire; 2 : Miocène; F : forage; N : niveau piézométrique; RA : résistance transversale de l’ensemble mio-plio-quaternaire; RB : résistance transversale des lentilles perméables.
Simplified cross-section of the Haouz aquifer showing the different transverse resistances assumed in this study. 1: Plio-Quaternary; 2: Miocene; F: well; N: water table; RA: transverse resistance of the whole Mio-Plio-Quaternary; RB: transverse resistance of the pervious layers.
Figure 7
Diagramme de régression Log-Log entre les transmissivités (Tmes) et les résistances transversales des lentilles perméables saturées (RB).
Log-Log regression diagram between measured transmissivities (Tmes) and transverse resistances of the pervious layers (RB).
Figure 8
Distribution spatiale de la transmissivité estimée de l’aquifère. 1 : Test ≥ 10‑2 m2/s; 2 : 610‑3 ≤ Test < 10‑2 m2/s; 3: 310‑3 ≤ Test < 610‑3 m2/s; 4: Test < 310‑3 m2/s.
Spatial distribution of estimated transmissivity in the aquifer. 1: Test > = 10‑2 m2/s; 2: 610‑3 ≤ Test < 10‑2 m2/s; 3: 310‑3 ≤ Test < 610‑3 m2/s; 4: Test < 310‑3 m2/s.
Figure 9
Distribution de fréquences de la transmissivité estimée. Ajustement à une loi lognormale.
Frequency distribution of estimated transmissivity. Adjustment with a lognormal law.
Liste des tableaux
Tableau 1
Paramètres statistiques de la résistance transversale des lentilles perméables (RB), de la transmissivité mesurée par pompages d’essai (Tmes) et de la transmissivité estimée par régression (Test). N : effectif; m : moyenne arithmétique; s : écart-type; CV : coefficient de variation; Min : valeur minimum; Max : valeur maximum.
Statistical parameters of the transverse resistance (RB) of the pervious layers, measured transmissivity (Tmes) and estimated transmissivity (Test). N: size; m: arithmetic mean; S: standard deviation; CV: coefficient of variation; Min: minimum value; Max: maximum value.
Tableau 2
Régression géométrique entre les valeurs de transmissivité mesurées par pompage d’essai et les résistances transversales (les calculs sont effectués après transformation logarithmique des variables). t(exp) = paramètre expérimental de Student obtenu par transformation du coefficient de corrélation; t(théo) = paramètre t théorique de Student au seuil de signification de 1 % et pour un nombre de degrés de libertés = N-2 (la régression est d’autant plus significative que t(exp) est supérieur à t(théo)); RA = résistance transversale de l’ensemble mio-plio-quaternaire; RB = résistance transversale des lentilles perméables; Tmes = transmissivité mesurée; Tcor = transmissivité corrigée de l’effet des variations piézométriques.
Geometrical regression between measured transmissivities and transverse resistances (calculations are carried out after logarithmic transformation of the variables). t(exp) = Student experimental parameter obtained by transformation of the correlation coefficient; t(théo) = Student theoretical parameter at a significance level of 1% and for a number of degrees of freedom = N-2 (the greater the difference between t(exp) and t(théo), the more significant the regression); RA = transverse resistance of the whole Mio-Plio-Quaternary formation; RB = transverse resistance of the pervious lenses; Tmes = measured transmissivity; Tcor = corrected transmissivity for the effect of the piezometric variations.