Corps de l’article

Introduction

Un petit retour en arrière

Les auteurs en psychométrie ont traditionnellement été peu diserts sur le sujet des normes et, a fortiori, sur leur précision. Un survol des grands textes publiés sur les théories des tests et l’élaboration des instruments de mesure verbale, en psychologie et en éducation, permet de trouver quelques pages sur les types de normes et leur méthode de fabrication, sans plus. Les grands classiques que sont Gulliksen (1950) et Guilford (1954) sont muets sur la question. L’article de Flanagan, Units, scores, and norms, paru dans le premier grand collectif de référence Educational measurement dirigé par Lindquist (1951), fait une présentation honnête des principaux types de normes ; le seul commentaire formulé concernant la précision suggère d’utiliser quelques centaines de répondants pour le groupe normatif[1]. Angoff (1971) va un peu plus loin en soulignant le fait que les calculs présentés sur la précision relative à l’échantillonnage concernent la moyenne de l’ensemble normatif et que, en ce qui regarde la médiane et les centiles inférieurs et supérieurs de la distribution, leur erreur-type varie et augmente avec l’éloignement par rapport à la valeur centrale. Ces propos ne semblent pas avoir été repris, encore moins développés, dans les éditions ultérieures du collectif Educational measurement (Brennan, 2006 ; Linn, 1989 ; Thorndike, 1971). L’exhaustive revue des procédés de création de normes de passage présentée en 2007 par Cizek et Bunch, tout intéressante qu’elle soit, concerne quasi exclusivement des normes édictées, c’est-à-dire produites par le concours d’un groupe d’experts et selon leurs appréciations des contenus du test ou des niveaux de score ; rien sur les seuils psychométriques à proprement parler.

Dans un article intitulé Test reliability for what?, Bloom (1942) introduit un concept, nouveau en psychométrie, relatif à la capacité d’un test à catégoriser les personnes de manière fiable. En fait, il présente une formule,

en la décrivant ainsi : « Ce quotient indique le nombre de classes qu’on peut créer à partir de l’étendue des scores de telle sorte que les chances qu’une donnée d’une classe recoupe une donnée correspondante dans la classe voisine sont à peu près d’une sur mille » (Bloom, 1942, p. 521). Thurlow (1950), qui réclame la copaternité de cette formule, parle aussi de « discriminations stables », qu’il relie verbalement au coefficient de fidélité, c’est-à-dire à la précision du test, sans plus. Enfin, Laurencelle (1997, 1998, 2014) redécouvre le concept de Bloom, l’élaborant de A à Z à partir du « pouvoir discriminant » de Ferguson (1949) et de la résolution statistique de la base de mesure, et il en propose la formule suivante,

sous l’appellation de « capacité discriminante ». Semblablement à Bloom (1942), cette formule indiquerait le nombre d’intervalles de mesure efficaces, ou catégories efficaces, parmi lesquels l’instrument de mesure à fidélité ρXX peut répartir une population statistique normale de telle façon qu’un élément mesuré ait une probabilité d’au moins ½ d’être classé dans son intervalle propre. Cette incursion dans la propriété d’un test consistant à classer les objets mesurés tout en tenant compte de l’erreur de mesure, autrement dit du coefficient de fidélité du test, nous semble être la première du genre, associant de manière explicite et structurée l’erreur de mesure et la fonction normative des tests.

Finalement, Laurencelle, en 1998, décrit une première forme de traitement probabiliste des normes en présentant une « norme diagnostique », soit un seuil psychométrique ayant pour propriété de sanctionner une décision normative sous un contrôle explicite de l’erreur. L’erreur ici contrôlée, il faut le noter, est l’erreur d’échantillonnage ou erreur positionnelle du seuil, non pas l’erreur de mesure, et son traitement suppose une mesure parfaitement précise, c.-à-d. à fidélité de 1. Les développements qui suivent amplifient la question.

Un bref rappel de la théorie classique des tests et de la notation

Avant d’aborder le problème spécifique des seuils psychométriques, rappelons brièvement les éléments de la théorie classique des tests et sa notation, tels qu’ils ont été fixés par les auteurs de référence (Guilford, 1954 ; Gulliksen, 1950 ; Lord & Novick, 1968). Chaque mesure Xi,o, prise d’un individu i à l’occasion o, est susceptible de fluctuer d’une occasion à l’autre, et ce, même en stipulant que la caractéristique évaluée reste quant à elle invariable. Le train virtuel de mesures Xi,1, Xi,2, Xi,3,… présente donc des valeurs changeantes, mais ces valeurs oscillent de façon structurée en s’agglutinant plus ou moins près d’une valeur imaginaire, la valeur vraie de la caractéristique mesurée chez l’individu évalué. Cette constatation axiomatique aboutit au modèle classique :

en vertu duquel la valeur mesurée Xi,o apparaît comme le composé linéaire de la valeur propre, dite « valeur vraie », de l’individu évalué i et d’une « erreur de mesure » eo, associée aux circonstances de la mesure (imprécision de l’instrument, variation non systématique de contexte, etc.), ce composant eo variant au hasard.

Le modèle (1) ci-dessus pose que, dans le double univers des individus et des occasions de mesure, les variables Vi et eo sont stochastiquement indépendantes (et non corrélées). La précision d’une mesure X (ou de l’instrument qui la porte) est caractérisée par deux indices globaux. D’abord, la fidélité ρXX, que nous dénoterons ici R, soit :

et l’erreur-type de mesure σe, habituellement présentée par :

les méthodes d’estimation de l’un et de l’autre indices méritant réflexion (Allaire & Laurencelle, 1998 ; Laurencelle, 1998).

Il est d’usage de stipuler que la variable aléatoire eo est de distribution normale[2]. Quant à la loi de distribution des valeurs vraies Vi, elle est laissée ad lib. et est occasionnellement rapportée aussi au modèle normal. D’autres aspects complémentaires de la théorie classique seront présentés au fur et à mesure des besoins de l’exposé.

L’incertitude positionnelle et ses effets sur les seuils psychométriques et leurs taux de capture

Les seuils centiles et leurs taux de capture nominal et réel

Les normes psychométriques, qui permettent de classer les personnes, qualifier un candidat ou repérer un cas déviant, apparaissent sous forme de centiles ou reposent essentiellement sur eux. Tantôt la médiane[3] servira de norme de référence, tantôt ce sera le centile 75 qui permettra d’établir l’âge de développement moteur d’un enfant, tantôt on cherchera le candidat exceptionnel logé au-delà du centile 99. Le centile 75 doit par définition sommer 75 pour cent, ou la portion 0,75, de la population concernée, tout comme on devrait retrouver 1 % des gens au-delà du centile 99 d’une distribution normative. C’est à ces considérations et, surtout, à leur degré de précision relative que cette étude s’attarde maintenant.

Soit une population d’éléments de taille N (pratiquement) infinie et de mesure X, et soit P, une fraction allant de 0 à 1 ou indifféremment un pourcentage allant de 0 à 100. En ordonnant les éléments selon leur mesure, de la plus petite à la plus grande, nous donnons à l’élément X de rang r (1 ≤ r ≤ N) le rang centile P (aussi désigné « quantile » dans la littérature statistique), où P = r / N, la valeur marquant ce rang étant le centile vrai XP. Appliquant alors le centile (vrai) XP afin de repérer les éléments dont la mesure déborde la valeur XP, un élément est dit capturé si X ≥ XP, et le taux de capture est enfin K = Pr{X ≥ XP} = 1 – P. Cependant, les centiles qui nous intéressent, ceux exploités dans les normes des tests psychométriques, reposent non pas sur la population, mais sur un échantillon de taille n modeste : le centile échantillonnal CP est un estimateur du vrai centile XP, et son taux de capture k = Pr{X ≥ CP} est un estimateur de K ; CP et k ont donc les propriétés d’un estimateur, c.-à-d. qu’ils sont échantillonnalement imprécis, peuvent être biaisés et dépendent à la fois du modèle distributionnel sur lequel la mesure X repose vraiment et de la taille n de la série normative qui a permis d’établir CP.

Cette étude examinera d’abord les centiles calculés sur des échantillons issus d’une population de mesures « pures », c.-à-d. dépourvues d’imprécision ou d’erreur. Dans un article ultérieur (Partie II), l’étude portera vers des mesures plus coutumières en sciences humaines, celles composées d’une valeur vraie et d’une erreur aléatoire qui s’y ajoute.

Les centiles estimés à partir d’un échantillon normatif

Pour estimer la valeur d’un centile ou de quelques centiles à partir d’un échantillon, celui-ci doit être normatif, c.-à-d. représentatif et suffisant. La représentativité, qui dépend essentiellement du mode d’échantillonnage, ne permet pas à elle seule l’obtention d’une estimation satisfaisante. Par exemple, posant une population à composition homogène, si la mesure de 1 élément pris au hasard dans la population permet d’obtenir une estimation non biaisée de la moyenne de celle-ci, elle ne permet pas d’en estimer adéquatement le centile 95 (X0,95). Ce ne serait pas non plus le cas si nous mesurions, par exemple, n = 3 ou 10 éléments. La taille n suffisante dépend d’abord du rang centile à estimer[4], mais aussi du mode d’estimation appliqué et, le cas échéant, du modèle paramétrique invoqué.

On peut distinguer deux grandes catégories d’estimation, deux types de centiles à estimer : les centiles à modèle paramétrique stipulé et les centiles non paramétriques. La première catégorie, celle des centiles à modèle paramétrique stipulé, réfère aux situations dans lesquelles le chercheur sait ou stipule que sa population et son échantillon normatif relèvent d’un modèle paramétrique (une loi de distribution) auquel il peut se fier. Le modèle prééminent est évidemment celui de la loi normale, modèle qui sera invoqué ici. Dans la seconde catégorie, aucun modèle distributionnel ne s’impose avec force, car la loi de distribution empirique ne semble correspondre à rien de connu ou de sûr. Ce type de centile admet tout de même une sous-espèce, celle d’un système de centiles à comportement local paramétrique. En d’autres mots, si la distribution globale des mesures ne se conforme pas à un modèle paramétrique disponible, l’étalement statistique des centiles dans la zone d’intérêt, par exemple à l’extrémité droite de la distribution, est suffisamment proche de celui d’un modèle paramétrique donné pour que ce dernier serve à en estimer les caractéristiques.

Cette taxonomie heuristique nous amène à proposer trois types de centiles empiriques, différant entre eux par leur contexte paramétrique et leur mode d’estimation:

  • le centile à modèle stipulé normal (1C);

  • le centile ordinal simple (2C);

  • le centile ordinal normalisé (3C).

Le centile à modèle stipulé normal

Le centile à modèle stipulé normal repose sur l’invocation du modèle paramétrique normal à la fois pour la population de référence et pour l’échantillon normatif, celui fournissant les mesures qui basent l’estimation. Posons que la densité et la fonction de répartition normales standards sont dénotées respectivement par φ(X) et Φ(X). Soit zP, le centile de rang P dans la loi normale standard tel que Pr{z ≥ zP} = 1 – Φ(zP) = 1 – P, et soit X̅ et s, la moyenne et l’écart-type calculés à partir des n données de l’échantillon normatif. Alors,

est le centile de rang P estimé sous un modèle stipulé normal. La méthode appliquée pour l’obtenir étant linéaire par la formule (4), elle est désignée aussi sous ce nom. Par exemple, le questionnaire Minnesota Multiphasic Personality Inventory (MMPI) original, publié vers 1943, utilise des cotes T (moyenne 50, écart-type 10) linéaires pour ses multiples échelles.

Le centile ordinal simple

Le centile ordinal simple désigne une valeur d’échantillon servant à estimer la valeur bornant la fraction inférieure P de la population de référence, sans invocation aucune d’un modèle paramétrique. Le défaut de modèle paramétrique induit un certain flou dans l’estimation, et une forme d’estimation avantageuse pour une population ne le sera pas également pour une autre. Il faut donc se replier sur le modèle paramétrique uniforme standard, soit la loi X ~ U[0,1], de densité 1 et de fonction de répartition X, et proposer comme estimateur la statistique d’ordre:

laquelle a pour avantage d’être sans biais pour une variable de loi uniforme, c.-à-d. E{2CP} = XP = P, et, en généralisant, sans biais non plus pour le rang centile de toute loi, connue ou non, c.-à-d. E{rang(2CP)} = P (David, 1981). Cet estimateur peut aussi être dit consistant, en ce sens que, pour n ⟶ ∞, E{2CP} ⟶ XP pour toute loi. Cette forme de positionnement revient en somme à attribuer le rang centile P à la personne évaluée. Nonobstant sa simplicité, ce type de centile n’est guère employé : sa distribution (uniforme) est certes rébarbative par rapport aux statistiques usuelles qu’on voudrait y appliquer, d’autant plus que, du point de vue de la psychométrie, l’échelle de rangs centiles permet peu de discrimination aux zones extrêmes, zones souvent les plus intéressantes pour les testeurs.

Le centile ordinal normalisé

Le centile ordinal normalisé, ou centile normalisé, est un centile ordinal projeté sur le modèle paramétrique normal, d’abord par commodité d’interprétation parce que le modèle normal répond aux habitudes d’interprétation du scientifique moderne, mais aussi parce qu’un tel procédé récupère les avantages inhérents à un modèle paramétrique. Naturellement, la forme initiale de la distribution empirique de même que la granularité de son axe de mesure doivent assurer la plausibilité d’une telle imposition. Chaque mesure X de l’échantillon normatif a un rang r = r(X), numéroté de 1 à n, dans l’ensemble des mesures : il s’agit de la statistique d’ordre X(r), parfois notée X(r : n). Ce rang r étant converti en fraction P′ par P′ = r / (n + 1), la fraction P′ est projetée sur le modèle paramétrique choisi (normal), sur lequel la valeur normalisée est alors lue, soit:

où la notation Φ–1(P) indique l’inversion de la fonction de répartition normale standard et équivaut à zP ; μ et σ étant respectivement l’espérance (ou moyenne) et l’écart-type choisis pour l’échelle. Le centile ordinal, faut-il le dire, peut, selon le contexte ou le besoin, être projeté sur une forme paramétrique autre que la normale. Le QI (avec moyenne 100 et écart-type 15) et le T normalisé (encore avec moyenne 50 et écart-type 10) en sont des exemples courants.

L’incertitude positionnelle associée à chaque type de centile

Tout estimateur basé sur un échantillon de taille n souffre d’une forme ou d’une autre d’imprécision. En premier lieu, l’estimateur CP est imprécis par rapport à sa cible paramétrique XP. Cette imprécision en est une de variabilité, telle qu’on peut l’évaluer par son erreur-type σC, en ce sens que la valeur de CP fluctue d’un échantillon (de taille n) à l’autre ; et une de biais BC, tel qu’évalué par son espérance E(CP), où BC = E(CP) – XP. L’erreur quadratique moyenne (EQM) permet de globaliser ces deux erreurs par l’équivalence : EQM = E{(CP – XP)2} = σ2C +B2C .

En second lieu, l’imprécision de l’estimateur CP se répercute sur son taux de capture kn, lequel est une proportion dont l’espérance E(kn) peut être biaisée par rapport au taux prescrit K, selon Bk = E(kn) – K, et l’erreur-type estforme: 1983569n.jpg (voir note 10). Ces deux classes d’estimateurs, et les variantes d’estimation répertoriées ici, sont consistantes pour un modèle de population, en ce sens que, pour une taille d’échantillon n croissante, variabilité et biais décroissent jusqu’à disparition.

La précision du centile linéaire à modèle stipulé normal

Dans le contexte ordinaire et rassurant d’une population à distribution normale, la fonction d’estimation du centile linéaire (à modèle normal), soit la fonction (4), repose sur deux statistiques : la moyenne (X̅) et l’écart-type (s). Sa densité de probabilité s’obtient par :

h étant la densité normale centrée d’une moyenne basée sur n observations et g étant la densité de l’écart-type (de type Khi) basé sur n – 1 degrés de liberté. Par référence au modèle normal standard, de moyenne 0 et de variance 1, l’espérance et la variance de chacune sont:

L’écart-type échantillonnal (s) a un biais de sous-estimation par rapport à son pendant paramétrique σ, c.-à-d. E(s) < σ. En approximation, l’espérance[5] et la variance de l’écart-type (s) sont estimées par :

Rappelons que, dans le modèle normal, moyenne et écart-type sont des statistiques mutuellement indépendantes.

La fonction d’estimation (4) est donc biaisée par la contribution de l’espérance de s,

et sa variance est approximativement:

laquelle, à sa tour, est approchée par:

L’EQM est alors estimée approximativement par:

La précision du centile ordinal simple

Rappelons que, par « centile ordinal simple » (2CP), est désigné ici un centile de la distribution d’une variable X, variable dont la forme paramétrique n’est pas connue ou dont l’utilisateur n’entend pas exploiter les propriétés.

Supposons que le modèle paramétrique de X soit déterminé par une fonction de répartition F avec densité f, alors l’erreur-type d’un centile normatif de rang P serait approchée en première instance par:

une expression dérivée de la variance d’un centile de la loi U(0,1), P(1 – P)/n (Kendall & Stuart, 1977). En seconde instance, David et Johnson (1954), reprenant une proposition de K. Pearson, présentent des expansions en séries de Taylor (basées sur les dérivées de la variable) pour les moments des statistiques d’ordre. Ces approximations seront reprises à la section suivante.

Si, par prudence ou par dépit, on renonce à toute forme d’invocation paramétrique, on ne trouve aucun moyen répertorié pour estimer la variance du centile empirique 2CP. Toutefois, l’examen de l’expression (13) et la réflexion suggèrent une approximation grossière, que voici. Il est apparent dans (13), et de même il est logique, que la variance du centile varie en relation inverse de la densité de la distribution à cette position. Aussi, dans un échantillon de taille finie n, l’espacement entre les statistiques d’ordre successives reflète vraisemblablement cette propriété de densité et constitue un intervalle dans lequel le centile estimé peut s’inscrire. Cet intervalle, plus court sous une densité forte et plus large sous une densité moindre, est défini par les « intervars »[6] qui flanquent le centile. En guise d’illustration, supposons que r = P × (n + 1) est un entier (1 < r < n), alors l’intervalle approximatif que peut occuper le centile 2CP est ]X(r – 1). X(r + 1)[. En admettant que, dans la zone distributionnelle touchée, la densité inconnue f (X) est relativement égale et peut être estimée par les 2t intervars adjacents, alors cette densité devient approximativement f (Xr) ≈ (2t – 1) / n[X(r + t) – X(r – t)], et la variance cherchée[7] est approchée par :

cette expression fournissant un ordre de grandeur plutôt qu’une mesure précise.

La distribution de la statistique 2CP dépend essentiellement de la loi inconnue sous-jacente. Dans le cas d’une variable à distribution normale, le centile 2CP a une asymétrie orientée vers son extrémité proche, tandis que, pour une distribution uniforme, l’asymétrie est tournée vers le centre. Par exemple, pour C95 dans une série normale standard de n = 99 données correspondant à la statistique d’ordre X(95) de rang 95, nous calculons γ1 ≈ 0,223, une asymétrie positive, avec un mode de 1,659, une médiane de 1,674 et une espérance de 1,682, tandis que, pour une série uniforme standard équivalente, l’asymétrie de C95 est de –0,849, le mode de 0,959 (= (r – 1)/(n – 1)), la médiane de 0,953 et l’espérance de 0,950 (pour tout n). Comme ces deux exemples le montrent et lorsque le modèle distributionnel sous lequel les données évoluent est vraiment inconnu, il est quasi impossible et serait hasardeux de supposer le comportement du centile.

Dans le cadre de cette étude, diverses expérimentations selon la méthode Monte Carlo ont été conduites pour tester la capacité de capture d’un centile simple, et ce, sous différentes populations statistiques (par ex., normale, uniforme, Khi-deux). Dans tous les cas, les taux de capture se sont montrés justes, à savoir E(kn) ≈ 1 – P = K, à la variabilité près[8].

Les propriétés de ce type de centile n’ont pas été explorées plus avant.

La précision du centile ordinal normalisé et de son taux de capture

Le centile normalisé 3CP, basé sur la distribution empirique des statistiques d’ordre, est en fait la projection d’un rang centile approximatif P sur un modèle paramétrique, ici le modèle normal [voir l’expression (6)]. Ce centile invoque la loi normale comme modèle cible, mais pas explicitement comme modèle d’origine. Par conséquent, il n’exploite aucun des deux paramètres clés de ce modèle, à savoir la moyenne (X̅) et l’écart-type (s) de l’échantillon normatif.

Exprimée pour la re statistique d’ordre d’une série de n variables normales, pour laquelle P = r / (n + 1), la fonction de densité f (3CP) = f (x[r]) de 3CP est fournie (David, 1981) par :

avec, comme fonction de répartition:

Tel qu’indiqué plus haut, l’invocation du modèle normal permet d’établir une première approximation de la variance du centile normalisé, soit:

Plus studieusement, David et Johnson (1954) ont élaboré les moments d’une statistique d’ordre X(r) en en faisant l’expansion de Taylor sous la fonction de répartition paramétrique F. Posant que F(Xr) = r / (n + 1), nous avons:

où dr = F(X(r)) – F(Xr) = F(X(r)) – r / (n + 1) et Xru = dux / dFu évaluée à x = Xr, l’expansion se faisant sur les dérivées de la variable plutôt que les dérivées de la fonction. Une fois faite, l’expansion permet d’obtenir, à la précision voulue selon le nombre de termes retenus, les différents moments de la statistique d’ordre, notamment son espérance (ou biais) et sa variance. La réalisation de cette expansion pour la loi normale standard permet de trouver par exemple les premiers coefficients pour l’estimation de quelques centiles sélectionnés, l’espérance et la variance s’obtenant alors par:

où XP = Φ–1(P). Ainsi, la somme à la droite de XP dans (19) donne la valeur du biais positif de X(r), reflétant l’excès de cette statistique qui retourne paresseusement vers sa cible XP. Le tableau 1 (tiré de Laurencelle, 2000) donne, en approximation, les trois premiers coefficients ai et bi pour quelques rangs centiles choisis.

Tableau 1

Coefficients ai et bi appliqués pour l’estimation de l’espérance et la variance des centiles 3CP tirés d'une série de n données provenant de la loi normale standard, d’après David et Johnson (1954)

Coefficients ai et bi appliqués pour l’estimation de l’espérance et la variance des centiles 3CP tirés d'une série de n données provenant de la loi normale standard, d’après David et Johnson (1954)

-> Voir la liste des tableaux

Prenons l’exemple d’un centile, ou seuil, situé au rang centile 95, soit C95, basé sur un échantillon de n = 99 données normales[9]. Ce seuil correspondrait ici à la re = P´(n + 1) = 95e statistique d’ordre, X(95). Son espérance se calcule donc par :

donnant un biais de 1,682 – 1,64485 ≈ + 0,037. Quant à sa variance,

soit une erreur-type de 0,217. Ces données « normalisées » n’étant finalement qu’une transposition ordonnée des valeurs originales, leur comportement ordinal leur est semblable et les données de capture sont aussi les mêmes, c.-à-d. justes.

Les taux de capture et leur incertitude

Même si le centile linéaire 1CP n’avait pas été biaisé, sa seule variabilité autour de la valeur cible XP suffirait à faire craindre un biais de capture puisque, sous le modèle normal, la relation entre la variable X et la fonction de répartition Φ(X) est non linéaire ; le biais lui-même n’arrange pas les choses. Prenons l’exemple du centile de rang P = 95, dont la valeur et le taux de capture nominaux sont X0,95 = 1,645 et K = 0,05 sous le modèle normal. Les statistiques Monte Carlo suivantes (basées sur 106 échantillons) illustrent la situation (voir la première rangée du tableau 2). Il faut noter que les tailles échantillonnales ont été fixées à des nombres de type n = r × 20 – 1 de façon à permettre une estimation exacte des centiles ordinaux 95 et 99.

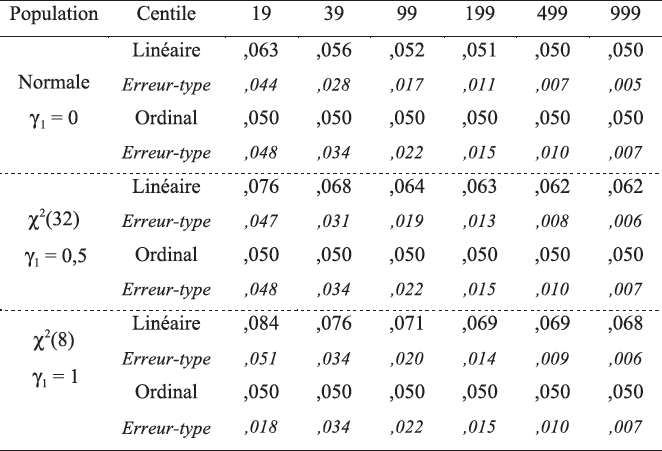
Le tableau 2 rapporte une étude du taux de capture (kn) réalisé par les estimateurs linéaire (1CP) et ordinal normalisé (3CP), d’abord sous une population normale. Le biais du taux kn encouru par le seuil linéaire 1CP, vis-à-vis du taux paramétrique K = 0,05, est imputable principalement au biais de l’écart-type (s) [voir les expressions (9) et (10)], générant un taux excessif dont l’excédent se résorbe peu à peu à mesure que la taille de l’échantillon normatif augmente. Il faut toutefois noter qu’il s’agit là de moyennes, et que les taux kn individuels fluctuent, ce à quoi cette étude reviendra un peu plus loin[10]. Tout redondant qu’il soit, le tableau 2 montre aussi, à l’évidence, que le centile ordinal (de type 2CP ou 3CP) est lui aussi fluctuant et produit une capture fluctuante, quoique systématiquement non biaisée.

Tableau 2

Taux de capture moyen (kn) des centils C95 linéaire et ordinal sous trois populations

Taux de capture moyen (kn) des centils C95 linéaire et ordinal sous trois populations

-> Voir la liste des tableaux

Le cas de populations à distribution asymétrique

Qu’arrive-t-il aux seuils et à leur taux de capture si la population concernée n’est pas « normale » ? Parmi la pléthore de formes de distribution non normales possibles, une classe de formes se distingue par son importance en psychométrie et par ses effets : la classe des distributions asymétriques. Il s’agit de distributions dans lesquelles une masse de données se trouve tassée plus ou moins dans les valeurs inférieures, alors que leur fréquence va en diminuant vers les positions plus élevées sur l’axe de mesure. Ces distributions caractérisent les échelles psychométriques adressées à la population générale, mais qui visent à repérer des personnes, moins nombreuses, à aptitudes ou à comportements exceptionnels. Le questionnaire MMPI, déjà cité, est un cas d’espèce avec ses échelles psychiatriques, mais le sont aussi les tests d’intérêt vocationnel, de motivation, d’attitude. La loi lognormale, utilisée en biométrie comme dans la mesure du temps de réalisation d’une tâche, et la loi du Khi-deux (ou loi Gamma) sont deux importants modèles de distributions d’asymétrie positive. Pour ces lois, non seulement la moyenne et l’écart-type ne sont plus indépendants l’un de l’autre[11], mais, au contraire, ils sont positivement corrélés, un fait peu connu et qu’ont noté Wagenmakers et Brown (2007) dans leur étude sur les temps de réaction et la loi lognormale. Afin d’étudier les effets de la non-normalité sur l’efficacité de capture des centiles, des populations Khi-deux ont été choisies, leur niveau d’asymétrie, mesuré par l’indice 𝛾1, dépendant simplement du paramètre dl, les degrés de liberté, soit 𝛾1 =forme: 1983783n.jpg. Les deux populations choisies correspondent à dl = 32, pour une asymétrie modérée de 𝛾1 = 0,5, et dl = 8, pour une forme plus marquée de 𝛾1 = 1. La figure 1 illustre ces deux distributions.

Figure 1

Tracé de la densité d’une distribution du Khi-deux avec dl = 32 (à gauche) et dl = 8 (à droite)

Tracé de la densité d’une distribution du Khi-deux avec dl = 32 (à gauche) et dl = 8 (à droite)

-> Voir la liste des figures

Les deux dernières rangées du tableau 2 fournissent des données comparatives du taux de capture kn pour ces populations asymétriques. Étant donné que le centile linéaire 1CP tombe un peu court dans la zone de droite de la distribution, il capture un important excédent de la population, et ce, d’autant plus que l’asymétrie est prononcée. De plus, s’il diminue quelque peu avec la taille n, le biais de capture ne s’efface pas puisqu’il dépend en fait de la discordance entre l’intervalle normal imposé dans la fonction (4) et l’intervalle réel du centile paramétrique 95 de la loi 𝜒2 étudiée[12]. Ces effets apparaîtraient encore plus importants pour le centile 99, tels qu’ils ont été vérifiés par ailleurs. Quant au centile ordinal, il n’est manifestement pas affecté par la non-normalité de la population.

Figure 2a

Taux de capture du centile linéaire C95, selon n (population normale)

Taux de capture du centile linéaire C95, selon n (population normale)

Figure 2b

Taux de capture d’un centile 𝜒2(8) linéaire C95, selon n

Taux de capture d’un centile 𝜒2(8) linéaire C95, selon n

Figure 2c

Taux de capture d’un centile 𝜒2(8) ordinal C95, selon n

Taux de capture d’un centile 𝜒2(8) ordinal C95, selon n

-> Voir la liste des figures

Au biais éventuel du taux de capture s’ajoute sa variabilité, qui dépend à son tour de la variabilité de l’estimateur échantillonnal CP. Dans un contexte normal bien défini à la figure 2a, le centile linéaire génère une marge d’erreur importante, qui ne devient raisonnable que vers n = 500. À n = 199 notamment, l’intervalle de confiance de capture est IC95(k199) = {0,032 ; 0,076}, soit plus de 50 % en déficit ou en excès par rapport au taux nominal K = 0,05. Dans le cas d’une distribution à asymétrie marquée, la 𝜒2(8) à la figure 2b, le même centile 1CP montre une erreur amplifiée, à la fois par son biais persistant et sa forte variabilité : à n = 199, les valeurs IC95(k199) = {0,045 ; 0,100} sont observées, la borne supérieure indiquant une capture deux fois plus importante que le taux prescrit. Pour la même population 𝜒2(8), le centile ordinal (2CP ou 3CP), présenté en figure 2c, reste sans biais et affiche par contre une variabilité légèrement plus forte que son émule linéaire, l’intervalle de confiance étant ici IC95(k199) = {0,024 ; 0,084}. La figure 3, où sont combinés biais et variabilité dans la racine de l’erreur quadratique moyenne, r(EQM), illustre l’efficacité comparative des différents seuils analysés.

Le contrôle de la variabilité et le concept de norme sûre

Quel que soit le type de centile ou seuil appliqué, sa variabilité, comme il a été démontré, interférera avec sa précision de capture, de sorte que la qualité des individus sélectionnés pourra laisser à désirer. Par exemple, la personne non qualifiée, selon Xi < XP, sera tout de même retenue parce que le seuil normatif CP sera inférieur à XP. Pour pallier ce risque, il suffit de relever la valeur générale des seuils CP en déplaçant leur distribution échantillonnale vers le haut, de sorte que le risque encouru, celui de retenir une personne non qualifiée, ne déborde pas un niveau de probabilité donné : c’est cette classe de seuils normatifs, protégés en probabilité, qui sera désignée ici par le concept de « norme sûre ». Selon le besoin de favoriser la spécificité de sélection (réduire le risque de retenir une personne non qualifiée) ou sa sensibilité (réduire le risque de ne pas retenir une personne qualifiée), il nous faut appliquer respectivement une norme sûre « exigeante » ou « permissive ». Le développement du concept de norme sûre apparaîtra dans un article ultérieur, où le contexte du contrôle de la décision normative sera complété en y intégrant la part importante qu’y joue l’erreur de mesure.

Figure 3

Racine de l’erreur quadratique moyenne (EQM) pour différents contextes d’estimation du centile C95

Racine de l’erreur quadratique moyenne (EQM) pour différents contextes d’estimation du centile C95

-> Voir la liste des figures

Conclusion

Vers un modèle intégrant incertitude positionnelle et erreur de mesure

Le but d’un seuil psychométrique, il faut le rappeler, est de capter, c.-à-d. discriminer, les individus qui relèvent d’une portion extrême significative d’une population, et ce, à des fins diverses (qualification, diagnostic, contrôle). Par rapport à la portion de population visée, soit K, l’incertitude positionnelle des seuils CP donne lieu à une capture variable kn, qui dépend évidemment de la taille échantillonnale n, mais aussi du mode de définition du centile (1CP, 2CP, 3CP) et de la forme de distribution des scores de la population. À cette première source d’erreur, déjà étudiée par Laurencelle (1998, 2000, 2002, 2008a, 2008b), doit s’ajouter l’erreur de mesure, notée eo. Tandis que la norme, le seuil normatif CP, est une valeur fixée dans une situation de sélection, l’erreur eo, elle, est variable d’une personne à l’autre, voire d’une mesure à l’autre de la même personne, et elle est en fait attachée à chaque mesure X, selon le modèle (1) de la théorie des tests. Au moment de confronter la mesure Xi = Vi + eo au seuil normatif CP, l’erreur eo surimposera sa propre marge d’incertitude à l’imprécision du seuil CP, ajoutant ainsi sa part de variabilité au taux de capture.

La théorie intégrant la mesure Xi avec erreur et l’incertitude échantillonnale du centile CP sera développée et présentée dans un prochain article, où sera formulé explicitement le concept de norme sûre, permettant de garantir en probabilité, à un niveau a prescrit, la qualité de la sélection. Un dernier article pourra enfin donner des exemples illustratifs, avec données à l’appui, de l’application et de l’utilisation de ces outils dans différents contextes.