L’effet lundi sur les marchés d’Europe Centrale et Orientale : un élément à intégrer dans une stratégie d’investissement internationale ?

Nivoix, Sophie; Boulerne, Sandrine

doi:https://doi.org/10.7202/1072647ar

A une époque où l’internationalisation des portefeuilles d’investissement et les algorithmes de trading sont choses communes, les investisseurs demeurent à la recherche de poches de rentabilité pour battre leurs benchmarks. La connaissance des caractéristiques spécifiques de chaque marché peut naturellement les y aider, et plus particulièrement lorsqu’il s’agit de places boursières moins souvent étudiées que d’autres dans la littérature académique. Ainsi, bien que les économies en transition et émergentes aient donné lieu à de nombreuses analyses empiriques, il s’avère que l’évolution et l’efficience des places boursières de l’ex-bloc de l’Est sont relativement moins documentées. C’est donc sur ces marchés financiers que porte notre étude, avec pour objectif la détection et l’analyse sur le long terme de la présence d’un effet lundi, en utilisant des outils statistiques tels que la dominance stochastique, non utilisée jusqu’à présent pour ces pays. Si l’effet lundi existe, il peut s’intégrer avec profit dans une stratégie d’investissement et de diversification de portefeuille d’actions. Si cet effet n’existe pas ou s’est atténué, comme dans de nombreux pays industrialisés, l’investisseur peut se tourner vers d’autres sources de rentabilité, liées à l’efficience faible ou semi-forte.

Nous mobilisons la théorie de l’efficience informationnelle des marchés financiers afin de mettre en évidence l’existence de phénomènes ou de biais remettant en cause cette efficience informationnelle, sans nécessairement déterminer la nature exacte de ces phénomènes. Sur un marché financier efficient, les investisseurs peuvent faire confiance au marché pour évaluer correctement les actions des firmes dans la mesure où toute l’information disponible est intégrée dans les cours. Cependant, l’hypothèse d’efficience des marchés financiers (EMH) proposée par Fama (1970) a été remise en cause par la mise en évidence de phénomènes dénommés d’« anomalies calendaires ou temporelles ». Ces observations ont été qualifiées d’anomalies au sens de Berk (1995) dans la mesure où les chercheurs avaient du mal à expliquer leur présence en référence à une théorie existante. Ces anomalies calendaires, à l’origine d’arbitrages et de rentabilités anormales, suggèrent ainsi une certaine inefficience des marchés sous la forme semi-forte. En effet, ainsi que l’a souligné Tadjeddine (2013, p. 16), « le paradigme classique de la finance repose sur deux postulats : la rationalité de la décision et l’efficience des prix. » Pourtant, dès les années 1980, plusieurs travaux dont ceux de De Bondt et Thaler (1985) sur la surréaction des marchés à certains événements, ou ceux de Shiller (1981) sur l’incapacité des prix à s’ajuster sur la valeur fondamentale des actifs, ont montré les limites de ce paradigme classique de la finance. Le rejet de l’efficience des prix et la mise en défaut de la rationalité de la décision ont permis de prendre en compte de nouveaux facteurs explicatifs dans le cadre de la finance comportementale. Celle-ci intègre dans les choix financiers des individus des aspects psychologiques, culturels ou sociologiques, ainsi que l’ont montré Akerlof et Shiller (2013).

Des biais décisionnels tels que la myopie, l’absence de représentativité ou la routine d’ancrage dans un ensemble partiel d’informations (Kahneman et Tversky, 1979) peuvent sous-tendre des inefficiences de marché. Il en va de même pour des paramètres émotionnels comme l’excès de confiance en soi, l’optimisme (De Bondt et Thaler, 1995) ou le mimétisme. Toutefois, certaines anomalies, peuvent persister ou résister aux explications proposées par la finance comportementale.

Ainsi, les anomalies calendaires les plus testées sont les effets jour de la semaine, les effets semaine du mois et les effets mois de l’année. Les effets jour de la semaine se réfèrent à la tendance des actions à afficher des rentabilités relativement faibles un jour donné (souvent le lundi) par rapport aux autres jours de la semaine. Elles permettent d’anticiper les variations de prix de certains jours et sont utilisées par les investisseurs afin de réaliser des profits avec une stratégie de trading.

De nombreuses études ont démontré que les anomalies calendaires existent sur tous les marchés boursiers du monde, incluant les marchés émergents au Moyen-Orient (Pettengill, 2003) et en Asie (Anwar et Muluyadi (2012) ou Hla et al. (2015)), dont la Chine et l’Inde (Doyle et Chen (2009) ou Chia et Liew (2010)). D’autres études tentent de démontrer la disparition de certaines de ces anomalies calendaires sur les marchés développés comme les marchés boursiers américains et certains marchés européens (Connolly (1989), Keef et al. (2009), Alt et al. (2011) et Zhang et al. (2017)). Rares sont les études réalisées spécifiquement sur les marchés boursiers des pays d’Europe centrale et orientale (PECO).

L’objectif principal de cet article est d’étudier l’effet jour de la semaine, tout particulièrement l’effet lundi, sur le principal indice boursier de 11 PECO. Les périodes testées sont variables selon les pays, allant de 11 années pour la Slovénie (2006-2017) à 25 années pour la Pologne (1993-2017). Selon Connolly (1989), les anomalies boursières sont sensibles à la méthode économétrique utilisée. Dès lors, pour analyser cet effet lundi, plusieurs tests économétriques ont été réalisés afin de confirmer la robustesse de nos résultats (tests de dominance stochastique, modélisations GARCH), qui permettent d’affirmer l’existence d’un effet lundi pour tous les marchés des PECO sauf la république Tchèque et la Slovaquie, qui présentent un effet inversé. Quel que soit le pays, des possibilités d’intégration de cette anomalie calendaire existent donc pour générer des rentabilités excédentaires dans le cadre d’une gestion internationale de portefeuille d’actions. Les analyses ayant été menées sur les indices de marché, une marge d’amélioration des performances existe en outre dans le cadre du choix des titres par l’investisseur, dans une optique de gestion active de portefeuille et non de réplication passive des indices. Concernant la volatilité, les équations GARCH ont été estimées avec des modèle tels que GARCH-M, EGARCH-M et GJR-GARCH, avec pour chacun d’entre eux une distribution sous-jacente des résidus de type Normale, de Student ou GED. Cette distribution n’est pas neutre quant aux valeurs de la rentabilité (Boubaker et al. (2017)). De plus, les tests de stationnarité des rentabilités de Dickey-Fuller augmenté et de Phillips-Perron indiquent un rejet de l’efficience de forme faible pour l’ensemble des marchés. Enfin, les tests de rupture structurelle indiquent une influence inégale de la période de crise des subprimes sur les rentabilités et volatilités des marchés étudiés. Précisons aussi que la variété des types de modèles testés renforce la robustesse de nos conclusions.

Cette étude approfondit la connaissance des marchés boursiers émergents des PECO, tout particulièrement sur les rentabilités moyennes journalières des indices boursiers. La situation de ces marchés boursiers est donc similaire à celle des places boursières des autres pays industrialisés en termes d’efficience semi-forte. De plus, nos résultats complètent les résultats antérieurs pour certains de ces marchés boursiers et apportent de nouvelles informations pour les autres.

La structure de cet article est la suivante. Dans un premier temps est présentée la revue de la littérature relative à l’effet lundi, puis la partie méthodologique décrit les tests réalisés dans la partie empirique. Suite aux statistiques descriptives des données utilisées, les résultats des différents tests sont exposés, avant de laisser place à une partie consacrée à la discussion.

Revue de littérature

Les anomalies de rentabilité sur le marché des actions sont nombreuses, en contradiction avec ce que laisse espérer l’hypothèse de marchés efficients, sous la forme semi-forte en ce qui concerne les anomalies calendaires. Ainsi, l’existence d’un effet lundi, générateur de rentabilités plus faibles, a été relevée dès le début des années 70 par Cross (1973) puis par French (1980) et Gibbons et Hess (1981), qui ont noté que les rentabilités sont plus inférieures ce jour-là. Keim et Stambaugh (1984) le relèvent sur le marché américain de façon persistante depuis 1928. Cette anomalie, qui devrait en théorie disparaître rapidement grâce aux arbitrages des opérateurs, a donné lieu à de nombreuses études, réalisées sur des périodes, dans des pays et avec des tests variés. Les résultats ne convergent pas systématiquement, notamment en raison des fenêtres d’observation, des méthodes statistiques employées et des places boursières considérées.

La persistance de décalages entre les rentabilités observées et celles auxquelles on peut s’attendre laisse la place à des stratégies d’arbitrage de la part des investisseurs et des opportunités pour les gestionnaires de portefeuilles. Toutefois, une zone géographique a fait l’objet d’une attention moindre, en dépit de ses caractéristiques particulières. Il s’agit des PECO, qui ont connu des transformations majeures depuis la chute du mur de Berlin. Depuis le début de la décennie 1990, ils sont progressivement passés par une transition d’un régime communiste à économie planifiée à un système capitaliste incluant la libre circulation des capitaux. La (ré)ouverture de leurs marchés boursiers constitue alors un événement majeur, dont les effets ont une portée de long terme. Cependant, les études dédiées à ces marchés des actions ne sont pas fréquentes dans les publications internationales. C’est pourquoi nous avons souhaité savoir si l’effet lundi a fait ou fait encore partie des caractéristiques de ces marchés, et donc si les stratégies d’investissement qui peuvent y être mises en place sont proches de ce qui est observé dans les marchés d’actions des économies occidentales matures. Plus largement, notre question de recherche est de savoir si l’effet lundi a existé et vite disparu de ces marchés, comme le soutiennent Olson et al. (2015) pour le marché américain, ou s’il persiste et résiste encore à une explication complète, comme le notent Dicle et Levendis (2014).

Chang et al. (1993) notent que sur la période 1985-1992 pour 24 pays occidentaux, l’effet lundi est confirmé pour 13 d’entre eux. Il s’agit des Etats-Unis, du Canada, de Hong Kong, et de 10 pays européens (Allemagne, Belgique, Danemark, Espagne, France, Italie, Pays-Bas, Royaume-Uni, Suède, et Suisse). Dans leur recherche d’une cause à cet effet, ils ont vérifié si les annonces d’indicateurs économiques importants, tels que l’indice des prix à la consommation, les statistiques monétaires, le niveau du chômage ou autres, avaient plutôt lieu à un moment particulier dans la semaine. Il s’avère que les annonces macro-économiques sont réparties de manière équilibrée sur les cinq jours de la semaine, donc les explications relèvent davantage de paramètres micro-économiques. Ainsi, l’effet lundi n’apparaît pas de manière régulière chaque semaine de l’année, mais sur la moitié d’entre elles environ. Toujours dans une optique internationale, Dubois et Louvet (1996) concluent que sur la période 1969-1992 pour les 9 pays qu’ils observent l’effet lundi semble s’atténuer, et pour les Etats-Unis ils indiquent une disparition au cours des années 80, ce qu’observe également Connolly (1989). Ce constat de disparition est confirmé par Marquering et al. (2006) pour le marché américain sur la période 1960-2004, et par Alt et al. (2011) pour les marchés américain, britannique et allemand durant les années 90 et 2000. L’instabilité de l’effet lundi peut être mise en parallèle avec la corrélation entre les rentabilités des vendredis et des lundis, notée par Abraham et Ikenberry (1994). Sur le marché américain, pour la période 1963-1991, ils constatent que cette corrélation est plus sensible lorsque les rentabilités sont négatives le vendredi.

Cho et al. (2007) utilisent le test de dominance stochastique, plus solide que la comparaison de moyennes, sur les marchés américain, britannique et japonais. Ils observent sur la période 1970-2004 que l’effet lundi s’est réduit pour l’indice Dow Jones et S&P 500 depuis 1987, mais s’est maintenu pour le NASDAQ, le Russel 2000 et le CRSP. Toujours sur le marché américain, Berument et Dogan (2012) notent que sur la période 1952-2006 la relation entre la rentabilité et la volatilité varie selon les jours de la semaine, et qu’elle est défavorable au lundi. Cela provient selon eux d’une fréquence plus forte de mauvaises nouvelles économiques le week-end, ce qui affaiblit directement les rentabilités des lundis.

Plus récemment, sur la période 1993-2007, Doyle et Chen (2009) notent un effet lundi instable au fil des années, sur les marchés américain, chinois, indien, britannique, allemand et français. Cette variabilité de l’effet lundi est également notée par Levy et Yagil (2012), avec des résultats significatifs pour 5 pays parmi 20, leur échantillon ne comportant pas de PECO. Une étude très large a été menée par Dicle et Levendis (2014) sur 33 pays pour la période 2000-2007, sans toutefois comporter de PECO. L’effet lundi persiste sur la plupart des marchés, et l’explication majeure que ces auteurs retiennent est une moindre liquidité, qui affaiblit les rentabilités le lundi (Kiymaz et Berument, 2003). D’autres facteurs, tels que la taille (effet lundi plus sensible pour les firmes moins grandes) et la contagion (par un indice du même pays ou d’un pays voisin), sont également présents, mais l’effet calendrier dû à deux jours sans Bourse le week-end s’avère moins sensible, tout comme la composition des opérateurs (plus d’investisseurs individuels le lundi). Kamara (1997) quant à lui remarque un déclin de l’effet lundi sur la période 1962-1993 pour le S&P500, lié selon lui à l’accroissement du poids des investisseurs institutionnels. Toutefois, l’effet persiste pour les petites firmes et lorsque les coûts de transaction sont élevés.

Dans son analyse des indices par secteurs d’activité sur le marché italien pour la période 1999-2009, Guidi (2010) ne note pas d’effet jour de semaine, ce qui est cohérent avec l’hypothèse d’efficience des marchés sous la forme semi-forte. Avec une modélisation GARCH(1,1), il observe cependant une volatilité plus élevée les lundis.

La taille est également signalée comme élément de nuance des conclusions de Brusa et al. (2005) sur le marché américain sur le période 1988-1998. En effet, ces auteurs remarquent un effet week-end inverse pour les grandes firmes, avec des rentabilités plus élevées le lundi, tandis que l’effet lundi classique (rentabilités plus faibles) persiste pour les entreprises de moindre envergure. Une large revue de littérature est fournie à ce propos par Pettengill (2003). Dans une autre étude, Brusa et al. (2003) remarquent que l’effet week-end inversé n’est pas présent sur la période 1988-1995 pour les 8 autres pays qu’ils analysent (dont la France, le Royaume-Uni, le Japon et Hong Kong). Plus récemment, Morey et Rosenberg (2012), dans leur étude du marché américain sur la période 1966-2007, concluent à une dissipation de l’effet lundi quelle que soit la taille des firmes.

S’agissant des marchés émergents, Chia et Liew (2010) relèvent des rentabilités significativement positives le lundi sur le marché de Bombay sur la période 1998-2008, et des rentabilités négatives le vendredi sur la période 1998-2001. Sur les marchés d’Indonésie, de Singapour et de Malaisie, pour la période 2003-2008, Anwar et Mulyadi (2012) notent des rentabilités anormalement positives le vendredi pour l’Indonésie et la Malaisie, mais pas d’effet lundi. A contrario, Hla et al. (2015) observent pour la Malaisie, sur la période 1996-2014, un effet lundi (avec rentabilités négatives) et un effet vendredi avec rentabilités positives, significatifs par rapport aux autres jours de la semaine.

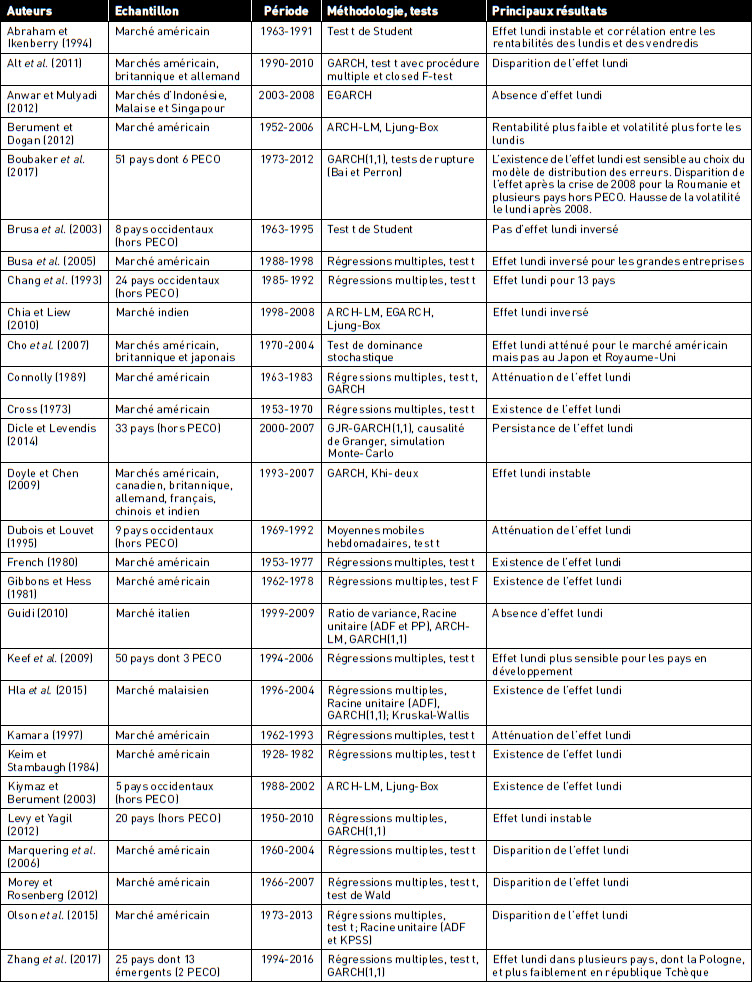
Les études des marchés des actions incluant les PECO sont relativement peu nombreuses, et en particulier celles qui leur sont spécifiquement consacrées. Une étude internationale récente incluant 6 de ces pays, parmi 51 en tout, sur plus de 20 années d’observations, est celle de Boubaker et al. (2017), dont l’apport majeur est de nature économétrique. Ainsi, les auteurs soulignent que les tests détectant les effets lundi sont sensibles à la distribution sous-jacente des erreurs, qui peuvent entre autres suivre une loi gaussienne, de Student, ou GED (Generalized Error Distribution) qui permet d’inclure les caractéristiques du coefficient d’aplatissement (kurtosis). Il apparaît en effet que les distributions non gaussiennes reflètent mieux la réalité des rentabilités. En outre, après la crise des subprimes de 2008, bien que l’effet lundi ait eu tendance à décroître, les volatilités ont quant à elles augmenté pour ce jour de la semaine. Dans une analyse des différences entre pays riches et pauvres sur la période 1994-2006, Keef et al. (2009) concluent que l’effet lundi se réduit au fil du temps mais qu’il reste plus sensible pour les indices des marchés des actions des pays pauvres. La Pologne, la république Tchèque et la Hongrie étant incluses dans le groupe des pays riches, elles n’ont pas fait l’objet d’une observation individuelle. Une autre étude internationale récente a été menée par Zhang et al. (2017), et parmi 25 pays dont 13 émergents, elle inclut la Pologne et la république Tchèque sur la période 1994-2016. Parmi tous les effets calendrier analysés (jour, semaine, mois), l’effet lundi est observé en Pologne avec un test par fenêtres glissantes sur 500, 1000 et 1500 jours de Bourse, mais pour 500 jours seulement en république Tchèque. Le tableau 1 synthétise les résultats de ces différentes études académiques.

Méthodologie

Comme cela a été signalé dès 1989 par Connolly, les résultats des analyses empiriques, pour l’effet lundi comme pour bien d’autres anomalies boursières, sont sensibles à la méthode employée. C’est pourquoi nous avons opté pour l’utilisation de plusieurs méthodes en parallèle, chacune ayant déjà montré sa pertinence dans des études antérieures.

Les tests de stationnarité

Plusieurs tests ont été réalisés afin de permettre une comparabilité pertinente de nos résultats avec ceux des études antérieures. Celles-ci s’appuient généralement sur le test de racine unitaire de Dickey-Fuller augmenté (ADF), le test de Phillips-Perron, le ratio de variance développé par Lo et MacKinlay (1988) ou le test de ratio de variance multiple de Chow et Denning (1993). Le test de Dickey-Fuller et le test de Phillips-Perron, lui-même une adaptation non paramétrique du test de Dickey-Fuller augmenté, ont pour objet de détecter la non stationnarité d’une série temporelle. Depuis la contribution de Lo et MacKinlay (1988), le test du ratio de variance et ceux qui s’inscrivent dans son prolongement – comme le test multiple de Chow et Denning (1993) – permettent de tester la stationnarité des séries, ce qui constitue une condition de la marche au hasard. Ces tests sont devenus les outils privilégiés d’analyse de l’efficience des marchés et ont été grandement utilisés pour toutes les places financières à travers le monde (Boya, 2012).

Le test de Ljung-Box (Ljung et Box, 1978) permet quant à lui de tester l’hypothèse nulle d’indépendance sérielle d’une série, autrement dit que cette série a la forme d’un bruit blanc[2], à travers l’hypothèse de nullité des coefficients d’autocorrélation des résidus. Le test se réalise en fixant un nombre de jours de décalage pour l’autocorrélation. Sous l’hypothèse nulle, la statistique Q de ce test suit asymptotiquement une loi de Khi-deux. Lorsque l’hypothèse d’indépendance sérielle (ou bruit blanc) n’est pas rejetée, les rentabilités présentent une autocorrélation. Si celle-ci est significative, il convient de compléter la modélisation temporelle des rentabilités avec des facteurs explicatifs complémentaires.

Les tests de dominance stochastique

Afin de compléter l’étude des valeurs moyennes des rentabilités, nous avons réalisé une représentation de la fonction de densité de la distribution des rentabilités des lundis, ainsi qu’une représentation de la fonction de répartition des rentabilités des lundis. Ainsi que l’ont indiqué et calculé Cho et al. (2007), l’intérêt qualitatif de ces tests de dominance stochastique d’ordre 1 pour notre étude est la comparaison qui peut être établie entre les rentabilités des lundis et celles des autres jours de la semaine, mais de façon plus robuste qu’un test de différence de moyenne. Les traitements statistiques ont été réalisés avec le logiciel R, et celui-ci utilise pour sa modélisation l’algorithme de Vinod (2004).

Les tests sur la volatilité

Ainsi que l’ont réalisé Morey et Rosenberg (2012) sur le marché américain, Guidi (2010) pour le marché italien, McGowan et Ibrihim (2009) sur le marché russe, il est possible de mettre en relation la rentabilité avec la volatilité, tout en introduisant l’effet jour de semaine. Le modèle GARCH à moyenne (GARCH-M) d’Engle et al. (1987) introduit la volatilité comme un déterminant de la rentabilité, tout en permettant de prendre en considération l’effet jour de semaine. Cependant, le modèle GARCH-M est un modèle linéaire qui suppose que l’amplitude du choc, c’est à dire le degré d’importance d’une nouvelle, détermine la volatilité. Les chocs positifs et négatifs de même amplitude ont un impact identique sur la volatilité (variance conditionnelle). Or, la réaction de la volatilité à un choc sur la rentabilité peut être différente selon l’amplitude du choc, mais également selon le signe du choc. Le modèle non linéaire GARCH exponentiel (EGARCH) [3], introduit par Nelson (1991), autorise une forme d’asymétrie qui dépend non seulement du signe positif ou négatif du choc, mais aussi de l’amplitude de ce choc. Par ailleurs, le modèle EGARCH présente l’avantage, par rapport au modèle GARCH standard, de ne nécessiter aucune restriction de non négativité sur les paramètres afin de garantir la positivité de la variance conditionnelle. Une autre approche permettant de capter l’effet d’asymétrie des perturbations sur la variance conditionnelle a été introduite par Glosten et al. (1993). Il s’agit de la formulation GJR-GARCH qui constitue un modèle GARCH avec l’ajout d’une variable muette multipliée par le carré du terme d’erreur de la période passée dans l’équation de variance conditionnelle. C’est un modèle à seuil où la variable muette est égale à 1 si le résidu de la période précédente est négatif, et nulle dans le cas contraire. De cette façon, la variance conditionnelle suit deux processus différents selon le signe du terme d’erreur. Selon Andersen et al. (2005), le modèle GARCH exponentiel (EGARCH) est l’un des modèles d’asymétrie les plus utilisés dans la littérature financière, avec le modèle à seuil GJR-GARCH. Nous avons donc estimé les modèles GARCH-M, EGARCH-M et GJR-GARCH, d’ordre 1 et d’ordre 5, selon trois distributions sous-jacentes pour le terme d’erreur, comme le suggèrent Boubaker et al. (2017) : une distribution Normale, une distribution de Student, suggérée par Bollerslev (1987), et une distribution GED[4] proposée par Nelson (1991). Ainsi, pour chaque PECO, 18 modèles ont été estimés et 198 modèles ont été comparés pour les onze pays de notre échantillon. Comme Morey et Rosenberg (2012), le choix du meilleur modèle a été réalisé suite à l’analyse des log-vraisemblances c’est-à-dire selon le meilleur niveau d’ajustement.

TABLEAU 1

**Synthèse des principaux résultats académiques concernant l’effet lundi**

Au final, le modèle EGARCH-M(1,1), avec un terme d’erreur qui suit soit une distribution de Student, soit une distribution GED, a été celui qui présentait la log-vraisemblance la plus élevée. L’écriture du modèle EGARCH-M(1,1) porte sur le logarithme de la variance conditionnelle du processus considéré.

La rentabilité conditionnelle, s’exprime alors avec :

R_t représente la rentabilité d’un indice boursier R_t-i et la rentabilité retardée de i jours, σ_t la volatilité des rentabilités, e_t le terme d’erreur, et L, M, J et V les variables muettes pour lundi, mardi, jeudi et vendredi. Lorsque les quatre variables muettes valent 0, le jour considéré est donc le mercredi, dont l’ordonnée à l’origine rend directement compte de la valeur, qui sert de référence. Ce choix se justifie par le fait que le mercredi est le jour le plus éloigné du week-end, moment crucial pour l’effet lundi. L’existence de l’effet lundi (hypothèse que nous testons) implique l’observation de rentabilités plus faibles ce jour-là, et donc un coefficient µ₁ négatif et significatif.

Et la variance conditionnelle s’écrit :

ω est une constante et z_t désigne un bruit blanc faible homoscédastique tel que E(z_t)=0 et Var(z_t)= σ²_z. Le paramètre ARCH (α_i) capture l’effet signe et permet de modéliser une asymétrie liée au signe d’un choc. Le paramètre γ_i capture l’effet taille et permet de prendre en considération une asymétrie liée à l’amplitude d’un choc mesurée par l’écart |z_t| - E (|z_t | : pour γ > 0, un choc de forte amplitude aura relativement plus d’effet (en valeur absolue) sur la variance conditionnelle (volatilité) qu’un choc de faible ampleur et inversement pour γ < 0.

Les tests de rupture structurelle

Dans le but de déterminer si des changements importants ont eu lieu dans les niveaux de rentabiltié et de volatilité des indices, notamment en liaison avec la crise des subprimes en 2008, nous avons procédé à des tests de ruptures structurelles. Cette analyse s’appuie sur les tests de Bai (1997) et Bai et Perron (1998 et 2003), réalisés avec le logiciel R. Ils permettent de voir l’impact de chocs exogènes sur les moments d’ordre 1 et 2 des séries de rentabilités et de détecter des points de rupture dans la fenêtre d’observation pour chacun des pays.

Analyse empirique

Après une présentation des statistiques descriptives relatives à chaque marché, nous exposerons les principaux résultats des tests réalisés.

Les données utilisées

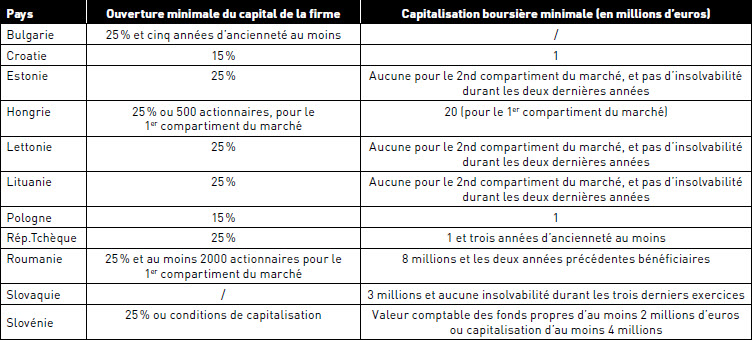
Afin de mener une étude aussi exhaustive que possible, nous avons analysé les données des indices boursiers des PECO sur la période la plus longue à notre disposition. L’historique a cependant été limité par la date de réouverture de ces places boursières après la période communiste et par le nombre réduit de sociétés cotées pour certains pays. Globalement, et suivant la disponibilité des données, la période d’étude s’étend selon les pays de 13 à 24 ans. Les sources de données furent : les sites des places boursières de chaque pays pour les événements historiques et les conditions de cotation, la base internationale Factset pour les cours des indices, et la World Federation of Exchanges pour les capitalisations boursières des marchés. Les conditions d’entrée sur chaque marché sont résumées dans le tableau 2.

TABLEAU 2

**Conditions d’entrée sur les marchés des actions, outre l’approbation des documents d’information par les autorités locales de marché**

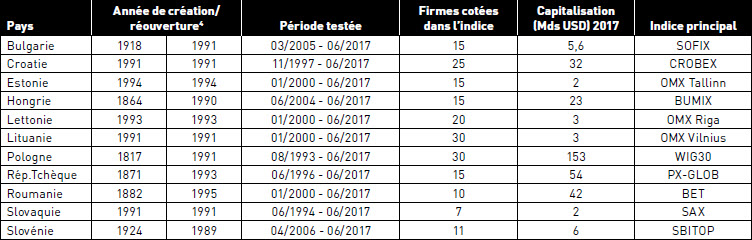
Concernant les conditions d’admission des sociétés sur ces différents marchés, on retrouve des seuils d’ouverture du capital, assez voisins d’un pays à l’autre, variant de 15 à 25 %, et une capitalisation minimale d’un million d’euros ou davantage. Le tableau 3 précise les périodes analysées, les indices de chaque pays et leur capitalisation.

Statistiques descriptives

Afin de fournir les principales caractéristiques des marchés des actions étudiés, le tableau 4 rassemble les statistiques descriptives des rentabilités des cours des 11 indices des pays considérés. Les colonnes 2 et 3 indiquent, respectivement, la date de disponibilité des données sur Factset et le nombre d’observations pour chaque série de rentabilités, sachant que les 11 séries se terminent toutes le 6 juin 2017, date de fin de collecte des données. L’indice slovène est celui qui présente le moins d’observations puisque les données sont disponibles à partir du 1^er avril 2006, alors que la série temporelle la plus longue est celle de l’indice polonais qui débute le 1^er août 1993, soit 5773 observations.

Les rentabilités moyennes quotidiennes des indices boursiers des PECO sont positives, excepté pour la Slovénie (-0,0095 %). Les rentabilités moyennes de 5 indices boursiers sur 11 sont supérieures à 0,04 %, mais elles présentent une volatilité plus importante, notamment pour la Pologne, la Roumanie ou la Lettonie. On remarque que les indices affichant les rentabilités moyennes les moins élevées sont ceux de pays de taille modeste (Slovénie, Slovaquie et Croatie), et que leur écart-type n’est pas plus faible que ceux des autres places boursières. Concernant le coefficient d’asymétrie (skewness), il est faiblement négatif pour tous les pays, sauf pour la Hongrie et l’Estonie, qui affichent une valeur légèrement positive. Quant au coefficient d’aplatissement (kurtosis), il a tendance à être plus important pour les marchés les plus petits (Slovaquie, Lituanie et Lettonie notamment), signe qu’une liquidité plus faible crée davantage d’incertitude pour les investisseurs, ce qui se traduit par des fluctuations de rentabilité plus marquées.

L’hypothèse de normalité des rentabilités des indices boursiers est significativement rejetée au seuil de 1 % par le test de Jarque-Bera, en raison de distributions fortement leptokurtiques. Les résultats obtenus ici sont proches de ceux de Guidi et al. (2010) pour le marché italien, de Boubaker et al. (2017) obtenus dans leur étude internationale et de Reboredo et al. (2015) lors de leur comparaison entre les marchés financiers d’Europe de l’Ouest et ceux des PECO (Pologne, Hongrie, République Tchèque et Roumanie).

Indicateurs financiers des marchés d’actions analysés4 — TABLEAU 3

**Indicateurs financiers des marchés d’actions analysés[4]**

TABLEAU 4

**Statistiques descriptives des rentabilités des cours de clôture des indices boursiers des pays d'Europe Centrale et Orientale**

Principaux résultats

Tests de stationnarité

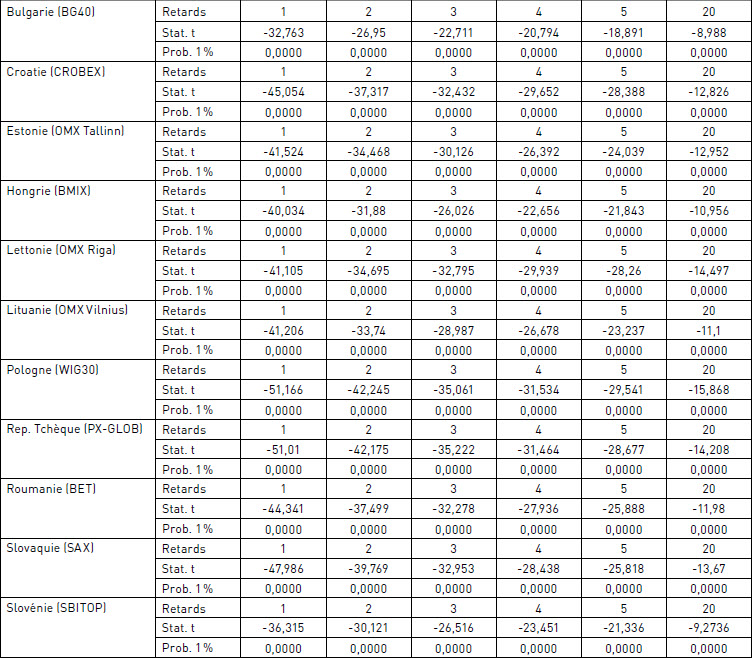
L’analyse de la stationnarité des rentabilités dans les différents pays a été réalisée avec le test ADF, avec des retards de 1, 2, 3, 4, 5 et 20 jours, ainsi que présenté[5] dans le tableau 5.

A la lecture des résultats, l’hypothèse de racine unitaire au seuil de 1 % est rejetée. Ainsi, les rentabilités des indices des PECO ne suivent pas un processus stationnaire. Ces résultats sont confirmés par les résultats du test de Phillips-Perron. Pour quatre PECO, Reboredo et al. (2015) obtiennent des résultats similaires concernant les tests de Dickey-Fuller augmenté et de Phillips-Perron. Entre outre, cela rejoint ce qui est usuellement observé sur les autres marchés des pays industrialisés, et conduit à un rejet de cette condition de l’efficience des marchés. Les résultats[6] du ratio de variance de Lo et MacKinlay (1988) démontrent qu’aucune des séries de rentabilités ne suit une marche au hasard, telle que la requiert l’efficience des marchés. La situation des marchés des PECO est donc similaire à celle des places boursières des autres pays industrialisés. La transition économique qu’ont vécue ces pays n’a donc pas eu d’impact durable sur la structure de leurs rentabilités boursières. Notons que ces résultats convergent avec ceux de Guidi (2010) pour le marché italien.

TABLEAU 5

**Tests de racine unitaire sur les rentabilités par pays : Test de Dickey-Fuller augmenté**

Test de dominance stochastique

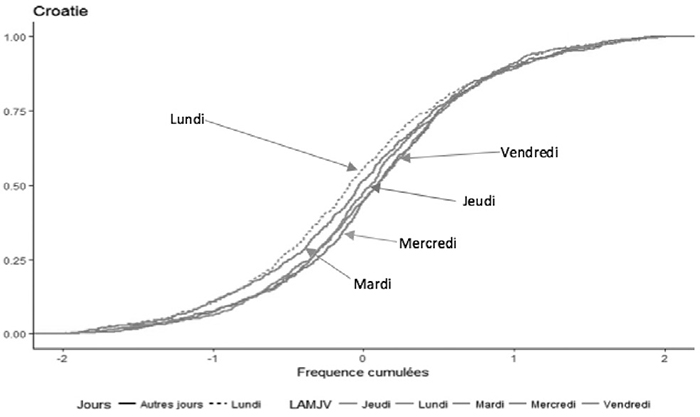
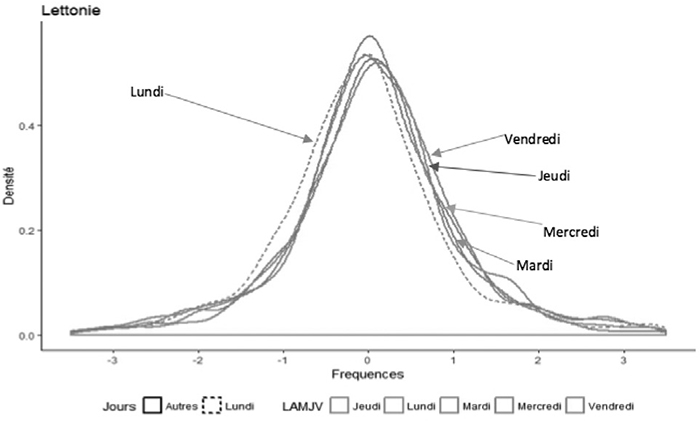
Afin de mettre en évidence l’effet lundi observé sur certains marchés des PECO, deux représentations graphiques ont été réalisées pour chaque indice : la première traduit la distribution de probabilité des rentabilités du lundi par rapport aux autres jours de la semaine et la seconde, la probabilité cumulée du lundi par rapport aux autres jours. Outre ces représentations graphiques, le tableau 6 présente les résultats de la dominance stochastique au premier ordre.

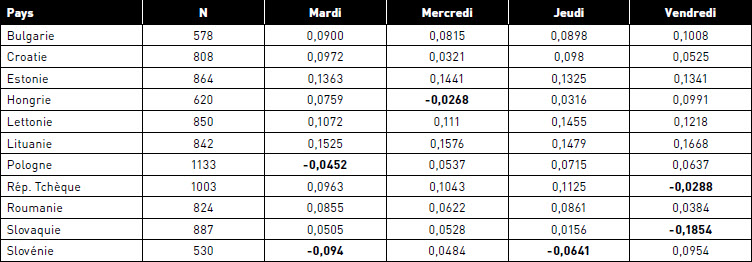
Suite à l’analyse des résultats du tableau 6 et des représentations graphiques, notamment celles de la Croatie et la Lettonie à titre d’exemple (graphiques 1 à 4)[7], l’effet lundi est particulièrement visible pour la Bulgarie, la Croatie, l’Estonie, la Lettonie, la Lituanie, et la Roumanie puisque les rentabilités du lundi sont dominées par celles des autres jours de la semaine. En revanche, comme le confirment quelques résultats négatifs reportés dans le tableau 6 (en caractère gras), les rentabilités du lundi dominent celles du mardi pour la Pologne et la Slovénie, celles du mercredi pour la Hongrie, celles du jeudi pour la Slovénie, et celles du vendredi pour la République Tchèque et la Slovaquie.

Tests sur la volatilité

Les équations (1) et (2) ont été estimées avec un modèle de type GARCH (p,q), incluant des modèles tels que GARCH-M, EGARCH-M et GJR-GARCH, avec pour chacun d’entre eux, une distribution sous-jacente Normale, de Student ou GED. En effet, Boubaker et al. (2017) montrent que les tests détectant les effets lundi sont sensibles à la distribution sous-jacente des erreurs. L’intérêt est ici d’incorporer la variance conditionnelle comme variable explicative dans l’équation du rendement excédentaire, en vue de connaître l’impact de la volatilité sur le rendement excédentaire conditionnel. Dit autrement, la variance conditionnelle du rendement a la possibilité de changer pour chaque jour de la semaine lorsque l’on modélise la variance conditionnelle dans l’équation du rendement excédentaire, ce qui permet de détecter la présence d’un effet jour de semaine dans la volatilité. Selon l’analyse des log-vraisemblance, le modèle EGARCH-M(1,1)[8] avec une distribution de Student ou GED, est celui qui donne les estimations les plus pertinentes pour étudier la relation entre le rendement excédentaire conditionnel et la variance conditionnelle des indices boursiers des PECO[9]. On peut donc rejeter la configuration d’une distribution gaussienne des résidus dans ces modèles. Morey et Rosenberg (2012) obtiennent également des niveaux de log-vraisemblance plus élevés pour le modèle EGARCH sur le marché américain.

Les estimations d’un effet lundi et des volatilités boursières obtenues avec le modèle EGARCH-M(1,1) sont reportées dans le tableau 7. Un effet lundi est confirmé pour tous les PECO, excepté pour la République Tchèque. Les coefficients (μ_Lundi) sont négatifs et significatifs au seuil de 1 % pour la Bulgarie, la Croatie, l’Estonie, la Lettonie, la Lituanie et la Slovénie, et significatifs au seuil de 5 % et 10 % respectivement pour la Roumanie et la Hongrie. Par contre, un effet week-end inversé est présent pour la Pologne et la Slovaquie puisque les coefficients (μ_Lundi) positifs et significatifs indiquent des rentabilités plus élevées le lundi. Cet effet lundi a déjà été observé précédemment avec le test de dominance stochastique, pour la Bulgarie, la Croatie, l’Estonie, la Lettonie, la Lituanie, et la Roumanie, ainsi que l’effet week-end inversé pour la Slovaquie.

TABLEAU 6

**Dominance stochastique d'ordre 1**

En outre, les coefficients de l’écart-type conditionnel λ de l’équation du rendement (risque) sont négatifs et significatifs au seuil de 1 % pour la Hongrie, la Lettonie, la Pologne, la République Tchèque et la Slovaquie et au seuil de 5 % pour la Bulgarie et la Slovénie. Ainsi, un accroissement de la volatilité diminuerait le rendement conditionnel et donc l’effet lundi. Selon Berument et Dogan (2012), une accumulation de mauvaises nouvelles économiques le week-end tendrait à réduire les rentabilités des lundis. Au contraire, les coefficients positifs de l’écart-type conditionnel λ dans l’équation du rendement excédentaire, pour l’Estonie et la Lituanie, suggèrent qu’un accroissement de la volatilité augmenterait l’effet lundi, mais ces coefficients ne sont pas significatifs. L’effet lundi est totalement absent pour la République Tchèque, ce qui nous conduit à penser que l’effet volatilité significatif et négatif, observé dans l’équation du rendement conditionnel, serait généré par d’autres facteurs qu’un effet jour de semaine. La volatilité la plus élevée, dans l’équation de la variance conditionnelle, est observée uniquement le lundi pour la Roumanie (ω_Lundi = 0,128283, significatif au seuil de 10 %), mais cette volatilité du lundi ne semble avoir aucun effet dans l’équation du rendement conditionnel (λ = -0,013028 non significatif). Les volatilités les plus faibles, dans l’équation de la variance conditionnelle (ω), apparaissent essentiellement le lundi (ω_Lundi), le jeudi (ω_Jeudi) et le vendredi (ω_Vendredi) pour la Croatie, mais génèrent finalement une absence de significativité de l’écart-type conditionnel (λ) dans l’équation du rendement. Seule la faible volatilité du mardi (ω_Mardi), observée pour la Lettonie dans l’équation de la variance conditionnelle, pourrait avoir un effet significatif sur l’écart-type conditionnel λ de l’équation du rendement (risque). En d’autres termes, un faible accroissement de la volatilité le mardi, sur le marché boursier letton, diminuerait le rendement conditionnel (λ) et donc l’effet lundi (μ_Lundi). Ainsi, l’inclusion des volatilités fait apparaître une spécificité plus marquée des lundis. On peut donc en conclure que ces résultats apportent la preuve d’un effet lundi dans les équations du rendement excédentaire pour la majorité des PECO, atténué ou accentué par l’écart-type conditionnel.

FIGURE 1

**Fonctions de distribution cumulatives pour les jours de la semaine : la Croatie**

FIGURE 2

**Distribution de probabilité des rentabilités des jours de la semaine : la Croatie**

FIGURE 3

**Fonctions de distribution cumulatives pour les jours de la semaine : la Lettonie**

FIGURE 4

**Distribution de probabilité des rentabilités des jours de la semaine : la Lettonie**

TABLEAU 7

**Détermination de l'existence d'un effet lundi avec le modèle EGARCH-M (1,1)**

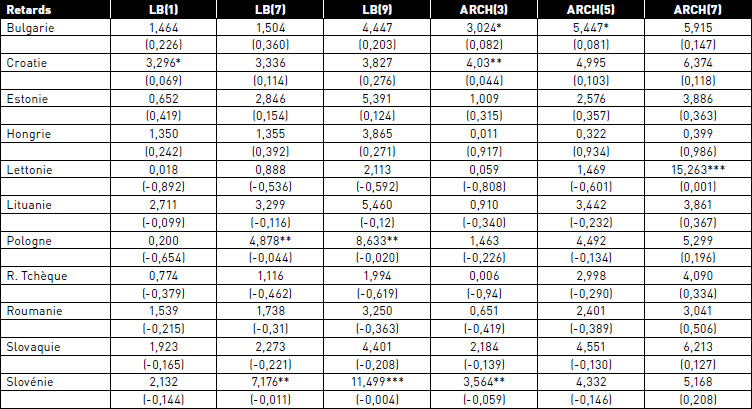
Si l’on s’intéresse à présent à l’analyse des résidus des modèles, on peut voir dans le tableau 8 les résultats des tests de Ljung-Box. Ils sont calculés pour les résidus normalisés, avec des retards de 1, 7 et 9 jours et les tests du Multiplicateur de Lagrange ARCH sont réalisés[10] avec des retards de 3, 5 et 7 jours. Les résultats des tests de Ljung-Box pondéré indiquent pour tous les pays la présence d’autocorrélation positive, mais non significative, parmi les résidus.

En outre, les résultats des tests du modèle ARCH-LM, traduisent l’absence de preuves d’effets ARCH résiduels. Le calibrage de nos modèles apparaît donc comme suffisamment complet avec ce type de décalage temporel. Sachant que 5 jours de Bourse de décalage correspondent à une semaine de cotation, il n’est pas surprenant que des décalages dépassant 10 jours (soit deux semaines de cotation) soient non significatifs, car ils impliqueraient un processus à mémoire assez longue.

Tests de rupture

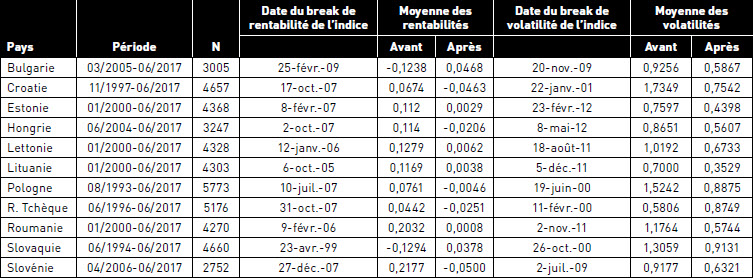
Enfin, les tests de rupture pour les moments d’ordre 1 et 2 ont permis de déceler des dates suggérant une modification sensible des niveaux de rentabilité et de volatilité des indices. Les résultats sont présentés dans le tableau 9, qui indique la date de changement structurel la plus significative pour chaque pays. La moyenne des rentabilités et des volatilités quotidiennes des indices a été déterminée avant et après cette date.

Plusieurs constats intéressants peuvent être faits. L’hypothèse de stabilité structurelle est rejetée pour tous les pays, et l’on constate que les rentabilités quotidiennes de 6 indices boursiers sur 11 ont subi une rupture durant l’année 2007, très probablement générée par la crise financière des subprimes. Pour les autres pays, le break le plus notable s’est situé à une autre date, sans que cela n’implique une absence d’influence de la crise financière de 2007-2008. L’effet de contagion fut alors plus faible. Ces résultats viennent compléter ceux de Boubaker et al. (2017) qui ont étudié pour 6 PECO l’existence d’une rupture suite à la crise financière.

Les indices boursiers de la Pologne et de la République Tchèque ont subi des changements structurels majeurs au cours des mêmes années, à savoir en 2007 pour les rentabilités et en 2000 pour les volatilités, ce qui tend à confirmer les résultats de Reboredo et al. (2015) quant à une dépendance positive très forte entre les marchés financiers polonais et tchèque. Les élections présidentielles de 1999 en Slovaquie, de 2009 en Bulgarie, de juillet 2011 en Estonie et août 2011 en Lettonie, semblent avoir eu un impact non négligeable sur les marchés financiers de ces pays. Pour la Slovaquie et la Bulgarie, la moyenne des rentabilités est devenue positive et la moyenne des volatilités des indices a diminué de près de 30 %, signe de plus de stabilité sur ces marchés. On retrouve cette situation de baisse de la volatilité sur l’ensemble des marchés observés. Pour la Lettonie, la moyenne des volatilités a chuté de plus de 40 %. Concernant l’Estonie, la baisse de la volatilité de plus de 30 % dès février 2012, fut probablement la conséquence de deux évènements majeurs, l’élection présidentielle d’août 2011 et l’adoption de l’euro en janvier 2011. En fin d’année 2011, la volatilité sur le marché financier Lituanien fut au plus haut, suite à l’annonce par la Banque Centrale de la liquidation de Snoras, la quatrième banque lituanienne, pour fraudes et détournements de fonds en fin d’année 2011. Suite à cet évènement, la volatilité du marché lituanien a, en moyenne, été divisée par deux. Le marché financier polonais, le plus actif parmi les PECO, a connu une forte rupture de volatilité en 2000, certainement suite à l’éclatement de la bulle internet en avril 2000. Globalement, on note donc une amélioration de l’équilibre rentabilité-risque sur l’ensemble des marchés après les dates de rupture.

TABLEAU 8

**Tests de Ljung-Box pondéré et Tests du Multiplicateur de Lagrange ARCH pondéré pour différents retards**

TABLEAU 9

**Tests sur les breaks de rentabilité et de volatilité (changements de structure)**

Discussion

L’existence de l’effet lundi dans la plupart des pays étudiés comporte plusieurs conséquences en termes d’allocation internationale des ressources pour les investisseurs. Tout d’abord, la diversification internationale des portefeuilles d’actions devrait éviter si possible les techniques de gestion passive consistant à répliquer les indices puisque les marchés ne sont pas efficients au sens semi-fort. Il convient donc d’opter pour des techniques de gestion active intégrant l’effet lundi dans le cadre d’arbitrages temporels (market timing). Ensuite, au sein de la zone géographique considérée, la stratégie à appliquer en liaison avec l’effet lundi sera inverse pour la République Tchèque et la Slovaquie comparativement aux autres pays. Cela permet d’être, selon les jours, présent (long) sur une partie des marchés des PECO et absent (short) des autres.

Sur un plan opérationnel, l’application de ces résultats pour les investisseurs internationaux est immédiate. En effet, extraire des rentabilités anormales des indices des marchés des PECO est concrètement utile pour un certain nombre d’investisseurs. A titre d’exemple, un des fonds d’investissement gérés par « Conseq Invest plc », dont le dépositaire est BNP Paribas Securities Services à Dublin, a pour orientation d’investissement les actions des PECO. Il est valorisé en couronnes tchèques et a pour objectif de performance (ou benchmark) un panier composé de l’indice polonais WIG30 pour 38 %, l’indice tchèque PX pour 28 %, l’indice hongrois BUX pour 28 % et l’indice slovène SBITOP pour 6 %, avec un horizon d’investissement de 5 ans. Autre exemple, le fonds luxembourgeois « NN (L) International Czech Equity - P Cap CZK » a pour objectif d’investir au moins 51 % de son portefeuille dans des actions cotées à la Bourse de Prague. Son benchmark est composé de l’indice PX pour 52 %, l’indice WIG30 pour 28 %, l’indice BUX pour 10 %, et l’indice roumain BET pour 10 %. Concernant les produits dérivés sur indices de marchés d’actions, ils n’existent pas pour tous les PECO, mais des options sur indice sont négociables sur l’indice polonais WIG30 et l’indice slovène SBITOP.

Conclusion

Afin d’analyser l’existence d’un effet lundi sur les marchés des actions de 11 pays d’Europe centrale et orientale, nous avons réalisé plusieurs types de tests, relatifs à la rentabilité, à la volatilité et à la dominance stochastique. Ce dernier point n’avait à notre connaissance jamais été étudié pour ces pays. Les résultats des différents tests réalisés montrent l’existence d’un effet lundi sur la plupart des marchés boursiers étudiés, au travers de rentabilités plus faibles. Un effet week-end inversé est en outre à signaler pour la Slovaquie et la république Tchèque. Ces résultats obtenus sont robustes du fait de la variété des modèles utilisés, linéaires et non linéaires. Ils peuvent être utilisés par les investisseurs pour prévoir les tendances boursières en exploitant les anomalies calendaires et pour maximiser les rentabilités de leurs portefeuilles internationaux tout en optimisant leur diversification. Les implications de ces conclusions sont donc directes en termes de gestion d’actifs et de stratégie active d’investissement en actions.

Le benchmark utilisé étant l’indice de référence, il existe une marge de manoeuvre pour un choix de titres au sein même de chaque indice (au moyen du stock picking). Ce volet constitue une voie de recherche prometteuse, notamment pour les pays dont les titres cotés sont nombreux (cas de la Pologne, de la Hongrie et de la république Tchèque). Toujours dans l’idée d’intégrer les anomalies des marchés dans une stratégie de gestion internationale active, il serait utile d’étudier pour ces pays l’existence ou la persistance d’autres effets présents sur les marchés d’actions, tels que l’effet janvier ou d’autres effets de calendrier.

Enfin, nos résultats ayant montré des différences entre les pays considérés, une piste de recherche future intéressante sera de vérifier si la taille des marchés influence l’effet lundi. Concernant les sociétés cotées à l’intérieur de chacun de ces marchés, il importe également d’analyser quelles sont les conséquences en termes d’accès au financement et d’opportunités d’investissement à l’international (Benkraiem et Miloudi, 2014).

Résumé

Abstract

Resumen

Revue de littérature