Régionalisation des débits moyens mensuels en Algérie du nord Regionalization of the mean regimes of the monthly runoff in northern Algeria

Résumé

L'identification des régions ayant des caractéristiques hydrologiques homogènes en Algérie du Nord représente l'objectif principal de cette étude. L'analyse en composantes principales (ACP) et la classification par les composantes principales dynamiques (CPD) ont été appliquées sur les débits moyens mensuels de 51 stations hydrométriques. Les résultats de l'ACP ont montré l'existence de trois groupes hydrologiquement homogènes. La mise en oeuvre de la méthode CPD a aussi mis en évidence les trois mêmes groupes. Les types de régimes mis en évidence avec les deux méthodes sont de types simple, mixte et complexe. Le type de climat qui caractérise ces groupes est méditerranéen pour le premier, transition entre méditerranéen et semi-aride pour le deuxième et semi-aride pour le troisième groupe.

Mots-clés :

• Algérie du Nord,
• analyse en composantes principales,
• analyse en composantes principales dynamiques,
• débits

Abstract

Identification of regions with homogeneous hydrological characteristics in Northern Algeria was the main objective of this study. Principal Component Analysis (PCA) and Principal Dynamic Components (PDC) were applied to monthly mean discharge data from 51 hydrometric stations. The PCA results showed the existence of three hydrologically homogeneous groups. The implementation of the CPD method highlighted the same three groups. The types of regimes identified with the two methods are single, mixed and complex. The type of climate that characterizes these groups is Mediterranean for the first, transition between Mediterranean and semi-arid for the second, and semi-arid for the third group.

Keywords:

• Northern Algeria,
• Principal components analysis,
• Principal dynamic components,
• discharge

1. Introduction

Les relevés des débits d’une rivière, pendant une longue série d’années, montrent des variations saisonnières des hautes et basses eaux en fonction des principaux facteurs influençant l’écoulement (le régime des précipitations, la nature géologique du bassin versant, sa situation géographique, sa surface, etc.). En général, en hydrologie, on résume sous la dénomination « régime » les variations relatives et absolues d’un élément du régime hydrologique dans un laps de temps déterminé. Sous « régime d’écoulement », on entend souvent le comportement hydrologique global d’un cours d’eau. Le régime hydrologique se définit par l’évolution de l’écoulement mensuel moyen (appelé débit « intermensuel » ou « module mensuel ») calculé sur un certain nombre d’années d’observations. Il est possible de caractériser les écoulements dans un bassin versant en adoptant une classification du régime des cours d’eau basée, d’une part, sur l’allure de la fluctuation saisonnière systématique des débits et, d’autre part, sur son mode d’alimentation, c’est-à-dire, la nature et l’origine des hautes eaux (pluviales, nivales). En général, l’étude du régime hydrologique fait référence aux régimes définis par PARDÉ (1955). Il s’agit de l’étude des variations saisonnières des moyennes interannuelles des débits mensuels. Sur la base de cette description des débits mensuels, la classification de PARDÉ (1955) s’intéresse à la répartition des apports mensuels au cours de l’année ainsi qu’à l’origine des écoulements.

Le régime méditerranéen est calqué, en grande partie, sur le régime des précipitations. Les hautes eaux sont enregistrées en saison froide et les basses eaux en saison chaude. Les études des dernières années (ANRH, 1993; TOUAZI et LABORDE, 2000; TOUAZI, 2001; TOUAZI et al., 2004) ont montré une tendance à la baisse des précipitations qui a eu pour conséquence une diminution des débits et qui a engendré le tarissement de certains cours d’eau.

L’Algérie dispose de ressources en eau douce limitées qui sont réparties à travers des régions présentant une grande diversité climatique et géographique. La meilleure gestion de ces eaux à l’échelle du bassin versant nécessite la connaissance des écoulements. Malheureusement, les bassins versants ne sont pas tous équipés de stations de jaugeage qui permettent de mesurer les débits. À cet effet, il est nécessaire de définir des régions hydrologiquement homogènes. Les méthodes qui ont été développées dans cette optique peuvent être définies comme étant l’utilisation des données provenant de plusieurs sites afin d’estimer la distribution de données observées à un site où l’on dispose de peu ou d’aucune information (HOSKING et WALLIS, 1993). La détermination des régions homogènes constitue donc un élément important dans toute méthodologie d’estimation régionale. Il existe plusieurs méthodes de régionalisation des débits de crues qui ont été utilisées dans diverses régions du monde. Ces techniques sont basées sur des théories complètement distinctes. Il importe donc de faire une brève description de ces différentes méthodes. Certaines de ces méthodes ont été décrites par plusieurs auteurs (GREHYS, 1996a, GREHYS, 1996b; OUARDA et al., 1999) dont l’essentiel se résume comme suit :

1.1 Approche basée sur des régions fixes

Ensemble de stations d’une région homogène. Deux sous-groupes peuvent être considérés :

• Régions géographiquement contiguës : Ces régions peuvent être définies, par exemple, à partir de la similarité des densités non paramétriques des débits de crues (ADAMOWSKI et al., 1994; GINGRAS et ADAMOWSKI, 1992; GINGRAS et al., 1994; HOSKING et WALLIS, 1993). La validation de cette méthode est réalisée avec l’application des L-moments. Cette technique a été popularisée en hydrologie par HOSKING (1986).

• Régions non contiguës : Ces régions peuvent être définies, par exemple, par analyse factorielle par correspondance et classification hiérarchique ascendante (BENZECRI, 1973; JAMBU, 1976).

1.2 Approche basée sur des régions de type voisinage

On associe à chaque station cible son propre voisinage. Les voisinages peuvent être définis par la méthode des régions d’influence (BURN, 1988, 1990a, b; ZRINJI et BURN, 1994) et par l’analyse de corrélations canoniques (CAVADIAS, 1989, 1990), dont le détail se résume comme suit :

• Méthode des régions d’influence : Dans la méthode des régions d’influence (BURN, 1988, 1990a, b; ZRINJI et BURN, 1994), chaque site peut être considéré comme le centre d’une région formée de sites dont les caractéristiques de crue sont similaires. Cette approche implique généralement que l’on dispose d’un minimum d’informations hydrologiques sur le site pour lequel on souhaite définir une région d’influence. L’identification d’une région d’influence d’un site donné est basée sur la distance euclidienne entre les sites dans l’univers des variables (attributs) sélectionnées. Dans l’espace des attributs physiographiques et/ou hydrologiques, la distance entre deux sites i et j est définie par :

(1)

où M est le nombre d’attributs considérés, , la valeur standardisée de l’attribut d’ordre m au site i et est le poids associé à l’attribut.

Plusieurs variantes de la méthode ont été présentées en fonction des attributs utilisés et selon que le site cible soit partiellement jaugé ou non (BURN, 1988, 1990a, b; GREHYS, 1996a; ZRINJI et BURN, 1994).

• Méthode d’analyse des corrélations canoniques : La méthode d’analyse des corrélations canoniques permet d’identifier les sites dont le régime des crues est similaire (CAVADIAS, 1989, 1990; OUARDA et al., 1997; OUARDA et al., 1999; OUARDA et al., 2001; RIBEIRO-CORRÉA et al., 1995). Cette technique est un outil d’analyse statistique multivariée qui permet de décrire la relation de dépendance existant entre deux ensembles de variables aléatoires. Cette technique permet de déterminer des paires de combinaisons linéaires de chaque ensemble de variables, de sorte que la corrélation entre les variables d’une paire soit maximisée et la corrélation entre les variables de paires différentes soit nulle.

En Algérie, l’état des connaissances concernant la détermination des régions hydrologiquement homogènes est embryonnaire. Néanmoins, quelques études ont déjà été réalisées par TAÏBI (1990) et BELDJOUDI et OULD YAHIA (1997). Dans le cadre des travaux réalisés par TAÏBI (1990) sur la régionalisation des écoulements en Algérie septentrionale, 104 stations, dont la période d’observation varie de sept à 36 ans, ont été utilisées. La procédure utilisée consiste en la mise en oeuvre de l’analyse factorielle des correspondances pour étudier les régimes d’écoulement. Il a ainsi identifié cinq zones hydrologiques homogènes : (1) zone tellienne Ouest; (2) zone tellienne Est; (3) zone de la Macta; (4) zone de la Mina; et (5) zone Atlas saharien et Hautes Plaines.

Les travaux réalisés par BELDJOUDI et OULD YAHIA (1997), qui consistent en l’étude des hydrogrammes de différentes stations de la zone d’étude, ont mis en évidence l’existence de deux régimes d’écoulement :

• Un régime simple, caractérisé par un seul minimum et un seul maximum et un régime complexe, composé de plusieurs minima et maxima.

• D’après ces auteurs, 60 % des bassins étudiés présentent un régime simple. Les 40 % à régime complexe concernent essentiellement les bassins de la Medjerda (BV 12) et des Hauts Plateaux constantinois (BV 07), qui sont situés à l’est de la région d’étude (Figure 1).

Figure 1

Stations hydrométriques disponibles (+) et utilisées (^*) et bassins versants

Hydrometric stations that were available and used and their catchments

Notre étude consiste à avancer la connaissance de l’hydrologie en Algérie du Nord où peu d’études ont été réalisées. Nous allons procéder à la régionalisation des régimes hydrologiques en utilisant les analyses multivariées : l’analyse en composantes principales (ACP) et la classification par les composantes principales dynamiques (CPD). Ce type de méthodes (statistiques multivariées) est en popularité croissante dans plusieurs domaines de recherche (psychologie, biologie, etc.), car il permet l’analyse de bases de données complexes. Cette approche est pertinente lorsque l’on veut analyser plusieurs variables dépendantes et plusieurs variables indépendantes qui sont corrélées entre elles à différents degrés. De même, ces méthodes présentent aussi un avantage dans leur facilité à être mises en oeuvre. Ces deux méthodes (ACP et CPD) seront appliquées aux débits moyens mensuels de 51 stations hydrométriques.

2. Présentation du cas d'étude

2.1 Zone d’étude

Localisée au sud de la bordure méditerranéenne, avec une superficie de 2 381 741 km², l’Algérie forme la partie centrale du Maghreb. Elle est limitée à l’est par la Tunisie et la Libye, au sud par le Niger et le Mali, au sud-ouest par la Mauritanie et à l’ouest par le Maroc (Figure 2).

Le territoire algérien est subdivisé en deux grandes zones géographiques distinctes. La première est constituée par une bande large de 200 à 300 km du nord au sud et qui s’étend sur 1 200 km de littoral. La seconde zone, située au sud de cette bande, concerne l’immense Algérie saharienne (plus de 2 millions de km²).

Du point de vue orographique, l’Algérie septentrionale correspond au prolongement de l’Atlas marocain (Moyen et Haut Atlas). Elle se présente sous la forme de deux chaînes parallèles : l’Atlas tellien (ou Tell), orienté est-ouest et l’Atlas saharien, orienté nord-est, sud-ouest (Figure 2).

Figure 2

Situation géographique de la zone d’étude

Geographical location of the study area

L’Atlas tellien s’étend sur une longueur d'environ 1 000 km et sur une largeur de 125 km. Sa partie orientale est composée des massifs du Djurdjura en Kabylie et de l’Edough et sa partie occidentale se distingue par les massifs du Dahra, Ouarsenis et Trara. Du point de vue hydrographique, le fleuve Cheliff est considéré comme le plus important d’Algérie. Long de 725 km, il prend sa source dans l’Atlas tellien et se jette dans la Méditerranée.

Du point de vue climatique, la région du Tell est caractérisée par un climat méditerranéen, avec des étés chauds et secs et des hivers doux et pluvieux. Les précipitations annuelles varient entre 400 et 1 800 mm. Le massif du Djurdjura, situé en Kabylie et le massif de l’Edough, situé plus à l’est, sont les zones les plus arrosées de l’Algérie.

En ce qui concerne les températures, les minima sont atteints au mois de janvier, alors que les maxima sont atteints en juillet ou août. Le contraste saisonnier est bien marqué entre l’hiver et l’été. Les températures moyennes en été varient entre 25 et 30 degrés, alors qu’en hiver, elles oscillent entre 10 et 15 degrés. Dans les régions montagneuses dépassant les 1 000 m d’altitude, ces températures peuvent atteindre des valeurs négatives.

2.2 Données disponibles

Les données utilisées concernent les débits journaliers de 51 stations hydrométriques. Elles sont structurées suivant l’année hydrologique allant du 1^er septembre au 31 août.

Elles proviennent de la banque de données de l’Agence Nationale des Ressources Hydrauliques (ANRH). La répartition spatiale des stations hydrométriques est très hétérogène (Figure 1). Le réseau hydrométrique algérien est constitué de 200 stations (Figure 1). Malheureusement, 51 stations de jaugeage seulement ont été utilisées, puisqu’elles présentent une période d’observation suffisamment longue pour permettre un traitement statistique. Les autres points de mesures disposent d’observations qui sont courtes et de fiabilité moindre, vu les difficultés de mesures.

En raison d’intérêts économiques, le réseau hydrométrique est plus dense au nord qu’au sud. La durée d’observation varie d’une station à une autre. Néanmoins, les stations retenues disposent d’une vingtaine d’années d’observations pendant la période commune allant de 1970 jusqu’à 1993. La surface des bassins versants utilisés dans cette étude varie entre 107 km² (Aïn Berda) et 42 756 km² (Cheliff). L’analyse générale du coefficient d’hydraulicité des différentes stations se traduit par de fortes fluctuations des débits d’une année à l’autre. Ces valeurs sont en majorité inférieures à l’unité, ce qui montre une forte dissymétrie positive de la distribution des apports annuels. Le régime est de type pluvial et les périodes de basses et hautes eaux se déplacent sensiblement d’une année à l’autre, suivant la répartition temporelle des pluies. Globalement, la répartition des débits suit celle des pluies, mais pour certains bassins, le rôle régularisateur des nappes souterraines peut devenir important. En ce qui concerne la qualité des données, elle a fait l’objet de vérification lors des travaux de TOUAZI (2001). Les débits moyens interannuels des stations utilisées dans le cadre de cette étude ont fait l’objet d’ajustement à différentes lois statistiques et la loi log-normale était la mieux adaptée.

3. Méthodologie utilisée

L’analyse en composantes principales (ACP) et la classification par les composantes principales dynamiques (CPD) ont été appliquées aux débits de 51 stations hydrométriques afin de proposer une classification des régimes hydrologiques. L’analyse en composantes principales a été décrite pour la première fois par PEARSON (1901). Depuis, cette technique d’analyse de données est couramment utilisée dans différents domaines (hydrologie, climatologie, chimie et géographie, etc.) (CERÓN et al., 1999; LABORDE, 1984; LEBART et al., 1977; LÓPEZ et al., 1994; RICHMAN, 1986). Cette méthode permet d’analyser un ensemble de n variables (espace à n dimensions) à travers leurs projections dans un sous-espace à nc dimensions (nc<<n). Ce sous-espace est choisi de façon à engendrer la plus petite déformation possible. Cette projection permet non seulement de conserver une part essentielle de l’information, mais aussi de la filtrer. Cette méthode d’analyse est très pratique lorsqu’on est en présence d’une masse de données importante difficile à manipuler. Les projections des variables sur les composantes permettent une vision claire lorsque l’on ne retient que deux ou trois composantes (projection sur un plan ou dans l’espace). Il faut cependant que ces dernières expliquent une part de variance significative.

Le principe de l’analyse en composantes principales consiste donc à construire un sous-espace sur lequel la projection des variables de départ se fait avec le moins de déformation possible. Les variables utilisées peuvent avoir des ordres de grandeur très différents, ce qui les rend difficilement comparables. Pour éliminer ce problème, il est recommandé de travailler sur une matrice des valeurs centrées réduites. On parle alors d’analyse en composantes principales sur la matrice des coefficients de corrélation. En effet, si l’on impose que les composantes principales définissant le sous-espace soient des combinaisons linéaires des variables et que ces composantes soient orthogonales entre elles, on démontre ainsi que les composantes principales sont portées par les vecteurs propres de la matrice des coefficients de corrélation entre les variables de départ. De même, la variance des projections des observations sur chaque composante est proportionnelle à la valeur propre associée à la composante (au vecteur propre).

Enfin, il est à noter que la somme des valeurs propres est égale au nombre de dimensions de l’espace originel (en général n, le nombre de variables). Les composantes principales sont numérotées dans l’ordre décroissant des valeurs propres , la somme des valeurs propres correspond à la variance totale. Le pourcentage de la variance initiale expliquée retrouvé en projection sur les i premières composantes est :

(2)

Il est également possible de projeter non seulement les observations, mais aussi les variables. En effet, le cosinus de l’angle formé entre une variable de départ et une composante n’est autre que le coefficient de corrélation entre les valeurs prises par une variable et les projections de toutes les observations sur la composante. Dans ces conditions, les variables de départ peuvent être représentées en fonction de leur coefficient de corrélation avec les composantes. En tant que telle, l’analyse en composantes principales n’est pas une méthode de classification, mais un mode de représentation des variables sur un support le moins déformant possible, qui rend une classification la moins subjective possible.

La méthode de classification automatique par les composantes principales dynamiques (CPD) a été développée dans le cadre des travaux de recherche pour le ministère de l’Agriculture français (LABORDE, 1984). Depuis, de nombreuses utilisations ont été faites avec succès dans de nombreux domaines tels que l’hydrologie, la climatologie et l’hydrochimie (CUGNY et REY, 1981; DIDAY, 1971; LEFEBVRE et DAVID, 1977).

Le principe de cette méthode, décrit par LABORDE (1991), consiste à proposer une partition de n variables en k classes. La particularité de cette méthode est de s’intéresser à des variables et non à des individus, comme dans la plupart des méthodes de classification. Cette méthode s’inspire des techniques d’agglomération autour de centres mobiles et des propriétés de l’analyse en composantes principales.

L’agglomération autour des centres mobiles est une démarche de classification d’individus. Elle permet de regrouper n individus notés en k classes. À la première étape, k points notés qui serviront à initialiser le processus sont donnés arbitrairement. Après avoir calculé les distances   , chaque point est affecté à la classe j pour laquelle la distance est minimale. Si l’on note les points affectés à la classe j à cette première étape, chaque centre initial est remplacé par le barycentre des points . Après avoir recalculé les distances , de nouvelles affectations ont été effectuées suivant le même critère de distance minimale et le nombre de points qui ont changé de groupe est noté. Au bout de quelques itérations, le processus se stabilise (le nombre de points changeant de groupe tend vers zéro). La partition en classes est alors terminée.

Les limites de cette méthode sont bien connues et sont essentiellement de deux ordres : (1) le nombre de classes doit être fixé a priori et il se peut qu’au cours des itérations, certaines classes se vident; et (2) la partition finale dépend des centres initiaux que l’on s’est donnés.

Pour utiliser cette méthode, non plus sur des individus, mais sur des variables, il suffit de trouver une notion de distance entre variables, ce qui est très simple, en utilisant les coefficients de corrélation. Mais il faut également trouver l’équivalent pour des variables, aux barycentres d’individus et, de plus, savoir calculer la distance entre cet équivalent et chaque variable de départ. Pour ce faire, nous allons combiner cette approche avec celle de l’analyse en composantes principales. Le principe se résume comme suit :

Soit n variables notées x_i qui vont être groupées en k classes. À la première étape, k variables centrales notées c_j0 qui serviront à initialiser le processus sont données arbitrairement. Ces centres c_j0 seront en fait k des variables x_i tirées au hasard parmi les variables. Après avoir calculé les coefficients de corrélation r(x_i,c_j0) entre les variables et les centres initiaux, chaque variable x_i est affectée à la classe j pour laquelle le coefficient maximal de corrélation est en valeur absolue. Si l’on note x_ij les variables affectées à la classe j à cette première étape, chaque centre initial c_j0 est remplacé par la première composante principale c_j1 calculée sur les variables x_ij. Après avoir recalculé les coefficients de corrélations r(x_i,c_j1) entre les variables et les centres, de nouvelles affectations suivant le même critère du coefficient maximal de corrélation en valeur absolue ont été effectuées et le nombre de variables qui ont changé de groupe est noté. Au bout de quelques itérations, le processus se stabilise et le nombre de variables changeant de groupe tend vers zéro. Sous cette forme, la méthode des CPD présente des défauts analogues à ceux décrits pour l’agglomération autour de centres mobiles qui sont : (1) la nécessité de choisir a priori le nombre de classes; et (2) la classification dépend en partie des centres initiaux.

La méthode des CPD a donc été couplée avec une phase initiale d’analyse. Cette phase consiste à réaliser un grand nombre de classifications en un nombre restreint de classes (deux ou trois). L’analyse des résultats montre que certaines variables sont toujours (ou presque toujours) dans le même groupe. Elles constituent donc des « noyaux durs » et le nombre de ces noyaux durs donne une indication plus objective sur le nombre de classes à choisir. En prenant pour centre initial de chacune des classes définitives une variable de chacun des noyaux durs, le problème de l’initialisation s'ammenuise.

4. Résultats

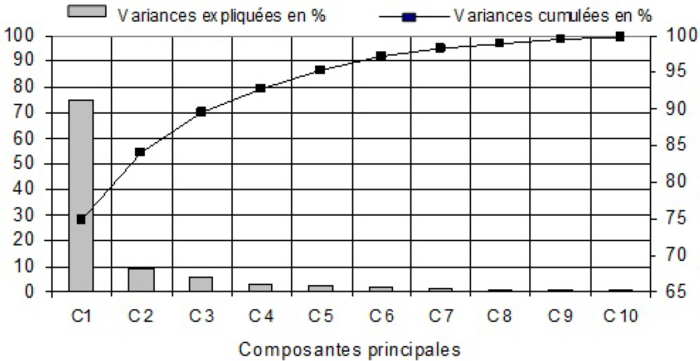
Dans le cadre de la mise en oeuvre de l’analyse en composantes principales, les stations ont été prises comme variables (colonnes) et les mois comme observations (lignes). Les dix premières composantes ont été retenues pour être présentées sur les figures, quel que soit leur pouvoir explicatif pour interpréter les résultats. En effet, la première composante C1 permet de donner des informations du point de vue temporel sur les variations saisonnières des régimes des cours d’eaux et la seconde composante C2 donne plutôt des informations spatiales. Les résultats ont montré qu’une bonne part de la variance (84 %) est expliquée par les deux premières composantes; la composante C1 en explique à elle seule 74,8 %, (Figure 3). La projection des variables sur la composante C1 a montré que toutes les stations sont corrélées positivement avec cette dernière (Figure 4) et que le coefficient de corrélation décroît lorsqu’on s’éloigne du nord vers le sud. Cette première composante explique le comportement « moyen » des débits mensuels sur l’Algérie du Nord.

Figure 3

Représentation de la variance expliquée et cumulée des résultats de l’ACP sur la zone d’étude

Representation of the explained and cumulative variance of the results of the PCA in the study area

Figure 4

Cartographie de la projection des variables sur la première composante C1 de la zone d’étude

Mapping of the projection of the variables on the first component C1 in the study area

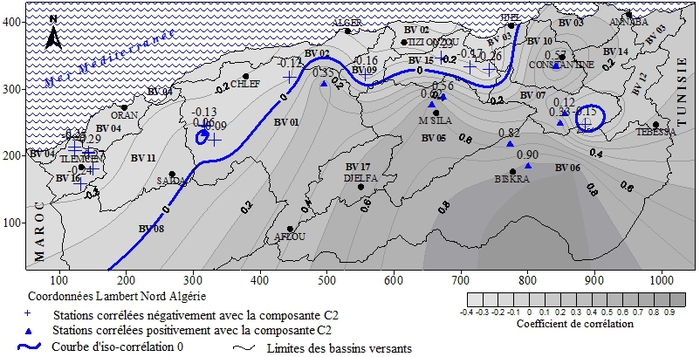
La projection des variables sur le plan C1/C2 (Figure 5) montre que les stations qui sont corrélées négativement avec la composante C2 forment un nuage de points compact, contrairement à celles qui le sont positivement, qui sont très éparpillées. Afin de pouvoir analyser ces résultats et les interpréter, la cartographie de la composante C2, qui explique 9,1 % de variance, a été réalisée. Les résultats ont mis en évidence deux groupes de stations (Figure 6). Les stations situées au-dessus de la ligne d’isocorrélation zéro, que l’on va appeler dans la suite du texte « groupe Nord », sont corrélées négativement avec cette composante C2. Par contre, les stations situées en dessous de cette ligne d’isocorrélation zéro, que l’on nommera « groupe Sud », sont corrélées positivement avec cette composante. La cartographie de la troisième composante C3 ne présente aucune structure spatiale en raison de la faible part de variance qu’elle explique. Il en est de même pour toutes les autres composantes. Ces dernières sont considérées représentatives des anomalies ponctuelles de mesures.

Figure 5

Projection des variables dans les plans C1 et C2

Projection of the variables in the C1 and C2 spaces

Figure 6

Cartographie de la projection des variables sur la deuxième composante C2 de la zone d’étude

Mapping of the projection of variables on the second component C2 in the study area

La projection des observations sur la composante C1 (Figure 7a) montre que le régime moyen est de type simple, avec un maximum en mars qui est associé aux fortes précipitations du printemps et un minimum en août qui est atteint pendant la sécheresse estivale. La projection des observations sur la deuxième composante montre un régime de type complexe et met en évidence la particularité des stations qui sont corrélées positivement avec cette composante. Ces dernières sont caractérisées par de forts débits au mois de septembre (Figure 7b). Afin de répondre à l’objectif principal fixé au préalable, qui était la régionalisation des apports moyens mensuels, on va procéder à une analyse de chaque groupe séparément.

Figure 7

Projection des observations a) sur la première composante C1 et b) sur la deuxième composante C2 de la zone d’étude

Projection of the observations a) on the first component C1 and b) on the second component C2 in the study area

4.1 Analyse en composantes principales sur le groupe Nord

La même procédure a été réalisée sur le groupe Nord qui est composé de 29 stations. En effet, toutes les stations sont corrélées positivement avec la première composante notée C1N (N : Nord). Cette dernière explique à elle seule 90,4 % de variance alors que les autres composantes n’expliquent qu’une faible part de variance (Figure 8). Avec 3,3 % de variance expliquée, la cartographie de la composante C2N ne présente aucune structure spatiale nette. La projection des observations sur la composante C1N a mis en évidence un régime hydrologique de type simple (Figure 9) similaire à celui déjà illustré dans le cas de l’application de l’ACP sur toute la zone d’étude. La seule différence est que le maximum est atteint en février au lieu de mars.

Figure 8

Représentation de la variance expliquée et cumulée des résultats de l’ACP sur le groupe Nord

Representation of the explained and cumulative variance of the results of the PCA on the northern group

Figure 9

Projection des observations sur la première composante C1N du groupe Nord

Projection of the observations on the first component C1N of the northern group

4.2 Analyse en composantes principales sur le groupe Sud

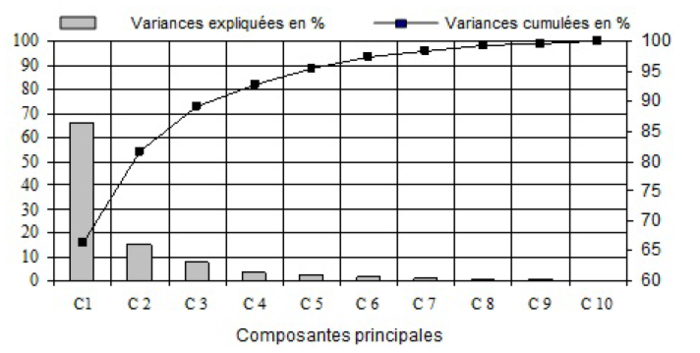
L’analyse en composantes principales appliquée au groupe Sud, dont le nombre de stations est de 22, montre que la première composante notée C1S (S : Sud) explique 66,3 % de variance (Figure 10). De même, toutes les stations sont corrélées positivement avec cette composante. Par rapport aux autres résultats, la composante C2S explique une plus grande partie que pour le groupe Nord, soit 15,2 % de la variance totale. Les trois premières composantes expliquent ensemble 89,1 % de variance.

Figure 10

Représentation de la variance expliquée et cumulée de l’analyse de l’ACP sur le groupe Sud

Representation of the explained and cumulative variance of the results of the PCA on the southern group

La cartographie de la composante C2S (Figure 11) montre des stations qui sont corrélées positivement, et d’autres qui le sont négativement avec cette composante. La répartition spatiale de ces dernières est hétérogène. En effet, en dehors du bassin versant 16, dont toutes les stations sont corrélées négativement et les bassins versants 05 et 06, dont toutes les stations sont corrélées positivement, les autres stations sont réparties à travers différents bassins. Ceci peut s’expliquer par une succession de cas particuliers qui sont liés à la rivière drainant le bassin ou sous-bassin versant. Les types de régimes ainsi mis en évidence sont de types mixte et complexe. En effet, les stations des bassins versants 16, 01, 15, 10 et 09 sont caractérisées par un régime mixte, alors que celles des bassins versants 05, 06 et 07 sont de type complexe. Contrairement aux deux cas précédents, la projection des observations sur la composante C1S montre un régime de type mixte avec deux minima, soit en août et novembre et deux maxima, soit en mars et septembre (Figure 12a). Cette figure montre deux périodes, une hivernale qui s’étend de janvier à mai et une estivale, qui commence en juin et se poursuit jusqu’en décembre. La projection des observations sur la deuxième composante montre la particularité des stations qui sont corrélées positivement avec cette composante. Ces dernières sont caractérisées par de forts débits au mois de septembre (Figure 12b). Ceci peut s’expliquer par les fortes précipitations qui tombent sous forme d’orages violents pendant ce mois.

Figure 11

Cartographie de la projection des variables sur la deuxième composante C2S du groupe Sud

Mapping of the projection of variables on the second component C2S of the southern group

Figure 12

Projection des observations a) sur la première composante C1S et b) sur la deuxième composante C2S du groupe Sud

Projection of the observations a) on the first component C1S and b) on the second component C2S of the southern group

D’après les résultats obtenus pour les trois groupes, on s’aperçoit qu’il existe une forte corrélation entre les variables d’origine. Le calcul du coefficient de corrélation entre certaines stations issues du même groupe a montré des coefficients de 0,99. Le calcul du coefficient moyen entre toutes les stations est de 0,89.

4.3 Application de la classification par les composantes principales dynamiques (CPD)

Dans une première phase d’analyse, les 51 stations hydrométriques ont été classées dix fois en deux groupes. La figure 13 présente le nombre de fois où deux stations ont été classées dans des groupes différents. Les plages de zéros, centrées sur la diagonale, constituent des noyaux durs. Ainsi, dix noyaux durs ont été obtenus. Il faut noter, parmi les dix regroupements, que beaucoup sont très proches. Certains de ces noyaux ne différent des autres que pour une ou deux itérations. Cette observation nous montre qu’il est possible d’associer des noyaux durs pour obtenir des régions hydrologiques homogènes.

Figure 13

Regroupement des stations en noyaux durs après une dizaine d’itérations

Grouping of the hard core stations after ten iterations

Sur les 51 stations, seules neuf stations n’appartiennent à aucun groupe. En fait, la quasi-totalité des stations se classe en trois groupes (distingués par des gammes de gris). Les résultats (Figure 13) montrent les trois groupes auxquels les stations ont été affectées après les différentes itérations. Ce regroupement se base sur les différents noyaux durs qui sont disposés en diagonale. Ces derniers sont les groupes qui constituent des régions hydrologiquement homogènes. À chacun d’eux on associe les différents groupes avec lesquels ce regroupement ne diffère que d’une seule itération. Il est à noter que les stations regroupées par deux ou trois ne peuvent être considérées comme des zones homogènes, mais plutôt comme une succession de cas particuliers liés à la rivière considérée. Il en est de même pour les stations qui n’ont été associées à aucun groupe dans cette classification. La figure 14 illustre la répartition spatiale des différents groupes mis en évidence. Nous avons gardé la courbe d’isocorrélation zéro, obtenue avec l’ACP appliquée sur toutes les stations de la région d’étude, afin de pouvoir comparer les résultats. On s’aperçoit que les stations qui sont situées au-dessus de cette ligne forment un groupe semblable à celui mis en évidence par la méthode ACP. Ces stations sont caractérisées par un régime hydrologique de type simple. Concernant le groupe 2, dont les stations sont localisées dans les bassins 01, 09, 15 et 16, il marque la transition entre le climat méditerranéen et semi-aride : il est caractérisé par un régime de type mixte. Le groupe 3, situé au sud, est constitué essentiellement de stations qui sont localisées dans les bassins versants 05, 06, 07 et 10. Ce groupe est caractérisé par un climat semi-aride. Le régime qui caractérise cette région est de type complexe. Les stations qui n’ont été associées à aucun groupe sont caractérisées par un régime de type mixte dont des minima et maxima sont différents d’une station à l’autre.

Figure 14

Représentation spatiale des stations appartenant aux trois groupes mis en évidence par l’analyse en composantes principales dynamiques

Spatial representation of the stations belonging to the three groups identified by the principal dynamic component analysis

5. Discussion

Dans le cadre de la gestion des ressources en eau, de la prévention du risque d’inondation et de la prédiction de la sécheresse, il est intéressant de connaître les variations saisonnières des régimes hydrologiques dans l’espace géographique et dans le temps. L’application des méthodes statistiques à l’évaluation des ressources en eau doit rendre compte de la complexité des variables à qualifier ou à quantifier en raison de leur variabilité spatio-temporelle. La bonne connaissance des caractéristiques physiques et climatiques d’une région donnée, qui conditionnent les débits mesurés à l’exutoire des bassins versants, permet de mieux cerner le comportement des régimes hydrologiques des cours d’eaux. De même, la meilleure analyse du comportement d’un bassin versant passe par la connaissance de l’interaction des différents paramètres qui conditionnent le devenir des pluies, depuis leur précipitation jusqu’à leur arrivée à l’exutoire de ce bassin versant. En Algérie du Nord, ces paramètres présentent de fortes variabilités spatiales pour certains d’entre eux (géologie, pentes, etc.) (TOUAZI, 2001) et spatio-temporelles pour d’autres (précipitations, températures, etc.) (ANRH, 1993; TOUAZI et LABORDE, 2000; TOUAZI, 2001; TOUAZI et al., 2004). C’est ainsi que la réponse d’un bassin versant à des sollicitations externes est différente d’une région à une autre. Ce comportement a une grande importance sur la répartition temporelle des débits et la nature du régime des rivières drainant ce bassin versant.

Des recherches sur l’évaluation des ressources en eau ont été réalisées par l’entremise de modèles pluie-débit à différentes échelles par BELDJOUDI et LARBI (1995), BELDJOUDI et OULD YAHIA (1997), KABOUYA (1990), TAÏBI (1990) et TOUAZI (2001). Ces modèles permettent de donner une estimation assez générale des ressources en eau. Pour une meilleure gestion de la ressource en eau et la mise en place d’infrastructures hydrauliques, il est nécessaire de connaître les variations saisonnières des cours d’eau et d’identifier ainsi des zones hydrologiquement homogènes. À cet effet, l’analyse des débits moyens mensuels de 51 stations hydrométriques a été réalisée par l’analyse en composantes principales et la classification par les composantes principales dynamiques.

Les résultats des deux méthodes montrent une certaine concordance. En effet, l’analyse en composantes principales a montré l’existence de deux groupes : un au nord et un autre au sud. Si le groupe Nord, délimité par la ligne d’isocorrélation zéro, caractérisé par un régime de type simple était bien défini, il n’en est pas de même pour le groupe Sud, dont les résultats de l’ACP ont montré une forte hétérogénéité spatiale. En effet, on y distingue des stations corrélées positivement et négativement avec la composante C2. Les stations corrélées négativement concernent essentiellement le bassin versamt 16 et les autres stations sont réparties à travers d’autres bassins versants : 01, 09, 15 et 16. Il en est de même pour les stations corrélées positivement avec la composante C2, où l’on retrouve les stations qui sont réparties à travers les bassins versants 05, 06, 07 et 10. Les régimes ainsi mis en évidence sont de types mixte et complexe. En effet, les stations des bassins versamts 01, 09, 10, 15 et 16 sont caractérisées par un régime mixte alors que celles des bassins versants 05, 06 et 07 sont de type complexe.

Concernant l’analyse en composantes principales dynamiques, on retrouve le groupe 1, dont les stations sont situées au-dessus de la ligne d’isocorrélation zéro, issue des résultats de l’ACP et qui sont caractérisées par un régime simple. Le groupe 2, qui est composé des stations des bassins versants 01, 09, 15 et 16, est caractérisé par un régime mixte et le groupe 3, qui est constitué des stations des bassins versants 05, 06 et 07, est caractérisé par un régime complexe. Ces résultats sont résumés dans le tableau 1.

Tableau 1

Résumé des résultats des deux méthodes (ACP et CPD)

Summary of results of the two methods (PCA and CPD)

Concernant les stations non classées, elles présentent des régimes qui diffèrent d’une station à une autre. Elles sont réparties à travers différents bassins versants. Ces résultats peuvent s’expliquer par le fait que la zone d’étude d’une superficie de 300 000 km² est caractérisée par une forte variabilité spatiale des paramètres climatiques (climat méditerranéen au nord et semi-aride au sud), qui peuvent influencer les débits ainsi que les paramètres physiques (géologie et relief). D’ailleurs, OBERLIN et HUBERT (1999) ont souligné que les progrès récents de l’analyse et de la modélisation des processus hydrologiques ont renforcé la prise de conscience de l’extrême complexité de ces processus, qui résultent de la variabilité dans le temps et dans l’espace des variables hydrologiques et des paramètres des milieux, comme de multiples interactions entre échelles de temps et d’espace, mais aussi entre phénomènes.

6. Conclusion et perspectives

Dans l’ensemble, la régionalisation des régimes hydrologiques obtenue par les deux méthodes semble concordante. Le contraste climatique de la zone d’étude, la variabilité spatiale et temporelle des précipitations et le contraste des paramètres physiques ont conditionné les régimes des cours d’eau. C’est ainsi que trois types de régimes hydrologiques (simple, mixte et complexe) ont été mis en évidence. De même, trois groupes hydrologiquement homogènes mis en évidence sont aussi la résultante de l’interaction de ces différents paramètres.

Afin de mesurer la qualité et la fiabilité des résultats, il sera intéressant de faire une analyse comparative avec d’autres méthodes, telles que la méthode Débit Durée Fréquence (QDF), la méthode Cluster (méthode qui permet de regrouper les individus proches en k-classes, en fonction de leur distance), la méthode d’analyse de corrélations canoniques, etc.

Dans cette étude, seuls les débits moyens mensuels ont été pris en considération, mais il serait intéressant de procéder à une classification des régimes hydrologiques qui tiendrait compte des paramètres qui influencent les débits, tels que la pluviométrie, la géologie, la surface et la pente du bassin versant. Ces résultats permettront de faire progresser l’état des connaissances des régimes hydrologiques en Algérie du Nord, où les études dans le domaine sont très restreintes.

Les auteurs remercient l’Agence Universitaire de la Francophonie pour avoir financé ce projet, dans le cadre d’une bourse d’excellence postdoctorale et le Centre d’études nordiques pour son soutien technique et logistique.