Évaluateurs évalués : évaluation diagnostique des compétences en évaluation des correcteurs d’une épreuve d’expression écrite à forts enjeux

Casanova, Dominique; Demeuse, Marc

doi:https://doi.org/10.7202/1040137ar

Introduction

L’évaluation diagnostique concerne en général les apprenants, dont il s’agit de mettre en lumière les forces et faiblesses pour mieux les accompagner dans leurs apprentissages. Cependant, une ambition similaire peut être portée auprès des évaluateurs eux-mêmes pour mieux les accompagner dans leur pratique et pour améliorer la qualité du dispositif d’évaluation. Cette ambition prend toute son importance dans le cas d’évaluations à grande échelle de compétences complexes (p. ex., les compétences d’expression écrite et d’expression orale) pour lesquelles plusieurs évaluateurs sont mobilisés et dont il faut assurer la fidélité des résultats, notamment quand elles présentent un enjeu important comme l’accès à un territoire ou à des études.

De nombreux paramètres interviennent dans l’acte d’évaluation (Eckes, 2011). Ils peuvent conduire à la présence d’une variance non désirée dans la distribution des scores et menacer la qualité du dispositif. Si certains de ces paramètres sont difficilement contrôlables en raison de leur caractère aléatoire (fatigue, intérêt pour le contenu de la copie, etc.), des caractéristiques potentiellement plus stables, comme la sévérité des correcteurs ou la difficulté relative des tâches, peuvent être mises en évidence par des expérimentations ad hoc ou par des analyses de données de production et prises en considération dans le dispositif d’évaluation afin de limiter l’erreur de mesure (Casanova & Demeuse, 2011).

Le courant docimologique a montré à de multiples reprises (Laugier & Weinberg, 1938 et Piéron, 1963, cités dans Cardinet, 1986) la variabilité des résultats constatés quand des échantillons identiques de copies étaient confiés à différents correcteurs. Des études récentes concernant le baccalauréat français (Merle, 1996 ; Suchaut, 2008) témoignent de la persistance de ce phénomène. De nombreuses recherches concernant la fidélité des dispositifs d’évaluation de l’expression écrite ou orale se sont concentrées sur les correcteurs, en raison de la subjectivité que comporte tout jugement humain et de leur sensibilité possible à des variables extérieures au contexte de l’évaluation (Engelhard, 1994 ; Leclercq, Nicaise & Demeuse, 2004 ; Artus & Demeuse, 2008). Les correcteurs constituent en effet un maillon essentiel du dispositif d’évaluation d’une épreuve d’expression et peuvent être sujets à des variations dans leurs jugements (manque de consistance interne) ou évaluer différemment un même ensemble de productions (différence de sévérité, sensibilité à des effets parasites). Cette variabilité des correcteurs justifie que leurs jugements fassent fréquemment l’objet d’analyse, que ce soit pour la mise en évidence de différents profils de correcteurs (McNamara & Adams, 1991), pour le suivi des écarts de sévérité (Eckes, 2005) ou pour le contrôle de la fidélité intraévaluateurs et interévaluateurs (Weigle, 1998).

Nos travaux de 2011 ont montré l’intérêt de tenir compte du niveau de sévérité des correcteurs pour constituer des jurys de correcteurs dits « équilibrés » afin de renforcer la fidélité d’une épreuve d’expression écrite. Cependant, un simple indice de sévérité ne saurait rendre compte de la diversité des profils d’évaluateurs et ce système de compensation peut s’avérer inopérant si, pour un niveau donné parmi les niveaux évalués, les correcteurs constituant le jury présentent une même tendance marquée à la sévérité alors que leur indice global diffère. Il ne fournit par ailleurs pas suffisamment d’informations pour les accompagner de façon pertinente.

Dans cet article, nous montrerons comment déterminer des profils de sévérité plus précis des correcteurs à partir d’une analyse des données d’évaluation pour renforcer la fidélité de l’épreuve d’expression écrite du Test d’évaluation de français (TEF) du Centre de langue française de la Chambre de commerce et d’industrie de région Paris Île-de-France (Noël-Jothy & Sampsonis, 2006) et pour améliorer l’accompagnement individuel des correcteurs en ciblant leurs particularités.

Deux méthodes ont été utilisées à cet effet, dans un contexte où chaque copie est corrigée indépendamment par deux correcteurs. La première méthode s’appuie sur les différences entre les scores attribués par les correcteurs à un ensemble de copies pour déterminer des indices rendant compte des profils. La seconde méthode mobilise un modèle multifacettes de Rasch (Linacre, 1989 ; Eckes, 2011). Les résultats des deux méthodes sont comparés, puis leurs avantages et inconvénients sont exposés.

Contexte : l’épreuve d’expression écrite du TEF

Déroulement

L’épreuve d’expression écrite est constituée de deux tâches standardisées indépendantes, qui placent les candidats dans deux situations de communication différentes. Chaque tâche comporte un sujet qui précise le type de production attendu et fournit des éléments de contexte (support déclencheur) permettant au candidat de mener à bien la tâche.

Elle est organisée collectivement dans une salle d’un centre agréé. La durée totale de la passation est de 1 heure, pendant laquelle les candidats répondent aux deux sujets. (La durée passée sur chaque tâche est laissée à la discrétion des candidats.) Dans la première situation, le candidat doit raconter une histoire en imaginant la fin d’un article de presse insolite, alors que, dans la seconde situation, le candidat doit exposer son point de vue et argumenter en réponse à une affirmation lue dans la presse.

À l’issue de la passation, le centre agréé remet les copies d’expression écrite au Centre de langue française, où sont évaluées toutes les copies.

Correction

La correction des copies de l’épreuve d’expression écrite est assurée par une équipe de correcteurs du Centre de langue française. Chaque copie est corrigée de manière indépendante par deux correcteurs différents, au moyen d’une grille d’évaluation analytique (voir section suivante). En cas d’écart important entre les résultats des deux correcteurs, le responsable des corrections peut solliciter une troisième correction et décider des deux corrections à retenir pour l’établissement des résultats[1].

Détermination du score et du niveau

Une grille unique d’évaluation est utilisée pour la correction des copies, quels que soient les sujets traités par les candidats pour la réalisation des deux tâches standardisées. Les productions sont évaluées par les correcteurs selon:

3 critères communicatifs propres à chacune des deux tâches;
6 critères linguistiques s’appliquant à l’ensemble du contenu des deux productions.

Pour chaque critère, des descripteurs illustrent chaque niveau (un niveau correspondant à l’absence de données observables pertinentes et les six niveaux principaux spécifiés dans le Cadre européen commun de référence pour les langues [CECR]) et sont gradués en un nombre variable d’échelons selon les niveaux. Cette échelle permet au correcteur de réduire la subjectivité de son jugement « en ajoutant à la simple impression une évaluation consciente en relation à des critères spécifiques», ce que le Cadre européen appelle le jugement guidé. Cette approche suppose, entre autres, « un ensemble de critères définis pour permettre la distinction entre les notes ou les différents résultats et une formation à l’application d’une norme » (Conseil de l’Europe, 2005, p. 143). L’annexe A présente l’échelle globale des niveaux communs de compétences en production écrite générale du CECR (Conseil de l’Europe, 2005), qui fournit une description de la compétence associée à chacun des niveaux A1 à C2.

Les notes finales relatives à chacun des critères (obtenues par moyennage) sont combinées, selon un système de pondération, pour aboutir à l’expression d’un score total sur une échelle allant de 0 à 450 points[2]. Des points de césure préétablis sur cette échelle déterminent, sur la base du score total, le niveau global de compétence du candidat, exprimé sur l’échelle de niveaux du CECR (de A1 à C2).

Management des correcteurs de l’épreuve d’expression écrite du TEF

La mise en place d’un nouveau système d’information pour le TEF offre des possibilités supplémentaires pour le suivi des correcteurs. Ce nouveau système permet en effet de disposer des évaluations de chacun des correcteurs des jurys au format numérique, données qui peuvent être exploitées pour la définition de différents profils d’évaluation. Cela a conduit le Centre de langue française à revoir son processus de management des correcteurs.

Sélection et formation initiale des correcteurs

Compte tenu des enjeux entourant le test (accès au territoire, à la citoyenneté, etc.), le Centre de langue française doit veiller à la performance de l’équipe de correcteurs. Par ailleurs, pour des raisons économiques, les nouveaux correcteurs doivent pouvoir être intégrés le plus rapidement possible au sein de l’équipe, ce qui laisse un temps limité au développement des compétences. C’est pourquoi le processus de sélection occupe une place centrale. Il s’agit de repérer des « talents » et de les amener rapidement à une activité opérationnelle en conditions réelles.

Processus de sélection

Le processus de sélection des correcteurs de l’épreuve d’expression écrite du TEF a pour objectif de choisir des professionnels de l’évaluation en français langue étrangère qui possèdent des compétences didactiques, pédagogiques et interculturelles qui les rendent capables:

de connaître et d’utiliser adéquatement le référentiel de niveaux de compétence du TEF et le Cadre européen commun de référence pour les langues (CECR) ;
de connaître et d’utiliser adéquatement la grille d’évaluation de l’épreuve d’expression écrite du TEF ;
d’être conscient des critères parasites de l’évaluation ; et
d’apprécier une production écrite et de lui attribuer un niveau.

Le profil attendu est celui de spécialistes de l’enseignement du français langue étrangère possédant un diplôme reconnu dans ce domaine (Master) et au moins trois ans d’expérience de l’enseignement auprès d’un public varié (en niveaux et en contextes d’apprentissage).

Les candidats-correcteurs sont présélectionnés sur la base de leur curriculum vitae et se voient proposer un test de sélection en ligne. Le test consiste à évaluer quatre productions écrites de façon holistique (c.-à-d. attribuer un niveau global en regard de l’échelle des niveaux du CECR) et à justifier ces évaluations. Les productions sont représentatives des performances des candidats au TEF et ont fait au préalable l’objet d’un calibrage (évaluation par plusieurs correcteurs et arbitrage final par le responsable pédagogique du TEF). La sélection est effectuée au regard des niveaux de compétence attribués et de la pertinence des justifications.

Formation et intégration des nouveaux correcteurs

La formation des nouveaux correcteurs s’opère en deux temps : une séance de formation en présentiel, puis une séance de standardisation à distance. Une fois sélectionnés, les nouveaux correcteurs assistent d’abord à une demi-journée de formation pratique axée sur les échelles du CECR correspondant à cette épreuve et sur la grille d’évaluation du TEF. Cette formation les sensibilise aux biais de l’évaluation et leur permet de s’entraîner à évaluer des épreuves en bénéficiant de corrigés et de commentaires personnalisés. L’accent est également mis sur les enjeux liés aux contextes d’utilisation du TEF. L’objectif de cette formation est principalement de garantir une compréhension partagée du construit évalué et de la grille d’évaluation. À l’issue de cette formation, les nouveaux correcteurs se voient remettre le Guide du correcteur, qui détaille les procédures et fournit des conseils pour l’évaluation des différents critères.

Ils suivent ensuite une séance de standardisation, qui consiste à évaluer 12 copies selon la procédure suivante :

À l’issue de l’évaluation des six premières copies, leurs évaluations sont comparées aux évaluations calibrées du Centre de langue française. Ils se voient proposer une restitution personnalisée comprenant des grilles corrigées ainsi que des commentaires sur les copies évaluées. L’accent est mis sur les écarts d’évaluation constatés.
À l’issue de l’évaluation des six copies suivantes, si leurs évaluations sont conformes, ils pourront intégrer le groupe de correcteurs. Au contraire, si leurs évaluations comportent encore des écarts significatifs, ils ne se verront pas confier de corrections. Un entretien individuel leur est accordé afin de justifier cette décision et de fournir des conseils de remédiation. Ils pourront alors se présenter à une nouvelle séance de standardisation après un minimum de six mois.

Cette activité permet un nouveau filtre en n’intégrant dans le groupe de correcteurs que des personnes dont les évaluations sont a priori proches de celles du Centre de langue française, ce qui n’empêche pas la présence de différences de sévérité entre ces nouveaux correcteurs, mais leur impact devrait s’avérer limité.

Suivi des profils et accompagnement des correcteurs

Jusqu’à présent, l’accompagnement des correcteurs consistait en des activités collectives de standardisation et en des remédiations individuelles lorsque des écarts récurrents de notation étaient constatés. Pour limiter l’importance de la variation due aux correcteurs, il est en effet conseillé d’organiser régulièrement des séances de formation et de standardisation (Lumley & McNamara, 1995). à défaut de faire disparaître les différences de sévérité entre correcteurs (McNamara, 1996)[3], ces séances contribuent à l’amélioration de la consistance individuelle[4] et renforcent la validité des évaluations.

Les activités collectives, qui sont l’occasion de préciser le construit du test, ne ciblent cependant pas les difficultés propres à chaque correcteur et peuvent avoir parfois un effet déstabilisateur. Ainsi, un correcteur qui prend conscience, sur un échantillon limité, qu’il est plus sévère que la norme, sans pour autant déterminer précisément les critères ou les niveaux de performance concernés, pourra chercher à modifier globalement ses représentations des niveaux et à modifier, parfois seulement pour un temps, son profil d’évaluateur, ce qui pourra conduire à un manque de consistance de ses évaluations ou déséquilibrer les jurys auxquels il participera.

Objectifs du suivi des profils des correcteurs

Le suivi des profils des correcteurs s’inscrit dans le système de management de la qualité du dispositif d’évaluation, qui vise une amélioration continue de la validité et de la fidélité des évaluations. Nos travaux menés en 2011 ont montré que les différences de sévérité entre correcteurs pouvaient constituer une part importante de l’erreur de mesure et qu’une manière de réduire leur impact était de tenir compte de ces différences dans la stratégie d’appariement des correcteurs pour constituer des jurys dits « équilibrés ».

L’objectif premier du suivi des profils des correcteurs était donc, jusqu’à présent, de caractériser le niveau de sévérité de chacun des correcteurs (catégories Sévère, Généreux et Neutre) pour déterminer les jurys à favoriser[5] (paires de correcteurs dont le niveau de sévérité se compense ou paires de correcteurs de sévérité neutre). Cette catégorisation n’est toutefois pertinente que si les correcteurs font preuve de constance dans la sévérité avec laquelle ils évaluent les copies des candidats. Or, des fluctuations peuvent apparaître, soit de manière sporadique et apparemment aléatoire, soit de manière plus systématique en fonction de facteurs liés au dispositif d’évaluation (sévérité différentielle selon la tâche traitée ou les critères d’évaluation) ou au référentiel d’évaluation (sévérité variable selon les niveaux de performance).

Le dispositif de suivi du profil des correcteurs est donc en cours de révision pour collecter, au fil des corrections, des informations sur la consistance des évaluations et pour procéder à des remédiations individuelles.

Organisation du suivi

Lorsqu’un nouveau correcteur rejoint le groupe, un tableau de suivi personnalisé est créé. Les premières évaluations du correcteur sont suivies de près, notamment à l’occasion de leur comparaison avec les évaluations des autres correcteurs des jurys auxquels il participe. Des régulations individuelles ad hoc peuvent alors intervenir afin d’ajuster sa maîtrise du construit et de la grille d’évaluation. Elles sont mentionnées dans le tableau de suivi.

Un premier bilan des interventions du nouveau correcteur est réalisé sur la base de ses 30 premières corrections et son tableau de suivi est actualisé. D’une manière plus générale, ce tableau de suivi est mis à jour de façon trimestrielle pour l’ensemble des correcteurs sur la base des données de correction.

L’accompagnement individuel s’effectue sur la base des données traitées trimestriellement et du tableau de suivi. Un entretien est organisé avec chacun des correcteurs montrant une tendance particulièrement marquée à la sévérité ou à la générosité à un ou plusieurs endroits de l’échelle de niveaux ou montrant un manque de consistance manifeste dans ses évaluations.

Modèles de mesure pour le suivi des profils des correcteurs

Données de production

Description de l’échantillon

L’échantillon à notre disposition est constitué des corrections de 2561 copies de candidats ayant passé le test au cours du premier semestre de l’année 2015, chaque copie étant évaluée individuellement par deux correcteurs parmi un ensemble de 23. La corrélation entre ces deux séries de scores est de 0,825, tandis que l’estimation de l’erreur de mesure de la correction[6] (EMC) est de 32 points. (Les scores sont attribués sur une échelle allant de 0 à 450 points.) Chaque correcteur a corrigé plusieurs copies (entre 33 et 751) et a été associé en jury à plusieurs correcteurs (entre 3 et 17). Le brassage des jurys et le niveau d’activité sont importants pour disposer d’un jeu de données suffisamment interreliées dans les analyses de profils, qui s’appuient sur les différences entre correcteurs.

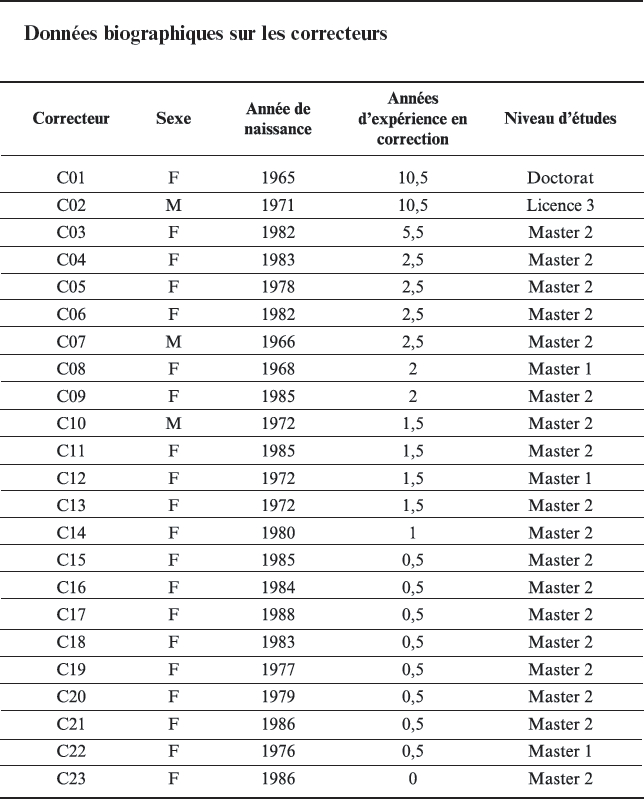
L’annexe B décrit les caractéristiques biographiques des correcteurs : 20 des 23 correcteurs sont des femmes. Ils sont d’âge varié : 6 correcteurs ont entre 25 et 30 ans ; 10 entre 31 et 40 ans ; et 7 entre 41 et 50 ans. Un correcteur est titulaire d’un doctorat, 18 correcteurs ont fait des études de niveau Master 2 ; 3 de niveau Master 1 ; et 1 de niveau licence 3. Concernant leur expérience en correction, 9 correcteurs ont moins d’une année d’expérience en correction pour le TEF ; 11 ont entre 1 et 3 années d’expérience ; et 3 correcteurs ont entre 5 et 11 années d’expérience.

Le tableau 1 présente la répartition des candidats par niveaux de compétence du CECR. La plupart des candidats passent l’épreuve d’expression écrite dans le cadre d’un projet d’immigration au Canada ou au Québec ou encore d’un projet d’études en France. La plupart du temps, le niveau minimal exigé correspond au B2, ce qui explique le nombre limité de copies de niveau inférieur.

Tableau 1

***Répartition des candidats à l’épreuve d’expression écrite du TEF sur l’échelle globale de niveaux de compétence du Cadre européen commun de référence (CECR)***

Structure factorielle de la grille de correction

Comme nous l’avons expliqué dans la partie Contexte, la grille d’évaluation comporte 12 critères :

3 critères communicatifs correspondant à la première tâche, que nous regrouperons sous la rubrique COMA ;
3 critères communicatifs correspondant à la seconde tâche, que nous regrouperons sous la rubrique COMB ; et
6 critères linguistiques s’appliquant à l’ensemble du contenu des deux productions, sous la rubrique LING.

Une analyse factorielle a été menée à partir des données de l’échantillon (scores moyennés) au moyen de la librairie psych du logiciel R. L’analyse des valeurs propres (voir Figure 1) montre la présence d’une dimension prépondérante, qui explique à elle seule 87 % de la variance.

Figure 1

***Diagramme en éboulis des valeurs propres***

Une analyse parallèle menée avec la librairie psych suggère de considérer une composante dans le cadre d’une analyse en composantes principales (ce qui légitime l’utilisation d’un score unique pour restituer la performance des candidats) et trois facteurs dans le cadre d’une analyse factorielle (ce qui était attendu compte tenu de l’organisation des critères de la grille).

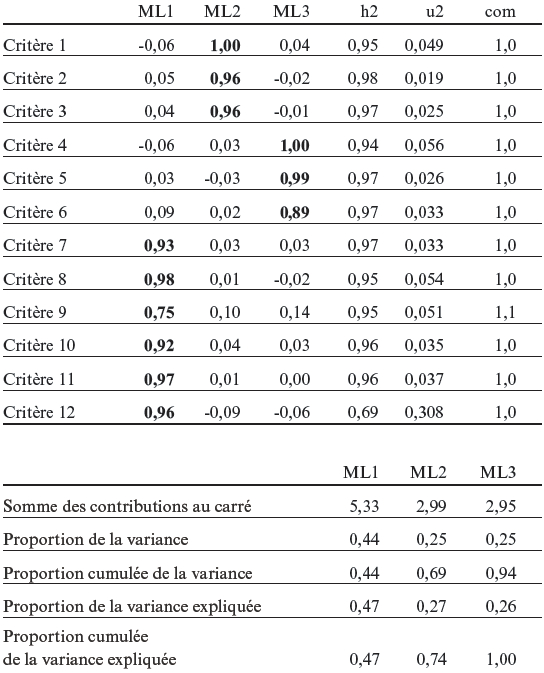
Une analyse factorielle pour une solution à trois facteurs, menée avec la méthode de maximum de vraisemblance et une rotation oblique (oblimin), permet de retrouver la structure de la grille : le premier facteur regroupe les 6 critères linguistiques ; le deuxième, les 3 critères communicatifs de la section A ; et le troisième, les 3 critères communicatifs de la section B. (Les résultats de cette analyse factorielle sont présentés dans l’annexe C.) Les corrélations entre les facteurs sont cependant très fortes (entre 0,85 et 0,89). Les saturations des critères sur les facteurs sont toutes supérieures à 0,89, à l’exception d’un critère linguistique pour lequel la saturation est de 0,75 sur le premier facteur. Ces trois facteurs permettent d’expliquer 94 % de la variance. Lorsque nous cherchons une solution à quatre facteurs, les saturations sur les trois premiers facteurs évoluent très peu et le plus grand poids constaté sur le quatrième facteur est de -0,14.

Au vu de ces résultats, il semble peu pertinent d’analyser le profil des correcteurs critère par critère (sauf peut-être pour le critère dont la saturation est la plus faible) et plus efficace de regrouper les critères selon la structure logique de la grille (COMA, COMB et LING).

Analyses basées sur la théorie classique des tests

La théorie classique des tests offre un cadre intéressant pour le traitement et l’analyse des données de production, qui conserve la richesse des données et qui permet de s’appuyer sur des sorties graphiques pour faciliter l’interprétation des résultats. La méthode décrite ci-après a été mise en oeuvre au moyen du logiciel R.

Tendance générale à la générosité

Le principe de cette méthode revient à considérer, pour chaque correcteur, les différences entre son évaluation et celle de l’autre correcteur du jury, sur l’ensemble des copies qu’il a traitées. La moyenne divisée par 2 de ces différences constitue un indice de la générosité du correcteur. Ainsi, pour un correcteur généreux, la moyenne des différences de scores, dont la significativité pourra être testée, devrait être positive. Toutefois, ces valeurs sont directement dépendantes de la constitution des jurys, qui doivent être suffisamment variés pour disposer de données croisées entre correcteurs.

Si un correcteur généreux se trouve régulièrement apparié avec un autre correcteur généreux, son indice risque d’être proche de 0 d’après cette moyenne des différences de scores. Il est donc nécessaire de procéder à une correction itérative des indices de générosité des correcteurs. Pour cela, à partir des indices déterminés lors de la dernière itération, il est nécessaire de calculer, pour chaque correcteur, la différence de moyenne entre les scores qu’il a attribués, ajustés au moyen de son indice de générosité (score ajusté = score – indice de générosité), et les scores ajustés des secondes corrections, ce qui aboutit à la détermination de nouveaux indices. Le cycle d’itération prend fin lorsque la variation de l’écart-type de l’ensemble des différences des scores ajustés devient inférieure à un critère de convergence (la meilleure solution est alors reportée, ainsi que la valeur de l’écart-type minimal). L’indice de générosité étant essentiellement déterminé par des moyennes portant sur le même échantillon (le nombre de copies corrigées par le correcteur), une erreur de mesure peut lui être associée (erreur type de la moyenne).

Si la tendance à la générosité des correcteurs était la seule variable interférant avec l’acte d’évaluation, alors les scores ajustés des deux correcteurs devraient être identiques, ce qui n’est en général pas le cas. La moyenne des différences entre les scores ajustés d’un correcteur donné et ceux des secondes corrections correspondantes est nulle, mais son écart-type constitue un indice de « l’imprévisibilité » (à défaut de trouver d’autres variables explicatives) du correcteur.

Prise en considération des dimensions de la grille d’évaluation

Un indice de générosité peut être exprimé pour chacune des dimensions de la grille d’évaluation en appliquant le même algorithme non plus à partir des scores attribués, mais de la moyenne des notes aux critères représentant chacune des dimensions. Cela permettra de déterminer, pour certains correcteurs, des tendances différentielles à la générosité selon la dimension considérée.

Prise en considération du niveau des performances

Rien ne garantit que les correcteurs aient une tendance uniforme à la générosité tout au long de l’échelle des scores. De même, en dépit de la formation et de l’accompagnement reçus, les correcteurs n’ont pas nécessairement tous la même représentation des degrés de performance attendus à un niveau donné du CECR.

Il semble donc opportun de déterminer des indices de générosité (sur l’ensemble de la compétence et sur chacune des dimensions de la grille) pour chacun des niveaux du CECR. Pour cela, nous procédons comme précédemment, mais en sélectionnant, pour chaque correcteur et chacun des niveaux du CECR, les copies dont la moyenne des scores des deux corrections (en réalité, la moyenne des scores ajustés à partir des indices de sévérité globale) correspond au niveau considéré. Ces indices peuvent également être déterminés pour chacune des dimensions de la grille d’évaluation, le profil d’un correcteur pouvant différer d’un critère à l’autre.

Une autre possibilité est de s’intéresser non pas aux niveaux mais aux frontières entre niveaux, les décisions étant en général prises en fonction de points de césure démarquant les niveaux de performance. Pour cela, nous procéderons de façon similaire en associant la moyenne des scores au point de césure le plus proche sur l’échelle des scores.

Analyses basées sur la théorie de réponse aux items

La théorie de réponse aux items fournit un autre moyen de décrire les profils des correcteurs. Les modèles multifacettes de Rasch permettent en effet d’analyser des données en tenant compte simultanément de différentes variables (les facettes) et d’interactions entre ces variables. Ils font partie de la famille des modèles de Rasch, fréquemment mise en oeuvre lors des analyses de réponse aux items.

Modèle de Rasch et ses extensions

Le modèle de Rasch (Bertrand & Blais, 2004) a été initialement développé pour des items dichotomiques et part du principe selon lequel la probabilité de bonne réponse d’un candidat à un item donné est fonction de son aptitude, qui est un trait latent (inobservé). La relation existant entre cette aptitude et la probabilité de bonne réponse, appelée fonction caractéristique de l’item, est une fonction monotone croissante pouvant être formulée ainsi :

où x_ni = le score du candidat n à l’item i (x_ni = 1 si la réponse est correcte, sinon 0), où Ɵ_n = l’aptitude du candidat et où β_i = la difficulté de l’item. (Cette difficulté est définie comme la valeur de l’aptitude pour laquelle un candidat a une probabilité de réussite de l’item égale à 50 %.) La fonction logit correspondante s’exprime simplement sous la forme :

Ce modèle a été étendu au cas des items polytomiques (items dont le score est attribué sur une échelle ordinale à plus de deux valeurs pour représenter des niveaux/catégories de réponse différents), notamment par Andrich (1978 ; le rating scale model [RSM]) et par Masters (1982 ; le partial credit model [PCM]).

Modèles multifacettes de Rasch

Les modèles multifacettes de Rasch sont une nouvelle extension introduite par Linacre (1989), qui propose d’introduire de nouveaux paramètres pour tenir compte de la variance introduite par différentes variables faisant partie du dispositif d’évaluation (les facettes). Considérons, comme dans notre étude, les facettes Correcteurs et Critères d’évaluation pour une épreuve d’expression écrite. Différents modèles peuvent alors être envisagés selon la pertinence de modéliser des interactions entre facettes et celle d’utiliser des paramètres seuils différents pour chacun des critères d’évaluation ou chacun des correcteurs. Le choix d’un modèle particulier s’appuie sur des informations préexistantes concernant l’interaction entre facettes et sur la qualité de l’ajustement global des données au modèle.

Des modèles multifacettes de Rasch ont été utilisés à plusieurs reprises dans le domaine de l’évaluation en langue pour analyser différentes caractéristiques des correcteurs (sévérité, exploitation de l’échelle de notation et différence d’application de l’échelle selon le critère d’évaluation ; McNamara & Adams, 1991), pour mesurer l’effet de la formation des correcteurs (Weigle, 1994) ou pour mettre en évidence l’impact des facettes Correcteurs et Sujets dans l’évaluation (Bachman, Lynch & Mason, 1995).

Utilisation dans le cadre du TEF

Dans le cas du TEF, les modèles multifacettes de Rasch ne sont pas applicables directement. Les résultats attribués par les correcteurs consistent en 12 notes exprimées sur une échelle de 0 à 20. Compte tenu du fait que le calibrage des données au moyen d’un modèle multifacettes de Rasch nécessite que chacune des valeurs doive être observée au moins une fois pour chacun des critères considérés et pour chacun des correcteurs (pour modéliser correctement l’interaction entre facettes), il est nécessaire de réduire l’information en limitant le nombre de catégories de scores sur l’échelle de notation. En effet, il est rare de disposer d’une observation pour chacun des 21 échelons de notation pour chaque couple (Critère, Correcteur). De surcroît, le nombre de catégories considérées a un impact direct sur le nombre de paramètres qu’il sera nécessaire d’estimer. Le choix a donc été fait de considérer une catégorie par niveau observable pour chacun des correcteurs. (Compte tenu de la répartition par niveau des candidats de l’échantillon, quatre catégories sont considérées, correspondant aux niveaux <B2, B2, C1 et C2.)

Un autre problème tient aux fortes corrélations entre les notes des différents critères, qui évaluent une même copie. Cela contrevient à la contrainte d’indépendance locale des items que réclame le modèle de Rasch. La réduction à trois « supercritères » sur la base des résultats de l’analyse factorielle permet de limiter les corrélations entre critères en dessous de 0,9 ainsi que le nombre de paramètres à estimer. Le score associé à chacun de ces supercritères est déterminé en considérant la moyenne des notes des critères portant sur une même dimension, puis le « niveau » correspondant.

Le modèle utilisé pour la détermination des profils de correction (modèle 1) est le suivant:

où P_nijk = la probabilité que le correcteur j situe le candidat n dans la catégorie k pour le critère i, où P_nik-1= celle qu’il le situe dans la catégorie k-1, où Ɵ_n = l’aptitude du candidat n, où β_i = la difficulté du critère i, où γ_j = la sévérité du correcteur j, où φ_ij = l’interaction entre le critère i et le correcteur j, et où τ_ijk = le paramètre seuil représentant la difficulté relative de transition de la catégorie k-1 à la catégorie k pour le critère i quand la copie est évaluée par le correcteur j.

Les analyses ont été menées au moyen du logiciel ACER ConQuest 4.0 (Adams, Wu & Wilson, 2015).

Résultats

Statistiques générales

La première méthode a été appliquée à partir des données non transformées afin d’exploiter tout leur potentiel. Toutefois, pour faciliter la comparaison avec les résultats de la seconde méthode, ce sont les indices autour des points de césure (et non les indices par niveau) qui ont été calculés pour la détermination d’un profil détaillé. Le critère de convergence choisi pour sa mise en oeuvre était d’arrêter les itérations lorsque la diminution de l’écart-type de la différence des scores ajustés devenait inférieure à 0,01.

Pour le calcul des indices globaux (sans prise en considération du niveau de performance des copies), il y a eu 6 itérations. La moyenne initiale de l’écart-type des différences des scores était de 45,106 lors de la 1re itération, et celle des scores ajustés était de 40,493 lors de la 5e itération et de 40,491 lors de la 6e itération. Ce sont donc les indices de la 5e itération qui ont été retenus. Sept itérations ont été nécessaires pour le calcul des indices par point de césure, et l’écart-type des différences des scores à l’issue de la 6e itération était de 34,694 points.

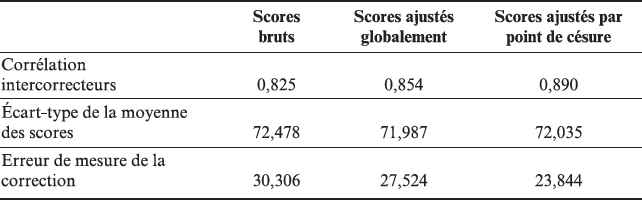
Ces résultats donnent une première information sur l’amélioration de la fidélité des résultats attendue en tenant compte des profils des évaluateurs pour l’expression de scores ajustés. Une démarche plus classique consiste à calculer la corrélation entre les scores ajustés, à la comparer à celle entre les scores initiaux et à estimer les erreurs types de correction correspondantes (voir Tableau 2).

Tableau 2

Comparaison de la fidélité et de l’erreur type de correction sur la base des scores bruts, des scores ajustés en tenant compte de la générosité globale et des scores ajustés en tenant compte de la générosité aux points de césure

Nous constatons que la prise en compte des profils détaillés devrait permettre d’améliorer sensiblement la fidélité des résultats, pour peu que les correcteurs montrent une stabilité dans leur profil puisqu’en pratique ce seront les profils établis pour les correcteurs à la date de la dernière estimation des indices de générosité (calculés sur la base d’un échantillon différent) qui seront pris en considération.

La mise en oeuvre du modèle multifacettes de Rasch avec ConQuest a nécessité, pour le respect des critères de convergence, de relancer plusieurs fois le fichier de commande, en prenant comme données d’entrée pour la N+1^ième tentative les matrices résultant de la meilleure solution de la N^ième tentative. L’information sur l’ajustement global des données au modèle est donnée sous la forme d’une déviance (log-vraisemblance), d’une valeur de 26 295 pour 207 paramètres estimés. Des statistiques d’ajustement (infit et outfit) sont également déterminées pour chacun des paramètres du modèle.

Compte tenu du modèle utilisé dans les traitements multifacettes de Rasch, lorsque les paramètres des correcteurs ou des critères seront positifs, cela traduira une sévérité des correcteurs ou une difficulté des items supérieure.

Difficulté relative des critères d’évaluation

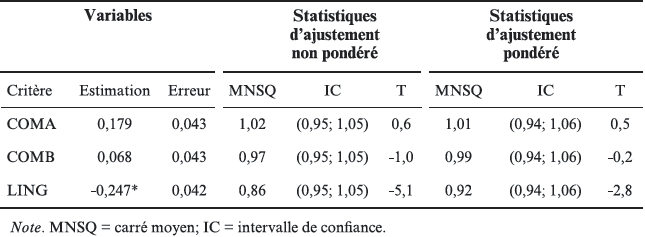
Le tableau 3 présente les estimations par le modèle multifacettes de Rasch des paramètres de difficulté des critères d’évaluation et les statistiques d’ajustement correspondantes (paramètres β_i de l’équation 5).

Tableau 3

***Estimation de la difficulté relative moyenne des supercritères d’évaluation correspondant aux dimensions principales de la grille d’évaluation (COMA, COMB et LING)***

Ces estimations sont en cohérence avec les moyennes pouvant être établies à partir des notes brutes en les regroupant par dimension (COMA, COMB et LING), qui sont respectivement de 14,99, de 15,12 et de 15,31 points. Le premier critère est en effet en moyenne plus sévèrement noté que le deuxième, lui-même plus sévèrement noté que le troisième.

Les statistiques d’ajustement (infit et outfit) sont plutôt satisfaisantes (carrés moyens [MNSQ] proches de 1), même si elles sortent de l’intervalle de confiance pour le critère LING. En effet, selon Linacre (2012), des valeurs du carré moyen comprises entre 0,5 et 1,5 sont acceptables pour que la mesure soit productive. C’est là une des caractéristiques de la méthode basée sur la théorie de réponse aux items : compte tenu du modèle sous-jacent, la confiance dans les résultats obtenus sera d’autant plus grande que les données des évaluations s’ajusteront au modèle proposé.

Comparaison des profils des correcteurs

Sévérité globale

L’annexe D présente les indices de sévérité globale estimés selon les différentes méthodes. Afin que l’interprétation des indices soit similaire pour chacune des méthodes, l’indice de générosité générale a été transformé en un indice de sévérité (changement de signe) et rapporté à la plus petite différence de scores entre deux points de césure consécutifs sur l’échelle de scores du TEF, soit 66 points. Les estimations des paramètres du modèle multifacettes de Rasch (paramètres γ_j de l’équation 5) ont pour leur part été rapportées à la plus petite différence entre les estimations de seuils du modèle, soit la valeur 3,33. Ainsi, un correcteur dont l’indice serait supérieur à 1 aurait en moyenne tendance à attribuer l’équivalent d’un niveau de moins à ses copies que la moyenne des correcteurs ou que le correcteur de référence (selon la méthode utilisée pour centrer les indices).

La corrélation entre les deux séries d’indices est élevée (0,908), voire très élevée (0,952) s’il est fait abstraction du correcteur C3[7]. Cette différence (pour un correcteur) tient à ce que, pour le calcul de l’indice global de sévérité, le modèle classique ne considère pas le niveau de la copie et évalue indépendamment la sévérité par critère, alors que le modèle multifacettes de Rasch génère, pour un correcteur dans une même analyse, un indice global de sévérité, une sévérité différentielle pour chacun des critères et une sévérité différentielle pour chacun des seuils par critère. Une analyse multifacettes de Rasch ne tenant pas compte des interactions entre facettes conduit à des indices de sévérité très proches de ceux de la méthode classique (0,950) et il n’y a pas de correcteur qui se distingue[8].

Une autre différence concerne l’écart-type de la distribution des indices de sévérité et, donc, l’appréciation du niveau de sévérité d’un correcteur. Cet écart-type est plus important avec le modèle multifacettes de Rasch (avec ou sans interactions) qu’avec la méthode classique. Cela tient probablement au fait que le modèle multifacettes de Rasch construit sa propre échelle de mesure (sur laquelle il peut fournir une estimation de la compétence des candidats), alors que la méthode classique se réfère à l’échelle prédéterminée du TEF. Ainsi, le rapport de l’écart-type des estimations Rasch des individus (4,04) par la plus petite différence entre les estimations de seuils du modèle (3,32) est supérieur au rapport de l’écart-type des scores moyens des copies (72,48 points) par la plus petite différence de scores entre deux points de césure consécutifs sur l’échelle de scores du TEF (66 points). L’utilisation du modèle multifacettes de Rasch pose donc davantage de difficultés d’interprétation de la valeur des indices de sévérité et risque de conduire à juger comme trop généreux ou trop sévères des correcteurs dont les évaluations sont en moyenne conformes à un critère d’appréciation (comme le fait qu’en moyenne ils attribuent moins que l’équivalent d’un quart de niveau en plus ou en moins à une copie que ne le ferait un évaluateur de référence ou la moyenne des évaluateurs).

En matière d’erreur type des estimations, les valeurs sont plus faibles (de l’ordre de la moitié) avec la méthode classique, et l’indice de consistance des évaluations déterminé par la méthode classique n’a qu’une relation modérée avec les valeurs d’infit et d’outfit des paramètres du modèle multifacettes de Rasch. (Les corrélations respectives sont de 0,610 et 0,571 lorsque les interactions entre facettes sont modélisées, sinon elles sont de 0,740 et 0,757.) Cela n’est guère surprenant étant donné la différence des méthodes de calcul. Lors d’une analyse avec le modèle multifacettes de Rasch en tenant compte des interactions entre facettes, seul 1 correcteur (C1) a une valeur d’infit en dehors de l’intervalle [0,5 ; 1,5] et ils sont 3 à avoir un outfit supérieur à 1,5. Les valeurs sont cependant inférieures à 1,6 et, selon Linacre (2012), des paramètres dont les valeurs du carré moyen sont comprises entre 1,5 et 2 ne sont pas productifs pour la construction de la mesure, mais ne la dégradent pas. Les ajustements sont moins satisfaisants en l’absence de modélisation des interactions entre facettes, avec 6 valeurs d’infit et 8 valeurs d’outfit comprises entre 1,5 et 2, ce qui montre les limites d’une telle modélisation.

Sévérité moyenne par critère

Pour comparer les indices de sévérité par critère établis selon la méthode classique aux résultats du modèle multifacettes de Rasch, il faut les comparer à la somme β_i+ γ_j+ φ_ij des paramètres de l’équation 5. Le tableau 4 présente les corrélations entre ces séries d’indices de sévérité pour chacun des critères considérés, avec et sans prise en considération du correcteur C3, qui constitue un point extrême repérable par une analyse graphique des indices de sévérité du critère COMB.

Tableau 4

***Concordance entre les indices de sévérité par critère***

La différence d’estimation de la sévérité du correcteur C3 et les problèmes d’ajustement éprouvés s’expliquent en analysant les paramètres τ_ijk (cf. formule 3) d’interaction entre les facettes croisées Correcteurs, Critères et Seuils du modèle multifacettes de Rasch (paramètres de l’équation 5). En effet, il n’y a pas d’estimation du paramètre représentant la difficulté relative de transition de la catégorie 2 à la catégorie 3 pour le critère COMB avec prise en considération du correcteur C3. Cela tient au fait que le correcteur C3 n’a jamais attribué le niveau C2 pour le critère COMB aux copies de l’échantillon qu’il a corrigées. Comme le modèle multifacettes de Rasch fixe la moyenne des seuils à 0, l’absence du troisième seuil pour la compétence COMB s’est répercutée sur le paramètre d’interaction entre C3 et COMB et, dans une moindre mesure, sur le paramètre de sévérité du correcteur. Comme le modèle multifacettes de Rasch fixe à 0, pour chaque critère, la moyenne des paramètres d’interaction Correcteurs X Critères, l’estimation erronée du paramètre d’interaction entre C3 et COMB se répercute sur les valeurs des autres paramètres d’interaction (et explique les corrélations plus faibles observées pour le critère COMB). Cela provoque un défaut d’ajustement pour certains d’entre eux : pour 6 paramètres sur 23, les valeurs d’infit se situent en dehors de l’intervalle [0,5 ; 1,5].

Sévérité par point de césure et selon les critères

La méthode classique permet de calculer un indice de sévérité pour chacun des points de césure (ou chacun des niveaux, selon l’information souhaitée), ainsi que la sévérité différentielle des correcteurs par critère, ce qui permet de disposer d’un profil détaillé des correcteurs. Telle qu’elle a été programmée, cette méthode ne cherche pas à trouver une explication optimale des données en calculant des indices de générosité par critère qui minimiseraient les différences entre correcteurs à chaque point de césure considéré, en ajustant dynamiquement la catégorie de rattachement des copies à partir du score ajusté de l’itération en cours. Elle s’attache à déterminer de bonnes approximations des indices de sévérité par point de césure en affectant une fois pour toutes une copie à une catégorie (p. ex., point de césure) à partir du score ajusté estimé d’après l’indice global de sévérité des correcteurs, puis à en déduire des indices par critère sur les bases des mêmes sous-échantillons.

Pour exprimer la sévérité différentielle des correcteurs selon les critères pour chacun des points de césure avec les résultats de la méthode multifacettes de Rasch, il faut combiner les indices de sévérité des correcteurs, de difficulté des critères, d’interaction entre correcteurs et critères, et d’interaction avec les différentes catégories de performance (paramètres β_i+ γ_j+ φ_ij+ τ_ijkde l’équation 5). Il est à noter toutefois que, pour le paramètre τ_ijk, dans 38 % des cas, le critère d’ajustement (carré moyen infit) est en dehors de l’intervalle [0,5 ; 1,5] et, dans 6 % des cas, il est supérieur à 2. Les estimations de ces paramètres, dont l’erreur type est en moyenne de 0,36, sont donc à considérer avec précaution. (En comparaison, la moyenne des erreurs types des indices de sévérité au moyen de la méthode classique est de 0,05.)

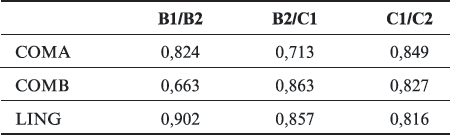
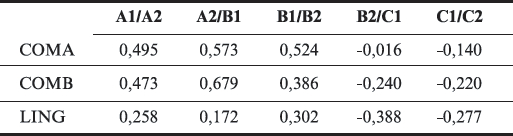
Le tableau 5 présente les corrélations entre les indices de sévérité obtenus selon les deux méthodes pour chacun des critères.

Tableau 5

***Concordance entre les indices de sévérité par critère aux différents points de césure***

Pour le modèle multifacettes de Rasch, l’expression d’un indice de sévérité moyen pour chacun des points de césure peut être dérivée en calculant la moyenne des indices par critère pour le point de césure considéré. La concordance avec les indices de sévérité établis au moyen de la méthode classique est alors élevée pour chacun des points de césure : elle est de 0,887 pour la césure B1/B2, de 0,858 pour la césure B2/C1 et de 0,954 pour la césure C1/C2.

Discussion

Choix de la méthode pour le suivi des profils

Deux méthodes ont été proposées pour rendre compte des profils des correcteurs au moyen d’indices synthétiques. Les deux méthodes donnent des résultats concordants jusqu’à un certain point : quand il s’agit de préciser la sévérité des correcteurs pour un (super)critère à un point donné de l’échelle (autour du point de césure sur l’échelle de score du TEF pour la méthode classique, en tenant compte de la valeur de seuil proposée pour le correcteur et le critère pour l’entrée dans la catégorie supérieure pour la méthode multifacettes de Rasch), quelques différences surgissent. Les indices d’ajustement des paramètres Rasch relatifs à ces seuils étant peu satisfaisants, cela montre peut-être les limites de son utilisation dans le cadre de l’objectif.

L’application du modèle multifacettes de Rasch pose par ailleurs un ensemble de contraintes sur les données. Afin de ne pas démultiplier les paramètres à évaluer, les données doivent être réduites avant traitement, et le modèle peut poser problème quand certaines informations sont manquantes, notamment si un niveau n’a jamais été attribué pour un critère par un correcteur. Enfin, l’information sur les différences de sévérité d’un correcteur selon le niveau de performance de la copie n’est disponible qu’en regard des points de césure, alors qu’il pourrait parfois être plus intéressant de savoir si le correcteur est sévère ou généreux en regard d’un niveau donné du CECR.

La méthode classique offre plus de souplesse : elle permet d’exploiter les notes détaillées, de considérer des données de correcteurs n’ayant pas évalué des copies de niveaux variés (ces correcteurs n’auront simplement pas d’estimation de sévérité pour les niveaux manquants) et donc de travailler avec des échantillons plus restreints. Elle permet également d’établir des profils d’évaluation tant par niveau qu’autour des points de césure. Couplée à une analyse graphique portant sur le même échantillon de données, elle simplifie l’interprétation des profils d’évaluation et leur communication aux correcteurs.

Profils des correcteurs

Le tableau 6 présente les indices de sévérité (et l’erreur type associée) pour chacun des points de césure des correcteurs de l’échantillon tels qu’ils ont été établis au moyen de la méthode classique. La valeur S. O. correspond aux cas où il n’y a pas d’observation disponible pour calculer cet indice. Les cellules du point de césure A1/A2 sont grisées, car aucun correcteur n’a corrigé plus de 9 copies dont le score moyen est inférieur au score médian du niveau A2.

Cette information peut être utilisée par exemple pour choisir le second correcteur d’un jury une fois une copie évaluée par un premier correcteur dont le profil est connu. Ainsi, si une copie s’est vu attribuer en première correction le niveau C1 par le correcteur C01, qui est réputé attribuer ce niveau avec générosité (sa valeur de sévérité au point de césure B2/C1 est de -0,653), il pourra être plus opportun de confier la seconde évaluation à C02 (indice de sévérité de 0,569 pour ce point de césure) qu’à un correcteur qui a lui aussi une tendance à attribuer le niveau C1 avec générosité.

Tableau 6

***Sévérité aux points de césure des correcteurs au moyen de la méthode classique***

Ces indices montrent clairement que la sévérité des correcteurs peut varier selon le niveau des copies qu’ils sont amenés à corriger. Ainsi, le correcteur C07, qui a un indice global de générosité proche de 0 (voir Annexe D), a une tendance générale à la sévérité pour les copies de niveau inférieur ou égal à B2, mais attribue généreusement les niveaux C1 ou C2.

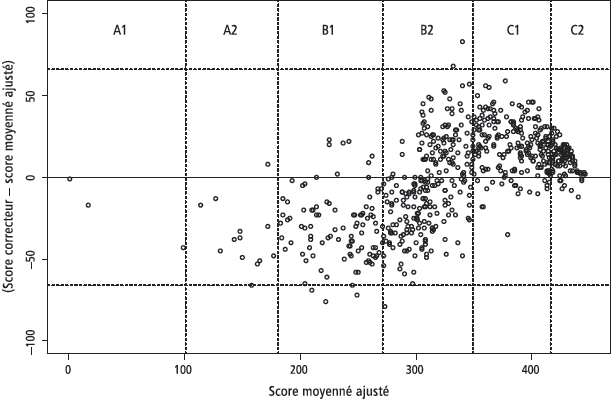
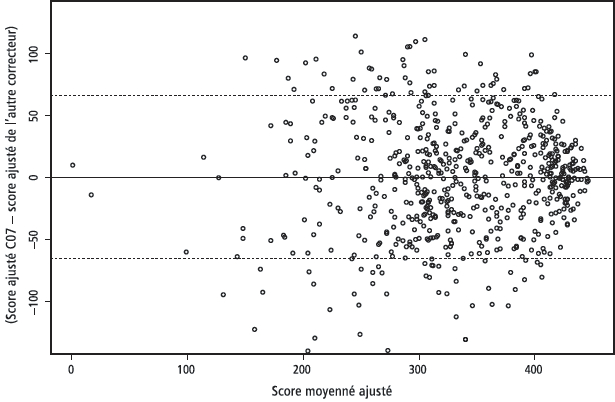
L’analyse graphique permet de vérifier cette tendance à partir des données d’évaluation détaillées et d’informer sur la régularité avec laquelle elle est appliquée. Dans la figure 2, chaque point représente une copie corrigée par le correcteur C07 avec, en abscisse, l’estimation du score du candidat (moyenne des scores ajustés des deux correcteurs du jury) et, en ordonnée, la différence entre le score attribué par C07 et cette estimation du score. Les lignes pointillées verticales délimitent les niveaux du CECR, affichés dans la partie supérieure du graphique. Les lignes pointillées horizontales indiquent les seuils de -66 et de +66 points. Pour la plupart des copies situées entre le niveau A1 et le milieu du B2, cette différence est négative, traduisant la sévérité du correcteur pour l’évaluation des copies, mais cela s’inverse nettement à partir de la fin du B2, où C07 se montre en effet plus généreux. Dans une dizaine de cas (sur 659), l’écart est d’environ un niveau.

Figure 2

***Écarts d’évaluation en fonction du score moyenné ajusté (N=659)***

L’analyse des indices de sévérité par critère donne des précisions sur le profil de l’évaluation. Ainsi, le tableau 7 montre une certaine régularité du correcteur C07, qui évalue tous les critères sévèrement avant le point de césure B2/C1 et généreusement après, et qui est systématiquement plus sévère pour les critères communicatifs que pour le critère linguistique.

Tableau 7

***Sévérité aux points de césure du correcteur C07 pour chacun des critères***

Consistance et stabilité des profils

Si la tendance à la sévérité des correcteurs était la seule variable externe intervenant dans l’évaluation des copies, alors les scores ajustés des deux correcteurs d’un jury seraient identiques. La figure 3 représente les écarts entre scores ajustés (en ordonnée) le long de l’échelle des scores pour le correcteur C07. Ces valeurs sont réparties autour de 0, car les ajustements prennent en compte les différences de sévérité, mais elles sont loin d’être nulles. Leur écart-type est de 36,5 points, alors que l’écart-type des différences entre scores bruts était de 47,5 points, ce qui montre que d’autres facteurs interviennent dans la notation.

La valeur de cet écart-type varie selon les correcteurs. Elle est par exemple de 16,7 pour C22. L’écart-type fournit donc une indication sur la prévisibilité des correcteurs, même s’il est imparfait puisqu’un correcteur parfaitement prédictible aurait un indice supérieur à 0 du fait de l’imprévisibilité des autres correcteurs des jurys auxquels il a participé.

Figure 3

***Écart entre scores ajustés (N=659)***

Au-delà de cette variabilité, la stabilité dans le temps des profils des correcteurs doit être questionnée. À cet effet, l’échantillon a été subdivisé en deux sous-échantillons de taille identique, sur la base de la date de passation de l’épreuve. Des profils ont été établis pour chacun des sous-échantillons et, pour chaque point de césure, les correcteurs ont été rangés dans une des cinq catégories suivantes, selon la valeur de leur indice de générosité pour le point de césure:

Très généreux si l’indice est inférieur à -0,5 ;
Généreux si l’indice est compris dans l’intervalle [-0,5 ; -0,25] ;
Neutre si l’indice est compris dans l’intervalle [-0,25 ; +0,25] ;
Sévère si l’indice est compris dans l’intervalle [+0,25 ; +0,5] ; et
Très sévère si l’indice est supérieur à 0,5.

Le tableau 8 présente, globalement et pour chacun des points de césure, la corrélation entre les indices obtenus, le nombre de cas où un correcteur a été affecté à la même catégorie, le nombre de cas où il a été affecté à deux catégories adjacentes (p. ex., Neutre pour le premier sous-échantillon et Généreux ou Sévère pour le second échantillon) et le nombre de cas où le changement de profil s’est avéré plus important. Le nombre de correcteurs pour lesquels un indice a pu être calculé pour chacun des deux sous-échantillons est cependant variable, certains correcteurs n’étant présents que dans l’un des sous-échantillons et les autres n’ayant pas corrigé de copies pour chacun des niveaux dans les deux sous-échantillons.

Tableau 8

***Évolution dans le temps de la sévérité des correcteurs***

Si les corrélations sont modérées pour chacun des points de césure considérés, une majorité de correcteurs est classée dans une catégorie identique pour chacun des deux sous-échantillons et les modifications importantes de profil sont rares. Il faut par ailleurs préciser que, dans de nombreux cas, les indices ont été calculés sur la base d’un nombre restreint de copies disponibles pour le correcteur au point de césure considéré, et que l’erreur type associée est parfois importante.

Conclusion

Cet article présente deux méthodes permettant de dresser un portrait individuel du comportement d’évaluation des correcteurs de l’épreuve d’expression écrite du Test d’évaluation de français, l’une basée sur la théorie classique des tests et l’autre, sur la théorie de réponse aux items. Les deux méthodes donnent en général des résultats très concordants, sauf pour les paramètres d’interaction entre l’ensemble des facettes, où la méthode classique ne cherche pas à déterminer des indices optimums et où les indices proposés par le modèle multifacettes de Rasch présentent une erreur type importante et des statistiques d’ajustement peu satisfaisantes. L’application de ce dernier modèle impose par ailleurs des contraintes sur les données d’entrée, ce qui nécessite notamment de procéder au préalable à une réduction de l’information. Dans ces conditions, l’utilisation de la méthode issue de la théorie classique, qui présente une plus grande souplesse d’utilisation et une plus grande simplicité d’interprétation, semble devoir être privilégiée.

Une des limites de l’étude menée tient à la taille des échantillons et au manque de copies de niveau A1 et A2, ce qui fait que certains paramètres de sévérité n’ont pas pu être déterminés pour certains correcteurs. De même, la période limitée sur laquelle elle a été conduite ne permet pas d’étudier réellement la stabilité des profils des évaluateurs. Une étude longitudinale à partir de l’ensemble des données recueillies depuis janvier 2015 devra être menée pour observer les évolutions des profils de correction.

Si les indices de sévérité par niveau présentent un intérêt pour l’accompagnement des correcteurs, il faut tenir compte également des différences qui peuvent apparaître selon les critères évalués. Se pose alors la question d’une catégorisation pertinente des correcteurs en profils-types, qui permettrait d’envisager des actions de remédiation propres à ces sous-groupes de correcteurs, compromis appréciable entre des actions communes à tous d’une portée limitée et des remédiations individuelles chronophages. Une étude complémentaire serait donc de procéder à une analyse de grappes (cluster analysis) des indices détaillés pour dégager des profils-types.

Par ailleurs, cette étude n’a pas tiré profit des informations biographiques à disposition concernant les correcteurs. Des analyses discriminantes permettraient de montrer si certaines de ces variables permettent de prédire l’appartenance d’un correcteur à un profil donné.

Enfin, si une catégorisation des évaluateurs sur la base de leur sévérité aux différents points de césure présente un intérêt pour la constitution de jurys « équilibrés » (qui permettent de neutraliser la sévérité relative des deux correcteurs au niveau de performance considéré), elle ne permet qu’une réduction appréciable mais limitée de l’erreur de mesure. D’autres facteurs sont susceptibles d’agir sur l’acte d’évaluation, qui restent à identifier.

Abstracts

Résumé

Abstract

Resumo

Article body