Abstracts
Résumé
Cet article décrit l’articulation de l’activité d’une enseignante avec celle de ses élèves lors d’une séance de résolution de problème de mathématiques à l’école primaire. Cette articulation est étudiée à l’aide d’une grille d’analyse inspirée de la sémiotique peircéenne et de la théorie du cours d’action. L’activité y est abordée, selon une approche d’anthropologie cognitive située, comme une action quotidienne, conduite en contexte par les élèves pour trouver la solution du problème et par l’enseignante pour les aider et valider ou invalider leurs propositions. La convergence ou la divergence des préoccupations des acteurs est analysée. Elle met en évidence tout à la fois la viabilité et l’efficacité relative de cette articulation.
Abstract
This article describes the verbal interaction between a primary school teacher and his students during a lesson in mathematics problem solving. This interaction is examined using an analytical grid developed from Peirce’s semiotics and the course of action theory. The activity is described according to an approach used in cognitive anthropology as a daily action, developed in this context by the students as they search for a solution to the problem and by the teacher who helps them and validates or refutes their propositions. The authors analyse the convergence or divergence of these participants’ preoccupations. The results show both the viability and the relative efficacy of this formulation.
Resumen
Este artículo describe la articulación de la actividad de una maestra con la de sus alumnos durante una sesión de resolución de problema en matemáticas en la escuela primaria. Se estudia esta articulación por medio de una red de análisis dictada por la semiótica peircena y de la teoría del “curso de acción”. Se emprende la actividad según un enfoque antropológico cognitivo situado, como una acción cotidiana, conducida en contexto, por los alumnos para encontrar la solución al problema, y para la maestra para ayudarles y validar o invalidar sus propuestas. Se analiza la convergencia o la divergencia de las preocupaciones de los actores. Hace resaltar a la vez la viabilidad y la eficacia relativa de esta articulación.
Article body
Les préconisations sont fortes en faveur d’un enseignement des mathématiques à l’école primaire à partir de « situations-problèmes » ou de démarches de « résolution de problèmes » (ministère de l’Éducation du Québec, 2001 ; ministère de l’Éducation nationale, 2002). Mais les résultats de cet enseignement sont contrastés : en France, une proportion importante des élèves obtient des scores médiocres aux tests de résolution des problèmes mathématiques, alors qu’au Canada, par exemple, ces scores sont sensiblement plus élevés (Organisation de coopération et de développement économiques, 2001). Les difficultés des élèves avaient déjà été constatées et expliquées par des recherches antérieures. Elles avaient mis en évidence l’effet des connaissances conceptuelles déficientes des enseignants (Romberg et Carpenter, 1986), des manques ou des insuffisances concernant les stratégies cognitives, computationnelles des élèves ou leurs bases de connaissances (Jordan et Montani, 1997 ; Verschaffel, De Corte et Vierstraete, 1999) ainsi que de la nature scolairement contextualisée des problèmes mathématiques (Lave, 1988 ; Nuñes, Schliemann et Carraher, 1993) sur ces difficultés.
Selon l’approche adoptée, faire des mathématiques est une pratique sociale située : l’activité mathématique scolaire se distingue de celle qui peut advenir au travail, à la maison ou dans la rue par les stratégies computationnelles utilisées, le rôle des artefacts ou l’utilisation de calculs mentaux (Lave, 1988, 1992 ; Nuñes, Schliemann et Carraher, 1993). Des normes culturelles construites dans l’action quotidienne, des plus générales aux plus typiques à chaque classe, caractérisent les mathématiques scolaires (Cobb, 2002 ; Gallego, Cole et The Laboratory of Comparative Human Cognition, 2001). L’activité des élèves est une participation à un processus de mathématisation, basée sur des négociations implicites qui contribuent à la fluctuation permanente de la situation. La résolution des problèmes suppose une coordination d’activités sémiologiques et culturelles : construire la signification de la situation et des données, abstraire des nombres et des opérations de cette situation, faire des opérations sur ces nombres, dégager des conclusions (Lave, 1992).
Cette recherche adopte l’approche de l’action située (Lave, 1988 ; Suchman, 1987) afin d’étudier la résolution d’un problème de mathématiques à l’école primaire comme une action quotidienne, sous un angle d’anthropologie cognitive située (Theureau, 1992). Elle vise à décrire in situ le niveau individuel des préoccupations et des actions, mais également le niveau collectif de l’articulation de l’activité de l’enseignante avec celle des élèves lors d’une « période ordinaire » de classe. Elle vise ainsi à mettre en évidence la dynamique collective de l’activité en classe et ses ressorts.
Présupposés sur l’activité humaine
L’activité humaine est située dynamiquement. Elle est indissociable de la situation matérielle, sociale et culturelle au sein de laquelle elle prend forme et doit, par conséquent, être étudiée in situ (Lave, 1988 ; Suchman, 1987). L’activité d’un acteur se développe dans une situation dont les éléments significatifs constituent des ressources que ce dernier utilise pour agir (Norman, 1993). Cette situation émerge de la dynamique des interactions qui sont à la fois sociales (l’acteur interagit avec les autres acteurs composant l’environnement) et contextualisées (l’acteur interagit avec l’espace et le monde des objets environnants). L’activité humaine ne peut donc être considérée en dehors de la situation de laquelle elle émerge. Issue d’une adaptation idiosyncrasique à cette situation, elle lui est spécifique. Réciproquement, les éléments de la situation sont des « ressources pour l’action » qu’offre l’environnement à l’acteur selon ses intentions (Norman, 1993).
Au niveau où nous l’appréhendons, l’activité humaine est cognitive. Lors de son activité, l’acteur manifeste, valide et construit à tout instant des connaissances, des modes d’action, des perceptions nouvelles (Theureau, 2004). De ce point de vue, il n’est pas d’activité sans apprentissage ni construction de connaissances (Rogoff et Lave, 1984 ; Varela, 1989). Analyser l’activité d’un acteur revient finalement à analyser sa mobilisation et/ou sa construction constante de significations et de connaissances au cours de celle-ci.
L’activité humaine est culturellement située. Action et culture sont envisagées au cours de pratiques réelles. Au sein des contextes d’action, les objets fabriqués par l’homme représentent une part importante de la culture et du social (Gallego et al., 2001). Ils guident l’action et assurent une économie cognitive, notamment en amplifiant l’efficience des fonctions mentales des acteurs (Cole et Griffin, 1980). Leur analyse fonctionnelle offre l’occasion de comprendre la nature de l’action qui s’accomplit à travers leur médiation. La présence des objets à l’école a pour effet de structurer l’action de l’enseignant et des élèves. De plus, des caractéristiques culturelles, des règles, des conventions, des pratiques sociales sont attachées aux objets ; ces derniers constituent, dans un environnement pédagogique, une concrétisation des intentions éducatives des enseignants (Gal-Petitfaux et Durand, 2001) et un véhicule de la culture scolaire (Gallego et al., 2001).
Analyse sémiologique du cours d’action
L’activité est analysée à partir de la théorie du cours d’action (Theureau, 2004) issue de la tradition ergonomique francophone (Pinsky, 1992 ; Theureau, 1992) et déjà exploitée dans des recherches sur l’enseignement (Durand, Ria et Flavier, 2002 ; Flavier, Bertone, Hauw et Durand, 2002 ; Gal-Petitfaux et Durand, 2001 ; Ria, Sève, Saury, Theureau et Durand, 2003). Ces travaux ont mis en évidence, au-delà des résultats empiriques, l’intérêt d’une étude à grain fin de l’action en contexte. Le cours d’action est l’activité d’un acteur déterminé, « significative pour ce dernier, c’est-à-dire montrable, racontable et commentable par lui à tout instant de son déroulement » (Theureau, 2004, p. 48).
À partir d’une adaptation de quelques propositions de Peirce (1978), l’activité est analysée comme un flux, décomposable en unités d’action (U) significatives pour l’acteur. Chacune de ces unités émerge de l’articulation dynamique de trois composantes qui constituent un signe : l’objet (O), le représentamen (R) et l’interprétant (I). L’objet (O) est une « totalité de possibles ouverte pour l’acteur du fait de son engagement dans la situation, qui est transformée à l’occasion de chaque signe » (Theureau, 2004, p. 139). Cette totalité, relativement indéterminée, est délimitée à chaque instant, dans la situation. Les préoccupations (P) constituent un élément de l’objet (O). Elles émergent de l’ensemble des possibles liés à l’histoire de l’acteur. Ces préoccupations sont floues et indéterminées, mais, en même temps, elles sont précisées dans l’action par le représentamen (R), en fonction de ce qui fait signe pour l’acteur. À chaque unité d’action (U) correspond alors une ou plusieurs préoccupations. Le représentamen (R) est une « actualité déterminée pour l’acteur » (Theureau, 2004, p. 139). Il correspond à ce qui fait signe pour l’acteur dans la situation et qui s’impose à lui. L’interprétant (I) est « la mise en oeuvre de types » (Theureau, 2004, p. 139). Il traduit l’intervention dans la cognition, ici et maintenant, d’éléments de généralité issus des cours d’action passés. Pour rendre compte de l’articulation de l’activité des acteurs, il faut rendre compte en premier lieu de l’activité individuelle. Cette articulation est décrite à partir de la convergence ou de la divergence des préoccupations. Les préoccupations convergent lorsqu’elles correspondent à des attentes proches. Par exemple, la préoccupation de l’enseignante d’aider les élèves à résoudre le problème converge avec celle des élèves à trouver la solution du problème. Les composantes du signe sont liées entre elles : chacune d’elles ne peut être décrite qu’à partir de l’identification des autres. Les préoccupations sont identifiées à partir de l’objet (O), du représentamen (R) et des signes précédents.
Ainsi, la théorie du cours d’action permet une analyse de l’activité individuelle accordant un crédit au point de vue des acteurs. Elle permet de décrire l’activité comme une totalité complexe et d’en extraire les préoccupations et les actions sans dénaturer cette totalité. Elle constitue un niveau de l’activité humaine considéré comme relativement autonome et qui contribue à sa compréhension. Elle permet également une description de l’activité collective prenant en considération le sens que les acteurs lui attribuent.
La recherche présentée dans cet article s’inscrit dans un programme plus vaste (nombre de participants, séquences de classe analysées, matières enseignées, etc.), mené en collaboration avec des enseignants débutants (Veyrunes, Bertone et Durand, 2003 ; Veyrunes, 2004). Le cas de Véronique a été sélectionné, car il a été considéré comme caractéristique de l’articulation de l’activité des acteurs lors des séances de mathématiques étudiées. En effet, des préoccupations et des types d’articulation proches ou identiques ont été repérés dans cinq des autres séances étudiées dans ce programme.
Méthode
Véronique, une enseignante débutante, s’est portée volontaire pour participer à cette recherche. Elle était une professeure des écoles dans sa troisième année d’enseignement. Elle avait suivi la formation à l’Institut Universitaire de Formation des Maîtres et enseignait dans une petite école à trois classes, en zone rurale, où elle était chargée de la classe de CM1-CM2 (« cours moyen 1 et 2 » : les deux derniers niveaux de l’enseignement primaire en France) qui regroupait dix-huit élèves (sept de CM1 et onze de CM2) âgés de dix à douze ans.
La séance de mathématiques étudiée portait sur la notion d’échelles et faisait suite à un travail sur le même thème, conduit à partir de cartes routières. L’articulation de l’activité de l’enseignante avec celle des élèves a été analysée pendant une durée de 37 minutes. Ce segment a été considéré d’un commun accord par l’enseignante et le chercheur principal comme significatif de l’ensemble de la séance.
Des données d’observation, d’autoconfrontation avec l’enseignante et d’entretien avec les élèves ont été recueillies. Les données d’observation et d’enregistrement des actions de l’enseignante et des élèves pendant la classe ont été recueillies à l’aide d’un caméscope muni d’un objectif grand angle (enregistrement en plan fixe large) couplé à un micro HF porté par l’enseignante et à un micro d’ambiance captant les verbalisations des élèves. Nous avons procédé ensuite à la collecte de données d’autoconfrontation lors d’entretiens consécutifs à la leçon : l’enseignante était confrontée à l’enregistrement de la leçon et invitée à commenter le déroulement de ses actions, en explicitant ce qu’elle faisait, ce à quoi elle pensait, ce qu’elle percevait, ce qu’elle ressentait. Ces données ont été recueillies lors d’entretiens au cours desquels l’enseignante et le chercheur visionnaient ensemble la cassette vidéo de la leçon. L’enseignante et le chercheur pouvaient arrêter le défilement de la bande afin de faciliter les descriptions et commentaires. Les relances du chercheur avaient pour but d’isoler un événement et d’inciter l’enseignante à décrire et à commenter ses actions tout en évitant les interprétations a posteriori ou les généralisations. Enfin, des entretiens ont été conduits avec quelques élèves, dans le but de connaître leurs préoccupations en classe et lors de la séance.
Le traitement a consisté en quatre étapes. Premièrement, une mise en vis-à-vis de l’enregistrement vidéo et des verbatim de l’autoconfrontation a été réalisée, afin de reconstruire la trame événementielle de l’action au niveau où elle est significative pour l’enseignante et pour les élèves. Deuxièmement, les unités d’action ont été identifiées, puis étiquetées à partir de la description des actions et des communications. Les composantes du signe (Objet, Représentamen, Interprétant) ont été documentées et les préoccupations ont été identifiées précisément (Tableau 1). Troisièmement, les unités d’action relatives au cours d’action de l’enseignante et celles relatives à celui des élèves ont été mises en vis-à-vis afin de décrire leur articulation. Quatrièmement, la convergence ou la divergence des unités d’action et des préoccupations ont été mises en évidence. Enfin, les quatre chercheurs se sont réunis pour lever les points de désaccord sur le découpage, l’étiquetage des unités d’action, la documentation des signes, l’articulation des préoccupations. Ils sont parvenus à un taux d’accord de 97 %.
Tableau 1
Exemple d’étiquetage d’une unité d’action de l’enseignante
Activité de l’enseignante
L’enseignante a formé des groupes homogènes de trois ou quatre élèves en fonction de l’estimation de leur niveau général en mathématiques. Les élèves devaient résoudre un problème portant sur la question des échelles, distribué sous forme de photocopies (Encadré 1). Les notations des échelles (1/45 et 1/20), bien que complexes pour des élèves à ce niveau de scolarité, avaient déjà été abordées lors d’une séance précédente portant sur les cartes routières.
L’enseignante attendait que les élèves comparent la longueur et la largeur des véhicules en fonction de l’échelle en multipliant les dimensions de chaque maquette par son échelle, puis qu’ils comparent les résultats obtenus. Pour la Maquette 1 : 9 x 45 = 405 et 3,2 x 45 = 144 ; pour la Maquette 2 : 22 x 20 = 440 et 7 x 20 = 140. Les élèves ont effectué de nombreux calculs avant de parvenir à la solution attendue par l’enseignante.
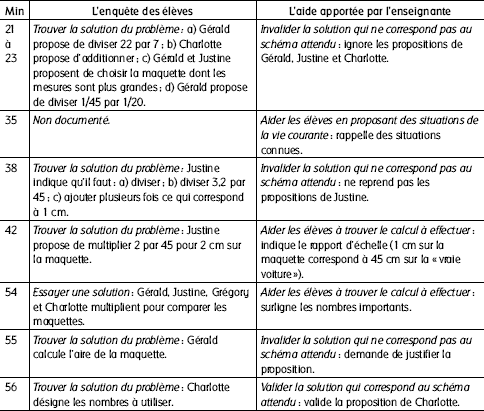
Les premières propositions des élèves du groupe composé de Gérald, Grégory, Justine et Charlotte[1] ont été invalidées par l’enseignante : à la minute 25, elle a invalidé une proposition de Gérald qui proposait de diviser les échelles entre elles. Puis l’enseignante a apporté une aide au groupe de Charlotte de la minute 35 à la minute 38. Elle considérait que ces élèves avaient besoin d’établir des liens entre cette situation et des éléments de leur vie en dehors de l’école : la voiture familiale, les modèles réduits de véhicules avec lesquels jouent les enfants et le travail effectué par les concepteurs de ces modèles réduits. Elle attendait que les élèves découvrent, à partir de cette notion de « réduction », l’opération à effectuer : « Je veux qu’ils comprennent que ce sera le même modèle, mais qu’il va falloir trouver quelque chose pour, justement… un calcul… » Ses préoccupations étaient : a) aider les élèves à comprendre le problème en imaginant une situation de la vie courante ; b) expliquer aux élèves qu’une maquette est une réduction d’un véhicule « grandeur nature » ; et c) aider les élèves à trouver le calcul à effectuer.
À la minute 38, l’enseignante a invalidé la proposition de Justine de diviser la mesure de la largeur de la première maquette par son échelle. Elle lui a demandé d’entourer d’autres données que 3,2 sur laquelle Justine semblait se focaliser. Dans la mesure où la proposition de Justine ne correspondait pas à ses attentes, elle l’a invalidée et lui a demandé implicitement de prendre en compte les autres données numériques. Ses préoccupations étaient : a) aider les élèves à trouver le calcul à effectuer ; b) invalider les propositions de Justine.
Comme dans deux groupes sur trois, les élèves ne trouvaient pas la solution, l’enseignante leur a donné des explications complémentaires (minute 42). Elle a illustré au tableau noir par des schémas les rapports d’échelles et le fait que 1 cm sur la maquette représentait 20 cm ou 45 cm, selon l’échelle, sur la voiture réelle (Tableau 2). Ses préoccupations étaient : a) aider les élèves à comprendre le problème en imaginant une situation de la vie courante ; b) aider les élèves à trouver le calcul à effectuer. L’enseignante était satisfaite de ce que disait Justine et validait implicitement sa réponse : avec un grand sourire, elle a exprimé sa satisfaction par des « Aaaaah ! ».
Quand elle est revenue près du groupe de Charlotte, à la minute 54, elle a repris les explications, car, selon elle, les élèves « faisaient fausse route » : ils étaient, en effet, en train de comparer les maquettes au lieu de comparer les véhicules « grandeur nature ». Elle a repris le texte du problème afin de les aider à repérer les données importantes en utilisant un marqueur fluorescent (« fluo ») (Tableau 3).
Tableau 2
Verbalisations en classe et lors de l’entretien d’autoconfrontation (min 54)
L’enseignante a utilisé le marqueur fluorescent pour faire repérer les données pertinentes aux élèves. En surlignant les dimensions des maquettes, elle rendait visibles et repérables, dans le corps du texte, les données essentielles. Mais elle attendait également que les élèves repèrent les relations entre les données. Ce repérage devait, selon elle, aider les élèves à identifier que la longueur et la largeur des deux maquettes étaient de même nature (ce sont des mesures) et qu’elles se distinguaient des données non surlignées qu’étaient les échelles (1/45 et 1/20). Elle voulait ainsi les guider vers les opérations qu’elle attendait. Ses préoccupations étaient : a) aider les élèves à établir les relations pertinentes entre les données ; b) aider les élèves à trouver le calcul à effectuer.
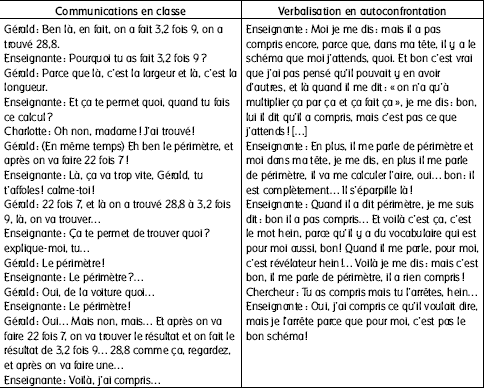
L’enseignante a été interrompue par Charlotte et Gérald, qui avançaient chacun une solution. La proposition de Gérald (Tableau 4) de calcul de ce qu’il appelait le « périmètre » de la voiture – et qui est en fait l’aire occupée par la maquette – a été immédiatement interprétée comme erronée par l’enseignante et invalidée, car elle ne correspondait pas au schéma de résolution attendu. Elle lui a demandé de justifier le calcul effectué avant de l’interroger sur le terme de « périmètre ». Elle a ensuite interrompu brusquement les explications de Gérald dans la mesure où elles ne permettaient pas d’approcher la solution. Ses préoccupations étaient : a) obliger Gérald à justifier sa proposition ; b) invalider la proposition de Gérald.
Tableau 3
Verbalisations en classe et lors de l’entretien d’autoconfrontation (min 55 à 56)
L’enseignante a donné ensuite la parole à Charlotte (Tableau 4). Après avoir rappelé la mesure de la longueur, celle-ci a montré successivement de la pointe de son stylo, directement sur le texte-problème, les nombres indiquant les mesures des maquettes et ceux indiquant les échelles. Elle a désigné successivement le Nombre 9 puis la notation de l’Échelle 1/45, ensuite le Nombre 3,2 et à nouveau 1/45, et de même pour l’autre maquette. Charlotte a accompagné ses gestes de déictiques successifs, indiquant qu’il fallait « faire ça et ça ». Après les avoir surlignées au marqueur fluorescent, l’enseignante attendait que Charlotte associe les mesures des maquettes avec leurs échelles. Elle attendait également la mise en oeuvre du schéma de résolution qu’elle avait conçu. Aussi, la validation de la proposition de Charlotte a-t-elle été directe. L’enseignante l’a interprétée en la validant dans un même mouvement par des « oui ! » successifs. L’enchaînement des gestes de Charlotte sur le texte-problème associé à son discours a été interprété comme une proposition de multiplication. Elle a considéré que Charlotte avait compris que, pour agrandir, il fallait multiplier. Du coup, la nécessité d’indiquer précisément l’opération à effectuer ne lui apparaissait plus indispensable. Sa préoccupation était : Valider la proposition de Charlotte.
Tableau 4
Verbalisations en classe et lors de l’entretien d’autoconfrontation (min 57)
Activité des élèves
Entre les minutes 21 et 25, un échange a eu lieu entre le groupe de Charlotte et l’enseignante. Gérald, Justine et Grégory avaient proposé de diviser 22 par 7. Gérald a abandonné rapidement cette proposition que l’enseignante ne relevait pas. Charlotte a alors proposé d’additionner, puis Gérald et Justine ont tenté de trouver directement une réponse dans le texte. Ils interprétaient tous les deux les mesures données, indépendamment de toute échelle, et considéraient que la voiture réelle la plus grande était celle qui correspondait à la seconde maquette dont les mesures étaient les plus grandes : « Elle, elle est plus petite, parce que : 9 cm et 3,2 cm. Et que elle, elle fait : 22 et 7 cm. » Enfin, Gérald a proposé de faire une autre division : il considérait les échelles comme des nombres décimaux qu’il divisait entre eux : « On n’a qu’à faire 1,45 divisé par 1,20. » Leurs préoccupations étaient : a) proposer des solutions d’addition, de division, de comparaison directe des mesures ; b) obtenir la validation de l’enseignante.
Entre les minutes 35 et 38, Gérald et Justine ont interprété ce que l’enseignante leur avait dit auparavant et tenté de trouver la solution (Tableau 5). Justine avait indiqué, à la demande de l’enseignante, que la mesure de 1 cm de la maquette correspondait à la mesure de 45 cm sur le véhicule grandeur nature. Elle a tenté en vain d’expliquer (minute 38) que ce rapport de 1 à 45 pouvait être ajouté autant de fois que nécessaire. Elle envisageait une solution additive : elle a indiqué qu’elle voulait ajouter ce qui correspondait à 1 cm sur la maquette. En effet, elle était guidée par l’explication précédente qu’elle ramenait au calcul additif suivant : « si 1 cm représente 45 cm, alors 2 cm représentent 45 cm + 45 cm ». Les préoccupations de Justine étaient : a) proposer la solution de l’addition réitérée ; b) obtenir la validation de l’enseignante.
Les solutions de l’addition et de la division ont alors été abandonnées par les élèves. À la minute 42, comme l’enseignante donnait des explications au tableau noir, Justine a indiqué qu’on calculait la correspondance entre une mesure de 2 cm sur une maquette à l’échelle 1/45 et sa mesure sur une vraie voiture en multipliant 45 par 2. Cette proposition a été validée par l’enseignante.
À la minute 54, l’enseignante est revenue près de ce groupe d’élèves. Lorsqu’elle a utilisé le marqueur fluorescent, Gérald a proposé immédiatement une solution. Il a multiplié entre elles la longueur et la largeur des maquettes, calculant ainsi l’aire occupée par la maquette. Il semblait interpréter le surlignage des données comme une mise en relation des nombres 3,2 et 9, puis 22 et 7 et non comme une relation de ces nombres vers les échelles. Aussi proposait-il de les multiplier entre eux. Il a poursuivi avec persévérance, malgré les demandes de l’enseignante et ses invalidations implicites, la recherche d’une solution, calculant l’aire occupée par chacune des maquettes. Il considérait probablement qu’il pouvait comparer les maquettes en comparant l’aire qu’elles occupaient.
Charlotte a ensuite obtenu la parole. Elle a montré les nombres du texte-problème de la pointe de son stylo en accompagnant ses gestes de déictiques successifs (« ça et ça »). Elle paraissait alors soucieuse de montrer les nombres qu’elle mettait en relation, sans éprouver la nécessité d’indiquer l’opération par laquelle elle établissait cette relation. Elle considérait que cette indication était suffisante et qu’elle était claire pour l’enseignante. Les préoccupations de ces élèves étaient : a) proposer une solution ; b) obtenir la validation de l’enseignante.
L’articulation des préoccupations
L’articulation de l’activité de l’enseignante avec celle des élèves est analysée au niveau des unités d’action et des préoccupations qui leur correspondent (Tableau 5).
Tableau 5
Articulation des préoccupations et des unités d’action de l’enseignante et des élèves
Les propositions et demandes de validation des élèves sont articulées avec les actions de l’enseignante : elles entraînent soit une validation ou une invalidation, soit l’apport d’aides qui sont suivies à leur tour de nouvelles propositions. Ces aides sont articulées de façon dynamique avec l’enquête menée par les élèves. Les propositions des élèves prennent en compte à la fois les validations et invalidations de l’enseignante, certaines des aides apportées et les propositions précédentes. Les propositions invalidées par l’enseignante ne sont pas reprises : les premières propositions portant sur l’addition et la division cèdent la place, après la minute 38, à des propositions portant sur la division. Cette dynamique conduit à la découverte de la solution du problème.
Discussion
Préoccupations de l’enseignante
L’analyse du cours d’action et des préoccupations dont l’enseignante fait état permet d’identifier deux grandes préoccupations : aider les élèves et valider leurs propositions.
L’aide apportée par l’enseignante est structurée par le texte-problème. Sa conception par l’enseignante a entraîné la mise en place d’une structure d’attente sous la forme de ce qu’elle appelle un « schéma » de résolution. Le choix de données numériques complexes empêche, pour des élèves de cet âge, de trouver la solution par un calcul mental, celui des échelles les contraint également à des calculs écrits. Le nombre des données incite les élèves à effectuer des choix difficiles de mise en relation des nombres. L’enseignante apporte une aide aux élèves en ce qui concerne le tri des données, la nature des relations à établir entre elles et les opérations à effectuer. Elle aide les élèves en fonction des indices topologiques du texte-problème (la place des nombres dans le texte-problème). Par exemple, lorsqu’elle surligne les mesures des maquettes, elle souhaite que les élèves remarquent non pas les nombres qu’elle surligne, mais les relations à établir avec ceux qu’elle n’a pas surlignés. Lorsque Justine propose de diviser 3,2 par 45, l’enseignante lui demande d’« [entourer] autre chose que 3,2 ». Enfin, le caractère décontextualisé du problème par rapport à la vie quotidienne des élèves contraint l’enseignante à les aider à comprendre la situation proposée en leur permettant d’établir des relations avec leur vie hors de l’école (minutes 35 à 38).
La validation est le processus par lequel une action est instituée et admise en fonction des normes et des règles plus ou moins explicites de la communauté (De Munck, 1999). Les validations sont fréquentes, dissymétriques, indirectes et implicites. La fréquence de la validation évite les temps morts. Nous avons observé neuf validations des propositions des élèves du groupe de Charlotte pendant le segment étudié aux minutes 25, 29, 36, 38, 42, 47, 54, 55 et 57. L’enseignante relance ainsi les élèves qui sont sur la bonne voie et qui attendent pour poursuivre. La fréquence des validations évite aux élèves de s’engager de façon durable dans des voies qui ne correspondraient pas à ce qu’elle attend. Elle entretient et guide à la fois l’activité des élèves. La validation et l’invalidation sont dissymétriques : la validation est rapide et directe, l’invalidation généralement indirecte et implicite. Lorsque les propositions des élèves sont interprétées par l’enseignante comme allant dans le sens attendu, elle les valide immédiatement (minutes 42, 47 et 57). Lorsque les propositions sont interprétées comme n’allant pas dans le sens attendu, elle les invalide de façon plus progressive et lente. Pour invalider, l’enseignante utilise des demandes successives de justification, des intonations dubitatives, des moues de perplexité que les élèves doivent interpréter comme une invalidation. Elle ignore également les propositions des élèves ou les presse de questions. La validation est souvent plus directe, mais peu explicite : elle passe par un sourire, une onomatopée, par une brève interjection (voilà !) ou un adverbe (oui !).
Préoccupations des élèves
L’analyse du cours d’action des élèves permet d’identifier la préoccupation : trouver la solution du problème. Cette recherche de la solution se traduit par une enquête de type pragmatique (Dewey, 1993) dont la progression est lente et complexe. Les élèves envisagent de nombreuses pistes, en abandonnent certaines, partent dans de mauvaises directions jusqu’à trouver la solution du problème. Ils utilisent tous les indices qui sont à leur disposition : des validations et des invalidations, les unes explicites, les autres implicites, des explications données par l’enseignante, les propositions d’élèves du groupe et celles d’élèves d’autres groupes, les données du texte-problème.
Dans un premier temps, ils considèrent que la réponse est contenue dans le texte-problème et que la voiture réelle la plus grande est celle dont on peut lire les plus grandes mesures. Cependant, cette solution est peu satisfaisante : pour les élèves, faire des mathématiques, c’est faire des opérations avec les nombres. L’enquête se poursuit alors par la recherche de l’opération à effectuer, des nombres à utiliser. Trois opérations sont envisagées : l’addition, la division et la multiplication. Celles-ci associent les nombres de diverses manières, y compris en divisant les deux échelles entre elles. Puis les élèves s’orientent vers la multiplication : les propositions portant sur l’addition ou sur la division ont été invalidées. Après la minute 38, toutes les propositions comportent des multiplications. L’enquête porte alors sur le choix des nombres à multiplier. Justine a indiqué à deux reprises qu’il fallait multiplier 45 par 2 pour trouver la mesure correspondant à 2 cm sur la maquette. Mais cette indication n’a pas suffi. Les élèves ne parviennent pas à déduire de cet énoncé qu’il faut ensuite multiplier 45 par 9, puis par 3,2. Leur raisonnement ne procède pas selon une logique hypothético-déductive, mais selon une démarche d’enquête. Ils retiennent certains indices (il faut multiplier des nombres), en éliminent certains (il ne faut ni additionner ni diviser) et en recherchent d’autres (quels nombres faut-il utiliser ?). Aussi, la proposition de Gérald (minute 54) ne doit-elle rien au hasard : il utilise la multiplication et associe des nombres pour calculer l’aire. Le surlignage des données l’incite à mettre ces nombres en relation. Les indices que sont le regroupement spatial et la nature des mesures (longueur et largeur) évoquent les leçons récentes sur les notions de périmètre et d’aire. Bien qu’il amalgame ces deux notions, sa proposition est cohérente à la fois avec les indices recueillis lors de l’enquête et avec ses connaissances. Lorsque Charlotte propose la solution attendue par l’enseignante, elle n’a pas à mentionner la multiplication. Les protagonistes ont construit collectivement l’idée qu’il faut multiplier. Il ne lui reste qu’à désigner sans erreur les nombres qu’il faut multiplier entre eux.
L’enquête se traduit également par les demandes fréquentes de validation adressées à l’enseignante qui circule parmi les élèves. La concurrence entre les groupes empêche les élèves de développer par écrit les solutions qu’ils proposent : celles-ci ne sont jamais suffisamment développées pour que les élèves parviennent à une véritable résolution du problème. Lorsqu’ils font état de leurs propositions, la validation est plus ou moins explicitement demandée. Les propositions se succèdent parfois très rapidement et s’apparentent à des sondes lancées en direction de l’enseignante et visant à recueillir des indices. Elles permettent de réduire peu à peu la complexité du problème et d’éliminer certaines propositions.
Coopération entre élèves
L’activité de recherche de la solution est collective et coopérative (Decortis, Noirfalise et Saudelli, 2000 ; Salembier et Zouinar, 2000). Pour ces auteurs, la coopération se définit selon deux axes, spatial et temporel. Les acteurs coopèrent quand ils sont engagés côte à côte dans des interactions verbales ou non verbales, lorsque leurs actions et les buts qu’ils poursuivent sont coordonnés et leurs actions synchronisées.
Lors de cette séance de mathématiques, l’articulation décrite entre les préoccupations d’aide de l’enseignante et celles de recherche de la solution des élèves participe de ces processus de production d’intelligibilité mutuelle et de compréhension partagée. Les processus improvisés et informels – de validation, d’institution des actions, d’enquête – relèvent de mécanismes d’adaptation et d’auto-organisation. Ils permettent aux acteurs de se coordonner et de réaliser la tâche de recherche de la solution. La coopération se manifeste de plusieurs manières. Les interactions verbales et non verbales entre les élèves ainsi que la visibilité des actions des uns et des autres permettent le partage des indices recueillis : lorsque la proposition d’un élève est éliminée, les autres ne la reprennent pas. Les acteurs partagent des préoccupations proches, relatives à la découverte de la solution du problème. Les propositions des élèves sont coordonnées temporellement et tiennent compte des indices recueillis précédemment : après la minute 38, toutes les propositions portent sur la multiplication.
Articulation des préoccupations
Un équilibre s’instaure entre les préoccupations de l’enseignante et celles des élèves, malgré les difficultés qu’éprouvent l’enseignante à aider les élèves et ceux-ci à résoudre le problème. La dynamique de cette articulation permet la progression de l’enquête. Le texte-problème – en particulier sa topologie – est utilisé par l’enseignante comme un support pour l’aide apportée et par les élèves comme un support pour l’enquête. En dépit du nombre limité d’interactions entre les élèves, une forme de coopération s’instaure au sein de ce groupe.
Conclusion
Cette étude met en évidence les ressorts de l’articulation de l’activité des acteurs au sein de la classe, dans une situation quotidienne, perçue comme difficile aussi bien par l’enseignante que par les élèves. L’activité de ces élèves est une activité d’enquête plutôt qu’une activité de raisonnement logico-mathématique. Elle procède, d’une part, sur le plan individuel par des généralisations « d’actions qui conviennent » (« quand on dispose de la longueur et de la largeur d’un quadrilatère on peut calculer son aire ou son périmètre ») et, d’autre part, sur le plan collectif par l’institution d’actions valides dans la communauté plus ou moins étendue (« quand on demande la validation, on l’obtient »). L’activité de l’enseignante consiste à aider les élèves à trouver la solution du problème. Cette aide est une aide à l’action plutôt qu’une aide à l’apprentissage. L’enseignante aide les élèves afin qu’ils surmontent leurs difficultés dans la réalisation de la tâche de résolution du problème, mais elle ne recherche pas la généralisation des relations de proportionnalité. En ce sens, le problème et sa résolution sont bien « scolairement contextualisés », étroitement enchâssés dans un contexte scolaire qui les structure et éloignés de la généralisation attendue.
Les résultats de cette étude ouvrent sur la question de l’efficacité de l’enseignement. Le segment étudié peut être considéré comme globalement viable pour les acteurs : les élèves cherchent activement, longuement, sans se distraire de la tâche. Du point de vue de l’enseignante, tous parviennent à la solution du problème. En dépit de cette viabilité, cette situation peut être considérée à maints égards comme peu efficace en ce qui concerne les apprentissages des élèves. Cette tâche apparaît sans doute difficile aux élèves de ce groupe du fait des implicites qui la caractérisent. Elle demande d’interpréter un texte complexe comme les approbations et les demandes de l’enseignante en termes d’attentes. Ils peinent à attribuer une signification mathématique claire à cette situation ; ils peinent à choisir les données pertinentes et à voir les rapports de proportionnalité qui les unissent. Cependant, ils cherchent opiniâtrement et, après une heure de travail sur le problème, construisent divers scénarios, effectuent des opérations, proposent des solutions.
L’approche de l’action située et celle de la tradition ergonomique francophone développées ici butent, lorsqu’elles étudient l’enseignement, sur le problème de la validité des pratiques observées. En accordant un primat au point de vue des acteurs, elles sont amenées à considérer ces derniers comme les experts de l’enseignement et leurs pratiques comme indépassables. Par ailleurs, la question de l’efficacité a été abordée à ce jour selon une perspective naturaliste exclusive (McIlrath et Huitt, 1995) qui se réfère à des normes imposées et à un point de vue extrinsèque. Notre étude pourrait permettre de prolonger cette façon d’aborder l’efficacité de l’enseignement. Elle permet de valoriser le point de vue des acteurs et de lui apporter des réponses plus compréhensives. Elle permet aussi de considérer l’efficacité de l’enseignement comme liée à l’articulation de l’activité de l’enseignante avec celle des élèves et pas seulement aux compétences des enseignants ou à leurs connaissances.
Cette étude concerne aussi le statut de l’articulation des actions en classe. Des articulations présentant des caractéristiques analogues ont déjà été observées dans d’autres contextes scolaires (Gal-Petitfaux et Durand, 2001). Ces articulations dynamiques émergent de l’action des élèves et de celle de l’enseignante et contribuent en retour à les définir. Elles intègrent plusieurs éléments : a) l’organisation du travail des élèves dans la classe (ici un travail en petits groupes d’élèves) ; b) les relations entre individus ; c) les modes d’action de l’enseignant (l’aide apportée aux élèves) ; d) la présence et la fonction structurante des objets (le texte-problème) ; e) l’organisation spatiale de la classe (les tables des élèves regroupées par quatre) ; f) les formes d’interaction ; g) les normes culturelles (le problème appelle des opérations) ; h) l’organisation temporelle ; i) les modes d’institution des actions (la validation et l’invalidation des propositions). Ces formes émergentes, dont l’épisode décrit ici est un exemple, ont été dénommées des « configurations d’activité » (Durand, 2004). De notre point de vue, elles constituent un niveau d’organisation pertinent pour l’étude des apprentissages scolaires et leur évaluation, tant d’un point de vue scientifique que de la conception pratique de dispositifs d’aide.
Appendices
Note
-
[1]
Ce groupe d’élèves est désigné par la suite comme le « groupe de Charlotte ».
Références
- Cobb, P. (2002). Reasoning with tools and inscriptions. The Journal of the Learning Sciences, 11(2-3), 187-215.
- Cole, M. et Griffin, P. (1980). Cultural amplifiers reconsidered. In D.R. Olson (dir.), The social foundations of language and thought (p. 343-364). New York, NY : Norton.
- Decortis, F., Noirfalise, S. et Saudelli, B. (2000). Activity theory, cognitive ergonomics and distributed cognition : Three views of a transport company. International Journal of Human Computer Studies, 53, 5-33.
- De Munck, J. (1999). L’institution sociale de l’esprit. Paris : Presses universitaires de France.
- Dewey, J. (1993). Logique. La théorie de l’enquête. Paris : Presses universitaires de France (1re éd. 1938).
- Durand, M. (2004). Les configurations de classe : un niveau autonome d’articulation de l’activité de l’enseignant et des élèves. In D. Biron, M. Cividini et J.F. Desbiens (dir.), La profession enseignante au temps des réformes. Sherbrooke : CRP.
- Durand, M., Ria, L. et Flavier, E. (2002). La culture en action des enseignants. Revue des sciences de l’éducation, 28(1), 83-104.
- Flavier, E., Bertone, S., Hauw, D. et Durand, M. (2002). The organization of physical education teachers’ action during conflict which opposes them with student(s). Journal of Teaching in Physical Education, 22, 20-38.
- Gal-Petitfaux, N. et Durand, M. (2001). L’enseignement de l’éducation physique comme « action située » : propositions pour une approche d’anthropologie cognitive. STAPS, 55, 79-100.
- Gallego, M.A., Cole, M. et The Laboratory of Comparative Human Cognition (2001). Classroom culture and cultures in the classroom. In V. Richardson (dir.), Handbook of research on teaching (p. 951-997). Washington, DC : American Educational Research Association.
- Jordan, N.C. et Montani, T.O. (1997). Cognitive arithmetic and problem solving : A comparison of children with specific and general mathematics difficulties. Journal of Learning Disabilities, 30(6), 624-634.
- Lave, J. (1988). Cognition in practice. Cambridge : Cambridge University Press.
- Lave, J. (1992). Word problems : A microcosm of theories of learning. In P. Light et G. Butterworth (dir.), Context and cognition. Ways of learning and knowing (p. 74-92). Exeter : BPCC Wheatons.
- McIlrath, D. et Huitt, W. (1995). The teaching-learning process : A discussion of models. Valdosta, GA : Valdosta State University.
- Ministère de l’Éducation du Québec (2001). Programmes de formation de l’école québécoise. Éducation préscolaire. Enseignement primaire. Québec : Gouvernement du Québec.
- Ministère de l’Éducation nationale (2002). Qu’apprend-on à l’école élémentaire ? Paris : CNDP/XO Éditions.
- Norman, D.A. (1993). Things that make us smart. New York, NY : Addison Wesley.
- Nuñes, T., Schliemann, A.D. et Carraher, D.W. (1993). Street mathematics and school mathematics. Cambridge : Cambridge University Press.
- Organisation de coopération et de développement économiques (2001). Connaissances et compétences : des atouts pour la vie. Premiers résultats du programme international de l’OCDE pour le suivi des acquis des élèves (PISA) 2000. Paris : OCDE.
- Peirce, C.S. (1978). Écrits sur le signe. Paris : Seuil.
- Pinsky, L. (1992). Concevoir pour l’action et la communication : essai d’ergonomie cognitive. Berne : Peter Lang.
- Ria, L., Sève, C., Saury, J., Theureau, J. et Durand, M. (2003). Beginning teacher’s situated emotions : Study about first classroom’s experiences, Journal of Education for Teaching, 29(3), 219-233.
- Rogoff, B. et Lave, J. (1984). Everyday cognition : Its development in social context. Cambridge, MA : Harvard University Press.
- Romberg T.A. et Carpenter, T.P. (1986). Research on teaching and learning mathematics : Two disciplines of scientific inquiry. In M. Wittrock (dir.), Handbook of research on teaching (p. 850-873). New York, NY : Macmillan.
- Salembier, P. et Zouinar, M. (2000). Analysing and assessing mutual awareness in cooperative work settings. Document téléaccessible à l’adresse URL : <http://www-sv.cict.fr/cotcos/pjs>.
- Suchman, L. (1987). Plans and situated action. Cambridge : Cambridge University Press.
- Theureau, J. (1992). Le cours d’action : analyse sémio-logique. Berne : Peter Lang.
- Theureau, J. (2004). Le cours d’action. Méthode élémentaire. Toulouse : Octarès.
- Varela, F. (1989). Autonomie et connaissance. Paris : Seuil.
- Verschaffel, L., De Corte, E., Vierstraete, H. (1999). Upper elementary school pupils’ difficulties in modeling and solving nonstandard additive word problems involving ordinal numbers. Journal for Research in Mathematics Education, 30(3), 265-285.
- Veyrunes, P. (2004). Les configurations d’activité : un niveau de description de l’articulation de l’activité de l’enseignant et des élèves. Étude située en mathématiques et en français à l’école primaire. Thèse de doctorat non publiée, Université de Montpellier, Montpellier.
- Veyrunes, P., Bertone, S. et Durand, M. (2003). L’exercice de la pensée critique en recherche-formation : vers la construction d’une éthique des relations entre chercheurs et enseignants débutants. Savoirs,2, 53-70.
List of tables
Tableau 1
Exemple d’étiquetage d’une unité d’action de l’enseignante
Tableau 2
Verbalisations en classe et lors de l’entretien d’autoconfrontation (min 54)
Tableau 3
Verbalisations en classe et lors de l’entretien d’autoconfrontation (min 55 à 56)
Tableau 4
Verbalisations en classe et lors de l’entretien d’autoconfrontation (min 57)
Tableau 5
Articulation des préoccupations et des unités d’action de l’enseignante et des élèves





 10.7202/007150ar
10.7202/007150ar