Résumés
Résumé
La généalogie des textes des évangiles synoptiques reste un sujet d’actualité. Différentes hypothèses existent quant à l’explication des similitudes ou des reprises de textes entiers d’un évangile à l’autre, dans les trois évangiles selon Matthieu, Marc et Luc. Une équipe de chercheurs japonais a réussi à identifier tous les segments communs entre les différents auteurs des évangiles de Marc, Luc et Matthieu et a construit un tableau de contingence qui décrit ces similitudes. Le tableau de contingence obtenu par le calcul des similarités dans les textes des évangiles synoptiques a été soumis à l’analyse des correspondances du taxi (ACT). L’ACT nous a permis d’obtenir des résultats interprétables et stables permettant de déduire une variante de l’hypothèse des deux évangiles.
Mots-clés :
- Évangiles synoptiques,
- paternité de textes,
- analyse des correspondances du taxi
Abstract
The genealogy of the synoptic gospels is still of current interest. Different hypotheses exist regarding the similarities or the repetition of entire texts from one gospel to the next among the 3 gospels according to Matthew, Mark, and Luke. A team of Japanese researchers has identified all the segments common to these three gospel authors and has built a contingency table describing their similarities. A statistical Analysis of the contingency table calculated from the synoptic gospels is done by taxicab correspondence analysis (TCA). TCA produced stable and interpretable results, from which we deduced a variant of two gospel hypothesis.
Keywords:
- synoptic gospels,
- text genealogy,
- taxicab correspondence analysis
Corps de l’article
Introduction
Les évangiles constituent une étude de cas de paternité, particulièrement intéressante. Hormis l’évangile selon Jean qui présente une structure bien différente des trois autres, les évangiles selon Matthieu, Marc et Luc ont une construction proche et sont donc appelés « évangiles synoptiques ». Ces trois évangiles se composent de plusieurs segments ou paragraphes communs de formats différents et donnent l’impression d’une sorte de rapiéçage de textes. En effet, dans les études bibliques, le « problème synoptique » cherche à savoir si les évangiles synoptiques ont été écrits littéralement par trois individus, ou s’il y a interdépendance entre eux, puisque chacun de ces évangiles contient des mots, phrases, extraits, quasiment identiques aux trois ou deux évangiles. Le problème synoptique a généré les études les plus controversées dans les recherches sur le Nouveau Testament. Nous allons décrire cela plus en détail dans la section 2.
Peu d’études jusqu’à présent ont essayé de donner des explications objectives basées sur des analyses statistiques concernant les relations entre les différents évangiles de Matthieu, Marc et Luc. Parmi ces études, citons par exemple, celle de Conzelmann et Lindemann (1988). Aussi, un certain nombre d’études ont proposé différentes explications ou hypothèses sur leurs relations généalogiques basées sur une comparaison subjective des textes. Le site web - www.hypotyposeis.org/synoptic-problem/2004/09/overview-of-proposed-solutions.html présente plus de 20 hypothèses à propos de la source originale de ces trois évangiles. Ceci étant dit, ces hypothèses peuvent être regroupées autour de deux hypothèses majeures : l’hypothèse des deux sources (H2S–Weisse 1838) et l’hypothèse des deux évangiles (H2E–Griesbach 1783).
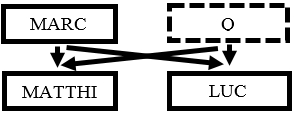
L’hypothèse des deux sources (H2S, Figure 1) est basée sur la supposition que les trois évangiles synoptiques ont deux sources originales, Marc et « Q » (l’ensemble des segments qui n’appartiennent pas à Marc).
Figure 1
Hypothèse des deux sources selon Weisse (1838)
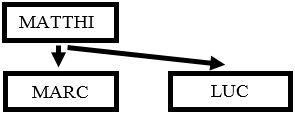
En revanche l’hypothèse des deux évangiles (H2E, figure 2) est basée sur la supposition que 1) l’évangile de Matthieu a été écrit en premier et qu’il aurait été utilisé par Luc, 2) que Marc serait une confluence de Matthieu et Luc. Il existe plusieurs variantes ou modifications de ces deux hypothèses H2S et H2E.
Figure 2
Hypothèse des deux Évangiles selon Griesbach (1783)
Cet article représente une étude statistique sur la paternité de ces trois évangiles par l’analyse des correspondances du taxi. Aussi, la suite de notre article comprendra trois parties : la section 2 introduira le corpus et la construction du tableau de contingence, l’analyse statistique sera présentée dans la section 3, enfin nous interpréterons les résultats et conclurons dans la section 4.
1. Corpus et méthodologie
Nous avons voulu étudier les textes, en grec, des trois évangiles[1] selon Matthieu, Marc et Luc, par une analyse statistique, l’Analyse des Correspondances du Taxi (ACT) développée par Choulakian (2006). Pour cela, nous avons divisé en 7 parties disjointes (a, b, c, d, e, f, g) l’union des trois évangiles, tels qu’illustrés dans les figures 3 et 4 ci-dessous, qui montrent bien cette composition en patchwork des évangiles. Les parties communes aux différents textes y sont identifiées par des couleurs : la partie en turquoise (a) est l’ensemble des textes communs aux trois évangiles; la partie en vert (b) est l’ensemble des textes communs à Marc et à Matthieu; la partie en rose (c) est l’ensemble des textes communs à Marc et Luc; la partie en orange (d) est l’ensemble des textes communs à Luc et à Matthieu.
Les sept parties disjointes sont donc définies ainsi : union (MATTHIEU, MARC, LUC) = union (a, b, c, d, e, f, g) où
|
a |
= |
MATTHIEU ∩ MARC ∩ LUC |
|
b |
= |
MATTHIEU ∩ MARC ∩ LUC′ |
|
c |
= |
MATTHIEU′∩ MARC ∩ LUC |
|
d |
= |
MATTHIEU ∩ MARC′ ∩ LUC |
|
e |
= |
MATTHIEU ∩ MARC′ ∩ LUC′ |
|
f |
= |
MATTHIEU′∩ MARC ∩ LUC′ |
|
g |
= |
MATTHIEU′∩ MARC′ ∩ LUC, |
et, où E′ désigne le complément de E, E étant un ensemble quelconque et ∩ indiquant l’intersection de deux ensembles.
Voici deux exemples de ces intersections entre les évangiles (Figures 3 et 4) : surlignés en turquoise, les textes communs aux trois évangiles dans la figure 3; surlignés en orange, les textes communs à Matthieu et Luc dans les figures 3 et 4.
Figure 3
Exemple de l’intersection entre les trois textes des évangiles
Figure 4
Exemple de l’intersection entre les deux textes des évangiles de Matthieu et Luc
Pour aborder l’étude des évangiles synoptiques objectivement, deux étapes sont nécessaires : tout d’abord, construire un tableau de contingence dans lequel le lexique complet des trois évangiles est distribué dans les sept catégories citées plus haut. La construction de ce tableau de données pour l’analyse statistique a été réalisée grâce au logiciel Tele-Synopsis, logiciel biblique en ligne développé par Miyake et coll. (2004), qui permet de manipuler des données textuelles de façon à les mettre en parallèle et ressortir leurs variantes. La version NA26 de Nestle et Aland (1979) et Aland (1989) des textes en grec des trois évangiles a été utilisée pour l’étude. Ainsi, nous considérons le tableau de contingence du lexique des évangiles synoptiques selon les sept catégories ou ensembles définis plus haut (a, b, c, d, e, f, g). Ce tableau de contingence tient compte de 7 276 unités de segments lexicaux. En éliminant les mots outils, comme les articles, les prépositions, les pronoms et les conjonctions, le nombre des segments lexicaux a été réduit à 7 099. Le tableau de contingence croisant les 7 099 segments du lexique en lignes et les sept catégories en colonnes est désigné par T1.
2. Une analyse statistique par l’analyse des correspondances du taxi
Dans la seconde étape, le tableau T1 a été soumis à l’analyse statistique dans le but de discerner les structures valides et stables de ces évangiles.
Nous avons donc appliqué l’analyse des correspondances du taxi (ACT) pour analyser ces données et voir si les résultats obtenus permettent de valider une hypothèse quant à la paternité de ces trois évangiles.
2.1. L’analyse statistique
Le tableau de contingence T1 ainsi construit a été soumis à l’ACT qui produit les mesures de dispersion des facteurs représentées dans la colonne de gauche du tableau 1 ci- dessous. Dans le tableau 1, D2i représente la mesure de dispersion de l’axe i et DCRi sa mesure de dispersion cumulée relative en %. Il paraît évident que ce sont les trois premières dimensions qui sont significatives, car elles expliquent 92,2 % de la dispersion cumulée relative.
La colonne de gauche du tableau 2 présente les quatre premiers facteurs principaux obtenus par l’ACT pour les sept catégories (a, b, c, d, e, f, g), mais nous n’interprétons que les trois premiers qui sont représentés dans les figures 5 et 6 qui suivent.
Tableau 1
Les mesures de dispersion D2i, et les mesures de dispersion cumulées relatives DCRi de l’ACT pour les tableaux T1 et T10
Tableau 2
Les quatre premiers facteurs principaux obtenus par l’ACT pour les tableaux T1 et T10
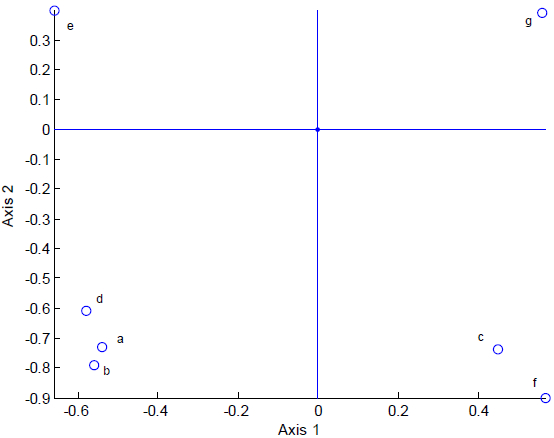
Le premier axe de l’ACT (Figure 5) sépare les sept catégories de T1 en deux grands groupes {a, b, d, e} et {c, f, g}, tandis que le second et le troisième axe (Figure 6) séparent respectivement chacun de ces groupes en deux sous-groupes : {a, b, d, e} en {a, b, d} et {e}, et {c, f, g} en {c, f} et {g}.
Donc, à partir des figures 5 et 6 nous remarquons que les sept catégories sont regroupées en quatre classes distinctes : {a, b, d}, {c, f}, {e} et {g} qui peuvent être représentées par l’arbre suivant (Figure 7).
Figure 5
Axes 1 et 2 de l’ACT des 7 catégories
Figure 6
Axes 2 et 3 de l’ACT des 7 catégories
Figure 7
Arbre montrant le regroupement des sous-ensembles a, b, c, d, e, f et g
2.2. Stabilité des résultats
Avant d’aller plus loin dans l’interprétation de ces résultats dans une optique de généalogie de ces textes, nous aimerions aborder la question de la stabilité de l’arbre représenté par la figure 7. Afin de vérifier la stabilité de cet arbre, nous avons utilisé deux approches : la première basée sur le rééchantillonnage (bootstrapping) du tableau de contingence T1 (Greenacre 1984, ch. 8; Alvarez, Bécue et Valencia, 2004; Lebart, 2004) tandis que la deuxième est basée sur l’analyse des sous-tableaux Tk, pour k = 1,..., 10.
Dans la méthode de rééchantillonnage, 1 000 tableaux de contingence échantillonnés de T1 ont été choisis et l’ACT a été appliquée à chacun d’eux. Chacune de ces analyses a produit l’arbre de la figure 7, ce qui montre une grande stabilité de l’arbre.
Dans la seconde méthode, l’ACT a été appliquée aux sous-tableaux Tk qui ne contiennent que les segments de T1 ayant un effectif marginal plus grand ou égal à k. Les dimensions des sous-tableaux Tk sont données dans le tableau 3. Par exemple, dans le tableau T1, on observe qu’il y a 4 433 lignes qui ont une fréquence marginale de 1; en les éliminant, on obtient le tableau T2 ayant 7 099 – 4 433 = 2 666 lignes, et ainsi de suite jusqu’à k=10. L’ACT de chacun des sous-tableaux de Tk a produit le même arbre la figure 7. Le tableau 2 illustre cette stabilité en montrant parallèlement les sorties des tableaux de contingence de T1 et T10. Remarquons que les facteurs ou scores des sept modalités de T1 et T10 ont la même interprétation, donc produisent le même arbre de la figure 7.
Tableau 3
Nombre des segments (lignes) dans les sous-tableaux Tk
3. Interprétation des résultats et conclusion
La stabilité de l’arbre étant démontrée, que pouvons-nous conclure de ces résultats obtenus quant à la généalogie ou la paternité des textes des trois évangiles de MATTHIEU, LUC et MARC ? Les résultats de l’ACT peuvent être interprétés par deux approches : soit par les axes séparément, soit par le groupement géométrique des modalités.
Dans la première approche, l’axe 1 montre l’opposition entre MATTHIEU = union (a, b, d, e) et le reste des catégories (c, f, g,) ; donc cet axe 1 est l’axe de MATTHIEU. L’axe 2 montre l’opposition entre MARC = union (a, b, c, f) et (d) et les autres catégories (e, g); donc ce 2e axe est l’axe de MARC. L’axe 3 montre l’opposition entre les groupes (a, b, d, g) et (c, e, f); on peut en déduire que LUC = union (a, c, d, g) donc un amalgame de MATTHIEU et MARC.
La deuxième approche, basée sur le groupement géométrique des modalités, nous donne l’arbre de la figure 7; cet arbre regroupe les sept variables en quatre catégories à partir desquelles on définit :
(3) proto - MATTHIEU = union (a, b, d).
On voit alors que
MATTHIEU = union (proto - MATTHIEU, e)
(4) MARC = union (c, f, parties de proto - MATTHIEU),
LUC = union (g, proto - MATTHIEU, partie de MARC).
À partir de ces considérations, on peut émettre l’hypothèse selon laquelle Matthieu, qui est dominant sur le 1er axe, vient en premier, donc constitue la source première; il est suivi de Marc, qui est dominant sur le 2e axe et qui constitue la deuxième source; Luc vient en dernier sur le 3e axe, son texte est un amalgame, il aurait utilisé des textes de Matthieu et de Marc.
Ces résultats stables et interprétables obtenus grâce à l’ACT nous permettent donc de nuancer et de proposer une variante de l’hypothèse des deux évangiles de Griesbach 1783.
Parties annexes
Note
-
[1]
Les textes des évangiles ont été étudiés dans leur version en grec. Bien qu’il n’y ait pas de traces convaincantes de la langue initiale des évangiles, on pense qu’ils ont été écrits en grec. L’évangile de Matthieu aurait été écrit à Antioche de Syrie; la couche finale de l’Évangile de Marc, à Rome; l’Évangile de Luc à Achaïe en Grèce; la couche finale de l’Évangile de Jean à Éphèse. Comme le dit Yolande Girard, Bibliste de Montréal dans sa chronique du 25 janvier 2008, « ... les évangélistes ont utilisé, par contre pour les écrire, des collections de Paroles de Jésus qui provenaient de Galilée (araméen, hébreu) ainsi que des traditions particulières (traditions orales) qu’ils ont agencées différemment dans chaque Évangile selon leurs perspectives théologiques et le vécu de leurs communautés ». Elle ajoute aussi que ces récits s’adressaient à des gens de langue grecque.
Bibliographie
- Aland, K. (1989). Synopsis of the Four Gospels. 9 th ed. Stuttgart : German Bible Society.
- Alvarez, R., Bécue, M., et Valencia, O. (2004). Étude de la stabilité des valeurs propres de l’AFC d’un tableau lexical au moyen de procédures de reéchantillonage. Actes JADT’2004, 7es Journées internationales d’analyse statistique de données textuelles, Lexicométrica. 42-51.
- Choulakian, V. (2006). Taxicab correspondence analysis. Psychometrika. 71:2.1-13.
- Choulakian, V., Kasparian S., Miyake M., Akama H., Makoshi M., et Nakagawa, M. (2006). A statistical Analysis of Synoptic Gospels. In J.-M. Viprey, et C. Condé (dir.), LASELDI, Université de Franche – Comté, France. Actes JADT’2006, 8es Journées internationales d’analyse statistique de données textuelles, Lexicométrica. 281-288.
- Conzelmann, H., et Lindemann, A. (1988). Interpreting The New Testament. Trans. Siegfried S. Schatzmann. Peabody, Mass.: Hendrickson Publishers.
- Girard, Y. (2008). La langue des Évangiles : langue de Jésus ? À la découverte du monde biblique. 25 janvier. http://www.interbible.org/interBible/decouverte/comprendre/2008/clb_080125.html
- Greenacre, M. J. (1984). Theory and Applications of Correspondence Analysis. Academic Press : N.Y.
- Lebart, L. (2004). Validité des visualisations de données textuelles. Actes JADT’2004, 7es Journées internationales d’analyse statistique de données textuelles, Lexicométrica. 708-715.
- Miyake, M., Akama, H., Sato, M., et Nakagawa, M. (2004). Tele-Synopsis for biblical research. Proceedings of the IEEE ICALT. 931-935.
- Nestle, E., et Aland, K. (1979). Nestle-Aland Novum Testamentum Graece. 26 th ed. Stuttgart : Deutsche Bibelstiftung.
Liste des figures
Figure 1
Hypothèse des deux sources selon Weisse (1838)
Figure 2
Hypothèse des deux Évangiles selon Griesbach (1783)
Figure 3
Exemple de l’intersection entre les trois textes des évangiles
Figure 4
Exemple de l’intersection entre les deux textes des évangiles de Matthieu et Luc
Figure 5
Axes 1 et 2 de l’ACT des 7 catégories
Figure 6
Axes 2 et 3 de l’ACT des 7 catégories
Figure 7
Arbre montrant le regroupement des sous-ensembles a, b, c, d, e, f et g
Liste des tableaux
Tableau 1
Les mesures de dispersion D2i, et les mesures de dispersion cumulées relatives DCRi de l’ACT pour les tableaux T1 et T10
Tableau 2
Les quatre premiers facteurs principaux obtenus par l’ACT pour les tableaux T1 et T10
Tableau 3
Nombre des segments (lignes) dans les sous-tableaux Tk