Modélisation des rizières irriguées et intégration dans hydrotel : application au bassin versant de la rivière Cau au Vietnam

Nguyen, Xuan Tuan; Kokutse, Nomessi; Duchesne, Sophie; Toumbou, Babacar; Villeneuve, Jean-Pierre

doi:https://doi.org/10.7202/1054304ar

1. Introduction

Le riz est la deuxième céréale alimentaire la plus produite dans le monde avec une production mondiale de 479,2 millions de tonnes (2013-2014) de riz par an. Le riz peut être cultivé en terrain inondé, avec apport d’eau par irrigation, ou en terrain non inondé. La culture du riz en terrain non inondé est la plus ancienne, mais elle ne produit pas les rendements fournis par les rizières inondées. La croissance du riz nécessite en effet de fortes chaleurs et de grandes quantités d’eau. Malgré ses grands besoins en eau, la « riziculture irriguée » est le type de culture du riz le plus répandu, en raison de ses meilleurs rendements, et aussi le plus intensif. Ainsi, environ les trois quarts de la production de riz proviennent de cet agrosystème. Dans les régions chaudes et fertiles, on obtient jusqu’à trois récoltes par an. Toutefois, cette utilisation intensive de l’eau pour produire le riz modifie le cycle hydrologique naturel sur les bassins versants où sont implantées les rizières.

La présente démarche s’inscrit dans le projet de gestion intégrée de l’eau sur le bassin versant de la rivière Cau au Vietnam. La prise en compte de l’impact des rizières sur le régime hydrologique est essentielle à une prise de décision rationnelle sur l’aménagement du territoire. À notre connaissance, les modèles hydrologiques de bassin versant existants (WATFLOOD [KOUWEN et al., 2005]; SWAT [NEITSCH et al. 2002]; MIKE SHE [ABBOTT et al., 1986a et 1986b]; MIKE 11 NAM [DHI, 2000]; CEQUEAU [MORIN et al., 1981]; GAWSER/GRIFFS [BOYD et al., 2000]; Hydrotel [FORTIN et al., 1995; FORTIN et ROYER, 2004]) ne permettent pas de faire une distinction entre les rizières et les autres types de surfaces agricoles. Dans le cadre du projet de la rivière Cau le logiciel GIBSI (VILLENEUVE et al. 1998) est utilisé. Or la constituante hydrologique de ce logiciel est Hydrotel. Hydrotel a été développé en région méridionale et ne permet pas de prendre en compte facilement le comportement hydrologique des rizières. Cependant, dans Hydrotel, le calcul de l’évapotranspiration réelle tient compte de la saturation du sol avec possibilité d’inondation et du type de culture en zone agricole. Dans le contexte du projet global de la rivière Cau, nous devons intégrer au modèle Hydrotel un sous-modèle qui permet d’évaluer l’impact des rizières sur le système hydrologique d’un bassin versant. Ce développement permettra finalement de mettre en oeuvre le logiciel GIBSI. Au demeurant, une approche similaire a été adoptée par XIE et CUI (2011). Ces derniers ont intégré dans le modèle hydrologique SWAT de nouveaux processus pour l’irrigation et le drainage et ont montré que le nouveau modèle obtenu était plus adapté pour les rizières que le modèle original (XIE et CUI, 2011). Sur la base des concepts répertoriés dans la littérature, une approche de modélisation sera développée pour modéliser le fonctionnement hydrologique d’une rizière irriguée. L’ajout de cette démarche dans Hydrotel se fera suivant la logique de discrétisation spatiotemporelle adoptée dans ce modèle (FORTIN et al., 1995).

Un cas d’application du modèle est présenté sur le bassin versant de la rivière Cau au Vietnam, en amont de la station de mesure Gia Bay. Bien que les rizières ne constituent que 4,3 % de la superficie de cette zone d’étude, on croit pouvoir démontrer que, sur ce bassin, la consommation d’eau pour l’irrigation des rizières modifie le régime hydrologique.

2. Méthodologie

Pour simuler l’influence des rizières sur le régime hydrologique d’un bassin versant, on implantera dans le modèle Hydrotel un sous-modèle qui représente le fonctionnement hydrologique du système « rizières irriguées ». La revue de littérature conduira au choix d’une approche de modélisation adaptée à la structure de modélisation d’Hydrotel. Pour vérifier l’impact des rizières, le modèle Hydrotel sera calibré sur le bassin de la rivière Cau, d’abord sans le modèle « rizière irriguée ». Dans un deuxième temps, le modèle modifié tenant compte des rizières sera recalibré. La comparaison des simulations permettra d’évaluer l’importance de prendre en compte les rizières.

2.1 Modèles

Après une brève description du modèle Hydrotel, la démarche d’implantation du modèle « rizière irriguée » sera décrite.

2.1.1 Hydrotel

Le modèle Hydrotel (FORTIN et al., 1995) est un modèle hydrologique distribué à base physique. Il a été développé au départ pour être utilisé en zone tempérée, dans un contexte où il n’y a pas de culture du riz, donc pas de rizière. Le modèle intègre six sous-modèles qui permettent de simuler les processus hydrologiques suivants : l’interpolation des données météorologiques, l’évolution du couvert nival, l’évapotranspiration, le bilan d’eau vertical, l’écoulement sur la partie terrestre du bassin et l’écoulement par le réseau hydrographique.

Les données d’entrée d’Hydrotel sont obtenues à partir d’un système d’information géographique (SIG), Physitel (TURCOTTE et al., 2001), développé pour les besoins du modèle Hydrotel. Ce SIG permet de traiter l’ensemble des données physiographiques du bassin versant. Ces données sont : la topographie du bassin sous la forme d’un modèle numérique de terrain (MNT), le réseau hydrographique sous forme vectorielle, l’occupation du sol et le type de sol.

2.1.2 Modèle de rizières irriguées

2.1.2.1 Choix du concept

À partir de la revue de la littérature (AZAMATHULLA et al., 2008; GUPTA et al., 2008; MASUMOTO et al., 2008; SOMETH et al., 2009), le principe de base adopté pour le sous-modèle de rizières est celui qui consiste à assimiler une rizière à un réservoir et à exprimer l’équation de continuité sous la forme de variations de l’emmagasinement. La figure 1 résume les processus hydrologiques dans la rizière.

Figure 1

**Illustration des variables du bilan de masse à l’échelle d’un casier rizicole.**

**Illustration of mass balance variables at the rice field scale.**

La variation de l’emmagasinement (ΔV) s’exprime par :

où
A : surface de rizière (m²);
V : volume d’eau dans la rizière (m³);
h : hauteur d’eau dans la rizière (m);
ΔV, Δh : variation du volume (m³) et variation de la hauteur d’eau (m) dans la rizière;
P : précipitation (m);
Irr : irrigation (m);
Re : ruissellement de surface en entrée (m);
Ap.e : apports latéraux souterrains (m);
Inf : infiltration (m);
ET : évapotranspiration (m);
Rs : ruissellement de surface en sortie (m);
Ap.s : pertes latérales souterraines (m).

Dans cette équation, deux variables (Irr et Rs) sont influencées par les prises de décision en lien avec les seuils de hauteurs maximale et minimale définies pour la rizière. La contrainte supérieure (seuil maximal ou optimal) est définie en fonction du stade de croissance de la plante. Elle permet d’éviter une submersion des plantes en saison des pluies et conduit à une utilisation rationnelle de l’eau en saison sèche :

où k : stade de la plante dans son cycle de croissance; h_opt : seuil optimal de la hauteur d’eau dans la rizière (m).

La contrainte inférieure (seuil minimal ou critique) pour la hauteur d’eau dans la rizière est également définie en fonction du stade de croissance du riz afin d’éviter que la plante ne se retrouve en état de stress hydrique en cas de baisse du niveau d’eau. C’est le seuil à partir duquel le besoin d’irrigation est nécessaire pour assurer une bonne croissance de la plante et assurer une bonne productivité de la culture :

où h_crit : seuil critique de la profondeur d’eau dans la rizière (m).

Ces contraintes sur le niveau de l’eau dans la rizière permettent une gestion rationnelle de l’eau et l’optimisation de la croissance.

2.1.2.2 Intégration dans Hydrotel

Pour pouvoir implanter le modèle de rizière dans Hydrotel, il est très important de bien comprendre la structure spatiale de simulation. Dans Hydrotel, le bassin étudié est discrétisé en UHRH (unités hydrologiques relativement homogènes) (FORTIN et ROYER, 2004). Les quatre premiers processus hydrologiques d’Hydrotel (interpolation des données météorologiques, évolution du couvert nival, évapotranspiration et bilan d’eau vertical) sont simulés au niveau des UHRH. Notons que l’évapotranspiration réelle dans chaque UHRH et dans chaque couche est calculée comme la somme pondérée des ETR de chaque classe d’occupation en fonction de sa superficie. Cette approche permet de mieux prendre en compte la variabilité spatiale des caractéristiques physiographiques (topographie, occupation du sol, etc.) du bassin (FORTIN et ROYER, 2004).

Afin de pouvoir simuler le comportement hydrologique des rizières, on ajoute à Hydrotel une couche « rizière ». Dans chaque UHRH, on détermine la fraction occupée par les rizières (Figure 2) pour la modélisation des processus.

Figure 2

**Ilustration d’une UHRH (unité hydrologique relativement homogène) avec les surfaces en rouge occupées par des rizières (1 carreau = 20 x 20 m).**

**Illustration of a UHRH with red surfaces occupied by rice fields (1 square = 20 x 20 m).**

2.1.3 Algorithme ajouté à Hydrotel pour le sous-modèle des rizières

Dans Hydrotel, le sous-modèle BV3C (bilan vertical en trois couches) modélise le bilan d’eau sur chaque UHRH. Puisque la couche des rizières aura un impact sur les quantités d’eau qui seront attribuées au ruissellement de surface et à l’écoulement souterrain à l’exutoire de l’UHRH, le sous-modèle BV3C doit être modifié pour prendre en compte la classe d’occupation « rizière ». Pour tenir compte des quantités d’eau apportées par l’irrigation et des surfaces de rizières, les teneurs en eau peuvent être exprimées comme indiqué au tableau 1. L’apport en eau provenant de l’irrigation sera pris en compte dans l’expression de la teneur en eau de la première couche de sol. Ce tableau illustre les différences entre le sous-modèle BV3C initial et celui modifié pour prendre en compte les rizières.

Tableau 1

**Équations du BV3C (bilan vertical en trois couches) initial et du BV3C modifié.**

**Equations of initial BV3C and modified BV3C.**

Pour chaque unité spatiale de simulation, ou UHRH, les processus hydrologiques dans une rizière sont intégrés dans la structure d’Hydrotel selon la figure 3. Les données météorologiques disponibles sont fournies au pas de temps journalier. Le pas de temps retenu pour les simulations des processus hydrologiques dans les rizières est également une journée.

Figure 3

**Illustration des processus hydrologiques sur une UHRH (unité hydrologique relativement homogène) avec une classe d’occupation rizière.**

**Illustration of hydrological processes on a UHRH with the rice field land use.**

Les variables de la figure 3 sont présentées au tableau 2; le lien entre chacune d’entre elles et la façon dont elles sont prises en compte dans le modèle sont décrits aux paragraphes suivants.

Tableau 2

**Définition des variables de la Figure 3.**

**Definition of the variables in Figure 3.**

où
hⁱ^-1 : hauteur d’eau dans la rizière au jour i-1 (m);
hⁱ : hauteur d’eau dans la rizière au jour i (m);
Pⁱ : précipitation au jour i (m);
Irrⁱ : apport d’eau par irrigation dans la rizière au jour i (m);
Reⁱ : lame d’eau stockée par ruissellement de surface dans la rizière au jour i (m).

FORTIN et al. (1995) et FORTIN et ROYER (2004) ont défini que, sur la surface de l’UHRH, une lame d’eau de ruissellement est déterminée comme étant la différence entre la pluie et l’infiltration. Une portion de cette lame d’eau provenant du ruissellement est stockée dans la rizière selon la fraction des terres occupées par les rizières dans l’UHRH. Le reste du ruissellement sur l’UHRH rejoint directement le réseau hydrographique par l’entremise d’un hydrogramme géomorphologique (HGM) (FORTIN et al., 1995). Ainsi, la variable Reⁱ est calculée selon l’équation suivante :

où α_rizière : fraction de la surface de l’UHRH occupée par les rizières; : lame d’eau de ruissellement calculée par BV3C dans Hydrotel (m) pour cette UHRH au jour i.

Rsⁱ : lame d’eau nécessaire au drainage d’une rizière pour maintenir la hauteur d’eau dans la rizière à la hauteur optimale selon la période de croissance du riz. Pour le développement du sous-modèle de rizières, la quantité d’eau de drainage (Rs) est ajoutée à la lame de ruissellement sur l’UHRH préalablement calculée par Hydrotel.

Ap.eⁱ et Ap.sⁱ : infiltration latérale en entrée et en sortie de la rizière au jour i. Selon la loi de la conservation de la masse, l’écoulement souterrain dans chaque couche du sol d’une UHRH comportant une aire de rizière peut être calculé de la manière suivante :

où α_rizière : fraction de surface des rizières sur l’UHRH; h_opt : hauteur optimale d’eau (m); Z₁; Z₂; Z₃ : profondeurs des couches 1, 2 et 3 dans le sous-modèle BV3C (m); : lame d’eau (m) dans l’écoulement hypodermique vers la deuxième couche selon BV3C (FORTIN et al., 1995; FORTIN et ROYER, 2004); : lame d’eau (m) dans l’écoulement de base dans la troisième couche par BV3C (FORTIN et al., 1995; FORTIN et ROYER, 2004).

: infiltration dans la rizière au jour i. Le processus d’infiltration varie selon l’état du sol, à savoir selon que le sol est inondé ou non inondé.

Dans la phase de sol non inondé, l’infiltration sur les rizières est déterminée selon la simulation d’infiltration de l’UHRH par BV3C :

où : infiltration dans la première couche de sol de l’UHRH.

Dans la phase de sol inondé, l’équation adaptée pour calculer l’infiltration considère l’infiltration comme une fonction du type de sol et de la couche de labour (TUONG et al., 2005) ainsi que du stade de croissance des rizières (FAO, 1990; KHEPAR et al., 2000; JANSSEN et LENNARTZ, 2007). Ainsi, l’équation suivante a été adoptée :

où : gradient de charge hydraulique qui tient compte de l’influence du labour de la rizière. Cette variable est appelée coefficient d’infiltration des rizières. Il s’agit d’un paramètre d’ajustement du modèle.

ETⁱ : évapotranspiration dans une rizière au jour i. Son estimation est obtenue à partir de l’évaporation potentielle et doit tenir compte de l’état de la rizière au cours de l’année. La méthode adoptée pour la détermination de l’évapotranspiration réelle du riz est celle d’ALLEN et al. (1998) et de SOMETH et al. (2009). Elle permet de déterminer l’évapotranspiration réelle comme une fonction de l’évapotranspiration de référence et d’un coefficient de culture du riz. La quantité d’eau perdue par évapotranspiration réelle du riz étant plus élevée que celle de la majorité des autres plantes, l’évapotranspiration sur la fraction de l’UHRH occupée par les rizières doit aussi être modifiée.

Ainsi, l’évapotranspiration dans une rizière est calculée en fonction de l’état du sol. Dans une rizière, il existe trois états possibles du sol au cours de l’année :

État du sol inondé avec riz, qui correspond à la période de culture du riz, avec le coefficient de culture du riz qui tient compte de la période de croissance du riz :

où k : stade de la plante dans son cycle de croissance (1, 2 ou 3); : coefficient cultural du riz; : évapotranspiration potentielle sur l’UHRH au jour i calculée par Hydrotel (m).

État du sol inondé sans riz, qui correspond aux trois phases suivantes : (1) période de repos du sol avec eau, (2) phase de préparation du sol en saison des pluies et (3) phase de préparation du sol en saison sèche. Pour cet état du sol, l’évapotranspiration pour une rizière est calculée selon l’équation suivante :

État du sol non inondé sans riz, qui correspond à la phase de repos du sol en saison sèche. L’évaporation réelle dans ce cas est fonction de l’ETP et de l’humidité du sol au jour i. Elle est calculée tel qu’indiqué dans le manuel d’Hydrotel pour les sols nus.

Dans l’équation 4, les sous-modèles actuels de Hydrotel permettent de déterminer toutes les variables sauf trois, à savoir : hⁱ, Irrⁱ et Rsⁱ. Le bilan d’eau dans la rizière selon l’équation 4 doit être contraint par les règles de gestion de l’irrigation et du drainage des rizières pour chaque période de croissance, énoncées aux équations 2 et 3.

2.1.4 Simulation des processus hydrologiques dans les rizières : résolution des équations dans Hydrotel

Dans l’équation 4, on doit déterminer à chaque pas de temps les valeurs des inconnues qui sont Irrⁱ , Rsⁱ et hⁱ tandis que les autres variables sont fournies par Hydrotel ou par d’autres calculs. D’abord, au premier pas de temps i-1, la hauteur d’eau initiale dans la rizière est connue (valeur initiale). Ensuite, on vérifie les conditions suivantes :

Si , alors l’irrigation est nécessaire sur une hauteur d’eau de : ;
À l’opposé, si alors Irrⁱ = 0;
De plus, si , l’eau excédentaire doit être drainée; la hauteur d’eau à drainer est donnée par : ;
À l’opposé, si hⁱ^-1 est inférieure à alors Rsⁱ = 0.

Enfin, pour chaque pas de temps, la hauteur d’eau dans la rizière est calculée à partir du bilan de masse (voir équation 4).

2.1.4.1 Mise à jour des variables dans Hydrotel

L’utilisation du concept de couches rizières dans une UHRH amène à apporter des modifications dans les différentes variables pour tenir compte du stockage d’eau dans une rizière ou du drainage d’eau excédentaire sur l’UHRH. Le nouvel algorithme intégré dans Hydrotel permet de trouver les valeurs inconnues des variables associées aux processus hydrologiques des rizières. Ainsi, des modifications sont apportées aux différentes lames d’eau initialement calculées par Hydrotel pour tenir compte de l’effet de la présence des rizières sur l’UHRH. En d’autres termes, l’algorithme de simulation des rizières modifie certaines variables du modèle Hydrotel pour simuler le fonctionnement hydrologique de celles-ci, soit certaines variables associées à l’écoulement terrestre et à l’écoulement souterrain, tel que détaillé ici-bas.

Modifications dans l’écoulement sur la partie terrestre (ruissellement de surface)

Dans Hydrotel, l’écoulement à l’exutoire d’une UHRH est basé sur les équations de Saint-Venant (modèle de l’onde cinématique). Le débit de ruissellement à l’exutoire dépend de la lame d’eau calculée par le sous-modèle BV3C et des coefficients de frottement (Manning), lesquels varient selon la classe d’occupation du sol. Le calcul du débit de ruissellement à l’exutoire de chaque UHRH est réalisé via un hydrogramme géomorphologique de référence (MOUSSA, 1991; MOUSSA, 1997; MOUSSA et BOCQUILLON, 1996; FORTIN et ROYER, 2004). En présence de rizières, il est nécessaire de recalculer, dans BV3C, la lame d’eau à la surface de l’UHRH. En effet, cette lame d’eau sera modifiée par la lame d’eau stockée dans la rizière (Re) et par la lame d’eau de drainage éventuel de la rizière (Rs). On recalcule alors la lame d’eau de ruissellement à la surface de l’UHRH à chaque pas de temps :

où
: valeur initiale calculée par l’algorithme actuel de BV3C;
: nouvelle lame d’eau sur l’UHRH mise à jour et devant servir au calcul de l’hydrogramme géomorphologique pour l’écoulement vers l’exutoire de l’UHRH;
: stockage d’eau dans la rizière;
: lame d’eau due au drainage des rizières (en temps de pluie).

Modifications dans l’alimentation des écoulements souterrains

Hydrotel représente les écoulements souterrains, par le débit hypodermique dans la deuxième couche du sol (Q₂) et le débit de base dans la troisième couche (Q₃). Selon FORTIN et al. (1995), dans BV3C, ces variables sont calculées par l’équation de Richards. Q₂ est calculé en fonction de la gravité, parallèle à la pente, et Q₃ est une fonction de la teneur en eau de la troisième couche du sol. Les écoulements souterrains Q₂ et Q₃, seront automatiquement mis à jour sur chaque UHRH avec modification de la teneur en eau de chaque couche. Ainsi, en présence de rizières, la lame d’eau dans la deuxième couche sera influencée par l’infiltration à partir des rizières, qui change en fonction des conditions comme le labour du sol et le degré de saturation du sol. En saison sèche, la quantité d’eau d’infiltration provenant de la rizière est considérée comme négligeable. En saison des pluies, la nouvelle valeur mise à jour dans Hydrotel, est la suivante :

Les variables utilisées dans cette équation sont présentées au tableau 3.

Tableau 3

**Variables dans le code du sous-modèle des rizières.**

**Variables in the rice sub-model code.**

En ce qui concerne la lame d’eau dans la troisième couche, le processus de l’écoulement est automatiquement simulé à partir du débit provenant de la couche supérieure et de la teneur en eau dans la couche 3.

Structure générale

À partir de la structure de simulation dans Hydrotel (FORTIN et al., 1995), un organigramme incluant les sous-modèles de rizières et de gestion de la source d’eau pour l’irrigation synthétise les liens entre les données et les différents sous-modèles (Figure 4). Cette structure permet de mieux visualiser, en fonction de l’irrigation, du drainage des rizières et de la gestion de la source d’eau, comment le sous-modèle des rizières s’insère au sein de l’architecture actuelle d’Hydrotel. On doit noter que le modèle de gestion de la source d’alimentation en eau n’est pas discuté ici, puisqu’il n’est pas utilisé dans le cas d’application présenté dans cet article (bassin versant de la rivière Cau). Ce module fera l’objet d’un autre article en préparation.

Figure 4

**Nouvelle structure intégrée au modèle Hydrotel (les cases rosées correspondent aux modifications apportées au modèle).**

**New structure implemented in the Hydrotel model (pink boxes correspond to the modifications made to the model).**

2.2 Cas d’application : bassin versant de la rivière Cau

La zone d’étude (Figure 5) s’étend sur près de 4 500 km². Le bassin versant se situe dans le nord du Vietnam, dans une région au climat de type mousson. En été, les conditions météorologiques y sont chaudes, humides et ponctuées de fortes précipitations. En hiver, le climat y est relativement froid et sec. La température annuelle moyenne varie entre 21 et 23 °C. Dans cette région, la période estivale s’étend de mai à septembre alors que l’hiver commence au mois de novembre pour se terminer en mars. Ainsi, les mois d’avril et d’octobre correspondent à une période de transition entre les deux principales saisons.

Figure 5

**Localisation du bassin versant de la rivière Cau : (a) Vietnam et (b) zone d’étude (en jaune).**

**Location of the Cau River watershed: (a) Vietnam and (b) study area (in yellow).**

La topographie du bassin versant est relativement diversifiée. Elle présente trois types de milieux : les terrains montagneux, les vallées et les plaines. Les précipitations annuelles sur le bassin versant se situent entre 1 500 et 2 700 mm. La saison des pluies coïncide, paradoxalement, avec la période ensoleillée, soit d’avril à octobre. Au cours de cette période, la région reçoit des précipitations qui représentent 85 à 90 % des précipitations annuelles totales. Le régime hydrologique de la région est clairement divisé en deux saisons. En outre, le débit des rivières de juin à octobre représente 75 à 85 % du débit total annuel.

Les données de débit qui sont utilisées pour la calibration du modèle Hydrotel sont celles de la station Gia Bay. Ce sont les seules données disponibles en aval du bassin versant. La surface du bassin versant utilisée dans la modélisation est donc celle en amont de cette station, telle que représentée à la figure 6, qui illustre l’utilisation du territoire. La superficie du bassin versant en amont de la station Gia Bay est de 2 925 km² tandis que la superficie des rizières sur cette partie du bassin est de 126 km² (données observées au printemps 2010).

Figure 6

**Carte de l'occupation du territoire.**

**Land use map.**

2.3 Calage, validation et évaluation de la performance du modèle

2.3.1 Période de calage et de validation

Les deux paramètres intervenant dans le sous-modèle des rizières pour l’ajustement des débits en rivière sont le paramètre d’infiltration K_inf, qui intervient dans le processus d’infiltration au fond des rizières, et le coefficient de culture Kc, servant à ajuster l’évapotranspiration dans les rizières. Pour l’ajustement, la procédure adoptée est celle d’un ajustement en deux étapes : d’abord l’ajustement des paramètres du modèle Hydrotel à partir des travaux de NGUYEN (2012), ensuite l’ajustement des paramètres intervenant dans le sous-modèle de rizières. Une valeur initiale de Kc de 1,3 a été utilisée, à partir de données de la littérature pour les différentes étapes de croissance (ALLEN et al., 1998; LE, 2011). Pour la valeur initiale du paramètre d’infiltration K_inf, celle-ci a été déterminée en tenant compte des caractéristiques hydrauliques des sols et des valeurs de la littérature (TUONG et al., 2005).

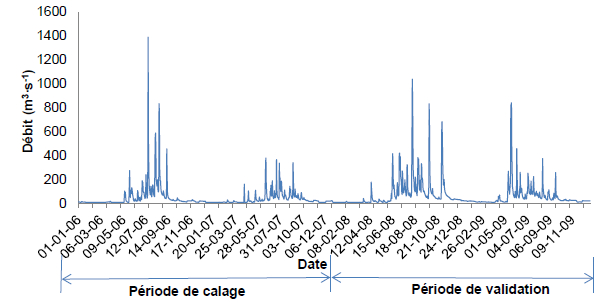
La carte d’occupation du territoire avec la classe rizière a été réalisée à partir d’images satellitaires et de mesures de terrain de 2006 à 2009 (HOANG, 2014). Le calage et la validation du modèle rizière ont donc été réalisés sur cette même période. Ainsi, le calage du sous-modèle de rizières a été réalisé à partir des observations des saisons des pluies 2006 et 2007, puis le modèle a été validé sur la base des observations des saisons des pluies de 2008 et 2009. La figure 7 présente une synthèse des données de débits observées à la station Gia Bay pendant la période 2006-2009. Même si ces périodes de calage et de validation peuvent être considérées comme courtes au regard des conditions optimales en matière de quantité de données pour le calage, elles sont supposées suffisantes pour obtenir un modèle acceptable pour l’aide à la décision. En effet, en matière de gestion intégrée par bassin versant, une situation de référence acceptable suffit pour analyser l’impact d’aménagements sur l’hydrologie d’un bassin versant.

Figure 7

**Débits observés à la station Gia Bay.**

**Observed discharges at Gia Bay station.**

Tableau 4

**Algorithmes sélectionnés pour les simulations hydrologiques.**

**Selected algorithms for hydrological simulations.**

Tableau 5

**Valeurs des indices foliaires et des profondeurs racinaires.**

**Values of foliar indices and root depths.**

Tableau 6

**Hauteurs d’eau utilisées dans les rizières pour les simulations.**

**Water heights used in rice fields for simulations.**

Pour tous les résultats présentés dans cet article, les algorithmes d’Hydrotel utilisés pour les simulations sont ceux apparaissant au tableau 4. Étant donné que les applications précédentes sur le bassin versant de la rivière Cau avaient été réalisées en utilisant ces algorithmes, nous avons choisi de poursuivre avec ceux-ci, bien que l’utilisation d’autres algorithmes ait pu être possible. Les valeurs des paramètres d’indices foliaires et de profondeurs racinaires sont données au tableau 5, alors que les valeurs de hauteurs d’eau minimales et maximales dans les rizières, pour les différents stades de croissance du riz, apparaissent au tableau 6.

L’objectif du calage d’un modèle est de déterminer les valeurs de ses paramètres de sorte que le modèle reproduise au mieux le comportement général du bassin à l’étude (VILLENEUVE et al., 1998). La méthode de calage qui a été appliquée est un ajustement manuel en appréciant les courbes simulées et observées et en calculant les valeurs des indicateurs de performance. Selon FORTIN et al. (1995), plusieurs critères permettent d’estimer la performance d’un modèle hydrologique. Chaque critère joue un rôle particulier dans le processus de jugement. En général, trois critères, soit le coefficient de Nash-Sutcliffe (NASH et SUTCLIFFE 1970), la racine carrée de l’écart quadratique moyen (RCEQM) et l’erreur relative sur le volume d’écoulement total sont utilisés.

Les deux premiers critères s’expriment ainsi :

où N : nombre de valeurs observées; Q_sim : débits simulés (m³∙s-¹); Q_obs : débits observés (m³∙s^-1); : valeur moyenne des débits observés (m³∙s^-1).

Une comparaison entre le bilan mensuel d’eau simulé et celui observé a aussi été effectuée lors du calage et de la validation du modèle. Cette comparaison est exprimée par le critère de l’erreur relative sur le volume d’écoulement total :

où V_sim : volume total simulé (m³); V_obs : volume total observé (m³).

Pour l’analyse des résultats de simulation, une valeur de 1 pour le critère de Nash-Sutcliffe signifie que les simulations coïncident exactement avec les observations. De plus, les résultats sont d’autant meilleurs que le critère de Nash se rapproche de 1. Par contre, une valeur inférieure à 0 signifie que la simulation est moins bonne pour représenter les valeurs observées que la moyenne des observations. Pour la RCEQM, celle-ci permet de mesurer si la simulation a tendance à surestimer ou à sous-estimer les apports. L’objectif est d’obtenir une valeur proche de 0. Enfin, la valeur de l’ERSVET recherchée est celle qui est proche de 0.

3 Résultats et discussion

Suite au calage, les valeurs de Kc obtenues varient entre 0,7 et 1,3 selon chaque stade de croissance, tel qu’indiqué au tableau 7.

Tableau 7

**Paramètres ajustés du sous-modèle des rizières.**

**Adjusted parameters of the rice field sub-model.**

Les hydrogrammes simulés pour la période de calage, en tenant compte du fonctionnement hydrologique des rizières, et observés en période de culture du riz en saison des pluies dans le bassin versant de la rivière Cau sont présentés à la figure 8. Ces résultats montrent que les courbes de débits simulés et observés se superposent assez bien. Les pics principaux des crues de simulation et d’observation ont la même amplitude; il existe une seule différence plus marquée, soit celle du pic simulé le 15/07/2007. Les décalages entre les deux courbes de débits simulés et observés sont acceptables.

Figure 8

**Hydrogrammes simulés et observés à la station Gia Bay en saison des pluies sur la période 2006-2007 (période de calage).**

**Simulated and observed hydrographs at Gia Bay station in rainy season during the 2006-2007 period (calibration period).**

Le calcul des trois indicateurs de performance du modèle a permis d’obtenir sur la période de calage les valeurs suivantes : 0,72 pour le coefficient de Nash, 1,08 pour la RCEQM et 6 % pour l’ERSVET. On considère que ces valeurs sont très acceptables.

On retrouve à la figure 9 les hydrogrammes observés et simulés à la station Gia Bay pour la période de validation. Pendant cette période, les débits simulés représentent assez bien les débits observés. Les courbes de débits simulés et observés se superposent bien. Les pics des crues simulés et observés ont des amplitudes similaires. Les trois indicateurs de performance du modèle dans la période de validation sont : 0,78 pour le coefficient de Nash, 2,17 pour la RCEQM et 11 % pour l’ERSVET. Ces résultats montrent que les valeurs des paramètres de calage du modèle Hydrotel avec le fonctionnement hydrologique des rizières sont acceptables.

Figure 9

**Hydrogrammes simulés et observés à la station Gia Bay en saison des pluies sur la période 2008-2009 (période de validation).**

**Simulated and observed hydrographs at Gia Bay station in rainy season during the 2008-2009 period (calibration period).**

Enfin, la comparaison des résultats de simulations hydrologiques avec et sans la prise en compte du fonctionnement des rizières a été effectuée. L’objectif est d’évaluer le niveau d’amélioration des résultats de simulation. Pour ce faire, deux situations différentes ont été considérées : 1) simulation sans faire de distinction entre le fonctionnement hydrologique des rizières et celui des autres surfaces agricoles (sans prise en compte du sous-modèle des rizières) et 2) simulation en tenant compte d’une différence de fonctionnement hydrologique entre les rizières et les autres surfaces agricoles (en utilisant le nouveau sous-modèle des rizières). Dans le cadre de cette évaluation, la carte d’occupation du territoire élaborée par HOANG (2014) (Figure 6) a été utilisée. Tel que présenté au tableau 8, les résultats ont permis d’améliorer les indicateurs de performance des modèles, c’est-à-dire que l’ajout du sous-modèle des rizières a conduit à une amélioration de la simulation hydrologique. Le coefficient de Nash passe de 0,66 à 0,73; la RCEQM est quasiment constante et l’erreur relative sur le volume de l’écoulement total passe de 6,6 à 2,2 %. Même si le niveau d’amélioration peut apparaître comme n’étant pas significatif, il est important de rappeler que, dans le bassin versant de la rivière Cau, la surface de rizières représente seulement 4,3 % de la surface du bassin versant.

Tableau 8

**Comparaison des indicateurs de performance sur la période 2006-2009.**

**Comparison of performance indicators over the 2006-2009 period.**

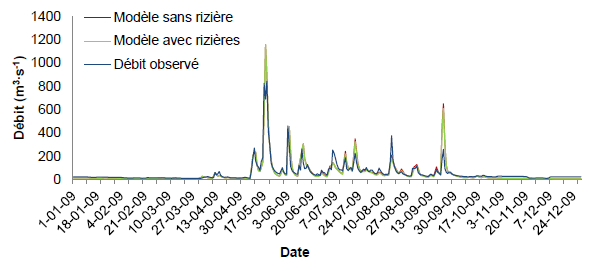
Les hydrogrammes simulés et observés sont également présentés aux figures 10 à 14. Ces courbes montrent que la simulation avec le sous-modèle des rizières reproduit généralement mieux les observations qu’ Hydrotel sans les rizières. Notamment, on peut observer sur ces figures que sans les rizières, les débits de pointe sont plus élevés et que l’impact de la modélisation des rizières a pour effet de réduire les débits de pointe, ce qui de fait les rapproche des débits observés. Cet impact apparaît donc comme significatif, malgré le fait que la superficie des rizières soit faible sur le bassin versant de la rivière Cau.

Figure 10

**Amélioration de la simulation de 2006 à la station Gia Bay.**

**Improvement of the 2006 simulation at Gia Bay station.**

Figure 11

**Amélioration de la simulation de 2007 à la station Gia Bay.**

**Improvement of the 2007 simulation at Gia Bay station.**

Figure 12

**Amélioration de la simulation de l'été 2007 à la station Gia Bay.**

**Improvement of the summer of 2007 simulation at Gia Bay station.**

Figure 13

**Amélioration de la simulation 2008 à la station Gia Bay.**

**Improvement of the 2008 simulation at Gia Bay station.**

Figure 14

**Amélioration de la simulation de 2009 à la station Gia Bay.**

**Improvement of the 2009 simulation at Gia Bay station.**

4 Conclusion

Nous avons présenté dans cet article un sous-modèle qui rend compte du fonctionnement des rizières. Bien que la surface des rizières ne représente que 4,3 % de la superficie du cas d’étude, la différence entre les résultats avec ou sans modélisation des rizières démontre l’importance de la simulation des rizières à l’échelle du bassin versant. Ces résultats démontrent aussi l’efficacité du modèle de rizière à bien simuler leur comportement et leurs impacts sur le régime hydrologique du bassin.

Le modèle pourra donc être utilisé pour réaliser des études sur l’impact des rizières sur les ressources en eau de bassins versants. Il pourra être très utile pour évaluer la capacité d’un système hydrologique à faire face à l’implantation de nouvelles rizières. Dans le cas où les rizières sont alimentées à partir d’un réservoir, il permettra d’effectuer une gestion rationnelle de celui-ci.

Modélisation des rizières irriguées et intégration dans hydrotel : application au bassin versant de la rivière Cau au VietnamIrrigated rice fields modeling and implementation in Hydrotel: application to the Cau River watershed in Vietnam

Résumé

Abstract

1. Introduction