Régionalisation d'une méthode de prédétermination de crue sur l'ensemble du territoire français : la méthode SHYREG Regionalization of a flood frequency estimation method over metropolitan France: the SHYREG method

Résumé

La méthode SHYREG a été développée pour la connaissance régionale des quantiles de débits de crue (débit de pointe et lames d'eau maximales écoulées sur les durées de 1 h à 72 h) pour les périodes de retour de 2 à 100 ans suivant une approche spatialisée. Elle associe un simulateur de pluies horaires et une modélisation simple pluie-débit, mis en oeuvre à une résolution kilométrique. Les quantiles de débits se déduisent directement des distributions de fréquence empiriques des valeurs maximales extraites des très longues chroniques de débit simulées. On obtient alors une base de quantiles de crues que l'on peut agréger à l'échelle de n'importe quel bassin versant, moyennant une règle d'abattement avec la surface. La régionalisation de la méthode a été réalisée sur la France métropolitaine, à l'exclusion de la Corse, en exploitant les données hydrométriques de 1 359 stations de jaugeage et des caractéristiques hydro-climatiques et hydrogéologiques spatialisées permettant de décrire la variabilité du paramètre saisonnier du modèle. Au final, cette régionalisation permet la connaissance des quantiles de débits de crue en tout bassin versant de la France métropolitaine avec une bonne restitution des quantiles de débit de pointe et journalier, pour les périodes de retour comprises entre 2 et 10 ans : un critère de Nash minimum de 80 % est obtenu sur les quantiles de débit de pointe pseudo-spécifique et de débit journalier spécifique des bassins versants non utilisés pour la régionalisation.

Mots clés:

• prédétermination des crues,
• approche spatialisée,
• modèle pluie-débit,
• régionalisation,
• territoire français

Abstract

The SHYREG method was developed for regional flood frequency analysis to estimate peak flow and flood discharges for various durations (1 h to 72 h) and return periods (2 to 100 years), according to a spatialized approach. For each 1-km² pixel, the method combines an hourly rainfall model with a simple rainfall-runoff model. The discharge flood frequency estimates are deduced directly from the empirical frequency distributions for the maximum values, which are extracted from very long simulated discharge time series. This gives a database of 1-km² gridded flood quantiles that can be aggregated for any catchment by using an areal averaging method. The method was regionalized for metropolitan France, excluding Corsica, using flow data from 1,359 gauging stations and regional hydroclimatic and hydrogeological characteristics to describe the variability of the rainfall-runoff model parameter. Such regionalization provides flood discharge quantiles for any catchment in metropolitan France for various durations and return periods. Regarding the method performance, accurate estimates of flood quantiles were produced for peak discharge and mean daily discharge for return periods of two to 10 years for gauged basins in dependent validation and cross-validation. A minimum NASH criterion of 80% is obtained for peak flow and mean daily discharge for the catchments not used in the regionalization process.

Key words:

• flood frequency estimation,
• spatialized approach,
• rainfall-runoff model,
• regionalization,
• French territory

1. Introduction

En France métropolitaine, les enjeux humains et économiques liés au « risque inondation » étant, du fait de l'accroissement de l'urbanisation, de plus en plus importants, une politique de prévention a été mise en place par le ministère de l'Écologie, du Développement durable et de l'Énergie (MEDDE) à travers l'élaboration de Plans de Prévention des Risques inondation -PPRi- (MATE-METL, 1999). Le débit de référence retenu pour ces PPRi est défini par le débit centennal ou par le plus fort débit historique s'il excède le débit centennal. Les mesures de débits sur les bassins versants de superficie inférieure à quelques centaines de kilomètres carrés étant très peu nombreuses, la plupart des PPRi sont élaborés sur la base d'une estimation du débit centennal par des méthodes faisant appel à l'extrapolation (spatiale et fréquentielle).

La détermination de ce débit centennal repose généralement soit sur une étude statistique de la chronique des débits observés, soit sur une modélisation de la pluie en débit, et nécessite donc des informations hydro-climatologiques qui ne sont disponibles que pour les bassins versants jaugés.

La majorité des bassins versants n'étant pas jaugés ou ne disposant pas d'une chronique de mesures suffisamment longue et fiable, le débit centennal est alors déterminé par les méthodes classiques de l'hydrologie française que l'on peut classer en trois catégories (HINGRAY et al., 2009; LANG et LAVABRE, 2007) :

Les formules empiriques régionalisées pour lesquelles le débit est directement relié à la superficie du bassin versant et à des paramètres intégrant, d'une part, la pluviométrie et l'aptitude au ruissellement du bassin versant et, d'autre part, l'abattement des pluies et l'amortissement de l'hydrogramme de crue dans le réseau hydrographique. Dans cette catégorie, on retiendra la formule dite de Bressand-Golossof, établie pour les bassins versants du département du Gard à partir des courbes enveloppes de 150 bassins versants du Languedoc et du Roussillon et de superficie allant de 20 à 400 km² (BRESSAND et GOLOSSOF, 1996), qui fournit des débits de pointe de périodes de retour proches de 100 ans et 1 000 ans, la synthèse des débits de période de retour 1 000 ans calculée par la méthode du Gradex (DUBAND et al., 1988) sur 170 bassins versants de superficie comprise entre quelques km² et quelques milliers de km², et les courbes-enveloppes de FRANCOU et RODIER (1967) établies à partir des crues maximales de 1 400 bassins versants dans le monde de superficies de 0,01 à 1 000 000 km². Notons également les formules Crupedix (MINISTÈRE DE L'AGRICULTURE, 1980a) et Socose (MINISTÈRE DE L'AGRICULTURE, 1980b) qui nécessitent la connaissance de variables climatiques (pluviométrie et température) pour l'estimation du débit de pointe décennal.

La méthode rationnelle (KUICHLING, 1889) et la méthode SCS (Soil Conservation Service) (UNITED STATES DEPARTMENT OF AGRICULTURE, 1985) sont des exemples de modèles hydrologiques simplifiés préparamétrés largement utilisés en ingénierie.

Notons enfin deux exemples de modèles fréquentiels régionaux calés au préalable sur des sites jaugés : les courbes QdF adimensionnelles de référence (GALÉA et PRUDHOMME, 1997) permettent, moyennant la connaissance de deux descripteurs locaux (la durée caractéristique de crue et le débit de pointe décennal), de déterminer les débits toutes durées et toutes fréquences sur un site quelconque et le modèle QdF régional convergent (JAVELLE et al., 2002) inspiré de la méthode de l'Indice de crue (DALRYMPLE, 1960).

Ces méthodes peuvent donner des résultats très différents, ce qui génère une hétérogénéité des débits de référence des PPRi non souhaitée du fait du caractère réglementaire de ces dossiers.

Dans ce contexte, la méthode SHYREG, basée sur une régionalisation de la méthode SHYPRE (ARNAUD et LAVABRE, 1999; ARNAUD et LAVABRE, 2001; ARNAUD et LAVABRE, 2002; ARNAUD et al., 2006; ARNAUD et al., 2007), a la particularité de synthétiser l'ensemble de l'information pluie et de l'information débit d'une région, pour proposer des estimations de débits de crue en tout point du réseau hydrographique de cette région.

Elle a été appliquée aux régions Languedoc-Roussillon et Provence-Alpes-Côte-d'Azur puis au sud de la France (LAVABRE et al., 2003, ORGANDE, 2008).

Cet article décrit la méthode SHYREG et le travail réalisé pour son application à l'ensemble du territoire de la France Métropolitaine.

2. La méthode SHYREG

La méthode SHYREG (LAVABRE et ARNAUD, 2010) est la version régionalisée de la méthode SHYPRE (Simulation d'HYdrogrammes pour la PREdétermination des crues) développée au groupement d'Aix-en-Provence de Irstea. Elle s'appuie sur les travaux de CERNESSON (1993), CERNESSON et al. (1996), ARNAUD (1997) et ARNAUD et LAVABRE. (1999). La méthode associe un générateur de chroniques de pluies horaires et une transformation de la pluie en débit. Des scénarios de pluies horaires sont générés suivant des caractéristiques déterminées pour deux saisons distinctes : la « saison hiver », de décembre à mai, et la « saison été », de juin à novembre. Les techniques de simulation stochastiques permettent de générer de très longues chroniques de pluies horaires (sur 100 000 ans, par exemple) transformées en hydrogrammes de crue par application d'une modélisation simple de la pluie en débit. Un simple classement des pluies maximales et des débits maximums simulés permet de tracer les distributions de fréquence « empiriques » des pluies et des débits de toutes durées (de 1 h à 72 h par exemple) et d'en déduire les quantiles pour une large gamme de périodes de retour, de 2 à 100 ans par exemple.

Le générateur de pluie horaire de SHYREG est paramétré par trois paramètres journaliers, NE (nombre moyen d'événements par saison) caractérisant l'occurrence des pluies fortes, PJmax (moyenne des pluies journalières maximales de chaque événement) permettant de caractériser l'intensité des pluies et Dtot (durée moyenne des événements) informant sur la durée des événements pluvieux, qui ont été régionalisés sur la France, au km² par la méthode Aurelhy (MÉTÉO FRANCE, 2005). La seule connaissance de ces trois paramètres permet d'estimer les paramètres décrivant la structure temporelle des événements pluvieux nécessaires à la génération stochastique de pluie horaire.

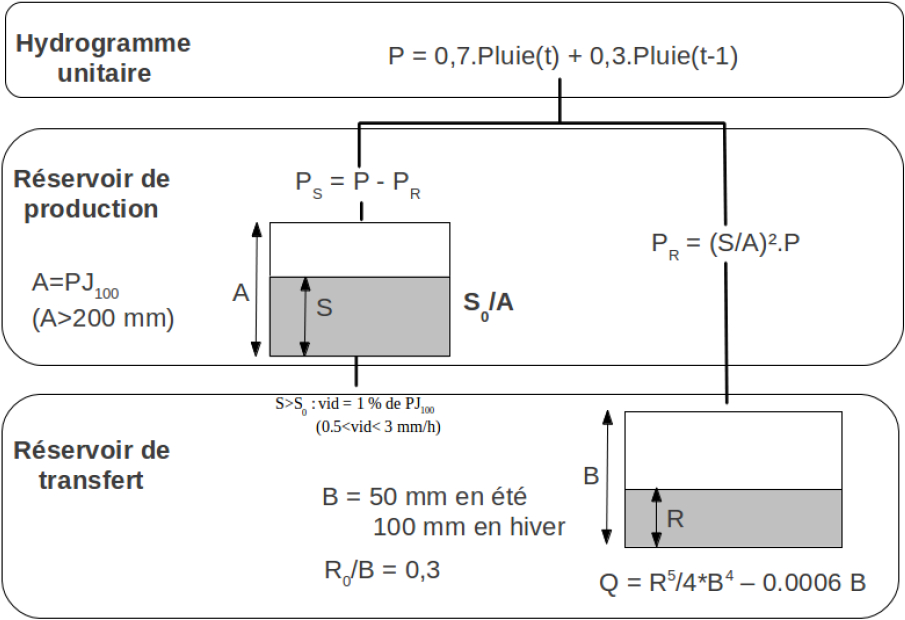
Les pluies horaires générées à chaque pixel du territoire sont transformées par le modèle pluie-débit au pas de temps horaire GR simple (GRS) (ARNAUD et al., 2011) pour disposer de longues chroniques d'hydrogrammes de crue (Figure 1).

Figure 1

Structure de GR3H simplifié : GR simple (GRS).

Simplified GR3H structure: simple GR model (GRS).

Le modèle GRS est une version simplifiée du modèle GR3H (MICHEL, 1989; YANG, 1993). Il est composé de deux réservoirs non linéaires : un premier réservoir de capacité maximale notée A et de niveau de remplissage noté S sert à modéliser la production du ruissellement de la pluie, et un second réservoir de capacité maximale B et de niveau de remplissage R sert à modéliser le transfert du ruissellement de la pluie à l'exutoire.

La pluie passe tout d'abord par un hydrogramme unitaire (HU) très simple qui la répartit sur 2 h (70 % de la pluie au pas de temps t et 30 % au pas de temps suivant t + 1), afin d'effectuer un lissage des intensités de pluies.

Le réservoir A assure une production non linéaire : la part de la pluie qui ruisselle vers le réservoir B (P_R) est proportionnelle au carré du niveau de remplissage du réservoir A (S/A). La part de la pluie qui ne ruisselle pas (P_S) remplit le réservoir A qui se vidange par un débit perdu constant (vid) valant 1 % de la pluie journalière centennale du pixel (1 % de PJ100) tout en respectant l'intervalle [0,5 mm•h^‑1; 3 mm•h^‑1]. Le volume de A est égal à la pluie journalière centennale du pixel avec une borne inférieure à 200 mm. Cette paramétrisation permet, d'une part, de s'assurer d'une saturation du modèle pour les pluies de fréquences rares et, d'autre part, de ne pas ajouter de paramètre à caler.

Le réservoir B assure un transfert non linéaire : le débit sortant de B est proportionnel au niveau de remplissage R⁵ de B. Le volume de B est unique pour tous les pixels mais fonction de la « saison » : 100 mm pour la « saison hiver » et 50 mm pour la « saison été ». Ces valeurs ont été choisies suite à l'étude de petits bassins versants (GRAFF, 2005).

À chaque pas de temps, le niveau des réservoirs (S et R) sont mis à jour de façon à respecter le bilan de masse.

L'initialisation du modèle pour chaque événement de pluie consiste à définir le niveau de remplissage des réservoirs A (noté S₀/A) et B (noté R₀/B). R₀/B est fixé à 30 %. Le paramètre S₀/A est alors l'unique paramètre que l'on s'autorisera à faire varier lors du calage de la méthode, les autres paramètres étant fixés aux valeurs présentées ici.

Les crues générées par le modèle GRS sont ensuite analysées de façon classique, comme un échantillon de crues observées, pour en extraire les distributions de fréquence des débits de différentes durées et ainsi les quantiles de débit au km². Ces valeurs sont alors tributaires de la valeur du paramètre S₀/A que l'on aura choisi.

L'intégration des quantiles de débit au km² à l'échelle du bassin versant est assurée par une fonction d'abattement notée FTS (RONSOUX FOUCHIER, 2010). Cette règle d'addition des débits des pixels contenus dans le bassin versant se caractérise par un abattement fonction de la superficie du bassin qui intègre à la fois l'abattement de la pluie avec la surface et l'abattement des débits dans le réseau hydrographique. Elle varie avec la durée (d) du débit considéré. La formulation mathématique de la FTS établie pour les débits de durée supérieure et de durée inférieure à 24 h est la suivante :

(1)

(2)

où Q(d,T) représente le débit de durée d et de période de retour T à l'exutoire du bassin versant de superficie S. q_i est le quantile de débit estimé au pixel i de 1 km² et n le nombre de pixels contenus dans le bassin versant. La formulation proposée permet ainsi de créer un abattement plus fort pour les débits de courte durée, afin d'intégrer l'étalement des hydrogrammes pour les bassins les plus grands.

Ainsi, la détermination des quantiles de débit par SHYREG repose sur la régionalisation de l'unique paramètre S₀/A, variant entre les valeurs 0 et 1.

La première partie de cet article vise à présenter les données utilisées pour le calage du paramètre S₀/A. La seconde partie traite de la méthode employée pour la régionalisation du paramètre S₀/A; les résultats obtenus et le contrôle de leur pertinence font l'objet des deux dernières sections.

3. Données hydrométriques

Le calage du paramètre S₀/A sur un bassin jaugé est basé sur la capacité de la méthode SHYREG à retrouver les quantiles de débits de pointe (Qp) et journaliers (QJ) de périodes de retour 2, 5 et 10 ans pour les deux saisons étudiées. Ces quantiles ont été calculés à partir des chroniques de débit disponibles dans la banque HYDRO (http://www.hydro.eaufrance.fr/), base de données hydrométriques nationale. Une sélection des stations de mesures a été effectuée de façon à retenir seulement les bassins versants de moins de 2 000 km² (domaine d'application actuel de la méthode) et présentant au moins dix années d'observation pour s'assurer une représentativité minimale de la chronique lors de l'estimation des quantiles dits « courants » (périodes de retour 2, 5 et 10 ans). Ces conditions conduisent à retenir 1 751 stations hydrométriques pour lesquelles les contours des bassins versants (tracé automatique sous SIG à partir du Modèle Numérique de Terrain issu de la mission SRTM pour la France et son voisinage au pas de 75 m : srtm.usgs.gov) présentent un écart de superficie avec celle fournie par la banque HYDRO (http://www.hydro.eaufrance.fr/) inférieure à 20 %.

Une analyse critique de la fiabilité de ces données a été réalisée en s'appuyant sur les éléments suivants : (i) informations qualitatives disponibles auprès de la banque HYDRO, (ii) analyse visuelle des distributions et des ajustements des débits de crues, (iii) analyse de l'homogénéité géographique de la station.

Compte tenu de la quantité importante de stations, seules les stations répondant à des critères précis sont analysées plus spécifiquement. Ces critères sont d'ordre qualitatif (disponibles auprès de la banque HYDRO) : stations influencées (e.g. barrages), bassins versants à caractère karstique, stations de qualité « douteuse » en hautes eaux.

Concernant les critères d'ordre quantitatif, le premier critère permet de juger de la pertinence de l'ajustement statistique : une loi GEV (Generalized Extreme Value) est ajustée sur les chroniques de débit maximum, la fonction de répartition étant donnée par l'équation 3 :

(3)

avec :

• a : paramètre de position;

• b : paramètre d'échelle;

• c : paramètre de forme.

Les stations dont le paramètre de forme c (équation 3) est inférieur à -0,5 sont analysées.

Pour le deuxième critère quantitatif, la formule Crupedix (équation 4) (Ministère de l'Agriculture, 1980b) d'estimation du débit de pointe décennal est utilisée pour juger de l'homogénéité régionale de ces débits pour chaque station.

(4)

• S : superficie du bassin versant en km²

• Pj : pluie journalière décennale en mm

• R : coefficient régional.

La formule classique suppose les valeurs suivantes : k = 1, P₀ = 80 mm, α = 0,8 et β = 2.

Pour chaque « saison », les paramètres k, P0, α et β de l'équation 4 sont ajustés afin de maximiser le critère de Nash (Équation 5) entre le débit de pointe décennal dit « observé » d'après l'ajustement de la loi GEV et le débit de pointe décennal calculé avec la formule Crupedix. Afin de faire disparaître l'influence de la superficie des bassins versants, le critère de Nash est calculé à partir des débits pseudo-spécifiques (QI₁₀/S^0,8; S superficie en km²).

(5)

On obtient des critères de Nash de respectivement 72 % et 79 % en hiver et en été. Les bassins versants dont le débit de pointe décennal « observé » s'éloigne de la tendance régionale proposée par l'équation 4 optimisée (i.e. ratio Q_p¹⁰_observé/Q_p¹⁰_calculé inférieur à 0,5 ou supérieur à 2) sont alors examinés.

Sur les 1 751 stations retenues initialement, 839 ont fait l'objet d'une critique spécifique sur la base des critères évoqués précédemment.

Cette analyse conduit à trois types d'actions distinctes :

1. Station conservée : distribution et ajustement statistique fiables;

2. Station rejetée : distribution et ajustement statistique non fiables ou non homogène régionalement et informations qualitatives défavorables;

3. Demande d'informations complémentaires auprès des gestionnaires : doute sur l'homogénéité régionale et absence d'informations qualitatives pour orienter la décision.

L'analyse de ces stations a amené à rejeter 185 stations et à questionner les gestionnaires au sujet de 183 autres. Après traitement des réponses des gestionnaires, l'échantillon exploité pour le calage du paramètre du modèle pluie-débit (S₀/A) est de 1 493 stations.

4. Régionalisation du modèle pluie-débit

4.1. Détermination des valeurs optimales du paramètre unique du modèle

Suite à l'analyse critique des données hydrométriques, les quantiles de débit de pointe de crue et les quantiles de débit journalier de période de retour 2, 5 et 10 ans, pour chaque « saison », ont été déterminés par l'ajustement d'une loi GEV pour les 1 493 stations sélectionnées. Le choix de la loi de probabilité a relativement peu d'influence sur les résultats de la méthode car elle n'est pas utilisée en extrapolation, mais pour estimer des quantiles courants (2, 5 et 10 ans).

Le calage du paramètre S₀/A pour un bassin versant est réalisé de la façon suivante. Le générateur de chroniques de pluie horaire est activé pour chaque pixel (1 km x 1 km) du bassin, avec son paramétrage régional. Au total, 50 000 années sont simulées de manière à obtenir une stabilisation de la distribution de fréquence des débits jusqu'à la période de retour millennale. Le modèle pluie-débit qui assure la transformation de ces chroniques de pluie en hydrogrammes de crue en chaque pixel, est mis en oeuvre avec une valeur de S₀/A homogène sur tous les pixels du bassin excepté les pixels spécifiques (voir ci-dessous). Les quantiles fournis en chaque pixel sont ensuite agglomérés et abattus par la FTS et comparés avec les quantiles courants ajustés précédemment par la loi GEV. Puis, de façon itérative, on cherche à optimiser la valeur de S₀/A (homogène sur le bassin) de façon à minimiser les écarts entre les quantiles de débit dits « observés », issus de l'ajustement statistique des débits, et les quantiles de débits « simulés » par la méthode. Le critère d'écart utilisé est la somme des valeurs absolues des écarts relatifs entre les quantiles « observés » et les quantiles « simulés » pour les trois périodes de retour de 2, 5 et 10 ans. Après différents tests, l'optimisation offrant les meilleures résultats est celle donnant plus de poids à la période cinq ans (poids de 2), les autres périodes de retour ayant un poids de 1.

Pour les pixels concernés par une occupation des sols spécifique, associée à un ruissellement fort et que nous supposons peu sensible à d'autres caractéristiques (types de sol, de végétation, de topographie, etc.), une valeur minimale du paramètre S₀/A est imposée comme suit :

• « tissu urbain continu » (classe 1.1.1 de Corine Land Cover) : S₀/A = 0,9 (ruissellement important);

• « tissu urbain discontinu » (classe 1.1.2 de Corine Land Cover) et « zones industrielles ou commerciales » (classe 1.2.1 de Corine Land Cover) : S₀/A_hiv = 0,7; S₀/A_été = 0,6 (ruissellement plutôt important);

• « zones humides intérieures et eaux continentales » (respectivement classes 4.1 et 4.2 de Corine Land Cover) : S₀/A = 1 et B = 300 mm (ruissellement total et effet d'amortissement du plan d'eau).

Les autres types d'occupation des sols ne permettent pas de dégager des valeurs de S₀/A a priori. Ils seront utilisés si une corrélation est observée avec les valeurs optimisées du paramètre.

Les résultats du calage sont synthétisés par le graphique de la figure 2 où chaque point correspond à la valeur optimale du paramètre pour les saisons « hiver » et « été » pour un bassin versant. De façon générale, la « saison hiver » conduit à un paramètre globalement plus fort que pour la « saison été », traduisant une saturation des sols plus marquée pour cette période de l'année. On note également une liaison significative (R² = 0,54) entre les valeurs saisonnières du paramètre (i.e., les bassins productifs en hiver le sont aussi en été).

Figure 2

Résultats de calage : relation entre S₀/Astat hiver et S₀/Astat été.

Calibration results: relationship between S₀/Astat «winter» and S₀/Astat «summer».

La détermination du paramètre optimal saisonnier de chaque bassin versant conduit à une très bonne restitution des quantiles de débit dits « observés », avec un critère de Nash variant de 90 % à 97 % sur les débits pseudo-spécifiques (Q_P/S^0,8) et spécifiques (Q_J/S). Qp et QJ sont respectivement le débit de pointe et le débit journalier en m³•s^‑1 et S la superficie en km². Ces résultats montrent qu'en calant seulement un paramètre, la méthode est capable de rendre compte de la distribution de fréquences des débits d'un bassin versant.

Les bassins versants pour lesquels l'« écart moyen » entre les quantiles « simulés » et les quantiles « observés » est supérieur à 20 % pour au moins une des deux « saisons » sont examinés : 28 bassins versants sont alors rejetés car jugés peu fiables et 106 autres sont retirés de la régionalisation en l'absence de réponse aux questionnaires soumis aux gestionnaires pour obtenir des éléments nécessaires à l'argumentation du choix. On considère alors que, pour les 1 359 bassins versants restant pour effectuer la régionalisation, la méthode est capable de fournir des quantiles en adéquation avec les observations, moyennant la connaissance d'un seul paramètre, S₀/A. Le fait que la méthode puisse se caler avec un unique paramètre facilite les possibilités de régionalisation.

Sélection de variables explicatives spatialisées

L'objectif est d'identifier des variables spatialisées pour estimer les valeurs optimales saisonnières du paramètre S₀/A pour tout bassin, jaugé ou non jaugé.

Une difficulté apparaît dans le cas où un pixel est associé à plusieurs bassins versants emboîtés, et donc à plusieurs valeurs de S₀/A optimales. Dans ce cas, après plusieurs essais de combinaison des différentes valeurs de S₀/A communes au pixel, il a été choisi de donner la priorité à la valeur associée au plus petit bassin : ainsi, lors de la création de la grille du paramètre S₀/A, la valeur pour un pixel commun à plusieurs bassins versants sera associée à celle du plus petit bassin versant. À partir de cette grille, certains bassins verront leur paramètre optimum modifié. Le tableau 1 présente un exemple de modification de la valeur optimale du paramètre, lors de sa mise en forme de grille, nécessaire pour avoir une valeur par pixel dans la version régionale de la méthode.

Tableau 1

Règle de traitement des bassins emboités.

Processing rule for nested catchments.

L'objectif suivant est alors d'identifier des variables spatialisées permettant d'expliquer au mieux la variabilité du paramètre cartographié (Figure 3).

Figure 3

Cartographie du paramètre S₀/A optimum pour la « saison été ».

Mapping of the optimum S₀/A parameter for the summer season.

Pour cela, des variables explicatives de différents types sont étudiées dans le but de retenir la meilleure régression linéaire possible.

Des variables journalières régionalisées du modèle de génération de pluie horaire SHYPRE : PJMAX (moyenne des pluies journalières maximales de chaque événement, en mm); DTOT ( durée moyenne des événements, en jours); NE (nombre moyen d'événements par « saison »).

Des indices statistiques de bilan hydrique : S/A_clim et S/A_clim20, correspondant au niveau de remplissage moyen du réservoir de production d'une version journalière et continue du modèle GR : GR4J (PERRIN et al., 2003) fonctionnant avec des données de pluie journalière et d'évapotranspiration potentielle (ETP) fournies par Météo-France (données SAFRAN). Le premier indice est calculé à partir de toutes les pluies journalières, le second avec les pluies journalières dépassant 20 mm.

Des caractéristiques climatiques issues des données SAFRAN (Météo-France) : valeur annuelle moyenne d'évapotranspiration potentielle (ETP_an), valeur annuelle moyenne de pluie journalière (PJ_an) et valeur annuelle moyenne de précipitation neigeuse (NEI_an).

Indice de drainage : cumul_reseau calculé à partir du réseau hydrographique de base de données CARTHAGE. Ce paramètre calculé au km² correspond au pourcentage de pixel de 100 m par 100 m traversé par le réseau hydrographique. La variable peut théoriquement varier de 0 à 100.

L'occupation des sols caractérisée à l'aide de la base de données Corine Land Cover (http://www.eea.europa.eu).

Variables morphometriques : l'altitude moyenne et la pente moyenne (moyenne de la pente aux pixels contenus dans le bassin versant) du bassin versant calculées à partir d'un Modèle Numérique de Terrain (mission SRTM au pas de 75 m).

Toutes ces variables sont disponibles sous forme de grille au km² et sur l'ensemble du territoire français, ce qui permet de calculer une valeur moyenne par bassin versant.

Il est ensuite recherchée la meilleure régression linéaire des valeurs moyennes des variables explicatives pour estimer la valeur saisonnière optimale de S₀/A des bassins. Pour cela, les régressions linéaires à deux et trois variables explicatives sont évaluées par validation croisée. L'ensemble des 1 359 bassins versants est aléatoirement séparé en un échantillon de calage (2/3 de l'ensemble) et en un échantillon de validation (1/3 de l'ensemble). À partir de l'échantillon de calage sont recherchées toutes les régressions linéaires possibles, puis ces régressions sont appliquées aux bassins versants de l'échantillon de validation. Un processus itératif permet alors de retenir les variables les plus performantes pour estimer les valeurs saisonnières optimales de S₀/A.

Ces variables sont enfin utilisées pour déterminer les paramètres des régressions linéaires sur l'échantillon complet des 1 359 bassins versants, explicitées dans les équations 6 et 7 .

(6)

(7)

Ces relations sont significatives et permettent d'expliquer une partie de la variabilité du paramètre. Cependant, elles ne sont pas suffisantes et vont être améliorées par la prise en compte de variables supplémentaires et par la spatialisation des résidus (partie du paramètre non expliquée) comme cela est décrit par la suite.

4.2. Élaboration des grilles régionales du paramètre saisonnier

L'élaboration des grilles régionales est réalisée en plusieurs étapes. La première étape consiste à établir une grille de valeur de S₀/A à partir des formules 6 et 7 : notée grille S₀/A_reg. Cette grille est ensuite améliorée grâce à l'utilisation de l'information issue de la carte hydrogéologique de la France (MARGAT, 1980) qui a été digitalisée pour les besoins de l'étude. Les entités hydrogéologiques ont été regroupées, selon leur capacité à produire du ruissellement, en 13 classes distinctes. Cette information étant qualitative, il a été fait le choix d'appliquer un coefficient correcteur associé à chacune des 13 classes hydrogéologiques. Cette correction est déterminée de manière à expliquer au mieux la variabilité du paramètre optimal. On obtient alors une grille notée S₀/A_reg-cor (Figure 4). Pour chaque pixel i, on a : S₀/Aⁱ_reg-cor = αⁱ_j x S₀/Aⁱ_reg; αⁱ_j, coefficient correcteur du pixel i lié à la classe hydrogéologique j du pixel.

Figure 4

Cartographie du paramètre S₀/A obtenu par régression et amélioré par l'hydrogéologie pour la « saison été ».

Mapping of the S₀/A obtained by regression analysis and enhanced by hydrogeological data for «summer season».

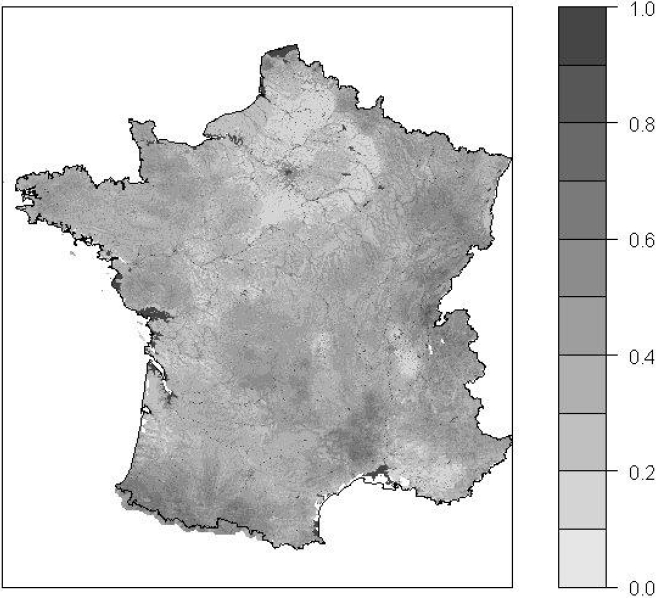
Enfin, les résidus calculés entre la valeur optimale du paramètre et celle obtenue par la régression linéaire multiple améliorée par l'hydrogéologie sont spatialisés par la fonction inverse du carré de la distance puis lissés par moyenne glissante. La carte finale est obtenue en sommant la grille des résidus à la précédente grille obtenue : grille S₀/A_regio (Figure 5).

Figure 5

Cartographie du paramètre S₀/A régionalisé pour la « saison été ».

Mapping of the regionalized S₀/A parameter for the « summer season ».

La spatialisation et le lissage des résidus sont un moyen de prendre en compte la partie de variabilité non expliquée, et pouvant être attribuée aux diverses incertitudes provenant de la modélisation hydrologique, de la pluviométrie mais également des difficultés métrologiques et statistiques (estimation des quantiles issus des observations).

Ainsi, bien que la prise en compte des résidus vise à restituer au mieux les quantiles « observés » aux stations jaugées, le processus d'élaboration des cartes régionales du paramètre S₀/A privilégie l'émergence d'une tendance régionale correcte nécessaire à une utilisation de la méthode en site non jaugé.

La cartographie finale permet la restitution de la valeur optimale du paramètre S₀/A avec un Nash de 78 % pour la « saison hiver » et de 84 % pour la « saison été ».

4.3. Qualité de la méthode de régionalisation

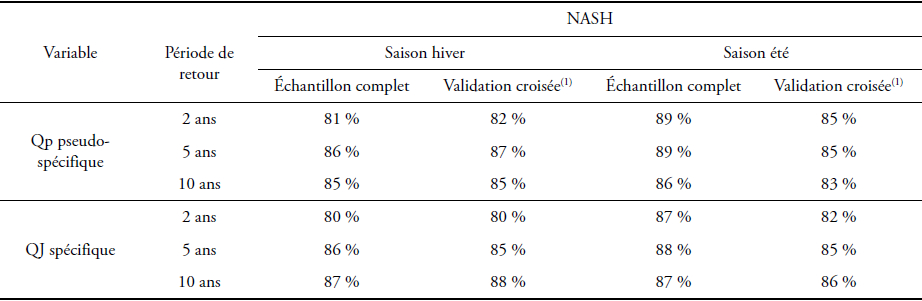
Afin de qualifier de façon objective la qualité de la restitution du paramètre S₀/A, dix grilles régionales de S₀/A ont été établies selon la méthodologie de validation croisée à partir de dix échantillons de bassins versants calage/validation choisis aléatoirement. À chaque étape de la méthode, le Nash est calculé sur les bassins versants de validation pour évaluer la qualité de restitution du paramètre optimal.

Le tableau 2 synthétise les critères de Nash obtenus entre la valeur optimale de S₀/A et sa valeur calculée aux différentes étapes de la régionalisation. Les valeurs des critères sont calculées, d'une part, à partir des grilles établies sur la base de tous les bassins versants et, d'autre part, à partir des dix grilles établies dans le cadre de la validation croisée.

Tableau 2

Critère de Nash caractérisant la qualité de la régionalisation de S₀/A (1 359 bassins versants).

Nash-Sutcliffe model efficiency coefficient (NSME) used to characterize S₀/A regionalization efficiency (1,359 catchments).

(1) : valeur médiane des 10 Nash calculés sur les 10 échantillons de validation

Les critères de Nash calculés par la validation croisée sur les bassins versants non utilisés pour la régionalisation sont très proches de ceux calculés à l'aide de tous les bassins versants. Ce point atteste de la robustesse des régressions linéaires (Équations 6 et 7) qui dépendent peu du choix des bassins versants qui ont servi à leur élaboration. Les résultats mettent également en évidence l'intérêt apporté par la prise en compte de l'hydrogéologie qui permet d'améliorer le critère de Nash de quatre à cinq points en été et de trois points en hiver.

La prise en compte des résidus spatialisés et lissés (passage de S₀/A_reg-cor à S₀/A_regio) augmente le critère de Nash de 17 points en été et de sept points en hiver pour l'approche validation croisée. Ceci tend à montrer que l'information contenue dans les résidus présente une signification régionale qui constitue une part non expliquée de la variabilité du paramètre S₀/A.

5. Résultats et discussion

La cartographie du paramètre S₀/A permet la mise en oeuvre du modèle pluie-débit et ainsi l'obtention de grilles de quantiles de débits au km² pour différentes périodes de retour (de 2 à 100 ans) et différentes durées (du débit de pointe à la lame d'eau en 72 h).

La figure 6 présente les cartes des débits décennaux et centennaux. Sur la majeure partie du territoire, on obtient des débits spécifiques inférieurs à 1,5 m³•s^‑1•km^‑2 pour l'occurrence décennale et inférieurs à 3 m³•s^‑1•km^‑2 pour l'occurrence centennale. Les débits supérieurs à ces valeurs sont localisés sur les zones urbaines (production importante), sur les secteurs montagneux, sur l'arc méditerranéen et plus particulièrement sur les Cévennes (zone qui connaît des épisodes orageux de pluviométrie importante).

Figure 6

Cartographie du débit de pointe décennal (a) et centennal (b) SHYREG en m³•s^‑1•km^‑2.

Mapping of SHYREG decennial (a) and hundred-year (b) peak flows in m³•s^‑1•km^‑2.

(a)

(b)

L'application de la FTS fournit alors les quantiles de débit de tout bassin versant de superficies comprises entre 10 et 2 000 km².

Les quantiles SHYREG ainsi obtenus peuvent être comparés aux valeurs issues des ajustements statistiques sur les distributions empiriques des débits « observés » aux stations hydrométriques ayant servi à la régionalisation (Tableau 3).

Tableau 3

Comparaison des quantiles SHYREG 1) avec les quantiles « observés » sur les bassins versants de la régionalisation, et 2) par validation croisée (1 359 bassins versants).

Comparison of SHYREG quantiles 1) with quantiles «observed» for regionalization catchments and 2) by cross-validation (1,359 catchments).

(1) : valeur médiane des 10 Nash calculés sur les 10 échantillons de validation

Les grilles de débit sont élaborées de manière à privilégier l'émergence d'une tendance régionale mais également avec l'objectif de restituer au mieux les quantiles « observés ». De ce fait, il paraît plus objectif de contrôler la méthode en comparant les quantiles SHYREG aux quantiles « observés » pour des bassins versants n'ayant pas servi à la régionalisation. C'est donc par le principe de la validation croisée que les critères de Nash sont établis entre les quantiles estimés par SHYREG et les quantiles « observés » (Tableau 3).

Les Nash médians obtenus par la validation croisée sont très proches de ceux obtenus sur les bassins versants de la régionalisation. Ce constat est très encourageant car il montre notamment que tous les critères de Nash calculés sur les quantiles pseudo-spécifiques (Q/S⁰,⁸) et spécifiques (Q/S : lame journalière) dépassent 80 % pour des bassins versants qui n'ont pas été utilisés pour la régionalisation du modèle pluie-débit.

Ces résultats sont à comparer aux performances obtenues avec l'optimisation de la formule Crupedix pour l'estimation du débit de pointe décennal (Section 3) qui, en phase de calage, aboutit à des Nash respectifs de 72 % et 79 % pour les saisons hiver et été.

Une autre façon d'analyser les performances de la méthode est de s'intéresser au rapport entre le débit « simulé » et le débit « observé ». Il est calculé pour le débit décennal de pointe et journalier pour chaque « saison » (Tableau 4).

Tableau 4

Statistiques des ratios Débit « simulé » / Débit « observé » (1 359 bassins versants).

Statistics on «simulated» discharge / «observed» discharge ratios (1,359 catchments).

Malgré une dispersion des ratios (minimum de 0,2 et maximums de 4,2 en « saison hiver » et 8 en « saison été »), leur distribution montre que l'estimation du débit de pointe décennal est comprise entre la moitié et le double du quantile « observé » pour 92 % des bassins versants pour la « saison hiver » et pour 96 % des bassins versants pour la « saison été ».

6. Conclusion et perspectives

La régionalisation du modèle hydrologique permet de disposer sur la zone d'étude (France métropolitaine) d'une base de quantiles de débits (débit de pointe et lames d'eau écoulées sur les durées de 1 h à 72 h pour les périodes de retour de 2 ans à 100 ans) qui permet, par l'application de la FTS (fonction d'abattement), d'obtenir les quantiles de débits de tout bassin versant de superficie comprise entre 10 et 2 000 km².

L'application de la méthode aboutit à des critères de Nash sur les quantiles pseudo-spécifiques (Q/S⁰,⁸) et spécifiques (Q/S : lame journalière) dépassant 80 % pour des bassins versants non utilisés pour la régionalisation du modèle pluie-débit.

Le processus d'élaboration des cartes du paramètre hydrologique saisonnier privilégie l'émergence d'une tendance régionale globale. La difficulté de l'exercice consiste à fournir une information pour tout bassin versant non jaugé. Le contrôle de la qualité de la méthode par validation croisée sur 1 359 bassins apporte la confirmation que celle-ci fournit une information pertinente, non pas uniquement sur les seuls bassins versants utilisés pour la régionalisation, mais sur tout le territoire étudié.

Bien que la méthode apporte des résultats plus performants au regard des méthodes régionales actuellement disponibles, des approfondissements restent à être menés afin de fiabiliser l'estimation des quantiles dans les fréquences rares et d'améliorer les résultats de la méthode en particulier en zones montagneuses (impact de la fonte des neiges sur le débit de base) et karstiques (bassins non traités par la méthode actuelle).