Résumés
Résumé
Le bassin hydrographique du Timis-Bega, d’une superficie d’environ 13 000 km2, est situé à l’ouest de la Roumanie. Le contexte orographique, l’influence climatique méditerranéenne, la nature et l’occupation du sol font que cette zone géographique relativement restreinte présente une assez grande diversité des écoulements. Cette dernière est considérée à travers le choix de 19 sous-bassins, de quelque km2 à plusieurs centaines de km2. La régionalisation des modules et des débits d’étiage du Timis-Bega a été entreprise à la suite de travaux analogues réalisés sur le bassin hydrographique de la Moselle française (GALÉA et CANALI, 2005). Ces travaux avaient montré l’adéquation de la loi de Weibull à deux paramètres pour décrire la variabilité temporelle et spatiale des modules annuels et des étiages des sous-bassins observés. Deux principaux résultats avaient été soulignés, l’un concernait la faible différenciation des lois régionales établies pour les modules et les étiages des années moyennes à « sèches » (F ≤ 0,5), l’autre mettait l’accent sur l’usage de jaugeages épisodiques d’étiage pour améliorer la performance des modèles régionaux. Notre propos est de vérifier ces considérations, établies pour le bassin de la Moselle, dans le contexte hydro-climatique du Timis-Bega. Les résultats obtenus permettent de confirmer tant l’aspect peu différencié des lois régionales que l’aspect amélioration de la performance des modèles régionaux. Plus précisément, cette amélioration résulte d’une meilleure précision, que celle obtenue par régression multiple classique, de l’estimation du descripteur de régime local, le module annuel médian ou le débit journalier médian d’étiage qui représente une source d’incertitude importante du modèle régional respectif. L’usage d’une information épisodique sur les débits d’étiage, concomitante à un site étudié et à un sous-bassin de référence, permet l’estimation du débit journalier médian et, par extension, celle du module annuel médian. Une explication à cette extension pourrait être trouvée dans la faible différenciation des lois régionales pour les fréquences moyennes à « sèches ». L’intérêt des jaugeages épisodiques d’étiage nous semble assez porteur pour être pris en considération lors d’une démarche ultérieure de régionalisation à bases géostatistiques des descripteurs de régime. Enfin, un résultat inattendu concerne la quasi similitude des lois régionales de la Moselle et du Timis-Bega tant en ce qui concerne les modules annuels que les étiages. Ce résultat, à considérer avec prudence, abonderait dans le sens de la théorie des régions hydrologiques homogènes.
Mots clés:
- Régionalisation,
- module annuel,
- étiage,
- modélisation statistique QdF
Abstract
The catchment area of Timis-Bega (13,000 km2) is located in the western part of Romania. The orographical context, the Mediterranean climatic influence, the nature of the ground and the vegetation contribute to this relatively restricted geographical area’s great diversity of flows. This latter characteristic is based on a study of 19 sub-basins, ranging in size from a few km2 to several hundred km2. The regionalization of annual mean discharge and low flow in the Timis-Bega catchment was undertaken following similar work realized on the French Moselle catchment. This earlier work showed that the two-parameter Weibull distribution adequately described the spatial and temporal variability of annual mean discharge and low flow for the studied sub-catchments. The two principal results of the preceding study were the weak differentiation among the regional models established for annual mean discharge and low flow, and the recommended use of episodic gauging of low flows for the improvement of the regional models. Our intention was to verify these preceding considerations, established for the French Moselle basin, in the hydro-climatic context of Timis-Bega. The results obtained allowed us to confirm the weak differentiation among the regional models as well as the improvement of the regional models. More specifically, this improvement resulted from the better precision, compared to that obtained by traditional multiple regression methods, of the estimation of the local discharge descriptor, the median annual mean discharge or the median minimal daily low flow discharge. The use of low flow episodic discharge measurements, that are concomitant between the studied and reference sub-catchments, allows the estimation of the median minimal daily low flow discharge and the median annual mean discharge. This fortuitous result is explained by the weak differentiation observed between the regional annual mean discharge model and the regional average low flow discharge model for average to dry years. We believe episodic measurements of low flow should be considered when collecting data that will be used for the generation of regionalization flow descriptors by geostatistical methods. Lastly, the similarities between the regional distributions of annual mean discharge and low flow for both the Moselle and Timis-Bega regions were unexpected. This result should, however, be considered with caution, as it implies the existence of homogeneous hydrological regions.
Key words:
- regionalization,
- annual mean discharge,
- low flow,
- statistical QdF modelling
Corps de l’article
1. Avant‑propos
Notre démarche de régionalisation des modules et des étiages des sous‑bassins du Timis-Bega s’inscrit logiquement dans la continuité des travaux menés sur le bassin hydrographique de la Moselle française (GALÉA et CANALI, 2005). Nous avions montré l’adéquation de la loi de Weibull à deux paramètres pour décrire la variabilité temporelle et spatiale des modules annuels et des étiages des sous-bassins observés. Deux principaux résultats avaient été soulignés. L’un concernait la faible différenciation des lois régionales établies pour les modules et les étiages des années moyennes à « sèches » (F ≤ 0,5), l’autre mettait l’accent sur l’usage de jaugeages épisodiques d’étiage pour améliorer la performance des modèles régionaux. Notre intention est de voir, entre autres, si ces considérations établies pour le bassin de la Moselle se vérifient dans le contexte hydro-climatique du Timis-Bega.
2. Contexte général et chroniques de débit disponibles des sous-bassins du Timis–Bega retenus
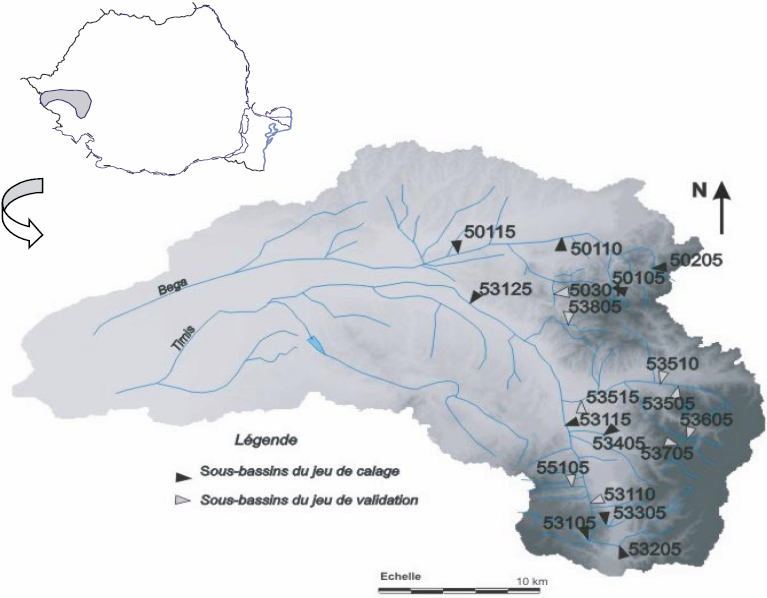
Le bassin hydrographique du Timis-Bega, d’une superficie d’environ 13 000 km2, est situé à l’ouest de la Roumanie. Les rivières Timis et Bega drainent respectivement 7 489 km2 et 5 248 km2. L’altitude moyenne (Zm) est de 415 m pour le bassin du Timis et de 236 m pour le bassin du Bega, elle culmine à 2 000 m environ au sud-est du bassin hydrographique. Le substratum d’origine cristalline et éruptive est recouvert de dépôts récents (quaternaires) favorables aux cultures et prairies (51 % de la superficie) ainsi qu’à la forêt (35 % de la superficie). Du réseau d’observation des débits, nous retiendrons 19 sous‑bassins (Tableau 1) dont les étiages et les modules annuels ne sont pas influencés (Figure 1), soit 14 sous-bassins pour le bassin du Timis et cinq sous-bassins pour le bassin du Bega. Certains d’entre eux font l’objet d’un suivi de la production des fines, favorisée par la nature du sol et l’influence climatique méditerranéenne sur la région (GALÉA et al., 2004).
La taille, le contexte orographique, la nature et l’occupation du sol des 19 sous-bassins retenus expliquent, entre autres, les écoulements diversifiés qui y sont observés, en crue notamment (MIC et GALÉA, 2004) mais aussi des modules et des étiages. Pour fixer les idées, les modules annuels médians varient de 7 L/s/km2 à 41 L/s/km2 et les débits journaliers médians d’étiage varient de 2 L/s/km2 à 10 L/s/km2.
Tableau 1
Présentation des 19 sous-bassins du Timis-Bega retenus.
Presentation of the 19 sub-catchments of the Timis-Bega region.
Bassin hydrographique du Timis : 14 sous-bassins | |||||
|---|---|---|---|---|---|
Sous-bassins |
Code |
Observations de débit |
S |
Zm |
|
|
|
Période |
Durée (an) |
(km2) |
(m) |
Timis à TEREGOVA |
53105 |
1953-2001 |
49 |
167 |
906 |
Timis à SADOVA |
53110 |
1971-2001 |
31 |
560 |
936 |
Timis à CARANSEBES |
53115 |
1974-2001 |
28 |
1 072 |
769 |
Timis à LUGOJ |
53125 |
1970-2001 |
32 |
2 706 |
665 |
Raul Rece à RUSCA |
53205 |
1953-2001 |
49 |
163 |
1157 |
Fenes à FENES |
53305 |
1964-2001 |
38 |
125 |
973 |
Sebes à TURNU RUENI |
53405 |
1964-1998 |
35 |
122 |
819 |
Bistra à VOISLOVA BUCOVEI |
53505 |
1951-2001 |
51 |
232 |
886 |
Bistra à VOISLOVA |
53510 |
1963-2001 |
39 |
404 |
827 |
Bistra à OBREJA |
53515 |
1982-2001 |
20 |
863 |
880 |
Bistra Marului à POIANA MARULUI |
53605 |
1953-2001 |
49 |
79 |
1 442 |
Sucu à POIANA MARULUI |
53705 |
1953-2001 |
49 |
77 |
1 434 |
Nadrag à NADRAG |
53805 |
1963-2001 |
39 |
35 |
742 |
Golet à GOLET |
55105 |
1982-2001 |
20 |
41 |
751 |
Bassin hydrographique du Bega : 5 sous-bassins | |||||
Sous-bassins |
Code |
Observations de débit |
S |
Zm |
|
|
|
Période |
Durée (an) |
(km2) |
(m) |
Bega à LUNCANI |
50105 |
1976-2001 |
26 |
73,5 |
739 |
Bega à FAGET |
50110 |
1974-2001 |
28 |
474 |
470 |
Bega à BALINT |
50115 |
1970-2001 |
32 |
1 064 |
329 |
Sasa à POIENI |
50205 |
1966-2001 |
36 |
80 |
763 |
Gladna à FIRDEA |
50301 |
1980-2001 |
22 |
57 |
456 |
Nota - Parmi ces 19 sous-bassins, deux jeux sont constitués: de 10 (en gris) et 9 sous-bassins, respectivement utilisés pour le calage et la validation des régressions ultérieures.
Figure 1
Localisation des stations hydrométriques des sous-bassins retenus
Location of the hydrometric measurement stations.
3. Régionalisation des modules du bassin hydrographique du Timis – Bega
3.1 Bassin du Timis : 14 sous-bassins
Pour chacun des 14 sous-bassins, la distribution théorique des modules annuels échantillonnés sur la période d’observation (Tableau 1) est représentée par une loi de Weibull à deux paramètres :
où : UF = - ln (1-F) avec F : fréquence au non‑dépassement;QAL (UF) = Quantile théorique de module annuel, localement « observé », déduit des observations de débit (m3/s).
Nous avons choisi la loi de Weibull à deux paramètres par antériorité (GALÉA et CANALI, 2005) et parce qu’elle est conseillée par un groupe de travail (MASSON et al., 1994). C’est une loi simple, adaptée à l’étude fréquentielle des débits de faible valeur, ce qui est le cas des modules, notamment en années sèches, ainsi que des étiages sévères.
Pour obtenir les paramètres αR et βR de la loi régionale (2) des modules annuels du bassin du Timis (Tableau 2 et Figure 2a), nous avons appliqué aux modules (et ultérieurement aux étiages) la méthode de l’indice de crue de DALRYMPLE (1960). Les paramètres régionaux αR et βR résultent respectivement de la moyenne des paramètres αL et β*L (βL/q̅a̅l̅) des sous-bassins, pondérés par le nombre d’années d’observation.
où : QAR (UF) = Quantile de module déduit de la loi régionale, en un site quelconque observé ou non (m3/s).
Pour une période d’observation plus homogène (Figure 2b) et ainsi éviter un éventuel biais temporel dans l’approche régionale des modules, la loi de Weibull a été ajustée sur les 22 dernières années communes (1980-2001), excepté pour trois des sous-bassins (cf. tableau 1). Nous noterons une relative sensibilité des paramètres locaux et régionaux à la durée d’observation considérée (Tableaux 2 et 3).
3.2 Bassin du Bega : 5 sous-bassins
De même que précédemment, les paramètres des modélisations effectuées sont plus ou moins sensibles à la période d’observation (Tableau 4).
Tableau 2
Paramètres locaux et régionaux de la loi sur les modules (durée : cf. Tableau 1).
Local and regional parameters of the annual mean discharge distribution (chronicle: cf. Table 1).
Station |
53105 |
53110 |
53115 |
53125 |
53205 |
53305 |
53405 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73,5 |
560 |
1 072 |
2 706 |
163 |
125 |
122 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
Paramètres locaux (1) et quantile médian q̅a̅l̅ | ||||||||||||||
αL |
3,28 |
5,26 |
3,70 |
3,83 |
6,14 |
4,95 |
3,61 |
4,06 |
4,25 |
3,62 |
4,77 |
4,14 |
3,12 |
3,64 |
βL (m3/s) |
2,49 |
11,5 |
21,1 |
44,5 |
5,06 |
3,07 |
3,20 |
4,30 |
7,55 |
12,9 |
3,05 |
3,41 |
0,799 |
0,759 |
q̅a̅l̅ (m3/s) |
2,23 |
10,7 |
19,1 |
40,5 |
4,76 |
2,85 |
2,89 |
3,93 |
6,93 |
11,7 |
2,82 |
3,12 |
0,710 |
0,686 |
β*L |
1,12 |
1,07 |
1,10 |
1,10 |
1,06 |
1,08 |
1,11 |
1,09 |
1,09 |
1,11 |
1,08 |
1,09 |
1,12 |
1,11 |
Paramètres Régionaux :αR = 4,24 et βR = 1,09 |
Tableau 3
Paramètres locaux et régionaux de la loi de Weibull sur les modules (1980-2001).
Local and regional parameters of the Weibull distribution of annual mean discharge (1980-2001).
Station |
53105 |
53110 |
53115 |
53125 |
53205 |
53305 |
53405 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73,5 |
560 |
1 072 |
2 706 |
163 |
125 |
122 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
Paramètres locaux (1) et quantile médian q̅a̅l̅ | ||||||||||||||
αL |
3,21 |
4,94 |
3,45 |
3,67 |
5,34 |
4,66 |
3,38 |
4,35 |
4,22 |
3,62 |
4,75 |
4,08 |
2,98 |
3,64 |
βL (m3/s) |
2,06 |
11,0 |
20,6 |
42,8 |
4,76 |
2,95 |
3,16 |
4,31 |
7,18 |
12,9 |
2,99 |
3,44 |
0,74 |
0,76 |
q̅a̅l̅ (m3/s) |
1,84 |
10,2 |
18,5 |
38,7 |
4,45 |
2,73 |
2,84 |
3,96 |
6,58 |
11,7 |
2,77 |
3,15 |
0,678 |
0,686 |
β*L |
1,12 |
1,08 |
1,11 |
1,11 |
1,07 |
1,08 |
1,11 |
1,09 |
1,09 |
1,11 |
1,08 |
1,09 |
1,09 |
1,11 |
Paramètres Régionaux : αR = 4,03 et βR = 1,10 |
Figure 2
Loi régionale des modules : a) chronique complète (cf. tableau 1) et b) période 1980-2001 pour le bassin du Timis.
Regional distribution of the annual mean discharges: a) time series available (cf Table 1) and b) period 1980- 2001 for the Timis catchment.
(a)
(b)
3.3 Bassin hydrographique du Timis-Bega : modèle régional des modules
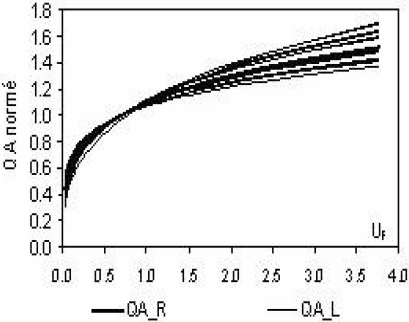
Le biais temporel éventuel sur les paramètres de la loi régionale des bassins du Timis et du Bega est faible (Tableaux 2 et 3, Tableau 4). Pour plus d’objectivité sur le choix du modèle régional du Timis-Bega, nous retiendrons les résultats associés à la période d’observation commune aux deux bassins (1980‑2001). Les lois régionales des modules du Timis et du Bega sont peu différenciées, notamment pour les faibles valeurs de UF (Figure 3).
Un critère d’erreur quadratique moyenne (3), inspiré des critères utilisés par OUARDA et ASHKAR (1994), permet d’apprécier l’adéquation du calage des modèles régionaux (Tableau 5). Ce critère d’erreur (Er) a été appliqué entre quantiles « observés » (1) et quantiles déduits de la loi régionale (2) où q̅a̅site est connu grâce aux observations.
avec s, le nombre de sous-bassins par bassin; n, le nombre d’années de la période d’observation considérée.
Tableau 4
Paramètres locaux et régionaux de la loi de Weibull sur les modules – influence de différentes périodes d’observation.
Local and regional parameters of the Weibull distribution of annual mean discharge – influence of different observation periods.
Station |
50105 |
50110 |
50115 |
50205 |
50301 |
50105 |
50110 |
50115 |
50205 |
50301 |
|---|---|---|---|---|---|---|---|---|---|---|
Période |
1976-2001 |
1974-2001 |
1970-2001 |
1966-2001 |
1980-2001 |
1980-2001 |
||||
S (km2) |
73,5 |
474 |
1 064 |
80 |
57 |
73,5 |
474 |
1 064 |
80 |
57 |
Paramètres locaux (1) et quantile médian q̅a̅l̅ | ||||||||||
αL |
4,55 |
3,56 |
2,80 |
3,12 |
2,87 |
4,61 |
3,47 |
3,07 |
3,27 |
2,87 |
βL (m3/s) |
1,49 |
5,66 |
8,52 |
1,36 |
0,63 |
1,46 |
5,32 |
7,86 |
1,20 |
0,63 |
q̅a̅l̅ (m3/s) |
1,38 |
5,10 |
7,47 |
1,21 |
0,55 |
1,35 |
4,78 |
6,97 |
1,07 |
0,55 |
β*L |
1,08 |
1,11 |
1,14 |
1,12 |
1,14 |
1,08 |
1,11 |
1,13 |
1,12 |
1,14 |
Paramètres Régionaux : αR = 3,36 et βR = 1,12 |
Paramètres Régionaux : αR = 3,46 et βR = 1,12 |
Figure 3
Lois régionales sur les modules des bassins du Timis et du Bega (1980-2001); (a) 0<UF<4,0 et (b) 0<UF<1,0.
Regional distribution of the annual mean discharges for the Timis and Bega catchments; (a) 0<UF<4.0 and (b) 0<UF<1.0.
(a)
(b)
Tableau 5
Erreur quadratique moyenne sur les modules de chaque bassin.
Average quadratic error on the annual mean discharges quantiles for each catchment.
Bassin du Timis (14 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||
Erreur quadratique (%) (Éq. 3) |
Erreur quadratique (%) (Éq. 3) |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
5,6 |
3,5 |
7,1 |
5,5 |
4,0 |
6,6 |
Ce critère d’erreur à l’échelle des bassins du Timis et du Bega peut être diversifié pour les sous-bassins du Timis, par exemple (Tableau 6).
Les résultats précédemment obtenus nous permettent de considérer que le bassin hydrographique du Timis-Bega est une région hydrologique homogène pour laquelle un seul modèle régional des modules peut être envisagé. Si chaque bassin joue tour à tour un rôle de calage et de validation, nous pouvons noter les incertitudes qui en résultent (Tableau 7).
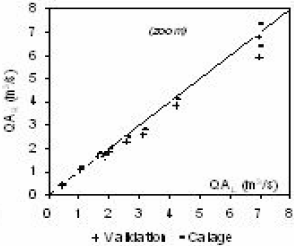
Comparativement aux incertitudes régionales (Tableau 5), nous en déduisons que le modèle régional des modules du Bega est représentatif du bassin hydrographique du Timis-Bega. Ce modèle, appliqué au bassin du Timis, dégrade peu les quantiles « humides » (Fi > 0,5) et pas du tout les quantiles « secs » (Fi < 0,5). Une illustration peut en être donnée pour des quantiles « secs » et des quantiles « humides » particuliers du bassin du Timis (Figure 4). Nous comparons les quantiles « observés » (Éq. 1) aux quantiles régionalisés (Éq. 2). La comparaison est effectuée dans un premier temps avec les quantiles régionalisés selon le modèle du Bega (validation), et, dans un deuxième temps, selon le modèle du Timis (adéquation du calage). La bonne correspondance observée entre calage et validation nous permet de retenir pour le bassin hydrographique du Timis-Bega le modèle régional des modules de paramètres αR = 3,46 et βR = 1,12 (Tableau 4).
4. Régionalisation des étiages du bassin hydrographique du Timis-Bega
4.1 Modélisation débit-durée-fréquence (QdF) locale des étiages
Elle concerne 13 sous-bassins du Timis et les cinq sous-bassins du Bega. Pour le quatorzième sous-bassin du Timis (55105), en effet, l’adéquation de la loi de Weibull n’est pas vérifiée.
Pour ce qui concerne les étiages, nous nous intéressons à une variable caractéristique d’étiage, le débit moyen minimum sur une durée continue d, noté VCNd. Cette variable associée à d est extraite par échantillonnage annuel, noté vcnd, de la chronique de débits journaliers. Dans le cas de notre étude, nous étudierons plus précisément les durée d de 1 j, 3 j, 6 j, 10 j, 30 j et 90 jours.
Pour les étiages, comme pour les modules annuels, c’est la loi de Weibull à deux paramètres (Éq. 4) qui a été choisie et nous noterons Vd(UF) les quantiles théoriques associés à l’échantillon vcnd.
Tableau 6
Erreur quadratique moyenne par sous-bassin du Timis.
Average quadratic error for each Timis sub-catchment.
Station |
53105 |
53110 |
53115 |
53125 |
53205 |
53305 |
53405 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73,5 |
560 |
1072 |
2706 |
163 |
125 |
122 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
Bassin du Timis : Erreur quadratique moyenne par sous-bassin (%) | ||||||||||||||
∀ Fi confondues |
8,0 |
5,4 |
5,1 |
2,9 |
7,0 |
3,9 |
6,0 |
2,2 |
1,3 |
3,4 |
4,4 |
0,5 |
12,8 |
3,1 |
∀ Fi>0,5 |
5,2 |
3,9 |
3,4 |
2,4 |
5,7 |
3,2 |
3,7 |
1,5 |
1,1 |
2,6 |
3,4 |
0,7 |
4,7 |
2,6 |
∀ Fi<0,5 |
10,0 |
6,5 |
6,4 |
3,2 |
8,1 |
4,5 |
7,7 |
2,7 |
1,5 |
3,9 |
5,2 |
0,3 |
17,5 |
3,6 |
Tableau 7
Erreur quadratique moyenne sur les modules du bassin du Timis-Bega.
Average quadratic error on the annual mean discharges quantiles of the Timis-Bega catchment.
Bassin du Timis (14 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||
Er. quadratique (%), avec paramètres régionaux Bega |
Er. quadratique (%), avec paramètres régionaux Timis |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
6,4 |
5,4 |
7,3 |
8,5 |
5,3 |
10,8 |
Figure 4
Comparaison des quantiles « observés » et régionalisés sur le bassin du Timis; (a) QA «sec» T = 5 ans; (b) QA «sec» T = 5 ans; (c) QA «sec» T = 10 ans; (d) QA «sec» T = 10 ans; (e) QA «humide» T = 5 ans; (f) QA «humide» T = 5 ans; (g) QA «humide» T = 10 ans; (h) QA «humide» T = 10 ans.
Comparison of local and regional quantiles for the Timis catchment; (a) QA «dry» T = 5 yr; (b) QA «dry» T = 5 yr; (c) QA «dry» T = 10 yr; (d) QA «dry» T = 10 yr; (e) QA «humid» T = 5 yr; (f) QA «humid» T = 5 yr; (g) QA «humid» T = 10 yr; (h) QA «humid» T = 10 yr.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Une modélisation statistique peut être généralisée à l’ensemble des durées d par calage d’une fonction locale VL(d, UF) sur les échantillons vcnd. Cette modélisation fait référence à l’analyse QdF qui, d’une manière générale, fournit une description fréquentielle théorique multi-durée des quantiles de crue ou d’étiage, et ce, indépendamment des lois de probabilité retenues (JAVELLE, 2001). Le concept de modélisation (GALÉA et al., 2000) repose sur une propriété observée des différents ajustements Vd(UF) à converger vers les fortes périodes de retour des années « sèches » et sur une propriété d’affinité orthogonale des lois de probabilité théorique relatives aux échantillons vcnd (GALÉA et CANALI, 2005). L’application du modèle QdF convergent nous permet de donner une description théorique (Éq. 5) selon VL(d, UF) des régimes d’étiage observés.
avec ![]() , la distribution théorique locale adimensionnelle des débits d’étiage consolidée par modélisation (GALÉA et CANALI, 2005), car toutes les durées de 1 j à 90 j participent à l’estimation des deux paramètres de la distribution théorique; ∆e, le paramètre à caler sur les échantillons vcnd constitués, homogène à un temps et relié à la dynamique des étiages. Autrement dit, il permet de déduire, de la distribution théorique consolidée des débits journaliers d’étiage (
, la distribution théorique locale adimensionnelle des débits d’étiage consolidée par modélisation (GALÉA et CANALI, 2005), car toutes les durées de 1 j à 90 j participent à l’estimation des deux paramètres de la distribution théorique; ∆e, le paramètre à caler sur les échantillons vcnd constitués, homogène à un temps et relié à la dynamique des étiages. Autrement dit, il permet de déduire, de la distribution théorique consolidée des débits journaliers d’étiage (![]() ), les distributions relatives à d = 3 j, 6 j…90 j.
), les distributions relatives à d = 3 j, 6 j…90 j.
4.2 Modélisation QdF régionale des étiages
Les paramètres régionaux αR et βR du Timis et du Bega sont estimés à partir d’une moyenne pondérée (nombre d’années d’observation) des paramètres consolidés βc et αc (Tableau 8). Pour chaque bassin, un modèle régional permet d’estimer les quantiles d’étiage des sites particuliers (Éq. 6).
où ![]() , la distribution théorique régionale des débits d’étiage; v̅d=1,site, le quantile journalier d’étiage médian déduit de (Éq. 4) ou estimé (cf. ultérieurement); ∆esite, le temps caractéristique d’étiage déduit des observations (Éq. 5) ou estimé (cf. ultérieurement).
, la distribution théorique régionale des débits d’étiage; v̅d=1,site, le quantile journalier d’étiage médian déduit de (Éq. 4) ou estimé (cf. ultérieurement); ∆esite, le temps caractéristique d’étiage déduit des observations (Éq. 5) ou estimé (cf. ultérieurement).
Un critère d’erreur quadratique moyenne, analogue à celui des modules (Éq. 3), appliqué aux sous-bassins du Timis et du Bega entre quantiles théoriques locaux (Éq. 5) et régionaux (Éq. 6) permet d’apprécier l’adéquation des modèles régionaux (Tableau 8) ainsi que le caractère hydrologique homogène de la région (Figure 5).
Tableau 8
Erreur quadratique moyenne sur les quantiles d’étiage de chaque bassin.
Average quadratic error on low flow quantiles for each catchment.
Bassin du Timis (13 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||
|---|---|---|---|---|---|
Paramètres régionaux |
Paramètres régionaux |
||||
αR = 2,78 et βR = 1,20 |
αR = 3,25 et βR = 1,23 |
||||
Erreur quadratique (%) |
Erreur quadratique (%) |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
10,1 |
9,3 |
10,8 |
6,1 |
5,2 |
6,9 |
Figure 5
Lois régionales sur les étiages des bassins du Timis et du Bega; (a) 0<UF<4,5 et (b) 0<UF<1,0.
Low flow regional distributions for the Timis and Bega catchments; (a) 0<UF<4.5 et (b) 0<UF<1.0.
(a)
(b)
Tableau 9
Erreur quadratique moyenne sur les quantiles d’étiage du Timis-Bega.
Average quadratic error on low flow quantiles of the Timis-Bega catchment.
Bassin du Timis (13 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||
|---|---|---|---|---|---|
Er. Quadratique (%), avec paramètres régionaux Bega |
Er. quadratique (%), avec paramètres régionaux Timis |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
16,3 |
9,7 |
20,9 |
9 |
5,9 |
11,3 |
L’application du modèle régional d’étiage du Bega aux sous-bassins du Timis et vice-versa accroît significativement l’erreur quadratique moyenne des quantiles « secs » en particulier (Tableaux 8 et 9).
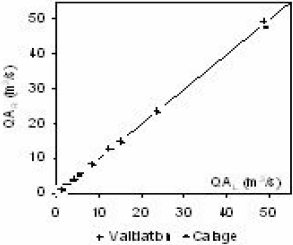
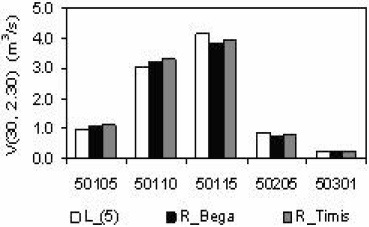
Le choix d’un modèle régional d’étiage unique pour le bassin hydrographique du Timis-Bega est cependant possible. En effet, la généralisation du modèle régional d’étiage du bassin du Timis (αR = 2,78 et βR = 1,20) au bassin du Bega ne dégrade pas l’estimation des quantiles « humides » (∀ Fi > 0,5). Seuls les quantiles « secs » (∀ Fi < 0,5) voient leur estimation sensiblement dégradée, conformément à la différenciation des modèles régionaux (Figure 5), mais cela reste tout de même acceptable. Nous en donnons une illustration pour la norme d’usage : le débit moyen d’étiage de 30 jours (Figure 6).
Figure 6
Comparaison des quantiles d’étiage sur 30 jours pour le bassin du Bega; (a) quinquennal «sec»; (b) décennal «sec»; (c) quinquennal «humide»; (d) décennal «humide»;
Comparison of low flow 30-day quantiles for the Bega catchment; (a) five-year «dry»; (b) 10-year «dry»; (c) 5-year «humid»; (d) 10-year «humid».
(a)
(b)
(c)
(d)
5. Similitudes régionales avec le bassin de la Moselle
5.1 Différenciation des lois régionales sur les modules et les étiages du Timis-Bega
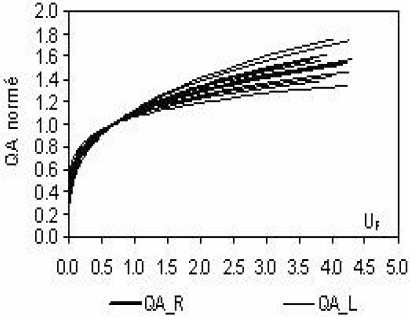
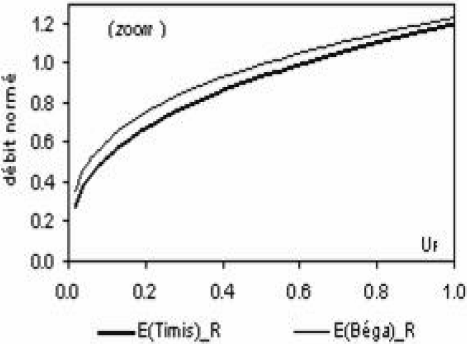
Les lois régionales établies pour les modules annuels et les étiages du Timis-Bega montrent une faible différenciation pour les quantiles des années moyennes à « sèches » (∀ UF < 0,7), ce qui n’est pas le cas pour les quantiles des années « humides » (Figure 7). Ce résultat est à rapprocher de celui trouvé pour le bassin hydrographique de la Moselle française (GALÉA et CANALI, 2005).
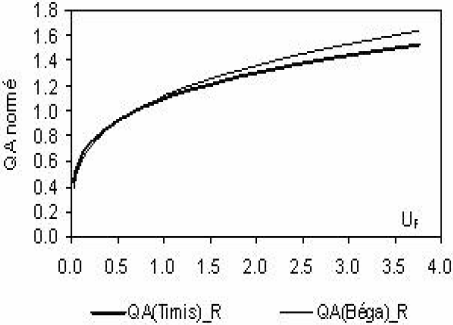
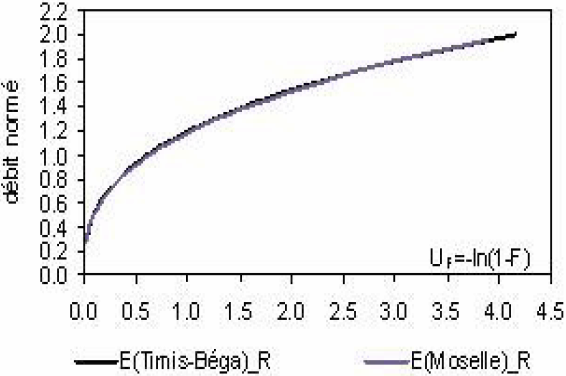
5.2 Comparaison des lois régionales du Timis-Bega et de la Moselle
Nous notons la quasi similitude des lois régionales du Timis-Bega et de la Moselle, tant en ce qui concerne les modules que les étiages (Figure 8). C’est un résultat inattendu, d’autant plus qu’il s’agit de deux entités géographiques contrastées, entre autres, par le climat et le régime des crues (MIC et GALÉA, 2004; GALÉA et BLUM, 2005). Par référence à certains travaux sur la modélisation statistique des crues, nous pourrions avancer deux éléments d’explication. Cela militerait, d’une part, pour la théorie des régions hydrologiques homogènes (RIBEIRO-CORRÉA et al., 1995; OUARDA et al., 2001 ) et, d’autre part, pour le concept de modélisation QdF à référence typologique (MIC et al., 2002).
Figure 7
Comparaison des lois régionales sur les modules et étiages du Timis-Bega; (a) 0<UF<4,5 et (b) 0<UF<1,0.
Comparison of regional distributions of annual mean discharge and low flow in the Timis-Bega catchment; (a) 0<UF<4.5 and (b) 0<UF<1.0.
(a)
(b)
Figure 8
Comparaison des lois régionales des bassins hydrographiques du Timis-Béga et de la Moselle; (a) lois régionales sur QA et (b) lois régionales d’étiage.
Comparison of regional distributions for the Timis-Bega and Moselle catchments (a) QA regional distributions and (b) low flow regional distributions.
(a)
(b)
6. Estimation des descripteurs de régime
6.1 Estimation du module médian d’un sous-bassin non observé
Pour estimer les quantiles du module annuel en un site donné, le modèle régional (Éq. 2) est proposé avec la régression linéaire sur variables normalisées (Éq. 7). Les coefficients de corrélation partielle RS (0,985) et RZm (0,869) sont significatifs. Ils sont en effet supérieurs à R (0,76), coefficient relatif au test de validité des coefficients de corrélation partielle au seuil d’erreur de 1 % de la variable de STUDENT. La relation (7) explique 97 % de la variance du module médian et pour un intervalle de confiance raisonnable (70 %), la vraie valeur de q̅a̅ est comprise entre 0,80 fois et 1,24 fois la valeur estimée selon l’équation 7. Au tableau 10, nous présentons le contrôle du calage de la relation (Éq. 7).
avec S, la Superficie (km2); Zm, l’altitude moyenne (m).
L’erreur quadratique moyenne obtenue en validation est du même ordre de grandeur (Tableau 11).
Ultérieurement, nous vérifierons une procédure mise en oeuvre pour le bassin hydrographique de la Moselle (GALÉA et CANALI, 2005) et qui permet, à partir de quelques mesures d’étiage par an concomitantes au site non observé et aux sous-bassins observés, une estimation appréciable du module médian. Nous nous intéresserons en particulier au sous-bassin 53105 du jeu de calage et au sous-bassin 53515 du jeu de validation pour lesquels l’estimation selon (7) induit la plus forte erreur relative sur le module médian.
6.2 Estimation du quantile journalier médian d’étiage d’un sous-bassin non observé
Pour estimer les quantiles d’étiage, le modèle régional (Éq. 6) est proposé avec l’équation 8, régression multiple (R2 = 0,97) qui permet d’estimer, en l’absence d’observation de débit, le quantile journalier médian d’étiage en un site donné v̅d=1,site. Comme précédemment, pour le module médian, les coefficients de corrélation partielle RS (0,985) et RIb (0,843) sont significatifs, l’intervalle de confiance à 70 % est comparable. Le tableau 12 présente le contrôle du calage de la relation (8).
avec S, la Superficie (km2); Ib, la pente moyenne du sous-bassin (%0).
En ce qui concerne le jeu de validation (Tableau 13), nous rappelons que la loi de Weibull à deux paramètres n’est pas acceptable pour décrire les étiages du sous-bassin 55105. La valeur du quantile journalier médian peut être cependant approchée à partir de la médiane de l’échantillon.
Tableau 10
Calage de la relation (Éq. 7).
Calibration of the relationship (Eq. 7)
Code |
50105 |
50110 |
50115 |
50205 |
53105 |
53115 |
53125 |
53205 |
53305 |
53405 |
|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73.5 |
474 |
1064 |
80 |
167 |
1 072 |
2 706 |
163 |
125 |
122 |
q̅a̅ (Éq. 1) observé (m3/s) |
1,35 |
4,78 |
6,97 |
1,07 |
1,84 |
18,5 |
38,7 |
4,45 |
2,73 |
2,84 |
q̅a̅ (Éq. 7) (m3/s) |
1,14 |
4,58 |
7,07 |
1,29 |
3,21 |
17,4 |
37,6 |
4,06 |
2,59 |
2,11 |
Erreur relative (%) |
16 |
4 |
-1 |
-21 |
-74 |
6 |
3 |
9 |
5 |
26 |
Erreur quadratique (%) |
19 |
Tableau 11
Validation de la relation (7).
Validation of the relationship (7).
Code |
50301 |
53110 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|
S (km2) |
57 |
560 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
q̅a̅ (1) observé (m3/s) |
0,550 |
10,2 |
3,96 |
6,58 |
11,7 |
2,77 |
3,15 |
0,680 |
0,690 |
q̅a̅ (7) (m3/s) |
0,530 |
11,2 |
4,36 |
7,06 |
16,1 |
2,48 |
2,40 |
0,550 |
0,650 |
Erreur relative (%) |
4 |
-10 |
-10 |
-7 |
-38 |
10 |
24 |
19 |
6 |
Erreur quadratique (%) |
17 |
Tableau 12
Calage de la relation (8).
Calibration of the relationship (8).
Code |
50105 |
50110 |
50115 |
50205 |
53105 |
53115 |
53125 |
53205 |
53305 |
53405 |
|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73.5 |
474 |
1 064 |
80 |
167 |
1 072 |
2 706 |
163 |
125 |
122 |
v̅d=1 (4) observé (m3/s) |
0,633 |
1,81 |
2,08 |
0,417 |
0,440 |
3,63 |
8 |
1,04 |
0,646 |
0,633 |
v̅d=1 (8) (m3/s) |
0,460 |
1,39 |
2,13 |
0,440 |
0,530 |
3,84 |
7,85 |
1,08 |
0,760 |
0,660 |
Erreur relative (%) |
27 |
23 |
-2 |
-6 |
-20 |
-6 |
2 |
-4 |
-18 |
-4 |
Erreur quadratique (%) |
15 |
Tableau 13
Validation de la relation (8).
Validation of the relationship (8).
Code |
50301 |
53110 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|
S (km2) |
57 |
560 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
v̅d=1 (4) observé (m3/s) |
0,128 |
2,38 |
0,839 |
1,50 |
2,69 |
0,759 |
0,784 |
0,144 |
0,136 |
v̅d=1 (8) (m3/s) |
0,210 |
2,32 |
1,29 |
1,99 |
3,64 |
0,640 |
0,510 |
0,310 |
0,370 |
Erreur relative (%) |
-64 |
3 |
-54 |
-33 |
-35 |
16 |
35 |
-115 |
-172 |
Erreur quadratique (%) |
55 |
L’erreur quadratique de 55 % sur le jeu de validation (huit sous-bassins) est à relativiser dans la mesure où nous sommes en présence de faibles débits. Ce qui est à rechercher est essentiellement l’ordre de grandeur et nous verrons ultérieurement comment cela peut être amélioré à partir d’une information épisodique sur les étiages des sous-bassins. Comme pour les modules, nous nous intéresserons aux sous-bassins présentant la plus forte erreur relative sur l’estimation de v̅d=1.
6.3 Estimation du temps caractéristique d’étiage ∆e
Pour le temps caractéristique d’étiage, nous avons été amené à différencier son estimation, en fonction de l’altitude moyenne, selon qu’il s’agisse des sous-bassins du Timis (Éq. 9) ou du Bega (Éq. 10).
Pour le bassin du Timis, la relation (9) a été calée sur huit des 14 sous-bassins et validée sur les six autres. Pour le bassin du Bega, la relation (10) a été exclusivement calée, étant donné le faible nombre de sous-bassins (Tableau 14).
L’incertitude sur ce paramètre est acceptable compte tenu de sa relative faible sensibilité dans le modèle d’étiage (GALÉA et al., 2000).
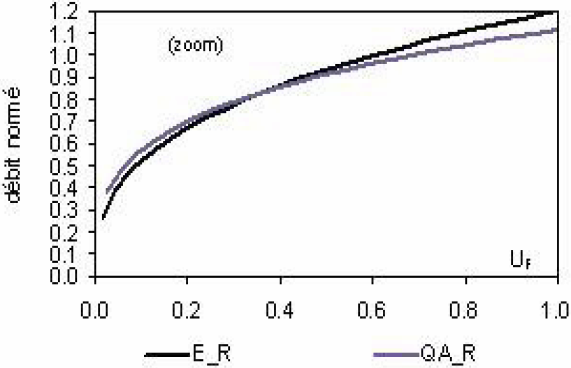
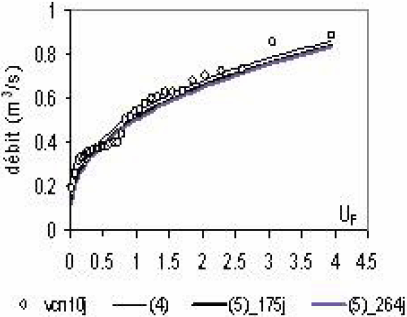
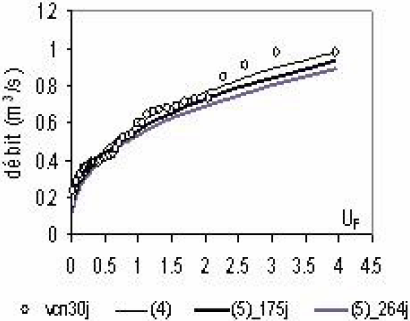
On peut montrer l’influence de ∆e sur les quantiles relatifs aux durées d (1 j, 3 j, 6 j, 10 j, 30 j et 90 j) des sous-bassins 50205 et 50105 qui présentent la plus forte erreur d’estimation de ∆e, respectivement 51 % et -36 % (Tableau 14). L’erreur quadratique moyenne est établie toutes durées d confondues entre modélisation locale (Éq. 5) et ajustements directs (Éq. 4). Pour le sous-bassin 50205, l’incertitude sur les quantiles associés aux valeurs respectives de ∆e de 175 j et 264 j est donnée au tableau 15.
Une visualisation de cette incertitude peut être montrée à partir des distributions obtenues pour les échantillons de durées 10 j, 30 j et 90 j. L’influence de ∆e est surtout sensible à 90 j (Figure 9).
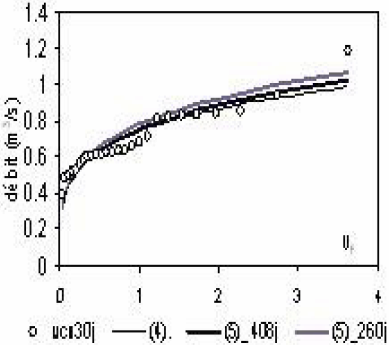
Nous faisons de même pour le sous-bassin 50105 (Tableau 16).
La visualisation de cette incertitude à la figure 10 (comme à la figure 9) pour les distributions relatives aux durées 10 j, 30 j et 90 j montre que l’incertitude d’estimation de ∆e a peu d’impact sur les quantiles modélisés (5) de quelques jours à 30 jours. L’impact est relativement sensible pour les quantiles d’étiage sur 90 j.
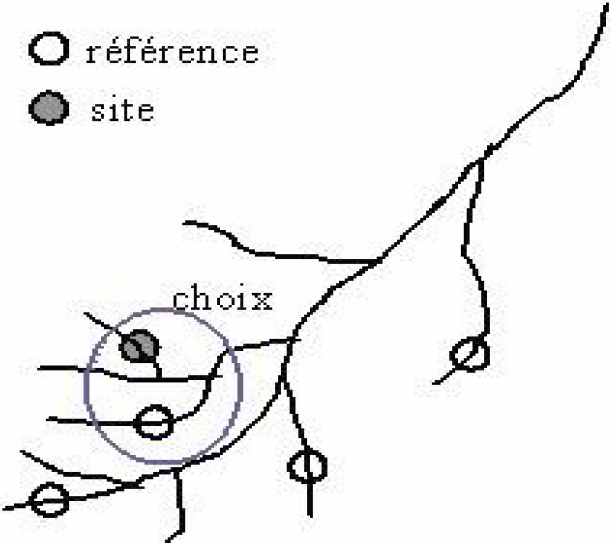
6.4 Prise en compte d’une information épisodique sur les débits d’étiage
Le principe a déjà été éprouvé pour le bassin hydrographique de la Moselle (GALÉA et CANALI, 2005). Nous rappelons que l’information épisodique sur les débits d’étiage concerne des mesures concomitantes au sous-bassin étudié (site) et au sous-bassin de référence qui lui est associé (Figure 11). Selon la nomenclature des réseaux d’observation en vigueur, le sous-bassin de référence appartient en général au réseau primaire tandis que le site étudié est celui associé au réseau tertiaire, en principe instrumenté au stade des avant-projets. Le critère de choix du sous-bassin de référence n’est pas l’objectif de notre propos, le choix est effectué a priori. Notre intention première est l’évaluation du principe dans le contexte hydro-climatique du Timis-Bega, différent de celui de la Moselle.
Tableau 14
Estimation de ∆e et de son incertitude.
Estimation and relative error of ∆e.
Bassin du Timis (14 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||||||
|---|---|---|---|---|---|---|---|---|---|
Sous-bassins |
S |
Δe (j) |
Sous-bassins |
S |
Δe (j) |
||||
|
(km2) |
observé (5) |
estimé (9) |
erreur (%) relative |
|
(km2) |
observé (5) |
estimé (10) |
erreur (%) relative |
53105 |
167 |
96 |
109 |
14 |
50105 |
73,5 |
408 |
260 |
-36 |
53110 |
560 |
110 |
110 |
0 |
50110 |
474 |
224 |
203 |
-9 |
53115 |
1072 |
99 |
102 |
3 |
50115 |
1064 |
172 |
167 |
-3 |
53125 |
2706 |
109 |
96 |
-12 |
50205 |
80 |
175 |
264 |
51 |
53205 |
163 |
113 |
120 |
6 |
50301 |
57 |
168 |
200 |
19 |
53305 |
125 |
109 |
112 |
3 |
|
||||
53405 |
122 |
97 |
104 |
7 |
|
||||
53505 |
232 |
97 |
108 |
11 |
|
||||
53510 |
404 |
97 |
105 |
8 |
Erreur quadratique (%) |
||||
53515 |
863 |
118 |
107 |
-9 |
Timis |
Bega |
|||
53605 |
79 |
164 |
131 |
-20 |
Calage (9) |
validation |
Calage (10) |
||
53705 |
77 |
145 |
130 |
-10 |
9 |
11 |
29,5 |
||
53805 |
35 |
107 |
100 |
-7 |
|
||||
55105 |
41 |
93 |
101 |
9 |
|
Tableau 15
Incertitude sur les quantiles d’étiage du sous-bassin 50205 liée à l’estimation de ∆e.
Low flow quantile uncertainty induced by the estimation of ∆e for the (50205) sub-catchment.
50205 : Modélisation (5) avec α = 2,74 β = 1,26 et v̅c̅n̅d=1 = 0,385 m3/s | |||||
|---|---|---|---|---|---|
Δe = 175 j (observé) |
Δe = 264 j (estimé) |
||||
Erreur quadratique (%) |
Erreur quadratique (%) |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
4 |
3 |
4,7 |
5,9 |
6 |
5,8 |
Figure 9
Influence de ∆e sur les quantiles d’étiage modélisés (Éq. 5) du sous-bassin 50205 (S = 80 km2; (a) vcn 10 j; (b) vcn 30 j; (c) vcn 90 j
Influence of ∆e on the modelling of low flow quantiles (5) for the (50205) sub-catchment (S = 80 km2; (a) vcn 10 d; (b) vcn 30 d; (c) vcn 90 d.
(a)
(b)
(c)
Tableau 16
Incertitude sur les quantiles d’étiage du sous-bassin 50105 liée à l’estimation de ∆e.
Low flow quantile uncertainty induced by the estimation of ∆e for the (50105) sub-catchment.
50105 : Modélisation (5) avec α = 4,13 β = 1,18 et v̅c̅n̅d=1 = 0,595 m3/s | |||||
|---|---|---|---|---|---|
∆e = 408 j (observé) |
∆e = 260 j (estimé) |
||||
Erreur quadratique (%) |
Erreur quadratique (%) |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
2,2 |
1,5 |
2,7 |
6 |
5,2 |
6,7 |
Figure 10
Influence de ∆e sur les quantiles d’étiage modélisés (5) du sous-bassin 50105 (S = 73,5 km2); (a) vcn 10 j; (b) vcn 30 j; (c) vcn 90 j.
Influence of ∆e on the modelling of low flow quantiles (5) for the (50105) sub-catchment (S = 73.5 km2); (a) vcn 10 d; (b) vcn 30 d; (c) vcn 90 d.
(a)
(b)
(c)
Figure 11
Site et sous-bassin de référence associé.
Study site and associated reference sub-catchment.
Pour le site étudié (non observé continûment) et pour le sous-bassin de référence, un échantillon de 50 valeurs est constitué à partir des chroniques de débit journalier, à raison de cinq mesures par an sur les dix dernières années, pour fixer les idées. Les deux échantillons concomitants, une fois constitués, un simple coefficient d’affinité k entre cumuls des débits d’étiage échantillonnés, du site étudié en fonction du sous-bassin de référence, est proposé pour estimer le descripteur du régime d’étiage v̅d=1,site(11). Si cela est vérifié et compte tenu de la faible différenciation observée entre les lois régionales (Figure 7), pour les années moyennes à « sèches » (∀ UF < 0,7), nous faisons l’hypothèse forte que ce même coefficient d’affinité k, établi sur les débits d’étiage, peut permettre une estimation satisfaisante du module médian q̅a̅site (Éq. 12).
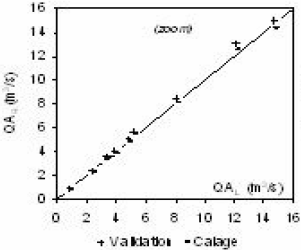
Les relations précédentes peuvent être testées à partir de quelques exemples choisis afin d’évaluer leur performance par rapport aux relations respectives (Éq. 8) et (Éq. 7). En ce qui concerne les modules, nous nous intéressons aux sous-bassins pour lesquels l’estimation (Éq. 7) induit par rapport à l’observation (Éq. 1) une erreur relative de ‑75 % (53105, Tableau 10) et de ‑38 % (53515, Tableau 11). Conformément au principe énoncé précédemment, sont associés respectivement aux sites étudiés 53105 et 53515 les sous-bassins de référence 53205 et 53510 dont la localisation est donnée à la figure 1. Nous faisons de même pour ce qui concerne l’estimation du débit journalier médian d’étiage des sous-bassins 50301, 53805 et 55105 qui présentent les trois plus fortes erreurs relatives (Tableau 13). À ces sites étudiés, nous associons respectivement les sous-bassins de référence 50205, 50301 et 53105 (Figure 1). Pour ces cinq sites étudiés, la prise en compte d’une information épisodique sur les débits d’étiage, selon la démarche préconisée, permet de réduire significativement l’erreur relative associée aux régressions (Figure 12).
Au tableau 17, nous présentons les éléments de calcul associés, entre autres, à la représentation de la figure 12. À des fins prospectives, nous avons étendu notre exploration des doublets site étudié – sous-bassin de référence sans a priori sur le choix du sous-bassin de référence compte tenu de la superficie et de la localisation géographique du site étudié. Par ailleurs, et pour chaque doublet, une inversion des rôles a été considérée, autrement dit le site étudié devient sous-bassin de référence et vice-versa.
De manière générale, l’erreur quadratique moyenne associée aux différentes estimations confirme les résultats présentés antérieurement (Figure 12). Bien que le critère de choix du sous-bassin de référence ne soit pas l’objet de notre propos, nous pouvons souligner de manière expérimentale le meilleur choix possible du sous-bassin de référence pour un site d’étude donné. Pour le site étudié 50301, par exemple, nous pouvons l’associer tour à tour aux sous-bassins de référence 50205 et 53805. Dans le premier cas, le doublet appartient au bassin du Bega et à deux affluents indépendants (Figure 1, Tableau 1). Dans le deuxième cas, le sous-bassin de référence appartient au bassin du Timis (Figure 1). Dans les deux cas, l’ordre de grandeur des superficies est comparable à celle du site étudié. Quel que soit le sous-bassin de référence le quantile d’étiage v̅d=1 est bien estimé, ce qui n’est pas le cas du module médian q̅a̅. Le meilleur choix pour le site étudié 50301, compte tenu de notre investigation non exhaustive (Tableau 17), serait le sous-bassin de référence 53805, situé de l’autre coté de la crête (Figure 1). Si nous prenons comme autre exemple le site étudié 53105, selon le sous-bassin de référence associé 53205 (affluent amont) ou 55105 (affluent aval) le rapport de superficie varie de un à trois. Les estimations sont d’un ordre de grandeur comparable, cependant l’erreur relative sur q̅a̅ est de 10 % au lieu de 20 % (Figure 12) avec le sous-bassin de plus faible superficie (55105). Les exemples peuvent être multipliés sur la base des combinaisons présentées au tableau 17.
7. Conclusion
Les résultats issus de la régionalisation des modules annuels et des étiages du bassin du Timis-Bega montrent dans l’ensemble une grande similitude avec ceux du bassin de la Moselle française (GALÉA et CANALI, 2005). En particulier, les lois régionales sont peu différenciées pour les années moyennes à « sèches » des modules et des étiages des sous-bassins (Figure 7). De même que pour la Moselle, l’usage d’une information épisodique sur les débits d’étiage a permis d’améliorer l’estimation du débit journalier médian d’étiage v̅d=1,site (Éq. 11) mais aussi l’estimation (Éq. 7) du module annuel médian q̅a̅site (12). La conservation du même coefficient d’affinité k dans les relations (Éq. 11) et (Éq. 12) ne nous semble pas être a priori le fait de la proximité ou non du sous-bassin de référence, d’après les résultats du tableau 12. Cette extension de l’usage de l’information épisodique sur les débits d’étiage à l’estimation du module annuel médian q̅a̅site peut trouver une explication dans la faible différenciation des lois régionales pour les fréquences moyennes à « sèches ». Ces descripteurs de débit, des régimes de module et d’étiage des sous-bassins, constituent une source d’incertitude importante des modèles régionaux (Éq. 2) et (Éq. 6). Il serait donc ultérieurement envisageable, compte tenu des résultats obtenus (Figure 12 et Tableau 17), d’entreprendre une régionalisation à bases géostatistiques de ces descripteurs prenant en compte, par exemple, l’effet structurant du réseau hydrographique (SAUQUET et al., 2003) ainsi qu’une information épisodique sur les débits d’étiages. Celle-ci n’est pas rare, car il existe en effet des suivis ponctuels épisodiques pour évaluer la qualité de la ressource disponible mais aussi sa quantité, notamment au stade des avants‑projets.
Figure 12
Erreur relative sur v̅d=1,site et q̅a̅site selon les estimations; (a) entre débit journalier médian d’étiage observé (Éq. 4) et estimé selon l’éq. 8 ou l’éq. 11; (b) entre module médian observé (Éq. 1) et estimé selon l’éq. 7 ou l’éq. 12.
Estimation of v̅d=1,site and q̅a̅site relative error; (a) between observed median daily flow (Eq. 4) and estimated as per eq. 8 or eq. 11; (b) between observed median modulus (Eq. 1) and estimated as per eq. 7 or eq. 12.
(a)
(b)
Tableau 17
Poids de l’information épisodique d’étiage sur l’estimation des descripteurs de régime.
Impact of the low flow episodic information on the estimation of regime descriptors.
Sous-bassin de référence |
K |
Site étudié |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Code |
S (km2) |
v̅d̅=̅1̅ (m3/s) |
q̅a̅ (m3/s) |
Code |
S (km2) |
v̅d̅=̅1̅ (m3/s) |
q̅a̅ (m3/s) |
|||||||||
|
|
(4) |
(1) |
|
|
|
(4) |
(8) |
Er.(8) % |
(11) |
Er.(11) % |
(1) |
(7) |
Er.(7) % |
(12) |
Er.(12) % |
50110 |
474 |
1,81 |
4,78 |
0,317 |
50105 |
73,5 |
0,633 |
0,460 |
27 |
0,573 |
9 |
1,35 |
1,14 |
16 |
1,51 |
‑12 |
50105 |
73,5 |
0,633 |
1,35 |
3,15 |
50110 |
474 |
1,81 |
1,39 |
23 |
2 |
‑10 |
4,78 |
4,58 |
4 |
4,25 |
11 |
50301 |
57 |
0,128 |
0,550 |
3,32 |
50205 |
80 |
0,417 |
0,440 |
‑6 |
0,425 |
‑2 |
1,07 |
1,29 |
‑21 |
1,83 |
‑71 |
50205 |
80 |
0,417 |
1,07 |
0,3 |
50301 |
57 |
0,128 |
0,210 |
‑64 |
0,125 |
2 |
0,550 |
0,530 |
4 |
0,320 |
42 |
53110 |
560 |
2,38 |
10,2 |
1,74 |
53115 |
1072 |
3,63 |
3,84 |
6 |
4,13 |
‑14 |
18,5 |
17,4 |
6 |
17,7 |
4 |
53115 |
1072 |
3,63 |
18,5 |
0,57 |
53110 |
560 |
2,38 |
2,32 |
3 |
2,07 |
13 |
10,2 |
11,2 |
‑10 |
10,5 |
‑3 |
53205 |
163 |
1,04 |
4,45 |
0,497 |
53105 |
167 |
0,440 |
0,530 |
‑20 |
0,517 |
‑18 |
1,84 |
3,21 |
‑75 |
2,21 |
‑20 |
53105 |
167 |
0,440 |
1,84 |
2 |
53205 |
163 |
1,04 |
1,08 |
‑4 |
0,883 |
15 |
4,45 |
4,06 |
9 |
3,68 |
17 |
53505 |
232 |
0,839 |
3,96 |
2,17 |
53510 |
404 |
1,50 |
1,99 |
‑33 |
1,80 |
‑20 |
6,58 |
7,06 |
‑7 |
8,60 |
‑31 |
53510 |
404 |
1,50 |
6,58 |
0,459 |
53505 |
232 |
0,839 |
1,29 |
‑53 |
0,690 |
18 |
3,96 |
4,36 |
‑10 |
3,02 |
24 |
53510 |
404 |
1,50 |
6,58 |
1,87 |
53515 |
863 |
2,69 |
3,64 |
‑35 |
2,81 |
‑5 |
11,7 |
16,1 |
‑38 |
12,3 |
‑5 |
53515 |
863 |
2,69 |
11,7 |
0,532 |
53510 |
404 |
1,50 |
1,99 |
‑33 |
1,43 |
5 |
6,58 |
7,06 |
‑7 |
6,20 |
6 |
53515 |
863 |
2,69 |
11,7 |
0,174 |
53605 |
79 |
0,759 |
0,640 |
16 |
0,468 |
38 |
2,77 |
2,48 |
11 |
2,04 |
26 |
53605 |
79 |
0,759 |
2,77 |
5,73 |
53515 |
863 |
2,69 |
3,64 |
‑35 |
4,35 |
‑62 |
11,7 |
16,1 |
‑38 |
15,9 |
‑36 |
53705 |
77 |
0,784 |
3,15 |
0,874 |
53605 |
79 |
0,759 |
0,640 |
16 |
0,686 |
10 |
2,77 |
2,48 |
11 |
2,75 |
1 |
53605 |
79 |
0,759 |
2,77 |
1,14 |
53705 |
77 |
0,784 |
0,510 |
35 |
0,867 |
‑11 |
3,15 |
2,40 |
24 |
3,17 |
‑1 |
53805 |
35 |
0,144 |
0,680 |
0,802 |
50301 |
57 |
0,128 |
0,210 |
‑64 |
0,115 |
10 |
0,550 |
0,530 |
4 |
0,545 |
1 |
50301 |
57 |
0,128 |
0,550 |
1,23 |
53805 |
35 |
0,144 |
0,310 |
‑115 |
0,158 |
‑10 |
0,680 |
0,550 |
19 |
0,678 |
0 |
55105 |
41 |
0,136 |
0,690 |
2,39 |
53105 |
167 |
0,440 |
0,530 |
‑21 |
0,325 |
26 |
1,84 |
3,21 |
‑75 |
1,65 |
10 |
53105 |
167 |
0,440 |
1,84 |
0,418 |
55105 |
41 |
0,136 |
0,370 |
‑172 |
0,184 |
‑35 |
0,690 |
0,650 |
6 |
0,769 |
‑11 |
55105 |
41 |
0,136 |
0,690 |
5,74 |
53205 |
163 |
1,04 |
1,08 |
‑4 |
0,781 |
25 |
4,45 |
4,06 |
9 |
3,96 |
11 |
53205 |
163 |
1,04 |
4,45 |
0,174 |
55105 |
41 |
0,136 |
0,370 |
‑172 |
0,181 |
‑33 |
0,690 |
0,650 |
6 |
0,774 |
‑12 |
Erreur quadratique moyenne (%) |
65 |
|
23 |
|
|
28 |
|
23 |
Parties annexes
Références bibliographiques
- DALRYMPLE T. (1960). Flood frequency analysis. U.S. Geol. Surv. Water Supply Pap., 1543A.
- GALÉA G., P. JAVELLE et N. CHAPUT (2000). Un modèle débit-durée-fréquence pour caractériser le régime d’étiage d’un bassin versant. Rev. Sci. Eau, 13, 421-440.
- GALÉA G., P. RAMEZ, M.J. ADLER et E. ROTARU (2004). Modélisation statistique des apports de MES associés au régime des crues d’un sous-bassin du Timis-Béga (Roumanie). Rev. Sci. Eau, 17, 471-488.
- GALÉA G. et S. CANALI (2005). Régionalisation des modules annuels et des régimes d’étiage du bassin hydrographique de la Moselle française : lien entre modèles régionaux. Rev. Sci. Eau, 18, 331-352.
- GALÉA G. et M. BLUM (2005). Modélisation régionale des régimes de crue du bassin hydrographique de la Moselle française. Houille blanche, 5, 88-96.
- JAVELLE P. (2001). Caractérisation du régime des crues : le modèle débit-durée-fréquence convergent. Approche locale et régionale. Thèse de Doctorat, Institut National Polytechnique de Grenoble, France, 1er mars 2001, 268 p.
- MASSON J.M, H. LUBES, P. RAOUS et M. TAPIAU (1994). Safarhy, logiciel de calculs statistiques et d’analyse fréquentielle adapté à l’évaluation du risque en hydrologie. Montpellier : ORSTOM, Laboratoire d’hydrologie.
- MIC R., G. GALÉA et P. JAVELLE (2002). Modélisation régionale des débits de crue du bassin hydrographique du Cris (Roumanie) : approche régionale classique et par modèles de référence. Rev. Sci. Eau, 15, 677-700.
- MIC R. et G. GALÉA (2004). Local and regional estimation of floods in the Timis and Bega hydrographic basins. Application of converging QdF model concept. Conference on Water Observation and Information System for Decision Support, Ohrid, FY Republic of Macedonia, 25‑29 May 2004.
- OUARDA T.B.M.J. et F. ASHKAR (1994). Bootstrap-based intercomparison of regional flood frequency models. Rapport technique, Département de mathématiques, Université de Moncton, 13p.
- OUARDA T.B.M.J., C. GIRARD, G.S. CAVADIAS et B. BOBÉE (2001). Regional flood frequency estimation with canonical correlation analysis. J. Hydrol., 254, 157-173.
- RIBEIRO-CORRÉA J., G.S. CAVADIAS, B. CLÉMENT et J. ROUSSELLE (1995). Identification of hydrological neighborhoods using canonical correlation analysis, J. Hydrol., 173, 71-89.
- SAUQUET E., E. LEBLOIS et G. GALÉA (2003). Mapping flood regime descriptors for flow duration-frequency characterisation at ungauged location. EGS-2003, Nice, France (affiche).
Liste des figures
Figure 1
Localisation des stations hydrométriques des sous-bassins retenus
Location of the hydrometric measurement stations.
Figure 2
Loi régionale des modules : a) chronique complète (cf. tableau 1) et b) période 1980-2001 pour le bassin du Timis.
Regional distribution of the annual mean discharges: a) time series available (cf Table 1) and b) period 1980- 2001 for the Timis catchment.
(a)
(b)
Figure 3
Lois régionales sur les modules des bassins du Timis et du Bega (1980-2001); (a) 0<UF<4,0 et (b) 0<UF<1,0.
Regional distribution of the annual mean discharges for the Timis and Bega catchments; (a) 0<UF<4.0 and (b) 0<UF<1.0.
(a)
(b)
Figure 4
Comparaison des quantiles « observés » et régionalisés sur le bassin du Timis; (a) QA «sec» T = 5 ans; (b) QA «sec» T = 5 ans; (c) QA «sec» T = 10 ans; (d) QA «sec» T = 10 ans; (e) QA «humide» T = 5 ans; (f) QA «humide» T = 5 ans; (g) QA «humide» T = 10 ans; (h) QA «humide» T = 10 ans.
Comparison of local and regional quantiles for the Timis catchment; (a) QA «dry» T = 5 yr; (b) QA «dry» T = 5 yr; (c) QA «dry» T = 10 yr; (d) QA «dry» T = 10 yr; (e) QA «humid» T = 5 yr; (f) QA «humid» T = 5 yr; (g) QA «humid» T = 10 yr; (h) QA «humid» T = 10 yr.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Figure 5
Lois régionales sur les étiages des bassins du Timis et du Bega; (a) 0<UF<4,5 et (b) 0<UF<1,0.
Low flow regional distributions for the Timis and Bega catchments; (a) 0<UF<4.5 et (b) 0<UF<1.0.
(a)
(b)
Figure 6
Comparaison des quantiles d’étiage sur 30 jours pour le bassin du Bega; (a) quinquennal «sec»; (b) décennal «sec»; (c) quinquennal «humide»; (d) décennal «humide»;
Comparison of low flow 30-day quantiles for the Bega catchment; (a) five-year «dry»; (b) 10-year «dry»; (c) 5-year «humid»; (d) 10-year «humid».
(a)
(b)
(c)
(d)
Figure 7
Comparaison des lois régionales sur les modules et étiages du Timis-Bega; (a) 0<UF<4,5 et (b) 0<UF<1,0.
Comparison of regional distributions of annual mean discharge and low flow in the Timis-Bega catchment; (a) 0<UF<4.5 and (b) 0<UF<1.0.
(a)
(b)
Figure 8
Comparaison des lois régionales des bassins hydrographiques du Timis-Béga et de la Moselle; (a) lois régionales sur QA et (b) lois régionales d’étiage.
Comparison of regional distributions for the Timis-Bega and Moselle catchments (a) QA regional distributions and (b) low flow regional distributions.
(a)
(b)
Figure 9
Influence de ∆e sur les quantiles d’étiage modélisés (Éq. 5) du sous-bassin 50205 (S = 80 km2; (a) vcn 10 j; (b) vcn 30 j; (c) vcn 90 j
Influence of ∆e on the modelling of low flow quantiles (5) for the (50205) sub-catchment (S = 80 km2; (a) vcn 10 d; (b) vcn 30 d; (c) vcn 90 d.
(a)
(b)
(c)
Figure 10
Influence de ∆e sur les quantiles d’étiage modélisés (5) du sous-bassin 50105 (S = 73,5 km2); (a) vcn 10 j; (b) vcn 30 j; (c) vcn 90 j.
Influence of ∆e on the modelling of low flow quantiles (5) for the (50105) sub-catchment (S = 73.5 km2); (a) vcn 10 d; (b) vcn 30 d; (c) vcn 90 d.
(a)
(b)
(c)
Figure 11
Site et sous-bassin de référence associé.
Study site and associated reference sub-catchment.
Figure 12
Erreur relative sur v̅d=1,site et q̅a̅site selon les estimations; (a) entre débit journalier médian d’étiage observé (Éq. 4) et estimé selon l’éq. 8 ou l’éq. 11; (b) entre module médian observé (Éq. 1) et estimé selon l’éq. 7 ou l’éq. 12.
Estimation of v̅d=1,site and q̅a̅site relative error; (a) between observed median daily flow (Eq. 4) and estimated as per eq. 8 or eq. 11; (b) between observed median modulus (Eq. 1) and estimated as per eq. 7 or eq. 12.
(a)
(b)
Liste des tableaux
Tableau 1
Présentation des 19 sous-bassins du Timis-Bega retenus.
Presentation of the 19 sub-catchments of the Timis-Bega region.
Bassin hydrographique du Timis : 14 sous-bassins | |||||
|---|---|---|---|---|---|
Sous-bassins |
Code |
Observations de débit |
S |
Zm |
|
|
|
Période |
Durée (an) |
(km2) |
(m) |
Timis à TEREGOVA |
53105 |
1953-2001 |
49 |
167 |
906 |
Timis à SADOVA |
53110 |
1971-2001 |
31 |
560 |
936 |
Timis à CARANSEBES |
53115 |
1974-2001 |
28 |
1 072 |
769 |
Timis à LUGOJ |
53125 |
1970-2001 |
32 |
2 706 |
665 |
Raul Rece à RUSCA |
53205 |
1953-2001 |
49 |
163 |
1157 |
Fenes à FENES |
53305 |
1964-2001 |
38 |
125 |
973 |
Sebes à TURNU RUENI |
53405 |
1964-1998 |
35 |
122 |
819 |
Bistra à VOISLOVA BUCOVEI |
53505 |
1951-2001 |
51 |
232 |
886 |
Bistra à VOISLOVA |
53510 |
1963-2001 |
39 |
404 |
827 |
Bistra à OBREJA |
53515 |
1982-2001 |
20 |
863 |
880 |
Bistra Marului à POIANA MARULUI |
53605 |
1953-2001 |
49 |
79 |
1 442 |
Sucu à POIANA MARULUI |
53705 |
1953-2001 |
49 |
77 |
1 434 |
Nadrag à NADRAG |
53805 |
1963-2001 |
39 |
35 |
742 |
Golet à GOLET |
55105 |
1982-2001 |
20 |
41 |
751 |
Bassin hydrographique du Bega : 5 sous-bassins | |||||
Sous-bassins |
Code |
Observations de débit |
S |
Zm |
|
|
|
Période |
Durée (an) |
(km2) |
(m) |
Bega à LUNCANI |
50105 |
1976-2001 |
26 |
73,5 |
739 |
Bega à FAGET |
50110 |
1974-2001 |
28 |
474 |
470 |
Bega à BALINT |
50115 |
1970-2001 |
32 |
1 064 |
329 |
Sasa à POIENI |
50205 |
1966-2001 |
36 |
80 |
763 |
Gladna à FIRDEA |
50301 |
1980-2001 |
22 |
57 |
456 |
Nota - Parmi ces 19 sous-bassins, deux jeux sont constitués: de 10 (en gris) et 9 sous-bassins, respectivement utilisés pour le calage et la validation des régressions ultérieures.
Tableau 2
Paramètres locaux et régionaux de la loi sur les modules (durée : cf. Tableau 1).
Local and regional parameters of the annual mean discharge distribution (chronicle: cf. Table 1).
Station |
53105 |
53110 |
53115 |
53125 |
53205 |
53305 |
53405 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73,5 |
560 |
1 072 |
2 706 |
163 |
125 |
122 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
Paramètres locaux (1) et quantile médian q̅a̅l̅ | ||||||||||||||
αL |
3,28 |
5,26 |
3,70 |
3,83 |
6,14 |
4,95 |
3,61 |
4,06 |
4,25 |
3,62 |
4,77 |
4,14 |
3,12 |
3,64 |
βL (m3/s) |
2,49 |
11,5 |
21,1 |
44,5 |
5,06 |
3,07 |
3,20 |
4,30 |
7,55 |
12,9 |
3,05 |
3,41 |
0,799 |
0,759 |
q̅a̅l̅ (m3/s) |
2,23 |
10,7 |
19,1 |
40,5 |
4,76 |
2,85 |
2,89 |
3,93 |
6,93 |
11,7 |
2,82 |
3,12 |
0,710 |
0,686 |
β*L |
1,12 |
1,07 |
1,10 |
1,10 |
1,06 |
1,08 |
1,11 |
1,09 |
1,09 |
1,11 |
1,08 |
1,09 |
1,12 |
1,11 |
Paramètres Régionaux :αR = 4,24 et βR = 1,09 |
Tableau 3
Paramètres locaux et régionaux de la loi de Weibull sur les modules (1980-2001).
Local and regional parameters of the Weibull distribution of annual mean discharge (1980-2001).
Station |
53105 |
53110 |
53115 |
53125 |
53205 |
53305 |
53405 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73,5 |
560 |
1 072 |
2 706 |
163 |
125 |
122 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
Paramètres locaux (1) et quantile médian q̅a̅l̅ | ||||||||||||||
αL |
3,21 |
4,94 |
3,45 |
3,67 |
5,34 |
4,66 |
3,38 |
4,35 |
4,22 |
3,62 |
4,75 |
4,08 |
2,98 |
3,64 |
βL (m3/s) |
2,06 |
11,0 |
20,6 |
42,8 |
4,76 |
2,95 |
3,16 |
4,31 |
7,18 |
12,9 |
2,99 |
3,44 |
0,74 |
0,76 |
q̅a̅l̅ (m3/s) |
1,84 |
10,2 |
18,5 |
38,7 |
4,45 |
2,73 |
2,84 |
3,96 |
6,58 |
11,7 |
2,77 |
3,15 |
0,678 |
0,686 |
β*L |
1,12 |
1,08 |
1,11 |
1,11 |
1,07 |
1,08 |
1,11 |
1,09 |
1,09 |
1,11 |
1,08 |
1,09 |
1,09 |
1,11 |
Paramètres Régionaux : αR = 4,03 et βR = 1,10 |
Tableau 4
Paramètres locaux et régionaux de la loi de Weibull sur les modules – influence de différentes périodes d’observation.
Local and regional parameters of the Weibull distribution of annual mean discharge – influence of different observation periods.
Station |
50105 |
50110 |
50115 |
50205 |
50301 |
50105 |
50110 |
50115 |
50205 |
50301 |
|---|---|---|---|---|---|---|---|---|---|---|
Période |
1976-2001 |
1974-2001 |
1970-2001 |
1966-2001 |
1980-2001 |
1980-2001 |
||||
S (km2) |
73,5 |
474 |
1 064 |
80 |
57 |
73,5 |
474 |
1 064 |
80 |
57 |
Paramètres locaux (1) et quantile médian q̅a̅l̅ | ||||||||||
αL |
4,55 |
3,56 |
2,80 |
3,12 |
2,87 |
4,61 |
3,47 |
3,07 |
3,27 |
2,87 |
βL (m3/s) |
1,49 |
5,66 |
8,52 |
1,36 |
0,63 |
1,46 |
5,32 |
7,86 |
1,20 |
0,63 |
q̅a̅l̅ (m3/s) |
1,38 |
5,10 |
7,47 |
1,21 |
0,55 |
1,35 |
4,78 |
6,97 |
1,07 |
0,55 |
β*L |
1,08 |
1,11 |
1,14 |
1,12 |
1,14 |
1,08 |
1,11 |
1,13 |
1,12 |
1,14 |
Paramètres Régionaux : αR = 3,36 et βR = 1,12 |
Paramètres Régionaux : αR = 3,46 et βR = 1,12 |
Tableau 5
Erreur quadratique moyenne sur les modules de chaque bassin.
Average quadratic error on the annual mean discharges quantiles for each catchment.
Bassin du Timis (14 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||
Erreur quadratique (%) (Éq. 3) |
Erreur quadratique (%) (Éq. 3) |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
5,6 |
3,5 |
7,1 |
5,5 |
4,0 |
6,6 |
Tableau 6
Erreur quadratique moyenne par sous-bassin du Timis.
Average quadratic error for each Timis sub-catchment.
Station |
53105 |
53110 |
53115 |
53125 |
53205 |
53305 |
53405 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73,5 |
560 |
1072 |
2706 |
163 |
125 |
122 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
Bassin du Timis : Erreur quadratique moyenne par sous-bassin (%) | ||||||||||||||
∀ Fi confondues |
8,0 |
5,4 |
5,1 |
2,9 |
7,0 |
3,9 |
6,0 |
2,2 |
1,3 |
3,4 |
4,4 |
0,5 |
12,8 |
3,1 |
∀ Fi>0,5 |
5,2 |
3,9 |
3,4 |
2,4 |
5,7 |
3,2 |
3,7 |
1,5 |
1,1 |
2,6 |
3,4 |
0,7 |
4,7 |
2,6 |
∀ Fi<0,5 |
10,0 |
6,5 |
6,4 |
3,2 |
8,1 |
4,5 |
7,7 |
2,7 |
1,5 |
3,9 |
5,2 |
0,3 |
17,5 |
3,6 |
Tableau 7
Erreur quadratique moyenne sur les modules du bassin du Timis-Bega.
Average quadratic error on the annual mean discharges quantiles of the Timis-Bega catchment.
Bassin du Timis (14 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||
Er. quadratique (%), avec paramètres régionaux Bega |
Er. quadratique (%), avec paramètres régionaux Timis |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
6,4 |
5,4 |
7,3 |
8,5 |
5,3 |
10,8 |
Tableau 8
Erreur quadratique moyenne sur les quantiles d’étiage de chaque bassin.
Average quadratic error on low flow quantiles for each catchment.
Bassin du Timis (13 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||
|---|---|---|---|---|---|
Paramètres régionaux |
Paramètres régionaux |
||||
αR = 2,78 et βR = 1,20 |
αR = 3,25 et βR = 1,23 |
||||
Erreur quadratique (%) |
Erreur quadratique (%) |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
10,1 |
9,3 |
10,8 |
6,1 |
5,2 |
6,9 |
Tableau 9
Erreur quadratique moyenne sur les quantiles d’étiage du Timis-Bega.
Average quadratic error on low flow quantiles of the Timis-Bega catchment.
Bassin du Timis (13 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||
|---|---|---|---|---|---|
Er. Quadratique (%), avec paramètres régionaux Bega |
Er. quadratique (%), avec paramètres régionaux Timis |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
16,3 |
9,7 |
20,9 |
9 |
5,9 |
11,3 |
Tableau 10
Calage de la relation (Éq. 7).
Calibration of the relationship (Eq. 7)
Code |
50105 |
50110 |
50115 |
50205 |
53105 |
53115 |
53125 |
53205 |
53305 |
53405 |
|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73.5 |
474 |
1064 |
80 |
167 |
1 072 |
2 706 |
163 |
125 |
122 |
q̅a̅ (Éq. 1) observé (m3/s) |
1,35 |
4,78 |
6,97 |
1,07 |
1,84 |
18,5 |
38,7 |
4,45 |
2,73 |
2,84 |
q̅a̅ (Éq. 7) (m3/s) |
1,14 |
4,58 |
7,07 |
1,29 |
3,21 |
17,4 |
37,6 |
4,06 |
2,59 |
2,11 |
Erreur relative (%) |
16 |
4 |
-1 |
-21 |
-74 |
6 |
3 |
9 |
5 |
26 |
Erreur quadratique (%) |
19 |
Tableau 11
Validation de la relation (7).
Validation of the relationship (7).
Code |
50301 |
53110 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|
S (km2) |
57 |
560 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
q̅a̅ (1) observé (m3/s) |
0,550 |
10,2 |
3,96 |
6,58 |
11,7 |
2,77 |
3,15 |
0,680 |
0,690 |
q̅a̅ (7) (m3/s) |
0,530 |
11,2 |
4,36 |
7,06 |
16,1 |
2,48 |
2,40 |
0,550 |
0,650 |
Erreur relative (%) |
4 |
-10 |
-10 |
-7 |
-38 |
10 |
24 |
19 |
6 |
Erreur quadratique (%) |
17 |
Tableau 12
Calage de la relation (8).
Calibration of the relationship (8).
Code |
50105 |
50110 |
50115 |
50205 |
53105 |
53115 |
53125 |
53205 |
53305 |
53405 |
|---|---|---|---|---|---|---|---|---|---|---|
S (km2) |
73.5 |
474 |
1 064 |
80 |
167 |
1 072 |
2 706 |
163 |
125 |
122 |
v̅d=1 (4) observé (m3/s) |
0,633 |
1,81 |
2,08 |
0,417 |
0,440 |
3,63 |
8 |
1,04 |
0,646 |
0,633 |
v̅d=1 (8) (m3/s) |
0,460 |
1,39 |
2,13 |
0,440 |
0,530 |
3,84 |
7,85 |
1,08 |
0,760 |
0,660 |
Erreur relative (%) |
27 |
23 |
-2 |
-6 |
-20 |
-6 |
2 |
-4 |
-18 |
-4 |
Erreur quadratique (%) |
15 |
Tableau 13
Validation de la relation (8).
Validation of the relationship (8).
Code |
50301 |
53110 |
53505 |
53510 |
53515 |
53605 |
53705 |
53805 |
55105 |
|---|---|---|---|---|---|---|---|---|---|
S (km2) |
57 |
560 |
232 |
404 |
863 |
79 |
77 |
35 |
41 |
v̅d=1 (4) observé (m3/s) |
0,128 |
2,38 |
0,839 |
1,50 |
2,69 |
0,759 |
0,784 |
0,144 |
0,136 |
v̅d=1 (8) (m3/s) |
0,210 |
2,32 |
1,29 |
1,99 |
3,64 |
0,640 |
0,510 |
0,310 |
0,370 |
Erreur relative (%) |
-64 |
3 |
-54 |
-33 |
-35 |
16 |
35 |
-115 |
-172 |
Erreur quadratique (%) |
55 |
Tableau 14
Estimation de ∆e et de son incertitude.
Estimation and relative error of ∆e.
Bassin du Timis (14 sous-bassins) |
Bassin du Bega (5 sous-bassins) |
||||||||
|---|---|---|---|---|---|---|---|---|---|
Sous-bassins |
S |
Δe (j) |
Sous-bassins |
S |
Δe (j) |
||||
|
(km2) |
observé (5) |
estimé (9) |
erreur (%) relative |
|
(km2) |
observé (5) |
estimé (10) |
erreur (%) relative |
53105 |
167 |
96 |
109 |
14 |
50105 |
73,5 |
408 |
260 |
-36 |
53110 |
560 |
110 |
110 |
0 |
50110 |
474 |
224 |
203 |
-9 |
53115 |
1072 |
99 |
102 |
3 |
50115 |
1064 |
172 |
167 |
-3 |
53125 |
2706 |
109 |
96 |
-12 |
50205 |
80 |
175 |
264 |
51 |
53205 |
163 |
113 |
120 |
6 |
50301 |
57 |
168 |
200 |
19 |
53305 |
125 |
109 |
112 |
3 |
|
||||
53405 |
122 |
97 |
104 |
7 |
|
||||
53505 |
232 |
97 |
108 |
11 |
|
||||
53510 |
404 |
97 |
105 |
8 |
Erreur quadratique (%) |
||||
53515 |
863 |
118 |
107 |
-9 |
Timis |
Bega |
|||
53605 |
79 |
164 |
131 |
-20 |
Calage (9) |
validation |
Calage (10) |
||
53705 |
77 |
145 |
130 |
-10 |
9 |
11 |
29,5 |
||
53805 |
35 |
107 |
100 |
-7 |
|
||||
55105 |
41 |
93 |
101 |
9 |
|
Tableau 15
Incertitude sur les quantiles d’étiage du sous-bassin 50205 liée à l’estimation de ∆e.
Low flow quantile uncertainty induced by the estimation of ∆e for the (50205) sub-catchment.
50205 : Modélisation (5) avec α = 2,74 β = 1,26 et v̅c̅n̅d=1 = 0,385 m3/s | |||||
|---|---|---|---|---|---|
Δe = 175 j (observé) |
Δe = 264 j (estimé) |
||||
Erreur quadratique (%) |
Erreur quadratique (%) |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
4 |
3 |
4,7 |
5,9 |
6 |
5,8 |
Tableau 16
Incertitude sur les quantiles d’étiage du sous-bassin 50105 liée à l’estimation de ∆e.
Low flow quantile uncertainty induced by the estimation of ∆e for the (50105) sub-catchment.
50105 : Modélisation (5) avec α = 4,13 β = 1,18 et v̅c̅n̅d=1 = 0,595 m3/s | |||||
|---|---|---|---|---|---|
∆e = 408 j (observé) |
∆e = 260 j (estimé) |
||||
Erreur quadratique (%) |
Erreur quadratique (%) |
||||
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
∀ Fi confondues |
∀ Fi>0,5 |
∀ Fi<0,5 |
2,2 |
1,5 |
2,7 |
6 |
5,2 |
6,7 |
Tableau 17
Poids de l’information épisodique d’étiage sur l’estimation des descripteurs de régime.
Impact of the low flow episodic information on the estimation of regime descriptors.
Sous-bassin de référence |
K |
Site étudié |
||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
Code |
S (km2) |
v̅d̅=̅1̅ (m3/s) |
q̅a̅ (m3/s) |
Code |
S (km2) |
v̅d̅=̅1̅ (m3/s) |
q̅a̅ (m3/s) |
|||||||||
|
|
(4) |
(1) |
|
|
|
(4) |
(8) |
Er.(8) % |
(11) |
Er.(11) % |
(1) |
(7) |
Er.(7) % |
(12) |
Er.(12) % |
50110 |
474 |
1,81 |
4,78 |
0,317 |
50105 |
73,5 |
0,633 |
0,460 |
27 |
0,573 |
9 |
1,35 |
1,14 |
16 |
1,51 |
‑12 |
50105 |
73,5 |
0,633 |
1,35 |
3,15 |
50110 |
474 |
1,81 |
1,39 |
23 |
2 |
‑10 |
4,78 |
4,58 |
4 |
4,25 |
11 |
50301 |
57 |
0,128 |
0,550 |
3,32 |
50205 |
80 |
0,417 |
0,440 |
‑6 |
0,425 |
‑2 |
1,07 |
1,29 |
‑21 |
1,83 |
‑71 |
50205 |
80 |
0,417 |
1,07 |
0,3 |
50301 |
57 |
0,128 |
0,210 |
‑64 |
0,125 |
2 |
0,550 |
0,530 |
4 |
0,320 |
42 |
53110 |
560 |
2,38 |
10,2 |
1,74 |
53115 |
1072 |
3,63 |
3,84 |
6 |
4,13 |
‑14 |
18,5 |
17,4 |
6 |
17,7 |
4 |
53115 |
1072 |
3,63 |
18,5 |
0,57 |
53110 |
560 |
2,38 |
2,32 |
3 |
2,07 |
13 |
10,2 |
11,2 |
‑10 |
10,5 |
‑3 |
53205 |
163 |
1,04 |
4,45 |
0,497 |
53105 |
167 |
0,440 |
0,530 |
‑20 |
0,517 |
‑18 |
1,84 |
3,21 |
‑75 |
2,21 |
‑20 |
53105 |
167 |
0,440 |
1,84 |
2 |
53205 |
163 |
1,04 |
1,08 |
‑4 |
0,883 |
15 |
4,45 |
4,06 |
9 |
3,68 |
17 |
53505 |
232 |
0,839 |
3,96 |
2,17 |
53510 |
404 |
1,50 |
1,99 |
‑33 |
1,80 |
‑20 |
6,58 |
7,06 |
‑7 |
8,60 |
‑31 |
53510 |
404 |
1,50 |
6,58 |
0,459 |
53505 |
232 |
0,839 |
1,29 |
‑53 |
0,690 |
18 |
3,96 |
4,36 |
‑10 |
3,02 |
24 |
53510 |
404 |
1,50 |
6,58 |
1,87 |
53515 |
863 |
2,69 |
3,64 |
‑35 |
2,81 |
‑5 |
11,7 |
16,1 |
‑38 |
12,3 |
‑5 |
53515 |
863 |
2,69 |
11,7 |
0,532 |
53510 |
404 |
1,50 |
1,99 |
‑33 |
1,43 |
5 |
6,58 |
7,06 |
‑7 |
6,20 |
6 |
53515 |
863 |
2,69 |
11,7 |
0,174 |
53605 |
79 |
0,759 |
0,640 |
16 |
0,468 |
38 |
2,77 |
2,48 |
11 |
2,04 |
26 |
53605 |
79 |
0,759 |
2,77 |
5,73 |
53515 |
863 |
2,69 |
3,64 |
‑35 |
4,35 |
‑62 |
11,7 |
16,1 |
‑38 |
15,9 |
‑36 |
53705 |
77 |
0,784 |
3,15 |
0,874 |
53605 |
79 |
0,759 |
0,640 |
16 |
0,686 |
10 |
2,77 |
2,48 |
11 |
2,75 |
1 |
53605 |
79 |
0,759 |
2,77 |
1,14 |
53705 |
77 |
0,784 |
0,510 |
35 |
0,867 |
‑11 |
3,15 |
2,40 |
24 |
3,17 |
‑1 |
53805 |
35 |
0,144 |
0,680 |
0,802 |
50301 |
57 |
0,128 |
0,210 |
‑64 |
0,115 |
10 |
0,550 |
0,530 |
4 |
0,545 |
1 |
50301 |
57 |
0,128 |
0,550 |
1,23 |
53805 |
35 |
0,144 |
0,310 |
‑115 |
0,158 |
‑10 |
0,680 |
0,550 |
19 |
0,678 |
0 |
55105 |
41 |
0,136 |
0,690 |
2,39 |
53105 |
167 |
0,440 |
0,530 |
‑21 |
0,325 |
26 |
1,84 |
3,21 |
‑75 |
1,65 |
10 |
53105 |
167 |
0,440 |
1,84 |
0,418 |
55105 |
41 |
0,136 |
0,370 |
‑172 |
0,184 |
‑35 |
0,690 |
0,650 |
6 |
0,769 |
‑11 |
55105 |
41 |
0,136 |
0,690 |
5,74 |
53205 |
163 |
1,04 |
1,08 |
‑4 |
0,781 |
25 |
4,45 |
4,06 |
9 |
3,96 |
11 |
53205 |
163 |
1,04 |
4,45 |
0,174 |
55105 |
41 |
0,136 |
0,370 |
‑172 |
0,181 |
‑33 |
0,690 |
0,650 |
6 |
0,774 |
‑12 |
Erreur quadratique moyenne (%) |
65 |
|
23 |
|
|
28 |
|
23 |