Corps de l’article

1. Introduction

Dans le programme québécois, la résolution de problèmes, désignée par RP dans la suite du texte, est une compétence. L’élève doit montrer qu’elle⋅il maitrise plusieurs stratégies et qu’elle⋅il les mobilise dans un ensemble organisé pour répondre à une question ou à une consigne dans une tâche (Jonnaert, 2017). Elle nécessite alors plusieurs stratégies pédagogiques convergentes de la part des enseignant⋅e⋅s (Lajoie et Bednarz, 2016).

Par ailleurs, les classes primaires québécoises, comme partout dans le monde, sont de plus en plus hétérogènes. Elles comptent en leur sein des élèves en difficulté d’apprentissage ou à risque, des élèves issu⋅e⋅s de l’immigration, des élèves de différents milieux socioéconomiques, des élèves doué⋅e⋅s. Pour répondre à cette grande variété de profils, la politique et la recherche en psychopédagogie recommandent la mise en place de la différenciation pédagogique, notée DP dans la suite du texte.

Dans cette étude, nous présentons comment des enseignant⋅e⋅s prévoient cette DP en résolution de situation-problème mathématique et parviennent à mettre en place de nombreuses adaptations en général, mais aussi pour un⋅e ou des élèves en particulier, ce qui nous conduit à parler d’une différenciation pédagogique potentiellement de qualité selon les indicateurs de Tomlinson (1999).

2. Problématique

2.1 Le défi de l’enseignement de la compétence de résolution de problèmes

Puisque la RP est considérée comme une compétence du 21e siècle, son enseignement doit permettre le développement du potentiel de tou⋅te⋅s les élèves (Cai et coll., 2020). Dans l’école inclusive, l’enseignant⋅e doit se doter de pratiques inclusives et, notamment, elle⋅il peut se tourner vers la mise en place de la DP, pratique qui permet de chercher comment faire fructifier les différences pour permettre l’épanouissement de chacun⋅e (Bergeron et coll., 2021).

Au Québec, la RP est une des trois compétences du programme en mathématiques. Bien que la province fasse figure de bonne élève dans les palmarès internationaux, les écarts de performance entre les élèves à risque et les autres restent préoccupants (Oubenaïssa et Poirier, 2021). Par ailleurs, l’enseignement-apprentissage est une source de stress avérée pour tou⋅te⋅s les élèves et les enseignant⋅e⋅s (Rajotte et Rochette-Parent, 2017).

La RP réclame de mobiliser connaissances et processus mathématiques à partir d’un énoncé qui fait appel à la culture de l’élève et à la découverte de données qui n’ont pas toujours de référence ou sont implicites (Giroux, 2013 ; Koichu et coll., 2022). L’élève doit organiser sa démarche et la réajuster au besoin. L’expression situation-problème est choisie dans les programmes québécois notamment pour souligner la différence avec le problème d’application d’une règle ou d’une connaissance. Une situation-problème engendre « un processus de recherche » (Lajoie et Bednarz, 2016, p. 5) qui va différer d’un⋅e élève à l’autre. Elle⋅il peut rencontrer un certain nombre d’obstacles (Brousseau, 2012). Les enseignant⋅e⋅s doivent par conséquent se doter de pratiques qui lèvent les obstacles à l’équité.

Il est donc intéressant de se pencher sur le cas québécois et de se demander quelles pratiques inclusives, parmi celles qui sont prévues par les enseignant⋅e⋅s du primaire lors de l’enseignement-apprentissage de la RP, permettent la réussite d’un grand nombre d’élèves et la réduction des écarts entre elles⋅eux.

2.2 Enseigner le défi de la résolution de problèmes dans une classe hétérogène

Les classes québécoises primaires sont hétérogènes. Pour les élèves issu⋅e⋅s de milieux défavorisés, les enseignant⋅e⋅s doivent s’assurer que la situation proposée fait bel et bien référence à une situation quotidienne connue. Au Québec, les énoncés de problèmes décrivent généralement une sortie, une activité scolaire (Lajoie et Bednarz, 2016). Or, l’habillage du problème dans une situation concrète peut ne pas être compris. En effet, tou⋅te⋅s les enfants n’ont pas l’occasion d’aller dans un parc d’attractions, au restaurant ou ne possèdent pas forcément de nombreux jeux et livres à la maison. Il se peut que certain⋅e⋅s élèves ne connaissent pas ce à quoi font référence les énoncés des problèmes. L’enseignant⋅e doit s’assurer de créer une culture de classe commune pour ne pas creuser les inégalités (Dutercq, 2001), de supprimer les obstacles de l’ordre de la culture générale afin d’entretenir une interaction entre l’élève et la situation (Giroux, 2013).

Pour les élèves issu⋅e⋅s de l’immigration, c’est la compréhension des mots de l’énoncé qui pourrait faire obstacle ainsi que la double difficulté de devoir acquérir des concepts nouveaux dans une langue et une culture qu’elles⋅ils ne maitrisent pas (McTighe et Brown, 2005).

Pour les élèves handicapé⋅e⋅s ou en difficulté d’apprentissage et d’adaptation (HDAA), l’enseignant⋅e doit veiller à considérer leurs besoins spécifiques et variés pour qu’elles⋅ils comprennent la situation-problème (Côté, 2015 ; Giroux, 2013). Accompagnement accru, utilisation du matériel de manipulation, aide à la lecture des énoncés, aide à l’écriture des résultats, accompagnement en classe par l’orthopédagogue, ces moyens visent à lever les obstacles dus à leurs difficultés (Giroux, 2013).

La classe compte aussi généralement des élèves avancé⋅e⋅s, voire doué⋅e⋅s, pour qui la situation-problème est vite résolue et qui se retrouvent à attendre leurs pairs (Berdonneau, 2009). Les praticien⋅ne⋅s nomment généralement qu’il faut leur préparer plus de travail (Bergeron, 2016), et la recherche s’est interrogée sur la nature de ce travail : rien ne sert de leur demander de faire plus que ce qu’elles⋅ils savent déjà faire (Côté, 2015). Elles⋅ils sont à risque de se désintéresser de la tâche (Hattie et coll., 2020), voire, pour les élèves doué⋅e⋅s, de décrocher plus tard au secondaire (Audibert et Baudrit, 2009). Des défis doivent être créés à la hauteur de leur potentiel.

Si on ajoute à tou⋅te⋅s ces élèves celles⋅ceux que l’on qualifie parfois d’ordinaires, mais qui rencontrent certainement aussi des difficultés plus ou moins ponctuelles en RP, nous avons ici le portrait de nombreuses différences et intérêts à prendre en compte.

Pour l’enseignant⋅e, gérer la classe hétérogène entraine un questionnement sur l’articulation entre les exigences de la RP dans le programme et les besoins des élèves. C’est le principe de la DP recommandée à la fois par les politiques d’adaptation québécoises et par la recherche en psychopédagogie, mais qui reste encore à comprendre dans son application pratique.

2.3 Un manque de repères clairs sur la différenciation pédagogique en pratique

La présence d’une définition de la DP se fait rare dans les textes officiels québécois. Les référentiels qui relatent des pratiques inclusives ont été longs à être publiés et leurs publications ne se sont pas accompagnées de formations (Tremblay, 2020). Le référentiel en mathématiques est apparu en 2019 seulement. En 2021, enfin, est sorti ce que le ministère nomme un « document », accompagné de ses outils complémentaires (ministère de l’Éducation, 2021), qui donne des pistes concrètes de dispositifs à déployer en classe selon la typologie de Tomlinson (1999), à savoir des pistes pour différencier les processus, produits, structures et contenus d’apprentissage. En 2017, la politique de réussite indique qu’il faut prendre en compte les capacités intellectuelles de tou⋅te⋅s les élèves, qu’elles⋅ils soient doué⋅e⋅s, en situation de handicap ou aient simplement besoin d’encouragement ; issu⋅e⋅s de milieux défavorisés ou des élèves venant de parcours migratoires variés, des élèves qui ont donc des caractéristiques linguistiques, culturelles et religieuses variées ; des élèves avec des caractéristiques personnelles, identitaires (genre, sexe, orientation sexuelle) (ministère de l’Éducation et de l’Enseignement supérieur, 2017).

En théorie, le concept est présenté comme étant une pédagogie ou un ensemble de pratiques prometteur (Moldoveanu et coll., 2021). Les études sur la DP en psychopédagogie s’accordent à dire que les principes sont clairs, mais restent encore à opérationnaliser dans la pratique (Frèrejean et coll., 2021 ; Nilholm, 2021). Ainsi, les recherches empiriques ne sont pas encore parvenues à avoir accès à la manière dont les enseignant⋅e⋅s perçoivent la DP et la mettent en oeuvre (Nilholm, 2021). Les études sur les pratiques rapportées des enseignant⋅e⋅s concluent alors à une mise en oeuvre apparemment partielle de la DP (Pozas et coll., 2020). Ainsi, de manière surprenante, la recherche qui ne parvient pas à faire consensus sur le concept de DP s’étonne du flou qui demeure pour les praticien⋅ne⋅s, ce que nous désirions questionner.

En outre, plusieurs articles montrent que, quand on les interroge sur leurs pratiques inclusives, les enseignant⋅e⋅s ne nomment pas forcément l’ensemble des pratiques qu’elles⋅ils emploient quotidiennement parce qu’on ne leur pose peut-être pas la question comme il faut (Kingsdorf et Krawec, 2016 ; Roditi, 2003). Bergeron (2016) explique, par exemple, que les enseignant⋅e⋅s agissent plutôt par expérience ; elles⋅ils savent aussi que ce qui est prévu est toujours modifié lors de l’intervention auprès des élèves. C’est ainsi que des études ne questionnent plus directement les enseignant⋅e⋅s en utilisant le terme DP dans leurs questions ou en cherchant les adaptations visibles dans la classe, mais vont plutôt faire émerger cette dernière en posant des questions sur les pratiques qu’elles⋅ils réfléchissent selon les besoins et intérêts des élèves (Goddard et coll., 2015 ; Nilholm, 2021 ; Roditi, 2003). C’est ce que nous avons fait dans cette étude. Nous avons demandé aux participantes quelles adaptations elles prévoyaient mettre en place pour des élèves identifié⋅e⋅s préalablement. Leur conclusion à l’issue des entretiens est d’ailleurs éloquente ; une des enseignantes ayant déclaré : « Finalement, on ne s’en rend pas compte, mais je fais beaucoup de choses pour préparer la RP et aider mes élèves ».

En somme, la RP est une compétence complexe pour tou⋅te⋅s et les classes québécoises sont hétérogènes, ce qui entraine un ensemble hétérogène de besoins à gérer. Ajoutons à cela que les enseignant⋅e⋅s n’ont pas reçu de prescriptions claires et que la recherche peine à comprendre comment elles⋅ils mettent en oeuvre une pratique aussi changeante. On se demande donc comment, concrètement, les enseignant⋅e⋅s font pour gérer la complexité de la RP et en plus réfléchissent à la gérer en DP. On peut penser que les enseignant⋅e⋅s savent différencier, mais on a peu de données là-dessus (van Geel et coll., 2019). On comprend mal comment elles⋅ils parviennent à tenir compte des besoins et intérêts de tou⋅te⋅s ou si elles⋅ils favorisent des besoins plus que d’autres. Nous nous sommes ainsi demandé : comment, au primaire, les enseignant⋅e⋅s prévoient-elles⋅ils la différenciation pédagogique de la résolution de situations-problèmes mathématiques ?

3. Contexte théorique

Notre cadre conceptuel s’appuie sur le modèle de Verschaffel et coll. (2000). Ce modèle cyclique décrit plusieurs phases dans la démarche de l’élève. Dans chaque phase, il est possible de voir dans quel lieu et quel temps les enseignant⋅e⋅s peuvent prévoir les adaptations nécessaires pour tou⋅te⋅s et pour chacun⋅e. Les adaptations reflètent alors les pratiques de différenciation pédagogique des enseignant⋅e⋅s.

3.1 Le modèle de résolution de problèmes mathématiques de Verschaffel et coll. (2000)

Les situations-problèmes choisies par les enseignant⋅e⋅s sont des tâches complexes en plusieurs étapes, juxtaposées ou combinées entre elles, qui sont mises en contexte par deux énoncés : un habillage de problème dans un énoncé non mathématique pour la mise en contexte et un énoncé mathématique qui décrit l’ensemble des contraintes à prendre en compte pour résoudre la situation.

Les mathématiques ne sont pas des savoirs isolés, mais plutôt « une série d’activités faites en cohérence » (Verschaffel et De Corte, 2008, p. 1). À cet égard, le modèle met de l’avant les allers-retours entre les différentes actions requises pour résoudre une situation-problème (figure 1).

Figure 1

Diagramme schématique du processus de modélisation (Fagnant et coll., 2003, p. 30)

Diagramme schématique du processus de modélisation (Fagnant et coll., 2003, p. 30)

  • Lors de la phase de compréhension, l’élève doit déterminer les éléments importants et les relations entre ces derniers.

  • Lors de la phase de modélisation, l’élève cherche comment opérationnaliser sa réponse. Le modèle de situation se transforme en modèle mathématique.

  • Lors de la phase d’analyse, il s’agit d’effectuer les opérations et de proposer un ou plusieurs résultats. L’élève analyse alors le modèle mathématique qu’elle⋅il a trouvé.

  • La phase d’interprétation est le moment où l’élève vérifie si les résultats coïncident avec le modèle de situation. Dans le cas contraire, il faut reprendre à la phase 1.

  • La phase de communication consiste à présenter son résultat sous la forme d’une trace explicite.

-> Voir la liste des figures

Ce modèle montre donc que l’élève ne fait pas qu’une simple opération, mais met bel et bien en oeuvre une démarche de raisonnement complexe. L’enseignant⋅e doit donc s’adapter pour s’adresser à sa classe hétérogène (Goulet, 2018).

3.2 La différenciation pédagogique et les adaptations

La différenciation pédagogique apparait dans le discours de la recherche en psychopédagogie avec le constat que tout⋅e enseignant⋅e fait quand elle⋅il rencontre un nouveau groupe d’élèves : elles⋅ils sont différent⋅e⋅s, elles⋅ils ont des besoins, des intérêts différents (Tomlinson, 1999). C’est un constat qui a toujours été interrogé par les enseignant⋅e⋅s qui cherchent à tenir compte de tou⋅te⋅s et de chacun⋅e (Prud’homme et coll., 2011). C’est une forme d’entéléchie morale, comme dirait Aristote. En grec, le thélos est le but à atteindre, il est en toute chose, comme une force qui pousse à la croissance. Les enseignant⋅e⋅s recherchent la réussite de tou⋅te⋅s leurs élèves.

Cette reconnaissance des différences entraine deux principes dont les ajustements semblent incompatibles, si on pense en matière d’ajout d’adaptation. D’une part, l’enseignant⋅e doit transmettre les savoirs du curriculum, s’assurer que les élèves en difficulté puissent bénéficier d’un soutien accru quand c’est nécessaire. C’est le principe d’équité. D’autre part, l’enseignant⋅e est guidé⋅e par le principe d’excellence : le savoir ne doit pas être amoindri pour ces élèves en difficulté, mais la situation doit aussi faire progresser les élèves les plus avancé⋅e⋅s. La recherche parle des deux extrémités du spectre de l’apprentissage (Celik, 2019) ou encore de viser à mettre à la fois en place du soutien et des défis (Dulfer et coll., 2021). Pourtant, si on pense à la richesse du partage de stratégies, les pratiques inclusives peuvent aussi se saisir de ces différences pour enrichir le débat (Ainscow, 2020 ; Prud’homme et coll., 2016).

Ainsi, la différenciation consiste à mettre en place des situations didactiques (van Geel et coll., 2019) qui permettent le progrès du plus grand nombre d’élèves à la fois, en déterminant des variables dans l’organisation des ressources, mais aussi dans le contenu de l’enseignement-apprentissage : la DP, c’est à la fois des considérations pratiques et des comportements (Finkelstein et coll., 2021) ; c’est la flexibilité (Frèrejean et coll., 2021) et la pensée critique de l’enseignant⋅e (Wright, 2018).

Tomlinson (1999) propose de ranger les stratégies d’intervention en quatre axes : différenciation des processus, des produits, des structures et des contenus. Ce sont les actions que l’enseignant⋅e peut poser. La recherche reprend souvent cette typologie pour chercher les marqueurs visibles de la DP dans les classes. Nous ne faisons pas exception ici puisqu’il est vrai qu’avant de chercher à comprendre comment s’organise la pensée critique des enseignant⋅e⋅s, cette typologie a l’avantage de faire voir la partie émergée de l’iceberg.

Le processus est la manière dont l’élève arrive à comprendre ce qui est enseigné. Ce sont les stratégies de l’apprenant⋅e. En RP, l’enseignant⋅e peut proposer du matériel de manipulation à certains élèves et faire varier le niveau de maitrise des processus requis en employant des nombres plus ou moins complexes, par exemple.

La production constitue les différentes manières pour l’élève de prouver qu’elle⋅il a compris. Ce sont les travaux de l’élève. Elle⋅il peut témoigner de l’acquisition d’une connaissance en laissant des traces différentes : faire un dessin, trouver des stratégies personnelles de calcul mental ou utiliser les algorithmes traditionnels.

S’ajoute à cela l’organisation des tâches dans la classe. Ce sont les structures. On peut, par exemple, envisager de placer les élèves en groupes hétérogènes ou homogènes afin d’adapter l’intervention durant l’enseignement-apprentissage.

Le contenu correspond aux connaissances à acquérir. Par exemple, l’enseignant⋅e peut penser à intervenir auprès des élèves en difficulté sur le sens de la connaissance en jeu en travaillant avec du matériel de manipulation, tout en proposant des activités qui vont explorer les applications de la connaissance aux élèves plus avancé⋅e⋅s (un jeu mathématique, par exemple).

Pour différencier en RP, l’enseignant⋅e doit enseigner en tenant compte des « grandes idées » (Small et Lin, 2022, p. 5, traduction libre), c’est-à-dire faire percevoir aux élèves la cohérence des mathématiques plutôt que leur enseigner des processus isolés. Cela nécessite de les évaluer régulièrement pour s’assurer que la situation choisie corresponde aux habilités de chacun⋅e. Enseigner les situations-problèmes requiert alors de poser des questions ouvertes durant le pilotage et de proposer parfois des tâches parallèles selon le niveau de connaissances des élèves en variant la grandeur des données numériques, par exemple (Small et Lin, 2022).

Dans notre recherche, nous avons choisi d’interroger les participantes sur une situation-problème qu’elles avaient choisie et leur avons demandé de faire un portrait des besoins de leurs élèves en RP (ce que nous nommons portrait-classe, annexe 1), avant de mener avec elles des entretiens d’explicitation (Vermersch, 2006). Nous les avons questionnées sur la manière dont elles anticipaient offrir du soutien aux élèves identifié⋅e⋅s et les adaptations qu’elles prévoyaient.

L’adaptation est une action mise en place afin de permettre à un ou des élèves de comprendre le savoir. C’est un ajustement à court ou à long terme (Shumm, 1999). C’est un soutien qui veille à ne pas amoindrir la connaissance en jeu. Nous avons organisé les choix prévus de nos participantes entre adaptations générales ou adaptations pour un⋅e ou des élèves en particulier.

À travers la description des cinq phases du modèle de Verschaffel et coll. (2000), nous faisons ressortir les adaptations générales et les adaptations pour un⋅e ou des élèves en particulier prévues et décrivons la DP selon la typologie de Tomlinson (1999).

4. Méthodologie

La DP, en classe primaire, est par nature un principe de décision flexible et est sujette à changement selon des considérations pédagogiques et didactiques. Ainsi, nous avons laissé la parole aux enseignant⋅e⋅s. Cette étude suit les principes du paradigme descriptif/interprétatif : nous tentons de cerner les besoins ressentis des participantes, les caractéristiques de ces besoins et leur perception (Gallagher et Garceau, 2020).

Ont été recrutées quatre enseignantes considérées expertes au deuxième cycle du primaire, à Montréal, Québec, soit auprès d’élèves de huit ou neuf ans (tableau 1). Nous les avons interrogées en février/mars, à un moment de l’année où elles connaissaient leurs élèves et avaient déjà enseigné la RP.

Tableau 1

Description des participantes de cette étude

Description des participantes de cette étude

-> Voir la liste des tableaux

Nous nous sommes dotée de plusieurs outils de collecte afin de multiplier les points de vue possibles sur la pratique. Tout d’abord, le portrait-classe est une carte conceptuelle que les participantes devaient nous envoyer une semaine avant l’entretien (annexe 1). L’examen de ce document nous a permis de préparer les questions, car nous avons demandé de justifier les choix prévus en fonction des élèves du portrait. Une analyse à priori des situations-problèmes nous a permis d’identifier les obstacles que pourraient rencontrer les élèves. Nous avons choisi la grille d’analyse de Berger (2017), que nous avons modifiée pour l’adapter au primaire.

Les entretiens d’explicitation permettent un partage d’expertise. Nous voulions comprendre les choix et, en tant que praticienne, nous nous étions forgé une conception générale de la manière dont pourraient se piloter les situations choisies. Nous nous sommes basée sur notre compréhension personnelle des classes primaires en général et de la situation choisie pour guider les entretiens et confronter notre expertise à celle des participantes, comme si, en quelque sorte, nous nous projetions aussi à la place des participantes pour lever tous les implicites dans leurs discours, au fur et à mesure de leurs explications, quand cela ne nous semblait pas familier. La construction de sens est donc le fruit d’une interaction. Par exemple, nous avons demandé à une enseignante pourquoi elle n’anticipait pas la gestion du budget de la sortie comme un obstacle pour les élèves. Cela nous avait en effet semblé majeur lors de l’analyse à priori. Nous avons donc insisté sur cet aspect dans l’entretien et elle nous a expliqué que le budget avait déjà été l’objet d’une situation précédente, donc implicitement, elle le considérait comme non prioritaire cette fois-ci. Nous croyons que les entretiens que nous avons menés sont alors très pertinents pour comprendre comment est réellement opérationnalisée la DP.

À ces outils s’ajoute le journal de bord de la chercheuse. Ce dernier contient entre autres des fiches synthèses réalisées après la transcription de chaque entretien, mais aussi avant l’entretien suivant, qui ont eu l’avantage de mettre en lumière les points d’ombre à expliciter d’un entretien à l’autre. Par exemple, le premier entretien nous a éclairée sur la nécessité de dire que la situation n’était qu’un prétexte pour parler de la DP en général. Les entretiens suivants ont été orientés pour que les enseignantes évoquent aussi ce qu’elles font le plus souvent et pas seulement ce qu’elles prévoyaient strictement pour la situation choisie.

Nos entretiens ont duré en moyenne 40 minutes. Nous les avons immédiatement retranscrits grâce à un logiciel (QDA Miner 6.0). Nous avons relu plusieurs fois les retranscriptions pour obtenir un texte fluide. Pour analyser ces données, nous avons suivi le modèle de Miles et Huberman (2003). Les données ont donc été traitées au fur et à mesure que nous les avons recueillies et nous avons fait des allers-retours entre les verbatims retranscrits et les notes de notre journal de bord afin d’ancrer nos résultats dans les propos des participantes. C’est donc un modèle interactif, cyclique. Tout d’abord, nous avons procédé à la condensation des données et avons produit des résumés-synthèses de chaque entretien d’explicitation. Ensuite, nous avons présenté les données de manière à montrer notre compréhension de ces dernières et leur agencement. Nous avons notamment réalisé un récit d’évènements pour présenter le déroulement de l’enseignement-apprentissage de la RP. Les conclusions ont été élaborées dans un troisième temps, notamment par le truchement de discussions avec des enseignant⋅e⋅s de notre entourage et une autre chercheuse.

5. Résultats

Nous proposons le récit d’évènements, résultat de la présentation des données. Ensuite, nous expliquons les adaptations générales et les adaptations pour un⋅e ou des élèves en particulier, évoquées par les participantes selon les quatre axes de la DP selon Tomlinson (1999) : différenciation des processus, des productions, des structures et des contenus.

5.1 Les portraits-classes et les analyses des situations-problèmes mathématiques par les participantes

En premier lieu, nous avons bel et bien constaté que nos quatre participantes montréalaises enseignent dans des classes hétérogènes. Elles côtoient des élèves à risque et HDAA avec des besoins assez épars : dyslexie, dyspraxie, trouble du déficit de l’attention avec hyperactivité (TDAH), des élèves issu⋅e⋅s de l’immigration récente, des élèves avancé⋅e⋅s et d’autres élèves avec toutes sortes de besoins.

En deuxième lieu, les situations choisies ont des contextes variés : organisation d’activités, gestion de projet, gestion de budget. Les participantes ont précisé avoir l’intention de prioriser certaines notions mathématiques par rapport à d’autres. Les situations combinent des notions maitrisées depuis longtemps, par les élèves, et qui, alors, ne nécessiteront pas d’intervention (addition/soustraction). Il y a ensuite des notions plus difficiles qu’elles veulent faire mettre en oeuvre dans une situation complexe (le calcul du budget total). Finalement, on trouve des notions nouvelles qui demanderont une explication collective (l’enseignante 3 [E3] va enseigner le calcul de la surface d’une pièce).

5.2 Le récit d’évènements de l’enseignement-apprentissage de la résolution de problèmes

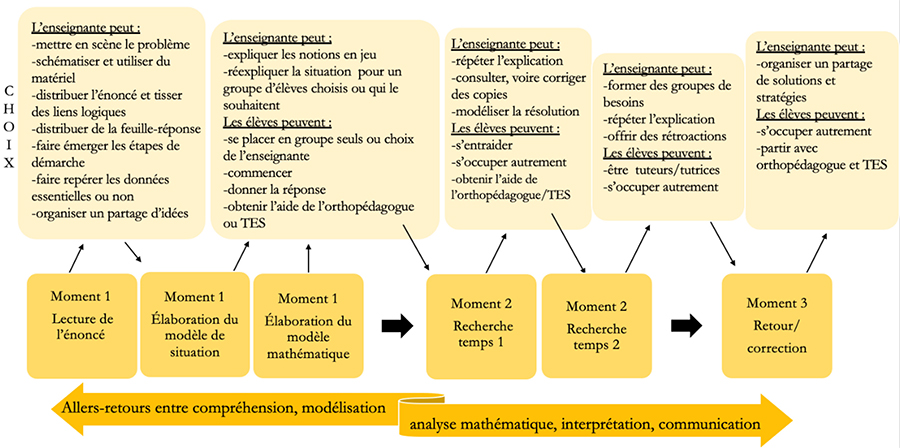
Les participantes ont décrit chronologiquement leurs intentions. Leurs discours ont concordé pour dire que l’enseignement-apprentissage se déroule en général en trois moments : la lecture de l’énoncé, la recherche et le retour avec toute la classe après l’analyse des solutions par l’enseignante.

Tout d’abord, les élèves parviendront à comprendre la situation grâce à la lecture de l’énoncé. Les participantes pensent mettre l’accent sur la mise en contexte. Elles expliquent qu’elles font souvent des schémas pour articuler les données entre elles. Par exemple, elles organisent des discussions autour de l’énoncé et du contexte pour vérifier la compréhension. Elles vont donc généralement mettre l’accent sur le phénomène à l’étude, première phase du modèle de Verschaffel et coll. (2000). Elles liront l’énoncé elles-mêmes ou le feront lire. Les participantes précisent qu’il faut faire des liens avec des activités familières pour les élèves ou vécues à l’école (E1). Elles prévoient faire une véritable mise en scène de l’énoncé, elles disent qu’elles le liront comme elles lisent un album de littérature jeunesse (E3), qu’elles utiliseront l’intonation et des gestes. La théâtralisation semble donc importante. Elles visent que cela soit « le plus logique possible » (E1). Par exemple, l’enseignante 2 va changer « cadeau de fin d’année » en « cadeau de fête » puisqu’on est en février. Elles prévoient aussi apporter des objets comme la boite à chaussure dont il est question dans le texte (E3). Les énoncés sont accompagnés d’une liste de contraintes à combiner entre elles et sont associés à des schémas et à des tableaux pour construire la réponse (annexe 2). Lors des échanges avec les élèves, elles prendront des notes sur ces contraintes selon les remarques des élèves, insisteront sur des mots-clés pour « pister » les élèves (E2). Par exemple, elles vont écrire « budget total », indiquer le nombre de personnes participant à l’activité.

Lors de ce moment de lecture, elles déclarent aussi qu’elles soutiendront les élèves dans la construction de la démarche de résolution. Nous associons cette intention aux phases de la modélisation de la situation et de la modélisation mathématique. Les élèves pourront poser des questions ou échanger en petits groupes. Elles pensent alors que cela permet l’autorégulation dans le sens où les élèves commentent leurs idées entre elles⋅eux. L’enseignante 3 nous a expliqué que « des fois, il y a des idées farfelues : “Oh moi, j’aimerais des meubles ronds”. C’est le temps de remettre cela dans la logique ». Elles les laissent libres de faire tous les commentaires.

Les participantes pourraient projeter l’énoncé au tableau, l’annoter, donner une copie à chaque élève, ne pas le donner du tout et juste le narrer. En général, au Québec, les situations-problèmes contiennent une feuille-réponse avec un tableau prérempli (annexe 2) qui fournit en quelque sorte les étapes de la démarche. L’enseignante 4 précise qu’elle se réserve la possibilité de ne pas donner cette feuille à certain⋅e⋅s élèves, voire à son groupe, selon la teneur des échanges.

La manière d’accompagner les élèves à trouver la démarche de résolution sans « la mâchouiller » (E1) est très présente dans leurs discours. Trois d’entre elles expliquent vouloir s’assurer que tout le monde sait quoi faire avant de commencer seul⋅e, mais « sans leur dire quoi faire exactement » (E1). L’enseignante 2, en revanche, prévoit faire toutes les étapes de la démarche avec tou⋅te⋅s les élèves. Elle validera ces étapes et ne laissera pas les élèves résoudre seul⋅e⋅s la situation. L’élève devrait garder seulement la charge des opérations.

Le moment de la lecture est donc anticipé comme une période collective, riche en explications, voire en guidage. Les participantes précisent pourtant qu’elles savent que ce moment ne sera pas profitable pour tou⋅te⋅s. En effet, elles déclarent que pour certain⋅e⋅s élèves, « il ne se passera rien » (E2), qu’elles⋅ils ne sauront pas comment résoudre la situation du tout. L’enseignante 3 parle même d’un élève qui ne fera que « subir cette période ». Elles disent aussi que les élèves avancé⋅e⋅s de leur classe pourraient ne pas participer à ce moment, mais elles insistent sur le fait qu’elles⋅ils doivent tout de même être présent⋅e⋅s. C’est la période où elles prévoient répondre aux questions et anticipent être moins disponibles par la suite, car elles consacreront leur temps à accompagner les élèves à risque.

Nous avons demandé aux enseignantes comment elles organiseraient la classe pendant le moment de recherche. Elles ont déclaré que, quand les élèves se lancent en général dans la résolution, certain⋅e⋅s commencent tout de suite seul⋅e⋅s, car elles⋅ils savent quoi faire. D’autres demandent de se faire réexpliquer l’énoncé avant de partir travailler seul⋅e⋅s ou en groupe. Cependant, un groupe d’élèves à risque restera certainement avec elles pendant tout l’enseignement-apprentissage. Elles anticipent que le travail de recherche connaitra des soubresauts : à un moment donné, certain⋅e⋅s élèves pourraient ne plus savoir « comment s’enligner » (E1) et auront des questions. Elles vont alors aller voir les élèves au cas par cas ou bien pourraient arrêter toute la classe pour faire une intervention auprès de tout le groupe.

Elles travailleront avec un groupe homogène d’élèves en difficulté, mais elles prévoient se déplacer dans la classe pour évaluer l’avancée des élèves et décrèteront des pauses au besoin. Ces pauses se justifient par la baisse de concentration ou de motivation des élèves, mais aussi par leur besoin d’évaluation, car elles reliront alors les copies. Nous avons donc découpé le temps de recherche en deux moments, entre une période où les élèves cherchent de manière plus autonome et une période où l’enseignante sait ce dont les élèves ont besoin et peut donner des rétroactions adaptées (puisqu’elle a consulté les copies).

Les participantes ont aussi évoqué que certain⋅e⋅s élèves bénéficient de l’aide de l’orthopédagogue qui soit vient en classe (E3), soit accueille les élèves dans une autre classe (E1 et E2). De surcroit, nous avons demandé comment elles gèreraient les différences de rythmes. L’enseignante 4 prévoit mettre en place du tutorat en sollicitant l’aide de celles⋅ceux qui ont réussi ; les participantes en général disent que celles⋅ceux qui réussissent facilement finissent ce moment par des activités occupationnelles, la lecture notamment.

Le troisième moment de la RP est celui du retour. Après avoir analysé les productions des élèves, les participantes prévoient un moment de validation collective pendant lequel elles organisent des discussions autour de la solution et des procédures de résolution choisies. Certain⋅e⋅s élèves pourraient alors partir refaire la situation avec l’orthopédagogue. Elles déclarent que ce moment est surtout consacré à l’analyse des erreurs et que cela pourrait ne pas être profitable aux élèves avancé⋅e⋅s.

Nous avons regroupé les différentes actions variées prévues par les enseignantes pour elles-mêmes et pour leurs élèves dans un récit d’évènements, tel que le recommandent Miles et Huberman (2003). Cette représentation graphique permet de montrer la flexibilité de la pratique enseignante dans l’enseignement-apprentissage de la RP (figure 2).

Figure 2

Relevé d’évènements de la prévision de l’enseignement-apprentissage de la RP

Relevé d’évènements de la prévision de l’enseignement-apprentissage de la RP

-> Voir la liste des figures

5.3 La différenciation pédagogique dans les discours de prévision

Lors de l’analyse, nous avons distingué les adaptations pour tou⋅te⋅s et les adaptations pour une élève ou des élèves en particulier. En ressort un portrait de la DP prévue : nous avons constaté que les enseignantes prévoient faire usage de tous les dispositifs. Elles mettent toutefois l’accent sur la DP des processus, productions et structures. C’est la DP des contenus qui semble la plus difficile à articuler entre tou⋅te⋅s les élèves.

Une analyse de fréquence en pourcentages des codes avec QDA Miner nous a permis d’établir la figure 3 : tous les dispositifs de la différenciation pédagogique selon Tomlinson sont évoqués dans les discours. La différenciation des processus est la plus présente des quatre dispositifs dans les discours.

Figure 3

Pourcentage des extraits en lien avec les dispositifs de la DP selon Tomlinson (1999) dans les discours de prévision

Pourcentage des extraits en lien avec les dispositifs de la DP selon Tomlinson (1999) dans les discours de prévision

-> Voir la liste des figures

Les participantes prévoient-elles les adaptations générales et les adaptations pour un⋅e ou des élèves en particulier dans ces dispositifs ? La réponse est contrastée. Les extraits en lien avec les adaptations des processus sont présents en plus grande proportion que ceux en lien avec les autres dispositifs (tableau 2). Pour les processus, nos participantes évoquent des adaptations générales et des adaptations pour un⋅e ou des élèves en particulier en parts égales. Cependant, quand elles parlent des structures, ce sont les extraits en lien avec les adaptations pour tou⋅te⋅s qui sont les plus nombreux. Enfin, quand elles parlent des contenus, un plus grand nombre d’extraits fait référence à des adaptations pour un⋅e ou des élèves.

Tableau 2

Fréquence des extraits sur les adaptations en général et les adaptations pour un⋅e ou des élèves en particulier dans les discours de prévision en fonction des dispositifs de la DP selon Tomlinson (1999)

Fréquence des extraits sur les adaptations en général et les adaptations pour un⋅e ou des élèves en particulier dans les discours de prévision en fonction des dispositifs de la DP selon Tomlinson (1999)

-> Voir la liste des tableaux

5.3.1 Les adaptations dans la différenciation pédagogique des processus

Très présente dans les discours des participantes, la DP des processus réfère à la manière dont les enseignant⋅e⋅s laissent les élèves s’organiser pour résoudre la situation-problème. Les élèves seraient libres de présenter leur solution avec des moyens personnels, qu’il s’agisse des ressources qu’elles⋅ils utiliseront ou la manière de présenter leur réponse. Elles⋅ils bénéficieront de tout le temps que cela requiert. Les rythmes des élèves seront donc pris en compte.

Pour ce qui est des adaptations générales, les participantes parlent d’un matériel de manipulation varié, accessible dans leur classe. Comme l’évoque le contexte, l’enseignante 3 ira sur Internet montrer les circulaires de magasin sur la peinture afin de rendre concrète la situation qui demande de repeindre une chambre (annexe 2).

Les ressources humaines reviennent souvent dans les discours. Les enseignantes prévoient que les élèves poseront des questions et que les élèves à risque seront épaulé⋅e⋅s par l’orthopédagogue ou la technicienne en éducation spécialisée. L’enseignante 3 parle alors d’un de ses élèves qui habituellement se greffe à un groupe d’élèves plus talentueux « comme à la queue d’une étoile filante ». Les élèves avancé⋅e⋅s peuvent donc être une ressource experte pour leurs camarades. Les adaptations pour un⋅e ou des élèves en particulier sont surtout présentes dans les extraits en lien avec le degré de soutien aux élèves. Les participantes prévoient accompagner pas à pas les élèves à risque tout en se rendant disponibles pour les autres élèves. Les élèves avancé⋅e⋅s devraient rester autonomes tout au long de la recherche.

5.3.2 Les adaptations dans la différenciation pédagogique des productions

Les participantes anticipent plusieurs moyens pour que les élèves présentent leur solution. En RP, la différenciation des productions se retrouve principalement dans la présentation écrite de la solution, ce qu’elles nomment les traces, ou dans l’ouverture à laisser aux apprenant⋅e⋅s le choix du processus mathématique employé. L’enseignante 4 s’est démarquée sur ce point, car elle a parlé de laisser la forme des traces très libre et donner la feuille-réponse le moins souvent possible. Les autres participantes ont parlé plutôt de ne pas intervenir sur les traces pendant le moment de recherche, mais d’y revenir spécifiquement au moment du retour.

5.3.3 Les adaptations dans la différenciation pédagogique des structures

La différenciation pédagogique des structures consiste à faire varier l’aménagement de la classe et les regroupements entre élèves. Revient surtout la préoccupation de créer une ambiance de classe pour favoriser la concentration et l’utilisation des ressources. L’enseignante 1 le répète même plusieurs fois dans l’entretien en s’excusant « d’être fatigante » : installation de paravent, pupitre dans le corridor, casque antibruit, espaces aménagés dans la classe. La DP des structures semble principalement être abordée sous le thème de la concentration des élèves.

Également, nos questions ont orienté les participantes à expliquer comment elles organisent les sous-groupes lors du moment de la recherche. En février, elles déclarent qu’elles ont déjà expérimenté la création de groupes homogènes et hétérogènes. Elles craignent que certain⋅e⋅s travaillent plus que d’autres dans certains groupes. Elles trouvent efficace de laisser travailler les élèves avancé⋅e⋅s en groupe homogène et autonome. L’enseignante 3 déclare même : « je ne vois pas pourquoi je ferais d’autres choses », car elles⋅ils « ont le même genre de cerveau et travaillent très bien ensemble ». Elles ont déjà prévu leur groupe homogène d’élèves en difficulté.

5.3.4 Les adaptations dans la différenciation pédagogique des contenus

La différenciation des contenus apparait surtout dans les extraits sur le moment de la lecture. L’enseignante 1 déclare réécrire l’énoncé « pour qu’il soit le plus universel possible » et que les tournures de phrases « ne soient pas trop compliquées pour rien ».

Les participantes anticipent un écart important de niveau de compréhension entre tou⋅te⋅s leurs élèves. Elles nomment que cette différenciation est délicate à orchestrer, car dans le cadre d’une RP, on ne peut pas morceler la tâche, la « mâchouiller » (E1). Elles déclarent donc qu’elles savent qu’elles vont « exemplifier » plus qu’il ne le faudrait pour les élèves en difficulté. Elles ne prévoient toutefois pas donner une situation plus simple, signe du maintien du haut niveau d’exigence dans leurs classes.

Lorsque nous avons posé des questions sur les élèves avancé⋅e⋅s présenté⋅e⋅s dans le portrait-classe, les participantes ont déclaré qu’elles anticipaient qu’elles⋅ils répondraient vite et bien. Elles reconnaissent qu’elles devraient mettre en place d’autres avenues pour elles⋅eux, mais qu’elles ne le font pas faute de contraintes de temps et de matériel. Elles⋅ils devraient recevoir des explications non sollicitées et elles⋅ils devraient se retrouver à attendre leurs camarades. C’est à travers ce résultat que notre entretien d’explicitation s’est révélé le plus pertinent. En effet, après la rencontre, l’enseignante 3 nous a recontactée pour nous expliquer que la réflexion entamée alors lui avait fait changer son enseignement-apprentissage et qu’elle avait remanié l’énoncé de sa situation-problème pour proposer un défi à ces élèves. Elle précisait d’ailleurs à quel point elle percevait un impact sur l’engagement et la motivation de ces dernier⋅ère⋅s.

Dans le tableau 3, nous réunissons l’ensemble des marques des dispositifs de la différenciation pédagogique de Tomlinson prévus par les enseignantes. Cela permet de clarifier quels dispositifs sont prévus pour le groupe en général et lesquels sont prévus pour un⋅e ou des élèves en particulier.

Tableau 3

Adaptations en lien avec les dispositifs de la différenciation pédagogique de Tomlinson (1999) dans les discours de prévision

Adaptations en lien avec les dispositifs de la différenciation pédagogique de Tomlinson (1999) dans les discours de prévision

-> Voir la liste des tableaux

6. Discussion

6.1 Les enseignantes ont une expertise à différencier, mais elles ont le potentiel de la bonifier

Le relevé d’évènements met en lumière un grand nombre d’adaptations prévues. Cependant, les participantes déclarent prévoir prendre beaucoup de temps pour mener les RP en classe et donc ne pas en faire souvent. Or, le temps alloué ne semble pas être utilisé adéquatement. Il est vrai que la différenciation des structures dirigée vers la création d’une disponibilité accrue des enseignantes pour les élèves à risque permet d’offrir un étayage expert, celui de l’enseignante aux élèves en difficulté (Nootens, 2010). Cependant, la perception des enseignantes qu’il faille s’assurer que tou⋅te⋅s les élèves comprennent quelle démarche opérer nuit aux apprentissages de tou⋅te⋅s.

En effet, afin d’avoir un regard critique sur les constats que nous venons de présenter, nous choisissons de confronter nos résultats à ceux de Demonty et coll. (2015), dans une étude sur la compréhension des énoncés de problèmes ; le guidage des enseignant⋅e⋅s aurait tendance à découper le problème en sous-problèmes et à orienter les élèves vers la démarche la plus adéquate, selon leur perspective. Les autrices qualifient cette manière de piloter la lecture de l’énoncé de « guidage directif ». Il a pour conséquence de priver les élèves à risque des discussions autour du phénomène à l’étude et du choix de la démarche. Les élèves plus avancée⋅s se voient donner des explications non sollicitées, ce qui conduit à une perte de l’essence de la RP pour certain⋅e⋅s (qui n’apprennent pas la démarche de RP) et à un risque de décrochage pour d’autres (qui se voient dévoiler le savoir avant de s’y confronter, seule⋅s).

Par ailleurs, nos participantes s’appuient bel et bien sur la connaissance des obstacles de la situation-problème et des erreurs usuelles de leurs élèves, mais leur pilotage ne laisse pas la place à la discussion autour de ces obstacles.

Notre recherche met toutefois en relief qu’elles sont conscientes de cette exemplification et qu’elles essaient de faire émerger la démarche en questionnant les élèves, le plus souvent. C’est un levier important dans de futures discussions avec des enseignant⋅e⋅s. Les adaptations prévues pourraient paradoxalement contribuer au maintien des écarts de réussite entre les élèves.

Il serait même intéressant de s’interroger sur la pertinence de l’énergie qu’elles mettent à planifier la tâche avant de laisser les élèves dans le moment de recherche. Peut-être faudrait-il le supprimer ? Cette manière de faire, présente dans les discours de toutes nos participantes, est certainement induite par la manière dont la présentation des situations-problèmes est recommandée par les examens du ministère québécois, passés à toutes les fins de cycle au primaire, les demandes officielles ayant un poids sur l’autonomie professionnelle et étant prouvées comme ayant une influence directe sur les pratiques enseignantes (Marcoux et Crahay, 2017). Elles semblent d’ailleurs avoir tous les outils pour organiser des groupes flexibles dans leurs classes pour pallier cette suppression. Nous avons en effet vu qu’elles savent organiser leur classe, qu’elles expérimentent les groupes homogènes et hétérogènes à différents moments de l’année et qu’elles sont capables de regrouper les élèves selon la connaissance de leur potentiel cognitif à travailler ensemble.

Enfin, leur enseignement de la RP pourrait être appuyé par l’enseignement quotidien du raisonnement mathématique. Les participantes prévoient que certain⋅e⋅s élèves arriveront devant la situation-problème et ne sauront ni quelle démarche mettre en oeuvre ni quels processus et concepts mobiliser. Le manque d’automatismes et de maitrise des concepts et processus mathématiques rend l’autonomie dans la démarche impossible puisque cela conduit à une surcharge de la mémoire de travail (Cabot-Thibault et Dumas, 2017 ; Frèrejean et coll., 2021 ; Kingsdorf et Krawec, 2016). Les participantes n’ont pas non plus évoqué l’enseignement de stratégies de RP, pourtant présentes dans le programme québécois.

6.2 Des pistes pour comprendre la différenciation pédagogique en contexte

Les adaptations de la DP relevées dans les discours de prévision prennent plusieurs formes, se situent à plusieurs endroits et à plusieurs moments. Nous avions repéré que la DP était saisie difficilement par la recherche, qu’elle se contentait de constater les dispositifs sur le vif, pendant le pilotage. Questionner des enseignant⋅e⋅s sur chaque geste prévu dans le pilotage en faisant spécifiquement le lien avec leurs élèves donne accès à tous les gestes de la DP dans la pratique. L’intérêt des entretiens d’explicitation est donc réitéré ici. Ils permettent de saisir le contexte et de comprendre les tenants et aboutissants des pratiques différenciées et les dilemmes quotidiens des praticien⋅ne⋅s. Nos participantes confirment qu’elles ne mesurent pas spontanément l’ampleur de l’ensemble des besoins qu’elles prennent en compte, toutes les adaptations qu’elles prévoient et elles reconnaissent qu’elles font des choix déchirants faute de temps et de ressources. Notre étude contribue donc à enrichir le portrait de la DP dans les classes : les pratiques de la DP sont bel et bien présentes, mais pas forcément nommées comme telles spontanément.

7. Conclusion

Notre recherche qualitative/interprétative auprès de quatre enseignantes expertes du primaire québécois permet de faire un portrait de la manière dont les enseignant⋅e⋅s prévoient leur enseignement-apprentissage en RP au primaire.

Par le truchement du modèle de Verschaffel et coll. (2000), nous sommes parvenue à établir un récit d’évènements qui montre les nombreuses adaptations à considérer dans le pilotage de la compétence complexe de la RP. En analysant les discours de prévisions selon les quatre axes de la DP de Tomlinson (1999), nous obtenons une liste non exhaustive des adaptations pour tou⋅te⋅s et pour chacun⋅e dans tous les aspects de la DP.

Les entretiens d’explicitation ont permis de valoriser le contexte et l’expertise des enseignant⋅e⋅s. Ils mettent aussi de l’avant le besoin de poursuivre le dialogue au bénéfice de tou⋅te⋅s les élèves. En effet, les participantes semblent prévoir organiser des groupes de travail pour que les élèves parviennent à trouver la démarche, mais leurs explications font peu de liens avec les concepts et processus en jeu. Seule l’enseignante 3 évoque le fait que les élèves vont se confronter à de nouvelles notions. Elles semblent donc privilégier un enseignement de la RP plutôt qu’un enseignement par la RP.

En définitive, il semble que les participantes de notre étude mettent en oeuvre les dispositifs de la DP, mais bénéficieraient du développement professionnel afin d’articuler ces savoir-faire et les enjeux spécifiques de la RP : cela nécessite, comme elles le décrivent, de trouver quelles connaissances mathématiques sont en jeu dans l’énoncé et comment les organiser dans une démarche pour produire une solution. Toutefois, elles semblent occulter ici que la RP doit aussi être exploitée comme posture de recherche en classe. Les obstacles qu’elles évoquent dans l’entretien pourraient faire l’objet de débats dans la classe afin que les apprenant⋅e⋅s construisent leurs connaissances mathématiques.

forme: 2348210.jpg
Florence Croguennec
Étudiante au doctorat, Université de Montréal