Exploration et classification de livres à compter : interactions et complémentarités entre apprentissages littéraires et mathématiques

Camenisch, Annie

doi:https://doi.org/10.7202/1024538ar

1. Introduction et problématique

Les livres à compter sont fréquemment utilisés en complément d’apprentissages mathématiques, en particulier en classe de maternelle ; dans la francophonie et ailleurs, de nombreux albums à compter étant des traductions. Destinataire exclusif du livre à compter, l’enfant, incité à des activités de dénombrement ou de comptage, se familiarise ainsi avec des nombres. Ces livres à usage documentaire ou scolaire ont été peu étudiés en tant qu’ouvrages appartenant à la littérature de jeunesse. Une analyse systématique des structures mathématiques et narratives de ces livres à compter a pour principal objectif de montrer que, sous certaines conditions, les livres à compter appartiennent à une forme littéraire particulière qui construit des réseaux de signification entre un texte narratif et une structure mathématique. Ces ouvrages, apparemment élémentaires, révèlent une réelle complexité et une richesse indéniable tant du point de vue littéraire que de leur exploitation mathématique. Comment un travail sur les caractéristiques littéraires, notamment narratives de ces livres, est-il propice à une meilleure perception de concepts mathématiques ? Et inversement, comment les structures mathématiques sous-jacentes peuvent-elles donner sens à une lecture littéraire ?

La réponse à ces questions passe d’abord par une exploration de livres à compter pour déterminer des critères de classement rigoureux, en relation avec les apprentissages mathématiques visés.

Les livres à compter seront ensuite examinés pour déterminer les conditions qui permettent de les définir en tant que forme littéraire où ils prennent alors le statut d’album. Une seconde exploration des albums en fonction de la complexité des structures narratives permettra d’affiner la première classification. Ces analyses aboutiront à des propositions didactiques visant des apprentissages interactifs et complémentaires entre mathématiques et littérature à partir de ces albums à compter.

2. Contextes théoriques

2.1 En mathématiques

Le livre à compter peut se définir comme un livre qui comporte une activité de comptage ou de dénombrement. Il est destiné à de jeunes enfants dont les compétences et connaissances liées au dénombrement et aux désignations orales ou écrites des nombres sont en construction (Valentin, 1992-1993). Les livres à compter sont très présents en classe de maternelle, utilisés notamment comme supports pour des productions dans le cadre de projets interdisciplinaires. De nombreux ouvrages de didactique des mathématiques proposent des démarches pour réaliser des livres à compter (Ermel, 2005) ou des séquences d’apprentissages sur la numération à partir des livres à compter (Guitton, Renault-Girard et Vouhé, 2008 ; Miri et Rabany, 2004). Certains chercheurs ont établi des inventaires critiques de livres à compter en fonction des apprentissages mathématiques visés ou des obstacles didactiques qu’ils posent (Petit et Camenisch, 2008, 2009 ; Pierrard, 2003 ; Valentin, 1992-1993). Les classements opérés dans les sélections de livres à compter analysés séparent notamment les suites numériques croissantes et décroissantes (Valentin, 1992-1993). Pierrard propose des critères de classement plus disparates : suite numérique croissante, comptines pour mémoriser les suites de nombres, suite numérique décroissante, association de l’approche ordinale et cardinale, grands nombres et/ou calculs (Pierrard, 2003). D’autres chercheurs ont classé les ouvrages en fonction des apprentissages mathématiques dominants qu’ils favorisent : approcher le concept de cardinal, travailler le zéro, construire le 10, compter et calculer, construire la notion de nombre (Petit et Camenisch, 2007, 2008). Plus rares sont les études qui prennent en compte les aspects linguistiques ou littéraires de ces ouvrages (Guitton et al., 2008 ; Petit et Camenisch, 2007, 2008). Aucune ne construit explicitement de relations entre les caractéristiques mathématiques et littéraires des livres à compter.

Le critère de classement récurrent concerne l’ordre dans lequel apparaissent les nombres. La plupart des livres à compter comportent des ensembles à dénombrer dont les cardinaux constituent des suites croissantes ou décroissantes : le cardinal d’une collection d’objets correspond au nombre d’éléments de cette collection. Ces deux structures se rencontrent de manière prégnante dans l’abondante production, toujours renouvelée, et quelque peu éphémère, des livres à compter.

Certains livres à compter constituent le scénario simplifié, car réduit à une opération mathématique élémentaire d’ajout ou de soustraction d’une seule unité, d’un type de problème appelé problème additif à une transformation (Vergnaud, 1982, 1986). Il s’agit de problèmes, résolus avec une addition ou une soustraction, comprenant un état initial, une transformation d’état et un état final. Ces énoncés de problèmes à la trame narrative minimaliste, souvent réduite à trois phrases, mettent encore de nombreux élèves en échec, non en raison de leur complexité mathématique, mais à cause de certaines difficultés liées à la langue et à la temporalité (Camenisch et Petit, 2007). En effet, le passage d’un état à un autre par l’intermédiaire d’une transformation fait intervenir trois périodes qui se réalisent selon un ordre chronologique.

Dans le cadre de la didactique des mathématiques, la recherche s’appuie sur les études concernant l’acquisition du nombre chez l’enfant, en particulier les procédures de quantification, les principes de dénombrement et l’apprentissage de la suite verbale des nombres (Fayol, 1990). Le développement des structures mentales qui favorisent l’apprentissage du nombre passe par cinq principes, appelés principes de comptage (Bideaud, Lehalle et Vilette, 2004), inspirés des travaux de Gelman (Gelman et Gallistel, 1986). On peut ainsi distinguer :

le principe de correspondance terme à terme, où à chaque objet compté correspond un seul nom de nombre ;
le principe de suite stable, où les noms de nombres se succèdent dans le même ordre à chaque comptage ;
le principe cardinal, où le dernier nom de nombre énoncé désigne la totalité des éléments comptés et représente donc le nombre total d’éléments ;
le principe d’abstraction, où le comptage s’applique à tout objet ou entité quelle que soit sa nature ou sa fonction (Bideaud et al., 2004) ;
le principe de non-pertinence de l’ordre, où l’ordre d’énonciation n’a aucune incidence sur le comptage.

Les livres à compter peuvent contribuer à l’acquisition des connaissances propres à ces cinq principes, en particulier, la compétence de cardinalité où les élèves doivent comprendre que le nom de nombre renvoie à la totalité des éléments comptés à chaque étape précédente du comptage incluant tous les nombres inférieurs (Fayol, 1990). La construction de la compétence de cardinalité passe par différents niveaux d’apprentissages de la chaîne numérique, dont l’un, appelé niveau de la chaîne dénombrable, renvoie à la capacité de l’enfant de compter à rebours et de placer un nombre en relation avec le précédent et le suivant (Bideaud et al., 2004). Le principe d’abstraction est acquis tardivement. Il est loin d’être construit par la totalité des enfants de 6 à 7 ans, nombreux à montrer des difficultés à considérer tous les éléments d’un ensemble comme des unités équivalentes (Van Nieuwenhoven, 1996).

2.2 En littérature

2.2.1 Histoire littéraire des livres à compter

Les livres à compter à suites croissantes ou décroissantes ont une origine différente : les premiers sont issus de la tradition scolaire alors que les seconds ont une origine populaire et littéraire.

Les premiers livres à compter, apparus simultanément aux abécédaires dans le cadre d’un apprentissage familial, illustraient la file numérique pour initier les enfants aux rudiments du comptage (Weber, 2010). Pendants numériques de l’abécédaire ou de l’imagier, les livres à compter utilisent les nombres en place d’alphabet ou d’images, ce qui explique que la plupart des études associent les fonctionnements de ces trois types d’ouvrages (Miri et Rabany, 2004 ; Weber, 2010). La fonction principale de l’imagier est de faire nommer les choses et découvrir le monde aux enfants. Les activités mentales mises en jeu pour construire une relation entre un objet et sa représentation favorisent ainsi un premier pas vers l’abstraction. L’abécédaire a longtemps contribué à l’apprentissage des premiers rudiments de la lecture par la présentation de l’ordre conventionnel de l’alphabet, organisant des liens entre des écrits, des images et les représentations construites par le jeune enfant sur le monde (Observatoire national de la lecture, 2003). Le livre à compter constitue donc une sorte d’imagier avec une représentation iconographique d’éléments liés à un nombre et, le plus souvent, à une désignation par l’intermédiaire d’un texte. Mais, par son classement ordonné en fonction d’une suite numérique, le livre à compter s’apparente aussi à l’abécédaire, suite rangée par ordre alphabétique.

Poslaniec (2007) ne s’intéresse pas aux livres à compter, mais ses conclusions concernant l’évolution des abécédaires et des imagiers peuvent aussi s’appliquer aux livres à compter. Considérés avant tout comme des ouvrages documentaires, abécédaires et imagiers se trouvent exclus du champ de la littérature. Pourtant, certains de ces ouvrages tendent de plus en plus vers la narrativité (Poslaniec, 2007, p. 24) et deviennent des oeuvres de fiction. Ils comprennent ainsi un système de narration avec un narrateur plus ou moins explicite, des personnages et la représentation d’un univers fictionnel. C’est la fonction narrative de l’image qui confère essentiellement à un ouvrage le statut d’album et le différencie du livre illustré (Poslaniec, 2007). Ainsi, un album se caractérise par la présence simultanée de deux narrateurs qui racontent la même histoire de manière complémentaire : un narrateur textuel avec des mots et un narrateur imagier par les images. Il devient alors une forme littéraire qui se distingue essentiellement des autres (poésie, roman, nouvelle, théâtre, conte, bande dessinée) par des critères formels (Poslaniec, 2007). L’écriture d’un album régi par l’ordre alphabétique ou par une file numérique peut s’apparenter à une technique oulipienne (Observatoire national de lecture, 2003), l’Oulipo (ouvroir de littérature potentielle) utilisant la contrainte comme moteur de sa création littéraire (Oulipo, 1988). Les auteurs d’albums à compter issus de la tradition scolaire utilisent la file numérique comme contrainte d’écriture.

L’origine plus populaire des albums à suite décroissante date de 1868, où l’Américain Septimus Winner (1827-1902) a écrit une chanson intitulée Ten Little Injuns. Elle avait pour sujet les Américains natifs, les Indiens éponymes et s’est rapidement répandue sous le titre Ten Little Niggers, traduite en français par Dix petits nègres (Lukasch, 2008). Inscrite dans une période de l’histoire américaine marquée par la fin de la guerre de Sécession et des guerres contre les tribus indiennes, cette chanson, nullement destinée aux enfants, véhiculait une idéologie raciste et coloniale. Chaque strophe, sauf la dernière, se termine par la mort violente d’un des personnages, Noir ou Indien. Pourtant, dès 1880, Ten little niggers se retrouve parmi des nursery tales, nurses rhymes, comme une comptine pour enfants (Lukasch, 2008). Devenue chansonnette traditionnelle, elle a été reprise dans de nombreuses éditions illustrées de la littérature anglaise, allemande et française, avec de nombreuses variantes.

Dix petits nègres peut ainsi être considéré comme un hypotexte (Genette, 1982), puisqu’il est à la source des livres à compter construits sur une suite numérique décroissante. En effet, dès les années 1950, apparaissent de nombreux pastiches des Dix petits nègres faisant intervenir d’autres personnages (souvent des animaux) au destin souvent moins tragique (Lukasch, 2008). Les nouvelles histoires imitent la chansonnette avec un texte rimé dont chaque strophe se termine par Et il n’en resta plus que… Avec une production illustrée abondante, la chanson traditionnelle des Dix petits nègres a donné naissance à un procédé formel, lui-même devenu forme littéraire dans la production récente.

En effet, au tournant des années 1970, la littérature de jeunesse a connu une véritable mutation (Poslaniec, 2008) tant par l’évolution du style graphique que par la libération du texte remettant en cause les cohérences image-texte-lectorat qui avaient fait le succès des albums avant 1968 (Gourévitch, 1998). Cette mutation de la littérature de jeunesse s’applique ainsi au livre à compter, qu’il soit issu d’ouvrages scolaires ou qu’il provienne d’une tradition plus littéraire. Grâce à la multiplicité de leurs formes et à des usages renouvelés, les livres à compter sont devenus des objets culturels (Guitton et al., 2008 ; Weber, 2010).

2.2.2 Didactique de la lecture littéraire

La recherche s’appuie aussi sur les travaux menés sur la lecture littéraire, lancés par Catherine Tauveron. La lecture littéraire se conçoit comme un jeu interactif entre le livre et le lecteur où le texte, avec la complémentarité des images pour un album, propose un itinéraire virtuel à parcourir qui s’actualise au fur et à mesure que le lecteur résout les énigmes disposées sur le chemin (Tauveron, 2004, p. 31). Cette lecture passe par un travail interprétatif, demandant la coopération cognitive active du lecteur (Tauveron, 1999, p. 11). Elle constitue donc une activité de résolution de problèmes, problèmes que le texte pose de lui-même ou que le lecteur construit dans sa lecture (Tauveron, 1999, p. 17). Le texte littéraire est donc par essence un texte résistant qui pose des problèmes d’interprétation et dont l’accès au sens symbolique n’est pas immédiat (Tauveron, 1999).

La lecture littéraire nécessite alors le développement de compétences spécifiques : linguistiques, encyclopédiques, logiques, rhétoriques et idéologiques (Rouxel, 2004), qui peuvent toutes être convoquées dans la lecture d’un album à compter. La compétence logique suppose par exemple la compréhension du fonctionnement de la suite numérique. La compétence rhétorique renvoie à des connaissances littéraires et à la compétence interprétative qui en découle. En effet, les albums à compter s’inscrivent dans la production littéraire d’un auteur, d’un genre, d’une époque ou d’une certaine esthétique et se réfèrent implicitement à d’autres oeuvres antérieures avec lesquelles ils tissent des liens d’intertextualité (Rouxel, 2004, p. 25), liens qui demandent à être explicités pour accéder à une lecture littéraire. Ces connaissances littéraires favorisent la compétence interprétative qui met en jeu culture et activité cognitive du jeune lecteur dans une lecture sensible à la forme, attentive au fonctionnement du texte et à sa dimension esthétique (Rouxel, 2004, p. 26). Enfin, la compétence idéologique met en jeules valeurs que le lecteur construit à partir du texte littéraire et construit une vision du monde (Rouxel, 2004, p. 29).

Considéré comme objet d’une lecture littéraire, l’album à compter constitue une oeuvre complexe résistante qui passe par l’interprétation croisée d’une représentation iconographique, d’un texte et d’une suite numérique. Le rôle alors signifiant de la suite numérique constitue une énigme à résoudre. Elle ouvre à un niveau symbolique de lecture et renvoie à des valeurs éthiques. Cette dimension idéologique du texte littéraire engage le lecteur dans une appropriation active (Rouxel, 2004).

Une telle appropriation ne peut se mener sans l’intervention d’un enseignant, éclairé et éclaireur, passeur culturel (Zakhartchouk, 1999), donnant accès aux élèves au patrimoine artistique, littéraire et scientifique de l’humanité, mais aussi meneur de jeu et arbitre (Tauveron, 2004, p. 35) dans le travail interactif entre l’élève et la littérature. Il est donc nécessaire de développer à la fois la propre culture littéraire des enseignants, en particulier des variétés de formes de la production à destination de la jeunesse, et les compétences professionnelles des enseignants, qui favorisent notamment des démarches interdisciplinaires (Zakhartchouk, 1999) et permettent d’imaginer des dispositifs propices à des lectures littéraires (Tauveron, 2004).

Notre recherche vise à mieux faire connaître ces oeuvres littéraires méconnues que sont les albums à compter afin de pouvoir proposer des dispositifs didactiques adaptés et pertinents. En effet, ces albums se situent à la lisière des ouvrages documentaires, destinés à participer à la construction du concept de nombre en mathématiques, et constituent des ouvrages littéraires qui véhiculent aussi des valeurs et posent notamment des difficultés d’interprétation. Comprendre les fonctionnements et les structures de ces albums revient à donner des clés pour classer ces albums et ainsi à mettre en évidence les complémentarités et les interactions qui se tissent entre mathématiques et littérature. L’enjeu d’une telle recherche est non seulement de développer la culture littéraire des élèves, mais aussi de promouvoir des démarches interdisciplinaires, car c’est dans l’interaction entre littérature et mathématiques que s’éclairent à la fois des concepts mathématiques et des compétences littéraires.

3. Méthodologie

La méthodologie passe donc par le choix d’un corpus d’analyse et par le classement des albums en fonction de leurs structures pour aboutir à une analyse fine des complémentarités et des interactions entre littérature et mathématiques.

3.1 Le corpus : des suites croissantes et des suites décroissantes de raison 1

Notre recherche consiste en une analyse de contenu portant sur un corpus spécifique de livres à compter. Ce corpus se restreint aux ouvrages présentant des suites numériques croissantes ou décroissantes de raison 1 et dont les nombres correspondent sans équivoque aux cardinaux des collections iconographiques associées.

Ce type d’ouvrages est de loin le plus représentatif, par son abondance, des livres à compter édités. Ces livres sont aussi les plus aptes à permettre des apprentissages sur le concept de nombre, puisque nous avons délibérément écarté les ouvrages présentant des collections iconographiques difficilement quantifiables. Mais surtout, l’analyse comparative des livres à compter ne peut se mener que sur des ouvrages aux caractéristiques globales similaires. Ces ouvrages présentent donc des collections d’éléments représentés (personnages ou objets) dont le cardinal augmente de 1 (pour les suites croissantes) ou diminue de 1 (pour les suites décroissantes) à chaque double page avec, dans la majorité des cas, une inscription explicite du nombre total d’objets de la collection.

Une même double page contient ainsi une représentation iconographique des éléments dénombrés le plus souvent accompagnée d’un nombre, écrit en chiffres, en lettres et/ou dans une représentation figurale. Ce corpus d’analyse est composé de trente-quatre livres à compter sélectionnés en fonction de leur représentativité dans les principaux corpus recensés par Valentin (1992-1993) et Pierrard (2003). Ainsi, les suites croissantes, largement majoritaires, sont présentées dans le plus grand nombre d’ouvrages recensés, soit vingt-six livres à compter. Les suites décroissantes, plus rares, ne sont présentées que dans huit livres à compter.

3.2 Les critères d’analyse : des structures mathématiques aux structures littéraires

Une première étude porte sur les structures mathématiques sous-jacentes. Partant du classement traditionnel séparant suites croissantes et décroissantes, nous examinons la manière dont les suites de collections se présentent et s’enchaînent dans les ouvrages. Il s’agit donc d’observer la nature des éléments iconographiques d’une collection, c’est-à-dire d’une double page à la suivante, afin de déterminer les fonctionnements mathématiques de ces suites. Ce premier examen s’intéresse donc aux structures mathématiques profondes des livres à compter en faisant abstraction des structures de surface que sont la formulation du texte, les représentations iconographiques, voire la croissance ou décroissance de la suite des nombres. Cette analyse permet de définir des critères de distinction entre les livres à compter et pointe les apprentissages mathématiques favorisés par l’une ou l’autre de ces structures profondes. Elle aboutit à une classification originale opératoire de tout livre à compter de suites numériques de raison 1, faisant coïncider structures et apprentissages mathématiques, classification servant de base à l’ensemble de l’analyse.

Une seconde étude vise à déterminer des formes littéraires prototypiques dans les albums à compter à partir de leurs systèmes de narration. Il s’agit d’analyser la progression de l’histoire, c’est-à-dire le passage d’un état initial à un état final entre deux doubles pages, par l’intermédiaire du texte, de la représentation iconographique et/ou de l’écriture mathématique. Elle conduit au classement des albums à compter en fonction des structures narratives complémentaires aux structures mathématiques sous-jacentes.

Enfin, une troisième étude pointe quelques interactions entre apprentissages mathématiques et littéraires. D’une part, elle explicite la manière dont la fiction et notamment les structures narratives peuvent contribuer à la compréhension d’énoncés de problèmes additifs. D’autre part, elle analyse la manière dont les suites numériques participent à l’interprétation littéraire des albums, notamment par les jeux sur le langage et la valeur symbolique des nombres.

4. Résultats

4.1 Vers un nouveau classement mathématique des suites de collections

Le classement des livres à compter est opéré en fonction des structures mathématiques profondes régissant les suites de collections et des apprentissages mathématiques qui en découlent. On peut ainsi distinguer des suites de collections indépendantes et des suites de collections par ajout ou retrait d’un élément.

4.1.1 Les suites de collections indépendantes

Ces livres à compter rassemblent des collections d’éléments (objets, animaux, personnages, etc.) exclusivement représentés, dans notre corpus, en nombre croissant. Ces collections seront appelées indépendantes si et seulement si la nature des entités représentées varie d’une collection à l’autre : Un corbeau, Deux chèvres, Trois chiens, Quatre chats, etc. (Blake, 1997). Les collections, indépendantes les unes des autres, ne reprennent pas d’éléments communs d’une collection à l’autre même si elles appartiennent souvent à une même thématique ou peuvent être désignées par un hyperonyme commun. Le cardinal de chaque collection apparaît alors sous la forme d’un égrainage de la suite des nombres entiers de manière croissante sans saut de page en page. Si l’habillage des ouvrages (c’est-à-dire l’univers représenté, la nature des éléments de la suite iconographique, les structures linguistiques, etc.) varie considérablement d’un ouvrage à l’autre, leur structure mathématique sous-jacente correspond à la suite des entiers naturels, les variantes mathématiques ne concernant que l’écriture du nombre (en chiffres et/ou en lettres) et le choix du premier nombre (zéro ou un) et du dernier nombre de la collection :

[(0), 1, 2, 3, …, 9, 10, …]

Les livres à compter construits à partir de cette structure se différencient en fonction de la nature des éléments qui composent chaque collection. On dira que les éléments iconographiques sont homogènes si et seulement si les entités à dénombrer dans chaque collection sont de même nature.

Figure 1

Suite de collections indépendantes d’éléments homogènes

-> Voir la liste des figures

Ces livres à compter répondent à la configuration suivante : compter des collections d’éléments homogènes à partir de zéro ou un jusqu’à un nombre terminal (3, 9, 10 ou un nombre supérieur à 10) en langue naturelle et/ou en représentation symbolique mathématique. Les ouvrages de ce type représentent plus de la moitié des livres à compter du corpus (dix-huit ouvrages), l’étendue numérique de 1 à 10 étant majoritairement représentée (onze ouvrages).

Les élèves peuvent ainsi apprendre à dénombrer, c’est-à-dire associer des cardinaux à des collections d’objets. Ils peuvent aussi articuler différentes représentations sémiotiques du nombre, à savoir sa représentation dans les écritures symboliques mathématiques (écritures chiffrées) et sa représentation en langue naturelle (en français) sous forme écrite ou orale (Duval, 1995). La fréquentation de ces albums contribue ainsi à l’apprentissage de la comptine numérique et du dénombrement. Elle permet notamment de développer la compétence de cardinalité.

D’autres livres à compter présentent des collections indépendantes d’éléments non homogènes. On dira que les éléments iconographiques sont non-homogènes si et seulement s’il existe au moins une collection à dénombrer dont les éléments ne sont pas de même nature.

Figure 2

Suite de collections indépendantes d’éléments non homogènes

-> Voir la liste des figures

Ces ouvrages peu fréquents (trois ouvrages du corpus) indiquent le cardinal de chaque collection, mais comme les éléments iconographiques sont de nature différente, l’écriture en langue naturelle est rendue difficile par absence d’hyperonyme.

Par exemple, la page du 2 des Contes du bout des doigts (Calleja, 2008) montre bien deux personnages, mais la légende renvoie à deux dénominations, le loup et le petit chaperon rouge. La page du 4 mêle aussi des expressions du nombre sous forme de déterminant (article défini ou indéfini) et de chiffres : une blondinette et 3 ours. Dans Un pour l’escargot, dix pour le crabe (Sayre et Sayre 2003), les éléments non homogènes renvoient à l’hyperonyme pieds comme l’indique le sous-titre de l’album Combien de pieds ? Pourtant les pieds (pattes, estomac-pied pour le gastéropode, pinces) appartiennent à des êtres de nature différente (escargot, enfant, chien, insecte, araignée, crabe) et leurs représentations graphiques sont aussi différentes. Cet album montre ainsi des décompositions additives, l’hyperonyme pied permettant de compter et d’additionner des nombres, indépendamment de leur identité physique (Petit et Camenisch, 2007). Dans Et si on comptait (Houblon, 2003), les décompositions additives d’éléments iconographiques de nature différente sont complétées par une légende comprenant une décomposition additive explicite :

1 héron et 1 robinet maigrichon ;1 + 1 = 2.

Tous ces ouvrages comprenant des collections indépendantes d’éléments non homogènes font donc apparaître une décomposition additive toujours indiquée en langue naturelle par la conjonction de coordination et rassemblant les éléments additionnés et, parfois, sous la forme plus abstraite d’une égalité en représentation symbolique mathématique. Ces pages d’éléments non homogènes permettent de comprendre que le cardinal est indépendant de la nature des éléments. La fréquentation de ce type de livres peut favoriser le développement du principe d’abstraction.

4.1.2 Les suites de collections par ajout ou retrait d’un élément

Les suites iconographiques de ce type de livres à compter comprennent des éléments communs, repris d’une collection à l’autre. Ces collections seront appelées collections par ajoutou retrait d’un élément si et seulement si à chaque nouvelle collection, un élément iconographique nouveau est rajouté ou retiré aux éléments déjà présents dans la collection précédente, augmentant ou diminuant la collection d’un élément. Contrairement aux suites de collections indépendantes, exclusivement croissantes, ces suites rassemblent des collections croissantes et décroissantes correspondant à la structure mathématique sous-jacente :

[n ; n + 1 ; (n+1) +1 ; ((n + 1) + 1) + 1 ; etc.] pour les suites croissantes ;
[n ; n – 1 ; (n – 1) – 1 ; ((n – 1) – 1) – 1 ; etc.] pour les suites décroissantes.

On constate un emboîtement des collections, puisque toute collection est incluse dans la suivante ou la précédente.

Dans les suites de collections par ajout d’un élément (six ouvrages du corpus), le texte souligne parfois la structure profonde de nature additive : moi ça fait un, plus le veau, ça fait deux, plus sa mère la vache ça fait trois : 1, 2, 3 (Prøysen, 1992).

Figure 3

**Suites de collections par ajout d’un nouvel élément**

L’ajout des éléments peut aussi être explicité par les mots ou le symbole mathématique + : Et il ajoute la tortue pour porter la patience du temps. 3 + 1 = 4 (Rosano, 2002). Les éléments iconographiques de ces livres à compter sont le plus souvent de nature non homogène : animaux variés (Prøysen, 1992), jouets différents (Crowther, 2005) ou les broderies ajoutées par un couturier à l’oeuvre qu’il crée (Rosano, 2002).

Tous ces albums prennent appui sur l’axiomatique de Peano qui pose, entre autres, que tout nombre entier naturel n possède un unique successeur noté n + 1. Dans cette axiomatique, 0 peut être considéré comme le premier des entiers naturels, il est postulé qu’il n’est le successeur d’aucun entier naturel (Peano, 1889 ; Petit et Camenisch, 2007, 2008). Dans tous ces albums, tout nombre trouve donc son existence à partir d’un premier, le plus souvent un, parfois zéro.

Les suites de collections par retrait d’un élément (huit ouvrages du corpus) sont le plus souvent composées d’éléments de même nature, qui apparaissent fréquemment dans les titres commençant par Dix petits…

Figure 4

**Suite de collections par soustraction d’un nouvel élément**

Ces livres à compter peuvent favoriser l’apprentissage du comptage à rebours. Cependant cet aspect reste relativement mineur d’autant que le décomptage se termine souvent par un au lieu de se terminer naturellement par zéro ou par une expression équivalente dans la langue naturelle.

Les livres à compter présentant des suites de collections par ajout ou retrait d’un élément sont propices au développement de la capacité à repérer le successeur ou le prédécesseur immédiat d’un nombre dans la file numérique. Ils correspondent donc à un stade évolué du développement des enfants situé au niveau de la chaîne dénombrable (Bideaud et al., 2004).

L’analyse des livres à compter présentant des suites de collections a permis de distinguer des collections indépendantes homogènes ou non homogènes et des collections emboîtées par ajout ou retrait d’un élément. Les structures mathématiques ainsi dégagées correspondent à différentes étapes de développement du principe d’abstraction chez les enfants.

4.2 Complémentarité entre suites de collections et structures narratives

4.2.1 Du livre à l’album à compter

Les livres à compter permettent de construire des relations entre les références portées par les images et les représentations construites par le jeune enfant sur le nombre organisées par l’arbitraire de la comptine numérique. Les livres à compter présentant des suites de collections décroissantes par retrait d’un élément proviennent d’une tradition littéraire et ont été peu à peu utilisés, de manière incidente, à des fins mathématiques. Le thème des Dix petits nègres se trouve ainsi réinterprété dans le cadre de l’avènement d’une lecture plurielle et ludique. L’imitation de la chansonnette avec rimes et disparitions tragiques reste par exemple le moteur de 10 p’tits pingouins (Fromental et Jolivet, 2010), dont le sous-titre souligne l’aspect ludique et mathématique : un livre animé pour jouer à compter. La conclusion sous forme de farce neutralise l’effet tragique de la disparition des pingouins.

Comme les abécédaires et les imagiers, de nombreux livres à compter sont devenus des objets culturels où la suite numérique constitue une contrainte oulipienne, devenue procédé littéraire, rappelant celui formalisé par les Oulipiens sous l’appellation boule de neige (Oulipo, 1988). Cette contrainte liée à la suite numérique constitue ainsi l’origine d’un univers fictif, faisant interagir texte, nombre et représentation iconographique. À cela s’ajoute l’émergence d’une narrativité, avec ses personnages, son univers fictionnel et la présence simultanée d’un narrateur textuel et d’un narrateur iconographique. Cette double narration suppose donc l’existence d’un récit, texte référentiel à déroulement temporel (Ducrot et Todorov, 1972). Ce dernier critère est essentiel pour sélectionner les livres à compter du corpus devenus albums à compter narratifs. On peut ainsi constater que les ouvrages avec suites de collections par ajout ou retrait d’un élément entrent tous dans cette catégorie, alors que les livres à compter de suites de collections indépendantes d’éléments non homogènes en sont tous exclus. Parmi les suites de collections indépendantes d’éléments homogènes, quatorze ouvrages peuvent être considérés comme des albums.

Ainsi, de nombreux auteurs/illustrateurs comme Douzou (1997), Voltz (1999), Texier (1998), Ramos (1999), Chichester Clark (2004), Rand et Rand (1992), Crowther (2005), Brown (2001), Erlbruch (1997), etc. se sont saisis de cette contrainte numérique facilement imitable et ancrée dans l’imaginaire collectif pour élaborer une histoire. Le rapport entre mathématiques et littérature y semble alors inversé, la suite numérique n’étant plus l’objectif d’un apprentissage, mais le moteur d’une entreprise esthétique. Les deux structures mathématiques sous-jacentes s’appuient alors sur un habillage présentant des formes potentiellement infinies (Tauveron, 1996). Cet habillage dessine les premiers contours de la représentation d’un univers fictif. La nature même de la collection influe sur la trame narrative des livres à compter.

4.2.2 Narrations et transformations dans les suites par ajout ou retrait d’un élément

La structure mathématique des albums avec suites de collections par ajout ou retrait d’un élément fait apparaître une égalité comprenant une addition ou une soustraction : 2 + 1 = 3 ; 3 – 1 = 2. Ces phrases mathématiques correspondent à la solution de problèmes additifs à une transformation, problèmes issus d’une histoire formée d’un état initial (un nombre n d’éléments) qui subit une transformation (on ajoute ou on enlève un élément) pour aboutir à un état final (Petit et Camenisch, 2007 ; Vergnaud, 1982, 1986). Les trois périodes de ces problèmes additifs sont schématisées de la manière suivante, E marquant les états, T la transformation :

Einitial ➔ T ➔ Efinal

Tout récit minimal s’identifie par deux attributs et un processus de transformation qui permet le passage de l’un à l’autre (Ducrot et Todorov, 1972). Le schéma induit par la structure mathématique fonctionne donc comme un moteur narratif qui nécessite un habillage textuel permettant de désigner la transformation (Camenisch et Petit, 2007).

Les albums avec suites de collections par ajout ou retrait d’éléments imposent donc, par leur structure mathématique, la création d’une histoire qui justifie l’accroissement ou la diminution de la collection de départ. Ils emboîtent ainsi successivement des histoires minimales à partir de la transformation d’un état initial en état final, l’état final devenant souvent l’état initial de la péripétie suivante.

Selon les albums, les trois périodes de cette trame narrative sont plus ou moins explicitées par le texte, par l’illustration ou par une phrase mathématique.

Dans les albums dont le texte est fortement inspiré par l’hypotexte des Dix petits nègres, la narration textuelle rend ces trois périodes explicites :

État initial 1 : Dixharengs verts dociles dormaient près des boeufs.
Transformation 1 : L’un attrapa le rhume des foins.
État final 1 : Il n’en resta que neuf.
État initial 2 : Neuf harengs verts graciles dansaient dans la nuit.
Etc. (Erlbruch, 1997)

Les doubles pages de ce type d’album se succèdent de la manière suivante :

Einitial₁ ➔ T₁ ➔ Efinal₁Einitial₂ ➔ T₂ ➔ Efinal₂ Einitial₃ ➔ T₃ ➔ Efinal₃ , etc.

Dans d’autres albums, seules deux périodes sont explicitées par le texte, l’état final étant confondu avec l’état initial suivant :

État initial 1 : Ils étaient dix poussins […].
Transformation 1 : Alors le tout-petit s’en fut dehors […].
État final 1 et État initial 2 : Ils étaient neuf, neuf poussins […].
Transformation 2 : Alors, le rondouillet s’en fut dans les bois […].
État final 2 et État initial 3 : Ils étaient huit, huit poussins […].
Etc. (Naumann-Villemin et Oriol, 2008)

Ce type de séquence narrative se termine par la transformation, l’état final doit être reconstitué mentalement pour coïncider avec l’état initial suivant. La compréhension de l’histoire nécessite donc de faire des inférences :

Einitial₁ ➔ T₁Einitial₂ ➔ T₂ Einitial₃ ➔ T₃ , etc.

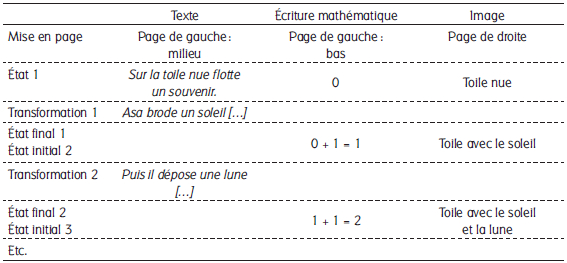
Dans Au fil des nombres (Rosano, 2002), album à suite croissante, deux périodes sont explicitées dans trois registres différents, soulignés par des mises en page particulières : langage naturel, iconographique et symbolique mathématique.

La même histoire est donc racontée complémentairement par trois narrateurs, iconographique, textuel et mathématique en fonction des périodes du récit : l’écriture mathématique et l’image montrent les situations finales qui deviennent les situations initiales suivantes, la transformation exclusivement racontée par le narrateur textuel s’opère au moment où la page est tournée. Le lecteur doit donc inférer chaque état initial nouveau :

Einitial₁ T₁ ➔ Efinal₁ T₂ ➔ Efinal₂ , etc.

Schéma narratif de Au fil des nombres (Rosano, 2002) — Tableau 1

**Schéma narratif de *Au fil des nombres* (Rosano, 2002)**

Dans certains albums, les différentes périodes ne sont pas explicitées par le texte. Par exemple dans Salut ! (Dorin, 2008), le texte se réduit à quelques dialogues. Les nombres inscrits sur les doubles pages et la succession des images doivent être interprétés pour rétablir mentalement les différentes périodes du récit.

Schéma narratif de Salut ! (Dorin, 2008) — Tableau 2

**Schéma narratif de *Salut !* (Dorin, 2008)**

La transformation n’est pas montrée ni même suggérée, mais se situe dans un espace imaginaire entre deux pages. L’état final apparaît sur la page suivante, confondu avec l’état initial suivant. L’album montre donc une succession d’états nécessitant la construction mentale de la transformation qui a lieu hors champ. Seule la suite des nombres constitue un indice de la transformation qui a eu lieu :

E₁ T₁ E₂ T₂ E₃ etc.

Tous les albums à suite numérique par ajout ou retrait d’un élément contiennent des trames narratives, représentées le plus souvent par le texte, l’image et des représentations symboliques mathématiques. Ces mini-récits successifs sont à leur tour enchâssés dans une trame narrative dont la chute connaît trois variantes : la boucle où la même histoire peut recommencer avec d’autres personnages, la disparition des personnages ou leur réunion.

Tableau 3

**Narrations des suites de collections par ajout ou retrait d’un élément**

La structure narrative plus ou moins explicite conduit à des obstacles liés aux inférences nécessaires à la compréhension de l’histoire et, donc, à la représentation de la structure mathématique sous-jacente. Une explicitation de la trame narrative constitue donc un outil pour l’interprétation mathématique des albums.

4.2.3 Narrations dans les collections indépendantes

Les livres à compter à suite de collections indépendantes sont moins susceptibles de contenir une trame narrative. Comment en effet motiver littérairement une suite de collections disparates ? Certains auteurs de livres à compter ne s’en préoccupent guère et enchaînent les collections sans introduire de temporalité ni d’intrigue. La majorité des ouvrages tentent cependant de développer un récit avec une temporalité marquée. Deux procédés sont ainsi mis en oeuvre : celui de la double suite numérique et celui des rencontres successives.

Le texte d’Un deux trois dans l’arbre (Ravishankar, Rao et Bay, 2006) ne raconte aucune histoire, mais égraine l’arrivée d’un nombre croissant d’animaux grimpant successivement dans un arbre. Une chronologie est cependant marquée par certains verbes du texte qui montrent une succession d’événements : les lézardssuivent ; les hyènesbousculent tout le monde. L’illustration y participe en faisant varier la place des animaux dans l’arbre, indiquant un déplacement. L’arbre aussi se modifie : son tronc s’épaissit, ses branches se multiplient.

L’organisation de l’album montre deux étapes dans l’ascension des animaux : sur une première double page, les animaux isolés sont désignés par un groupe nominal : 1 pou un peu fou, 2 lézards rêveurs, etc. Sur une seconde double page, ils apparaissent perchés dans l’arbre tranchant par leur couleur, et une phrase souligne leur action : Un pou un peu fou saute dans un arbre, Deux lézards rêveurs suivent sans se presser, etc. Un examen attentif de l’arbre montre que les animaux précédents y sont toujours, moins visibles par leur teinte grisée. Ainsi, une seconde suite croissante textuellement implicite, mais perceptible par l’illustration, se superpose à la première suite explicite. La collection totale des éléments augmente chaque fois du nombre des nouveaux arrivants :

1
1 + 2 = 3
(1 + 2) + 3 = 6
(1 + 2 + 3) + 4 = 10
(1 + 2 + 3 + 4) + 5 = 15
Etc.

Cette seconde suite correspond aussi à une transformation d’état, puisque l’ajout des éléments de la collection suivante modifie un état initial :

État initial 1 : (image) Il n’y a aucun animal dans l’arbre.
Transformation 1 : Un pou un peu fou saute dans un arbre.
État final 1 et État initial 2 : (image) Il y a un animal dans l’arbre.
Transformation 2 : Deux lézards rêveurs suivent sans se presser.
État final 2 et État initial 3 : (image) Il y a trois animaux dans l’arbre.
Transformation 3 : Trois petits rats fouineurs pointent leur museau.
État final 3 et État initial 4 : (image) Il y a six animaux dans l’arbre.
Etc.

Ces deux suites révèlent la structure mathématique d’une trame narrative par réunions successives des différentes collections (marquées C) :

Première suite : [C1 ; C2 ; C3 ; …]
Seconde suite : [C1 ; C1 U C2 ; C1 U C2 U C3 ; …]

L’histoire implicite racontée dans Un deux trois… dans l’arbre demande alors à être interprétée par la lecture croisée du texte, des nombres et de l’image.

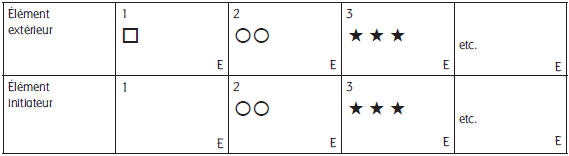
La rencontre constitue un autre moyen pour introduire un lien narratif dans l’énumération des collections indépendantes. Ainsi, un élément rencontre successivement les différentes collections d’éléments. Personnage ou narrateur, il est souvent investi d’une quête ou d’un projet qui constitue le moteur de l’histoire et sa présence est récurrente dans les illustrations ou le texte. Deux cas de figure peuvent alors se présenter : soit cet élément récurrent reste constamment extérieur aux collections, soit il en constitue l’initiateur en étant l’élément unique premier selon les schémas suivants :

Figure 5

**Éléments récurrents de suites de collections indépendantes**

Dans l’ensemble des albums à compter de suites croissantes de collections indépendantes, une situation initiale explicite ou implicite indique le début d’une quête ou d’un projet. La situation finale implique toujours la fin des rencontres ainsi que l’issue de la quête ou du projet.

On peut constater que le fonctionnement narratif des livres à compter coïncide avec leur structure mathématique. Ainsi les collections par ajout ou soustraction d’éléments élaborent des trames narratives fondées sur des transformations d’état alors que les collections indépendantes d’éléments, soit introduisent une transformation d’état grâce à une seconde suite implicite, soit inventent une quête ou un projet justifiant des rencontres successives.

De nombreux livres à compter peuvent être considérés comme des oeuvres littéraires, dans la mesure où, réalisés par des auteurs et illustrateurs de littérature de jeunesse, ils créent cet univers fictionnel par la combinaison d’une narration réalisée par la représentation iconographique, le texte et les structures mathématiques. Mais, cette fiction narrative constitue-t-elle un simple habillage, un prétexte pour donner du sens à un usage avant tout mathématique ? Ou, au contraire, la visée mathématique est-elle passée au second plan, les préoccupations premières des auteurs n’étant alors pas d’enseigner le comptage, mais de l’utiliser à des fins éthiques ou esthétiques ? Les deux aspects, littéraire et mathématique, peuvent s’entrecroiser et interagir grâce à la mise en place de dispositifs didactiques spécifiques.

Tableau 4

**Types de narrations dans les suites de collections indépendantes d’éléments homogènes**

4.3 Interactions entre littérature et mathématiques

Littérature et mathématiques peuvent s’entrelacer dans des albums à compter pour un double enjeu. Une lecture littéraire centrée sur la compréhension de l’histoire et notamment de l’implicite peut favoriser des apprentissages mathématiques sur les nombres ou dans le cadre de l’initiation à la résolution d’énoncés de problèmes. À l’inverse, la structure numérique des albums peut aussi se charger de valeurs symboliques propres à une lecture littéraire qui demandent à être interprétées. L’enseignant se fait alors passeur de littérature mais aussi, en quelque sorte, passeur de mathématiques.

4.3.1 Une initiation aux problèmes additifs : de l’histoire aux problèmes

Les problèmes additifs donnent l’occasion aux enseignants de faire construire des représentations figuratives par les élèves comme outil de résolution. Cependant ces dessins ne tiennent guère compte de la temporalité, c’est-à-dire l’inscription des événements dans une chronologie. Or, il est nécessaire de distinguer les trois périodes : celle qui précède la transformation, la période de la transformation et celle qui suit la transformation (Camenisch et Petit, 2007). Si à chacune des deux périodes extrêmes correspond un état que l’on peut représenter par un dessin, la période de la transformation ne peut se représenter par une image fixe (Camenisch et Petit, 2007). En effet, comment indiquer par un dessin la disparition ou l’apparition progressive d’éléments ? Les ouvrages de mathématiques utilisent certaines conventions peu satisfaisantes, car non explicites : barrer, diminuer la taille, etc. En effet, seul le langage verbal permet d’exprimer sans équivoque la transformation.

Or, la représentation des transformations se pose aussi dans les albums à compter. Dans le livre animé 10 p’tits pingouins (Fromental et Jolivet, 2010), l’animation consiste à faire disparaître un pingouin en activant la languette correspondante. Le lecteur réalise donc lui-même la transformation. Le texte construit pour cette dynamique commence par l’énonciation du nombre de pingouins présents dans l’état initial et se termine par une phrase inachevée : Les pingouins ne sont plus que… encourageant, après manipulation, le décompte des pingouins restants. Une représentation astucieuse est aussi mise en oeuvre dans Dix petites graines (Brown, 2001) : à la double page du huit, on découvre par exemple huit graines dont une est attrapée par une souris, indice d’un début de transformation qui demande explicitation. Les élèves peuvent alors reconstruire la trame narrative manquante et simplement initiée par l’image : une souris prend une graine, la souris va manger une graine, etc. La transformation suggérée impose une verbalisation. Les élèves doivent en effet comprendre que tout dessin fixe reste ambigu pour représenter la transformation et que seul le langage peut l’exprimer de manière explicite.

Certains albums à suite de collections par ajout ou retrait d’un élément peuvent donc être utilisés pour apprendre à exprimer verbalement les transformations dans les problèmes additifs. Ainsi les moments d’apprentissage de résolution de problèmes additifs peuvent être combinés avec la lecture littéraire d’albums à compter comprenant des transformations d’état. Les élèves sont amenés à expliciter leur compréhension des histoires et à verbaliser les transformations. Le fonctionnement de ces albums et celui d’énoncés de problèmes additifs similaires peuvent alors être mis en évidence, conduisant ainsi les élèves à mieux se représenter les situations décrites dans les problèmes.

4.3.2 Une initiation à la littérature : du nombre aux valeurs

Une lecture littéraire conçue comme la construction d’une interprétation à partir d’indices apportés, dans le cas de l’album à compter, par le texte, l’image et la suite numérique, s’appuie aussi sur l’intertextualité et, donc, sur les oeuvres avec lesquelles l’album entre en résonance. Les suites numériques peuvent être signifiantes, indices essentiels d’une valeur symbolique à construire par le lecteur. Le thème des Dix petits nègres est ainsi réinterprété par Erlbruch qui parodie la chansonnette et dénonce par la dérision les aspects contestables de l’idéologie initiale. Les dix petits harengs (Erlbruch, 1997) imite la structure rimée et le motif de la chanson. Le titre original Zehn grüne Heringe signifie littéralement Dix harengs verts, où le vert s’oppose au rouge ou au noir des personnages initiaux. Le hareng lui-même est issu de la chanson :

Four Little Nigger Boys going out to Sea ;
A Red Herring swallowed one, and then there were Three.

Au Red Herring (hareng saur) fait écho le Grüne Hering, de couleur complémentaire, mais qui désigne aussi en allemand le hareng frais (par opposition au hareng saur). Erlbruch joue sur le langage en opposant le vert au rouge, mais aussi la fraîcheur aux relents saumâtres de la chanson. La compétence rhétorique sollicitée pour la connaissance de l’hypotexte donne accès à l’ironie et la dérision du message initial qui échappent au lecteur non averti. Si, avec des élèves de 5-7 ans, cet album peut être lu comme toute comptine un peu absurde, il gagne cependant à être mis en réseau avec une des versions de la chanson originale ou avec d’autres albums fortement liés à l’hypotexte.

L’album Dix petits poussins (Naumann-Villemin et Oriol, 2008) s’éloigne du modèle d’origine en abandonnant les rimes et en introduisant une trame narrative plus construite. À peine éclos, des poussins chassent un à un d’autres poussins pour toutes sortes de raisons : la force, la taille, le poids, le sexe, etc. Cette description de la loi du plus fort, de l’intolérance ou de la normalité contre la différence tourne cependant à l’avantage des poussins rejetés. En effet, grâce à leur éloignement du nid, ces derniers s’ouvrent à la découverte du monde et des autres et trouvent leur épanouissement dans d’autres valeurs. Le dernier poussin dans le nid, encore couvé par sa mère, subit en fait un immobilisme immature. L’idéologie et le fonctionnement de l’hypotexte se trouvent donc totalement renversés dans cet album, par la dénonciation de toute discrimination, mais aussi par un retournement des valeurs, puisque les personnages exclus sont tournés vers la vie et non vers la mort.

L’ajout d’un élément peut aussi se révéler signifiant. Ainsi, Au fil des nombres fait progressivement surgir du néant, figuré par la toile nue, les éléments et les animaux jusqu’au tableau final de la création du monde. Le couturier Asa recrée le monde par son art, comme l’écrivain crée un univers fictif qu’il peuple de ses créatures selon l’interprétation construite par le lecteur. Une analyse détaillée de l’album à double suite croissante Un, deux, trois… dans l’arbre ! (Ravishankar, Rao et Bay, 2006), réalisée par Petit et Camenisch (2009), pointe ses qualités littéraires, à la fois éthiques et esthétiques. Cet album, traduit de l’anglais (Inde) One, Two, Tree ! joue sur un double sens, par la proximité sonore, de la prononciation de three (trois) et de tree (arbre). Ce titre révèle les deux acteurs essentiels de l’album : les nombres et l’arbre, tissant d’emblée entre eux un lien originel (Petit et Camenisch, 2009). Du pou à l’éléphant, les animaux qui grimpent successivement dans l’arbre s’accroissent non seulement en nombre, mais aussi en taille. L’arbre, qui croît en taille et en volume, doit porter une charge de plus en plus lourde. La chute de l’histoire conduit à la conclusion à tirer de l’histoire :

Dix éléphants balourds… Pourront-ils aussi se percher ?

L’histoire implicitement racontée semble donc porter sur la capacité d’accueil de l’arbre et sur la volonté de cohabitation des animaux. Image et texte y répondent de manière complémentaire. En effet, l’illustration qui accompagne cette question anticipe la réponse, puisqu’on les voit déjà tous perchés dans l’arbre. La page suivante donne la réponse explicitement :

Oui ! Si chacun laisse une place à l’autre !

Mais, sur l’illustration, vingt oiseaux attendent leur tour. La dernière page, qui montre les oiseaux perchés, semble apporter une réponse plus définitive et plus universelle. La démultiplication des oiseaux semble ainsi indiquer que d’autres animaux chercheront à se percher et seront accueillis de la même manière. La compétence idéologique se trouve alors sollicitée pour construire une interprétation : il peut exister une harmonie entre différentes espèces à condition que chacun y prenne part. Cette entente entre les espèces doit cependant s’accompagner d’une harmonie entre l’arbre et ses occupants dans la mesure où leur nombre respecte la capacité d’accueil de l’arbre au fur et à mesure de sa croissance. Cette harmonie-là est totalement implicite dans l’album et uniquement perceptible par la mise en relation entre l’illustration et les nombres. Dans une interprétation plus métaphorique, cette histoire pourrait aussi symboliser l’harmonie possible entre l’homme et la nature ou le monde, qui progressivement se remplit avec l’accroissement de la population, mais où néanmoins, dans le respect de la nature, l’entente peut faire place à la concurrence.

Le point d’eau (Base, 2001) suscite une interprétation proche. Des animaux qui se rassemblent près de la mare pour s’abreuver croissent en nombre, alors que la mare diminue de plus en plus (en aire) et que la végétation s’assèche. Cet accroissement, souligné par les nombres inscrits, est contrebalancé par une structure décroissante implicite. En effet, des grenouilles, anthropomorphisées, différenciables par leur forme ou leurs vêtements, peuplent la mare. À chaque accroissement des autres animaux, leur population diminue d’un membre. Cet album dissimule donc une suite numérique décroissante qui se termine par la fuite de toutes les grenouilles, concomitante avec l’assèchement du point d’eau. La disparition des grenouilles sonne comme un compte à rebours et illustre la fin de toute vie sans eau.

Par les interprétations suscitées et le rôle signifiant des suites numériques dans la construction d’une interprétation, certains albums à compter constituent donc de véritables oeuvres littéraires.

5. Discussion des résultats

L’exploration de livres à compter comportant des suites de collections croissantes ou décroissantes de raison 1 remet en question les classements opérés par Valentin (1992-1993) ou Pierrard (2003). En effet, ces derniers se sont essentiellement livrés à un inventaire de livres comprenant des nombres et ont proposé plusieurs pistes d’exploitations mathématiques. Leurs classements restent cependant superficiels, car ils ne s’intéressent ni aux structures mathématiques profondes ni à la nature des suites iconographiques présentées. Notre recherche a permis de dégager un autre classement original et opérant du point de vue des apprentissages mathématiques et des structures narratives complémentaires aux structures mathématiques :

les collections indépendantes d’éléments iconographiques homogènes ou non homogènes sont plutôt propices à des apprentissages sur le dénombrement, sur le concept de nombre, en particulier, son aspect cardinal, et sur la décomposition additive des nombres. Lorsqu’ils sont narratifs, ces albums à compter nécessitent une part d’invention pour justifier la succession des collections. En effet, l’auteur doit créer une intrigue qui fasse progresser une action, quête ou projet, le plus généralement rattachée au personnage ;
les collections par ajout ou retrait d’un élément favorisent plutôt des apprentissages sur la chaîne dénombrable et la construction des entiers naturels. De par leur histoire et surtout par la nature de leur structure mathématique, ces albums comportent naturellement une trame narrative minimale. Ils peuvent ainsi contribuer à une meilleure représentation mentale des énoncés de problèmes additifs par l’explicitation des transformations d’état et par leur inscription dans une chronologie.

Le critère de croissance ou de décroissance révèle une absence de symétrie dans la répartition des livres à compter :

Tableau 5

**Répartition des livres à compter du corpus**

On peut ainsi constater qu’aucun livre à compter du corpus ne propose de suite décroissante indépendante, mais cette configuration n’est pas théoriquement impossible. Ce classement est ainsi opérant pour tout livre à compter comprenant une suite numérique de raison 1 dont les collections sont clairement identifiables et dénombrables et constitue un outil pratique pour proposer des apprentissages mathématiques adaptés.

Tous les livres à compter ne peuvent cependant pas être considérés comme des ouvrages littéraires. Nous avons retenu essentiellement deux caractéristiques pour considérer ce que nous appelons alors album à compter comme une forme littéraire. Pour la première caractéristique, nous avons étendu aux albums à compter les analyses de Poslaniec (2007) portant initialement sur les albums et plus spécifiquement sur les abécédaires et les imagiers. Cette caractéristique concerne l’émergence de structures narratives complexes dans la production récente de ces ouvrages initialement à destination scolaire. Pour la seconde caractéristique, nous nous sommes appuyée sur les recherches de Tauveron (1999, 2004) concernant la lecture littéraire et les textes résistants qui demandent un travail participatif du lecteur.

Nous considérons donc comme des albums à compter les seuls ouvrages qui possèdent une structure narrative double à la fois textuelle et iconographique et dont la suite numérique crée la résistance du texte. Cette suite numérique demande alors un travail d’interprétation en faisant sens en interaction avec toutes les dimensions du texte et de l’image.

Nous avons constaté que la structure des problèmes additifs établie par Vergnaud (1982, 1986), fondée sur des transformations d’états, s’appliquait aussi aux albums à compter comprenant des suites de collections par ajout ou soustraction d’éléments. Cet outil nous a permis d’analyser précisément les structures narratives de ces albums et d’établir des critères de complexité dans leur compréhension en fonction de l’expression, verbale, iconographique et/ou mathématique, des différentes périodes des histoires. Cependant, les interactions entre littérature et mathématiques peuvent aussi être prises en défaut, notamment d’un point de vue mathématique. En effet, la plupart des auteurs-illustrateurs ne se soucient guère de la correction mathématique de l’album, et certains de leurs choix sont discutables, voire erronés, comme cela a d’ailleurs été relevé par Valentin (1992-1993) et Pierrard (2003). L’usage en classe de tels ouvrages doit donc s’accompagner d’une véritable réflexion sur la validité des contenus mathématiques à moins de proposer des dispositifs didactiques adaptés pour rectifier les éventuelles erreurs. Ces erreurs ou maladresses portent en particulier sur l’écriture 10 comme symbole succédant à la suite 1, 2, […], 9, sans que le 0 n’ait été rencontré, explicité et construit (Petit et Camenisch, 2007). Cette construction est en effet indispensable pour comprendre le fonctionnement du système de numération de position décimal.

Un certain nombre de propositions didactiques découlent de cette recherche. Elles s’inscrivent dans le fil des recherches et des dispositifs décrits par Poslaniec et Houyel (2000) et Tauveron (2002), adaptées aux spécificités des albums à compter (Petit et Camenisch, 2008). Ainsi nous proposons que l’exploitation mathématique de l’album se réalise dans un second temps de l’exploitation de l’album. En effet, la première approche d’un album à compter dans une classe doit être fondée sur la réception et la découverte de l’objet-livre (Poslaniec et Houyel, 2000). Cette approche personnelle et impliquée vise d’abord à éveiller un ressenti et des réactions libres chez l’élève. La présence des nombres émergera sans doute naturellement de cette première découverte, mais les dispositifs mis en place, spécifiques aux particularités de chaque album, doivent mettre en évidence l’univers représenté, les personnages et la progression de la narration. Différents dispositifs peuvent être convoqués pour entrer dans une lecture plus experte de l’album, que ce soit d’un point de vue littéraire ou mathématique. Un des plus opérants reste la mise en réseaux (Tauveron, 2002) avec des albums de même structure ou de structure contrastée pour les aspects mathématiques ou des albums comparables d’un point de vue éthique ou esthétique. Enfin des dispositifs de questionnement du texte, des images et des suites numériques doivent permettre d’interroger l’implicite et conduire à des hypothèses d’interprétation à croiser avec tous les indices fournis dans l’album. L’utilisation d’outils d’analyse littéraire appliqués au cas particulier des livres à compter ouvre donc un champ de recherche nouveau où le livre à compter, devenu album à part entière, tisse des liens entre mathématiques et littérature.

6. Conclusion

L’objectif spécifique de cette analyse de contenu était de déterminer les conditions qui permettent de faire entrer les livres à compter, habituellement considérés comme des ouvrages documentaires, dans le champ de la littérature.

Notre recherche a exclusivement porté sur des livres à compter présentant des suites numériques croissantes ou décroissantes de raison 1, associant sans équivoque nombres cardinaux et collections d’objets, soit un corpus de trente-quatre ouvrages. Nous avons passé ces livres à compter au crible de trois analyses successives.

La première a conduit au dépassement du classement usuel et évident de ces livres en fonction de la croissance ou de la décroissance pour déboucher sur un classement original tenant compte des structures mathématiques profondes, fondées sur des fonctionnements rigoureux et applicables à tout livre à compter de même type. Ce classement a permis de retenir deux catégories de livres à compter, chacune correspondant à des apprentissages mathématiques relatifs à différents moments de la construction du concept de nombre. Il présente aussi l’avantage de coïncider avec les structures narratives des ouvrages considérés comme des albums en fonction de la présence d’une double narration, textuelle et iconographique. Nous avons constaté que ces structures narratives étaient complémentaires aux structures mathématiques.

La seconde analyse des albums a permis de mettre en évidence les complexités de ces structures narratives et de déterminer des schémas narratifs, clairement identifiables, applicables aux deux catégories d’albums à compter, les uns fonctionnant à partir d’une succession de transformations d’états, les autres greffant une quête ou un projet sur une structure additive. Les apprentissages mathématiques semblent alors secondaires pour les auteurs, plus sensibles aux aspects esthétiques et littéraires.

Pourtant une lecture littéraire des albums à compter comprenant des transformations d’état peut contribuer à une meilleure représentation et compréhension d’énoncés de problèmes additifs, la similarité de fonctionnement entre ces albums et ces énoncés ayant été établie.

Notre troisième analyse a donc porté sur les interactions entre lecture littéraire et mathématiques, au bénéfice de l’une ou de l’autre discipline. Elle s’est soldée par une analyse littéraire de quelques albums à compter où la suite numérique constitue une contrainte signifiante nécessitant une interprétation.

Notre recherche comprend cependant plusieurs limites. Ainsi, les analyses des interactions entre littérature et mathématiques, qui n’ont porté que sur quelques exemples, mériteraient d’être étendues sur l’ensemble des albums retenus. Elles permettraient de cerner davantage la valeur narrative des nombres ou leur rôle dans la « résistance » des albums au contenu « réticent » ou « proliférant » (Tauveron, 1999), dans la construction d’une interprétation littéraire. Le rapport texte/image resterait ainsi à approfondir, notamment dans une analyse plus systématique de la fonction narrative des images, du texte et de la suite numérique. Une autre limite de la recherche concerne certains apprentissages mathématiques qui peuvent se trouver renforcés par une approche littéraire. Il serait, par exemple, intéressant d’exploiter les pages consacrées au zéro dans les albums qui le présentent parmi les autres nombres, soit au début d’une suite croissante, soit en fin de suite décroissante. Les sens du nombre zéro peuvent ainsi être approchés grâce à différentes mises en scène dans les histoires racontées (Petit et Camenisch, 2010). Enfin, les situations explicitées dans des albums à compter auraient aussi pu nourrir des réflexions sur la notion de pluralité et de quantité, exprimée par le nombre, tant au sens mathématique qu’au sens grammatical. Il existe, en effet, une relation entre le nombre en langue, marqué par le singulier et le pluriel, et les nombres en mathématiques. Les albums à compter peuvent favoriser la conceptualisation du nombre en langue par l’observation des situations mises en scène qui permettent de comprendre et de relever les indices de la pluralité par opposition à la singularité (Camenisch et Petit, 2008).

Une analyse de contenu pourrait aussi s’étendre à d’autres livres à compter volontairement exclus de la recherche. Ainsi, certains ouvrages sans narration ni collections clairement distinguées, plus proches du poétique par le symbolisme des nombres ou les jeux de langage, nécessitent une lecture plus tabulaire tant des nombres que du texte. On pourrait ainsi proposer une classification notamment en fonction des structures linguistiques ainsi que des valeurs, notamment culturelles, attribuées aux nombres.

Résumé

Abstract

Resumen

1. Introduction et problématique