Les représentations : étude en théorie des situations didactiques

Brousseau, Guy

doi:https://doi.org/10.7202/012669ar

Introduction

Le terme « représentation » désigne l’action de « rendre présent à nouveau » et son résultat. Son usage est très répandu dans de nombreuses branches de l’activité humaine, avec des sens parfois très différents. Mais il est aujourd’hui un concept important de la psychologie cognitive et de la psychologie sociale, d’où il diffuse vers tous les secteurs de l’analyse des connaissances, notamment vers le secteur de l’éducation, donc vers celui de l’éducation mathématique. Depuis plus de trente ans, à la suite notamment de Janvier (1994, 1998), les éducateurs en mathématiques s’intéressent à l’usage des représentations et un flux régulier de travaux sur cette question alimente les revues de recherche. Aujourd’hui, la notion de « modélisation » fait florès auprès des enseignants et des responsables. Il est donc étonnant de constater que ce concept ne tient qu’une place mineure dans des théories comme celle des situations didactiques, de la transposition didactique ou de l’approche anthropologique. De ce fait peut-être, un certain nombre de travaux français de didactique des mathématiques, qui traitent pourtant de divers aspects importants de la « représentation », ne font pas figurer ce terme parmi les mots clés de leur travail et restent donc à l’écart des débats sur ce point. L’existence d’« écoles » où le choix des termes et de la langue sert autant à exclure certaines références et certaines idées qu’à les rassembler et à les confronter ne suffit pas à expliquer cette différence. Plus qu’un simple glissement de vocabulaire, et plus que des hypothèses et des méthodes de travail différentes, certains n’y voient qu’une différence de position épistémologique. Pour réussir à jeter un pont entre les chercheurs qui étudient directement « la représentation » avec les instruments habituels de la psychologie cognitive et ceux qui l’approchent avec d’autres instruments théoriques, cet article [1] doit relever le défi de souligner ces différences épistémologiques.

Pour tous ceux qui voient la didactique comme un champ d’application de la psychologie cognitive, il semble naturel d’importer sans façon un concept du second domaine dans le premier. Il en résulte que dans ce genre de travaux, le terme « représentation » est utilisé de façon très souple, tantôt avec un de ses sens communs, tantôt avec un de ses sens scientifiques, comme s’il était transparent.

Cette importation est-elle légitime ? Est-elle sans inconvénient ? C’est la question que les approches indépendantes permettent de poser et que nous allons poser ici. Il s’agit donc d’abord de repérer et de définir les différentes acceptions et usages du terme « représentation » en psychologie, en mathématiques et en général, puis dans la théorie des situations à usage didactique. Nous examinerons ensuite un processus presque « adidactique », effectivement mis en oeuvre avec des enfants de 5 ans pour leur faire construire des représentations d’objets, de collections et de propriétés. Nous entamerons ensuite l’étude des rôles des représentations dans les situations didactiques elles-mêmes. Cet article s’appuie sur de nombreuses recherches menées entre 1979 et 2002. La plupart n’ont pas été identifiées comme des travaux sur les représentations. Elles n’ont pas été proposées comme des recherches sur les représentations et elles n’ont pas été reconnues comme telles par les chercheurs spécialisés dans ce domaine, non pas à cause de leur nature ou de leur contenu ou de leur manque d’intérêt pour ce sujet, mais à cause des différences de présupposés théoriques et de langage. Elles se plaçaient par rapport à des questions et à des priorités différentes, avec un vocabulaire différent. Elles montrent, de façon précise, le rôle de la représentation dans la construction et l’apprentissage des mathématiques.

Le concept de représentation

Sans chercher de justifications qui sortiraient du cadre de cet article, nous admettrons qu’une représentation comporte au moins trois objets : un objet représenté, un objet représentant qui est souvent appelé « représentation » et une certaine relation qui relie le représentant au représenté. Cette relation est aussi appelée « représentation ».

En fait, une représentation met de plus en présence deux univers : l’un contient la chose représentée, l’autre contient la chose représentante. Représentant et représenté ont des relations avec leurs univers respectifs. À titre d’exemple, suivant une acception courante, « une représentation mentale » est une « entité de nature cognitive reflétant “dans le système mental” d’un individu, une fraction de l’univers extérieur à ce système [2] » (Denis, 1999). Le schéma proposé par Vergnaud (1998) illustre ce concept dans une perspective piagétienne.

En mathématiques, nous retrouvons le triplet <S, f, S’> où S et S’ sont deux structures et f un morphisme – une correspondance – qui associe à chacun des composants de S – éléments, relations, propriétés ou opérations – certains des éléments de S’. Remarquons que la représentation est maintenant le triplet <S, f, S’> et non pas seulement S’ comme précédemment. Une représentation doit de plus satisfaire une propriété de commutativité : l’image f(R(a,b)) d’une relation R entre deux objets a et b de l’univers représenté doit coïncider avec la relation image fR appliquée aux images f(a) et f(b) de a et de b. Ce qui s’exprime par f(R(a,b)) = fR ((f(a), f(b)) et qui signifie que l’on peut indifféremment considérer d’abord les relations dans l’univers représenté, puis les traduire dans l’univers représentant ou commencer par traduire les objets et les relations et considérer les relations images dans le représentant. Cette condition, ignorée du sens général, joue pourtant un rôle fondamental dans toutes les études de représentations. C’est elle qui permet de réimporter une signification ou un résultat obtenu de l’univers représentant dans l’univers du représenté, donc d’utiliser la représentation. Remarquons que la définition mathématique ne donne pas au représentant et au représenté un rôle symétrique, sauf dans les cas d’isomorphismes – où l’inverse de la représentation est aussi une représentation. Ces cas sont si nombreux que la représentation est souvent perçue de façon symétrique comme une analogie.

Ladrière (1995) regroupe les représentations, au sens général, sous deux métaphores : la représentation théâtrale et la représentation diplomatique, où les objets peuvent être des personnes. La représentation en psychologie relèverait plutôt de la représentation théâtrale. L’approche de Ladrière nous met sur la voie de l’attribution de certaines fonctions à la relation de représentation.

Or, pour envisager les divers usages de la notion de représentation en didactique, nous aurons besoin de préciser ces fonctions. Quels sont donc ces usages ?

Dans la mesure où on admet que toutes les connaissances sont des représentations, au sens d’images d’une réalité, alors ces représentations sont les « objets même de l’enseignement ». À ce titre, elles sont aussi des « moyens de connaissances pour les élèves », elle doivent donc être enseignées comme telles. Cette dualité est particulièrement évidente en mathématiques, où certains objets d’étude sont explicitement des représentations au sens mathématique, c’est-à-dire des triplets <représentant, représentation, représenté>. On y enseigne des modèles et aussi la modélisation, en tant que processus scientifique, avec parfois des justifications qui font de cet enseignement une véritable formation épistémologique. La représentation apparaît aussi comme un moyen de provoquer l’apprentissage et, par là, elle peut être un moyen d’enseignement. Enfin, elle apparaît comme un moyen d’analyse et de connaissance de l’enseignement lui-même. Elle joue un rôle important dans les conceptions épistémologiques du professeur. En particulier, si le professeur centre ses efforts sur l’enseignement des représentations et les connaissances canoniques, il a affaire, à chaque instant, à des représentations spontanées ou induites réelles « différentes », suivant les élèves, les sujets d’études et les moments de ces études. Sa connaissance, ou ses croyances sur le fonctionnement de ces représentations dans les processus d’enseignement et d’apprentissage, joue un rôle important.

Nous sommes ainsi conduits à nous demander de quelle utilité peuvent être, pour la didactique, les théories de la connaissance qui font abstraction de l’action didactique. Le réalisme platonicien met en scène une réalité éternelle dans un rapport statique avec son image unique. L’apprentissage consiste pour le sujet à reproduire ce couple, soit par un hasard improbable, soit dans une maïeutique logique et figée. L’empirisme offre des possibilités d’évolutions plus variées quoique, dans une dynamique diversifiée, il postule que le rapport au monde tend irrésistiblement à établir « la » connaissance, celle, unique, qui correspond à « la » réalité. Dans ces deux conceptions, le couple réalité/connaissance, représenté/représentant est déterminé à l’avance, sans rapport avec l’histoire du sujet et de son apprentissage. La seule incertitude qui demeure est celle de l’accès ou non à ce couple. Le succès ou l’insuccès de l’apprentissage et de l’enseignement ne dépend que des trois partenaires : le sujet lui-même, l’enseignant et la difficulté propre à la connaissance en jeu. La connaissance doit être la même pour le savant et pour l’élève, pour tous les élèves. Si « la connaissance de l’élève » différait de celle du savant, elle serait une erreur ; elle ne pourrait donc pas être une connaissance. Il nous semble que l’emploi du terme « représentation » permet d’échapper en partie à cette logique. Le terme « connaissances » étant réservé aux connaissances « vraies », le terme « représentation » peut s’en écarter un peu pour désigner les idées qu’en ont divers sujets.

Pourtant, ces conceptions épistémologiques conduisent immanquablement à utiliser un vocabulaire, des méthodes d’études et des concepts différents pour l’objet de l’enseignement, la connaissance, et pour son résultat, l’erreur, ou la représentation, entre lesquels une irréductible opposition s’établit. Ainsi, le psychologue ne peut rien dire d’un sujet qui manifeste une connaissance correcte, alors qu’il peut faire nombre de conjectures à propos d’une réponse erronée. Finalement, ces théories désarment l’action de l’enseignant en renvoyant à des lois d’apprentissage et en le déchargeant ainsi de la tâche de recréer l’histoire et la fonction de chaque connaissance. Elles vident à l’avance les processus didactiques de leur substance.

La méthode d’étude propre à la théorie des situations didactiques en mathématiques

La théorie des situations didactiques en mathématiques (TSDM) propose une autre voie. Un objet mathématique étant déterminé par une de ces définitions classiques, il s’agit de concevoir un ensemble de conditions qui fasse qu’un sujet doive nécessairement utiliser cet objet comme moyen pour obtenir un certain résultat. Ces conditions ne sont pas a priori indépendantes les unes des autres ni indépendantes de l’objet ainsi défini. Elles seront modélisées par un ou des systèmes mathématiques appelés « situations » et formellement structurées comme des « jeux » mathématiques.

Un objet mathématique sera donc défini par sa fonction dans au moins un tel jeu. Une situation détermine les enjeux et les possibilités de décision d’un actant dans un certain milieu. Elle est choisie de telle manière que la stratégie de résolution ne puisse être mise en oeuvre que grâce à une certaine connaissance mathématique, l’apparition de cette décision sans la connaissance étant hautement improbable. La méthode qui consiste à définir un objet mathématique par un ensemble de relations qu’il est seul à satisfaire est classique. La seule différence ici est que l’ensemble des relations est un « jeu ». La détermination d’une connaissance mathématique par un problème, dont cette connaissance est la solution, est un procédé aussi ancien que les mathématiques. La TSDM est simplement une théorisation de ce procédé. Il existe de nombreuses situations relatives à une même connaissance. De même, de nombreuses connaissances peuvent intervenir dans une décision unique. Un des objets de cette théorie est de classer les situations et, par conséquent, les connaissances non seulement en fonction de leurs rapports logiques, mais aussi suivant leurs propriétés ergonomiques et les possibilités d’apprentissage et d’enseignement qu’elles offrent.

La méthode de définition des objets mathématiques par leur fonction peut être étendue à tous les objets non primitifs et non mathématiques de la TSDM. Ainsi, nous allons essayer de déterminer par cette méthode l’objet « représentation » : quelles sont les situations qui exigent une représentation, et seulement une représentation ?

Mais au lieu de donner d’emblée une définition « générale » et complète de toutes les situations de représentation, nous allons au contraire utiliser une méthode ascendante et progressive, classique en TSDM, qui consiste à composer des situations simples pour décrire les plus complexes [3].

Elle consiste, dans un premier temps, à ne considérer que les acceptions mathématiques du terme, sans évoquer le sujet qui les utilise (connaissance objective). Nous l’avons fait très succinctement pour le concept de « représentation » dans le paragraphe précédent et nous ne l’approfondirons pas davantage.

Dans un deuxième temps, la méthode conduit à étudier les situations objectives associées à ces acceptions – les situations objectives de représentation – et à nous demander :

Comment la représentation joue-t-elle un rôle dans l’action et dans l’apprentissage d’un sujet « isolé » ? Sans nous occuper pour l’instant des circonstances didactiques, ce qui nous permettra de nous référer à la théorie des situations mathématiques non didactiques (TSM).
Vis-à-vis de quel « milieu » est elle nécessaire comme moyen de formulation ou de communication ?
Quel rôle joue-t-elle dans la genèse des systèmes de validation culturels logiques et mathématiques ?

Nous illustrerons cette étude par un exemple : le jeu des trésors.

Ce n’est que dans un troisième temps que nous « plongerons » ces situations dans des situations « didactiques », beaucoup plus complexes, où apparaîtront de nouvelles fonctions – spécifiquement didactiques – de la représentation.

Les situations objectives de représentation

Définition et présentation

Considérons un milieu M (un dispositif) et un actant A, lié à ce milieu par des possibilités d’action et des objectifs modélisés par une situation ∑. Et considérons le sujet O (observateur) qui observe l’activité de A sur M dans les conditions ∑. Ce milieu M est dit objectif pour A dans la mesure où A le tient pour tel, c’est-à-dire où A ne remet pas en cause ce qu’il en perçoit – la situation pourrait être fictive, mais tenue pour vraie ou réalisable et bien connue par A. Supposons que O, théoriquement muni de toutes les connaissances du moment, identifie dans M tous les éléments d’une représentation formelle. Cette « représentation » R fait partie du milieu objectif de A. Il peut en avoir conscience ou non et devoir s’en occuper ou non, suivant ∑. La présence de R pour O n’entraîne pas qu’elle joue un rôle quelconque dans la solution théorique de ∑ ou dans celle, effective, qu’en donne A. Par contre, si ∑ est tel que A doive nécessairement utiliser la représentation R pour résoudre le problème que lui pose ∑, nous dirons que ∑ est une situation objective de représentation. Dans le cas où une représentation R est observable dans M, mais ne joue pas de rôle dans la solution de ∑, nous dirons que R est pertinente dans M, mais pas adéquate à ∑.

Remarquons plusieurs différences avec les approches habituelles :

A est un actant (comme les noirs ou les blancs aux échecs). Il sert à décrire un simple assujettissement, mais pas un sujet, lequel pourrait peut-être se définir par un ensemble d’assujettissements.
Mettre en présence un milieu objectif caractéristique d’une connaissance (ici R) avec un sujet A ne suffit pas pour obtenir une situation objective relative à cette connaissance comme ce serait le cas dans l’approche empiriste ou réaliste. Il faut qu’une situation rende obligatoire l’usage de cette connaissance par l’actant pour obtenir un résultat connu préalablement de l’actant.

Une situation objective de représentation est donc déterminée par le « septet » < ∑, A, S, f, S’, U-é, U-ant>. Nous dirons en abrégé que « f est la représentation que A fait de S dans la situation ∑, S est pris dans l’univers représenté U-é, et S’ dans l’univers représentant U-ant [4] ».

Les univers peuvent être des milieux au sens large de branches ou de cadres mathématiques. Douady (1986) a montré l’importance des cadres mathématiques qui offrent des occasions de fabriquer des représentations : du cadre géométrique au cadre arithmétique, algébrique ou graphique. Les jeux de cadres sont ainsi des générateurs de représentations, aussi précieux pour la compréhension et l’apprentissage que pour la recherche.

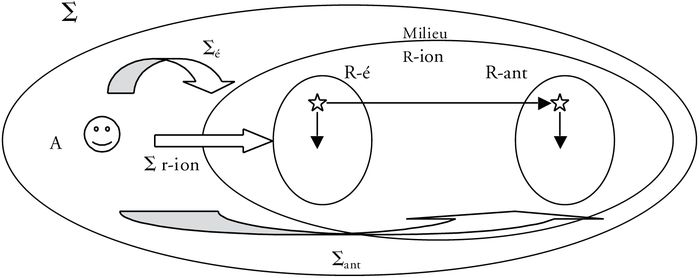
Le schéma de la figure 1 donne une idée des composants de la situation. Un actant A est confronté à un milieu objectif M formé essentiellement d’une représentation <Ré, Rant, Rion> telle qu’elle apparaît à un observateur O extérieur. Mais celui-ci doit supposer qu’il entretient avec les univers réprésenté et représentant des rapports autonomes modélisés par des situations composantes : ∑_é la situation représentée, Sant, la situation représentante, Sr-ion la situation de représentation (flèches doubles). Le sujet ne voit a priori qu’un seul milieu et c’est lui qui doit y distinguer un R-é, un R-ant et une R-ion pour ses besoins dans ∑. Nous avons à déterminer lesquels.

Figure 1

**Composants d’une situation objective de représentation**

Dans certains cas, A peut mettre en oeuvre une « représentation » qui lui est familière et l’utiliser directement. Souvent, il devra n’effectuer que des « tentatives de représentations », à ses risques et périls, en particulier au cours d’une action non algorithmique. Il s’agit maintenant de la situation telle que l’observateur pense que l’actant la perçoit, compte tenu de son comportement. Une tentative infructueuse est structurée comme une représentation réussie, mais elle peut être non pertinente ou inadéquate.

Dans le meilleur des cas, les univers U-é et U-ant peuvent être matériellement suffisamment distincts. Alors, les rapports ∑é de A avec U-é, et ∑ant de A avec U-ant peuvent être identifiés comme des situations distinctes, au point parfois que seule R-ion est problématique. Tous les cas sont possibles.

Nous n’avons pas encore évoqué les raisons qui rendent nécessaires la séparation puis la mise en correspondance des situations ∑é et ∑ant. Pour que l’utilisation de ∑ant soit nécessaire, il faut que A ne puisse réaliser un certain projet dans ∑é, – que ce soit pour des raisons matérielles, logiques ou ergonomiques, mais qu’il envisage de faire dans ∑ant une action qu’il pourra ensuite transporter dans ∑é, où elle réalisera le projet initial.

Prenons, à titre d’exemple, la célèbre expérience du singe de Wolfgang Kohler (1964), placé devant une banane qu’il convoite, mais qu’il ne peut atteindre : c’est la situation ∑é. Le milieu comprend non loin deux cannes qui, mises bout à bout, permettraient d’atteindre la banane. Le singe a déjà joué avec ces cannes. Il peut envisager de les adapter ; ce jeu constitue ∑ant. La représentation réside dans la mise en correspondance de la distance à la banane dans Ré avec celle des cannes dans Rant et l’anticipation de ce que la somme des longueurs des cannes dans ∑ant peut excéder la distance à la banane dans ∑é. Remarquons que c’est la propriété fondamentale qui permet de ramener avec succès le résultat de l’opération de ∑ant dans ∑é. Une représentation consiste donc en l’utilisation d’un univers représentant, pour y accomplir une action a priori directement impossible dans un univers représenté, afin de pouvoir, par la suite, ramener dans ce dernier le résultat de cette action.

Premières conséquences

L’analyse de la notion de représentation à l’aide de la théorie des situations met en évidence un fait dont l’importance n’est pas toujours reconnue : l’accent est surtout mis sur les objets <S, f, S’> qui entrent dans la définition d’une représentation particulière. Les objets qui ne sont pas mis en correspondance semblent ne jouer aucun rôle. Nous venons de montrer que dans une représentation, le rôle des dissemblances entre les deux univers est aussi important que celui de leurs ressemblances, dont une partie seulement est prise en compte dans la représentation. Cette condition a tendance à être un peu sous-évaluée dans les études qui ne font pas appel à la théorie des situations (comme dans l’article de Brian Greer et Guershon Harel, 1998).

En psychologie, l’univers représentant est assimilé à la connaissance par le sujet d’un univers représenté considéré comme le réel. Ce n’est qu’un cas particulier de situation de représentation qui laisse très ouvertes des questions essentielles sur la façon dont le sujet établit des correspondances et construit sa représentation, ou plutôt ses modèles implicites d’action pour utiliser le vocabulaire de la TSM. L’avantage en a été souligné par Sarrazy (2002).

Piaget (1996) et Freud (1920) ont apporté des éclaircissements substantiels à ce sujet. Ainsi, en commentant le jeu du « fort-da » de Freud (1981), Lacan (1966, dans Brousseau et Otte, 1991) montre bien que l’enfant qui fait disparaître et réapparaître sa bobine reproduit une situation réelle dans laquelle il n’est pas le maître des apparitions et des disparitions de sa mère par une situation où lui-même peut provoquer les apparitions et les disparitions d’une bobine. Une situation est représentée par une autre, semblable mais différente par la place et par le pouvoir de l’actant. La deuxième équilibre l’angoisse provoquée par la première et en constitue le sens. En aucun cas cette bobine isolée de son contexte ne représente la mère absente. Cet exemple montre la proximité de la notion de représentation avec celle du sens. Pour Lacan (1966, dans Brousseau et Otte, 1991), la chaîne du sens est ouverte, car la représentation – le jeu de la bobine – perd vite son pouvoir d’équilibrer les frustrations dues aux disparitions incontrôlables de la mère. Lorsque l’enfant n’y voit plus qu’un effet banal de ses actions, le symbole s’écroule ou, plus précisément, l’échec de la représentation doit être à son tour équilibré par la création d’un nouveau symbole. Cette interprétation fonctionnalise la connaissance et le sens ; elle nous rapproche ainsi de la méthode des situations.

Naturellement les types fondamentaux de situations non didactiques déterminent des fonctions différentes des représentations. Dans les situations d’action, la décision peut être fondée ou non sur la reconnaissance explicite ou implicite d’une représentation « objective ». Remarquons que ce que les psychologues appelleraient « représentation » du milieu est, dans la TSM, une collection de modèles implicites d’action associés aux diverses situations d’action concernant ce milieu. Ces modèles implicites ne comprennent peut-être aucune représentation objective, ils sont une forme de représentation mentale. De même, la façon vraisemblablement dialectique dont le sujet envisage ou rejette des interprétations de sa situation pour en élire une de façon durable importe peu. Il suffit que cela ait de bonnes chances de se produire grâce aux rétroactions de la situation. Ceci montre bien la différence des points de vue.

Mais dans les situations de formulation ou de communication et, par conséquent, dans les situations de validation explicite, l’usage d’une représentation linguistique ou iconique est obligatoire. L’essentiel des exemples d’utilisation des représentations dans les classes rapportés dans la littérature didactique relève de ce type de situations, que les interlocuteurs soient effectifs ou fictifs, qu’ils soient des élèves, seuls ou en groupes, ou des professeurs. L’exemple que nous commenterons plus loin relève de ce type de situations. Nous n’insistons donc pas sur ce point qui nous entraînerait à regarder plus précisément les possibilités des langues et répertoires pour construire et générer des représentations.

Avant d’avancer dans l’étude de la représentation, il est nécessaire de rappeler que l’observateur, ou le chercheur, fait partie du système et que son action peut se modéliser avec les mêmes moyens. Supposons que l’observateur O recueille des indices que l’actant A utilise bien certains objets et certaines relations comme des représentants d’autres, et que ce dernier s’attend à ce que le résultat soit celui que devrait donner la représentation, si elle était objectivement correcte et adéquate. Supposons également que cette représentation soit impropre, c’est-à-dire qu’elle ne satisfait pas la relation fondamentale. Objectivement, et notamment pour un observateur mathématicien, la correspondance utilisée par A n’est pas alors une représentation. Nous parlerons d’une tentative de représentation. Le sujet l’utilise comme une représentation et, pour lui, si la situation ne lui donne pas des raisons et des moyens de renoncer à son interprétation, il la conservera. Ce point illustre l’importance de rapporter les éléments de l’analyse à leurs situations d’utilisation.

Le didacticien construit des « modèles implicites » des représentations impropres dont il observe ou peut observer les effets. Il s’en sert pour prévoir et expliquer la distribution des réponses d’une population. Il cherche à expliquer sa présence, comme le ferait un psychologue. Dans la mesure où ces modèles implicites expliquent des décisions par des « croyances », ils jouent le jeu d’énoncés qu’il est pratique d’appeler « connaissances du sujet », étant entendu que ces connaissances peuvent être justes ou fausses et distinctes ou non des connaissances d’autres sujets, d’autres institutions et, en particulier, des connaissances scientifiques. Rien dans cette option n’empêche d’utiliser les résultats de psychologie.

L’essentiel est de montrer le rôle, la fonction de ces connaissances dans la gestion et l’évolution des situations. Il est important de noter que la modélisation, en termes de situation, facilite l’indispensable distinction entre les diverses assignations des « connaissances » à un sujet (élève, professeur, observateur, institution savante, etc.) et leur statut [5].

Situations objectives de représentations en mathématiques

Nous n’étudions, pour l’instant, que des conditions internes au système du schéma de la figure 1. La fonction de la représentation ne doit répondre qu’à des besoins du sujet pour son action. S’il avait recours à une représentation pour « illustrer » son propos, lui donnant ainsi une fonction poétique, cela relèverait d’un système de communication plus complexe.

À quoi une représentation peut-elle servir en mathématiques ? Un actant engagé dans une situation ∑₁ et qui peut la résoudre n’a pas besoin à la base de chercher à lui en adjoindre une autre. C’est donc dans la mesure où ∑₁ ne peut pas être résolu facilement que l’actant va chercher à construire une autre situation ∑₂, dans laquelle il pourra transporter une partie S de ∑₁ avec l’espoir que dans ∑₂ une solution lui apparaîtra et qu’il pourra la rapatrier dans ∑₁.

Il faut remarquer que l’actant ne peut pas nécessairement identifier exactement la structure S, c’est pourquoi c’est une situation qu’il recrée et non pas seulement une structure.
De plus, ce dont il a besoin est quelque chose qui ne se trouve pas immédiatement dans ∑₁ ; les différences entre ∑₁ et ∑₂ sont aussi importantes que les ressemblances.
Il est nécessaire de pouvoir utiliser une représentation inverse (pas nécessairement l’inverse de la première).

Il y a de nombreux exemples où un objet nouveau est « construit » grâce à une représentation. À tout nombre rationnel, Dedekind (1981) fait correspondre une coupure, c’est-à-dire une partition de l’ensemble Q. En raisonnant sur les coupures, il prouve l’existence des irrationnels et définit la structure R des réels. Alson (2000) reprend cet exemple dans sa thèse et en dérive le concept de « description ». Ce concept, qui prend en charge une autre acception des représentations, mériterait ici beaucoup plus qu’une simple allusion.

Il peut arriver que, dans la recherche, le jeu des représentations ne soit pas utilisé dans un point de vue aussi strict et que seules les questions transportées d’une situation dans une autre soient utilisées. Il arrive fréquemment que la représentation soit déjà connue et qu’elle soit utilisée pour diverses raisons. Nous n’en évoquons ci-après que deux.

La première, pour des raisons d’économie : les objets pertinents pour la résolution sont plus faciles à manier, plus familiers, dans U-ant que dans U-é. Les représentations iconiques permettent de traiter presque simultanément un nombre d’objets plus important, pour peu que les traitements correspondent à des relations spatiales. Ainsi, la représentation des quantités par des longueurs de segment permet de passer subrepticement d’un problème d’arithmétique à une résolution algébrique, du moins pour les élèves qui acceptent de représenter des quantités inconnues par un segment de longueur déterminée (Broin-Ferguson, 2002). Autres exemples, la représentation des sommes de fractions par des sommes de décimaux ou celle des produits de nombres par les sommes de leurs logarithmes.
La deuxième, pour effectuer une comparaison : le sujet doit comparer deux objets (deux longueurs, deux expressions algébriques, etc.), pour les remplacer l’un par l’autre, entre autres raisons. La situation détermine explicitement ou implicitement les conditions, la relation d’ordre ou les conditions d’équivalence, mais le sujet doit plonger les deux objets dans un même univers ou représenter l’un dans l’univers de l’autre. Derrière toute comparaison, il y a une représentation.

Ces exemples absorbent la plus grande partie des représentations utilisées dans les mathématiques scolaires. La classification des situations objectives de représentation suit naturellement celle proposée par la TSDM, dont les modèles génèrent un grand nombre de situations particulières.

Dans les exemples évoqués précédemment, il n’y a qu’un seul actant, sujet ou institution, engagé dans des situations d’action. Ces situations conduisent à inventer une représentation, utiliser la représentation déjà là pour trouver un objet, pour traduire une relation, etc.
Dans les situations de formulation, il y a deux actants. Il s’agit pour eux d’utiliser une représentation dans une communication, de décrire la représentation, de traduire d’un langage à un autre, etc. Entre de nombreux autres exemples, on peut signaler l’ostension : un sujet montre à son interlocuteur un objet pour évoquer une classe d’objets – un arbre représente la forêt ou une essence particulière. La réduction des ambiguïtés liées à la représentation tient une place importante dans les communications.
Dans les situations de preuve, la représentation joue un rôle rhétorique dans un débat entre deux actants. La discussion de la valeur de preuve d’une représentation est toujours délicate, comme le montre (Lakatos, 1984) dans un des meilleurs exemples de situation de « preuve » que nous connaissons.
Dans les situations d’institutionnalisation, les représentations jouent aussi un rôle important : elles sont citées comme sources et on s’y réfère constamment.

Un exposé exhaustif de ces différents usages sort du cadre de cet article, mais nous en donnerons plusieurs exemples détaillés ultérieurement.

Situations d’invention ou d’apprentissage de la représentation dans l’action

Nous suivons toujours l’ordre ascendant de la complexité des situations. Supposons que l’actant – ce peut être un sujet ou une institution, mais il se contente de « jouer le jeu rationnel et économique » déterminé par la situation – se trouve en présence d’un échec dans une situation objective dont il pressent qu’elle se reproduira souvent ou qu’elle est importante. Il doit « adapter » ses stratégies de résolution et les connaissances qui leur sont associées à ce qu’il connaît, avec l’espoir d’améliorer ses chances dans des situations qu’il ne connaît pas encore exactement.

L’exemple des décimaux révèle ce genre de difficulté : beaucoup de fractions n’ont pas de correspondant décimal exact. On ne peut pas trouver l’inverse de tous les naturels dans les décimaux. La solution a été trouvée par des méthodes qui illustrent la deuxième fonction des représentations : suppléer une impossibilité.

Considérons les décimaux et les rationnels (suivant la définition ci-dessus, D ne peut être que S, et Q ne peut être que S’ puisque D ⊂ Q). Soit S” les rationnels représentant les décimaux. La représentation transporte la somme, la différence, le produit de deux décimaux de D dans Q. Mais le quotient défini dans Q n’est le correspondant d’aucune opération de D. Cependant, la représentation transporte aussi l’ordre et la topologie : tout élément de S’ (de Q) peut être approché d’aussi près qu’on veut par des éléments de S”, c’est-à-dire de S (de D).

Cette propriété permet de définir une nouvelle représentation R^–1, inverse de la première, de Q par D, telle qu’un quotient non décimal (dans Q) sera représenté dans D par toutes les suites de décimaux qui convergent vers lui et, en particulier, par la suite canonique (décimaux à n décimales). Cette nouvelle représentation de Q par D permet de rapatrier dans le représentant initial un objet du représenté qu’il ne possédait pas précédemment et de bénéficier de la facilité des calculs dans D sans abandonner la facilité que donne la conception algébrique du corps Q [6].

Notons que pour appeler représentation l’inverse R^–1 de R, il faut admettre que la définition de la représentation autorise que certains objets de l’univers des représentés (ici Q) ne soient pas représentés par des objets de même nature, puisqu’un nombre de Q est représenté par une suite de D [7].

L’utilisation concomitante d’une représentation et de son inverse conduit souvent, par abus, à les confondre et à utiliser le terme « représentation » comme une relation symétrique. Cet exemple révèle donc que l’intérêt des représentations réside dans ce qui peut être fait dans un univers et qui ne peut pas être fait dans l’autre.

À ce moment, les deux univers – et pas seulement le couple (R-é, R-ant) – fonctionnent comme un nouveau couple générateur d’un nouvel objet. Les recherches dont nous parlons plus loin, en particulier celles d’Alson (2000), ont donné des exemples de telles inventions dans l’histoire ou en didactique.

L’étude de la représentation en termes de situations nous permet d’envisager de façon beaucoup plus précise et concrète les conditions dans lesquelles elle est susceptible d’apparaître comme solution d’un problème, soit pour des raisons logiques, soit à cause des économies qu’elle permet. On comprend, par exemple, que le passage d’une représentation formelle à une représentation iconique permet de bénéficier de possibilités sémiologiques et physiologiques intéressantes dans certains cas (par le nombre d’objets et de structure appréhendés d’un coup). Les vertus de ces représentations ne peuvent être étudiées qu’au cas par cas à cause et en fonction de leur sensibilité aux variables de la situation.

Pourtant, en dehors de quelques mises au point, on ne peut pas dire que ce qui précède apporte des résultats très originaux. La notion de représentation est apparemment trop générale pour déterminer des catégories spécifiques de travaux en didactique. Une étude particulière sera caractérisée par bien d’autres conditions plus importantes et plus particulières. L’intérêt de cette approche est peut-être de permettre de poser les questions suivantes : dans quelles conditions et dans quelle mesure l’enseignement peut-il utiliser les représentations ? Peut-il le faire sans adaptation spécifique ?

Avant d’aborder ce point, il sera sans doute agréable au lecteur de trouver une illustration de nos propos peut-être un peu théoriques.

Le « jeu des trésors »

Tous les ans, entre 1977 et 1990, les élèves de l’école maternelle J. Michelet (l’école pour l’observation de l’IREM de Bordeaux), âgés de 5 ans, se sont vu proposer une suite de situations qui les conduisaient à construire des « codes » pour représenter des objets, des collections, des propriétés, des relations, etc. Cette suite de situations est organisée suivant les principes théoriques exposés au paragraphe précédent. C’était l’activité dite « des trésors ».

Les différentes phases du « jeu des trésors »

Pour mieux cerner les questions soulevées par la représentation de quelques objets, il est plus commode d’évoquer d’abord les différentes étapes du processus et de résumer les situations caractéristiques.

Première phase : la collecte d’objets

L’enseignante présente à tous les enfants assis en rond devant elle deux ou trois petits objets nouveaux, appartenant au monde des enfants. Elle les fait passer de mains en mains, les fait nommer, puis les met dans une boîte grise qu’elle ferme et qu’elle met sur ses genoux. Elle demande alors : qu’est-ce qu’il y a dans ma boîte ? Un élève à la fois nomme un objet, l’enseignante le sort alors de sa boîte et le pose à la vue de tout le monde. Ma boîte est-elle vide ?, demande-t-elle et, si non, le jeu se poursuit, etc.

Le jeu s’effectue tous les matins. Tous les deux ou trois jours de nouveaux objets apparaissent et s’ajoutent aux précédents. Bientôt, avec une vingtaine d’objets, le jeu devient plus difficile : il faut penser à un objet, vérifier qu’il n’est pas déjà sorti de la boîte, lever le doigt, etc. et changer de proposition si un camarade interrogé avant nous fait sortir cet objet. Aucun élève n’est capable, à ce moment-là, d’énumérer tout seul le référentiel. Les enfants ont un répertoire réduit (de 7 à 28 objets suivant les sujets), mais cela suffit pour vider la boîte collectivement. Ce jeu quotidien dure au plus quinze minutes. Après un mois, la classe entière arrive à vider une boîte d’une quarantaine d’objets en apparence disparates mais soigneusement choisis.

Cette phase a pour objet d’introduire progressivement les éléments d’un référentiel, de rendre leur reconnaissance et leur dénomination verbale (le répertoire) collectives, fluides. Elle permet de présenter le jeu « devine ce qu’il y a dans ma boîte » sous sa forme la plus simple. Certaines connaissances logiques et mathématiques sont déjà implicitement mobilisées par les enfants.

Deuxième phase : le jeu des listes

Le jeu de la mémoire – L’enseignante choisit trois objets du référentiel, les montre aux enfants, les fait circuler, les leur fait désigner verbalement et les place dans une nouvelle boîte colorée : « Tout à l’heure, je vous demanderai de me dire ce que nous venons de cacher dans cette boîte. » Au bout de trois séances, tous les enfants ont compris le jeu et sont capables de le réussir, c’est-à-dire de mémoriser de courtes listes d’objets du matin pour le soir.

Le « saut informationnel » – En atelier, un matin, les élèves reçoivent sans transition non pas trois, mais une dizaine d’objets qu’ils peuvent examiner à loisir. Puis on range les objets dans la boîte colorée ; il faudra se rappeler la liste des objets. Panique ! Le passage de 3 à 10 introduit une complexification considérable de la situation [8]. L’enseignante impavide constate les échecs, mais reste encourageante. « Réfléchissez, nous y arriverons. » Au cours de plusieurs séances collectives, les élèves commencent à obtenir des réussites partielles en aidant leur mémoire par des dessins.

Aucun enfant de cet âge ne peut inventer ni même concevoir d’un coup la réponse qui consiste à faire la liste des objets à l’aide d’une collection de petits dessins des objets, car le processus ne peut réussir que si on en maîtrise en même temps la totalité des composantes. D’autre part, le projet ne peut avoir de sens que si les enfants envisagent, au préalable, des moyens de le mener à bien. La situation paraît bloquée, ce qui angoissait les enseignants. Et pourtant, nous avons observé que chaque année, des dessins et des listes apparaissent. Chaque année, quelques élèves ont demandé du papier pour « dessiner », pour faire comme maman avec les commissions. Ce qui est loin de résoudre le problème, car il faut dessiner chaque objet de façon à le reconnaître (lui et pas un autre auquel on ne pensait pas), les dessiner tous (et pour cela les énumérer), le dessiner une seule fois, ne pas en oublier, etc. Or les éléments de la solution apparaissent et se répandent dans la classe : la culture (la liste de maman pour les commissions), l’intuition de l’un, l’imitation d’un second, la critique d’un troisième, la chance d’un quatrième, etc. suffisent pour des succès encourageants. Aucune connaissance effective et définitive n’apparaît d’emblée, seulement ce qui est nécessaire pour s’engager dans la partie suivante. La méthode qui consiste à faire des listes de dessins est vite adoptée ; il reste à maîtriser les conditions de la réussite.

Troisième phase : le jeu de communication des listes

Dans un atelier, une liste des objets cachés dans une boîte colorée est réalisée par un « auteur ». Elle est essayée, dans un deuxième temps, successivement par trois « lecteurs ». Le lecteur essaie de reconnaître un objet d’après le dessin et le nomme. Un autre enfant, le « contrôleur », tient la boîte cachée et dit si elle contient ou non l’objet nommé. Le lecteur recommence ou continue jusqu’au succès ou à l’abandon.

Après le contrôle, l’enseignante écoute, et enregistre pour l’observation, les trois enfants qui commentent et discutent entre eux les réussites, les échecs et les difficultés du jeu. Ses sollicitations restent discrètes et courtes. Pour cette phase, qui n’est plus d’autocommunication, le nombre des objets est ramené à quatre.

Une des principales difficultés pour les enfants réside dans la compréhension de la répartition des responsabilités entre l’auteur et le lecteur : ils doivent coopérer pour gagner, bien qu’au moment de la critique finale, ils se trouvent avoir des intérêts opposés. C’est dans cette phase que se mettent au point tous les embryons de techniques de la représentation des objets et de l’énumération des listes sur lesquelles nous allons revenir.

Quatrième phase : la construction d’un code commun

L’enseignante instaure des séances d’études et de discussions sur les difficultés et les malentendus de la veille. La confrontation des diverses représentations données d’un même objet fait apparaître des variables iconiques et des choix motivés par des raisonnements d’ordre logique. Ils aboutissent à la construction progressive d’un code collectif, affiché et mis à jour.

Le processus avait fait l’objet d’une étude minutieuse des conditions susceptibles de provoquer ces apprentissages par le jeu des modifications des variables de situations « adidactiques ». L’intervention des enseignants ne concernait jamais le « contenu » des apprentissages, mais seulement les conditions, le déroulement et la motivation des élèves.

L’organisation des situations et du processus présente un intérêt pour la présente étude, car ils réalisent le paradigme de toutes les situations de représentations.

Conditions de la genèse des représentations

Il s’agit donc pour les élèves de pouvoir utiliser des « signes », des combinaisons de signifiants et des listes de signes pour décrire et communiquer le contenu d’une boîte à un autre enfant ou pour interpréter son message. Cette boîte contient quelques petits objets ou jouets pris dans un référentiel d’une quarantaine d’objets.

Voici un échantillon des conditions et des raisonnements qui soutiennent la construction du processus. Comme dans toutes les études d’ingénierie didactique, il faut commencer par la situation terminale et remonter la chaîne des conditions didactiques nécessaires. Ce raisonnement est habituellement caché par l’habitude de prendre connaissance des dispositifs à l’aide de la chronique de leur déroulement, ce qui permet une bien meilleure compréhension, mais qui masque totalement sa technicité [9].

Nous nous sommes intéressés essentiellement à la fonction référentielle (le discours se fait en fonction de ce qu’on a à dire) d’un « langage iconique » et à son élaboration spontanée dans des conditions spécifiques « adidactiques ». Un enfant qui dessine une maison représente-t-il une maison ? ou accomplit-il une activité rituelle de dessin dont les éléments symboliques lui sont fournis par son milieu ? Dans le premier cas, il prend effectivement en charge certaines relations entre son modèle et le dessin : à titre d’exemple, il fait deux portes parce que sa maison en a effectivement deux. Son dessin a une fonction référentielle. Dans le deuxième, non, l’enfant ne travaille que sur le plan symbolique : une maison icône ou métaphore a toujours une seule porte, deux fenêtres placées symétriquement et une cheminée, quatre fenêtres et c’est un château.
Les objets du référentiel sont soigneusement choisis de façon à poser les principaux problèmes de représentation repérés à l’époque.
Le code final doit être discuté par l’ensemble des enfants qui choisiront, en les justifiant, les sèmes : les caractères et les signes les plus propres à identifier un objet, en le distinguant d’autres similaires et en le dessinant facilement. La structure du référentiel joue évidemment encore ici un rôle très spécifique.
Pour que ce débat puisse avoir lieu et amener l’émergence d’un discours sur les qualités des représentations, il faut que les « signes » ou « symboles » en débat soient ceux que les enfants ont eux-mêmes construits (et non choisis parmi des dessins déjà là) individuellement, essayés et discutés dans des situations d’autocommunication (individuelles) ou de communication (duelles).
Pour échapper à la culture que les enfants de cet âge ont du dessin libre, la consigne de « dessiner » ne doit pas émaner de l’enseignante (condition un peu arbitraire, mais défi intéressant).
La situation de base devra satisfaire toutes les conditions de la situation non didactique typique. C’est-à-dire qu’elle sera telle que les enfants auront besoin de désigner exactement un objet, quel que soit ce moyen, avec un résultat, réussite ou échec, qu’ils pourront immédiatement apprécier directement eux-mêmes, mais surtout avec des possibilités de prévoir ce résultat et de corriger l’exactitude de leurs prévisions dans des tentatives multiples et répétées.
Si le jeu complet est trop complexe dans sa forme utile (devoir dessiner pour prévoir), des jeux préparatoires seront proposés, mais tous auront une structure non didactique typique complète. Il faut noter les particularités de ce processus où la succession des situations est déterminée par des variations des variables de commande d’une même situation et non pas directement par l’articulation de situations différentes relevant d’une même connaissance. La logique des situations vient ainsi doubler ou même se substituer à la seule logique des connaissances (topogenèse) qui préside habituellement aux chronogenèses didactiques.
Ainsi, l’enseignante peut changer les jeux, mais n’a pas à apporter des informations ni à approuver : ce n’est pas une maïeutique socratique. De plus, l’objet d’une situation n’est pas toujours l’acquisition d’une connaissance ou d’une partie des connaissances visées. Il peut être simplement de permettre à un enfant de se glisser dans une situation, de comprendre à quoi on joue, d’éprouver le plaisir qu’on peut y prendre, réussite totale ou non.
Les enfants de cet âge n’ont aucune difficulté à nommer verbalement et à discriminer les dénominations des objets du référentiel (la voiture avec une étoile, le porte-monnaie, la grenouille, etc.), mais ils ne savent pas écrire ces dénominations. Les situations devront pouvoir être résolues d’abord verbalement, puis plus tard devront l’être par un dessin.
Le passage de la phase verbale à la phase graphique sera commandée par un saut informationnel, en ce sens que la tâche habituelle facile (se souvenir des trois ou quatre objets contenus dans une boîte) deviendra impossible par le seul jeu d’un « saut » d’une variable ergonomique : le nombre d’objets. Celui-ci passera d’un coup à une dizaine.
De nombreuses autres variables ont été prises en compte dans la conception de l’organisation générale, dans celle de chaque situation particulière et aussi dans leur gestion (l’enseignante participait étroitement aux recherches). Il serait oiseux de les rapporter ici.

Quelques-uns des résultats établis dans cette expérience

Jean-Marie Digneau (1980) a rapporté, étudié et justifié les principaux paramètres du processus, en particulier dans ses deux premières phases. Puis Jacques Péres (1984) a étudié le processus dans son intégralité, notant au passage de nombreux aspects plus psychologiques. En particulier, il a précisé les conditions et les étapes du passage des représentations iconiques, graphiques ou schématiques (analogiques) à des codes formels. Les résultats établis dans cette expérience sont nombreux et divers.

Tout d’abord, les phases « adidactiques » fonctionnent bien et provoquent les apprentissages annoncés. En particulier, le saut informationnel, malgré un aspect assez angoissant et même un peu dramatique pour les élèves, ne provoque pas le blocage redouté. Sa résolution provoque un certain plaisir qui sert de paradigme pour les situations suivantes et d’encouragement pour les difficultés. Fragmenter la difficulté en une multitude de situations de plus en plus évidentes ou faciles, mais considérées comme des petits pas dont la succession est nécessaire, n’est pas toujours la meilleure stratégie.
En suivant de près la progression du répertoire des enfants, une différence assez grande apparaît entre le répertoire de la classe, celui qu’un élève mobilise dans l’action et celui qu’il peut fournir en réponse à un questionnaire.

On peut en tirer des conclusions dont voici des exemples.

Les connaissances d’un élève, qui se manifestent dans une situation collective familière, sont souvent beaucoup plus riches que ce qu’il peut produire « formellement » dans d’autres conditions. Dans des conditions différentes, ces mêmes connaissances n’ont pas le même sens puisque les situations objectives sont différentes et les situations didactiques superposent des effets de contrat. À titre d’exemple, Péres (1984) rapporte un effet de contrat : un élève s’interdit de dessiner et déclare en protestant qu’il fera faire ce dessin par sa soeur ou par sa mère.
Les connaissances disponibles dans une collectivité sont la réunion des connaissances de ses membres, les connaissances « communes » – celles repérées dans la plupart des évaluations – en sont l’intersection. La différence entre ces deux répertoires peut être grande. La variété des situations d’enseignement mobilise des répertoires qui se situent entre ces deux extrêmes. Les situations proposées sollicitent les deux répertoires qui progressent ensemble.

Les enseignants fondent leurs stratégies didactiques sur une certaine « représentation » du savoir des élèves, en particulier sur des « évaluations » individuelles. Suivant que leurs conceptions pédagogiques utilisent plutôt la réunion (par exemple, dans la maïeutique collective) ou plutôt l’intersection (par exemple, dans des exercices individuels en parallèle) et suivant que leurs techniques didactiques sont plus ou moins adaptées à ces conceptions, de très grands écarts entre les attentes et les observations de « résultats » peuvent être constatés. Ce phénomène joue un rôle important dans la sous-évaluation et le sous-emploi des ressources des élèves.

L’énumération d’une collection n’est pas une acquisition immédiate. Bien qu’invisible, puisque cette « connaissance » ne figure pas comme objet d’enseignement et qu’elle s’acquiert spontanément lors de l’apprentissage du comptage, elle pose des problèmes aux enfants ; cette observation fera par la suite l’objet des travaux de Briand (1993).
La nécessité de représenter des objets pour les reconnaître parmi d’autres fait développer par les élèves des stratégies diverses mais régulières dans un ordre « génétique » presque immuable et général. Le premier procédé qui apparaît est la trace. Les enfants décalquent le contour de l’objet à représenter, ensuite ils enrichissent le dessin de caractères oppositifs ou de détails distinctifs (tableau 1).

Un caractère est « distinctif » lorsqu’il suffit à déterminer un objet dans le référentiel (par exemple, dans cette collection, seul l’indien est un bonhomme qui porte des plumes ; un seul camion porte une étoile). Un caractère est « oppositif » lorsqu’il contribue, avec d’autres, à déterminer une classification de tout ou d’une partie importante du référentiel. Les objets qui ont ce caractère et les objets qui ne le présentent pas sont à peu près aussi nombreux.

Les éléments représentant ces caractères peuvent être figuratifs : ils tendent à évoquer l’aspect de l’objet. Mais il n’y a aucun caractère analogique qui puisse représenter la terre, le verre, l’acier, la porcelaine dont est faite une bille. Il faut donc inventer et convenir d’un « signe » arbitraire : hachures, pointillés, croix, etc.

La grenouille, beaucoup plus grande que la feuille de dessin, leur pose un réel problème. Impossible de relever sa trace : elle est trop grande. L’idée d’inventer un dessin petit qui ressemble à – mais qui présente quelques traits de – son grand modèle ne vient pas immédiatement. Mais lorsqu’un enfant résout le problème, la plupart des autres l’imitent et tous envisagent cette « découverte » comme une conquête précieuse.

Mais les progrès lors des phases d’action ne sont pas assurés. Le modèle est trop grossier et d’autres variables d’ordre psychogénétique interviennent. Les phases successives de débat et d’institutionnalisation du code sont alors cruciales.
Le processus n’est pas ponctuellement reproductible, en ce sens que les réactions et les remarques des élèves ne se superposent pas exactement, et les « histoires », c’est-à-dire les déroulements, bien que proches, sont différents. Par contre, il est globalement reproduit en ce sens que les résultats, les successions de phases, les comportements essentiels, les apprentissages et autres sont bien similaires. Définir ce qu’est la reproductibilité didactique est un problème fondamental de la didactique théorique, et c’est un facteur essentiel de la connaissance de l’enseignement, entre autres par les professeurs.

Tableau 1

**Les représentations des objets**

En conclusion, dans des situations appropriées, il est possible de faire apparaître chez les enfants une réelle pratique de diverses méthodes de représentation des objets et de développer chez eux une « culture sémiologique », c’est-à-dire de les voir argumenter les propriétés de diverses méthodes de représentation. Inversement, la nécessité d’effectuer ces représentations met en évidence les objets (éléments, propriétés et relations) et prépare leur reconnaissance, leur emploi dans d’autres situations, leur étude et leur connaissance explicite. De sorte que le processus décrit ci-dessus constitue une genèse didactique et même scolaire des premières représentations. De plus, les situations présentées peuvent servir de référence pour d’autres acquisitions du même type, tant pour les professeurs que pour les élèves. En ce sens, le jeu des trésors est une situation fondamentale pour la représentation. La place de la représentation dans les recherches en didactique liées à la théorie des situations sera reprise plus loin dans l’article, mais auparavant, il est temps de continuer notre étude théorique.

Situations didactiques de représentation

Dans les activités d’enseignement, qu’il s’agisse pour l’élève de faire un problème ou de comprendre un discours du professeur, les représentations peuvent jouer des rôles différents de ceux que nous venons d’évoquer. Leur étude est plus complexe.

Rôles des représentations dans les situations didactiques

L’élève A est assujetti à la fois à une situation objective de représentation ∑ et à une situation didactique SD_R gérée par le professeur P. La figure 2 représente l’inclusion des milieux et des situations [10] dans les situations didactiques, mais nous ne représentons toujours pas l’observateur O. Il est fréquent de devoir envisager l’existence simultanée de plusieurs assujettissements, qu’ils réagissent ou non les uns sur les autres. La question est de savoir si cette imbrication oblige à envisager d’autres usages, d’autres rôles pour les représentations ou d’autres types de situations, et aussi de savoir ce que serait une situation didactique de représentation.

Figure 2

**Situation didactique d’une représentation**

Le schéma fait apparaître deux situations objectives de représentation au fonctionnement similaire à celui que nous avons étudié précédemment : celle qui a pour actant l’élève et celle qui a pour actant le professeur. Elles font apparaître respectivement :

une représentation comme « moyen pour l’élève A de dominer la situation objective » ou comme objet de « connaissance ». C’est R, celle que nous venons d’étudier (flèches doubles).

Dans le jeu des trésors, un dessin représente le contenu d’une boîte, une collection d’objets tente de réaliser ce que représente un dessin, etc. Le jeu des trésors comporte de nombreux autres exemples.

R_P, des représentations comme « connaissances » pour le professeur :
- R_PE comme « connaissance à enseigner » (confondue avec R pour la clarté du schéma).
- R_PS comme objet de savoir pour lui, en tant que sujet (flèche simple).

À titre d’exemple, il sait que tel dessin d’objet est ambigu ou que des ajouts de caractères correspondent à des intersections de listes, etc.

Les différences entre R_PE et R_PS constituent une composante de la transposition didactique particulière à ce professeur.

Mais le schéma fait apparaître aussi :

R_d, la position d’une représentation comme moyen didactique pour l’enseignant (flèche pennée). Son fonctionnement est fondamentalement différent des deux précédents.

À titre d’exemple, devant la difficulté de ses élèves à comprendre la notion dans son univers d’origine U-é, le professeur fait appel à une représentation de cette notion dans un univers plus familier U-ant : « C’est comme si… », dit-il. Si l’étude de l’image de cette représentation permet à l’élève de comprendre le fonctionnement de la notion, la représentation est utilisée comme précédemment. Mais si l’existence de cette représentation et de cette image est tenue par le professeur ou par les élèves comme une raison explicite ou implicite d’accepter la notion sans réellement la comprendre, alors la représentation a joué le rôle d’un argument inductif, d’un moyen rhétorique ou didactique direct, destiné à influencer l’élève et à modifier ses convictions pour des raisons sans rapport avec l’objet de savoir. Ce rôle, sa légitimité et sa nécessité vont être étudiés dans le paragraphe suivant.

Ainsi, une même situation didactique effective peut comporter des représentations R, R_P et R_d différentes, ces différences étant faibles lorsqu’il s’agit de sous-représentations d’une même représentation ou radicales si elles n’ont à peu près rien en commun.

Une même représentation peut être utilisée dans chacun des trois rôles ci-dessus. Nous distinguerons donc :

des « situations didactiques portant sur la représentation », où une représentation figure comme objet d’enseignement ou comme moyen de connaissance pour l’élève ;
et des « situations didactiques de représentation » où, pour influencer l’élève, une représentation est utilisée comme moyen d’enseignement par le professeur, comme argument rhétorique ou comme moyen didactique indépendant de l’objet d’enseignement.

Exemple de représentations objets d’enseignement : l’enseignement des entiers au collège

Pour introduire les entiers relatifs, il est courant d’évoquer des altitudes et des profondeurs, des avoirs et des dettes, des escaliers, des positions sur une droite numérique, des températures, etc. Il s’agit de représentations du type R ci-dessus, « objets de savoir » pour les élèves. Si ces représentations sont inscrites au programme du collège, elles deviennent R_PE.

Il y a bien représentation, même si ces représentations sont impropres, en ce sens que seule une partie de la structure visée <Z, <, +, χ> est représentée : l’ordre et l’addition, mais pas la multiplication.

Le professeur est en mesure d’en connaître une représentation propre R_PS, celle des translations numériques de N, par exemple. Il sait aussi que la température, par contre, ne représente que l’ordre, pas l’addition.

Lorsqu’il faudra comprendre la multiplication de deux entiers, les représentations impropres se constitueront en obstacles comparables à l’obstacle épistémologique et historique bien connu. Les élèves ne comprendront pas le produit de deux entiers parce que les représentations utilisées pour introduire les entiers les ont associés à des mesures et que toutes les opérations arithmétiques sont soutenues, conçues à partir de situations de mesurage.

Le choix qui s’offre à l’enseignant est alors, soit d’introduire des représentations impropres pour récupérer une compréhension liée à la mesure ou au comptage, quitte à les modifier plus tard avec des difficultés et des risques, soit de préférer l’introduction directe d’une représentation propre plus complexe et plus insolite avec tout de suite d’autres difficultés et d’autres risques. La décision ne se prend pas sur des considérations uniquement mathématiques, mais surtout sur des considérations didactiques : ergonomiques, psychologiques, de développement, etc.

Il ne faudrait donc pas interpréter les propos ci-dessus comme une condamnation de l’usage didactique des représentations, même impropres. Les naturels se constituent aussi en obstacle, comme tous les plongements dans des surstructures ; il n’empêche qu’on ne peut pas les enseigner après les décimaux.

La presque totalité de la littérature sur les représentations publiée dans les revues et ouvrages sur l’enseignement des mathématiques et, en particulier, les articles contenus dans cet ouvrage, traitent des « situations didactiques portant sur la représentation ». Très peu sur la transposition didactique, c’est-à-dire sur la différence entre les représentations utilisées par les élèves et celles utilisées par leurs professeurs et sur les deux aspects suivants [11].

Les représentations comme instruments d’influence didactique non spécifique

Pourtant, l’utilisation des représentations comme moyen d’expliquer, de faire comprendre, de faire admettre, de convaincre, de faire apprendre, de faire retenir, etc., c’est-à-dire comme moyen logique ou « formel », indépendant de la connaissance à enseigner est très fréquente et très banale.

On la trouve dans toutes les formes classiques de situations didactiques :

comme introduction à une connaissance nouvelle ;
comme illustration pour augmenter « le sens » ;
comme moyen inductif de définition ;
comme moyen d’organiser et de hiérarchiser l’ensemble des connaissances, « donc » de démontrer les énoncés ;
comme argument inductif, l’« explication par analogie » ;
comme explication ;
comme moyen de démultiplier des exercices similaires pour obtenir l’apprentissage par répétition, par un serinage un peu perfectionné.

Attachons-nous un instant, à l’usage des représentations comme moyen inductif de la définition d’un objet ou de l’enseignement d’un théorème. L’ostension consiste à présenter un objet pour désigner une classe d’objets, lorsque la reconnaissance de la classe « exacte » à partir d’un seul objet est trop difficile. La présentation d’un petit ensemble de représentants de cette classe, et qui sont des représentations les uns des autres, peut induire un meilleur résultat : A est P, B est P, C est P, ceci doit permettre de reconnaître que D est P.

Le procédé rhétorique est, somme toute, assez innocent. Mais il peut devenir « principe » et s’ériger en exigence didactique à l’égard de l’élève. L’exemple le plus clair est sans doute celui des exercices structuraux. Le principe est le suivant : l’élève doit décoder le discours du professeur et trouver l’objet d’enseignement dissimulé par le professeur derrière une représentation. La théorie du contrat didactique montre que ce genre de dissimulation est inévitable, voire nécessaire.

Mais lorsque le procédé s’étend à la présentation et à l’enseignement des propositions mathématiques et qu’il intervient comme argument inductif pour faire admettre un énoncé, enfin et surtout lorsqu’il se substitue à la preuve, lorsqu’il opère sous la pression d’une exigence didactique implicite mais impérieuse – « ce qui est répété doit être appris » –, il y a conflit entre l’objet et le moyen de la connaissance et de l’apprentissage. Explicitement, la règle didactique inductive serait la suivante :

Le professeur a montré que :

R possède la propriété P ;
que la représentation R1 de R possède la propriété P ;
que la représentation R2 de R possède la propriété P ;
si une représentation R3 de R se présente, je dois conclure qu’elle possède la propriété P.

Syllogisme évidemment faux, éminemment contraire à l’objet de l’enseignement des mathématiques où comme ailleurs « comparaison n’est pas raison », mais dont l’usage s’impose à l’élève s’il ne veut pas apparaître comme réfractaire à l’enseignement. De même que la répétition des exercices permet d’obtenir une « connaissance » qui remplace et simule la compréhension, la répétition de l’usage de théorèmes à l’occasion d’une accumulation de représentations peut simuler un savoir mathématique.

Les justifications de ces procédés sont les plus diverses, scientifiques ou méthodologiques. Il est souvent implicitement admis que la multiplication des liens cognitifs, en particulier des illustrations, participe à une meilleure « connaissance » d’une notion. Ce point de vue tend à autoriser et même à favoriser la multiplication des représentations d’une notion, propres ou impropres. Les avantages mais aussi les inconvénients de cette croyance sont évidents. Seule une étude cas par cas peut indiquer dans quelles limites il convient de se tenir, et l’analyse en termes de situations est inévitable pour cela.

L’importance des représentations, sous la forme mathématique d’isomorphismes, est apparue tellement forte à certains auteurs comme Dienes [12] (1970) qu’ils en ont fait la base d’une théorie de la connaissance, de l’apprentissage, de l’enseignement et même de l’histoire des mathématiques à l’usage des enseignants. Brousseau (1986) a dénoncé « l’abus de l’analogie ».

Le succès des représentations dans l’« épistémologie de professeurs » est sans aucun doute dû à la proximité de leur fonctionnement avec toutes sortes de procédés rhétoriques – l’analogie, la comparaison, etc. – ou didactiques – la réification, la répétition –, et à l’appui que semblent leur apporter des formulations mathématiques comme l’isomorphisme.

Les exemples familiers et personnels abondent, mais ils ne sont pas tous l’effet d’une tentative furtive et personnelle. L’usage didactique des représentations comprend une part très importante de rhétorique, et cette part est profondément liée à la culture, et aux croyances de toutes sortes, des professeurs et des élèves : cultures scientifique et populaire, cultures épistémologique et didactique.

Différence entre les deux usages didactiques de la représentation

L’utilisation des représentations y compris « impropres » par le sujet d’une situation d’action objective relève de l’heuristique. Le sujet peut tenter une représentation dans la mesure où il engage sa responsabilité et assume les conséquences de sa tentative.

II faut que la méthode de projection soit contenue dans le processus de projection ; le processus de représentation atteint ce qu’il représente par le moyen d’une règle de projection. Si je copie quelque chose, les erreurs de ma copie seront compensées par la colère, les regrets, etc. que je manifesterai à leur égard. Le résultat global – c’est-à-dire la copie plus l’intention – est l’équivalent de 1’original. Le résultat effectif – la simple copie visible – ne représente pas la totalité du processus de copiage ; nous devons y inclure l’intention. Le processus contient la règle, le résultat ne suffit pas à décrire le processus […].

Nous comprenons un symbole (la copie du plan du métro) comme partie d’un système, et le système est décrit par sa grammaire (non par une proposition supplémentaire).

[B VI] 1. II faut que ce que la pensée et la réalité ont « en commun » soit déjà exprimé dans l’expression de la pensée. Vous ne pouvez pas l’exprimer dans une proposition supplémentaire, et il est égarant d’essayer de le faire. L’« harmonie » entre la pensée et la réalité, harmonie que les philosophes qualifient de « fondamentale », est quelque chose dont nous ne pouvons parler ; aussi n’est-elle pas le moins du monde harmonie au sens ordinaire, étant donné que nous ne pouvons la décrire. Ce qui fait qu’il nous est possible de porter des jugements justes sur le monde, fait aussi que nous pouvons en porter de faux.
Wittgenstein, 1971, p. 42

Dans la relation didactique, au contraire, l’usage d’une représentation s’apparente en fait à des usages rhétoriques très généraux et très variés puisqu’elle sert à influencer, convaincre, enseigner à un autre. Nous venons d’évoquer l’analogie, mais une représentation impropre peut aussi fonctionner comme figure de sens, les exemples de symbolisations métaphoriques ou métonymiques abondent en mathématiques (Bauersfeld et Zavadowski, 1981) et aussi dans des stratégies plus modestes, comme figures de répétition et d’accumulation.

Il est donc essentiel de distinguer les représentations objets d’enseignement des représentations comme moyens rhétoriques et didactiques des enseignants et, parmi ces derniers, ceux qui peuvent être contrôlés et justifiés ainsi que les autres. Cela nous amènerait à étudier les rapports entre ces deux usages didactiques de la représentation.

S’il est assez évident que l’usage des représentations est soumis à des obligations liées à la contingence, qu’en est-il de l’usage rhétorique de la représentation dans la relation didactique ? Jusqu’à quel point est-il fécond de substituer des procédés formels à des procédés signifiants ? Chercher une réponse à cette question sort du cadre de cet article. Cela impliquerait d’entrer dans l’analyse des diverses formes du « contrat didactique », c’est-à-dire des différentes façons de répartir la responsabilité de l’apprentissage et de la connaissance entre le professeur et son élève.

La représentation comme connaissance préalable à la relation didactique

La relation didactique présente plusieurs propriétés paradoxales qui font que son établissement et sa réussite ont toujours quelque chose de hasardeux, de fragile et de provisoire. Si l’établissement premier des connaissances ne suppose pas l’intervention d’une connaissance extérieure à l’humanité et peut donc satisfaire l’hypothèse constructiviste, c’est parce qu’elle profite de deux circonstances originales par rapport à la diffusion didactique des connaissances. D’une part, les connaissances à établir et surtout leur forme et les processus pour le faire ne sont pas déterminés : il existe bien des façons équivalentes d’établir les connaissances. L’histoire en réalise une ; elle aurait pu en réaliser d’autres. D’autre part, cette relation dispose, de fait, d’un temps non limité a priori. Ces conditions restent valides aussi pour la plupart des acquisitions de connaissances qui ne répondent pas à un projet didactique, mais qui proviennent d’une adaptation spontanée, autonome à son environnement.

La relation didactique entre deux institutions P (professeur) et E (élève) s’instaure, par définition, lorsqu’une institution S (société) décide que E devrait acquérir une certaine connaissance, lorsqu’elle juge que E ne pourra pas le faire par une adaptation spontanée et autonome à son environnement M (milieu), et lorsqu’elle juge qu’une institution P est en mesure de l’obtenir par d’autres moyens, S charge P de réaliser le projet (P, E et S peuvent être des institutions ou des sujets) [13].

Une des raisons pour laquelle E ne peut pas acquérir la notion de façon autonome est que le milieu n’en fournit aucun emploi ou s’il y en a un, alors la construction de la notion nécessaire à été si complexe que la probabilité de voir un sujet la produire dans le temps dont il dispose est trop faible. Souvent, l’institution ou l’élève ne peuvent pas apprendre ce dont ils n’envisagent pas l’emploi. De plus, ils ne peuvent concevoir l’emploi de la connaissance nouvelle et en comprendre l’adéquation qu’après l’avoir acquise. Dans certaines circonstances, même l’enseignement de la notion par d’autres moyens peut ne pas aboutir à une connaissance utilisable.

Il en résulte pour l’enseignant une sorte d’alternative absurde : soit il doit organiser des situations d’autoapprentissage et attendre une improbable genèse spontanée de connaissances semblables aux savoirs actuels, soit il enseigne directement ce « savoir », mais il est incompréhensible et inutilisable, et ne sera donc pas converti en connaissance pour le sujet [14]. Mais l’autoapprentissage ne se réduit pas à une adaptation inconsciente. L’adaptation s’effectue toujours avec le concours nécessaire d’un autoenseignement qui obéit au même schéma que la relation didactique. Si la relation didactique est impossible, l’autodidactisme et la transformation des connaissances en savoirs (Conne, 1992) le sont également. Il s’agit bien d’un paradoxe de la situation didactique (Brousseau, 1990, 1998).

Cette hypothèse est évidemment contredite par l’observation. Tous les organismes humains peuvent, plus ou moins facilement, acquérir des connaissances aussi bien par l’autoapprentissage que par l’enseignement direct. Avant de « posséder » une connaissance, un sujet ou une institution doit s’en faire une idée, dont la fonction serait de permettre la mise en route des processus d’apprentissage et d’enseignement.

Concrètement, nous supposons qu’un sujet ne peut entrer dans une situation que s’il la « comprend », c’est-à-dire non seulement s’il peut en connaître les objets, les relations et les règles données dans l’« énoncé » de la situation, mais aussi s’il envisage quelles décisions bonnes ou mauvaises il pourrait prendre. Cette façon de répondre, qui peut être fausse ou inefficace, constitue la stratégie de base, le « modèle d’action » initial et indispensable qui permet à l’élève d’entrer dans la dialectique des questions, des réponses et des corrections qui amèneront une connaissance adaptée. En théorie des situations, l’apprentissage n’est donc jamais qu’une transformation d’une « connaissance » ou son remplacement par une autre.

Cette approche conduit à distinguer, d’une part, les « connaissances » et les « savoirs » que l’enseignant peut déterminer comme nécessaires ou utiles, sous quelque forme que ce soit, à la résolution des situations qu’il organise pour en susciter la manifestation ou pour les faire apprendre et, d’autre part, la nébuleuse des connaissances que le sujet est susceptible d’engager dans cette opération pour l’investir et la mener à bien. Les connaissances relèvent de l’intention et de l’action du professeur. Elles peuvent être prises en charge dans la théorie des situations didactiques. Elles sont contenues dans la nébuleuse des connaissances qui semble correspondre à ce que les psychologues appellent les représentations.

Nous pourrons utiliser le terme « représentation » pour désigner cette idée de la connaissance en question, idée propre à l’apprenant, idée construite à partir d’idées véhiculées par la culture et travaillées par son expérience « personnelle ». Cette représentation comprendrait non seulement des caractères et des opinions, exacts ou non, relatifs à la connaissance et à la situation en question, mais aussi des caractères et des opinions sur l’institution elle-même et sur les situations d’emploi de la connaissance. Ainsi, cette nouvelle définition ferait des représentations des sortes d’accoucheuses de l’apprentissage.

La solution pourrait convenir si elle n’est pas seulement une « fuite en avant », car les mêmes paradoxes peuvent se retrouver en amont. Le rapport entre représentation, connaissance, savoir et action ne peut être bien déterminé en didactique que par des classes de situations identifiables.

Conclusion

Cet article avait pour objet premier de montrer comment la théorie des situations didactiques en mathématiques aborde l’étude du fonctionnement et de l’enseignement d’une notion mathématique comme celle de représentation et d’homomorphisme. Il devrait se prolonger par le recensement, la discussion, la confrontation et la reprise des nombreux et riches travaux qui ont étudié l’utilisation de représentations particulières ; nous avons donc essayé de montrer que chacune peut être modélisée par une situation spécifique. Comment la modélisation en termes de situation permet-elle de juger des avantages et des inconvénients de l’introduction d’une représentation dans l’étude, l’apprentissage ou l’enseignement de telle ou telle notion mathématique ? Est-il intéressant de glisser à nouveau une étude générale des représentations comme cela avait été tenté, en d’autres termes, dans les années 1960 et 1970 [15] ?

Le lecteur n’y trouvera qu’un exemple simple d’emploi de cette modélisation, de ses prolongements et de la méthodologie, pour un sujet « élémentaire » mais fondamental : la genèse de la représentation à l’école. D’aucuns pourront penser que la contingence sur laquelle s’appuient nos réflexions est bien mince. C’est pourquoi nous évoquons, en annexe, des exemples plus avancés et les questions de didactique qui leur sont liées.

La généralité même de la notion de représentation, au coeur de la modélisation, et la grande variété de ses manifestations – arguments pour certains en faveur de son enseignement – risquent de générer des méprises et des déceptions. L’enseignement d’une représentation, même correcte et riche, peut manquer d’intérêt didactique, peut même introduire une substitution illégitime. L’analyse des situations propose des moyens de contrôler leur usage et, notamment, leur usage rhétorique. Comment déceler et éviter les glissements métadidactiques, les ostensions douteuses (Brousseau, 1998), les abus de l’analogie, les débordements de l’usage des métaphores et des métonymies, etc. ? Il ne s’agit pas de diminuer l’importance de l’emploi des représentations, mais d’augmenter leur adéquation. L’étude du fonctionnement des représentations ouvre la voie à une méthode pour en contrôler l’usage : déterminer quand elles sont utiles, quand elles sont superflues et quand elles sont nocives.

Un premier résultat de notre étude conduit à distinguer les représentations comme objets d’enseignement et comme moyens heuristiques enseignés a priori, et les représentations et tentatives de représentations comme moyens effectifs dans l’activité mathématique en cours.

L’examen de ce dernier cas conduit alors à s’intéresser aux rôles complémentaires de ce qui est similaire et de ce qui est différent dans les univers représentés et représentants. La prise en considération des différences d’efforts que le sujet doit déployer dans l’univers représenté et dans le représentant, entre les difficultés ou les facilités qu’il y rencontre est un argument récurrent classique. Notre deuxième résultat met en évidence l’importance des propriétés logiques et ergonomiques des différentes connaissances dans les situations en présence et donne les moyens de les quantifier.

Essentielles en situation de recherche lorsque les représentations sont des tentatives, les différences n’apparaissent plus comme pertinentes dans la présentation des résultats établis. Les représentations reconnues deviennent de simples faits et les tentatives échouées doivent être rejetées. Ainsi, le troisième résultat, le rôle essentiel que joue la représentation dans la connaissance, tend à disparaître dans l’organisation et dans la transmission des savoirs, ce qui appelle des études d’ingénierie didactique pour pallier cette composante de la transposition didactique.

L’existence et la prospérité du thème de la représentation dans le domaine de la psychologie semblent être parmi les raisons pour lesquelles de nombreux travaux de didactique se sont rassemblés autour de ce thème. Nous avons fermement montré la différence de point de vue entre les deux domaines et mis en suspicion les importations naïves d’un domaine à l’autre. De nouvelles études devraient être entreprises dans ce sens. Il me semble difficile, voire illégitime, contraire à l’éthique, dans son principe, d’importer directement en didactique des prescriptions, des suggestions ou même de simples concepts issus des sciences cognitives, directement, c’est-à-dire sans les intégrer spécifiquement dans une analyse du système didactique.

Les représentations : étude en théorie des situations didactiques

Résumé

Abstract

Resumen

Zusammenfassung

Introduction

Le concept de représentation

La méthode d’étude propre à la théorie des situations didactiques en mathématiques