Résumés
Résumé
Dans cet article, nous présentons une analyse de la pauvreté chez les 0-17 ans au Québec et au Canada dans une perspective comparative et une analyse des impacts des politiques publiques sur la pauvreté dans ce groupe d’âge. Nous montrons que la pauvreté chez ces personnes au Québec est moins élevée que partout ailleurs au Canada et que dans une perspective internationale, le classement du Québec et du Canada est relativement bon en ce qui a trait à la pauvreté des 0-17 ans. Nos résultats indiquent aussi que, si l’objectif du décideur public est de faire diminuer la pauvreté chez ces jeunes au Québec, une augmentation des prestations familiales et des prestations d’aide sociale serait l’option à privilégier.
Abstract
In this article, we present an analysis of poverty among 0-to-17-year-olds in Quebec and Canada from a comparative perspective and an analysis of the impact of public policies on poverty. We show that the poverty rate among 0-to-17-year-olds in Quebec is lower than elsewhere in Canada and that, from an international perspective, Quebec and Canada rank relatively well. Our results also indicate that, provided it is the objective of public decision-makers to decrease poverty among 0-to-17-year-olds in Quebec, an increase in family benefits and social assistance would be two measures to prioritize.
Corps de l’article
Partout en Occident, il est généralement reconnu que les conditions matérielles d’existence sont un des déterminants majeurs de la réussite scolaire et de l’état de santé des jeunes[1]. Au sujet de la réussite scolaire, Clark (1960), Christofides, Cirello et Hoy (2001), Conley (2001), Hutchings et Archer (2001), Willis (1981) ainsi que le Conseil supérieur de l’éducation du Québec (2004) reconnaissent tous que l’origine sociale et les conditions matérielles d’existence expliquent en grande partie l’espérance de scolarisation des jeunes ainsi que leur accès aux diplômes postsecondaires. À propos de l’état de santé, Paquet (2005) relate que la plupart des études internationales en santé publique mettent en lumière un gradient social de santé. Elle insiste aussi sur le fait que la causalité va largement dans le sens de la position sociale vers la santé et que la causalité inverse est un phénomène relativement marginal. À titre d’exemple, Case, Lubotsky et Paxson (2002), Currie et Stabile (2003) et Currie, Shields et Wheatley Price (2007) démontrent l’existence d’un tel gradient social pour les États-Unis, le Canada et la Grande-Bretagne. Il convient de noter tout de même que Nahum (2007) montre qu’un tel gradient social n’existe pas en Suède. À l’aide d’un modèle probabiliste, elle montre que la présence de contraintes de liquidité[2] expliquerait un moins bon état de santé psychologique chez les enfants. Dans un tel contexte, il est intéressant d’analyser la pauvreté chez les jeunes de 0-17 ans ainsi que l’impact des différentes politiques de soutien de revenu sur celle-ci.
L’objectif de cet article consiste, dans un premier temps, à analyser la pauvreté chez les jeunes de 0-17 ans au Québec. Pour ce faire, nous décomposons celle-ci par types de familles et comparons la performance du Québec à celle des autres provinces canadiennes ainsi qu’à d’autres pays industrialisés. Par la suite, nous analysons l’impact qu’ont les principaux programmes publics de transferts du revenu sur la pauvreté des jeunes de 0-17 ans au Québec et au Canada. La prochaine section présente la méthodologie de la mesure de la pauvreté ainsi que ses fondements normatifs et la suivante, un portrait de la pauvreté chez les 0-17 ans. La section 4 propose une analyse de l’impact des politiques publiques sur la pauvreté des 0-17 ans, suivie d’une brève conclusion.
Méthodologie
L’analyse des comparaisons de pauvreté fait normalement face à deux problèmes majeurs : un problème d’identification (dans le cas de la pauvreté) et un problème d’agrégation (pour l’inégalité et la pauvreté). Pour identifier les personnes ou les ménages pauvres, l’analyste utilise normalement un seuil de pauvreté, dégagé selon plusieurs méthodes. Un ménage ayant un revenu inférieur à ce seuil sera considéré comme pauvre alors qu’un ménage ayant un revenu au-dessus du seuil sera considéré comme non pauvre. Comme le souligne Ravallion (1996), les économistes qui s’intéressent au concept de niveau de vie font traditionnellement référence à l’« utilité » ou au niveau de satisfaction qu’une personne peut atteindre à l’aide d’un certain panier de biens de consommation. Ce niveau d’utilité est déterminé par les préférences de l’individu. Cette façon de voir le problème est en lien direct avec la pensée de la philosophie utilitariste développée par Bentham et Mill aux dix-huitième et dix-neuvième siècles.
Mais les préférences d’un individu ne sont pas déterminées dès la naissance. Bourdieu (1970) a d’ailleurs montré que le caractère de celles-ci est en partie cognitif car elles se développent à partir du cadre socioéconomique et culturel dans lequel l’individu évolue. Par contre, il est opportun de se demander si cette différence dans les préférences individuelles est pertinente sur le plan de l’évaluation de la justice sociale et distributive. Pour certaines personnes, la réponse est non. Pour cette raison, Rawls (1971) propose une approche différente. Adoptant une démarche contractualiste, il arrive à la conclusion qu’il faut considérer la distribution des « biens premiers » disponibles aux individus afin d’évaluer la justice sociale. Ces biens premiers sont définis comme étant tout ce qu’une personne normale peut désirer afin de mener une bonne vie selon sa propre philosophie compréhensive individuelle. Rawls classe ces biens premiers en deux grands groupes. Le premier groupe comprend les biens premiers naturels tels les talents et la santé. Le second groupe est composé de biens premiers sociaux. Ces biens sociaux sont les libertés fondamentales (droit de vote, liberté d’expression, etc., les chances d’accès aux différentes positions sociales et les avantages socioéconomiques (revenu, richesse, base sociale du respect de soi, etc.). C’est dans cet espace des avantages socioéconomiques que l’évaluation du niveau de vie doit alors être effectuée. Rawls propose aussi le principe de différence qui consiste à maximiser les avantages socioéconomiques du groupe le moins bien nanti. Ce faisant, Rawls élimine les différences entre les individus dans la procédure d’évaluation de la justice sociale.
Plusieurs travaux ont par la suite proposé différentes façons d’évaluer la distribution des revenus et de la qualité de vie[3]. Ainsi, Sen (1992) suggère une méthode d’évaluation basée sur ce qu’il nomme les « capabilités »[4]. Ces capabilités sont définies comme étant la capacité qu’a un individu de bien fonctionner socialement et de saisir les opportunités socioéconomiques qui s’offrent à lui. Sen argumente que, bien que Rawls ait de bonnes raisons de rejeter l’utilitarisme, celui-ci va trop loin dans son élimination des différences entre les individus. Sen soutient que la société ne doit pas tenir compte des différences dans les préférences entre les individus dans ses jugements de justice sociale, mais qu’elle doit tout de même tenir compte d’autres différences. Par exemple, une personne handicapée aura besoin de plus de ressources pour se déplacer qu’une personne non handicapée. Ce surplus de ressources ne permet pas à cette personne de réaliser plus de modes de fonctionnement qu’une autre mais ne lui permet que de se déplacer, tout comme la personne non handicapée. C’est pourquoi Sen propose plutôt d’évaluer la justice distributive et la qualité de vie sur les capabilités qui sont définies comme les ensembles de modes de fonctionnement social parmi lesquels la personne peut choisir. Sen illustre le concept à l’aide d’une bicyclette. La bicyclette est un bien de consommation qui, de par ses caractéristiques, permet à la personne de se déplacer d’une certaine façon. La caractéristique de transport de la bicyclette permet de réaliser la capabilité « se déplacer d’une certaine façon » et c’est cette capabilité qui procure à la personne de l’utilité ou de la satisfaction. Sen considère que c’est cette capabilité, et non pas la satisfaction qu’elle procure, qui s’approche le plus du concept de niveau de vie. La société n’est pas responsable du niveau de satisfaction atteint par l’individu. C’est la responsabilité individuelle qui intervient à cet égard. Par contre, il est facile de constater que, pour la personne handicapée, la réalisation du même fonctionnement social exigera plus de ressources. Il lui faudra acheter, par exemple, un fauteuil roulant électrique.
Lorsqu’une analyse des standards de vie par l’approche des capabilités est réalisée, il faut donc tenir compte des éléments qui permettent aux individus de pouvoir fonctionner à l’intérieur de la société. De même, il est probable que la définition de la pauvreté devienne relative dans la dimension du revenu bien que la pauvreté fasse référence à une notion qui est absolue dans l’espace des capabilités. Ceci est dû au fait qu’une personne puisse avoir besoin de plus de ressources afin de pouvoir satisfaire certains modes de fonctionnement social si elle vit dans une société dans laquelle le niveau de revenu général est plus élevé.Implication du choix épistémologique sur la sélection du seuil de pauvreté
Figure 1
Implication du choix épistémologique sur la sélection du seuil de pauvreté
Le schéma ci-dessus dresse une esquisse du raisonnement de Sen. Dans un premier temps il considère que l’individu possède des ressources (revenus, richesse) qu’il utilise pour accomplir certains fonctionnements sociaux. Dans un second temps, l’accomplissement des fonctionnements sociaux sélectionnés par l’individu procure à ce dernier un certain niveau de satisfaction. Pour Rawls, la justice sociale devrait être évaluée dans l’espace des ressources (ou biens premiers) mises à la disposition de l’individu. Pour les utilitaristes, c’est le niveau de satisfaction atteint par les individus qui est la variable d’intérêt. Sen quant à lui adopte une position intermédiaire qui consiste à évaluer la justice sociale par l’ensemble des modes de fonctionnements sociaux parmi lesquels l’individu peut choisir. La définition de la pauvreté peut donc être absolue dans cet espace des capabilités mais impliquer en même temps une définition relative dans l’espace des ressources disponibles, donc des revenus. C’est cette position épistémologique que nous adoptons dans ce texte. Nous faisons le choix d’établir notre seuil de pauvreté relatif correspondant à 50 % de la médiane des revenus après transferts et impôts.
L’autre problème auquel l’analyste fait face est celui d’agrégation. Il doit utiliser les statistiques sur les revenus des ménages afin d’établir un portrait de la pauvreté pour l’ensemble de la société ou d’un sous-groupe de la population qui l’intéresse. Pour ce faire, l’analyste doit choisir un indice de pauvreté. L’indice de pauvreté le plus fréquemment utilisé est l’indice numérique de pauvreté. Celui-ci donne tout simplement la proportion de ménages pauvres dans la population. Sa simplicité d’interprétation est probablement la meilleure explication de la popularité de cet indice. Par contre, comme le souligne Sen (1976), l’utilisation de celui-ci comporte deux problèmes majeurs : il est insensible à la profondeur de la pauvreté et à l’inégalité entre les pauvres. Pour illustrer le premier problème, prenons un exemple. Considérons une société composée de 10 individus dont les revenus sont respectivement de 7 000 $, 8 000 $, 11 000 $, 13 000 $, 14 000 $, 15 000 $, 16 000 $, 17 000 $, 18 000 $ et 20 000 $. Imaginons que dans cette société, 10 000 $ serait un seuil de pauvreté acceptable. Si nous calculons l’indice numérique de pauvreté, nous obtenons un résultat de 20 % (soit 2 personnes ayant un revenu de moins de 10 000 $ divisé par 10 personnes). Imaginons maintenant qu’un changement économique provoque une chute des revenus des deux personnes pauvres, soit de 7 000 $ à 5 000 $ pour l’une et de 8 000 $ à 6 000 $ pour l’autre. Nous souhaiterions considérer cette perturbation comme facteur aggravant de la pauvreté. Toutefois l’indice numérique de pauvreté demeure inchangé. Les deux situations sont donc considérées comme étant équivalentes.
Afin de tenir compte de la profondeur de la pauvreté nous pouvons utiliser un autre indice, l’indice de déficit normalisé de pauvreté (l’expression mathématique exacte de cet indice est présentée dans l’encadré 1). En calculant le déficit normalisé du revenu de chaque ménage pauvre par rapport au seuil de pauvreté et en calculant une moyenne de ces déficits pour l’ensemble de la population, cet indice permet de prendre en compte les variations de profondeur de la pauvreté en plus de l’incidence de celle-ci. Par contre, cet indice comporte aussi un problème si nous considérons que le manque de ressources d’un pauvre est un problème qui devient de plus en plus grave au fur et à mesure que nous nous éloignons du seuil de pauvreté. Nous dirons alors vouloir tenir compte de l’inégalité dans la distribution de l’écart de pauvreté. Afin de comprendre ce problème, reprenons la situation initiale de notre exemple dans laquelle un des pauvres a un revenu de 7 000 $ tandis que l’autre a un revenu de 8 000 $. Imaginons maintenant deux situations différentes. Soit la situation (A) où 500 $ est enlevé à celui qui a 7 000 $ et la situation (B) où 500 $ est retiré à celui qui a 8 000 $. Si nous considérons que le fait d’enlever des ressources à un pauvre est un problème qui devient de plus en plus grave au fur et à mesure que nous nous éloignons du seuil de pauvreté, nous aimerions avoir un indice qui indique que la situation (A) est pire que la situation (B). Malheureusement, en ne prenant en compte que le déficit moyen, l’indice de déficit normalisé de pauvreté va considérer ces deux situations comme équivalentes. Nous avons donc besoin d’un autre indice pour pouvoir tenir compte de ce facteur, c’est-à-dire un indice qui prenne en compte l’inégalité dans la distribution de l’écart de pauvreté. Une classe d’indices qui permet de tenir compte de cette dimension de la pauvreté est la classe d’indices de Foster, Greer et Thorbecke (1984). Cette classe d’indices est intéressante parce qu’elle inclut, entre autres, l’indice numérique de pauvreté, P0 et l’indice de déficit normalisé de pauvreté, P1. Nous choisirons l’indice P2 dans cette classe afin de tenir compte de la dimension inégalité de la pauvreté en plus de la profondeur et de l’incidence. De plus, les indices de pauvreté de cette classe sont décomposables, ce qui permet de pouvoir comparer la pauvreté de différents sous-groupes de la population.
Lorsque deux analystes utilisent des seuils et (ou) des indices de pauvreté différents, leurs résultats peuvent diverger. Dans un tel contexte, il est tout de même possible d’effectuer des tests de dominance stochastique. Ces tests, proposés par Atkinson (1987), identifient les situations dans lesquelles le classement de la pauvreté entre différents groupes démographiques demeure le même pour tous les choix de seuils ou d’indices de pauvreté potentiels. Imaginons que nous fixons une limite maximale à 20 000 $ pour un individu vivant seul pour le seuil de pauvreté. Le test de dominance stochastique permettrait alors d’affirmer que le classement entre deux groupes demeure valide quel que soit le seuil de pauvreté entre 0 $ et 20 000 $ et quel que soit l’indice de pauvreté dans l’ensemble des indices considérés. Dans cet article, nous effectuerons le test de dominance stochastique du premier degré qui consiste à comparer les distributions cumulatives de revenu[5] des différents groupes démographiques. Lorsque deux distributions cumulatives ne se croisent pas avant le seuil de pauvreté maximal (c.-à.-d. 20 000 $ dans le cas qui nous intéresse), le groupe ayant la distribution cumulative la plus élevée sera considéré plus pauvre que l’autre groupe et cette conclusion demeure valide quel que soit le seuil de pauvreté choisi et quel que soit l’indice de pauvreté choisi (c.-à.-d. tout indice existant dans la littérature ou tout autre indice qu’un analyste pourrait construire et qui aurait les propriétés exigées pour un indice de pauvreté). L’application de ces tests permet de vérifier si les classements de pauvreté obtenus dans cet article sont contingents à notre choix de seuil à 50 % de la médiane. De plus, si les deux distributions cumulatives du revenu ne se croisent jamais, même au-dessus du seuil de pauvreté maximal, Duclos et Makdissi (2004) ont montré que le test de dominance stochastique devient alors un test de bien-être pour l’ensemble du groupe démographique. On peut alors affirmer que le bien-être de l’ensemble des individus du groupe ayant la distribution cumulative la plus élevée est alors inférieur au bien-être de l’ensemble des individus de l’autre distribution et que cette conclusion est valide pour tous les indices de bien-être existants et pour tous ceux qu’on pourrait inventer. Dans une telle situation, on analyse l’ensemble de la distribution de revenu plutôt que de nous concentrer sur les pauvres seulement. Il existe aussi des tests de dominance stochastique de degré supérieur (c.-à.-d. de degré 2, 3,…). Ces tests restreignent l’ensemble des choix d’indices pour lequel la comparaison demeure valide[6]. Nous n’effectuerons pas ce type de tests dans cet article.
L’analyse de l’impact des différentes politiques sur la pauvreté peut se faire selon deux types d’approches. Le premier type d’approche consiste à identifier quel est l’apport des politiques existantes sur la réduction de la pauvreté ou de l’inégalité. L’analyste évalue alors, de façon ex-post, dans quelle mesure les politiques mises en place ont permis de réduire la pauvreté ou l’inégalité observée par rapport à ce qu’elle aurait été en absence d’intervention publique. Ce type d’approche est utilisé dans Makdissi, Therrien et Wodon (2006). Le deuxième type d’approche est plus approprié lorsqu’on veut faire des recommandations de modifications aux politiques économiques. L’analyste calcule alors l’élasticité des indices par rapport à chacun des programmes de transferts. Ces élasticités indiquent quel pourcentage de diminution de l’indice peut être obtenu en augmentant les transferts d’un programme de 1 %, tout en laissant les critères de sélections constants. C’est cette approche que nous adoptons dans cet article.
Portrait de la pauvreté chez les 0-17 ans
Afin d’effectuer nos comparaisons de pauvreté entre les différentes provinces canadiennes, nous utilisons l’Enquête sur la dynamique du travail et du revenu (EDTR) de Statistique Canada pour l’année 2002. Nous retenons la définition de revenu selon la mesure de panier de consommation. Cette définition ajuste le revenu disponible après impôts et transferts du ménage en lui retranchant toutes les dépenses obligatoires liées au travail telles que les cotisations syndicales et les frais de garde d’enfants. Cette définition prend en compte, entre autres choses, les différences interprovinciales dans les prix des services de garde. Pour ajuster le revenu pour les différentes tailles de famille, nous utilisons la classe d’échelles d’équivalence paramétriques de Buhmann, Rainwater, Schmaus et Smeeding (1987). Ces auteurs suggèrent de diviser le revenu disponible des ménages par n?, où n représente le nombre d’individus dans le ménage et ?, l’élasticité de l’échelle d’équivalence par rapport à la taille du ménage. Théoriquement, la valeur de ? est comprise entre 0 et 1 mais Buhmannet al. (1987) soulignent que les échelles les plus fréquemment utilisées par les analystes donnent des valeurs ? comprises entre 0,23 et 0,84. Tel que suggéré dans plusieurs études de l’OCDE, nous utiliserons une valeur de 0,5 pour ? (voir Föster (2000)).
Afin d’ajuster pour les différences de prix entre les régions, nous avons utilisé les mêmes déflateurs régionaux que Makdissi et Groleau (2002) que nous avons ajustés pour l’année 2002 en tenant compte des différentiels d’inflation entre les régions[7]. Une fois ces ajustements effectués, nous avons calculé la médiane des revenus au Canada et avons par la suite calculé notre seuil de pauvreté à 50 % de cette médiane. Pour l’année 2002, ce seuil de pauvreté (en équivalent revenu d’une personne seule) est de 13 290 $.
Pour les comparaisons internationales, nous avons utilisé les données du Luxembourg Income Study (LIS) pour les années 2000. Nous avons ajusté les revenus de la même façon à l’exception des différences régionales dans les prix des biens puisque l’information sur la province de résidence n’est pas disponible dans les données du LIS. Les indices pour le Canada tels que calculés avec l’EDTR 2000 ou le LIS 2000 seront donc quelque peu différents. Comme l’information sur la province de résidence n’est pas incluse dans le LIS 2000, nous ne pouvons pas estimer les indices pour le Québec. Nous utilisons donc l’EDTR 2000 pour calculer les indices du Québec que nous ajustons par la suite en multipliant par le ratio de l’indice LIS sur l’indice EDTR pour le Canada. Bien que n’étant pas exact, cet ajustement est le meilleur qu’on puisse faire compte tenu des informations disponibles.
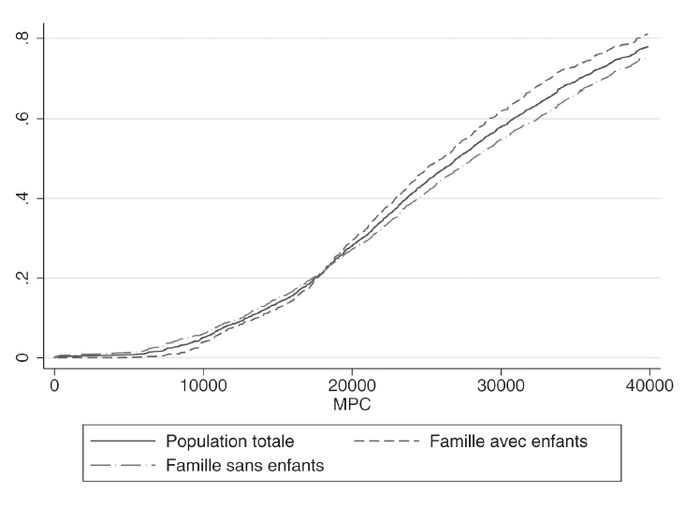
À la lecture du graphique 1, on constate que la distribution cumulative des revenus pour les familles avec enfants (c.-à-d. pour les 0-17 ans aussi) est située sous celle des ménages n’ayant pas d’enfants jusqu’à un croisement qui se situe aux alentours de 18 000 $. Ceci signifie qu’il y a moins de pauvreté chez les 0-17 ans que chez les personnes vivant dans des familles sans enfants pour tout indice de pauvreté et pour tout seuil de pauvreté inférieur à 18 000 $. En comparant la distribution cumulative des revenus des 0-17 ans avec celle de la population totale, on arrive à la même conclusion. Par contre, on ne distingue pas ici les 0-17 ans selon le type de famille à laquelle ils appartiennent. Les données pour le Québec seulement ne permettent pas d’effectuer des tests de dominance stochastique pour une décomposition plus fine. Nous devons donc prendre l’ensemble des données canadiennes pour effectuer une décomposition plus précise.
Graphique 1
Tests de dominance stochastique entre les types de familles au Québec, 2000
Une première constatation émerge lorsqu’on lit le graphique 2 : la dominance de la distribution cumulative des revenus des 0-17 ans sur les personnes sans enfants n’est vraie que pour les seuils de 0 $ à environ 12 000 $. Il faut considérer les 0-17 ans vivant dans des familles biparentales ou avec un père seul pour avoir une dominance aussi claire que pour le Québec. Si on ne considère maintenant que les 0-17 ans vivant dans des familles monoparentales, on constate que leur distribution cumulative des revenus est en tout point supérieure à celle des autres personnes et qu’il ne semble y avoir aucun croisement. Ceci signifie qu’il y a plus de pauvreté chez les 0-17 ans vivant dans des familles monoparentales au Canada que chez toutes les autres personnes et que cette conclusion est vraie, quels que soient le seuil de pauvreté et l’indice de pauvreté utilisés. De plus, comme il n’y a pas de croisement, on peut utiliser le résultat de Duclos et Makdissi (2004) pour affirmer que le bien-être des 0-17 ans vivant dans des familles monoparentales est moins élevé au Canada que pour les personnes vivant dans les autres types de familles et ceci est vrai, quel que soit l’indice de bien-être utilisé.
Graphique 2
Tests de dominance stochastique entre les types de familles au Canada, 2000
À la lecture du graphique 3, on remarque qu’il y a moins de pauvreté chez les 0-17 ans du Québec que pour les 0-17 ans des Prairies et ceci est vrai pour tout indice de pauvreté et pour tout seuil de pauvreté compris entre 0 $ et 18 000 $. De plus, il y a moins de pauvreté chez les 0-17 ans du Québec que pour les 0-17 ans de l’Ontario, de l’Atlantique et de la Colombie-Britannique et ceci est vrai pour tout indice de pauvreté et pour tout seuil de pauvreté. De plus, comme il n’y a pas de croisement, on peut encore une fois utiliser le résultat de Duclos et Makdissi (2004) pour affirmer que le bien-être des 0-17 ans du Québec est supérieur au bien-être des 0-17 ans de l’Ontario, de l’Atlantique et de la Colombie-Britannique et ceci est vrai pour tout indice de bien-être possible.
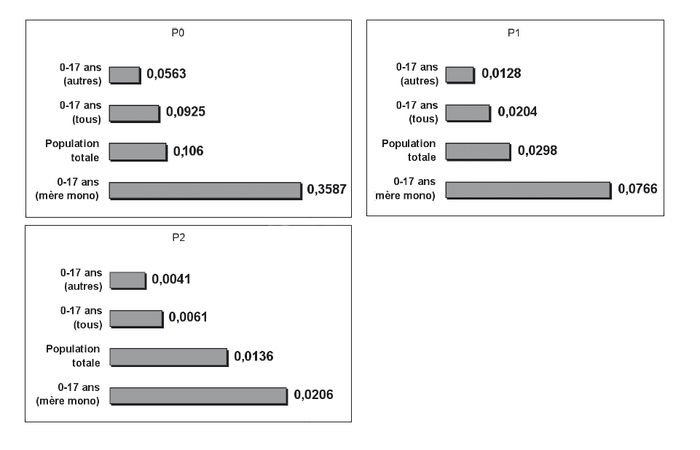
Le graphique 4 présente les estimations de nos trois indices de pauvreté pour la population totale ainsi que chez les 0-17 ans par type de famille au Québec. On constate que les 0-17 ans vivant dans des familles dirigées par des mères monoparentales sont plus pauvres que la population totale alors que les 0-17 ans vivant dans les autres types de familles sont moins pauvres que la population totale. Ces résultats sont valides pour nos trois indices de pauvreté, ce qui est cohérent avec les tests de dominance stochastique effectués sur l’ensemble de la population canadienne.
Graphique 3
Tests de dominance stochastique pour les 0-17 ans entre les différentes provinces au Canada, 2000
Graphique 4
Trois indices de pauvreté P0 , P1 et P2 chez les 0-17 ans par type de famille au Québec
Le tableau 1 présente respectivement les indices P0 , P1 et P2 pour les 0-17 ans résidant dans les différentes provinces au Canada. On constate que pour les trois indices, le classement du Québec par rapport aux autres provinces est cohérent avec les tests de dominance stochastique effectués pour les cinq régions du Canada.
Tableau 1
Taux de pauvreté P0 , P1 et P2 chez les 0-17 ans par province canadienne, 2000
|
P0 |
P1 |
P2 |
Colombie-Britannique |
0,2683 |
0,0746 |
0,0341 |
Terre-Neuve |
0,1981 |
0,0508 |
0,0192 |
Nouvelle-Écosse |
0,1803 |
0,0469 |
0,0187 |
Nouveau-Brunswick |
0,1428 |
0,0306 |
0,0094 |
Île-du-Prince-Édouard |
0,1419 |
0,0348 |
0,0145 |
Canada |
0,1376 |
0,0368 |
0,0161 |
Manitoba |
0,1355 |
0,0334 |
0,0157 |
Ontario |
0,1293 |
0,0358 |
0,0165 |
Saskatchewan |
0,116 |
0,0225 |
0,0081 |
Alberta |
0,1069 |
0,0349 |
0,0186 |
Québec |
0,0925 |
0,0204 |
0,0061 |
Il est pertinent d’analyser la situation de la pauvreté chez les enfants de 0-5 ans puisque certains des parents de ceux-ci ont accès à des services de garde subventionnés au Québec. Le graphique 6 présente un test de dominance stochastique pour les familles avec enfants de 0 à 5 ans selon leur région de résidence. La première constatation est qu’il y a moins de pauvreté chez les enfants de 0 à 5 ans du Québec que pour les familles avec enfants de 0 à 5 ans résidant dans n’importe quelle autre région canadienne et ceci est vrai pour tout indice de pauvreté et pour tout seuil de pauvreté. La deuxième constatation est qu’il y a plus de pauvreté avec enfants de 0 à 5 ans de la Colombie-Britannique que pour les familles avec enfants de 0 à 5 ans résidant dans n’importe quelle autre région canadienne et ceci est vrai pour tout indice de pauvreté et pour tout seuil de pauvreté.
Graphique 6
Tests de dominance stochastique entre les familles ayant des enfants de 0 à 5 ans selon leur région de résidence au Canada
Tableau 2
Taux de pauvreté P0 , P1 et P2 chez les 0-5 ans par province canadienne, 2000
|
P0 |
P1 |
P2 |
Colombie-Britannique |
0,3373 |
0,0843 |
0,0352 |
Terre-Neuve |
0,242 |
0,0672 |
0,0253 |
Nouvelle-Écosse |
0,2085 |
0,0528 |
0,0196 |
Nouveau-Brunswick |
0,157 |
0,0259 |
0,0079 |
Île-du-Prince-Édouard |
0,1829 |
0,0539 |
0,0254 |
Canada |
0,1691 |
0,0433 |
0,0179 |
Manitoba |
0,2127 |
0,0437 |
0,0173 |
Ontario |
0,148 |
0,0427 |
0,0194 |
Saskatchewan |
0,1567 |
0,0274 |
0,008 |
Alberta |
0,1293 |
0,0404 |
0,0191 |
Québec |
0,1168 |
0,0224 |
0,0059 |
Le tableau 2 présente respectivement les indices P0 , P1 et P2 pour les 0-5 ans résidant dans les différentes provinces au Canada. On constate que pour les trois indices, le classement du Québec par rapport aux autres provinces est encore une fois cohérent avec les tests de dominance stochastique effectués pour les cinq régions du Canada.
Tournons-nous maintenant vers des comparaisons internationales. Comment le Québec se compare-t-il à d’autres pays pour la pauvreté chez les 0-17 ans. Pour répondre à cette question, nous utilisons les données de la vague 5 du LIS (« around 2000 » tel qu’indiqué sur le site du LIS[8]). La base de données du LIS n’indique pas la province de résidence de telle sorte que nous ne pouvons calculer les indices pour le Québec. La façon dont nous procédons pour effectuer la comparaison internationale est la suivante. Avec l’EDTR 2000, nous calculons les indices de pauvreté pour le Canada et pour le Québec. Nous comparons les résultats de l’EDTR 2000 et de la vague 5 du LIS pour le Canada et construisons un facteur d’ajustement implicite que nous imputons par la suite aux indices calculés à l’aide de l’EDTR 2000 pour le Québec.
Tableau 3
Calcul du facteur d’ajustement automatique pour le Canada
|
P0 |
P1 |
P2 |
LIS |
0,129 |
0,033 |
0,015 |
EDTR |
0,137 |
0,036 |
0,016 |
Facteur d’ajustement |
0,942 |
0,917 |
0,938 |
Le tableau 3 donne le facteur d’ajustement implicite calculé à partir des données du LIS et de l’EDTR pour le Canada. Nous appliquons ce facteur aux indices québécois afin de construire les trois figures suivantes. Par contre, il convient à ce point de faire une mise en garde. Premièrement, les indices pour le Canada calculés à l’aide du LIS et de l’EDTR sont relativement semblables. Ceci est un facteur positif. Par contre, nous ne savons pas ce qui explique la faible différence. Celle-ci pourrait être due, par exemple, à l’absence d’ajustement pour les différences de prix entre les provinces dans le LIS puisque l’information sur la province de résidence n’est pas incluse dans cette base de données. Il faut donc interpréter les résultats suivants avec une certaine réserve.
Figure 9
Comparaison internationale de l’incidence de la pauvreté chez les 0-17 ans
À la lecture de la figure 9, on constate que l’incidence de la pauvreté chez les 0-17 ans, tant au Canada qu’au Québec, est moins élevée qu’aux États-Unis, qu’en Italie, qu’en Irlande, qu’en Espagne, qu’en Grande-Bretagne et qu’en Australie. L’incidence de la pauvreté chez les 0-17 ans au Canada est plus élevée qu’en Grèce tandis qu’au Québec, elle est moins élevée qu’en Grèce. Tous les autres pays sur le graphique ont une incidence de la pauvreté chez les 0-17 ans moins élevée qu’au Canada et qu’au Québec. Pouvons-nous conclure que la pauvreté des 0-17 ans est nécessairement moins élevée dans ces pays ? Cette réponse est loin d’être robuste. Il faut se souvenir que l’incidence de la pauvreté n’est qu’un indice de pauvreté parmi d’autres et qu’il a certaines propriétés qui ne sont pas réellement désirables lorsqu’on analyse la pauvreté. Notamment, il ne prend pas en compte la profondeur de la pauvreté et l’inégalité dans la distribution de cette profondeur de la pauvreté. Il est donc impératif d’examiner ce qui se passe avec les autres indices de la classe FGT.
La lecture du tableau 4 indique qu’au niveau de l’indice P1 (qui mesure la profondeur moyenne de la pauvreté en plus de son incidence), les États-Unis, l’Italie, l’Irlande, l’Espagne, la Grande-Bretagne et l’Australie affichent toujours une pauvreté chez les 0-17 ans plus élevée qu’au Canada et qu’au Québec. De plus, la Grèce et les Pays-Bas affichent pour cet indice une pauvreté chez les 0-17 ans plus élevée qu’au Canada et qu’au Québec. En utilisant un indice de pauvreté plus complet, le Canada et le Québec font meilleure figure qu’en utilisant simplement l’incidence de la pauvreté. Qu’en est-il maintenant si on incorpore la dimension de l’inégalité dans la distribution de la pauvreté ? En d’autres termes, qu’arrive-t-il lorsqu’on prend en considération le niveau de vie des plus pauvres d’entre les pauvres ?
Tableau 4
Comparaison internationale des indices P1 etP2 chez les 0-17 ans
|
P1 |
P2 |
États-Unis |
0,062 |
0,032 |
Italie |
0,051 |
0,026 |
Espagne |
0,045 |
0,023 |
Grande-Bretagne |
0,043 |
0,035 |
Pays-Bas |
0,040 |
0,030 |
Australie |
0,040 |
0,036 |
Irlande |
0,036 |
0,013 |
Grèce |
0,034 |
0,018 |
Canada |
0,033 |
0,015 |
Québec |
0,025 |
0,009 |
Allemagne |
0,021 |
0,008 |
Suisse |
0,018 |
0,019 |
Belgique |
0,018 |
0,009 |
Autriche |
0,017 |
0,008 |
France |
0,016 |
0,015 |
Luxembourg |
0,013 |
0,003 |
Suède |
0,012 |
0,016 |
Norvège |
0,010 |
0,011 |
Finlande |
0,006 |
0,002 |
La lecture du tableau 4 indique que le Canada et le Québec font bien meilleure figure au niveau international lorsqu’on prend en compte toutes les dimensions de la pauvreté. Dans les pays qui affichaient une pauvreté plus élevée chez les 0-17 ans pour l’indice P1 , seule l’Irlande fait mieux que le Canada concernant de la pauvreté chez les 0-17 ans mesurée par l’indice P2 (qui prend en compte l’inégalité dans la distribution de la profondeur de la pauvreté en plus de l’incidence et de la profondeur elle-même). Par contre, le Québec fait encore mieux que l’Irlande quant à l’indice P2 chez les 0-17 ans. Le Canada a aussi une pauvreté moins élevée chez les 0-17 ans que la Suisse et la Suède. En plus de ces deux pays, le Québec a une pauvreté chez les 0-17 ans moins élevée que la France et la Norvège. La situation au Québec est maintenant comparable à celle de la Belgique. En résumé, si on tient compte des trois dimensions de la pauvreté que sont l’incidence, la profondeur et l’inégalité, il y a moins de pauvreté chez les 0-17 ans au Québec qu’en Australie, qu’en Grande-Bretagne, qu’aux États-Unis, qu’aux Pays-Bas, qu’en Italie, qu’en Espagne, qu’en Suisse, qu’en Grèce, qu’en Suède, qu’en France, qu’en Irlande et qu’en Norvège. La pauvreté chez les 0-17 ans en Belgique est comparable à celle des 0-17 ans au Québec. Il y a plus de pauvreté chez les 0-17 ans au Québec, qu’en Allemagne, qu’en Autriche, qu’au Luxembourg et qu’en Finlande.
Impact des politiques publiques
Cette section présente une analyse de l’impact des politiques de soutien du revenu sur la pauvreté. Comme nous l’avons expliqué dans la seconde section de cet article, l’indice de pauvreté P2 constitue l’indice de pauvreté le plus complet parmi ceux mentionnés puisqu’il prend en compte simultanément l’incidence de la pauvreté, la profondeur moyenne de celle-ci et l’inégalité dans la distribution de cette profondeur de la pauvreté. Nous avons donc calculé les élasticités de P2 par rapport aux différentes politiques de transferts, pour le Québec et l’ensemble du Canada et ceci pour la population totale, pour le groupe des 0-17 ans et pour le sous-groupe des 0-17 ans vivant avec une mère monoparentale.
Le tableau 5 présente l’élasticité de l’indice P2 aux différentes catégories de programmes de transferts au Québec et au Canada. On constate que pour l’ensemble du Canada c’est une augmentation des prestations familiales qui ferait le plus diminuer la pauvreté dans la population tandis qu’au Québec ce serait une augmentation des prestations d’aide sociale qui ferait le plus diminuer la pauvreté totale. Tournons-nous maintenant vers l’impact de ces mêmes politiques sur les 0-17 ans. La lecture du tableau 5 indique que, tant pour le Canada que pour le Québec, une augmentation des prestations familiales serait la politique qui ferait diminuer le plus la pauvreté chez les 0-17 ans. Une augmentation de 1 % de ces prestations ferait diminuer la pauvreté chez les 0-17 ans de 1,063 % au Canada et de 1,252 % au Québec. Une augmentation de 1 % des prestations d’aide sociale permettrait de faire diminuer la pauvreté des 0-17 ans de 0,831 % au Québec et de 0,428 % au Canada. La lecture du tableau donne le même type de résultats pour l’impact des politiques publiques sur la pauvreté des 0-17 ans vivant avec des mères monoparentales. Une augmentation de 1 % des prestations familiales ferait diminuer la pauvreté chez les 0-17 ans vivant avec des mères monoparentales de 1,156 % au Canada et de 1,405 % au Québec. Une augmentation de 1 % des prestations d’aide sociale permettrait de faire diminuer la pauvreté des 0-17 ans vivant avec des mères monoparentales de 0,973 % au Québec et de 0,679 % au Canada.
Tableau 5
Élasticité de la pauvreté (P2) de différents programmes de transferts au Québec et au Canada selon différents groupements
Population totale
Programmes |
Québec |
Canada |
Sécurité de vieillesse |
0,04 |
0,041 |
Régime d’assurance-chômage |
0,058 |
0,038 |
RPC et RRQ |
0,061 |
0,112 |
Prestations familiales |
0,294 |
0,371 |
Aide sociale |
0,55 |
0,298 |
0-17 ans
Programmes |
Québec |
Canada |
Sécurité de vieillesse |
0 |
0,012 |
Régime d’assurance-chômage |
0,092 |
0,054 |
RPC et RRQ |
0,005 |
0,036 |
Prestations familiales |
1,252 |
1,063 |
Aide sociale |
0,831 |
0,428 |
0-17 ans vivant avec une mère monoparentale
Programmes |
Québec |
Canada |
Sécurité de vieillesse |
0 |
0,004 |
Régime d’assurance-chômage |
0,031 |
0,042 |
RPC et RRQ |
0,007 |
0,027 |
Prestations familiales |
1,405 |
1,156 |
Aide sociale |
0,973 |
0,679 |
En conclusion, si l’objectif du décideur public est de faire diminuer la pauvreté au Québec, que ce soit pour la population en général ou pour les 0-17 ans en particulier, une augmentation des prestations familiales et des prestations d’aide sociale serait l’option à privilégier. Ce résultat est important si on considère le fait que Audet et Makdissi (2007) montrent que la seule non-indexation des prestations d’aide sociale durant les années 1990 a eu pour conséquence que l’indice de pauvreté P2 observé chez les 0-17 ans vivant dans des familles biparentales est de 21,5 % plus élevé que s’il y avait eu simple indexation. Pour les 0-17 ans vivant avec des mères monoparentales, Audet et Makdissi (2007) montrent que cette non-indexation des prestations d’aide sociale entraîne un indice P2 de 10,6 % plus élevé.
⁂
Dans cet article, nous avons montré que la pauvreté chez les 0-17 ans au Québec se compare avantageusement au niveau de pauvreté observé ailleurs au Canada ou dans le monde. Si nous désirons nous comparer avec les pays qui affichent une meilleure performance que nous à ce chapitre, l’Autriche, l’Allemagne, la Belgique, le Luxembourg et la Finlande seraient des exemples à analyser plus en profondeur. La Finlande est le pays affichant les niveaux de pauvreté les moins élevés pour les 0-17 ans.
Nous avons aussi analysé l’impact des politiques publiques sur la pauvreté. Une conclusion claire émerge : si le décideur public désire faire diminuer la pauvreté, c’est à travers une augmentation des prestations familiales et des prestations d’aide sociale qu’il y parviendra le mieux. Il convient tout de même de souligner l’effort récent du gouvernement du Québec en matière de lutte à la pauvreté chez les 0-17 ans. Celui-ci a significativement augmenté son aide financière directe aux parents avec la mise en place du programme de Soutien aux enfants en janvier 2005 et a augmenté le revenu des prestataires du Programme d’assistance-emploi grâce à l’indexation de l’aide sociale à compter de janvier 2004 (voir Gouvernement du Québec, 2004). Cela va exactement dans le sens des recommandations qui émergent de cet article. Il serait donc intéressant d’effectuer une analyse ex-post des changements survenus lorsque les données seront disponibles.
Parties annexes
Notes biographiques
Paul Makdissi
Paul Makdissi est professeur titulaire de science économique à l’Université d’Ottawa depuis 2007. Auparavant, il a occupé des postes à l’Université de Sherbrooke et à la Vrije Universiteit, Amsterdam. Ses champs principaux de recherche sont la distribution du revenu et la politique fiscale. Il a publié plus de 40 articles dans des revues telles que International Economic Review, Social Choice and Welfare, Journal of Development Economics et Journal of Public Economic Theory.
Mathieu Audet
Mathieu Audet est analyste en recherche à Ressources humaines et Développement des compétences Canada depuis 2007. Auparavant il a occupé des postes au Groupe de recherche en économie et développement internationale de l'Université de Sherbrooke et à la Banque Mondiale. Il a publié ses travaux dans plusieurs revues telles que Review of Income and Wealth, Applied Economics Letters, Journal of Development and Economic Policies, Interventions économiques et Revista Perspectivas Sociales/Social Perspectives.
Notes
-
[1]
Les auteurs ont bénéficié d’une subvention de recherche du ministère de la Santé et des Services sociaux du Québec. La contribution de Mathieu Audet dans le cadre de ce projet de recherche a été effectuée alors que celui-ci était professionnel de recherche dans l’équipe du professeur Makdissi à l’Université de Sherbrooke. Les opinions exprimées dans ce rapport sont celles des auteurs et ne représentent pas nécessairement celles de Ressources humaines et Développement social Canada.
-
[2]
Les contraintes de liquidité indiquent qu’un ménage n’a pas accès à son épargne ou à du crédit pour faire face aux aléas qui peuvent survenir.
-
[3]
Le lecteur désirant un bon survol peut consulter Arnsperger et Van Parijs (2000).
-
[4]
Le terme « capabilité » est introduit par Sophie Marnat, traductrice de Sen (1993).
-
[5]
La distribution cumulative de revenu pour un groupe démographique est une fonction mathématique qui donne, pour chaque niveau de revenu possible, la proportion de personnes ayant un revenu inférieur à ce niveau.
-
[6]
Le lecteur intéressé peut consulter Duclos et Makdissi (2004).
-
[7]
L’étude de Makdissi et Groleau portait sur des données de 1997.
- [8]
Bibliographie
- Arnsperger, C. et p. Van Parijs, 2000 Éthique économique et sociale, La Découverte, Paris.
- Atkinson, A.B., 1987 « On the measurement of poverty », Econometrica, 55 : 759-764.
- Audet, Mathieu et Paul Makdissi, 2007 « Assessing the impact of historical changes in social protection on poverty in Canada », à paraître dans Applied Economics Letters.
- Bourdieu, Pierre, 1970 La distinction, Éditions de Minuit, Paris.
- Buhman, B., Lee Rainwater, G. Schmaus et Thimoty M. Smeeding, 1987 « Equivalence scales, well-being, inequality, and poverty : Sensitivity estimates across ten countries using the Luxembourg income study (LIS) database », Review of Income and Wealth, 34 : 115-142.
- Case, A., D. Lubotsky et C. Paxson, 2002 « Economic status and health in childhood : The origins of the gradient », American Economic Review, 92 : 1308-1334.
- Christofides, L.N., J. Cirello et M. Hoy, 2001 « Family income and post-secondary education in Canada », The Canadian Journal of Higher Education / La revue canadienne d’enseignement supérieur, 31 : 177-208.
- Clark, B.R., 1960 « The Cooling-out function in higher education », American Journal of Sociology, 65 : 569-576.
- Conley, D., 2001 « Capital for college : Parental assets and postsecondary schooling », Sociology of Education, 74 : 59-72.
- Conseil supérieur de l’éducation, 2004 « L’accessibilité financière à la réussite du projet d’études », Avis du comité consultatif sur l’accessibilité financière aux études », Québec, Conseil supérieur de l’éducation.
- Currie A., M. Shields et p. Wheatley Price, 2007 « The child health/family income gradient : Evidence from England », Journal of Health Economics, 26 : 213-232.
- Currie, J. et M. Stabile, 2003 « Socioeconomic status and child health : Why is the relationship stronger for older children ? », American Economic Review, 93 : 1813-1823.
- Duclos, Jean-Yves et Paul Makdissi, 2004 « Restricted and unrestricted dominance for welfare, inequality and poverty orderings », Journal of Public Economic Theory, 6, 1 : 145-164.
- Foster, J.E., J. Greer et E. Thorbecke, 1984 « A class of decomposable poverty measures », Econometrica, 52, 3 : 761-776.
- Föster, M.F., 2000 Trends and Driving Factors in Income Distribution and Poverty in the OECD Area, Organisation for Economic Cooperation and Development.
- Gouvernement du Québec, 2004 Concilier liberté et justice sociale : un défi pour l’avenir. Plan d’action gouvernemental en matière de lutte contre la pauvreté et l’exclusion sociale, Ministère de l’Emploi et de la Solidarité sociale.
- Hutchings, M. et L. Archer, 2001 « Higher than Einstein : Construction of going to University among working-class non-participants », Research Papers in Education, 16 : 69-91.
- Makdissi, Paul et Y. Groleau, 2002 « Que pouvons-nous apprendre des profils de pauvreté canadiens ? », Actualité économique - Revue d’analyse économique, 78, 2 : 257-286.
- Makdissi, Paul, Y. Therrien et Q. Wodon, 2006 « L’impact des transferts publics et des taxes sur la pauvreté au Canada et aux États-Unis », Actualité économique - Revue d’analyse économique, 82 : 377-394.
- Nahum, R.A., 2007 « Child health and family income : Physical and psychosocial health », Rapport de recherche, Institute for Future Studies.
- Paquet, Ginette, 2005 Partir au bas de l’échelle. Des pistes pour atteindre l’égalité sociale en matière de santé, Presses de l’Université de Montréal.
- Ravallion, M., 1996 Comparaisons de la pauvreté. Concepts et méthodes, Études sur la mesure des niveaux de vie, Document de travail n° 122, Banque Mondiale, Washington.
- Rawls, John, 1971 A Theory of Justice, Cambridge (Mass.), Harvard University Press.
- Sen, A., 1976 « Poverty : An ordinal approach to measurement », Econometrica, 44, 2 : 219-231.
- 1992 Inequality Reexamined, Cambridge (Mass.), Harvard University Press., 1993 Éthique et économie, Presses Universitaires de France.
- Willis, P., 1981 Learning to Labor. How Working Class Kids get Working Class Jobs, New York, Columbia University Press.
Liste des figures
Figure 1
Implication du choix épistémologique sur la sélection du seuil de pauvreté
Graphique 1
Tests de dominance stochastique entre les types de familles au Québec, 2000
Graphique 2
Tests de dominance stochastique entre les types de familles au Canada, 2000
Graphique 3
Tests de dominance stochastique pour les 0-17 ans entre les différentes provinces au Canada, 2000
Graphique 4
Trois indices de pauvreté P0 , P1 et P2 chez les 0-17 ans par type de famille au Québec
Graphique 6
Tests de dominance stochastique entre les familles ayant des enfants de 0 à 5 ans selon leur région de résidence au Canada
Figure 9
Comparaison internationale de l’incidence de la pauvreté chez les 0-17 ans
Liste des tableaux
Tableau 1
Taux de pauvreté P0 , P1 et P2 chez les 0-17 ans par province canadienne, 2000
|
P0 |
P1 |
P2 |
Colombie-Britannique |
0,2683 |
0,0746 |
0,0341 |
Terre-Neuve |
0,1981 |
0,0508 |
0,0192 |
Nouvelle-Écosse |
0,1803 |
0,0469 |
0,0187 |
Nouveau-Brunswick |
0,1428 |
0,0306 |
0,0094 |
Île-du-Prince-Édouard |
0,1419 |
0,0348 |
0,0145 |
Canada |
0,1376 |
0,0368 |
0,0161 |
Manitoba |
0,1355 |
0,0334 |
0,0157 |
Ontario |
0,1293 |
0,0358 |
0,0165 |
Saskatchewan |
0,116 |
0,0225 |
0,0081 |
Alberta |
0,1069 |
0,0349 |
0,0186 |
Québec |
0,0925 |
0,0204 |
0,0061 |
Tableau 2
Taux de pauvreté P0 , P1 et P2 chez les 0-5 ans par province canadienne, 2000
|
P0 |
P1 |
P2 |
Colombie-Britannique |
0,3373 |
0,0843 |
0,0352 |
Terre-Neuve |
0,242 |
0,0672 |
0,0253 |
Nouvelle-Écosse |
0,2085 |
0,0528 |
0,0196 |
Nouveau-Brunswick |
0,157 |
0,0259 |
0,0079 |
Île-du-Prince-Édouard |
0,1829 |
0,0539 |
0,0254 |
Canada |
0,1691 |
0,0433 |
0,0179 |
Manitoba |
0,2127 |
0,0437 |
0,0173 |
Ontario |
0,148 |
0,0427 |
0,0194 |
Saskatchewan |
0,1567 |
0,0274 |
0,008 |
Alberta |
0,1293 |
0,0404 |
0,0191 |
Québec |
0,1168 |
0,0224 |
0,0059 |
Tableau 3
Calcul du facteur d’ajustement automatique pour le Canada
|
P0 |
P1 |
P2 |
LIS |
0,129 |
0,033 |
0,015 |
EDTR |
0,137 |
0,036 |
0,016 |
Facteur d’ajustement |
0,942 |
0,917 |
0,938 |
Tableau 4
Comparaison internationale des indices P1 etP2 chez les 0-17 ans
|
P1 |
P2 |
États-Unis |
0,062 |
0,032 |
Italie |
0,051 |
0,026 |
Espagne |
0,045 |
0,023 |
Grande-Bretagne |
0,043 |
0,035 |
Pays-Bas |
0,040 |
0,030 |
Australie |
0,040 |
0,036 |
Irlande |
0,036 |
0,013 |
Grèce |
0,034 |
0,018 |
Canada |
0,033 |
0,015 |
Québec |
0,025 |
0,009 |
Allemagne |
0,021 |
0,008 |
Suisse |
0,018 |
0,019 |
Belgique |
0,018 |
0,009 |
Autriche |
0,017 |
0,008 |
France |
0,016 |
0,015 |
Luxembourg |
0,013 |
0,003 |
Suède |
0,012 |
0,016 |
Norvège |
0,010 |
0,011 |
Finlande |
0,006 |
0,002 |
Tableau 5
Élasticité de la pauvreté (P2) de différents programmes de transferts au Québec et au Canada selon différents groupements
Population totale
Programmes |
Québec |
Canada |
Sécurité de vieillesse |
0,04 |
0,041 |
Régime d’assurance-chômage |
0,058 |
0,038 |
RPC et RRQ |
0,061 |
0,112 |
Prestations familiales |
0,294 |
0,371 |
Aide sociale |
0,55 |
0,298 |
0-17 ans
Programmes |
Québec |
Canada |
Sécurité de vieillesse |
0 |
0,012 |
Régime d’assurance-chômage |
0,092 |
0,054 |
RPC et RRQ |
0,005 |
0,036 |
Prestations familiales |
1,252 |
1,063 |
Aide sociale |
0,831 |
0,428 |
0-17 ans vivant avec une mère monoparentale
Programmes |
Québec |
Canada |
Sécurité de vieillesse |
0 |
0,004 |
Régime d’assurance-chômage |
0,031 |
0,042 |
RPC et RRQ |
0,007 |
0,027 |
Prestations familiales |
1,405 |
1,156 |
Aide sociale |
0,973 |
0,679 |







 10.7202/007253ar
10.7202/007253ar