Résumés
Résumé
Dans une étude antérieure (Vohl & Loye, 2024), nous avons montré qu’en moyenne, les filles québécoises francophones de 15 ans se disent davantage anxieuses à l’égard des mathématiques que les garçons et ce, sur l’ensemble du continuum des performances. Nous avons également montré que performances en mathématique et anxiété mathématique sont deux phénomènes négativement corrélés. Dans le présent article, nous souhaitons identifier des facteurs qui pourraient permettre d’expliquer les écarts d’anxiété mathématique observés entre les filles et les garçons. En prenant appui sur le modèle du contrôle et de la valeur de Pekrun (2006), nous vérifions si les écarts de concept de soi, de valeur intrinsèque et de valeur utilitaire observés entre les filles et les garçons expliquent complètement les écarts d’anxiété mathématique. Nos résultats révèlent que les écarts de concept de soi expliquent près de 70 % des écarts d’anxiété mathématique relevés chez les élèves francophones du Québec.
Mots-clés :
- anxiété mathématique,
- concept de soi en mathématiques,
- valeur intrinsèque des mathématiques,
- valeur utilitaire des mathématiques,
- PISA
Abstract
In a previous study (Vohl & Loye, 2024), we showed that, on average, 15-year-old French-speaking Quebec girls are more anxious about mathematics than French-speaking Quebec boys across the performance continuum. We also showed that performances in mathematics and mathematical anxiety are two negatively correlated phenomena. In this article, we wish to identify factors that could explain the differences in mathematical anxiety observed between girls and boys and that would have the potential, eventually, to reduce the observed differences. Based on the Pekrun (2006) Model of Control and Value for Academic Emotions, we verify whether differences in self-concept, intrinsic value and utilitary value observed between girls and boys completely explain the differences in mathematical anxiety. Our results show that differences in self-concept explain nearly 70% of the differences in mathematical anxiety observed among francophone students in Quebec.
Keywords:
- mathematical anxiety,
- self-concept in mathematics,
- intrinsic value of mathematics,
- utilitary value of mathematics,
- PISA
Resumo
Num estudo anterior (Vohl & Loye, 2024), mostramos que, em média, as raparigas francófonas do Quebec de 15 anos se sentem mais ansiosas em relação à matemática do que os rapazes e em todo o contínuo das performances. Mostramos também que o desempenho em matemática e a ansiedade matemática são dois fenómenos negativamente correlacionados. No presente artigo, pretendemos identificar fatores que possam explicar as diferenças de ansiedade matemática observadas entre raparigas e rapazes. Baseando-nos no modelo de controlo e valor de Pekrun (2006), procuramos verificar se as diferenças de autoconceito, valor intrínseco e valor utilitário observadas entre raparigas e rapazes explicam completamente as diferenças de ansiedade matemática. Os nossos resultados revelam que as diferenças de autoconceito explicam cerca de 70% das diferenças de ansiedade matemática observadas entre os alunos francófonos do Quebec.
Palavras chaves:
- ansiedade matemátic,
- autoconceito em matemática,
- valor intrínseco da matemática,
- valor utilitário da matemática,
- PISA
Corps de l’article
Problématique
Les mathématiques constituent l’un des fondements de notre société hautement technologique. De ce fait, bien performer dans le domaine constitue un atout de taille. À preuve, des études longitudinales montrent que les performances en mathématiques sont liées positivement à la probabilité d’obtenir un diplôme au secondaire, de réussir la transition vers les études supérieures, puis d’obtenir un diplôme post-secondaire (Chiu & Klassen, 2010 ; Ma, 1999 ; OCDE, 2014a ; Parsons & Bynner, 2005 ; Stokke, 2015). D’autres études révèlent que ces mêmes performances permettent de prédire le niveau d’employabilité des personnes ainsi que leurs revenus professionnels éventuels (p. ex., Fonseca et al., 2021 - pour des résultats empiriques québécois ; Joensen & Nielsen, 2009 ; Ma, 1999 ; Parsons & Bynner, 2005).
Dans ce contexte, il apparaît prioritaire, pour les systèmes éducatifs, de veiller à ce que chaque apprenant performe à la hauteur de ses capacités, en mathématiques (OCDE, 2014b). Heureusement, les résultats des grandes enquêtes internationales en éducation, comme TIMSS[1] et PISA[2], révèlent qu’en la matière, le système québécois réussit plutôt bien. En effet, à chacun des cycles de l’enquête PISA, par exemple, les élèves québécois de 15 ans se sont classés dans les premiers rangs, à l’international. De surcroît, à toutes ces occasions, ils se sont hissés en tête des provinces canadiennes (sauf en 2003 : à ce cycle, l’Alberta et la Colombie-Britannique ont devancé le Québec) (Bussière et al., 2004). Les analyses selon le genre, elles, font toutefois état de disparités qui méritent une attention particulière, au vu des enjeux évoqués ci-haut. En effet, les résultats du TIMSS et du PISA ont montré, à plusieurs reprises depuis le début des années 2000, des différences statistiquement significatives entre les scores moyens des garçons et ceux des filles, à l’avantage des garçons. Les résultats du PISA de 2003, de 2012 et de 2018 ont de plus révélé que, toute proportion gardée, les filles québécoises sont moins nombreuses que les garçons à se hisser dans les premiers rangs[3] (Brochu et al., 2013 ; Mullis et al., 2016 ; OCDE, 2014a ; OCDE, 2016 ; O’Grady et al., 2016, 2019).
Préoccupées par ces écarts de performances selon le genre, dans un article précédent (Vohl & Loye, 2024), nous avons voulu vérifier si l’anxiété mathématique, un concept défini comme « une sensation de tension et d’anxiété qui interfère avec la manipulation des nombres et la résolution de problèmes mathématiques dans une grande diversité de situations de la vie courante et de situations académiques [traduction libre] » (Richardson & Suinn, 1972, p. 551), pourrait être un phénomène qui contribue aux différences observées entre les performances des garçons et celles des filles, en mathématiques, comme le stipulent notamment Stoet et al. (2016). Les résultats obtenus nous permettent de soutenir cette hypothèse.
En effet, en analysant de manière secondaire les données des élèves québécois francophones[4] de 15 ans ayant participé au PISA de 2003 et de 2012, nous avons montré notamment les deux éléments suivants : 1) en moyenne, les filles québécoises francophones de 15 ans se disent davantage anxieuses à l’égard des mathématiques que les garçons québécois francophones et ce, sur l’ensemble du continuum des performances et 2) les performances en mathématique et l’anxiété mathématique sont deux phénomènes négativement corrélés. Ainsi, les élèves québécois francophones qui se disent plus anxieux vis-à-vis des mathématiques tendent à réussir moins bien en mathématiques, en moyenne, que ceux qui se disent moins anxieux. Ces deux éléments sont d’ailleurs en adéquation avec les tendances générales relevées par le PISA de 2003 et de 2012 quant aux liens entre le genre, l’anxiété mathématique et les performances en mathématiques. En effet, en 2003 et en 2012, dans l’ensemble des pays de l’OCDE participants, les filles se sont dites davantage anxieuses à l’égard des mathématiques que les garçons, en moyenne (OCDE, 2014b). Également, les analyses réalisées par l’OCDE en 2003 et en 2012 ont fait état de corrélations respectives de -0,37 et de -0,39, entre l’anxiété mathématique et les performances en mathématiques, dans les pays de l’OCDE (OCDE, 2014b).
Dans le présent article, nous souhaitons poursuivre le travail amorcé dans l’article de Vohl et Loye (2024). De manière plus précise, nous désirons identifier des facteurs qui pourraient expliquer les écarts d’anxiété mathématique observés entre les garçons et les filles francophones au Québec, en vue d’envisager, éventuellement, la mise en oeuvre de stratégies d’intervention permettant de réduire ces écarts. De ce fait, nous énonçons la question générale du présent article comme suit : quels sont les facteurs qui permettent d’expliquer la disparité d’anxiété mathématique observée, selon le genre, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012, et qui auraient éventuellement le potentiel de réduire ces écarts ?
Cadre théorique
Depuis le début des années 2000, trois hypothèses ont été proposées afin d’expliquer le lien négatif anxiété mathématique/performances en mathématiques. Comme les facteurs mis en cause pour expliquer les écarts d’anxiété mathématique selon le genre sont des facteurs qui gravitent autour de ces trois hypothèses, à la section suivante, nous présentons ces trois hypothèses. Puis, nous présentons un modèle théorique, appelé modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006), qui comporte notamment comme avantages d’intégrer les trois hypothèses explicatives du lien négatif anxiété mathématique/performances, de proposer une piste principale pour expliquer la disparité d’anxiété mathématique selon le genre, puis d’intégrer l’ensemble des autres facteurs évoqués à ce jour pour expliquer la disparité d’anxiété mathématique selon le genre.
Les trois hypothèses explicatives du lien négatif anxiété mathématique/performances
La première hypothèse explicative du lien négatif anxiété mathématique/performances en mathématiques a été proposée par Ashcraft et Kirk (2001). Il s’agit de l’hypothèse de l’interférence (traduction libre de disruption account, Ramirez et al., 2018, p. 146). Selon Ashcraft et Kirk (2001), c’est l’anxiété mathématique (la cause) qui nuirait aux performances (la conséquence). Pour ce faire, la mémoire de travail, un système cognitif lié à la mémoire à court terme, responsable de la gestion des informations nécessaires à la résolution de tâches mathématiques (inhibition des informations non pertinentes et emmagasinage des informations pertinentes) (Baddeley, 1992 ; Baddeley & Hitch, 1974 ; Beilock & Carr, 2005 ; Geary & Widaman, 1992 ; Miyake & Shah, 1999 ; Raghubar et al., 2010) entrerait en jeu. En effet, l’anxiété mathématique engendrerait des ruminations et des pensées négatives qui, en consommant une partie des ressources limitées de la mémoire de travail, nuirait aux performances en mathématiques.
En outre, les manifestations physiques désagréables du phénomène (augmentation du rythme cardiaque, sudation, tremblements, etc.) pousseraient les personnes qui se disent anxieuses à l’égard des mathématiques à éviter les situations mathématiques. Pour elles, éviter les mathématiques serait aussi naturel que de chercher à éviter une douleur (OCDE, 2014b). En agissant de la sorte, elles se priveraient d’un certain nombre d’occasions d’apprentissage. L’évitement contribuerait donc également à expliquer le lien négatif anxiété mathématique/performances en mathématiques, selon Ashcraft et Kirk (2001).
La seconde hypothèse explicative du lien négatif anxiété mathématique/performances a été proposée entre autres par Maloney et al. (Ferguson et al., 2015 ; Maloney, 2016 ; Maloney et al., 2010 ; Maloney et al., 2011 ; Maloney et al., 2012). Il s’agit de l’hypothèse du déficit (traduction libre de reduced competency account, Ramirez et al., 2018, p. 146). Selon ces auteurs, l’anxiété mathématique émanerait d’un déficit au niveau de trois habiletés élémentaires en mathématiques que sont l’habileté à dénombrer des objets, l’habileté à ordonner des nombres et l’habileté spatiale. Comme ces habiletés sont considérées essentielles au bon développement d’habiletés mathématiques de haut niveau, leur déficit engendrerait, dès l’enfance, de moins bonnes performances en mathématiques (la cause), ce qui déclencherait l’anxiété mathématique (la conséquence).
La troisième hypothèse explicative du lien négatif anxiété mathématique/performances en mathématiques a été proposée par Ramirez et al. (2018). Il s’agit de l’hypothèse de l’interprétation (traduction libre de interpretation account, Ramirez et al., 2018, p. 151). Celle-ci découle de la théorie de l’évaluation cognitive (appraisal theory) pour la genèse des émotions (Arnold, 1950 ; Barrett, 2006 ; Lazarus, 1991 ; Schacter et Singer, 1962, cités dans Ramirez et al., 2018, p. 151) et de la théorie des attitudes construites (attitude-as-constructions view) (Bem, 1972 ; Chaiken et Yates, 1985 ; Wilson et al., 2000, cités dans Ramirez et al., 2018, p. 151). Ces deux théories définissent les émotions/attitudes comme la résultante d’une interprétation : l’interprétation des événements vécus. Ainsi, selon l’hypothèse de l’interprétation, l’anxiété mathématique découlerait davantage de la manière dont la personne interprète ses expériences d’apprentissage présentes et passées en mathématiques, de même que les résultats de ces apprentissages, plutôt que des expériences et des résultats, eux-mêmes. Des interprétations négatives, inadaptées ou irréalistes engendreraient l’anxiété mathématique.
La majorité des résultats empiriques proposés par Ramirez et al. (2018) afin de soutenir l’hypothèse de l’interprétation font état de liens entre l’anxiété mathématique, les performances en mathématiques et diverses perceptions de l’apprenant telles que la perception de ses compétences en mathématiques, opérationnalisée, notamment, par le sentiment d’efficacité personnelle (self-efficacy) de Bandura (1977, 1997, 2003) et le concept de soi en mathématiques (self-concept) (p. ex., Marsh et al., 1988 ; Marsh & Hau, 2004 ; Marsh & Yeung, 1998 ; Martin & Marsh, 2008), puis la perception de la valeur des mathématiques, opérationnalisée, notamment, par la valeur intrinsèque et par la valeur utilitaire des mathématiques (Ryan & Deci, 2009 ; Viau, 2009 ; Wigfield & Eccles, 2000). Les concepts de sentiment d’efficacité personnelle, de concept de soi en mathématiques, de valeur intrinsèque et de valeur utilitaire sont définis dans ce qui suit.
Pour Bandura, le concept de sentiment d’efficacité personnelle se rapporte à « la croyance de l’individu en sa capacité d’organiser et d’exécuter la ligne de conduite requise pour produire des résultats souhaités » (Bandura, 2003, p. 12). Le concept est vu comme « un motivateur puissant, qui incite à agir et à persévérer en cas de difficultés » (OCDE, 2014b, p. 91). Selon Bandura (2003), quatre sources influencent le sentiment d’efficacité personnelle d’une personne : « les expériences actives de maîtrise qui servent d’indicateur de capacités ; les expériences vicariantes qui modifient les croyances de capacités par la transmission de compétences et la comparaison avec ce que font les autres ; la persuasion verbale et des formes proches d’influence sociale » (Berger, 2015, p. 67), et enfin, les états physiologiques et émotionnels ressentis.
Marsh et al. (1988) et Shavelson et al. (1976) décrivent le concept de soi comme la confiance de la personne en ses capacités (OCDE, 2014b). Tout comme le sentiment d’efficacité personnelle, le concept de soi est fortement corrélée aux performances dans un domaine (Marsh et al., 1985a, 1985c ; Marsh & Shavelson, 1985b). Les sources principales du phénomène sont les évaluations fournies par les personnes significatives (les parents, les enseignants), les attributions causales (la manière dont la personne s’explique ses succès/échecs), la comparaison avec les pairs et enfin, la comparaison des performances entre divers domaines d’étude (Marsh & Scalas, 2011).
La valeur intrinsèque et la valeur utilitaire font toutes deux référence au jugement de la valeur d’un domaine ou d’une activité dans un domaine donné (Viau, 2009 ; Wigfield & Eccles, 2000). La valeur intrinsèque se rapporte au plaisir qu’une personne retire de l’accomplissement d’une tâche (Berger, 2015 ; Viau, 2009 ; Wigfield & Eccles, 2000) ou à « l’envie de mener à bien une activité pour le simple plaisir qu’elle procure » (OCDE, 2014b, p. 75). La valeur utilitaire, pour sa part, fait référence aux avantages qu’une personne retire de l’accomplissement d’une activité (Viau, 2009) et « à sa fonction pour le futur » (Berger, 2015, p. 71), dans sa vie académique, professionnelle et/ou personnelle (Wigfield & Eccles, 2000). La valeur intrinsèque s’apparente au concept de motivation intrinsèque de la théorie de l’autodétermination (Ryan & Deci, 2009) et à celui d’intérêt (Hidi & Renninger, 2006). La valeur utilitaire s’apparente au concept de motivation extrinsèque de la théorie de l’autodétermination de Ryan et Deci (2009).
Dans ce qui suit, nous présentons le modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006), tout en mentionnant de quelle manière l’hypothèse de l’interférence, l’hypothèse du déficit et l’hypothèse de l’interprétation s’y intègrent.
Le modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006)
Le modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006) place le concept d’anxiété mathématique au sein d’un groupe de 15 émotions reconnues pour être ressenties spécifiquement en contexte académique. Ces 15 émotions, appelées émotions académiques, peuvent être divisées en trois catégories : 1) les émotions liées à une activité d’apprentissage en cours (plaisir, rage, frustration, ennui), 2) les émotions liées aux résultats anticipés d’une activité d’apprentissage (anxiété, joie anticipatoire, espoir, désespoir, soulagement anticipatoire) et 3) les émotions liées aux résultats passés d’une activité d’apprentissage (joie, fierté, gratitude, tristesse, honte, rage) (Pekrun, 2006).
Le postulat de base du modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006) est le suivant : les émotions académiques résultent, d’abord et avant tout, d’une évaluation cognitive de contrôle et de valeur – le contrôle que la personne croit pouvoir exercer sur l’activité et sur ses résultats, puis la valeur de l’activité et de ses résultats. Selon Pekrun (2016), le concept de soi permet de témoigner de l’évaluation cognitive de contrôle, alors que la valeur intrinsèque et la valeur utilitaire permettent de témoigner de l’évaluation cognitive de la valeur. Ce postulat de base permet donc d’établir le parallèle avec l’hypothèse de l’interprétation, lorsque l’émotion d’intérêt est l’anxiété mathématique, en privilégiant toutefois le concept de soi seul plutôt qu’à la fois le sentiment d’efficacité personnelle et le concept de soi, en regard de la perception de compétences.
Le modèle du contrôle et de la valeur de Pekrun (2006) est composé de quatre sphères principales qui interagissent entre elles : 1) l’environnement d’apprentissage, 2) l’évaluation cognitive du contrôle et de la valeur, 3) les émotions académiques et enfin, 4) l’apprentissage/la réussite/les performances où l’apprentissage fait référence aux ressources cognitives, aux stratégies employées, à l’engagement/évitement, alors que les performances se rapportent aux résultats issus de l’évaluation des apprentissages. À ces quatre sphères s’ajoutent les prédispositions individuelles affectives (p. ex., la génétique et le tempérament) et les prédispositions individuelles cognitives (p. ex., l’intelligence et les habiletés).
Pekrun (2006) propose une série de liens entre les diverses sphères du modèle (voir la figure 1) Ces liens sont les suivants :
-
l’évaluation cognitive du contrôle et de la valeur engendre les émotions académiques – le postulat de base du modèle (lien 1) (qui permet, avec les liens 2 et 3 qui suivent, de faire le parallèle avec l’hypothèse de l’interprétation) ;
-
l’apprentissage/la réussite/les performances influencent l’évaluation cognitive du contrôle et de la valeur (lien 2) ;
-
l’environnement d’apprentissage, notamment l’interaction entre l’apprenant, ses pairs, ses enseignants et ses parents, influence l’évaluation cognitive du contrôle et de la valeur (lien 3) ;
-
les émotions académiques agissent sur les ressources cognitives (dont la mémoire de travail), sur le choix des stratégies d’apprentissage (flexibles ou rigides), sur l’engagement/l’évitement, ce qui a un impact sur la réussite/les performances (lien 4) (ce qui permet de faire le parallèle avec l’hypothèse de l’interférence) ;
-
les prédispositions individuelles cognitives (p. ex., l’intelligence et les habiletés) influencent l’apprentissage/la réussite/les performances (lien 5) (ce qui, en combinaison avec le lien 7, permet de faire le parallèle avec l’hypothèse du déficit) ;
-
les prédispositions individuelles affectives (p. ex., la génétique et le tempérament) influencent les émotions académiques (lien 6) ;
-
l’apprentissage/la réussite/les performances influencent les émotions (lien 7) et enfin,
-
l’apprentissage/la réussite/les performances influencent l’environnement (lien 8).
En s’appuyant sur les travaux de Meece et al. (1990) et de Seegers et Boekaerts (1996), Pekrun (2006) suppose que l’ensemble des liens énoncés ci-haut sont invariants, selon le genre et selon la culture. Autrement dit, selon Pekrun, il n’y a pas d’effet de modération attendu des liens proposés, par le genre et par la culture.
Dans ce qui suit, nous présentons la piste, proposée par le modèle du contrôle et de la valeur de Pekrun (2006), afin d’expliquer la disparité d’anxiété mathématique selon le genre.
La piste permettant d’expliquer la disparité d’anxiété mathématique entre les garçons et les filles, selon le modèle du contrôle et de la valeur de Pekrun (2006)
Selon le modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006), le genre influencerait directement l’évaluation cognitive du contrôle et de la valeur (lien 9, figure 1) et, à son tour, l’évaluation cognitive engendrerait les émotions académiques : l’anxiété mathématique, dans le cas qui nous occupe. Ainsi, la relation entre le genre et l’anxiété mathématique serait médiée par l’évaluation cognitive faite par l’apprenant, opérationnalisée par le concept de soi, la valeur intrinsèque et la valeur utilitaire.
Comme les liens entre le concept de soi, la valeur intrinsèque, la valeur utilitaire et l’anxiété mathématique sont présumés invariants selon le genre, si la médiation est complète, la disparité d’anxiété mathématique entre les garçons et les filles s’expliquerait par la disparité d’évaluation cognitive, selon le genre : un concept de soi en mathématiques, une valeur intrinsèque des mathématiques et une valeur utilitaire accordée aux mathématiques plus faibles chez les filles que chez les garçons (Frenzel et al., 2007).
Afin de vérifier empiriquement cette piste explicative, il est nécessaire de procéder en trois étapes : 1) vérifier s’il existe un écart dans le niveau moyen de concept de soi, de valeur intrinsèque et de valeur utilitaire, selon le genre, 2) vérifier si la relation entre le genre et l’anxiété mathématique est médiée complètement par le concept de soi, la valeur intrinsèque et la valeur utilitaire et 3) vérifier si les liens entre concept de soi, valeur intrinsèque, valeur utilitaire et anxiété mathématique sont invariants selon le genre. Il est attendu que ces liens soient négatifs entre le concept de soi, la valeur intrinsèque et l’anxiété mathématique, mais que le lien soit positif entre la valeur utilitaire et l’anxiété mathématique. Ainsi, un concept de soi plus faible serait associé à un niveau d’anxiété mathématique plus élevé, une valeur intrinsèque plus faible serait associée à un niveau d’anxiété mathématique plus élevé et une valeur utilitaire plus faible serait associée à un niveau d’anxiété mathématique moins élevé (Pekrun, 2006, cité dans Henschel & Roick, 2017).
Figure 1
Modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006)
Lorsque ces trois étapes sont vérifiées, il est adéquat d’affirmer que la disparité d’anxiété mathématique entre les garçons et les filles s’explique par une disparité de concept de soi, de valeur intrinsèque et de valeur utilitaire, selon le genre. Dans ce qui suit, nous faisons état de résultats empiriques qui permettent de soutenir chacune de ces étapes.
En lien avec la première étape, plusieurs recherches (Frenzel et al., 2007 ; Goetz et al., 2008 ; Goetz et al., 2013 ; Kyttälä & Björn, 2010, Meece et al., 1990 ; Mullis et al., 2000), dont des méta-analyses (Else-Quest et al., 2010 ; Hyde et al., 1990), ont révélé des écarts entre les garçons et les filles en ce qui a trait au concept de soi, à la valeur intrinsèque et/ou à la valeur utilitaire des mathématiques. La méta-analyse de Hyde et al. (1990) a révélé que les filles ont tendance à rapporter un concept de soi en mathématiques plus faible que celui des garçons (avec une taille d’effet de 0,25). Ensuite, la méta-analyse d’Else-Quest et al. (2010) a montré que les filles ont tendance à rapporter un concept de soi, une valeur intrinsèque des mathématiques et une valeur utilitaire accordée aux mathématiques inférieurs à ceux des garçons (avec des tailles d’effet respectives de 0,33, 0,20, 0,24).
Les données du PISA de 2003 et de 2012 ont aussi permis de relever des écarts selon le genre, en ce qui a trait au concept de soi, à la valeur intrinsèque et à la valeur utilitaire. En effet, les filles de 15 ans ayant participé au PISA de 2003 et de 2012 ont fait état d’un concept de soi, d’une valeur intrinsèque et d’une valeur utilitaire statistiquement plus faibles que ceux des garçons, en moyenne, dans les pays de l’OCDE (p < 0,05). Il en a été de même au Canada. Les différences d’indices moyens observés au Canada entre les garçons et les filles (G-F) pour les trois concepts ont été respectivement de 0,36, de 0,18 et de 0,13 en 2003 et de 0,39, de 0,23 et de 0,13 en 2012 (des indices calibrés de manière à ce que la moyenne soit de 0 et l’écart-type de 1, dans les pays de l’OCDE) (OCDE, 2005a, 2014b).
En contrôlant les performances antérieures, l’étude de Frenzel et al. (2007), menée auprès de 2 053 élèves allemands âgés de 11 ans en moyenne, a révélé des écarts statistiquement significatifs selon le genre pour les trois perceptions (avec des tailles d’effet de 0,49, 0,31 et 0,02 pour le concept de soi, la valeur intrinsèque et la valeur utilitaire, respectivement). D’autres études ayant documenté spécifiquement les écarts de concept de soi selon le genre ont montré qu’à performance égale, les filles font état d’un concept de soi en mathématiques plus faible que celui des garçons, en moyenne (Correll, 2001 ; Goldman & Penner, 2016 ; Mejía-Rodríguez et al., 2021).
En lien avec la deuxième étape, l’étude menée par Frenzel et al. (2007) a montré que le concept de soi, la valeur intrinsèque et la valeur utilitaire médient complètement la relation entre le genre et l’anxiété mathématique. Pour ce faire, les auteurs ont procédé comme le proposent Kenny et al. (1998, cité dans Frenzel et al., 2007) et ont montré qu’en ajoutant les trois perceptions comme variables indépendantes, le coefficient de régression de la variable indépendante genre passe de statistiquement significatif à non significatif dans un modèle de régression multiple où l’anxiété mathématique est définie comme variable dépendante (b = 0,13, p < 0,01, pour la variable genre avant l’inclusion des trois perceptions et b = 0, après inclusion des trois perceptions). Une autre étude, celle de Kyttälä et Björn (2010), menée sur deux ans auprès de 116 élèves finlandais de 13 et 14 ans, a montré une médiation complète de la relation genre/anxiété mathématique via le concept de soi. Pour ce faire, les auteurs ont étudié les effets directs et les effets indirects entre les variables genre et anxiété mathématique par des analyses de liens structurels. Ils ont obtenu un coefficient de régression non-significatif pour l’effet direct de la variable genre sur l’anxiété mathématique (coefficient de régression standardisé de -0,07, p = 0,350) et un coefficient de régression statistiquement significatif pour l’effet indirect du genre sur l’anxiété mathématique via le concept de soi (coefficient standardisé statistiquement significatif de 0,14, p < 0,05). Cette étude n’a toutefois pas révélé de lien indirect significatif entre le genre et l’anxiété mathématique via la valeur utilitaire.
En lien avec la troisième étape, l’étude de Frenzel et al. (2007) a montré, à partir d’analyses multigroupes, que les liens structurels entre le concept de soi, la valeur intrinsèque, la valeur utilitaire des mathématiques (variables indépendantes) et l’anxiété mathématique (variable dépendante) peuvent être considérés invariants selon le genre, tout en contrôlant les performances antérieures. Pour arriver à cette conclusion, ils ont comparé l’indice d’ajustement du khi carré du modèle multigroupes non contraint (modèle dans lequel les paramètres de régression sont libres de varier, entre le groupe fille et le groupe garçon) et celui du modèle multigroupes contraint (modèle dans lequel les paramètres sont forcés à l’égalité entre les deux groupes). Comme l’indice d’ajustement du khi carré n’a pas varié de manière statistiquement significative en passant du modèle non contraint au modèle contraint, ils ont conclu que les liens peuvent être considérés invariants selon le genre (∆χ2 = 4,93, ddl = 4, p = 0,29). L’étude a aussi fait état d’un lien négatif entre le concept de soi en mathématiques et l’anxiété mathématique, d’un lien négatif entre la valeur intrinsèque et l’anxiété mathématique, puis d’un lien positif entre la valeur utilitaire et l’anxiété mathématique. L’étude de Kyttälä et Björn (2010) a aussi révélé, par des analyses multigroupes, que les liens structurels entre le concept de soi, la valeur utilitaire (variables indépendantes) et l’anxiété mathématique (variable dépendante) peuvent être considérés invariants selon le genre. Le lien concept de soi/anxiété mathématique s’est avéré négatif et le lien valeur utilitaire/anxiété mathématique, positif.
Enfin, comme l’étude de Frenzel et al. (2007) a procédé aux vérifications des trois étapes, les auteurs ont conclu que les écarts d’anxiété mathématique observés entre les filles et les garçons ayant participé à leur étude s’expliquent par les écarts de perception entre les filles et les garçons : un concept de soi en mathématiques, une valeur intrinsèque des mathématiques et une valeur utilitaire accordée aux mathématiques plus faibles chez les filles.
Dans le cadre de la présente recherche, nous souhaitons vérifier si la disparité observée entre l’anxiété mathématique des filles et celle des garçons francophones de 15 ans du Québec ayant participé au PISA de 2003 et de 2012 s’explique par la disparité d’évaluation cognitive selon le genre : un concept de soi, une valeur intrinsèque et une valeur utilitaire plus faibles chez les filles que chez les garçons. Pour ce faire, nous définissons trois objectifs spécifiques de recherche :
OS1 : Vérifier s’il existe une disparité de concept de soi, de valeur intrinsèque et de valeur utilitaire, selon le genre, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012, en contrôlant les performances en mathématiques.
Hypothèse de recherche en lien avec OS1 : les filles québécoises francophones rapportent un niveau plus faible de concept de soi, de valeur intrinsèque et de valeur utilitaire que les garçons québécois francophones, même en contrôlant les performances en mathématiques.
OS2 : Vérifier si la relation entre le genre et l’anxiété mathématique est médiée complètement par le concept de soi, la valeur intrinsèque et la valeur utilitaire, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012, en contrôlant les performances.
Hypothèse de recherche en lien avec OS2 : le concept de soi, la valeur intrinsèque et la valeur utilitaire médient complètement la relation entre le genre et l’anxiété mathématique, en contrôlant les performances.
OS3 : Vérifier si les liens structurels entre le concept de soi, la valeur intrinsèque et la valeur utilitaire (variables indépendantes), puis l’anxiété mathématique (variable dépendante) sont invariants selon le genre, chez les élèves québécois francophones ayant participé au PISA de 2003 et de 2012.
Hypothèse de recherche en lien avec OS3 : les liens structurels sont invariants selon le genre. Les liens concept de soi/anxiété mathématique et valeur intrinsèque/anxiété mathématique sont négatifs, alors que le lien valeur utilitaire/anxiété mathématique est positif, en contrôlant les performances.
La mise en commun de OS1, OS2 et OS3 et l’hypothèse de recherche qui en découle : Si, pour les trois perceptions considérées, les filles ont un niveau moyen inférieur à celui des garçons, si le lien genre/anxiété mathématique est médié complètement par les trois perceptions et si les liens perceptions/anxiété mathématique sont invariants selon le genre, nous concluons que les écarts d’anxiété mathématique observés entre les filles et les garçons francophones de 15 ans du Québec ayant participé au PISA de 2003 et de 2012 s’expliquent par un concept de soi, une valeur intrinsèque et une valeur utilitaire plus faible chez les filles que chez les garçons. Le fait d’avoir contrôlé les performances nous permettra de nous assurer que les écarts observés ne sont pas attribuables simplement à des écarts de performances entre les garçons et les filles. L’hypothèse de recherche qui découle de la mise en commun des résultats OS1, OS2 et OS3 est la suivante : les écarts d’anxiété mathématique entre les filles et les garçons s’expliquent par un concept de soi, une valeur intrinsèque et une valeur utilitaire plus faible chez les filles que chez les garçons.
Méthodologie
Les données analysées dans la présente recherche sont des données secondaires issues du PISA de 2003 et de 2012. Ces données ont trois caractéristiques particulières qui doivent être considérées au moment de les analyser. Dans Vohl et Loye (sous presse), nous présentons ces trois caractéristiques dans le détail ainsi que les techniques d’analyse à mettre en oeuvre afin de les traiter adéquatement. Au besoin, le lecteur est invité à consulter l’article de Vohl et Loye (sous presse), pour de plus amples détails. Toutefois, de manière à permettre une meilleure compréhension du présent article, les trois caractéristiques particulières inhérentes aux données du PISA sont brièvement décrites dans ce qui suit, de même que les techniques d’analyse à utiliser.
La première considération méthodologique inhérente aux données du PISA
Dans le cadre du PISA, les échantillons sont générés, dans chacun des pays participants, au moyen d’un plan d’échantillonnage dit plan d’échantillonnage complexe (complex sampling design) (p. ex., Lohr, 2019 ; Rutkovski et al., 2010 ; Skinner & Wakefield, 2017 ; Stapleton, 2013). Le plan d’échantillonnage complexe du PISA est un plan aléatoire stratifié en deux niveaux : au premier niveau, des écoles sont sélectionnées, puis au deuxième niveau, à l’intérieur de chacune des écoles, des élèves sont sélectionnés. Dans un tel plan d’échantillonnage, les probabilités de sélection des élèves peuvent être inégales. Cela explique en partie pourquoi les bases de données du PISA incluent, pour chaque élève, une pondération appelée poids de sondage. Les poids de sondage permettent également d’ajuster pour la non-réponse. Ils doivent être incorporés aux calculs au moment d’estimer des paramètres, par exemple, la moyenne d’un groupe.
De plus, dans un plan aléatoire stratifié à deux niveaux, comme les élèves sont nichés à l’intérieur des écoles, les données relatives aux élèves ne peuvent être considérées indépendantes. Pour cette raison, le PISA fournit, pour chaque élève, des poids de sondage répliqués, qui permettent d’estimer la variance des paramètres estimés, par méthode de rééchantillonnage, sans que l’analyste ait lui-même à procéder au rééchantillonnage. De ce fait, au moment d’analyser de manière secondaire des données issues du PISA, il faut employer les poids de sondage et les poids de sondage répliqués, à moins d’opter pour la modélisation multiniveau (voir Vohl & Loye, sous presse). Les poids de sondage et les poids de sondage répliqués sont intégrés au plan d’analyses présenté plus loin.
La deuxième considération méthodologique inhérente aux données issues du PISA
Lors des épreuves du PISA de 2003 et de 2012, les participants ont été invités à répondre à deux types de questionnaires : les épreuves cognitives et le questionnaire contextuel (OCDE, 2005b, 2014c). Les épreuves cognitives, de type papier-crayon, d’une durée de 120 minutes ont servi à évaluer la culture mathématique, la culture scientifique et la compréhension de l’écrit. Le questionnaire contextuel, de type papier-crayon, d’une durée de 30 minutes, a servi à documenter divers facteurs non-cognitifs liés aux performances dans les trois domaines évalués. Comme la culture mathématique a été identifiée comme domaine majeur d’évaluation lors de ces deux cycles, ce sont principalement des facteurs non-cognitifs liés aux performances en mathématiques qui ont été documentés. C’est pour cette raison que l’anxiété mathématique, le concept de soi, la valeur intrinsèque et la valeur utilitaire des mathématiques ont été documentés lors de ces cycles.
En 2012, le PISA a employé une méthode de rotation des items appelée devis en trois formes (three-form design) (Graham et al., 1996) au moment de développer les questionnaires contextuels : trois formes de cahier ont été produites (les formes A, B et C), puis, chaque facteur non-cognitif a été inclus dans uniquement deux des trois formes. Comme chaque élève a répondu à une seule des trois formes (la forme A ou B ou C) qui lui a été administrée aléatoirement, la base de données du PISA de 2012 contient minimalement un tiers de données manquantes au regard de l’anxiété mathématique, du concept de soi, de la valeur intrinsèque et de la valeur utilitaire des mathématiques. Afin de traiter adéquatement ces données manquantes, il faut intégrer une méthode adaptée au plan d’analyse. L’état de l’art dans le contexte consiste à employer la méthode de vraisemblance maximale (full information maximum likelihood, FIML) (Enders, 2010). Cette méthode est intégrée au plan d’analyse de données présenté plus loin.
La troisième considération méthodologique inhérente aux données issues du PISA
Pour rendre compte des performances, en 2003 et en 2012, le PISA n’a pas fourni des scores, mais plutôt cinq estimations du niveau d’habileté des élèves en fonction des réponses fournies aux items des épreuves cognitives et en fonction du niveau de difficulté des items. Ces cinq estimations sont appelées des valeurs plausibles. L’approche des valeurs plausibles est employée depuis 2000 par le PISA, afin de rendre compte du niveau d’habileté des élèves. Pour toute analyse impliquant le niveau d’habileté, les cinq valeurs plausibles doivent être combinées selon une approche particulière, l’approche de Little et Rubin (2002). Cette méthode est intégrée au plan d’analyse des données présenté plus loin.
Les échantillons
Les deux échantillons analysés dans la présente recherche sont : 1) le sous-échantillon d’élèves québécois en provenance d’écoles dont le français était la langue principale d’enseignement lors du PISA de 2003, issu de l’échantillon canadien du PISA de 2003 et 2) le sous-échantillon d’élèves québécois en provenance d’écoles dont le français était la langue principale d’enseignement lors du PISA de 2012, issu de l’échantillon canadien du PISA de 2012.
Le sous-échantillon de participants québécois francophones de 2003 est constitué de 2 151 élèves de 15 ans, soit 1 102 filles et 1 049 garçons (51,2 % et 48,8 %, respectivement, avec ou sans l’utilisation des poids de sondage), provenant de 119 écoles. Le sous-échantillon de 2012 contient 2 385 élèves de 15 ans, soit 1 251 filles et 1 134 garçons (52,5 % et 47,5 %, respectivement, sans les poids de sondage, puis 50,9 % et 49,1 %, lorsque les données sont pondérées à l’aide des poids de sondage), en provenance de 109 écoles.
Les aspects éthiques considérés
Lors des enquêtes du PISA de 2003 et de 2012, le consentement écrit des parents a été exigé afin que les élèves puissent participer aux épreuves (dans l’ensemble des pays et des économies où la réglementation en vigueur exigeait un tel consentement) (OCDE, 2005b, 2014c). Par ailleurs, afin de mener la présente recherche, une demande de certification éthique a été soumise au Comité d’éthique de la recherche en éducation et en psychologie (CEREP) de l’Université de Montréal. Celle-ci a été acceptée et la présente recherche est considérée à faible risque pour les participants.
Les variables étudiées et les données analysées
Afin de répondre aux objectifs spécifiques de notre recherche, six variables sont utilisées : le genre, les performances en mathématiques et les quatre variables non-cognitives que sont le concept de soi en mathématiques, la valeur intrinsèque des mathématiques, la valeur utilitaire accordée aux mathématiques et l’anxiété mathématique.
Le genre
En 2003 et en 2012, le PISA a documenté le genre des participants au moyen d’un item dichotomique[5].
Les performances en mathématiques
Depuis 2003, en mathématiques, le PISA s’intéresse à une compétence appelée la culture mathématique. Cette compétence est définie comme « l’aptitude d’un individu à formuler, employer et interpréter des mathématiques dans un éventail de contextes, c’est-à-dire à raisonner en termes mathématiques et à utiliser des concepts, procédures, faits et outils mathématiques pour décrire, expliquer et prévoir des phénomènes. Elle aide les individus à comprendre le rôle que les mathématiques jouent dans le monde et à se comporter en citoyens constructifs, engagés et réfléchis, c’est-à-dire à poser des jugements et à prendre des décisions en toute connaissance de cause » (OCDE, 2014a, p. 42).
Afin de rendre compte du niveau de compétence de chacun des participants en regard de la culture mathématique, le PISA fournit cinq valeurs plausibles[6]. En 2000, l’OCDE a calibré chacune des valeurs plausibles de manière à ce que la moyenne soit de 500, dans les pays de l’OCDE, et l’écart-type de 100.
Les quatre variables non-cognitives
Sur la base de considérations théoriques et empiriques, quatre instruments de mesure ont été élaborés dans le cadre du PISA de 2003 et repris, de manière intégrale en 2012, afin d’appréhender le concept de soi en mathématiques, la valeur intrinsèque des mathématiques, la valeur utilitaire accordée aux mathématiques et l’anxiété mathématique (OCDE, 2005b, 2014b, 2014c).
Pour chacun des quatre instruments, en 2003 et en 2012, à partir des réponses fournies par les participants, le PISA a calculé un indice. Pour ce faire, une généralisation du modèle de Rasch à un paramètre (Rasch, 1960), le modèle de crédit partiel (Masters & Wright, 1997, cité dans OCDE, 2005b) a été utilisé pour la mise à l’échelle de chacun des items de l’instrument, puis une estimation ponctuelle de l’indice a été dérivée sur la base « d’une estimation pondérée des réponses les plus vraisemblables (weighted likelihood estimate, WLE) (Warm, 1989, cité dans OCDE, 2014b, p. 199). Ces indices ont été calculés et calibrés de manière à ce que la moyenne, dans les pays de l’OCDE, soit de 0 et l’écart-type de 1.
Le tableau 1 présente, pour chacune des quatre variables non-cognitives étudiées dans la présente recherche, le nom et la définition de l’indice tels que proposés par le PISA, le libellé des items de chacun des instruments, les qualités psychométriques de ces instruments, telles que documentées par l’OCDE lors du PISA de 2003 et de 2012, pour le Canada et, enfin, les qualités psychométriques des quatre instruments telles que documentées, dans le cadre de la présente recherche, à partir des deux échantillons étudiés. Les indices d’ajustement issus des analyses factorielles confirmatoires (AFC) menées, tant par l’OCDE que dans la présente recherche, indiquent un ajustement adéquat entre le modèle théorique sous-jacent aux instruments et les résultats empiriques, sauf les indices RMSEA qui, dans certains cas, révèlent un mauvais ajustement puisque supérieurs à 0,1 (Byrne, 2012). Comme la majorité des indices révèlent un bon ajustement, les valeurs élevées de RMSEA ne compromettent pas l’usage des données. En outre, l’ensemble des indices de fidélité révèlent une bonne consistance interne.
Comme notre premier objectif spécifique de recherche s’intéresse aux écarts de concept de soi, de valeur intrinsèque et de valeur utilitaire en mathématiques, selon le genre, nous avons mené des analyses factorielles confirmatoires multigroupes (Bollen, 1989 ; Hayduk, 1987 ; Jöreskog, 1971 ; Sörbom, 1974) de manière à vérifier l’invariance métrique (égalité des coefficients de saturation du facteur, entre les groupes, pour chacun des items de l’instrument de mesure) et l’invariance scalaire (égalité des ordonnées à l’origine entre les groupes pour chacun des items) (Meredith, 1993 ; Widaman & Reise, 1997) de ces trois instruments, sur les échantillons de 2003 et de 2012.
En effet, bien que peu de recherches aient vérifié l’invariance métrique et scalaire des instruments de mesure de concept de soi, de valeur intrinsèque et de valeur utilitaire selon le genre, avant de comparer les moyennes observées entre les garçons et les filles, jusqu’à aujourd’hui, il est fortement recommandé de le faire avant de tirer quelque conclusion que ce soit lorsque des moyennes sont comparées entre des groupes (Meredith, 1993 ; Steenkamp & Baumgartner, 1998 ; Steinmetz, 2011 ; Vandenberg & Lance, 2000). Cette vérification est nécessaire avant de conclure que les écarts moyens observés reflètent bien des écarts moyens du trait latent d’intérêt, puisqu’ils pourraient aussi refléter la non-invariance métrique et/ou la non-invariance scalaire, entre les groupes (voir Steinmetz, 2011 pour une explication détaillée).
Pour vérifier l’invariance métrique et scalaire, nous avons procédé par étapes, en vérifiant d’abord l’invariance configurale, suivie de l’invariance métrique, puis de l’invariance scalaire, entre les groupes (Meredith, 1993 ; Widaman & Reise, 1997, Wang & Wang, 2020). En passant d’une étape à l’autre, nous avons étudié les changements (∆) des indices d’ajustement suivants : l’indice d’ajustement comparatif (CFI pour Comparative fit index) (Bentler, 1990), la racine carrée de l’erreur quadratique moyenne d’approximation (RMSEA pour Root mean square error of approximation) (Steiger, 1990) et la valeur moyenne quadratique pondérée (SRMR pour Standardized Root Mean-Square Residual) (Bentler, 1995 ; Muthén, 1998-2004) Afin de conclure, nous avons suivi les recommandations de Chen (2007, p. 501) : un ∆|CFI|≥,010 auquel s’ajoute un ∆RMSEA≥,015 ou un ∆SRMR≥,030 entre le modèle non-contraint (modèle d’invariance configurale) et le modèle où les coefficients de saturation du facteur sont contraints à l’égalité (modèle d’invariance métrique), entre les groupes pour chacun des items, indique de rejeter l’hypothèse de l’invariance métrique de la mesure, puis, pour tester l’invariance scalaire, un ∆|CFI|≥,010 auquel s’ajoute un ∆RMSEA≥,015 ou un ∆SRMR≥,010, entre le modèle d’invariance métrique et le modèle d’invariance scalaire indique de rejeter l’hypothèse d’invariance scalaire de la mesure.
Tableau 1
Instruments de mesure du concept de soi en mathématiques, de la valeur intrinsèque des mathématiques, de la valeur utilitaire des mathématiques et de l’anxiété mathématique, tels que proposés par le PISA en 2003 et en 2012
Note. AFC = analyses factorielles confirmatoires, RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation (Root-Mean Square Error of Approximation), RMR = racine carrée de l’erreur quadratique moyenne des résidus (Root Mean Square Residual), SRMR = valeur moyenne quadratique pondérée (Standardized Root Mean-Square Residual), CFI = indice d'ajustement comparatif (Comparative Fit Index), TLI = indice de Tucker Lewis (Tucker Lewis index), α = coefficient alpha de Cronbach (1951), ω = coefficient omega de McDonald (1985, 1999). Des valeurs de RMSEA sous 0,05 indiquent un bon ajustement, puis des valeurs au-dessus de 0,1 sont interprétées comme un ajustement inacceptable. Des valeurs de RMR ou de SRMR sous 0,08 indiquent un bon ajustement et de moins de 0,10, un ajustement acceptable. Des valeurs de CFI, NNFI et TLI entre 0,9 et 0,95 indiquent un ajustement acceptable, puis des valeurs de CFI, NNFI et TLI supérieures à 0,95 indiquent un bon ajustement (Hu & Bentler, 1999). Les informations des colonnes 2 et 3 sont tirées de OCDE (2014b, p. 75, 81, 97, 101). Les informations de la colonne 4 sont tirées de OCDE (2005b, p. 290, 291, 293, 294). Les informations de la colonne 5 proviennent d’analyses personnelles effectuées sur l’échantillon de 2003 et de 2012 de la présente recherche.
Les résultats de ces analyses sont présentés dans le tableau 2. Ceux-ci indiquent de ne pas rejeter l’hypothèse d’invariance métrique et l’hypothèse d’invariance scalaire de la mesure de valeur intrinsèque et de la mesure de valeur utilitaire des mathématiques, entre les filles et les garçons, pour 2003 et pour 2012. Toutefois, pour le concept de soi, les résultats de 2003 et de 2012 indiquent de rejeter l’hypothèse de l’invariance scalaire, entre les garçons et les filles.
L’étude des indices de modification nous a amenées à relâcher la contrainte d’égalité sur l’ordonnée à l’origine de l’item 2, en 2003, puis à relâcher la contrainte d’égalité sur les ordonnées à l’origine des items 2 et 5, pour 2012. En procédant de la sorte, les variations d’indices d’ajustement se sont avérées acceptables (voir le tableau 2). De là, comme nous avons pu vérifier l’invariance scalaire de plus de deux items pour l’instrument de concept de soi, nous avons conclu qu’il est adéquat de comparer les moyennes entre les filles et les garçons, en regard de cette perception (Byrne et al., 1989 ; Steenkamp & Baumgartner, 1998 ; Steinmetz, 2011).
Les procédures ayant permis d’obtenir les données des échantillons de participants québécois francophones du PISA de 2003 et de 2012
Pour 2012, la base de données internationale du PISA de 2012 a été téléchargée à partir de l’adresse[7] https://www.oecd.org/pisa/data/pisa2012database-downloadabledata.htm. Pour 2003, comme le Canada avait décidé, à l’époque, de ne pas rendre publique l’information relative à la province, dans la base de données internationale du PISA, nous avons soumis une demande de renseignement au Conseil des ministres de l’Éducation du Canada (CMEC). Celui-ci nous a transmis la base de données de l’échantillon d’élèves québécois du PISA de 2003[8].
Tableau 2
Étude de l’invariance de la mesure de concept de soi en mathématiques, de valeur intrinsèque des mathématiques, de valeur utilitaire des mathématiques
Note. CFI = indice d'ajustement comparatif (Comparative Fit Index), RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation (Root-Mean Square Error of Approximation), SRMR = valeur moyenne quadratique pondérée (Standardized Root Mean Square Residual), ∆ = changement.
Les analyses de données
Le logiciel employé
Afin de traiter adéquatement les trois considérations méthodologiques inhérentes aux données du PISA, les données sont analysées en intégrant les poids de sondage, les poids de sondage répliqués[9], la méthode de vraisemblance maximale et l’approche de Little et Rubin (2002). L’ensemble de analyses est mené à l’aide du logiciel Mplus, Version 8, qui possède les particularités suivantes : 1) il prend en charge les poids de sondage et les poids de sondage répliqués des élèves, 2) il intègre la méthode de vraisemblance maximale (full information maximum likelihood, FIML) (Arbuckle, 1996 ; Little & Rubin, 2002) « en conjonction avec l’estimateur ML » (traduction libre de Wang et Wang, 2020, p. 47), l’estimateur de vraisemblance maximale et enfin, 3) il prend en charge les valeurs plausibles qu’il traite selon l’approche de Little et Rubin (2002). Pour traiter adéquatement le tout, Mplus, Version 8 utilise l’estimateur MLR[10] (maximum likelihood robust) (Muthén & Muthén, 2017).
Le plan d’analyse de données
Le plan d’analyse prévu afin de répondre à chacun de nos objectifs de recherche est défini dans ce qui suit.
Les analyses permettant de répondre à l’OS1
Afin de répondre à l’objectif spécifique 1, pour chacune des trois perceptions, un modèle de régression linéaire à deux covariables est employé. Ce modèle se présente comme suit :
Dans ce modèle, la variable genre est une variable dichotomique. ![]() estime, pour chacune des trois perceptions, l’écart moyen de cette
perception selon le genre, en contrôlant les performances.
estime, pour chacune des trois perceptions, l’écart moyen de cette
perception selon le genre, en contrôlant les performances.
Pour les perceptions où l’écart selon le genre est statistiquement significatif, la taille d’effet est estimée au moyen du d de Cohen. En posant θgarçons et θfilles, la moyenne de la perception chez les garçons et chez les filles, d s’obtient par la formule
Selon Feingold (2019), la valeur de l’expression:  de l’équation (2) s’obtient en prenant la variance résiduelle du
coefficient de régression de la variable genre dans le modèle de régression à
une seule covariable qui suit :
de l’équation (2) s’obtient en prenant la variance résiduelle du
coefficient de régression de la variable genre dans le modèle de régression à
une seule covariable qui suit :
Les analyses permettant de répondre à OS2
Afin de répondre à l’objectif spécifique 2 et, ainsi, vérifier si la relation entre le genre et l’anxiété mathématique est médiée complètement par le concept de soi, la valeur intrinsèque et la valeur utilitaire, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012, en contrôlant les performances, le lien direct entre le genre et l’anxiété mathématique et le lien indirect entre le genre et l’anxiété mathématique via le concept de soi, la valeur intrinsèque et la valeur utilitaire sont étudiés au moyen d’analyse de liens structurels (p. ex., Byrne, 2012 ; Kline, 2016 ; Wang & Wang, 2020). Un lien direct non significatif et un lien indirect statistiquement significatif nous amènent à conclure que les perceptions médient complètement le lien entre le genre et l’anxiété mathématique. Un lien direct significatif et un lien indirect significatif nous amènent à conclure que les perceptions médient partiellement le lien entre le genre et l’anxiété mathématique.
Afin de vérifier si le lien indirect est significatif, un intervalle de confiance à 95 % est fourni. Un intervalle de confiance est aussi fourni pour chacun des liens indirects spécifiques, à savoir le lien genre/anxiété mathématique via la valeur intrinsèque, le lien genre/anxiété mathématique via la valeur utilitaire, le lien genre/anxiété mathématique via le concept de soi et le lien genre/anxiété mathématique via les performances. Les intervalles de confiance fournis tiennent compte du fait que la distribution des paramètres estimés peut être non normale. En conséquence, ils ne sont pas nécessairement symétriques autour du paramètre estimé (Muthén & Muthén, 2017, p. 613). La figure 2 propose une représentation des liens étudiés afin de répondre à l’objectif spécifique 2 (elle montre également le parallèle avec la figure 1).
Comme l’analyse de ces liens implique la variable anxiété mathématique comme variable dépendante, il est nécessaire de vérifier l’invariance métrique de la mesure d’anxiété mathématique (Wang & Wang, 2020). Cette procédure a été effectuée dans Vohl et Loye (2024)[11]. Les résultats ont suggéré de ne pas rejeter l’hypothèse d’invariance métrique.
Figure 2
Liens direct et indirects spécifiques tels qu’étudiés afin de répondre à l’objectif spécifique 2
Note. c représente le lien direct entre le genre et l’anxiété mathématique, les liens indirects spécifiques sont donnés par les produits suivants : a1 • b1, a2 • b2, a3 • b3 et a4 • b4. Le lien indirect total entre le genre et l’anxiété mathématique est donné par la somme a1 • b1 + a2 • b2 + a3 • b3 + a4 • b4.
Les analyses permettant de répondre à OS3
Afin d’étudier l’invariance des liens structurels entre les trois perceptions et l’anxiété mathématique, selon le genre, en contrôlant les performances, des analyses de liens structurels multigroupes sont menées (p. ex., Byrne, 2012 ; Wang & Wang, 2020). Pour ce faire, il faut effectuer une démarche en trois étapes. Dans un premier temps, nous étudions la qualité de l’ajustement du modèle non contraint, celui où les coefficients de régression sont libres de varier selon le genre. Dans un second temps, nous étudions la qualité de l’ajustement du modèle multigroupes contraint, celui dans lequel les coefficients de régression sont contraints à l’égalité dans les deux groupes. À chacune de ces deux étapes, afin de juger de la qualité de l’ajustement global des données au modèle proposé, nous utilisons les indices suivants : racine carrée de l’erreur quadratique moyenne d’approximation (RMSEA, root mean square error of approximation) (Steiger, 1990), l’indice d’ajustement comparatif (CFI, comparative fit index) (Bentler, 1990), l’indice de Tucker Lewis (TLI, Tucker-Lewis index) (Bentler & Bonett, 1980 ; Tucker & Lewis, 1973) et la valeur moyenne quadratique pondérée (SRMR, standardized root mean-square residual) (Bentler, 1995 ; Muthén, 1998-2004). Les balises d’interprétation utilisées sont celles proposées par Hu et Bentler (1999) qui stipulent qu’une valeur de RMSEA inférieure à 0,05, des valeurs de CFI et de TLI supérieures à 0,95 et une valeur de SRMR inférieure à 0,08 indiquent un bon ajustement.
À l’étape 3, afin de vérifier l’hypothèse de l’invariance des liens structurels, nous comparons la qualité de l’ajustement entre le modèle non contraint et le modèle contraint. Pour ce faire, nous utilisons la différence de l’indice d’ajustement comparatif (∆CFI) et concluons qu’il n’y a pas lieu de rejeter l’hypothèse d’invariance lorsque la diminution de CFI est de moins de 0,01 entre les deux modèles nichés[12] (Cheung & Rensvold, 2002 ; Wang & Wang, 2020).
Résultats
Les statistiques descriptives des six variables étudiées dans l’échantillon de 2003 et dans l’échantillon de 2012, de même que les pourcentages de données manquantes pour chacune de ces variables sont présentées à l’annexe A.
Les résultats en lien avec l’objectif spécifique 1
Le tableau 3 montre les paramètres de régression de la variable genre dans chacun des modèles de régression à deux covariables (équation 1) effectués, de même que les tailles d’effet associées telles que calculées à partir du modèle à une covariable (équation 3). Les résultats montrent, dans un premier temps, que les filles québécoises francophones ont fait état d’un niveau moyen de concept de soi, de valeur intrinsèque et de valeur utilitaire statistiquement inférieur à celui des garçons québécois francophones, en 2003 et en 2012, en contrôlant les performances (avec p < 0,10). Ces résultats confirment l’hypothèse de recherche évoquée en lien avec OS1.
En outre, tout comme l’ont révélé des recherches antérieures (Else-Quest et al., 2010 ; Frenzel et al., 2007 ; OCDE, 2005a, 2014b), nos résultats montrent que les garçons et les filles diffèrent davantage en regard du concept de soi qu’en regard de la valeur intrinsèque et de la valeur utilitaire accordée aux mathématiques (tailles d’effet de 0,32 et 0,22 pour le concept de soi et des tailles d’effet entre 0,10 et 0,17 pour la valeur intrinsèque et la valeur utilitaire, pour 2003 et 2012).
Les résultats en lien avec l’objectif spécifique 2
Afin de vérifier si la relation entre le genre et l’anxiété mathématique est médiée complètement par le concept de soi, la valeur intrinsèque et la valeur utilitaire, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012, en contrôlant les performances, nous avons étudié les liens direct et indirect entre le genre et l’anxiété mathématique pour 2003 et 2012. Le tableau 4 fait état des résultats obtenus.
Les résultats montrent, qu’à la fois en 2003 et en 2012, le lien direct et le lien indirect entre le genre et l’anxiété mathématique se sont avérés statistiquement significatifs, en contrôlant les performances. De là, nous déduisons que la médiation de la relation genre/anxiété mathématique par les trois perceptions est partielle, plutôt que complète, comme le stipulait l’hypothèse de recherche en lien avec OS2.
Le coefficient de régression du lien indirect s’est toutefois avéré supérieur à celui du lien direct, aux deux cycles étudiés. En effet, en 2003, le lien indirect total a représenté 69,2 % du lien total et en 2012, il a compté pour 65,3 %. Parmi les liens indirects spécifiques étudiés, toutefois, seul le lien indirect genre/anxiété mathématique via le concept de soi s’est avéré significatif, en 2003 et en 2012. En effet, alors que les intervalles de confiance à 95 % des autres liens indirects spécifiques incluent la valeur de 0, le lien indirect spécifique genre/anxiété mathématique via le concept de soi n’inclut pas la valeur de 0.
Les résultats en lien avec l’objectif spécifique 3
Les tableaux 5 et 6 montrent les résultats des analyses multigroupes menées afin de vérifier si les liens structurels entre concept de soi, valeur intrinsèque, valeur utilitaire et anxiété mathématique peuvent être considérés invariants, selon le genre.
Le tableau 5 montre que, pour 2003 et pour 2012, le modèle multigroupes non contraint s’ajuste parfaitement aux données. Le tableau 6 montre que, pour 2003 et pour 2012, le modèle contraint rend compte d’un bon ajustement. Comme le changement de valeur de CFI entre le modèle non contraint et le modèle contraint est de moins de 0,01 pour 2003 et pour 2012, nous concluons que les liens structurels entre concept de soi, valeur intrinsèque, valeur utilitaire et anxiété mathématique peuvent être considérés invariants selon le genre.
En outre, les valeurs de paramètres obtenues dans le modèle contraint, pour 2003 et pour 2012, révèlent que le lien invariant valeur intrinsèque/anxiété mathématique est non significatif contrairement à ce qui était proposé dans l’hypothèse de recherche en lien avec l’objectif spécifique 3. Toutefois, conformément à cette hypothèse de recherche, le lien invariant valeur utilitaire/anxiété mathématique s’est avéré positif et le lien invariant concept de soi/anxiété mathématique s’est révélé négatif.
La mise en commun des résultats obtenus en réponse aux objectifs spécifiques 1, 2 et 3 nous amène à conclure qu’en 2003 et en 2012, la relation entre le genre et l’anxiété mathématique est médiée par le concept de soi et que cette médiation est partielle. Il était attendu, selon l’hypothèse de recherche stipulée, que la médiation soit complète et que les trois perceptions médient la relation genre/anxiété mathématique.
Ainsi, en 2003, 69,2 % des écarts d’anxiété mathématique entre les filles et les garçons québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012 s’expliquent par les écarts de concept de soi entre les filles et les garçons. En 2012, ce pourcentage s’élève à 65,3 %. Le modèle de 2003 explique 43,2 % de la variance de l’anxiété mathématique et le modèle de 2012 en explique 47,2 %.
L’invariance des liens structurels nous amène à conclure que, chez les garçons comme chez les filles, une augmentation d’une unité de l’indice de concept de soi diminue l’indice d’anxiété mathématique d’environ 2/3 d’écart-type, soit 0,601 en 2003 et 0,660 en 2012, et qu’une augmentation d’une unité de l’indice de valeur utilitaire augmente l’indice d’anxiété mathématique de 0,078 et 0,070, soit environ 7/100 d’écart-type en 2003 et 2012, respectivement (puisque ces indices sont calibrés de manière à ce que l’écart-type soit de 1, dans les pays de l’OCDE).
Tableau 3
Écarts de concept de soi, de valeur intrinsèque et de valeur utilitaire, selon le genre, observés chez les élèves québécois francophones ayant participé au PISA de 2003 et de 2012 et tailles d’effets associées
Note.  = coefficient de régression non standardisé estimé de la
variable genre dans le modèle de régression donné par Perception =
= coefficient de régression non standardisé estimé de la
variable genre dans le modèle de régression donné par Perception =  genre +
genre +  performances avec la
référence genre = 0 pour fille ; Er.t. = erreur type du coefficient de
régression
performances avec la
référence genre = 0 pour fille ; Er.t. = erreur type du coefficient de
régression  ; p = valeur p ;
d = taille d’effet ; SCMAT =
concept de soi en mathématiques ; INTMAT = valeur intrinsèque des
mathématiques ; INSTMOT = valeur utilitaire des mathématiques.
; p = valeur p ;
d = taille d’effet ; SCMAT =
concept de soi en mathématiques ; INTMAT = valeur intrinsèque des
mathématiques ; INSTMOT = valeur utilitaire des mathématiques.
Tableau 4
Résultats des liens directs et indirects pour 2003 et 2012, en contrôlant les performances
Note. Les couleurs correspondent à celles employées dans la figure 2. Genre = 0 pour fille, Coeff. = coefficient de régression standardisés par rapport à y, Er.t. = erreur type, p = valeur p, %T = pourcentage de l’effet total, i.c. = intervalle de confiance à 95 %, SCMAT = concept de soi en mathématiques, INTMAT = valeur intrinsèque en mathématiques, INSTMOT = valeur utilitaire en mathématiques, ANXMAT = anxiété mathématique. Pour 2003, le pourcentage de variation expliquée par le modèle et les indices d’ajustement des données au modèle : R2 = 43,2 %, RMSEA = 0,000, CFI = 1,000, TLI = 1,000, SRMR = 0,000. Pour 2012, le pourcentage de variation expliquée par le modèle et les indices d’ajustement sont R2 = 47,2 %, RMSEA = 0,000, CFI = 1,000, TLI = 1,000, SRMR = 0,000.
Tableau 5
Résultats du modèle multigroupes non contraint pour 2003 et pour 2012
Note. Coeff. = coefficient de régression non standardisés, Er.t. = erreur type, p = valeur p, R2 = pourcentage de variation expliquée par le modèle, INTMAT = valeur intrinsèque en mathématiques, INSTMOT = valeur utilitaire en mathématiques, SCMAT = concept de soi en mathématiques, RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation, CFI = indice d’ajustement comparatif, TLI = indice de Tucker et Lewis, SRMR = valeur moyenne quadratique pondérée.
Tableau 6
Résultats du modèle multigroupes contraint pour 2003 et pour 2012
Note. Coeff. = coefficient de régression non standardisés, Er.t. = erreur type, p = valeur p, R2 = pourcentage de variation expliquée par le modèle, INTMAT = valeur intrinsèque en mathématiques, INSTMOT = valeur utilitaire en mathématiques, SCMAT = concept de soi en mathématiques, RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation, CFI = indice d’ajustement comparatif, TLI = indice de Tucker et Lewis, SRMR = valeur moyenne quadratique pondérée, ∆CFI = changement de l’indice d’ajustement comparatif entre le modèle contraint et le modèle non contraint.
Discussion
L’objectif général du présent article visait à identifier des facteurs qui pourraient permettre d’expliquer la disparité d’anxiété mathématique observée, selon le genre, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012, et qui auraient éventuellement le potentiel de réduire ces écarts. Pour ce faire, nous avons retenu la piste proposée par le modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006). Conformément à ce que propose cette piste, nous avons émis l’hypothèse que les écarts d’anxiété mathématique selon le genre pourraient s’expliquer par des écarts de perceptions de compétence, de valeur intrinsèque et de valeur utilitaire entre les garçons et les filles. Afin de vérifier cette hypothèse, nous avons énoncé et vérifié trois objectifs spécifiques de recherche.
En combinant les résultats obtenus en réponse à ces trois objectifs, il ressort que la disparité d’anxiété mathématique selon le genre, observée chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012 peut s’expliquer par un concept de soi en mathématiques plus faible chez les filles que chez les garçons et par la présence d’un lien direct genre/anxiété mathématique négatif. Les écarts de concept de soi expliquent la majeure portion des écarts d’anxiété mathématique : 69,2 % en 2003 et 65,3 % en 2012.
Ces conclusions ont des implications scientifiques et pratiques importantes. En effet, dans un premier temps, la présence du lien direct invite à se pencher sur les facteurs qui, en plus du concept de soi, de la valeur intrinsèque et de la valeur utilitaire, pourraient expliquer les écarts d’anxiété mathématique observés entre les filles et les garçons. Justement, la piste proposée par le modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006) n’est pas la seule évoquée dans les écrits pour expliquer les écarts d’anxiété mathématique selon le genre. En effet, des facteurs qui se rapportent aux composantes prédispositions affectives et prédispositions cognitives du modèle du contrôle et de la valeur de Pekrun pour les émotions académiques (2006) sont mis en cause pour expliquer les écarts d’anxiété mathématique entre les filles et les garçons.
En regard des prédispositions individuelles affectives, certains auteurs ont proposé que la disparité d’anxiété mathématique selon le genre pourrait s’expliquer par des différences dans le niveau moyen d’anxiété ressenti par les garçons et par les filles (p. ex., Dowker et al., 2016 ; Frenzel et al., 2007 ; Hill et al., 2016). En effet, des études indiquent que les filles ont un niveau moyen d’anxiété générale supérieur à celui des garçons (p. ex., Chapman et al, 2007 ; Costa et al., 2001 ; Feingold, 1994) et une prévalence de troubles anxieux plus élevée que les garçons (p. ex., McLean et al., 2011). À cet égard, Szczygiel (2020) a montré, auprès d’élèves de 1re et de 2e année du primaire, que l’anxiété générale médie la relation entre le genre et l’anxiété mathématique. L’auteure a conclu que les filles pourraient se dire davantage anxieuses à l’égard des mathématiques parce que leur niveau d’anxiété générale est supérieur à celui des garçons, en moyenne.
En regard des prédispositions cognitives, et en lien avec l’hypothèse du déficit, des recherches menées par Delage et al. (2022), Ferguson et al. (2015), Gibeau et al. (2023), Maloney et al. (2012) et Sokolowski et al. (2019), auprès de populations adultes, révèlent qu’une disparité d’habileté spatiale entre les hommes et les femmes pourrait expliquer, à tout le moins en partie, les écarts d’anxiété mathématique observés selon le genre. En effet, ces auteurs ont montré que l’habileté spatiale médie la relation entre le genre et l’anxiété mathématique
Ces divers facteurs liés aux prédispositions cognitives et aux prédispositions affectives du modèle du contrôle et de la valeur de Pekrun pour les émotions académiques (2006) n’ont pas été documentés lors des épreuves du PISA et, en conséquence, ils n’ont pas été étudiés dans le contexte de la présente recherche. Il serait donc des plus pertinents qu’ils soient explorés ou à tout le moins considérés, à titre de covariables, dans le cadre de recherches futures visant à expliquer la disparité d’anxiété mathématique entre les garçons et les filles via le concept de soi, la valeur intrinsèque et la valeur utilitaire des mathématiques. Parallèlement, le fait que les écarts d’anxiété mathématique observés entre les filles et les garçons francophones du Québec s’expliquent en grande partie par un concept de soi en mathématique plus faible chez les filles que chez les garçons, en moyenne, invite, d’un point de vue pratique, à faire du concept de soi un levier d’intervention incontournable en vue de réduire les écarts d’anxiété mathématique entre les filles et les garçons.
De ce fait, ci-après, nous nous intéresserons aux principaux facteurs qui sous-tendent les écarts de concept de soi entre les filles et les garçons. De ces facteurs, nous déduisons des recommandations en vue de réduire les écarts de concept de soi observés entre les garçons et les filles et ainsi, réduire les écarts d’anxiété mathématique entre les filles et les garçons.
Les sources des écarts de concept de soi selon le genre et les recommandations visant à les réduire
Les stéréotypes de genre en mathématiques sont fortement mis en en cause pour expliquer les écarts de concept de soi, selon le genre (p. ex., Ertl et al., 2017 ; Makarova et al., 2019 ; Rossi et al., 2022). En effet, des études ont révélé qu’à compétence égale, les filles qui adhèrent aux stéréotypes de genre en mathématiques font état d’un concept de soi en mathématiques plus faible que les garçons (Ertl et al., 2017 ; Guimond & Roussel, 2001). Au contraire, les garçons qui adhèrent aux stéréotypes de genre en mathématiques révèlent un concept de soi plus élevé que celui de leurs camarades féminines (Rossi et al., 2022).
Les personnes significatives (parents et enseignants) joueraient un rôle clé en regard de la transmission implicite et explicite des stéréotypes de genre (p. ex., Ertl et al., 2017). En effet, en plus d’être susceptibles de transmettre explicitement leurs croyances (Gunderson et al., 2012 ; Herbert & Stipek, 2005), les personnes significatives qui y adhèrent auraient tendance à formuler, envers les filles, des attentes de succès moins élevées en mathématiques qu’envers les garçons (Dresel et al., 2007, cité dans Ertl et al., 2017).
Aussi, les personnes significatives qui adhèrent aux stéréotypes de genre en mathématiques auraient tendance à attribuer les succès et les échecs des apprenants, de manière différenciée selon le genre. Par exemple, ils auraient tendance à attribuer les succès des garçons à leur habileté en mathématiques et ceux des filles à leur diligence (Kessels, 2015), puis à attribuer les échecs des garçons à un manque d’effort et ceux des filles à un manque d’habileté (Dresel et al., 2007, cité dans Ertl et al., 2017). Or, attribuer les succès à l’effort et les échecs à un manque d’effort favoriserait le bon développement du concept de soi, en mathématiques (Ertl et al., 2017).
Toujours en regard des stéréotypes de genre en mathématiques, il appert que les parents et les enseignants qui adhèrent aux stéréotypes de genre en mathématiques auraient aussi tendance à adopter, envers les apprenants, des comportements différenciés, selon le genre. Ils proposeraient, par exemple, davantage de jeux orientés vers la numératie aux garçons et davantage de jeux orientés vers la littératie aux filles (Gunderson et al., 2012). Ils soumettraient des défis mathématiques plus importants aux garçons qu’aux filles (Gunderson et al., 2012), puis ils auraient tendance à s’immiscer davantage dans les travaux des filles liés aux mathématiques. Ces comportements nuiraient au concept de soi des filles en mathématiques. En effet, en agissant de la sorte, les parents et les enseignants laisseraient moins d’occasions aux filles de développer leur familiarité et leurs habiletés dans le domaine (Ertl et al., 2017 ; Mejía-Rodríguez et al., 2021 ; Skaalvik & Skaalvik, 2004). Dans ce contexte, lutter contre les stéréotypes de genre en mathématiques s’avère un levier d’intervention incontournable en vue de réduire les écarts de concept de soi entre les filles et les garçons (Encinas-Martín & Cherian, 2023).
Toutefois, d’autres croyances associées aux mathématiques mériteraient aussi d’être ciblées dans le cadre de cette lutte. En effet, le stéréotype lié au caractère inné des mathématiques (p. ex., « en mathématiques certains et certaines l’ont, d’autres ne l’ont pas ! ») pourrait, lui aussi, nuire au concept de soi des apprenants, notamment celui des filles (Ertl et al., 2017). De ce fait, lutter aussi contre ce stéréotype serait des plus importants, dans le contexte, tout comme le fait de valoriser l’erreur pour apprendre (p. ex., Ertl et al., 2017 ; Ramirez et al., 2018), puis de promouvoir l’effort et le travail bien fait en mathématiques. Comme l’évoque Gourdeau (2019, cité dans Kinnard, 2019) : « La réussite en mathématiques ne dépend pas tant de l’intelligence que de la discipline et du travail. Tous les grands mathématiciens expliquent leur succès par leur travail acharné ».
Afin de réduire les écarts de concept de soi en mathématiques, il serait aussi des plus important, selon Stoet et al. (2016), de favoriser, chez les jeunes filles, la valeur intrinsèque des mathématiques. En effet, à partir d’une analyse secondaire des données du PISA de 2012, Stoet et al. (2016) ont montré que les pays dans lesquels les indices d’égalité sont les plus élevés (une liste de pays qui inclut le Canada) sont aussi les pays où les écarts d’anxiété mathématique, les écarts de concept de soi et les écarts de valeur intrinsèque selon le genre sont les plus élevés. Selon les auteurs, dans les pays plus égalitaires et aussi plus développés, les filles seraient moins fortement assujetties à des considérations économiques au moment de faire des choix de nature académique. En conséquence, elles seraient davantage libres de choisir en fonction des intérêts qui leur sont propres. Dans ce contexte, comparativement aux garçons, elles opteraient dans une mesure moindre, pour les mathématiques, ce qui ferait en sorte qu’elles auraient moins d’occasions de développer leur familiarité avec le domaine et leur habileté dans le domaine. De là, comparativement aux garçons, elles feraient état d’un concept de soi en mathématiques plus faible.
Afin de mener à bien la lutte contre les stéréotypes en mathématiques et de favoriser, chez les jeunes filles, la valeur intrinsèque des mathématiques, il serait essentiel d’amener les parents, les enseignants et autres personnes significatives qui se disent anxieux à l’égard des mathématiques à prendre en charge leur propre anxiété mathématique (p. ex., Beilock et al., 2010 ; Casad et al., 2015 ; Maloney et al., 2015 ; Vukovic et al., 2013). En effet, les personnes qui se disent anxieuses à l’égard des mathématiques sont susceptibles non seulement d’adhérer aux stéréotypes de genre en mathématiques (Beilock et al., 2010 ; Casad et al., 2015 ; Ertl et al., 2017 ; Maloney et al., 2015 ; Vukovic et al., 2013) et de les transmettre (Beilock et al., 2010 ; Bieg et al., 2015 ; Casad et al., 2015 ; Goetz et al., 2013), mais également, de faire état de perceptions négatives à l’égard des mathématiques et de les transmettre. Or, des études ont montré que les adultes peuvent surmonter leur anxiété mathématique, améliorer leur rendement en mathématiques (p. ex., Jamieson et al., 2016 ; Park et al., 2014 ; Passolunghi et al., 2020), puis accroître leur concept de soi en mathématiques (p. ex., Gresham, 2007 cité dans Casad et al., 2015).
En résumé, en vue de réduire les écarts de concept de soi entre les filles et les garçons, il serait essentiel de : 1) lutter contre les stéréotypes en mathématiques, 2) promouvoir l’effort et la persévérance en mathématiques, 3) favoriser, chez les jeunes filles, la valeur intrinsèque des mathématiques et 4) favoriser, chez les personnes significatives, la prise en charge de leur propre anxiété mathématique. Au-delà de tout cela, cependant, selon Goetz et al. (2013), il serait essentiel de lever le voile, auprès des filles, sur le décalage entre performances en mathématiques et concept de soi en mathématiques. En effet, selon ces auteurs, il serait primordial d’amener les filles à réaliser que, même à compétence égale, elles font état, en moyenne, d’un concept de soi en mathématiques plus faible que les garçons. Le simple fait pour elles de se percevoir, à tort, comme étant moins compétentes les amène à se dire davantage anxieuses à l’égard des mathématiques, à moins bien performer en mathématiques et à se détourner des STIM. Il s’agit-là d’une cascade négative qui nuit aux femmes et à la société, en général (OCDE, 2017). Pour Devine et al. (2012), cette cascade est d’autant plus déplorable que, malgré les importants écarts d’anxiété mathématique et de concept de soi observés entre les filles et les garçons, les filles parviennent à obtenir des résultats à peine inférieurs à ceux des garçons, en moyenne, lorsque des écarts de performances en mathématiques sont effectivement observés. Dans ce cas, Devine et al. (2012) en déduisent que les filles sont possiblement dotées d’un très grand potentiel en mathématiques.
Limites
La nature transversale des données analysées dans notre recherche ne nous permet pas de conclure à l’existence d’une relation causale entre le concept de soi, la valeur intrinsèque, la valeur utilitaire et l’anxiété mathématique.
Aussi, « Dans l’optique de réduire au minimum le risque de biais de réponse, les normes de qualité des données du PISA exigent des taux minimums de participation pour les écoles et les élèves. À l’échelle du Canada, un taux de réponse minimum de 85 p. 100 était exigé pour les écoles sélectionnées initialement » (O’Grady et al., 2016, p. 53). « Le PISA exige en outre un taux de participation minimum des élèves de 80 p. 100 dans l’ensemble des écoles participantes (échantillon initial et échantillon de remplacement) à l’échelle du pays » (O’Grady et al., 2016, p. 53). Or, en 2012, au Québec, le taux de participation des écoles au PISA a été supérieur au seuil minimal requis, mais le taux de réponse des élèves a été de 75,6 %, une valeur inférieure au seuil de 80 % fixé par l’OCDE (Brochu et al., 2013). Une analyse des caractéristiques de répondants et des non-répondants a révélé que le phénomène « […] pourrait avoir une incidence marginale sur les résultats du Québec […] » (Brochu et al., 2013, p. 55-56).
En outre, bien que contrairement à la vaste majorité des études, nous ayons documenté, pour les quatre concepts non-cognitifs étudiés dans notre recherche, l’invariance scalaire ou l’invariance scalaire partielle, avant de procéder aux comparaisons de moyennes entre les garçons et les filles, l’idée selon laquelle les écarts observés selon le genre peuvent s’expliquer par des considérations méthodologiques ne peut être exclue (p. ex., Devine et al., 2012 ; Frenzel et al., 2007 ; Hill et al., 2016). En effet, les instruments de mesures autorapportées, comme ceux employés afin de documenter le concept de soi en mathématiques, la valeur intrinsèque, la valeur utilitaire et l’anxiété mathématique, sont reconnus pour être associés à divers types de biais tels que le biais de réponse lié au genre (gender-linked response bias) (Devine et al., 2012, p. 6), le biais de désirabilité sociale (Paulhus, 2017) ou encore le biais de réponse attribuable au calibrage inadéquat des perceptions et des jugements relatifs à l’apprentissage, chez les élèves (Winne & Jamieson-Noel, 2002), etc.
Conclusion
Dans le cadre de cette recherche, nous avons voulu identifier des facteurs qui pourraient permettre d’expliquer les écarts d’anxiété mathématique observés entre les garçons et les filles francophones du Québec de 15 ans, documentés à partir des données du PISA de 2003 et de 2012. En prenant appui sur le postulat de base du modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006), nous avons voulu vérifier si les écarts de concept de soi, de valeur intrinsèque et de valeur utilitaire entre les garçons et les filles peuvent expliquer les écarts d’anxiété mathématique. Nos résultats ont révélé que les écarts de concept de soi et un lien direct genre/anxiété mathématique expliquent les écarts d’anxiété mathématique relevés chez les élèves francophones du Québec. De là, nous avons proposé des pistes à explorer dans le cadre de futures recherches afin d’expliquer le lien direct genre/anxiété mathématique et nous avons proposé une série de recommandations qui pourraient favoriser le bon développement du concept de soi des filles et, ultimement, permettre au plus grand nombre d’entre elles de performer à la hauteur de leur potentiel en mathématiques (OCDE, 2014a).
Parties annexes
Annexe
Annexe A
Tableau A.1
Principales statistiques descriptives des variables étudiées dans l’échantillon de participants francophones du Québec - 2003
Note. ANXMAT = anxiété mathématique, INTMAT = valeur intrinsèque des mathématiques, INSTMOT = valeur utilitaire des mathématiques, SCMAT = concept de soi en mathématiques, PV1 à PV5 = valeurs plausibles 1 à 5, PVMATH = cinq valeurs plausibles combinées, Coeff. asym. = coefficient d’asymétrie, Coeff. apl. = coefficient d’aplatissement. Résultats issus d’analyses personnelles.
Tableau A.2
Principales statistiques descriptives des variables étudiées dans l’échantillon de participants francophones du Québec - 2012
Note. ANXMAT = anxiété mathématique, INTMAT = valeur intrinsèque des mathématiques, INSTMOT = valeur utilitaire des mathématiques, SCMAT = concept de soi en mathématiques, PV1 à PV5 = valeurs plausibles 1 à 5, PVMATH = cinq valeurs plausibles combinées, Coeff. asym. = coefficient d’asymétrie, Coeff. apl. = coefficient d’aplatissement. Résultats issus d’analyses personnelles.
Tableau A.3
Pourcentage de données manquantes dans l’échantillon d’élèves québécois francophones ayant participé au PISA de 2003 et dans l’échantillon d’élèves québécois francophones ayant participé au PISA de 2012
Note. ANXMAT = anxiété mathématique, INTMAT = valeur intrinsèque des mathématiques, INSTMOT = valeur utilitaire des mathématiques, SCMAT = concept de soi en mathématiques, PV1 à PV5 = valeurs plausibles 1 à 5. Résultats issus d’analyses personnelles.
Notes
-
[1]
TIMSS pour Trends In International Mathematics And Science Study, des enquêtes internationales mises en oeuvre par l’IEA (International Association for the Evaluation of Educational Achievement).
-
[2]
PISA pour Programme international pour le suivi des apprentissages, lancé en 2000 par l’OCDE (Organisation de coopération et de développement économiques).
-
[3]
À titre d’exemple, en 2003, 25,9 % des garçons québécois se sont classés dans les niveaux 5 et 6 du PISA, les niveaux de compétence les plus élevés, alors que seulement 19,3 % des filles y sont parvenues (p < 0,05). En 2012, toujours dans le cadre du PISA, 25,3 % des garçons se sont classés dans les niveaux 5 et 6, comparativement à 19,5 % de filles (p < 0,05). Des différences comparables ont aussi été observées dans le cadre du PISA de 2015 et de 2018.
-
[4]
Nous avons privilégié les élèves québécois francophones, car ce groupe constitue la majorité au Québec. Ce choix est par ailleurs justifié dans Vohl (2023) et Vohl et Loye (2024). Notons que, dans le présent article tout comme dans Vohl et Loye (2024), l’appellation « élèves québécois francophones » désigne les élèves québécois issus d’écoles du système scolaire francophone ayant participé au PISA de 2003 et de 2012.
-
[5]
L’item ST01Q03 en 2003 et l’item ST01Q04, en 2012.
-
[6]
Dans les bases de données du PISA de 2003 et de 2012, les cinq valeurs sont identifiées par les variables PV1MATH, PV2MATH, PV3MATH, PV4MATH et PV5MATH.
-
[7]
Dans cette base de données, les participants canadiens ont été identifiés par la variable CNT = CAN, puis les participants québécois francophones ont été identifiés par la variable STRATUM = CAN0545 ou CAN0546 ou CAN0547.
-
[8]
Dans cette base de données, la variable lang_sector a permis d’identifier les participants québécois issus d’écoles francophones.
-
[9]
Les poids de sondage des élèves sont identifiés par la variable W_FSTUWT dans ces bases de données, puis les poids de sondage répliqués par W_FSTR1 à W_FSTR80 (80 poids de sondage répliqués).
-
[10]
« L’estimateur MLR est l’estimateur de vraisemblance maximale qui estime les paramètres, leur erreur type et la statistique du khi carré de manière à ce qu’ils soient robustes à la non-normalité et à la non-indépendance des observations lorsqu’il est utilisé avec TYPE = COMPLEX» [traduction libre] (Muthén & Muthén, 2017, p. 668).TYPE = COMPLEX est utilisé ici, car le plan d’échantillonnage est un plan d’échantillonnage complexe (voir Vohl & Loye, sous presse).
-
[11]
Pour comparer des moyennes latentes, il faut vérifier l’invariance scalaire de l’instrument de mesure. Lorsque des variables latentes sont impliquées dans un modèle de régression linéaire, il faut vérifier leur invariance métrique.
-
[12]
En général, lorsque l’estimateur de vraisemblance maximale robuste (MLR) est employé, un test sur la différence de khi carré par la méthode de Satorra-Bentler (scaled chi-square difference test) (Satorra & Bentler, 2001) entre le modèle multigroupes non contraint et le modèle multigroupes contraint est effectué afin de vérifier l’invariance de deux modèles nichés. Toutefois, ce test n’a pu être mené dans la présente recherche vu l’utilisation des valeurs plausibles (les facteurs de correction fournis par Mplus pour effectuer un test sur la différence de khi carré par la méthode de Satorra-Bentler ne sont pas disponibles lorsque des données imputées sont analysées). Le test sur la différence de khi carré par la méthode de Satorra-Bentler aurait aussi été d’une utilité limitée dans la présente recherche, vu sa grande sensibilité à la taille d’échantillon (p. ex., Kline, 2016).
Liste des références
- Arbuckle, J. L. (1996). Full information estimation in the presence of incomplete data. Dans G. A. Marcoulides & R. E. Schumacker (dir.), Advanced structural equation modeling: Issues and techniques (p. 243–277). Lawrence Erlbaum Associates.
- Ashcraft, M. H. & Kirk, E. P. (2001). The relationships among working memory, math anxiety, and performance. Journal of Experimental Psychology: General, 130(2), 224-237. https://doi.org/10.1037/0096-3445.130.2.224
- Baddeley, A. (1992). Working memory. Science, 255(5044), 556-559. https://doi.org/10.1126/science.1736359
- Baddeley, A. D. & Hitch, G. (1974). Working memory. Psychology of learning and motivation, 8, 47-89.
- Bandura, A. (1977). Self-efficacy: Toward a unifying theory of behavioral change. Psychological Review, 84(2), 191-215. https://doi.org/10.1037/0033-295X.84.2.191
- Bandura, A. (1997). Self-efficacy: The exercise of control. W.H. Freeman.
- Bandura, A. (2003). Auto-efficacité : Le sentiment d’efficacité personnelle (traduit par Jacques Lecomte). De Boeck.
- Beilock, S. L. & Carr, T. H. (2005). When high-powered people fail: Working memory and “choking under pressure” in math. Psychological Science, 16(2), 101-105. https://doi.org/10.1111/j.0956-7976.2005.00789.x
- Beilock, S. L., Gunderson, E. A., Ramirez, G. & Levine, S. C. (2010). Female teachers’ math anxiety affects girls’ math achievement. Proceedings of the National Academy of Sciences of the United States of America, 107(5), 1860-1863. https://doi.org/10.1073/pnas.0910967107
- Bentler, P. M. (1990). Comparative fit indexes in structural models. Psychological Bulletin, 107(2), 238-246. https://doi.org/10.1037/0033-2909.107.2.238
- Bentler, P. M. (1995). EQS structural equations program manual (Vol. 6). Multivariate software.
- Bentler, P. M. & Bonett, D. G. (1980). Significance tests and goodness of fit in the analysis of covariance structures. Psychological bulletin, 88(3), 588-606. https://doi.org/10.1037/0033-2909.88.3.588
- Berger, J.-L. (2015). Apprendre : la rencontre entre motivation et métacognition. Autorégulation dans l’apprentissage des mathématiques en formation professionnelle. Peter Lang.
- Bieg, M., Goetz, T., Wolter, I. & Hall, N. C. (2015). Gender stereotype endorsement differentially predicts girls’ and boys’ trait-state discrepancy in math anxiety. Frontiers in psychology, 6, Article 1404, 1-8. https://doi.org/10.3389/fpsyg.2015.01404
- Bollen, K. A. (1989). Structural equations with latent variables. John Wiley & Sons.
- Brochu, P., Deussing, M.-A., Houme, K. & Chuy, M. (2013). À la hauteur : Résultats canadiens de l’étude PISA de l’OCDE - Le rendement des jeunes du Canada en sciences, en lecture et en mathématiques - Premiers résultats de 2012 pour les jeunes du Canada âgés de 15 ans. Conseil des ministres de l’Éducation (Canada). https://www.cmec.ca/Publications/Lists/Publications/Attachments/318/PISA2012_CanadianReport_FR_Web.pdf
- Bussière, P., Knighton, T. & Cartwright, F. (2004). À la hauteur : Résultats canadiens de l’études PISA de l’OCDE : la performance des jeunes du Canada en mathématiques, en lecture, en sciences et en résolution de problèmes : premiers résultats de 2003 pour les Canadiens de 15 ans. Statistique Canada. https://www.cmec.ca/docs/pisa2003.fr.pdf
- Byrne, B. M. (2012). Structural equation modeling with Mplus: Basic concepts, applications, and programming. Routledge.
- Casad, B. J., Hale, P. & Wachs, F. L. (2015). Parent-child math anxiety and math-gender stereotypes predict adolescents’ math education outcomes. Frontiers in psychology, 6, Article 1597,1-21. https://doi.org/10.3389/fpsyg.2015.01597
- Chapman, O. (2007). Facilitating preservice teachers’ development of mathematics knowledge for teaching arithmetic operations. Journal of Mathematics Teacher Education, 10, 341-349. https://doi.org/10.1007/s10857-007-9046-8
- Chen, F. F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Structural equation modeling: a multidisciplinary journal, 14(3), 464-504. https://doi.org/10.1080/10705510701301834
- Cheung, G. W. & Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Structural equation modeling, 9(2), 233-255. https://doi.org/10.1207/S15328007SEM0902_5
- Chiu, M. M. & Klassen, R. M. (2010). Relations of mathematics self-concept and its calibration with mathematics achievement: cultural differences among fifteen-year-olds in 34 countries. Learning Instruction, 20(1), 2-17. https://doi.org/10.1016/j.learninstruc.2008.11.002
- Correll, S. J. (2001). Gender and the career choice process: The role of biased self-assessments. American journal of Sociology, 106(6), 1691-1730. https://psycnet.apa.org/doi/10.1086/321299
- Costa Jr, P. T., Terracciano, A. & McCrae, R. R. (2001). Gender differences in personality traits across cultures: robust and surprising findings. Journal of personality and social psychology, 81(2), 322-331. https://doi.org/10.1037/0022-3514.81.2.322
- Cronbach, L. J. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16(3), 297-334.
- Delage, V., Trudel, G., Retanal, F. & Maloney, E. A. (2022). Spatial anxiety and spatial ability: Mediators of gender differences in math anxiety. Journal of Experimental Psychology: General, 151(4), 921-933. https://psycnet.apa.org/doi/10.1037/xge0000884
- Devine, A., Fawcett, K., Szűcs, D. & Dowker, A. (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behavioral and brain functions, 8, 1-9. https://doi.org/10.1186/1744-9081-8-33
- Dowker, A., Sarkar, A. & Looi, C. Y. (2016). Mathematics anxiety: What have we learned in 60 years ? Frontiers in psychology, 7, Article 508, 1-16. https://doi.org/10.3389/fpsyg.2016.00508
- Else-Quest, N. M., Hyde, J. S. & Linn, M. C. (2010). Cross-national patterns of gender differences in mathematics: a meta-analysis. Psychological bulletin, 136(1), 103. http://dx.doi.org/10.1037/a0018053
- Encinas-Martín, M. & M. Cherian (2023). Gender, Education and Skills: The Persistence of Gender Gaps in Education and Skills, OECD Skills Studies. Éditions OCDE. https://doi.org/10.1787/34680dd5-en
- Enders, C. K. (2010). Applied missing data analysis. Guilford press.
- Ertl, B., Luttenberger, S. & Paechter, M. (2017). The impact of gender stereotypes on the self-concept of female students in STEM subjects with an under-representation of females. Frontiers in Psychology, 8, Article 703, 1-11. https://doi.org/10.3389/fpsyg.2017.00703
- Feingold, A. (1994). Gender differences in personality: a meta-analysis. Psychological bulletin, 116(3), 429. https://doi.org/10.1037/0033-2909.116.3.429
- Feingold, A. (2019). New approaches for estimation of effect sizes and their confidence intervals for treatment effects from randomized controlled trials. The quantitative methods for psychology, 15(2), 96-111. https://doi.org/10.20982%2Ftqmp.15.2.p096
- Ferguson, A. M., Maloney, E. A., Fugelsang, J. & Risko, E. F. (2015). On the relation between math and spatial ability: The case of math anxiety. Learning Individual Differences, 39, 1-12. https://doi.org/10.1016/j.lindif.2015.02.007
- Fonseca, R., Fontaine, M. M. & Haeck, C. (2021). Le lien entre les compétences en numératie et les rendements sur le marché du travail au Québec (2021RP-11, CIRANO). https://www.cirano.qc.ca/fr/sommaires/2021RP-11
- Frenzel, A. C., Pekrun, R. & Goetz, T. (2007). Girls and mathematics—A “hopeless” issue ? A control-value approach to gender differences in emotions towards mathematics. European Journal of Psychology of Education, 22(4), 497-514. https://doi.org/10.1007/BF03173468
- Geary, D. C. & Widaman, K. F. (1992). Numerical cognition: On the convergence of componential and psychometric models. Intelligence, 16(1), 47-80. https://doi.org/10.1016/0160-2896(92)90025-M
- Gibeau, R. M., Maloney, E. A., Béland, S., Lalande, D., Cantinotti, M., Williot, A., Chanquoy, L., Simon, J., Boislard-Pépin, M.-A. & Cousineau, D. (2023). The Correlates of Statistics Anxiety: Relationships with Spatial Anxiety, Mathematics Anxiety and Gender. Journal of Numerical Cognition, 9(1), 16-43. https://doi.org/10.5964/jnc.8199
- Goetz, T., Bieg, M., Lüdtke, O., Pekrun, R. & Hall, N. C. (2013). Do Girls Really Experience More Anxiety in Mathematics ? Psychological Science, 24(10), 2079-2087. https://doi.org/10.1177%2F0956797613486989
- Goetz, T., Frenzel, A. C., Hall, N. C. & Pekrun, R. (2008). Antecedents of academic emotions: Testing the internal/external frame of reference model for academic enjoyment. Contemporary Educational Psychology, 33(1), 9-33. https://doi.org/10.1016/j.cedpsych.2006.12.002
- Goldman, A. D. & Penner, A. M. (2016). Exploring international gender differences in mathematics self-concept. International Journal of Adolescence and Youth, 21(4), 403-418. https://doi.org/10.1080/02673843.2013.847850
- Graham, J. W., Hofer, S. M. & MacKinnon, D. P. (1996). Maximizing the usefulness of data obtained with planned missing value patterns: An application of maximum likelihood procedures. Multivariate Behavioral Research, 31(2), 197-218. https://doi.org/10.1207/s15327906mbr3102_3
- Guimond, S. & Roussel, L. (2001). Bragging about one’s school grades: Gender stereotyping and students’ perception of their abilities in science, mathematics, and language. Social psychology of education, 4, 275-293. https://doi.org/10.1023/A:1011332704215
- Gunderson, E. A., Ramirez, G., Levine, S. C. & Beilock, S. L. (2012). The role of parents and teachers in the development of gender-related math attitudes. Sex roles, 66, 153-166.
- Hayduk, L. A. (1987). Structural equation modeling with LISREL: Essentials and advances. Jhu Press.
- Henschel, S. & Roick, T. (2017). Relationships of mathematics performance, control and value beliefs with cognitive and affective math anxiety. Learning and Individual Differences, 55, 97-107. https://doi.org/10.1016/j.lindif.2017.03.009
- Herbert, J. & Stipek, D. (2005). The emergence of gender differences in children’s perceptions of their academic competence. Journal of applied developmental Psychology, 26(3), 276-295. https://doi.org/10.1016/j.appdev.2005.02.007
- Hidi, S. & Renninger, K. A. (2006). The four-phase model of interest development. Educational Psychologist, 41(2), 111-127. https://doi.org/10.1207/s15326985ep4102_4
- Hill, F., Mammarella, I. C., Devine, A., Caviola, S., Passolunghi, M. C. & Szűcs, D. (2016). Maths anxiety in primary and secondary school students: Gender differences, developmental changes and anxiety specificity. Learning and individual differences, 48, 45-53. https://doi.org/10.1016/j.lindif.2016.02.006
- Hu, L.-t. & Bentler, P. M. (1999). Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Structural Equation Modeling: A Multidisciplinary Journal, 6(1), 1-55. https://doi.org/10.1080/10705519909540118
- Hyde, J. S., Fennema, E. & Lamon, S. J. (1990). Gender differences in mathematics performance: A meta-analysis. Psychological Bulletin, 107(2), 139-155. https://doi.org/10.1037/0033-2909.107.2.139
- Jamieson, J. P., Peters, B. J., Greenwood, E. J. & Altose, A. J. (2016). Reappraising stress arousal improves performance and reduces evaluation anxiety in classroom exam situations. Social Psychological and Personality Science, 7(6), 579-587. https://psycnet.apa.org/doi/10.1177/1948550616644656
- Joensen, J. S. & Nielsen, H. S. (2009). Is there a causal effect of high school math on labor market outcomes ? Journal of Human Resources, 44(1), 171-198.
- Jöreskog, K. G. (1971). Simultaneous factor analysis in several populations. Psychometrika, 36(4), 409-426.
- Kessels, U. (2015). Bridging the gap by enhancing the fit: How stereotypes about STEM clash with stereotypes about girls. International Journal of Gender, Science and Technology, 7(2), 280-296. https://genderandset.open.ac.uk/index.php/genderandset/article/view/392
- Kinnard, N. (2019, hiver). Qui a peur des mathématiques ? Contact, 26-29. https://contact.ulaval.ca/article_magazine/qui-a-peur-des-mathematiques/index.html
- Kline, R. B. (2016). Principles and practice of structural equation modeling (4e éd.). Guilford Press.
- Kyttälä, M. & Björn, P. M. (2010). Prior mathematics achievement, cognitive appraisals and anxiety as predictors of Finnish students’ later mathematics performance and career orientation. Educational Psychology Review, 30(4), 431-448. https://doi.org/10.1080/01443411003724491
- Little, R. J. & Rubin, D. B. (2002). Statistical analysis with missing data (2e éd.). John Wiley & Sons.
- Lohr, S.L. (2019). Sampling: Design and Analysis (2e éd.). Chapman et Hall/CRC. https://doi.org/10.1201/9780429296284
- Ma, X. (1999). A meta-analysis of the relationship between anxiety toward mathematics and achievement in mathematics. Journal for Research in Mathematics Education, 30(5), 520-540. https://doi.org/10.2307/749772
- Makarova, E., Aeschlimann, B. & Herzog, W. (2019). The gender gap in STEM fields: The impact of the gender stereotype of math and science on secondary students’ career aspirations. Frontiers in Education, 4, Article 60, 1-11.
- Maloney, E. A., Ansari, D. & Fugelsang, J. A. (2011). The effect of mathematics anxiety on the processing of numerical magnitude. The Quarterly Journal of Experimental Psychology, 64(1), 10-16. https://doi.org/10.1080/17470218.2010.533278
- Maloney, E. A., Ramirez, G., Gunderson, E. A., Levine, S. C. & Beilock, S. L. (2015). Intergenerational effects of parents’ math anxiety on children’s math achievement and anxiety. Psychological Science, 26(9), 1480-1488. https://doi.org/10.1177/0956797615592630
- Maloney, E. A., Risko, E. F., Ansari, D. & Fugelsang, J. (2010). Mathematics anxiety affects counting but not subitizing during visual enumeration. Cognition, 114(2), 293-297. https://doi.org/10.1016/j.cognition.2009.09.013
- Maloney, E. A., Waechter, S., Risko, E. F. & Fugelsang, J. (2012). Reducing the sex difference in math anxiety: The role of spatial processing ability. Learning Individual Differences, 22(3), 380-384. https://doi.org/10.1016/j.lindif.2012.01.001
- Maloney, E. A. (2016). Math anxiety: Causes, consequences, and remediation. Dans K. R. Wentzel et D. B. Miele (dir.), Handbook of motivation at school (2e éd., p. 408-423). Routledge.
- Marsh, H. W., Barnes, J. & Hocevar, D. (1985a). Self–other agreement on multidimensional self-concept ratings: Factor analysis and multitrait–multimethod analysis. Journal of Personality and Social Psychology, 49(5), 1360-1377. https://doi.org/10.1037/0022-3514.49.5.1360
- Marsh, H. W., Byrne, B. M. & Shavelson, R. J. (1988). A multifaceted academic self-concept: Its hierarchical structure and its relation to academic achievement. Journal of Educational Psychology, 80(3), 366-380. https://doi.org/10.1037/0022-0663.80.3.366
- Marsh, H. W. & Hau, K.-T. (2004). Explaining paradoxical relations between academic self-concepts and achievements: Cross-cultural generalizability of the internal/external frame of reference predictions across 26 countries. Journal of Educational Psychology, 96(1), 56-67. https://doi.org/10.1037/0022-0663.96.1.56
- Marsh, H. W. & Scalas, L. F. (2011). Self-concept in learning: Reciprocal effects model between academic self-concept and academic achievement. Dans S. Jarvela (dir.), Social and emotional aspects of learning (p. 191-198). Elsevier.
- Marsh, H. W. & Shavelson, R. (1985b). Self-concept: Its multifaceted, hierarchical structure. Educational Psychologist, 20(3), 107-123. https://doi.org/10.1207/s15326985ep2003_1
- Marsh, H. W., Smith, I. D. & Barnes, J. (1985c). Multidimensional self-concepts: Relations with sex and academic achievement. Journal of Educational Psychology, 77(5), 581-596. https://doi.org/10.1037/0022-0663.77.5.581
- Marsh, H. W. & Yeung, A. S. (1998). Longitudinal structural equation models of academic self-concept and achievement: Gender differences in the development of math and English constructs. American Educational Research Journal, 35(4), 705-738. https://doi.org/10.3102/00028312035004705
- Martin, A. J. & Marsh, H. W. (2008). Workplace and academic buoyancy: Psychometric assessment and construct validity amongst school personnel and students. Journal of Psychoeducational Assessment, 26(2), 168-184. https://doi.org/10.1177/0734282907313767
- McDonald, R. P. (1985). Factor analysis and related methods. Lawrence Erlbaum.
- McDonald, R. P. (1999). Test theory: A unified treatment. Lawrence Erlbaum.
- McLean, C. P., Asnaani, A., Litz, B. T. & Hofmann, S. G. (2011). Gender differences in anxiety disorders: prevalence, course of illness, comorbidity and burden of illness. Journal of psychiatric research, 45(8), 1027-1035. https://doi.org/10.1016/j.jpsychires.2011.03.006
- Meece, J. L., Wigfield, A. & Eccles, J. S. (1990). Predictors of math anxiety and its influence on young adolescents’ course enrollment intentions and performance in mathematics. Journal of Educational Psychology, 82(1), 60-70. https://doi.org/10.1037/0022-0663.82.1.60
- Mejía-Rodríguez, A. M., Luyten, H. & Meelissen, M. R. (2021). Gender differences in mathematics self-concept across the world: An exploration of student and parent data of TIMSS 2015. International Journal of Science and Mathematics Education, 19, 1229-1250. https://doi.org/10.1007/s10763-020-10100-x
- Meredith, W. (1993). Measurement invariance, factor analysis and factorial invariance. Psychometrika, 58, 525-543. https://doi.org/10.1007/BF02294825
- Miyake, A. & Shah, P. (dir.). (1999). Models of working memory: Mechanisms of active maintenance and executive control. Cambridge University Press.
- Mullis, I. V., Martin, M. O., Foy, P. & Hooper, M. (2016). TIMSS 2015 International Results in Mathematics. Boston College, TIMSS & PIRLS International Study Center website.
- Mullis, I.V., Martin, M. O., Gonzalez, E. J., Gregory, K. D., Smith, T. A, Chrostowski, S. J. & O’Connor, K. M. (2000). TIMSS 1999 International Mathematics Report Findings from IEA’s Repeat of the Third International Mathematics and Science Study at the Eighth Grade. https://timssandpirls.bc.edu/timss1999i/pdf/T99i_Math_All.pdf
- Muthén, B. O. (1998-2004). Mplus technical appendices. Muthén & Muthén.
- Muthén, L. K. & Muthén, B. O. (2017). Mplus User’s guide (8e éd.). Muthén & Muthén.
- O’Grady, K., Deussing, M.-A., Scerbina, T., Fung, K. & Muhe, N. (2016). À la hauteur : Résultats canadiens de l’étude PISA de l’OCDE – Le rendement des jeunes du Canada en sciences, en lecture et en mathématiques - Premiers résultats de 2015 pour les jeunes du Canada âgés de 15 ans. Conseil des ministres de l’Éducation (Canada). https://www.cmec.ca/Publications/Lists/Publications/Attachments/365/PISA2015-CdnReport-FR.pdf
- O’Grady, K., Deussing, M.-A., Scerbina, T., Tao, Y., Fung, K., Elez, V. & Monk, J. (2019). À la hauteur : Résultats canadiens de l’étude PISA 2018 de l’OCDE – Le rendement des jeunes de 15 ans du Canada en lecture, en mathématiques et en sciences. Conseil des ministres de l’Éducation (Canada). https://www.cmec.ca/Publications/Lists/Publications/Attachments/396/PISA2018_PublicReport_FR.pdf
- OECD (2005a), Apprendre aujourd’hui, réussir demain : Premiers résultats de PISA 2003. Éditions OCDE. https://doi.org/10.1787/9789264007260-fr
- OCDE (2005b). PISA 2003 Technical Report. Éditions OCDE. https://doi.org/10.1787/9789264010543-en
- OCDE (2014a). Résultats du PISA 2012 : Savoirs et savoir-faire des élèves (vol. I). Éditions OCDE. https://doi.org/10.1787/9789264208827-fr
- OCDE (2014b). Résultats de PISA 2012 : Des élèves prêts à apprendre (vol. III). Éditions OCDE. https://doi.org/10.1787/9789264205345-fr
- OCDE (2014c). PISA 2012 Technical Report. Éditions OCDE.
- OCDE (2016). Résultats du PISA 2015 : L’excellence et l’équité dans l’éducation (vol. 1). Éditions OCDE. https://doi.org/10.1787/9789264267534-fr
- OCDE (2017). Recommandation de 2013 du Conseil de l’OCDE sur l’égalité hommes-femmes en matière d’éducation, d’emploi et d’entrepreneuriat. Éditions OCDE. https://doi.org/10.1787/9789264279407-fr
- Park, D., Ramirez, G. & Beilock, S. L. (2014). The role of expressive writing in math anxiety. Journal of Experimental Psychology: Applied, 20(2), 103-111. https://doi.org/10.1037/xap0000013
- Parsons, S. & Bynner, J. (2005). Does numeracy matter more ? National Research and Development Centre for Adult Literacy and Numeracy.
- Passolunghi, M. C., De Vita, C. & Pellizzoni, S. (2020). Math anxiety and math achievement: The effects of emotional and math strategy training. Developmental science, 23(6), e12964 https://doi.org/10.1111/desc.12964
- Paulhus, D. L. (2017). Socially desirable responding on self-reports. Encyclopedia of personality and individual differences, 1-5.
- Pekrun, R. (2006). The control-value theory of achievement emotions: Assumptions, corollaries, and implications for educational research and practice. Educational Psychology Review, 18, 315-341. https://doi.org/10.1007/s10648-006-9029-9
- Raghubar, K. P., Barnes, M. A. & Hecht, S. A. (2010). Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches. Learning Individual Differences, 20(2), 110-122. https://doi.org/10.1016/j.lindif.2009.10.005
- Ramirez, G., Shaw, S. T. & Maloney, E. A. (2018). Math anxiety: Past research, promising interventions, and a new interpretation framework. Educational Psychologist, 53(3), 145-164. https://doi.org/10.1080/00461520.2018.1447384
- Rasch, G. (1960). Studies in mathematical psychology: I. Probabilistic models for some intelligence and attainment tests. Nielsen & Lydiche.
- Richardson, F. C. & Suinn, R. M. (1972). The mathematics anxiety rating scale: psychometric data. Journal of Counseling Psychology, 19(6), 551-554. https://doi.org/10.1037/h0033456
- Rossi, S., Xenidou-Dervou, I., Simsek, E., Artemenko, C., Daroczy, G., Nuerk, H. C. & Cipora, K. (2022). Mathematics–gender stereotype endorsement influences mathematics anxiety, self-concept, and performance differently in men and women. Annals of the New York Academy of Sciences, 1513(1), 121-139. https://doi.org/10.1111/nyas.14779
- Rutkowski, L., Gonzalez, E., Joncas, M. & von Davier, M. (2010). International large-scale assessment data: Issues in secondary analysis and reporting. Educational Researcher, 39(2), 142-151. https://doi.org/10.3102/0013189X10363170
- Ryan, R. M. & Deci, E. L. (2009). Promoting self-determined school engagement. Dans K. R. Wentzel & A. Wigfield (dir.), Handbook of motivation at school (p. 171-195). Routledge.
- Satorra, A. & Bentler, P. M. (2001). A scaled difference chi-square test statistic for moment structure analysis. Psychometrika, 66(4), 507-514. https://doi.org/10.1007/BF02296192
- Seegers, G. & Boekaerts, M. (1996). Gender-related differences in self-referenced cognitions in relation to mathematics. Journal for Research in Mathematics Education, 27(2), 215-240. https://doi.org/10.5951/jresematheduc.27.2.0215
- Skaalvik, S. & Skaalvik, E. M. (2004). Gender differences in math and verbal self-concept, performance expectations, and motivation. Sex roles, 50, 241-252. https://doi.org/10.1023/B:SERS.0000015555.40976.e6
- Shavelson, R. J., Hubner, J. J. & Stanton, G. C. (1976). Self-concept: Validation of construct interpretations. Review of educational research, 46(3), 407-441. https://doi.org/10.3102/00346543046003407
- Skinner, C. & Wakefield, J. (2017). Introduction to the design and analysis of complex survey data. Statistical Science, 32(2), 165-175. https://doi.org/10.1214/17-STS614
- Sokolowski, H. M., Hawes, Z. & Lyons, I. M. (2019). What explains sex differences in math anxiety ? A closer look at the role of spatial processing. Cognition, 182, 193-212. https://doi.org/10.1016/j.cognition.2018.10.005
- Sörbom, D. (1974). A general method for studying differences in factor means and factor structure between groups. British Journal of Mathematical and Statistical Psychology, 27(2), 229-239. https://doi.org/10.1111/j.2044-8317.1974.tb00543.x
- Stapleton, L. M. (2013). Multilevel structural equation modeling with complex sample data. Dans G. R. Hancock & R. O. Mueller (dir.), Quantitative methods in education and the behavioral sciences: Issues, research, and teaching. Structural equation modeling: A second course (p. 521–562). IAP Information Age Publishing.
- Steenkamp, J. B. E. & Baumgartner, H. (1998). Assessing measurement invariance in cross-national consumer research. Journal of consumer research, 25(1), 78-90. https://doi.org/10.1086/209528
- Steinmetz, H. (2011). Estimation and comparison of latent means across cultures. Dans Davidov, P. Schmidt & J. Billiet (dir.), Cross-cultural analysis: Methods and applications (p. 85–116). Routledge/Taylor & Francis Group.
- Stoet, G., Bailey, D. H., Moore, A. M. & Geary, D. C. (2016). Countries with higher levels of gender equality show larger national sex differences in mathematics anxiety and relatively lower parental mathematics valuation for girls. PloS One, 11(4), Article e0153857. https://doi.org/10.1371/journal.pone.0153857
- Stokke, A. (2015). What to do about Canada’s declining math scores ? C.D. Howe Institute Commentary 427. https://doi.org/10.2139/ssrn.2613146
- Szczygiel, M. (2020). Gender, general anxiety, math anxiety and math achievement in early school-age children. Issues in Educational Research, 30(3), 1126-1142. https://search.informit.org/doi/10.3316/informit.465488906598804
- Tucker, L. R. & Lewis, C. (1973). A reliability coefficient for maximum likelihood factor analysis. Psychometrika, 38(1), 1-10. https://doi.org/10.1007/BF02291170
- Vandenberg, R. J. & Lance, C. E. (2000). A review and synthesis of the measurement invariance literature: Suggestions, practices, and recommendations for organizational research. Organizational research methods, 3(1), 4-70.
- Viau, R. (2009). La motivation en contexte scolaire (2e éd.). De Boeck.
- Vohl, P. (2023). Étude des écarts d’anxiété mathématique selon le genre et des facteurs ayant le potentiel de les réduire, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012 [thèse de doctorat, Université de Montréal]. Papyrus. https://papyrus.bib.umontreal.ca/xmlui/handle/1866/32456
- Vohl, P. & Loye, N. (2024). Portrait des écarts d’anxiété mathématique selon le genre et du lien anxiété mathématique/performances en mathématiques, chez les élèves québécois francophones de 15 ans ayant participé au PISA de 2003 et de 2012. Mesure et évaluation en éducation, 46(2), 128-170. https://doi.org/10.7202/1111101ar
- Vohl, P. & Loye, N. (sous presse). Les défis liés à l’analyse secondaire de données issues des évaluations à grande échelle en éducation. Dans N. Loye & N. Duroisin (dir.), Évaluation des apprentissages et technologies numériques : évolution, nouveautés et défis actuels. Peter Lang.
- Vukovic, R. K., Kieffer, M. J., Bailey, S. P. & Harari, R. R. (2013). Mathematics anxiety in young children: Concurrent and longitudinal associations with mathematical performance. Contemporary Educational Psychology, 38(1), 1-10. https://doi.org/10.1016/j.cedpsych.2012.09.001
- Wang, J. & Wang, X. (2020). Structural equation modeling: Applications using Mplus. Wiley.
- Warm, T. A. (1989). Weighted likelihood estimation of ability in item response theory. Psychometrika, 54(3), 427-450. https://doi.org/10.1007/BF02294627
- Widaman, K. F. & Reise, S. P. (1997). Exploring the measurement invariance of psychological instruments: Applications in the substance use domain. Dans K. J. Bryant, M. Windle & S. G. West (dir.), The science of prevention: Methodological advances from alcohol and substance abuse research (p. 281–324). American Psychological Association. https://doi.org/10.1037/10222-009
- Wigfield, A. & Eccles, J. S. (2000). Expectancy–value theory of achievement motivation. Contemporary Educational Psychology, 25(1), 68-81. https://doi.org/10.1006/ceps.1999.1015
- Winne, P. H. & Jamieson-Noel, D. (2002). Exploring students’ calibration of self reports about study tactics and achievement. Contemporary Educational Psychology, 27(4), 551-572. https://doi.org/10.1016/S0361-476X(02)00006-1
Liste des figures
Figure 1
Modèle du contrôle et de la valeur pour les émotions académiques de Pekrun (2006)
Figure 2
Liens direct et indirects spécifiques tels qu’étudiés afin de répondre à l’objectif spécifique 2
Note. c représente le lien direct entre le genre et l’anxiété mathématique, les liens indirects spécifiques sont donnés par les produits suivants : a1 • b1, a2 • b2, a3 • b3 et a4 • b4. Le lien indirect total entre le genre et l’anxiété mathématique est donné par la somme a1 • b1 + a2 • b2 + a3 • b3 + a4 • b4.
Liste des tableaux
Tableau 1
Instruments de mesure du concept de soi en mathématiques, de la valeur intrinsèque des mathématiques, de la valeur utilitaire des mathématiques et de l’anxiété mathématique, tels que proposés par le PISA en 2003 et en 2012
Note. AFC = analyses factorielles confirmatoires, RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation (Root-Mean Square Error of Approximation), RMR = racine carrée de l’erreur quadratique moyenne des résidus (Root Mean Square Residual), SRMR = valeur moyenne quadratique pondérée (Standardized Root Mean-Square Residual), CFI = indice d'ajustement comparatif (Comparative Fit Index), TLI = indice de Tucker Lewis (Tucker Lewis index), α = coefficient alpha de Cronbach (1951), ω = coefficient omega de McDonald (1985, 1999). Des valeurs de RMSEA sous 0,05 indiquent un bon ajustement, puis des valeurs au-dessus de 0,1 sont interprétées comme un ajustement inacceptable. Des valeurs de RMR ou de SRMR sous 0,08 indiquent un bon ajustement et de moins de 0,10, un ajustement acceptable. Des valeurs de CFI, NNFI et TLI entre 0,9 et 0,95 indiquent un ajustement acceptable, puis des valeurs de CFI, NNFI et TLI supérieures à 0,95 indiquent un bon ajustement (Hu & Bentler, 1999). Les informations des colonnes 2 et 3 sont tirées de OCDE (2014b, p. 75, 81, 97, 101). Les informations de la colonne 4 sont tirées de OCDE (2005b, p. 290, 291, 293, 294). Les informations de la colonne 5 proviennent d’analyses personnelles effectuées sur l’échantillon de 2003 et de 2012 de la présente recherche.
Tableau 2
Étude de l’invariance de la mesure de concept de soi en mathématiques, de valeur intrinsèque des mathématiques, de valeur utilitaire des mathématiques
Tableau 3
Écarts de concept de soi, de valeur intrinsèque et de valeur utilitaire, selon le genre, observés chez les élèves québécois francophones ayant participé au PISA de 2003 et de 2012 et tailles d’effets associées
Note.  = coefficient de régression non standardisé estimé de la
variable genre dans le modèle de régression donné par Perception =
= coefficient de régression non standardisé estimé de la
variable genre dans le modèle de régression donné par Perception =  genre +
genre +  performances avec la
référence genre = 0 pour fille ; Er.t. = erreur type du coefficient de
régression
performances avec la
référence genre = 0 pour fille ; Er.t. = erreur type du coefficient de
régression  ; p = valeur p ;
d = taille d’effet ; SCMAT =
concept de soi en mathématiques ; INTMAT = valeur intrinsèque des
mathématiques ; INSTMOT = valeur utilitaire des mathématiques.
; p = valeur p ;
d = taille d’effet ; SCMAT =
concept de soi en mathématiques ; INTMAT = valeur intrinsèque des
mathématiques ; INSTMOT = valeur utilitaire des mathématiques.
Tableau 4
Résultats des liens directs et indirects pour 2003 et 2012, en contrôlant les performances
Note. Les couleurs correspondent à celles employées dans la figure 2. Genre = 0 pour fille, Coeff. = coefficient de régression standardisés par rapport à y, Er.t. = erreur type, p = valeur p, %T = pourcentage de l’effet total, i.c. = intervalle de confiance à 95 %, SCMAT = concept de soi en mathématiques, INTMAT = valeur intrinsèque en mathématiques, INSTMOT = valeur utilitaire en mathématiques, ANXMAT = anxiété mathématique. Pour 2003, le pourcentage de variation expliquée par le modèle et les indices d’ajustement des données au modèle : R2 = 43,2 %, RMSEA = 0,000, CFI = 1,000, TLI = 1,000, SRMR = 0,000. Pour 2012, le pourcentage de variation expliquée par le modèle et les indices d’ajustement sont R2 = 47,2 %, RMSEA = 0,000, CFI = 1,000, TLI = 1,000, SRMR = 0,000.
Tableau 5
Résultats du modèle multigroupes non contraint pour 2003 et pour 2012
Note. Coeff. = coefficient de régression non standardisés, Er.t. = erreur type, p = valeur p, R2 = pourcentage de variation expliquée par le modèle, INTMAT = valeur intrinsèque en mathématiques, INSTMOT = valeur utilitaire en mathématiques, SCMAT = concept de soi en mathématiques, RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation, CFI = indice d’ajustement comparatif, TLI = indice de Tucker et Lewis, SRMR = valeur moyenne quadratique pondérée.
Tableau 6
Résultats du modèle multigroupes contraint pour 2003 et pour 2012
Note. Coeff. = coefficient de régression non standardisés, Er.t. = erreur type, p = valeur p, R2 = pourcentage de variation expliquée par le modèle, INTMAT = valeur intrinsèque en mathématiques, INSTMOT = valeur utilitaire en mathématiques, SCMAT = concept de soi en mathématiques, RMSEA = racine carrée de l’erreur quadratique moyenne d’approximation, CFI = indice d’ajustement comparatif, TLI = indice de Tucker et Lewis, SRMR = valeur moyenne quadratique pondérée, ∆CFI = changement de l’indice d’ajustement comparatif entre le modèle contraint et le modèle non contraint.
Tableau A.1
Principales statistiques descriptives des variables étudiées dans l’échantillon de participants francophones du Québec - 2003
Note. ANXMAT = anxiété mathématique, INTMAT = valeur intrinsèque des mathématiques, INSTMOT = valeur utilitaire des mathématiques, SCMAT = concept de soi en mathématiques, PV1 à PV5 = valeurs plausibles 1 à 5, PVMATH = cinq valeurs plausibles combinées, Coeff. asym. = coefficient d’asymétrie, Coeff. apl. = coefficient d’aplatissement. Résultats issus d’analyses personnelles.
Tableau A.2
Principales statistiques descriptives des variables étudiées dans l’échantillon de participants francophones du Québec - 2012
Note. ANXMAT = anxiété mathématique, INTMAT = valeur intrinsèque des mathématiques, INSTMOT = valeur utilitaire des mathématiques, SCMAT = concept de soi en mathématiques, PV1 à PV5 = valeurs plausibles 1 à 5, PVMATH = cinq valeurs plausibles combinées, Coeff. asym. = coefficient d’asymétrie, Coeff. apl. = coefficient d’aplatissement. Résultats issus d’analyses personnelles.
Tableau A.3
Pourcentage de données manquantes dans l’échantillon d’élèves québécois francophones ayant participé au PISA de 2003 et dans l’échantillon d’élèves québécois francophones ayant participé au PISA de 2012





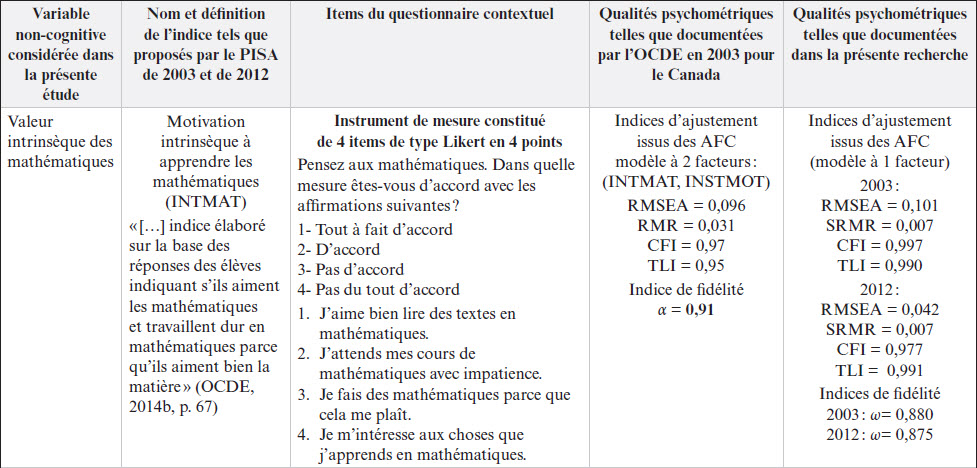


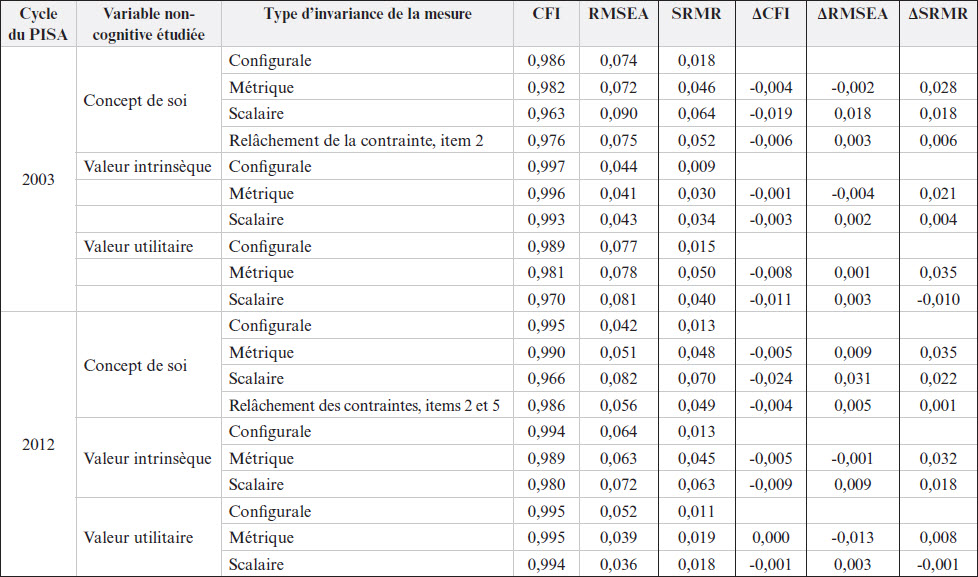






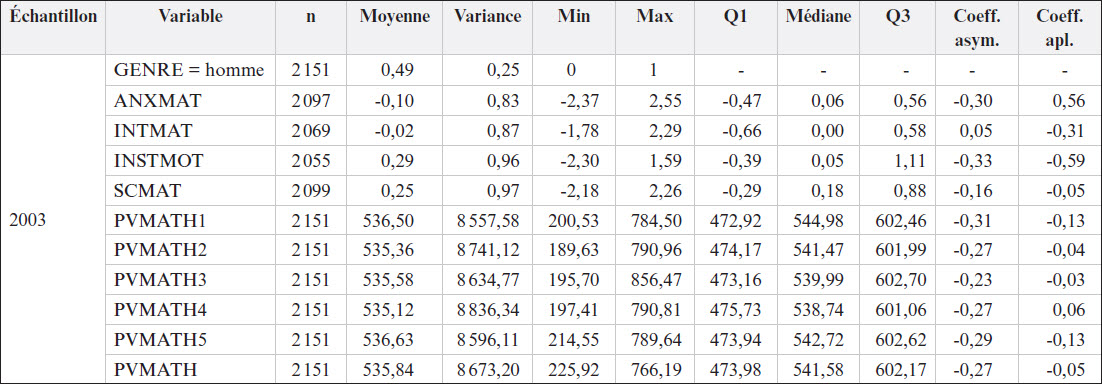


 10.7202/1111101ar
10.7202/1111101ar