Étude des liens entre les variables sociodémographiques et scolaires par rapport au rendement des élèves du primaire et à la perception des enseignants des difficultés d’apprentissage en mathématiques

Rajotte, Thomas; Dufour, Raphaëlle; Boivin, Émilie

doi:https://doi.org/10.18162/fp.2024.802

Contexte de l’étude

Au cours des dernières décennies, des efforts considérables ont été mis en oeuvre par les instances ministérielles ainsi que les professionnels issus du milieu de l’éducation afin de soutenir la réussite des élèves en mathématiques. Cet intérêt découle notamment du fait que les mathématiques sont considérées comme une source importante de développement intellectuel qui constitue un atout significatif des élèves dans la société québécoise où les retombées pratiques de cette discipline sont aussi nombreuses que diversifiées (MELS, 2012; MEES, 2019).

Le regard sur la réussite des élèves et son apport dans la vie courante a amené le gouvernement du Québec à mettre en oeuvre un processus de réflexion visant à approfondir la nature des difficultés d’apprentissage ainsi que les interventions efficaces permettant d’accompagner les élèves vers la réussite (MELS, 2012). Par ailleurs, les modalités d’interprétation des difficultés et de la mise en place des interventions qui en découlent sont au coeur d’importants débats au sein de la communauté scientifique.

Pour notre part, notre étude corrélationnelle réalisée auprès d’un bassin de 262 dyades impliquant des élèves du primaire et leur titulaire de l’autorité parentale vise justement à étudier les facteurs sociodémographiques et scolaires explicatifs du rendement en mathématique des élèves et de la perception des dix-neuf enseignants interrogés à l’égard des difficultés d’apprentissage relevant de cette discipline.

Introduction

Des perspectives opposées pour interpréter les difficultés d’apprentissage

Dans le domaine des mathématiques, les écrits scientifiques se rapportent essentiellement à deux perspectives explicatives distinctes permettant d’interpréter les difficultés en mathématiques des élèves du primaire (Rajotte et al., 2014). La première perspective est essentiellement centrée sur l’identification et la description des dysfonctionnements propres à l’élève (Giroux, 2010). Selon le regard de Martin et Mary (2010) ainsi que de Rajotte et ses collaborateurs (2014), celle-ci s’appuie principalement sur les travaux de chercheurs oeuvrant dans les domaines de la neuropsychologie, de la psychologie cognitive ainsi que de la psychologie développementale. Les tenants de cette perspective cognitive attribuent les difficultés d’apprentissage directement à l’élève. Celles-ci sont alors considérées comme étant la résultante des caractéristiques fonctionnelles et cognitives de l’apprenant (Lemoyne et Lessard, 2003) et peuvent être mesurées à l’aide d’instruments d’évaluation standardisés (Giroux, 2010). Cette méthode d’évaluation consiste à attribuer un diagnostic (tel que la dyscalculie) ou à mettre en lumière des caractéristiques cognitives particulières en ciblant les élèves qui s’éloignent de la moyenne établie pour les élèves de leur âge (Houle, 2019). Comme le rapportent Barallobrès (2018) et Monnin (2010), cette vision concernant la nature des difficultés en mathématiques, ainsi que l’idéologie sous-jacente à la normalisation des processus cognitifs des élèves, ouvrent la porte à la médicalisation de l’éducation.

D’un autre côté, comme rapporté par Roiné (2009), les travaux de recherche se rapportant à la deuxième perspective explicative relèvent du domaine de la didactique des mathématiques. Dans le cadre de cette perspective, les difficultés d’apprentissage sont présentées comme étant la résultante de l’interaction de l’élève avec le système scolaire ainsi que de l’interprétation des phénomènes qui découlent de cette interaction (Perrin-Glorian, 1993; Rajotte et al., 2014). De ce fait, les tenants de cette perspective suggèrent d’intervenir auprès des élèves en considérant simultanément la spécificité du savoir, le niveau de connaissances mathématiques des élèves ainsi que la nature de la relation qu’entretient l’enseignant auprès de l’apprenant (Martin et Mary, 2010).

Un regard sur l’évolution des législations et des politiques propres à l’adaptation scolaire permet de relever que le ministère de l’Éducation et les orientations qu’il promeut se rapportent à la première perspective explicative, soit la perspective cognitive (Rajotte, 2014). Dégagé de la Politique de l’adaptation scolaire (MEQ, 1999), ce positionnement a pour objectif de recadrer les grandes orientations de la dernière réforme québécoise quant aux besoins particuliers et aux caractéristiques particulières des élèves handicapés ou rencontrant des difficultés d’adaptation ou d’apprentissage (EHDAA). Comme le souligne Giroux (2013), cette politique comprend une injonction ministérielle à l’égard des enseignants afin qu’ils adaptent leur pédagogie ainsi que leurs modalités d’enseignement aux caractéristiques et aux besoins des élèves. Toutefois, il s’avère difficile pour les enseignants d’appliquer ces visions de l’adaptation de l’intervention aux élèves en difficulté puisqu’il existe peu de données scientifiques permettant de mettre en lumière les caractéristiques particulières se rapportant à cette catégorie d’élèves (Houle, 2019) ni de moyens didactiques et d’appuis théoriques permettant d’effectuer ce type d’adaptation (Rajotte et al., 2020).

À ce sujet, Houle (2019) ajoute que ce type de centration sur les difficultés des élèves peut conduire à négliger la prise en compte des conditions didactiques nécessaires à l’apprentissage. Ainsi, l’aide apportée aux élèves en difficulté consiste alors à simplifier les tâches et à viser la réussite sans prendre en compte les connaissances véritablement engagées par les élèves (Houle, 2019).

Par ailleurs, des restrictions concernant la portée des résultats ont aussi été mises en lumière concernant l’application des postulats sous-jacents à la deuxième perspective explicative, qui relève essentiellement du domaine de la didactique des mathématiques (Rajotte et al., 2020). En effet, bien que de nombreux travaux réalisés par les chercheurs se rapportant à cette perspective aient permis de documenter les spécificités de l’enseignement dispensé aux différentes catégories d’élèves en difficulté, ce type de recherche implique généralement des analyses approfondies nécessitant un échantillon restreint d’individus (Giroux, 2013).

À la lumière de ce constat, Giroux (2013) soutient que les difficultés en mathématiques et la problématique de l’échec scolaire sont si complexes qu’elles nécessitent des outils d’analyse provenant des sciences sociales. Par ailleurs, les écrits scientifiques se rapportant aux sciences sociales, ayant pour objectif d’expliquer la nature des difficultés d’apprentissage, sont peu nombreux étant donné qu’ils ont été supplantés dans les dernières années par les travaux se rapportant aux sciences cognitives (Giroux, 2013). À ce sujet, il s’avère pertinent de prendre en considération les travaux issus des sciences sociales pour expliquer les difficultés des élèves, ce qui a d’ailleurs été mis en lumière par une récente étude (Rajotte et al., 2020). En fait, cette recherche a permis de relever que des professionnels issus du milieu de l’éducation (enseignants du primaire, orthopédagogues, conseillers pédagogiques) se basent parfois simultanément sur les postulats sous-jacents aux trois perspectives (sciences cognitives, didactique des mathématiques et sciences sociales) lorsqu’ils se positionnent concernant les modalités permettant d’identifier et d’intervenir auprès d’élèves caractérisés comme ayant des difficultés d’apprentissage en mathématiques.

Interpréter les difficultés en mathématiques : regard sur les postulats issus des sciences sociales

Différents débats ont eu lieu au cours des dernières années entre les tenants des deux principales approches explicatives. Dans cette foulée, une troisième perspective a alors émergé de certains travaux européens qui abordaient les difficultés d’apprentissage en mathématiques (Ahmad, 2014; Chopin, 2011; Rajotte et al., 2020; Roiné, 2012). Cette perspective provient essentiellement des sciences sociales et considère que la genèse des difficultés relève d’un processus collectif d’acculturation (Roiné, 2015).

Pour interpréter les difficultés des élèves en mathématiques, l’approche utilisée par les tenants de cette troisième perspective réfère à l’anthropodidactique (Bergeron, 2017), qui se situe au croisement de l’anthropologie et de la didactique (Sarrazy, 2001). Selon cette approche, les situations d’enseignement et les difficultés qui en découlent sont déterminées à la fois par les conditions didactiques et par les conditions non didactiques (des arrière-plans culturel et social). Cela signifie qu’elles sont interprétées au regard des habitudes et des manières de faire de l’enseignant ou de l’élève par rapport à l’enseignement d’un savoir mathématique spécifique, mais aussi en fonction des croyances, des désirs, des valeurs sociales ainsi que des idéologies de l’enseignant, de l’élève et des institutions (Bergeron, 2017). L’approche anthropodidactique met l’accent sur l’importance de considérer l’ensemble de ces facteurs afin d’interpréter la nature des interactions entre l’élève et l’enseignant (Rajotte et al., 2020). Celle-ci met en lumière le rôle de l’arrière-plan scolaire et social, ainsi que le statut scolaire de l’élève, comme étant des facteurs prépondérants qui contribuent à moduler l’intervention pédagogique mise en oeuvre auprès de certaines catégories d’élèves (Bergeron, 2017).

L’approche anthropodidactique place donc en relation les inégalités scolaires et les positions sociales (Bourdieu, 2002; Ayala et Roditi, 2014; Rajotte, 2018). Conséquemment, cette approche s’intéresse aux mécanismes par lesquels l’institution scolaire agit en tant que système de reproduction des inégalités sociales (Van Haecht, 2006) ou, en d’autres mots, à la manière dont l’institution scolaire transforme le classement social des élèves en classement scolaire (Giroux, 2013). Selon ce point de vue, l’école contribuerait à transformer les différences de classes sociales en différences d’intelligence (Rajotte et al., 2018). Ainsi, au fil des générations, les classes considérées supérieures (en référence à un niveau socioéconomique plus élevé) préserveraient leur statut privilégié, et ce, en raison de ce mécanisme (Van Haecht, 2006). Rajotte (2014) propose une piste explicative à ce phénomène selon laquelle le contrat didactique, ainsi que la nature des interactions entre le milieu, les élèves et l’enseignant pourraient être modulés dans les classes du primaire en fonction de sous-catégories de classements sociaux d’apprenants. Au regard de cette troisième perspective interprétative des difficultés d’apprentissage, il serait pertinent de mettre à l’épreuve empiriquement cette hypothèse. Cela pourrait permettre de contribuer à documenter les liens possibles qu’entretiennent différents facteurs sociodémographiques concernant le rendement des élèves en mathématiques ainsi qu’en lien avec la perception de l’enseignant du rendement de l’élève dans cette discipline scolaire.

Synthèse des différentes perspectives interprétatives et de leurs postures

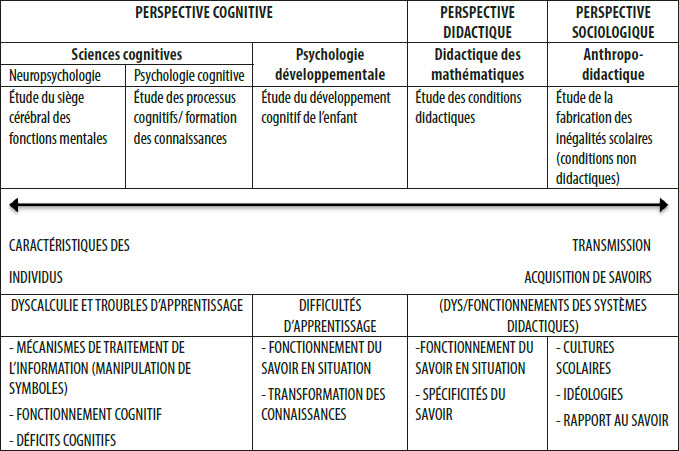
Giroux (2015) propose un schéma qui permet d’organiser les différentes disciplines qui étudient les difficultés d’apprentissage en mathématiques, et ce, en fonction de leur finalité ou de leur posture épistémologique. La figure 1 permet de refléter les finalités des différentes disciplines sur un axe transversal.

Les propos de Giroux (2015) permettent de relever que les tenants de la première perspective, soit la perspective cognitive, se situent à la gauche de l’axe. Cette perspective comprend, entre autres, les recherches issues de la psychologie développementale, de la neuropsychologie et des sciences cognitives. Le positionnement à la gauche de l’axe se justifie notamment par le fait que les chercheurs qui oeuvrent au sein de cette discipline adoptent un cadre explicatif centré sur les caractéristiques individuelles des apprenants. Ensuite, au centre droit du continuum se trouvent les tenants de la seconde perspective, soit les chercheurs rattachés à la perspective didactique qui axent leur objet d’étude sur les interactions entre l’élève et le système didactique. Finalement, il est possible de constater que pour ce qui est des chercheurs qui adhèrent à la troisième perspective, soit celle des sciences sociales, ces derniers se retrouvent à l’extrême droite du continuum. Cela se justifie par le fait que les tenants associés à cette perspective expliquent les difficultés d’apprentissage en portant un regard simultané sur la structure du savoir mathématique en jeu ainsi qu’en fonction des dimensions socioculturelles qui sont susceptibles de favoriser l’émergence de ces difficultés.

Figure 1

***Adaptation de Rajotte et al. (2020) du schéma de Giroux concernant l’organisation des disciplines qui étudient les difficultés d’apprentissage selon Giroux (2015)***

Objectifs de recherche

Au cours des dernières décennies, de nombreuses études ont contribué à mettre à l’épreuve les deux premières perspectives explicatives des difficultés d’apprentissage en mathématiques. Par ailleurs, la troisième piste explicative, se rapportant au domaine des sciences sociales, a fait l’objet d’un nombre plus restreint de travaux de recherche visant à éprouver sa pertinence et son bien-fondé[1]. À ce sujet, il importe de mentionner que d’autres recherches réalisées dans un champ plus large que celui de l’enseignement et de l’apprentissage des mathématiques ont permis d’établir que le milieu familial, notamment en ce qui a trait au niveau socioéconomique, constitue un facteur important pour favoriser le rendement scolaire. Basque et Bouchamma (2018) approfondissent ce propos en soutenant que les enseignants et les directeurs d’établissement scolaire perçoivent que la collaboration des parents, le statut socioéconomique qui caractérise la famille ainsi que l’encadrement et l’implication des parents constituent des facteurs extrinsèques à l’élève qui sont rattachés au rendement de celui-ci.

Dans le but de mettre à l’épreuve la perspective des sciences sociales, l’étude de Rajotte et ses collaborateurs (2018), réalisée en Abitibi-Témiscamingue, a relevé que les indicateurs ministériels de défavorisation (indice de milieu socioéconomique (IMSE) et indice du seuil de faible revenu (SFR)) sont liés à la perception qu’entretiennent les enseignants à l’égard du rendement des élèves en mathématiques. Par ailleurs, ces indicateurs agissent moindrement au niveau du rendement des élèves à répondre à un questionnaire écrit sollicitant des habiletés en mathématiques.

Cependant, en impliquant des participants issus de communautés majoritairement francophones et caucasiennes, l’étude de Rajotte et ses collaborateurs (2018) n’a pas permis de relever une relation qu’entretiennent certaines variables sociales, telles que l’ethnicité et la langue maternelle sur la perception des enseignants. Conséquemment, l’objectif général de la présente recherche consiste à mettre à l’épreuve la perspective explicative des sciences sociales quant à l’interprétation des difficultés d’apprentissage d’élèves issus de centres urbains caractérisés de cosmopolites. Des variables sociales qui n’ont pas été prises en compte dans l’étude de 2018 de Rajotte et ses collaborateurs seront alors étudiées.

En considérant une diversité de variables sociales susceptibles d’entretenir une relation avec la perception qu’entretiennent les enseignants à l’égard des difficultés des élèves en mathématiques ainsi qu’en lien avec le rendement des élèves en mathématiques, cette étude comporte deux objectifs distincts, soit :

Explorer et décrire les liens entre différents facteurs se rapportant au profil sociodémographique des élèves du primaire ainsi que celui des titulaires de leur autorité parentale par rapport au rendement de l’élève dans la résolution d’un questionnaire écrit de mathématiques ;
Explorer et décrire les liens entre différents facteurs se rapportant au profil sociodémographique des élèves du primaire ainsi que celui des titulaires de leur autorité parentale par rapport à la perception qu’entretiennent les enseignants à l’égard des difficultés des élèves en mathématiques.

Méthodologie

Afin de réaliser cette étude, un devis de recherche corrélationnel de type descriptif (Pelletier et al., 2000) a été mis en oeuvre. Dans ce type de devis, les variables sont étudiées et analysées sans être manipulées ou subir un contrôle expérimental. Plus spécifiquement, dans le cadre de ce type de devis, le chercheur transpose des données sous forme de variables, leur attribue une valeur et établit le niveau de relation entre chacune des variables à l’aide d’un coefficient de corrélation (Pelletier et al., 2000). Les chercheurs qui utilisent ce type de devis visent essentiellement à définir les facteurs ou les caractéristiques qui sont associées à un phénomène précis.

Participants à l’étude

Afin de constituer l’échantillon de l’étude, une technique non probabiliste de type accidentel a été mise en oeuvre (Fortin, 2010; Voyer et al., 2000). Des élèves de la deuxième année du deuxième cycle ainsi que des élèves du troisième cycle du primaire issus de trois centres de services scolaires distincts ont été ciblés (Centre de services scolaire des Navigateurs, Centre de services scolaire des Découvreurs, Centre de services scolaire de la Capitale). Au total, 262 élèves provenant de 14 écoles primaires différentes ont été rencontrés (115 élèves de quatrième année, 54 élèves de cinquième année et 96 élèves de sixième année[2]). Pour chaque élève participant au projet, des données ont aussi été collectées auprès des titulaires de l’autorité parentale par l’entremise du formulaire de consentement parental qui visait simultanément à recueillir des données sociodémographiques concernant les parents. De plus, pour chacun des participants, des données complémentaires ont été collectées auprès des enseignants ayant accepté de participer au projet d’étude. Cette collecte de données complémentaire a impliqué la participation de dix-neuf enseignants distincts.

Concernant la constitution de l’échantillon de l’étude, il importe de mentionner que nous anticipions de recueillir des données auprès de plus de 400 participants. À cet effet, plusieurs visites dans les milieux scolaires étaient prévues au courant du printemps 2020. Par ailleurs, la pandémie de la COVID-19 a entraîné la fermeture des écoles primaires sur plusieurs semaines. Dans la foulée, pour des raisons de santé publique, l’équipe de recherche ne s’est pas déplacée dans le milieu scolaire au courant des mois de mai et juin 2020.

Variables à l’étude et instruments de mesure

Afin de mettre en oeuvre le projet de recherche, pour chaque participant à l’étude, des données ont été recueillies auprès de trois catégories de répondants distincts, soit : 1) les titulaires de l’autorité parentale des élèves, 2) les élèves, 3) les enseignants titulaires de chacun des élèves. Les prochaines sections permettront de détailler les différentes variables recueillies auprès de ces trois catégories de participants ainsi que les instruments de mesure utilisés afin de procéder à la collecte de données.

Données recueillies auprès des titulaires de l’autorité parentale des élèves

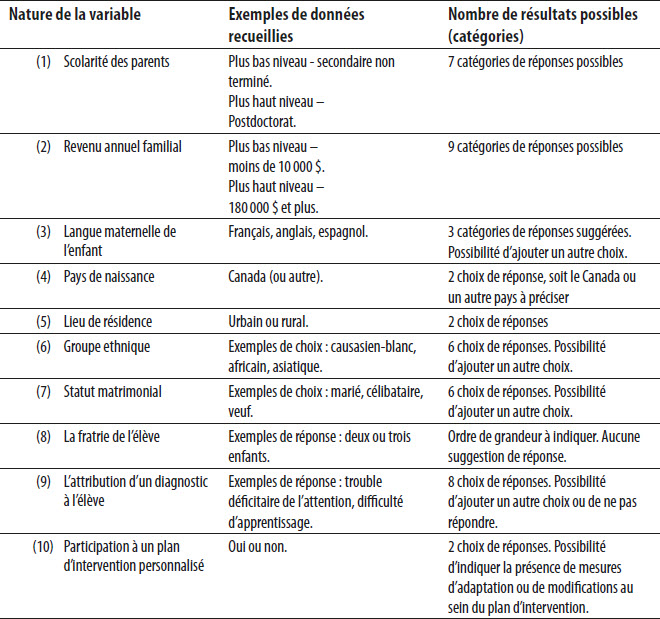
En remplissant le formulaire de consentement concernant la participation à l’étude, les titulaires de l’autorité parentale étaient invités à remplir un questionnaire visant à recueillir des données en lien avec leur profil sociodémographique et leur environnement familial. Les données ainsi recueillies se rapportaient en dix variables distinctes. Le tableau suivant présente une synthèse des variables ainsi qu’un aperçu des données recueillies.

Tableau 1

***Synthèse des variables et aperçu des données recueillies auprès des titulaires de l’autorité parentale***

Données recueillies auprès des élèves du primaire

Différentes données ont été recueillies auprès des élèves du primaire à l’aide d’un questionnaire comprenant quatre sections distinctes, soit : des données individuelles, leur niveau de motivation scolaire, leur perception des pratiques enseignantes en classe ainsi qu’un test de rendement en mathématiques impliquant six énoncés de problèmes élaborés par l’équipe de recherche et adaptés au degré scolaire des élèves.

Concernant les données individuelles sous-jacentes à l’élève, chaque participant devait inscrire son genre (garçon ou fille), son âge, son mois de naissance ainsi que son rang dans la famille (aîné, benjamin, cadet ou enfant unique). La section concernant le niveau de motivation scolaire comprenait quant à elle douze questions distinctes. Ces questions provenaient d’un test validé au Québec par une équipe de chercheurs en psychologie (Vallerand et al., 1993). Sur le plan de la consistance interne, l’équipe de recherche de Vallerand et al. (1993) a fixé l’alpha de Cronbach de l’outil à 0,80. Les différentes questions se rapportaient à une échelle de type Likert et impliquaient quatre possibilités de choix (1- tout à fait en désaccord ; 4 – tout à fait en accord). L’échelle de Vallerand et al. (1993) permet d’évaluer quatre sous-construits de la motivation scolaire, soit :

l’amotivation, qui désigne la perception d’un individu de mettre en place des efforts sans que ceux-ci ne portent fruit ;
la motivation intrinsèque, qui réfère au fait de réaliser une activité pour la satisfaction et le plaisir que l’on en retire ;
la motivation extrinsèque identifiée, qui consiste en la régulation d’un comportement par le choix libre d’un individu qui est en mesure de relever les motifs qui justifient ce choix ;
la motivation extrinsèque introjectée, qui consiste en la régulation d’un comportement par des sources de contrôle intériorisées par l’individu ; ces sources de contrôle exerçant une pression sur cette personne.

Finalement, une dernière section du questionnaire visait à évaluer le rendement en mathématiques des élèves du primaire selon des concepts mathématiques qui variaient en fonction du niveau scolaire des élèves. Cette section comportait six questions distinctes et avait fait l’objet d’une préexpérimentation auprès de deux classes afin d’assurer que le niveau de difficulté ainsi que la formulation des énoncés étaient adaptés au degré scolaire des élèves. Chaque question se rapportait à un énoncé de problèmes mathématiques. La majorité des questions se rapportait au champ des structures multiplicatives. Par ailleurs, le questionnaire acheminé aux élèves de quatrième année comportait une question en lien avec les structures additives, tandis que les élèves du troisième cycle devaient résoudre une question en lien avec le sens « partie-tout » de la fraction. L’évaluation était réalisée en fonction de l’adéquation des calculs relationnel et numérique par rapport aux énoncés proposés.

Données recueillies auprès des enseignants titulaires d’une classe du primaire

En s’appuyant sur la méthode proposée par Sovik, Frostrad et Heggberget (1999), les enseignants titulaires d’une classe du primaire devaient se prononcer concernant leur perception du rendement scolaire en attribuant une cote de 1 à 5 à chaque élève pour leur niveau de compétence en lecture ainsi que leur niveau de compétence en résolution de problèmes mathématiques (la cote 1 signifiait que le rendement de l’élève était nettement supérieur aux attentes, tandis que la cote 5 caractérisait un rendement nettement inférieur aux attentes).

Toujours en utilisant la méthode de Sovik et ses collaborateurs (1999), les enseignants portaient un jugement évaluatif concernant le niveau de risque de chaque élève de décrocher du système scolaire. Pour ce faire, cinq critères d’évaluation étaient utilisés : 1) aucun ; 2) faible ; 3) moyen ; 4) élevé ; 5) très élevé.

Des données ont aussi été recueillies en lien avec le milieu d’appartenance des enseignants titulaires. En effet, en se basant sur les indicateurs ministériels du niveau de défavorisation des écoles québécoises, il a été possible de créer deux variables supplémentaires, soit l’indice de milieu socioéconomique, qui est établi à partir du niveau de scolarité de la mère et du niveau d’employabilité des parents (IMSE) ainsi que le seuil de faible revenu (SFR), qui correspond à la proportion des familles avec enfants dont le revenu est situé près ou sous le seuil de faible revenu. En correspondance avec le document Indices de défavorisation des écoles publiques 2019-2020, publié par le gouvernement du Québec (2020), une valeur a été attribuée à chaque milieu scolaire pour ces deux indicateurs.

Déroulement de l’expérimentation

L’expérimentation, puisqu’elle a été pilotée par le même assistant de recherche, s’est déroulée de la même façon pour les 19 classes du primaire. La première étape de l’expérimentation touchait les titulaires de l’autorité parentale des élèves qui devaient, dans un délai de deux semaines, remplir un formulaire de consentement parental visant à recueillir des informations sur leurs données sociodémographiques.

La deuxième étape de l’expérimentation, d’une durée de 60 minutes, se déroulait en classe avec les élèves ayant reçu le consentement de l’autorité parentale. Pour débuter, l’assistant de recherche approchait les élèves avec une discussion sur les caractéristiques d’une recherche ainsi que sur les retombées des recherches dans le monde de l’éducation afin de les sensibiliser à l’importance de leur participation. Ensuite, l’assistant de recherche expliquait aux élèves les sections du questionnaire qu’ils devaient remplir. Durant l’expérimentation, les élèves étaient autorisés à lever leur main et à poser des questions à l’assistant de recherche en cas de besoin.

Finalement, la troisième étape, qui se déroulait simultanément avec l’étape précédemment énoncée, impliquait une collecte de données réalisée auprès des enseignants titulaires. En effet, en utilisant une grille de notation, ceux-ci devaient se prononcer sur leur perception du rendement scolaire et porter un jugement évaluatif concernant le niveau de risque de chaque élève de décrocher du système scolaire.

Analyses statistiques effectuées

Les analyses ont été réalisées en utilisant la version 27 du logiciel SPSS. Dans le but de répondre aux objectifs de recherche, des analyses de régression de type pas à pas (stepwise) ont été réalisées. Ce type d’analyse permet de mettre en relation un groupe de variables indépendantes avec une variable dépendante ainsi que de hiérarchiser les différentes variables corrélées selon leur ordre d’importance respective. Les données recueillies auprès des titulaires de l’autorité parentale, des élèves, des enseignants ont été insérées comme variables indépendantes susceptibles d’influer sur deux variables dépendantes distinctes, soit : le rendement des élèves à un questionnaire écrit de mathématiques ainsi que la perception de l’enseignant quant au rendement de l’élève en mathématiques.

Résultats de recherche

Afin de répondre aux deux objectifs de recherche, nous avons mis en oeuvre deux analyses de régression de type pas à pas. Les deux prochaines sections présentent les résultats des analyses qui ont été réalisées.

Analyse des facteurs liés au rendement à résoudre un questionnaire écrit de mathématiques

Afin de répondre au premier objectif de recherche, qui consiste à explorer et à décrire les liens entre différents facteurs se rapportant au profil sociodémographique des élèves du primaire ainsi que celui des titulaires de leur autorité parentale par rapport au rendement de l’élève à résoudre un questionnaire écrit de mathématiques, nous avons réalisé une première analyse de régression multiple. Ainsi, les différents modèles de régression multiple retenus à la suite de l’analyse sont présentés dans le tableau 2 et les valeurs de coefficient de régression sont mises de l’avant dans le tableau 3.

Tableau 2

***Première analyse : R-carré et R-carré ajusté des différents modèles de régression multiple retenus***

Tableau 3

***Coefficients standardisés (bêta), test T et degré signification des variables associées au rendement à résoudre un questionnaire écrit***

Le cinquième modèle de régression a été retenu puisque celui-ci permet de considérer le plus grand nombre de variables rattachées au rendement à résoudre un questionnaire écrit de mathématiques. Les résultats obtenus révèlent que cinq variables indépendantes sont reliées au rendement à résoudre un questionnaire écrit de mathématiques (F(5,259)=18,412 ; p < 0,001). En fait, la perception de l’enseignant des habiletés en lecture (9,5 %), le degré scolaire de l’élève (9,1 %), la participation de l’enfant à un plan d’intervention personnalisé (2,8 %), le sexe de l’élève (2,3 %) ainsi que la perception de l’enseignant du risque de décrochage de l’élève (1,3 %) justifient 24,8 % de la variabilité du rendement à résoudre un questionnaire écrit en mathématiques. En référence à l’indice de Cohen (1988), un regard à la valeur de la corrélation multiple du modèle permet de dégager une corrélation moyenne entre les cinq variables indépendantes retenues et le rendement de l’élève à résoudre un questionnaire écrit en mathématiques (r = 0,512).

Analyse des facteurs liés à la perception de l’enseignant par rapport au rendement de l’élève en mathématiques

Afin de répondre au deuxième objectif du projet, qui consiste à explorer et à décrire les liens entre différents facteurs se rapportant au profil sociodémographique des élèves du primaire ainsi que celui des titulaires de leur autorité parentale par rapport à la perception qu’entretiennent les enseignants à l’égard des difficultés des élèves en mathématiques, nous avons réalisé une seconde analyse de régression multiple. Le modèle de régression multiple retenu à la suite de l’analyse est présenté dans le tableau 4, tandis que les valeurs de coefficient de régression sont mises de l’avant dans le tableau 5.

Tableau 4

***Deuxième analyse : R-carré et R-carré ajusté des différents modèles de régression multiple retenus***

Tableau 5

Coefficients standardisés (bêta), test T et degré signification des variables associées à la perception de l’enseignant à l’égard du rendement de l’élève en mathématiques

Le premier modèle de régression a été retenu puisqu’il est le seul à avoir obtenu un résultat significatif permettant de relever au moins une variable permettant d’expliquer une part de la variance de la perception de l’enseignant concernant le rendement de l’élève en mathématiques (F(1,262)=11,314; p < 0,005)[3]. Plus spécifiquement, le modèle issu des analyses a permis de dégager que l’indicateur ministériel du seuil de faible revenu permet expliquer 23,5 % de la variance concernant la perception de l’enseignant à l’égard du rendement de l’élève en mathématiques. Au regard de l’indice de Cohen (1988), une corrélation moyenne est dégagée entre le seuil de faible revenu et la perception de l’enseignant concernant le rendement de l’élève en mathématiques (r = 0,508).

Interprétation des résultats

À la lumière des données obtenues, il est possible de relever des différences considérables concernant la nature des variables qui entretiennent une relation avec le rendement à résoudre un questionnaire écrit en mathématiques par rapport à celles qui sont associées à la perception de l’enseignant à l’égard du rendement de l’élève en mathématiques. Ce constat se traduit par les résultats des analyses de régression qui ont été réalisées.

En effet, les résultats issus du premier objectif de la recherche mettent en lumière le fait que les facteurs rattachés au rendement à résoudre un questionnaire écrit en mathématiques relèvent principalement de l’idée que se fait le professionnel de l’enseignement par rapport au potentiel de l’enfant dans le réseau scolaire (perception du niveau d’habiletés en lecture, perception du risque de décrochage de l’élève) ainsi qu’en fonction de facteurs qui se rapportent à l’élève (attribution d’un plan d’intervention, genre et degré scolaire). Concernant les variables retenues dans le modèle, les analyses ont permis de constater que la participation d’un élève à un plan d’intervention individualisé explique une part de la variance concernant le rendement à résoudre des énoncés de problèmes en mathématiques (2,8 %). Cependant, la perception de l’enseignant à l’égard du niveau d’habiletés en lecture de l’élève représente la principale variable explicative (9,5 %) de la variabilité du rendement de l’élève à résoudre un questionnaire écrit en mathématiques. Mentionnons également que la présence du genre (2,3 %) au sein du modèle de régression retenu est aussi documentée dans les écrits scientifiques, bien que les études à grandes échelles démontrent que cet écart entre les sexes tend à diminuer au fil des années (Rajotte et al., 2014). Finalement, il importe de mentionner que le degré scolaire a été relevé dans le cadre de cette première analyse. Cela signifie que les questionnaires qui ont été transmis aux élèves des différents degrés scolaires n’impliquaient pas des niveaux de difficulté homogènes et que les enseignants percevaient différemment le potentiel de réussite des élèves en mathématiques selon leur année scolaire. Dans le cadre d’études ultérieures, il serait pertinent de travailler auprès d’élèves se rapportant à un seul et même degré scolaire.

Par ailleurs, les résultats issus du second objectif de l’étude, qui consiste à poser un regard sur les facteurs rattachés à la perception de l’enseignant quant au rendement de l’élève en mathématiques, nous amènent à mettre en lumière la présence d’une autre variable explicative qui se rapporte au milieu de l’élève. En fait, la seconde analyse de régression permet de relever que l’indicateur ministériel du seuil de faible revenu (SFR) constitue la seule variable retenue qui entretient une relation avec la perception de l’enseignant par rapport au rendement en mathématiques de l’élève (23,5 %). Pour le milieu scolaire, les constats issus de ce résultat peuvent avoir des retombées considérables. En effet, ceux-ci permettent de mettre en lumière le fait que le milieu socioéconomique de l’élève peut être modérément rattaché à la perception de l’enseignement par rapport au potentiel de réussite de l’élève en mathématiques (r > 0,5). Ces résultats pourraient contribuer à alimenter une prise de conscience chez les enseignants quant à la possibilité de mettre en place des interventions différenciées en mathématiques selon une catégorisation d’élèves pouvant s’appuyer sur leur niveau socioéconomique d’appartenance.

Conclusion

Les récentes études effectuées dans le domaine des sciences de l’éducation ont permis de mettre en lumière l’importance de l’effet enseignant comme principal levier permettant de soutenir la réussite scolaire des élèves du primaire (Bissonnette, 2015). À cet effet, les résultats de cette étude permettent de dégager qu’un facteur se rapportant au profil sociodémographique des élèves, soit l’indicateur ministériel du seuil de faible revenu (SFR), entretient un lien modéré avec la perception de l’enseignant à l’égard du rendement de l’élève en mathématiques. Dans le souci de favoriser l’égalité des chances entre les différents élèves du primaire, nous suggérons aux pédagogues d’effectuer une analyse réflexive sur leur pratique afin de prendre conscience des facteurs se rapportant à leurs « arrière-plans » culturel et social pouvant potentiellement influer sur leur perception du rendement des élèves ainsi qu’en fonction de leurs interventions pédagogiques. En effet, cette prise de conscience pourrait faire en sorte que les enseignants évitent de mettre en place des interventions se rapportant à un contrat didactique différencié[4] selon le profil sociodémographique de certains élèves.

Parallèlement, les résultats issus de l’étude n’ont pas permis d’établir de relation entre les facteurs considérés en lien avec le profil sociodémographique de l’élève par rapport au rendement de celui-ci à résoudre un questionnaire écrit en mathématiques. Considérant que ce sont d’autres variables, notamment la perception du niveau d’habileté en lecture, qui sont principalement rattachées au rendement de l’élève en mathématiques, il serait possible d’envisager d’adopter un autre angle d’approche afin de prévenir les difficultés des élèves en mathématiques. À ce sujet, nous suggérons aux enseignants de viser une consolidation des habiletés en lecture et en écriture afin de favoriser le développement des compétences disciplinaires des élèves du primaire en mathématiques. De manière à consolider les habiletés en lecture qui sont les plus sujettes à être mises à profit en contexte de résolution de problèmes, Voyer, Beaudoin et Goulet (2012) suggèrent de prioriser le développement des habiletés des élèves à émettre des inférences ainsi que de prioriser la compréhension de textes informatifs. Selon ces auteurs, les liens qu’entretiennent les habiletés en lecture avec les activités mathématiques réalisées par les élèves pourraient être considérés comme un levier permettant de tirer profit de l’enseignement donné dans les classes de français afin d’aider les élèves à mieux réussir en mathématiques. De manière à réaliser un pont entre le français et les mathématiques, pour obtenir des effets bénéfiques chez les élèves, Forest et Voyer (2021) proposent notamment de miser sur un enseignement parallèle des stratégies liées aux inférences au sein de ces deux disciplines.

Résumé

Abstract

Contexte de l’étude

Introduction

Des perspectives opposées pour interpréter les difficultés d’apprentissage

Interpréter les difficultés en mathématiques : regard sur les postulats issus des sciences sociales