Résumés
Résumé
Cet article présente des modèles stochastiques de projection des taux de fécondité et du nombre d’adoptions. Le modèle de fécondité développé utilise les taux de fécondité les plus récents comme point de départ des projections et permet de faire évoluer la fécondité moyenne attendue dans le futur, en plus de prévoir des fluctuations aléatoires des taux de fécondité au fil des ans. Cette approche est complémentaire à l’utilisation d’une enquête d’opinion auprès d’experts comme celle utilisée récemment par Statistique Canada pour des projections de population. En ce qui a trait à l’adoption, il s’agit plutôt de refléter la réalité de changements de régime vécus dans les dernières années, c’est-à-dire des périodes pluriannuelles successives de forte et de faible adoption. À titre d’illustration, les modèles développés sont utilisés pour réaliser des projections stochastiques de la situation financière du Régime québécois d’assurance parentale.
Abstract
This paper presents stochastic projection models for fertility rates and number of adoptions. The fertility projection model uses the most recent fertility rates as a starting point, but it also allows for changing the expected average fertility in the future, in addition to incorporating random fluctuations in fertility rates over the years. Such an approach is complementary to the one based on expert opinion for population projections, as recently used by Statistics Canada. With regard to adoption, it aims to reflect the Quebec “regime-switching” reality of recent years: successive multi-year periods of high and low adoption. As an example, the models developed are used to make stochastic projections of the financial situation of the Quebec Parental Insurance Plan.
Corps de l’article
Introduction
La fécondité et les adoptions sont des facteurs à considérer pour réaliser des projections de population. Ils sont également nécessaires pour la réalisation des évaluations actuarielles requises pour le financement de régimes de sécurité sociale comme le Régime québécois d’assurance parentale (RQAP). Une grande incertitude est associée aux hypothèses concernant ces facteurs, notamment pour des projections sur plusieurs années (Lee, 1998). Le présent article propose des bases stochastiques de projection qui permettent de calibrer les hypothèses utilisées en fonction des résultats escomptés et ainsi éviter une référence excessive à l’expérience passée.
Les modèles de projection stochastique de la mortalité de Lee-Carter ont été adaptés afin de produire des projections de la fécondité (Lee, 1993). Une variante du modèle Lee-Carter, proposée par Myrskylä et ses collaborateurs (2013), a d’ailleurs été utilisée pour les projections de fécondité effectuées par Statistique Canada en 2015 (Dion et Bohnert, 2015). Les hypothèses associées à ces modèles sont généralement basées sur des données historiques. Ainsi, dans son article publié en 1993, Lee réfère aux données de la période 1917-1987 pour des projections effectuées jusqu’en 2065, alors que les projections de 2015 de Statistique Canada réfèrent plutôt aux années 2001 à 2011 pour des projections de la fécondité jusqu’en 2021. Dans ce dernier cas, la période historique de référence retenue varie selon le scénario de fécondité considéré (fécondité basse, moyenne ou élevée). Ces projections de Statistique Canada s’étendent jusqu’en 2038 pour les provinces et territoires et jusqu’en 2063 pour l’ensemble du Canada. Les taux de fécondité utilisés sont supposés constants au-delà de 2021 ; les hypothèses de fécondité font évoluer l’indice synthétique de fécondité (ISF) jusqu’en 2021, puis le garde constant pour le reste de la période de projection.
Contrairement à la mortalité, la fécondité est marquée par des changements de tendance significatifs au fil des ans. D’abord le reflet de choix personnels, l’évolution de la fécondité peut être influencée par différents facteurs, comme les conditions du marché du travail ou de l’économie. Les variations de la fécondité au fil des ans peuvent être le fait d’une volonté de retarder ou devancer la venue d’enfants, aussi bien qu’une évolution du nombre souhaité d’enfants. Comme montré plus loin, les variations des dernières années sont sans commune mesure avec la baisse enregistrée à compter des années 1960, mais elles sont suffisamment importantes pour avoir un impact notable sur les résultats obtenus des projections en fonction de la période de référence utilisée : « Les considérations précédentes montrent que dans un contexte de volatilité des taux de fécondité, il est difficile d’extrapoler les niveaux futurs de la fécondité des cohortes sans faire des choix quelque peu arbitraires, mais non moins significatifs en ce qui concerne la période de référence » (Dion et Bohnert, 2015). En fait, « fertility history tends to reveal relatively little predictive signal » (Tuljapurkar, 2019). Dans ce contexte, il ne faut pas se surprendre que la référence aux données du passé se traduise par des intervalles de projection très larges pour les taux de fécondité futurs : « This interval may seem to overstate the uncertainty, but it merely reflects the rapidity of changes that have occurred in the sample period. Planners should keep in mind the volatility of fertility, and its past history of long swings » (Lee, 1993).
Après une revue des modèles de Lee et de Myrskylä, et l’illustration de la sensibilité des résultats aux hypothèses utilisées, cet article présente une méthodologie définissant a priori, comme une hypothèse du modèle, l’intervalle de confiance de la distribution de la fécondité au terme de la période de projection. Un tel modèle ne vise donc pas à prédire la fécondité future, mais plutôt définir un ensemble de trajectoires vraisemblables. Cet ensemble de trajectoires sera caractérisé d’une part par l’amplitude de l’intervalle à l’intérieur duquel se situeront les résultats et par l’évolution des résultats moyens attendus dans le futur par rapport à l’expérience récente d’autre part. L’expérience récente constitue le point de départ des projections.
Considérant le caractère « quelque peu arbitraire » de la méthodologie utilisée dans le passé, Statistique Canada a revu la base de définition des hypothèses de fécondité pour les projections de population publiées en 2019 (Chagnon et collab. 2020). Les trajectoires à court terme ont été obtenues en extrapolant les tendances des variations des taux de fécondité par âge observées au cours de la période allant de 2007 à 2017 et les cibles nationales de l’ISF en 2043 tirées de l’Enquête auprès d’experts sur les tendances démographiques futures de 2018 ont été utilisées pour les trajectoires à long terme. Une telle approche fondée sur l’opinion d’experts est complémentaire à celle développée dans le présent article. Une telle enquête fournit les balises requises pour l’utilisation du modèle. Ainsi, Statistique Canada a retenu la médiane de la distribution comme cible de moyenne fécondité, le 90e centile a servi à obtenir une cible de forte fécondité et le 10e centile une cible de faible fécondité.
En plus de la fécondité, et bien que l’impact soit nettement moins important du fait de leur nombre réduit, l’accroissement de la population est également tributaire de l’adoption. Si on peut parler de changements de tendances au fil des ans concernant la fécondité, on peut aussi parler de « changements de régime » dans le cas de l’adoption.[2] L’expérience québécoise des dernières années témoigne d’une période pluriannuelle de forte adoption suivie d’une baisse considérable. Dans ce contexte, un modèle dit de changement de régime a été développé pour des fins de projection stochastique du nombre d’adoptions.
Les modèles de projection de la fécondité et des adoptions sont présentés dans les sections suivantes, après une revue de l’expérience québécoise et une discussion des deux modèles susmentionnés de projection de la fécondité. Des résultats de projection pour la période 2020-2050 sont aussi présentés, sur la base de trajectoires aléatoires générées avec les modèles développés. Un exemple d’application des modèles est l’objet de la dernière section de l’article. Il s’agit de projections relatives au financement du RQAP. La situation financière de ce régime de prestations parentales est très sensible à l’évolution du nombre de naissances et d’adoptions. Les résultats financiers sont simulés considérant les trajectoires de projection de la fécondité et des adoptions sur les horizons 2030 et 2050.
REVUE DE L’EXPÉRIENCE QUÉBÉCOISE
L’ISF se situait à près de quatre enfants par femme au début des années 1950. Une baisse significative a été enregistrée dans les années qui ont suivi, notamment de 1964 à 1971, alors qu’il est passé de 3,5 à 2,0. Depuis ce moment, l’ISF a toujours été inférieur au seuil de remplacement, soit 2,1 enfants par femme.
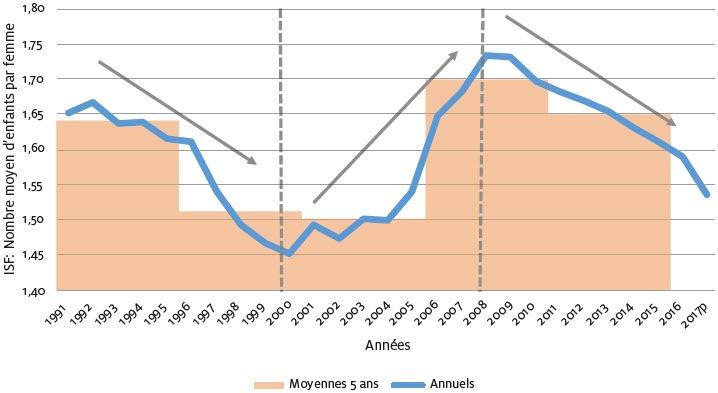
Des variations importantes ont été enregistrées depuis le début des années 1990. Cet indice est effectivement passé de 1,67 en 1992 à un creux historique de 1,45 en 2000 avant d’atteindre un sommet relatif à 1,73 en 2008. Il est en baisse depuis ce moment. La figure 1 témoigne de ces fluctuations significatives des 25 dernières années.
Figure 1
Indice synthétique de fécondité (ISF), Québec, 1991-2017
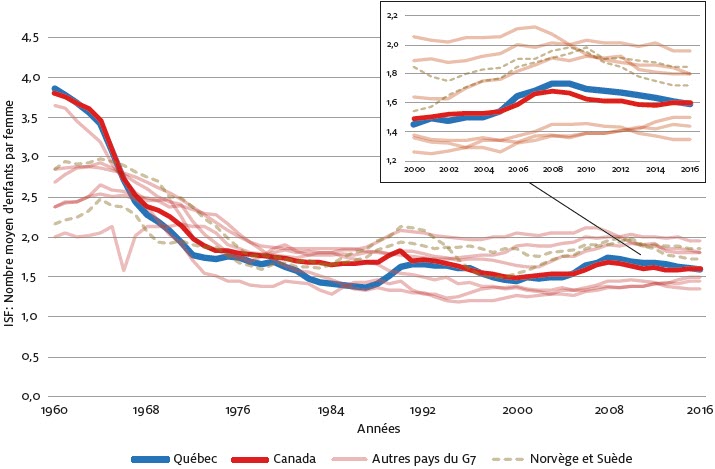
Il est également pertinent de comparer les valeurs de l’ISF enregistrées au Québec par rapport à celles de l’ensemble du Canada et d’autres pays développés. La figure 2 fait état de l’évolution de l’ISF dans les pays du G7 de même qu’en Norvège et en Suède, pour la période de 1960 à 2016. Les pays du G7 fournissent un échantillon varié quant aux réalités sociales et culturelles, de même qu’au regard des politiques publiques et des pratiques du marché du travail. La Norvège et la Suède ont également été retenues en raison de leurs politiques familiales avant-gardistes, un peu comme au Québec.
Depuis le début des années 2000, le Québec et l’ensemble du Canada sont qualifiés de « médians » ou « centristes » par rapport aux autres pays, leur ISF se situant au centre du spectre des valeurs obtenues. L’Allemagne, l’Italie et le Japon ont des valeurs plus faibles, alors que la France, les États-Unis, le Royaume-Uni, la Norvège et la Suède ont enregistré des ISF plus élevés. Il ressort également de ce graphique que, depuis 1980, les indices de fécondité les plus élevés se situent entre 1,8 et 2,0, alors que les plus faibles oscillent entre 1,3 et 1,5.
Figure 2
Comparaison de l’indice synthétique de fécondité du Québec par rapport à ceux de pays développés
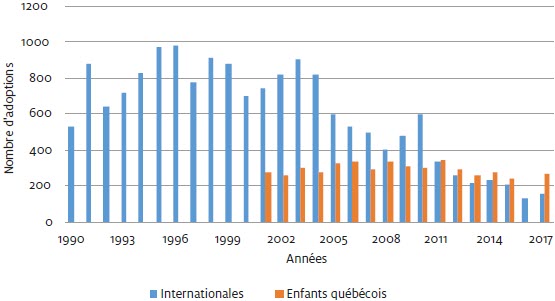
Les données présentées dans la figure 3 témoignent de l’évolution du nombre d’adoptions au Québec au cours des 20 dernières années. On remarque tout d’abord les variations importantes du nombre d’adoptions internationales, dans l’esprit des régimes de forte et de faible adoption explicités plus tôt. Ainsi, le nombre d’adoptions internationales a atteint un plafond de 977 en 1996, alors que, plus récemment, il a atteint des creux de 134 et 153 en 2016 et 2017. Pour la période 1991-2004, le nombre annuel moyen d’adoptions internationales était de 825, alors qu’il est en moyenne de 200 par année depuis 2012. Le nombre d’adoptions internationales est conditionné par la disponibilité d’enfants confiés à l’adoption dans différents pays. Cette disponibilité est tributaire des conditions prévalant dans ces derniers.
Les variations sont beaucoup moins importantes en ce qui a trait à l’adoption d’enfants nés au Québec, le nombre ayant varié de 239 à 336 par année de 2000 à 2017, pour une moyenne annuelle de 295.
Figure 3
Nombre d’adoptions au Québec entre 1990 et 2017
REVUE DE MODÈLES DE FÉCONDITÉ[3]
Modèle pour la fécondité de Lee
Le modèle proposé par Lee se fonde sur les taux de fécondité par âge et par année de calendrier. Il s’énonce comme suit[4] :
L’estimation de ax se fonde sur la moyenne des 𝑓x,t à l’âge x, alors qu’on peut recourir à la décomposition en valeurs singulières pour obtenir les estimations de bx et kt. Il est généralement souhaitable d’ajuster les valeurs obtenues pour kt au nombre total des naissances observées. Pour ce faire, on recourt généralement à des méthodes d’optimisation telle que la méthode de Newton-Raphson.[5] Pour projeter kt, Lee utilise un modèle avec bornes inférieures, bornes supérieures et valeurs d’équilibre quant aux valeurs calculées de l’ISF.[6]
En fait, dans son article paru en 1993, Lee a articulé son modèle autour d’une fécondité établie par année de calendrier et référant à l’ISF. Cet indice pour l’année t (ISFt) est donné par l’équation ci-dessous :
Comme nous le verrons ci-dessous avec Myrskylä et collaborateurs (2013), de tels modèles peuvent aussi être étudiés sur la base d’une fécondité par cohorte.
Modèle pour la fécondité de Myrskylä et collaborateurs (2013)
Les projections par année des taux de fécondité peuvent fluctuer de manière importante en comparaison avec les projections par cohorte. Myrskylä et collaborateurs (2013) ont proposé un modèle inspiré du modèle de Lee pour la fécondité et l’ont utilisé pour projeter des taux de fécondité par cohorte. Ce modèle se distingue par sa simplicité et la volonté de refléter l’expérience récente, pour une période de projection de quelques années. La méthode proposée se base sur l’extrapolation de la tendance de la fécondité des 5 dernières années sur une période de projection aussi de 5 ans.
Le modèle utilisé pour prédire la fécondité est similaire au modèle de Lee, soit :
Ceci dit, la méthode d’estimation des paramètres est différente :
ax = valeur la plus récente du taux de fécondité observé pour l’âge x
bx = variation annuelle moyenne des taux de fécondité au cours des cinq dernières années, soit :
L’estimation de ax sur la base des données les plus récentes suppose implicitement que la dernière année d’observation est fiable et représentative. À l’inverse, si on craint que les 𝑓x,t de la dernière année soient le fait d’une situation particulière, il est préférable d’opter pour une approche similaire à celle de Lee et d’utiliser des valeurs de 𝑓x,t issues d’un modèle, pour la dernière année, plutôt que celles observées.
Le vecteur de paramètres kt reflète le changement dans le niveau
de fécondité à travers le temps. Il est estimé en appliquant une régression
linéaire simple de 𝑓x,t – ax sur
bx, et ce, pour les 5 dernières années. Contrairement au
modèle de Lee, les ![]() ne font pas l’objet d’un rajustement avant d’être modélisés pour
la projection. Ils ne font l’objet d’aucune transformation et sont plutôt
modélisés par une marche aléatoire avec dérive comme montré ci-dessous :
ne font pas l’objet d’un rajustement avant d’être modélisés pour
la projection. Ils ne font l’objet d’aucune transformation et sont plutôt
modélisés par une marche aléatoire avec dérive comme montré ci-dessous :
À l’instar de la fécondité par période qui permet de définir l’indice synthétique de fécondité pour une période donnée, l’étude longitudinale de la fécondité permet de définir la descendance finale (DFc) qui est définie par la somme des taux de fécondité observés en suivant une génération ou cohorte de femmes nées en l’année c, et ce, tout au long de leur période de fécondité, soit de 15 ans à 49 ans. Autrement dit,
Nous avons projeté les taux de fécondité avec le modèle de Myrskylä et collaborateurs (2013), et ce, pour des périodes de référence passées de longueur variable se terminant en 2015. Ces périodes de référence sont respectivement 1991-2015, 1996-2015, 2001-2015, 2006-2015 et 2011-2015. Les projections ont été réalisées jusqu’en 2050 sur la base du modèle défini ci-dessus et il a été possible d’en déduire des valeurs de l’ISF comme présenté dans la figure 4 (2.7).[7]
De surcroît, la descendance finale a été projetée pour chacune des cohortes de femmes nées entre 1972 et 2000. Ces dernières atteignent l’âge de 15 ans entre 1987 et 2015 et l’âge de 49 ans entre 2021 et 2049. Les résultats sont présentés à la figure 5 (2.8).
Ces graphiques expriment clairement le risque exprimé plus tôt en ce qui a trait à l’utilisation de données historiques pour la formulation des hypothèses de projection : les résultats sont fort variables en fonction de la période de référence utilisée.
Figure 4
Projection de l’ISF avec le modèle de Myrskyla et collaborateurs (2013) pour le Québec et différentes périodes de référence
Figure 5
Projection de la descendance finale de différentes cohortes avec le modèle de Myrskyla et collaborateurs (2013) pour le Québec et différentes périodes de référence
PROJECTION STOCHASTIQUE CONTRÔLÉE DE LA FÉCONDITÉ
Dans le présent article, l’approche privilégiée pour la modélisation de la fécondité vise à prévoir une marge de manoeuvre par rapport aux valeurs historiques pour l’estimation des paramètres de projection, tout en référant aux données les plus récentes des taux de fécondité par âge comme point de départ des projections. On doit pouvoir faire évoluer de façon déterministe la fécondité attendue dans le futur, soit les résultats moyens escomptés, en plus de prévoir des fluctuations aléatoires des taux de fécondité au fil des années. Le volet déterministe permet d’apporter un ajustement aux données récentes, alors que le volet stochastique se doit d’être calibré de façon à obtenir des intervalles de confiance des valeurs projetées conformes aux attentes. Comme mentionné plus tôt, il s’agit de définir les valeurs limites à l’intérieur desquelles devrait se situer l’indice de fécondité avec un certain niveau de confiance.
En fait, les taux de fécondité sont modélisés sur la base d’une marche aléatoire avec dérive, sur la base de trois critères :
le taux récent de fécondité, ce qui, pour la simulation dans l’année t, correspond au taux de fécondité simulé pour l’année t−1 ;
l’application d’un facteur de dérive permettant une évolution déterministe des taux de fécondité par rapport aux taux récents ;
une composante aléatoire dont le paramètre d’amplitude est défini de façon à ce que la distribution des résultats se situe à l’intérieur de l’intervalle de confiance prédéfini.
En termes mathématiques, ce modèle peut être exprimé de la façon suivante :
et en supposant des données historiques disponibles jusqu’en 2017 et une période de projection débutant en 2018.
Cette méthodologie permet de développer un grand nombre de trajectoires applicables sur plusieurs années de projection et considérant des intervalles de confiance à l’intérieur desquels se situent les résultats, et ce, pour un niveau de confiance à 95 %. Dans l’illustration présentée ci-dessous, ces projections sont effectuées jusqu’en 2050, soit sur une trentaine d’années. L’utilisation d’une période aussi longue permet d’évaluer la variabilité ultime des taux de fécondité générés, de même que les fluctuations possibles au fil des années.
L’expérience québécoise fait état d’un ISF de 1,54 pour 2017, en baisse depuis 2008, où il avait atteint un plafond de 1,73[8]. Les taux de fécondité de 2017 correspondent au point de départ pour les fins des simulations. Un facteur de dérive est appliqué. Pour des fins d’illustration, il se fonde sur les hypothèses utilisées par les actuaires du Conseil de gestion de l’assurance parentale pour les fins de leur évaluation actuarielle du RQAP au 31 décembre 2017 (Conseil de gestion de l’assurance parentale, 2018). Cette évaluation actuarielle repose sur un scénario déterministe[9] et les actuaires ont alors supposé une baisse de l’ISF jusqu’à 1,52 en 2019, suivie d’une hausse entre 2020 et 2022 pour atteindre une valeur ultime de 1,59. Ces hypothèses ont été établies en considérant la tendance des femmes à avoir leurs enfants de plus en plus tard, en s’appuyant sur les statistiques publiées par l’Institut de la statistique du Québec (ISQ) et en prenant en compte l’estimation de l’évolution de l’indice de descendance finale (Conseil de gestion de l’assurance parentale, 2018).
Finalement, dans le cadre des présentes simulations, un facteur de volatilité stochastique est introduit, ce qui permet d’obtenir des distributions des valeurs de l’ISF se situant à l’intérieur d’intervalles prédéterminés en 2050, et ce, pour 95 % des 2000 trajectoires générées[10]. Ainsi, en supposant une valeur du paramètre σ égale à 0,4, l’intervalle de confiance se situe entre 1,46 et 1,75 en 2050. Pour un horizon de projection plus court, soit en 2030, l’intervalle de confiance oscille plutôt entre des valeurs de 1,50 et 1,70. Ces résultats sont présentés dans la figure 6[11].
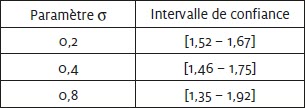
Le tableau 1 présente les intervalles obtenus pour l’indice synthétique de fécondité en 2050 avec un niveau de confiance à 95 % et pour des valeurs alternatives du paramètre σ. Une valeur du paramètre σ plus élevée se traduit par une distribution plus large des valeurs de l’ISF et inversement avec une valeur réduite de σ.
Tableau 1
Intervalles de confiance de l’ISF en 2050 selon les valeurs du paramètre de volatilité σ, Québec (niveau de confiance de 95 %)
Figure 6
Distribution des ISF simulés, Québec 2017-2050
L’intervalle [1,46 – 1,75] associé au paramètre σ de valeur 0,4 est le reflet de l’expérience québécoise des 25 dernières années, caractérisée par des valeurs extrêmes de 1,45 et 1,75. Les projections sont effectuées sur une période de longueur comparable, soit d’une trentaine d’années jusqu’en 2050. Il s’agit du scénario de référence pour les fins du présent document. L’intervalle plus large est associé à des valeurs limites de 1,35 et 1,92 et une valeur de 0,8 du paramètre σ. Il se rapproche davantage des valeurs extrêmes enregistrées dans différents pays développés tel que discuté dans la première section. Une valeur de l’ordre de 1,35 a été enregistrée pour une seule année au Québec, soit 1,359 en 1987. Il faut remonter en 1971 pour noter un indice supérieur à 1,9. Le scénario avec un paramètre σ de 0,2 correspond simplement à un scénario de faible volatilité, en-deçà de la volatilité enregistrée dans le passé.
En complément à l’indice synthétique de fécondité, les projections effectuées dégagent des résultats relatifs aux nombres de naissances et à la descendance finale. Il est aussi possible de se questionner sur l’âge moyen de la mère à la naissance. L’évolution du nombre de naissances est conditionnée à la fois par l’ISF et la structure de la population par âge. Les phénomènes du baby-boom et de la génération X (baby-bust generation) ayant été particulièrement importants au Québec, ils auront des échos dans l’avenir[12]. C’est ce que démontre la figure 7 avec une baisse du nombre de naissances de 2024 à 2033.[13] Le nombre de naissances (86 000) atteint comme valeur moyenne en 2023 correspond aux valeurs ultimes pour les dernières années de projection, soit de 2045 à 2050. À un niveau de confiance de 95 %, on retrouve à ce moment un nombre de naissances oscillant entre 79 000 et 94 000. Les valeurs des trajectoires extrêmes (minimum et maximum) sont de 74 000 et 104 000.
Figure 7
Distribution des trajectoires du nombre de naissances,Québec, 2017-2050
Les résultats relatifs à la descendance finale sont présentés à la figure 8, sur la même période 2017-2050, mais pour des femmes nées 49 ans plus tôt. Les résultats témoignent d’une volatilité réduite, du fait que bon nombre des enfants de ces générations successives de femmes sont déjà nés. Les valeurs ultimes de la descendance finale tendent vers 1,59, soit la valeur moyenne supposée pour l’ISF. L’intervalle de confiance à 95 % se situe alors entre 1,52 et 1,67.
Finalement, en ce qui a trait à l’âge de la mère à la naissance, il importe de se rappeler que le modèle utilisé est caractérisé par un facteur déterministe de l’évolution de la fécondité par âge au fil des ans et un facteur aléatoire de fluctuations statistiques autour des taux escomptés dans le futur. C’est véritablement par la composante déterministe qu’il serait possible d’intégrer une hypothèse d’évolution de l’âge à la naissance de la mère. Les taux utilisés pour illustration, selon les hypothèses retenues pour l’évaluation actuarielle du RQAP, sont établis pour une période de 5 ans et maintiennent inchangé l’âge moyen des mères à la naissance. Ces hypothèses ne font qu’ajuster l’indice synthétique de fécondité le plus récent[14].
Figure 8
Distribution des trajectoires de descendances finales simulées, Québec, 2017-2050
PROJECTION STOCHASTIQUE CONTRÔLÉE DES ADOPTIONS
Le Québec ne fait pas exception en ayant un nombre d’adoptions nettement plus faible que le nombre de naissances. Bien que moins important, il s’agit d’un facteur considéré dans les projections de population et les évaluations actuarielles de régimes comme le RQAP prévoyant le paiement de prestations aux nouveaux parents. Dans le cas du RQAP, les prestations découlant d’adoptions représentent moins de 1 % du total des prestations payées.
Bien que l’entrée en vigueur de ce régime demeure relativement récente, son histoire a été marquée par deux périodes successives : la période actuelle de « faible » adoption a été précédée d’une période caractérisée par un nombre significativement plus élevé d’adoptions internationales. Dans ce contexte, et comme mentionné plus tôt, la modélisation du nombre total d’adoptions est fondée sur un modèle de changement de régime qui, d’un point de vue mathématique, a été développé sur la base d’une chaîne de Markov. Les principales hypothèses et paramètres sont les suivants :
deux régimes d’adoption sont possibles, soit un régime correspondant à des années de forte adoption et un régime alternatif d’années de faible adoption ;
on suppose un nombre annuel d’adoptions de 1 100 en régime de forte adoption et de 500 en régime de faible adoption. Ces chiffres incluent l’ensemble des adoptions par des parents québécois, soit les adoptions internationales aussi bien que les adoptions d’enfants nés au Québec ;
les durées moyennes escomptées sont les mêmes pour les deux régimes et, par conséquent, les mêmes probabilités sont utilisées pour quantifier la possibilité de demeurer dans un régime ou de passer dans le régime alternatif ;
différentes valeurs de probabilités ont été testées de façon à définir une hypothèse raisonnable par rapport à l’expérience québécoise des dernières années ;
une probabilité annuelle de changement de régime d’adoption de 10 % a été retenue aux fins de la simulation.
Les résultats obtenus concernant la durée des régimes successifs d’adoption pour différentes probabilités annuelles de changement de régime sont présentés à la figure 9. Ainsi, avec une probabilité annuelle de changement de régime d’adoption de 10 %, on obtient une durée moyenne dans un même cycle d’adoption de 8,5 années. Pour un intervalle de confiance de 95 %, la distribution des durées de cycle se situe alors entre 3,6 et 19 années.
La définition de l’hypothèse d’adoption ne peut reposer sur des bases solides. L’expérience est limitée et le passé n’est pas garant de l’avenir, considérant notamment la disponibilité d’enfants pour adoption dans d’autres pays et les pratiques en la matière. Une telle situation rend d’autant plus pertinente l’utilisation de modèles stochastiques prévoyant de fortes variations dans la durée des cycles et le nombre d’adoptions qui y sont associés. Dans ce contexte, l’hypothèse fondée sur cette probabilité annuelle de changement de régime d’adoption de 10 % doit être vue comme un estimé raisonnable des anticipations futures.
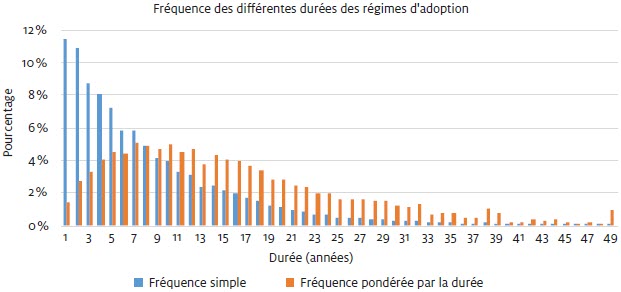
La figure 10 présente la fréquence de durées simulées des régimes successifs d’adoption en supposant une probabilité annuelle de changement de régime d’adoption de 10 %. La fréquence simple correspond au pourcentage des régimes simulés correspondant à chacune des durées, alors que la fréquence pondérée par la durée reflète l’influence de la durée des différents régimes. Ainsi, un régime d’adoption durant 10 ans a 10 fois plus d’impact qu’un régime d’une seule année au regard du nombre effectif d’adoptions. Dans le cas de la fréquence simple, la durée la plus fréquente est de 1 an, les fréquences étant décroissantes avec la durée. Dans le cas de la fréquence pondérée, les durées ayant le plus d’impact sur le nombre effectif d’adoptions se situent entre 7 et 13 ans.
Figure 9
Distribution des durées de régimes d’adoption selon les probabilités de changement de régime[15]
Figure 10
Fréquence des différentes durées des régimes d’adoption[16]
Finalement, la figure 11 présente la distribution du nombre annuel moyen d’adoptions pour la période 2018-2050, sur la base des 2000 trajectoires stochastiques générées.
Figure 11
Distribution du nombre annuel moyen d’adoptions au Québec sur l’horizon 2018-2050
LE FINANCEMENT DU RÉGIME QUÉBÉCOIS D’ASSURANCE PARENTALE
Le RQAP est entré en vigueur le 1er janvier 2006. Des prestations sont prévues pour les parents s’absentant du marché du travail dans l’année suivant la naissance ou l’adoption d’un enfant[17]. Le financement du régime est assuré par les cotisations versées par les salariés et leurs employeurs, de même que par les travailleurs autonomes.
L’évolution des coûts du régime est conditionnée notamment par le nombre de naissances et d’adoptions d’enfants de parents québécois. Les modèles stochastiques explicités dans les sections précédentes sont d’intérêt pour simuler l’évolution des résultats financiers, sur la base de la volatilité escomptée au niveau de la fécondité et des adoptions. Les modèles stochastiques de projection de la fécondité prennent en considération les taux courants de fécondité, de même que les hypothèses utilisées dans le cadre de l’évaluation actuarielle du régime au 31 décembre 2017 (Conseil de gestion de l’assurance parentale, 2018), en plus de prévoir une composante aléatoire. La méthodologie de projections stochastiques des contingents d’adoptions permet de définir des trajectoires de forte et de faible adoption intercalées dans le temps, pour des durées aléatoires, et fondées sur des probabilités reflétant l’expérience récente.
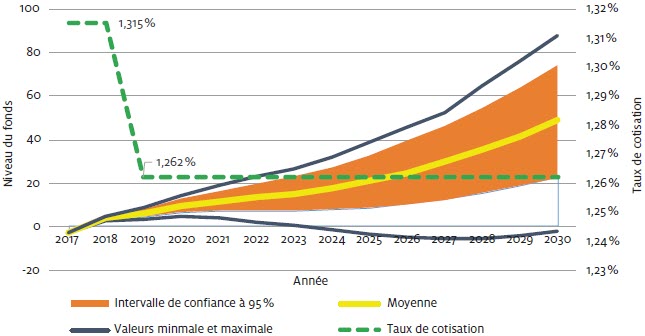
Figure 12
Projection du Fonds d’assurance parentale sur la base des taux de cotisation 2019 et 2020
12-A
Taux de cotisation 2019
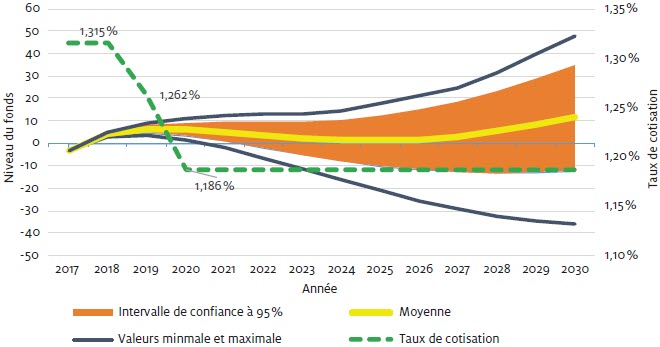
12-B
Taux de cotisation 2020
Note : Fonds exprimé en semaines de prestations (échelle de gauche).
Les résultats de l’évaluation actuarielle au 31 décembre 2017 font état d’un solde négatif du Fonds d’assurance parentale de -114 M $ à cette date. Par contre, l’excédent des cotisations perçues sur les prestations payées pour les années 2018 et 2019 devrait permettre de combler ce déficit et de voir émerger un surplus. En fait, la réalisation de projections stochastiques supposant le maintien des taux de cotisation de 2019 pour les prochaines années laisse entrevoir l’accumulation d’un surplus substantiel au fil des ans. Le fonds accumulé en 2030 se situerait à un niveau moyen équivalent à 49 semaines de prestations, mais susceptible de varier entre 22 et 74 semaines à un niveau de confiance de 95 %. En fait, la probabilité d’avoir un fonds négatif entre 2020 et 2029 est de 0,03 % sur la base des modèles de fécondité et d’adoption retenus et en supposant inchangés les taux de cotisation de 2019. Le détail est présenté à la figure 12-A.
Les taux de cotisation ont été réduits de 6 % à compter du 1er janvier 2020. Les résultats obtenus sur la base de ces nouveaux taux de cotisation sont présentés à la figure 12-B. Le niveau moyen du fonds accumulé en 2030 correspond alors plutôt à 11 semaines de prestations, l’intervalle se situant entre un fonds négatif de 13 semaines et un fonds positif de 35 semaines de prestations pour un niveau de confiance de 95 %. En fait, la probabilité d’avoir un fonds négatif entre 2020 et 2029 est alors de 25 %.
Le Fonds a néanmoins tendance à augmenter à compter de 2026, du moins pour la valeur moyenne escomptée. Cette tendance se maintient au-delà de 2030 lorsque la période de projection est étendue jusqu’en 2050. Ces résultats montrent qu’une réduction supplémentaire de l’ordre de 4 % du niveau des taux de cotisation serait requise à compter de 2031 pour maintenir la probabilité d’un fonds négatif à un niveau de 25 % sur l’horizon (très long) 2030-2049. Sans cette réduction supplémentaire des taux de cotisation, la probabilité d’un fonds négatif entre 2030 et 2049 serait plutôt de 9 %.
CONCLUSION
Les changements importants dans le niveau de la fécondité au fil du temps témoignent de la grande incertitude associée aux projections de la fécondité, notamment lorsqu’elles doivent être réalisées sur plusieurs années. Il y a aussi lieu de s’interroger sur les valeurs retenues comme point de départ de ces projections, les valeurs les plus récentes n’étant pas nécessairement représentatives des niveaux de fécondité escomptés dans les prochaines années. Concernant les adoptions, l’expérience des dernières décennies témoigne de changements importants dans le nombre annuel d’adoptions au terme d’une période de quelques années.
Dans ce contexte, le présent article présente une méthode de projection de la fécondité visant tout d’abord à refléter la grande incertitude associée à de telles projections, en plus de prendre de la distance par rapport aux valeurs historiques pour l’estimation des paramètres de projection. Si les taux de fécondité les plus récents sont utilisés comme point de départ des projections, il doit être possible de faire évoluer la fécondité moyenne attendue dans le futur, en plus de prévoir des fluctuations aléatoires des taux de fécondité au fil des ans. Le volet stochastique est calibré de façon à obtenir des intervalles de confiance des valeurs projetées conformes aux attentes.
Les projections de population sont le fait de différentes sources d’incertitude. Si les données utilisées pour caractériser l’expérience passée sont fiables, il n’en demeure pas moins que le futur pourrait s’avérer différent du passé du fait d’une évolution structurelle induisant des différences soutenues au fil des ans. Il pourrait aussi s’agir de fluctuations davantage cycliques ou conjoncturelles qui caractériseront l’expérience sur des périodes successives. Les deux composantes du modèle cherchent à refléter ces deux volets d’incertitude, soit une composante déterministe pour les aspects structurels et une composante stochastique pour les aspects cycliques ou conjoncturels.
Un tel modèle mathématique peut être utilisé conjointement avec une approche davantage centrée sur des opinions d’experts. Ainsi, les projections de population publiées par Statistique Canada en 2019 se fondent sur les cibles nationales de l’indice synthétique de fécondité en 2043 tirées de l’enquête d’opinion auprès d’experts. Ces résultats pourraient être utilisés pour définir les hypothèses importantes du modèle développé dans le présent article, soit les limites de l’intervalle requis pour les simulations de trajectoires et la valeur médiane utilisée pour définir l’évolution déterministe des taux futurs de fécondité.
Si l’expérience de la fécondité témoigne de fluctuations au fil des ans, l’adoption vécue au Québec a plutôt été le fait de « changements de régime », c’est-à-dire des périodes pluriannuelles successives de forte et de faible adoption. Le présent article élabore un modèle mathématique de projection des adoptions dit de changement de régime. Le modèle a été calibré sur la base de l’expérience québécoise récente et des probabilités annuelles de changement de régime d’adoption.
À titre d’exemple, les résultats des 2000 trajectoires de la fécondité et des adoptions ont été utilisés pour réaliser des projections stochastiques de la situation financière du RQAP sur les horizons 2030 et 2050. En plus de présenter une distribution des résultats financiers escomptés, de telles projections stochastiques sont d’intérêt pour évaluer la pertinence d’ajustement des taux de cotisation au fil des ans.
Parties annexes
Annexe
Des trajectoires de l’évolution de l’indice synthétique de fécondité ont été générées avec un nombre variable de simulations afin d’évaluer la sensibilité des résultats au nombre de simulations et la robustesse des résultats sur la base d’un nombre de 2000 simulations. Les résultats sont présentés ci-dessous. Ils ont été obtenus en supposant successivement 1 000, 2 000, 5 000 et 10 000 simulations.
Figure A-1
ISF simulés : Intervalle de confiance à 95 % selon le nombre de trajectoires simulées
Figure A-2
ISF simulés : Valeurs extrêmes selon le nombre de trajectoires simulées
Il en ressort que les résultats sont très similaires en ce qui a trait à l’intervalle de confiance à 95 %. Des écarts quelque peu plus importants sont générés pour les valeurs extrêmes, un nombre plus grand de simulations étant plus susceptibles de générer des valeurs particulièrement éloignées de la moyenne.
Notes
-
[1]
La méthodologie et les résultats présentés dans cet article prennent assise sur des travaux réalisés pour un essai de maîtrise (Boughal, 2019) et un contrat de recherche (Latulippe et collab. 2019). Bien qu’ils assument l’entière responsabilité du contenu du texte, les auteurs tiennent à remercier Claudia Giguère et Marie-Josée Dutil du Conseil de gestion de l’assurance parentale de même que Jean-François Therrien, Thomas Landry et Valérie Carrier de Retraite Québec pour leur soutien.
-
[2]
Comme cela se fait de plus en plus en matière de finance et d’investissement.
-
[3]
Référer à Boughal (2019) pour une discussion plus étoffée de ces modèles incluant l’estimation des paramètres.
-
[4]
Une version logarithmique de ce modèle peut être proposée dans le but d’avoir des taux de fécondité positifs quel que soit le niveau de fécondité. Afin de rendre la représentation des 𝑓x,t unique, on normalise bx et kt en imposant les contraintes suivantes : ∑xbx = 1 ; ∑tkt = 0.
-
[5]
La méthode de Newton-Raphson peut être utilisée pour résoudre l’équation suivante pour chaque t :
Les valeurs de kt obtenues lors du premier stade d’estimation permettent d’initialiser l’algorithme d’optimisation choisi. L’étape suivante consiste à modéliser les kt retenus dans l’étape précédente par un modèle de série chronologique pour projeter les taux de fécondité. Pour assurer le caractère plausible de ces projections, il est nécessaire de prendre en considération, lors de la modélisation, les contraintes imposées sur l’indice synthétique de fécondité.
-
[6]
Il s’agit en fait d’un modèle autorégressif ARIMA(1,0,1) sur la transformée logistique des valeurs de kt. Un tel modèle suppose que chaque point peut être prédit par la somme pondérée d’un ensemble de points précédents, plus un terme aléatoire.
-
[7]
Ces projections allant jusqu’en 2050, avec des périodes de référence de longueur variable, ne respectent pas la méthodologie de Myrskylä et collaborateurs (2013) car elles n’utilisent pas des périodes de même longueur pour les références historiques et celles des projections. Quoi qu’il en soit, les résultats obtenus montrent clairement la grande sensibilité à la période de référence utilisée, peu importe la période de projection.
-
[8]
Des informations véhiculées récemment par l’Institut de la statistique du Québec font état de valeurs différentes de l’ISF pour les dernières années. Ces changements sont attribuables à des révisions d’estimations de populations relatives aux dernières données de recensement. Le nombre de naissances est demeuré inchangé et c’est là la valeur importante du point de vue des projections. Dans ce contexte et par souci de cohérence de l’information, les données issues des plus récentes évaluations actuarielles du RQAP et du Régime de Rentes du Québec (RRQ) seront utilisées pour la fécondité et la population.
-
[9]
Le scénario principal est assorti d’une analyse de sensibilité des résultats aux principales hypothèses.
-
[10]
Différentes trajectoires ont été générées avec un nombre variable de simulations afin d’évaluer la sensibilité des résultats au nombre de simulations et la robustesse des résultats sur la base d’un nombre de 2000 simulations. Les résultats sont présentés en annexe.
-
[11]
Les projections de descendance finale découlant de ces projections de fécondité tendent vers la valeur de 1,59 retenue comme ISF. Pour un intervalle de confiance de 95 %, la descendance finale se situe entre 1,52 et 1,67 pour la cohorte atteignant 49 ans en 2050.
-
[12]
Si le baby-boom correspond à la période de forte fécondité des années 1950 et du début des années 1960, la génération X (baby-bust) correspond aux années de faible fécondité qui ont suivi.
-
[13]
Les projections du nombre de naissances ont été obtenues avec des données exogènes et déterministes quant à la population, soit les données de population des projections actuarielles du RRQ (Therrien et collab. 2016).
-
[14]
À l’inverse, les projections actuarielles du RRQ sont effectuées sur une période de 50 ans et les hypothèses utilisées pour l’évaluation en date du 31 décembre 2018 font état d’une hausse de l’âge moyen des mères à la naissance de 30,7 ans en 2018 à 32,0 ans en 2048. Cet âge moyen est maintenu constant après cette période initiale de 30 ans. Pour les illustrations dans le présent document, nous nous en sommes tenus aux hypothèses retenues pour l’évaluation du RQAP et avons supposé constant l’âge moyen des mères à la naissance.
-
[15]
Ces résultats ont été obtenus sur la base des 2000 trajectoires sur une période de 50 ans. La durée du régime d’adoption en vigueur à la fin de la période de projection de 50 ans est supposée se terminer à ce moment, bien que ce régime était susceptible de se poursuivre au-delà de la période de projection. Ainsi, les résultats présentés quant à la moyenne et la distribution les résultats obtenus s’éloignent de la moyenne théorique attendue dans les situations où la probabilité de changement de régime est faible (et la durée moyenne des régimes est longue). Les résultats obtenus pour chacune des années de projection demeurent cependant conformes aux résultats attendus d’un tel modèle.
-
[16]
Tout comme pour la figure 9, les résultats de la figure 10 ont été obtenus sur la base d’une période de projection de 50 ans
-
[17]
Les prestations payables au titre de la maternité débutent normalement quelques semaines avant la naissance de l’enfant. Des prestations de paternité sont également prévues de même que des prestations parentales et des prestations d’adoption partageables entre les deux parents.
Bibliographie
- BOUGHAL, H. 2019. « Modélisation de la fécondité par une variante du modèle Lee-Carter », (Essai de maîtrise en actuariat), Université Laval, Québec, Canada.
- CHAGNON, J., P. DION, N. GALBRAITH, E. SIRAG et Y. ZHANG. 2020. Projections démographiques pour le Canada (2018 à 2068), les provinces et les territoires (2018 à 2043) : rapport technique sur la méthodologie et les hypothèses, produit no 91-620-X au catalogue de Statistique Canada, Ottawa.
- CONSEIL DE GESTION DE L’ASSURANCE PARENTALE. 2018. Rapport actuariel du Régime québécois d’assurance parentale au 31 décembre 2017. RQAP.
- DION, P. et N. BOHNERT. 2015. Chapitre 3 : Projection de la fécondité. Projections démographiques pour le Canada (2013 à 2063), les provinces et les territoires (2013 à 2038) : rapport technique sur la méthodologie et les hypothèses, produit no 91-620-X au catalogue de Statistique Canada, Ottawa.
- DIRECTION DE LA PROTECTION DE LA JEUNESSE. 2019. Bilans annuels des directeurs de la protection de la jeunesse, Québec, disponible à la page : https://ciusss-centresudmtl.gouv.qc.ca/actualite/bilan-annuel-des-directrices-et-des-directeurs-de-la-protection-de-la-jeunesse-directeurs-provinciaux-du-quebec-une.
- INSTITUT DE LA STATISTIQUE DU QUÉBEC. 2018. Le bilan démographique du Québec. ISQ, Ste-Foy.
- INSTITUT DE LA STATISTIQUE DU QUÉBEC. 2019. Taux de fécondité selon le groupe d’âge de la mère, indice synthétique de fécondité et âge moyen à la maternité, Québec, 1951-2019, Québec, disponible à la page : http://www.stat.gouv.qc.ca/statistiques/population-demographie/naissance-fecondite/402.htm.
- LATULIPPE, D., P.C. MICHAUD et G. LACROIX. 2019. Étude stochastique sur le financement à long terme du Régime québécois d’assurance parentale — Rapport de recherche, Québec, disponible à la page : http://www.cgap.gouv.qc.ca/publications/pdf/RQAP_etude_shoch_financement.pdf.
- LEE, R.D. 1993. « Modeling and forecasting the time series of US fertility : Age distribution, range, and ultimate level », International Journal of Forecasting, 9, 2 : 187–202.
- LEE, R. 1998. « Probabilistic Approaches to Population Forecasting », Population and Development Review, 24, Supplement : Frontiers of Population Forecasting : 156-190.
- MYRSKYLÄ M., J.R. GOLDSTEIN et Y.A. CHENG. 2013. « New cohort fertility forecasts for the developed world : Rises, falls, and reversals », Population and Development Review, 39, 1 : 31-56.
- SECRÉTARIAT À L’ADOPTION INTERNATIONALE. 2019. Site officiel sur l’adoption internationale au Québec — Statistiques d’adoption, Québec, disponible à la page : http://adoption.gouv.qc.ca/fr_statistiques-dadoption.
- THERRIEN, J.F., P. GUÈVREMONT, V. CARRIER et E. POULIN. 2016. Évaluation actuarielle du Régime de rentes du Québec au 31 décembre 2015. Québec, Retraite Québec, 133 p.
- TULJAPURKAR, S. 2019. « Stochastic Forecasts of Mortality, Population and Pension Systems », dans T. BENGTSSON et N. KEILMAN (dir.), Old and New Perspectives on Mortality Forecasting, Springer Open, Max Planck Institute for Demographic Research : 145-156
- WORLD BANK. 2019. Data. Fertility rate, total (births per woman), disponible à la page : https://data.worldbank.org/indicator/SP.DYN.TFRT.IN.
Liste des figures
Figure 1
Indice synthétique de fécondité (ISF), Québec, 1991-2017
Figure 2
Comparaison de l’indice synthétique de fécondité du Québec par rapport à ceux de pays développés
Figure 3
Nombre d’adoptions au Québec entre 1990 et 2017
Figure 4
Projection de l’ISF avec le modèle de Myrskyla et collaborateurs (2013) pour le Québec et différentes périodes de référence
Figure 5
Projection de la descendance finale de différentes cohortes avec le modèle de Myrskyla et collaborateurs (2013) pour le Québec et différentes périodes de référence
Figure 6
Distribution des ISF simulés, Québec 2017-2050
Figure 7
Distribution des trajectoires du nombre de naissances,Québec, 2017-2050
Figure 8
Distribution des trajectoires de descendances finales simulées, Québec, 2017-2050
Figure 9
Distribution des durées de régimes d’adoption selon les probabilités de changement de régime[15]
Figure 10
Fréquence des différentes durées des régimes d’adoption[16]
Figure 11
Distribution du nombre annuel moyen d’adoptions au Québec sur l’horizon 2018-2050
12-A
Taux de cotisation 2019
12-B
Taux de cotisation 2020
Note : Fonds exprimé en semaines de prestations (échelle de gauche).
Figure A-1
ISF simulés : Intervalle de confiance à 95 % selon le nombre de trajectoires simulées
Figure A-2
ISF simulés : Valeurs extrêmes selon le nombre de trajectoires simulées
Liste des tableaux
Tableau 1
Intervalles de confiance de l’ISF en 2050 selon les valeurs du paramètre de volatilité σ, Québec (niveau de confiance de 95 %)