Résumés
Résumé
L’évolution dans le temps de la fonction des survivants par âge est très souvent présentée graphiquement, mais n’est pas mesurée précisément. Cela s’explique par le fait que la lecture directe de ce déplacement selon l’âge n’est pas possible dans la mesure où les tables de mortalité sont décrites âge par âge et non pas pour des proportions de survivants données. En fait, il est possible de détourner cette difficulté au moyen d’interpolations. Des mesures sont présentées pour une dizaine de pays à faible mortalité. Le déplacement de la fonction des survivants (Sx) au cours du temps — à droite, selon l’axe des âges x, se réduit au fur et à mesure que le niveau de Sx diminue ; cette liaison est pratiquement linéaire lorsque Sx est inférieur à 0,8. Une suggestion, basée sur cette démarche, est proposée pour établir une projection d’une table de mortalité nécessitant seulement de définir la trajectoire au fil du temps au moyen de deux paramètres facilement interprétables. Cette méthode présente l’avantage de tenir compte du fait que l’effet de l’âge évolue au fur et à mesure que l’âge au décès augmente.
Abstract
The evolution over time of the survival curve by age is very often presented graphically but is not precisely measured. This is due to the fact that direct reading of this age shift is not possible, in that mortality tables are described age by age, and not for given survivor proportions. In fact, it is possible to bypass this difficulty using interpolations. Measurements are presented for ten low-mortality countries. The shift of the survivor function Sx over time — to the right, along the age axis x — decreases as the level of Sx decreases ; the relation is almost linear when Sx is less than 0.8. A suggestion, based on this approach, is offered to establish a projection of a mortality table requiring only the definition of the trajectory over time using two easily interpretable parameters. This method has the advantage of taking into account the fact that the age effect evolves as the age at death increases.
Corps de l’article
INTRODUCTION
Alors que l’évolution dans le temps des courbes de survivants selon l’âge est souvent décrite graphiquement, il est intéressant d’aller plus loin dans cette démarche en mesurant précisément leur déplacement à droite, soit dans la direction de l’axe des âges vers des âges plus avancés. Ce déplacement sera évalué point par point pour un intervalle de temps choisi. Cette approche est non seulement utile pour décrire l’évolution de la mortalité passée, mais est aussi précieuse si on souhaite établir une projection des tables de mortalité basée sur une modélisation simple et efficace de l’évolution des survivants selon l’âge. Une analyse des résultats sur la base des données de quelques pays à faible mortalité est effectuée et quelques pistes pour établir des projections de tables sont ensuite proposées. Le modèle nécessite peu de paramètres et ceux-ci sont facilement interprétables. Cela permet de faire le compromis entre le simple déplacement à droite, vers des âges plus avancés, de la fonction des survivants par âge et une forte concentration de la mortalité aux âges élevés.
La grande majorité des modèles de projections utilisés (Caselli, 2004) s’appuient sur une extension de la formule de Gompertz (Duchêne, 1980) ou sur l’analyse de l’évolution des quotients de mortalité par âge. À cet effet, les travaux de Vincent peuvent être évoqués (Vincent, 1951), puis, au début des années 1990, le modèle bien connu de Lee-Carter (Lee et Carter, 1992) qui présente une formulation plus élégante qu’une série de régressions linéaires établies pour chaque âge sur le logarithme des quotients de mortalité. Ce dernier montre certaines faiblesses particulièrement aux âges élevés et suppose que l’effet d’âge est dissocié de l’effet temporel. Par la suite, les imperfections de ce modèle ont été réduites par de nombreux auteurs (Booth et collab. 2006 ; Bohk et Rau, 2016) au prix d’une complexification plus ou moins lourde. La démarche présentée ici offre l’intérêt de proposer une approche nouvelle qui décrit l’évolution de la mortalité avec peu de paramètres tout en tenant compte que les progrès pour un âge donné évoluent en lien avec la structure par âge de la mortalité (contrairement au modèle de Lee-Carter). Cette méthode a essentiellement comme objectif de bien décrire la mortalité induite par le vieillissement. En effet, la démarche proposée n’est guère pertinente en ce qui concerne la description de la mortalité des enfants et des jeunes adultes.
Dans le cadre de travaux sur les projections de tables, un modèle original avait été proposé (Menthonnex, 2015), proche de celui de Makeham (Duchêne, 1980, p 11-15) dans sa démarche, mais avec des coefficients parfois liés entre eux ou variables en fonction de l’âge et du temps. Bien qu’il présente certaines qualités, la difficulté de mise en oeuvre de l’estimation des nombreux paramètres restait un point faible. Ce constat a conduit à chercher une nouvelle voie simple et opérationnelle, expérimentée sur la base de l’évolution récente, observée au moyen des tables de survie de la « Human Mortality Database » (HMD)[1] de 13 pays : la France (FR), la Suisse (CH), l’Espagne (ES), l’Italie (IT), la Belgique (BE), l’Allemagne (DE), les Pays-Bas (NL), la Norvège (NO), la Suède (SU), le Royaume-Uni (GB), le Canada (CA), les États-Unis (US) et le Japon (JP).
LA MÉTHODE PROPOSÉE
Certes l’idée n’est pas nouvelle. La transformation au cours du temps de la fonction des survivants selon l’âge x, Sx(t), est souvent représentée graphiquement (Kannisto,1996 ; Vallin et Berlinguer, 2002 : 182). Cependant, cette observation n’est pas exploitée de façon optimale. Cela s’explique par le fait qu’il n’est pas aisé de lire directement le décalage à droite[2] des Sx(t) dans la mesure où les tables sont toujours présentées pour des âges x exprimés en nombres entiers. Il n’est pas habituel de produire des tables décrivant l’âge, exprimé en nombres réels, pour des nombres de survivants donnés ; or celles-ci permettraient de décrire le déplacement précis selon l’âge de la courbe de survie. Cette lacune peut être comblée en remplaçant les tables par une fonction Sx(t) déterminée analytiquement ou, plus simplement, au moyen d’interpolations sur la base des tables habituelles. La mise en place de formules d’interpolation simplement linéaire est présentée en annexe. Ce procédé permet de mesurer pour une vingtaine de niveaux de Sx (choisis arbitrairement) le déplacement à droite vers des âges plus avancés entre deux années et de décrire ainsi parfaitement le processus de rectangularisation des courbes de survie de manière plus complète que par l’usage d’un indicateur de mesure de la « rectangularité » (Vallin et Berlinguer, 2002). On peut souligner qu’un problème similaire se rencontre pour déterminer avec une certaine précision l’âge modal au décès à partir de la répartition des décès décrite point par point par les tables de mortalité ; pour cela des méthodes de lissage par fonctions splines sont utiles (Ouellette et Bourbeau, 2011).
Entre un simple décalage et une concentration des décès
Lorsque la courbe des survivants par âge se déplace de manière homogène à droite (shift), cela correspond à une situation où l’espérance de vie restante à l’âge x pour l’année t se retrouvera au même niveau quelques années plus tard pour un âge plus élevé. Autrement dit, pour un âge donné, la distance moyenne jusqu’au décès augmente pour les générations plus récentes ; il y a un simple déplacement à droite de la courbe des décès, le profil de l’espérance de vie qui reste selon l’âge est aussi simplement décalé. Il est pertinent de souligner que dans leurs travaux sur cet aspect, Sanderson et Scherbov (2007) ont appelé « âge prospectif » l’espérance de vie restante, en symétrie de l’âge, la durée depuis la naissance, qu’ils intitulent « âge rétrospectif ». Dans un contexte de tables de mortalité par génération, l’espérance de vie restante devrait plutôt s’intituler simplement « la durée qu’il reste à vivre ».
Dans un autre cas de figure, l’évolution des tables de mortalité va dans le sens d’une « rectangularisation » en montrant un rapprochement d’un âge limite par une concentration accrue des décès aux âges élevés. Dans ce cas, le décalage à droite de Sx est de plus en plus faible au fur et à mesure que l’âge est élevé, et donc que le niveau de Sx se réduit.
L’OBSERVATION DU DÉCALAGE DE LA COURBE DES SURVIVANTS
Pour évaluer l’intérêt de la méthode proposée, la transformation de la structure d’une dizaine de tables de pays à faible mortalité a été analysée. L’objectif n’est pas ici de décrire les particularités spécifiques de la mortalité de chaque pays, mais plutôt de mettre en évidence les analogies. Une fois les données de base organisées dans un tableur, et les formules d’interpolation disposées, il devient aisé d’observer le comportement des courbes de survie entre deux années sélectionnées pour un pays donné. Pour faciliter la comparaison, le décalage vers des âges plus avancés des courbes de survie est systématiquement ramené à une évolution moyenne par année.
Pour chaque point mesuré, c’est-à-dire pour un niveau de Sx choisi, le décalage observé a été mis en regard de ce niveau. Le lien entre le décalage et l’âge est moins intéressant à analyser pour trois raisons : l’âge n’est pas fixe sur l’intervalle de temps observé, la liaison observée est plus complexe à décrire et elle est moins stable dans le temps. En effet, au fur et à mesure que l’âge au décès augmente, les variations de mortalité marquées se déplacent vers des âges plus élevés.
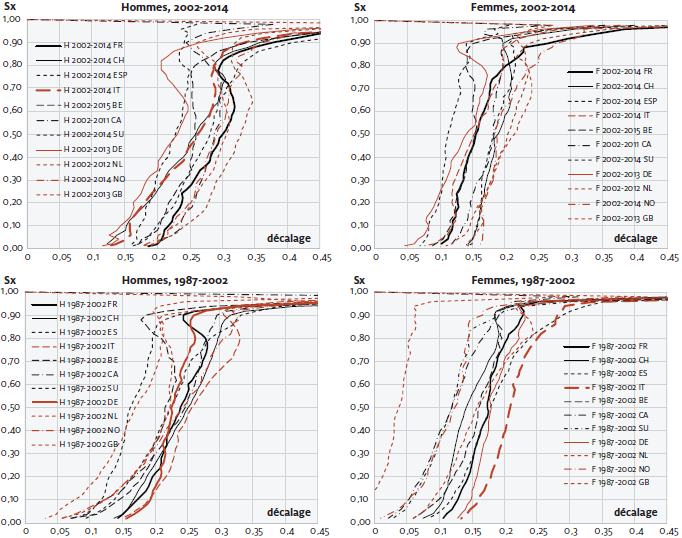
La figure 1 illustre les résultats obtenus pour onze pays[3] pour les périodes 1987-2002 et 2002-2014[4]. Bien que selon nous ce soit le décalage qui dépende du niveau de Sx, nous avons laissé les Sx sur l’axe des ordonnées prenant en considération la présentation habituelle de S(x). L’allure générale des courbes est relativement homogène. Dès que le niveau de Sx est inférieur à 0,7 chez les hommes et inférieur à 0,8 ou 0,9 chez les femmes, le décalage à droite évolue en diminuant de manière pratiquement linéaire à mesure que Sx diminue (et donc que l’âge x augmente). Ainsi, on constate que près des trois quarts des décès se situent dans l’intervalle où le décalage est linéaire en fonction du niveau de Sx (pour les hommes et les femmes de plus de 75 ans, approximativement). Près du mode des décès, vers le point d’inflexion de Sx (actuellement vers 0,35-0,4 selon le pays et le sexe), on remarque que pour les 13 tables, le décalage de Sx est pratiquement linéaire. Ainsi, on peut en déduire qu’un modèle s’appuyant sur ce constat devrait être efficace pour établir des projections de mortalité pour les personnes âgées. En revanche, aux âges très élevés, pour Sx inférieur à 0,05, on constate que, pour de nombreux pays, la courbe tend à s’infléchir un peu plus et indique donc un décalage moindre que la tendance linéaire pour les derniers survivants. Autrement dit, la tendance à la diminution de la mortalité (décrite par son décalage) présente un léger frein dès 95 ans pour les hommes et dès 97 ans pour les femmes[5]. Bien que ce phénomène présente des variations selon l’époque et le pays, il demeure suffisamment généralisé pour être souligné.
Pour les hommes, lorsque Sx se situe entre 0,7 et 0,9 (x entre 75 et 60 ans), la fonction est parfois plus complexe à décrire. En effet, bien que le décalage soit toujours positif, il se présente sous une forme convexe avec un minimum local aux alentours de 0,8. Chez les femmes, cette situation apparait plus rarement et de manière moins marquée. Une analyse plus fine montre que cette fluctuation du décalage, qui s’observe dans de nombreux pays, a eu lieu à la fin des années 1990 ou au début des années 2000 et correspond au contexte où les quotients de mortalité diminuent assez fortement pour les âges situés vers 65 à 85 ans alors qu’en même temps la mortalité évolue modestement pour les 50 à 65 ans. Ce phénomène ne s’observe toutefois pas de manière durable. Si tel était le cas, on observerait des situations étonnantes (des projections sont présentées plus loin, figure 6). En examinant l’évolution de la mortalité sur certaines périodes courtes (1992-1997), ou plus longues (1982-2012, ou 1960-2014 avec la figure 3), on constate que le décalage de la courbe de survie se déplace de manière pratiquement linéaire sur un grand segment (0,05 < Sx < 0,85) pour la large majorité des pays étudiés.
Pour Sx élevé (> 0,9), le décalage augmente fortement, car, compte tenu de la pente très faible de la courbe Sx à ces âges, il suffit d’une légère diminution de la mortalité des jeunes adultes pour que le décalage à droite soit important. Cette sensibilité particulière suggère que, pour l’analyse de la mortalité entre 0 et 35 ans, l’utilisation des quotients est préférable.
Figure 1
Décalage annuel en âge de la courbe des survivants (Sx) en fonction de son niveau. Mortalité de 11 pays pour les périodes 2002-2014 et 1987-2002, par sexea
a Jusqu’à la dernière année disponible, FR, CH, ESP, IT, SU et NO : 2014 ; Ca : 2011 ; NL : 2012 ; DE et GB : 2013 ; BE : 2015.
Figure 2
Décalage annuel de la fonction des survivants, comparaison pour le Japon et les États-Unis avec une situation de référencea
a La table de référence est constituée de la moyenne simple entre les 11 tables (pays de la figure 1).
Le niveau du décalage est propre à chaque pays. On constate par exemple que, pour la période 2002-2014, le décalage moyen des Sx des Pays-Bas (NL) est particulièrement élevé alors que celui de la Suède (SU) se situe à un niveau modeste quel que soit le sexe. Pour la période 1987-2002, c’est l’Italie qui a vu sa mortalité fortement diminuer (décalage particulièrement important de Sx) alors que la mortalité des Pays-Bas (NL) a nettement moins évolué. Une analyse plus pointue de la situation au cours du temps montre que l’évolution est plutôt instable et ne présente donc pas de tendances temporelles aisées à décrire. Le comportement de la mortalité au Japon et aux États-Unis conforte cette remarque (figure 2). Au Japon, la comparaison des courbes de survie entre 1987 et 2002 montre un simple décalage à droite indépendant du niveau de Sx. Cela veut donc dire que la fonction des décès selon l’âge se déplace uniformément à droite au fil du temps, et ce, tant chez les hommes que chez les femmes. Pour ces dernières, les progrès sont particulièrement importants. Au cours de la période suivante, pour les deux sexes, le décalage est clairement plus élevé lorsque Sx est élevé, et faible lorsque Sx est faible (aux âges x élevés). Autrement dit, il y a concentration des âges au décès. Il est à noter qu’entre 2012 et 2014 on retrouve un simple déplacement vers les âges élevés tant chez les hommes que chez les femmes japonaises. Cela suggère qu’il soit utopique de chercher trop de régularité à court terme. Aux États-Unis, si on se focalise sur la partie de la table où Sx est inférieur à 0,65, on observe une situation bien différente avec un déroulement dans le temps inverse. Alors qu’il y a concentration des décès lors de la première période, il y a « simple » décalage à droite de la courbe des décès sur la période 2002-2014. Pour faciliter la comparaison, le troisième graphique de cette figure décrit l’évolution des Sx(t) correspondant à la moyenne des tables de 11 pays[6]. On constate ainsi que la mortalité des femmes suit une évolution comparable sur les deux périodes, alors pour les hommes, le décalage de Sx est plus important en seconde période et résulte d’un effet de rattrapage de la mortalité des hommes sur celle des femmes.
SYNTHÈSE DES RÉSULTATS ET MODÉLISATION DE LA MORTALITÉ DES PERSONNES ÂGÉES
Comme le décalage suit une fonction pratiquement linéaire pour les deux sexes, sur les intervalles {0,03 < Sx < 0,9} pour les femmes, et {0,05 < Sx < 0,7} pour les hommes[7], les valeurs de chaque constante et chaque pente par pays et par sexe ont été calculées par régression pour synthétiser cette information. Pour la modélisation du décalage annuel de la courbe des survivants (noté décal) en fonction du niveau de cette dernière (Sx), on utilise comme notation α pour la valeur de la constante et β pour la valeur de la pente.
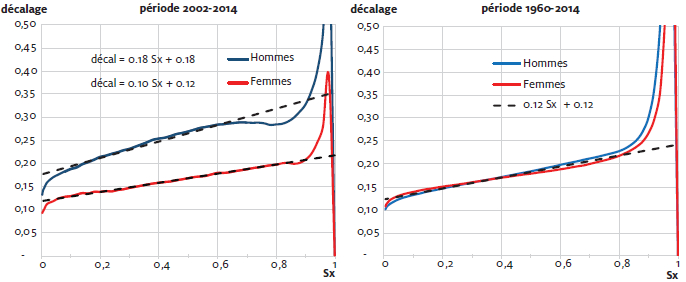
A priori, ces deux paramètres dépendent de la période d’observation, du pays et du sexe. Pour la table de référence (moyenne sur 10 pays observés[8]), les valeurs des paramètres selon le sexe sont présentées dans la figure 3. Il est à noter que par rapport à la figure précédente, les axes ont été intervertis pour laisser en ordonnée la variable expliquée et en abscisse la variable de contrôle.
Pour la période 2002-2014, (α, β) = (0,18 0,18) pour la mortalité masculine, et (0,12 0,10) pour la mortalité féminine (figure 3). Ainsi, tant le déplacement à droite que la concentration de la mortalité est plus forte chez les hommes. Cependant, sur le graphique de droite, qui décrit la situation moyenne sur une période d’un peu plus de 50 ans, on constate que la progression des tables de mortalité est comparable selon le sexe. Les paramètres α et β sont tous les deux proches de 0,12, quel que soit le sexe. On retrouve un décalage similaire à celui observé sur la période récente chez les femmes. Cette stabilité montre que ce modèle présente empiriquement une certaine robustesse. La partie linéaire de la fonction du décalage annuel des survivants selon l’âge se localise aux âges plutôt élevés où ont lieu plus des trois quarts des décès. Cela justifie ainsi de bénéficier de cette situation aisée à décrire pour établir un modèle sur cette base.
Alors que la table de référence facilite une vision globale, la comparaison entre les évolutions des tables nationales peut enrichir la description. L’observation des coefficients de régression mesurés sur la partie linéaire du décalage de Sx pour chaque pays facilite l’analyse. En utilisant l’espérance de vie à la naissance (e0) comme un indicateur du niveau relatif de la mortalité, qui situe indirectement chaque pays par rapport à un niveau maximum possible (mais inconnu) dans les conditions du moment, cela permet de décrire le comportement du niveau des deux paramètres en regard de e0. On valide ainsi l’idée que la rectangularisation de Sx se traduit par un mouvement de concentration des décès aux âges élevés d’autant plus marqué que e0 est grand (c’est-à-dire que la surface du « rectangle » est grande).
Figure 3
Décalage annuel de la courbe des survivants, comparaison selon le sexe et la périodea
a Table de référence sur la base de 10 pays (les 11 sans DE). Droites de régression ajustées sur la partie pratiquement linéaire
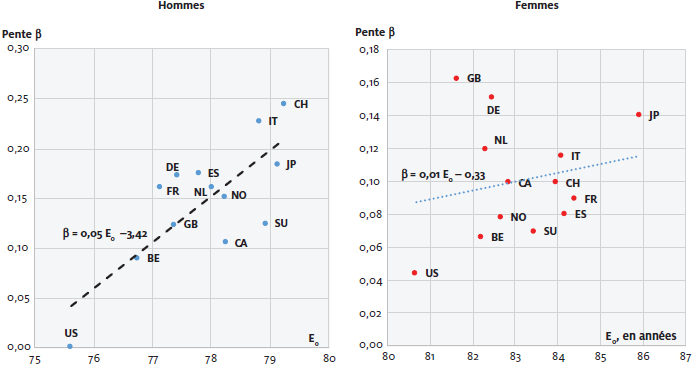
Ainsi pour la période 2002-2014, on constate que le coefficient de pente β est généralement d’autant plus élevé que l’espérance de vie à la naissance est élevée (figure 4). Une corrélation entre ces deux variables semble se confirmer. Calculé pour la mortalité des hommes, le coefficient de détermination (R2) vaut 0,6 ; mais sans les points CA et SU, il est de 0,81. Pour les femmes, calculé avec les 13 pays, R2 est proche de 0, cependant sans les trois points de NL, DE et GB, il est de 0,72. Bien qu’une tendance générale semble bien établie, la dispersion observée entre les pays n’est pas surprenante compte tenu des caractéristiques socio-économiques largement différentes de leurs populations (Eggerickx et collab. 2018).
Symétriquement, la constante α de chaque droite est en général d’autant plus faible que l’espérance de vie à la naissance est élevée. Cela s’explique par la liaison constatée entre une pente élevée et la constante faible (figure 5). L’observation des courbes de la figure 1 rend plausible la présomption que si α était nul, la pente β serait relativement élevée, alors que si α était très élevé, β serait probablement proche de 0 ; ainsi une fonction de type exponentielle (formule 2, en traitillé sur la figure 5) permet de décrire assez bien la disposition des droites de régression observées.
L’observation de l’évolution au cours du temps de la fonction du décalage montre cependant que l’on ne peut pas en déduire que, pour un pays donné, au fur et à mesure que l’espérance de vie augmente, la constante diminue et la pente augmente de manière inexorable. L’évolution dans le temps de la mortalité, par pays, suggère qu’elle puisse parfois présenter des fluctuations imprévisibles. Certains pays qui ont un retard relatif, du point de vue du niveau de leur mortalité, ont des difficultés à progresser (constante faible et pente élevée, progrès mais avec une concentration des décès), peut-être induit par des conditions-cadres défavorables. Cela n’empêchera pas ces derniers de voir leur table de mortalité refaire parfois un bond en avant lorsque le contexte sera plus favorable (situation économique, progrès sanitaire, profil socioprofessionnel, etc.). L’observation par pays montre des niveaux de mortalité qui évoluent par à-coups et de façon non synchronisée. Sur la longue durée, il semble cependant vraisemblable que le décalage à droite de la courbe des survivants selon l’âge diminue plutôt et que les décès se concentrent un peu plus aux âges élevés. Autrement dit, on pourrait s’attendre à ce que la constante diminue et que la pente augmente au fur et à mesure que la mortalité s’atténue.
Figure 4
Valeur de la pente de la régression (β) en correspondance avec le niveau de l’espérance de vie à la naissance (e0) selon le paysa pour la période 2002-2014, par sexe
a e0 au milieu de la période observée
UN MODÈLE DE PROJECTION
Dans la logique de notre description, pour établir une projection d’une table de mortalité en décalant la table des survivants selon l’âge, il est nécessaire de formaliser le niveau du décalage en fonction de celui de Sx pour un sexe donné.
Figure 5
Lien entre la pente β et la constante α de la droite de régression, pour la période 2002-2014 selon le pays, par sexe
Le modèle « sophistiqué » n’est pas vraisemblable sur le long terme
Dans un premier temps, une formulation « complexe » du décalage a été déterminée afin que la physionomie de la fonction décal(Sx) du modèle corresponde de manière fidèle aux observations récentes de l’évolution de la table de mortalité (table de référence telle la figure 3, période 2002-2014). En gardant constante la fonction de décalage ainsi formalisée pour établir une projection des tables de mortalité sur une longue période, le résultat obtenu pour la mortalité de la table de référence montre des conséquences déconcertantes pour les hommes. Alors que la mortalité diminue de manière importante, les quotients de mortalité restent particulièrement élevés aux alentours de 65 ans. Par contre, aux autres âges, la diminution de mortalité semble irréaliste. Pour les jeunes adultes, la diminution de la mortalité semble excessive tant pour les femmes que pour les hommes. Autrement dit, les particularités de décal(Sx) observées sur la période 2002-2014 ne peuvent pas être supposées durables sans que les tables projetées correspondantes deviennent surprenantes (figure 6). Cet essai est intéressant dans la mesure où il démontre qu’une prise en compte d’un comportement observé sur une brève période peut être influencée par des caractéristiques spécifiques à des personnes de groupes d’âge particuliers, ou par les comportements particuliers de certaines générations (qui ne dureront donc pas). Pour élaborer des projections sur le long terme, il semble plus réaliste de s’appuyer sur une vision plus large et suggère ainsi d’utiliser le modèle simple validé sur une durée suffisante et pour plusieurs pays à mortalité relativement comparable.
Finalement, nous suggérons d’utiliser dans un premier temps une modélisation établie sur la base d’une formalisation de décal(Sx) simplifiée (figure 7). Elle présente l’avantage d’utiliser peu de paramètres — ce qui facilite aussi la compréhension de leurs rôles respectifs — tout en présentant des tables qui affichent une structure par âge qui reste vraisemblable. On verra que ce modèle simple semble efficace.
Figure 6
Projection de la mortalité 2014-2060 établie avec un décalage de Sx constant sur la période
Pour cet exercice, la prise en compte de la surmortalité observée avant 35 ans qui n’est pas induite par les effets de la sénescence est traitée de manière sommaire. La limite de 35 ans correspond approximativement (selon l’époque, le pays et le sexe) à l’âge à partir duquel le logarithme du quotient de mortalité évolue de manière linéaire. Bien que cette surmortalité des jeunes soit largement documentée et reconnue en démographie, elle n’a jamais été clairement définie et ni expliquée. Une recherche récente (Remund, 2015) comble ces lacunes et montre que la présence d’une très petite sous-population vulnérable suffit à générer une bosse de surmortalité sans qu’aucun individu ne connaisse une élévation de son risque de décès.
Description du modèle simplifié
La fonction qui précise le décalage de la fonction des survivants est définie selon des intervalles d’âge. Dès 35 ans, l’importance du décalage de Sx est dépendante du niveau de celui-ci par une fonction linéaire :
Il est à noter que, comme S0 ne change pas de valeur, par définition, pour x = 0 décal(1,t) = 0.
Pour décrire l’évolution de la mortalité[9] aux âges jeunes (0 < x < 35), un simple « raccord » a été effectué. Nous proposons un processus rudimentaire pour décrire ce groupe à faible mortalité, mortalité qui n’est pratiquement pas induite par le processus de sénescence. Le niveau retenu pour décal(S22,t) est ajusté empiriquement par l’observation des quotients de mortalité par âge résultant du modèle et par l’idée que nous nous faisons de l’évolution de la mortalité des jeunes adultes.
|
Pour 0 < x < 22 |
décal(x, t) résulte d’une simple interpolation linéaire selon l’âge x entre décal(0,t) = 0 et décal(22,t) déterminé sur une base empirique (0,1 pour les hommes et 0,08 pour les femmes, par exemple). |
|
Pour 22 < x < 35 |
décal(x, t) résulte d’une interpolation linéaire entre décal(22,t) et décal(S35,t). Cela permet de conserver un profil de mortalité relativement stable pour ce groupe d’âge tout en intégrant le progrès escompté à 35 ans. |
Une difficulté pratique subsiste pour pouvoir décrire la table de mortalité de l’année suivante. Effectivement, il est nécessaire d’ajuster Sx(t) pour estimer Sx(t+1).Cela correspond au déplacement de Sx, âge après âge, dans le sens de l’axe du nombre de survivants (verticalement) alors que nous avons observé, puis projeté, l’évolution du décalage de la fonction Sx dans le sens de l’axe des âges (noté décal). La stratégie utilisée est l’interpolation décrite en annexe (explications de la formule 8 en annexe, avec l’aide de la figure 11).
Test de la méthode sur la base de la table de référence
Une première illustration des résultats obtenus avec ce modèle simplifié sur la base de la table de référence est présentée, sans intention « prédictive ». Les valeurs suivantes pour déterminer décal(Sx) ont été choisies et ont été maintenues constantes entre 2012 et 2060 afin de simplifier la démonstration. Dans le contexte d’une projection, il serait bien entendu possible d’envisager un scénario avec les paramètres qui seraient variables au cours du temps et choisis en fonction des caractéristiques de la mortalité du pays concerné :
(α, β) = (0,12 0,12) pour les hommes,
(α, β) = (0,10 0,10) pour les femmes.
Ce choix (figure 7) correspond à une évolution de la mortalité inférieure à celle observée entre 2002 et 2014 sur les 10 pays mais proche de celle observée sur la période 1960-2014 (figure 3, droites en traitillé).
Figure 7
Décalage pris en compte pour estimer les tables de 2060a
a décalage constant sur toute la période de calcul
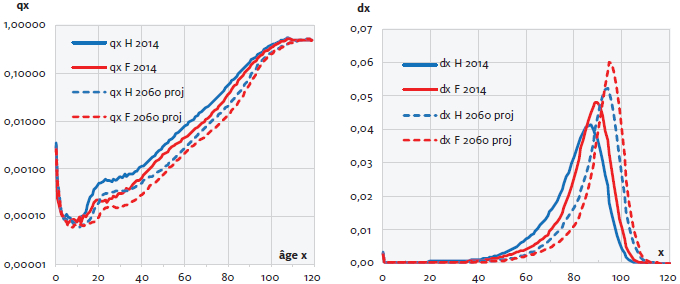
La projection établie[10] pour les tables de mortalité avec décal(Sx) jusqu’en 2060 aboutit à une évolution de la mortalité assez marquée et avec une évolution des quotients de mortalité plausible. Pour les hommes, e0 passe ainsi de 79,9 ans en 2014 à 88,1 ans (+ 8,2 ans) et, pour les femmes e0 passe de 84,1 ans à 91 ans (+ 6,9 ans). La fonction décal(Sx) est constante dans le temps, mais son effet évolue avec Sx(t).Cela explique que la concentration des décès augmente vers des âges de plus en plus élevés. La figure 8 visualise les décès dx(t) et les quotients par âge qx(t) pour t = 2014 et 2060.
Pour illustrer la souplesse du modèle proposé, des projections ont été établies avec des paramètres (α, β) fixes illustrant des situations typiquement différentes. La figure 9 présente les résultats obtenus pour trois projections (2060, mortalité de référence des hommes). Les résultats montrent qu’en interprétant α comme un indicateur de l’importance de la diminution de mortalité et β comme un indicateur de la concentration des décès, cela est empiriquement assez représentatif de l’évolution observée.
Projection 1 avec (α, β) = (0,05 0,16) : la diminution des quotients de mortalité est bien visible particulièrement pour les personnes de moins de 90 ans.
Projection 2 avec (α, β) = (0,1 0,24) : diminution encore plus importante qui conduit à une concentration marquée des décès vers 95 ans, toujours sans progrès important au niveau de la mortalité aux âges élevés.
Projection 3 avec (α, β) = (0,3 0) : cette projection (avec une pente nulle) correspond pratiquement à un simple décalage des tables de mortalité S(x) vers les âges x élevés.
Figure 8
Quotients de mortalité (qx) et décès par âge (dx) avec la méthode simple. Évolution 2014-2060, table de référence pour les hommes (H) et les femmes (F)
Figure 9
Trois projections pour illustrer l’impact de la constante α et de la pente β(a). Table de référence, Hommes 2014 et projections pour 2060
Il est à noter que « l’effet d’âge » sur le niveau d’évolution des quotients de mortalité varie dans le temps avec un profil dépendant tant de décal(Sx(t)) choisi que de la table de départ Sx(t0).
Dans le cadre de cet exercice, l’évolution de la distribution des décès selon l’âge calculée (figures 8 et 9) dépend des deux paramètres α et β qui traduisent le décalage à droite de la fonction des survivants selon l’âge ; cela permet d’avoir une description de la mortalité complémentaire à celles que l’on trouve dans de nombreuses publications relatives à l’âge modal et à la variance des décès selon l’âge (par exemple, Martel et Bourbeau, 2003 ; Cheung et Robine, 2007 ; Cheung et collab. 2009).
La liaison entre ces deux paramètres et les indicateurs qui permettent de décrire la distribution des décès est intéressante. Dans le contexte décrit précédemment, avec α et β maintenus constants entre l’année t0 et t, deux simples équations, formulent relativement bien (pour α < 0,4 et β < 0,3) le lien empiriquement observé entre ces paramètres et la croissance de M, le mode des décès selon l’âge, ainsi qu’avec l’évolution de C50 (l’intervalle d’âge rassemblant la moitié des décès autour du mode, Kannisto, 2000) :
Ainsi, en se fixant les évolutions du mode et de C50 souhaitées, on pourrait en déduire les valeurs des paramètres α et β correspondant.
Ajustements pour rendre un scénario vraisemblable
Afin d’établir des projections nationales acceptables en décalant la fonction Sx (formule 3), une analyse spécifique est indispensable pour comprendre les caractéristiques de la table et les particularités de son évolution récente. L’expertise permettra de faire évoluer α(t) et β(t) au fil du temps selon l’appréciation de l’évolution et en commençant avec des valeurs proches des estimations correspondant à l’évolution récente observée. Le paramètre α(t) permet de régler l’importance du décalage à droite des Sx au cours du temps, et le paramètre β(t) règle le niveau de la concentration des décès aux âges élevés. Pratiquement, il faudra procéder à un calcul année par année. En général, on recherche des tables projetées qui sont cohérentes avec certains indicateurs-cibles choisis pour chaque sexe (habituellement e0(t), e60(t)) et la vraisemblance des quotients de mortalité par âge obtenus doit être vérifiée et plus particulièrement pour l’année « horizon ».
La figure 5 montre qu’il y a une certaine corrélation entre les deux paramètres α(t) et β(t). Pour établir une projection, il pourrait être intéressant de tenir compte du lien observé entre eux (formule 2). Avec ce choix, les projections se réduisent alors à déterminer le cheminement de α(t) compte tenu de a et b choisis (a étant éventuellement adapté sur la durée). Le paramètre α faible induit une pente β moindre, donc un décalage à droite moins dépendant du niveau de Sx. Il pourrait encore être utile de perfectionner la fonction linéaire en complexifiant la fonction linéaire de décalage aux deux extrémités pour ajuster la diminution de la mortalité chez les moins de 50 ans et pour restreindre légèrement le décalage de la fonction de survivants pour la mortalité des très âgés ; par exemple, pour Sx < 0,08, diminuer le décalage de 3(0,08-Sx)2.
CONCLUSION
L’observation du décalage à droite, vers des âges plus avancés, des courbes de survie (figure 1) est intéressante pour décrire la mortalité des adultes en fournissant un regard complémentaire aux méthodes habituelles. Le procédé proposé présente l’avantage d’être logique et simple à mettre en oeuvre.
Cependant, deux problèmes pratiques doivent être surmontés. Premièrement il faut mesurer le déplacement à droite des courbes de survie. Comme une lecture directe n’est pas possible, la mesure peut se faire en recourant à des interpolations entre les points de la table de mortalité. Deuxièmement, une fois la nouvelle table projetée (par un déplacement à droite de Sx), il faut déterminer le niveau des survivants pour chaque âge, les âges étant définis en valeur entière. Pour cela, on a aussi recouru à des interpolations, bien que la formule d’interpolation soit plus complexe (formule 8 en annexe) car il est nécessaire de tenir compte de la courbure de la fonction des survivants.
L’évolution des tables de mortalité peut être ajustée pour rendre les projections vraisemblables en choisissant le niveau de deux paramètres. Les deux paramètres ont un rôle respectif interprétable : l’un, α(t), règle l’importance du décalage à droite de la fonction des survivants par âge, et l’autre, β(t), règle la vitesse de concentration par âge des décès.
Ce procédé comporte une analogie avec la méthode « Lee-Carter » dans la mesure où le modèle s’appuie directement sur une table de référence, mais exprimée avec la fonction de survie, et non pas avec le logarithme des quotients de mortalité. Par contre, il présente des résultats clairement différents de ceux obtenus par cette méthode car l’interférence entre « l’effet d’âge » et l’évolution temporelle de la mortalité est ici prise en compte de manière efficace.
L’objectif de cet exercice est volontairement axé sur la description de la méthode proposée plutôt que sur les résultats obtenus qui ne sont utilisés ici que pour illustrer concrètement notre proposition de modélisation (figures 7 et 8). La projection jugée vraisemblable d’une table nationale nécessite une analyse de l’évolution passée et une comparaison avec d’autres tables. Cela permettra de tenir compte de leurs particularités, requérant toutefois de devoir parfois complexifier le modèle de base.
Parties annexes
Annexe
Description des procédés par interpolations
Lecture de l’écart d’âge entre deux courbes de survie et détermination d’une nouvelle table redéfinie âge par âge.
Mesure du décalage à droite de Sx
La méthode retenue consiste à estimer l’écart d’âge entre les deux courbes, Sx(t2) et Sx(t1), pour toute une série de niveaux de survivants choisis arbitrairement. À chaque niveau choisi, il faut simplement interpoler les points de la table concernés pour chacune des deux tables à comparer.
Afin que la lecture des résultats ne soit pas trop influencée par des variations dues aux aspects techniques de la construction des tables (qualité des relevés, lissage des courbes pour certains pays) et au fait que les tables de certaines années peuvent présenter des caractéristiques exceptionnelles (effet de la grippe, par exemple), il est logiquement avantageux de comparer les tables sur un intervalle de plusieurs années (cinq par exemple) et de ramener le résultat en écart moyen par année. Cela permet en plus de diminuer le poids relatif de l’erreur d’interpolation (considérée à tort comme linéaire) par rapport à l’écart mesuré et d’obtenir des résultats moins sensibles à certaines caractéristiques exceptionnelles. Il est à noter que comme les deux courbes présentent des allures semblables (en t1 et t2), l’erreur due à la linéarisation de l’interpolation devrait être très faible.
Figure 10
Illustration de la méthode de mesure du décalage entre deux courbes de survivants
Modalité des calculs pour un des niveaux de Sx choisi = Schoix pour les années t1 et t2 :
Recherche sur la table de l’année t1 pour quel âge xa, Sxa est juste supérieur à Schoix (fonction Equiv dans un tableur Excel). Ainsi Sxa > Schoix > Sxb où xb=xa+1
Estimation de x1 correspondant à Schoix par interpolation
Ainsi dans l’exemple illustré, (hommes suisses), t1 = 2007 :
pour Schoix = 0,8, xa = 70 et xb = 71 x1 = 70 + (0,811 – 0,8) / (0,811 - 0,795) = 70,7
En faisant de même avec la table de l’année t2 = 2014, on obtient l’âge x2 :
Le décalage annuel à droite pour Sx = Schoix est alors :
Concrètement, après avoir préparé, sur une feuille de calcul, les formules pour déterminer le décalage à droite entre deux tables de mortalité sur une vingtaine de niveaux (Schoix), il devient aisé de mesurer différentes variantes (choix d’autres années, choix de tables d’un autre pays). Nous avons pu vérifier, empiriquement, que le résultat obtenu est peu sensible au nombre de points et à leurs positions. Un test, au moyen d’une table et d’un décalage décrit mathématiquement, a permis de vérifier que la précision était nettement suffisante.
Calcul d’une nouvelle table pour des âges entiers (décalage vertical de Sx)
Cette autre situation, symétrique à la précédente, se présente lorsque l’on établit une projection des tables de mortalité sur la base d’une estimation du décalage à droite de Sx pour les années à venir.
Après avoir déterminé le modèle qui décrit le décalage potentiel à droite des courbes de survie, les valeurs décal(Sx, t) sont déterminables pour chaque valeur de Sx(t), x prenant successivement les valeurs de 0, 1, 2, 3, etc. Sx(t) correspondant d’abord à la dernière table connue, puis jusqu’à l’avant-dernière calculée.
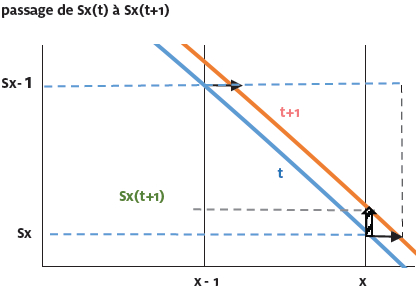
Pour passer de la table Sx(t) à la table Sx(t + 1), il faut décaler verticalement, de manière adéquate, la table Sx(t). Le croquis ci-dessous permet de comprendre comment passer du décalage par âge à droite décal(Sx -1,t) et décal(Sx, t) (les deux flèches noires) au décalage pour un x donné (la flèche large et hachurée qui correspond au décalage vertical, pour un âge entier donné) :
Figure 11
Schéma explicatif du passage d’une description selon des niveaux de Sx à celle selon des âges entiers
Les propriétés du théorème de Thalès permettent de déduire la taille du déplacement vertical de Sx(t + 1) - Sx(t). Ainsi on déduit la formule suivante :
Un exercice de simulation utilisant ce procédé a montré que le résultat était trop influencé par la courbure de la fonction Sx, concave ou convexe selon l’âge. En utilisant la même interpolation qui s’appuie sur la situation entre x et x+1, l’erreur d’interpolation est dans le sens opposé. Ainsi, pour avoir un calcul suffisamment précis, nous proposons d’utiliser une moyenne entre les deux interpolations, chacune présentant un biais qui se compense :
Empiriquement, avec w = 0,66, nous avons constaté un résultat pratiquement sans erreur.
Remerciements
L’auteur remercie Philippe Wanner et Adrien Remund, de l’Université de Genève, ainsi que les évaluateurs anonymes des Cahiers pour leurs commentaires constructifs.
Note biographique
Anciennement chef de section de recherche à « Statistique Vaud » en Suisse, l’auteur a régulièrement élaboré (durant une trentaine d’années) des projections démographiques au niveau régional pour plusieurs cantons suisses.
Notes
-
[1]
Sources : « Human Mortality Database », Institut Max Planck pour la recherche démographique, Allemagne, Université de Californie, Berkeley. www.mortality.org
-
[2]
Dans le sens de l’axe des âges en abscisse.
-
[3]
Les résultats particuliers des États-Unis et du Japon sont traités dans la figure 2.
-
[4]
Parfois 2011 ou 2015, selon la dernière mise à jour de la base de données.
-
[5]
Âges indicatifs dans la situation actuelle.
-
[6]
Moyenne arithmétique simple entre les onze tables utilisées pour la figure 1.
-
[7]
Ce qui correspond approximativement à {75 < x < 100 ans} tant pour les hommes que les femmes.
-
[8]
Les 11 pays de la figure 1 sans l’Allemagne (DE).
-
[9]
Il est supposé que le niveau du décalage dépend essentiellement de l’âge pour les personnes jeunes, puis du niveau de Sx à partir de 35 ans.
-
[10]
Cet exemple de calcul n’est pas une prévision.
Bibliographie
- BOHK, C. et R. RAU. 2016. « Changing Mortality Patterns and their Predictability : The Case of the United States », dans R. SCHOEN, Dynamic Demographic Analysis, Springer : 69-89.
- BOOTH, H., R. HYNDMAN, L. TICKLE et P. de JONG. 2006. « Lee-Carter mortality forecasting : a multi-country comparison of variants and extension », Demographic Research, 15, 9 : 289-310.
- CASELLI, G. 2004. « Projections de mortalité : hypothèses et méthodes », Démographie : analyse et synthèse, Vol V, Histoire du peuplement et prévisions, Paris, INED : 301-322.
- CHEUNG, S.L.K. et J.M. ROBINE. 2007. « Increase in Common Longevity and the Compression of Mortality : The Case of Japan », Population Studies, 61, 1 : 85-97.
- CHEUNG, S.L.K. et J.M. ROBINE, F. PACCAUD, A. MARAZZI. 2009. « Dissecting the Compression of Mortality in Switzerland, 1876-2005 », Demographic Research, 21,19 : 569-598.
- DUCHÊNE, J. 1980. Un essai de modélisation de la répartition des décès selon l’âge et la cause dans les pays industrialisés. Louvain-la-Neuve, Cabay, 182 p.
- EGGERICKX, T., J-F. LÉGER, J-P. SANDERSON et C. VANDESCHRICK. 2018. « Inégalités sociales et spatiales de mortalité dans les pays occidentaux. Les exemples de la France et de la Belgique », Espace populations sociétés, 2018/1-2.
- KANNISTO, V. 1996. The Advancing Frontier of Survival : Life Tables for Old Age. Odense, Denmark, Odense University Press.
- KANNISTO, V. 2000. « Measuring the Compression of Mortality », Demographic Research, 3, 6.
- LEE R. et L. CARTER. 1992. « Modeling and Forecasting US Mortality », Journal of the American Statistical Association, 87, 419 : 659-675.
- MARTEL, S. et R. BOURBEAU. 2003. « Compression de la mortalité et rectangularisation de la courbe de survie au Québec au cours du XXe siècle »,Cahiers québécois de démographie, 32, 1 : 43-75.
- MENTHONNEX, J. 2015. Estimation des durées de vie par génération, Évolution 1900-2150 et tables de mortalité par génération 1900-2030, Rapport technique pour la Suisse, août 2015, Neuchâtel, Office fédéral de la statistique (OFS), 65 p.
- OUELLETTE, N. et R. BOURBEAU. 2011. « Changes in the Age-at-death Distribution in Four Low Mortality Countries : A Nonparametric Approach », Demographic Research, 16, 19 : 595-628.
- REMUND, A. 2015. Jeunesses vulnérables ? Mesures, composantes et causes de la surmortalité des jeunes adultes. Université de Genève. Thèse.
- SANDERSON, W. et S. SCHERBOV. 2007. « A New Perspective on Population Aging », Demographic Research, 16, 2 : 27-58.
- VALLIN, J. et G. BERLINGER. 2002. « De la mortalité endogène aux limites de la vie humaine », dans G. CASELLI, J. VALLIN et G. WUNSCH (dir.), Démographie : analyse et synthèse, Vol III, Les déterminants de la mortalité, Paris, INED : 169-204.
- VINCENT, P. 1951. « La mortalité des vieillards », Population, 2 : 181-204.
Liste des figures
Figure 1
Décalage annuel en âge de la courbe des survivants (Sx) en fonction de son niveau. Mortalité de 11 pays pour les périodes 2002-2014 et 1987-2002, par sexea
Figure 2
Décalage annuel de la fonction des survivants, comparaison pour le Japon et les États-Unis avec une situation de référencea
Figure 3
Décalage annuel de la courbe des survivants, comparaison selon le sexe et la périodea
Figure 4
Valeur de la pente de la régression (β) en correspondance avec le niveau de l’espérance de vie à la naissance (e0) selon le paysa pour la période 2002-2014, par sexe
Figure 5
Lien entre la pente β et la constante α de la droite de régression, pour la période 2002-2014 selon le pays, par sexe
Figure 6
Projection de la mortalité 2014-2060 établie avec un décalage de Sx constant sur la période
Figure 7
Décalage pris en compte pour estimer les tables de 2060a
Figure 8
Quotients de mortalité (qx) et décès par âge (dx) avec la méthode simple. Évolution 2014-2060, table de référence pour les hommes (H) et les femmes (F)
Figure 9
Trois projections pour illustrer l’impact de la constante α et de la pente β(a). Table de référence, Hommes 2014 et projections pour 2060
Figure 10
Illustration de la méthode de mesure du décalage entre deux courbes de survivants
Figure 11
Schéma explicatif du passage d’une description selon des niveaux de Sx à celle selon des âges entiers