Résumés
Résumé
Au moyen d’un registre de population informatisé intitulé « Vallouise en Briançonnais », qui regroupe la population d’une vallée des Alpes sur une période allant de 1370 environ à nos jours, nous considérons les enfants nés sur ce site et les enfants utiles. Le concept d’enfant utile, émanant de la génétique des populations, est un paramètre essentiel de la dynamique évolutive des populations. Il concerne les enfants qui, naissant en un lieu donné, grandiront, se marieront et se reproduiront de telle façon que leurs descendants formeront une génération supplémentaire. En stratifiant l’ensemble en sept cohortes trentenaires, nous observons son comportement en matière de reproduction générationnelle. En ce qui a trait à la fertilité efficace, sur dix couples fondés, seulement sept participent localement à la génération suivante. Par contre, en termes de descendance, sur dix enfants naissants, seulement quatre seront des enfants utiles. Finalement, quand nous examinons cette contribution, nous nous apercevons que moins du quart des couples (23 pour cent) concourent à près des trois cinquièmes de l’effectif reproductif (56 pour cent). Durant l’Époque moderne, seule une faible partie des enfants naissants assure en montagne la dynamique de cette population qui compte plus de 3200 personnes. Ce comportement spécifique présente une telle homogénéité au cours du temps que nous sommes sans doute face à des stratégies matrimoniales et reproductives adaptées.
Abstract
By means of a computerized population register entitled “Vallouise en Briançonnais,” which includes the population of an Alpine valley over a period from approximately 1370 AD to the present, we consider the children born in this area and so-called “useful children.” The concept of “useful children,” derived from population genetics, is an essential parameter in the evolutionary dynamics of populations. It concerns children who, being born in a given place, will grow up, get married and reproduce in such a way that their descendants will form a new generation. By stratifying the population into seven 30-year age groups, we observe generational reproductive behaviour. As regards effective fertility, for every 10 legal couples, only 7 are locally involved in producing the next generation. On the other hand, in terms of descent, for every 10 children born, only 4 will be “useful children.” Finally, when we examine this contribution, we notice that less than 1/4 of the couples [23%] are responsible for about 3/5 of the number of children who will in turn reproduce [56%]. Thus, during the period from 1600 to 1809, only a small portion of the children born in this Alpine area ensured the dynamics of this population, which includes over 3,200 persons. This specific behaviour is so similar over time that it suggests the existence of adaptive marital and reproductive strategies.
Corps de l’article
Dans leur étude consacrée au concept d’enfant utile, Heyer et Cazes (1999) préconisaient l’emploi de ce type de recherche pour la connaissance de la dynamique des populations. Lorsqu’un enfant naît, il devient un sujet susceptible de s’unir puis de se reproduire; il transmettra alors ses gènes, son nom, son patrimoine, il sera un chaînon de l’évolution humaine et un acteur de la dynamique de la population dans laquelle il s’insère (Sauvain-Dugerdil, 1996). Cependant, aux prémices d’un nouveau cycle familial, quand un couple se forme et tente de procréer, nombre d’obstacles viennent obérer cette volonté créatrice. Ce sont d’abord des contingences biologiques de tous ordres qui feront que la famille pourra être stérile ou subira les affres de la mortinatalité (Sutter et Tabah, 1953). Et, quand les naissances se succèdent, il sera nécessaire de pallier autant que possible la mortalité infantile, qui écarte une part plus ou moins importante d’enfants dans les premiers âges de la vie. Néanmoins, il s’agira que l’enfant passe du stade de nourrisson à celui d’adolescent puis de jeune adulte, et là demeurent d’autres paramètres culturels et éducatifs qui rendront ou non cette accession possible. À toutes ces occurrences, nous pouvons ajouter celle concernant le comportement familial en matière de transmission patrimoniale, qui déterminera, selon le sexe, le célibat définitif mais aussi les migrations matrimoniale et viagère (Goy et al., 1992). Nous nous intéressons donc ici aux enfants qui, échappant à tous ces obstacles biologiques et culturels, grandissent et parviennent à leur tour à procréer, au point d’assurer le renouvellement générationnel familial.
Matériel et méthodes
Pour réaliser cette recherche, nous prenons appui sur un registre de population nommé « Vallouise en Briançonnais », qui se présente comme un ensemble de familles reconstituées en généalogies ascendantes dont le nombre de générations est variable selon l’ancienneté des personnes sur le site. Ainsi, « Vallouise en Briançonnais » est une base de données qui regroupe les personnes nées sur le territoire de cette vallée des Alpes françaises située entre Gap et Briançon. Cependant, il ne s’agit pas d’un listing patronymique, car chaque individu de ce registre est relié par des liens généalogiques à partir de fondateurs nés, pour la plupart, aux XIVe et XVe siècles, si bien que les générations successives s’étendent jusqu’à nos jours pour former un ensemble comprenant 22 générations, parfois plus (Prost et Boëtsch, 2001a). À partir de cette structure arborescente viennent se greffer les unions, c’est-à-dire le ou les mariages de certains individus. Ce sont ces unions entre les membres des familles qui déterminent en quelque sorte les noeuds d’un maillage plus ou moins compliqué et instaurent, de fait, des réseaux plus ou moins imbriqués selon le degré de parenté des familles. Il en résulte un assemblage d’autant plus inextricable que la population est nombreuse et que les membres de celle-ci entretiennent une proximité d’apparentement importante.
C’est le cas pour la vallée de Vallouise, qui compte à la fin du XVIIe siècle environ 3200 personnes, et encore près de 3400 au début du XIXe. Par ailleurs, durant la période 1780-1809, neuf unions de ce site sur dix s’effectuent entre apparentés [1], et si l’on raisonne en termes de personnes, plus de 92 pour cent des individus naissants en Vallouise sont consanguins (Prost, 1998; Boëtsch et al., 2002). Ainsi, sans le secours d’un programme informatique approprié, une structure aussi complexe ne peut être gérée. Informatisé à l’aide du logiciel canadien-français Analypopopus 6.01 (laboratoire Ediph-Cinbiose de l’Université du Québec à Montréal, dirigé par Francine M. Mayer; voir Boisvert et al., 1996), le registre de population prend actuellement en compte environ 43 000 personnes et 12 500 unions. À titre informatif, il convient de préciser qu’Analypop ne se contente pas de gérer et d’ordonnancer une base de données généalogiques. Il permet, grâce à une interface multimodulaire, d’effectuer de multiples applications de biodémographie (Boisvert et Mayer, 1994; Bachand et al., 1997; Lima et al., 1997, 1998; Boëtsch et Prost, 2001; Boëtsch et al., 2002).
Sept cohortes d’unions de chacune 30 années ont été prises en compte pour appréhender le temps long et les éventuelles évolutions qui s’y produisent et, pour chacune d’elles, nous établirons la descendance généalogique. L’élément particulier que nous tentons de cerner, l’enfant utile, met en jeu, nous le verrons explicitement plus loin, trois générations : c’est donc sur une période de trois siècles que porteront nos analyses. Notre démarche sera mixte; nous empruntons les cohortes aux historiens-démographes et les descendances généalogiques aux biodémographes (Sauvain-Dugerdil et Richard, 1998; Bley et Boëtsch, 1999; Boëtsch et Prost, 2001). En optant pour cette approche plurielle, nous devrions pouvoir rendre compte plus justement du phénomène évolutif. Il est certain que le découpage du temps en cohortes ne s’accorde guère avec les descendances, qui peuvent s’étaler parfois sur de longues périodes. Néanmoins, des travaux ont montré que certains résultats calculés selon les deux méthodes ne présentaient que des écarts très faibles (Roberts et Rawling, 1974). Récemment, une étude théorique portant sur cette recherche particulière proposait d’opérer à partir de cohortes (Heyer et Cazes, 1999); nous allons donc procéder en quantifiant et comparant, au niveau de chacune des périodes trentenaires figurant les générations humaines, différents paramètres issus de la biodémographie : la descendance finale, le nombre d’enfants par famille, le nombre moyen d’enfants contenu dans les descendances généalogiques et les enfants utiles. Pour ce dernier paramètre, le concept provient de la génétique des populations. Si sa définition est simple, sa mise en oeuvre reste complexe, surtout si nous prenons en compte plusieurs milliers de familles. Le terme « nombre d’enfants utiles » (Jacquard, 1974; Roberts, 1976) résulte de l’effet global :
de la fécondité du couple (nombre d’enfants procréés),
de la mortalité (nombre d’enfants morts entre la naissance et l’âge au mariage),
de l’émigration (nombre d’enfants ayant quitté la population avant de se marier),
de la nuptialité (nombre d’enfants restés célibataires).
Ainsi, on qualifie d’enfants utiles des enfants qui, naissant en un lieu donné, grandiront, se marieront et (ou) se reproduiront de telle façon que leurs descendants formeront une génération supplémentaire. À lui seul, cet élément serait la résultante de tous les indices synthétiques qui peuvent s’élaborer en démographie historique. Néanmoins, sa comptabilité nécessite deux outils particulièrement adaptés : un registre de population et un logiciel ad hoc. Dans notre cas, après une programmation idoine, un des modules d’Analypop, dénommé « Création et analyse de descendance d’unions », délivre pour chaque union plusieurs informations, telles que le nombre d’individus contenu dans la descendance, d’unions que les descendants ont contractées, de fratries, de descendants qui se sont reproduits. C’est donc ce dernier résultat qui est pris en compte, relativement au premier, qui, lui, comptabilise la totalité des descendants. Comme tout registre de population, la base de données ne s’intéresse qu’aux personnes qui demeurent sur place. Donc, tous les descendants qui vont migrer et s’unir ailleurs n’entrent pas dans la catégorie des enfants utiles. Et même s’ils appartiennent à celle-ci, ils ne sont pas recensés dans notre présente étude. Analypop ne renvoie que des données qu’il peut calculer; il s’agit donc d’une « catégorie spécifique » d’enfants utiles, ceux qui sont restés sur place. Néanmoins, comme nous cherchons à connaître uniquement la dynamique reproductive en place de cette population d’altitude, si des Vallouisiens se sont reproduits hors du contexte, cela n’intervient aucunement dans notre problématique. D’ailleurs, une étude est en cours pour savoir comment se reproduisaient les Alpins hors de leur contexte et si des migrations « alléliques de retour » (Heyer et Cazes, 1999) n’entraient pas dans les habitudes montagnardes.
Résultats et discussion
Spécifions qu’afin de mesurer l’homogénéité des données chiffrées au cours du temps, nous utiliserons le coefficient de variation [cv], qui est le rapport de l’écart type [σ] sur la moyenne [μ] exprimé en pourcentage [cv = σ/μ * 100]. Explicitement, plus le coefficient de variation est faible, plus l’homogénéité est importante (Zakharov, 1992; Wachter, 1992).
D’emblée, il faut stipuler que, pour la période 1600-1629, un sous-enregistrement des naissances est à déplorer. Le nombre 2,6 enfants par couples paraît bien faible au regard des suivants. En effet, les familles ont été reconstruites à l’aide de multiples séries d’archives (Prost et Boëtsch, 2001a), et les enfants morts en bas âge ou adolescents n’ont pu être véritablement tous intégrés. Il y a aussi le fait que cette cohorte particulière succède aux importantes crises de peste qui se déroulèrent en Vallouise entre 1586 et 1589 puis en 1596 et en 1598. Perte de population, migrations temporaires puis définitives pour échapper aux foyers épidémiques ont créé des désordres qui se sont prolongés durant plusieurs décennies. Les deux premières colonnes du tableau 1 synthétisent les données recueillies en découpant le temps long en périodes trentenaires et en programmant le logiciel pour obtenir la descendance des unions à la première génération seulement [2]. Les 5401 mariages observés entre le XVIIe et le début du XIXe siècle ont généré plus de 21 500 individus déterminant une moyenne de quatre enfants par couple. En fait, le tableau ne rend pas réellement compte de la dimension diachronique puisque, pour les unions qui se sont déroulées au XIXe siècle [cohorte 1780-1809], les descendances s’étalent, pour les extrema, de 1782 à 1839, soit une « génération profonde » de 58 ans. Quant aux unions comptabilisées dans la quatrième colonne, il s’agit d’unions au sens large (mariages et remariages [3]) que les descendants de la deuxième colonne ont contractées. Là encore, pour ces dernières, si nous examinons les dates auxquelles elles se sont déroulées, nous trouvons un créneau compris entre 1801 et 1874 : il s’agit là d’un véritable « saut générationnel ». Ces quelques nombres montrent bien l’important décalage qui subsiste entre une cohorte démographique, artificiellement stratifiée, et un saut de génération vraiment enregistré, ici 74 ans. D’ailleurs, quantitativement, il devrait y avoir quelques distorsions. À titre d’exemple, si nous examinons les 817 unions recensées entre 1690 et 1719 (voir la cinquième ligne du tableau 1), elles ont « produit » 3281 descendants, qui eux-mêmes ont contracté un total de 1126 mariages. Pour la cohorte suivante, 1720-1749 (sixième ligne du même tableau), nous ne tablons que sur 778 unions d’où émaneront 3461 descendants puis successivement 1098 unions. C’est cette dichotomie entre cohorte et génération qui nous a fait opter pour une méthode mixte. Toutefois, il y a là un problème méthodologique nouveau généré par l’avènement des registres de population informatisés. En tout cas, hormis la première période, pour laquelle les enfants morts en bas âge n’ont pas été comptabilisés faute de données démographiques complètes, les six cohortes suivantes présentent une homogénéité moyenne de 11 pour cent pour l’ensemble des données réunies dans les cinq colonnes. Finalement, on constate que les comportements matrimoniaux apparaissent comme particulièrement stables dans la montagne briançonnaise durant l’Époque moderne. En effet, en effectuant le rapport entre les unions contractées par les descendants et celles contractées par les parents, on aboutit à un ratio moyen de 1,4 qui ne varie que très faiblement [cv = 7 pour cent] au cours des presque 300 ans de l’observation (des années 1600 à 1874 pour les extrêmes).
Tableau 1
Distribution des données démographiques du corpus de travail, en nombres absolus, observées selon sept cohortes trentenaires
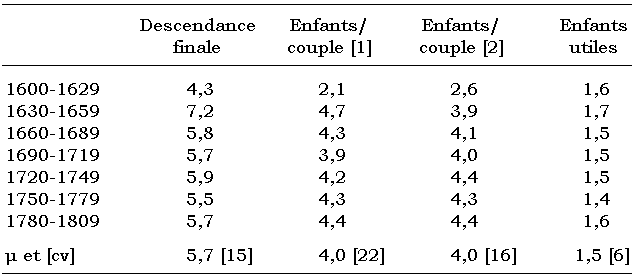
La première colonne du tableau 2 présente le résultat de l’indice synthétique qu’est la « descendance finale », calculé grâce aux taux de fécondité. Or, « les descendances calculées à partir des taux de fécondité ne correspondent pas au nombre d’enfants produit par les mariages mais au nombre d’enfants qui auraient été produits en l’absence de mortalité, comme si toutes les unions avaient duré jusqu’au terme de la vie procréatrice de la femme » (Dupâquier et al., 1988 : 356). Remarquons l’important indice de la cohorte 1630-1659, qui prouve la capacité réactive de la population montagnarde à l’égard de la dernière peste connue dans les Alpes. Passé cette crise, les indices retrouvent une stabilité remarquable autour de 5,7. Il en est de même pour les deux autres colonnes, qui aboutissent à des moyennes identiques en dépit des différentes méthodologies employées; toutefois, la méthode généalogique (unions et descendance à la première génération) offre une meilleure homogénéité eu égard à la méthode de la démographie historique et à ses rapports par cohortes : 16 pour cent contre 22 pour cent. Dans une précédente étude comparative (Bideau et al., 1995), nous obtenions pour la Vallouise 3,7 enfants par couple pour deux périodes relativement « courtes », 1670-1684 puis 1750-1764, les calculs portant alors respectivement sur 315 puis 424 mariages. Ainsi, il semblerait avantageux d’opérer sur des corpus plus conséquents afin de mieux rendre compte de la réalité car, en matière de démographie, oeuvrer sur de faibles effectifs entraîne de facto des effets aléatoires néfastes (Wachter, 1992). Avec l’ultime colonne, nous comptabilisons le nombre absolu d’enfants utiles recueillis au fil des générations dans la vallée de Vallouise : 1,5 en moyenne, avec un très faible coefficient de variation de 6 pour cent. Alors que l’on observe deux importantes crises dues aux épidémies de peste de la fin du XVIe siècle (1586-1589) et du début du XVIIe (1630), tout porte à croire que les familles montagnardes tentent de s’adapter. Ainsi, nous supposons qu’elles résolvent leurs déficits démographiques et leurs problèmes de transmission patrimoniale en accroissant le nombre moyen d’enfants utiles jusqu’à 1,7. Puis la moyenne reprend son cours aux générations suivantes, en laissant à peine plus qu’un héritier. En tout état de cause, nous voyons bien l’imposante dichotomie qui s’établit entre les indices synthétiques que nous pouvons obtenir et la réalité familiale en matière de dynamique de population.
Tableau 2
Distribution de différents indices a calculés concernant la descendance des couples vallouisiens
Ici, nous avons voulu comparer certains résultats concernant la descendance selon différentes méthodologies. Le premier (colonne 1) concerne l’indice synthétique que l’on calcule en démographie historique à l’aide des taux de fécondité par groupes d’âge quinquennaux. Les valeurs enregistrées se situent dans la norme de l’enquête de l’INED pour le quart sud-est de la France : 1720-1739 (6,30), 1740-1769 (5,87) et 1770-1789 (5,67). Le deuxième indice (colonne 2, nommée enfants/couple [1]) résulte lui du calcul effectué selon les principes de la démographie historique, c’est-à-dire par cohortes. C’est le rapport du nombre d’enfants nés durant une certaine période (ou cohorte) sur le nombre de mariages qui se sont déroulés durant cette même période. Or, entre les unions et les naissances, il y a un décalage générationnel. Cependant, tous les mariages qui se sont déroulés en fin de cohorte ont très bien pu avoir des naissances non prises en compte durant ce laps de temps. C’est pour cela que nous tentons de vérifier ici la validité du corpus en considérant maintenant la descendance généalogique. Un algorithme particulier du programme Analypop permet de définir, sur une ou plusieurs générations, la descendance exacte des couples à une période donnée que l’on aura programmée. C’est une méthode davantage utilisée en anthropologie. De cette programmation, nous obtenons un troisième indice (colonne 3, nommée enfants/couple [2]). Ce dernier est obtenu par le rapport du nombre de descendants effectifs, à la première génération, sur le nombre des unions enregistrées durant une période choisie. À notre sens, cette dernière méthode est beaucoup plus pertinente que les autres, surtout lorsque les cohortes envisagées sont décennales. Ce n’est pas le cas ici et, si des variations indiciaires sont de mise durant certaines périodes, les résultats des colonnes 2 et 3 s’accordent véritablement.
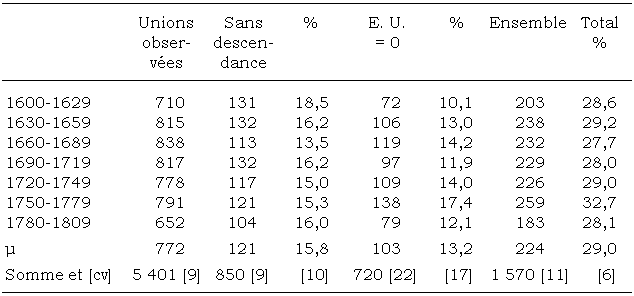
Sur la totalité des unions qui se réalisent en Vallouise, nous distinguons, dans le tableau 3, celles qui sont stériles de celles pour lesquelles aucun enfant utile n’est détecté. Le résultat d’ensemble donne 15,8 pour cent, avec un coefficient de variation faible de 9 pour cent d’un siècle à l’autre. Néanmoins, face à cette incapacité à procréer, nous découvrons une quantité non négligeable (720 couples, soit plus de 13 pour cent de l’ensemble des unions) ayant eu une descendance, cette dernière décédant ou migrant. Au total, plus de 29 pour cent de couples vallouisiens ne jouent aucun rôle dans la reproduction générationnelle de la vallée et ne transmettent pas leurs gènes au pool génique existant. Par comparaison, les rares études comptabilisant ce paramètre donnent des taux semblables ou supérieurs. Ainsi, dans la population québécoise du Saguenay-Lac-Saint-Jean, ce sont 30 pour cent des couples qui n’ont pas d’enfant utile (Austerlitz et Heyer, 1998). Plus près de nous, dans les collines du Jura, ils sont 47 pour cent pour une période couvrant les XVIIIe et XIXe siècles (Heyer, 1991). À « l’effectif efficace » des généticiens pourrait s’opposer un paramètre plus concret, « l’effectif inefficace » de la biodémographie. Par ailleurs, en Vallouise, ce résultat final s’accompagned’un coefficient de variation de 6 pour cent (voir la dernière colonne du tableau 3) évalué sur plusieurs siècles. Ce type de résultat amène à présumer qu’en Briançonnais, et sans doute ailleurs, un « contingent » homogène d’unions se constituerait au cours des générations en évitant toute participation génétique à la population en place. Un certain groupe de montagnards s’uniraient en sachant pertinemment leur non-participation au renouvellement [4] ? Peut-être s’agit-il de stratégies mises au point afin que la transmission patrimoniale et la circulation des biens s’effectuent plus facilement dans une province de droit écrit, le Dauphiné, où la coutume est « de faire autant d’héritiers qu’un père a d’enfants » (Prost et Revol, 2001). Au reste, les recherches conduites sur la population du Saguenay ont montré l’impact des facteurs sociodémographiques et culturels en matière de reproduction humaine. Ailleurs, d’autres études témoignent de l’impact direct des groupes sociaux sur les structures génétiques (Cannings et Skolnick, 1975; Abelson, 1978).
Tableau 3
Distribution en nombres absolus et relatifs des couples qui ne participent pas au renouvellement des générations
Le tableau 4 montre comment s’opère la distribution dans le temps de la descendance généalogique pour chacune des cohortes prises en compte, soit un total de 21 551 Vallouisiens, avec une partition selon le sexe qui détermine que 50,3 pourcent sont des garçons. Pour chaque période considérée figure le nombre exact d’enfants utiles. Ainsi, un total de 8369 personnes appartiennent à cette catégorie et, du fait de leur statut de descendants, leur naissance et leur existence se situent jusqu’à la fin du XIXe siècle.
Tableau 4
Distribution selon le temps et le sexe des naissances vallouisiennes et indication du nombre d’E. U. recensé avec, en regard, le pourcentage qu’il représente
Les deux dernières colonnes du tableau 4 appellent plusieurs remarques.
D’abord, le nombre d’enfants utiles s’accompagne d’un coefficient de variation de 10 pour cent qui démontre une fois encore une permanence de stratégies en matière démographique. Il paraît certain que cette variabilité aurait été plus faible encore si, au cours des deux premières cohortes, les Alpins n’avaient effectué une sorte de « rattrapage » après les crises épidémiques de peste. Ces données montrent bien l’adaptabilité continuelle et la capacité réactive des montagnards face aux conditions difficiles auxquelles ils sont soumis. Alors qu’habituellement la vallée ne « garde » qu’environ 35 pour cent d’enfants utiles, les temps de peste génèrent des mortalités qu’il faut pallier en augmentant très sensiblement le potentiel reproducteur vers 40 et même 60 pour cent. Au cours de ces deux générations, la migration viagère a dû forcément connaître un arrêt brutal.
Sans vraiment, comme pour les descendants, discriminer précisément le nombre réel de garçons et de filles parmi les enfants utiles [5], des travaux précédents permettent d’en avoir une idée : globalement, au XVIIe siècle, près de 60 pour cent des enfants utiles sont des garçons, tandis qu’au siècle suivant, ces derniers ne représentent plus que 53 pour cent. Un calcul sommaire fait ressortir que les 8369 enfants utiles recensés dans la Vallouise se scinderaient en 4788 garçons (57,2 pour cent) pour 3581 filles (42,8 pour cent), soit un sexe-ratio de 133,7. En tout cas, le résultat le plus pertinent s’avère être celui concernant le rapport du nombre d’enfants utiles sur celui des naissances, avec une moyenne de 40 pour cent.
Seulement un petit nombre d’individus participe à la dynamique de la population montagnarde. Ainsi, six enfants naissants sur dix ne contribuent aucunement, sur près de trois siècles, au renouvellement générationnel de la Vallouise. Nous mesurons ici toute la dichotomie entre enfants naissants et enfants utiles. Concrètement, dans la montagne briançonnaise, il ne s’agit pas seulement de naître, mais il s’agit de grandir, de perdurer et de se reproduire.
On peut aussi s’interroger sur le devenir des enfants non « utiles ». Voici quelques proportions émanant de travaux antérieurs : si, en moyenne sur deux siècles, 40 pour cent des naissants sont des enfants utiles, 30 pour cent meurent célibataires et 30 pour cent ont un destin inconnu puisqu’ils quittent le site d’observation (Bideau et al., 1995).
Dans le tableau 5, nous récapitulons la contribution propre de chacun des 5401 couples pris en compte, pour appréhender globalement la cohérence du comportement montagnard en matière de reproduction. Nous avons distribué les couples selon leur nombre d’enfants utiles en nous restreignant au nombre de 5 pour ne pas agrandir démesurément un tableau déjà important. En effet, parmi les couples marqués d’un astérisque, nous comptons 6 et 7 enfants utiles (ainsi, les sept astérisques de la cohorte 1720-1749 synthétisent cinq familles avec 6 E. U. et deux autres avec 7 E. U.). Quant aux doubles astérisques, ils signalent des couples ayant 8 et 9 E. U.; ce sont les extrêmes rencontrés en Vallouise. Par contraste, au Saguenay en terre québécoise, durant les XVIIIe et XIXe siècles, les chercheurs observent plusieurs couples avec plus de 10 enfants utiles. Nous remarquons que ces familles si reproductives se contingentent dans les premières cohortes et semblent agir comme pour compenser face aux crises démographiques citées plus haut. D’autre part, le tableau 5 montre que ce sont les familles ayant un seul E. U. qui sont les plus nombreuses (1443, soit 26,7 pour cent du total des couples), suivies de celles n’ayant que 2 E. U. (1137, soit 21 pour cent du total). Si nous adjoignons les 665 couples du groupe suivant, ceux qui ont 3 E. U., nous obtenons alors 60 pour cent des 5401 familles de la vallée. Ainsi, une forte majorité d’autochtones, les trois cinquièmes exactement des couples montagnards, fait naître un potentiel d’enfants tel, qu’une fois ceux-ci arrivés à l’âge adulte, il ne reste au sein des familles que majoritairement 1, 2 ou 3 enfants utiles. À l’inverse, un groupe non négligeable de 586 couples ont des familles pourvues de 4, 5, 6 héritiers et plus, jusqu’à 9 au maximum. Il y a là un gisement d’études concernant ces familles particulières : comment font-elles pour gérer cette multitude ? Comment résolvent-elles l’entrée de leur descendance dans un marché matrimonial hautement contrôlé ? Comment procèdent-elles en matière de dévolution des biens patrimoniaux pour éviter une « atomisation » des immeubles ? Comment opèrent-elles la recomposition du patrimoine aux générations suivantes ?
Tableau 5
Distribution, en nombres absolus, des couples observés selon le nombre d’enfants utiles recensés ou bien selon leur non-contribution
Néanmoins, plusieurs résultats importants se situent aux extrêmes du tableau 5. Avec une moyenne de 71 pour cent, les coefficients de variation à chaque période indiquent une homogénéité remarquable; seule la cohorte 1630-1659 déroge, pour les raisons évoquées précédemment (épidémie de peste). De même, les coefficients de chaque ligne oscillent autour d’un coefficient de variation de 22 pour cent que seule la dernière ligne, qui est un assemblage disparate de données, vient bousculer. Ces moyennes semblent suggérer une réelle continuité comportementale en Vallouise. Il s’avérerait que chaque famille de la vallée gère et tente de résoudre son ou ses problèmes de pérennité familiale; néanmoins, de l’observation de l’ensemble des couples résulte une telle régularité que les solutions adoptées ne doivent guère être dissemblables, au point de délivrer presque constamment le même indice.
Un autre angle d’observation peut être envisagé, celui concernant la contribution des couples au renouvellement générationnel en fonction du nombre d’E. U. qu’il a engendrés.
Les nombres absolus et proportionnels du tableau 6 sont cumulatifs et prennent en compte tous les couples observés et leur descendance à la génération suivante, c’est-à-dire sur une période allant de 1600 à 1874 exactement. Au total, nous observons 5401 couples qui vont procréer ou non un ensemble de 8369 enfants utiles. Nous avons vu que 1570 couples (720 + 850) étaient de facto exclus de la dynamique reproductive; ils figurent explicitement dans les deux dernières lignes du tableau 6. Néanmoins, il reste 3831 couples qui, eux, participent activement mais à différents degrés, selon la quantité d’enfants utiles qu’ils ont élevés puis « conservés ». Dès lors, si un peu plus de 10 pour cent des couples ont 4 E. U. et plus, ils concourent à près de 32 pour cent du renouvellement générationnel, et si nous examinons les familles ayant 2 E. U. et plus, nous pouvons dire qu’un peu plus des deux cinquièmes des couples (44 pour cent) participent à plus des quatre cinquièmes (83 pour cent) de ce même renouvellement dynamique. En Vallouise, donc, sur une période pluriséculaire, nous constatons qu’un nombre restreint de couples contribue, pour une part très importante, à l’évolution de la structure biodémographique de l’ensemble de la population.
Tableau 6
Distribution cumulée des couples et de leur descendance utile selon le nombre d’enfants utiles dans la famille à laquelle ils appartiennent
Conclusion
Le concept « d’enfant utile » est le seul indice de la dynamique évolutive des populations capable de concentrer en un paramètre unique la mesure d’une contribution génétique non nulle à la génération suivante. « Le terme “enfants utiles” fait référence, en fait, à trois générations successives : celle de leurs parents; la leur; celle des enfants proprement dite; et celle de leur progéniture puisqu’ils seront “utiles” » (Heyer et Cazes, 1999 : 686). Cependant, cet élément est relativement délicat à mettre en oeuvre, et cela pour deux raisons. Il faut au moins avoir accès à un corpus généalogique pouvant s’étendre sur de nombreuses générations et représenter des ensembles populationnels fiables (Cazes et al, 1993). Ensuite, il convient d’opérer des analyses sur plusieurs centaines de familles et sur de longues périodes, sous peine de déboucher sur des études de cas qui obèrent la réalité. Ces contraintes s’accompagnent de la nécessité d’employer un programme informatique spécifique qui discriminera, dans l’ensemble des descendances généalogiques, les enfants qui se reproduiront et formeront une nouvelle génération. Le registre « Vallouise en Briançonnais », géré par Analypop 6.01, répond amplement à tous ces critères méthodologiques.
Rares étant les recherches concrètes sur ce concept particulier de la dynamique reproductive, nous ne possédons que très peu de points de comparaison avec d’autres populations françaises et européennes. D’ailleurs, les communautés montagnardes, considérées jadis comme des isolats (Jacquard et al., 1976; Chaventré et al., 1990), sont souvent restées à l’écart des grandes synthèses de démographie (Dupâquier et al., 1988; Bardet et Dupâquier, 1997). Pourtant, depuis quelques années, différentes études et quelques programmes pluridisciplinaires se sont intéressés aux populations d’altitude (Morton et al., 1973; Serre et al., 1985; Viazzo, 1989; Prost et Boëtsch, 2001b et 2002; Boëtsch et al., 2002). Ainsi, la vallée de Vallouise en France et celle de Chiomonte en Italie font l’objet de travaux comparatifs d’anthropologie biologique et de démographie, pour lesquels nous étudions, entre autres choses, les structures biodémographiques. Comprise dans cette recherche européenne, cette étude sur l’enfant utile en Briançonnais met en évidence plusieurs résultats originaux.
D’abord, en termes d’unions, sur dix mariages qui unissent ces montagnards, seulement sept ont un rôle dans la constitution de la génération suivante. Cependant, si nous analysons l’ensemble en termes de descendance sur place, sur dix enfants naissants en Vallouise au cours des XVIIe et XIXe siècles, plus de six ne participent aucunement à la dynamique de la population.
Ensuite, nous remarquons que ces Alpins font preuve de continuité. Les comportements matrimoniaux et reproductifs perdurent au point de produire des indices ou des données dont les coefficients de variation présentent une stabilité remarquable. Certes, nous ne recueillons ici que des éléments macroscopiques résultant de l’observation de plusieurs milliers de familles; pourtant, il semble bien que les Briançonnais aient en matière démographique des comportements, sinon homogènes, en tout cas fort peu dissemblables, en sorte que la résultante que nous recueillons n’offre que très peu de fluctuations. À la lumière de cette recherche, l’adaptabilité apparaît comme un trait marquant de ces populations : nous discernons ici leur capacité de réactivité face aux mortalités épidémiques.
Enfin, la connaissance de l’enfant utile relativement à celle de l’enfant naissant nous dévoile un pan de la reproduction humaine : si environ la moitié des couples vallouisiens (48 pour cent) laissent un ou deux héritiers, leur contribution au renouvellement générationnel de l’ensemble de la vallée reste faible. En revanche, un peu plus d’un couple sur cinq (23 pour cent) ayant trois héritiers et plus participe amplement à la génération suivante, puisque la contribution de ce groupe s’élève à presque trois cinquièmes (56 pour cent) du nombre d’enfants utiles recensés.
Ainsi, constamment durant une longue période historique, dans la haute montagne dauphinoise, la dynamique de la population est le résultat d’un nombre réduit de familles autochtones ayant assuré une forte descendance utile. Cette pérennité comportementale, qui paraît être le fruit d’une adaptabilité répétée aux contraintes de l’écosystème d’altitude, fait qu’une partie du potentiel « efficace » disparaît du site. La migration viagère ou définitive tend à priver la Vallouise d’une fraction de sa diversité génétique. Cet état de fait aura sans doute pour conséquence que son pool génique, observé au XIXe siècle, sera pratiquement homogène, neuf montagnards sur dix ayant un coefficient de consanguinité non nul [6].
Parties annexes
Annexe
Annexe
En ce qui concerne l’information généalogique, voici les données quantitatives que nous relevons dans chacune des cohortes du registre de population. Les trois paramètres cités, respectivement la profondeur généalogique moyenne, l’entropie et la variance, sont définis par des algorithmes spécifiques inclus dans le module de génétique du programme Analypop. Si le premier est facilement compréhensible, les deux autres s’élaborent avec des équations plus complexes. Les lecteurs se reporteront à des références qui les renseigneront parfaitement : Kouladjian, 1986, de Braekeleer et al., 1991; Boisvert et Mayer, 1994.
À titre comparatif, dans le registre de population de l’Île-aux-Coudres (Boisvert et Mayer, 1994), on recueillait durant la période 1800-1819 une entropie moyenne de 2,77 et une variance de 0,38, tandis qu’en 1820-1839, les deux paramètres croissaient respectivement à 3,23 et à 0,51 (tableau, p. 690). En Vallouise, ces mêmes critères moyens s’établissent respectivement, pour la cohorte 1810-1839, à 7,40 et à 4,51, avec une profondeur généalogique moyenne de 14,2. On indiquera simplement qu’une entropie moyenne de rang 7 signifie que l’on répertorie, dans le registre de population, pour les couples mariés en 1810-1839, 128 ancêtres des époux et 128 ancêtres des épouses (rang 1 = 2 ancêtres, rang 2 = 4 ancêtres, rang 3 = 8 ancêtres, etc.). La variance quant à elle est beaucoup plus élevée en Briançonnais; cela marque un déséquilibre entre les branches masculine et féminine des arbres généalogiques. La vallée alpine s’ouvrant peu à peu à l’exogamie de proximité (vallées circumvoisines), on observe dans le registre des couples exogames dont l’un des membres est autochtone et possède une ascendance d’une quinzaine de générations, tandis que l’autre n’a aucun ancêtre répertorié.
Tableau A
Distribution par cohortes de trois paramètres quantifiant le registre de population « Vallouise en Briançonnais » : profondeur généalogique moyenne (PGm), entropie et variance; [cv] étant le coefficient de variation
Notes
-
[1]
En anthropologie biologique, on parle d’apparentement pour des couples et de consanguinité pour les individus qui, éventuellement, en descendent. « Le concept de consanguinité repose sur une recherche d’identité génétique entre deux individus qui produiront une descendance. On dit que deux personnes sont apparentées si, parmi les ascendants de l’une, figurent les ascendants de l’autre, ou l’autre lui-même (parent-enfant). La transmission simultanée des gènes des deux parents est le départ du processus de formation biologique d’un individu. Lorsque deux individus ne possèdent pas d’ancêtre commun, le coefficient d’identité est nul et leur distance génétique est maximale » (Bley et Boëtsch, 1999 : 35 et passim). Mais d’autres auteurs peuvent être cités, tels Boisvert et Mayer (1994 : 688) : « cette consanguinité de l’individu est elle-même déterminée par le degré d’apparentement de ses parents ». De même, voir la version française de Jacquard (1974), publiée en 1970 : Structure génétique des populations, Paris, Masson : 47 et passim. On se reportera à l’annexe pour connaître les différents paramètres généalogiques (profondeur généalogique, etc.) utilisés pour calculer les coefficients d’apparentement ou de consanguinité.
-
[2]
Voir la note suivante.
-
[3]
Le programme Analypop ne distingue pas, pour ce module, les premiers mariages des remariages successifs. Ceux-ci sont assez nombreux, de l’ordre de 18 pour cent durant la période 1650-1749, et croissent encore entre 1750-1851, vers 23 pour cent. Néanmoins, pour le module consacré à l’objet de notre recherche, c’est-à-dire l’enfant utile, chaque union est compilée l’une après l’autre, et c’est dans cette configuration que nous recueillons le nombre de descendants et celui d’enfants utiles. Il est certain cependant que l’absence de distinction entre premiers mariages et remariages peut entraîner différents biais, en particulier celui de la variabilité du nombre d’enfants par couple.
-
[4]
Nous avons peut-être affaire à des remariages entre veufs ou entre personnes ne pouvant plus procréer, ayant pour but de réunir un certain patrimoine foncier par apport dotal, puis de rétrocéder ce patrimoine par donation à différentes personnes choisies dans l’entourage respectif des époux, neveux, petits-neveux, etc.
-
[5]
Le module du programme Analypop « Création et analyse de descendances d’unions » que nous avons utilisé ne discrimine pas le sexe des enfants utiles.
-
[6]
Durant la période 1780-1839, les époux ont un ou plusieurs ancêtres communs dans neuf mariages sur dix. Mais, en ce qui concerne les personnes naissant dans la vallée, c’est pour les années 1750-1839 qu’on observe parmi les autochtones les plus forts taux de consanguinité : ceux-ci passent de 90,7 à 92 pour cent d’un bout à l’autre de la période. Si l’on décompte de l’ensemble de nombreuses unions où l’un des époux est un enfant naturel qui ont eu lieu durant la période post-révolutionnaire et pour lesquelles on ne peut calculer d’apparentement, les taux sont certainement très proches de 95 pour cent. Entre 1750 et 1839, le registre de population présente une profondeur généalogique moyenne de 13, une entropie moyenne de 6,77 (rangs 6 et 7 : entre 64 et 128 ancêtres connus pour chaque époux) et une variance moyenne de 3,58. En Vallouise, le coefficient moyen de consanguinité, calculé par les généalogies, s’établit à 0,00538 pour la période 1780-1809 et à 0,006514 pour 1840-1869, et il est encore de 0,0082929 pour les premières années du XXe siècle (1900-1929). Des conclusions analogues sont émises pour des populations suisses et italiennes d’altitude, en particulier dans la synthèse effectuée par Sauvain-Dugerdil (1990).
Références bibliographiques
- ABELSON, A. 1978. « Population structure in the Western Pyrenees: Social class, migration and the frequency of consanguineous marriage, 1850 to 1910 », Annals of Human Biology, 5 : 165-178.
- AUSTERLITZ, F., et É. HEYER. 1998. « Social transmission of reproductive behavior increases frequency of inherited disorders in a young-expanding population », Proceedings of the National Academy of Science, 95 : 15140-15144.
- BACHAND, M., N. VACHON, M. BOISVERT, F. M. MAYER et D. CHARTRAND. 1997. « Clinical reassessment of malignant hyperthermia in Abitibi-Témiscamingue », Canadian Journal of Anaesthesia, 44, 7 : 696-701.
- BARDET, J.-P., et J. DUPÂQUIER. 1997. Histoire des populations de l’Europe. Paris, Fayard, 2098 p.
- BIDEAU, A., G. BRUNET, B. DESJARDINS et M. PROST. 1995. « La reproduction de la population aux XVIIe et XIXe siècles. Exemples français et québécois », Annales de démographie historique : 137-148.
- BLEY, D., et G. BOËTSCH. 1999. L’anthropologie démographique. Paris, PUF, 127 p.
- BOËTSCH, G., et M. PROST. 2001. « Descendances différentielles, reproduction générationnelle et enfants-utiles dans une population isolée de la montagne alpine », Bulletins et mémoires de la Société d’anthropologie de Paris, 13, 1-2 : 39-59.
- BOËTSCH, G., M. PROST et E. RABINO-MASSA. 2002. « Evolution of consanguinity in a French alpine valley: The Vallouise in the Briançon region (17th-19th centuries) », Human Biology, 74, 2 : 285-300.
- BOISVERT, M., et F. M. MAYER. 1994. « Mortalité infantile et consanguinité dans une population endogame du Québec », Population, 3 : 685-724.
- BOISVERT, M., F. M. MAYER et É. LABELLE. 1996. « Multi-usage du registre de population et pluri-disciplinarité (biologie, démographie, anthropologie, histoire) au service d’une problématique unique », Cahiers de la société historique acadienne, 27, 2-3 : 60-74.
- CANNINGS, C., et M. H. SKOLNICK. 1975. « Genetic drift in exogamous marriage system », Theoretical Population Biology, 7: 39-54.
- CAZES, M. H., E. BROWN, B. FLOURY, A. JACQUARD et C. SAUVAIN-DUGERDIL. 1993. Les Dogon de Boni : approche démo-génétique d’un isolat du Mali. PUF-INED, Travaux et Documents, Cahier 132, 306 p.
- CHAVENTRÉ, A., et D. K. ROBERTS. 1990. Approche pluri-disciplinaire des isolats humains. Paris, INED, Congrès et colloques, 3, 459 p.
- DE BRAKELEER, M., G. BOUCHARD et M. GRADIE. 1991. « Consanguinité et parenté au Saguenay », dans G. BOUCHARD et M. DE BRAKELEER, éd. Histoire d’un génome. Québec, PUQ, 607 p. : 323-342.
- DUPÂQUIER, J., dir. 1988. Histoire de la population française. Tome 2, chapitre 8. Paris, PUF, 2310 p.
- GOY, J., G. BOUCHARD et R. BONNAIN. 1992. Transmettre, hériter, succéder. La reproduction familiale en milieu rural. France-Québec, XVIIIe-XXe siècles. Lyon, PUL, 433 p.
- HEYER, É. 1991. Étude démogénétique d’une population humaine. Le cas de la maladie Rendu-Osler. Lyon, 203 p. (dactylographié).
- HEYER, É., et M. H. CAZES. 1999. « Les enfants-utiles. Une mesure démographique pour la génétique des populations », Population, 54, 4-5 : 677-692.
- JACQUARD, A. 1974. The Genetic Structure of Populations (Biomathematics, vol. 5). Berlin, Heidelberg, New York, 569 p.
- JACQUARD, A., dir. 1976. L’étude des isolats. Espoirs et limites. Paris, EPHE-INED, 334 p.
- KOULADJIAN, K. 1986. Une mesure d’entropie généalogique. Chicoutimi, SOREP, document III-C43, 4 p.
- LIMA, M., F. M. MAYER, P. COUTINHO et A. ABADE. 1997. « Prevalence, geographical distribution and genealogical investigation of Machado-Joseph disease in the islands of the Azores (Portugal) », Human Biology, 69, 3 : 383-393.
- LIMA, M., F. M. MAYER, P. COUTINHO et A. ABADE. 1998. « Origins of a mutation: Population genetics of Machado-Joseph disease in the islands of the Azores (Portugal) », Human Biology, 70, 6 : 1011-1023.
- MORTON, N. E., D. KLEIN, I. E. HUSSELS, P. DODINVAL, A. TODOROV, R. LEW et S. YEE. 1973. « Genetic structure of Switzerland », American Journal of Human Genetics, 25 : 347-361.
- PROST, M. 1998. « Évolution comparée de l’apparentement dans les deux paroisses de la vallée de Vallouise en Briançonnais (XVIIe et XVIIIe siècles) », dans Le choix du conjoint. Lyon, Programme Rhône-Alpes : Recherches en sciences humaines, Les chemins de la recherche, no 43 : 151-166.
- PROST, M., et G. BOËTSCH. 2001a. « Un outil au service de la transdisciplinarité appliquée aux sciences de l’homme : le registre de population informatisé », Histoire et mesure, XVI, 1-2 : 93-111.
- PROST, M., et G. BOËTSCH. 2001b. « Choix du conjoint et apparentement dans les populations montagnardes du Dauphiné aux XVIIe et XVIIIe siècles », Revue de géographie alpine, 89, 3 : 21-40.
- PROST, M., et G. BOËTSCH. 2002. « Mobilité et aires matrimoniales dans les populations alpines du Dauphiné : le cas des 20 communautés de l’Oisans du XVIe au XIXe siècle », Anthropologica et Praehistorica, 113 : 121-133.
- PROST, M., et M. REVOL. 2001. « Hériter ou migrer dans la montagne dauphinoise. Le cas des Briançonnais de la Vallouise », dans Les écosystèmes alpins : approches anthropologiques. Gap, CDDP, 160 p. : 100-111.
- ROBERTS, D. F. 1976. « Les concepts d’isolats », dans A. JACQUARD, éd. L’étude des isolats, espoirs et limites. Paris, EPHE-INED : 75-92.
- ROBERTS, D. F., et C. P. RAWLING. 1974. « Secular trends in genetic structure: An isonymic analysis of Northumberland parish records », Annals of Human Biology, 4 : 393-410.
- SAUVAIN-DUGERDIL, C. 1990. « Les isolats alpins ont-ils existé ? Réflexion à partir de 250 ans d’histoire généalogique d’une vallée valaisanne », dans A. CHAVENTRÉ et D. K. ROBERTS, éd. Approche pluri-disciplinaire des isolats humains. Paris, INED, Congrès et colloques, no 3 : 297-322.
- SAUVAIN-DUGERDIL, C. 1996. « The reproductive cycle and population dynamics: The case of the Bagnes Valley (Valais, Switzerland) in the XIXth century », International Journal of Anthropology, 11, 2-4 : 167-183.
- SAUVAIN-DUGERDIL, C., et Philippe RICHARD. 1998. « Le cercle des unions : une définition dynamique de la population, ou de la pertinence d’une convergence entre l’anthropologie biologique et la démographie historique », dans Le choix du conjoint. Lyon, Programme Rhône-Alpes : Recherches en sciences humaines, Les chemins de la recherche, no 43 : 27-45.
- SERRE, J. L., L. JAKOBI et M. C. BABRON. 1985. « A genetic isolate in the French Pyrenees: Probabilities of origin of genes and inbreeding », Journal of Biosocial Sciences, 17 : 405-414.
- SUTTER, J., et L. TABAH. 1953. « Structure de la mortalité dans les familles consanguines », Population, 8 : 511-526.
- VIAZZO, P. P. 1989. Upland Communities. Environment, Population and Social Structure in the Alps since the Sixteenth Century. Cambridge, Cambridge University Press, 325 p.
- WACHTER, K. W. 1992. « Variabilité aléatoire des phénomènes démographiques : enseignements des séries paroissiales de Wrigley et Schofield », dans Modèles de la démographie historique. Paris, INED-PUF, Congrès et colloques, no 11 : 77-98.
- ZAKHAROV, S. 1992. « La transition démographique en Russie et l’évolution des disparité démographiques régionales », dans Modèles de la démographie historique. Paris, INED-PUF, Congrès et colloques, no 11 : 353-370.
Liste des tableaux
Tableau 1
Distribution des données démographiques du corpus de travail, en nombres absolus, observées selon sept cohortes trentenaires
Tableau 2
Distribution de différents indices a calculés concernant la descendance des couples vallouisiens
Ici, nous avons voulu comparer certains résultats concernant la descendance selon différentes méthodologies. Le premier (colonne 1) concerne l’indice synthétique que l’on calcule en démographie historique à l’aide des taux de fécondité par groupes d’âge quinquennaux. Les valeurs enregistrées se situent dans la norme de l’enquête de l’INED pour le quart sud-est de la France : 1720-1739 (6,30), 1740-1769 (5,87) et 1770-1789 (5,67). Le deuxième indice (colonne 2, nommée enfants/couple [1]) résulte lui du calcul effectué selon les principes de la démographie historique, c’est-à-dire par cohortes. C’est le rapport du nombre d’enfants nés durant une certaine période (ou cohorte) sur le nombre de mariages qui se sont déroulés durant cette même période. Or, entre les unions et les naissances, il y a un décalage générationnel. Cependant, tous les mariages qui se sont déroulés en fin de cohorte ont très bien pu avoir des naissances non prises en compte durant ce laps de temps. C’est pour cela que nous tentons de vérifier ici la validité du corpus en considérant maintenant la descendance généalogique. Un algorithme particulier du programme Analypop permet de définir, sur une ou plusieurs générations, la descendance exacte des couples à une période donnée que l’on aura programmée. C’est une méthode davantage utilisée en anthropologie. De cette programmation, nous obtenons un troisième indice (colonne 3, nommée enfants/couple [2]). Ce dernier est obtenu par le rapport du nombre de descendants effectifs, à la première génération, sur le nombre des unions enregistrées durant une période choisie. À notre sens, cette dernière méthode est beaucoup plus pertinente que les autres, surtout lorsque les cohortes envisagées sont décennales. Ce n’est pas le cas ici et, si des variations indiciaires sont de mise durant certaines périodes, les résultats des colonnes 2 et 3 s’accordent véritablement.
Tableau 3
Distribution en nombres absolus et relatifs des couples qui ne participent pas au renouvellement des générations
Tableau 4
Distribution selon le temps et le sexe des naissances vallouisiennes et indication du nombre d’E. U. recensé avec, en regard, le pourcentage qu’il représente
Tableau 5
Distribution, en nombres absolus, des couples observés selon le nombre d’enfants utiles recensés ou bien selon leur non-contribution
Tableau 6
Distribution cumulée des couples et de leur descendance utile selon le nombre d’enfants utiles dans la famille à laquelle ils appartiennent
Tableau A
Distribution par cohortes de trois paramètres quantifiant le registre de population « Vallouise en Briançonnais » : profondeur généalogique moyenne (PGm), entropie et variance; [cv] étant le coefficient de variation






![Distribution par cohortes de trois paramètres quantifiant le registre de population « Vallouise en Briançonnais » : profondeur généalogique moyenne (PGm), entropie et variance; [cv] étant le coefficient de variation](/fr/revues/cqd/2002-v31-n2-cqd466/000665ar/media/000665art007n.png)