Le jeu de l’ultimatum, une méta-analyse de 30 années de recherches expérimentales

Tisserand, Jean-Christian

doi:https://doi.org/10.7202/1039879ar

Introduction

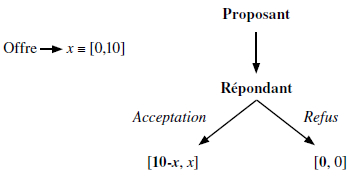
Avec un total de plus de 2800 citations sur Google Scholar (Güth et Kocher, 2013), le jeu de l’ultimatum de Güth et al. (1982) constitue l’expérience initiale de l’un des jeux les plus étudiés en économie expérimentale. Dans le jeu de l’ultimatum, deux joueurs se partagent une somme d’argent. Le premier joueur, qualifié de proposant, est chargé de proposer un partage de la somme entre lui-même et le second joueur[1]. Le second joueur, qualifié de répondant, a le choix entre deux actions. Il peut accepter l’offre du proposant, auquel cas la somme d’argent mise en jeu sera partagée telle que le proposant l’aura souhaité. Le répondant peut également décider de refuser le partage proposé par le proposant, auquel cas les deux joueurs obtiennent un gain nul. Le graphique 1 présente le jeu de l’ultimatum lorsque la somme à partager entre les deux joueurs est égale à 10. Selon la prédiction de l’équilibre de Nash parfait en sous-jeu (ENPSJ), le proposant offre la plus petite somme positive possible et le répondant accepte cette proposition.

Graphique 1

**Représentation du jeu de l’ultimatum**

Les nombreuses études expérimentales menées sur le jeu de l’ultimatum ont montré que les joueurs adoptent un comportement différent de celui prédit par l’ENPSJ : l’offre moyenne proposée par le joueur ayant l’initiative se situe entre 40 et 50 % de la somme à partager. Pour leur part, les répondants déclinent très souvent les offres en dessous de 20 % de la somme à partager. Si ces déviations robustes constatées lors des différentes expériences du jeu de l’ultimatum conduisent au rejet des hypothèses d’égoïsme et de simple maximisation monétaire traditionnelles, elles ne remettent pourtant pas en question la rationalité des agents économiques. La régularité des constats empiriques mis en évidence par le jeu de l’ultimatum permet d’enrichir la théorie en tenant compte de différents facteurs tels que les préférences sociales, les émotions, l’aversion à l’inégalité, l’aversion au risque ou encore l’altruisme (Güth et Kocher, 2013). L’analyse du comportement des agents économiques « réels » constitue un enjeu important : il s’agit de remettre en question les hypothèses relatives au comportement de ces agents et ainsi contribuer à l’enrichissement de la théorie standard qui semble sous-estimer l’importance de certaines composantes de l’utilité individuelle. La validation de théories existantes ou l’émergence de nouvelles théories peuvent alors orienter les choix du décideur, notamment en matière de politique publique. En effet, la mise en évidence de faits stylisés et de déviations robustes par rapport aux prédictions théoriques conduit à reconsidérer les effets des instruments institutionnels à disposition de la puissance publique (Ferey et al., 2013). L’apport de l’économie expérimentale en tant qu’outil d’aide à la décision a été confirmé de nombreuses fois par le passé à l’image de Roth (2002) qui, grâce à ses recherches expérimentales, a notamment contribué à la conception de la procédure de vente aux enchères des fréquences radio aux États-Unis.

Afin d’étudier les diverses composantes non monétaires qui guident les choix individuels, nous avons réalisé une analyse statistique de la littérature expérimentale du jeu de l’ultimatum de ces trois dernières décennies. Notre article vise d’une part à procurer une estimation précise de la somme moyenne offerte par le proposant dans le jeu de l’ultimatum, et d’autre part à identifier les facteurs déterminants des choix des offreurs qui s’écartent de l’équilibre théorique. Afin de répondre à ce double objectif, nous avons conduit une méta-analyse ainsi qu’une métarégression incluant 97 observations du jeu de l’ultimatum simple recueillies au sein de 41 articles et d’un ouvrage d’économie expérimentale dont les références figurent à la fin de l’article.

La méta-analyse est un puissant outil statistique très fréquemment utilisé dans le domaine de la médecine depuis les années 1950[2]. Cet outil permet d’analyser des données issues de différentes études indépendantes portant toutes sur une même variable. Dans ce cadre, la forte puissance statistique conférée par la méta-analyse permet d’obtenir des estimations très précises des effets des différents médicaments sur les sujets traités. Alors qu’une simple lecture de la littérature empirique dans son ensemble peut mener à des intuitions erronées, la méta-analyse permet une lecture synthétique et quantifiée des données agrégées, dont la précision ne peut être égalée par une étude individuelle. Cette précision est naturellement croissante avec le nombre d’études incluses dans l’analyse et dépend également de la méthode d’estimation utilisée. Sur ce dernier point, notre méta-analyse se distingue de celle menée sur le jeu de l’ultimatum par Oosterbeek et al. (2004). En effet, dans leur article, les auteurs précisent ne pas avoir la totalité des données concernant la dispersion des offres relatives à chaque étude. Pour pallier cette insuffisance, nous avons obtenu les données manquantes auprès des auteurs. D’un point de vue méthodologique, la prise en compte de la dispersion de l’effet étudié est un élément fondamental qui permet au statisticien de définir les pondérations adéquates des différentes études dans la méta-analyse et ainsi d’obtenir une estimation fiable[3].

Nos résultats montrent que le joueur ayant l’initiative dans le jeu de l’ultimatum offre en moyenne 41,04 % (écart-type = 0,05) de la somme mise en jeu au répondant qui lui fait face. Cette estimation, de loin supérieure à l’offre théorique, s’explique principalement par le pouvoir de refus du répondant qui force l’offreur à proposer une offre généreuse. Une simple comparaison des offres moyennes du jeu du dictateur dans lequel le répondant n’a aucun pouvoir stratégique et du jeu de l’ultimatum permet d’identifier cet effet (Cooper et Ducther, 2011). Toutefois, les sommes non nulles offertes par les dictateurs soulignent que l’altruisme entre également en compte dans la fonction d’utilité des joueurs. De nombreuses études du jeu de l’ultimatum ont tenté d’analyser précisément les déterminants des choix des offreurs par le biais de différents protocoles expérimentaux en modifiant trois catégories majeures de variables. Tout d’abord, les variables contextuelles s’intéressent aux modifications des paramètres du jeu de l’ultimatum simple. Les deux variables contextuelles les plus importantes sont le choix de la somme d’argent à partager ainsi que la répétition du jeu. Les variables démographiques ont ensuite pour objectif d’estimer l’influence des caractéristiques observables des sujets participant à l’expérience. Finalement, les variables structurelles visent à analyser le comportement des joueurs dans les variantes et extensions du jeu de l’ultimatum simple. Les expériences menées sur les variables contextuelles ne permettent pas d’établir un lien de causalité robuste entre ces variables et la somme offerte par les proposants. Les variables relatives à la population étudiée présentent une influence modérée sur la somme proposée au travers des différentes études. Les résultats de notre métarégression montrent que les étudiants en sciences économiques conservent en moyenne 5,4 % de plus de la somme à partager que les sujets non-économistes. Par ailleurs, les offres formulées par les proposants issus de pays industrialisés sont en moyenne supérieures de 3,35 % aux offres formulées par les proposants issus de pays non industrialisés. En ce qui concerne les variables structurelles, notre base de données composée exclusivement de jeux de l’ultimatum simples[4] ne nous permet pas d’analyser leur influence dans le cadre d’une métarégression. Par ailleurs, l’analyse de variables additionnelles à travers notre métarégression telles que l’âge moyen des sujets, le PIB ou l’IDH des pays dans lesquels les expériences se sont déroulées n’a abouti à aucun résultat significatif.

La suite de cet article s’articule de la manière suivante : dans la section 1, nous abordons successivement les divers travaux menés sur les trois champs de variables mentionnés précédemment à travers une revue de la littérature. La section 2 est dédiée à l’analyse successive du comportement des répondants et des proposants dans le jeu de l’ultimatum. La section 3 conclut cet article en présentant l’intérêt de nos résultats pour des recherches ultérieures.

1. Les variables du jeu de l’ultimatum, revue de la littérature

Afin d’étudier le comportement des sujets, l’arsenal de variables dont dispose l’expérimentaliste est vaste. En effet, les choix concernant le protocole expérimental, la population qui participe à l’expérience ou encore la structure du jeu sont autant d’outils d’analyse des composantes de l’utilité des sujets. Dans cette revue de la littérature, nous présentons les résultats principaux des diverses expériences du jeu de l’ultimatum. Par souci de clarté, l’argumentaire sera exposé de manière à systématiquement dissocier, quand les études relatées le permettent, l’analyse du comportement des offreurs de celui des répondants. Cette section préalable à notre méta-analyse constitue un point de référence important pour l’analyse des effets marginaux des différentes variables obtenus par notre métarégression.

1.1 Les variables contextuelles

La modification des paramètres d’une expérience est susceptible d’influencer les choix des sujets. Parmi les variables contextuelles du jeu de l’ultimatum, la répétition et la somme d’argent en jeu sont celles qui ont suscité le plus grand nombre de recherches.

1.1.1 Les conséquences monétaires

En économie, contrairement à d’autres disciplines de recherche telles que la psychologie, les sujets qui participent aux expériences sont généralement rémunérés en fonction de leurs choix dans le jeu. Il est donc naturel de se demander si les choix des joueurs varient lorsque la somme mise en jeu est plus ou moins importante.

De nombreuses études ayant pour but d’analyser cet effet ont montré qu’en réalité, le montant de la somme à partager dans un jeu de l’ultimatum n’a pas d’influence sur le comportement des offreurs. Hoffman et al. (1996) ainsi que Slonim et Roth (1998) proposent des expériences du jeu de l’ultimatum dans lesquelles les sommes mises en jeu sont respectivement multipliées par 10 et par 25 entre les différents traitements et ne trouvent aucune différence entre les offres formulées. Cameron (1999) est le premier à réaliser une expérience du jeu de l’ultimatum dont la somme en jeu est multipliée par 40 entre les différents traitements. Le traitement le plus généreux propose aux joueurs le partage d’une somme de 20 000 roupies indonésiennes soit environ 600 heures de travail rémunérées au salaire d’un emploi sans qualifications. Malgré l’importance des sommes mises en jeu, les résultats ne révèlent pas de différence significative entre les offres formulées lors des différents traitements. L’étude de Cameron permet également de mettre en évidence qu’en l’absence d’incitations monétaires (argent fictif), la variance concernant les offres formulées est significativement plus élevée.

En ce qui concerne les répondants, l’étude de Cameron met en évidence un changement de comportement significatif de leur part : plus la somme en jeu est importante, plus les chances qu’une certaine proportion de la somme à partager soit acceptée sont élevées. Les offreurs pourraient alors profiter de cet effet pour conserver une plus grande proportion de la somme à partager mais leur crainte du rejet de leur offre est également plus forte lorsque la somme à partager augmente. La compensation de ces deux effets explique l’inélasticité des offres formulées par rapport à la somme à partager. Lorsqu’il s’agit d’argent fictif, les résultats de l’expérience de Cameron montrent que le taux de rejet des offres formulées est significativement plus élevé.

1.1.2 La répétition

Lorsqu’ils sont confrontés à un jeu expérimental, les joueurs suivent un processus d’apprentissage et leurs décisions évoluent au fil de leurs essais et de leurs erreurs. La découverte d’une situation inconnue nécessite une phase d’adaptation de la part des sujets : on peut alors se demander si les choix des joueurs ayant acquis de l’expérience se rapprochent de l’ENPSJ dans le jeu de l’ultimatum.

Roth et Erev (1995) se sont intéressés à l’évolution des choix des joueurs dans les jeux expérimentaux les plus populaires sous leur forme répétée. Alors que les choix des joueurs convergent rapidement vers l’équilibre théorique dans le jeu de biens publics et le jeu de marché, ce n’est pas le cas pour le jeu de l’ultimatum. Les auteurs soulignent même que la variance à travers les offres formulées est croissante à mesure que les proposants accumulent de l’expérience. Afin de tester l’effet de l’expérience sur les choix des proposants tout en écartant les considérations altruistes, Brenner et Vriend (2006) proposent un protocole expérimental dans lequel les proposants sont conscients de faire face à des répondants informatisés pendant 100 périodes de jeu. Afin que le comportement des répondants informatisés soit proche de celui d’un joueur humain et que l’équilibre théorique du jeu ne soit pas perturbé, les auteurs se sont assurés que la probabilité d’acceptation de l’offre soit croissante avec la part du gâteau proposée par l’offreur et que l’offre minimale (1 $ sur 9 $) soit celle qui procure aux joueurs l’espérance de gains la plus élevée. Malgré les 100 périodes de jeu, les résultats de l’expérience montrent que les offres formulées par les joueurs ne convergent pas vers l’ENPSJ. Les sommes positives offertes ne pouvant pas être justifiées par des considérations altruistes, ces résultats ont donc 2 explications potentielles : il est possible que les joueurs soient fortement averses au risque malgré les 100 périodes de jeu et préfèrent maximiser leur probabilité de paiement plutôt que leur gain espéré. Il est également possible que les limites cognitives des sujets ne leur permettent pas d’identifier le choix qui maximise leur paiement.

Cooper et Dutcher (2011) ont réalisé une méta-analyse orientée sur les effets d’expérience dans le jeu de l’ultimatum. Leur méta-analyse regroupe sept études indépendantes menées sur des jeux de l’ultimatum simples répétés. Les auteurs parviennent à trois conclusions majeures qui concernent en grande partie le comportement des répondants. Tout d’abord, l’expérience a pour effet d’augmenter le taux d’acceptation des offres conséquentes (20 % ou plus) et de diminuer le taux d’acceptation des offres faibles (moins de 20 %). Ensuite, la probabilité d’acceptation d’une offre donnée est plus élevée si cette offre est supérieure à la précédente et inversement. Enfin, les réactions des proposants face aux acceptations et rejets de leurs offres montrent que leurs choix s’expliquent en grande partie par une volonté de maximiser leur gains plutôt que par des considérations altruistes. Cette flexibilité de la part des offreurs face aux acceptations et rejets de leurs offres rationalise donc, in fine, à l’échelle globale, le comportement des répondants et le refus des sommes jugées trop faibles.

1.2 Les variables démographiques

En règle générale, la sélection des sujets testés est une variable importante de l’économie expérimentale. Des populations différentes par leurs caractéristiques sont susceptibles de présenter des préférences divergentes. Parmi les nombreuses variables démographiques, la culture et le fait d’étudier l’économie sont celles qui ont suscité le plus grand intérêt.

1.2.1 L’influence des cultures

Chaque culture présentant des conceptions distributives potentiellement différentes, il est intéressant de se demander si les origines des joueurs ont un impact sur leurs décisions dans le jeu de l’ultimatum.

Roth et al. (1991) sont, à notre connaissance, les premiers à s’intéresser à cette question. Par le biais d’un seul protocole expérimental traduit dans différentes langues, les auteurs réalisent leur expérience dans quatre pays différents (Japon, USA, Slovénie, Israël) afin de comparer les décisions des proposants dans un jeu de l’ultimatum simple. Les résultats obtenus permettent de mettre en évidence une différence significative entre les décisions des joueurs des différents pays. En revanche, rien ne confirme que ces différences soient dues aux cultures respectives des joueurs. Henrich (2000) réalise une expérience du jeu de l’ultimatum au Pérou ainsi qu’aux États-Unis. Son étude met en évidence le fait que la moyenne des offres des proposants péruviens est significativement plus faible que la moyenne des offres formulées par les proposants américains. Alors que les joueurs américains offrent en moyenne 40 % du gâteau, les Péruviens proposent en moyenne 26 %. Henrich et al. (2005) ont mené des expériences du jeu de l’ultimatum à travers 15 pays non-industrialisés. Selon les auteurs, les préférences et attentes des joueurs sont influencées par les normes d’équité des différentes cultures. Ainsi, un joueur d’un pays industrialisé où le système redistributif joue un rôle important sera davantage susceptible d’offrir une forte proportion de la somme à partager qu’un joueur issu d’une tribu où chaque famille survient à ses besoins. Les auteurs supposent que lorsque les joueurs font face à un jeu qu’ils ne connaissent pas, ils tentent de l’assimiler à une situation quotidienne similaire pour effectuer leur choix. Les résultats obtenus au travers des 15 études menées sur des populations rurales de pays non industrialisés vont dans le sens de ces explications : les communautés les plus solitaires et indépendantes sont également celles dont les offres sont les plus faibles. Si ces tendances sont observables, les auteurs ne sont toutefois pas en mesure de communiquer des résultats statistiquement significatifs. Afin de répondre plus précisément à la question de l’influence des cultures sur les choix dans le jeu de l’ultimatum, Oosterbeek et al. (2004) ont mené une méta-analyse ciblée sur les effets culturels. Leurs résultats montrent que les offres proposées dans les différents pays ne sont pas statistiquement différentes.

Henrich s’est également intéressé au comportement des répondants des différents pays. Il explique que les notions d’équité et de partage égalitaire ne font pas partie de la culture de tous les joueurs. Par exemple, les répondants péruviens interrogés par Henrich expliquent qu’ils n’ont donc pas d’attente vis-à-vis des offreurs et donc aucune raison de les punir. Malgré la très faible moyenne des offres constatée au Pérou (26 %), le taux de rejet global constaté n’est pas plus élevé que le taux de rejet global moyen de l’ensemble des pays. Si les traits culturels du peuple du Machiguenga (Pérou) poussent les joueurs à faire fi de la notion d’équité ou de partage égalitaire, Oosterbeek et al. montrent qu’il n’en va pas de même pour les répondants asiatiques dont le taux de rejet est statistiquement plus élevé que celui des répondants américains.

1.2.2 Les étudiants en sciences économiques

De manière générale, l’économie expérimentale a permis de montrer que les étudiants en sciences économiques, toutes choses égales par ailleurs, adoptaient souvent un comportement plus proche de l’équilibre théorique lors des expériences. Par exemple, Marwell et Ames (1981) ont montré que dans un jeu de financement de bien public, le comportement de passager clandestin s’observe davantage chez les étudiants en sciences économiques.

En ce qui concerne le jeu de l’ultimatum, l’étude de Carter et Irons (1991) montre que les choix des étudiants en sciences économiques sont plus proches de l’ENPSJ que ceux des étudiants issus d’autres filières. Alors que les proposants non-économistes offrent en moyenne 45,6 % de la somme à partager, les proposants économistes n’offrent en moyenne que 38,5 % de cette somme. Certains auteurs n’identifient toutefois aucune différence entre les offres des étudiants en économie et celles des autres étudiants (Eckel et Grossman, 1996 et Stanley et Tran, 1998).

Parmi les répondants, les choix des étudiants en sciences économiques sont également plus proches de l’ENPSJ : là où l’offre minimum acceptable moyenne des répondants non-économistes s’établit à 24,4 % de la somme à partager, celle des répondants économistes se situe à 17 %. La différence entre les offres minimum acceptables des deux populations est significative.

1.3 Les variables structurelles

Il existe une multitude de variantes qui modifient la structure de base du jeu simple de l’ultimatum. Les variantes du jeu de l’ultimatum présentent un grand intérêt pour étudier les motivations qui guident les choix des joueurs. Le jeu de l’ultimatum simple sert alors de traitement de contrôle à l’expérimentaliste qui a pour objectif de mesurer l’impact des modifications structurelles sur les décisions individuelles.

1.3.1 Les choix limités

En règle générale, les actions à la disposition du proposant lui permettent d’opter pour l’allocation de son choix. Falk et al. (2008) souhaitent tester le rôle des intentions des joueurs et proposent un jeu de l’ultimatum dans lequel le proposant n’a que deux actions à sa disposition. Dans un premier protocole expérimental, le proposant a le choix d’offrir 20 % de la somme à partager au répondant et de garder 80 % pour lui-même ou de partager les gains de manière égalitaire (50 %, 50 %). Dans un second protocole, le proposant peut offrir 20 % de la somme au répondant et conserver 80 % ou garder la totalité de la somme (100 %, 0 %).

Les résultats de cette expérience du jeu de l’ultimatum aux choix limités montrent que les répondants sont fortement sensibles aux intentions qui guident les choix du proposant. En effet, lorsque l’offre alternative est égoïste, les offres de 20 % sont rejetées dans 8,9 % des cas par les répondants contre 44,4 % lorsque l’offreur aurait pu partager le gâteau de manière égalitaire. Ces résultats confirment le rôle prépondérant des intentions d’autrui dans la prise de décision individuelle, tel qu’il a été suggéré par Rabin (1993), et montrent que les répondants ont davantage tendance à adopter un comportement punitif envers les proposants qu’ils ont jugés injustes envers eux. Si les proposants sont capables d’anticiper le fait que les offres perçues comme insultantes vont être rejetées, alors leur objectif devrait être de proposer une offre suffisamment élevée pour être acceptée. De ce point de vue, les offres largement positives constatées dans l’ensemble des jeux de l’ultimatum s’expliquent en partie par des considérations stratégiques.

1.3.2 L’information incomplète

Afin de modifier le jeu simple de l’ultimatum, il est également possible de modifier la structure de l’information en favorisant l’un des deux joueurs.

Mitzkewitz et Nagel (1993) sont les premiers à proposer une version expérimentale du jeu de l’ultimatum en information incomplète. Ils proposent deux traitements distincts appelés « demand game » et « offer game » dans lesquels seuls les proposants sont informés du montant de la somme à partager. La somme à partager est déterminée aléatoirement au début de chaque période de jeu et le répondant connaît uniquement la procédure de détermination aléatoire de cette somme. Dans le demand game, l’offreur demande une somme d’argent au répondant : ce dernier ne connaît alors que le paiement de l’offreur au moment d’accepter ou non. Dans le offer game, l’offreur propose une somme d’argent au répondant qui ne connaît alors que son propre paiement au moment de prendre sa décision. Alors qu’ils devraient proposer le montant minimal de la somme en jeu, de nombreux offreurs optent pour un partage égalitaire dans le offer game. Dans le demand game, la théorie prédit que les offreurs choisissent de garder la quasi-totalité de la somme à partager, pourtant cette décision n’est observée que dans 30 % des cas et principalement lorsque la somme en jeu est faible. De nombreuses études similaires ont par la suite mis en évidence des résultats identiques. Les décisions individuelles semblent être influencées par des considérations d’équité qui ne font pas partie des hypothèses de la théorie standard.

Plus récemment dans le domaine de l’information incomplète, Conrads et Irlenbusch (2013) ont réalisé une expérience du jeu de l’ultimatum dans laquelle le répondant, contrairement au proposant, détient l’information concernant le montant de la somme à partager. Les résultats de leur étude montrent que le fait de ne pas être informé peut être un avantage dans les situations où la structure informationnelle est endogène et que l’ignorance peut être une stratégie : le taux de rejet des offres égoïstes est significativement plus faible lorsque l’offreur n’est pas informé de la somme à partager.

1.3.3 Le jeu d’offres alternées

Dans la catégorie des extensions du jeu simple, le jeu de l’ultimatum avec contre-offre(s) a été très largement étudié. Il s’agit d’un jeu de l’ultimatum sous forme extensive étudié pour la première fois par Stahl (1972) puis approfondi par Rubinstein (1982). Le jeu se déroule de la manière suivante : un offreur initial propose un partage d’une somme d’argent à un répondant. Si le répondant accepte le partage alors le jeu est terminé et les gains sont partagés tels que l’offreur initial l’a souhaité. Si le répondant refuse l’offre, il devient à son tour offreur et propose le partage d’une somme plus faible que la somme mise en jeu lors de la période précédente. Ce processus peut être répété plusieurs fois et la dernière période du jeu s’apparente à jeu de l’ultimatum simple dans lequel le refus du répondant entraîne la perception de gains nuls. La réduction de la somme à partager matérialise l’inefficacité provenant du fait que les parties ne soient pas parvenues à trouver un accord immédiatement : les coûts de transaction de la nouvelle recherche d’un accord sont donc imputés sur la somme à partager.

En 1985, Binmore, Shaked et Sutton sont les premiers à réaliser une expérience du jeu de l’ultimatum avec contre-offre. Leur protocole expérimental propose un jeu à deux périodes dans lequel le refus de l’offre proposée en première période conduit à une seconde période de jeu où la taille du gâteau est réduite à 25 % de sa valeur initiale. Par la suite, de nombreux auteurs dont Güth et Tietz (1988) puis Ochs et Roth (1989) réalisent des expériences similaires dans lesquelles la diminution de la somme à partager entre la première et la seconde période est plus ou moins importante. L’équilibre théorique du jeu d’offres alternées à deux périodes prédit que l’offreur initial devrait proposer une somme légèrement supérieure à celle que le répondant pourrait avoir s’il gardait la totalité de la somme en jeu pour lui-même lors de la seconde période. Pourtant, comme dans le jeu de l’ultimatum simple, les joueurs semblent davantage être guidés par des normes qui leur sont propres plutôt que par la rationalité : les offres initiales correspondant à l’ENPSJ sont très rares et les partages égalitaires en première période restent très fréquents quel que soit le taux d’escompte appliqué en seconde période.

Du côté des répondants, l’hypothèse de maximisation monétaire est souvent violée : les résultats de l’ensemble des études montrent qu’il arrive fréquemment aux répondants de proposer une contre-offre dont les gains constituant la paire sont strictement inférieurs à ceux de l’offre initialement rejetée. Si ces choix ne semblent pas rationnels de prime abord, le modèle de paiement comparatif de Bolton (1991) ainsi que le modèle d’aversion à l’inégalité de Fehr et Schmidt (1999) permettent de modéliser le comportement des joueurs. En effet, en plus du paiement absolu perçu par chaque joueur, ces modèles prennent en compte le paiement relatif représenté par le rapport des gains des deux joueurs. Ainsi, un joueur peut préférer percevoir une somme d’argent plus faible pour augmenter son paiement relativement au second joueur formant la paire.

1.3.4 Le jeu à plus de 2 joueurs

On distingue trois catégories de jeux de l’ultimatum à trois joueurs ou plus. D’une part, le jeu de l’ultimatum en groupes permet de confronter un groupe de répondants à un groupe d’offreurs afin d’étudier la rationalité de groupe. D’autre part, le jeu de l’ultimatum en « monopole » confronte un seul répondant à plusieurs offreurs ou inversement afin d’étudier les situations concurrentielles. Enfin, le jeu à trois joueurs peut également inclure un joueur muet n’ayant aucun pouvoir stratégique afin de distinguer l’altruisme des considérations stratégiques.

Les résultats de l’expérience de Bornstein et Yaniv (1998) montrent que lorsque la réflexion en groupe est permise, les joueurs semblent se comporter de manière plus rationnelle que lorsqu’ils jouent individuellement. Les sujets en groupe offrent en moyenne 10 % de moins de la somme à partager que les sujets individuels et sont prêts à accepter des sommes plus faibles en tant que répondants. Selon Battigalli et Dufwenberg (2007), un tel résultat peut s’expliquer par le fait que l’absence d’altruisme ne peut pas être reprochée à un joueur en particulier lorsque le choix est effectué par un groupe de joueurs.

Lorsque les répondants ou les offreurs sont en situation de concurrence, les prédictions théoriques du jeu basculent alors d’un extrême à l’autre selon le rôle attribué aux joueurs additionnels. En présence de plusieurs offreurs et d’un seul répondant, le jeu de l’ultimatum se transforme alors en « jeu de marché » et la théorie prédit que la concurrence devrait profiter à l’unique répondant et lui permettre de récolter la quasi-totalité de la somme à partager. En présence de plusieurs répondants, l’équilibre du jeu reste identique à celui du jeu simple : la quasi-totalité de la somme à partager revient à l’offreur. Les résultats des diverses expériences impliquant de la compétition se rapprochent davantage des prédictions théoriques. En situation de concurrence, les sujets font davantage usage de leur pouvoir de négociation.

En ce qui concerne les joueurs muets, ils n’obtiennent qu’une proportion très faible de la somme en jeu. Güth et Van Damme (1998) montrent que l’offreur perçoit en moyenne 50 % de la somme à partager tandis que le répondant et le joueur muet reçoivent respectivement 35 % et 15 %. Les auteurs insistent également sur le fait que la somme perçue par le joueur muet décroit avec l’expérience des offreurs dans le jeu. La faible somme attribuée aux joueurs muets permet donc de confirmer que l’équité n’est pas la seule composante de la fonction d’utilité des joueurs et que ceux-ci cherchent à maximiser leurs gains.

1.3.5 Le jeu du dictateur

Dans le jeu du dictateur, un joueur est chargé de partager une somme d’argent entre lui-même et un second joueur (le second joueur n’a aucun pouvoir et est contraint de recevoir la somme qui lui a été attribuée). Ce jeu est en tout point similaire au jeu de l’ultimatum à l’exception que le joueur initialement appelé « répondant » dans le jeu de l’ultimatum ne peut refuser la somme proposée dans le jeu du dictateur. Pour cette raison, le jeu du dictateur constitue une variante structurelle du jeu de l’ultimatum qui permet d’isoler les considérations stratégiques des considérations altruistes qui guident les choix du proposant. La première expérience visant à comparer les offres d’un jeu de l’ultimatum et d’un jeu du dictateur a été menée par Forsythe et al. (1994). D’une manière générale, les nombreuses expériences montrent que les dictateurs offrent en moyenne 20 % de la somme à partager. Cette somme peut être plus faible si l’expérience est menée en double aveugle (Hoffman et al., 1994) afin d’assurer aux joueurs que leurs choix ne pourront pas être observés par les expérimentalistes. En supposant que les joueurs cherchent à maximiser leur utilité, les sommes positives offertes dans le jeu du dictateur prouvent que l’altruisme est une composante de cette utilité. Le surplus offert dans le jeu de l’ultimatum peut alors être interprété comme la part relevant des considérations stratégiques de l’offreur. A priori, les sommes moyennes offertes lors des diverses expériences des jeux de l’ultimatum (environ 40 %) et du dictateur (environ 20 %) laissent supposer que les considérations altruistes et stratégiques jouent un rôle équivalent dans les choix des joueurs. Toutefois, une estimation précise de ces deux effets nécessiterait la réalisation d’une méta-analyse comparative entre les deux jeux.

Dans la seconde section de cet article, nous analysons dans un premier temps le comportement des joueurs dans le jeu de l’ultimatum. Ensuite, par le biais d’une métarégression, nous revenons sur les différentes variables énumérées dans cette première partie et en estimons l’influence sur les décisions des proposants dans notre échantillon d’études.

2. Méta-analyse

Dans la plupart des expériences du jeu de l’ultimatum, l’offre moyenne des proposants se situe en moyenne entre 40 et 50 % de la somme totale à partager. Afin d’obtenir une estimation précise de cette offre, nous réalisons une méta-analyse sur un total de 97 expériences du jeu simple de l’ultimatum.

2.1 Les données

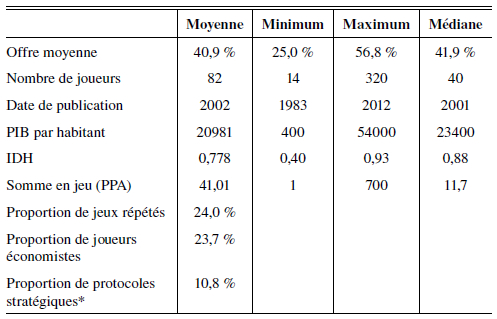
La base de données que nous avons construite dans le cadre de cette méta-analyse contient un total de 97 observations recueillies au sein de 41 articles et d’un ouvrage d’économie expérimentale portant sur le jeu de l’ultimatum. Dans un souci de représentativité des 30 années de recherches expérimentales menées sur le jeu de l’ultimatum nous avons sélectionné un grand nombre d’articles dont les dates de publication s’étendent de 1983 à 2011, 2001 étant la date médiane de notre échantillon. En ce qui concerne la diversité géographique des études, l’ensemble des données sur lesquelles nous travaillons ont été recueillies sur un ensemble de 29 pays différents. La pertinence des résultats obtenus est directement liée aux choix effectués concernant la construction de la base de données, c’est pourquoi nous avons établi certaines restrictions concernant les articles que nous avons sélectionnés qui doivent être comparables. Ainsi, chaque observation correspond à un jeu de l’ultimatum simple. Le « jeu de l’ultimatum « simple » fait référence au jeu sous sa forme initiale dans lequel un offreur et un répondant jouent de manière anonyme. Étant donné que nous cherchons à estimer la proportion moyenne de la somme en jeu offerte par un proposant, cette restriction vise à assurer que notre résultat soit le plus précis possible et ne soit pas altéré par les divergences protocolaires des diverses expériences. Ainsi, nous avons recensé l’ensemble des traitements correspondant à ces critères. L’effet moyen (somme moyenne offerte) de chaque traitement du jeu de l’ultimatum que nous avons sélectionné correspond à une observation de notre base de données. Pour un grand nombre d’articles, nous n’avons retenu qu’une seule observation : le traitement de contrôle. Le tableau 1 recense l’essentiel des statistiques descriptives concernant les études utilisées pour notre méta-analyse.

Dans les études sélectionnées, les proposants et répondants sont réappariés à chaque période de jeu pour former de nouvelles paires : les effets de réputation sont donc exclus (protocole « stranger »). Chaque expérience propose un minimum de 10 actions distinctes aux offreurs : cela exclut donc les jeux de l’ultimatum dans lesquels les ensembles individuels de stratégies sont trop restreints. Par ailleurs, nous avons choisi de ne conserver que les expériences dans lesquelles les sujets négocient une somme d’argent réelle. Cette condition fondamentale vise à assurer que les sujets sont soumis à des incitations monétaires dont l’importance est supposée par la théorie économique. Afin d’obtenir un maximum d’observations pour notre base de données, nous avons principalement utilisé Google Scholar comme outil de recherche des articles. Les différentes combinaisons de mots-clefs que nous avons utilisées nous ont permis de consulter plus de 200 articles expérimentaux dont le titre semblait avoir un rapport avec notre étude. Naturellement, seuls les articles dont les caractéristiques étaient en accord avec nos restrictions ont été conservés. Afin de limiter le risque de biais de sélection des articles, nous avons mis en oeuvre le « funnel plot » de notre méta-analyse que nous présentons dans la partie résultats. Pour chaque article pertinent, nous avons relevé les informations suivantes : offre moyenne du proposant, écart-type des offres, la somme d’argent à partager en PPA, le fait que les sujets sont économistes ou non, le fait que le jeu est répété ou non, le PIB et l’IDH du pays de l’étude, le fait que le pays est ou non industrialisé, l’âge moyen des sujets et le fait qu’il s’agit d’un jeu sous forme stratégique ou non[5]. Ces différentes variables explicatives nous permettent d’établir d’éventuels liens de causalité avec les offres formulées par le biais d’une métarégression.

Tableau 1

**Principales statistiques descriptives des données**

2.2 Résultats

Comme nous l’avons précédemment mentionné, l’ENPSJ du jeu de l’ultimatum prédit que le proposant doit garder la totalité de la somme à partager pour lui-même. Cependant, l’offre proposée par le joueur ayant l’initiative sera conforme à l’ENPSJ seulement si ce joueur anticipe que le répondant ne cherchera qu’à maximiser ses gains monétaires en occultant toute autre forme de réflexion. En revanche, si le proposant pense que ce dernier va refuser les offres trop faibles, pour diverses raisons, alors l’ENPSJ n’est pas le critère sur lequel le proposant doit se fonder pour formuler son offre. Cette réflexion simple et intuitive nous conduit à la conclusion que les offres des proposants sont conditionnées par leurs croyances concernant le comportement des répondants qui leur font face. Pour cette raison, il convient de s’intéresser au comportement des répondants avant de procéder à l’analyse des choix des proposants dans le jeu de l’ultimatum.

2.2.1 Les répondants

Dans le jeu de l’ultimatum, les répondants disposent d’un pouvoir de véto qui leur permet d’infliger des gains nuls aux deux joueurs si le partage de la somme qui leur est proposé ne leur convient pas. L’analyse de comportement des répondants, bien qu’indispensable pour se pencher par la suite sur les choix des offreurs, se confronte à deux problèmes majeurs. D’une part, les acceptations ou les rejets observés formulés par les répondants sont conditionnels à l’offre qui leur a été proposée. Or, les offres formulées par les proposants sont, pour la plupart, concentrées entre 30 % et 50 %. Il n’est donc pas chose aisée que d’établir une analyse robuste du comportement des répondants face aux offres inférieures à 30 % ou supérieures à 50 %. Par ailleurs, l’analyse du comportement des répondants suppose que les choix de ces derniers soient reportés dans les différents articles. Cependant, la plupart des articles du jeu de l’ultimatum n’optent pas pour un protocole stratégique et un grand nombre ne mentionnent pas le taux d’acceptation ou de refus en fonction de l’offre proposée.

Malgré ces difficultés, nous avons rassemblé l’ensemble des articles dans lesquels les choix des répondants sont reportés en détail. Lorsqu’il est demandé aux joueurs de lister leurs différentes stratégies ou lorsque la distribution des offres fait apparaître la proportion d’offres acceptées et refusées, l’analyse du comportement des répondants est possible. Parmi notre échantillon de 41 études, seules 13 répondaient à ces critères. Pour chacune de ces études, nous avons recensé le nombre d’offres correspondant à chaque valeur par tranche de 10 % pour des valeurs allant de 0 à 100 % de la somme à partager. Pour chaque valeur, nous avons relevé l’ensemble des offres acceptées et rejetées, tous articles confondus, que nous faisons apparaître dans le tableau 2.

Cette analyse du comportement des répondants sur un total de 1980 observations individuelles nous permet d’obtenir plusieurs informations. Tout d’abord, le taux d’acceptation des offres est croissant avec la valeur de l’offre jusqu’à 50 % de la somme à partager. Ensuite, le taux d’acceptation d’une certaine offre étant la probabilité que celle-ci soit acceptée par un répondant, il est alors possible de calculer le gain espéré d’une certaine offre qui apparaît dans la dernière colonne du tableau[6]. Selon les données de notre échantillon, le proposant maximise son gain espéré lorsqu’il propose 40 % de la somme à partager au répondant. Son gain espéré est alors égal à 50,96 % de la somme à partager. En outre, il convient également de souligner qu’offrir 30 % ou 50 % de la somme sont également des stratégies dont le gain espéré est élevé et s’établit respectivement à 50 % et 48,32 % de la somme à partager. Nous pouvons également constater que le fait de jouer l’ENPSJ du jeu de l’ultimatum ne serait pas profitable face aux répondants de cet échantillon d’études : cette décision procure un gain espéré de 7,69 % de la somme à partager.

2.2.2 Les proposants

Après avoir analysé le comportement des répondants face aux différentes offres, nous nous intéressons au choix des répondants et à leurs déterminants à travers une méta-analyse regroupant 97 observations.

Les deux principaux modèles d’estimation utilisés dans le cadre des méta-analyses sont le modèle à effets fixes et le modèle à effets aléatoires. Ces modèles à « effets fixes » et « effets aléatoires » utilisés dans le cadre de la méta-analyse ne reflètent pas les modèles du même nom communément utilisés dans le cadre du traitement des données de panel. Chacun de ces deux modèles présente des hypothèses différentes concernant les effets de taille des différentes études[7]. Le modèle à effets fixes est basé sur l’hypothèse que l’ensemble des études incluses dans l’analyse partage le même effet de taille réel, représenté par un rond dans le graphique 2[8]. Les différences entre les effets de taille observés, représentés par un carré dans le graphique 2, sont donc uniquement dues aux erreurs d’échantillonnage. À l’inverse, le modèle à effets aléatoires ne repose pas sur cette hypothèse restrictive et suppose que l’effet de taille réel que l’on souhaite estimer peut varier d’une étude à l’autre. Par exemple, l’effet de taille peut varier en fonction de l’âge des sujets, de leur nationalité, des paramètres expérimentaux ou d’autres variables.

Graphique 2

**Modèles à effets fixes (haut) et aléatoires (bas)**

Afin d’estimer la proportion moyenne de la somme en jeu offerte par un proposant dans le jeu de l’ultimatum, nous préférons utiliser le modèle à effets aléatoires dont le caractère non restrictif nous semble plus adapté au jeu de l’ultimatum. En effet, les caractéristiques des sujets ainsi que les nombreux paramètres expérimentaux sont susceptibles d’être à l’origine de variations entre les effets de taille réels des différentes études. Le choix d’un modèle à effets aléatoires nécessite toutefois un grand nombre d’études pour fournir une estimation précise de l’effet : la précision de l’estimateur de la variance interétudes (τ²) qui intervient dans la définition des pondérations des différentes études dépend du nombre d’études inclues dans l’échantillon. Dans notre cas, ce prérequis ne pose aucun problème étant donné que nous disposons de 97 observations. Les résultats obtenus sont présentés dans le tableau 3.

Tableau 3

**Méta-analyse, modèle à effets aléatoires**

Un proposant offre en moyenne 41,04 % de la somme mise en jeu au répondant qui lui fait face. La forte puissance statistique assurée par l’agrégation des 97 observations nous permet de nous assurer de la précision de cette estimation : l’erreur standard est égale à 0,005 et l’intervalle de confiance à 95 % pour la valeur de l’offre moyenne est donc [40,03 %; 42,05 %]. Compte tenu des résultats obtenus dans le tableau 2, ce résultat très proche de 40 %, laisse donc penser que les proposants ont une idée clairvoyante de la stratégie adoptée par les répondants. Avec une offre moyenne proche de 40 %, les offreurs de notre échantillon maximisent leur espérance de gain compte tenu des choix effectués par les répondants. Une analyse plus approfondie des offres individuelles montre que 86 % des offres effectuées sont concentrées entre 30 % et 50 % de la somme totale à partager[9]. Comme nous l’avons mentionné précédemment, le fait de formuler une offre comprise entre 30 % et 50 % de la somme à partager procure au proposant une espérance de gain relativement élevée par rapport aux autres offres possibles. S’il n’est pas statistiquement possible de distinguer l’ensemble des facteurs ayant conduit un proposant à choisir une certaine offre, une grande majorité des proposants agissent, in fine, de manière à maximiser leur d’espérance de gain en tenant compte de la stratégie des répondants.

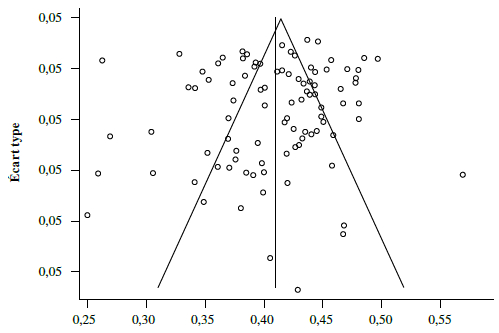
Afin de nous assurer de la robustesse de notre résultat, nous avons mis en oeuvre le funnel plot de notre méta-analyse. Il s’agit d’un outil aux nombreux usages permettant notamment de vérifier la présence d’un biais de sélection des articles dans l’échantillon d’études. La lecture du funnel plot offre au statisticien une vue d’ensemble sur les effets moyens et les erreurs standard des études qui composent l’échantillon. Sur le graphique, l’effet moyen de chaque étude est rapporté sur l’axe des abscisses et leur erreur standard sur l’axe des ordonnées. Les erreurs d’échantillonnage étant supposées aléatoires et distribuées selon une loi normale, les études devraient être réparties de manière symétrique de chaque côté de l’effet estimé par la méta-analyse (représenté par l’axe central). Si le nuage de points renvoyé par le funnel plot présente une forte asymétrie, il est probable que certaines études présentant des caractéristiques communes aient été omises lors de la phase de récolte des données. L’analyse du funnel plot de notre méta-analyse (graphique 3) ne présente pas d’asymétrie particulière. En effet, l’ensemble des observations sont réparties de manière quasi symétrique de part et d’autre de l’axe central : 52 observations à gauche, 45 à droite.

Funnel plot, modèle à effets aléatoires — Graphique 3

*Funnel plot*, modèle à effets aléatoires

Toutefois, une simple analyse graphique n’est pas suffisante pour déterminer la présence d’un biais. Nous procédons donc au test de Egger[10] pour analyser la symétrie de notre funnel plot. Les résultats du test présentés dans le tableau 4 montrent que l’hypothèse nulle de non-asymétrie n’est pas rejetée.

Tableau 4

**Résultats du test d’Egger**

Les statistiques relatives à l’hétérogénéité de notre échantillon d’études présentées dans le tableau 5 montrent que l’hypothèse nulle du test Q sur l’effet de taille identique pour toutes les études est rejetée (probabilité critique = 0,0001). Par ailleurs, 93,7 % de la variance totale est expliquée par des différences entre les effets de taille réels.

Tableau 5

Méta-analyse, statistiques relatives à l’hétérogénéité

-> Voir la liste des tableaux

Les statistiques du tableau 5 mettent en évidence une hétérogénéité de l’effet de taille étudié à travers notre échantillon d’études. Afin d’analyser l’origine de cette variance, nous avons conduit une méta-analyse sur l’ensemble des variables explicatives collectées. Les résultats de notre métarégression estimée par un modèle à effets mixtes apparaissent dans le tableau 6.

Tableau 6

**Métarégression, estimation par modèle à effets mixtes, variables explicatives de la somme offerte dans un jeu de l’ultimatum**

Nos résultats concernant les variables méthodologiques montrent que ni la somme d’argent en jeu (1), ni la répétition du jeu (2) n’influencent le choix de l’offreur dans le jeu de l’ultimatum. Ces résultats vont donc dans le sens des études menées par (1) Cameron (1999), Hoffman et al. (1996), Slonim et Roth (1998), puis (2) Roth et Erev (1995), Brenner et Vriend (2006), Cooper et Dutcher (2011). La rémunération modeste des joueurs et le manque de connaissance du jeu ne sont donc pas en mesure d’expliquer les offres moyennes observées dans notre échantillon de 97 observations. Concernant les variables démographiques, le fait d’être un étudiant en économie influence significativement (au seuil de 1 %) la somme offerte dans le jeu de l’ultimatum : un économiste conserve en moyenne 5,6 % de plus de la somme à partager pour lui-même. Cela confirme donc les résultats de Carter et Irons (1991) selon lesquels les choix d’un étudiant en sciences économiques sont plus proches de l’équilibre théorique que les choix d’un autre joueur dans le jeu de l’ultimatum. En ce qui concerne les nombreux pays dans lesquels les études ont été réalisées, les offres formulées dans les pays industrialisés[11] ne présentent pas de différence significative par rapport aux offres formulées dans les pays non industrialisés. Ce résultat va donc dans le sens de l’étude menée par Heinrich et al. (2005). Malgré la non-significativité de leurs résultats, Heinrich et al. précisent qu’ils observent une tendance d’offres plus généreuses dans les pays industrialisés. Selon les auteurs, les préférences et les attentes des joueurs sont influencées par le cadre institutionnel et les normes culturelles d’équité de l’environnement dans lequel ils évoluent. Ainsi, il semblera plus naturel à un joueur d’un pays industrialisé de redistribuer une plus grande partie de la somme qui lui a été allouée.

Conclusion

En définitive, il est intéressant de constater qu’une analyse approfondie des comportements individuels des répondants nous permet de réfuter la remise en cause de la rationalité des proposants dans le jeu de l’ultimatum dont les choix ne correspondent pas à l’ENPSJ. En effet, les choix des proposants qui, à priori, ne semblent pas conformes à la rationalité se révèlent l’être en moyenne compte tenu du comportement observé des répondants. Si cette divergence entre les choix des joueurs et l’ENPSJ du jeu de l’ultimatum peut être considérée comme une forme d’irrationalité, son analyse est à approfondir du côté des choix des répondants qui préfèrent renoncer à de gains positifs pour construire une menace crédible qui, a priori, ne l’est pas. L’analyse du comportement des répondants nécessite donc un approfondissement que nous ne proposons pas dans ce papier. Nous sommes toutefois conscients de l’importance d’une telle analyse qui constitue une piste de recherche pour des travaux ultérieurs.

Au-delà de ce constat, les nombreuses expériences du jeu de l’ultimatum et ses déclinaisons menées au cours de ces 30 dernières années ont fortement contribué à l’évolution de l’approche théorique des comportements individuels. En effet, les régularités empiriques mises en évidence ont notamment participé au développement du modèle de paiement comparatif de Bolton et Ockenfels (1991), à celui de Rabin (1993) lié au rôle des intentions ou encore au modèle d’aversion à l’iniquité de Fehr et Schmidt (1999). Au-delà de la rationalité supposée par l’approche économique standard, les individus manifestent des préoccupations différentes que les expériences du jeu de l’ultimatum ont en partie permis de révéler. S’il n’est pas possible d’établir un modèle théorique général permettant de prédire le comportement de l’ensemble des individus face à toute situation, la révélation de certaines composantes de la fonction d’utilité des individus telles que les préférences sociales, les différentes aversions, l’altruisme ou encore les émotions doit permettre à la microéconomie de mieux saisir le comportement réel des agents économiques.

Le jeu de l’ultimatum, une méta-analyse de 30 années de recherches expérimentales

Résumé

Introduction