Résumés
Résumé
Nous utilisons des méthodes de simulation pour analyser les impacts de certaines propositions de réforme visant à améliorer la couverture du risque de longévité. Ce risque, qui peut en principe être adéquatement couvert par les régimes de retraite classiques à prestations déterminées, fait l’objet d’une attention particulière au Québec depuis quelques années, notamment en raison du déclin de la participation à de tels régimes. Les propositions récentes visant à bonifier la couverture du risque de longévité se concentrent en grande partie sur l’expansion du « 2e pilier » du système de revenu de retraite, actuellement constitué du Régime de rentes du Québec. Nous considérons à ce titre une proposition-clé du Comité d’Amours (la rente longévité), ainsi que deux autres propositions : celle de Mintz et Wilson, qui vise à augmenter la générosité du régime actuel, et celle de Wolfson, qui introduit une notion de taux de cotisation et de prestations différenciés selon le revenu. À l’aide de données provenant des enquêtes de Statistique Canada, nous analysons pour plusieurs types d’individus le taux de rendement interne (TRI) de ces propositions en prenant en considération l’inégalité d’espérance de vie, la variabilité temporelle des revenus ainsi que les interactions avec la fiscalité et les différents programmes de soutien du revenu à la retraite. Nous contrastons les résultats avec ceux obtenus en effectuant des contributions additionnelles à des véhicules d’épargne volontaire existants combinées à l’achat d’une rente simple au moment de la prise de la retraite.
Corps de l’article
Introduction
Avec le vieillissement de la population et l’augmentation prévue de l’espérance de vie, la gestion du risque de longévité par les ménages deviendra un enjeu de plus en plus important. Bien que depuis Yaari (1965), les économistes s’entendent pour dire que l’annuitisation de la richesse à la retraite offre la meilleure protection contre le risque de longévité, une condition importante de cette supériorité est que le prix implicite de la rente ainsi achetée se transpose en un rendement à l’échelle individuelle qui est adéquat d’un point de vue actuariel. Le respect de cette condition dépendra entre autres du risque de mortalité de l’individu ainsi que du niveau des prestations nettes qui lui seront versées. Le recul des régimes complémentaires de retraite à prestations déterminées ainsi que la faible générosité des régimes publics de retraite pour les individus se situant dans le deuxième tercile de revenu ne font par ailleurs qu’accentuer le besoin de revoir la protection contre ce risque.
Dans cet article, nous souhaitons quantifier le rendement implicite — ou rendement interne — de propositions récemment mises de l’avant pour augmenter la protection contre le risque de longévité. Afin de bien jauger l’hétérogénéité individuelle des rendements possibles, nous prenons en compte les inégalités de risque de mortalité selon le niveau d’éducation (et donc, implicitement, selon le revenu espéré) ainsi que les interactions qu’auraient les réformes proposées avec i) les programmes existants de soutien du revenu à la retraite, et ii) les autres revenus de retraite que les individus obtiendraient dans un monde sans réforme.
En effet, il est bien connu que la mortalité est associée au revenu et au niveau d’éducation des individus. Au Canada par exemple, Adam (2012) démontre non seulement que les taux de mortalité des prestataires du Régime de rentes du Québec (RRQ) et du Régime de pensions du Canada (RPC) diffèrent selon leur revenu, mais aussi que l’amélioration de la mortalité semble plus rapide chez les plus fortunés. Puisque les taux de cotisation au RRQ/RPC ne sont pas différenciés par niveau de revenu (outre la différenciation qui s’effectue par le biais du maximum des gains admissibles), il est possible que la rente offerte procure un rendement implicite inférieur aux individus ayant un risque de mortalité plus élevé que la moyenne.
Les propositions de réforme que nous analysons — ainsi que plusieurs autres formulées ces dernières années — sont par ailleurs susceptibles d’offrir un rendement plus faible aux ménages moins fortunés, puisque ceux qui sont admissibles au Supplément de revenu garanti (SRG) fédéral pourraient voir leur prestation réduite suite à la mise en oeuvre de ces réformes. L’évaluation du rendement implicite de nouvelles modalités de cotisations et de prestations doit tenir compte de leur effet total sur les revenus nets d’impôts et de prestations (ou revenus disponibles, selon la terminologie de Statistique Canada) de l’individu à la retraite, et non pas seulement de l’effet isolé de ces modalités.
Le système canadien de revenu de retraite comporte trois composantes, qui sont détaillées à la section 2 et dont l’importance varie entre individus. Le « 1er pilier » comprend les programmes publics de base que sont la Pension de sécurité de la vieillesse et le SRG. Le 2e est constitué du RRQ et du RPC, tandis que le 3e inclut les régimes complémentaires de retraite et l’épargne privée, enregistrée ou non.
Nous considérons ici trois propositions de réforme aux programmes publics du 2e pilier pour améliorer la couverture du risque de longévité. Nous traitons tout d’abord de la proposition du Comité sur l’avenir des régimes de retraite présidé par Alban D’Amours, qui consiste à introduire une « rente longévité » similaire à une bonification de la prestation du RRQ à partir de l’âge de 75 ans (D’Amours et al., 2013). Cette rente serait financée par une cotisation additionnelle des travailleurs et employeurs et remplacerait au maximum 28,5 % des revenus de travail à partir de l’âge de 75 ans. Une deuxième proposition consiste à bonifier le régime actuel, une proposition faite par Jack Mintz de l’Université de Calgary et Thomas Wilson de l’Université de Toronto (Mintz et Wilson, 2013). Cette proposition vise à augmenter le taux de remplacement de la prestation actuelle du RRQ (et du RPC) à 35 % au lieu de 25 %. Finalement, une dernière proposition, faite par Michael Wolfson de l’Université d’Ottawa, écarterait le principe d’un taux de cotisation uniforme en modulant le taux de cotisation selon le revenu, tout en doublant à 105 000 $ le plafond des gains admissibles, par rapport au plafond actuel, qui est de 52 500 $ en 2014 (Wolfson, 2013).
Afin d’obtenir des alternatives comparables basées sur des véhicules d’épargne individuelle existants, nous considérons également deux possibilités simples d’épargne volontaire accrue, au sein du « 3e pilier », avec des paramètres et dans le cadre de véhicules précis. Ainsi, nous modélisons un scénario utilisant un Régime volontaire d’épargne retraite (RVER), véhicule récemment créé au Québec et similaire au Régime enregistré d’épargne retraite (REER); ainsi qu’un autre faisant appel au Compte d’épargne libre d’impôt, le CELI. Nous modélisons une contribution additionnelle faite dans chacun de ces véhicules par tous les travailleurs, en présumant que les sommes sont investies dans l’achat d’obligations canadiennes à long terme. Dans ces scénarios, les individus achètent une rente sur le marché privé au moment où ils prennent leur retraite, en utilisant la totalité du capital supplémentaire accumulé dans leur RVER ou leur CELI.
La section 1 de l’article présente la structure de la modélisation. La section 2 présente les différents scénarios considérés. La section 3 quantifie le rendement des propositions considérées pour des ménages possédant différentes caractéristiques, à la fois en termes de taux de remplacement du revenu et de rendement interne, et présente quelques analyses contrefactuelles. La section 4 conclut.
1. Modélisation
1.1 Les agents
Nous considérons un travailleur débutant sa carrière en 2011 à l’âge de 25 ans. Ce travailleur salarié peut avoir en début de carrière un niveau variable d’éducation et de revenu initial, c.-à-d. de revenu à 25 ans. Nous construisons des cas types en plaçant le travailleur dans chacune de 78 cellules possibles, définies par le niveau d’éducation e ∈ E (3 niveaux) et le revenu initial Y25 ∈ {2 000 $,…,102 000 $} (soit 26 tranches de revenu de 4 000 $ chacune). Ces deux sources d’hétérogénéité permettront de prendre en compte deux dimensions de la mortalité différenciée et les interactions possibles entre les nouvelles modalités proposées et les programmes existants.
Pour simplifier l’analyse et la présentation des résultats, le travailleur est présumé célibataire et sans enfants pour toute sa vie. Cette simplification n’enlève rien à la pertinence de l’analyse, puisque le système québécois de revenu de retraite est plutôt neutre par rapport à la situation familiale à quelques exceptions près : le SRG verse des prestations par personne moins élevées aux couples afin de tenir compte des économies d’échelle; et le RRQ ne pénalise pas les parents temporairement hors du marché du travail pour s’occuper d’enfants en bas âge. Qui plus est, le célibat et l’absence d’enfants ne sont pas des phénomènes marginaux au Québec : près d’une femme sur cinq y restera nullipare toute sa vie, tandis que près de 60 % des individus nés à la fin des années 1970 ne se seront jamais mariés lorsqu’ils auront 50 ans (Institut de la statistique du Québec, 2014).
1.2 Revenu de travail
Nous utilisons la structure de salaire proposée par Gourinchas et Parker (2002). Le modèle de revenu de travail suppose que le salaire annuel est donné par
où Y25 est le revenu de travail initial, Ge,t est une composante du salaire qui dépend de l’âge, t, et du niveau d’éducation, e (avec Ge,25 = 1), Ue,t est un choc transitoire avec ![]() , et Pe,t (avec Pe,25 = 1) est un choc permanent qui suit
, et Pe,t (avec Pe,25 = 1) est un choc permanent qui suit
où ![]() . L’agent prend sa retraite à 65 ans, après avoir travaillé 40 années sans interruption. Il cesse à ce moment de recevoir un revenu de travail. Ces processus sont estimés séparément par niveau d’éducation à l’aide des répondants des cycles 2 à 5 de l’Enquête sur la dynamique du travail et du revenu (EDTR) de Statistique Canada. L’annexe A présente les détails sur la méthode d’estimation ainsi que les résultats principaux. Les résultats montrent que les revenus ont un profil en U inversé sur le cycle de vie, atteignant un maximum aux environs de 55 ans. La croissance des revenus est beaucoup plus forte pour les individus ayant un diplôme universitaire. Pour ce qui est des estimations de la structure d’erreur, on trouve que diminue à mesure que le niveau d’éducation augmente, ce qui suggère que les revenus des individus les plus éduqués dépendent moins de leur situation passée. La variance estimée du choc transitoire décroît également avec le niveau d’éducation, alors que celle du choc permanent augmente avec le niveau d’éducation.
. L’agent prend sa retraite à 65 ans, après avoir travaillé 40 années sans interruption. Il cesse à ce moment de recevoir un revenu de travail. Ces processus sont estimés séparément par niveau d’éducation à l’aide des répondants des cycles 2 à 5 de l’Enquête sur la dynamique du travail et du revenu (EDTR) de Statistique Canada. L’annexe A présente les détails sur la méthode d’estimation ainsi que les résultats principaux. Les résultats montrent que les revenus ont un profil en U inversé sur le cycle de vie, atteignant un maximum aux environs de 55 ans. La croissance des revenus est beaucoup plus forte pour les individus ayant un diplôme universitaire. Pour ce qui est des estimations de la structure d’erreur, on trouve que diminue à mesure que le niveau d’éducation augmente, ce qui suggère que les revenus des individus les plus éduqués dépendent moins de leur situation passée. La variance estimée du choc transitoire décroît également avec le niveau d’éducation, alors que celle du choc permanent augmente avec le niveau d’éducation.
À l’aide de ces paramètres estimés nous simulons 100 fois, pour chaque combinaison de revenu initial et de niveau d’éducation, le parcours dynamique de revenus de travail (entre 26 et 64 ans). On prend ensuite pour chaque âge la moyenne des revenus des 100 simulations pour déterminer le revenu par âge pour chaque cas-type.
1.3 Mortalité
Il n’existe pas de tables de mortalité prospective par niveau de revenu ou d’éducation. Afin d’obtenir des taux de mortalité par niveau d’éducation pour un individu ayant 25 ans en 2011, nous combinons les projections des taux agrégés de mortalité et les différentiels actuels de taux de mortalité par niveau d’éducation. Cette méthode a été utilisée par French (2005). Elle suppose toutefois que les écarts actuels de taux de mortalité entre des individus avec différents niveaux d’éducation se maintiendront dans le futur, ce qui n’est pas assuré.
Nous utilisons d’abord la table de mortalité de 2009 de l’Institut de la statistique du Québec (ISQ). En dénotant l’indicateur de décès entre l’âge t et l’âge t +1 par Mt+1, nous obtenons une probabilité de décès donnée par ![]() . Nous calculons ensuite
. Nous calculons ensuite ![]() , en utilisant le fait que
, en utilisant le fait que
On estime ![]() et
et ![]() à partir de l’Enquête nationale sur la santé de la population (ENSP), cycles 1994-2010, pour ensuite calculer
à partir de l’Enquête nationale sur la santé de la population (ENSP), cycles 1994-2010, pour ensuite calculer ![]() . L’annexe B donne les détails de l’application de cette méthode ainsi que les résultats. Nous estimons que les écarts de mortalité sont plus importants avant 65 ans et qu’ils diminuent après 65 ans. Une des raisons probables est un effet de sélection dynamique : les individus survivant jusqu’à 65 ans au sein du groupe ayant un risque de mortalité structurel plus élevé ont sans doute des caractéristiques inobservables qui rendent leur probabilité individuelle de décès plus faible que la probabilité de décès moyenne du groupe d’individus ayant un risque de mortalité structurel plus faible. L’espérance de vie à la naissance ainsi estimée varie de 78,3 à 84,6 années, selon le niveau d’éducation, conditionnellement au fait d’avoir survécu jusqu’à l’âge de 25 ans (puisque c’est l’âge de nos agents au début des simulations).
. L’annexe B donne les détails de l’application de cette méthode ainsi que les résultats. Nous estimons que les écarts de mortalité sont plus importants avant 65 ans et qu’ils diminuent après 65 ans. Une des raisons probables est un effet de sélection dynamique : les individus survivant jusqu’à 65 ans au sein du groupe ayant un risque de mortalité structurel plus élevé ont sans doute des caractéristiques inobservables qui rendent leur probabilité individuelle de décès plus faible que la probabilité de décès moyenne du groupe d’individus ayant un risque de mortalité structurel plus faible. L’espérance de vie à la naissance ainsi estimée varie de 78,3 à 84,6 années, selon le niveau d’éducation, conditionnellement au fait d’avoir survécu jusqu’à l’âge de 25 ans (puisque c’est l’âge de nos agents au début des simulations).
2. Les scénarios
Afin d’analyser les différentes propositions de réforme, nous construisons tout d’abord un scénario de référence qui doit représenter la situation du système de retraite en 2011, c’est-à-dire telle que rencontrée par nos agents-type. Un scénario alternatif est ensuite construit pour chacune des trois propositions de réforme considérées et ses résultats sont comparés à ceux du scénario de référence afin d’en évaluer les impacts. Nous modélisons ainsi : (1) la rente longévité proposée par le Comité D’Amours (D’Amours et al., 2013), en raison de son originalité; (2) une version simplifiée de la proposition de bonification du RRQ/RPC formulée par Mintz et Wilson (2013), qui consiste surtout en un rehaussement du taux de remplacement; et (3) la proposition émise par Wolfson (2013), consistant à doubler le plafond du revenu assurable par le RRQ/RPC, et à introduire des taux de cotisations — et de prestations — différenciés selon le revenu.
Notons qu’un bon nombre d’autres propositions de réforme du système de revenu de retraite ont été formulées depuis quelques années, visant notamment la bonification du RRQ/RPC, en particulier depuis la crise financière de 2008 (voir par exemple Milligan et Schirle, 2014). Nous avons choisi ces trois propositions parce qu’elles constituent à notre avis un éventail pertinent et représentatif des propositions émises, en plus de différer substantiellement quant à leur esprit et à leurs paramètres.
2.1 Scénario de référence
Le scénario de référence tient compte des particularités du système fiscal et du système de retraite québécois existants. Le premier pilier du système de retraite est constitué de la Pension de sécurité de la vieillesse (PSV) et du Supplément de revenu garanti (SRG), deux programmes fédéraux. Le deuxième pilier est composé des prestations du Régime de rentes du Québec (RRQ). Le troisième pilier est composé des régimes complémentaires de retraite et de l’épargne privée, enregistrée ou non.
Les prestations des programmes publics (piliers 1 et 2) ainsi que la fonction d’imposition présentées ci-après sont calculées à l’aide de SimTax, un calculateur fiscal dont le fonctionnement et les détails sont présentés à l’annexe D.
2.1.1 Pension de sécurité de la vieillesse
La prestation de la PSV est donnée par BPV. Pour tout citoyen canadien ayant résidé au pays durant au moins 40 années depuis ses 18 ans (ce que nous supposons être le cas pour les individus dans notre simulation), cette prestation imposable est de 6 368 $ en 2011. Une récupération fiscale s’applique cependant à un taux de 15 % à partir d’un revenu de 67 700 $ après déductions (mais incluant la PSV).
2.1.2 Supplément de revenu garanti
La prestation de SRG est donnée par BSRG et elle est non imposable. En 2011, la prestation de base est de 8 039 $ pour un célibataire (le calcul pour les couples est différent) et elle diminue à un taux de 50 % en fonction des autres revenus, hormis la PSV et une exemption de 3 500 $ pour les revenus de travail. Depuis 2011, le SRG inclut également une prestation additionnelle de 600 $ pour les individus à très faible revenu, qui est réduite à un taux de 20 % à partir d’un revenu total de 2 000 $, excluant la PSV. Toutes ces particularités sont prises en compte dans SimTax.
2.1.3 Cotisations au RRQ
Les cotisations au Régime de rentes du Québec sont données par SRRQ. En 2011, elles correspondent à 9,90 % du revenu admissible, soit celui se situant entre l’exemption générale de 3 500 $ et le maximum des gains admissibles (MGA), soit 48 300 $. Ce taux est toutefois partagé moitié-moitié entre l’employeur et l’employé, à raison de 4,95 % chacun.[1] Les cotisations sont nettes, c’est-à-dire qu’on en déduit le crédit d’impôt non remboursable fédéral qui y est rattaché.
2.1.4 Prestations de retraite du RRQ
Les prestations de retraite du RRQ sont imposables et sont fonction de la moyenne des gains admissibles, APEt. Elles sont aussi fonction de l’âge lors du début des prestations, mais puisque tous les agents prennent ici leur retraite à 65 ans, soit l’âge normal, ce paramètre n’a pas d’impact. On dénote la prestation par BRRQ.
2.1.5 Revenus de marché une fois à la retraite : prestations de régimes complémentaires et revenus d’épargne personnelle
Les individus peuvent recevoir des revenus de retraite privés, provenant par exemple de régimes complémentaires, à prestations déterminées (PD) ou à cotisations déterminées (CD), ou encore provenant de régimes enregistrés d’épargne-retraite (REER) individuels ou collectifs ou d’épargne individuelle non enregistrée. Les comptes d’épargne libres d’impôt (CELI), dont le traitement fiscal diffère, ne sont pas modélisés dans le scénario de référence. Tous ces revenus, agrégés, sont dénotés ensemble par BPP, et dépendent notamment du dernier revenu de travail avant la retraite, Y64. Ils sont estimés de façon agrégée, à l’aide de la méthode décrite à l’annexe C.
2.1.6 Imposition des revenus de travail et de retraite
Le revenu net (ou revenu disponible) est donné par
La fonction τ() tient compte des taux d’imposition et de la structure des impôts provinciaux et fédéraux sur le revenu ainsi que des cotisations apparentées, comme la contribution santé (voir l’annexe D qui détaille SimTax). Elle ne s’applique qu’à Ytou à tous les autres types de revenus imposables réunis, jamais aux deux ensembles en même temps, puisque la retraite est définie comme un arrêt complet du travail. Nous présumons donc aussi que les travailleurs ne reçoivent aucune prestation de retraite.
2.2 Scénario alternatif 1 : ajout d’une rente longévité
Dans ce scénario, nous modélisons l’introduction d’une rente longévité payable à partir de 75 ans, selon les modalités prévues par le Comité D’Amours (D’Amours et al., 2013). Cette rente longévité s’ajoute à la structure existante décrite au scénario de référence.
Nous supposons donc un taux de cotisation de 3,3 % jusqu’au plafond fixé par le MGA. Ce taux est partagé moitié-moitié entre l’employeur et l’employé, de sorte que l’agent paie, aux fins fiscales, un taux de 1,65 %. À des fins de simplicité, un crédit d’impôt non remboursable est rattaché à cette cotisation, selon les mêmes modalités que pour les cotisations au RRQ. C’est la principale différence avec le programme proposé par le Comité D’Amours, qui recommandait plutôt une déduction fiscale, potentiellement plus avantageuse pour le travailleur. La cotisation nette est dénotée SRL et est soustraite du revenu disponible.
Nous considérons que la cotisation de l’employeur est en partie supportée par les travailleurs par le biais de salaires plus faibles. En nous basant sur Roy-Cesar et Vaillancourt (2010), nous supposons que la moitié de la cotisation employeur est refilée aux travailleurs. Ainsi, la cotisation totale du travailleur s’élève à 1,65 %*1,5, soit 2,475 % du salaire. Seule la cotisation directe de l’employé est toutefois prise en compte pour le calcul du crédit d’impôt non remboursable. Ces mêmes hypothèses seront aussi faites pour les autres propositions de réforme du 2e pilier.
La prestation est fonction de la même base que la prestation du RRQ, APEt. Le taux de remplacement dépend toutefois du nombre d’années de cotisations. Il est de 0,5 % par année de cotisation, de sorte qu’il est de 20 % pour nos simulations, dans lesquelles les agents travaillent durant 40 ans. La prestation est dénotée BRL et elle s’ajoute au revenu disponible (donc à l’intérieur de la fonction τ() ci-dessus).
2.3 Scénario alternatif 2 : bonification du RRQ (proposition de Mintz-Wilson)
Pour plusieurs raisons, Mintz et Wilson (2013) proposent de hausser simplement et modestement le taux de remplacement du revenu offert par le RRQ/RPC en le faisant passer de 25 % à 35 %. Ils recommandent de laisser le MGA inchangé, dans la mesure où les individus gagnant un revenu supérieur au MGA ont plusieurs autres options à leur disposition pour préparer leur retraite.
En contrepartie de la hausse des prestations, Mintz et Wilson suggèrent d’augmenter le taux de cotisation de 2,5 points de pourcentage, hausse payée à parts égales par les employeurs et employés — mais supportée aux 3/4 par les travailleurs, comme dans le cas de la rente longévité, ce qui donne un taux effectif de 1,875 % pour les travailleurs aux fins du calcul de taux de rendement (voir section 4). Dans le cas du RRQ de 2011, le taux de cotisation total passe donc de 9,9 % à 12,4 %. Il faut noter que les auteurs n’ont pas quantifié de façon détaillée le coût de la hausse de prestations qu’ils proposent, de sorte que la hausse des cotisations qu’ils suggèrent pourrait bien, dans la réalité comme dans nos simulations, s’avérer trop faible ou trop forte pour financer la hausse proposée des prestations. Toutefois, dans la mesure où les prestations de retraite du RRQ/RPC à leur niveau actuel coûtent environ 5,2 % du revenu de travail (Wolfson, 2013), il semble probable qu’une hausse des prestations de 40 % [soit (35 % – 25 %)/25 %] puisse effectivement être financée par la hausse de cotisations proposée de 2,5 points de pourcentage.
2.4 Scénario alternatif 3 : bonification du RRQ (proposition de Wolfson)
La dernière proposition de réforme que nous modélisons est celle de Wolfson (2013), construite en utilisant le modèle de microsimulation Lifepaths de Statistique Canada. Cette proposition consiste tout d’abord à doubler le MGA du RRQ pour le faire passer à deux fois le revenu moyen canadien, soit près de 97 000 $ pour 2011 (ou 105 000 $ en 2014). Cet élément fait aussi partie de nombreuses autres propositions de réforme mises de l’avant.
L’autre partie de la proposition consiste à introduire des taux de cotisations et de prestations différenciés selon le niveau de revenu. Ainsi, pour un revenu n’excédant pas la moitié du revenu moyen (c’est-à-dire 50 % du MGA préréforme), le taux de cotisation reste le même, soit 9,9 %. Puis, entre la moitié du revenu moyen et une fois le revenu moyen, donc entre 50 % et 100 % du MGA préréforme, le taux de cotisation augmente d’environ 3,1 points de pourcentage, sur la base du coût estimé du service courant mentionné plus haut[2]. Enfin, entre une fois et deux fois le revenu moyen, soit entre 100 % et 200 % du MGA préréforme, le taux de cotisation s’établit à 8,3 % (il est de 0 % dans le scénario de référence). Les taux de cotisation postréforme sont donc de 9,9 % jusqu’à la moitié du revenu moyen; de 13,0 % ensuite, jusqu’au revenu moyen; puis de 8,3 % entre une fois et deux fois le revenu moyen.
Du côté des prestations de retraite, cette structure de cotisations permet un taux de remplacement du revenu inchangé (soit de 25 %) pour les individus ayant gagné en deçà de 50 % du MGA préréforme, et un taux de remplacement de 40 % pour ceux ayant gagné entre 50 % et 200 % du MGA préréforme[3]. Selon l’auteur, cette structure vise à cibler le plus possible les besoins constatés dans son analyse prospective des revenus des futurs retraités. Le graphique 1 montre le taux de cotisation et le taux de remplacement provenant des prestations du RRQ/RPC dans le scénario de référence et avec la proposition de Wolfson, (2013).
Les caractéristiques principales des scénarios considérés de réforme du « 2e pilier » sont résumées dans le tableau 1.
2.5 Scénario alternatif 4 : épargne personnelle dans un RVER et achat d’une rente viagère
Afin de comparer les rendements des propositions de réforme aux programmes publics, nous souhaitons obtenir des alternatives comparables basées plutôt sur des véhicules d’épargne individuelle existants. Pour ce faire, nous considérons deux possibilités simples d’épargne volontaire additionnelle, avec des paramètres et dans le cadre de véhicules précis du 3e pilier[4]. Dans un premier cas, nous modélisons un scénario utilisant un Régime volontaire d’épargne retraite (RVER), véhicule récemment créé au Québec et similaire au Régime enregistré d’épargne retraite (REER) en ce sens que les cotisations sont défiscalisées (déductibles du revenu dans l’année où elles sont effectuées) tandis que les retraits sont, eux, imposables au taux marginal d’imposition applicable au moment du retrait. Les rendements s’accumulent à l’abri de l’impôt.
Tableau 1
Tableau synthèse des réformes
Graphique 1
Taux de cotisation et de remplacement en proportion du revenu, proposition de Wolfson (2013)
Taux de cotisation
Taux de remplacement
Plus précisément, nous modélisons une contribution annuelle de 2 % du revenu de travail (avant impôts) pour chaque travailleur-type. Ce taux de cotisation correspond au taux par défaut dans les RVER jusqu’à la fin de 2017. Nous supposons que le capital-épargne est investi dans des obligations gouvernementales de long terme fournissant un rendement de 3 %, soit le rendement approximatif d’une obligation canadienne à 30 ans[5]. Le choix du produit financier nous est dicté par un besoin de faible risque et de rendement stable afin de faciliter la comparaison avec les réformes aux programmes publics, mais il serait possible de modéliser des stratégies différentes d’investissement du capital.
Chaque travailleur contribue donc 2 % de son revenu à chaque année de travail, soit entre 25 et 64 ans inclusivement. Au moment de la prise de retraite à 65 ans, la totalité du capital accumulé — contributions plus rendements — est utilisée pour acheter une rente viagère simple, avec une garantie de paiement de 10 ans mais sans autre caractéristique optionnelle. Le prix de cette rente est la moyenne du prix pour un homme et de celui pour une femme, et correspond au prix moyen exigé mi-2014 par 11 grandes institutions canadiennes, obtenu de la base données CANNEX[6]. Puisque les sommes utilisées pour acheter la rente proviennent d’un RVER, les paiements de rente sont imposables. Cet aspect est pris en compte par le calculateur SimTax.
Le prix moyen utilisé correspond à 15,83 $ pour chaque dollar de revenu annuel versé par l’institution financière, calculé sur la base d’un versement annuel de 6 316 $ par tranche de 100 000 $ (homme : 6 660 $; femme : 5 972 $) : . On note que ce prix semble, en moyenne, assez juste d’un point de vue actuariel. En effet, en utilisant les tables de mortalité de l’ISQ et un rendement sur actif attendu de 3 %, on obtient des versements annuels allant de 6 239 $ à 7 237 $ selon le niveau d’éducation de l’individu (et donc son espérance de vie). Le diplômé universitaire a donc un léger avantage à se procurer une telle rente, tandis que l’individu sans diplôme reçoit des versements 14 % plus faibles que la juste valeur actuarielle du montant qu’il a versé pour acheter sa rente. On voit ainsi que la justesse actuarielle varie significativement selon le niveau d’éducation, ce qui risquerait de créer des problèmes d’antisélection si les pouvoirs publics souhaitaient promouvoir un usage volontaire d’une rente viagère. Cependant, on voit également à partir de ce calcul très approximatif que le prix moyen des rentes au Canada semble compétitif d’un point de vue actuariel, un constat qui s’applique à la plupart des pays, sauf l’Australie, selon Milevsky (2013).
2.6 Scénario alternatif 5 : épargne personnelle dans un CELI et achat d’une rente viagère
Le scénario alternatif 5 est en tous points identique au scénario 4, à l’exception du véhicule utilisé pour accumuler du capital à l’aide d’épargne personnelle. Ce scénario suppose ainsi que l’épargne additionnelle (le 2 % du scénario 4) est plutôt dirigée vers un Compte d’épargne libre d’impôt (CELI), un véhicule mis en oeuvre en 2009 par le gouvernement canadien. La principale différence qui en résulte est que le différentiel de taux d’imposition entre les années de travail et les années de retraite n’a plus d’impact — les contributions au CELI sont faites après impôts (c’est-à-dire que celles-ci ne donnent pas droit à une déduction) tandis que les retraits ne sont pas imposables. Avec de l’épargne personnelle accumulée dans un CELI, la rente viagère est donc achetée et versée en franchise d’impôts[7].
3. Remplacement du revenu et rendement interne
Le taux de remplacement du revenu à la retraite et le taux de rendement interne constituent deux outils simples et couramment utilisés pour évaluer l’impact de réformes proposées. Nous les appliquons dans cette section aux différentes propositions de réforme que nous étudions.
3.1 Taux de remplacement du revenu
Le taux de remplacement du revenu à la retraite est une mesure souvent utilisée par les analystes et les conseillers financiers et fréquemment citée dans les médias. Il n’existe toutefois pas de façon unique de calculer ce taux et plusieurs mesures différentes se côtoient dans la littérature. Pour des raisons de simplicité et de disponibilité des données, nous définissons ici ce taux comme étant le ratio entre le revenu disponible pour une année de retraite donnée, donc à partir de 65 ans, et le revenu disponible moyen sur la période avant la retraite, soit entre 25 et 64 ans. Il convient de souligner que le revenu à la retraite est constant dans tous les scénarios, sauf dans le scénario alternatif 1, où il change à 75 ans avec l’introduction de la rente longévité[8].
Si on dénote par Ht(k) le revenu disponible annuel de l’individu à l’âge t dans le scénario k = 0, 1,…,K, où k = 0 est le scénario de référence, on obtient pour chaque individu i et chaque scénario k le taux de remplacement à l’âge t
Ces taux de remplacement ne tiennent pas compte de l’espérance de vie ou du risque de mortalité, et sont donc conditionnels à ce que l’individu atteigne effectivement l’âge pour lequel le taux de remplacement est calculé. Le graphique 2 présente les taux de remplacement à 75 ans pour chacun des scénarios alternatifs, ainsi que pour le scénario de référence (soit la situation qui prévalait effectivement en 2011)[9]. On constate que c’est la rente longévité qui hausse le plus les taux de remplacement pour les individus avec un faible revenu moyen, et ce jusqu’à un revenu annuel de 60 000 $ environ. À l’opposé, la proposition Wolfson laisse les taux de remplacement largement inchangés pour les individus gagnant en moyenne 20 000 $ ou moins, et devient à partir d’un revenu brut (donc avant impôts) moyen de 60 000 $ la proposition de réforme qui hausse le plus les taux de remplacement. La hausse générée par la rente longévité, elle, est surtout concentrée entre des revenus initiaux de 15 000 $ et de 45 000 $, et c’est à partir d’un revenu moyen de 60 000 $ qu’elle cesse de hausser les taux de remplacement davantage que les autres réformes. Il faut rappeler toutefois que les hausses de taux de remplacement engendrées par l’introduction de la rente longévité, bien qu’elles soient les plus généreuses pour plusieurs tranches de revenu, ne s’appliquent qu’à partir de 75 ans, offrant donc jusqu’à 10 années de prestations de moins que les autres propositions.
Graphique 2
Taux de remplacement du revenu à 75 ans
La proposition Mintz-Wilson, elle, se situe entre les deux et offre une hausse modeste des taux de remplacement pour tous les niveaux de revenu, mais davantage pour les individus gagnant entre 20 000 $ et 85 000 $ en moyenne. On note que le profil de taux de remplacement de la proposition Mintz-Wilson est très similaire à celui du scénario RVER-rente, surtout jusqu’à un revenu moyen en carrière de 60 000 $. La différence entre les deux scénarios s’accroît par la suite mais reste faible. On voit enfin que le scénario CELI-rente performe assez bien selon la mesure du taux de remplacement, n’étant surpassé que par la rente longévité en deçà de 60 000 $ et par la proposition Wolfson au-delà.
On voit par ailleurs clairement que dans tous les cas les taux de remplacement sont très élevés pour des revenus faibles et qu’ils décroissent à mesure que ceux-ci augmentent. Les taux dépassent les 150 % à 10 000 $, et restent supérieurs à 125 % à un revenu moyen de 20 000 $. À partir de ce niveau de revenu, la pente devient graduellement moins abrupte et le taux décroît lentement pour atteindre tout de même 75 % à 95 % à 100 000 $, selon le scénario. L’écart de taux de remplacement entre les scénarios s’accroît donc à mesure que le revenu de travail moyen des individus augmente, ce qui témoigne du fait que les différentes réformes analysées visent d’abord les individus à revenu moyen ou élevé. Ainsi, toutes les réformes analysées ici haussent les taux de remplacement par rapport au scénario de référence, et ce, de façon plus marquée pour les individus gagnant plus de 20 000 $ par année en moyenne.
3.2 Taux de rendement interne
Le taux de rendement interne est une autre mesure communément utilisée par les analystes, surtout en évaluation de projets. Dans ce cas, il faut comparer les flux futurs associés à chaque réforme (scénario alternatif) à ceux associés au statu quo (scénario de référence). Cet exercice permet d’obtenir le taux de rendement qui rend nulle la valeur présente nette de chaque réforme. Pour un taux d’escompte r, la valeur escomptée à 25 ans du revenu disponible espéré LY d’un individu de niveau d’éducation e dans le scénario de référence ( k = 0 ) est donnée par
Nous avons fixé T, l’âge maximal possible, à 110 ans. Les taux de survie sont donnés par ![]() .
.
Les cotisations entrent dans le calcul de manière négative alors que les prestations entrent positivement. Le taux de rendement du scénario k est dénoté par ![]() et est donné implicitement par
et est donné implicitement par
On peut résoudre numériquement pour ![]() , en utilisant par exemple la bi-section (Judd, 1998 : chapitre 6).
, en utilisant par exemple la bi-section (Judd, 1998 : chapitre 6).
Le graphique 3 présente les taux de rendement interne par groupe d’éducation et de revenu dans chacun des scénarios alternatifs. On note que dans tous les scénarios, ces taux de rendement sont plus importants pour les individus ayant un niveau d’éducation plus élevé, en raison notamment de l’écart d’espérance de vie entre ces groupes. De plus, le profil général des rendements comporte un maximum entre 25 000 $ et 45 000 $ avec cependant plusieurs exceptions. De façon générale également, en raison de la croissance des salaires avec l’âge et de l’interaction de ceux-ci avec le MGA, les taux de rendement diminuent à mesure que le revenu moyen de l’individu augmente.
La rente longévité offre des rendements assez faibles, surtout pour les individus ayant le moins d’éducation. Les diplômés universitaires gagnant 35 000 $ à 55 000 $ environ obtiennent, eux, 2 %; tous les autres individus obtiennent un rendement inférieur. On note cependant que les diplômés universitaires obtiennent toujours un rendement supérieur à 1,5 % grâce à leur longévité plus grande. Le profil de rendement de la rente longévité est similaire à celui du scénario RVER-rente, ce dernier offrant toutefois un rendement plus faible aux individus à faible revenu — qui sont fortement désavantagés par un tel scénario en raison de l’interaction avec le SRG — et un rendement plus élevé aux individus gagnant plus de 35 000 $. Ce rendement identique de 2 % à 3 % pour tous ceux gagnant au-delà de ce seuil est aussi le rendement offert par le scénario CELI-rente, qui ne dépend pas du niveau de revenu. La neutralité fiscale du scénario CELI-rente génère un profil de rendement en fonction du revenu parfaitement horizontal — ce qui questionne la pertinence du RVER par rapport au CELI pour les individus à revenu faible ou moyen.
Graphique 3
Taux de rendement implicite
Rente longévité
Mintz-Wilson
Wolfson
RVER-rente
CELI-rente
![]() Moins que secondaire
Moins que secondaire
![]() Secondaire
Secondaire
![]() Université
Université
La proposition Mintz-Wilson diffère de la rente longévité et du scénario RVER-rente quant au taux de rendement qu’il offre, qui est comparable à celui du scénario RVER-rente pour les revenus moyens-élevés, mais également en raison de l’exemption de cotisation au RRQ pour des revenus allant jusqu’à 3 500 $. Cette exemption est unique à Mintz-Wilson, puisque Wolfson ne hausse les cotisations qu’à partir de 0,5*MGA, tandis que les trois autres scénarios ne prévoient aucune exemption de cotisation. Cette exemption explique la différence de profil de rendement aux niveaux de revenu plus faibles.
Enfin, la proposition de Wolfson semble offrir des rendements très élevés, de l’ordre de 4 % à 6 %, pour les individus gagnant entre 20 000 $ et 65 000 $ environ. Ceux gagnant davantage obtiennent tout de même entre 2 % et 4 %. On note que les individus gagnant 15 000 $ ou moins obtiennent des rendements bien plus faibles, voire négatifs. Bien qu’ils ne devraient pas être affectés par la réforme Wolfson, la variation des revenus en cours de carrière fait en sorte qu’ils sont affectés malgré tout (voir la sous-section suivante). Les dernières observations permettent néanmoins de conclure que la proposition Wolfson semble le mieux cibler les groupes souvent définis comme étant les plus à risque en termes de revenu à la retraite, soit les individus au milieu de la distribution des revenus de travail — avec un possible effet indésirable au bas de la distribution. Le scénario CELI-rente, qui serait sans doute difficile à mettre en oeuvre de façon volontaire, offre toutefois le rendement le plus neutre du point de vue des revenus de travail et de la fiscalité existante, et maintient un écart constant entre les groupes d’éducation.
3.3 Décomposition des taux de rendement interne
Il est instructif d’examiner l’effet sur les taux de rendement interne de la présence i) du SRG, et ii) de taux de mortalité différenciés par niveau d’éducation. En simulant des situations contrefactuelles, il est possible d’identifier le rôle que jouent la présence du SRG (de par sa structure, notamment son taux de récupération de 50 %) et les différentiels de mortalité entre individus de niveau d’éducation différent. Le graphique 4 montre tout d’abord l’effet sur les taux de rendement interne de supprimer le SRG dans chacun des 5 différents scénarios. Le graphique présente l’effet de la suppression du SRG ceteris paribus en points de pourcentages supplémentaires de rendement qu’offre chacun des scénarios dans ce monde hypothétique. Nous montrons uniquement ici le cas des individus sans diplôme secondaire, qui sont ceux ayant le risque de mortalité le plus élevé — et donc, en conséquence, ceux qui obtiennent le rendement le plus faible dans tous les scénarios de réforme.
Graphique 4
Augmentation du taux de rendement implicite dans un monde sans SRG
Effets pour les individus sans diplôme secondaire
Sans surprise, le scénario CELI-rente ne subit aucune modification, puisque les retraits d’un CELI n’entraînent aucune conséquence fiscale et aucune réduction des prestations de SRG. Au contraire, le scénario RVER-rente, tout comme la proposition Mintz-Wilson d’ailleurs, obtient une hausse de rendement appréciable pour les individus à faible revenu lorsque l’on supprime le SRG : près de 3 points de pourcentage pour ceux ayant gagné en moyenne 5 000 $, et plus de 2 points pour des revenus annuels moyens en carrière allant jusqu’à 15 000 $. C’est donc dire que ces scénarios de réforme sont particulièrement défavorisés pour ces individus dans la réalité, étant donné l’existence et la structure du SRG. Dans tous les scénarios de réforme, les impacts de la présence du SRG diminuent à mesure que le revenu moyen en carrière augmente jusqu’à disparaître complètement à 40 000 $ (raison pour laquelle, d’ailleurs, le graphique 4 s’arrête à ce niveau de revenu).
Dans le cas de la rente longévité, la présence du SRG a aussi pour effet de diminuer le taux de rendement chez les moins fortunés mais de façon un peu moins importante. La différence avec les autres scénarios tient surtout au fait que la rente longévité n’est versée qu’à partir de 75 ans, ce qui vient en quelque sorte réduire le désavantage dont souffrent les individus à faible revenu. Malgré cette différence, la rente longévité connaît un rendement rehaussé de 2 points de pourcentage en l’absence de SRG pour les individus gagnant 5 000 $, et toujours de 1,5 point de pourcentage environ à un revenu moyen de 15 000 $.
Avec la proposition Wolfson, le SRG devrait avoir peu d’impact puisque les faibles revenus sont exclus de la réforme. Or on observe un certain effet, généralement plus faible que pour les autres scénarios de réforme. Cet effet est principalement dû à la variation des revenus en cours de carrière : notre processus de génération des revenus de travail inclut plusieurs chocs au fil des ans, ce qui fait en sorte que même un individu gagnant un très faible revenu moyen en carrière est susceptible de connaître quelques années lors desquelles son revenu sera suffisamment élevé pour qu’il soit touché par la hausse des taux de cotisation — avec seulement une contrepartie partielle en termes de prestations une fois à la retraite, son revenu moyen en carrière ne le rendant pas admissible à des prestations supplémentaires. Cet aspect illustre la grande importance de prendre en compte la trajectoire complète des revenus de travail sur l’ensemble d’une carrière, particulièrement lorsque des réformes à la Wolfson sont envisagées, c’est-à-dire avec des taux de cotisation et des prestations différenciés selon le revenu.
Une autre source potentielle de variation du rendement des différents scénarios de réforme est la mortalité — ou l’espérance de vie — différenciée par niveau d’éducation. Or le graphique 5 indique que ce facteur a un impact plus limité sur le rendement des différentes propositions, qui s’établit à environ 0,4 point de pourcentage pour les individus sans diplôme secondaire. Dit autrement, dans un monde où ces individus auraient un risque de mortalité identique à la moyenne, le rendement supplémentaire qu’ils obtiendraient dans chaque scénario de réforme serait supérieur de 0,4 point de pourcentage. Cet effet est loin d’être insignifiant, mais on voit qu’il est beaucoup plus petit que l’effet du SRG pour les individus à plus faible revenu. Ce sont les individus gagnant plus de 30 000 $ par an qui sont davantage désavantagés par la mortalité différenciée que par la présence du SRG, ce qui est attendu puisque ce dernier s’adresse aux individus à plus faible revenu.
3.4 Simulation des rendements internes en l’absence de revenus de retraite privés
Une critique possible de notre analyse tient au mode d’imputation des revenus de retraite privés avant toute réforme. Nous explorons donc l’effet sur les taux de rendement des différents scénarios de réforme de supprimer complètement ces revenus de retraite privés, autres que ceux générés par les propositions de réforme elles-mêmes, bien entendu. Le graphique 6 montre ces taux de rendement en l’absence de revenus de retraite privés (REER ou régimes complémentaires de retraite).
On voit que toutes les réformes, sauf à nouveau le CELI-rente, offrent un rendement plus faible en l’absence de revenus privés de retraite. Dans le cas de la rente longévité, ce constat s’applique surtout aux individus gagnant moins de 75 000 $. Mintz-Wilson offre un rendement très faible, voire négatif, à partir du milieu de la distribution des revenus de travail; la proposition de Wolfson voit toutes ses courbes de rendement déplacées vers le bas de façon marquée pour les individus gagnant moins de 65 000 $; et le scénario RVER-rente offre désormais des rendements inférieurs pour les individus gagnant moins de 85 000 $. Pour comprendre ces différences, il faut faire appel à l’interaction des différentes propositions avec le SRG.
Graphique 5
Augmentation du taux de rendement implicite dans un monde sans différences d’espérance de vie
Effets pour les individus sans diplôme secondaire
En effet, dans un monde sans revenus de retraite privés, tous les individus dans notre simulation sont admissibles au SRG avant réforme puisque des revenus de retraite provenant uniquement de la PSV et du RRQ donnent droit à de petites prestations de SRG. Avec l’introduction d’une réforme, plusieurs perdent l’accès aux prestations du SRG, ce qui se traduit par une baisse marquée du rendement qu’ils obtiennent de chaque réforme, surtout pour les individus à revenu de travail moyen-élevé (qui, eux, ne reçoivent pas de SRG dans la réalité, avec revenus de retraite privés). Les différences de baisse de rendement reflètent les différences de structure des cotisations-prestations des différents scénarios de réforme.
Graphique 6
Taux de rendement implicites en l’absence de revenus de retraite privés (%)
Rente longévité
Mintz-Wilson
Wolfson
RVER-rente
CELI-rente
![]() Moins que secondaire
Moins que secondaire
![]() Secondaire
Secondaire
![]() Université
Université
Conclusion
Nos résultats suggèrent que les trois propositions de réformes des programmes publics considérés dans cet article ont des particularités communes. D’abord, toutes haussent les taux de remplacement du revenu par rapport au scénario de référence, surtout à partir d’un revenu annuel moyen de 25 000 $. Le profil de cette hausse diffère toutefois substantiellement entre les différentes réformes, la rente longévité offrant les hausses plus importantes pour un revenu en deçà de 60 000 $ et la proposition de Wolfson étant la plus généreuse au-delà de ce seuil. Les deux options d’épargne privée accrue avec achat de rente viagère, elles, génèrent des hausses contrastées de taux de remplacement : une contribution de 2 % du revenu à un RVER procure une hausse modeste du taux de remplacement, tandis qu’une contribution identique dirigée vers un CELI procure une hausse plus importante pour tous les niveaux de revenu. Toutes les observations faites dans le cas des scénarios avec achat de rente privée sont conditionnelles à ce que de la nouvelle épargne soit effectivement générée et dirigée vers les véhicules concernés, ce qui ne va pas nécessairement de soi dans la réalité.
Ensuite, tous les scénarios sauf le CELI-rente procurent un rendement faible pour les individus ayant des revenus de travail modestes et ce, en raison surtout de la présence du SRG mais aussi de leur risque de mortalité plus grand. Pour les individus ayant des revenus de travail en carrière plus importants, c’est la mortalité différenciée qui joue un plus grand rôle, puisqu’ils ne sont pas admissibles aux prestations du SRG. Cet ordonnancement vaut pour tous les scénarios de réforme à partir d’un seuil de 35 000 $ de revenus de travail environ.
On note par ailleurs que le profil de rendement en fonction du revenu varie considérablement d’un scénario à l’autre, tout comme le niveau du rendement. Si la rente longévité offre un rendement assez faible pour tous, le CELI-rente offre un rendement moyen pour tous, de l’ordre de 2 % à 3 %. On peut donc penser que la rente longévité serait moins attrayante que certaines alternatives privées, ce qui n’est pas nécessairement le cas des propositions de Mintz-Wilson et de Wolfson. Mintz-Wilson offre des rendements moyens pour tous, à un niveau semblable au CELI-rente, tandis que Wolfson offre des rendements élevés aux individus gagnant plus de 20 000 $ par an, mais avec des effets négatifs au bas de la distribution. Le scénario RVER-rente génère également des rendements négatifs au bas de la distribution des revenus de travail en raison, comme pour tous les scénarios, de l’interaction avec le SRG. Ainsi, la rente longévité et le RVER-rente semblent être supplantés par d’autres scénarios analysés, Wolfson offrant le meilleur rendement à un groupe ciblé de classe moyenne et le CELI-rente offrant un rendement neutre par rapport au revenu et à la fiscalité (c’est-à-dire ne dépendant pas des différences entre les taux d’imposition marginaux durant la vie active et à la retraite).
Enfin, il convient de souligner que notre modélisation, par construction, ne permet de tenir compte d’aucun effet de comportement. Bien que de tels effets seraient peu susceptibles de varier entre les différents scénarios, ils pourraient s’avérer non négligeables. Par exemple, les travailleurs bénéficiant d’une prestation accrue du RRQ, ou même d’une rente longévité à compter de 75 ans, pourraient très bien décider de prendre leur retraite plus tôt. Or, une retraite hâtive se traduirait par des cotisations ou de l’épargne totales plus faibles que dans nos scénarios, prenant possiblement la forme de pénalités actuarielles. Ces changements pourraient par la suite venir modifier les taux de remplacement et les taux de rendement obtenus pour les différents scénarios. De tels effets ne modifieraient cependant les résultats de notre analyse que s’ils diffèrent selon le niveau de revenu ou d’éducation des individus, ce qui reste possible étant donné notamment la présence de programmes conditionnels au revenu comme le SRG.
Nous avons calculé dans cet article les taux de remplacement du revenu et les taux de rendement interne associés à différents scénarios de réforme, soit trois modifiant les programmes publics du 2e pilier et deux scénarios de comparaison faisant appel à des véhicules d’épargne privée existants. Nous avons illustré l’effet qu’ont sur le rendement de ces réformes potentielles i) les variations de revenu de travail; ii) la présence et la structure du SRG; et iii) la présence de différentiels de mortalité par niveau d’éducation. Nos conclusions n’ont cependant trait qu’au rendement financier des différents scénarios analysés. Un autre aspect qui mériterait d’être inclus dans une analyse future concerne la valeur d’assurance des différentes propositions et, par extension, la valeur de celles-ci en termes d’utilité pour les individus touchés. Ces considérations seront intégrées à nos travaux futurs.
Parties annexes
Annexes
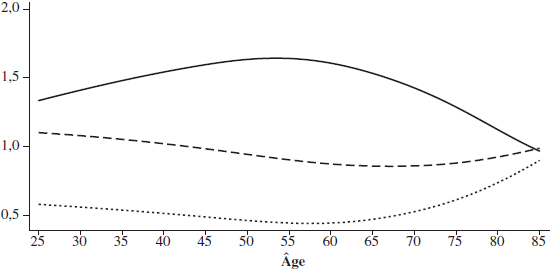
Annexe A. Revenus de travail avant la retraite
Nous utilisons les cycles 2 à 5 de l’EDTR, qui offrent un échantillon de répondants i=1…N, chacun observé au maximum 6 fois entre 1996 et 2010. Nous sélectionnons les hommes québécois qui ne sont pas travailleurs autonomes et qui sont âgés de 25 à 100 ans; nous n’utilisons pas les femmes simplement pour avoir un historique de travail le plus complet possible. On élimine les observations avec des revenus de travail de plus de 250 000 $ et on utilise l’indice des prix à la consommation de Statistique Canada pour convertir les valeurs monétaires en dollars de 2011.
Puisque nous estimons les processus de revenu de travail par niveau d’éducation, nous omettons cette dimension. En prenant le log du processus du salaire et en dénotant les variables en log par des lettres minuscules, on obtient pour l’individu i à la période t :
En dénotant ![]() et en supposant pour l’instant
et en supposant pour l’instant ![]() , on peut estimer les gj en déviation par rapport à la moyenne. On retrouve également l’effet fixe de chaque répondant, qui correspond à yi,25.
, on peut estimer les gj en déviation par rapport à la moyenne. On retrouve également l’effet fixe de chaque répondant, qui correspond à yi,25.
Le graphique 7 montre les profils d’âge-éducation Ge,t. Ceux-ci sont lissés à l’aide d’un estimateur non-paramétrique lowess à partir des valeurs estimées de gj.
Graphique 7
Facteurs de croissance du salaire
On estime les paramètres (![]() ) par distance minimale en utilisant le fait que
) par distance minimale en utilisant le fait que ![]() , s > 0 et
, s > 0 et ![]() .
.
Dénotons les paramètres à estimer θ et la vraie valeur des paramètres θ0. Dénotons par ![]() (θ0) la matrice variance-covariance des données et par
(θ0) la matrice variance-covariance des données et par ![]() (θ0) la matrice variance-covariance théorique basée sur les hypothèses ci-dessus. L’estimateur est donné par
(θ0) la matrice variance-covariance théorique basée sur les hypothèses ci-dessus. L’estimateur est donné par
On utilise MN = I comme matrice de pondération. Le tableau 2 présente les résultats pour chaque niveau d’éducation.
Tableau 2
Paramètres estimés des processus de revenu de travail
Annexe B. Mortalité
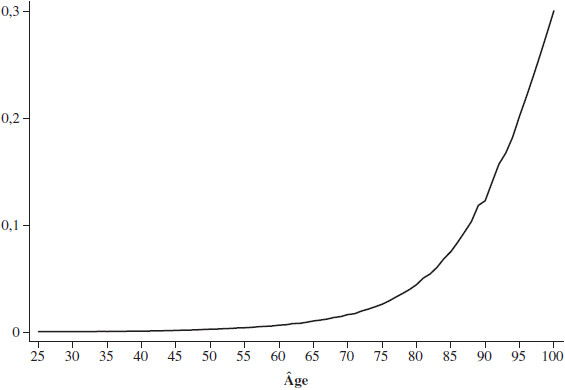
Le graphique 8 donne les taux de mortalité périodiques de 2009 rapportés par l’ISQ. On dénote ce taux à la période t par ![]() .
.
On utilise les cycles (biennaux) de 1994 à 2010 de l’ENSP pour estimer le processus de mortalité spécifique par niveau d’éducation, pour les deux sexes combinés puisque nos cas-types simulés sont en quelque sorte asexués. Nous considérons seulement le volet ménages de l’enquête. Nous estimons d’abord ![]() pour j = 0 et j = 1 à l’aide d’un logit multinomial et en incluant un effet linéaire d’âge pouvant s’ajuster à 50 ans (spline). On peut ensuite corriger les taux de l’ISQ pour les rendre spécifiques au niveau d’éducation par la formule suivante :
pour j = 0 et j = 1 à l’aide d’un logit multinomial et en incluant un effet linéaire d’âge pouvant s’ajuster à 50 ans (spline). On peut ensuite corriger les taux de l’ISQ pour les rendre spécifiques au niveau d’éducation par la formule suivante :
Graphique 8
Taux de mortalité par âge (ISQ)
Le graphique 9 présente les facteurs de correction ![]() estimés.
estimés.
Le taux de survie à l’âge t étant donné la survie à 25 ans est donné par
Le graphique 10 donne les courbes de survie par niveau d’éducation alors que le graphique 11 montre les courbes d’espérance de vie restante étant donné la survie à l’âge t.
Graphique 9
Facteurs de correction des taux de mortalité
Graphique 10
Probabilité de survie jusqu’à l’âge t
Graphique 11
Espérance de vie restante à l’âge t
Annexe C. Estimation des revenus de marché une fois à la retraite
Nous sélectionnons dans les cycles 2 à 5 de l’EDTR les individus ayant cessé de travailler une seule fois, sans recommencer, entre 50 et 70 ans. En raison du faible nombre d’observations disponible, nous utilisons cette fois les observations portant sur des hommes et celles portant sur des femmes et ce, pour l’ensemble du Canada. Procéder autrement ne permet pas, avec les données de l’EDTR, d’avoir un nombre d’observations suffisant pour nos simulations.
Nous estimons pour chaque individu i son revenu de travail avant retraite par la moyenne de ses revenus de travail juste avant qu’il ne cesse de travailler. Notons que l’EDTR est conçue pour interviewer au maximum 6 fois un même individu. Le nombre de périodes utilisées pour calculer le revenu avant retraite varie donc entre 1 et 5 selon l’individu. Pour faire le lien avec notre modèle où l’âge de la retraite est forcément de 65 ans, nous dénotons ce revenu de travail avant retraite par Yi,64. On supprime les observations pour lesquelles Yi,64 < 10 000 $, afin d’éliminer autant que possible du calcul les travailleurs à temps partiel, et celles pour lesquelles Yi,64 > 250 000 $.
Nous calculons ensuite, toujours avec l’EDTR, les revenus de marché à la retraite. Une fois que l’individu a cessé de travailler, nous additionnons ses revenus provenant de régimes complémentaires ou de placements et prenons la moyenne sur les périodes observées après la prise de retraite (périodes dont le nombre varie entre 1 et 5 selon l’individu). On dénote ce revenu par BPP,i. On élimine les observations pour lesquelles BPP,i > 100 000 $. On estime finalement par moindres carrés ordinaires les effets de salaire et d’éducation sur le taux de remplacement privé, ![]() , par le modèle suivant :
, par le modèle suivant :
Le tableau 3 montre les paramètres estimés de ce modèle. Tous les paramètres sont positifs et statistiquement significatifs. Ces coefficients sont ensuite utilisés pour calculer les revenus de marché à la retraite en fonction du niveau d’éducation et du revenu de travail à 64 ans (soit « avant retraite »).
Tableau 3
Estimation par MCO du taux de remplacement privé
Note : * significatif à un seuil de 10 % ** significatif à un seuil de 5 % *** significatif à un seuil de 1 %
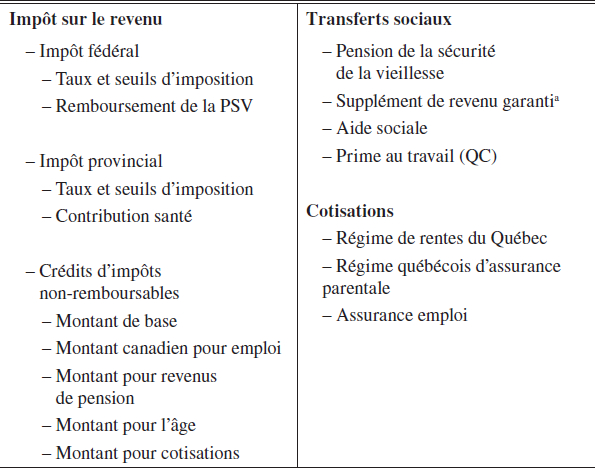
Annexe D. Taxation et transferts sociaux
Les revenus disponibles Ht présentés et utilisés dans l’article sont calculés en tenant compte de la complexité des systèmes d’imposition fédéral et provincial ainsi que des principaux transferts sociaux dont les individus peuvent bénéficier en fonction de leur revenu. Nous utilisons le calculateur SimTax, développé par des membres de l’équipe et d’autres chercheurs de l’Université Laval. Notons que la version disponible au moment de rédiger le présent article permet seulement d’utiliser les paramètres qui étaient en vigueur pour l’année fiscale 2011.
SimTax prend comme intrants les revenus de marché (revenus de travail, intérêts, pensions privées) et du RRQ ainsi que diverses caractéristiques individuelles pouvant affecter les crédits ou transferts (âge, situation conjugale, etc.). Le tableau 4 présente les éléments du système d’imposition et de transferts sociaux pertinents pour le Québec qui sont pris en compte dans SimTax. Pour le présent article, SimTax est également ajusté pour tenir compte des modifications qui sont requises pour simuler les réformes étudiées.
Tableau 4
Liste des éléments pris en compte dans SimTax
Remerciements
Nous remercions pour leurs commentaires et suggestions les participants au congrès 2014 de la Société canadienne de science économique et à la Grande conférence CIRPÉE 2014, ainsi qu’Oscar Becerra, Richard Guay et un évaluateur anonyme. Cet article s’en est trouvé fortement bonifié.
Notes
-
[1]
La question de savoir si une portion de la cotisation employeur est supportée par les employés sous la forme de salaires plus faibles n’est pas pertinente ici, contrairement aux scénarios alternatifs envisagés plus bas, puisqu’il s’agit d’un élément commun du scénario de référence auquel s’ajoutent les autres. Nous ne considérons donc que les cotisations payées par l’employé.
-
[2]
Pour une prestation de 25 %, ce coût est de 5,2 % selon Wolfson (2013) ce qui donne ici (15 %/ 25 %)*5,2 %= 3,1 % puisque la prestation supplémentaire est de 15 % — voir ci-après.
-
[3]
Malgré un taux de remplacement uniforme de 40 % à partir de la moitié du MGA préréforme, le taux de cotisation entre 50 % et 100 % du MGA préréforme est de 4,7 points de pourcentage plus élevé. Cette différence sert à financer les autres types de prestations du RRQ, mais aussi et surtout à compenser le sous-financement passé du Régime, entraîné par des taux de cotisation historiquement trop faibles.
-
[4]
Tel qu’expliqué à la section 2 et à l’annexe C, l’épargne volontaire déjà effectuée dans les différents régimes enregistrés est prise en compte dans le scénario de référence. Il s’agit, dans le cadre des scénarios alternatifs 4 et 5, de modéliser une épargne additionnelle dans les véhicules considérés, afin de comparer les résultats avec ceux obtenus à l’aide des scénarios de réforme du 2e pilier.
-
[5]
Nous postulons que ce rendement est net de frais de gestion et d’administration, ce qui peut paraître optimiste dans le cas d’un RVER mais qui peut se justifier si une obligation simple est achetée. Certains comptes d’épargne offerts dans le cadre des RVER comportent des frais aussi faibles que 0,25 % de l’actif, incluant les taxes de vente.
-
[6]
Voir www.cannex.com.
-
[7]
Il s’agit ici d’une approximation, puisque dans la réalité une petite proportion des paiements de rentes prescrites est considérée comme du rendement sur le capital investi dans l’achat de la rente. Jusqu’au 31 décembre 2016, la formule en vigueur prévoit ainsi que pour une femme de 65 ans, la proportion du revenu annuel considérée imposable est de 6,8 % environ, tandis qu’elle est de 0 % pour un homme du même âge. À compter de 2017, ces proportions seront révisées à la hausse afin de refléter les espérances de vie accrues.
-
[8]
Dans la réalité, les prestations des programmes publics — PSV, SRG et RRQ — sont indexées à l’inflation. Nous omettons cet aspect de notre modélisation; il ne ferait que compliquer l’analyse en obligeant à considérer des rentes privées indexées dans les scénarios alternatifs 4 et 5, et aurait peu de valeur ajoutée dans la mesure où cette caractéristique serait identique dans tous les scénarios.
-
[9]
Nous présentons les taux à 75 ans car le revenu à la retraite étant supposé constant, avant cet âge, les résultats pour tous les scénarios seraient identiques à ce qui est présenté ici, sauf pour la rente longévité, dont la courbe se confondrait presque avec celle du scénario de référence. En effet, aucune prestation n’est versée avant l’âge de 75 ans dans le scénario de rente longévité, tandis que les cotisations affectent très légèrement le revenu disponible avant la retraite et, par ricochet, les taux de remplacement obtenus entre 65 et 74 ans. Les taux calculés et montrés ici correspondent, rappelons-le, à des taux de remplacement totaux, c’est-à-dire utilisant les revenus de toutes sources à la retraite, et non seulement ceux provenant des programmes publics ou du 2e pilier.
Bibliographie
- Adam, L. (2012), « The Canadian Pensioners’ Mortality Table », Rapport technique, Institut canadien des actuaires.
- D’Amours, A., R. Beaudry, L. Godbout, C. Lamoureux, M. N. Marchon, B. Morency et M. Rochette (2013), « Innover pour pérenniser le système de retraite : Un contrat social pour renforcer la sécurité financière de tous les travailleurs québécois », Rapport technique, Comité d’experts sur l’avenir du système de retraite québécois.
- French, E. (2005), « The Effects of health, wealth, and wages on labour supply and retirement behaviour », The Review of Economic Studies, 72(2) : 395–427.
- Gourinchas, P. O. et J. Parker (2002), « Consumption over the Life Cycle », Econometrica, 59 : 779–813.
- Institut de la Statistique du Québec (2014), Le bilan démographique du Québec, Gouvernement du Québec.
- Judd, K. L. (1998), Numerical Methods in Economics, MIT press.
- Milevsky, M. A. (2013), « Life Annuities : An Optimal Product for Retirement Income », Rapport technique, Research foundation of CFA institute.
- Milligan, K. et T. Schirle (2014), « Simulated replacement rates for CPP reform options », SPP Research Papers 7-7, Social Science Research Network.
- Mintz, J. et Wilson, T. (2013), « Reform proposals for replenishing retirement savings », SPP Research Papers 6-9, University of Calgary School of Public Policy.
- Roy-Cesar, E. et Vaillancourt, F. (2010), « The incidence of payroll taxes in Ontario and Quebec; evidence from collective agreements for 1985-2007 », Cahier scientifique 2010s-36, CIRANO.
- Wolfson, M. (2013), « Not-so-modest options for expanding the CPP/QPP », Étude IRPP 41, IRPP.
- Yaari, M. E. (1965), « Uncertain Lifetime, Life Insurance, and the Theory of the Consumer », The Review of Economic Studies, 32(2) : 137–150.
Liste des figures
Graphique 1
Taux de cotisation et de remplacement en proportion du revenu, proposition de Wolfson (2013)
Taux de cotisation
Taux de remplacement
Graphique 2
Taux de remplacement du revenu à 75 ans
Rente longévité
Mintz-Wilson
Wolfson
RVER-rente
CELI-rente
![]() Moins que secondaire
Moins que secondaire
![]() Secondaire
Secondaire
![]() Université
Université
Graphique 4
Augmentation du taux de rendement implicite dans un monde sans SRG
Effets pour les individus sans diplôme secondaire
Graphique 5
Augmentation du taux de rendement implicite dans un monde sans différences d’espérance de vie
Effets pour les individus sans diplôme secondaire
Rente longévité
Mintz-Wilson
Wolfson
RVER-rente
CELI-rente
![]() Moins que secondaire
Moins que secondaire
![]() Secondaire
Secondaire
![]() Université
Université
Graphique 7
Facteurs de croissance du salaire
Graphique 8
Taux de mortalité par âge (ISQ)
Graphique 9
Facteurs de correction des taux de mortalité
Graphique 10
Probabilité de survie jusqu’à l’âge t
Graphique 11
Espérance de vie restante à l’âge t
Liste des tableaux
Tableau 1
Tableau synthèse des réformes
Tableau 2
Paramètres estimés des processus de revenu de travail
Tableau 3
Estimation par MCO du taux de remplacement privé
Tableau 4
Liste des éléments pris en compte dans SimTax




 Référence
Référence  Wolfson
Wolfson
 Référence
Référence  Wolfson
Wolfson
 Référence
Référence  Rente longévité
Rente longévité  Wolfson
Wolfson  Mintz-Wilson
Mintz-Wilson  RVER-Rente
RVER-Rente  CELI-Rente
CELI-Rente





 Rente longévité
Rente longévité  Mintz-Wilson
Mintz-Wilson  Wolfson
Wolfson  RVER-Rente
RVER-Rente  CELI-Rente
CELI-Rente
 Rente longévité
Rente longévité  Mintz-Wilson
Mintz-Wilson  Wolfson
Wolfson  RVER-Rente
RVER-Rente  CELI-Rente
CELI-Rente





 Moins que secondaire
Moins que secondaire  Secondaire
Secondaire  Université
Université
 Moins que secondaire
Moins que secondaire  Secondaire
Secondaire  Université
Université
 Moins que secondaire
Moins que secondaire  Secondaire
Secondaire  Université
Université
 Moins que secondaire
Moins que secondaire  Secondaire
Secondaire  Université
Université