Résumés
Résumé
Dans cet article, nous étudions l’impact des différences de longévité sur la conception des politiques publiques, en particulier celles liées au départ à la retraite. Nous montrons premièrement qu’alors même que l’espérance de vie a augmenté de manière très importante tout au long du siècle dernier, il subsiste encore de fortes disparités. Deuxièmement, nous étudions d’un point de vue normatif comment les différences de longévité sont généralement prises en compte dans les modèles de cycle de vie et montrons que certaines hypothèses peuvent avoir des implications fortes en terme de redistribution intragénérationnelle. Nous identifions au moins trois arguments en faveur d’une redistribution vers les agents à faible longévité : l’aversion à l’inégalité multipériodes, l’aversion au risque de mortalité et la compensation pour des caractéristiques dont les agents ne sont pas responsables. Nous étendons ensuite notre analyse de manière à tenir compte du fait que les individus puissent être en partie responsables de leur longévité.
Finalement, nous lions ces résultats aux débats actuels sur la réforme des systèmes de retraite. Nous montrons qu’en général, parce que les pensions de retraite sont conditionnelles à la survie des bénéficiaires, les systèmes de retraite publics vont redistribuer des ressources des agents dont la durée de vie est courte vers ceux dont la durée de vie est longue. Nous fournissons des pistes de réformes qui viseraient à mieux prendre en compte ces différences de longévité et en particulier, celles relatives à la création d’une « rente longévité » telle que souhaitée par le Comité d’Amours et au développement de l’assurance autonomie, qu’elle soit privée ou publique.
Corps de l’article
Introduction
À l’exception des périodes de conflits mondiaux, l’espérance de vie n’a cessé d’augmenter au cours du siècle dernier. Selon l’OCDE (2011), l’espérance de vie à 65 ans a progressé de 3,9 ans pour les hommes et de 5,4 ans pour les femmes entre 1960 et 2010. Au Québec, en 2012, l’espérance de vie à 65 ans pour les femmes était de 22 ans et de 19 ans pour les hommes alors qu’en 1921, elle n’était que de 13,5 ans pour les femmes et de 13 ans pour les hommes[1]. Les progrès de la médecine, de meilleures conditions de vie et de travail ont permis des gains de durée de vie sans précédent. Des politiques économiques et sociales, telles que les systèmes de retraite, ont été mises en place et même déjà réformées de manière à s’adapter à ces nouvelles réalités démographiques.
Ces gains en longévité ne doivent cependant pas faire oublier que des inégalités d’espérance de vie persistent entre des individus appartenant à une même génération. Comme nous l’avons mentionné ci-dessus, au Québec, l’écart d’espérance de vie à 65 ans entre hommes et femmes était de 3 ans en 2012. En France, en 2010, l’espérance de vie à 60 ans d’une femme était de 27,1 années contre 22,4 années pour les hommes, soit un écart de presque 5 ans (données INSEE).
Les différences de mortalité sont aussi notables en fonction de la situation matrimoniale des individus. En France, les personnes entre 40 et 60 ans vivant seules de manière continue ont un risque jusqu’à deux fois plus important de décéder que les personnes vivants en couple et ce à caractéristiques socioéconomiques comparables (chiffres INSEE). De la même manière, le risque de décès est plus élevé pour les personnes séparées et cet effet est plus important dans les catégories sociales les moins favorisées[2].
Le niveau d’éducation et la catégorie socioprofessionnelle, reflétant le niveau de revenu jouent aussi un rôle important dans les différences d’espérance de vie. En France, en 2000-2008, l’espérance de vie à 35 ans d’une femme cadre était de 52 ans alors que celle d’une ouvrière était de 49 ans. De la même manière, l’espérance de vie d’un homme cadre était de 47 ans alors que celle d’un ouvrier était de 41 ans. À noter que ces écarts d’espérance de vie sont stables depuis les années soixante-dix. Ces différences entre catégories socioprofessionnelles peuvent s’expliquer d’une part par des différences d’éducation et de revenus, ayant pour conséquences des modes de vie différents, découlant d’une plus grande méconnaissance des facteurs influençant l’espérance de vie mais aussi d’une moins grande capacité à investir dans des dépenses de santé. D’autre part, elles proviennent du type même de professions exercées, les ouvriers étant généralement plus à risque que les cadres. Nous reviendrons sur ces différents aspects par la suite.
Finalement, les différences d’espérance de vie peuvent aussi être associées au lieu de résidence. Au Québec, on vit plus longtemps dans la région de Laval où l’espérance de vie est de 80,4 ans pour les hommes et moins longtemps dans la région Nord du Québec où l’espérance de vie des hommes n’est plus que de 72,4 ans. Ces différences se retrouvent dans d’autres pays. En France, on vit le plus longtemps en Île de France et le moins longtemps dans la région Nord-Pas de Calais (INSEE-2001-2002), même si ces écarts ont diminué depuis les années quatre-vingt-dix[3].
Ces différentes statistiques montrent bien qu’il existe de fortes inégalités sociales face à la mort, selon le genre, la situation matrimoniale, la catégorie socioprofessionnelle, le niveau d’éducation, etc. au sein d’un même pays[4]. Delavande et Rohwedder (2011) montrent que ces inégalités d’espérance de vie entre différents groupes socioéconomiques sont aussi plus ou moins importantes selon les pays considérés. Non seulement les probabilités de survie subjectives (dont ces auteurs montrent qu’elles sont de bons prédicteurs des probabilités de survie objectives au niveau de la population) augmentent avec la richesse des individus mais surtout le gradient dépend du pays considéré. Ces auteurs montrent que le lien entre survie et richesse est plus faible en Belgique, en France et en Espagne qu’aux États Unis, en Suède et en Angleterre. Ceci peut s’expliquer par les différences institutionnelles, politiques et sociales entre les différents pays.
Dans certains groupes de population, ces inégalités ont même parfois augmenté avec le temps. Comme l’indique le graphique 1 pour le Canada, l’écart d’espérances de vie entre hommes et femmes a varié au cours du siècle dernier et a même eu tendance à augmenter[5]. Au Québec, les écarts d’espérance de vie entre hommes et femmes ont augmenté au cours du siècle, passant de 6 mois à 3 ans[6].
Graphique 1
Espérance de vie à la naissance au Canada (Human Mortality Database, 2014)
Dans une étude récente sur les États-Unis, Cristia (2009) montre aussi que les différences de longévité par revenus ont augmenté sur la période 1983-2003. En effet, alors qu’entre 1983 et 1997, les hommes entre 35 et 49 ans appartenant au quintile le plus faible de revenus avaient un taux de mortalité 5,9 fois (1,8 pour les femmes) plus élevé que ceux appartenant au quintile le plus élevé, cet écart est passé à 8,3 (4,8 pour les femmes) sur la période 1998-2003. Cet accroissement des inégalités a été causé en particulier par le fait que l’espérance de vie dans le quintile le plus faible n’a pas changé alors que celle des autres quintiles a augmenté. Pour les femmes, l’espérance de vie a même diminué pour les deux quintiles de revenus les plus faibles.
L’objectif de cet article consiste à se concentrer sur les différences de longévité intragénérationnelles et à étudier leurs conséquences sur le bien-être individuel et collectif. Nous étudierons aussi leurs conséquences sur la taille de la redistribution opérée par les programmes publics ainsi que les avenues de réformes à mettre en place de manière à mieux prendre en compte ces disparités. Notre approche est théorique et essentiellement normative.
Dans cette perspective, nous distinguerons deux catégories de facteurs pouvant influencer les différences de longévité entre individus d’une même cohorte. En s’appuyant sur les travaux de Fleurbaey (2008), nous étudierons d’une part, ceux qui relèvent de la responsabilité individuelle et d’autre part, ceux qui ne relèvent pas de la responsabilité mais qui découlent de circonstances externes aux individus (comme, par exemple, des opportunités que les individus ont eues à la naissance). Cette distinction conditionnera dans une large mesure le type de politiques publiques mises en place pour tenir compte des différences de longévité. En effet, Fleurbaey (2008) utilise cette distinction pour esquisser les contours optimaux des politiques publiques de redistribution : les inégalités dues exclusivement aux circonstances devraient, selon lui, être annulées par les politiques de redistribution (au nom du principe de compensation), tandis que les inégalités dues exclusivement aux variables de responsabilité devraient être laissées telles quelles (au nom du principe de responsabilité). On notera par ailleurs que la frontière entre responsabilité ou non-responsabilité est parfois difficile à établir[7].
Ainsi, de nombreuses études ont montré que les agents peuvent influencer leur espérance de vie. Kaplan et al. (1987) montrent qu’un risque de mortalité des 60-94 ans plus important est associé au fait de fumer, d’avoir peu d’activité physique, d’être en surpoids et de ne pas prendre de manière régulière de petit déjeuner. Dans un article plus récent, Balia and Jones (2008) montrent que le mode de vie (consommation d’alcool, de cigarettes, petit déjeuner régulier, temps de sommeil, surpoids et activité physique) explique environ 1/4 des inégalités de longévité au sein d’une cohorte, et influence donc de manière non négligeable ces inégalités. En particulier, fumer et dormir de manière régulière ont un impact important. On peut considérer que ces facteurs relèvent de la responsabilité individuelle.
Au contraire, d’autres facteurs peuvent être considérés comme ne relevant pas de la responsabilité individuelle ou comme étant prédéterminés. Christensen (1999) a montré, en comparant des jumeaux monozygotes et dizigotes que les facteurs génétiques expliquent 1/4 des différences de santé reportée par un panel de personnes agées de 75 ans et plus. Skytthe et al. (2003) et Christensen et al. (2006) ont recensé les travaux sur les déterminants génétiques de la longévité et indiquent que la plupart des études épidémiologiques se basant sur l’étude de jumeaux s’accordent sur le fait qu’environ 25 % des variations d’espérance de vie sont liées à des différences génétiques (voir entre autres, Herskind et al., 1996)[8].
Par ailleurs, comme nous l’avons illustré ci-dessus, le genre et l’appartenance ethnique sont également corrélés avec la longévité. Les femmes ont des taux de mortalité plus faibles que ceux des hommes, en partie pour des raisons biologiques (bien sûr, ce biais peut varier en fonction de leurs conditions de vie). De la même façon, même si on contrôle pour les différences de revenus, les noirs américains ont des taux de survie plus faibles que ceux des blancs[9]. Finalement, si l’on considère que le célibat prolongé est un état subi plutôt que réellement souhaité, les individus ne peuvent être tenus pour responsables des différences de longévité liées à leur situation matrimoniale.
L’endogénéité ou non de la longévité aura alors un impact sur la question de savoir si le gouvernement devrait intervenir pour réduire les écarts de longévité et, si oui, de quelle manière. Finalement, il faut attirer l’attention sur le fait que ces facteurs ne sont pas indépendants les uns des autres et qu’ils peuvent influencer la longévité de manière complémentaire ou substituable, en fonction des types de facteurs considérés. Nous reviendrons sur ces points dans les sections suivantes.
Notons aussi que, dans cet article, nous nous concentrons sur les différences de mortalité et non de morbidité, même si dans les faits, l’aspect « qualité » de la vie est indissociable de l’aspect « quantité » : on souhaite vivre plus longtemps pour autant que la vie vaille la peine d’être vécue[10]. Ici, nous supposerons que c’est toujours le cas et que la longévité, comme d’autres variables économiques telles que le revenu, fait partie intégrante du bien-être individuel.
L’article s’organise de la manière suivante. La section 1 présente notre modélisation de la fonction d’espérance de vie individuelle et les facteurs susceptibles de l’influencer. La section 2 traite des différents problèmes de maximisation du bien-être social et de leurs conséquences en terme de redistribution lorsque la longévité est exogène. La section 3 montre comment ces résultats sont modifiés quand la longévité dépend des comportements individuels. La section 4 présente plusieurs avenues de réformes publiques possibles de manière à mieux tenir compte des différences de longévité intragénérationnelles.
1. Modélisation de la longévité
Dans cette section, nous allons montrer comment modéliser la longévité et les différences de longévité individuelles.
Lorsqu’on parle de la mesure des conditions de survie, l’indicateur le plus répandu est l’espérance de vie. Cet indicateur mesure l’espérance mathématique de la durée d’une vie conditionnellement aux probabilités de décès par âge qui prévalent sur une période donnée. Il est cependant important de noter que cet indicateur constitue une sorte de moyenne. En ce sens, l’indicateur d’espérance de vie ne nous dit pas grand-chose sur les inégalités qui existent en termes de durées de vie réalisées par les différents membres d’une population[11].
Afin de distinguer les variations de l’espérance de vie associées à une amélioration générale des conditions de survie, de celles qui ne sont partagées que par un petit nombre de personnes, nous allons modéliser les conditions de survie de la manière suivante. Considérons une économie à deux périodes et une population constituée de groupes d’individus identiques de type i. Chaque groupe de population est de taille ni. La première période, de longueur unitaire, est vécue par tous les membres de la population. En revanche, la seconde période, de longueur Ti(0 < Ti < 1), n’est vécue que par une fraction πi > 0 du groupe de type i. Dès lors, l’espérance de vie pour chaque groupe i est donnée par : (1− πi )1+ πi (1+ Ti ) = 1+ πiTi. La variable Ti reflète le niveau de la durée de vie maximale au sein du groupe i, tandis que la variable πi capture les inégalités dans la longévité. Notons que le cas où πi = 1 correspond au cas spécial d’une absence de risque quant à la durée de vie : tous les individus appartenant au groupe i ont la même durée de vie, égale à 1+ Ti. C’est le cas lorsque la courbe de survie est un simple rectangle. En revanche, dès que πi < 1, des inégalités existent dans la durée de vie réalisée au sein du groupe i.
Il est clair que des facteurs encourageant la convergence de πi vers 1 contribuent, en réduisant la prévalence d’une mortalité précoce, à réduire les inégalités de durée de vie au sein du groupe i. Au contraire, lorsque πi < 1, une hausse de Ti augmente les inégalités dans la durée de vie, car seule une fraction πi des individus de type i bénéficie de cette amélioration de la survie.
Cette probabilité de survie est une fonction (non exhaustive) de plusieurs éléments : [12]
où ei représente un investissement individuel en santé que l’on pourrait assimiler à un effort non monétaire (psychologique ou physique) mais pénible dans le sens où il entraîne une certaine désutilité pour l’agent. La variable mi représente les dépenses de santé individuelles, telles que le fait de procéder à des examens réguliers, aller chez le médecin, prendre des vitamines[13]. La variable εi représente une caractéristique exogène propre à l’agent i. Notons ici que nous faisons abstraction d’autres variables qui pourraient éventuellement influencer les chances de survie et nous concentrons sur celles qui sont essentielles pour le reste de notre analyse[14]. L’impact de ces variables sur la probabilité de survie est positif de telle sorte que ∂π(ei,mi;εi) / ∂x ≥ 0 avec x = {ei,mi;εi}. Cependant le rendement marginal de chacun de ces facteurs est décroissant : ∂2π(ei,mi;εi) / ∂2x ≤ 0, laissant supposer qu’il existe une limite aux possibilités d’augmenter la probabilité de survie.
Le signe des dérivées croisées est plus ambigu et dépendra des types d’investissement en santé considérés. On parlera de complémentarités dans les inputs lorsque le rendement marginal d’un facteur sur la longévité est d’autant plus élevé que l’autre facteur est important, soit ∂2π(ei,mi;εi ) / ∂x∂y ≥ 0 avec y ≠ x = {ei,mi;εi}. Par exemple, on peut supposer que le rendement (l’efficacité) marginal(e) des dépenses de santé, mi est d’autant plus élevé(e) que l’agent est en bonne forme physique ( ei élevé), ou a de bons gênes ( εi élevé). Par exemple, une opération à coeur ouvert a d’autant plus de chances de réussir que la personne est en bonne condition physique. Au contraire, on parlera de substituabilité entre les inputs, lorsque le rendement marginal d’un facteur sur la longévité est d’autant plus faible que l’autre facteur est important de telle sorte que ∂2π(ei ,mi;εi) / ∂x∂y ≤ 0. Ceci peut être lié au fait qu’il y a une limite aux bénéfices liés à l’investissement en santé. Pour quelqu’un dont la santé est bonne, soit parce qu’il est en bonne condition physique, soit parce qu’il a de bons gênes, le rendement marginal d’une intervention médicale pourrait en théorie être plus faible que pour quelqu’un dont la santé est mauvaise.
La durée maximale de vie (ou de manière équivalente ici, la longueur maximale de la deuxième période) de l’individu i peut aussi être modélisée comme étant une fonction du comportement et des caractéristiques individuels :
où comme précédemment, ei représente des efforts non monétaires, mi des dépenses de santé individuelles et εi représente la caractéristique exogène propre à l’agent[15]. Ces variables peuvent donc augmenter à la fois la probabilité de survie et la durée de vie. Comme pour la probabilité de survie, nous faisons les hypothèses suivantes : ![]() avec
avec ![]() ,
, ![]() et
et ![]() avec
avec ![]() . Cette liste de facteurs, encore une fois, n’est pas exhaustive.
. Cette liste de facteurs, encore une fois, n’est pas exhaustive.
Finalement, d’autres caractéristiques individuelles que les gènes (la variable εi) vont aussi jouer sur l’espérance de vie et ce de manière indirecte. En particulier, le revenu est une source importante de différences d’espérance de vie mais ne jouera pas directement sur le niveau de πi et de Ti. Le revenu influence indirectement la probabilité de survie en influençant le niveau des dépenses de santé, mi. Le goût pour l’effort va aussi influencer les efforts non monétaires (ei) que l’agent pourra faire pour augmenter sa longévité : par exemple, les individus vont avoir des préférences différentes pour le sport, indépendemment du fait que celui-ci soit coûteux en termes monétaires ou non. Nous reviendrons sur ces questions par la suite.
Notons ici que dans le reste de cet article, nous allons essentiellement faire l’hypothèse qu’il n’y a pas d’asymétrie d’information. Nous supposerons donc que les individus et le gouvernement partagent la même information concernant les caractéristiques individuelles (par exemple, de revenus et de longévité). Nous pourrions étendre notre analyse à un contexte où il existe de l’asymétrie d’information, mais cela ne ferait que compliquer notre analyse sans rien modifier à nos conclusions.
2. Modélisation des préférences individuelles et sociales lorsque la longévité est exogène
2.1 Le problème de base
En économie publique, il est généralement supposé que les préférences des agents satisfont l’hypothèse de l’utilité attendue, et que l’utilité associée à une période de vie est égale à la somme des utilités associées aux différentes sous-périodes de cette vie. Comme nous allons le montrer dans cette section, ces deux hypothèses, lorsqu’elles sont jointes à un objectif social de type utilitariste, légitiment des politiques de redistribution peu intuitives, au sens où elles recommandent rien de moins qu’une redistribution des individus à vie courte vers ceux à vie longue.
Pour comprendre ceci, prenons un exemple simple où l’on s’abstrait du risque intragroupe et où l’on suppose que ![]() . Nous supposons deux groupes d’individus i = {1,2} qui ne sont différents qu’en terme de la longueur de la deuxième période qu’ils vont vivre : T1 > T2. Les différences de longévité résultent, par exemple de facteurs génétiques et sont donc ici uniquement la conséquence du hasard. En dehors de ces différences, les individus sont identiques. Les préférences individuelles sont représentées par la fonction d’utilité additive suivante :
. Nous supposons deux groupes d’individus i = {1,2} qui ne sont différents qu’en terme de la longueur de la deuxième période qu’ils vont vivre : T1 > T2. Les différences de longévité résultent, par exemple de facteurs génétiques et sont donc ici uniquement la conséquence du hasard. En dehors de ces différences, les individus sont identiques. Les préférences individuelles sont représentées par la fonction d’utilité additive suivante :
avec u(c), l’utilité de la consommation par unité de temps et ![]() ,
, ![]() Étant donné ces préférences, un planificateur social utilitariste résoud le problème suivant :
Étant donné ces préférences, un planificateur social utilitariste résoud le problème suivant :
avec W, un montant donné de ressources à disposition dans l’économie et ci,di, les consommations par unité de temps d’un agent de type i. La résolution de ce modèle montre qu’il est optimal d’égaliser les consommations de sorte que ![]() . Ainsi, les individus dont l’espérance de vie est plus grande bénéficient au cours de leur cycle de vie d’une utilité et de ressources plus importantes :
. Ainsi, les individus dont l’espérance de vie est plus grande bénéficient au cours de leur cycle de vie d’une utilité et de ressources plus importantes : ![]() et
et ![]() . La fonction de bien-être utilitariste favorise donc les agents vivant plus vieux.
. La fonction de bien-être utilitariste favorise donc les agents vivant plus vieux.
Bommier et al. (2011a) montrent que cette conclusion reste vraie quand on introduit une offre de travail de cycle de vie endogène et de ce fait des ressources variables. Pour comprendre ceci, supposons que dans leur deuxième période de vie, les agents travaillent un certain temps avant de partir à la retraite. Supposons en outre que la désutilité du travail soit indépendante de la longévité. Dans ce cas, quelle que soit l’espérance de vie des agents, l’optimum social utilitariste recommande qu’ils partent tous à la retraite au même âge : ![]() où zi est la durée de vie active ou de manière équivalente, l’âge de départ à la retraite. Si l’on suppose des salaires identiques, leur contribution nette,
où zi est la durée de vie active ou de manière équivalente, l’âge de départ à la retraite. Si l’on suppose des salaires identiques, leur contribution nette, ![]() , est donc décroissante avec la longévité. Il s’opère alors une redistribution des agents ayant une espérance de vie plus faible vers ceux ayant une espérance de vie plus grande.
, est donc décroissante avec la longévité. Il s’opère alors une redistribution des agents ayant une espérance de vie plus faible vers ceux ayant une espérance de vie plus grande.
Notons que cette conclusion est aussi indépendante du caractère exogène de la probabilité de survie. Si celle-ci dépendait des dépenses de santé, sous l’hypothèse de complémentarité entre dépenses de santé et caractéristiques individuelles, cette conclusion serait même renforcée par le fait qu’il est optimal d’investir plus dans la santé des individus avec de meilleures dispositions génétiques. Ceci a été montré dans Leroux et al. (2011). Nous revenons là-dessus en section 3.
Il apparaît alors que cette hypothèse de double additivité (à l’échelle des préférences individuelles et sociales) pose problème lors de la conception de politiques publiques impliquant des agents ayant des durées de vie différentes. On peut considérer que dans nos sociétés développées, mourir jeune est associé à une perte de bien-être que l’on souhaiterait éviter (pour preuve, les individus investissent dans leur santé de manière à réduire leur risque de décès). Ainsi, le risque de mortalité et les différences de longévité font partie intégrante du bien-être d’un individu et il semble alors crucial que cela soit pris en compte dans les politiques publiques telles qu’un système de retraite ou de santé.
Une première question allant dans le sens d’une modélisation adéquate consiste à se demander si en effet, la redistribution des ressources entre agents dont les espérances de vie sont différentes est souhaitable. Cette question renvoie à la question de la responsabilité individuelle. Un planificateur voudrait sans doute compenser les agents malchanceux, nés en mauvaise santé et qui mourront sans doute plus jeunes[16]. Cependant, un planificateur voudrait-il redistribuer des ressources vers ces mêmes agents si leur plus faible espérance de vie est liée à des comportements individuels à risque? Voudrait-il redistribuer vers le fumeur, si ce dernier est totalement conscient des méfaits du tabagisme[17]? Un planificateur bienveillant souhaiterait donc limiter son intervention à la correction des différences de longévité découlant seulement de facteurs exogènes. C’est l’objet du reste de cette section.
2.2 Introduction de l’aversion à l’inégalité multipériodes
Si la durée de vie est certaine comme dans notre exemple précédent, une manière simple de tenir compte des différences de longévité consiste à introduire la notion d’aversion à l’inégalité multipériodes du planificateur social[18]. Dans ce cas, la fonction de bien-être social s’écrit de la manière suivante :
où G(.) est une transformation croissante des utilités individuelles. Si la fonction G(.) est concave, le planificateur social présente de l’aversion à l’inégalité multipériodes. Si G(.) est linéaire, le planificateur est neutre alors que si G(.) est convexe, le planificateur social a une préférence pour l’inégalité multipériodes. Le problème auquel le planificateur social fait face s’écrit alors :
Si ![]() , il est possible de montrer que la seule solution possible implique que
, il est possible de montrer que la seule solution possible implique que ![]() (voir Bommier et al., 2011a). Plus la fonction G(.) est concave, plus le planificateur social est opposé à l’inégalité et plus la différence entre c1et c2 est importante. L’introduction de l’aversion à l’inégalité multipériodes va donc entraîner des consommations par unité de temps plus faibles pour les individus à forte espérance de vie que pour ceux à faible espérance de vie. Toutefois, il est possible de montrer que
(voir Bommier et al., 2011a). Plus la fonction G(.) est concave, plus le planificateur social est opposé à l’inégalité et plus la différence entre c1et c2 est importante. L’introduction de l’aversion à l’inégalité multipériodes va donc entraîner des consommations par unité de temps plus faibles pour les individus à forte espérance de vie que pour ceux à faible espérance de vie. Toutefois, il est possible de montrer que
Ainsi, même si les individus avec une espérance de vie plus importante obtiennent toujours une utilité espérée supérieure à celle des individus avec une espérance de vie plus faible, les écarts d’utilité sont inférieurs à ceux que l’on obtenait lorsque l’on ne tenait pas compte de l’aversion à l’inégalité (puisque, dans le problème (1), les consommations individuelles étaient identiques), ces écarts d’utilité diminuant à mesure que G(.) devient de plus en plus concave. Donc, contrairement au cas où le planificateur social était neutre à l’inégalité multipériodes, les individus sont maintenant au moins partiellement « compensés » pour leur espérance de vie plus faible.
Bommier et al. (2011a) montrent grâce à une formulation identique à (2), que les agents avec une espérance de vie plus élevée devraient aussi travailler plus longtemps, réduisant encore les écarts d’utilités de cycle de vie entre agents avec des espérances de vie différentes.
Finalement, une méthode alternative visant à tenir compte des caractéristiques individuelles responsables des différences de longévité, consiste à considérer une fonction utilitariste qui attribuerait des poids différents à chaque agent en fonction de ses caractéristiques. Si l’on suppose toujours des fonctions d’utilité individuelles additives, la fonction de bien-être social s’écrit alors :
La pondération βi décroît avec la durée de la vie[19]. Ainsi, si T1 > T2 (par exemple, en raison de facteurs génétiques différents) alors β1 < β2 et à l’optimum, les individus dont la durée de vie est plus grande obtiennent des consommations par unité de temps plus faibles, ![]() de manière à redistribuer des ressources vers les agents dont la probabilité de survie est plus faible.
de manière à redistribuer des ressources vers les agents dont la probabilité de survie est plus faible.
2.3 Aversion au risque sur les durées de vie
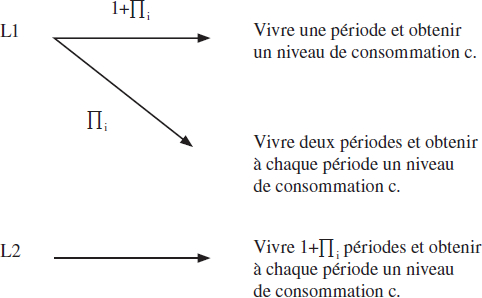
Dans le cas où la durée de vie serait incertaine, c’est-à-dire que ![]() le concept d’aversion au risque de mortalité ou aversion au risque sur les durées de vie, introduit par Bommier (2006), justifierait aussi de redistribuer des ressources des agents ayant une forte probabilité de survie vers ceux ayant une faible probabilité de survie. Pour comprendre ce concept, considérons les deux loteries représentées sur le graphique ci-dessous. Ces deux loteries L1 et L2 sont caractérisées par la même espérance de vie :
le concept d’aversion au risque de mortalité ou aversion au risque sur les durées de vie, introduit par Bommier (2006), justifierait aussi de redistribuer des ressources des agents ayant une forte probabilité de survie vers ceux ayant une faible probabilité de survie. Pour comprendre ce concept, considérons les deux loteries représentées sur le graphique ci-dessous. Ces deux loteries L1 et L2 sont caractérisées par la même espérance de vie : ![]() . De plus, ces deux loteries sont caractérisées par des profils de consommation constants.
. De plus, ces deux loteries sont caractérisées par des profils de consommation constants.
Supposons que l’individu ne présente pas de préférences temporelles pures[20]. L’individu est neutre au risque sur la durée de vie si et seulement si il est indifférent entre des loteries caractérisées par la même espérance de vie (sous un profil de consommation constant). En revanche, quand, dans cette situation, l’individu préfère la loterie où le risque sur la durée de vie est moindre (en l’occurrence, la loterie L2), alors il est averse au risque sur la durée de vie.
Graphique 2
Loteries présentant deux scénarios de survie
Afin de modéliser l’attitude des individus face au risque de mortalité, il suffit de faire une transformation croissante F(.) de l’utilité obtenue dans chaque état de la nature. L’utilité obtenue grâce à la loterie 1, s’écrit alors
et celle obtenue grâce à la loterie 2 s’écrit
L’agent est indifférent entre les deux loteries, et donc neutre au risque, si et seulement si U(L1) = U(L2 ). Ceci n’est possible que dans le cas où F(.) est linéaire. Cependant, l’individu est dit averse au risque de mortalité si la loterie certaine est strictement préférée, U(L2 ) > U(L1). Ceci n’est possible qu’en supposant que F(.) est concave. Au contraire, l’agent a une préférence pour le risque si U(L1) > U(L2 ) et donc si F(.) est convexe. Dans une étude récente, Delprat et al. (2013) ont montré grâce à un questionnaire proposé à un panel de répondants de l’American Life Panel, qu’effectivement, les individus ne sont en général pas neutres au risque sur les durées de vie lorsqu’on leur propose des loteries similaires à L1 et L2. Dans le scénario de base, environ 26,5 % des répondants sont neutres au risque alors que 38,2 % sont averse au risque et 35,4 % sont preneurs de risque.
Ainsi, lorsque les utilités individuelles sont additives au travers du temps, et lorsque l’on fait l’hypothèse de l’utilité espérée, cela revient à faire l’hypothèse implicite que les individus sont neutres au risque de mortalité. Par conséquent, il n’est pas nécessaire de conditionner l’allocation optimale sur un risque qui les laisse indifférent[21]. Dans ce cas, ils n’attachent pas d’importance au fait de vivre une vie risquée ou non. Au contraire, si on considère que les individus ne sont pas neutres au risque de mortalité, comme le montrent Delprat et al. (2013), la fonction de bien-être social devrait en tenir compte. C’est l’objet du papier de Bommier et al. (2011b) qui suppose que les individus sont averses au risque de mortalité. L’utilité individuelle est modélisée en faisant une transformation concave des utilités obtenues dans chaque état de la nature et ces auteurs montrent qu’à l’optimum, les individus dont la probabilité de survie à chaque période est plus faible devraient obtenir un profil de consommations par période plus élevées et décroissant plus lentement au cours du temps que les individus dont la probabilité de survie est plus élevée[22].
2.4 Compensation ex ante
Jusqu’à présent, nous avons utilisé des critères qui permettent de faire de la redistribution vers les agents dont l’espérance de vie est plus faible. Si G(.) est extrêmement concave ou si βi est infini, alors les fonctions de bien-être social définies en (2) et (3) correspondent à un critère maximin et le planificateur social souhaite alors « compenser parfaitement » les agents pour leur espérance de vie plus faible. Un tel critère est étudié dans Fleurbaey et al. (2014a). Nous en présentons ici une version simplifiée dans laquelle l’offre de travail de cycle de vie est inélastique. Les deux individus i = {1,2} vivent au maximum deux périodes de vie. La première période de vie (la période d’activité) est certaine alors que la deuxième période de vie (la retraite) est incertaine. Nous supposons que parmi ces deux agents, l’un a une meilleure prédisposition génétique à vivre longtemps, ε1 > ε2 de telle sorte que π1 > π2. L’espérance de vie individuelle, 1+ πi est donc différente entre ces deux agents. Un planificateur qui souhaite compenser les individus en fonction de leur espérance de vie maximise alors la fonction de bien-être social suivante :
L’allocation optimale implique que de sorte que ![]() les utilités espérées soient égalisées :
les utilités espérées soient égalisées :
Les travaux de Fleubaey et al. (2014b) montrent aussi que si l’offre de travail est endogène, il serait optimal que les agents dont l’espérance de vie est plus grande travaillent plus longtemps. Cette approche (et celles développées dans les sections précédentes) justifie donc la mise en place de politiques publiques qui indexeraient l’âge de la retraite et la durée de cotisation aux systèmes de retraite sur la pénibilité du travail. En effet, un travail plus pénible conduit à une espérance de vie plus faible : la politique que nous proposons ci-dessus propose de différencier l’âge de la retraite et le montant des cotisations versées et des prestations reçues selon l’espérance de vie individuelle.
2.5 Compensation ex post pour les différences de longévité
Le principal défaut des approches que nous venons de développer vient du fait que nous raisonnons en terme d’espérance de vie et d’utilité espérée. Cependant, est-il juste de redistribuer des ressources sur base de différences d’espérance de vie, même si celles-ci sont exogènes alors que l’espérance de vie ne représente pas un évènement certain? Par exemple, une personne avec une espérance de vie faible ne mourra pas forcément jeune et si les politiques pronées dans les sections précédentes étaient mises en place, celle-ci obtiendrait un double dividende en cas de survie : celui de vivre longtemps et de disposer de plus de ressources. Inversement, une personne avec une espérance de vie plus grande peut avoir la malchance de mourir jeune et serait doublement pénalisée.
La difficulté de tenir compte de ces différences de longévité réalisée dans les politiques de redistribution du revenu vient du fait qu’ex ante, le type de l’agent (c’est-à-dire le fait qu’il meure jeune ou plus âgé) est inconnu. Or, lorsque le type de l’agent est révélé, il est malheureusement trop tard pour compenser cet agent pour la perte d’utilité générée par une vie courte.
L’approche que nous allons développer maintenant se base sur les travaux de Fleurbaey et al. (2014a, 2014b) et vise à introduire de la compensation pour des durées de vie plus faibles. De manière cruciale, nous faisons ici l’hypothèse que la vie vaut toujours la peine d’être vécue et donc qu’une vie plus longue constitue toujours un gain de bien-être pour les agents. On supposera alors que les ressources dans l’économie sont toujours suffisantes pour assurer que chaque individu obtienne à chaque période de sa vie un niveau de consommation supérieur à c0 où u(c0 ) = 0[23].
Cette approche, qu’on appelle égalitarisme ex post, plaide pour une compensation individuelle sur base de durées de vie réalisées plutôt qu’anticipées. L’objectif du planificateur social égalitariste ex post, consiste alors en la résolution du problème suivant :
où, comme dans la section précédente, l’indice i = {1,2} représente le type ex ante de l’agent, c’est-à-dire sa probabilité de survie à la deuxième période avec π1 > π2. Avec ce type d’approche, le nombre de types ex ante (2) diffère du nombre de types ex post (4), puisqu’il faut distinguer les individus qui sont morts à la fin de la première période de ceux qui vivent deux périodes, en plus des différences ex ante d’espérance de vie. À la différence de l’égalitarisme ex ante, l’objectif social défini en (4) s’intéresse non pas aux utilités espérées mais aux utilités réalisées.
Il est alors optimal d’égaliser les utilités entre tous les types, c’est-à-dire à la fois entre les agents avec des probabilités de survie différentes et entre ceux qui ont des durées de vie différentes :
ce qui conduit à l’allocation optimale :
Plusieurs remarques méritent ici d’être faites. Premièrement, sous l’approche égalitariste ex post, l’allocation optimale ne fait pas de différences entre des individus qui ont des espérances de vie différentes puisque les agents obtiennent tous l’allocation ![]() . C’est la conséquence directe de notre objectif social qui considère comme non pertinentes les différences ex ante. Deuxièmement, les individus ne devraient consommer que le minimum de subsistance en deuxième période. En effet, de manière à éviter toute inégalité entre les agents qui vivent une seule période et ceux qui en vivent deux, il est souhaitable de donner un niveau de consommation tel que l’utilité obtenue en deuxième période soit nulle. Ceci constitue la seule manière de compenser les agents dont la vie sera finalement courte. Troisièmement, cette allocation préconise de réallouer les consommations vers la première période, puisque dans ce cas tous les individus sont encore vivants. Ceci découle de l’hypothèse qu’il est toujours mieux de vivre plus longtemps.
. C’est la conséquence directe de notre objectif social qui considère comme non pertinentes les différences ex ante. Deuxièmement, les individus ne devraient consommer que le minimum de subsistance en deuxième période. En effet, de manière à éviter toute inégalité entre les agents qui vivent une seule période et ceux qui en vivent deux, il est souhaitable de donner un niveau de consommation tel que l’utilité obtenue en deuxième période soit nulle. Ceci constitue la seule manière de compenser les agents dont la vie sera finalement courte. Troisièmement, cette allocation préconise de réallouer les consommations vers la première période, puisque dans ce cas tous les individus sont encore vivants. Ceci découle de l’hypothèse qu’il est toujours mieux de vivre plus longtemps.
Finalement, Fleurbaey et al. (2013) montrent que lorsque l’offre de travail de cycle de vie est endogène, l’allocation égalitariste ex post implique une durée d’activité indépendante des probabilités de survie des agents, puisque seules les différences de longévité réalisées importent du point de vue du bien-être social. Ainsi, à la différence de l’optimum égalitariste ex ante, l’égalitarisme ex post ne pourrait justifier la mise en place de politiques sociales prônant des âges de retraite différenciés selon l’espérance de vie individuelle, puisque cela créerait des inégalités ex post.
Dans cette section, nous venons de montrer pour quelles raisons et de quelle manière il serait souhaitable de redistribuer du revenu lorsque les agents ont des durées de vie différentes. Cependant, le schéma de compensation dépend ici de manière cruciale de l’hypothèse d’exogénéité de la longévité[24]. Dans la section suivante, nous allons montrer comment tenir compte du fait que la longévité dépend aussi de choix individuels.
3. Tenir compte de la responsabilité individuelle dans la redistribution intragénérationnelle
Notre première approche présente une version simplifiée de Leroux et al. (2011)[25]. Dans ce papier, les auteurs supposent que des agents de type i = {1,2} peuvent tous vivre jusqu’à deux périodes de même durée, la première étant certaine, alors que la deuxième est conditionnelle à la réalisation d’une probabilité de survie, ![]() où mi sont des dépenses de santé individuelles préventives et εi, une caractéristique génétique telle que ε1 > ε2. Nous allons montrer que la relation de complémentarité ou de substituabilité entre dépenses de santé mi et caractéristique génétique εi joue un rôle crucial dans la taille et la direction de la redistribution. Comme précédemment, les préférences individuelles sont additives et les agents n’ont pas de préférence temporelles pures.
où mi sont des dépenses de santé individuelles préventives et εi, une caractéristique génétique telle que ε1 > ε2. Nous allons montrer que la relation de complémentarité ou de substituabilité entre dépenses de santé mi et caractéristique génétique εi joue un rôle crucial dans la taille et la direction de la redistribution. Comme précédemment, les préférences individuelles sont additives et les agents n’ont pas de préférence temporelles pures.
Un planificateur social utilitariste résoud alors le problème suivant :
où W est le montant total de ressources disponibles dans l’économie et ni dénote le nombre de personnes de type i. La résolution de ce modèle nous permet d’obtenir les conclusions suivantes :
Il est donc optimal que les consommations soient lissées au cours du temps et entre les types d’agents. Le rendement marginal de l’investissement en santé devrait aussi être identique entre les agents[26]. Comme nous l’avons mentionné en première section, ![]() ≥ 0 et
≥ 0 et ![]() ≤ 0. Il en résulte qu’en cas de complémentarité entre les dépenses de santé individuelles et les caractéristiques génétiques (
≤ 0. Il en résulte qu’en cas de complémentarité entre les dépenses de santé individuelles et les caractéristiques génétiques (![]() ≥ 0 ), il est optimal que m1 > m2 lorsque ε1 > ε2. Au contraire en cas de substituabilité (
≥ 0 ), il est optimal que m1 > m2 lorsque ε1 > ε2. Au contraire en cas de substituabilité ( ![]() ≤ 0), m1 < m2 serait optimal[27].
≤ 0), m1 < m2 serait optimal[27].
L’intuition derrière ce résultat est la suivante. Dans l’optique utilitariste qui consiste à aggréger les utilités individuelles, il est optimal de concentrer les ressources sur l’individu qui est le plus à même d’en tirer le maximum de bénéfices, sans aucune considération de compensation pour la chance initiale dont les agents ont bénéficié. S’il existe une complémentarité (resp. substituabilité) entre caractéristiques génétiques et dépenses de santé, il est alors optimal de concentrer les ressources de l’économie sur l’individu qui a les meilleurs (resp. les moins bons) gènes puisqu’il est mieux à même de « transformer » ces ressources en une longévité plus grande et de créer le maximum de bien-être social.
En cas de complémentarité, il s’opèrera alors une redistribution des ressources de l’économie vers l’agent ayant de meilleurs gènes, puisqu’il est optimal de dépenser plus pour sa longévité :
Cet individu se retrouve alors doublement avantagé : d’une part grâce à ses meilleures chances initiales (c’est-à-dire de meilleurs gènes) et d’autre part grâce au processus de réallocation des ressources.
En présence d’asymétrie d’information, c’est-à-dire quand le planificateur n’observe pas les caractéristiques génétiques individuelles, il est même optimal de subventionner les dépenses de santé de l’individu avec de meilleurs gènes (type ε1) de manière à décourager l’agent avec des moins bons gènes (type ε2) de prétendre qu’il a des bons gènes (dans ce cas, il se retrouverait à investir trop en santé par rapport à ce qu’il souhaiterait réellement).
Les dépenses de santé ne sont pas seules responsables des différences de longévité. Comme nous l’avons indiqué dans l’introduction, le mode de vie, tel que le fait de pratiquer une activité sportive, dormir suffisamment, prendre un petit déjeuner, est aussi à l’origine des différences de longévité observées au sein d’une population. Leroux (2011) aborde ce problème et fait l’hypothèse que les différences de mode de vie découlent de différences de préférences individuelles. Les individus s’astreignent à un certain mode de vie en fonction de leur préférences individuelles, ou plus particulièrement en fonction de leur « goût » pour un effort visant à augmenter leur espérance de vie. Par exemple, pour certaines personnes, il est extrêmement coûteux en terme de bien-être de faire du sport alors que pour d’autres, c’est un plaisir; or il est reconnu que faire de l’exercice va augmenter l’espérance de vie. De la même manière, pour certains arrêter de fumer représente un effort insurmontable alors que pour d’autres, cela sera plus facile.
Leroux (2011) modélise les préférences individuelles lorsque les agents ont des « goûts » pour l’effort différents de la manière suivante :
où γi représente l’intensité de la désutilité engendrée par un effort non monétaire e pour l’individu de type i[28]. La survie dépend uniquement du comportement individuel avec ![]() et
et ![]() et tous les autres facteurs susceptibles d’influencer la longévité sont tenus constants. De la même manière que précédemment, si le planificateur social est utilitariste, il est optimal que l’agent pour qui la désutilité de l’effort est la plus faible fasse le plus d’effort, c’est-à-dire si γ1 > γ2, e1 < e2. Il aura alors une probabilité de survie plus élevée :
et tous les autres facteurs susceptibles d’influencer la longévité sont tenus constants. De la même manière que précédemment, si le planificateur social est utilitariste, il est optimal que l’agent pour qui la désutilité de l’effort est la plus faible fasse le plus d’effort, c’est-à-dire si γ1 > γ2, e1 < e2. Il aura alors une probabilité de survie plus élevée : ![]() Ceci maximisera le bien-être social au moindre coût total en terme d’effort. Cette allocation est identique à celle obtenue au laissez-faire. Si on considère que les individus sont responsables de leurs différences de préférences, le laissez-faire est optimal et le planificateur ne devrait donc pas intervenir. Les différences de longévité sont alors justifiées d’un point de vue social. Si au contraire, on considère que les agents ne sont pas responsables de leurs différences de préférences (cela serait la conséquence par exemple de différences d’éducation, de milieu social d’origine), alors le critère utilitariste ne semble pas adéquat puisqu’il n’entraîne aucune compensation et laisse intactes des différences de longévité résultant de différences dont les agents ne peuvent pas être tenus responsables.
Ceci maximisera le bien-être social au moindre coût total en terme d’effort. Cette allocation est identique à celle obtenue au laissez-faire. Si on considère que les individus sont responsables de leurs différences de préférences, le laissez-faire est optimal et le planificateur ne devrait donc pas intervenir. Les différences de longévité sont alors justifiées d’un point de vue social. Si au contraire, on considère que les agents ne sont pas responsables de leurs différences de préférences (cela serait la conséquence par exemple de différences d’éducation, de milieu social d’origine), alors le critère utilitariste ne semble pas adéquat puisqu’il n’entraîne aucune compensation et laisse intactes des différences de longévité résultant de différences dont les agents ne peuvent pas être tenus responsables.
Finalement, le niveau de prévention optimale en présence de préférences hétérogènes a été également étudié par Fleurbaey et Ponthière (2013). Contrairement aux deux articles présentés ci-dessus, cet article propose, dans un premier temps, de construire une fonction d’objectif social pertinente dans le contexte d’une économie à durée de vie risquée, où les individus peuvent, par des efforts préventifs, influencer leurs chances de survie. Comme dans Fleurbaey et al. (2014), ces auteurs se concentrent exclusivement sur des objectifs de type égalitarien ex post, c’est-à-dire accordant un poids très important à la réduction des inégalités, entre les individus, dans le bien-être réalisé–et non attendu–sur la vie. Pour ce faire, Fleurbaey et Ponthière (2013) mettent l’accent sur deux propriétés de l’objectif social. D’une part, il est légitime d’attendre d’un objectif social qu’il compense les personnes malchanceuses, c’est-à-dire, dans notre contexte, les personnes victimes d’une mortalité prématurée. Cette propriété de compensation est plausible dans ce contexte, tout simplement parce que les efforts préventifs ne conduisent qu’à une hausse de la durée de vie attendue, et non de la durée de vie certaine. D’autre part, il semble également légitime d’attendre d’un objectif social qu’il encourage, toutes autres choses étant égales d’ailleurs, les comportements de prévention, afin de permettre, ceteris paribus, de sauver, de façon certaine, un certain nombre de vies (à condition que ces sauvetages soient évidemment désirables pour les personnes concernées, ce qui est, en général, une condition très faible).
Bien que plausibles, ces deux propriétés–intérêt pour la compensation et intérêt pour la prévention–ne sont pas logiquement compatibles. En effet, Fleurbaey et Ponthière (2013) montrent qu’un objectif social ne peut, sous des conditions générales (notamment concernant la structure des préférences individuelles), satisfaire ces deux propriétés simultanément. La raison de cette incompatibilité est simple : dès que l’on impose, collectivement, un effort de prévention plus important permettant de sauver une vie, cet effort préventif additionnel va avoir comme conséquence, outre d’allonger une vie, de réduire le bien-être des personnes malchanceuses à vie courte, pour qui les efforts préventifs ont été uniquement coûteux.
Cette incompatibilité peut être illustrée grâce à la fonction d’utilité présentée ci-dessus. Supposons que la population compte une nombre N d’individus et que la situation initiale soit caractérisée par un niveau d’effort e0 > 0. Supposons maintenant une hausse de l’effort, vers un niveau e1 > e0, permettant la survie d’une personne additionnelle sur les N personnes concernées. Le bien-être réalisé sur la vie de cette personne augmente de ![]() à
à ![]() (sinon, le niveau d’effort e1 ne serait pas réalisé). En revanche, pour les N - 1 personnes ne profitant pas d’un allongement de la vie, le bien-être réalisé sur la vie est égal à :
(sinon, le niveau d’effort e1 ne serait pas réalisé). En revanche, pour les N - 1 personnes ne profitant pas d’un allongement de la vie, le bien-être réalisé sur la vie est égal à :
ce qui est inférieur au niveau de bien-être initial. Il apparaît alors qu’une augmentation générale du niveau de prévention en vue de sauver une vie certaine, bien que recommandée du point de vue de la prévention, entre en conflit avec le critère de compensation, puisque celle-ci conduit à une baisse du niveau de bien-être sur la vie des personnes faisant face à un décès prématuré.
Un intérêt pour la prévention est donc difficilement compatible avec un intérêt pour la compensation. Bien entendu, cette incompatibilité peut être surmontée dès lors que l’on impose des restrictions sur le domaine des préférences individuelles. Si, par exemple, on suppose que tous les individus retirent une utilité positive de l’effort préventif (c’est-à-dire, dans notre modèle, le coût de l’effort γ est négatif) quelles que soient ses conséquences en termes de survie, alors prévention et compensation seraient logiquement compatibles. Il est cependant clair qu’une telle restriction n’est justifiable que pour certains individus.
À la lumière de cette tension entre prévention et compensation, Fleurbaey et Ponthière (2013) proposent de construire d’autres objectifs sociaux reposant soit sur la propriété d’intérêt pour la compensation, soit sur la propriété d’intérêt pour la prévention. Une première approche consiste à ne garder que l’intérêt pour la compensation, ce qui conduit à un objectif de type maximin défini sur un indice du bien-être réalisé sur la vie. Cet objectif conduit à une différentiation extrême des niveaux de prévention optimaux : seuls les individus avec un γ < 0 (la prévention est toujours désirable) devraient faire de la prévention, tandis que les individus avec un γ > 0 (pour qui l’effort préventif crée de la désutilité) ne devraient pas en faire, afin de protéger les malchanceux pour qui ces efforts ne seront pas fructueux en terme de survie[29]. Une autre approche consiste à se focaliser sur la prévention, tout en renonçant à la propriété de compensation. L’objectif social obtenu est alors, sous des conditions générales, une somme d’indices du bien-être réalisé sur la vie, indices transformés par une fonction concave. Ce deuxième objectif, contrairement au premier, accorde une importance à la taille relative des différents effectifs en termes de durée de vie réalisée, et, ce faisant, permet d’encourager la prévention et le sauvetage d’un grand nombre de vies. Cependant, le revers de cet objectif réside dans le fait qu’un tel encouragement de la prévention tend, en général, à détériorer la situation des personnes malchanceuses décédant prématurément malgré les efforts de prévention. Il s’ensuit que la tension identifiée plus haut entre compensation et prévention est bien réelle : la question de la prévention optimale est donc bien, avant tout, une question de choix social, dont la résolution exige l’explicitation des fondations normatives sous-jacentes.
Dans les sections précédentes, nous avons étudié différents objectifs sociaux et leurs conséquences en terme de redistribution intragénérationnelle, quand les agents ont des durées de vie différentes. Nous avons insisté sur le fait que cette modélisation devait tenir compte à la fois des caractéristiques endogènes et exogènes de la longévité, influençant alors le type de redistribution qui serait désirable.
Au regard de ces conclusions, nous allons, dans la section suivante, étudier des pistes de réformes publiques visant à prendre en compte plus adéquatement les différences de longévité.
4. Implications politiques et avenues de réformes
Dans cette section, nous allons premièrement établir qu’à l’heure actuelle, les systèmes de retraite ont tendance à redistribuer des ressources des agents ayant une durée de vie courte vers ceux ayant une durée de vie longue. Ce faisant, et à cause de la corrélation positive entre revenus et longévité, la redistribution de cycle de vie opérée par ces systèmes est plus faible qu’il n’y paraît. Dans un deuxième temps, nous allons étudier quelques pistes de réformes visant à mieux prendre en compte les aspects liés à la longévité.
4.1 Implications des différences de longévité sur les politiques publiques
Les conséquences de la longévité différentielle sur la redistribution opérée par les systèmes de retraite sont relativement peu connues du grand public. En dehors de leur rôle principal d’assureur, les systèmes de retraite visent aussi à redistribuer des revenus au sein d’une même cohorte. Ce faisant, ceci génère aussi de la redistribution implicite entre agents ayant des durées de vie différentes. Pour comprendre l’impact de la longévité différentielle sur la redistribution opérée par les systèmes de retraite, il est important de distinguer la redistribution faite sur base annuelle, de la redistribution opérée sur l’ensemble du cycle de vie. Par exemple, les taux de remplacement bruts des systèmes de retraite sont décroissants avec le revenu comme l’indique le tableau 1.
Ce calcul, par la définition même du taux de remplacement, est annuel. Il ne tient donc pas compte de la durée de la vie des pensionnés et du fait que certains individus bénéficieront plus longtemps que d’autres de leur pension de retraite. Ce phénomène a été détaillé dans plusieurs études, pour plusieurs pays et provient du fait que les systèmes de retraite offrent une rente constante et vont ainsi transférer des ressources (non utilisées) des individus qui meurent plus tôt vers ceux qui meurent plus tard[30]. Coronado et al. (2000) montrent, en utilisant des données du PSID, que si l’on tient compte des différences d’espérance de vie selon les niveaux de revenus, le système de retraite ne peut plus être considéré comme progressif[31]. Liebman (2001) s’intéresse en particulier aux différences de redistribution de cycle de vie induites par les différences de situations matrimoniales et de longévité, et ce, en tenant compte des différences de revenus des agents. Ainsi, il montre que tenir compte des différences de longévité par sexe, âge, race et éducation fait baisser la valeur présente des bénéfices reçus par les agents appartenant aux deux quintiles les plus pauvres mais augmente la valeur présente des bénéfices reçus par les agents appartenant aux deux quintiles les plus riches. La redistribution entre quintile est donc plus faible qu’il n’y paraît.
De la même manière, Bommier et al. (2006) montrent que dans le cas français, la mortalité différentielle annule entre le quart et la moitié de la redistribution faite sur base des revenus. Ils concluent que même si le système de retraite reste redistributif, les taux de remplacement constituent une mesure imparfaite de cette redistribution. Dans la même ligne mais en utilisant comme mesure le taux de rendement interne (défini comme le taux d’actualisation pour lequel la somme actualisée de toutes les cotisations est égale à celle de toutes les prestations sur le cycle de vie) et en supposant que la mortalité est identique au sein d’une cohorte donnée, Walraet et Vincent (2003) montrent que le taux de rendement pour les hommes augmenterait et celui pour les femmes diminuerait par rapport à la situation réelle où leurs espérances de vie sont différenciées. Ceci corrobore le résultat selon lequel il existe de la redistribution liée aux différences de longévité allant des individus à faible longévité (les hommes) vers ceux à forte longévité (les femmes).
Tableau 1
Taux de remplacement brut du revenu offert à 65 ans par les régimes obligatoires, selon un multiple du salaire moyen (pour les hommes)
Note : Les chiffres pour le Québec sont issus de la Régie des Rentes du Québec (2012).
Finalement, Brown (2002) montre que la taille des transferts antiredistributifs, c’est-à-dire allant des agents avec une mortalité plus élevée vers ceux ayant une mortalité plus faible (les femmes, les plus éduqués, les blancs), dépend de la structure des annuités suivant qu’elles sont fixes, variables, qu’elles autorisent des paiements au conjoint survivant, etc.
Les études mentionnées ci-dessus mettent en avant le fait que les différences de longévité au sein d’une cohorte ont des conséquences non négligeables et non désirables sur la redistribution intragénérationnelle selon le revenu. Ces effets ne sont pourtant pour le moment pas pris en compte dans la plupart des régimes de retraite. Dans les sections suivantes, nous allons traiter de quelques avenues de réformes possibles ainsi que des écueils à éviter de manière à mieux prendre en compte la longévité individuelle.
4.2 Réforme des retraites et pénibilité du travail
Une réforme des retraites efficace et juste, qui tiendrait compte des différences de longévité, devrait aussi tenir compte du fait que ces différences peuvent être en partie liées aux emplois, plus ou moins pénibles, que les travailleurs ont occupés pendant leur vie active.
À l’heure actuelle, on ne trouve pas de systèmes de retraite tenant compte adéquatement de la pénibilité du travail. Les dispositifs existants sont restrictifs : ils n’ont en fait que peu à voir avec la pénibilité du travail, entendue comme un facteur de réduction de l’espérance de vie future, et se focalisent plutôt sur les handicapés graves du travail. Il faut dire que les difficultés sont nombreuses, la pénibilité étant une notion aux contours flous. Elle désigne l’exposition à des contraintes et à des nuisances professionnelles susceptibles de réduire la durée de vie des travailleurs. Il faut donc être en mesure d’observer parfaitement les conditions de travail de chacun et de déterminer ces facteurs de risque, des tâches qui s’avèrent complexes. Il n’est pas facile de s’accorder sur plusieurs critères : les contraintes physiques marquées, un environnement agressif, et, enfin, certains rythmes de travail (de nuit, répétitifs ou en horaires alternés).
Pour toutes ces raisons, dans de nombreux pays, la réforme des retraites se heurte au dossier sensible de la pénibilité du travail. L’enjeu est de taille. Alors que la hausse continue de la longévité pousse à relever l’âge minimal du départ à la retraite, il s’agit de définir les conditions qui permettraient aux travailleurs usés de partir plus tôt que les autres, et ce afin de les compenser pour le risque d’une vie plus courte. Les inégalités sociales en matière de santé sont en effet flagrantes. En France, à 35 ans, les hommes cadres supérieurs peuvent espérer vivre encore en moyenne pendant 47 ans. Les hommes ouvriers, eux, n’ont pas cette chance : à 35 ans, leur espérance de vie est inférieure de six ans à celle des cadres, et leur espérance de vie sans incapacité est plus courte de dix ans (INSEE 2011). Bien que l’usure professionnelle ne soit pas seule en cause, elle joue un rôle non négligeable dans cette « double peine ». De quoi légitimer un départ en retraite anticipé pour cause de pénibilité.
Même si tout le monde est d’accord avec ce constat, la difficulté réside dans l’application d’une réforme qui tienne compte de la complexité de la réalité du marché du travail. Premièrement, un métier pénible aujourd’hui ne le sera peut être plus demain et si tel est le cas, il sera difficile de revenir sur ce que d’aucuns considèreront comme des droits acquis. Ensuite, un régime qui serait trop favorable à des professions dangereuses pourrait encourager des choix professionnels qui ne seraient pas socialement désirables. Enfin et surtout, il n’existe pas de professions totalement pénibles et d’autres qui ne le seraient pas du tout. Il existe certes des professions où les conditions de travail sont éprouvantes pour la majorité et d’autres où elles ne sont éprouvantes que pour une minorité, mais adopter une réforme qui accorderait un régime particulier à certaines professions aurait pour conséquence que certains travailleurs qui n’en ont pas besoin bénéficieraient d’un régime de faveur et certains travailleurs qui au contraire en auraient besoin, en seraient exclus.
Certes, dans un monde d’information parfaite, il serait possible d’accorder un régime favorable aux travailleurs dont les conditions de travail sont pénibles avec pour conséquence une longévité faible. Dans un monde d’information imparfaite, il faut recourir à des mécanismes d’autosélection ou à des tests de santé. C’est l’approche de Pestieau et Racionero (2013a, b) qui adoptent un modèle où les travailleurs peuvent être employés par deux entreprises dans lesquelles le travail est plus ou moins pénible. L’entreprise dite « pénible » est celle où la probabilité d’y occuper une activité qui s’avérera à terme pénible est plus élevée. Les travailleurs sont identiques ex ante et indifférents entre l’une et l’autre entreprise, l’entreprise dite pénible offrant un salaire plus élevé. L’état de santé des travailleurs est révélé à la fin de la première période (celle où ils travaillent) et constitue une information privée. Le système de retraite optimal varie selon l’entreprise et la pénibilité du travail. Cette dernière caractéristique n’étant pas observable, le système de retraite consiste en une double taxe non linéaire sur l’âge de départ à la retraite et sur l’épargne de telle sorte que dans chaque entreprise, le travailleur révèle son véritable état de santé. Afin de dissuader les travailleurs qui ne souffrent pas de conditions pénibles de se faire passer pour des travailleurs qui en sont les victimes, le système de retraite optimal incite ces derniers à consommer relativement plus dans leur première période de vie et à partir à la retraite plus tôt. Il se peut aussi que les travailleurs fragilisés par leurs conditions de travail partent à la retraite plus tôt s’ils appartiennent à la firme dite non pénible qu’à la firme dite pénible. Ce mécanisme permet alors de résoudre le problème d’asymétrie d’information.
Alternativement ou conjointement, le gouvernement peut décider d’introduire des tests (coûteux) de santé à un certain âge prédéterminé. Si à la suite d’une visite médicale, le travailleur est reconnu souffrir d’un handicap grave, il a alors droit à une retraite anticipée dont le montant peut varier d’une entreprise à l’autre[32]. Si ces tests étaient gratuits, on retrouverait l’optimum de premier rang. Ces tests seraient aussi utiles afin de contrer la possibilité d’utiliser l’assurance invalidité comme moyen de retraite anticipée, mécanisme utilisé par les travailleurs âgés dans de nombreux pays tels que les Pays Bas (voir Wise, 2012).
4.2 Mortalité différentielle et pauvreté
Une constante démographique, déjà documentée par Malthus (1798), est la surmortalité des personnes les plus pauvres (Pamuk, 1985; Duleep, 1986; Jusot, 2003). Avec l’allongement de la vie, cela n’a pas changé, loin de là. Pour l’économiste, cette surmortalité des plus pauvres a plusieurs implications.
Une première implication est d’ordre statistique. La surmortalité des pauvres a en effet pour conséquence de conduire, par un simple effet de sélection, à une sous-estimation du taux de pauvreté chez les personnes âgées. En d’autres termes si les pauvres avaient le même taux de survie que les riches, il y aurait beaucoup plus de personnes âgées sous le seuil de pauvreté. Pour corriger ce biais de sélection, Kanbur et Mukherjee (2007) et Lefebvre et al. (2013) ont proposé de corriger les mesures de pauvreté en assignant aux personnes disparues prématurément un revenu fictif. L’intuition sous-jacente est de faire comme si les personnes disparues prématurément étaient encore en vie, et pouvaient par conséquent être, elles aussi, comptées comme pauvres. Ces mesures ajustées de la pauvreté ont été calculées par Lefebvre et al. (2013, 2014) pour différents pays de l’OCDE. Ces travaux montrent que le taux de pauvreté que l’on connaîtrait si les pauvres vivaient aussi longtemps que le reste de la population et disposaient d’un certain revenu pendant ces années additionnelles, est significativement plus élevé que le taux de pauvreté observé, de par le biais de sélection induit par la mortalité différentielle selon le revenu. En effet, ces auteurs montrent, sur base de données euroéennes de l’enquête EU-SILC, que le taux de pauvreté chez les Belges de plus de 60 ans augmenterait de près d’un point en cas de prise en compte des personnes disparues prématurément (passage de 20,8 % à 21,7 %).
Notons toutefois que cet ajustement exige la sélection d’un niveau de revenu fictif, niveau qui dépend de la définition sous-jacente de la pauvreté. Si on considère la surmortalité des pauvres comme générant un simple biais de sélection, alors l’objectif des mesures de pauvreté ajustées est simplement de neutraliser ce biais de sélection, et les revenus fictifs assignés se doivent donc de refléter le processus de mobilité de revenu entre vivants (voir Lefebvre et al. 2014)[33]. En revanche, si on considère, comme Sen (1998), qu’un décès prématuré est une source majeure de pauvreté et de déprivation, alors les revenus fictifs assignés aux personnes décédées prématurément se doivent d’être plus faibles encore afin d’incorporer la déprivation générée par un décès prématuré. À cette fin, Lefebvre et al. (2013, 2014) proposent d’utiliser comme revenu fictif le revenu neutre pour la continuation de l’existence, qui est l’équivalent monétaire du concept de niveau neutre de bien-être pour la continuation de l’existence introduit par Broome (2004).
Au delà des difficultés de mesure de la pauvreté impliquées par la surmortalité des plus pauvres, une autre implication de cette constante démographique est qu’elle conduit à des choix cornéliens pour de nombreux gouvernements. Pour illustrer cela, supposons qu’un état doive choisir entre deux politiques ayant le même coût : une politique de santé publique qui permette à une partie des pauvres de voir leur vie s’allonger ou une politique visant à faire sortir une partie des pauvres âgés de leur état de pauvreté. On voit de suite qu’un État qui se soucie uniquement de réduire la pauvreté chez les personnes âgées préfèrera cette seconde politique, alors qu’un État utilitariste préfèrera la première[34]. Ceci nous amène naturellement à la question de la subvention de la longévité et des facteurs qui l’influencent.
4.4 Sortie en rente obligatoire et myopie
Pour les individus, l’espérance de vie est sans doute une des dimensions de l’existence qui se prête le plus à des perceptions irrationnelles, des anticipations erronées et des comportements myopes. Quand on demande aux futurs retraités sous quelle forme ils souhaiteraient toucher leur épargne, ils sont une majorité à demander le versement d’un capital plutôt qu’une sortie en rente. Et pourtant l’expérience indique que pour une partie d’entre eux qui ont le bonheur de vivre longtemps cette décision peut tourner au cauchemar dès lors qu’ils ont liquidé tout leur capital. La solution dans les États providence modernes est de fournir une retraite de base. Dans les pays, où le pilier public est ténu, il arrive que l’on oblige les retraités à une sortie en rente pour une partie de leur épargne à partir d’un certain âge. C’est le cas du Royaume-Uni où les retraités qui possèdent des fonds de pension placés en bourse sont tenus de les « annuitiser » avant 75 ans (voir Brown, 2003). Cette mesure qui veut éviter la pauvreté aux grands âges est pourtant remise en question par le gouvernement actuel.
Au Québec, dans le même esprit, le comité D’Amours a proposé, en 2013, d’introduire une « rente longévité » à savoir un nouveau régime de retraite à prestations définies, totalement capitalisé, qui offrirait à tous les travailleurs québécois une rente viagère payable à compter de 75 ans, sans possibilité d’anticipation ni d’ajournement. Ce type de politique qui vise à éviter les dommages que la sortie en capital ou l’épargne peuvent avoir pour les travailleurs qui ont la chance de vivre longtemps, plus longtemps qu’ils ne l’anticipaient, peut se justifier parce que l’État veut éviter de jouer au « bon samaritain », lorsque ces personnes se retrouvent sans ressources, à des âges avancés. Il demeure qu’elle peut se discuter pour plusieurs raisons. Premièrement, des individus rationnels anticiperont ce « bonus » de ressources et diminueront leur épargne individuelle en conséquence : il n’est donc pas certain qu’une fois arrivés à un âge avancé, ce problème de sous-épargne ne se pose pas à nouveau. Deuxièmement, dans la mesure où ce sont les riches bien plus que les pauvres qui courent le risque d’une longue vie, ce genre de mesure va donc dans le sens de la redistribution des personnes vivant peu de temps vers celles vivant longtemps[35]. Comme nous l’avons vu précédemment, cela n’est pas forcément justifiable du point de vue de l’équité sociale. En revanche, cette rente longévité pourra servir à couvrir des dépenses en cas de perte d’autonomie, qui sont généralement importantes et encourues principalement par des personnes très âgées. Ceci fait l’objet de notre dernière section.
4.5 Longévité et perte d’autonomie aux grands âges
La perte d’autonomie est définie par l’OCDE (2011) comme étant liée à l’incapacité d’effectuer des tâches de la vie quotidienne, comme celles de se lever du lit, se laver, s’habiller, se nourrir, etc. Nous allons nous concentrer dans cette section sur la perte d’autonomie liée à la vieillesse, comme, par exemple, suite au développement de la maladie d’Alzheimer. Selon Brown et Finkelstein (2009), aux États Unis, entre 35 et 50 % des personnes ayant aujourd’hui 65 ans utiliseront une maison médicalisée à un moment dans leur vie. Cette perte d’autonomie chez les personnes âgées est d’autant plus courante que leur âge est avancé. Or, comme la longévité est elle-même positivement corrélée avec le revenu, ce sont essentiellement les personnes les plus riches qui font face au risque de dépendance. Une telle corrélation pose alors la question de l’intervention de l’État pour couvrir le risque de dépendance. En effet, à la différence du risque de chômage, les conséquences redistributives d’une assurance publique dépendance sont moins évidentes, tout simplement car les personnes dépendantes constituent, en moyenne, un groupe moins défavorisé que les chômeurs par exemple (surtout les chômeurs de longue durée). Une telle assurance aurait donc une portée redistributive moins importante.
Néanmoins, plusieurs autres arguments plaident en faveur de la mise en place de politiques publiques visant à couvrir les dépenses liées à la dépendance aux grands âges. Premièrement, les individus ont tendance à sous-estimer le risque de dépendance, quel que soit leur niveau de revenu et ils n’investissent pas suffisamment dans des annuités visant spécifiquement à couvrir ce risque. L’étude de Finkelstein et McGarry (2006) montre que la plupart des individus autour de 78 ans sous-estiment leur probabilité de rentrer dans une maison de soins dans les 5 ans, par rapport à la réalisation de cette probabilité après 5 ans[36]. L’État devrait alors intervenir pour inciter les agents à investir plus dans ce type de produits financiers. Deuxièmement, les systèmes de taxation ne sont pas forcément optimaux et la mise en place d’une assurance dépendance pourrait alors servir à des fins de redistribution puisque compte tenu du coût élevé des soins en cas de perte d’autonomie, certaines personnes ne pourraient pas assumer ces dépenses.
Ce sont des questions que traitent Cremer et Roeder (2014) et Cremer et Pestieau (2013) dont la problématique commune repose sur le fait de déterminer s’il vaudrait mieux subventionner l’achat d’assurances privées ou la création d’une assurance publique visant à couvrir le risque de dépendance aux grands âges. Ces auteurs adoptent une approche utilitariste où les individus peuvent se procurer une assurance privée qui n’est généralement pas actuariellement juste (en raison de l’existence de coûts de gestion importants) et où la corrélation entre revenu et longévité est positive.
Cremer et Pestieau (2014) supposent en particulier que la taxation des revenus n’est pas optimale. En cas de taxation linéaire des revenus, une subvention à l’achat d’assurances privées est désirable et, une assurance publique (c’est-à-dire un transfert uniforme en cas de dépendance) n’est souhaitable que si le gouvernement ne fournit pas de transfert uniforme. Si la taxation des revenus est non linéaire, une subvention à l’achat d’assurance privée n’est jamais souhaitable et, une assurance publique n’est désirable que si le système de taxation se restreint à une taxe proportionnelle et que l’allocation obtenue en cas de dépendance peut être non linéaire.
Cremer et Roeder (2013) considèrent un modèle de taxation non linéaire et ajoutent un élément important dans ce type de problématique, à savoir que certains individus ont vis-à-vis de la perspective de dépendance une certaine myopie. Ces auteurs montrent, dans un modèle où longévité, productivité et dépendance sont (parfaitement) corrélées positivement, que sous l’hypothèse d’information parfaite, l’achat d’assurance privée devrait être subventionné pour inciter les agents myopes à se couvrir contre ce risque. De manière parfaitement équivalente, le gouvernement peut fournir directement le niveau optimal d’assurance publique. Cependant, lorsque l’assurance privée n’est pas actuariellement juste, la provision directe (comptant ou en nature) de soins visant à palier la dépendance par le gouvernement s’avère être une meilleure solution. Lorsque le gouvernement ne peut pas observer les caractéristiques individuelles, si l’assurance privée est actuariellement juste, une assurance publique n’est jamais optimale car elle redistribue dans le « mauvais » sens, et ce indépendamment de la proportion de myopes dans la population. En revanche, si les coûts de gestion de l’assurance privée sont très élevés, l’assurance privée n’est jamais optimale : on préfèrera l’assurance publique. Pour des niveaux intermédiaires de frais de gestion, un système dans lequel les deux types d’assurance coexistent s’avère optimal.
Ces deux papiers montrent bien que le choix entre subvention de l’assurance privée (qui bénéficiera plutôt aux classes moyennes et aux riches, ayant une forte probabilité de dépendance) ou provision publique directe (qui bénéficiera à toute la population) n’est pas toujours évident et dépendra entre autres de la capacité de l’État à taxer les revenus de manière optimale et de l’ampleur des frais de gestion des assurances privées.
Conclusion
L’espérance de vie n’a cessé d’augmenter au cours du siècle dernier. Ce progrès social, s’accompagnant aussi le plus souvent de meilleures conditions de vie, n’a pourtant pas toujours été synonyme de réduction des inégalités de longévité dans la plupart des pays. Si vivre plus longtemps est considéré comme un évènement heureux, alors les différences de longévité se traduisent aussi par des différences en terme de bien-être. Malheureusement, les politiques publiques ne prennent encore que peu en compte les différences de longévité, au contraire d’autres différences telles que les inégalités de revenu.
L’objet de cet article a donc été de décrire les différences de longévité et leur évolution dans le temps. Nous avons montré ensuite que la plupart des modèles théoriques de cycle de vie ne permettent pas de tenir compte adéquatement de ces différences de longévité et que de ce fait, la redistribution intragénérationnelle va souvent dans le « mauvais » sens. Nous avons alors proposé plusieurs pistes de modélisation visant à redistribuer des ressources des agents ayant une forte espérance de vie vers ceux ayant une faible espérance de vie. Nous avons aussi abordé la question de la compensation des individus ayant la malchance de mourir jeunes. Finalement, dans la dernière section, nous avons analysé la redistribution inverse qu’opèrent les systèmes de retraite et nous avons identifié plusieurs pistes de réformes visant à mieux tenir compte des différences de longévité.
Certes, ces réformes pourraient s’avérer difficiles à mettre en place pour des raisons tant politiques qu’éthiques. Par exemple, différencier les pensions, les cotisations et l’âge de départ à la retraite en fonction des espérances de vie–comme le prônerait une approche égalitarienne ex ante–pourrait être perçu comme de la discrimination. Par ailleurs, introduire des considérations de compensation ex post pourrait aussi susciter une certaine hostilité, car la compensation des personnes à vie courte se fait nécessairement au prix d’une baisse de bien-être pour les personnes profitant d’une vie longue. Par conséquent, prendre en compte, dans les programmes publics de redistribution les différences de longévité, semble être une tâche extrêmement ardue, quels que soient les fondements éthiques mobilisés. Pourtant, étant donné les évolutions démographiques à l’oeuvre, cette prise en compte pourrait occuper une place importante dans l’agenda des réformes futures.
Parties annexes
Remerciements
Nous souhaiterions remercier notre rapporteur pour les commentaires très utiles faits sur ce papier.
Notes
-
[1]
Données Institut de la Statistique du Québec (2012).
-
[2]
Par exemple, les hommes employés et ouvriers non diplômés séparés ont un risque de décès 2,1 fois plus important que celui des cadres séparés, à caractéristiques comparables.
-
[3]
Ces différences peuvent en partie être expliquées par des différences de revenus. Voir Woods et al. (2005) qui étudient le lien entre revenu, région et espérance de vie en Angleterre et au Pays de Galles.
-
[4]
Notons ici que nous n’établissons pas de lien causal entre caractéristiques individuelles et espérance de vie. Nous considérons plutôt des corrélations entre ces différents facteurs et une plus ou moins grande mortalité.
-
[5]
Notons que le graphique 1 porte sur l’espérance de vie à la naissance, et, ce faisant, reflète les modifications dans les conditions de survie prévalant aux plus jeunes âges de la vie. Bien que notre article portera plutôt sur la mortalité aux âges adultes, nous montrons ici l’évolution de l’espérance de vie à la naissance, car cet indicateur constitue une mesure classique de la durée de vie moyenne conditionnellement aux probabilités de décès par âge observées sur une période donnée.
-
[6]
Ces écarts d’espérance de vie ont atteint leur apogée dans les années quatre-vingt, en raisons de facteurs comme la mortalité associée au tabagisme, pour ensuite se réduire.
-
[7]
Dans ces deux catégories, il est aussi important de faire la distinction entre facteurs monétaires et non monétaires. Nous y reviendrons dans le reste du papier mais l’enjeu principal réside dans le fait de pouvoir taxer ou subventionner une habitude de vie. Cela semble plus compliqué que des dépenses de santé, d’une part de par leur observabilité mais aussi de part la nature même de la dépense (en termes d’utilité ou monétaire).
-
[8]
Dans le même ordre d’idée, l’article de Perls et al. (2002) mentionne aussi que vivre centenaire pourrait avoir une explication génétique.
-
[9]
Voir Sen (1998). Brown (2002) documente aussi les différences de mortalité pouvant s’expliquer par des différences de race, de sexe et de statut économique aux États Unis.
-
[10]
Les données sur la morbidité sont aussi beaucoup plus subjectives que celles sur la mortalité.
-
[11]
À titre d’exemple, une espérance de vie de 60 ans peut être compatible avec deux situations très différentes. D’une part, la situation A, où 100 % des membres d’une cohorte décèdent à l’âge de 60 ans (courbe de survie rectangulaire); d’autre part, la situation B, où 50 % des membres d’une cohorte décèdent à l’âge de 30 ans, et 50 % des membres de cette cohorte décèdent à l’âge de 90 ans. Dans les deux cas, l’espérance de vie est identique, mais les inégalités en termes de durées de vie sont beaucoup plus importantes dans le cas de la situation B, où la moitié de la population décède prématurément, à seulement 30 ans.
-
[12]
Dans les pages qui suivent, nous allons, pour simplifier la présentation, utiliser les expressions « individu de type » et « groupe d’individus de type » d’une manière équivalente, sauf lorsque la présence d’hétérogénéité à l’intérieur d’un groupe exige des précisions additionnelles.
-
[13]
Quand ces dépenses sont faites en première période et influencent la probabilité de survie, ces dépenses sont préventives.
-
[14]
Par exemple, on pourrait inclure l’intervention de l’État par le biais de la fourniture de biens publics contribuant à l’amélioration de la santé de la population dans son ensemble.
-
[15]
Notons que dans la fonction T(.), mi peut représenter à la fois des dépenses de santé préventives, si elles sont engagées en premiére période ou curatives (telles que des traitements contre le cancer) si elles sont engagées en deuxième période.
-
[16]
Comme nous l’avons défini plus haut, espérance de vie et durée de vie sont deux concepts distincts. Le premier concept est une notion ex ante qui peut être différente de sa réalisation ex post,Ti. Nous reviendrons sur cette distinction dans les deux prochaines sous-sections.
-
[17]
D’aucuns prétendent que le fait de fumer ne relève pas nécessairement d’un choix mais d’un mode de vie imposé par le milieu. La distinction entre non-responsabilité (c’est-à-dire ce qui est du aux circonstances) et responsabilité est donc parfois difficile à établir. Voir Roemer (1993).
-
[18]
Ce concept est défini formellement dans Atkinson et Bourguignon (1982) et dans Bommier et al. (2011a).
-
[19]
Voir Leroux et al. (2011) qui utilisent le même type d’objectif social dans un modèle où les agents ont des probabilités de survie différentes en fonction de facteurs exogènes et endogènes différents
-
[20]
Par préférences pures, nous voulons dire une préférence pour le présent ou le futur indépendamment des conditions de survie. Il est clair qu’une probabilité positive de décéder dans un futur proche agit, dans le cadre de la théorie de l’utilité espérée, comme un facteur d’escompte.
-
[21]
Notons que la neutralité pour le risque sur la durée de vie provient de la combinaison de ces deux hypothèses. Il est donc possible de réintroduire de l’aversion pour le risque sur la durée de vie en relâchant l’hypothèse d’additivité dans le temps (comme le fait Bommier, 2006), ou en relâchant l’hypothèse d’utilité attendue (comme le font Leroux et Ponthière, 2009, qui utilisent une approche par moments dans l’utilité).
-
[22]
Dans ce papier, il est supposé que les agents ont tous le même degré d’aversion au risque, c’est-à-dire la fonction F(.) est la même pour tous, même si, comme le montre l’étude de Delprat et al. (2013), tous les individus d’une même économie n’ont pas la même attitude face au risque de mortalité.
-
[23]
Fleurbaey et al. (2014) étudient aussi comment les résultats sont modifiés quand les ressources sont insuffisantes pour garantir qu’une durée de vie plus grande soit toujours souhaitable. Dans ce cas, il faudrait compenser les individus qui ont eu le malheur de vivre longtemps.
-
[24]
Nous avons supposé que soit les comportements individuels étaient identiques, soit qu’ils n’avaient pas d’impact sur l’espérance de vie.
-
[25]
En particulier, nous ne modélisons pas les différences de productivité et faisons l’hypothèse d’une offre de travail individuelle inélastique. Nous ne tenons pas compte non plus des biais comportementaux qui ont pour conséquences que les individus ne vont pas correctement estimer leur longévité. Finalement, nous ne modélisons pas l’externalité positive que génèrent les dépenses de santé individuelles sur le reste de la société. Ces deux derniers aspects nous permettent de ne pas considérer les problèmes d’efficacité de manière à nous concentrer sur la redistribution opérée par le planificateur social lorsque les agents ont des espérances de vie différentes en raison de comportements individuels différents.
-
[26]
Notons que si les individus avaient aussi des productivités différentes, nous obtiendrions la même conclusion que les dépenses de santé optimales ne devraient dépendre que des caractéristiques génétiques.
-
[27]
Notons ici que nous étudions des cas où les dépenses en santé et le mode de vie ont toujours un impact positif sur la probabilité de survie. Or, il existe des types de biens, dits peccamineux, qui peuvent réduire cette probabilité, comme par exemple la cigarette. Dans cette optique, Pestieau et Ponthière (2012) étudient les déterminants d’une taxe optimale sur ces biens, dans une économie où les individus présentent différents degrés de myopie, et différentes propensions au regret vis-à-vis de leurs comportements passés. La taxe optimale sur les biens peccamineux est croissante avec la proportion de consommateurs qui regrettent leurs consommations passées.
-
[28]
Puisque cet effort est non monétaire, il n’apparaît pas dans la contrainte budgétaire de l’agent.
-
[29]
Avec cette approche, les agents à vie courte sont tous compensés au sens où la consommation de première période est augmentée par rapport au laissez-faire, tandis que la consommation de seconde période est minimale et égale à la consommation neutre pour la continuation de l’existence.
-
[30]
Dans ces études, la problèmatique des régimes spéciaux de retraite, qui vont octroyer une rente plus importante aux individus qui ont occupé des postes à risque, n’est pas abordée.
-
[31]
Ces auteurs adoptent une procédure étape par étape et font varier d’autres aspects du système de retraite et des caractéristiques individuelles qui le rende de moins en moins redistributif au fur et à mesure que ces éléments sont pris en compte dans le calcul du rendement du système de retraite. Tenir compte de la mortalité différentielle arrive à l’étape 5 quand la redistribution intragénérationnelle est déjà faible.
-
[32]
Si ces tests étaient effectués par d’autres instances que le gouvernement (par exemple, un médecin de famille), des problèmes d’agence pourraient alors survenir.
-
[33]
Notons que l’attribution d’un revenu fictif aux personnes décédées prématurément ne neutralise pas nécessairement l’impact de la surmortalité des personnes démunies. Comme cela est démontré par Lefèbvre et al. (2014), c’est seulement sous certaines conditions (égalité des matrices de mobilité de revenu et de mobilité de revenu fictif) que le biais de sélection induit par la mortalité différentielle disparaît.
-
[34]
C’est ce qu’on appelle communément « la solution répugnante ». Étant donné des ressources limitées, un planificateur social utilitariste qui peut choisir la taille de sa population préferera un grand nombre de pauvres à un petit nombre de riches.
-
[35]
La rente longévité est toutefois financée à hauteur de 1,65 % du salaire individuel par l’employeur et par l’employé. Ce type de financement permet donc d’effectuer de la redistribution de revenus, mais comme pour la pension de retraite, cette redistribution est exagérée si l’on ne tient pas compte des différentiels de longévité liés aux différences de revenus.
-
[36]
Environ 50 % des répondants considère que leur probabilité de rentrer dans une maison de soins est nulle, alors même que la probabilité objective est strictement positive.
Bibliographie
- Atkinson, A.B. et F. Bourguignon (1982), « The Comparison of Multi-Dimensioned Distributions of Economic Status », The Review of Economic Studies, 49(2) : 183-201.
- Balia, S. et A. Jones (2008), « Mortality, Lifestyles and Socio-economic Status », Journal of Health Economics, 27 : 1-26.
- Bommier, A. (2006), « Uncertain Lifetime and Intertemporal Choice: Risk Aversion as a Rationale for Time Discounting », International Economic Review, 47(4) : 1223-1246.
- Bommier, A., T. Magnac, B. Rapoport et M. Roger (2006), « Droit à la retraite et mortalité différentielle », Economie et Prévision, 168 : 1-16.
- Bommier, A., M.-L. Leroux et J.-M. Lozachmeur (2011a), « Differential Mortality and Social Security », Canadian Journal of Economics, 44(1) : 273-289.
- Bommier, A., M.-L. Leroux et J.-M. Lozachmeur (2011b), « On the Public Economics of Annuities with Differential Mortality », Journal of Public Economics, 95 (7-8) : 612-623.
- Broome, J. (2004), Weighing Lives, Oxford University Press.
- Brown, J. (2002), « Differential Mortality and the Value of Individual Account Retirement Annuities » inThe Distributional Aspects of Social Security and Social Security Reform, University of Chicago Press.
- Brown, J. (2003), « Redistribution and Insurance: Mandatory Annuitization with Mortality Heterogeneity », Journal of Risk and insurance, 70(1) : 17-41.
- Brown, J.R. et A. Finkelstein (2009), « The Private Market for Long-Term Care Insurance in the United States: A Review of the Evidence », Journal of Risk and Insurance, 76 : 5-29
- Coronado, J.L., D. Fullerton et T. Glass (2000), « The Progressivity of Social Security », NBER Working Paper 7520.
- Christensen, K., T. Johnson et J. Vaupel (2006), « The Quest for Genetic Determinants of Human Longevity : Challenges and Insights », Nature Reviews of Genetics, 7 : 436- 448.
- Cremer, H. et K. Roeder (2013), « Long-term Care Policy, Myopia and Redistribution », Journal of Public Economics, 108 : 3-43.
- Cremer, H. et P. Pestieau (2014), « Social Long-term Care Insurance and Redistribution », International Tax and Public Finance, 21 : 955-974.
- Cristia, J. (2009), « Rising Mortality and Life Expectancy Differentials by Lifetime Earning in the United States », Journal of Health Economics, 28 : 984-995.
- Delavande, A. et S. Rohwedder (2011), « Differential Survival in Europe and the United States: Estimates Based on Subjective Probabilities of Survival », Demography, 48 : 1377-1400.
- Delprat, G., M.-L. Leroux et P-C Michaud (2013), « Evidence on Individual Preferences for Longevity Risks », à paraître Journal of Pension Economics and Finance.
- Duleep, H.O. (1986), « Measuring the Effect of Income on Adult Mortality Using Longitudinal Administrative Record Data », Journal of Human Resources, 21(2) : 238-251.
- Finkelstein, A. et K. McGarry (2006), « Multiple Dimensions of Private Information: Evidence from the Long-term Care Insurance Market », The American Economic Review, 96 : 938-58.
- Fleurbaey, M. (2008), Fairness, Responsibility and Welfare, Oxford University Press.
- Fleurbaey, M. et G. Ponthière (2013), « Prevention Against Equality », Journal of Public Economics, 103(1) : 68-84.
- Fleurbaey, M., M-L Leroux et G. Ponthière (2014a), « Compensating The Dead », Journal of Mathematical Economics, 51 : 28-41.
- Fleurbaey, M., M-L Leroux, G. Ponthière et P. Pestieau (2014b), « Fair Retirement under Risky Lifetime », à paraître International Economic Review.
- Gan, L., M. Hurd et D. McFadden (2005), « Individual Subjective Survival Curves », in D.Wise (Ed.), Analyses in the Economics of Aging, Cambridge: NBER Books, National Bureau of Economic Research
- Hammermesh, D. S. (1985), « Expectations, Life Expectancy, and Economic Behavior », Quarterly Journal of Economics, 100(2) : 389-408.
- Herskind, A. M., M. McGue, N.V. Holm, T.I. Sorensen, B. Harvald et J. W. Vaupel (1996), « The Heritability of Human Longevity: A Population-based Study of 2872 Danish Twin Pairs born 1870-1900 », Human Genetics, 97 : 319-323.
- Hurd, M. D. et K. McGarry (1995), « Evaluation of the Subjective Probabilities of Survival in the Health and Retirement Study », Journal of Human Resources, 30(0) : 268-S292.
- Institutde la Statistique du Québec (2012), « Le vieillissement démographique : de nombreux enjeux à déchiffrer ».
- INSEE (2006), « Dans quelles régions meurt-on le plus tard au début du XXIe siècle? », INSEE Première, 1114.
- INSEE (2011), « L’espérance de vie s’accroît, les inégalités sociales face à la mort demeurent », INSEE Première, 1372.
- Jusot, F. (2003), « Inégalités sociales de mortalité : effet de la pauvreté ou de la richesse », mimeo.
- Kanbur, R. et D.Mukherjee (2007), « Premature Mortality and Poverty Measurement », Bulletin of Economic Research, 59 : 339-359.
- Kaplan, G.A, T.E. Seeman, R.D. Cohen, L.P. Knudsen et J. Guralnik (1987), « Mortality among the Elderly in the Alameda County Study: Behavioral and Demographic Risk Factors », American Journal of Public Health, 77(3) : 307-312
- Lefebvre, M., P. Pestieau et G. Ponthière (2013), « Measuring Poverty without the Mortality Paradox », Social Choice and Welfare, 40 : 285-316.
- Lefebvre, M., P. Pestieau et G. Ponthière (2014), « FGT Poverty Measures and the Mortality Paradox: Theory and Evidence », mimeo, Paris School of Economics.
- Leroux, M-L. (2011), « Endogenous Differential Mortality, Non-contractible Effort and Non-linear Taxation », International Tax and Public Finance, 18(1) : 56-73.
- Leroux, M-L., P. Pestieau et G. Ponthière (2011), « Longevity, Genes and Efforts: An Optimal Taxation Approach to Prevention », Journal of Health Economics, 30(1) : 62-76.
- Leroux, M.L. et G. Ponthière (2009), « Optimal Tax Policy and Expected Longevity. A Mean and Variance Utility Approach », International Tax and Public Finance, 16(4) : 514-537.
- Liebman, J.B. (2001), « Redistribution in the Current U.S Social Security System », NBER Working Paper 8625.
- Ludwig, A. et A. Zimper (2013), « A Parsimonious Model of Subjective Life Expectancy », Theory and Decision, 75 : 519-541.
- Malthus, T. (1798), An Essay on the Principle of Population, London.
- OCDE (2011), « Panorama des pensions 2011, les systèmes de retraites dans les pays de l’OCDE et du G20 ».
- OECD (2011),« Help Wanted? Providing and Paying for Long-Term Care », http://www.oecd.org/health/health-systems/helpwantedprovidingandpayingforlong-termcare.htm, dernier accès en août 2014.
- Pamuk, E.R. (1985), « Social Class Inequality in Mortality from 1921 to 1972 in England and Wales », Population Studies, 39 : 17-31.
- Payeur, F. (2013), « La mortalité et l’espérance de vie au Québec en 2012 », Institut de la Statistique du Québec.
- Perls, T., R. Levenson, M. Regan et A. Puca (2002), « What does it Take to Live to 100 », Mechanisms of Ageing and Development, 123 : 231-242.
- Pestieau, P. et G. Ponthière (2012), « Myopia, Regrets and Risky Behaviors », International Tax and Public Finance, 19 (2) : 288-317.
- Pestieau, P. et M. Racionero (2013a), « Harsh Occupations, Life Expectancy and Social Security », CEPR Discussion Papers 678.
- Pestieau P. et M. Racionero (2013b), « Harsh Occupations, Health Status and Social Security », à paraître Journal of Economics.
- Régie des Rentes du Québec (2012), « Évaluation du système québécois de sécurité financière à la retraite par rapport à celui d’autres pays industrialisés ».
- Roemer, J. (1993), « A Pragmatic Theory of Responsibility for the Egalitarian Planner », Philosophy and Public Affairs, 22(2) : 146-166.
- Sen, A. (1998), « Mortality as an Indicator of Economic Success and Failure », Economic Journal, 108 : 1-25.
- Skytthe, A., L. Nancy, J. Kaprio, M.-A. Stazi, J. v.B. Hjelmborg, I. Lachine, J. W. Vaupel et K. Christensen (2003), « Longevity Studies in GenomEUtwin », Twin Research, 6 (5) : 448-454.
- University of California, Berkeley (USA), et Max Planck Institute for Demographic Research (Allemagne) (2014), « Human Mortality Database », Disponible sur www.mortality.org ou www.humanmortality.de (données téléchargées en juillet 2014).
- Walraet, E. et A. Vincent (2003), « La redistribution intragénérationnelle dans le système de retraite des salariés du privé : une approche par microsimulation », Economie et Statistique, 366 : 31-61.
- Wise, D. (2012), « Social Security and Retirement around the World: Historical Trends in Mortality and Health, Employment, and Disability Insurance Participation and Reforms », NBER and University of Chicago Press.
- Woods, L., B. Rachet, M. Riga, N. Stone, A. Shah et M. Coleman (2005), « Geographical Variation in Life Expectancy at Birth in England and Wales is Largely Explained by Deprivation », Journal of Epidemiology & Community Health, 59 : 115-120.
Liste des figures
Graphique 1
Espérance de vie à la naissance au Canada (Human Mortality Database, 2014)
Graphique 2
Loteries présentant deux scénarios de survie
Liste des tableaux
Tableau 1
Taux de remplacement brut du revenu offert à 65 ans par les régimes obligatoires, selon un multiple du salaire moyen (pour les hommes)



 Femmes
Femmes  Hommes
Hommes