La demande domestique d’eau potable : une étude sur un panel de communes ivoiriennes

Résumé

Dans cet article, nous estimons une fonction de demande d’eau potable pour les communes ivoiriennes, en présence d’une tarification progressive par paliers. Sur la base des applications de Nordin (1976), Corral et al. (1998) et Martinez-Espiñeira (2003) et en l’absence de données individuelles, nous estimons dans une première étape la proportion d’usagers associée à chaque tranche du tarif. L’estimation de la fonction de demande agrégée dans la seconde étape fait apparaître des élasticités-prix et revenu assez fortes et significatives, évaluées respectivement à -0,81 et 0,15. Ces estimations sont utilisées pour simuler l’impact de réformes tarifaires et leur impact sur le bien-être des usagers.

Introduction

L’eau en général et l’eau potable en particulier sont au coeur de la plupart des activités humaines aussi bien de production que de consommation. Au niveau mondial, les consommations d’eau ont augmenté ces 35 dernières années à un rythme annuel de 4 à 8 %. Selon la Banque mondiale (1996), 69 % des 3240 km³ d’eau douce prélevés chaque année sont utilisés par l’agriculture, 23 % par l’industrie et 8 % par les usages domestiques.

Cependant, bien qu’elle constitue une ressource indispensable pour toute l’humanité, la problématique de l’eau se pose en des termes différents d’une région à une autre du globe, notamment entre pays développés et pays en voie de développement (PED). Si les consommations se stabilisent voire diminuent dans les pays industrialisés, elles augmentent considérablement dans les PED, en raison de la croissance démographique, du développement de l’irrigation et de la modification des pratiques de consommation. Dans les pays riches, les caractéristiques économiques du secteur sont maintenant bien connues et maîtrisées. À l’opposé, la situation des PED, surtout en Afrique subsaharienne, est différente à bien des égards, notamment en ce qui concerne la composition de la demande totale en eau, et la configuration des réseaux d’alimentation et d’assainissement.

La connaissance de la demande pour chacun des types d’usagers (ménages, industriels et agriculteurs) est indispensable pour une gestion de la ressource efficace d’une part (affecter la ressource en eau à ceux qui la valorisent le mieux) et d’autre part, équitable (garantir l’accès à tous). Parler de fonction de demande en eau revient à considérer l’eau comme un bien économique. La conférence de Dublin en 1992 sur l’eau et l’environnement dans son accord de principe lui a d’ailleurs reconnu cette qualité. Cet accord de principe stipule en effet que « l’eau a une valeur économique dans tous ses usages concurrentiels et doit être reconnue en tant que bien économique ». La valeur de l’eau pour un usager est le montant maximum que cet usager est prêt à payer pour disposer d’une unité supplémentaire. Cependant, comme il n’existe pas de marché à proprement parler pour l’eau, il est difficile d’en estimer la valeur. L’on doit alors se limiter à estimer des fonctions de demande ou de coût de production afin d’en déduire un indicateur de sa valorisation économique. L’estimation d’une fonction de demande en eau constitue un moyen parmi d’autres de mesurer la valorisation du bien eau pour un usager et de contribuer à la mise en place de schémas de partage efficace de la ressource.

L’objectif de cet article est d’estimer une fonction de demande d’eau des ménages en Côte d’Ivoire, afin d’en déduire l’élasticité-prix et l’élasticité-revenu. Notre travail porte exclusivement sur l’usage résidentiel de l’eau et nous ne traiterons donc pas de la demande pour les deux autres types d’usage (industrie et agriculture). L’analyse empirique porte sur une base de données de 156 localités observées sur 5 années (de 1998 à 2002). La particularité de l’approche proposée réside dans l’utilisation de données agrégées au niveau communal, en l’absence de variables collectées au niveau des ménages. Nous proposons dans cet article une spécification de la fonction de demande individuelle, compatible avec la version agrégée et s’inspirant du cadre d’analyse de Nordin (1976), Corral et al. (1998) et Martinez-Espiñeira (2003), ainsi qu’une méthode d’estimation convergente et efficace des paramètres d’intérêt. Contrairement à la plupart des études antérieures, nous exploitons la double dimension individuelle et temporelle des données de consommation, permettant par exemple d’explorer les disparités régionales de la demande en eau potable. Plus précisément, nous estimons dans une première étape les proportions d’abonnés au réseau dans chaque tranche de tarification, puis nous estimons la fonction de demande agrégée au niveau communal dans une seconde étape. Nous appliquons les tests de spécification et les estimateurs dédiés aux données de panel à chaque étape, et plus précisément ceux permettant de contrôler la présence d’effets individuels communaux inobservables corrélés avec les variables explicatives. La première section contient une revue de la littérature existante sur l’estimation de la demande en eau potable. Nous présentons dans la deuxième section les modèles économique et économétrique envisagés, adaptés à la tarification par paliers. Les données utilisées, obtenues pour la plupart auprès de l’opérateur SODECI (Société de Distribution d’Eau de Côte d’Ivoire), sont détaillées à la section 3. Les résultats d’estimation sont présentés à la quatrième section, concernant le choix des tranches de consommation, les élasticités-prix et revenu et les spécificités régionales de la demande en eau. L’analyse de bien-être de la section 5 est associée à l’évaluation de l’impact de réformes tarifaires (modification du prix moyen ou de certaines composantes du tarif). Les remarques de conclusion figurent dans la sixième section.

1. Une revue de la littérature

Les premières études sur la demande d’eau à usage résidentiel sont apparues aux États-Unis à la fin des années soixante (Howe, 1967; Gibbs, 1978; Danielson, 1979 et Foster, 1979). Suite à des sécheresses de plus en plus fréquentes, les responsables des services d’approvisionnement en eau potable cherchaient les moyens de gérer la rareté périodique de la ressource. À cette époque, il était déjà question de réguler, à travers les prix comme instrument économique privilégié, la demande d’eau étant donné les limites d’une politique d’offre basée sur la mobilisation de plus en plus coûteuse de nouvelles ressources. Les économistes ont alors estimé l’élasticité-prix afin d’évaluer l’impact sur la demande domestique des politiques de gestion de la demande (demand-side management) basées sur la tarification. Les années quatre-vingt virent ensuite se développer de nombreux travaux selon deux axes, le premier concernant la spécification appropriée de la fonction de demande domestique en eau et le second relatif au développement des méthodes économétriques adaptées à son estimation.

La spécification généralement retenue est la forme linéaire, et plus particulièrement celle dite log-log car elle permet une lecture directe des élasticités, qui sont alors supposées être constantes pour tous les niveaux de consommation. Il existe un large consensus entre les économistes concernant les déterminants de la fonction de demande domestique d’eau potable. En effet, tous s’accordent à considérer que le prix, le revenu, les caractéristiques du ménage (sa taille, sa composition) ainsi que de l’habitat (zone rurale ou urbaine, habitat collectif ou individuel, équipements électroménagers,...) sont les principales variables qui conditionnent le choix des ménages. Certaines études ont également montré l’influence du climat notamment sur les usages externes (arrosage de jardins ou bien lavage de voitures) dans des régions soumises à de fortes pénuries d’eau.

En revanche, la spécification du prix dans la fonction de demande a suscité de nombreux débats entre les chercheurs et a constitué un domaine d’étude important pendant les années quatre-vingt. L’objet du désaccord est le type de prix à inclure dans la fonction de demande. Les uns, faisant l’hypothèse d’information parfaite des consommateurs, préconisent l’utilisation du prix marginal (le prix de la dernière unité consommée). Les autres, rejetant cette hypothèse, prônent l’introduction du prix moyen (montant de la facture divisé par le volume consommé). La théorie (1986) du consommateur, basée sur l’égalisation du surplus marginal au coût marginal, conduit à préférer le prix marginal plutôt que le prix moyen. Pour Opaluch (1982), Shin (1985) et Chicoine et Ramamurthy (1986), la question de l’information possédée par les usagers est plus empirique que théorique. Opaluch (1982) propose une méthode pour tester à quel type de prix le ménage est le plus sensible. Sur la base de cette méthode, Chicoine et al. (1986) concluent que les ménages semblent plutôt réagir au prix moyen. Nauges et Thomas (2000) montrent avec le même test qu’aucun des deux prix ne peut être rejeté. Shin (1985), adversaire de l’hypothèse d’information parfaite, propose un test de perception du prix. En utilisant cette technique, Nieswadomy et Molina (1989) montrent que les prix perçus diffèrent selon le type de tarification adopté. Les consommateurs semblent réagir au prix marginal sous une tarification progressive par paliers (IBR, Increasing Block Rate) et au prix moyen sous une tarification dégressive par paliers (DBR, Decreasing Block Rate).

Cette tarification par paliers ou tranches est une des caractéristiques essentielles de la tarification de l’eau dans de nombreux pays en développement ou en transition. Dans un tel système de tarification, les prix marginaux varient selon la tranche dans laquelle la consommation d’eau d’un usager donné se situe. On a une structure DBR si les prix marginaux pratiqués dans les tranches baissent avec la quantité d’eau consommée. À l’opposé, si les prix marginaux pratiqués dans les tranches augmentent avec le volume d’eau consommée alors on parlera de structure IBR. Sous une telle tarification, les ménages ne font pas face à un prix unique, mais à un barème composé en général d’une charge fixe et surtout de prix marginaux (prix du m³) différents selon les niveaux de consommation. Leur contrainte budgétaire est donc non linéaire, de même que la fonction de demande qui en découle, cette dernière étant en outre non differentiable. Les premières études menées dans le cadre de ce type de tarification se contentaient d’utiliser le prix marginal ou le prix moyen correspondant à la tranche dans laquelle la consommation du ménage se situait.

Taylor (1975) et Nordin (1976) sont les premiers auteurs à avoir proposé une spécification qui tienne compte véritablement de cette structure par paliers. En effet, pour remédier à la non-prise en compte du barème complet de prix des études antérieures, ils proposent d’inclure une nouvelle variable désormais connue dans la littérature sous le nom de « différence ». Cette variable, définie comme la différence entre ce que le ménage aurait payé si toutes les unités avaient été facturées au prix de la dernière unité consommée et ce qu’il paie effectivement, est censée représenter l’effet revenu qu’impose cette structure tarifaire. Ainsi, dans le cadre d’une tarification progressive par paliers, cette variable est négative et s’assimile à une subvention appliquée aux premières unités consommées, en compensation des prix élevés payés pour les unités consommées dans les tranches supérieures. A contrario, dans une tarification dégressive par paliers, elle est positive et agit comme une taxe payée sur les premières unités en compensation des prix bas appliqués dans les tranches supérieures. En présence d’un tarif parfaitement linéaire, la variable différence est nulle. Par conséquent, le coefficient affectant cette variable devrait être de signe opposé et équivalent en magnitude à celui qui affecte le revenu. Cette conséquence théorique donna naissance à une série d’études empiriques, notamment celles de Billings et Agthe (1981), Foster et Beattie (1981) et Howe (1982), visant à tester de sa pertinence; mais à ce jour seuls Shefter et David (1985) ont réussi à valider empiriquement cette affirmation en utilisant des données simulées.

Jusqu’au milieu des années quatre-vingt-dix, il n’existait aucune étude sur l’eau modélisant de façon explicite le comportement des ménages face à une tarification par paliers. Pionniers sur ce terrain, Hewit et Hanemann (1995), en utilisant le modèle à deux étapes initialement élaboré par Burtless et Hausman (1979) puis Moffitt (1986 et 1990), proposent une modélisation en deux étapes de la demande d’eau où les ménages choisissent, dans un premier temps, le niveau optimal de consommation dans chacune des tranches puis, dans un second temps, la tranche leur procurant l’utilité maximale. Shefter et David (1985), bien qu’ayant fait des hypothèses sur la distribution des ménages entre les tranches, n’ont pas explicité la méthode d’obtention des proportions d’usagers dans chacune d’entre elles. Corral et al. (1998) ainsi que Martinez-Espiñeira (2003), forts de ces différentes avancées, utilisent certes des données réelles dans les estimations mais celles-ci ne sont disponibles que pour trois municipalités seulement. En général, les données sur le nombre d’abonnés dans les tranches ne sont pas disponibles.

Un autre point, largement abordé par la littérature sur la demande d’eau à usage résidentiel, est celui des méthodes économétriques à appliquer. Les premières études ont largement utilisé la méthode des moindres carrées ordinaires (Billings et Agthe, 1980; Shefter et David, 1985 puis Chicoine et Ramamurthy, 1986). Mais très vite, s’est posé le problème de l’endogénéité de la variable prix. Lorsqu’on utilise le prix moyen, la condition d’orthogonalité entre les régresseurs et le terme d’erreur n’est pas vérifiée car la consommation totale d’eau apparaît des deux côtés de l’équation; ce qui peut créer un biais dit de simultanéité[1].

Le prix marginal, dans le cas d’une tarification par paliers, peut aussi être source d’endogénéité car le prix marginal dépend de la tranche choisie par les ménages. Pour corriger ces problèmes d’endogénéité on assistera au cours des années quatre-vingt, à un usage de plus en plus fréquent des techniques par variables instrumentales (Jones et Morris, 1984 ainsi que Nieswiadomy et Molina, 1989). Dans ce type de tarification, l’estimation économétrique devient plus complexe en particulier pour traiter simultanément les décisions de choix de la tranche de tarification et celle du niveau de consommation. Hewitt et Hanemann (1995) utilisent à cet effet la méthode du maximum de vraisemblance, mais cette technique peut poser certaines difficultés car la fonction de vraisemblance peut être ni globalement concave ni differentiable en tout point. Les années quatre-vingt-dix et deux mille verront se développer les techniques de choix discret/continu dans les estimations des demandes en eau dans ce cadre de tarification par paliers (Corral et al., 1995 et Martinez-Espiñeira, 2003). D’autres études telles que Point (1993), Agthe et Billings (1996), Höglund (1997), Renwick et Archibald (1998), ont insisté sur des aspects nouveaux de la consommation domestique, notamment l’adoption par les ménages d’équipements économes en eau ou encore les conséquences en termes de bien-être des politiques de régulation. De nos jours, on assiste à l’utilisation des méthodes de panel dans l’estimation des fonctions de demande en eau (Höglund, 1997; Nauges et Thomas, 2000, 2003; et Nauges et Reynaud, 2001). Par ailleurs, le champ géographique jusque-là couvert (exclusivement les États-Unis) s’est progressivement élargi aux pays européens, notamment la France, la Suède, le Danemark et l’Espagne.

Enfin, se pose le problème crucial de la disponibilité des données pour les études sur l’eau potable notamment dans les pays en développement (PED). Les données idéales pour ces types d’analyse, comme le souligne Arbués et al. (2003) ainsi que Worthington et Hoffman (2008), sont les données individuelles. Mais la difficulté d’obtenir ces dernières poussent la plupart des auteurs à s’en remettre aux données agrégées. Or l’usage de données agrégées est source de controverse quant à la pertinence des coefficients estimés (Shefter et David, 1985; Arbués et al. , 2003 ainsi que Worthington et Hoffman, 2008). Ces problèmes peuvent être amplifiés selon que l’opérateur utilise des compteurs d’eau individuels ou non. En effet, si chaque compteur sert un et un seul ménage, l’approche du ménage représentatif est en général utilisée et les coefficients obtenus permettent d’analyser le comportement des ménages en question. Par contre, comme c’est souvent le cas dans les PED, s’il n’y pas de compteurs d’eau pour les ménages, les dépenses en eau de ceux-ci ne correspondront pas réellement aux volumes d’eau consommés. Les coefficients estimés alors expliqueraient en même temps tout et rien. Ils ne peuvent donc servir d’instruments d’analyse. Dans ces conditions, des données individuelles sont indispensables pour une analyse pertinente. Il arrive également qu’il y ait des compteurs d’eau pour les ménages mais que chaque compteur sert plus d’un ménage. Dans ce cas, il est certain que les dépenses en eau correspondront aux volumes consommés et l’approche du ménage représentatif restera utilisable mais les coefficients estimés perdront de facto une partie de leur pouvoir explicatif.

En Côte d’Ivoire, l’opérateur utilise systématiquement les compteurs d’eau. Cependant, dans notre base de données, nous avons un mélange de compteurs servant un seul ménage et de compteurs servant un groupe de ménages. Les proportions de chaque type varient d’une localité à une autre selon le type d’habitat prédominant. La SODECI ne tient malheureusement pas cette comptabilité et il nous est objectivement impossible de déterminer la proportion de compteurs collectifs dans l’ensemble.

2. Le modèle

La tarification en vigueur en Côte d’Ivoire est progressive par paliers (Increasing Block Rate). Ce type de tarif se matérialise par une contrainte de budget non linéaire pour le consommateur. Considérons un ménage qui dispose d’un revenu exogène I qu’il consacre à l’achat de deux biens, l’eau potable x et un bien composite y regroupant les autres biens consommés par le ménage. Le prix du bien y est normalisé à 1 (y est pris comme numéraire) et l’eau est vendue selon une structure tarifaire à m tranches dans lesquelles les prix marginaux (prix du m³) sont notés P_i pour i = 1,…, m. La contrainte budgétaire à laquelle fait face un ménage représentatif[2] s’écrit I_i = I – d_i = P_ix + y si x est dans la tranche i, i = 1,2,…, m, où d_i est la variable différence de la i^e tranche proposée par Nordin (1976) et I_i, souvent appelé revenu virtuel, est le revenu du ménage situé dans la tranche i corrigé de la variable différence. Partant de la spécification de Corral et al. (1998)[3], la variable différence définie ici est donnée par :

(1)

où x̅_j est la borne supérieure de la tranche j et donc la borne inférieure de la tranche j + 1.

Comme mentionné dans la revue de littérature, la construction de la fonction de demande dans ces conditions nécessite deux étapes. Dans la première étape, l’usager détermine (choix continu) son niveau optimal de consommation à l’intérieur de chaque segment de la contrainte de budget (on parle alors de demandes « conditionnelles »); dans la seconde, il détermine (choix discret) la demande conditionnelle qui maximise son utilité globale. Finalement, la combinaison des solutions issues de ces deux choix (continu et discret) fournit la fonction de demande dite « non conditionnelle »), qui peut s’écrire comme suit :

(2)

où x^*_i désigne le niveau optimal de consommation conditionné par le choix d’être dans la i^e tranche pour i = 1,2,…, m, et

Si l’on ne dispose pas de données individuelles (par ménage) mais seulement de données agrégées, la spécification correcte du modèle économétrique requiert l’agrégation des fonctions de demandes individuelles définies dans l’équation (2). Soit n le nombre total d’abonnés dans une commune donnée, n_j et q_j le nombre d’abonnés et la consommation moyenne dans la tranche j, x^*_ij (.) la demande conditionnelle du consommateur i dans la tranche j et . La somme des demandes individuelles sur l’ensemble des abonnés de la commune donne la fonction de demande agrégée suivante :

(3)

La composante discrète du choix des consommateurs détermine le nombre n_j de ménages qui se situe dans la tranche j, tandis que la composante continue définit la consommation moyenne q_j (.) des ménages conditionnée par le choix de se situer dans la tranche j. Ainsi, comme remarqué à juste titre par Corral et al. (1998), la structure de la fonction de demande non conditionnelle au niveau des données individuelles est préservée dans la fonction de demande agrégée[4]. Pour prendre en compte la dispersion du nombre d’abonnés entre communes, une normalisation s’avère nécessaire. En divisant la demande totale de chaque commune par le nombre total de ses abonnés, on aboutit à la fonction suivante :

(4)

où q est la consommation moyenne par ménage et s_j est la proportion de ménages dont la consommation se situe dans la tranche j. Comme dorénavant admis par la plupart des auteurs, des variables socioéconomiques sont à inclure dans la fonction de demande. En prenant en compte la dimension temporelle des données, ces variables additionnelles et le terme d’erreur permettent d’écrire la fonction agrégée sous la forme suivante :

(5)

où t est l’indice de la période, h l’indice de la commune, Z_ht le vecteur des variables socio-économiques, ε_ht le terme d’erreur et β le vecteur des paramètres à estimer. Notons que dans cette spécification, les prix sont identifiques entre les différentes communes, ce qui est le cas de nombreux pays en développement (prix administrés par un opérateur unique au niveau national et non déterminés au niveau de chaque commune). Si nous supposons une forme linéaire pour la demande, l’équation à estimer s’écrit explicitement :

(6)

où s_iht est la proportion de ménages dans la tranche i à la date t dans la commune h et δ le vecteur des paramètres associés à la matrice Z.

Les proportions ou probabilités s_iht d’être situé dans une tranche quelconque, à l’instar des demandes conditionnelles, dépendent des préférences des individus, et sont de ce fait corrélées avec le terme d’erreur. Il serait par conséquent inapproprié d’utiliser leurs valeurs observées pour estimer l’équation (6). Pour résoudre ce problème, on estime dans une première étape les probabilités, ŝ_iht correspondant aux proportions de ménages situés dans les différentes tranches. Afin d’obtenir des proportions estimées comprises entre 0 et 1, nous appliquons un modèle logit dont la forme générale est :

(7)

Prob[choix de la tranche i, comme h] = , i = 0,1,..., m

où la variable à expliquer est la proportion des ménages dans chaque tranche et la matrice X est constituée de variables socioéconomiques et techniques spécifiques à chaque commune. Une fois les proportions estimées, elles sont utilisées en lieu et place des valeurs observées pour pondérer les prix marginaux par tranche ainsi que le revenu virtuel (obtenu en additionnant le revenu et la variable différence). L’étape suivante consiste à estimer l’équation (6) au moyen des techniques de données de panel.

Contrairement à Corral et al. (1998) ainsi que Martinez-Espiñeira (2003), nous ne disposons pas du nombre d’abonnés dans chaque tranche de consommation. Pour résoudre ce problème, à l’instar de Shefter et David (1985), nous faisons l’hypothèse suivante : le rapport entre le nombre d’abonnés de deux tranches est proportionnel au rapport entre le volume d’eau facturé dans ces tranches. Ce coefficient de proportionnalité est spécifique à chaque commune et est calculé à partir des effets fixes obtenus en régressant le logarithme du rapport des quantités sur les variables de la matrice X définie ci-dessus.

Plus concrètement, reprenons le logit multinomial de l’équation (7). Ce modèle est utilisé dans le cas où les éléments de la matrice X ne sont pas les caractéristiques des choix à opérer (les tranches tarifaires), mais celles des individus observés (les ménages représentatifs de chaque commune), ces caractéristiques étant les mêmes pour les différents résultats possibles du choix. Considérons le ménage k de la ville h à la date t. La probabilité que ce ménage choisisse la tranche i est :

(8)

Prob[ménage k choisit tranche i] = , i = 1, 2,..., m.

En incluant dans X les variables socio-économiques et techniques propres aux communes et en prenant la tranche 1 comme modalité de référence, on peut réécrire l’équation (8) sous la forme du système suivant de (m – 1) équations[5] :

(9)

où s_iht est la proportion de ménages dans la tranche i à la date t et dans la ville h.

L’hypothèse énoncée ci-dessus revient à considérer :

(10)

Ainsi, nous commençons par estimer le système suivant :

(11)

où V_iht est le volume total d’eau facturé dans la tranche i à la date t et dans la commune h, et α_ih est l’effet individuel de cette dernière[6]. L’estimation du système d’équations défini en (11) donne le système suivant :

(12)

Les équations (9), (10) et (12) conduisent par identification (avec ) aux égalités suivantes :

(13)

(14)

(15)

Au total, une fois estimé le système d’équations (11), les effets fixes et les rapports entre volumes pour chacune des équations du système sont récupérés pour ensuite calculer les rapports de proportions définis par l’équation (15). En tenant compte de l’égalité , nous déterminons enfin les proportions d’abonnés dans chaque tranche de facturation.

3. Les données de l’étude

Les données sur les consommations, les prix et les abonnés ont été collectées essentiellement auprès de l’opérateur SODECI. Nous disposons pour l’ensemble du pays des données sur la période 1998-2002, mais nous avons retenu dans notre échantillon les 156 communes connectées au réseau de distribution d’eau potable avant le début de la période (1998)[7]. En Côte d’Ivoire, l’unité d’observation selon la terminologie de l’opérateur, est le centre d’imputation. Cependant dans la plupart des cas, le centre d’imputation correspond à une commune. Dans quelques cas, soit une grande commune est subdivisée en centres d’imputation, soit de petites communes proches sont rassemblées ou ajoutées à des grandes pour former un tel centre. Puisque cela ne change pas l’analyse, nous désignerons comme il est de coutume dans les travaux sur la demande d’eau les centres d’imputation par « commune », « localité » ou « ville ». Nous disposons au final d’une base de données de panel cylindrée de 780 observations.

Les données socio-économiques ont été collectées auprès de l’Institut National de la Statistique (INS) et sont issues du recensement général de la population et de l’habitat de 1998 ainsi que des enquêtes Niveau de vie des ménages de 1998 à 2002. Les données utilisées sont toutes des données annuelles. Des données complémentaires ont été collectées auprès de la Direction de l’hydraulique humaine du ministère des Infrastructures Économiques.

Les données sur la consommation d’eau potable sont obtenues par le biais des recettes contenues dans les rapports financiers de la SODECI. Ces recettes sont disponibles par tranche, par commune et par année pour toutes les communes du pays. Sur la base de ces rapports, nous calculons les consommations totales et moyennes pour les différentes communes.

Le système tarifaire est le même pour les 156 communes du fait de la politique de péréquation des prix en vigueur dans le pays. En termes nominaux, ces prix n’ont pas beaucoup varié durant la période d’étude. Ils ont cependant été déflatés au moyen de l’indice des prix à la consommation en prenant l’année 1998 comme base. De cette grille tarifaire, nous calculons un prix moyen du m³ par année et par commune. Ce prix moyen[8] est égal à la recette totale collectée auprès des ménages (vente d’eau ajoutée au frais de connections et autres dépenses liées à l’eau) divisée par le volume total d’eau distribué aux ménages. Il a été en moyenne de 396 FCFA/m3[9] durant la période 1998-2002. Cette variable PRIX est également déflatée avec toujours 1998 comme année de base. Lprix est son logarithme.

La variable REVENU (Lrevenu en log) représente les dépenses totales moyennes des ménages au cours de l’année, que nous assimilons au revenu permanent. En effet, il n’existe pas en Côte d’Ivoire une base de données fiable à l’échelle nationale sur le revenu imposable des ménages. Cet état de fait ajouté à la part assez prépondérante du secteur informel dans l’activité économique du pays font des dépenses moyennes la meilleure approximation des revenus. Les données de la SODECI permettent d’avoir pour chaque année et pour chaque commune, les dépenses totales en eau de ses abonnés. Quant à l’INS, ses différentes enquêtes sur le niveau de vie des ménages fournissent, au niveau régional, les parts des dépenses en eau dans les dépenses totales des ménages. Les coefficients obtenus grâce aux données de l’INS ajoutés aux dépenses en eau fournies par l’opérateur nous permettent d’obtenir les dépenses totales des ménages par année et par commune. Il suffit donc de diviser les dépenses ainsi obtenues par le nombre d’abonnés dans chaque commune pour obtenir notre variable revenu. Tout comme le prix, cette variable a également été déflatée avec 1998 comme année de base.

La variable CONSO est la variable dépendante dans le modèle de demande. Elle représente la consommation moyenne d’eau des ménages, par année et par ville. Elle est calculée en divisant le volume total d’eau distribué aux ménages par le nombre d’abonnés. Elle a été en moyenne (non pondérée par le nombre d’abonnés) de 120 m³/ abonné durant la période 1998-2002. Cette valeur masque de fortes disparités car la consommation moyenne par commune varie énormément d’une année à l’autre, mais également et surtout d’une localité à l’autre. Ainsi, en termes de consommation moyenne par localité, on enregistre 43 m³/an/abonné pour la ville de Yakassé Attobrou dans le sud-est du pays contre 332 m³/an/abonné pour la commune de Zone 4 (Abidjan). Selon les données individuelles de la SODECI, la consommation moyenne d’eau par jour et par habitant en Côte d’Ivoire est de 72 litres/jour/habitant.

La description des autres variables utilisées ainsi que les statistiques descriptives associées sont données en annexe.

4. Les résultats des estimations

4.1 Le choix des tranches

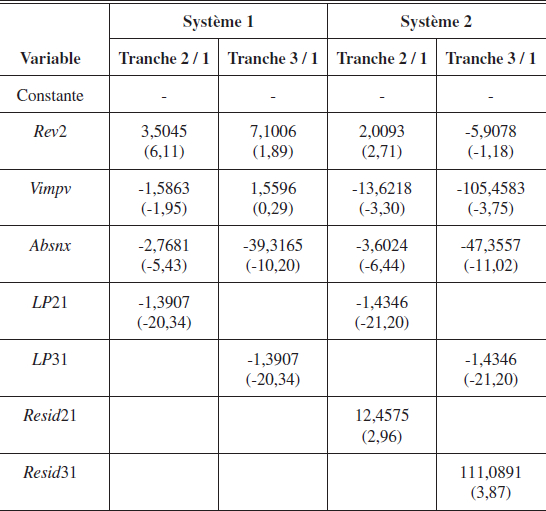
L’analyse économétrique débute par l’estimation du système d’équations de choix de tranches défini par (11) qui découle du logit multinomial afin d’obtenir les proportions de ménages dans chaque tranche. Puisqu’il y a trois tranches de facturation dans le barème tarifaire, le système à estimer se compose de deux équations dans notre étude. Les deux variables à expliquer sont le logarithme du rapport des volumes d’eau dans les tranches tarifaires (LA2 et LA31) et les variables explicatives[10] sont REV2, VIMPV, ABSNX, LP21 et LP31. Ces deux dernières variables sont des variables de prix et représentent le rapport entre les prix moyens du m³ d’eau dans chaque tranche. L’une des hypothèses fondamentales du logit que nous utilisons étant l’identité des caractéristiques pour les différents résultats possibles du choix, nous contraignons les coefficients de ces deux variables à être les mêmes dans le système estimé et les considérons ainsi comme une caractéristique des communes. Les variables VIMPV et ABSNX sont vraisemblablement liées au revenu ainsi qu’aux caractéristiques de logement, et par conséquent correlées à REV2 à travers les effets fixes spécifiques aux différentes localités. Ainsi, pour l’estimation de ce système, la procédure within - Triples Moindres Carrés[11] a été utilisée, car cette procédure est convergente en présence d’un effet individuel inobservable, constant tout au long de la période et éventuellement corrélé avec les variables explicatives. En outre, étant donné que tous nos régresseurs varient dans le temps, l’utilisation de cette procédure est bien appropriée pour cette estimation. Par ailleurs, la présence des impayés (VIMPV) dans les équations expose notre système à un éventuel biais d’endogénéité. Avant d’estimer le choix des tranches, nous traitons cette endogénéité à travers le test proposé par Nakamura et Nakamura (1981)[12], une version du test d’endogénéité de Hausman. Le tableau 1 donne les résultats de ce test.

Tableau 1

Test d’endogénéïté de Nakamura et Nakamura

Note : Les statistiques de Student sont entre parenthèses

Pour chacun des systèmes d’équations de choix des tranches, la tranche 1 est prise comme modalité de référence. La première équation de chaque système donne le choix de la tranche 2 sur la tranche 1 et la seconde, le choix de la tranche 3 sur la première. Le système 1 est l’estimation du logit multinomial décrit plus haut en supposant l’exogénéité des impayés. Le système 2 représente le test du biais d’endogénéité. Les biais d’endogénéité (Resid21 et Resid31) sont très significatifs dans ce système, ce qui nous permet de rejeter l’hypothèse d’exogénéité des impayés. Le système issu du logit est donc à nouveau estimé en prenant les valeurs prédites des impayés (Vimp21 et Vimp31) et non leurs valeurs observées.

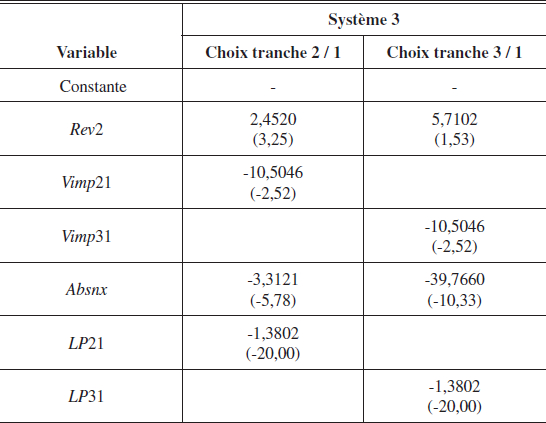
Une fois cette endogénéité traitée, nous estimons maintenant les choix des tranches opérés par les ménages. Pour respecter les hypothèses du logit utilisé, nous avons contraint les coefficients de Vimp21 et Vimp31 à être égaux. Les résultats de cette dernière estimation sont reportés dans le tableau 2.

Tableau 2

Estimation des équations de choix de tranche

Note : Les statistiques de Student sont entre parenthèses

Tous les coefficients de ce système sont significatifs au seuil de 5 % à l’exception de Rev2 dans le choix de la tranche 3 par rapport à la tranche 1, et ont le signe attendu. Ainsi, l’équation 1 (Choix tranche 2 / 1) montre que le revenu a un effet positif sur la probabilité de choisir la tranche 2 par rapport à la tranche 1 tandis que les impayés, le prix relatif et la proportion d’abonnés subventionnés dans les nouveaux abonnés ont un effet négatif sur la probabilité de choisir la tranche 2 par rapport à la tranche 1. On retrouve les mêmes conclusions dans l’équation 2 (Choix tranche 3 / 1) pour le choix entre les tranches 1 et 3. Ces résultats restent valables lorsqu’on change de tranche de référence. Ainsi, lorsque la tranche 3 est prise comme modalité de référence, tous les coefficients changent de magnitude, mais également et surtout de signe. Lorsque c’est la tranche 2 qui est prise comme référence, le revenu a un effet positif sur la proportion de ménages qui choisissent la tranche 3 et un effet négatif sur la proportion de ceux qui choisissent la tranche 1[13].

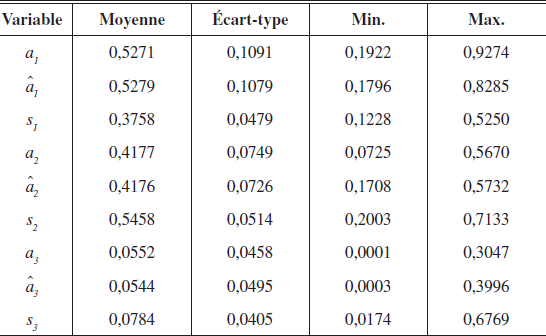
L’étape suivante consiste à déterminer les proportions estimées de ménages dans chaque tranche de facturation. Pour ce faire, comme indiqué dans la section 2, nous récupérons les effets fixes dans les équations 1 et 2 du système 3 précédent afin de calculer le coefficient qui permet de passer du rapport entre volumes au rapport entre proportions. En utilisant l’équation (15), les proportions s₁, s₂, et s₃ se calculent aisément. L’analyse des statistiques descriptives des rapports entre volumes prédits par le modèle et les proportions de ménages dans les tranches qui s’ensuit est assez instructive comme le montre le tableau 3.

Tableau 3

Proportions estimées de volume d’eau et de ménages par tranche

Note : 780 observations. a_i est la proportion du volume d’eau facturée dans la tranche i et â_i sa prédiction. s_i est la proportion de ménages situés dans la tranche i.

En effet, d’un côté le modèle prédit parfaitement les différentes variables à expliquer du système d’équations (a₁, a₂ et a₃) et de l’autre, les proportions de ménages simulées (s₁, s₂ et s₃) montrent que notre hypothèse n’implique pas la proportionnalité entre le volume d’eau facturé dans une tranche et le nombre de ménages dans cette dernière. Ainsi, on constate que la tranche 1 qui enregistre environ 52,71 % des volumes d’eau facturés (a₁) ne contient en fait que 37,58 % des ménages en moyenne (s₁). Par contre la tranche 2 qui ne compte que pour 41,77 % des volumes d’eau facturés (a₂) contient 54,58 % des ménages (s₂). Quant à la tranche 3, elle compte 5,20 % et 7,84 % respectivement pour les proportions de volumes d’eau (a₃) et de ménages (s₃). La tranche 2 représentant la tranche du milieu et ajoutant à cela son épaisseur (72 m³ contre seulement 18 m³ pour la tranche 1), ces approximations semblent assez proches de la réalité.

4.2 La demande agrégée

Une fois obtenues, les proportions sont utilisées pour créer les variables prix moyen et revenu virtuel moyen [14]. Ces deux variables ainsi créées mesureront respectivement, dans l’équation agrégée, l’effet du prix et du revenu sur la consommation d’eau. Pour compléter la fonction de demande, nous y avons inclus d’autres variables telles que le nombre de personnes ayant accès à l’eau potable grâce à un branchement domiciliaire (Acces), le rendement du réseau de distribution (Rendt) et l’équivalent en volume d’eau des factures impayés par ménage (Vimp).

L’étape finale consiste à estimer les paramètres structurels de la demande d’eau ainsi spécifiée. Pour ce faire, nous utilisons la procédure within avec des écarts-types robustes[15]. Par ailleurs, à titre de comparaison, nous avons estimé une autre fonction de demande qui utilise les variables PRIX et REVENU définies à la section 2. En substituant ces variables de prix et de revenu aux variables et précédemment définies, la fonction de demande d’eau est à nouveau estimée, dans une spécification log – log, avec la procédure within et écarts-types robustes. L’ensemble des résultats est présenté dans le tableau 4 où les résultats des estimations par moindres carrés ordinaires (MCO) et moindres carrés généralisés (MCG) ont été également reportés.

Tableau 4

Estimation de la demande agrégée

Note : 780 observations. Les statistiques de Student sont entre parenthèses.

Le coefficient du prix (en valeur absolue) est sous-estimé par les MCO, tandis que le paramètre sur le revenu est surestimé par les MCO et les MCG, comparé à celui obtenu avec la procédure within. De ces estimations, l’élasticité-prix et l’élasticité-revenu[16] sont aisément calculées de même que leur écart-type avec la méthode Delta. Les élasticité-prix et élasticité-revenu obtenues ont le signe attendu et sont statistiquement significatives (les ménages ajustent à la baisse leur consommation moyenne lorsque le prix de l’eau augmente, et ils augmentent leur consommation moyenne d’eau lorsque leur revenu s’accroît).

La procédure des MCO est convergente pour les modèles sans hétérogénéité inobservée spécifique à chaque localité, alors que les MCG sont convergents et efficaces sous l’hypothèse que les variables explicatives ne sont pas corrélées à l’effet individuel communal. La statistique du test de Hausman portant sur la comparaison entre les estimateurs within et MCG est χ²(5) = 70, par conséquent l’hypothèse nulle d’effets aléatoires, est fortement rejetée. Ainsi, les estimateurs MCO et MCG (tous convergents sous la spécification effets aléatoires) sont rejetés au profit du modèle à effets fixes.

Le modèle log-log du tableau 4 est une méthode d’estimation efficiente d’une fonction de demande d’eau. Dans un premier temps, nous analysons l’endogénéité de la variable prix utilisée. Pour ce faire, le prix est instrumenté par des variables censées être exogènes (reseau, rendt, nxabon et vmenv). Ces variables affectent les coûts de production mais n’expliquent pas a priori le niveau de consommation par tête en eau potable des ménages résidentiels. Même si les prix unitaires des tranches sont administrés et uniformes entre les communes, les prix moyens sont variables du fait des charges fixes et des frais de connexion, et dépendent en dernier ressort des coûts de production. Le test de validité des instruments utilisés (test de suridentification) est calculé, selon la procédure robuste à l’hétéroscédasticité de Wooldridge (2002 : 123). Avec trois conditions suridentifiantes, la statistique de test vaut χ²(3) = 2,0210 (p-value de 0,5659), l’hypothèse nulle de validité des instruments n’est donc pas rejetée. La statistique du test de Hausman pour la comparaison entre within et within instrumenté est χ²(4) = 0,41; par conséquent l’hypothèse nulle d’exogénéité du prix n’est pas rejetée et nous n’avons pas besoin d’instrumenter la variable prix.

Dans un second temps, nous étudions la corrélation éventuelle entre les variables explicatives et l’effet individuel. La statistique du test de Hausman pour la comparaison entre within et MCG est χ²(5) = 117,92, ce qui permet de rejeter fortement l’hypothèse nulle d’absence de corrélation entre effets fixes et variables explicatives. Ici, les estimateurs MCG sont également rejetés au profit du modèle à effets fixes[17]. L’avantage de ce modèle log-log est que ses paramètres estimés sont directement des élasticités. Cependant, de par sa construction, il ignore totalement la structure par paliers du tarif étudié et l’estimation perd du coup certaines informations notamment le choix des tranches opéré par les ménages. Ainsi, de toutes les spécifications du tableau 4, celle de la colonne dénommée within (colonne 3) semble la plus proche de la réalité. Par conséquent, nous utiliserons les estimations de paramètres structurels qui y sont reportées pour tirer les conclusions de notre étude.

Avec les paramètres estimés de la procédure within, l’élasticité-prix est égale à -0,8119 (écart-type de 0,1072) et l’élasticité-revenu est égale à 0,1453 (écart-type de 0,0406). Ces deux coefficients sont très significatifs et indiquent qu’en moyenne, en Côte d’Ivoire, pour une hausse de 1 % du prix de l’eau, les ménages diminuent de 0,81 % leur consommation d’eau; et pour une hausse de 1 % de leur revenu, les ménages augmentent de 0,15 % leur consommation de ce bien. Par conséquent, l’eau en Côte d’Ivoire peut être considérée, selon la théorie microéconomique, comme un bien de première nécessité; c’est-à-dire un bien normal (élasticité-revenu positive et inférieure à 1) dont la demande est inélastique (une élasticité-prix inférieure en valeur absolue à 1). Ces paramètres estimés sont cependant très élevés par rapport à ceux obtenus, en moyenne, dans des études similaires portant sur les pays riches. Cette différence de magnitude semble cohérente avec l’idée selon laquelle, en moyenne, plus les populations sont pauvres plus elles feront attention à leurs dépenses et aux fluctuations de prix des biens de consommation courante. Il n’existe malheureusement pas à notre connaissance d’études sur la demande d’eau pour les pays de la région permettant d’effectuer des comparaisons.

D’autres variables incluses dans la fonction de demande estimée permettent de faire ressortir certains effets. La variable Acces a un effet négatif sur la consommation moyenne des ménages. Cet effet est assez intuitif, car il montre que plus le nombre de personnes ayant accès à l’eau potable par le biais d’un robinet à domicile augmente, plus la consommation moyenne d’eau des ménages baisse. Ceci reflète une certaine réalité des PED en général et de la Côte d’Ivoire en particulier, à savoir la présence de compteurs collectifs dans les logements collectifs (« cours communes » selon la terminologie locale). Le compteur appartient en général à un ménage (le mieux nanti dans bien des cas) et les autres ménages de la cour commune viennent s’y approvisionner en eau potable (buvable et/ou utilisable pour la cuisine). À l’exception notable des communes d’Abidjan, ces cours communes sont le plus souvent équipées de puits où est puisée l’eau servant pour les autres usages domestiques (vaisselle, lessive, etc.). Partant de cette situation, la pose d’un second compteur dans une telle habitation – même si elle accroît la consommation totale d’eau – se traduit inéluctablement par la baisse de l’eau facturée au premier ménage. Ainsi, le développement des compteurs individuels encouragé par la SODECI par le biais des branchements subventionnés accroît certes la consommation totale d’eau mais entraîne la baisse de la consommation moyenne des ménages déjà connectés dans l’environnement décrit. Ceci est d’ailleurs assez intéressant pour les ménages car sous la tarification progressive par paliers en vigueur, l’usage collectif fait facilement monter la consommation d’eau dans les tranches supérieures où les prix marginaux sont plus élevés. Le rendement du réseau de distribution (Rendt) a un effet positif sur la consommation d’eau. Cela indique que les réseaux les plus efficaces (moins de fuites d’eau) sont également ceux où les niveaux de consommation d’eau sont relativement les plus élevés. Enfin, les impayés (Vimp) ont un effet positif sur la consommation des ménages. À première vue, cet effet paraît contre-intuitif. Mais une explication pourrait résider dans l’externalité positive sur les abonnés qu’ont les déconnections suites aux factures impayées. En effet, grâce à un système efficace de comptage et de facturation, le taux de recouvrement de la SODECI est assez élevé et par ricochet les déconnections pour arriérés également. Ainsi, l’interruption de la fourniture d’eau aux mauvais payeurs entraîne la décongestion du réseau et donc une réduction des baisses de pression aux heures de pointe. Cette réduction se traduit in fine par l’augmentation de la consommation des autres ménages restants connectés au réseau.

4.3 Spécificités régionales de la demande en eau

La SODECI est le seul opérateur d’eau potable en Côte d’Ivoire et sa concession couvre toutes les zones urbaines du pays. Cependant, les conditions climatiques, sociales et économiques sont assez différentes d’une région à l’autre dans le pays et il en résulte très certainement des consommations d’eau moyennes assez différentes. Dans l’optique d’une gestion plus efficace de ses activités, l’opérateur a découpé son périmètre de concession en 10 zones dénommées directions régionales (DR). Une DR est composée d’un ensemble de villes et le critère de regroupement est essentiellement la localisation géographique. Ainsi, pour prendre en compte l’hétérogénéité des différentes régions du pays, nous reprenons les estimations de la demande agrégée au niveau des directions régionales de la SODECI.

Comme pour l’estimation de la demande agrégée au niveau national, nous testons l’hypothèse nulle d’effets aléatoires par le biais d’un test d’Hausman. Les résultats des différents tests sont reportés dans le tableau 5. Tout comme dans la demande au niveau national les statistiques d’Hausman sont supérieures à la valeur du Khi-deux au seuil de 1 % pour quatre DR (Korhogo, Daloa, Man et Abidjan Nord). Il y a donc présence d’effets individuels tout au long de la période et nous utilisons comme précédemment la procédure within pour estimer la demande agrégée. À l’opposé, les statistiques d’Hausman sont inférieures à la valeur du Khi-deux au seuil de 5 % pour les six autres DR. Pour ces six régions, il n’y a donc pas d’effets fixes et nous estimons la fonction de demande d’eau par la méthode des moindres carrées généralisés.

Tableau 5

Test de spécification d’Hausman par DR

Note : DR : direction régionale. ddl désigne le nombre de degrés de liberté.

Pour les 10 demandes agrégées d’eau ainsi estimées, nous nous limiterons à l’analyse des élasticité-prix et élasticité-revenu que nous avons reportées dans le tableau 6. Les élasticités calculées sont en moyenne supérieures à celles obtenues au niveau national. En termes de revenu, l’élasticité régionale est inférieure à l’élasticité au niveau national (0,1453) pour trois DR (Bouaké, Abengourou et Man). Mais ces élasticités ne sont pas statistiquement significatives. En d’autres termes, le revenu n’a pas d’effets sur les décisions de consommation d’eau dans ces localités. A contrario, ces trois régions ont les élasticités-prix les plus élevées et celles-ci sont statistiquement très significatives. Pour ces régions, le prix semble donc être l’élément qui conditionne le plus les décisions de consommation d’eau potable. En termes de prix, seule la région de Yamoussoukro a une élasticité nettement inférieure à l’élasticité-prix nationale (-0,8119) mais celle-ci n’est pas statistiquement significative.

Tableau 6

Élasticité-prix et élasticité-revenu par DR

Note : DR : Direction Régionale. Les statistiques de Student sont entre parenthèses.

Au total, au niveau national et encore plus au niveau régional, les élasticités, notamment les élasticité-prix, sont assez élevées comparées à celles des pays riches. Cette situation pourrait en partie s’expliquer par la pauvreté de la plupart des ménages ivoiriens. En effet, selon l’indice de développement humain (IDH) de la Banque mondiale, la Côte d’Ivoire est classée 164^e sur 183 pays et 48,8 % de sa population vit avec moins de 2 dollars US par jour. Par ailleurs, à l’exception des communes de Zone 4 et Cocody (où vivent en général la frange la plus aisée de la population d’Abidjan), il existe des sources d’approvisionnement alternatives en eau potable. Ces solutions vont des revendeurs indépendants d’eau jusqu’aux puits, selon les localités.

5. Analyse de bien-être

Dans la section précédente, nous nous sommes limités à une approche positive de la théorie du consommateur en dérivant des fonctions de demande en eau. La connaissance de ces fonctions est cependant utile aux décideurs publics, à bien des égards, et permet de mener une approche normative du comportement des ménages. Plus particulièrement, les fonctions de demande permettent l’évaluation en termes monétaires du bien-être des usagers suite à un changement de prix. Les variations du bien-être peuvent être obtenues aisément et avec exactitude à partir des fonctions d’utilité indirectes. Cette méthode proposée par Hicks a permis de définir deux mesures couramment employées du bien-être des usagers suite à une variation de prix : la variation compensatoire (VC) et la variation équivalente (VE) du revenu. Dans la pratique, les fonctions d’utilité indirectes ainsi que les fonctions de demandes proposées par Hicks sont difficiles à quantifier et estimer. Ainsi, pour contourner cette difficulté, la plupart des études empiriques s’en remettent aux variations de surplus directement calculées à partir des fonctions de demande proposées par Alfred Marshall. Par ailleurs, Willig (1976) et Hausman (1981) démontrent – dans le cas d’une variation du prix d’un seul bien – qu’il est possible de calculer les variations exactes de bien-être directement à partir des estimations des fonctions de demande marshalliennes.

Dans ce qui suit, nous nous proposons d’évaluer l’impact monétaire dans deux cas de variation de prix en Côte d’Ivoire. D’un côté, nous simulons une hausse de 10 et 20 % du prix moyen du m³ d’eau en Côte d’Ivoire. De l’autre, nous simulons une politique tarifaire qui consisterait en une hausse de 10 % du prix marginal de la tranche 1 et une baisse de 5 % du prix marginal de la tranche 3, celui de la tranche 2 restant inchangé. L’année de référence est la dernière année de notre échantillon, c’est à dire 2002. Ces scénarii – même s’ils sont essentiellement exploratoires – sont motivés par le prix du m³ jugé assez bas pour les tranches inférieures.

5.1 Hausses du prix moyen

Le prix moyen considéré est celui obtenu en pondérant les prix marginaux des différentes tranches par la proportion de volume d’eau qui y est facturé. En termes de variation du bien-être, nous évaluons la variation du surplus ainsi que de la VC selon l’approche de Hausman. Nous obtenons sur l’échantillon les résultats présentés dans le tableau 7.

Tableau 7

Mesure de la variation de bien-être pour le prix moyen

Note : La variation du surplus a été directement calculée à partir des demandes marshaliennes. La variation compensatoire (VC) a été calculée à partir de la méthode de Hausman

La variation du surplus calculée directement à partir des demandes marshaliennes et la variation compensatoire (VC) calculée à partir de la méthode de Hausman donnent des résultats sensiblement différents. Dans les différents scénarios, la mesure exacte de la variation du bien-être représentée par la VC est supérieure à son approximation représentée par la variation du surplus, ce qui confirme l’approximation de Willig . En termes de variation compensatoire, une augmentation du prix moyen de l’eau de 10 % se traduirait en moyenne en Côte d’Ivoire par une réduction du bien-être des ménages de l’ordre de 1511 F CFA (2,30 euros) par ménage et par an. De même, une augmentation du prix moyen de l’eau de 20 % se traduirait en moyenne par une réduction du bien-être des ménages de l’ordre de 3153 F CFA (4,81 euros) par ménage et par an.

5.2 Variation des prix marginaux

Dans la pratique, les variations de prix moyens sont en fait induites par celles des prix marginaux. Envisageons donc les deux réformes tarifaires suivantes. La première (resp. le seconde) consiste en une hausse de 10 % (resp. 20 %) du prix marginal dans la tranche 1 et une baisse de 5 % (resp. 10 %) de celui de la tranche 3; le prix dans la tranche 2 restant constant. De telles réformes ont un effet sur le prix moyen de vente du m³, sur les choix de tranches opérés par les ménages ainsi que sur leur bien-être. Le tableau 8 résume les résultats de ces deux politiques tarifaires.

Tableau 8

Mesure de la variation de bien-être pour le prix marginal

Note : Les s_i sont les proportions de ménages dans les différentes tranches i. P est le prix moyen du m³ d’eau dans les différents schémas.

Avec la première politique (resp. la seconde) la proportion de ménages dans la tranche 1 (s₁) baisse et passe de 37,58 % à 34,38 % (resp. 31,53 %). À l’opposé, les deux autres tranches enregistrent plus de ménages que dans la situation initiale. Ainsi, s₂ passe de 54,58 % à 56,87 % (resp. 58,75 %) et s₃ passe de 7,84 % à 8,75 % (resp. 9,72 %) respectivement avec les réformes tarifaires 1 et 2. Ces mouvements de ménages dans les tranches tarifaires s’expliquent par le fait que les deux politiques simulées rendent la tranche 1 relativement plus coûteuse que la tranche 2, elle-même plus coûteuse que la tranche 3. Par conséquent certains ménages initialement dans la tranche 1 migrent vers la tranche 2 tandis que d’autres initialement dans cette dernière migrent vers la tranche 3.

Nous avons également reporté dans le tableau 8 les variations du prix moyen du m³ qui résulteraient de ces variations de prix marginaux. Ainsi, la première réforme (resp. la seconde) entraîne une hausse de 1,89 % (resp. 3,64 %) du prix moyen qui passe de 276,62 F CFA à 281,79 F CFA (resp. 286,69 F CFA). Avec ces variations de prix moyen, nous pouvons aisément évaluer, comme précédemment, les variations du bien-être induites par ces politiques tarifaires. Nous nous sommes limités au calcul de la variation compensatoire VC, également reportée dans le tableau 8.

Dans les deux cas, la perte de bien-être au niveau national est assez faible: en moyenne 258 F CFA avec la première politique et 515 F CFA avec la seconde. Il est certain que ces montants à l’échelle nationale cachent des disparités régionales que nous prenons en compte dans une autre étude (Diakité et al., 2009). Enfin, les variantes de ces politiques qui consisteraient en une variation des prix marginaux des tranches tout en laissant inchangé le prix moyen induit (ou de façon équivalente le bien-être) peuvent être envisagées. Elles auraient pour effets de modifier la répartition des ménages entre les tranches de consommation des schémas tarifaires.

Ces simulations de politiques tarifaires ainsi que les variations du bien-être et les choix de tranches qu’elles induisent, peuvent guider les décideurs publics à établir des schémas de partage efficace de la ressource en eau lorsque celle-ci est rare. Par exemple, calculée pour chaque type d’usagers, la variation compensatoire doit orienter les gestionnaires de l’eau dans leurs choix d’attribution de la ressource, un partage efficace d’une ressource rare étant obtenu en égalisant les prix de vente aux valorisations marginales des différents types d’usagers (ménages, agriculteurs, industriels, etc.).

Conclusion

L’objectif de cet article était d’estimer une fonction de demande d’eau afin d’évaluer la sensibilité de la consommation d’eau des ménages au prix et au revenu. La fonction de demande spécifiée repose sur l’hypothèse de séparabilité entre l’eau et les autres biens, justifiée par l’absence de biens totalement substituables à l’eau potable. En outre, cette fonction de demande, linéaire et localement flexible dans les paramètres, satisfait les conditions d’intégrabilité et on en dérive aisément la fonction d’utilité qui lui est associée.

À partir de travaux similaires sur le sujet, nous avons estimé une fonction de demande d’eau agrégée sous une tarification de type « progressive par paliers ». L’estimation en deux étapes que cette forme de tarification suggère a été appliquée. Dans la première étape, pour pallier l’absence d’informations sur les proportions d’individus à l’intérieur de chaque tranche, une méthode d’approximation de celles-ci basée sur le volume d’eau facturé dans chaque tranche a été adoptée. Le modèle considéré à cette étape indique que le revenu a un effet positif sur le choix des tranches de facturation supérieures tandis que le prix relatif de la tranche, les impayés et la proportion d’abonnés subventionnés conduisent les ménages à choisir les tranches inférieures. Dans la seconde étape, l’estimation globale de la fonction de demande agrégée fait apparaître, dans la spécification la plus appropriée à notre sens, une élasticité-prix de -0,81 et une élasticité-revenu de 0,15. Ces estimations confèrent à l’eau potable sa qualité de bien de première nécessité selon la théorie microéconomique. Par ailleurs, ces coefficients, assez élevés eu égard à ceux obtenus dans les pays riches (États-Unis, Canada, France et Espagne notamment), semblent cohérents avec l’hypothèse selon laquelle plus le ménage est riche, moins il est sensible à ses dépenses en biens de première nécessité en particulier sa facture d’eau.

Cette étude sur la demande d’eau est une première en Côte d’Ivoire et, à notre connaissance, l’une des rares disponibles pour l’Afrique occidentale. Mais le peu de variabilité du prix de l’eau durant notre période d’étude ajouté à la méthode d’approximation utilisée dans la première étape de l’estimation nous obligent à tempérer quelque peu notre enthousiasme vis-à-vis des résultats ainsi obtenus. Des études ultérieures avec notamment une base de données plus riche seraient nécessaires pour valider ces paramètres estimés. Cependant, faute de mieux, les élasticités qu’elle a permis d’obtenir peuvent servir dans des évaluations de politiques tarifaires à but exploratoire dans le système d’AEP en Côte d’Ivoire.

Notes

• [1] Le prix moyen s’écrit par exemple, dans le cas d’un tarif binôme, PM = pma + CF/q, où pma est le prix marginal, CF la charge fixe et q le volume consommé.
• [2] Dans notre étude, nous disposons de données agrégées à l’échelle de la commune. Nous les divisons par le nombre d’abonnés au service eau dans chaque commune afin d’obtenir des données par abonné ou ménage représentatif.
• [3] Dans cet article, la variable différence est définie comme suit : , où d₁ = –fc. Elle est l’opposée de celle de Taylor (1975) et Nordin (1976) et dans notre cas, fc = 0 car les ménages ne font pas face à des charges fixes.
• [4] Ces auteurs notent cependant la non-prise en compte par la demande agrégée des ménages situés aux « coudes » des contraintes budgétaires. Tout comme eux, une étude statistique de nos données montre très peu de points de ce type dans la base.
• [5] Voir Berry (1994).
• [6] Il y a autant de vecteurs d’effets fixes qu’il y a d’équations, à savoir (m – 1).
• [7] Nous nous sommes arrêtés à 2002 car depuis octobre de cette année-là, suite à une rébellion armée, la Côte d’Ivoire se trouve coupée en deux. La guerre a entraîné de vastes mouvements de populations et les données disponibles pour la partie sous contrôle rebelle sont des approximations.
• [8] Le tarif en vigueur ne comporte pas de partie fixe. Ainsi, une fois payés les frais de raccordement au service, les abonnés font face à une facture de montant égal à leur consommation multipliée par le prix des mètres cubes selon les tranches.
• [9] 1 euro équivaut à environ 655 FCFA.
• [10] Voir en annexe la description de ces différentes variables.
• [11] Pour ce faire, nous avons initialement transformé les variables selon la procédure within et ensuite appliqué les Triples Moindres Carrés aux variables transformées.
• [12] Pour ce test, on estime d’abord l’équation en supposant une absence totale d’endogénéité (système 1). Ensuite, la variable suspecte (Vimpv) est régressée sur les autres variables de l’équation en y ajoutant d’autres variables censées être exogènes (Rendt et Vmenv). On y récupère les résidus (Resid21 et Resid31), dénommés biais d’endogénéité, que l’on ajoute comme variables explicatives dans la première équation pour estimer à nouveau cette dernière (système 2). Si le biais d’endogénéité n’est pas significatif, on ne rejette pas l’hypothèse d’exogénéité et la toute première estimation est valide. Par contre, si le biais d’endogénéité est significatif, l’hypothèse d’exogénéité est rejetée et on estime de nouveau l’équation initiale (système 3) mais en remplaçant la variable suspecte (Vimpv) par sa prédiction (Vimpv21 et Vimpv31).
• [13] D’autres régressions du même type avec d’autres variables de prix ont été menées et confirment les résultats précédents. Mais, de toutes ces spécifications, celle dont les coefficients sont reportés dans le tableau 2 produit de loin les meilleurs résultats, nous les conservons donc dans la suite.
• [14] Étant donné le peu de variabilité des prix et donc de la variable différence, nous ne dissocions pas cette variable du revenu comme originellement préconisé par Taylor (1975) et Nordin (1976). Avec la spécification retenue, on ne peut tester la relation supposée en théorie entre la variable différence et le revenu.
• [15] Les écarts-types robustes sont obtenus en corrigeant de l’hétéroscédasticité inhérente aux données de panel, par la formule d’Huber-White.
• [16] Pour les modèles 1, 2 et 3, ces élasticités ont été évaluées au point moyen pondéré par le nombre d’abonnés de chaque commune, c’est à dire :

  Pour le modèle 4, étant donné la spécification log – log, la régression donne directement les élasticités.

• [17] L’analyse n’a pu être conduite jusqu’aux estimations plus efficientes proposées par Breusch, Schmidt et Mizon (1989) faute d’instruments valides. Cependant, tous nos régresseurs variant dans le temps, on peut se limiter à cette étape car tous nos paramètres sont identifiés.