Résumés
Résumé
Cet article présente la version statique du modèle d’équilibre général calculable (MEGC) développé pour le ministère des Finances du Québec. C’est un MEGC de grande taille, multisectoriel et birégional, du Québec et du reste du Canada. L’exposé est centré sur les taux effectifs marginaux d’imposition (TEMI) et la mobilité partielle du capital. L’objectif est de décrire une technique de modélisation qui permet d’aborder l’allocation du capital dans le cadre d’un modèle statique, bien que cette question soit fondamentalement dynamique. Les TEMI mesurent l’écart entre le taux de rendement payé aux détenteurs de capital et la valeur du produit marginal du capital. Ils synthétisent donc les multiples distorsions que peut créer la fiscalité dans les incitations touchant l’allocation des ressources. Leur utilisation devient intéressante lorsque le capital est mobile entre ses utilisations concurrentes. Dans la version statique du modèle, le capital n’est pas parfaitement mobile, comme cela serait approprié dans un modèle statique à très long terme; il est plutôt partiellement mobile entre industries et régions, la mobilité étant limitée par une borne supérieure sur la quantité de capital qui peut quitter une industrie donnée dans une région donnée. De plus, il y a dans le modèle un certain degré de mobilité internationale du capital, sous la forme d’une offre à élasticité-prix constante. Les résultats de simulation présentés montrent que le comportement du modèle est en accord avec les anticipations théoriques.
Abstract
This paper presents some of the outstanding innovations featured in the static version of the large, multisector, bi-regional computable general equilibrium (CGE) model of Quebec and the Rest-of-Canada developed for the ministère des Finances du Québec. It focuses on the marginal effective tax rate (METR) approach to capital taxation, and partial capital mobility. The objective is to describe a modelling technique to examine capital allocation with a static model, in spite of the fact that it is a fundamentally dynamic issue. METRs measure the “fiscal wedge” between the rate of return paid to capital owners, and the value of the marginal product of capital. So they synthetize the numerous distortions in resource allocation incentives which may result from the tax system. The introduction of METR’s becomes interesting when capital is mobile between competing uses. In the static version of the model, capital is not perfectly mobile, as would be appropriate in a very long term static model; rather, it is partially mobile between industries and regions, mobility being restrained by imposing an upper bound on the quantity of capital that may leave a given industry in a given region. In addition, there is some degree of international capital mobility in the model, in the form of constant price-elasticity supply. In simulation results, the model’s behaviour is consistent with analytical expectations.
Corps de l’article
Introduction
Les modèles d’équilibre général calculable (MEGC) sont une application empirique du modèle théorique d’équilibre général concurrentiel de Walras[1]. Les comportements des agents économiques y sont représentés par des relations dérivées de modèles microéconomiques d’optimisation. L’équilibre résulte de l’ajustement entre l’offre et la demande par le jeu des prix, puisque ceux-ci influencent effectivement les choix des agents économiques. Comme les modèles entrées-sorties (IO – input-output), les MEGC mettent l’accent sur les liens d’interdépendance, mais à travers un mécanisme de régulation par les prix, ce dont sont dépourvus les modèles IO. Les MEGC sont donc libérés des hypothèses rigides de stricte proportionnalité et d’offre parfaitement élastique des modèles IO.
La plupart des MEGC sont aussi détaillés que le serait un modèle IO correspondant. De plus, comparés aux modèles IO, les MEGC englobent le plus souvent l’ensemble de l’économie, à l’instar des modèles basés sur des matrices de comptabilité sociale (MCS)[2], et non seulement le système productif comme les modèles IO. Enfin, les MEGC sont très flexibles, ce qui a permis d’en généraliser la spécification pour représenter, par exemple, des situations de déséquilibre, de concurrence imparfaite, etc.
Grâce à leur capacité à représenter la complexité des interactions et de leurs influences sur le comportement des agents dans l’ensemble de l’économie, les MEGC sont donc des outils extrêmement puissants, voire indispensables, d’analyse des politiques économiques et fiscales ou de simulation des effets de changements exogènes de la structure des prix (comme par exemple, les variations du prix mondial du pétrole). Ils permettent aussi d’examiner certains effets d’offre : les conséquences d’une augmentation du stock de capital ou de l’offre de travail par exemple. Ce sont ces considérations qui ont poussé le ministère des Finances du Québec à se doter d’un tel modèle.
Cet article a un objectif méthodologique : il présente les innovations les plus remarquables que comporte le modèle d’équilibre général calculable (MEGC) développé pour le ministère des Finances du Québec (MEGFQ)[3]. Il s’agit d’un modèle multisectoriel birégional du Québec et du reste du Canada, de grandes dimensions. La version du modèle présentée ici est statique, tandis que la version couramment utilisée par le ministère des Finances est dynamique. C’est néanmoins dans la version statique qu’ont été développées les innovations mises en valeur ici : la représentation de la fiscalité au moyen des taux effectifs marginaux d’imposition (TEMI)[4], la mobilité partielle du capital et l’offre endogène de travail par les ménages. Cet article découle d’un document de recherche publié par le ministère des Finances du Québec (Decaluwé et al., 2005). Le même document est à la source de deux autres articles (Decaluwé et al., 2006 et 2010), dans lesquels l’accent est mis sur le marché du travail et l’offre endogène de travail et où sont discutées d’autres simulations que celles présentées ici.
Le reste de l’article est divisé en trois sections, suivies d’une brève conclusion synthèse. La prochaine section présente les traits saillants du modèle en mettant l’accent sur ses aspects plus novateurs, en particulier quant au marché du travail. La section suivante montre comment l’approche des TEMI s’applique dans le modèle et comment est représentée la mobilité partielle du capital. La dernière section expose les résultats de deux simulations qui mettent en relief les effets de la mobilité partielle du capital.
1. Approche générale et structure du modèle
1.1 Un modèle birégional
Le modèle d’équilibre général pour le Québec est un modèle d’équilibre général calculable (MÉGC) multisectoriel, adapté pour tenir compte des caractéristiques et spécificités du Québec, dans un contexte canadien et mondial. Concrètement, le Québec fait partie du Canada et, en tant que tel, est soumis aux politiques fiscales et monétaires du gouvernement fédéral ainsi qu’aux règles de libre circulation à l’intérieur des frontières canadiennes.
Étant donné l’imbrication du Québec dans le Canada, le modèle est donc un modèle birégional où, non seulement l’économie du Québec, mais aussi celle du reste du Canada (RdC) sont modélisées de façon explicite, tout en tenant compte de leurs relations mutuelles et avec le reste du monde. Cela permet de prendre en compte les effets de rétroaction (feedback effects) entre les deux économies. En outre, en plus de représenter les effets directs des politiques fédérales et provinciales, le modèle tient compte, grâce à sa structure birégionale, de leurs effets indirects, c’est-à-dire qui touchent le Québec par le biais des effets de ces mêmes politiques sur le reste du Canada et vice-versa.
Dans le modèle, les agents économiques sont classés en quatre catégories : les entreprises, les ménages, les gouvernements et l’étranger. Tous les agents prennent les prix comme donnés. Mais tandis que les deux premiers ont un comportement d’optimisation, les deux derniers n’en ont pas. Tous respectent néanmoins leurs contraintes budgétaires.
Il s’agit d’un modèle de grande envergure, très détaillé, où la classification des activités et des biens et services est proche de l’agrégation M des comptes entrées-sorties de Statistique Canada. Signalons que la modélisation du reste du Canada est aussi détaillée que celle du Québec, sauf pour ce qui est des gouvernements. Dans le cas des gouvernements, il n’est pas tenu compte de la subdivision du reste du Canada en provinces et territoires, de sorte que les gouvernements des neuf autres provinces sont agrégés en un seul agent, comme le sont tous les gouvernements locaux et régionaux hors-Québec. On distingue dans chacune des deux régions : 56 secteurs productifs, 121 catégories de biens et services et 48 catégories de dépenses personnelles de consommation. Les investissements sont répartis en 13 catégories. Il y a 150 types de ménages au Québec et 155 au Canada[5], définis selon la composition du ménage, le niveau de revenu et le groupe d’âge. Cette classification très fine des ménages permet d’évaluer les impacts sociaux des politiques fiscales, selon l’approche de l’agent représentatif, où tous les agents d’une même catégorie sont réputés avoir les mêmes caractéristiques et se comporter de manière identique (cela implique en particulier que la variance intragroupe des revenus des ménages soit nulle)[6]. La demande de travail distingue dans chaque région 11 types de main-d’oeuvre; cette nomenclature est une agrégation des grands groupes de la classification type des professions de 1980. Enfin, on trouve dans le modèle deux types de capital, qui correspondent aux deux agents entreprises : les sociétés et les entreprises individuelles[7].
Le caractère birégional du modèle apparaît nettement dans la matrice de comptabilité sociale, dont la structure générale est représentée dans le schéma de l’annexe 1. Deux séries parallèles de comptes représentent, l’une l’économie du Québec et l’autre, celle du RdC. Les échanges entre le Québec et le RdC apparaissent dans les secteurs de la matrice où les colonnes des comptes du Québec croisent les lignes des comptes du RdC et vice-versa. On trouve là les importations de chaque région en provenance de l’autre (qui, par définition, sont identiques aux exportations de l’autre région). On y trouve aussi les transferts entre ménages du Québec et du RdC, ainsi que les salaires versés à des résidants de l’autre région.
Une des originalités du modèle, inspirée de Round (1988), est l’introduction de comptes suprarégionaux, afin de prendre en compte les transactions entre agents qui ne peuvent être reliées à une notion de territorialité régionale. Dans notre modèle, les comptes de niveau suprarégional sont : les comptes d’intérêts et de dividendes, le compte du reste du monde (RdM, hors Canada), les comptes du gouvernement fédéral consolidé et le compte d’accumulation. Le lecteur trouvera des détails sur la raison d’être de chacun de ces comptes dans Decaluwé et al. (2005). La structure de la matrice de comptabilité sociale avec les comptes suprarégionaux est représentée dans le schéma de l’annexe 1.
Un soin particulier a été apporté à la représentation de la fiscalité. Chaque taxe s’applique dans le modèle à un flux qui représente d’aussi près que possible l’assiette fiscale correspondante. C’est le cas notamment des taxes indirectes, qui s’appliquent pour ainsi dire en couches successives les unes sur les autres. De plus, le modèle prévoit que les taux de taxes indirectes peuvent être différents, selon qu’il s’agisse de dépenses de consommation des ménages, d’investissement ou de consommation intermédiaire. L’impôt sur le revenu des particuliers et des sociétés est représenté par les taux effectifs marginaux d’imposition (TEMI); nous reviendrons sur ce point, brièvement à propos de l’offre de travail des ménages (section 1.3) et de façon plus détaillée à propos du capital (section 2.1).
Le modèle se distingue aussi par la présence d’une wage curve pour déterminer l’équilibre du marché du travail (section 1.2), par la spécification novatrice de l’offre de travail (section 1.3) et par la mobilité partielle du capital (section 2.2). Pour le reste, sa structure générale est relativement standard. Pour chaque région, le modèle reproduit le circuit classique des revenus et dépenses. Les facteurs de production (travail et capital) sont utilisés dans la production de biens et services qui sont, soit vendus localement, soit exportés vers l’autre région ou vers l’étranger. Conjointement, l’offre et la demande sur les marchés des facteurs déterminent les taux de salaire et de rendement du capital, et par là, la rémunération des facteurs. Celle-ci se traduit en revenu pour les agents économiques : une fois pris en compte les transferts entre agents (y compris les impôts sur le revenu) et l’épargne, les revenus engendrent la demande finale. Cette dernière, combinée à la demande intermédiaire, constitue la demande intérieure, qui interagit avec l’offre des producteurs locaux et celle de l’autre région et du reste du monde. Sont ainsi déterminés les prix et les quantités des produits achetés localement et importés, ce qui boucle la boucle. Il s’agit donc bel et bien d’un modèle d’équilibre général, où les prix et les quantités d’équilibre sont déterminés par l’interaction de l’offre et de la demande sur les marchés.
Dans la version statique présentée ici, le modèle ne s’intéresse toutefois pas à l’accumulation des facteurs (évolution du stock de capital, démographie et évolution de la main-d’oeuvre); les phénomènes dynamiques et intertemporels ne sont pas incorporés dans le comportement des agents. Le modèle décrit ici diffère donc de la version dynamique du MEGC couramment utilisée par le ministère des Finances : il est fondamentalement statique, même si le traitement de la mobilité du capital comporte implicitement une dimension temps.
1.2 Taux de salaire, taux de chômage et équilibre du marché du travail
Une représentation réaliste du fonctionnement du marché du travail ne saurait faire fi de la réalité du chômage. C’est pourquoi, dans notre modèle, les marchés du travail ne sont pas en équilibre au sens strict de la théorie microéconomique, puisque, au taux de salaire qui prévaut dans la solution du modèle, les quantités offertes et demandées ne sont pas égales. Il s’agit néanmoins d’un « équilibre » au sens large, en ce que le taux de chômage qui résulte de l’interaction entre l’offre et la demande doit être compatible avec le taux de salaire.
La compatibilité entre le taux de chômage et le taux de salaire est représentée par une « courbe salaire-chômage » (wage curve en anglais; Blanchflower et Oswald, 1995; Card, 1995). Cette notion, généralement acceptée aujourd’hui, est issue d’une série d’études empiriques, menées avec des données provenant de plusieurs pays, qui montrent une relation à pente négative entre le taux de chômage et le taux de salaire sur les marchés de travail locaux (dans notre modèle, nous considérons comme « local » le marché de travail d’une profession donnée dans une région donnée). La courbe salaire-chômage (CSC) est le lieu géométrique des couples de valeurs compatibles du taux de chômage et du taux de salaire. Le graphique 1 illustre la forme de la CSC telle que développée par Blanchflower et Oswald (1995).
Graphique 1
Détermination du salaire et du chômage selon une wage curve
Sa forme algébrique est donnée par
Selon Blanchflower et Oswald (1995) et Card (1995), il ressort des études réalisées sur plusieurs pays que la CSC est « virtuellement identique d’un pays à l’autre et stable dans le temps » avec une élasticité e généralement proche de –0,1[8]. Pour le cas spécifique du Canada, Blanchflower et Oswald (1995) trouvent une élasticité e globale égale à –0,09, une estimation basée sur des données statistiques de 1972-1987. L’élasticité des courbes salaire-chômage du MEGFQ ont été estimées par Danielle Bilodeau et Laurence Bargaud, de l’ISQ, au moyen de données microéconomiques de l’Enquête sur les finances des consommateurs (EFC) pour la période 1981-1997 et de l’Enquête sur la dynamique du travail et du revenu (EDTR) pour 1997-2001.
1.3 L’offre endogène de travail
On ne compte plus les MEGC avec offre de travail endogène. Mentionnons Ballard et al. (1985), Tarr (1989), de Melo et Tarr (1992), Berg et Reinert (1995), Blonigen et al. (1997), Decaluwé et al. (2002) et Annabi (2003). Dans tous les cas, on élargit la liste des biens de consommation pour y inclure le loisir, en supposant que celui-ci est un bien normal, dont le coût de renonciation est égal au taux de salaire. Un accroissement du taux de salaire a un effet de revenu et un effet de substitution. D’un côté, l’accroissement du taux de salaire fait monter le coût de renonciation du loisir et incite le consommateur à travailler davantage (consommer moins de loisir) : c’est l’effet de substitution. De l’autre côté, la hausse du taux de salaire augmente le revenu réel, ce qui pousse à une plus grande consommation de tous les biens normaux, y compris le loisir : c’est l’effet de revenu[9].
Mais comment modéliser l’offre de travail endogène dans un MEGC où l’on distingue plusieurs types de travail et où chaque catégorie de ménages du modèle est en fait un amalgame d’une grande diversité de ménages qui exercent des professions différentes? Par exemple, la catégorie « Couple marié avec deux enfants, de moins de 35 ans, avec un revenu entre 15 000 et 24 999 $ » regroupe autant des ménages agricoles que des fonctionnaires ou des membres de professions libérales.
L’approche adoptée consiste à supposer que chaque ménage dispose de différents types de temps de loisir, un par catégorie professionnelle de travail. Cette façon de voir peut surprendre, mais il faut se rappeler que chaque ménage dans le MÉGC est un ménage « représentatif », composé d’une multitude de ménages, dont les membres appartiennent à différentes catégories professionnelles. En outre, il existe bel et bien des ménages dont plus d’un membre travaille : or, si les ajustements au partage des tâches domestiques permettent jusqu’à un certain point de substituer le loisir de l’un(e) à celui de l’autre, il est raisonnable de penser que chacun des membres du ménage qui travaille consomme son propre loisir. D’ailleurs, c’est bien ce que l’on trouve dans les modèles de l’offre de travail des ménages à plusieurs travailleurs (Blundell et MaCurdy, 1999).
Avec cet a priori, et selon l’idée que l’on se fait des possibilités de substitution entre les types de loisir, il y a deux approches possibles. Suivant la première approche, le ménage représentatif est conçu comme une unité de décision intégrée par rapport à sa consommation de loisir, comme il l’est par rapport à sa consommation de biens : les offres de travail sont représentées comme si elles résultaient de décisions conjointes des membres. De cette conception, il découle que l’élasticité-prix croisée de l’offre de travail n’est pas nulle, puisque les différents types de loisir sont substituables les uns aux autres. Pour cette raison, nous préférons une autre approche, où l’on fait comme si chaque ménage était composé d’autant de membres individuels qu’il y a de types de travail et que chacun d’eux maximisait son utilité indépendamment des autres, tout en ayant les mêmes préférences quant à la consommation de biens. Il en résulte un modèle où la demande de consommation de biens est la même que dans un système linéraire de dépenses standard, tandis que l’offre de travail de chaque catégorie par un ménage donné est indépendante du taux de salaire des autres catégories.
Par ailleurs, l’approche des TEMI, appliquée à l’impôt sur le revenu personnel, est prise en compte dans la détermination de l’offre de travail. Les taux marginaux d’imposition représentent, non seulement l’impôt sur le revenu personnel, mais aussi l’imposition implicite que constitue la réduction de certains transferts. Le modèle peut donc simuler l’effet sur l’incitation au travail de certains programmes de transfert, comme l’aide sociale.
Enfin, pour tenir compte du chômage, le coût de renonciation du loisir est égal à l’espérance mathématique du taux de salaire net. L’espérance mathématique du taux de salaire est définie comme le produit du taux de salaire par la probabilité d’être employé, cette dernière étant égale au complément du taux de chômage de la profession concernée dans la région de résidence du ménage. Ainsi, le consommateur maximise son utilité en sachant qu’une fraction de son offre de travail risque de ne pas trouver preneur. D’un autre point de vue, on pourrait aussi dire que le chômage a sur le comportement des ménages le même effet qu’une taxe sur le salaire : il crée un écart entre, d’une part, le prix brut (taux de salaire) sur la base duquel les employeurs prennent leurs décisions d’embauche et, d’autre part, le prix net (espérance mathématique du taux de salaire) sur la base duquel les travailleurs décident de leur offre.
2. Fiscalité et mobilité partielle du capital
Le traitement du capital dans les MEGC est traditionnellement assez simple. Dans le cadre d’un modèle statique, ou bien les auteurs adoptent l’hypothèse de mobilité parfaite du capital entre les industries pour représenter les ajustements de long terme, ou bien ils supposent que le stock de capital est spécifique à chaque industrie. Il est évident que ces deux hypothèses extrêmes ne sont pas nécessairement satisfaisantes dans une perspective appliquée, lorsqu’un gouvernement cherche à évaluer différents scénarios de politique fiscale, comme réduire les taxes sur la masse salariale ou l’impôt sur les revenus du capital. Il est également clair que l’accumulation ou la mobilité du capital sont des phénomènes intrinsèquement dynamiques dont l’examen approfondi requiert un modèle dynamique (comme l’est la version la plus récente du MEGC du ministère des Finances du Québec). Toutefois, le passage d’un modèle statique à un modèle dynamique n’est pas une tâche facile et soulève quantité de problèmes conceptuels et empiriques, et d’autant plus s’il s’agit d’un modèle finement désagrégé. D’où la pertinence, du point de vue des méthodes de modélisation, de montrer comment un modèle statique peut :
représenter l’ensemble des impôts qui touchent la rémunération du capital, y compris l’impôt sur le revenu des sociétés, selon l’approche des taux effectifs marginaux d’imposition (TEMI);
représenter la mobilité du capital (mobilité entre branches, entre régions, et même internationale), sans pour autant faire l’hypothèse extrême de la mobilité parfaite.
Dans un modèle où le capital est immobile, spécifique à chaque branche dans chaque région, les TEMI n’ont aucune pertinence, puisque cette approche vise justement à mettre en lumière les distorsions que peut créer la fiscalité dans l’allocation du capital. Inversement, l’introduction d’une certaine mobilité du capital exige que soit pris en compte, non seulement le rendement du capital payé par les utilisateurs, mais aussi bien le rendement, net d’impôts, reçu par les détenteurs, qui allouent leur capital entre les utilisations concurrentes de manière à maximiser leur revenu.
Cela dit, l’inclusion des TEMI dans un MEGC n’est pas sans poser des difficultés conceptuelles. Car l’approche des TEMI a été développée dans un contexte d’analyse en équilibre partiel et, par surcroît, en référence à l’allocation des investissements, c’est-à-dire du nouveau capital[10]. Cela est d’autant plus évident à la lumière des éléments qui sont pris en compte dans le calcul des TEMI (valeur présente des déductions futures pour fins d’amortissement, crédits d’impôt à l’investissement) : il est clair que ceux-ci s’appliquent à de nouveaux investissements.
On le voit donc, les TEMI sont conçus comme une mesure synthétique de la façon dont la fiscalité influence l’allocation des investissements et, par là, du stock de capital. Cette problématique relève à proprement parler de la dynamique.
Or le modèle dont il est question ici est un modèle d’équilibre général calculable statique… Mais avec la mobilité partielle du capital, ce modèle ne devient-il pas « crypto-dynamique »? Le terme même « mobilité partielle » donne à entendre que le modèle représente deux états successifs de l’économie, « avant » et « après » un choc, alors que le temps écoulé est trop court pour que les ajustements soient complétés. On s’éloigne ainsi de la statique comparative au sens étroit, où l’on compare deux états de l’économie qui ne sont pas censés se succéder dans le temps.
La statique comparative au sens étroit est dénuée de référence temporelle et un seul des deux états comparés peut se réaliser : ou bien c’est l’état observé qui prévaut, ou bien c’est un état différent, hypothétique, c’est-à-dire qui aurait pu se réaliser à sa place, s’il s’était produit des conditions différentes de celles qui ont produit l’état observé (la différence par rapport à ces conditions étant ce qui définit le « choc »). Ainsi, dans un contexte de statique comparative au sens étroit, il est parfaitement légitime que l’allocation du capital entre ses diverses utilisations soit parfaitement flexible : l’allocation à laquelle aboutit une simulation est alors interprétée comme celle qui se serait réalisée si le choc avait eu lieu, auquel cas l’allocation observée ne se serait jamais réalisée. Selon ce point de vue, en somme, le modèle répond à la question : « Qu’aurait été l’économie si…? ».
Mais si nous parlons de « mobilité partielle » du capital, il est clair que notre intention implicite est que le modèle décrive un état de l’économie qui pourrait vraisemblablement se réaliser en réponse à un choc exogène, à partir de l’état initial, sans que ce nouvel état soit un équilibre définitif, bien que l’on s’abstienne d’expliciter quelle serait la trajectoire de l’économie entre les deux équilibres. Le modèle répond alors à la question : « Vers où irait l’économie si…? ». C’est en cela que le modèle devient « crypto-dynamique ». Car le déplacement du capital d’une utilisation vers une autre, même si cela se fait sans démantèlement-reconstruction, est tout de même un processus qui prend du temps, et qui, donc, pourra ou ne pourra pas se réaliser selon l’horizon temporel de la simulation (court terme-long terme).
2.1 Les taux effectifs marginaux d’imposition du capital (TEMI) dans le modèle
En équilibre, l’entreprise qui maximise son profit emploie chaque facteur de production jusqu’au point où la productivité marginale en valeur est égale au prix du facteur. Pour le facteur capital, le prix pertinent est le coût d’usage du capital.
L’impôt sur le revenu des sociétés a pour effet de réduire la valeur du produit marginal qui est disponible pour rémunérer le capital. Par contre, les paiements d’intérêt sont déductibles du revenu, de sorte que, si une fraction de chaque dollar de capital utilisé est financé par emprunt, alors l’impôt marginal à payer est réduit d’autant. En outre, suivant McKenzie et al. (1998), on peut ajuster le coût de remplacement du capital pour tenir compte d’éventuels crédits d’impôt à l’investissement et de la déductibilité des provisions pour consommation de capital.
Lorsque l’on prend tous ces éléments en considération, l’équilibre de l’entreprise est défini par l’égalité entre
le coût d’usage du capital, compte tenu de l’ajustement du coût de remplacement du capital pour tenir compte d’éventuels crédits d’impôt à l’investissement et de la déductibilité des provisions pour consommation de capital et
la valeur du produit marginal après impôt, augmentée de la valeur de la déductibilité des intérêts payés sur les emprunts.
On définit les TEMI à partir de cette condition d’équilibre microéconomique. Il y a plusieurs formulations particulières des TEMI : en plus de celle de Daly et Jung (1987), signalons celle de McKenzie et al. (1998), plus proche de la spécification appliquée dans le MEGFQ. Mais l’idée générale est de mesurer l’écart (tax wedge) entre le taux de rendement payé aux détenteurs de capital et la valeur du produit marginal. Les TEMI du modèle ont été calculés par la Direction de la taxation des entreprises du ministère des Finances du Québec (Drolet et Bahan, 2004). En plus des éléments déjà mentionnés, les TEMI tiennent compte de la taxe sur le capital[11] et de l’effet des taxes à la consommation[12].
Fullerton, Henderson et Shoven (1984) passent en revue plusieurs modèles appliqués à la fiscalité aux États-Unis[13], mettant l’accent sur leurs contributions méthodologiques, telles que l’introduction de la mobilité des facteurs et la mesure des taux de taxation effectifs. Ils soulignent que le seul MEGC qui permet que les taux moyens et marginaux de taxation soient substantiellement différents est celui qui a été développé par Fullerton et Gordon (1983) pour simuler les effets de l’intégration de l’impôt sur les sociétés et de l’impôt sur le revenu des particuliers[14].
Dans la même veine, Fullerton et Henderson (1989a, 1989b) font l’hypothèse que le taux effectif marginal est différent du taux moyen. Dans la première étude, ils intègrent un MEGC avec un modèle des TEMI, en vue d’analyser les distorsions intersectorielles créées par la fiscalité aux États-Unis. Dans la seconde, ils utilisent le modèle décrit dans Ballard et al. (1985), combiné aux taux effectifs marginaux d’imposition estimés dans Fullerton et Henderson (1984) pour étudier le fardeau excédentaire marginal qui découle de diverses formes d’imposition du capital.
Dans le MEGFQ, le concept de TEMI apparaît dans la fonction de calcul des recettes fiscales associées au capital :
Les taux marginaux d’imposition ttemigvt,k,infc,rg sont des paramètres libres, dont la valeur a été calculée par la Direction de la taxation des entreprises du ministère des Finances du Québec (Drolet et Bahan, 2004). Le taux moyen tmoygvt,k,infc,rg est calibré de façon à équilibrer l’équation pour l’année de base.
Dans chaque secteur, la rémunération des détenteurs du capital est égale au loyer du capital payé par les utilisateurs, moins les taxes et l’allocation pour consommation de capital :
Le taux marginal de rémunération des détenteurs du capital de type k utilisé dans l’industrie infc de la région rg, rsk,infc,rg est la dérivée de cette dernière expression par rapport KDk,infc,rg.
On a donc
Étant donné
et l’équation (2), on a, après développement,
En prenant la dérivée du membre de droite de (6), on trouve
On peut maintenant voir que la somme des taux effectifs marginaux d’imposition est égale au rapport de l’écart entre la valeur du produit marginal du capital rdk,infc,rg et son coût d’usage marginal (rsk,infc,rg + δk,infc,rg ) sur la valeur du produit marginal net de la dépréciation :
Cette définition des TEMI est équivalente à celle de Daly et Jung (1987).
2.2 Mobilité du capital
Dans la première version opérationnelle du modèle, le capital était fixe, c’est-à-dire que les KSk,infc,rg étaient exogènes. À l’autre extrême, l’hypothèse de parfaite mobilité du capital entre les branches et les régions se traduirait par la condition d’équilibre
Avec la mobilité imparfaite du capital, nous supposons, d’abord, que celui-ci est mobile entre les branches et entre les régions, mais pas entre les types k et, ensuite, que seule une partie du capital est mobile. Cette mobilité partielle est représentée par un paramètre θk,infc,rg, défini comme la fraction du capital qui est non mobile par rapport à l’état initial (« captive »). On a alors la contrainte que l’offre de capital de type k dans la branche infc de la région rg ne peut pas être inférieure au capital non mobile :
Grosso modo, plus les θk,infc,rg sont grands, moins le capital est mobile, et plus court est l’horizon implicite de la simulation (long terme/court terme). La mobilité parfaite est représentée par des θk,infc,rg égaux à zéro et l’hypothèse du capital spécifique, par des θk,infc,rg égaux à 1[15].
L’offre de capital de type k pour l’industrie infc de la région rg devient
où DELKk,infc,rg est la variation de l’offre de capital, bornée inférieurement par la fraction non mobile θk,infc,rg du capital; cela implique
La variation DELKk,infc,rg est aussi bornée supérieurement par la disponibilité de capital mobile. Avec l’ALENA et la continentalisation de l’économie nord-américaine, le phénomène de la mobilité géographique du capital n’est pas contenu à l’intérieur des frontières nationales. Aussi, avons-nous introduit une certaine mobilité internationale du capital, au moyen d’une fonction d’offre à élasticité constante[16] :
Quand le taux de rémunération est égal au taux international, l’entrée nette de capital physique étranger est nulle. Elle est positive ou négative, selon que le taux intérieur est supérieur ou inférieur au taux international.
On a donc
Le taux de rémunération reçu par les détenteurs du capital est spécifique à chaque branche, sous réserve de la condition d’orthogonalité et de la contrainte d’équilibre du marché du capital mobile (voir plus loin).
Mais le taux de rémunération du capital dans une industrie donnée ne peut pas dépasser le taux de rémunération du capital mobile du même type. Cette contrainte représente le comportement d’arbitragistes des détenteurs de capital mobile, qui s’assurent d’obtenir le meilleur rendement possible pour leur capital (contrainte d’équilibre de marché du capital mobile) :
On impose aussi la contrainte d’orthogonalité[17] :
Si une industrie n’utilise que du capital « captif » (non mobile), c’est-à-dire si
alors il est possible, étant donné la contrainte de plein emploi du capital, que le capital de cette industrie soit rémunéré à un taux inférieur à celui du capital mobile (les détenteurs de ce capital « captif » étant forcés d’accepter une rémunération moindre pour leur capital afin de persuader les utilisateurs d’employer tout le capital offert). Mais toute industrie dont une partie du capital utilisé est mobile doit rémunérer son capital au taux du capital mobile rskmobk.
Les rsk,infc,rg jouent donc dans notre modèle le rôle de prix qui motivent l’arbitrage entre les multiples utilisations du capital.
3. Quelques expériences de simulation avec le modèle du ministère des Finances du Québec
Nous allons analyser les résultats de deux simulations dans le but d’illustrer le fonctionnement de la mobilité partielle du capital dans le modèle. L’attention est donc concentrée sur les mouvements du capital entre les industries et les régions. Les chocs dont les effets sont simulés sont :
une augmentation proportionnelle de 10 % des TEMI du capital des sociétés pour toutes les industries au Québec;
une diminution de 25 % du taux de rémunération international du capital.
Les résultats détaillés sont présentés aux tableaux 1 à 5.
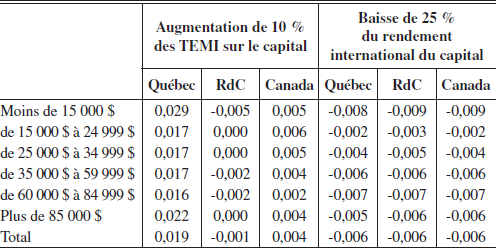
Tableau 1
Impact sur l’offre de travail des ménages
(variation en % par rapport à l’état initial)
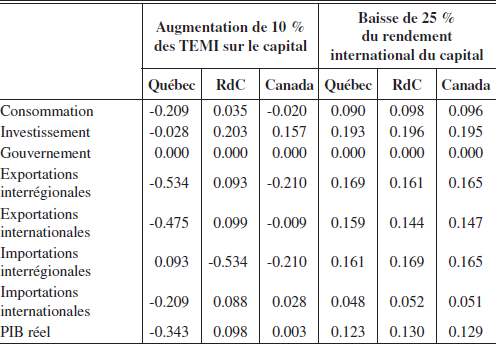
Tableau 2
Impact sur quelques indicateurs choisis
(variation en % par rapport à l’état initial)
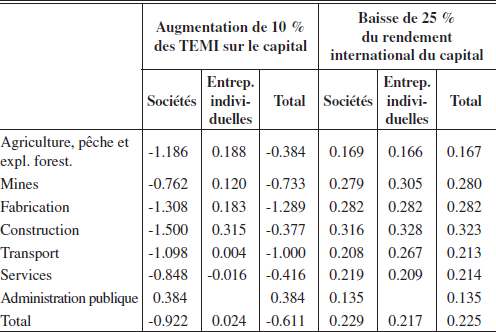
Tableau 3
Impact sur le taux de rémunération après impôt du capital au Québec
(variation en % par rapport à l’état initial)
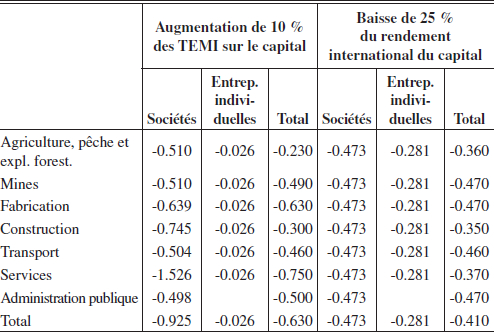
Tableau 4
Impact sur l’utilisation de capital au Québec
(variation en % par rapport à l’état initial)
Tableau 5
Impact sur le PIB réel
(variation en % par rapport à l’état initial)
3.1 Augmentation de 10 % des TEMI du capital au Québec
On considère ici que le montant des taxes qui affectent le capital est une fonction linéaire du revenu du capital, où la pente est le TEMI (équation 2). Le choc est défini comme une augmentation de 10 % de l’ordonnée à l’origine aussi bien que de la pente de la courbe.
L’augmentation de 10 % des taxes qui touchent le capital alourdit le fardeau fiscal des firmes. Il s’ensuit directement une hausse des coûts de production et un affaiblissement de la compétitivité des firmes établies au Québec. Naturellement, l’augmentation des coûts de production a un impact sur les prix à la consommation (0,250 %) et à la production (0,312 %). La baisse de la compétitivité du Québec a également un impact sur ses exportations interrégionales (-0,534 %) et internationales (-0,475 %).
En second lieu, l’augmentation des TEMI du capital accentue l’écart entre le rendement que les utilisateurs du capital doivent payer et le rendement net que reçoivent les détenteurs. Puisque le changement des TEMI n’affecte pas le rendement engendré pour les utilisateurs, l’effet immédiat est un affaissement du rendement aux détenteurs du capital des sociétés (-0,925 %) et des entreprises individuelles (-0,026 %). En outre, la baisse du rendement du capital entraîne une réallocation vers des industries et des régions offrant une meilleure rémunération. On constate en effet que l’utilisation totale de capital au Québec diminue (-0,611 %) et que l’utilisation totale au RdC augmente (0,155 %). Une partie du capital auparavant offert au Québec a été redirigé vers le RdC. Et bien que le « nouveau » capital utilisé dans le RdC ait une productivité marginale moindre, le taux de rémunération après impôt ex post demeure plus élevé dans le RdC qu’au Québec. Lors de l’interprétation de ces résultats, il est important de garder à l’esprit qu’une partie du capital utilisé au Québec est non mobile et qu’elle ne peut pas être transférée vers le RdC. Ainsi, la nature partielle de la mobilité explique pourquoi les taux de rémunération du capital des sociétés ne sont pas égaux entre le Québec et le RdC. L’égalité qui prévaut quant au taux de rémunération du capital des entreprises individuelles indique que la contrainte sur la mobilité de ce type de capital n’est pas « serrée ».
Le changement des TEMI du capital a aussi un impact sur le déplacement du capital entre le Canada et le RdM. L’impact global sur le capital utilisé au Canada est de -0,003 %. À cause d’une baisse du taux de rémunération au Canada, une certaine quantité de capital a fui vers le RdM pour obtenir un meilleur taux de rémunération.
Les industries à forte intensité de capital sont les plus touchées par l’augmentation des TEMI du capital. Si nous considérons l’utilisation du capital des sociétés, les industries les plus touchées sont la construction (-1,500 %) et la fabrication (-1,308 %), dans cet ordre. Toutefois, si nous regardons l’impact sur le taux de rémunération net, le plus durement frappé est le secteur des services (-1,526 %). Cela peut surprendre à première vue, mais la raison en est que le TEMI du capital est plus élevé pour les services.
Quels sont les impacts de la mobilité du capital sur le marché du travail? Il est clair que la réduction du taux de rémunération du capital a diminué la quantité de capital disponible au Québec. Cette fuite de capital a un effet négatif sur le PIB québécois (-0,343 %) et entraîne à la baisse la demande de travail, ce qui accentue la chute du revenu disponible réel (-0,213 %). L’utilisation du capital baisse (-0,616 %), l’emploi total diminue (-0,072 %) et le taux de chômage augmente.
L’impact positif sur les prix à la consommation au Québec exerce une pression sur les salaires. L’augmentation des taux de salaire (0,195 %) affecte l’offre et la demande de travail. La demande diminue, tandis que l’offre augmente pour tous les ménages au Québec. Les augmentations sont cependant minimes, variant de 0,016 % à 0,029 % .
Ensemble, la diminution de la demande de travail et de capital et la baisse du taux de rémunération du capital provoquent une chute de -0,213 % du revenu disponible réel, ce qui conduit à une diminution de la consommation réelle (-0,209 %). L’impact positif sur les salaires n’est pas suffisant pour compenser la hausse des prix, le plus faible niveau d’emploi et le moindre taux de rémunération du capital. Les revenus accrus de l’État permettent d’augmenter l’épargne des gouvernements fédéral et du Québec, ce qui alimente une hausse des investissements réels au Canada (0,157 %)[18]. Au Québec cependant, l’investissement réel diminue (-0,028 %). La hausse de l’investissement en termes nominaux n’est pas assez prononcée pour compenser l’augmentation des prix des biens d’investissement. La compétitivité des exportations du Québec est également touchée par l’augmentation des coûts de production. Les exportations, aussi bien vers le RdC (-0,534 %) que vers le RdM (-0.475 %) diminuent. L’accroissement de l’utilisation de capital (0,155 %) est le principal moteur de la croissance du PIB dans le RdC (0,098 %). Le niveau de l’emploi augmente aussi (0,036 %), à cause de la chute des taux de salaire (0.066 %), mais moins que l’utilisation de capital.
3.2 Diminution de 25 % du rendement international du capital dans le RDM
Ceteris paribus, la baisse du taux de rendement international implique que le taux de rendement relatif au Canada est plus élevé qu’avant le choc. Le capital étranger tendra à se déplacer vers le Canada, où il commande une meilleure rémunération. Les résultats montrent que l’augmentation de l’utilisation de capital est de 0,225 % au Québec, et de 0,230 % dans le RdC, ce qui donne un impact global sur le Canada de 0,229 %. Toutefois, l’offre supérieure de capital n’est pas sans effet sur son rendement. Puisque la contrainte sur la mobilité partielle du capital n’est pas « serrée » dans le cas présent, les taux de rémunération au Québec et dans le RdC sont les mêmes et à la baisse, tant pour les sociétés (-0,473 %) que pour les entreprises individuelles (-0,281 %). Les industries de la construction et de la fabrication montrent les plus fortes augmentations de la demande de capital. L’utilisation s’accroît de 0,323 % dans la construction, et de 0,282 % dans la fabrication.
Le coût plus faible du capital a un impact sur les prix aux producteurs et aux consommateurs. Au Québec, les prix aux producteurs baissent de -0,133 % et les prix aux consommateurs de -0,138 %. Au Québec, les salaires subissent eux aussi un impact négatif (-0,107 %), mais pas aussi considérable que les prix. L’entrée de capital génère une plus forte demande de travail, de telle sorte que l’emploi total croît au Québec et dans le RdC (0,061 % et 0,059 % respectivement), ce qui conduit à une baisse du taux de chômage (-0,480 %). Dans le RdC aussi, les salaires sont plus bas après le choc (-0,098 %), mais la chute est moindre qu’au Québec, puisqu’il y a une diminution plus prononcée du taux de chômage (-0,607 %). La variation du taux de chômage au Québec vient de la hausse de la demande de travail (0,061 %) et de la baisse de l’offre (-0,006 %). Ces changements de l’offre et de la demande sont un effet de la diminution des salaires au Québec.
L’utilisation accrue de facteurs résulte en une croissance du PIB réel au Québec (0,123 %) et dans le RdC (0,130 %). L’impact sur la consommation au Québec et dans le RdC est plutôt faible, puisque l’impact sur le revenu disponible nominal est négatif. Mais grâce à des prix à la consommation plus bas, l’impact sur le revenu disponible réel est positif (0,092 % au Québec et 0,099 % dans le RdC); il en est de même pour la consommation réelle. L’investissement au Québec et dans le RdC augmente à cause d’une plus grande abondance de l’épargne. L’impact combiné sur la consommation et l’investissement gonfle la demande de biens et services. Une partie de cette demande accrue peut être satisfaite par un accroissement de la production locale. Cependant, une part doit se satisfaire au moyen d’une augmentation des importations interrégionales et internationales. Il y a aussi une croissance des exportations internationales (Québec, 0,159 %; RdC, 0,144 %). Puisque la production a augmenté et que les prix locaux ont baissé, les firmes maximisent leur profit en vendant une partie de leur production dans le RdM.
Conclusion
Cet article présente certaines des innovations remarquables que contient le MEGC développé par les auteurs pour le ministère des Finances du Québec, en collaboration avec les autres membres de l’équipe et grâce à la coopération de l’Institut de la Statistique du Québec.
Il s’agit d’un MEGC de grande taille, multisectoriel et birégional du Québec et du reste du Canada. Notre présentation est centrée sur l’approche TEMI à la fiscalité et la mobilité partielle du capital dans le cadre d’une version statique du modèle.
La taxation du capital est représentée au moyen des taux effectifs marginaux d’imposition (TEMI), qui mesurent l’écart entre le taux de rendement payé aux détenteurs de capital et la valeur du produit marginal du capital. Les taux marginaux d’imposition du capital synthétisent donc les multiples distorsions de l’allocation des ressources qui peuvent résulter de la fiscalité.
L’introduction des TEMI devient intéressante lorsque le capital n’est pas fixe, mais au contraire mobile entre ses utilisations concurrentes. L’analyse de l’allocation du capital est une question fondamentalement dynamique. D’ailleurs, la version couramment utilisée du MEGC du ministère des Finances est dynamique. Il n’en demeure pas moins pertinent, du point de vue des techniques de modélisation, de voir comment cette question peut être abordée dans un modèle statique.
Dans la version statique du MEGFQ, le capital n’est pas parfaitement mobile, comme cela serait approprié dans un modèle statique à très long terme; il est plutôt partiellement mobile entre industries et régions, la mobilité étant limitée par une borne supérieure sur la quantité de capital qui peut quitter une industrie donnée dans une région donnée. De plus, il y a dans le modèle un certain degré de mobilité internationale du capital, sous la forme d’une offre à élasticité-prix constante.
Les résultats de simulation présentés montrent, en premier lieu, que les spécifications proposées sont réellement opérationnelles et, en second lieu, que le comportement du modèle est en accord avec les anticipations théoriques.
Parties annexes
Annexes
Annexe 1. Schéma de la matrice de comptabilité sociale birégionale Québec-RdC avec comptes suprarégionaux
Annexe 2. Élasticités estimées des courbes salaires-chômage
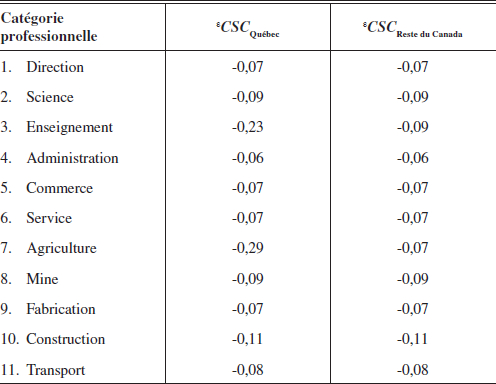
Selon Blanchflower et Oswald (1995) et Card (1995), il ressort des études réalisées sur plusieurs pays que la CSC est « virtuellement identique d’un pays à l’autre et stable dans le temps » avec une élasticité e généralement proche de –0,1[19]. Pour le cas spécifique du Canada, Blanchflower et Oswald (1995) trouvent une élasticité e globale égale à -0,09, une estimation basée sur des données statistiques de 1972-1987. L’élasticité des courbes salaire-chômage du MEGFQ ont été estimées par Danielle Bilodeau et Laurence Bargaud, de l’ISQ, au moyen de données microéconomiques de l’Enquête sur les finances des consommateurs (EFC) pour la période 1981-1997 et de l’Enquête sur la dynamique du travail et du revenu (EDTR) pour 1997-2001.
Tableau 6
Élasticités des courbes salaires-chômage par région et par profession dans le MEGFQ
Notes
-
[1]
Pour une description générale des MEGC, on peut consulter, entre autres, Decaluwé et al. (2001).
-
[2]
Pyatt et Thorbecke (1976).
-
[3]
En plus des auteurs de ce texte, il faut mentionner Véronique Robichaud et Christian Arnaud Emini, qui ont été membres de l’équipe de l’Université Laval. Brian Girard, Éric Fournier et Laurent Martin ont successivement assumé le rôle de leaders de l’équipe du ministère des Finances; ont fait notamment partie de cette équipe Daniel Florea, Hervé Lohouès et Sébastien Poirier. En plus de David Bahan, Danielle Bilodeau et Laurence Bargaud ont apporté des contributions significatives au développement du modèle, sous l’autorité de Camille Courchesne, directeur des statistiques économiques et sociales à l’Institut de la statistique du Québec (ISQ).
-
[4]
Cette approche est désignée dans les écrits anglo-saxons par le sigle METR – Marginal Effective Tax Rates.
-
[5]
Il y a cinq catégories qui ne comptent aucun ménage au Québec. Le groupe d’âge est défini par l’âge de la « personne de référence », selon la terminologie de Statistique Canada.
-
[6]
L’offre de travail, cependant, s’écarte quelque peu de l’approche habituelle de l’agent représentatif. Voir plus loin, 1.3.
-
[7]
Il n’y a que 2 types de capital, mais 13 catégories de biens d’investissement. Selon la structure de leur capital, les firmes sont sujettes à des taux d’imposition différents (voir plus loin, 2.1).
-
[8]
Voir Blanchflower et Oswald (1995 :156) et Card (1995 : 1 et 32-35).
-
[9]
Il peut arriver, à un taux de salaire suffisamment élevé, que l’effet de revenu soit supérieur à l’effet de substitution, auquel cas la courbe d’offre de travail a une pente négative dans sa partie supérieure. On dit alors que la courbe est « rebroussée » (Hanoch, 1965). Toutefois, même si les courbes individuelles d’offre de travail peuvent être rebroussées, il est raisonnable de penser que l’offre agrégée ne le soit pas. Alors, lorsque le consommateur-travailleur est un « agent représentatif » dans un MEGC, on s’attend à une courbe d’offre à pente positive.
-
[10]
Par exemple : « Policy issues often turn to questions related to the overall tax burden faced by companies, especially across sectors and jurisdictions. Two related partial equilibrium approaches are typically used to analyze this burden. The first involves measuring the effect of corporate income and other taxes on the return to capital, as in the case of project analysis. The second involves measuring the marginal effective tax rate on capital, which employs the concept of the user cost of capital. Using these approaches, tax burdens faced by firms in different jurisdictions are compared to see how investment might be influenced by the tax system » (McKenzie et al., 1997 : 337).
-
[11]
Elle demeure en vigueur au Québec jusqu’au premier janvier 2011; la taxe fédérale n’a été abolie qu’en 2008.
-
[12]
Bien que le système actuel de taxes à la consommation soit fondé sur le principe d’une taxe sur la valeur ajoutée et qu’il ne devrait donc pas avoir d’effet sur le coût d’usage du capital, certaines restrictions s’appliquent au niveau provincial et fédéral qui limitent de façon ciblée le remboursement des taxes sur les intrants.
-
[13]
La question de l’incidence des taxes au sein des MEGC a été abondamment discutée au cours des dernières décennies. Puisque nous nous préoccupons ici plus spécifiquement de l’introduction des TEMI dans les MEGC, nous nous contenterons de citer les principaux modèles appliqués qui ont contribué à ce domaine. Pour une revue complète de MEGC plus anciens appliqués à la taxation, voir Shoven et Whalley (1984) et Pereira et Shoven (1988).
-
[14]
Fullerton (1984) discute les raisons pour lesquelles les taux marginaux d’imposition devraient être différents des taux moyens. Il avance 11 raisons qui justifieraient cette différence et il souligne l’avantage de tenir compte des taux effectifs dans l’analyse des distorsions et des incitations à investir.
-
[15]
On peut d’ailleurs judicieusement rapprocher cette proposition du modèle dynamique de Fullerton (1983), un modèle à générations de capital (vintage).
-
[16]
Goulder et al. (1983) prennent en compte les flux internationaux de capital dans la modélisation des échanges avec l’étranger. Ils font l’hypothèse que l’entrée de capital étranger croît avec l’augmentation du loyer du capital sur le marché intérieur. Cette relation est spécifiée comme suit :
où WK et XK sont la dotation en capital étranger et la quantité de capital loué aux É.-U., et EK est l’élasticité du flux de capital. PK et PKF sont respectivement les loyers intérieur et étranger du capital. Pour leur simulation médiane, ils posent EK égale à –1 et ils mènent une analyse de sensibilité pour des valeurs variant de zéro à –10. Dans la solution de base, PK et PKF sont normalisés et XK est nul.
-
[17]
Van de Mensbrugghe (2003a et b) utilise une condition d’orthogonalité similaire, comme mécanisme de changement de régime pour représenter le fonctionnement du marché du travail (2003a, équations F-6 et F-7). Il se sert aussi d’une condition d’orthogonalité pour assurer que le taux de rendement sur le capital ancien soit égal au taux de rendement sur le nouveau si le capital (ancien) en place ne suffit pas à répondre à la demande courante (2003a, équation F-24). Cette approche est présentée plus explicitement dans Van de Mensbrugghe (2003b).
-
[18]
Aussi paradoxal que paraisse ce résultat, il est une simple conséquence des règles de fermeture du modèle et de l’absence de perspective dynamique dans la modélisation des investissement dans un cadre statique.
-
[19]
Voir Blanchflower et Oswald (1995 : 156) et Card (1995 : 1 et 32-35).
Bibliographie
- Annabi, N. (2003), « Modeling Labor Market in CGE Models, Endogenous Labour Supply, Unions and Efficiency Wages », Réseau Politiques économiques et pauvreté (PEP), Université Laval. http://www.pep-net.org/fileadmin/medias/pdf/Labormarket.pdf
- Annabi, N., J. Cockburn et B. Decaluwé (2003), « Formes fonctionnelles et paramétrisation dans les modèles d’équilibre général calculables », Centre de recherche en économie et finance appliquées, Université Laval, Québec : http://www.un.org/esa/policy/cairo_training_mdgs/annabi_cockburn_and_decaluwe_2003.pdf
- Armington, P. (1969), « A Theory of Demand for Products Distinguished by Place of Production, IMF Staff Papers 16 : 159-178.
- Bahan, D., D. Bilodeau, A. Lemelin et V. Robichaud (2003), « Une matrice de comptabilité sociale birégionale pour le modèle d’équilibre général du ministère des Finances du Québec (MEGFQ) », ministère des Finances du Québec, Collection Feuille d’argent, Travaux de recherche 2003-003. (http://www.finances.gouv.qc.ca/documents/feuille/fr/2003_003.pdf).
- Ballard, C. L., D. Fullerton, J. B. Shoven et J. Whalley (1985), A General Equilibrium Model for Tax Policy Evaluation, The University of Chicago Press.
- Becker, G. S. (1991), A Treatise on the Family, Harvard University Press, Cambridge, Mass.
- Berg, G. C. et K. A. Reinert (1995), « A Computable General Equilibrium Estimation of the Effects of the U.S. Meat Program », International Economic Journal, 9(1) : 53-66.
- Blanchflower, D. G. et A. J. Oswald (1995), « An Introduction to the Wage Curve », The Journal of Economic Perspectives, 9(3) : 153-167.
- Blonigen, B. A., J. E. Flynn et K. A. Reinert (1997), « Sector Focused General Equilibrium Modeling », inFrançois, J. F. et K. A. Reinert, Applied Methods for Trade Policy Analysis, A Handbook, Cambridge University Press p. 189-230.
- Blundell, R. et T. MaCurdy (1999), « Labour Supply: A Review of Alternative Approaches », in Ashenfelter O., et D. Card, (éd.), Handbook of Labour Economics, Elsevier Science, chap. 27.
- Boadway, R., N. Bruce et J. Mintz (1984), « Taxation, Inflation, and the Effective Marginal Tax Rate on Capital in Canada »,The Canadian Journal of Economics, 17 : 62-79.
- Boadway, R., N. Bruce et J. Mintz (1987), Taxes on Capital Income in Canada: Analysis and Policy, Canadian Tax Foundation.
- Boadway, R., N. Bruce, K. McKenzie et J. Mintz (1987), « Marginal Effective Tax Rates for Capital in the Canadian Mining Industry », The Canadian journal of Economics, 20 : 1-16.
- Brazel, Y. et R. J. McDonald (1973), « Assets, Subsistence, and the Supply of Labor », The American Economic Review, 63(4) : 621-633.
- Card, D. (1995), « The Wage Curve : A Review », Journal of Economic Literature, 33 : 785-799.
- Chiappori, P.-A. (1992), « Collective Labor Supply and Welfare », Journal of Political Economy, 100 : 437-467.
- Chiappori, P.-A., B. Fortin et G. Lacroix (2002), « Marriage Market, Divorce Legislation, and Household Labor Supply », Journal of Political Economy, 110(1) : 37-72.
- Daly, M. J. et J. Jung, (1987), « The Taxation of Corporate Investment Income in Canada : An Analysis of Marginal Effective Tax Rates », The Canadian Journal of Economics, 20(3) : 555-587.
- deMelo, J. et D. Tarr (1992), A General Equilibrium Analysis of US Foreign Trade Policy, The MIT Press, Cambridge, Mass.
- Deaton, A. et J. Muellbauer (1980), Economics and Consumer Behavior, Cambridge University Press.
- Decaluwé, B., A. Lemelin et D. Bahan (2006), « Oferta endógena de trabajo y capital parcialmente móvil en un MEGC birregional : Versión estática del modelo de equilibrio general computable del Ministerio de Hacienda de Québec », Investigación Económica, 258, octobre-décembre.
- Decaluwé, B., A. Lemelin et D. Bahan (2010), « Endogenous Labor Supply with Several Occupational Categories in a Bi-regional CGE Model ». Regional Studies, 44(10), p. 1401-1414
- Decaluwé, B., A. Lemelin, D. Bahan et N. Annabi (2005), « Offre de travail endogène et mobilité du capital dans un MEGC birégional : la version statique du modèle d’équilibre général calculable du ministère des Finances du Québec », ministère des Finances du Québec, collection Feuille d’argent, Travaux de recherche 2005-001, 62 pages. http://www.finances.gouv.qc.ca/documents/feuille/fr/2005_001.pdf
- Decaluwé, B., A. Lemelin, V. Robichaud, C. Emini et N. Annabi (2002), « La Modélisation du Marché du Travail dans les MEGC : offre endogène, syndicats et salaire d’efficience », Rapport soumis au ministère des Finances, Québec.
- Decaluwé, B., A. Lemelin, V. Robichaud et D. Bahan (2003), « Modèle d’équilibre général du ministère des Finances du Québec (MEGFQ) : caractéristiques et structure du modèle », ministère des Finances du Québec, Collection Feuille d’argent, Travaux de recherche 2003-002. (http://www.finances.gouv.qc.ca/documents/feuille/fr/2003_002.pdf).
- Decaluwé, B., A. Lemelin, V. Robichaud, D. Bahan et D. Florea (2004), « Le modèle d’équilibre général calculable du ministère des Finances, de l’Économie et de la recherche du Québec : un modèle birégional du Québec et du reste du Canada », in Cloutier, L., M. et C. Debresson, avec la collaboration d’Érik Dietzenbacher, Changement climatique, flux technologiques, financiers et commerciaux – nouvelles directions d’analyse entrée-sortie, Actes de la Quatorzième Conférence internationale de techniques d’analyse entrée-sortie, tenue à Montréal, 10-15 octobre 2002, Presses de l’Université du Québec.
- Decaluwé, B., A. Martens, et L. Savard (2001), La politique économique du développement et les modèles d’équilibre général calculable, Les Presses de l’Université de Montréal, Montréal.
- Drolet, S. et D. Bahan (2004), « Les taux effectifs marginaux d’imposition des sociétés : Estimations pour le Québec », ministère des Finances du Québec, à paraître.
- Fortin, B. et G. Lacroix (1997), « A Test of the Unitary and Collective Models of Household Labour Supply », Economic Journal, 107: 933-55.
- Fullerton, D. (1983), « Transition Losses of Partially Mobile Industry-Specific Capital », Quarterly Journal of Economics, 92(1) : 107-126.
- Fullerton, D. (1984), « Which Effective Tax Rate? », National Tax Journal, 37 : 23-43.
- Fullerton, D. et R. H. Gordon. (1983), « A Reexamination of Tax Distortions in General Equilibrium Models », sous la direction de M. Feldstein, Behavioral Simulation Methods in Tax Policy Analysis, Chicago : University of Chicago Press, p. 369-426.
- Fullerton, D. et M. A. King (1984), The Taxation of Income from Capital, The University of Chicago Press.
- Fullerton, D. et Y. K. Henderson (1984), « Incentive Effects of Taxes on Income from Capital: Alternative Policies in the 1980’s », NBER Working Paper No. 1262.
- Fullerton, D. et Y. K. Henderson (1989a), « A Disaggregate Equilibrium Model of the Tax Distortions among Assets, Sectors, and Industries », International Economic Review, 30(2) : 391-413.
- Fullerton, D. et Y. K. Henderson (1989b), « The Marginal Excess Burden of Different Capital Tax instruments », The Review of Economics and Statistics, 71(3) : 435-462.
- Fullerton, D., Y. K. Henderson et J. B. Shoven (1984), « A Comparison of Methodologies in Empirical General Equilibrium Models of Taxation », NBER Working Paper No. 911.
- Goulder, L. H., J. B. Shoven et J. Whalley (1983), « Domestic Tax Policy and the Foreign Sector Formulations to Results from a General Equilibrium Model », sous la direction de M. Feldstein, Behavioral Simulation Methods in Tax Policy Analysis, Chicago : University of Chicago Press.
- Hanoch, G. (1965), « The “Backward-bending” Supply of Labor », The Journal of Political Economy, 73 : 635-642.
- Jung, J. (1989), « The Calculation of Marginal Effective Corporate Tax Rates in The 1987 White Paper on Tax Reform », Working Paper No. 89-6, Department of Finance, Tax Policy and Legislation, Ottawa, Canada.
- McKenzie K. J., M. Mansour et A. Brûlé (1998), « Le calcul des taux effectifs marginaux d’imposition », Document de travail 97-15, ministère des Finances, Comité technique de la fiscalité des entreprises, Ottawa, Canada.
- McKenzie, K. J., J. M. Mintz et K. A. Scharf (1997), « Measuring Effective Tax Rates in the Presence of Multiple Inputs: A Production Based Approach », International Tax and Public Finance, 4 : 337-359.
- McKenzie, K. J. (1994), « The Implications of Risk and Irreversibility for the Measurement of Marginal Effective Tax Rates on Capital », The Canadian Journal of Economics, 27 : 604-619.
- Moes, A. (1998), « Effective Tax Rates on Capital in New Zealand – Changes 1972-1998 », Treasury Working Paper 99/12.
- Pereira, A. M. et J. B. Shoven, (1988), « Survey of Dynamic Computational General Equilibrium Models for Tax Policy Evaluation », Journal of Policy Modeling, 10(3) : 401-436.
- Pyatt, G. et E. Thorbecke (1976), Planning Techniques for a Better Future, Genève, ILO/OIT.
- Round, J. I. (1988), « Incorporating the International, Regional, and Spatial Dimension into a SAM : Some Methods and Applications », in Harrigan, F. et P. G. Mcgregor, (1988), Recent Advances in Regional Economic Modelling, Coll. London Papers in Regional Science; vol. 19, Pion Ltd., London, p. 24-45
- Shoven, J. B. et Whalley, J. (1984), « Applied General Equilibrium Models of Taxation and Trade: An Introduction and Survey », Journal of Economic Literature, 22(3) : 1007-1051.
- Stern, N. (1986), « On the Specification of Labour Supply Functions », in Blundell, R. et I. Walker, Unemployment Search and Labor Supply, Cambridge University Press, p. 143 à 189.
- Tarr, G. D. (1989), « A General Equilibrium Analysis of the Welfare and Employment Effects of US Quotas in Textiles, Autos and Steel », Bureau of Economics Staff Report to The Federal Trade Commission.
- Tchilinguirian, H. et K. Gordon (1998), « Marginal Effective Tax Rates on Physical », Human and R&D Capital, OECD Working Paper No. 199.
- vander Mensbrugghe, D. (2003a), « Linkage Technical Reference Document – Version 5.3 », The World Bank, Development Prospects Group.
- vander Mensbrugghe, D. (2003b), « A Simple Dynamic Model with Vintage Capital, unpublished.
- Whalley, J. (1997), « The Incidence of the Corporate Tax Revisited », Ottawa : Department of Finance, Technical Committee on Business Taxation, Working Paper 97-107.
Liste des figures
Graphique 1
Détermination du salaire et du chômage selon une wage curve
Liste des tableaux
Tableau 1
Impact sur l’offre de travail des ménages
(variation en % par rapport à l’état initial)
Tableau 2
Impact sur quelques indicateurs choisis
(variation en % par rapport à l’état initial)
Tableau 3
Impact sur le taux de rémunération après impôt du capital au Québec
(variation en % par rapport à l’état initial)
Tableau 4
Impact sur l’utilisation de capital au Québec
(variation en % par rapport à l’état initial)
Tableau 5
Impact sur le PIB réel
(variation en % par rapport à l’état initial)
Tableau 6
Élasticités des courbes salaires-chômage par région et par profession dans le MEGFQ