Résumés
Résumé
L’estimation de la conductivité hydraulique d’un aquifère de socle à l’échelle régionale demeure un défi majeur. À cette échelle, les données sont rares, en quantité et en qualité. Cette étude propose une approche d’estimation de la conductivité hydraulique des aquifères de socle à partir de la calibration d’un modèle d’écoulement au moyen des charges hydrauliques. Elle est appliquée au bassin du N’zo couvrant une superficie de 4 300 km2. La méthodologie adoptée fait l’hypothèse que la perméabilité de l’aquifère est liée à des fractures verticales, perméables sur 100 m à partir de la surface. Elle fait aussi l’hypothèse que ces fractures peuvent être identifiées sous forme de linéaments et que tous les linéaments sont des fractures et sont perméables. La première étape de cette méthodologie est la cartographie des zones discrètes de perméabilité de l’aquifère. Elles sont identifiées à partir de l’analyse de la densité et l’orientation des « fractures » à l’échelle de mailles de travail. Les fractures sont assimilées aux linéaments cartographiés à partir d’une image radar. Six configurations spatiales de zones discrètes de perméabilité sont générées avec des mailles carrées de 2 à 12 km de côté. La deuxième étape porte sur la construction du modèle numérique d’écoulement à partir des limites extérieures du bassin versant, du MNT (Modèle numérique de terrain), du réseau hydrographique et d’une recharge uniforme. Enfin, la troisième étape consiste à transférer chaque configuration de zones discrètes de perméabilité générée au sein du modèle numérique d’écoulement, puis à le calibrer en régime permanent au moyen de charges hydrauliques observées ponctuellement (86 points de mesure). Les résultats indiquent que le modèle optimal de distribution spatiale des zones discrètes de perméabilité est obtenu avec les mailles de 4 km de côté. Les conductivités hydrauliques calculées oscillent entre 1,1 x 10-6 et 2,4 x 10-5 m∙s-1. Cependant, ces valeurs doivent être prises avec précaution, car l’identification des zones homogènes du réseau de fractures est basée sur l’approche très controversée des linéaments et la calibration est effectuée seulement avec des charges hydrauliques et non avec des flux. Le modèle conceptuel ainsi élaboré pourrait être amélioré en caractérisant l’hétérogénéité de l’aquifère de socle à partir d’autres hypothèses telles que la lithologie et par l’introduction d’autres types de données dans la calibration (ex. : débits, carte piézométrique).
Mots-clés :
- Aquifère de socle,
- zones discrètes de perméabilité,
- conductivité hydraulique,
- charges hydrauliques,
- calibration,
- bassin versant du N’zo
Abstract
Estimating the hydraulic conductivity of hard rock aquifers at a regional scale remains a major challenge. At this scale the data are scarce in quantity and quality. This paper provides an approach to estimate the hydraulic conductivity of hard rock aquifers from the calibration of a numerical model using hydraulic heads. This approach is applied to the N’zo watershed, which extends over an area of 4 300 km2. The methodology assumes that the permeability of the aquifer is related to vertical fractures, which are permeable over a depth of 100 m down from the surface. It is also assumed that these fractures can be identified as fault lines and all fault lines are fractures and are permeable. The first step of this methodology is mapping the permeability in discrete zones of the hard rock aquifer. These are identified from analysis of the density and orientation of « fractures » at the mesh scale, which represent the work scale. The fractures are linked to fault lines that are mapped from a radar image. Six spatial configurations of discrete permeability zones are generated with mesh sizes from 2 to 12 km. The second step concerns the construction of the numerical model from the external limits of the watershed, the DEM (Digital elevation model), the river network and a uniform recharge. Lastly, the third step consists of transferring each configuration of the discrete permeability zones to the numerical model and calibration in a steady-state flow simulation, using hydraulic heads. The hydraulic heads are observed at 86 discrete measurement points. The results indicate that the optimal model of discrete permeability zones is obtained with a mesh of 4 km. Calculated hydraulic conductivities oscillate between 1.1 x 10-6 and 2.4 x 10-5 m∙s-1. However, these values should be taken with caution because the identification of the homogeneous zones from the fracture network is based on the controversial approach of using fault lines and the calibration is performed only with hydraulic heads and not with hydraulic fluxes. The conceptual model developed in this work could be improved by characterizing heterogeneity of the hard rock aquifer from other assumptions such as lithology and by the introduction of other types of data into the calibration (ex.: fluxes, groundwater maps).
Keywords:
- Hard rock aquifer,
- hydraulic conductivity,
- discrete zones,
- calibration,
- hydraulic heads,
- N’zo watershed
Corps de l’article
1. Introduction
La gestion et la protection des nappes d’eau souterraine requièrent la connaissance de leurs caractéristiques (structure, fonctionnement, etc.), dont la perméabilité. La perméabilité est définie comme la capacité de la roche à laisser s’écouler un fluide. Elle est susceptible d’exercer un contrôle significatif sur la recharge, les flux d’écoulement à travers l’aquifère et, par voie de conséquence, les gradients hydrauliques. Aujourd’hui, une grande partie des études scientifiques porte sur la caractérisation de la perméabilité à travers des essais in situ, des expériences en laboratoire et des modèles numériques (LONG et al., 1982; LONG et BILLAUX, 1987; CLAUSER, 1992; NEUZIL, 1994; INGEBRITSEN et MANNING, 1999, 2010; ILLMAN et NEUMAN, 2003; WELLMAN et POETER, 2005; GLEESON et al., 2011). Cependant, le calcul de la perméabilité des aquifères est loin d’être une chose facile en raison de son hétérogénéité. En milieu fracturé, elle peut varier de plus de huit ordres de grandeur (FREEZE and CHERRY, 1979; CLAUSER, 1992; DE MARSILY et al., 2005). Par ailleurs, la perméabilité est connue aussi pour sa dépendance de l’échelle d’étude. On considère que sa valeur augmente de l’échelle locale à l’échelle régionale et se stabilise à une très grande échelle (LONG et al., 1982; FAILLAT, 1986; ILLMAN, 2006). Des valeurs raisonnables de perméabilité à l’échelle régionale peuvent être accessibles à travers les méthodes géostatistiques (CLARK, 1979; DE MARSILY et al., 1984; GELHAR, 1993) ou numériques (CLAUSER, 1992; D'AGNESE et al., 1999; DE MARSILY et al., 2000; GLEESON et al., 2011). Les méthodes numériques donnent des résultats satisfaisants si le modèle est bien calibré (CACAS et al., 1990a, 1990b; WELLMAN et POETER, 2005). Cependant, la calibration se heurte à certaines difficultés dont la principale est la représentation des hétérogénéités de l’aquifère dans le modèle numérique (CACAS et al., 1990a, 1990b; VOSS, 2011a, 2011b). Les modalités de description de ces hétérogénéités sont nombreuses, elles sont le plus souvent basées sur les mesures ponctuelles, les propriétés géométriques du réseau de fractures, la lithologie, etc. Une revue synthétique des méthodes de description de l’hétérogénéité des aquifères est donnée par DE MARSILY et al. (2005).
Dans cette étude, l’hétérogénéité des aquifères de socle est décrite à partir de l’analyse des propriétés géométriques du réseau de fractures, notamment la densité et l’orientation. En milieu fracturé, la densité et l’orientation des fractures contrôlent la connectivité des fractures, dont dépend la perméabilité (BERKOWITZ, 2002). Le terme fractures fait référence ici à toutes sortes de ruptures d’une roche ou d’un ensemble rocheux. Elles regroupent les fissures, les joints et les failles. L’origine de ces fractures en milieu de socle connait quelques controverses dans la littérature. Ces fractures étaient attribuées anciennement à des phénomènes tectoniques ou de décompression dus à l’érosion (ACWORTH, 1987; WRIGHT, 1992). Cependant, les études récentes indiquent que ces fractures sont générées par les processus d’altération de la roche-mère (WYNS et al., 2004; LACHASSAGNE et al., 2011). Ainsi, au sein des roches de socle, le profil d’altération comporte, de haut en bas, une couche d’altérites meubles (la saprolite), peu perméable, mais capacitive, dont l’épaisseur peut atteindre plusieurs dizaines de mètres, puis un horizon fracturé, perméable, d’une épaisseur similaire. Au sein des granites, l’horizon fracturé comporte majoritairement des fractures subhorizontales. Dans les autres types de roche de socle, les fractures présentent tous types d’orientations et de pendages.
Les fractures, réseaux de fractures ou l’horizon fracturé peuvent être identifiés et caractérisés sur des échantillons récoltés sur le terrain, sur des affleurements, dans les forages, à partir d’approches géomorphologiques ou paléogéomorphologiques (LACHASSAGNE et al., 2011) ou, indirectement, à partir de méthodes géophysiques, des photographies aériennes et des images satellitaires. Dans le présent travail, les fractures sont considérées comme des objets discrets (et non comme un horizon fracturé) et cartographiées à partir des images satellitaires. Sur les images satellitaires, des linéaments sont identifiés. Toutefois, tous les linéaments ne sont pas forcément des fractures. Il peut s’agir, entre autres, de contacts géologiques, d’alignement d’arbres, de routes, lignes électriques, etc. Par conséquent, l’assimilation des linéaments à des fractures fait apparaître de nombreuses controverses en hydrogéologie (WISE, 1982; MABEE et al., 1994; SINGHAL et GUPTA, 1999; TAM et al., 2004; SANDER, 2007). Ces controverses vont au-delà des objectifs de cette étude. Cependant, les linéaments peuvent être assimilés aux fractures sous certaines conditions. Ces conditions sont abondamment illustrées dans la littérature (MABEE et al., 1994; SANDER et al., 1997; SANDER, 2007). Nous avons, entre autres, l’évaluation de la proximité des linéaments avec les débits des forages, la comparaison de l’orientation générale des linéaments avec celle des fractures ou failles formellement identifiées sur le terrain ou sur la carte géologique. Dans le présent travail, l’orientation des linéaments est comparée avec celle des fractures identifiées sur des affleurements et sur la carte géologique. Il est fait l’hypothèse que tous les linéaments correspondent à des fractures et que ces fractures sont verticales. Par ailleurs, tous les linéaments sont considérés comme des fractures perméables et aucune distinction n’est faite entre les fractures saturées et non saturées en eau.
Par ailleurs, deux approches sont généralement utilisées dans la littérature pour modéliser les écoulements en milieu de socle : le modèle discret et le modèle continu. Dans le modèle discret, les hétérogénéités sont représentées par des fractures individuelles. Ce modèle offre la possibilité d’examiner l’influence individuelle des fractures sur l’écoulement. Cependant, l’inconvénient majeur du modèle discret est que la définition détaillée des caractéristiques géométriques des fractures individuelles qui permettent le calcul de leur perméabilité telles que, la longueur, l’ouverture, l’espacement et l’orientation, est difficilement réalisable sur le terrain en pratique. Si bien que l’application de ce modèle est limitée à des échelles réduites (CACAS et al., 1987a, 1987b; DVERSTOP et ANDERSSON, 1989; DVERSTOP et al., 1992). Le modèle continu est par contre le modèle le plus classique et le plus simple employé dans les études du milieu fracturé. Il ne nécessite pas la connaissance précise de la géométrie du réseau de fractures. Le modèle continu suppose que l’écoulement à travers une masse rocheuse est similaire à celui d’un milieu poreux lorsque celle-ci est affectée par un réseau de fractures orientées dans toutes les directions et interconnectées (LONG et al., 1982; BERKOWITZ, 2002).
Dans ce travail, l’aquifère de socle est modélisé selon le modèle continu. La description des hétérogénéités qui contrôlent les champs de perméabilité dans ce modèle est basée sur la théorie des SER (surface élémentaire représentative), qui dérive du concept de VER (volume élémentaire représentatif) en milieu poreux. Une SER désigne une échelle pour laquelle une propriété hydrogéologique moyenne (ex. : la perméabilité) peut être trouvée. Ce concept a été défini pour la première fois par BEAR (1972) en milieu de socle. De nombreuses théories fondamentales actuelles de circulation d'eau en milieu de socle sont basées sur ce concept. Cependant, le concept de SER connait beaucoup de controverses depuis son apparition dans les sciences hydrologiques. En effet, de nombreux auteurs indiquent que la théorie des SER est trop simple et n’est pas applicable, car il n’est pas toujours possible de trouver des propriétés homogènes équivalentes (ou SER) pour les milieux naturels très hétérogènes (FREEZE, 1975; SMITH et FREEZE, 1979a, 1979b). D’autres auteurs montrent qu’en fonction de la complexité du milieu, plusieurs SER peuvent être identifiées et hiérarchisées à différentes échelles en milieu hétérogène (CUSHMAN, 1990). En dépit des limites liées à la définition des zones homogènes en milieu de socle, l’approche continue s’est avérée efficace dans de nombreuses études (TSANG, 1993; NRC, 1996; ANDO et al., 2003; LE GOC, 2009).
L’objectif principal de cette étude est de contribuer à la caractérisation de la géométrie des champs de perméabilité de la couche granitique de l’aquifère de socle du bassin versant du N’zo situé à l’Ouest de la Côte d’Ivoire. Cette couche contiendrait environ 80 % de la réserve en eau souterraine de l’aquifère de socle en général (WYNS et al., 2004). Les forages les plus productifs sont ceux qui captent cette couche granitique fissurée. L’aquifère est étudié comme un modèle continu où les hétérogénéités sont représentées par des zones discrètes de perméabilité déduites du concept de SER. Ces zones discrètes de perméabilité sont identifiées à partir de l’analyse de la densité et de l’orientation des linéaments. Plusieurs configurations possibles des zones discrètes de perméabilité sont générées en fonction de la taille de la maille d’analyse de la densité et de l’orientation des linéaments. L’évaluation de ces modèles de zones discrètes de perméabilité est faite au cours de la calibration en comparant les charges simulées et observées qui représentent respectivement les écoulements simulés et les écoulements naturels dans le système. Cette approche se présente comme une alternative aux méthodes existantes de calcul de la perméabilité dans cette région. Elles sont basées essentiellement sur la méthode de Franciss (FRANCISS, 1970) et sur l’interprétation des essais de pompage. Ces derniers sont le plus souvent rares et mal repartis.
2. Présentation de la zone d’étude
L’aquifère étudié dans le présent travail est un aquifère de socle situé en milieu tropical humide. La zone d’étude a été circonscrite à celle d’un bassin versant hydrologique, le bassin versant du N’zo à Kahin (Figure 1). Il est situé dans l’Ouest de la Côte d’Ivoire et s’étend sur une superficie de 4 300 km2. Sa topographie varie globalement de 1 250 m environ à 200 m dans la direction nord-sud. Les caractéristiques les plus importantes du relief sont les chaines des Dan et des Toura localisées dans la partie nord du bassin versant, dont les sommets dépassent les 1 000 m.
Sur le plan géologique, la lithologie du bassin est constituée de deux grands domaines : un domaine granulitique essentiellement localisé au Nord et un domaine migmatitique situé au Sud (Figure 1). Le domaine granulitique se compose de trois unités géologiques : 1) des gneiss gris rubanés, d’origine magmatique, composés de formations quartzo-feldspathiques à clinopyroxène et orthopyroxène, 2) des quartzites à magnétite et des formations associées (diopsidites, hypersthénites) reposant sur des basites et ultrabasites et 3) des charnockites intrusives formées de mégacristaux d’orthose. Le domaine migmatitique est aussi dominé par trois types de formations géologiques : 1) des migmatites à biotite et microcline qui sont des roches quartzo-feldspathiques assez homogènes, composées de bancs clairs et sombres millimétriques, rarement centimétriques, 2) des gneiss migmatitiques et des gneiss à deux micas et 3) des amphibolites, des pyroxénolites et des quartzites ferrugineuses.
Figure 1
Situation géographique et carte géologique de la zone d’étude
Geographic location and geological map of the study area
D’un point de vu structural, quatre phases de déformation allant de 2 817 à 1 670 Ma ont été inventoriées dans la zone d’étude (TAGINI, 1971; DJRO, 1998). Ces phases ont donné naissance à de nombreux accidents et fractures. Les études complémentaires basées sur la télédétection et les données de terrain effectuées par KOUAMÉ (1999) et SALEY (2003) montrent que cette région comporte de nombreux linéaments.
Le climat du bassin versant du N’zo est sous l’influence du régime de montagne, caractérisé par l'abondance des précipitations dont les valeurs annuelles varient de 1 600 à 2 500 mm. Il est constitué globalement de deux saisons : une longue saison pluvieuse qui dure huit mois (mars-octobre) et une saison sèche de quatre mois (novembre-février). Pendant la saison sèche, les précipitations moyennes mensuelles dépassent rarement 50 mm, tandis que les moyennes mensuelles dépassent 300 mm au cours de la saison des pluies. Concernant les températures, on observe une variation qui va de 21,4 °C en décembre (saison sèche) à 27,6 °C au mois de mars (début de saison sèche), avec une humidité de l’air très forte tout au long de l’année (98 %).
3. Matériel et méthodes
3.1 Données et matériel
La base de données du présent travail est constituée de : i) une image radar (RSO de RADARSAT-1 datant de 2002), ii) un MNT (modèle numérique de terrain) acquis en format SRTM (Shuttle Radar Topography Mission) avec une résolution spatiale de 90 m et une précision altimétrique de 16 m/10 m (absolu/relatif) et iii) 86 mesures de charges hydrauliques provenant d’archives de fiches techniques de forages.
Le logiciel de traitement d’image ENVI 4.5 est utilisé pour produire une carte linéamentaire détaillée à partir de l’image radar. Le traitement des linéaments (distribution des orientations et densités) est effectué avec le programme LINWIN. La carte de densité et d’orientation des linéaments a été produite avec ArcMap 9.3 à partir de la compilation des fichiers statistiques (distribution des orientations et densités) fournis par le programme LINWIN. Le maillage du modèle géométrique est effectué avec Triangle (SHEWCHUK, 1996) et le transfert précis des zones discrètes de perméabilité à ce maillage est réalisé avec Gridbuilder (MCLAREN, 2007). Le code numérique employé pour la simulation des écoulements est HydroGeoSphere (THERRIEN et al., 2006) et la calibration automatique ou modélisation inverse est effectuée à l’aide du code PEST (DOHERTY, 2005).
3.1.1 Caractéristiques des charges hydrauliques
Les charges hydrauliques utilisées pour la calibration des zones discrètes de perméabilité proviennent des niveaux piézométriques historiques contenus dans les fiches techniques de forages. La principale faiblesse de ces mesures piézométriques provient de leur date d’acquisition. En effet, la plupart de ces mesures piézométriques ont été réalisées lors de l’exécution des ouvrages, entre 1980 et 1981, dans le cadre des programmes nationaux d’équipements hydrauliques. Cependant, sur un effectif de 219, 167 mesures piézométriques ont été réalisées en 1981 soit environ 75 % de l’effectif total et le reste en 1980 soit 25 %. Nous avons donc utilisé pour cette étude seules les mesures effectuées en 1981 soit 167, afin d’éviter l’effet de la variation interannuelle de la pluviométrie sur la calibration. Il faut noter également que toutes les mesures ont été réalisées entre octobre et décembre. Cette période correspond à la période intermédiaire entre la saison des pluies et la saison sèche. En outre, pour obtenir de meilleurs résultats dans le processus de calibration automatique, les paramètres de calage doivent être uniformément répartis dans le bassin versant et les clusters (zones de fortes concentrations des mesures) doivent être évités (REILLY et al., 1987; REILLY et HARBAUGH, 2004; DOHERTY, 2005; HILL et TIEDEMAN, 2007). Ainsi, les données piézométriques rapprochées et semblables ont été supprimées. L’élimination de ces valeurs rapprochées n’a pas d’influence significative sur la calibration, car, pour une zone donnée dans le bassin versant, le niveau piézométrique varie très peu (OULARÉ et al., 2014). Finalement, le nombre de charges hydrauliques utilisées dans le processus de calibration est de 86. Elles couvrent assez uniformément le bassin versant (Figure 2). Une autre difficulté liée à l’exploitation des archives de forages se situe au niveau des mesures des altitudes qui sont le plus souvent imprécises. En effet, en comparant les altitudes (z) contenues dans les fiches techniques de forages avec le MNT, nous avons constaté des erreurs importantes. Les écarts entre les valeurs provenant des archives de forages et le MNT varient ainsi de 10 à 80 m. Compte tenu de l’importance de ce paramètre spatial pour le calcul des charges hydrauliques, les valeurs d’altitude provenant des archives ont été abandonnées au profit de celles déduites du MNT en raison de sa bonne résolution spatiale (90 m) et altimétrique (16 m/10 m). Cette résolution est jugée acceptable pour les objectifs de cette étude.
Figure 2
Répartition spatiale des mesures de charge hydraulique utilisées pour la calibration
Spatial repartition of the hydraulic head measurements used for the calibration
3.2 Méthodes
3.2.1 Acquisition du réseau de fractures
Le réseau de fractures employées dans le cadre de ce travail pour décrire les zones discrètes de perméabilité provient des linéaments. Dans le cadre de ce travail les linéaments ont été cartographiés à partir d’une image radar RSO. Une brève description de la méthodologie employée est donnée dans les sections ci-dessous.
3.2.1.1 Traitement de l’image
L’extraction des linéaments de la zone d’étude a été faite à partir d’une image RSO (radar à synthèse d’ouverture) de radarsat-1 ayant une résolution de 50 m. Le principal avantage de cette image est de pouvoir détecter les linéaments et autres objets géologiques à la surface de la Terre dans presque toutes les conditions atmosphériques, le jour ou la nuit, dans un brouillard, etc. (RUDANT et al., 1994; KOUAMÉ et al., 2009). Les linéaments multikilométriques sont observables sur l’image radar, ce qui n’est pas le cas des linéaments de faible extension compte tenu de la résolution de l’image (50 m).
Les traitements effectués se résument principalement en deux étapes. La première étape consiste à réduire le chatoiement qui est responsable de l’apparence bruitée de l’image. Les effets du chatoiement sont réduits par l’application respective des filtres de Lee, Kuan et Frost, disponibles dans le logiciel ENVI 4.5. La deuxième étape porte sur le rehaussement des discontinuités qui se fait également par l’application des filtres directionnels tels que les filtres Laplacien et de Sobel. Au cours de cette étude, ce sont les filtres directionnels de Sobel qui ont été appliqués à l’image. Ces filtres sont également disponibles dans ENVI 4.5.
3.2.1.2 Extraction des linéaments
Les traitements décrits ci-dessus permettent de produire une carte de gradient élevé. Il devient donc possible de repérer sur cette carte les linéaments qui sont représentés par les discontinuités-images. Les figures 3a et 3b montrent deux exemples de fenêtres ouvertes sur la zone d’étude à travers lesquels les discontinuités et les changements de tonalité sont observables. Sur ces discontinuités des segments sont tracés. Après avoir tracé les segments sur une vue globale de la zone d’étude, de petites fenêtres (permettant de faire un zoom) sont ouvertes et déplacées sur toute la surface de l’image afin de repérer et de cartographier les segments de petite taille. On enregistre ces segments supplémentaires dans le même fichier vecteur contenant les premiers segments cartographiés.
Figure 3
Discontinuités (linéaments) observées à travers deux fenêtres ouvertes dans la zone d’étude
Discontinuities (lineaments) observed through two windows opened in the study area
3.2.1.3 Validation de la carte linéamentaire
La validation de la carte linéamentaire constitue la dernière étape de l’établissement de la carte linéamentaire finale. Elle comporte globalement deux étapes. Dans un premier temps, les tracés rectilignes relatifs aux activités anthropiques (routes, pistes, lignes de transport d’énergie) sont éliminés de la carte linéamentaire produite par un croisement avec la carte routière (qui contient la plupart de ces tracés d’origine anthropique). Dans un second temps les directions majeures des linéaments, relevés sur l’image, sont analysées et comparées avec celles relevées sur le terrain.
3.2.1.3.1 Orientations des linéaments
La rosace directionnelle montre que les linéaments sont orientés dans toutes les directions (Figure 4). Cependant, trois directions se distinguent par leurs fréquences élevées, il s’agit des directions N-S, E-O et NE-SO. Ces trois directions sont comparées avec celles relevées sur le terrain dans les travaux antérieurs.
Figure 4
Rosace directionnelle des linéaments relevés de l’image satellitaire
Directional distribution of lineaments from the satellite image
3.2.1.3.2 Comparaison des orientations des linéaments avec celles des fractures
Les trois directions principales identifiées sur la carte de linéaments (N-S, E-O et NE-SO) concordent globalement avec les directions majeures des fractures relevées sur le terrain à Gbatodié et à San Maoulé (Figures 5a et 5b) dans la région de Man-Danané (KOUAMÉ, 1999). Cela montre l’existence d’une relation entre les fractures relevées sur le terrain et les linéaments. Les linéaments cartographiés ont donc un certain sens physique et par conséquent, ils peuvent être assimilés à des fractures (MABEE et al., 1994; SINGHAL et GUPTA, 1999; KOUAMÉ, 1999; SANDER et al., 1997; SANDER, 2007; JOURDA, 2005; YOUAN TA, 2008). La figure 6 résume les différentes étapes de l’élaboration de la carte de fracturation à partir de l’image radar.
Figure 5
Rosace directionnelle des fractures relevées sur le terrain
Directional distribution of fractures observed in the field
Figure 6
Principales étapes de l’élaboration de la carte de fracturation
Main steps in the development of the fracture map
3.2.2 Identification des zones discrètes de perméabilité du réseau de fractures
La définition des zones discrètes de perméabilité en milieu fracturé est basée sur de nombreuses hypothèses. Ces hypothèses sont le plus souvent fondées sur les propriétés géométriques telles que l’ouverture, la longueur, l’orientation et la connectivité des fractures (LONG et al., 1982; CHARLAIX et al., 1987; CACAS et al., 1990a, 1990b; DONADO et al., 2005). Il existe aussi des hypothèses basées sur la genèse et l’histoire des fractures (DE MARSILY et al., 2005). Ainsi, les zones discrètes de perméabilité peuvent être définies en regroupant les fractures en familles selon leurs ouvertures, longueurs, orientations, histoires géologiques, leurs degrés d’altération et de remplissage argileux, etc. Dans la région d’étude, les informations de terrain sur certaines propriétés géométriques, telles l’ouverture et la longueur précise des fractures et même sur l’histoire de ces fractures, sont rares. L’identification des zones discrètes de perméabilité du réseau de fracture est par conséquent basée sur la connectivité des fractures (BERKOWITZ, 2002), analysée à l’échelle des SER. La connectivité des fractures est étudiée indirectement à travers deux paramètres : la densité et de l’orientation des fractures. C’est une approche régionale, car elle est applicable facilement sur de grandes superficies, allant de l’échelle d’un grand bassin versant à l’échelle régionale. Globalement, elle est basée sur les hypothèses suivantes (BRACQ, 1994) : i) les fractures sont considérées comme des lignes (2D) d’extension finie dont la taille est fonction du pas de la maille choisie; cela revient aussi à considérer que toutes les fractures sont verticales, ii) les fractures sont considérées comme des unités sans largeur et iii) les fractures sont toutes considérées comme perméables et la matrice est considérée comme imperméable. La perméabilité est donc gouvernée essentiellement par la connectivité des fractures, analysée à travers la densité et l’orientation des fractures. Les mailles d’analyse de la fracturation doivent donc répondre aux critères de représentativité portant sur le nombre critique de fractures (au moins 30 fractures) et le poids relatif des classes directionnelles (seuil fixé à 10 %) nécessaire à la connectivité des fractures (BRACQ, 1994). Dans le réseau de fractures cartographiées, les mailles qui répondent à ces critères de représentativité mentionnés ci-dessus sont celles dont la taille varie de 2 à 12 km. La taille de ces mailles correspond également à celle des SER dans le présent travail. En effet, au-delà de 12 km, le nombre de classes directionnelles diminue considérablement dans les mailles et le critère lié à la classe directionnelle ne peut être atteint (seuil fixé à 10 %). À l’opposé, pour des tailles de mailles inférieures à 2 km, c’est plutôt le nombre de fractures qui est très faible (moins de 30 fractures). Par ailleurs, en raison de la superficie couverte (échelle d’un grand bassin versant), un pas de 2 km a été choisi afin de limiter le nombre de configurations des champs de perméabilité à traiter. Par conséquent, les tailles de mailles analysées sont respectivement 2, 4, 6, 8, 10 et 12 km de côté. Ces mailles qui sont représentatives des SER désignent les zones discrètes de perméabilité (HARDCASTLE, 1995). En considérant que toutes les fractures sont saturées en eau, une conductivité hydraulique équivalente peut être calculée dans ces zones discrètes de perméabilité à partir de la calibration d’un modèle d’écoulement en régime permanent (WELLMAN et POETER, 2005).
3.2.3 Évaluation des modèles possibles de zones discrètes de perméabilité
Les six modèles de configuration des zones discrètes de perméabilité, générés selon l’approche décrite ci-dessus, peuvent être évalués selon plusieurs approches, entre autres : i) la régression non-linéaire via la modélisation inverse (CARRERA et NEUMAN, 1986; COOLEY et NAFF, 1990; SUN et YEH, 1990a, 1990b; BURNHAM et ANDERSON, 2002), ii) les méthodes stochastiques (NEUMAN, 1987; BEVEN, 2000), iii) la géostatistique (MATHERON, 1973; CLARK, 1979) et iv) les méthodes bayésiennes (GRAHAM et TANKERSLEY, 1994; NEUMAN, 2002). Le choix de ces approches est le plus souvent guidé par l’échelle d’étude, les données disponibles et les objectifs de l’étude.
L’approche adoptée dans le cadre de cette étude est la modélisation inverse. Cette approche présente plusieurs avantages. Elle permet de calculer quantitativement la conductivité hydraulique équivalente des zones discrètes de perméabilité en utilisant les variables du système telles que les charges hydrauliques (niveaux piézométriques), les flux (débits), etc. (HILL, 1998; HILL et TIEDEMAN, 2007). En outre, la modélisation inverse ne nécessite pas un grand nombre d’observations pour calculer la conductivité hydraulique. Toutefois, le nombre d’observations doit être supérieur au nombre de paramètres (HILL, 1998; HILL et TIEDEMAN, 2007). A la fin de la calibration, de nombreuses informations sont fournies sous forme de fichiers. Elles peuvent être analysées statistiquement ou graphiquement pour évaluer les modèles de zones discrètes de perméabilités élaborés (WELLMAN et POETER, 2005, 2006). Ces informations sont classées globalement en deux groupes : 1) les paramètres d’ajustement et 2) les paramètres d’incertitude. Les paramètres d’ajustement sont la fonction objectif, l’erreur de modèle, la moyenne des résidus pondérés, etc. Les paramètres d’incertitude sont représentés par l’intervalle de confiance à 95 %. Nous avons aussi les paramètres statistiques tels que AIC (Akaike Information Criterion) et BIC (Bayesian Information Criterion) qui sont considérés comme des paramètres d’ajustement (HILL 1998; HILL et TIEDEMAN, 2007).
Les différentes configurations spatiales des zones discrètes de perméabilité générées sont toutes considérées comme des modèles possibles des champs de perméabilité du réseau de fractures étudié. Elles sont calibrées avec les mêmes observations, les mêmes conditions initiales et aux limites, puis comparées.
4. Résultats
4.1 Propriétés géométriques du réseau de fractures
Au total, 4 314 tracés de linéaments, assimilables à des fractures après validation, ont été recensés avec des longueurs variant de 0,5 km à quelques kilomètres sur l’ensemble du domaine (Figures 7a et 7b). Plus bas dans le texte, ces linéaments seront décrits comme des « fractures ». Les fractures sont orientées dans toutes les directions avec une prédominance dans les directions N-S, NE-SO et E-O (Figure 4). Le réseau de fractures est décrit par la loi de puissance avec un bon ajustement dans la plage comprise entre 3 et 20 km (Figure 7b). L’exposant de la loi de puissance est 2,86. Ce nombre est compris entre 1 et 3, ce qui confirme que le réseau de fractures cartographiées est un réseau interconnecté et comparable à un réseau percolant (DAVY, 1993; BOUR et DAVY, 1997). Il est donc assimilable à un milieu continu.
Figure 7
Caractéristiques géométriques des linéaments : a) répartition spatiale
Geometric characteristics of the lineaments
4.2 Distribution spatiale des modèles possibles de zones discrètes de perméabilité
Six configurations possibles de distribution spatiale de champs de perméabilité ont été générées en raison d’une configuration par pas de maille choisie (Figure 8). A l’intérieur de chaque configuration, des zones discrètes de perméabilité peuvent être associées à chaque maille. Cependant, cela engendrerait un trop grand nombre de zones de paramètres et il sera impossible de les calibrer en raison du nombre limité d’observations disponibles (moins d’une centaine pour cette étude). À titre d’exemple, pour une maille de 2 km on a environ 2 100 zones de paramètres. Ce nombre est largement supérieur au nombre d’observations disponibles. Les mailles ont donc été regroupées en quatre classes principales en fonction de leur similitude en termes de nombre de fractures et de classes directionnelles. Ainsi, en tenant compte de la valeur quantitative de ces variables, les classes définies sont considérées comme étant des zones potentielles de conductivité hydraulique élevée (K4), modérée (K3), faible (K2) et très faible (K1) (Figure 8). Ce nombre de classes est acceptable à l’échelle d’un grand bassin versant caractérisé par la rareté des observations (VOSS, 2011a, 2011b).
Figure 8
Zones discrètes de perméabilité produites respectivement avec les mailles de
Discrete permeability areas produced along with the meshes of
a) 2 km, b) 4 km, c) 6 km, d) 8 km, e) 10 km et f) 12 km
a) 2 km, b) 4 km, c) 6 km, d) 8 km, e) 10 km and f) 12 km
4.3 Calibration des modèles possibles de zones discrètes de perméabilité
4.3.1 Maillage du modèle d’écoulement
Le maillage ou la discrétisation de l’aquifère est effectué selon l’approche des éléments finis. L’avantage majeur de cette méthode réside dans la flexibilité du maillage, qui permet une approximation spatiale fine des limites irrégulières dans les zones de stress du système aquifère telles que les rivières, les limites latérales, etc. Dans cette étude, la taille des éléments varie de 100 m de côté aux alentours des zones de stress (limites latérales du bassin versant, rivières, etc.) à 500 m au maximum dans le reste du domaine. Ce maillage est jugé satisfaisant à l’échelle d’un grand bassin versant (REILLY et HARBAUGH, 2004). Sur le plan vertical, le maillage est subdivisé en plusieurs couches uniformes (environ une dizaine) afin d’obtenir un modèle en 3D. Au total, le modèle géométrique 3D construit est constitué de 607 782 noeuds et de 1 119 534 éléments.
4.3.2 Conditions aux limites du modèle d’écoulement
Pour résoudre l’équation d’écoulement dans le modèle numérique, il faut des informations supplémentaires sur l’état physique de l’aquifère (REILLY et HARBAUGH, 2004). Ces informations sont fournies par les conditions initiales et les conditions aux limites. Pour cette étude, étant donné que la calibration est effectuée en régime permanent, seules les conditions aux limites sont nécessaires (ANDERSON and WOESSNER, 1992; REILLY, 2001; REILLY et HARBAUGH, 2004). Mathématiquement, elles comprennent la géométrie des limites du domaine, les variables dépendantes (ex. : charge hydraulique) ou leurs dérivées (ex. : flux) imposées à ces limites (ANDERSON and WOESSNER, 1992; REILLY et HARBAUGH, 2004).
Les conditions aux limites correspondant à l’aquifère du bassin versant du N’zo sont définies sous certaines conditions. En effet, en contexte de socle, compte tenu de la faible perméabilité du milieu en général, on peut considérer que bassins versants topographique et souterrain coïncident. Par conséquent, les limites extérieures du bassin versant topographique d’étude sont considérées également comme des limites souterraines. Un flux nul a été donc imposé aux limites latérales du bassin versant du N’zo sur toute l’étendue de son épaisseur (Figure 9). L’épaisseur maximale de l’aquifère a été fixée à 100 m en tenant compte de la profondeur atteinte par les forages. Cette hypothèse est en bon accord avec l’épaisseur des horizons altérées (LACHASSAGNE et al., 2011). En outre, l’analyse des archives de fiches techniques de forage indique que les forages productifs dépassent rarement les 100 m de profondeur (KOUAMÉ, 1999; LASM, 2000). En réalité, l’épaisseur de la couche granitique fissurée est inférieure à 100 m, car la profondeur des forages englobe aussi l’épaisseur des altérites qui n’est pas considérée dans ce travail. Une étude de sensibilité s’avère donc nécessaire pour connaître l’influence de l’épaisseur de la couche granitique fracturée sur la conductivité hydraulique. Par ailleurs, un flux nul a été également imposé à la limite inférieure de l’aquifère correspondant à la couche granitique non fracturée. Un flux uniforme de 300 mm est appliqué sur toute la surface supérieure de l’aquifère. Ce flux, qui correspond à environ 15 % de la moyenne pluviométrique annuelle, est assimilé à la recharge annuelle. Une charge imposée a été appliquée le long des rivières afin de permettre l’exfiltration des eaux souterraines à ces endroits (Figure 9). La valeur de cette charge est égale à l’élévation du terrain dans les lits des cours d’eau. Cette valeur a été fournie par le MNT. Les rivières choisies sont considérées comme pérennes dans le bassin versant.
Figure 9
Conditions aux limites définies dans l’aquifère
Boundary conditions defined in the aquifer
4.3.3 Transfert des zones discrètes de perméabilité au modèle géométrique et exécution de la calibration
Avant la calibration, les différentes configurations spatiales de zones discrètes de perméabilité générées respectivement avec les mailles de 2, 4, 6, 8 , 10 et 12 km (Figure 8) sont transférées de manière précise au maillage du modèle géométrique 3D construit pour la simulation des écoulements. La figure 10 montre un exemple de zones discrètes de perméabilité transféré au maillage. Ces zones sont ensuite calibrées avec les conditions aux limites et les observations (charges hydrauliques). Les points de calage sont constitués de 86 charges hydrauliques et sont sélectionnés de sorte à couvrir l’ensemble du domaine d’étude de manière uniforme (Figure 2). Enfin, la calibration est effectuée en régime permanent en conditions saturées (zone non saturée non prise en compte).
Figure 10
Exemple de zones discrètes de perméabilité transférées au modèle géométrique
Example of discrete permeability areas transferred to the geometric model
Au début de la calibration, une valeur initiale de conductivité hydraulique est assignée à priori à chaque zone de paramètre prédéfinie dans le modèle d’écoulement (K1, K2, K3 et K4). Ces zones de paramètre correspondent aux quatre zones discrètes de perméabilités identifiées dans l’aquifère (très faible, faible, modérée, élevée). Après cette étape, le processus de calibration est lancé manuellement, ensuite le modèle d’écoulement est relancé à plusieurs reprises par l’estimateur de paramètre (PEST) qui prend en main le contrôle du modèle d’écoulement. En effet, après chaque exécution, le code PEST compare dans un premier temps les charges hydrauliques simulées et les charges hydrauliques observées puis, dans un second temps, détermine les modifications à apporter aux paramètres pour améliorer l’ajustement et, enfin, dans un troisième temps, il relance le modèle d’écoulement de façon automatique (sans intervention humaine). Le processus est ainsi répété jusqu’à l’obtention de la valeur minimum de la fonction objectif qui correspond au meilleur ajustement possible avec les charges hydrauliques observées. Après la calibration des différentes configurations spatiales des zones discrètes de perméabilité, les résultats obtenus sont analysés graphiquement.
4.4 Sélection du modèle optimal de zones discrètes de perméabilité et analyse des conductivités hydrauliques estimées
Les figures 11a et 11b montrent la relation entre la taille des mailles d’analyse des propriétés géométriques du réseau de fractures (densité et orientation) et les paramètres d’ajustement, désignés par la fonction objectif et l’erreur de modèle. Ces mailles contrôlent la configuration spatiale des zones discrètes de perméabilité définies dans l’aquifère (Figure 8). La maille qui donne les valeurs minimales de la fonction objectif et de l’erreur de modèle est 4 km. Les valeurs minimales des paramètres statistiques AIC et BIC sont également fournies pour cette maille (Figures 12a et 12b). Pour les mailles de taille inférieure et supérieure à 4 km, nous constatons une augmentation progressive de la fonction objectif, de l’erreur de modèle ainsi que des variables statistiques AIC et BIC. Donc la qualité de l’ajustement baisse lorsque les mailles sont trop petites ou trop grandes. Ces résultats sont conforment avec les hypothèses émises par BRACQ (1994) et par HARDCASTLE (1995) sur la sélection de la taille des mailles d’analyse des propriétés géométriques du réseau de fractures. En effet, les mailles ne doivent être ni trop petites, ni trop grandes. Lorsqu’elles sont trop petites, on aura beaucoup de valeurs nulles (ex. : nombre de fractures interconnectées). Par contre, si elles sont trop grandes, bien que le nombre de fractures interconnectées soit important, cela entraine une baisse de résolution au niveau des orientations de celles-ci. Par conséquent ces mailles ne peuvent plus représenter correctement le comportement discret des zones de perméabilité du réseau de fractures (BRACQ, 1994; HARDCASTLE, 1995).
Figure 11
Relation entre paramètres d’ajustement et pas de maillage
Relation between adjustment parameters and mesh size
Figure 12
Relation entre paramètres statistiques et pas de maillage
Relation between statistical parameters and mesh size
a) AIC (critère d'information d'Akaike), b) BIC (critère d'information bayésien)
a) AIC (Akaike Information Criterion); b) BIC (Bayesian Information Criterion)
Le modèle de configuration spatiale des zones discrètes de perméabilités le plus représentatif de la région étudiée (maille de 4 km) doit être capable aussi de calculer les conductivités hydrauliques avec des incertitudes minimales (WELLMAN et POETER, 2006). Ainsi, les conductivités hydrauliques moyennes calculées dans les différentes zones de paramètres définies avec la maille de 4 km (K1, K2, K3 et K4), varient de 1,1 x 10-6 à 2,4 x 10-5 m∙s-1 (Figure 13). Ces valeurs sont comparables à celles rencontrées dans les aquifères de socle (FREEZE et CHERRY, 1979; CLAUSER, 1992; MARÉCHAL et al., 2004; DEWANDEL et al., 2006, 2011). Par contre, les valeurs maximales de conductivités hydrauliques fournies par l’intervalle de confiances à 95 % dans les différentes zones discrètes de perméabilité varient de 6 x 10-3 à 4,4 x 10-1 m∙s-1 avec la maille de 4 km (Figure 10b). En effet, ces valeurs désignent les incertitudes associées aux valeurs de conductivité hydraulique calculée (qui varient de 1,1 x 10-6 à 2,4 x 10-5 m∙s-1), plus elles sont éloignées des valeurs connues du type d’aquifère étudié, plus les incertitudes sont significatives (HILL, 1998 ; HILL et TIEDEMAN, 2007). Les valeurs élevées de conductivité hydraulique maximale calculée dans cette étude (variant de 6 x 10-3 à 4,4 x 10-1 m∙s-1) indiquent que les valeurs estimées comportent des incertitudes. L’origine de ces incertitudes est diverse, elles pourraient provenir soit des erreurs de calibration (le nombre et la nature des paramètres de calibration), soit des erreurs liées au modèle conceptuel de l’aquifère (modèle de distribution spatiale des hétérogénéités et de la recharge dans l’aquifère, épaisseur de l’aquifère, etc.) (HILL, 1998, HILL et TIEDEMAN, 2007; DOHERTY, 2005). Certaines erreurs peuvent être mises en évidence à travers une étude de sensibilité qui sera abordée à la section suivante.
Figure 13
Intervalle de confiance à 95 % des conductivités hydrauliques calculées avec le modèle optimal des zones discrètes de perméabilité
Hydraulic conductivities and their 95% confidence intervals as calculated with the optimal model of discrete permeability zones
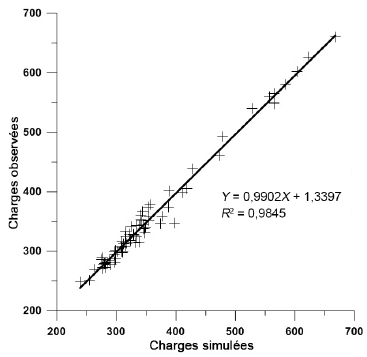
De manière globale, en dépit de ces incertitudes, la comparaison des charges simulées et observées montre que les écoulements reproduits par le modèle numérique de simulation sont comparables aux écoulements naturels dans l’aquifère, au moins en termes de gradient hydraulique puisque les flux ont été imposés de manière arbitraire. En effet, l’équation de la régression linéaire calculée en comparant les charges simulées et observées est y = 0,9902x + 1,3307 avec un coefficient de détermination R2 = 0,9845 (Figure 14). Toutefois, la calibration et la vraisemblance du modèle pourraient être améliorées en intégrant, par ordre d’importance décroissante : les débits des rivières, les flux étant la manière la plus sure de caler un modèle d’écoulement, en augmentant le nombre de charges hydrauliques et, mieux encore, en travaillant à partir d’une cartographie piézométrique observée au lieu de charges hydrauliques ponctuelles, éventuellement à partir de mesures directes de conductivité hydraulique recueillies sur le terrain ou à partir d’une analyse telle que celle menée par COURTOIS et al. (2009). Cela permettrait d’une part de réduire les incertitudes des conductivités hydrauliques calculées et, d’autre part, de résoudre le problème de non-unicité des valeurs calculées. En effet, les conductivités hydrauliques calculées seulement avec les charges hydrauliques ne sont pas uniques (HILL, 1998; HILL et TIEDEMAN, 2007; DOHERTY, 2005). La non-unicité des paramètres de l’aquifère (ex. : transmissivité, conductivité hydraulique) calculés à partir des observations est abondamment illustrée dans la littérature (HILL et TIEDEMAN, 2007; MOORE et DOHERTY, 2006). Pour autant, la problématique liée à la non-unicité des paramètres de l’aquifère calculés avec les charges hydrauliques va au-delà des objectifs de cette étude.
Figure 14
Comparaison des charges observées et charges simulées
Comparing observed and simulated heads
Par ailleurs, une étude de sensibilité a été effectuée afin d’évaluer l’influence de certains paramètres de l’aquifère sur les conductivités hydrauliques calculées.
5. Étude de sensibilité
L’étude de sensibilité porte sur certains paramètres utilisés dans l’élaboration du modèle conceptuel de l’aquifère. Les plus significatifs sont l’épaisseur de la couche productive (ou perméable) de l’aquifère de socle, la recharge et la perméabilité des fractures.
Dans la zone d’étude, l’épaisseur de la couche productive ou perméable de l’aquifère n’a pas été étudiée et n’est donc pas connue de façon précise. Alors, des simulations ont été effectuées avec plusieurs valeurs d’épaisseur afin de connaître l’influence de ce paramètre sur la conductivité hydraulique. Les valeurs considérées varient de 20 à 100 m au maximum avec un pas de 10 m. Les résultats indiquent de façon générale que, lorsque l’épaisseur de l’aquifère augmente, la conductivité hydraulique diminue (Figure 15). En effet, si nous considérons que la transmissivité est constante, le flux étant le même, une augmentation de l’épaisseur de l’aquifère entraine une diminution proportionnelle de la conductivité hydraulique. Le modèle conceptuel construit est donc sensible aux variations de la transmissivité et non à celles de l’épaisseur de l’aquifère ou de sa perméabilité.
Figure 15
Conductivité hydraulique en fonction de l’épaisseur de l’aquifère
Hydraulic conductivity as a function of the thickness of the aquifer
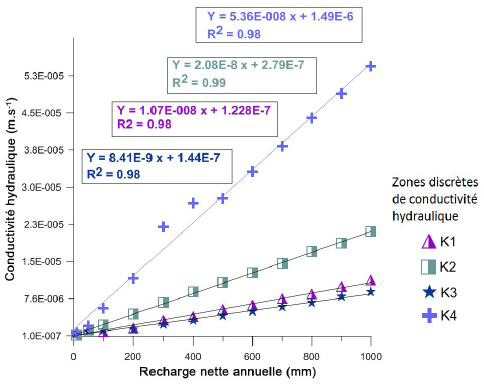
La conductivité hydraulique peut être influencée aussi par l’infiltration nette ou recharge. Les valeurs de recharges nettes utilisées dans l’étude de sensibilité varient de 10 à 1 000 mm∙an-1. Logiquement, les résultats montrent que la conductivité hydraulique (donc la transmissivité pour une épaisseur considérée comme constante) varie linéairement en fonction de la recharge (Figure 16). Lorsque nous considérons, par exemple, une recharge de 100 mm∙an-1, les valeurs de conductivité hydraulique diminuent au moins d’un facteur 3 par rapport aux moyennes calculées avec 300 mm∙an-1 dans l’ensemble des zones discrètes de conductivité hydraulique (Figure 16). À l’opposé, si la recharge augmente et atteint 600 mm∙an-1, cela entraine une augmentation de la conductivité hydraulique d’au moins un facteur 2 dans les zones de paramètres (Figure 16). Dans la zone d’étude, la distribution spatiale de la recharge n’est pas connue, si bien qu’une valeur unique de 300 mm∙an-1 censée représenter la moyenne annuelle a été utilisée dans le processus de calibration. Cela a pour conséquence une sous-estimation et une surestimation de la conductivité hydraulique dans les endroits du bassin versant où la recharge est respectivement inférieure et supérieure à la valeur fixée à 300 mm∙an-1.
Figure 16
Conductivité hydraulique en fonction de la recharge
Hydraulic conductivity as a function of the recharge
Une autre difficulté rencontrée dans le processus d’élaboration du modèle conceptuel développé dans ce travail porte sur la perméabilité des fractures cartographiées. L’approche de l’aquifère de socle par le modèle continu considère que le milieu est suffisamment fracturé et que toutes les fractures sont interconnectées. La perméabilité globale de l’aquifère dépend alors du degré de connexion entre les fractures (BERKOWITZ, 2002), de la même manière que l'est une structure poreuse et le degré de connexion entre ses pores. Notons que l’interconnectivité des fractures est étudiée ici indirectement et est basée principalement sur l’hypothèse suivante : plus la densité de la fracturation est élevée, plus les fractures ont une grande probabilité d’être interconnectées lorsqu’elles sont orientées dans différentes directions. Ainsi, la relation entre la densité de fracturation (dans les zones discrètes de perméabilité) et la conductivité hydraulique calculées après la calibration a été analysée. L’analyse détaillée des résultats après la calibration montre un gradient de densité de fracturation orienté globalement NO-SE (Figure 10), alors que les conductivités hydrauliques calculées ne semblent pas suivre une hiérarchisation dans ce sens. La zone discrète de conductivité hydraulique K3 a une densité de fracturation plus élevée que K2 (Figure 13), alors que la conductivité hydraulique équivalente calculée est plus faible dans K3 que K2 (Figure 13). Le modèle conceptuel ne montre pas ici, de façon claire une relation linéaire entre les zones discrètes de perméabilité et les conductivités hydrauliques estimées. L’absence de relation entre les zones discrètes de perméabilité et les conductivités hydrauliques pourraient avoir plusieurs origines : soit la méthode utilisée pour identifier les fractures connectées dans les zones discrètes (méthode linéamentaire) est inefficace, surtout si l’horizon fracturé est lié aux processus d’altération, soit les charges hydrauliques utilisées dans la calibration ne sont pas assez nombreuses pour mettre en évidence l’interconnectivité des fractures.
6. Discussion
Dans le présent travail, l’approche adoptée pour estimer la conductivité hydraulique est la modélisation inverse. Le principe de la modélisation inverse consiste à calculer les paramètres de l’aquifère difficilement accessibles sur le terrain (ex. : conductivité hydraulique, transmissivité) à partir des observations (ex. : charges hydrauliques, flux, piézométrie, etc.) qui par contre peuvent être récoltées facilement sur le terrain (CARRERA et NEUMAN, 1986; WELLMAN et POETER, 2005). La modélisation inverse est applicable à l’échelle régionale ou d’un grand bassin, car les hétérogénéités qui contrôlent les champs de perméabilité peuvent être spécifiées à partir des informations générales sur la géologie (KASENOW, 2002; FETTER, 2001) et/ou sur la géométrie du réseau de fractures (BEAR et al., 1993; WELLMAN et POETER, 2005, 2006). La modélisation se heurte cependant, à certaines difficultés notamment la construction du modèle conceptuel d’écoulement. En effet, le modèle conceptuel d’écoulement doit être le plus représentatif possible de l’aquifère étudié. L’une des étapes les plus importantes dans la construction d’un modèle conceptuel d’écoulement souterrain est la définition des conditions aux limites (REILLY, 2001; REILLY et HARBAUGH, 2004). Si elles ne sont pas définies correctement, le modèle peut ne pas être sensible aux paramètres de calage. L’étude de sensibilité effectuée dans ce travail indique globalement que les conditions aux limites définies dans le modèle conceptuel sont raisonnables, car les charges hydrauliques sont reproduites globalement de façon satisfaisante, en dépit de leur nombre limité pour cette étude et surtout ces conditions aux limites sont très proches de la réalité physique des aquifères de socle. Les charges hydrauliques sont couramment utilisées dans la modélisation hydrogéologique, car elles sont facilement accessibles sur le terrain (CARRERA et NEUMAN, 1986; HILL et TIEDEMAN, 2007). Elles permettent d’avoir des informations de base sur certains paramètres de l’aquifère notamment la conductivité hydraulique.
Une autre étape importante dans la construction du modèle conceptuel d’écoulement est la représentation des hétérogénéités de l’aquifère. Les hétérogénéités sont représentées ici en s’appuyant sur le concept de SER qui désigne les zones homogènes équivalentes. Le concept de SER permet de réduire l’aquifère de socle, très complexe, en un milieu homogène dont l’objectif est de rendre possible l’application des modèles mathématiques. C’est une simplification assez grossière de l’aquifère de socle, car ce concept ne tient pas compte des propriétés individuelles des fractures. Dans une SER, par exemple, aucune distinction n’est faite entre les fractures perméables et celles qui ne le sont pas. Toutes les fractures sont remplacées par une propriété hydraulique équivalente représentative de l’ensemble des fractures (ex. : connectivité, ouverture, etc.). De nombreux auteurs estiment que cette approche ne peut pas caractériser l’hétérogénéité du milieu fracturé, si bien que le concept de SER est beaucoup contesté depuis son apparition en sciences hydrologiques (FREEZE, 1975; SMITH ET FREEZE, 1979a, 1979b). Toutefois, une grande partie des études portant sur la modélisation des aquifères de socle est basée sur ce concept (NEUMAN, 1987; BEAR et al., 1993; VESSELINOV et al., 2001a, 2001b; WELLMAN et POETER, 2005, 2006). L’application du concept de SER dans la présente étude a montré quelques limites. En effet, la relation entre la densité des fractures et la conductivité hydraulique qui contrôle les écoulements n’a pu être établie dans toutes les zones de perméabilités équivalentes identifiées (Figure 10). En outre, certaines valeurs de conductivités hydrauliques calculées au cours du processus de calibration ne sont pas représentatives du milieu de socle (ex. : 5 x 10-1 m∙s-1, Figure 13). Ces erreurs pourraient être réduites soit en augmentant le nombre de charges hydrauliques utilisées dans la calibration, soit en simulant d’autres types d’observations tel le débit des rivières.
Par ailleurs, les résultats de cette étude peuvent être améliorés en redéfinissant les hétérogénéités dans le modèle conceptuel de l’aquifère de socle, par exemple à partir d’autres hypothèses sur l’origine de la perméabilité telles que le profil d’altération de la roche-mère, dont les propriétés hydrodynamiques dépendent de la lithologie (voir par exemple COURTOIS et al., 2009). En effet, de nombreuses études réalisées en milieu du socle au cours de ces quinze dernières années montrent que les propriétés géométriques et hydrodynamiques des aquifères de socle résultent principalement du processus d’altération profonde de la roche-mère (TAYLOR and HOWARD 2000; LACHASSAGNE et al. 2001; CHO et al., 2003; MARÉCHAL et al. 2004; DEWANDEL et al., 2006, 2011). En d’autres termes, ces travaux indiquent aussi qu’il existe une relation entre les propriétés hydrodynamiques de l’aquifère et le profil d’altération des roches-mères. À l’échelle régionale, les processus d’altération sont beaucoup plus homogènes que les phénomènes tectoniques qui, en région stable comme sur le craton ouest-africain, sont loin d’exister réellement. Notons que le profil d’altération n’est pas constitué que d’altérites meubles, mais il prend en compte la couche fracturée située en dessous de ces altérites. L’épaisseur de la couche fracturée est variable selon les zones géographiques. Elle est comprise entre 25 et 37 m au Burkina Faso (COURTOIS et al., 2009) et entre 40 et 60 m en Inde (WYNS et al., 1999, 2004). Par ailleurs, il est possible d’intégrer aussi les altérites meubles (saprolite) dans le modèle conceptuel de l’aquifère sous forme d’une couche. Sur le plan hydrodynamique cette couche est connue pour sa faible conductivité hydraulique et sa grande capacité de stockage (ACWORTH, 1987; WYNS et al., 2004; DEWANDEL et al., 2006). Cependant, à l’échelle régionale ou d’un grand bassin, du fait de l’érosion, l’épaisseur de la couche de saprolite peut varier plus fortement que celle de la couche fracturée sous-jacente (MARÉCHAL et al., 2004; COURTOIS et al., 2009). À cette échelle, la prise en compte de la couche altéritique dans le processus de calibration pourrait entrainer des biais en particulier dans les endroits où elle est absente ou peu épaisse. Une cartographie de ces deux couches serait nécessaire, ce qui est néanmoins possible (LACHASSAGNE et al., 2011), la modélisation numérique telle que présentée dans cet article pouvant concourir à cette cartographie.
En outre, la calibration peut être améliorée aussi en construisant une carte piézométrique (WYNS et al., 2004). Cette carte piézométrique permettrait d’augmenter le nombre de points d’observations (points de calage) qui seront comparés aux points simulés. Et lorsque cela est possible, une comparaison entre la carte piézométrique observée et celle simulée pourrait être envisagée afin de détecter certaines anomalies dans le modèle conceptuel (ex. : niveau piézométrique supérieur à la topographie de surface ou plus bas que les cours d’eau pérennes).
7. Conclusion
La conductivité hydraulique de l’aquifère de socle du bassin versant du N’Zo a été estimée à partir de la calibration des zones discrètes de perméabilité avec les charges hydrauliques. Ces zones discrètes de perméabilité sont identifiées à partir de l’analyse de la densité et de l’orientation des « fractures » déduites des linéaments. Six configurations spatiales de zones discrètes ont été générées en utilisant des mailles dont la taille varie de 2 à 12 km avec un pas de 2 km. Ces configurations sont représentatives des modèles possibles des champs de perméabilité de l’aquifère de socle du bassin versant du N’zo. La sélection du modèle optimal des champs de perméabilité est effectuée au cours du processus de calibration. L’analyse des résultats fournis à la fin de la calibration indique que le modèle optimal de distribution spatiale des zones discrètes de perméabilité du réseau de fractures de l’aquifère de socle est obtenu avec les mailles de 4 km. Les valeurs de conductivité hydraulique estimées par ce dernier dans les différentes zones discrètes de perméabilité oscillent entre 1,1 x 10-6 et 2,4 x 10-5 m∙s-1. Les incertitudes associées à ces valeurs ont été évaluées avec l’intervalle de confiance à 95 %. L’étude de sensibilité montre que ces valeurs sont influencées par l’épaisseur de l’aquifère et la recharge. Notons toutefois que ces résultats doivent être pris avec précaution en raison de nombreuses hypothèses simplificatrices utilisées pour identifier les champs de perméabilité du réseau de fractures et aussi en raison du caractère très controversé de la réalité physique des linéaments qui est la principale donnée utilisée dans cette étude. En outre, les conductivités hydrauliques estimées à partir des charges hydrauliques ne peuvent pas être utilisées dans toutes les études hydrogéologiques notamment celles portant sur la prédiction des écoulements. En effet, les conductivités hydrauliques estimées seulement à partir des charges hydrauliques ne sont pas uniques. Les charges hydrauliques doivent être utilisées avec d’autres types d’observations telles que les débits dans le processus d’estimation de la conductivité hydraulique.
En perspective, les résultats de cette étude peuvent être améliorés en caractérisant les champs de perméabilité de l’aquifère de socle à partir de la lithologie et du profil d’altération de la roche-mère. En effet, les études récentes en milieu de socle montrent une relation entre le profil d’altération et la perméabilité. En outre, la piézométrie et le débit des cours d’eau peuvent être pris en compte aussi dans le processus de calibration.
Parties annexes
Références bibliographiques
- ACWORTH R.I. (1987). The development of crystalline basement aquifers in a tropical environment. Q. J. Eng. Geol. Hydroge., 20, 265-272.
- ANDERSON M.P. et W.W. WOESSNER (1992). Applied Groundwater Modeling: Simulation of Flow and Advective Transport. Academic Press, San Diego, CA, États-Unis, 381 p.
- ANDO K., A. KOSTNER et S.P. NEUMAN (2003). Stochastic continuum modeling of flow and transport in a crystalline rock mass: Fanay-Augères, France, revisited. Hydrogeol. J., 11 (5), 521-535.
- BEAR J. (1972). Dynamics of Fluids in Porous Media. Elsevier, New York, NY, États-Unis, 794 p.
- BEAR J., C. TSANG et G. DE MARSILY (1993). Flow and Contaminant Transport in Fractured Rock. Elsevier, New York, NY, États-Unis, 560 p.
- BEVEN K.J. (2000). Uniqueness of place and non-uniqueness of models in assessing predictive uncertainty. Dans : Computational Methods in Water Resources XIII. BENTLEY L.R., J.F. SYKES, W.G. GRAY, C.A. BREBBIA et G.F. PINDER (Éditeurs), Balkema, Rotterdam, Pays-Bas, pp. 1085-1091.
- BERKOWITZ B. (2002). Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour., 25 (8), pp. 861-884.
- BOUR O. et P. DAVY (1997). Connectivity of random fault networks following a power law fault length distribution. Water Res., 33, 1567-1583.
- BRACQ P. (1994). L’effet d’échelle sur le comportement hydrodynamique et hydrodispersif de l’aquifère crayeux; apports de l’analyse morphostructurale. Thèse de Doctorat, Univ. Lille 1, France, 244 p.
- BURNHAM K.P. et D.R. ANDERSON (2002). Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach. Springer, New York, NY, États-Unis, 488 p.
- CACAS M.C., E. LEDOUX et G. DE MARSILY (1987a). Étude de l’effet d'échelle en milieu fissuré, Phase 2A, Étude des écoulements sur le site de Fanay-Augère. Rapport final, 2e partie, Interprétation et modélisation. École nationale supérieure des mines de Paris, Rep. LHL/RD/87/5, Fontainebleau, France, pp. 7-12.
- CACAS M.C., E. LEDOUX et G. DE MARSILY (1987b). Étude de l’effet d'échelle en milieu fissuré, Phase 2B, Étude des circulations sur le site de Fanay-Augère. Rapport final, 2e partie, Modélisation des essais de traçage. École nationale supérieure des mines de Paris, Rep. LHL/RD/87/74, Fontainebleau, France, pp. 9-14.
- CACAS M.C., E. LEDOUX, G. DE MARSILY, B. TILLIE, A. BARBEAU, E. DURAND, B. FEUGA et P. PEAUDECERF (1990a). Modeling fracture flow with a stochastic discrete fracture network: calibration and validation. 1. The flow model. Water Res., 26 (3), 479-489.
- CACAS M.C., E. LEDOUX, G. DE MARSILY, A. BARBEAU, P. CALMELS, B. GAILLARD et R. MAGRITTA (1990b). Modeling fracture flow with a stochastic discrete fracture network: calibration and validation. 2. The transport model. Water Res., 26 (3), 491-500.
- CARRERA J. et S. NEUMAN (1986). Estimation of aquifer parameters under transient and steady-state conditions: 2. Uniqueness, stability, and solution algorithms. Water Res., 22 (2), 211-227.
- CHARLAIX E., E. GUYON et S. ROUX (1987). Permeability of a random array of fractures of widely varying apertures. Transport Porous Med., 2 (1), 31-43.
- CHO M., K.M. HA, Y.S. CHOI, W.S. KEE, P. LACHASSAGNE et R. WYNS (2003). Relationship between the permeability of hard-rock aquifers and their weathered cover based on geological and hydrogeological observation in South Korea. IAH Conference on “Groundwater in fractured rocks”, 15 au 19 septembre, Prague, République tchèque.
- CLARK I. (1979). Practical Geostatistics. Elsevier, New York, NY, États-Unis, 129 p.
- CLAUSER C. (1992). Permeability of crystalline rocks. Eos, Trans. Amer. Geophys. Union, 73 (21), 233-238.
- COOLEY R.L. et R.L NAFF (1990). Regression modeling of ground-water flow. Dans : Techniques of Water-Resources Investigations. US Geological Survey, Livre 3, Chap. B4, Denver, CO, États-Unis, 232 p. http://pubs.usgs.gov/twri/twri3-b4/ (consultation le 16 mars 2013).
- COURTOIS N., P. LACHASSAGNE, R. WYNS, R. BLANCHIN, F.D. BOUGAÏRÉ, S. SOMÉ and A. TAPSOBA (2009). Country-scale hydrogeological mapping of hard-rock aquifers and its application to Burkina Faso. Ground Water, 48 (2), 269-283.
- CUSHMAN J. (1990). An introduction to hierarchal porous media. Dans : Dynamics of Fluids in Hierarchal Porous Media. CUSHMAN J. (Éditeur), Elsevier, New York, NY, États-Unis, pp. 1-6.
- D'AGNESE F.A., C.C. FAUNT, M.C. HILL et A.K. TURNER (1999). Death Valley regional ground-water flow model calibration using optimal parameter estimation methods and geoscientific information systems. Adv. Water Resour., 22 (8), 777-790.
- DAVY P. (1993). On the frequency-length distribution of the San Andreas Fault System. J. Geophys Res., 98 (B7), 12141–12151.
- DE MARSILY G., G. LAVEDU, M. BOUCHER et G. FADANINO (1984). Interpretation of interference tests in a well field using geostatistical techniques to fit the permeability distribution in a reservoir model. Dans : Geostatistics for Natural Resources Characterizations. VERLY G., M. DAVID, A. JOURNEL et A. MARECHAL (Éditeurs), Proceedings of the NATO Advanced Study Institute, South Lake Tahoe, CA, 6 au 17 septembre, Reidel, Dordrecht, Hollande, pp. 831-849.
- DE MARSILY G., J.P. DELHOMME, A. COUDRAIN-RIBSTEIN, A.M. LAVENUE (2000). Four decades of inverse problems in hydrogeology. Dans : Theory, modeling and field investigation in hydrogeology: A special volume in honor of Shlomo P. Neumans 60thbirthday. ZHANG D. et C.L. WINTER (Éditeurs), Geological Society of America Special Paper 348, pp. 1-17.
- DE MARSILY G., F. DELAY, J. GONÇALVES, P. RENNARD, V. TELES et S. VIOLETTE (2005). Dealing with spatial heterogeneity. Hydrogeol. J., 12, 161-183.
- DEWANDEL B., P. LACHASSAGNE, R. WYNS, J.C. MARECHAL et N.S. KRISHNAMURTHY (2006). A generalized 3D geological and hydrogeological conceptual model of granite aquifers controlled by single or multiphase weathering. J. Hydrol., 330 (1-2), 260-284.
- DEWANDEL B., P. LACHASSAGNE, S. CHANDRA et F.K. ZAIDI (2011). Conceptual hydrodynamic model of a geological discontinuity in hard rock aquifers: example of quartz reef in granitic terrain in South India. J. Hydrol., 405 (3-4), 474-487.
- DJRO S.C. (1998). Évolutions tectono-métamorphiques des gneiss granulitiques archéens du secteur de Biankouma-Touba (Nord-Ouest Côte d'Ivoire). Thèse de Doctorat, Univ. Cocody, Côte d’Ivoire, 121 p.
- DOHERTY J. (2005). PEST. Model-Independent Parameter Estimation User Manual. 5th Edition. Watermark Numerical Computing, États-Unis, 336 p.
- DONADO L.D., E. RUIZ, X. SANCHEZ-VILA, F.J. ELORZA, C. BAJOS et A. VELA-GUZMAN (2005). Calibration of hydraulic and tracer tests in fractured media represented by a DFN model. Dans : Calibration and Reliability in Groundwater Modelling: From Uncertainty to Decision Making. BIERKENS M.F.P., J.C. GEHRELS et K. Kovar (Éditeurs), IAHS Publication no. 304, Wallingford, Royaume-Uni, pp. 87-92.
- DVERSTOP B. et J. ANDERSSON (1989). Application of the Discrete Fracture Network concept with filed data: Possibilities of model calibration and validation. Water Resour. Res., 25 (3), 540-550.
- DVERSTOP B., J. ANDERSSON et W. NORDQVIST (1992). Discrete Fracture Network interpretation of field tracer migration in sparsely fracture rock. Water Resour. Res., 28 (9), 2327-2343.
- FAILLAT J.P. (1986). Hétérogénéité et effet d’échelle dans les aquifères fissurés. Approche par pompage d’essai sur station expérimentale (Afrique de l’Ouest). Hydrogéologie, 1, 65-76.
- FETTER C.M. (2001). Applied Hydrology. 4th Edition. Prentice-Hall, Upper saddle River, NJ, États-Unis, 598 p.
- FRANCISS F.O. (1970). Contribution à l'étude du mouvement d'eau à travers les milieux fissurés. Thèse de Doctorat, Univ. Grenoble I, Grenoble, France, 108 p.
- FREEZE R.A (1975). A stochastic-conceptual analysis of one-dimensional groundwater flow in non-uniform homogeneous media. Water Resour. Res., 11 (5), 725-741.
- FREEZE R.A. et J.A. CHERRY (1979). Groundwater. Prentice-Hall, Englewood Cliffs, NJ, États-Unis, 604 p.
- GELHAR L.W. (1993). Stochastic Subsurface Hydrology. Prentice-Hall, Old Trappan, NJ, États-Unis, 390 p.
- GLEESON T., L. SMITH, N. MOOSDORF, J. HARTMANN, H.H. DÜRR, A.H. MANNING, L.P.H. VAN BEEK et A.M. JELLINEK (2011). Mapping permeability over the surface of the Earth. Geophys. Res. Lett., 38, L02401.
- GRAHAM W. et C. TANKERSLEY (1994). Optimal estimation of spatially variable recharge and transmissivity fields under steady-state groundwater flow. Part 1. Theory. J. Hydrol., 157 (1-4), 247-266.
- HARDCASTLE K.C. (1995). Photolineament factor: a new computer-aided method for remotely sensing the degree to which bedrock is fractured. Photogram. Eng. Remote Sensing, 61 (6), 739-747.
- HILL M.C. (1998). Methods and guidelines for effective model calibration. US Geological Survey, Water-Resources Investigations Report 98-4005, Denver, CO, États-Unis, 98 p. https://water.usgs.gov/nrp/gwsoftware/modflow2000/WRIR98-4005.pdf
- HILL M.C. et C.R. TIEDEMAN (2007). Effective Groundwater Calibration, with Analysis of Data, Sensitivities, Prediction and Uncertainty. John Wiley & Sons, New York, NY, États-Unis, 480 p.
- ILLMAN W.A. (2006). Strong field evidence of directional permeability scale effect in fractured rock. J. Hydrol., 319, 227-236.
- ILLMAN W.A. et S.P. NEUMAN (2003). Steady-state analyses of cross-hole pneumatic injection tests in unsaturated fractured tuff. J. Hydrol., 281, 36-54.
- INGEBRITSEN S.E. et C.E. MANNING (1999). Geological implications of a permeability‐depth curve for the continental crust. Geology, 27, 1107-1110.
- INGEBRITSEN S.E. et C.E. MANNING (2010). Permeability of the continental crust: Dynamic variations inferred from seismicity and metamorphism. Geofluids, 10, 193-205.
- JOURDA J.P.R (2005). Méthodologie d’application des techniques de télédétection et du concept de l’hydrotechnique spatiale : cas des zones tests de la Côte d’Ivoire. Thèse de Doctorat, Univ. Cocody, Côte d’Ivoire, 430 p.
- KASENOW M. (2002). Determination of Hydraulic Conductivity from Gram Size Analysis. Water Resources Publications LLC, Littleton, CO, États-Unis, 110 p.
- KOUAMÉ K.F. (1999). Hydrogéologie des régions de montagne : apports des données de télédétection et des méthodes statistique et fractale à l'élaboration d'un Système d'Informations Hydrogéologiques à Référence Spatiale des aquifères discontinus du secteur Man-Danané (Ouest de la Côte d'Ivoire). Thèse de Doctorat, Univ. Cocody, Côte d’Ivoire, 210 p.
- KOUAMÉ K.F., T. LASM, M.B. SALEY, E. TONYÉ, M. BERNIER et S. WADE (2009). Extraction linéamentaire par morphologie mathématique sur une image RSO de Radarsat-1 : application au socle archéen de la Côte d’Ivoire. Journées d’Animation Scientifique, AUF (JAS 09), 8 au 11 novembre, Alger, Algérie, 8 p.
- LACHASSAGNE P., R. WYNS, P. BERARD, T. BRUEL, L. CHERY, T. COUTAND, J.F. DESPRATS et P. LE STRAT (2001). Exploitation of high-yield in hard-rock aquifers: Down scaling methodology combining GIS and multicriteria analysis to delineate field prospecting zones. Ground Water, 39 (4), 568-581.
- LACHASSAGNE P., R. WYNS et B. DEWANDEL (2011). The fracture permeability of hard rock aquifer is due neither to tectonics, nor to unloading, but to weathering processes. Terra Nova, 23, 145-161.
- LASM T. (2000). Hydrogéologie des réservoirs fracturés de socle : analyses statistique et géostatistique de la fracturation et des propriétés hydrauliques. Thèse de Doctorat. Univ. Poitiers, Poitiers, France, 233 p.
- LE GOC R. (2009). Caractérisation et modélisation des écoulements dans les milieux fracturés. Thèse de Doctorat, Univ. Rennes 1, Rennes, France, 238 p.
- LONG J.C.S., J.S. REMER, C.R. WILSON et P.A. WITHERSPOON (1982). Porous media equivalents for networks of discontinuous fractures. Water Res., 18 (3), 645-658.
- LONG J.C.S. et D. BILLAUX (1987). From field data to fracture network modeling: An example incorporating spatial structure. Water Res., 23 (7), 1201-1216.
- MABEE S.B., K.C. HARDCASTLE. et D.U. WISE (1994). A method of collecting and analyzing lineaments for regional-scale fractured-bedrock aquifer studies. Ground Water, 32 (6), 884-894.
- MARÉCHAL J.C., R. WYNS, P. LACHASSAGNE, K. SUBRAHMANYAM et F. TOUCHARD (2003). Anisotropie verticale de la perméabilité de l’horizon fissuré des aquifères de socle : concordance avec la structure géologique des profils d’altération. C. R. Géosci., 335, 451-460.
- MARÉCHAL J.C., B. DEWANDEL et K. SUBRAHMANYAM (2004). Use of hydraulic tests at different scales to characterize fracture network properties in the weathered-fractured layer of a hard rock aquifer. Water Resour. Res., 40, 11-17.
- MATHERON G. (1973). The intrinsic random functions and their applications. Adv. Appl. Probab., 5 (3), 439-469.
- MCLAREN R.G. (2007). Grid Builder: A Pre-processor for 2D, Triangular Element, Finite Element Programs. Groundwater Simulations Group, University of Waterloo, ON, Canada, 93p.
- MOORE C. et J. DOHERTY (2006). The cost of uniqueness in groundwater model calibration. Adv. Water Resour., 29 (4), 605-623.
- NATIONAL RESEARCH COUNCIL (1996). Rock Fractures and Fluid Flow. Contemporary Understanding and Applications. NRC, National Academy Press, Washington DC, États-Unis, 551 p.
- NEUMAN S.P. (1987). Stochastic continuum representation of fractured rock permeability as an alternative to the REV and fracture network concepts. Dans : Rock Mechanics, Proceedings of the 28th US Symposium. FARMER I.W., J.J.K. DALMEN, C.S. DESAI, C.E. GLASS, S.D. NEUMAN (Éditeurs), Balkema, Rotterdam, Pays-Bas, 533-561.
- NEUMAN S.P. (2002). Accounting for conceptual model uncertainty via maximum likelihood Bayesian model averaging. Dans : Calibration and Reliability in Groundwater Modelling: A Few Steps Closer to Reality. KOVAR K et Z. HRKAL (Éditeurs), IAHS Publications no. 277, Wallingford, Royaume-Uni, pp. 303-313.
- NEUZIL C.E. (1994). How permeable are clays and shales? Water Res., 30, 145-150.
- OULARÉ S., F.K. KOUAMÉ, M.B. SALEY, G.E. AKÉ, G.M. ADJA, A.K. KOUAMÉ et R. THERRIEN (2014). Estimation et validation de la profondeur des nappes du bassin versant du N’zo, en Côte d’Ivoire, par le modèle WTR. Physio-Géo, 8, 1-25.
- REILLY T.E. (2001). System and boundary conceptualization in ground-water flow simulation. Dans : Techniques of Water-Resources Investigations. US Geological Survey, Livre 3, Chap. B8, Denver, CO, États-Unis, 26 p. https://pubs.usgs.gov/twri/twri-3_B8/ (consultation le 16 mars 2013).
- REILLY T.E., O.L. FRANKE et G.D. BENNETT (1987). The principle of superposition and its application in ground-water hydraulics. Dans : Techniques of Water-Resources Investigations. US Geological Survey, Livre 3, Chap. B6, Denver, CO, États-Unis, 28 p. https://pubs.usgs.gov/twri/twri3-b6/ (consultation le 16 mars 2013).
- REILLY T.E. et A.W. HARBAUGH (2004). Guidelines for evaluating ground-water flow models. US Geological Survey, Scientific Investigations Report 2004-5038, Denver, CO, États-Unis, 37 p. https://pubs.usgs.gov/sir/2004/5038/PDF/SIR20045038_ver1.01.pdf
- RUDANT J.P., J.P. DEROIN et L. POLIDORI (1994). Multi-resolution analysis of radar images and its application to lithological and structural mapping, Larzac (southern France) test site. Int. J. Remote Sens., 15 (12), 2451-2468.
- SALEY M.B. (2003). Système d’Informations Hydrogéologiques à Référence Spatiale, discontinuités pseudo-images et cartographie thématique des ressources en eau de la région semi montagneuse de Man (Ouest de la Côte d’Ivoire). Thèse de Doctorat, Univ. Cocody, Côte d’Ivoire, 211 p.
- SANDER P. (2007). Lineaments in ground-water exploration: a review of applications and limitations. Hydrogeol. J., 15, 71-74.
- SANDER P., T.B. MINOR et M.M. CHESLEY (1997). Ground-water exploration based on lineament analysis and reproducibility tests. Ground Water, 35, 888-894.
- SHEWCHUK J.R. (1996). Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator. Dans : Applied Computational Geometry: Towards Geometric Engineering. FCRC'96 Workshop, WACG'96 Philadelphia, PA, 27-28 mai. LIN M.C. et D. MANOCHA (Éditeurs), Lecture Notes in Computer Science, Vol. 1148, Springer Berlin Heidelberg, Allemagne, pp. 203-222.
- SINGHAL B.B.S. et R.P. GUPTA (1999). Applied Hydrogeology of Fractured Rocks. Kluwer Academic Publishers, Dordrecht, Pays-Bas, 400 p.
- SMITH L. et R.A. FREEZE (1979a). Stochastic analysis of steady state groundwater flow in a bounded domain. 1. One-dimensional simulations. Water. Resour. Res., 15 (3), 521-528.
- SMITH L. et R.A. FREEZE (1979b). Stochastic analysis of steady state groundwater flow in a bounded domain. 2. Two-dimensional simulations. Water. Resour. Res., 15 (6), 1543-1559.
- SUN N.Z. et W. YEH (1990a). Coupled inverse problems in groundwater modeling. 1. Sensitivity analysis and parameter identification. Water Res., 26 (10), 2507-2525.
- SUN N.Z. et W. YEH (1990b). Coupled inverse problems in groundwater modeling. 2. Identifiability and experimental design. Water Res., 26 (10), 2527-2540.
- TAGINI B. (1971). Esquisse structurale de la Côte-d'Ivoire. Essai de géotectonique régionale. Thèse d’État, Univ. Lausanne, Bull. SODEMI no. 5, Abidjan, 302 p.
- TAM V.T., F. DE SMEDT, O. BATELAAN et A. DASSARGUES (2004). Study on the relationship between lineaments and borehole specific capacity in a fractured and karstified limestone area in Vietnam. Hydrogeol. J., 12 (6), 662-673.
- TAYLOR R. et K. HOWARD (2000). A tectono-geomorphic model of the hydrogeology of deeply weathered crystalline rock: evidence from Uganda. Hydrogeol. J., 8 (3), 279-294.
- THERRIEN R., R.G. MCLAREN, E.A. SUDICKY et S.M. PANDAY (2006). HydroGeoSphere: a three-dimensional numerical model describing fully-integrated subsurface and surface flow and solute transport. Unpublished User Manual, Groundwater Simulations Group, University of Waterloo, ON, Canada, 349 p.
- TSANG C.F. (1993). Tracer transport in fracture systems. Dans : Flow and Contaminant Transport in Fractured Rock. BEAR J, C.F. TSANG et G. DE MARSILY (Éditeurs), Academic Press, San Diego, CA, États-Unis, Chap. 5, pp. 237-266.
- VESSELINOV V.V., S.P. NEUMAN et W.A. ILLMAN (2001a). Three-dimensional numerical inversion of pneumatic cross-hole tests in unsaturated fractured tuff. 1. Methodology and borehole effects. Water Resour. Res., 37 (12), 3001-3018.
- VESSELINOV V.V., S.P. NEUMAN et W.A. ILLMAN (2001b). Three-dimensional numerical inversion of pneumatic cross-hole tests in unsaturated fractured tuff. 2 Equivalent parameters, high-resolution stochastic imaging and scale effects. Water Resour. Res., 37 (12), 3019-3041.
- VOSS C.I. (2011a). Editor’s message: Groundwater modeling fantasies - part 1, adrift in the details. Hydrogeol. J., 19 (7), 1281-1284.
- VOSS C.I. (2011b). Editor’s message: Groundwater modeling fantasies - part 2, down to earth. Hydrogeol. J., 19 (8), 1455-1458.
- WELLMAN T.P. et E.P. POETER (2005). Estimating spatially variable representative elementary scales in fractured architecture using hydraulic head observations. Water Resour. Res., 41 (3), doi:10.1029/ 2004WR003287
- WELLMAN T.P. et E.P. POETER (2006). Evaluating uncertainty in predicting spatially variable representative elementary scales in fractured aquifers, with application to Turkey Creek Basin, Colorado, Water Resour. Res., 42 (3), doi:10.1029/2005WR004431
- WISE D.U. (1982). Linesmanship and the practice of linear geo-art. Geol. Soc. Am. Bull., 93 (9), 886-888.
- WRIGHT E.P. (1992). The hydrogeology of crystalline basement aquifers in Africa. Geol. Soc. London Spec. Publ., 66, 1-27.
- WYNS R., J.C. GOURRY, J.M. BALTASSAT et F. LEBERT (1999). Caractérisation multi paramètres des horizons de subsufaces (0-100 m) en contexte de socle altéré. 2e colloque GEOFCAN, Bureau de recherches géologiques et minières, IRD UMPC, Orléans, France, pp. 105-110.
- WYNS R., J.M. BALTASSAT, P. LACHASSAGNE, A. LEGCHENKO, J. VAIRON et F. MATHIEU (2004). Application of SNMR soundings for groundwater reserves mapping in weathered basement rocks (Brittany, France). Bull. Soc. Géol. Fr., 175 (1), 21-34.
- YOUAN TA M. (2008). Contribution de la télédétection et des systèmes d'informations géographiques à la prospection hydrogéologique du socle précambrien d'Afrique de l'ouest : cas de la région de Bondoukou (Nord-Est de la Côte d'Ivoire). Thèse de Doctorat. Univ. Cocody, Côte d'Ivoire, 237 p.
Liste des figures
Figure 1
Situation géographique et carte géologique de la zone d’étude
Geographic location and geological map of the study area
Figure 2
Répartition spatiale des mesures de charge hydraulique utilisées pour la calibration
Spatial repartition of the hydraulic head measurements used for the calibration
Figure 3
Discontinuités (linéaments) observées à travers deux fenêtres ouvertes dans la zone d’étude
Discontinuities (lineaments) observed through two windows opened in the study area
Figure 4
Rosace directionnelle des linéaments relevés de l’image satellitaire
Directional distribution of lineaments from the satellite image
Figure 5
Rosace directionnelle des fractures relevées sur le terrain
Directional distribution of fractures observed in the field
Figure 6
Principales étapes de l’élaboration de la carte de fracturation
Main steps in the development of the fracture map
Figure 7
Caractéristiques géométriques des linéaments : a) répartition spatiale
Geometric characteristics of the lineaments
Figure 8
Zones discrètes de perméabilité produites respectivement avec les mailles de
Discrete permeability areas produced along with the meshes of
Figure 9
Conditions aux limites définies dans l’aquifère
Boundary conditions defined in the aquifer
Figure 10
Exemple de zones discrètes de perméabilité transférées au modèle géométrique
Example of discrete permeability areas transferred to the geometric model
Figure 11
Relation entre paramètres d’ajustement et pas de maillage
Relation between adjustment parameters and mesh size
Figure 12
Relation entre paramètres statistiques et pas de maillage
Relation between statistical parameters and mesh size
Figure 13
Intervalle de confiance à 95 % des conductivités hydrauliques calculées avec le modèle optimal des zones discrètes de perméabilité
Hydraulic conductivities and their 95% confidence intervals as calculated with the optimal model of discrete permeability zones
Figure 14
Comparaison des charges observées et charges simulées
Comparing observed and simulated heads
Figure 15
Conductivité hydraulique en fonction de l’épaisseur de l’aquifère
Hydraulic conductivity as a function of the thickness of the aquifer
Figure 16
Conductivité hydraulique en fonction de la recharge
Hydraulic conductivity as a function of the recharge