Analyse fréquentielle régionale des précipitations journalières maximales annuelles dans le bassin hydrographique - Chéliff, Algérie

Benhattab, Karima; Bouvier, Christophe; Meddi, Mohamed

doi:https://doi.org/10.7202/1027805ar

1. Introduction

De nombreuses applications hydrologiques s'appuient sur la connaissance des pluies extrêmes. Malheureusement, les données de pluie restent limitées à la fois dans le temps et dans l'espace, ce qui ne permet pas toujours d'obtenir des estimations fiables de ces extrêmes (OUARDA et al., 2008). La régionalisation est une possibilité pour pallier ce problème. La régionalisation consiste à regrouper les données des stations d'une région homogène (ou rendue homogène) pour estimer une fonction de distribution régionale de probabilité. L'échantillon étant plus riche, les estimateurs de cette distribution sont plus robustes que ceux obtenus par une distribution locale. Il a été montré que la distribution régionale menait, dans la plupart des cas, à de meilleurs résultats que la distribution locale, car elle tient compte d'une région en tant que tout (ANCTIL et al., 1998).

Plusieurs procédures de régionalisation des événements extrêmes ont été proposées. Les premiers travaux de régionalisation ont été menés par DALRYMPLE (1960), et reposent sur la distribution des valeurs extrêmes du type I (Gumbel) ajustée à l'aide de moments conventionnels (EV1/MC). Cette méthode, dite méthode de l’indice de crue (index flood) fait l’hypothèse de base que les données aux différents sites d’une région sont indépendantes et suivent la même distribution statistique à un facteur d’échelle près (DOMINGUEZ et al., 2005). Le coefficient de variation et le coefficient d’asymétrie sont alors constants à l’intérieur d’une région homogène. HOSKING (1990) a ensuite introduit les moments L pour l'ajustement des fonctions de distribution. Les moments L sont des combinaisons linéaires des moments conventionnels, ce qui leur confère une robustesse accrue et une plus grande insensibilité aux valeurs extrêmes (VOGEL et FENNESSEY, 1993). Les études de régionalisation peuvent faire appel à d'autres méthodes : interpolation spatiale par krigeage (MERZ et BLOSCHL, 2005), régressions multiples avec différents facteurs géographiques, notamment le relief (WOTLING et al., 2000). Les études les plus nombreuses s'appuient néanmoins sur les L-moments (e.g. ALLILA,1999; HOSKING et WALLIS, 1993; ONIBON et al., 2004).

L’objectif principal de la présente étude est la régionalisation des distributions des pluies extrêmes journalières, pour obtenir des quantiles fiables en des sites ayant peu ou aucune donnée, en utilisant la méthode des L-moments proposée par HOSKING et WALLIS (1997).

La région d'étude est le bassin versant de l’oued Cheliff qui couvre une superficie de 43 750 km². La faible densité des stations pluviométriques et leur répartition, assez concentrée dans le nord du bassin, nous ont conduits à mettre en place une approche régionale pour déterminer les pluies journalières maximales. La mise en place de l'approche régionale doit permettre d'obtenir de meilleures estimations des pluies extrêmes pour des périodes de retour comprises entre 10 et 100 ans, voire plus.

Cet article est structuré en trois étapes. Il propose, dans un premier temps, une présentation du site d'étude et des données disponibles puis une description des différents régimes pluviométriques qui se trouvent dans le bassin. En second lieu, nous présentons la méthode de régionalisation choisie. On y décrit les tests d’homogénéité utilisés pour la détermination des régions homogènes, la détermination de la fonction de distribution des précipitations et le principe de l’estimation régionale des quantiles associés aux différentes périodes de retour. Finalement, les résultats de la méthode de régionalisation appliquée au bassin du Cheliff concluent l'article.

2. Site d’étude et données utilisés

Situé au nord-ouest de l’Algérie, le bassin du Chéliff présente une superficie de 43 750 km².

De par ses 759 km de longueur, le Chéliff est le plus long oued du bassin, qui coule d’Est en Ouest depuis le barrage de Boughezoul jusqu’à la mer. Le bassin du Cheliff s’étend entre les longitudes 0° 7’ et 3° 31’ Est et les latitudes 33° 53’ et 36° 26’ Nord. Il est limité au Nord par les côtes de l'Algérois et de l'Oranais, à l’Est par les bassins de l’Isser, du Hodna, du Zahrez et des hauts plateaux Constantinois, à l’Ouest par les bassins de la Macta et des hauts plateaux Oranais et au Sud par l’Atlas saharien (Figure 1). Du point de vue du relief, le bassin comprend quatre régions naturelles diversifiées : les chaînes montagneuses du Dahra-Zaccar (chef-lieu de la wilaya de Chlef) (de 700 à 1 580 m d’altitude) au Nord et l’Ouarsenis au Sud (près de 2 000 m d’altitude), la vallée du Chéliff au centre et une région côtière.

Figure 1

**Isohyètes interannuelles et localisation des stations pluviométriques dans le bassin du Chéliff, nord-ouest de l'Algérie.**

**Interannual isohyetes and location of rain gauges in the Cheliff basin, northwestern Algeria.**

Le climat du Chéliff est caractérisé par des régimes pluviométriques irréguliers dans le temps et dans l'espace, des étés chauds et secs peu orageux et des hivers doux et humides et peut être appelé méditerranéen semi-aride (GOMER, 1994).

Les données utilisées dans le cadre de cette étude sont les précipitations journalières observées à 50 postes pluviométriques, pendant la période 1968 à 2004 (Tableau 1). Trente-trois stations ont fonctionné au moins 30 ans au cours de cette période, 47 stations au moins 20 ans. Nous avons conservé les années avec moins de 62 jours de pluie manquants par an, soit un taux de lacune maximal de 17 %. Le nombre moyen de lacunes sur l’ensemble des station-années conservées est sensiblement égal à 15 jours par an, soit 4 %. Les précipitations annuelles varient en moyenne de 154 à 600 mm, et sont plus élevées dans les zones montagneuses (Atlas tellien au Nord et Atlas saharien au Sud) que dans les zones de plaine (Figure 1). La variabilité saisonnière des pluies est très marquée, avec un minimum pendant l'été (juin, juillet, août, Figure 2).

Tableau 1

**Caractéristiques des stations pluviométriques (période 1968-2004).**

**Characteristics of rainfall stations (period 1968-2004).**

Figure 2

**Précipitations mensuelles moyenne, maximale et minimale à la station El Touaibia pour la période 1941- 2002.**

**Average maximum and minimum monthly precipitation at El Touaibia station for the period 1941-2002.**

Les pluies journalières maximales s’échelonnent de 44 à 190 mm sur l’ensemble des stations, avec une valeur médiane égale à 81 mm. Les pluies journalières maximales se produisent majoritairement de février à septembre (plus de 10 % d’occurrence pour chaque mois de cette période, avec un maximum de 14 % au mois de mars), et sont plus rares pendant la période octobre-janvier (moins de 5 % d’occurrence pour chaque mois de cette période, avec un minimum de 1 % au mois de décembre, Tableau 2).

Tableau 2

**Pourcentages d’occurrence des pluies maximales journalières.**

**Percentages of occurrence of the maximum daily rainfall.**

La stationnarité des pluies sur la période considérée a été étudiée avec le test de Mann-Kendall avec bootstrap, appliqué aux séries de pluies annuelles. Ce test, destiné à éliminer l’autocorrélation entre les valeurs des séries chronologiques, est effectivement recommandé (Önöz et Bayazit, 2007). Le test conduit à accepter l’hypothèse de stationnarité avec une confiance de 95 %, pour 49 des 50 stations. Les données utilisées par la suite sont les pluies journalières maximales annuelles (1 valeur par an), et tous les traitements ont été faits relativement à ces données.

3. Méthode de régionalisation

3.1 La méthode des L-Moments

Les L-moments sont des combinaisons linéaires des moments de probabilité pondérés. Le fait d'utiliser ces combinaisons linéaires réduit la dépendance aux événements extrêmes. Pour normaliser la méthode, HOSKING (1990) propose d’utiliser la forme standardisée des L-moments. Ainsi, le L-coefficient de variation (noté L-C_V), la L-asymétrie (notée L-C_S ) et le L-aplatissement (noté L-C_K) sont des formes standardisées des L-moments d’ordre 2, 3 et 4, estimées de la façon suivante (ONIBON et al., 2004) :

Une description détaillée des L-moments est donnée par HOSKING (1986; 1990).

3.2 Principes de la régionalisation

Le principe de la régionalisation consiste à caractériser la fonction de répartition associée à la variable aléatoire considérée, à partir d’informations locales recueillies sur une région homogène (ONIBON et al., 2004).

La mise en oeuvre de la régionalisation par les L-moments requiert trois étapes (HOSKING et WALLIS, 1993; 1997) : (i) identification des groupes de stations hydrologiquement homogènes, (ii) calcul des L-moments régionaux pour chaque groupe homogène et choix du type de loi régionale et (iii) estimation des quantiles locaux à partir de la distribution régionale et des caractéristiques de la pluie locale.

Ces étapes sont détaillées dans ce qui suit.

3.2.1 Constitution de régions homogènes

Pour valider l'homogénéité d'une région en matière de rapports de L-moments, nous avons utilisé le test d'homogénéité basé sur la statistique H proposé par HOSKING et WALLIS (1993).

L'objectif du test H est de vérifier que les pluies journalières maximales de différents sites peuvent être considérées comme étant issues d'une même distribution-mère.

Le principe du test H est de comparer la variance régionale observée des ratios des L-moments à la distribution de cette variance régionale sous l'hypothèse d'homogénéité de la région (hypothèse H₀). Cette distribution de variance régionale est obtenue par une méthode « Monte Carlo » qui consiste en une série de simulations basées sur la génération de variables distribuées selon la loi GEV, choisie a priori pour représenter les précipitations extrêmes.

La fonction de distribution cumulée F de la loi GEV est donnée par JENKINSON (1955) :

k, α et ζ représentent respectivement les paramètres de forme, d'échelle et de position.

La statistique H est calculée par :

où V est la valeur observée de V_r (r = 1, 2 ou 3), soit la variance pondérée V₁ du L-C_V :

La somme pondérée V₂ des distances de t et t₃ de chaque station à leurs moyennes respectives :

La somme pondérée V₃ des distances de t₃ et t₄ de chaque station à leurs moyennes respectives :

N désigne le nombre de postes d'observation, n_i l'effectif de l'échantillon du poste i; t⁽ⁱ⁾ t₃⁽ⁱ⁾ et t₄⁽ⁱ⁾ sont respectivement les L-C_V, L-C_S et L-C_K du poste i, et leurs moyennes pondérées, soit :

µ_v et σ_v sont respectivement la moyenne et l'écart-type des V_robtenus par simulation de Monte Carlo, dans une loi GEV dont les L-moments sont .

HOSKING et WALLIS (1993) montrent qu'une région peut être considérée comme étant homogène si H < 1, probablement hétérogène si 1 ≤ H < 2 et complètement hétérogène si H > 2.

En général, le test d'homogénéité est appliqué sur un découpage de stations en groupes supposés a priori homogènes. Ici, nous avons systématiquement testé toutes les combinaisons de stations, i.e. les combinaisons à p stations parmi les n stations possibles, en partant du plus grand nombre p = n, et en diminuant p d’une unité jusqu’à trouver un groupe homogène à p stations. Cette méthode est bien adaptée au cas d’une région probablement homogène, à condition d’enlever quelques stations posant problème pour des raisons diverses, liées davantage à des problèmes de données qu’à une réelle hétérogénéité physique. La méthode s’avère dans ce cas très efficace pour détecter ces quelques stations, et former le groupe homogène ayant le plus grand effectif. Elle s’est avérée notamment plus efficace que des méthodes classiques, consistant à chercher les stations discordantes, puis à tester l’hétérogénéité du groupe des stations non discordantes. Le cas échéant, cette méthode peut être combinée à une classification hiérarchique définissant plusieurs groupes au sens de la proximité des stations selon un caractère secondaire (par exemple, altitude ou pluie moyenne annuelle) lorsque la région n’est pas totalement homogène.

La statistique H a été calculée pour chaque combinaison de p stations parmi les n stations possibles par un programme R proposé par HOSKING (1997) (fonction regtst, voir en annexe 1), dans la bibliothèque lmomRFA, http://cran.r-project.org/web/packages/lmomRFA/lmomRFA.pdf. Les stations discordantes sont également détectées par ce programme.

3.2.2 Sélection d'une loi de distribution

Les L-moments de la distribution d'une région homogène sont identifiés aux moyennes pondérées des L-moments de chacun des postes d'observations, soit . On peut ensuite déterminer les paramètres de la loi régionale à partir des L-moments. Dans le cas d’une loi GEV, les paramètres sont liés aux L-moments par les relations :

Le paramètre de forme k est calculé par la formule suivante :

Les paramètres d'échelle α et de position ζ sont déduits des équations :

où représente la fonction Gamma.

Plusieurs méthodes peuvent être utilisées pour déterminer le type de la loi de distribution.

3.2.2.1 Le diagramme des L-Moments

Le choix de la loi peut être orienté par un diagramme des rapports des L-moments (HOSKING et WALLIS, 1997; VOGEL et al., 2009), en particulier le diagramme qui représente le L-coefficient d'aplatissement τ₄ en fonction du L-coefficient d'asymétrie τ₃ (MEYLAN et al., 2008). Les valeurs régionales moyennes des L-moments, estimés à partir des observations disponibles en chacun des sites de la région, peuvent être comparées aux L-moments théoriques de différentes lois de distribution.

3.2.2.2 Calcul de la statistique Zdist

BEN-ZVI et AZMON (1997) remarquent que le diagramme des L-moments permet de déterminer les distributions acceptables, mais pas nécessairement la distribution la plus adéquate. Des tests statistiques d'ajustement doivent être utilisés en complément au diagramme.

HOSKING et WALLIS (1997) ont développé le test de la statistique Z, dont l'objectif est de tester si un modèle fréquentiel théorique donné peut représenter le comportement statistique des pluies journalières maximales pour les différents sites d'une région homogène vis-à-vis de ces pluies.

Le test Z^dist mesure l'écart sur les ratios des L-coefficients d'aplatissement entre la valeur théorique de la loi choisie et la valeur moyenne obtenue sur la base des N_sim générations de « Monte Carlo ».

ratio du L-moment d'ordre 4 calculé à partir des valeurs régionales des coefficients de variation et d'asymétrie pour chaque distribution théorique candidate DIST. est la moyenne empirique des N_sim coefficients d'aplatissement régionaux générés par la loi Kappa. β₄ et σ₄ sont respectivement le biais et l'écart-type simulé des coefficients d'aplatissement régionaux (HINGRAY et al., 2009). La statistique Z^dist a été calculée à l’aide d’un programme R proposé par HOSKING (fonction regtst, voir en annexe 1) dans la bibliothèque lmomRFA, http://cran.r-project.org/web/packages/lmomRFA/lmomRFA.pdf.

3.2.3 Quantiles estimés pour différentes périodes de retour

Pour calculer pour chaque station les quantiles de période de retour T, nous excluons la station cible et calculons le L-C_V et la L-C_S régionaux. La distribution locale est estimée à partir de la distribution régionale, en déterminant d'abord le L-écart-type par multiplication du L-coefficient de variation régionale L-C_V par la moyenne des précipitations journalières maximales annuelles observées au site. Ensuite on calcule les paramètres de la loi GEV en utilisant la L-C_S régionale, le L-écart-type estimé à l'étape précédente et la moyenne de précipitations journalières maximales annuelles au site considéré à partir des équations 8 à 10). Enfin, on calcule les quantiles correspondant aux périodes de retour spécifiées en utilisant l'inverse de la fonction de distribution donnée par la formule suivante, dans le cas d’une loi GEV :

Les quantiles de cette distribution locale pourront être comparés à ceux obtenus par ajustement direct de la loi de distribution sur l'échantillon local. Les paramètres de la loi régionale ont été calculés par un programme R proposé par HOSKING (1997) (fonction regfit, voir annexe 1), dans la bibliothèque lmomRFA, http://cran.r-project.org/web/packages/lmomRFA/lmomRFA.pdf.

La fiabilité de la méthode régionale d’estimation des quantiles peut être évaluée en calculant par exemple la racine carrée de l’erreur quadratique moyenne (REQM) relative ainsi que le biais relatif lié à l’estimation régionale. Pour chaque station de la région homogène, nous calculons la racine de la moyenne des valeurs obtenues sur trois périodes de retour, à savoir 10 ans, 100 ans et 1 000 ans :

où et représentent les quantiles de période de retour T estimés pour le site i respectivement à partir des paramètres régionaux et locaux de la loi de distribution et N le nombre de stations.

4. Applications et résultats

4.1 Groupes homogènes

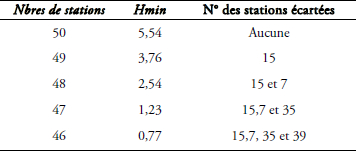
La méthode de calcul de la statistique H a été appliquée systématiquement à toutes les combinaisons de p (= 50, 49, 48, 47, 46 stations) parmi les 50 stations disponibles dans l’ensemble de la région. Pour chaque valeur de p, on a calculé le Hmin(p) correspondant à la valeur minimale de H pour toutes les combinaisons de p stations. On obtient finalement un groupe homogène avec 46 stations, après avoir éliminé quatre stations, N^os 15, 7, 35, 39 (Tableau 3).

Tableau 3

**Résultats des valeurs minimales de H pour toutes les combinaisons de p stations.**

**Results of the minimum values of H for all combinations of p stations.**

Les résultats présentés ont été obtenus avec H(L-C_V), des résultats similaires ont été obtenus avec H(L-C_S) et H(L-C_K).

4.2 Sélection de la loi régionale

Les résultats du diagramme des L-moments (Figure 3) et le test Z^dist (Tableau 4) valident l’hypothèse selon laquelle la loi GEV peut représenter de manière adéquate la distribution des pluies journalières maximales annuelles de la région homogène.

Relation entre la L-CS et le L-CK des précipitations journalieres maximales annuelles (Pearson, LogN, GEV, GPA représentent respectivement les lois Pearson, Lognormale, GEV et Pareto généralisée; Ens. est la désignation du point matérialisant les caractéristiques obtenues à partir des 46 stations). — Figure 3

Relation entre la L-C_S et le L-C_K des précipitations journalieres maximales annuelles (Pearson, LogN, GEV, GPA représentent respectivement les lois Pearson, Lognormale, GEV et Pareto généralisée; Ens. est la désignation du point matérialisant les caractéristiques obtenues à partir des 46 stations).

Relationship between L-C_S and L-C_K of annual maximum daily rainfall (Pearson, LogN, GEV, GPA represent respectively Pearson, Lognormal, GEV and generalized Pareto distributions; Ens. is the designation of the point materializing the characteristics obtained from 46 stations).

Tableau 4

**Caractéristiques statistiques du groupe homogène.**

**Statistical characteristics of the homogeneous group.**

4.3 Comparaison des quantiles locaux estimés par ajustement régional ou par ajustement local

Pour chaque site de la région homogène, on procède aux calculs des précipitations extrêmes correspondant aux quantiles de périodes de retour à partir des paramètres de la loi GEV régionale (cf. paragraphe 3.2.3).

Les quantiles locaux ont également été déterminés par ajustement local de la loi GEV. Ces quantiles ont ensuite été comparés à ceux calculés précédemment par ajustement régional (Figure 4).

Figure 4

**Distributions des quantiles estimés: (a) station Pontéba; b) station Sougueur; c) station El Asnam.**

**At-site and regional cumulative distribution functions (CDFs) for (a) Pontéba station; (b) Sougueur station and (c) El Asnam station.**

Comme le montre la figure 4, les écarts entre les quantiles estimés à partir de l'ajustement local ou régional de la GEV ont tendance à augmenter avec la période de retour. L’estimation des quantiles par ajustement régional donne des valeurs supérieures à celles estimées par ajustement local, dans le cas de la station Sougueur (Figure 4b), ou inférieures dans le cas de la station Ponteba (Figure 4a). Par ailleurs, il arrive que l'estimation régionale donne des valeurs similaires à l'estimation locale. C'est le cas, par exemple, de la station El Asnam (Figure 4c). Ces différences peuvent être imputables aux erreurs liées à l’échantillonnage, du fait de la durée relativement courte des périodes d’observation aux différentes stations.

Pour l’ensemble des 46 stations, l’écart REQM entre les quantiles obtenus par approche régionale ou locale est de 10 % pour la période de retour décennale, et de 35 % pour la période de retour centennale (Figure 5).

Figure 5

**Comparaison des quantiles des pluies journalières maximales obtenues par ajustement local et par ajustement régional : a) T = 10 ans; b) T = 100 ans.**

**Comparison of the quantiles of the daily maximal rainfalls derived from local fitting and regional fitting: a) T = 10 years; b) T = 100 years.**

Enfin, pour évaluer la pertinence du modèle régional, nous avons artificiellement retiré des valeurs de l’échantillon initial des pluies journalières maximales annuelles, et recalculé pour chaque nouvel échantillon les quantiles obtenus selon l’approche régionale ou selon l’approche locale : ces quantiles ont ensuite été comparés aux quantiles initiaux, obtenus avec l’échantillon complet. Les valeurs à supprimer ont été tirées aléatoirement, par simulation de type Monte Carlo; finalement, on travaille sur des échantillons comprenant entre 30 années d’observations par station (échantillon initial) et six années d’observations par station, pour un ensemble de 46 stations (Figure 6). On peut noter que l’erreur augmente en fonction de la longueur des séries d’observations, et que cette augmentation est relativement beaucoup plus importante pour l’approche locale. Le fait que l’approche régionale stabilise la variabilité de l’estimation des quantiles est naturellement lié au fait que l’échantillon régional est toujours plus important que l’échantillon local. Ceci peut apparaître comme un avantage important de l’approche régionale.

Figure 6

**Variation de l'erreur quadratique moyenne locale et régionale en fonction de la longueur de la série pour les périodes de retour décennale et centennale.**

**Local and regional variation of the relative root mean square error as a function of the length of the series for decennial and centennial return periods.**

5. Conclusion

Cette étude a porté sur la régionalisation des distributions des pluies extrêmes journalières, pour obtenir des quantiles fiables en des sites ayant peu ou aucune donnée. La méthode de régionalisation est basée sur les L-moments, et s’appuie sur trois étapes successives : 1) délimitation des régions homogènes par le test d’homogénéité basé sur la statistique H; 2) identification de la loi régionale basée sur le calcul de la statistique Z^dist; 3) comparaison des quantiles issus de l’approche régionale et de l’approche locale. Un algorithme original a montré que la région pouvait être considérée comme globalement homogène, si on considère un ensemble de 46 stations sur 50. La distribution GEV a été sélectionnée comme distribution régionale, et ses paramètres ont été estimés à partir des L-moments régionaux. Les REQM calculés entre quantiles régionaux et quantiles locaux sont de 10 et de 35 % respectivement pour des périodes de retour décennales et centennales. Les écarts entre les quantiles s’expliquent en partie par les erreurs d’échantillonnage liées à la durée relativement courte des observations locales; l’approche régionale, en utilisant des échantillons plus fournis, permet de réduire ces erreurs d’échantillonnage.

La méthodologie est généralisable à d'autres bassins algériens, et peut également s'appliquer à d'autres variables hydro-météorologiques que les précipitations. Ultérieurement, une comparaison de cette méthode L-moments est prévue avec d’autres méthodes de type « flood-index », consistant à regrouper toutes les données indépendantes dans un échantillon unique, après normalisation par un facteur d’échelle.

Résumé

Abstract

1. Introduction

2. Site d’étude et données utilisés