Résumés
Résumé
Ce travail évalue la pertinence d’une analyse en ondelettes appliquée à la consommation en eau potable, afin d’établir les habitudes de consommation des usagers et de détecter des changements. Cette démonstration exploite une série d’observations de débit au pas de temps horaire, couvrant une période de dix semaines dont le congé des Fêtes de fin d’année, tirée du réseau de distribution d’eau potable de la ville de Québec, Canada. Les résultats confirment la non-stationnarité du débit pour la gamme de périodes à l’étude, soit de 2 à 256 heures. Le principal cycle, qui explique la moitié de la variance naturelle de la série, possède une période de 24 heures dont l’intensité non stationnaire décrit un cycle de sept jours avec des pointes le dimanche matin et des creux au coeur de la semaine de travail. Le second cycle, responsable de plus du tiers de la variance, possède une période de 12 heures dont l’intensité suit également (mais un peu moins clairement) un cycle de sept jours avec des pointes la semaine et des creux le week-end. Ce comportement diffère pendant le congé des Fêtes de fin d’année, lorsque presque toute la variance naturelle est expliquée par la composante 24 heures de la série.
Mots-clés :
- Analyse en ondelettes,
- variance, débit de consommation,
- eau potable,
- réseau de distribution
Abstract
This study evaluates the relevance of wavelet analysis applied to water consumption in order to detect habits and changes in these habits. The demonstration is based on a series of one-hour flow observations from Quebec City’s water distribution flowmeter network for a 10-week period, which includes Christmas and the New Year holidays. Results confirm the non-stationarity of the flow data for all studied periods, which range from 2 to 256 h. The main cycle, which accounts for half of the natural variance of the series, has a period of 24 h, with a non-stationary intensity varying over 7 d, peaking on Sunday mornings and with lows during the work week. The second cycle, responsible for a third of the variance, has a period of 12 h, with an intensity which follows (although not as strongly as the previous cycle) a 7-d cycle, peaking during the week and with lows during the weekend. This behaviour differs during the Holidays, when most of the natural variance is explained by the 24-h component of the series.
Keywords:
- Wavelet analysis,
- variance, water consumption,
- drinking water,
- distribution network
Corps de l’article
1. Introduction
Le rendement des réseaux urbains de distribution d’eau potable évolue avec le temps. L’opération des pompes et des vannes ainsi que les fuites et les bris des équipements du système de distribution sont responsables de la perte de grandes quantités d’eau transportées en réseau. La gestion des pressions et des débits en vue d’optimiser l’efficacité de la distribution de l’eau potable en réseau ainsi que de minimiser la fréquence des bris de conduites représente un défi important pour les gestionnaires et les opérateurs. Pour des fins de détection et de régulation des fuites d’eau, il peut s’avérer très utile de disposer d’outils complémentaires d’aide à la gestion des réseaux d’alimentation en eau potable. Or, pour développer de tels outils, il est nécessaire d’avoir une très bonne connaissance des patrons de consommation des réseaux analysés. Dans cette perspective, l’étude en ondelettes des débits de consommation d’un réseau s’avère une voie intéressante à explorer car elle n’est pas contrainte par l’hypothèse de stationnarité des séries. En effet, la transformée continue en ondelettes admet des changements des propriétés du spectre de puissance en fonction du temps, traitant les domaines fréquentiel et temporel simultanément, en contraste avec la transformée de Fourier (DAUBECHIES, 1992).
La transformée continue en ondelettes est régulièrement utilisée en science hydrologique pour l’analyse de la variance de séries temporelles non stationnaires. Les applications hydrologiques incluent l’analyse fréquentielle de débits (SMITH et al., 1998; LAFRENIÈRE et SHARP, 2003; LABAT et al., 2005), de la teneur en eau du sol (LAUZON et al., 2004; PARENT et al., 2006), de la densité de la végétation (COSH et BRUTSAERT, 2003) et de propriétés du sol (LARK et WEBSTER, 2001; ANCTIL et al., 2008). Dans un contexte de gestion de la ressource en eau, notons aussi les travaux de WHITE et al. (2005) sur la détection de l’influence de l’opération d’un barrage sur les débits en aval.
Ce travail propose le recours de l’analyse en ondelettes pour la description temps-période d’une série de consommation en eau potable, au pas de temps horaire. Une telle analyse permettra de bien décrire les fluctuations du débit qui se révèlent non stationnaires pour la gamme de périodes à l’étude, soit de 2 à 256 heures. Il sera alors possible d’identifier précisément les habitudes de consommation des usagers et même de détecter des changements dans ces habitudes. La démonstration exploitera une série d’observations de débit tirées du réseau de distribution d’eau potable de la ville de Québec.
Trois sections suivent, soit une présentation des matériels et méthodes de l’étude, ce qui inclut notamment des descriptions de la base de données et de l’analyse en ondelettes; les résultats et une discussion et, finalement, une conclusion générale.
2. Matériels et méthodes
Le secteur à l’étude est un quartier résidentiel de la ville de Québec dont la population est en forte progression depuis une soixantaine d’années (MAHER et MATHIEU, 2005). Ces quelque 20 500 habitants se sont d’abord approvisionnés en eau potable à partir de cinq groupes de puits d’alimentation non traités. Dès 2001, cette ressource souterraine est devenue insuffisante pour satisfaire la demande. Le manque d’eau a alors été comblé par la construction d’un réservoir procurant un approvisionnement de pointe. Aujourd’hui, ce système est à nouveau sollicité au-delà de sa capacité, le déficit moyen entre la consommation journalière et la capacité de production en eau potable atteignant parfois jusqu’à 6 000 m3•j‑1.
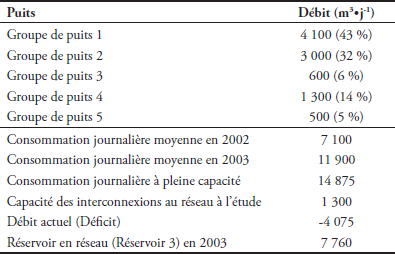
Les principaux paramètres de ces installations sont énumérés au tableau 1. En période de faible consommation, les excédents de débit des cinq groupes de puits sont acheminés jusqu’à un réservoir situé sur un point élevé du territoire. Le réseau supérieur est alimenté directement à partir de ce réservoir tandis que le débit acheminé vers le reste du réseau est contrôlé par des régulateurs de pression. Plusieurs éléments exacerbent la sous-production de ce réseau, dont son âge avancé, l’augmentation du nombre d’usagers, la forte sollicitation en matière de pression (conduites de faible diamètre et nombreuses extrémités de réseau) et l’isolement par rapport à d’autres sources d’eau potable.
Tableau 1
Capacité de production des puits et consommation des usagers selon MAHER et MATHIEU (2005).
Well production capacity and users' drinking water consumption according to MAHER and MATHIEU (2005).
2.1 Description de la base de données
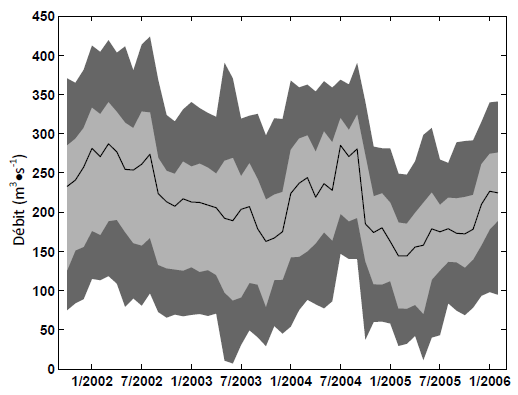
Une étude des patrons de consommation horaires a été réalisée à partir des données de débits du réseau de distribution d’eau potable. Les données brutes consistent en des mesures automatiques à la minute du groupe de puits 2, pour la période de quatre ans s’étendant d’octobre 2001 à mars 2006, desquelles ont été déduites une série de consommation horaire. Les caractéristiques statistiques de cette chronique horaire sont illustrées à la figure 1 : valeur médiane, bande regroupant 50 % des observations et bande regroupant 90 % des observations, chaque mois. La valeur médiane mensuelle varie de 150 à 300 m3•s‑1. La fluctuation des débits horaires durant chaque mois est toutefois plus importante, la bande 90 % s’étendant essentiellement sur 300 m3•s‑1. En fait, le débit oscille chaque journée entre 100 m3•s‑1 (nuit) et 400 m3•s‑1 (jour), tel qu’il est illustré à la figure 2 pour la période de dix semaines (1 680 heures) débutant le 8 novembre 2001 à 00 h le matin. Sur cette même figure, afin de distinguer les jours de travail de la majorité de la population (les lundis aux vendredis) des jours de repos (les samedis et dimanches), les dates indiquées sont les dimanches matin, 00 h.
Figure 1
Statistiques mensuelles de la série horaire des débits de consommation : valeur médiane (trait), partie de la distribution bornée par les quantiles 25 % et 75 % (gris pâle) et partie de la distribution bornée par les quantiles 5 % et 95 % (gris foncé).
Monthly statistics of the hourly water consumption series: median value (line), 25% and 75% quantiles (pale grey) and 5% and 95% quantiles (dark grey).
2.2 Analyse en ondelettes
Pour une chronique d’observations discrètes xn, la transformée continue en ondelettes Wn est définie par la convolution de xn avec une ondelette Ψ(η) mise à l’échelle et translatée à l’aide du paramètre adimensionnel η, positionnant l’ondelette le long de la série temporelle. La transformée continue s’écrit alors :
pour laquelle η est un indice temporel de positionnement, s est l’échelle de l’ondelette, δt est le temps écoulé entre deux prises de mesure, N est le nombre d’observations de la chronique et ψ* est la conjuguée complexe de ψ.
Plusieurs fonctions peuvent être utilisées pour le calcul de la transformée en ondelettes. Pour qu’une fonction soit admissible, sa moyenne doit être nulle dans les deux domaines (FARGE, 1992). La sélection d’une ondelette particulière dépend ensuite des objectifs de l’expérimentateur. Il est cependant préférable de choisir une ondelette dont la forme s’apparente au patron des fluctuations de la série temporelle (NAKKEN, 1999), ce qui est le cas de l’ondelette de Morlet qui trace des crêtes et des creux à la manière d’une onde. Cette caractéristique est compatible avec les oscillations de la série de débits observés (voir figure 2). Celle-ci consiste en une onde complexe modulée par une fonction Gaussienne. Cette ondelette s’écrit :
où ω0 est une fréquence adimensionnelle de valeur 6, afin de satisfaire la condition d’admissibilité décrite précédemment.
Figure 2
Série horaire des débits de consommation pour la période de dix semaines (1 680 valeurs) s'étendant du 8 novembre 2001 0 h (matin) jusqu'au 16 janvier 2002, 23 h.
Hourly water consumption series for the 10-week period (1680 values) from 8 November 2001, 0h00 (morning) to 16 January 2002, 23h00.
Le spectre de puissance en ondelettes, défini par ![]() , décrit les fluctuations de la variance de la série temporelle, à la fois dans le domaine temporel et dans le domaine fréquentiel.
, décrit les fluctuations de la variance de la série temporelle, à la fois dans le domaine temporel et dans le domaine fréquentiel.
Une analyse spectrale révèle souvent qu’une série temporelle de débits possède des bandes de fréquences préférentielles où se regroupe une partie importante de la variance (RAJAGOPALAN et LALL, 1998; ANCTIL et COULIBALY, 2004). Un spectre de puissance moyen par bandes de périodes permet souvent de bien illustrer les écarts entre la répartition fréquentielle de la variance, tout comme leur évolution temporelle. Un spectre de puissance moyen par bandes de périodes consiste en la somme pondérée du spectre de puissance entre deux échelles s1 et s2 sélectionnées par l’expérimentateur (TORRENCE et COMPO, 1998) :
où δj est un facteur définissant la résolution fréquentielle du spectre de puissance (sa valeur est ici fixée à 0,1) et Cδ est un facteur de reconstruction dont la valeur est spécifique à chaque ondelette. Précisions que j1 doit être inférieur à j2 afin de définir un intervalle non nul et que, dans le cas de l’ondelette de Morlet, Cδ égale à 0,776. Dans le cadre de ce projet, la série temporelle des débits horaires sera étudiée pour des bandes de périodes de 2 à 8 heures, de 8 à 16 heures, de 16 à 32 heures et de 32 à 256 heures, de manière à bien distinguer l’influence des deux périodes dominantes en jeu dans la série de consommation d’eau potable à l’étude, soit 24 h et 12 h, tel qu’il est décrit en détail à la section suivante.
3. Résultats et discussion
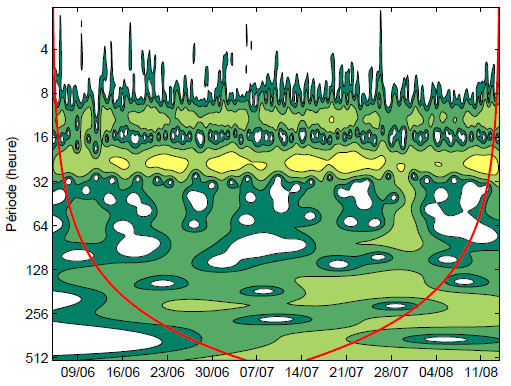
La figure 3 illustre la distribution temps-période de la variance (spectre de puissance) de la série des 1 680 débits horaires illustrée précédemment à la figure 2. Dans ce cas, la variance locale, calculée à l’aide d’une ondelette de Morlet, a été standardisée par la variance naturelle de la série, afin de simplifier l’illustration : les zones en blanc ont une variance standardisée inférieure à 0,25 et les quatre bandes de couleurs passant du vert au jaune illustrent des variances standardisées respectivement comprises entre 0,25 et 1, 1 et 4, 4 et 16, et 16 et plus. Lors de l’analyse, l’ondelette étant tour à tour centrée sur chacune des 1 680 valeurs de la série, il faut ajouter des valeurs nulles à chaque extrémité afin de procéder de part en part. Ceci crée un effet de bord pour lequel la variance des couples temps-période est affectée à la baisse par les valeurs nulles ajoutées. À la figure 3, la ligne rouge, en forme de coque de navire, identifie la portée de l’effet de bord. Il est alors d’usage de restreindre l’interprétation des résultats aux couples temps-période sis à l’intérieur de cette ligne rouge, soit, dans ce cas particulier, aux périodes de 2 à 256 heures. Finalement, tout comme pour la figure 2 et pour se situer dans la semaine, les dates indiquées à la figure 3 correspondent à des dimanches matin, 00 h.
Figure 3
Spectre de puissance de la série de 1 680 observations illustrée à la figure 2. Les variances sont standardisées par la variance naturelle de la série. Les couples tempspériode en blanc ont une variance standardisée inférieure à 0,25 et les quatre bandes de couleurs passant du vert au jaune illustrent des variances standardisées respectivement comprises entre 0,25 et 1, 1 et 4, 4 et 16, et 16 et plus. Les couples temps-période à l'extérieur de la ligne rouge ont une variance influencée par les effets de bord.
Power spectrum of the series of 1 680 values shown in Figure 2. Variances are standardized according to the natural variance of the series. Time-period couples in white have a standardized variance lower than 0.25 and the four colour bands going from green to yellow illustrate standardized variances between 0.25 and 1, 1 and 4, 4 and 16 and higher than 16, respectively. Time-period couples outside of the line in red are influenced by edge effects.
La figure 3 permet d’identifier deux périodes dominantes : 24 h puis 12 h. Tout d’abord, les variances standardisées de la période 24 h atteignent toujours plus de 4 et dépassent même 16 les week-ends. Ces résultats mettent en évidence un comportement fréquentiel différencié entre les habitudes en semaine et les habitudes en week-end, confirmant la propriété non stationnaire de la série des débits de consommation. L’analyse permet aussi d’identifier une différence de comportement des usagers pour la période s’étendant essentiellement du 23 décembre au 6 janvier, soit celle du congé scolaire de la période des Fêtes de fin d’année au Québec. Pendant toute cette période, une consommation de type « week-end » est maintenue. Pour sa part, la variance standardisée de la période 12 h est supérieur à 4, sauf pour la période des Fêtes de fin d’année où elle chute passablement. On note également une pulsation de la variance standardisée en fonction du temps, mais contrairement à la période 24 h, les minimums surviennent en week-end. Outre ces deux périodes dominantes, une variance standardisée plus faible est identifiée pour une période de 168 heures (sept jours) et de six heures. Dans ces cas aussi, les propriétés spectrales sont non stationnaires.
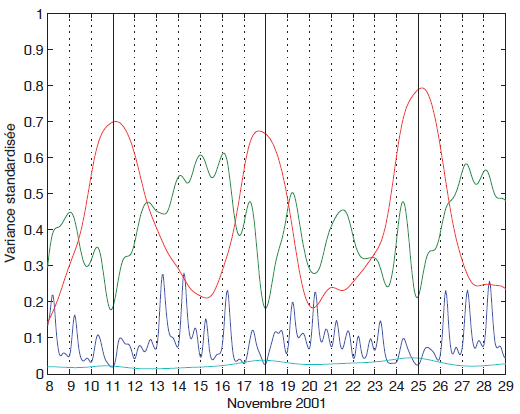
Le spectre de puissance à la figure 3 révèle également que la variance adopte préférentiellement certaines périodes. Les fluctuations non stationnaires de l’intensité de la variance standardisée sont alors souvent mieux décrites par un spectre de puissance moyen par bandes de périodes, tel qu’il est illustré à la figure 4. Dans ce cas, quatre bandes sont explorées : de 2 à 8 heures, de 8 à 16 heures, de 16 à 32 heures et de 32 à 256 heures. Les variances moyennes pour les bandes de périodes 16 à 32 heures et 8 à 16 heures, qui regroupent respectivement 51,2 % et 36,9 % de la variance naturelle de la série analysée, sont presque parfaitement déphasées – la bande 16 à 32 heures culmine le dimanche matin, alors que la bande 8 à 16 heures culmine en milieu de semaine. Pour leurs parts, les bandes 2 à 8 heures et 32 à 256 heures ne regroupent respectivement que 8,3 % et 2,7 % de la variance naturelle de la série, la première culminant en milieu de semaine et la seconde culminant le week-end. Il semble donc relativement facile de relier les diverses fluctuations temps-période de la variance en fonction des pratiques de consommation de la population. La figure 5, qui reprend l’information de la figure 4 pour les 21 premiers jours de la série, permet une analyse plus fine de ces habitudes. Entre autres, on constate que la valeur maximale de la variance moyenne de la bande 8 à 16 heures se produit la nuit en semaine et que la valeur maximale de la variance moyenne de la bande 2 à 8 heures se produit plutôt entre 6 h et 8 h du matin, également en semaine.
Figure 4
Spectre de puissance moyen par bandes de périodes de 2 à 8 heures (bleu foncé), de 8 à 16 heures (vert), de 16 à 32 heures (rouge) et de 32 à 256 heures (bleu pâle) de la série de 1 680 observations illustrée à la figure 2. Les variances sont standardisées par la variance naturelle de la série.
Mean power spectrum for period bands of 2 to 8 h (dark blue), from 8 to 16 h (green),from 16 to 32 h (red) and from 32 to 256 h (pale blue) of the series of 1680 values shown in Figure 2. Variances are standardized according to the natural variance of the series.
Figure 5
Spectre de puissance moyen par bandes de périodes tel qu'à la figure 4 mais uniquement pour les 21 premiers jours de la série de la figure 2. Les lignes verticales pointillées marquent 0 h et les lignes pleines identifient les dimanches matins.
Mean power spectrum for the same period bands as in Figure 4 but for the first 21 days only of the series shown in Figure 2. The dotted vertical lines mark the 0h00 times and the full lines identify the Sunday mornings.
À des fins comparatives, le spectre de la même série de dix semaines débutant le 8 novembre 2001, issu cette fois d’une analyse de Fourier, est illustré à la figure 6, pour laquelle les fréquences sont exprimées en cycle par jour. Cette analyse fréquentielle est cohérente avec l’analyse en ondelettes car elle identifie clairement la domination des fréquences 24 h et 12 h. Cependant, l’analyse de Fourier reste tout à fait silencieuse sur la non-stationnarité temporelle de ces oscillations, montrant bien l’intérêt de l’analyse en ondelettes.
Figure 6
Analyse de Fourier de la série de la figure 2. Le nombre de degrés de liberté du spectre est de 10, menant à une résolution fréquentielle de 0,071 cycle par jour.
Fourier analysis of the series shown in Figure 2. The spectrum has 10 degrees of freedom, for a frequency resolution of 0.071 cycle per day.
Une seconde série de dix semaines, cette fois débutant le 5 juin 2002, a fait l’objet d’une analyse en ondelettes (Figure 7) afin de permettre une comparaison entre les comportements de consommation d’été et d’hiver (voir figure 3). Si la consommation hivernale suit des patrons répétitifs, il n’en est pas de même pour la consommation estivale dont les cycles 24 h et 12 h ne se répètent pas systématiquement d’une semaine à l’autre. Il appert donc que des facteurs externes influencent les patrons de consommation. Par exemple, il est probable que le climat ait une influence sur la consommation tout comme une organisation différente des habitudes de vie de la population d’une saison à une autre.
Figure 7
Spectre de puissance comme à la figure 3, mais pour la série débutant le 5 juin 2002.
Power spectrum as in Figure 3, but for the time series starting 5 June 2002.
4. Conclusion
Une analyse visuelle détaillée d’une série temporelle, telle que celle tracée à la figure 2, permet l’identification qualitative des principaux cycles qui la constituent. Il s’agit toutefois d’une tâche colossale qu’il vaut mieux réaliser directement dans le domaine fréquentiel. En revanche, la non-stationnarité étant une qualité temporelle, elle ne peut pas être décrite par une analyse fréquentielle conventionnelle. Cette étude montre que l’analyse en ondelettes est une option adéquate pour l’analyse fréquentielle de séries non stationnaires de débits de consommation en réseau urbain. Un portrait des patrons de consommation horaires d’une zone urbaine de la province de Québec a ainsi été proposé pour une période de dix semaines, incluant un congé des Fêtes. Pour la série à l’étude, les analyses ont révélé un cycle principal d’une période de 24 heures dont l’intensité non stationnaire décrit un cycle de sept jours avec des pointes le dimanche matin et des creux au coeur de la semaine de travail. La moitié de la variance naturelle de la série est expliquée par cette fluctuation. Le second cycle en importance est responsable de plus du tiers de la variance naturelle de la série. Il s’agit d’un cycle d’une période de 12 heures, dont l’intensité suit également (mais un peu moins clairement) un cycle de sept jours avec des pointes la semaine et des creux le week-end. Les autres composantes jouent des rôles passablement secondaires.
Cette étude indique qu’une agence de gestion des eaux de consommation pourrait tirer profit d’une analyse en ondelettes pour étudier les patrons de consommation changeant de ces clients. Par exemple, la décomposition temps-période de l’analyse en ondelettes a révélé que, pendant la période d’environ deux semaines du congé des Fêtes, presque toute la variance naturelle est supportée par la composante 24 heures de la série, le cycle de 12 heures de période étant au mieux réduit à son niveau usuel des week-ends.
Parties annexes
Références bibliographiques
- ANCTIL F., A. PRATTE, L.-É. PARENT et M.A. BOLINDER. (2008). Non-stationary temporal characterization of the temperature profile of a soil exposed to frost in south-eastern Canada. Nonlin. Processes Geophys., 15, 409-416.
- ANCTIL F. et P. COULIBALY. (2004). Wavelet analysis of the interannual variability in southern Québec streamflow. J. Climate, 17, 163-173.
- COSH M.H. et W. BRUTSAERT. (2003). Microscale structural aspects of vegetation density variability. J. Hydrol., 276, 128-136.
- DAUBECHIES I. (1992). Ten lectures on wavelets. Society for Industrial and Applied Mathematics (SIAM) publication, 61.
- FARGE M. (1992). Wavelet transforms and their applications to turbulence. Ann. Rev. Fluid Mech., 24, 395-457.
- LABAT D., J. RONCHAIL et J.L. GUYOT. (2005). Recent advances in wavelet analyses: Part 2 - Amazon, Parana, Orinoco and Congo discharges time scale variability. J. Hydrol., 314, 289-311.
- LAFRENIÈRE M. et M. SHARP. (2003). Wavelet analysis of inter-annual variability in the runoff regimes of glacial and nival stream catchments, Bow Lake, Alberta. Hydrol. Process., 17, 1093-1118.
- LARK R.M. et R. WEBSTER. (2001). Changes in variance and correlation of soil properties with scale and location: Analysis using an adapted maximal overlap discrete wavelet transforms. Eur. J. Soil Sci., 52, 547-562.
- LAUZON N., F. ANCTIL et J. PETRINOVIC. (2004). Characterization of soil moisture conditions at temporal scales from few days to annual. Hydrol. Process., 18, 3235-3254.
- MAHER C. et P. MATHIEU. (2005). Étude hydraulique et interconnexion de Val-Bélair. Recherche de solution visant le transfert de 6 000 m3/j d’eau vers Val-Bélair. Ville de Québec, Tecsult inc., 41 p.
- NAKKEN M. (1999). Wavelet analysis of rainfall-runoff variability isolating climatic from anthopogenic patterns. Environ. Modell. Softw., 14, 283-295.
- PARENT, A.-C., F. ANCTIL et L.-É. PARENT (2006). Characterization of temporal variability in near-surface soil moisture at scales from 1 h to 2 weeks. J. Hydrol., 325, 56-66.
- RAJAGOPALAN B. et U. LALL. (1998). Interannual variability in western US precipitation. J. Hydrol., 210, 51-67.
- SMITH L.C., D.L. TURCOTTE et B.L. ISACKS. (1998). Stream flow characterization and feature detection using a discrete wavelet transform. Hydrol. Process., 12, 233-249.
- TORRENCE C. et G.P. COMPO. (1998). A practical guide to wavelet analysis. B. Am. Meteorol. Soc., 79, 61-78.
- WHITE M.A., J.C. SCHMIDT et D.J. TOPPING. (2005). Application of wavelet analysis for monitoring the hydrologic effects of dam operation: Glen Canyon Dam and the Colorado River at Lees Ferry, Arizona. River Res. Applic., 21, 551-565.
Liste des figures
Figure 1
Statistiques mensuelles de la série horaire des débits de consommation : valeur médiane (trait), partie de la distribution bornée par les quantiles 25 % et 75 % (gris pâle) et partie de la distribution bornée par les quantiles 5 % et 95 % (gris foncé).
Monthly statistics of the hourly water consumption series: median value (line), 25% and 75% quantiles (pale grey) and 5% and 95% quantiles (dark grey).
Figure 2
Série horaire des débits de consommation pour la période de dix semaines (1 680 valeurs) s'étendant du 8 novembre 2001 0 h (matin) jusqu'au 16 janvier 2002, 23 h.
Hourly water consumption series for the 10-week period (1680 values) from 8 November 2001, 0h00 (morning) to 16 January 2002, 23h00.
Figure 3
Spectre de puissance de la série de 1 680 observations illustrée à la figure 2. Les variances sont standardisées par la variance naturelle de la série. Les couples tempspériode en blanc ont une variance standardisée inférieure à 0,25 et les quatre bandes de couleurs passant du vert au jaune illustrent des variances standardisées respectivement comprises entre 0,25 et 1, 1 et 4, 4 et 16, et 16 et plus. Les couples temps-période à l'extérieur de la ligne rouge ont une variance influencée par les effets de bord.
Power spectrum of the series of 1 680 values shown in Figure 2. Variances are standardized according to the natural variance of the series. Time-period couples in white have a standardized variance lower than 0.25 and the four colour bands going from green to yellow illustrate standardized variances between 0.25 and 1, 1 and 4, 4 and 16 and higher than 16, respectively. Time-period couples outside of the line in red are influenced by edge effects.
Figure 4
Spectre de puissance moyen par bandes de périodes de 2 à 8 heures (bleu foncé), de 8 à 16 heures (vert), de 16 à 32 heures (rouge) et de 32 à 256 heures (bleu pâle) de la série de 1 680 observations illustrée à la figure 2. Les variances sont standardisées par la variance naturelle de la série.
Figure 5
Spectre de puissance moyen par bandes de périodes tel qu'à la figure 4 mais uniquement pour les 21 premiers jours de la série de la figure 2. Les lignes verticales pointillées marquent 0 h et les lignes pleines identifient les dimanches matins.
Mean power spectrum for the same period bands as in Figure 4 but for the first 21 days only of the series shown in Figure 2. The dotted vertical lines mark the 0h00 times and the full lines identify the Sunday mornings.
Figure 6
Analyse de Fourier de la série de la figure 2. Le nombre de degrés de liberté du spectre est de 10, menant à une résolution fréquentielle de 0,071 cycle par jour.
Fourier analysis of the series shown in Figure 2. The spectrum has 10 degrees of freedom, for a frequency resolution of 0.071 cycle per day.
Figure 7
Spectre de puissance comme à la figure 3, mais pour la série débutant le 5 juin 2002.
Power spectrum as in Figure 3, but for the time series starting 5 June 2002.
Liste des tableaux
Tableau 1
Capacité de production des puits et consommation des usagers selon MAHER et MATHIEU (2005).
Well production capacity and users' drinking water consumption according to MAHER and MATHIEU (2005).