Résumés
Résumé
Cet article propose de valoriser les jaugeages volants dans un cadre de régionalisation de débits caractéristiques d’étiage. La variable examinée est le débit mensuel minimal annuel de fréquence quinquennale sèche (QMNA5). Le jeu de données est formé de 133 stations hydrométriques réparties dans le bassin Seine-Normandie.
La méthode dite « des jaugeages épisodiques » calcule le QMNA5 en un site cible (peu jaugé) en multipliant la valeur de QMNA5 d’une station hydrométrique voisine par un coefficient k. Ce coefficient k est obtenu à partir d’observations concomitantes au site cible et à la station d’appui. Une étude de sensibilité à la stratégie de collecte des jaugeages et au degré de similitude entre le site cible et la station de référence montre une faible sensibilité au nombre de jaugeages volants (le risque d’erreur importante est cependant plus élevé avec peu de données). En outre, il semble préférable d’effectuer les mesures en période d’étiage, de rechercher une station d’appui sur le même linéaire et de calculer k selon le rapport des moyennes des débits synchrones. Cette méthode a été comparée à des méthodes d’interpolation classiques (régression et deux variantes du krigeage). Leur performance a été appréciée par validation croisée sur le jeu de données en considérant tour à tour chaque station comme peu jaugée. Les méthodes géostatistiques, équivalentes en matière d’efficience, sont plus fiables qu’une régression linéaire exploitant des données climatologiques, mais sont surpassées par la méthode des jaugeages volants. Enfin, la méthode des jaugeages épisodiques a été intégrée dans un cadre géostatistique pour extrapoler les valeurs obtenues aux sites peu jaugés. La validation croisée opérée montre que l’exploitation des jaugeages épisodiques, même en nombre réduit dans une méthode régionale, permet donc de mieux apprécier les valeurs de QMNA5.
Mots clés:
- étiage,
- jaugeage volant,
- krigeage,
- interpolation,
- Seine
Abstract
A general framework for improving the use of sporadic measurement data to estimate low flow characteristics is presented. The variable studied is QMNA5, the annual minimum monthly flow with a return period of 5 years. The dataset consists of 133 gauging stations of the Seine-Normandy basin.
The method using the sporadic measurement data provides estimates of QMNA5 at a poorly gauged site by multiplying QMNA5 computed at a nearby gauging station by a scale coefficient k. The value of k is obtained through synchronous measurements recorded at the poorly-gauged site and at the nearby station. A sensitivity analysis of the data collection strategy and of the similarity of the two sites indicated a weak sensitivity to the number of sporadic measurement data. However, the risk of a large bias is obviously higher when few measurements are involved. In addition, we recommend collecting measurements during the low flow period, choosing the donor site upstream or downstream from the poorly gauged site, and computing k as the ratio of the average of the synchronous discharges.
This method was compared to three regionalization procedures: regression analysis and two variants of kriging. Their efficiency was measured by cross validation. The procedure considered in turn each station from the dataset as a poorly gauged site. Regression analysis performed worse than the two kriging techniques, the efficiencies of which were comparable. The method using sporadic measurement data yielded the best predictive performance even when the collected data were few. This method was introduced into a geostatistical framework to extrapolate the values obtained at the poorly gauged sites. A cross validation was carried out and demonstrated that there was a significant gain in accuracy in the interpolated QMNA5 values, even when using only a few sporadic measurements to supplement regional information.
Key words:
- Low flow,
- spot gauging,
- kriging,
- interpolation,
- Seine
Corps de l’article
1. Introduction
La Directive Cadre Européenne sur l’Eau (DCE), adoptée en octobre 2000 par les membres de l’Union Européenne, définit un cadre juridique et réglementaire pour une politique durable et intégrée. Elle vise la protection et l’amélioration de la qualité des cours d’eau, lacs, eaux souterraines, eaux côtières ou estuaires et l’utilisation rationnelle de la ressource en eau. La DCE engage ainsi tous les pays à reconquérir la qualité de l’eau et des milieux aquatiques, à restaurer les milieux naturels dégradés et à préserver ceux qui sont actuellement en très bon état. Pour répondre à ces objectifs, une description exhaustive des flux (eau et matière) dans les cours d’eau s’avère nécessaire au travers de débits de référence. Ces variables de synthèse résument le régime hydrologique et dans une configuration naturelle renseignent sur le potentiel de dilution des pollutions et de développement de la vie aquatique. Leur estimation en site non jaugé requiert des opérations d’interpolation. Bien souvent, les données exploitées en régionalisation sont issues de longues chroniques continues. D’autres sources peuvent compléter un réseau de stations hydrométriques de référence : les jaugeages volants ou épisodiques, mesures ponctuelles effectuées sur des points non instrumentés. Ces données sont exploitées pour estimer un débit de référence en étiage au droit du point de mesure en s’appuyant sur une station hydrométrique voisine (GALEA et CANALI, 2005; OBERLIN et al., 1973). Leur usage dans un schéma d’interpolation n’est pas fréquent car une telle procédure se doit de distinguer les deux types de données.
Les objectifs de cet article sont de proposer une stratégie de collecte et d’exploitation des jaugeages volants visant à réduire les erreurs commises sur le débit de référence estimé aux sites peu jaugés et d’introduire finalement ces données dans une procédure de régionalisation. Les procédures intégrant les jaugeages volants seront comparées, en matière de performance, à trois méthodes purement régionales et d’usage courant en hydrologie : la régression linéaire et deux variantes du krigeage.
La régionalisation à base de relations empiriques simples entre débits de référence d’étiage et caractéristiques physiques et climatiques des bassins versants demeure une approche privilégiée par la communauté scientifique (HORTNESS, 2006; LACEY et GRAYSON, 1997; RIES et FRIESZ, 2000; TALLAKSEN et VAN LANEN, 2004). Le choix des variables explicatives se fonde sur les processus hydrologiques dominants, sur la facilité de calcul des variables et leur disponibilité dans les bases de données. De telles relations ont, pour la plupart, été établies au moyen de régression multiple sur les données brutes ou transformées récoltées sur des bassins jaugés. Les variables explicatives potentielles sont nombreuses (surface, statistique de pluie, caractéristiques du sol, altitude moyenne du bassin, proportion de bassin couverte par les étendues d’eau, pente, etc.) mais leur pertinence dans les formules empiriques n’est pas assurée. L’approche à base de formules empiriques n’exploite pas la notion de proximité contrairement aux méthodes dites « stochastiques ». Ces dernières sont des techniques de reconstitution de champs, chaque champ étant une réalisation d’un phénomène aléatoire. Leurs différences résident dans les hypothèses avancées sur la variable interpolée. Nous retenons ici la technique du krigeage (MATHERON, 1965). Les méthodes stochastiques présentent l’avantage de laisser les variables s’exprimer librement sans autre intervention que l’ajustement d’une fonction décrivant les liaisons spatiales, un modèle autorisé de variogramme ajusté sur les observations.
Dans la section suivante, nous décrirons le site d’étude et les données exploitées. Ensuite, nous présenterons un cadre d’analyse globale indispensable à l’utilisation optimale des jaugeages épisodiques. La quatrième section sera consacrée à une comparaison des méthodes d’estimation régionales et, finalement, nous proposerons l’insertion de la méthode des jaugeages épisodiques dans un schéma d’interpolation du type géostatistique avant de conclure.
2. Présentation de la zone d’étude et des données utilisées
2.1 Le secteur d’étude : le bassin de gestion Seine-Normandie
Le secteur d’application est le bassin de gestion de l’Agence de l’Eau Seine-Normandie. La zone d’étude couvre environ 100 000 km2. Elle inclut le bassin versant de la Seine, qui, à son débouché à la mer, draine une surface de 78 000 km2, et les bassins côtiers normands de tailles plus modestes. Les territoires traversés par les cours d’eau concernés sont peu accidentés. Moins de 1 % du territoire se situe à une altitude supérieure à 500 m et l’altitude moyenne de la zone est de 160 m.
Une représentation simplifiée du réseau hydrographique a été obtenue après traitement semi-automatique d’un modèle numérique de terrain raster à résolution kilométrique. Un algorithme a exploré le modèle numérique de terrain pour identifier le cheminement naturel de l’eau en surface (le plan de drainage). Des corrections locales manuelles ont été apportées, lorsque le réseau reconstitué dévie de sa « vraie » trajectoire définie par le référentiel hydrographique de la BDCarthage (http://services.sandre.eaufrance.fr). L’analyse du réseau sur la base des surfaces reconstituées montre que le réseau obtenu est fiable pour les points drainant plus de 50 km2 (SAUQUET, 2006). Le plan de drainage est indispensable au calcul des variables de bassin (coordonnées du centre de gravité, pluie de bassin, distance le long du linéaire).
2.2 Les données hydrométriques
Les données de base pour l’hydrologie sont les chroniques de débits journaliers (QJ) extraites de la banque nationale HYDRO et les séries agrégées au pas de temps mensuel (QM). Le choix des stations de référence, parmi les 494 référencées sur le bassin Seine-Normandie, est gouverné par la longueur des enregistrements. Les chroniques doivent être suffisamment longues pour garantir une estimation robuste des statistiques. Les stations de jaugeage n’ont malheureusement pas toutes fonctionné simultanément. En travaillant sur des périodes d’observation parfois disjointes, nous prenons le risque de représenter une variabilité temporelle plutôt qu’un effet spatial. Pour réduire ce risque, une solution est de manipuler des séries recouvrantes au moins partiellement. Le choix d’un échantillon résulte ainsi d’un compromis entre la durée de disponibilité et la densité du réseau de mesure. Dans cette étude, les lacunes sont autorisées mais un minimum de 20 ans de mesures entre 1976 et 2005 est requis. Cette période de référence présente l’avantage de caractériser les années les plus récentes.
De fait, nous avons écarté les stations aux mesures influencées ou de qualité médiocre sur la base d’informations présentes dans la base de données HYDRO, d’analyse des courbes de tarage mises à disposition ou/et sur les conseils des gestionnaires des stations. Finalement, 133 stations ont été conservées et exploitées dans la suite (Figure 1). La surface des bassins se situe entre 6 et 10 700 km2.
Figure 1
Réseau hydrographique principal (—) et stations de référence (•).
Mean river network (—) and location of the gauging stations (•).
2.3 Les données météorologiques
En complément des données hydrométriques, nous disposons de séries de cumuls mensuels de pluie en 177 stations pluviométriques. Ces postes ont fonctionné en continu sur la période 1976-2005 et sont référencés dans la base de données PLUVIO de Météo-France. Le secteur étant peu accidenté, les pluies de bassin ont été obtenues selon la méthode des polygones de Thiessen. La pluviométrie annuelle se situe entre 600 mm/an dans le bassin parisien et 1 400 mm/an sur le plateau de Langres.
L’évapotranspiration potentielle (ETP) mensuelle moyenne interannuelle est décrite par les douze cartes issues des travaux d’OUDIN et al. (2005). Nous en avons déduit les valeurs d’ETP de bassin.
2.4 Définition et modalités de calcul du débit de référence aux sites instrumentés
La variable d’intérêt est le débit mensuel minimal annuel de fréquence quinquennale sèche (ayant une probabilité 1/5 chaque année de ne pas être dépassé) (noté QMNA5). Ce descripteur renseigne sur la sévérité des étiages et intervient dans un cadre réglementaire français de gestion des eaux. Aux sites instrumentés, le QMNA5 est calculé par ajustement d’une loi de probabilité à un échantillon constitué des plus faibles débits mensuels observés pour chacune des années hydrologiques disponibles de la station hydrométrique (QMNA). Par la suite, nous utiliserons de manière préférentielle les quantiles exprimés en mm/mois pour une comparaison affranchie de l’effet de taille entre sites, d’une part, et entre variables hydrologiques et climatiques, d’autre part. La conversion en lame d’eau est obtenue en divisant le débit QMNA en m3/s par la surface en km2 et en multipliant par 2 440,8 ou 2 592 ou 2 678,4 selon le nombre de jours du mois considéré.
La zone d’étude est soumise majoritairement à un climat tempéré océanique. L’influence continentale se manifeste dans les secteurs plus accidentés du sud-est. Le régime hydrologique des cours d’eau au sens de PARDE (1955) est de ce fait pluvial avec une période d’étiage correspondant à l’été et au début de l’automne. L’année hydrologique à considérer pour l’extraction des minima mensuels QMNA est l’année civile. La figure 2 montre l’aspect fortement saisonnalisé de la variable QMNA : les valeurs échantillonnées se concentrent sur les mois d’août et de septembre (environ les deux tiers de l’échantillon). Dans la suite de l’article, la saison des étiages désigne la période juillet-octobre.
Figure 2
Proportion des valeurs QMNA extraites par mois, toutes stations confondues (%).
Proportion of QMNA values sampled by month, all the stations considered together (%).
En chaque station, nous avons testé l’ajustement de l’échantillon des valeurs non nulles de QMNA à deux lois de probabilité : la loi Log Normale, distribution privilégiée dans les services opérationnels français, et la distribution recommandée par la Théorie des Valeurs Extrêmes, la loi de Weibull. À des fins d’homogénéisation des traitements, nous avons souhaité conserver une seule loi, pour toutes les stations traitées. Pour chaque site, les paramètres ont été déterminés selon la méthode du maximum de vraisemblance. Le test du Khi 2 a ensuite été appliqué pour vérifier la qualité de l’ajustement avec un seuil α∈de signification de 10 %. Ce test a été mis en oeuvre sur 104 stations, pour lesquelles un nombre suffisant de valeurs non nulles permettait de créer au moins cinq classes contenant cinq éléments. Selon le test du Khi 2, la loi Log Normale semble la loi la plus en adéquation avec les observations; elle est acceptée dans 81 % des cas contre 74 % pour la loi de Weibull. Le nombre de stations rejetées est supérieur au risque de première espèce de 10 %. Cet écart peut s’expliquer par des échantillons non indépendants, compte tenu des dépendances amont-aval et de l’extension spatiale des phénomènes de sécheresse et de la même période de suivi. Nous utiliserons, par la suite, les quantiles obtenus par l’ajustement à une loi Log Normale. L’estimation du quantile QMNA5 est finalement obtenue à partir des fréquences corrigées des zéros le cas échéant. Les quantiles varient entre 0 et 20,2 mm/mois avec une médiane de 3,7 mm/mois.
3. Estimation des débits caractéristiques par la méthode des jaugeages épisodiques
3.1 Méthodologie
Les principes d’exploitation des jaugeages épisodiques sont énoncés dans CLAUSEN (1995), GALEA et CANALI (2005) et OBERLIN et al. (1973). Le débit caractéristique Q à un site peu jaugé est obtenu en multipliant la valeur estimée sur une longue chronique d’une station voisine multipliée par un coefficient k. Ce coefficient est établi sur des observations concomitantes. Trois méthodes de calculs peuvent être envisagées : k peut être assimilé à :1) la pente de la régression entre les débits bruts; 2) la pente de la régression entre les cumuls; ou 3) le simple rapport des moyennes des valeurs échantillonnées en simultané.
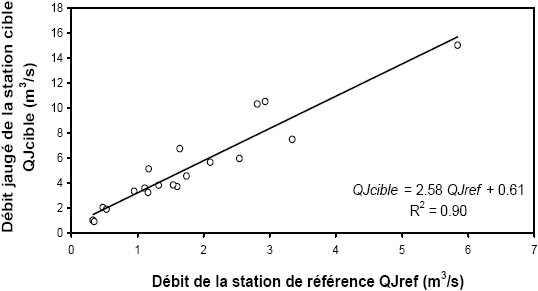
Pour illustrer cette méthode, prenons un couple de stations distantes de 11 km (site cible H0321030 l’Ource à Autricourt, S = 548 km2 – station de référence H0301010 l’Ource à Leuglay, S = 173 km2). Appliquons cette méthode avec vingt jaugeages effectués sur deux ans (Figure 3). La moyenne de l’échantillon des vingt débits de la station d’appui est égale à 1,69 m3/s et celle des débits du site cible égale à 4,97 m3/s. Sur cet exemple, les trois valeurs possibles de k sont 2,58 sur la base des débits bruts (Figure 4-a), 3,20 sur la base des débits cumulés (Figure 4‑b) et 2,94 selon le rapport des moyennes des échantillons. Connaissant QMNA5 à la station H0301010 (0,116 m3/s), les estimations du QMNA5 au site cible sont respectivement : 0,299, 0,370 et 0,340 m3/s. La valeur attendue, estimée selon la loi Log Normale ajustée au site cible, est égale à 0,409 m3/s. Pour ce cas, l’erreur d’estimation la plus petite est obtenue en exploitant les débits cumulés et la régression entre débits bruts semble la moins performante. Cependant, ce classement ne peut être généralisé. Une analyse globale est nécessaire pour établir des conclusions sur la stratégie de mesure et sur l’exploitation optimale des jaugeages épisodiques en contrôlant les paramètres qui régissent la méthode. Plusieurs éléments conditionnent l’efficience de la méthode : le mode de calcul de k, le nombre de valeurs M, la période de jaugeage à privilégier dans l’année et le « degré de similitude » entre les deux bassins définis par le couple de stations. Cette similitude renvoie à la notion de distance hydrologique entre bassins. Elle est évaluée ici au travers d’une distance dans le plan horizontal et du rapport des surfaces drainées. Compte tenu de la structure en réseau, nous pouvons distinguer deux types de distance :
la distance à parcourir le long du cours d’eau (elle existe si et seulement si les deux stations ont une liaison amont-aval directe);
la distance euclidienne entre les centres de gravité de leur bassin versant.
Figure 3
Chroniques de débits sur les deux années concomitantes 1986 et 1987 pour le couple de stations de l’Ource. Les valeurs concomitantes exploitées sont identifiées par des points.
Times series for the two concomitant years 1986 and 1987 for the pair of stations along the Ource River. The synchronous discharge measurements are identified by dots.
Figure 4
Estimation du rapport k à partir des débits bruts (a) et débits cumulés (b).
Estimation of the scale coefficient k from the regression equation between the synchronous discharge measurements (a) and between the sums of the synchronous discharge measurements (b).
(a)
(b)
Évaluer l’efficience de la méthode, préciser les incertitudes pesant sur les estimations et déterminer les conditions optimales de son usage ne sont possibles que dans un environnement contrôlé où nous pouvons agir sur les paramètres et où nous connaissons les valeurs de référence. Ces analyses sont utiles en condition opérationnelle pour mesurer les incertitudes autour des valeurs déduites des jaugeages épisodiques. Elles s’appuient sur le jeu de 133 stations pour lesquelles nous disposons du QMNA5. À tour de rôle, chaque station est considérée comme site peu jaugé et toutes les stations voisines dans un rayon de 100 km sont exploitées une fois en tant que station d’appui.
Pour chaque couple, cent échantillons de M jaugeages volants (M = 5, 15, 75, 150) sont créés par tirage aléatoire dans l’année ou la saison d’étiage. Le débit jaugé résulte en pratique d’une mesure à un instant t de la journée. Dans le cadre de nos analyses, nous l’assimilons à une valeur moyenne journalière QJ. Les débits jaugés sont choisis de façon aléatoire dans les chroniques de QJ avec pour contrainte la connaissance simultanée des débits journaliers aux deux stations. Les trois modes de calcul de k fournissent trois estimations du QMNA5 pour chaque échantillon. QMNA5 est fixé à zéro lorsque k est négatif (configuration possible lorsque la pente est calculée sur les débits bruts).
3.2 Sensibilité à la stratégie de mesure
L’analyse porte sur 3 612 couples de stations distantes de moins de 100 km selon la distance euclidienne. Nous privilégions cette mesure car les paires formées sont en plus grand nombre que celles pour lesquelles le calcul d’une distance le long du linéaire est possible (de l’ordre de 160).
La qualité de l’évaluation est mesurée par l’écart entre valeurs théoriques et estimées exprimées en mm/mois en chaque station. Nous retenons les valeurs minimales ErrMin, maximales ErrMax, la médiane Err50 et les premiers et derniers déciles Err10 et Err90 des erreurs toutes stations confondues.
Les tableaux 1 à 3 montrent de manière quasi systématique des erreurs Err90 et de ErrMax plus faibles lorsque les jaugeages se concentrent pendant la saison d’étiage. Le mode d’échantillonnage n’impacte pas la médiane Err50. La valeur estimée ne pouvant être inférieure à zéro, la valeur absolue de ErrMin est bornée par le maximum des QMNA5 observés (20,2 mm/mois). Le fait qu’un jaugeage sur la période des étiages soit plus efficace n’est guère surprenant. L’estimation repose implicitement sur un comportement identique au droit des deux points d’observation à un facteur d’échelle près, et donc, sur une forte corrélation temporelle des débits. En considérant l’année entière, nous piégeons éventuellement des valeurs relatives aux crues sur un des deux sites et la composante souterraine est noyée dans les processus multiples de génération des écoulements. La collecte des jaugeages en période des étiages permet d’isoler la composante « écoulement de base » qui conditionne principalement la variabilité spatiale du QMNA5.
Tableau 1
Erreurs de reconstitution du QMNA5 avec k obtenu par régression sur les valeurs brutes (statistiques exprimées en mm/mois).
Errors on QMNA5 estimates with k deduced from the regression analysis on discharge values (in mm/month).
Stratégie de jaugeage |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|
|---|---|---|---|---|---|---|
Nombre total de jaugeages (M) |
Période d’échantillonnage |
|||||
5 |
Année |
‑20,2 |
‑6,9 |
‑0,7 |
7,4 |
1140,7 |
|
Saison d’étiage |
‑20,2 |
‑6,7 |
‑1,1 |
4,5 |
609,9 |
15 |
Année |
‑20,2 |
‑6,8 |
‑0,6 |
7,3 |
226,6 |
|
Saison d’étiage |
‑20,2 |
‑6,5 |
‑1,1 |
4,0 |
234,2 |
75 |
Année |
‑20,1 |
‑6,8 |
‑0,6 |
7,2 |
109,4 |
|
Saison d’étiage |
‑20,1 |
‑6,6 |
‑1,1 |
4,1 |
86,6 |
150 |
Année |
‑20,0 |
‑6,8 |
‑0,6 |
7,1 |
88,8 |
|
Saison d’étiage |
‑20,0 |
‑6,7 |
‑1,1 |
4,0 |
98,6 |
Tableau 2
Erreurs de reconstitution du QMNA5 avec k obtenu par régression sur les valeurs cumulées (statistiques exprimées en mm/mois).
Errors on QMNA5 estimates with k deduced from the regression analysis on cumulative discharge values (in mm/month).
Stratégie de jaugeage |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|
|---|---|---|---|---|---|---|
Nombre total de jaugeages (M) |
Période d’échantillonnage |
|||||
5 |
Année |
‑19,6 |
‑4,5 |
0,0 |
4,6 |
117,0 |
|
Saison d’étiage |
‑19,5 |
‑3,3 |
0,0 |
2,4 |
113,4 |
15 |
Année |
‑19,1 |
‑4,6 |
0,0 |
4,7 |
49,2 |
|
Saison d’étiage |
‑18,3 |
‑3,5 |
0,0 |
2,3 |
42,3 |
75 |
Année |
‑18,4 |
‑4,6 |
0,0 |
4,8 |
33,8 |
|
Saison d’étiage |
‑16,8 |
‑3,5 |
0,0 |
2,2 |
17,6 |
150 |
Année |
‑18,1 |
‑4,6 |
0,0 |
4,9 |
29,9 |
|
Saison d’étiage |
‑16,5 |
‑3,5 |
0,0 |
2,2 |
15,4 |
Tableau 3
Erreurs de reconstitution du QMNA5 avec k obtenu par rapport des moyennes des valeurs brutes (statistiques exprimées en mm/mois).
Errors on QMNA5 estimates with k deduced from the ratio of the mean of the discharge values (in mm/month).
Stratégie de jaugeage |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|
|---|---|---|---|---|---|---|
Nombre total de jaugeages (M) |
Période d’échantillonnage |
|||||
5 |
Année |
‑19,4 |
‑4,4 |
0,0 |
4,5 |
101,3 |
|
Saison d’étiage |
‑19,0 |
‑3,3 |
0,0 |
2,4 |
81,9 |
15 |
Année |
‑18,7 |
‑4,5 |
0,0 |
4,7 |
48,1 |
|
Saison d’étiage |
‑17,4 |
‑3,4 |
0,0 |
2,3 |
32,0 |
75 |
Année |
‑18,3 |
‑4,6 |
0,0 |
4,8 |
32,6 |
|
Saison d’étiage |
‑16,6 |
‑3,5 |
0,0 |
2,2 |
15,5 |
150 |
Année |
‑17,9 |
‑4,6 |
0,0 |
4,8 |
29,3 |
|
Saison d’étiage |
‑16,5 |
‑3,5 |
0,0 |
2,2 |
14,1 |
Les meilleurs résultats sont obtenus en calculant k selon le rapport des moyennes. La méthode exploitant la régression sur les débits cumulés a une performance très légèrement inférieure. Celle utilisant les débits bruts présente un biais en moyenne et propose des valeurs hors normes. Le classement se justifie principalement sur la configuration la plus critique, avec M = 5 jaugeages.
Une tendance à la diminution des erreurs avec M est perceptible. La procédure est malgré tout peu sensible à M. Elle l’est, pour l’essentiel, sur Err90 et ErrMax. Au delà de 75 jaugeages, les statistiques semblent ne plus évoluer. Pour M < 75, la précision moyenne des estimations reste correcte mais le risque d’un biais important n’est pas exclu.
3.3 Sensibilité au choix de la station d’appui
Nous cherchons à connaître l’erreur de reconstitution selon les paramètres : distance (D) et rapport des surfaces (RS) entre bassins. Nous adoptons la convention suivante :
où Scible et Sref sont respectivement les surfaces drainées par le site cible et la station de référence, donc RS ≥ 1. La qualité des estimations est mesurée par l’erreur quadratique moyenne calculée sur les cent jeux de M jaugeages i, i = 1,…100 :
avec QMNA5obs la valeur observée et QMNA5estim (i) la valeur estimée pour la simulation i.
Les couples formés ne rendent pas compte de toutes les configurations possibles. Il n’est pas possible d’établir une relation continue entre ErrQ, Rs et D. L’échantillon a donc été scindé en deux classes selon le ratio (Rs < 10 et Rs ≥ 10) et une fonction simple a été ajustée sur les deux sous échantillons :
Cette formulation est cohérente avec le comportement attendu (pour une distance nulle, l’écart quadratique est nul) et simple (un seul paramètre à ajuster). Nous avons testé les configurations à M = 5, 15 et 75 jaugeages.
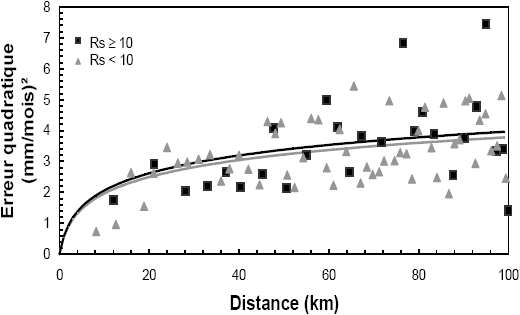
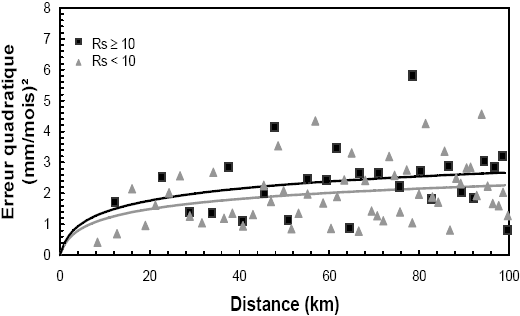
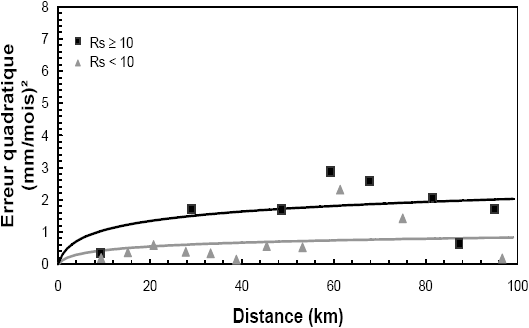
Pour chaque sous-échantillon (Rs < 10 et Rs ≥ 10) de NRs représentants, nous avons regroupé les couples ordonnés selon la distance croissante, P par P, P étant la racine carrée de NRs. Nous avons ensuite calculé la médiane des erreurs quadratiques et la distance moyenne par groupe. La figure 5 représente cette médiane en fonction de la distance euclidienne moyenne avec M = 5 et M = 75. Les courbes ajustées sont peu sensibles à Rs, en particulier pour le cas de 5 jaugeages. Le modèle (3) ajusté traduit une tendance observée : l’incertitude croit avec la distance, malgré une forte dispersion du nuage de points. La même analyse a été réalisée en considérant les distances le long du linéaire sur un nombre plus restreint de couples de stations (Figure 6). Nous obtenons les mêmes tendances avec cette fois un nuage moins dispersé. Cette impression peut être due à un nombre faible de couples.
Figure 5
Abaque des erreurs quadratiques en fonction des distances euclidiennes pour 5 jaugeages (a) et pour 75 jaugeages (b) pendant la saison des étiages.
Relation between the squared errors and the Euclidian distance for with 5 synchronous discharges (a) and 75 synchronous (b) discharges during the low flow season.
(a)
(b)
Figure 6
Abaque des erreurs quadratiques en fonction des distances linéaires pour 5 jaugeages (a) et pour 75 jaugeages (b) pendant la saison des étiages.
Relation between the squared errors and the distance along the river network for with 5 synchronous discharges (a) and 75 synchronous discharges (b) during the low flow season.
(a)
(b)
Le tableau 4 présente le paramètre α ajusté pour chaque configuration. α diminue et donc les erreurs sont globalement plus faibles lorsque M augmente. La valeur de α tend à se stabiliser à partir de 75 jaugeages. Pour un même nombre de jaugeages et une même distance, il est préférable de s’appuyer sur une station d’appui de surface équivalente à celle drainée en amont du site cible (Rs < 10). Pour une même valeur de distance, l’erreur d’estimation avec la distance le long du linéaire est inférieure à celle obtenue avec la distance euclidienne. En effet, la corrélation entre deux points sur le même linéaire est plus forte que entre deux points séparés de la même distance sur des tronçons indépendants, le point en amont contribuant aux écoulements en aval (GOTTSCHALK, 1992).
Tableau 4
Sensibilité du paramètre α à la stratégie de jaugeage.
Sensitivity of the parameter α to the sporadic measurement data collection.
Nombre total de jaugeages (M) |
Distance euclidienne entre centres de gravité |
Distance le long du linéaire |
||
|---|---|---|---|---|
α pour Rs <10 |
α pour Rs ≥10 |
α pour Rs <10 |
α pour Rs ≥10 |
|
5 |
0,82 |
0,86 |
0,28 |
0,62 |
15 |
0,59 |
0,67 |
0,21 |
0,46 |
75 |
0,49 |
0,58 |
0,18 |
0,44 |
150 |
0,48 |
0,56 |
0,18 |
0,44 |
3.4 Recommandations opérationnelles pour l’exploitation des jaugeages volants
La méthode des jaugeages épisodiques fournit globalement de bons résultats. Cependant, de manière exceptionnelle, elle peut proposer des valeurs hors normes lorsque le nombre de jaugeages volant est réduit.
La meilleure stratégie à adopter est d’utiliser une station de référence en amont ou en aval du site cible, sinon la plus proche possible et de préférence ayant une superficie de bassin versant équivalente, les jaugeages devant être réalisés plutôt en période estivale et le rapport k estimé par le rapport des moyennes. Il est difficile d’apporter un jugement objectif sur le nombre de jaugeages optimal compte tenu de la faible sensibilité à ce paramètre. Dans la suite du document, les calculs seront obtenus avec différents nombres de jaugeages volants.
Les conclusions énoncées sont propres au contexte climatique (le bassin Seine-Normandie) et à l’objectif recherché (la description des étiages). Elles pourraient être remises en cause dans un autre secteur ou/et si les débits de référence recherchés sont relatifs aux moyennes ou hautes eaux. Une analyse de sensibilité identique à celle proposée pour ce cas d’étude est vivement recommandée avant tout usage des jaugeages épisodiques.
4. Analyse comparative de méthodes d’estimation
Cette section a pour objectif de comparer les résultats obtenus par la méthode des jaugeages épisodiques à ceux issus des trois modes d’estimation : régression et deux variantes du krigeage. La technique employée pour évaluer leur efficience relative est la validation croisée. Chaque station est considérée partiellement jaugée; nous y estimons le QMNA5 selon les quatre méthodes, les écarts à la valeur issue des ajustements et finalement les valeurs ErrMin, ErrMax, Err50, Err10 et Err90 sur l’ensemble des données, toutes stations confondues.
4.1 La régression
La formule empirique est établie par régression linéaire sur les données exprimées en mm/mois. L’altitude moyenne, les données climatiques d’ETP et de précipitations (mensuelles de juillet à octobre, saisonnières et annuelles) sont des variables explicatives potentielles, la surface n’est pas retenue du fait de la conversion préalable des débits en lame d’eau. Plusieurs modèles ont été testés sur le jeu de 133 stations. Ceux dont les variables sont statistiquement significatives selon le test de Student appliqué aux coefficients de pondération ont été conservés. Les quatre modèles les plus performants sont :
ETPBA, ETPBJ-S et ETPBA-O sont respectivement la moyenne interannuelle de l’ETP de bassin, calculée sur le mois d’août, sur la période de juillet à septembre et sur la période d’août à octobre. PBJ représente la pluie moyenne de bassin de juillet et PBS celle de septembre. R désigne le coefficient de corrélation.
Les trois premières relations sont en accord avec le comportement physique attendu, à savoir que le débit et l’évapotranspiration varient en sens opposé; c’est moins le cas pour la relation (7). La variable la plus pertinente est une donnée d’ETP. Ceci est en contradiction avec la synthèse proposée par TALLAKSEN et VAN LANEN (2004), qui concluent à la prévalence des variables pluviométriques dans les formules en crue et en étiage. L’absence des précipitations dans la relation retenue pourrait être due au régime pluviométrique peu différencié et au relief peu accentué. Nous conservons finalement la relation (6), celle dont le coefficient de détermination est le plus élevé. En validation croisée, seule la variable ETPBA est exploitée.
4.2 Les méthodes géostatistiques
Les techniques de krigeage sont des interpolateurs linéaires. La valeur z* de la variable z recherchée au point x0 est donnée par :
où z(xi),i= 1,…,N sont les observations des N stations disponibles sur le domaine et λi leurs poids relatifs. Les méthodes de krigeage se différencient par la manière dont les pondérations sont calculés. Deux variantes sont testées. Nous supposons, dans un premier temps, que les variables de débit sont stationnaires dans l’espace. Le système d’équations linéaires à (N+1) inconnues à résoudre est celui du krigeage ordinaire :
µ est une inconnue supplémentaire (un « multiplicateur de Lagrange » au sens mathématique). di,j désigne la distance entre les points i et j et γ le variogramme théorique ajusté.
La seconde variante appliquée ‑ le krigeage des résidus ‑ s’apparente au krigeage à dérive externe. Elle suppose qu’un facteur explique la variabilité spatiale perçue dans les données. Cette méthode consiste à isoler la composante déterministe dans la variable étudiée par ajustement d’une formule empirique. Le résidu ε est la composante stochastique qui est interpolée par krigeage selon (9). Il reste à sommer le résidu interpolé et l’estimation issue de la formule empirique pour en déduire la valeur recherchée (BENICHOU et LE BRETON, 1987; FAULKNER et PRUDHOMME, 1998; SAUQUET et al., 2000).
La distance choisie di,j est la distance euclidienne entre les centres de gravité de leur bassin versant dans les deux variantes.
Pour chaque station exclue lors de la validation croisée, la composante déterministe est fournie par régression linéaire entre QMNA5 et ETPBA, et les variogrammes empiriques pour le résidu et le QMNA5 sont calculés sur les N-1 stations restantes. La figure 7 montre la stabilité des 133 variogrammes empiriques et la pertinence du modèle théorique ajusté, quelle que soit la station exclue du jeu de données. Le modèle exponentiel a été ajusté aux variogrammes empiriques :
avec a = 30 km, C = 14 mm2/mois2 et C0 = 0 pour z = QMNA5 et a = 25 km, C = 12 mm2/mois2 et C0 = 0 pour z = ε. Les paramètres du variogramme sont proches du fait d’une régression peu efficace.
Figure 7
Variogrammes théoriques (en noir) et empiriques (en gris) descriptifs des deux variables étudiées.
Empirical and theoretical variograms (respectively in grey and in black) for the two regionalized variables.
(a)
QMNA5
(b)
Résidu ε
4.3 La méthode des jaugeages épisodiques dans une configuration optimale
Nous reprenons la procédure d’exploitation des jaugeages volants mais cette fois avec les options optimales en ce qui concerne le choix de station et de calcul de k. Pour chaque site cible, au maximum quatre stations voisines sont identifiées. Ces stations doivent présenter au moins 15 années de données concomitantes avec le site cible et un débit de référence non nul. Nous repérons les stations aval et amont, si elles existent, et les deux stations les plus proches selon la distance euclidienne. Finalement, la station de référence choisie est celle qui, selon nos abaques, occasionne a priori les incertitudes les plus faibles. Nous réalisons une estimation avec des nombres de jaugeage différents pendant la période juillet-octobre (M = 5, 15 et 75). Les statistiques sont obtenues sur cent jeux de mesures, comme précédemment. La valeur est ramenée à zéro lorsque la procédure propose un débit négatif.
4.4 Résultats
Les quatre méthodes appliquées ne présentent pas de biais particulier : les médianes sont proches de zéro (Tableau 5; Figure 8).
Tableau 5
Statistiques issues de la validation croisée pour les trois approches régionales et la méthode des jaugeages épisodiques (en mm/mois).
Summary statistics derived from the cross validation for the three regional procedures and the method using sporadic measurement data (in mm/month).
Méthode |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|---|---|---|---|---|---|
Régression |
‑10,8 |
‑4,9 |
0,6 |
3,7 |
8,5 |
Krigeage du QMNA5 |
‑10,8 |
‑2,9 |
‑0,3 |
3,5 |
9,5 |
Krigeage des résidus |
‑9,9 |
‑3,1 |
0,2 |
3,5 |
9,2 |
Jaugeages épisodiques (5 valeurs) |
‑9,3 |
‑1,8 |
0,1 |
2,0 |
27,6 |
Jaugeages épisodiques (15 valeurs) |
‑8,9 |
‑1,9 |
0,0 |
1,9 |
14,4 |
Jaugeages épisodiques (75 valeurs) |
‑8,8 |
‑1,9 |
0,0 |
1,8 |
9,5 |
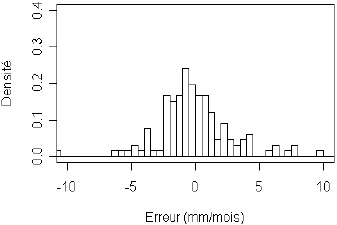
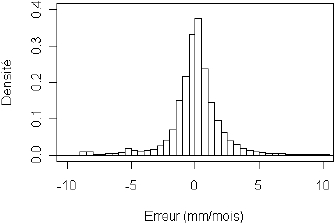
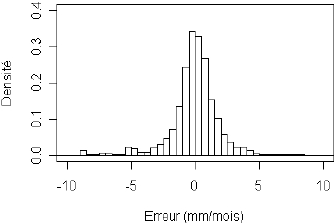
Figure 8
Erreurs de reconstitution du QMNA5 selon les trois approches régionales et la méthode des jaugeages épisodiques obtenues par validation croisée.
Errors on QMNA5 estimates for the three regional procedures and the method using sporadic measurement data derived from the cross validation.
(a)
Régression
(b)
Krigeage appliqué au QMNA5
(c)
Krigeage des résidus
(d)
Jaugeages épisodiques (5 valeurs)
(e)
Jaugeages épisodiques (15 valeurs)
(f)
Jaugeages épisodiques (75 valeurs)
Les erreurs d’estimation de la méthode des jaugeages épisodiques dans la configuration optimale sont fort heureusement plus faibles que celles observées lorsque le choix de la station d’appui n’est pas contraint (par comparaison aux statistiques du tableau 3). Comme précédemment, nous notons une faible sensibilité de la méthode des jaugeages épisodiques au nombre de jaugeages M. Une différence significative apparaît seulement sur la valeur maximale des erreurs. Plus M est élevé, plus les résultats sont stables et plus le risque d’erreur forte est faible.
La régression est peu fiable pour une estimation en site non jaugé. Nous observons peu de différence entre les deux méthodes de krigeage; ceci en raison du faible pouvoir explicatif de la relation reliant le QMNA5 à l’ETPBA. La méthode des jaugeages épisodiques est de loin la plus performante, même lorsque M est faible : dans 80 % des cas l’erreur d’estimation est inférieure à 1,9 mm/mois contre presque le double pour les autres méthodes régionales.
Nous pouvons conclure que l’information locale même minime s’avère plus efficace qu’une approche purement régionale. Du point de vue opérationnel, il y a un gain évident à procéder à quelques mesures pour compléter une information extraite d’un réseau de stations hydrométriques sur les sites sensibles où la connaissance précise des caractéristiques d’étiage est souhaitée.
5. Intégration des jaugeages épisodiques dans un schéma d’interpolation
Il n’est évidemment pas envisageable de réaliser des jaugeages en tout point d’un réseau hydrographique. Notre intention est d’intégrer les valeurs obtenues par la méthode des jaugeages épisodiques avec leurs incertitudes dans un système de type krigeage, approche régionale jugée la plus performante. Notre choix s’est porté sur le Krigeage Structural Ponctuel Universel à Variogramme Connu (MEYLAN, 1986). L’algorithme KSPUVC proposé est une extension du krigeage permettant d’introduire explicitement des données incertaines sous réserve de connaître la variance de l’erreur. Le principe d’estimateur linéaire optimal sans biais est conservé. Dans l’hypothèse de stationnarité, le système à résoudre fait apparaître des nouveaux termes, σi2, les variances des erreurs aux points i où la mesure est incertaine :
où di,j désigne la distance entre les points i et j et γ le variogramme théorique ajusté sur les données sans erreurs.
Lorsque σi2 est nul en tout point i, nous retrouvons la formulation classique du krigeage intrinsèque d’ordre 0. L’estimation est autorisée à s’éloigner de la valeur incertaine aux points i où σi2 > 0. L’écart est conditionné par l’incertitude locale σi2 et la proximité aux autres stations via le modèle de variogramme ajusté.
MERZ et BLÖSCHL (2004) ont appliqué avec succès cette approche aux quantiles de crue calculés sur des séries temporelles courtes. σi2 était alors déterminé par simulation de Monte-Carlo et rendait compte des fluctuations d’échantillonnage. Dans notre cas, ce sont les abaques écarts quadratiques ErrQ versus (M, D et Rs) qui fixent la variance σi2.
Il reste à mesurer le poids de chaque type d’information et l’efficience du couplage ainsi réalisé. Ceci est réalisé par validation croisée. Pour chaque station exclue i, nous supposerons que les données des autres stations j sont sans erreur (σj = 0, j ≠ i). La procédure est engagée sur le même échantillon de couples de stations que précédemment et les mêmes cent jeux de mesures.
L’estimation finale de KSPUVC s’éloigne peu de la valeur proposée par la méthode des jaugeages épisodiques (Tableau 5 versus Tableau 6). Ce résultat est certainement dû à la variance de l’erreur σi2 ‑ au maximum 3 (mm/mois)2 ‑ bien inférieure au palier du variogramme (14 (mm/mois)2). Nous obtenons donc de meilleurs résultats que ceux issus du krigeage de la variable brute ou du krigeage des résidus. Une performance légèrement supérieure à celle de la méthode des jaugeages épisodiques est perceptible sur ErrMax dans les configurations à 5 jaugeages. L’information régionale vient modérer les valeurs fortes proposées initialement par la méthode des jaugeages épisodiques (cf. ErrMax des tableaux 5 et 6) et donc réduire la plage de variation possible des débits estimés.
Tableau 6
Résultats de validation croisée pour l’estimation du QMNA5 selon KSPUVC (en mm/mois).
Summary statistics derived from the cross validation for the KSPUVC method (in mm/month).
Nombre de jaugeages (M) |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|---|---|---|---|---|---|
5 |
‑8,7 |
‑2,0 |
0,1 |
2,0 |
22,7 |
15 |
‑8,6 |
‑2,1 |
0,1 |
1,9 |
13,2 |
75 |
‑8,6 |
‑2,1 |
0,1 |
1,9 |
9,1 |
6. Conclusion
La méthode des jaugeages épisodiques permet d’estimer le QMNA5 en des sites faiblement jaugés de manière efficace. Nous avons proposé un cadre général d’analyse qui permet d’optimiser les paramètres de cette méthode sur les sites de mesure. L’étude de cas sur le bassin Seine-Normandie montre qu’il est préférable de réaliser les jaugeages volants pendant la période d’étiage et d’assimiler le coefficient k au rapport des moyennes des mesures synchrones aux deux sites. La méthode semble peu sensible au nombre de jaugeages. Les approches purement régionales sont moins performantes. Parmi elles, les interpolations à base de géostatistique apparaissent comme les plus efficaces.
Le couplage entre la méthode des jaugeages épisodiques et une technique de krigeage au travers du Krigeage Structural Ponctuel Universel à Variogramme Connu (KSPUVC) permet d’obtenir des estimations en des sites non jaugés à partir de données réputées sans erreur et d’autres plus incertaines. Appliqué au QMNA5, l’assemblage ainsi réalisé améliore significativement les résultats obtenus par krigeage appliqué dans sa formulation classique.
Les développements et analyses décrits sont applicables à d’autres variables caractéristiques. Il est cependant nécessaire de procéder à une analyse de sensibilité qui permet d’optimiser localement la méthode des jaugeages épisodiques avant d’appliquer le KSPUVC pour une cartographie exhaustive. Un gain d’efficience sera perceptible si l’incertitude autour des estimations issues des jaugeages volants est plus faible que le palier du variogramme théorique ajusté.
Parties annexes
Remerciements
Les auteurs tiennent à remercier l’Agence de l’Eau Seine- Normandie pour la mise à disposition des données nécessaires à cette étude, les gestionnaires des stations hydrométriques pour leur aide dans la sélection des chroniques de débits et M.H. Ramos pour ses suggestions lors de la rédaction de cet article. Cet article est également une contribution au projet VARIFLUX soutenu par le programme ECCO/CNRS.
Références bibliographiques
- BENICHOU P. et O. LE BRETON (1987). Prise en compte de la topographie pour la cartographie des champs pluviométriques statistiques. Météorol., 19, 23‑34.
- CLAUSEN B. (1995) Discharge data collection and analysis strategies in low flow studies. Nord. Hydrol., 26, 191-204.
- FAULKNER D.S. et C. PRUDHOMME (1998). Mapping an index of extreme rainfall across the UK. HESS, 2, 183‑194.
- GALEA G. et S. CANALI (2005). Régionalisation des modules annuels et des régimes d’étiage du bassin hydrographique de la Moselle française : lien entre modèles régionaux. Rev. Sci. Eau, 18, 331-352.
- GOTTSCHALK L. (1992). Correlation and covariance of runoff. Stochastic Hydrol. Hydraulics, 7, 85-101.
- HORTNESS J.E. (2006). Estimating low-flow frequency statistics for unregulated streams in Idaho. U.S. Geological Survey Scientific Investigations Report 2006-5035, 31 p.
- LACEY G.C. et R.B. GRAYSON (1997). Relating baseflow to catchment properties in south-eastern Australia. J. Hydrol., 204, 231-250.
- MATHERON G. (1965). Les variables régionalisées et leur estimation. Une application de la théorie des fonctions aléatoires aux sciences de la nature. Masson (Éditeurs), Paris, France, 306 p.
- MERZ R. et G. BLOSCHL (2004). Flood frequency regionalisation - spatial proximity vs. catchment attributes. J. Hydrol., 302, 283-306.
- MEYLAN P. (1986). Régionalisation de données entachées d’erreurs de mesure par krigeage structural - Application à la pluviométrie. Hydrol. Continent., 1, 25-34
- OBERLIN G., G.C. GALEA et J.T. TONI (1973). Intérêt des jaugeages épisodiques pour l’estimation des étiages de petits bassins non équipés. Cahiers de l’ORSTOM, série Hydrologie, X, 349-368.
- OUDIN L., F. HERVIEU, C. MICHEL, C. PERRIN, V. ANDREASSIAN, F. ANCTIL et C. LOUMAGNE (2005). Which potential evapotranspiration input for a lumped rainfall-runoff model? Part 2 Towards a simple and efficient potential evapotranspiration model for rainfall-runoff modelling. J. Hydrol., 303, 290-306.
- PARDE M. (1955). Fleuves et rivières. Collection Armand Colin, Paris, France, 224 p.
- RIES K.G. et FRIESZ P.J. (2000) Methods for estimating low-flow statistics for Massachusetts streams. U.S. Geological Survey Water-Resources Investigations Report 00-4135, 81 p.
- SAUQUET E., I. KRASOVSKAÏA et E. LEBLOIS (2000). Mapping mean monthly runoff pattern using EOF analysis. HESS, 4, 79-93.
- SAUQUET E. (2006) Mapping mean annual river discharges: geostatistical developments for incorporating river network dependencies. J. Hydrol., 331, 300-314.
- TALLAKSEN L.M. et H.A.J. VAN LANEN (2004) Hydrological drought: processes and estimation methods for streamflow and groundwater. Developments in water science, Elsevier (Éditeurs), Amsterdam, Pays‑Bas, 48, 579 p.
Liste des figures
Figure 1
Réseau hydrographique principal (—) et stations de référence (•).
Mean river network (—) and location of the gauging stations (•).
Figure 2
Proportion des valeurs QMNA extraites par mois, toutes stations confondues (%).
Proportion of QMNA values sampled by month, all the stations considered together (%).
Figure 3
Chroniques de débits sur les deux années concomitantes 1986 et 1987 pour le couple de stations de l’Ource. Les valeurs concomitantes exploitées sont identifiées par des points.
Times series for the two concomitant years 1986 and 1987 for the pair of stations along the Ource River. The synchronous discharge measurements are identified by dots.
Figure 4
Estimation du rapport k à partir des débits bruts (a) et débits cumulés (b).
Estimation of the scale coefficient k from the regression equation between the synchronous discharge measurements (a) and between the sums of the synchronous discharge measurements (b).
(a)
(b)
Figure 5
Abaque des erreurs quadratiques en fonction des distances euclidiennes pour 5 jaugeages (a) et pour 75 jaugeages (b) pendant la saison des étiages.
Relation between the squared errors and the Euclidian distance for with 5 synchronous discharges (a) and 75 synchronous (b) discharges during the low flow season.
(a)
(b)
Figure 6
Abaque des erreurs quadratiques en fonction des distances linéaires pour 5 jaugeages (a) et pour 75 jaugeages (b) pendant la saison des étiages.
Relation between the squared errors and the distance along the river network for with 5 synchronous discharges (a) and 75 synchronous discharges (b) during the low flow season.
(a)
(b)
Figure 7
Variogrammes théoriques (en noir) et empiriques (en gris) descriptifs des deux variables étudiées.
Empirical and theoretical variograms (respectively in grey and in black) for the two regionalized variables.
(a)
QMNA5
(b)
Résidu ε
Figure 8
Erreurs de reconstitution du QMNA5 selon les trois approches régionales et la méthode des jaugeages épisodiques obtenues par validation croisée.
Errors on QMNA5 estimates for the three regional procedures and the method using sporadic measurement data derived from the cross validation.
(a)
Régression
(b)
Krigeage appliqué au QMNA5
(c)
Krigeage des résidus
(d)
Jaugeages épisodiques (5 valeurs)
(e)
Jaugeages épisodiques (15 valeurs)
(f)
Jaugeages épisodiques (75 valeurs)
Liste des tableaux
Tableau 1
Erreurs de reconstitution du QMNA5 avec k obtenu par régression sur les valeurs brutes (statistiques exprimées en mm/mois).
Errors on QMNA5 estimates with k deduced from the regression analysis on discharge values (in mm/month).
Stratégie de jaugeage |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|
|---|---|---|---|---|---|---|
Nombre total de jaugeages (M) |
Période d’échantillonnage |
|||||
5 |
Année |
‑20,2 |
‑6,9 |
‑0,7 |
7,4 |
1140,7 |
|
Saison d’étiage |
‑20,2 |
‑6,7 |
‑1,1 |
4,5 |
609,9 |
15 |
Année |
‑20,2 |
‑6,8 |
‑0,6 |
7,3 |
226,6 |
|
Saison d’étiage |
‑20,2 |
‑6,5 |
‑1,1 |
4,0 |
234,2 |
75 |
Année |
‑20,1 |
‑6,8 |
‑0,6 |
7,2 |
109,4 |
|
Saison d’étiage |
‑20,1 |
‑6,6 |
‑1,1 |
4,1 |
86,6 |
150 |
Année |
‑20,0 |
‑6,8 |
‑0,6 |
7,1 |
88,8 |
|
Saison d’étiage |
‑20,0 |
‑6,7 |
‑1,1 |
4,0 |
98,6 |
Tableau 2
Erreurs de reconstitution du QMNA5 avec k obtenu par régression sur les valeurs cumulées (statistiques exprimées en mm/mois).
Errors on QMNA5 estimates with k deduced from the regression analysis on cumulative discharge values (in mm/month).
Stratégie de jaugeage |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|
|---|---|---|---|---|---|---|
Nombre total de jaugeages (M) |
Période d’échantillonnage |
|||||
5 |
Année |
‑19,6 |
‑4,5 |
0,0 |
4,6 |
117,0 |
|
Saison d’étiage |
‑19,5 |
‑3,3 |
0,0 |
2,4 |
113,4 |
15 |
Année |
‑19,1 |
‑4,6 |
0,0 |
4,7 |
49,2 |
|
Saison d’étiage |
‑18,3 |
‑3,5 |
0,0 |
2,3 |
42,3 |
75 |
Année |
‑18,4 |
‑4,6 |
0,0 |
4,8 |
33,8 |
|
Saison d’étiage |
‑16,8 |
‑3,5 |
0,0 |
2,2 |
17,6 |
150 |
Année |
‑18,1 |
‑4,6 |
0,0 |
4,9 |
29,9 |
|
Saison d’étiage |
‑16,5 |
‑3,5 |
0,0 |
2,2 |
15,4 |
Tableau 3
Erreurs de reconstitution du QMNA5 avec k obtenu par rapport des moyennes des valeurs brutes (statistiques exprimées en mm/mois).
Errors on QMNA5 estimates with k deduced from the ratio of the mean of the discharge values (in mm/month).
Stratégie de jaugeage |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|
|---|---|---|---|---|---|---|
Nombre total de jaugeages (M) |
Période d’échantillonnage |
|||||
5 |
Année |
‑19,4 |
‑4,4 |
0,0 |
4,5 |
101,3 |
|
Saison d’étiage |
‑19,0 |
‑3,3 |
0,0 |
2,4 |
81,9 |
15 |
Année |
‑18,7 |
‑4,5 |
0,0 |
4,7 |
48,1 |
|
Saison d’étiage |
‑17,4 |
‑3,4 |
0,0 |
2,3 |
32,0 |
75 |
Année |
‑18,3 |
‑4,6 |
0,0 |
4,8 |
32,6 |
|
Saison d’étiage |
‑16,6 |
‑3,5 |
0,0 |
2,2 |
15,5 |
150 |
Année |
‑17,9 |
‑4,6 |
0,0 |
4,8 |
29,3 |
|
Saison d’étiage |
‑16,5 |
‑3,5 |
0,0 |
2,2 |
14,1 |
Tableau 4
Sensibilité du paramètre α à la stratégie de jaugeage.
Sensitivity of the parameter α to the sporadic measurement data collection.
Nombre total de jaugeages (M) |
Distance euclidienne entre centres de gravité |
Distance le long du linéaire |
||
|---|---|---|---|---|
α pour Rs <10 |
α pour Rs ≥10 |
α pour Rs <10 |
α pour Rs ≥10 |
|
5 |
0,82 |
0,86 |
0,28 |
0,62 |
15 |
0,59 |
0,67 |
0,21 |
0,46 |
75 |
0,49 |
0,58 |
0,18 |
0,44 |
150 |
0,48 |
0,56 |
0,18 |
0,44 |
Tableau 5
Statistiques issues de la validation croisée pour les trois approches régionales et la méthode des jaugeages épisodiques (en mm/mois).
Summary statistics derived from the cross validation for the three regional procedures and the method using sporadic measurement data (in mm/month).
Méthode |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|---|---|---|---|---|---|
Régression |
‑10,8 |
‑4,9 |
0,6 |
3,7 |
8,5 |
Krigeage du QMNA5 |
‑10,8 |
‑2,9 |
‑0,3 |
3,5 |
9,5 |
Krigeage des résidus |
‑9,9 |
‑3,1 |
0,2 |
3,5 |
9,2 |
Jaugeages épisodiques (5 valeurs) |
‑9,3 |
‑1,8 |
0,1 |
2,0 |
27,6 |
Jaugeages épisodiques (15 valeurs) |
‑8,9 |
‑1,9 |
0,0 |
1,9 |
14,4 |
Jaugeages épisodiques (75 valeurs) |
‑8,8 |
‑1,9 |
0,0 |
1,8 |
9,5 |
Tableau 6
Résultats de validation croisée pour l’estimation du QMNA5 selon KSPUVC (en mm/mois).
Summary statistics derived from the cross validation for the KSPUVC method (in mm/month).
Nombre de jaugeages (M) |
ErrMin |
Err10 |
Err50 |
Err90 |
ErrMax |
|---|---|---|---|---|---|
5 |
‑8,7 |
‑2,0 |
0,1 |
2,0 |
22,7 |
15 |
‑8,6 |
‑2,1 |
0,1 |
1,9 |
13,2 |
75 |
‑8,6 |
‑2,1 |
0,1 |
1,9 |
9,1 |