Résumés
Résumé
Dans le présent article, on se propose d’évaluer la généralité et la robustesse du krigeage canonique, une méthode d’estimation régionale du débit, en l’appliquant pour l’estimation du débit moyen interannuel en régime hydrologique tropical et dans des conditions imparfaites de qualité et de disponibilité de données. Pour ce faire, la méthode du krigeage canonique a été appliquée au cas de Haïti dont le réseau de stations hydrométriques est très limité. Le krigeage canonique a été comparé à la régression linéaire, une méthode simple d’estimation régionale. Selon les critères de performance définis, le krigeage canonique paraît légèrement plus performant que la régression. Il produit des estimations moins biaisées (un biais relatif moyen de ‑ 13 % contre ‑ 20 % pour la régression) et des erreurs relatives légèrement moins importantes (54,4 % contre 59,6 %). Toutefois, le krigeage canonique a été moins performant pour l’estimation du débit des plus grands bassins versants, bien que ses performances globales demeurent acceptables. Par ailleurs, vu les conditions très défavorables dans lesquelles la méthode a été appliquée, il n’a pas été possible de relier la baisse dans les performances du krigeage canonique à une déficience dans la généralité de l’approche et/ou dans sa robustesse.
Mots clés:
- hydrologie,
- estimation régionale,
- régression linéaire,
- krigeage canonique,
- analyse canonique des corrélations,
- débit moyen
Abstract
The objective of this study was to test the general application and the robustness of canonical kriging, a new approach regional hydrological estimation. The evaluation of the robustness was carried out for the estimation of mean annual streamflow over the continental territory of Haiti, under a tropical climate and under non-optimal conditions of data quality and availability. The performances of canonical kriging were studied using cross validation. The results were compared to those of the linear regression between the mean annual streamflow and the watershed area applied for the same conditions. In general, canonical kriging yields slightly higher performances. It produces less biased estimates (mean relative bias of ‑ 13% against ‑ 20% for regression) with slightly less significant relative errors (54.4% against 59.6% for regression). However, the linear regression produced better estimates for the largest basins although the global performances of canonical krigeage remained acceptable. In addition, considering the very unfavourable conditions in which the method was applied, it was not possible to connect the decrease in the performances of canonical krigeage to a lack in the general application of the approach and/or its robustness.
Key words:
- hydrology,
- regional estimation,
- linear regression,
- canonical kriging,
- mean annual streamflow
Corps de l’article
1. Introduction
L’estimation des ressources hydriques est une étape primordiale pour la gestion rationnelle de l’eau. Or, estimer les ressources hydriques passe le plus souvent par l’analyse des écoulements (COSANDEY et ROBINSON, 2000). Généralement, le réseau de stations hydrométriques constitue la source principale d’information sur les débits. Toutefois, la densité et la répartition spatiale des sites d’observations hydrométriques sont rarement optimales. Dans un site donné, si on n’est pas confronté à une absence de toute observation, les données disponibles sont parfois de mauvaise qualité ou de courte durée. Pour pallier au manque d’information des sites d’intérêt, les hydrologues ont recours à des procédures d’estimation régionale (ou modèle régional) qui consistent à transférer les données d’écoulements disponibles à d’autres sites vers le site d’intérêt, où l’on ne dispose pas de suffisamment d’information.
Divers modèles régionaux ont été développés et appliqués de part le monde (BIRIKUNDAVYI et al., 1996; DURRANS et TOMIC, 1996; GREHYS, 1996; HAMZA et al., 2000; MIC et al., 2002; OUARDA et al., 1999). La plupart d’entre eux traitent des évènements extrêmes, en particulier les crues. CHOKMANI et OUARDA (2004) ont proposé une nouvelle approche d’estimation régionale qu’ils ont appliquée avec succès sur les bassins versants du Québec (Canada). Cette approche, connue sous le nom « krigeage canonique », consiste à interpoler les quantiles de crues à l’intérieur d’un espace mathématique construit à l’aide des caractéristiques physiographiques et météorologiques des bassins versants des sites jaugés. Les auteurs ont montré que cette méthode est aussi performante que les techniques conventionnelles d’estimation régionale les plus établies, telles que l’analyse canonique des corrélations (OUARDA et al., 2001). Cependant, la généralité et la robustesse de cette approche restent à démontrer. La robustesse statistique est souvent définie comme la capacité d’une méthode d’avoir de bons résultats dans une vaste gamme de situations et dans des conditions non optimales (OUARDA et ASHKAR, 1998). En effet, celle-ci a été développée et testée dans un régime hydrologique nordique et dans un contexte optimal, en présence d’une base de données exhaustive et de bonne qualité. Il serait alors intéressant de tester la généralité d’une telle approche sous un autre climat et/ou avec d’autres variables, et d’en vérifier la robustesse dans des conditions imparfaites de qualité et de disponibilité de données (séries courtes, données manquantes, faible densité spatiale, etc.).
L’objectif de la présente étude est d’évaluer la généralité et la robustesse du krigeage canonique pour l’estimation régionale des débits. Pour ce faire, le krigeage canonique sera appliqué au cas de Haïti pour l’estimation du débit moyen interannuel. Les performances de cette méthode d’estimation seront analysées et comparées à celles d’une méthode d’estimation régionale simple, à savoir la régression linéaire.
2. Méthodes d’estimation étudiées
2.1 Régression linéaire
La régression permet d’établir une relation linéaire entre la variable hydrologique (quantiles de crue, débit d’étiage, débit moyen, etc.) et une ou plusieurs variables explicatives de nature physiographique (superficie du bassin versant, couvert végétal, altitude, pente, etc.), climatique (précipitations, température, épaisseur de la neige, etc.) et/ou géomorphologique (type du sol, drainage, etc.). Ceci se base sur le fait que le ruissellement est une réponse hydrologique aux conditions climatiques et porte l’empreinte des caractéristiques physiographiques du bassin de drainage. L’estimation des paramètres du modèle régressif est effectuée à l’aide des sites jaugés pour lesquels on dispose à la fois de variables à expliquer et de variables explicatives. Par la suite, la variable hydrologique en question est estimée dans n’importe quel site non jaugé en appliquant le modèle ainsi étalonné, puisque pour ces sites, les variables explicatives sont facilement accessibles. Toutefois, les sites jaugés et non jaugés doivent appartenir à un même groupe dit hydrologiquement homogène. Cette condition d’homogénéité passe par la définition de régions hydrologiques homogènes ou par l’utilisation de la notion du voisinage hydrologique (OUARDA et al., 2001). Une région homogène pourrait être établie en regroupant des bassins versants appartenant à la même région géographique, en supposant que la proximité géographique soit garante de la similitude hydrologique (régions homogènes contiguës), ce qui n’est pas nécessairement vrai. Elle pourrait être aussi établie en rassemblant des bassins qui ne sont pas nécessairement géographiquement voisins, mais qui présentent des similarités dans leurs régimes hydrologiques en raison de leurs caractéristiques physiographiques et climatiques similaires (régions homogènes non contiguës). En revanche, la notion de voisinage se base sur la définition de régions homogènes non contiguës dynamiques : c’est-à-dire pour chaque site cible (site non jaugé), on définit une région hydrologique homogène (voisinage hydrologique) propre à ce site, constituée de sites jaugés présentant des similarités physiographiques et climatiques avec le site cible.
La régression a été fréquemment appliquée en estimation régionale des débits, en particulier sous sa forme loglinéaire (modèle de puissance). Dans ce cas, c’est le logarithme de la variable hydrologique en question qui est relié aux variables explicatives à l’aide d’une fonction linéaire. À titre d’exemple, PANDEY et NGUYEN (1999) ont appliqué la régression multiple loglinéaire pour estimer les quantiles de crues au Québec en fonction de la superficie du bassin. Ils ont comparé les performances de neuf méthodes d’estimation des paramètres de la régression. HAMZA et al. (2000) ont développé une régression loglinéaire entre les débits d’étiage et la surface des bassins versants dans une région homogène définie à l’aide d’une méthode d’invariance d’échelle. HACHÉ et al. (2002) ont estimé les quantiles de crue à différents sites non jaugés dans une même région homogène à l’aide d’une régression multiple loglinéaire entre la variable hydrologique (débits de crues) et des variables physiographiques (surface de drainage, pente du cours d’eau). Les régions hydrologiques homogènes ont été définies par l’analyse canonique des corrélations en adoptant l’approche du voisinage.
2.2 Krigeage canonique
Cette approche, développée par CHOKMANI et OUARDA (2004), utilise d’une manière explicite le concept de voisinage hydrologique. La variable hydrologique est interpolée dans l’espace physiographique en utilisant les valeurs observées aux sites jaugés hydrologiquement voisins du site d’intérêt. En effet, la variable en question peut être considérée comme étant une variable continue dans l’espace physiographique. L’espace physiographique est un espace mathématique construit à l’aide des caractéristiques physiographiques et/ou météorologiques de l’ensemble des bassins jaugés. CHOKMANI et OUARDA (2004) ont testé deux méthodes de définition de l’espace physiographique : l’analyse en composantes principales et l’analyse canonique des corrélations (ACC). Il s’est avéré que cette dernière, vu ses performances, est mieux adaptée pour cette tâche.
L’ACC est une méthode d’analyse statistique multivariée permettant de saisir la relation de dépendance entre deux séries de variables aléatoires, en l’occurrence, ici, une série de variables hydrologiques (Y) et une série de variables physiographiques (X). Elle permet de déterminer deux séries de variables canoniques W et V, constituées respectivement d’une combinaison linéaire de Y et de X. Les paramètres des combinaisons linéaires sont déterminés de façon telle que la corrélation entre une paire de V ou de W est nulle tout en maximisant la corrélation entre les V et W. Cette caractéristique permet d’utiliser l’une ou l’autre des variables canoniques comme la base orthogonale d’un espace multidimensionnel : physiographique dans le cas de V et hydrologique quand il s’agit de W. Connaissant les paramètres des combinaisons linéaires, un bassin jaugé pour lequel on dispose de variables physiographiques et de variables hydrologiques peut être localisé précisément dans l’un ou l’autre des deux espaces multidimensionnels. Pour plus d’information sur l’application de l’ACC pour l’estimation régionale des débits, se référer à OUARDA et al. (2000, 2001).
Puisque les caractéristiques physiographiques et climatiques des bassins non jaugés sont connues, il est alors possible de les positionner dans l’espace canonique physiographique/climatique. Celui-ci est défini à l’aide des deux premières variables canoniques physiographiques : V1 et V2. Il est, par conséquent possible, à la différence de l’espace géographique, d’employer une technique appropriée d’interpolation pour estimer sa valeur pour le bassin non jaugé d’intérêt. L’estimation est réalisée en utilisant sa position dans l’espace physiographique ainsi que l’information des bassins environnants pour lesquels les valeurs de la variable hydrologique sont déjà connues.
La technique d’interpolation retenue est le krigeage. Celle‑ci est une puissante technique géostatistique conçue pour étudier les variables spatialement autocorrélées (ARNAUD et EMERY, 2000). Elle permet d’estimer la valeur d’une variable à un point donné de l’espace en utilisant des mesures locales éparses. Le krigeage tient compte de la structure et de la distribution spatiales de la variable étudiée à l’aide d’une fonction de structure appelée variogramme. Cette fonction de structure est reliée à la covariance entre les points observés en fonction de la distance qui les sépare. Elle décrit l’intensité et la forme de l’autocorrélation spatiale de la variable. Le krigeage produit une estimation linéaire, non biaisée et optimale des valeurs inconnues. Ainsi, il fournit la meilleure estimation en utilisant l’information du voisinage. L’estimation est obtenue par la somme des valeurs voisines pondérées par leur degré de corrélation avec le point pour lequel l’estimation est effectuée. Les valeurs les plus proches reçoivent des poids plus élevés parce qu’elles ont plus de chance d’être semblables à la valeur inconnue. Les coefficients de pondération sont calculés en modélisant l’autocorrélation spatiale exprimée dans le variogramme observé. En effet, le variogramme expérimental (observé) ne peut pas être employé directement dans le calcul des coefficients de pondération, puisqu’il représente une mesure discrète de l’autocorrélation spatiale. Par conséquent, un modèle théorique est adapté au variogramme expérimental. Le choix du modèle est l’étape la plus cruciale et la plus difficile dans l’application du krigeage, puisque la qualité d’évaluation en dépend.
3. Cas d’étude
3.1 Contexte
Haïti fait face à un problème chronique d’approvision-nement en eau potable. D’aucuns estiment que l’eau ne manque pas dans la région. Le problème serait lié à la répartition spatiale et temporelle des ressources hydriques. L’eau souterraine est longtemps considérée comme la seule ressource susceptible d’être exploitée à des fins de consommation humaine. Afin de diminuer la pression sur la ressource d’eau souterraine et d’améliorer l’approvisionnement en eau potable, l’utilisation des eaux de surface nous paraît être la solution alternative. Cependant, la quantité disponible demeure peu connue. Pour s’assurer d’une gestion efficace de cette ressource, planifier les projets d’aménagement et en particulier d’approvisionnement en eau potable, il est nécessaire de connaître la ressource en eau de surface disponible à travers le territoire. Toutefois, le réseau de stations hydrométriques à Haïti est très limité. Certaines stations de jaugeage ont été abandonnées à cause des problèmes de budget, d’autres, emportées par les crues, n’ont jamais été remises en place. L’information hydrologique devient rare et n’est disponible que pour un nombre limité de cours d’eau. Pour une bonne estimation de la ressource, il est alors essentiel de connaître l’information hydrologique en tout point du territoire.
Par conséquent, le krigeage canonique et la régression seront appliqués au cas de Haïti pour l’estimation du débit moyen interannuel. Pour la régression, il sera question d’un modèle simple.
3.2 Région d’étude
Comme le montre la figure 1, Haïti fait partie des grandes Antilles. Elle occupe la partie ouest de l’île d’Hispaniola. Elle est comprise entre les latitudes 18° et 20° 6’ Nord et les longitudes 71° 20’ et 74° 30’ Ouest, et se trouve entièrement dans la zone tropicale. Haïti est limitée au nord par l’océan Atlantique, au sud par la mer des Caraïbes et à l’est par la République Dominicaine. Elle s’étend sur une superficie de 27 750 km2. Le pays possède un littoral marin évalué à 1 771 kilomètres (EMMANUEL et LINDSKOG, 2000).
Figure 1
Région d’étude et Modèle Numérique d’Altitude (MNA) d’Haïti (KUNZEL, 1999).
Location of the area of study and Digital Elevation Model (DEM) of Haïti (KUNZEL, 1999).
De par sa position géographique, le pays présente un climat extrêmement varié. La température, tout au long du littoral, est d’environ 27 °C avec une légère variation entre l’hiver et l’été. En montagne, la température peut osciller entre 18 et 22 ºC. La pluviométrie varie non seulement avec l’altitude mais aussi avec l’orientation des massifs par rapport aux alizés. Les pluies affichent une importante variation, allant du simple au quintuple. La façade occidentale de la péninsule du Nord est la région la moins arrosée avec, respectivement, 524 et 910 mm/an aux Gonaïves et à Saint-Marc. Inversement, certaines zones du Plateau central et la région des Cayes dans la péninsule du Sud reçoivent plus de 2 000 mm : 2 660 mm à Mirebalais, 2 107 mm/an aux Cayes. Cap-Haïtien et la Plaine du Nord affichent une pluviométrie intermédiaire d’environ 1 600 mm/an. À Port-au-Prince et à Pétion-Ville, la pluviométrie est, respectivement, de 1 437 mm/an et 1 326 mm/an. Jérémie et Jacmel (la dorsale méridionale) reçoivent environ 1 200 mm. La moyenne pluviométrique sur tout le territoire de Haïti est de 1 452 mm. Celle-ci a été estimée par interpolation (krigeage) des moyennes annuelles observées au niveau de 86 stations météorologiques (JOSEPH, 2005).
Le relief du pays est très accidenté et correspond à une topographie caractérisée par des plissements structuraux et synclinaux (Figure 1). Cinq chaînes de montagne couvrent 75 % de l’étendue du territoire. Le plus haut sommet (Massif de la Selle au sud-ouest) culmine à une élévation de 2 689 mètres. Le 1/3 restant est constitué de plaines. Les pentes varient de 0 à plus de 40 % (MDE, 1998). Cette topographie explique en grande partie la distribution de la précipitation à travers le territoire et influence le régime d’écoulement.
3.3 Données
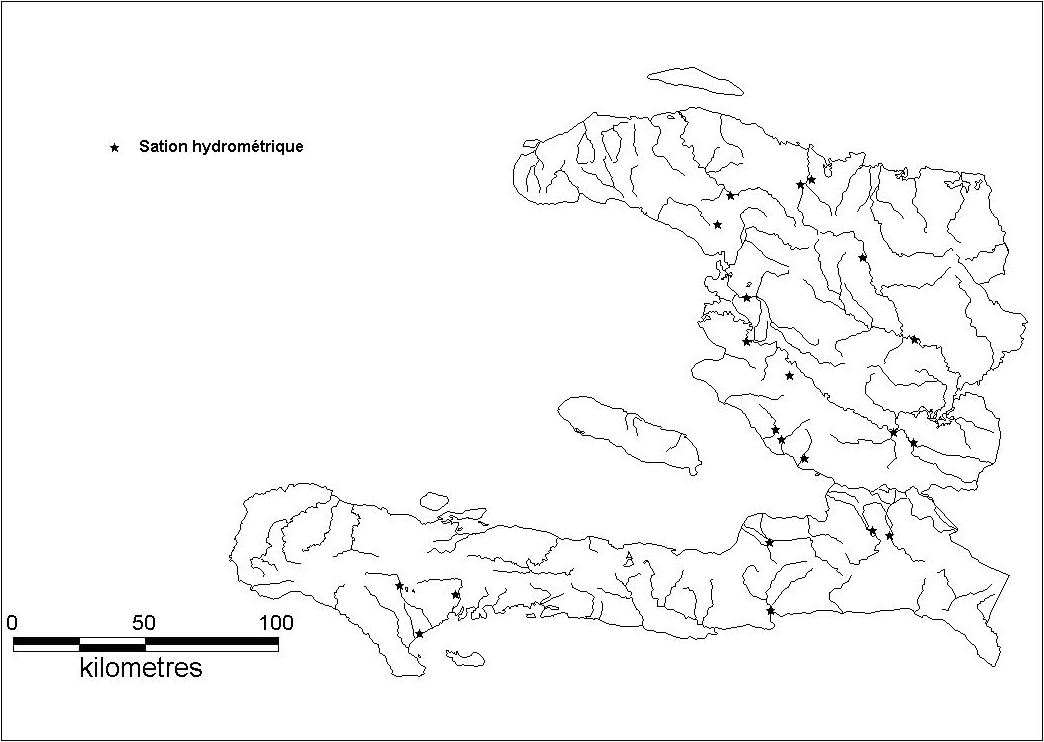
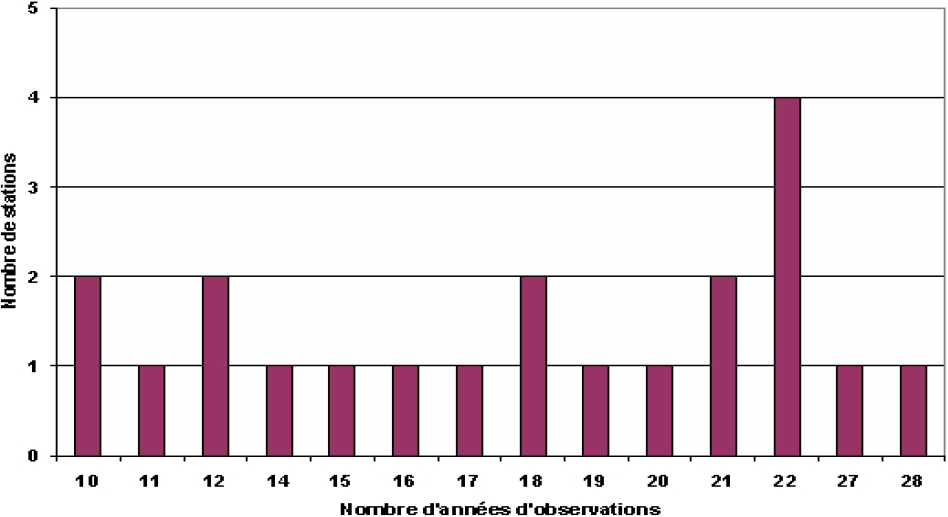
Pour les besoins de l’étude, nous avons utilisé les données du réseau hydrométrique de Haïti. 71 stations hydrométriques ont été recensées mais toutes ne sont pas utilisables. L’analyse de ces 71 stations a permis d’en retenir seulement 21 dont la période d’observation est supérieure à dix années (Figure 2). Le débit moyen interannuel et son écart type ont été calculés pour chacune des stations retenues. La figure 3 illustre le nombre de stations en fonction du nombre d’années d’observations.
Figure 2
Localisation des 21 stations hydrométriques retenues.
Location of the 21 hydrometric stations.
Figure 3
Nombre de stations en fonction du nombre d’années d’observation.
Number of stations as a function of the number of years of observation.
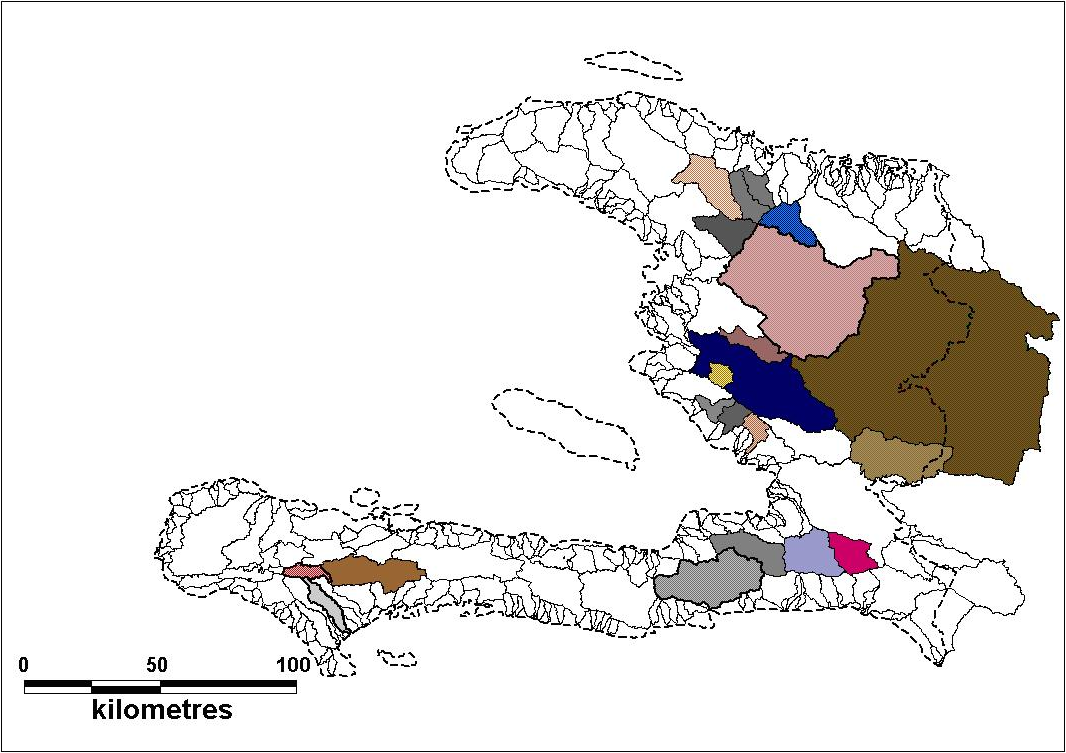
Par ailleurs, tous les bassins versants du territoire continental de Haïti ont été délimités à l’aide d’un modèle numérique de terrain d’une résolution spatiale de 90 m (Figure 1). Les bassins des 21 stations retenues ont été délimités grâce à la localisation de ces stations. En revanche, les bassins non jaugés ont été délimités en se référant à leurs exutoires (le point le plus bas drainant le bassin). Ainsi, plus de 1 000 bassins (grands, moyens et petits bassins) ont été identifiés. Toutes les caractéristiques géométriques et topographiques de tous les bassins (jaugés et non jaugés) ont été déterminées (superficie, périmètre, coefficient de forme, la longueur du cours d’eau, l’altitude ainsi que la pente). Les bassins délimités sont présentés à la figure 4.
Figure 4
Carte de délimitation des bassins jaugés (en couleur) et des bassins non jaugés (en blanc) – les limites de Haïti sont en pointillé.
Delineation map of gauged (coloured) and ungauged (white) basins – the dashed line represents the Haitian boundary.
3.4 Application des deux méthodes d’estimation
Le modèle de régression a été calibré à l’aide des données des 21 stations hydrométriques. En effet, étant donné la taille de l’échantillon de stations hydrométriques et celle du domaine géographique à l’étude, l’ensemble des 21 stations a été considéré comme faisant partie d’une même région hydrologique homogène. La superficie du bassin versant est la seule variable explicative incluse dans le modèle de régression. Étant donnée la taille limitée de l’échantillon, l’ajout de variables explicatives supplémentaires réduirait la précision avec laquelle les paramètres du modèle pourront être estimés. Les performances du modèle ont été vérifiées à l’aide de la validation croisée (ou « Jacknife »). Celle-ci consiste à retirer à chaque fois une station pour calibrer ensuite le modèle avec les données des stations restantes. La valeur du débit moyen interannuel de la station écartée est enfin calculée à l’aide du modèle nouvellement calibré. Cette opération est répétée pour l’ensemble des stations. Par la suite, une série de critères de performances, à savoir le coefficient de détermination (R2), le biais relatif moyen (BMR) et la racine carrée de l’erreur quadratique moyenne relative (REQMR), sont calculés à partir des valeurs estimées et des valeurs observées du débit moyen interannuel. Ces deux derniers sont définis comme suit :
où z est la valeur observée, ẑ est la valeur estimée et n est la taille de l’échantillon.
L’application du krigeage canonique pour l’estimation du débit moyen interannuel passe par différentes étapes :
Définition des variables : pour pouvoir construire l’espace physiographique à l’aide de l’ACC, il faut retenir au moins deux variables hydrologiques et deux variables physiographiques. En plus du débit moyen interannuel, l’écart type sur celui-ci a été retenu comme deuxième variable hydrologique. En ce qui concerne les variables physiographiques, nous disposons initialement d’une série de variables par bassin versant. Ceci comprend la superficie, le périmètre, le coefficient de forme (compacité) Kc, la longueur du rectangle équivalent L et les valeurs moyennes et médianes de l’altitude et de la pente. Après une analyse de la corrélation entre ces différentes variables et les deux variables hydrologiques, seules les variables suivantes ont été retenues : la superficie (S), le périmètre (P), le coefficient de forme (Kc), la longueur du rectangle équivalent (L), l’altitude et la pente médianes. Kc et L sont définis comme suit :
Transformation des variables : en prévision de l’application de l’ACC, les variables, dont la distribution présentait une asymétrie, ont été normalisées (i.e. rendre les distributions symétriques). Ainsi, le débit, l’écart type sur le débit interannuel et l’altitude médiane ont subi une transformation logarithmique; la superficie, une transformation racine réciproque (
 ); le périmètre et la longueur du rectangle équivalent, une transformation réciproque (
); le périmètre et la longueur du rectangle équivalent, une transformation réciproque ( );
);Standardisation des variables : toutes les variables ont été préalablement standardisées afin d’éliminer l’effet d’échelle. Celle-ci consiste à soustraire la moyenne de la valeur de la variable et à diviser le résultat par l’écart type;
Définition de l’espace canonique physiographique : celle‑ci consiste à appliquer l’ACC aux deux séries de variables transformées et standardisées : hydrologiques (débit moyen interannuel, l’écart type du débit interannuel) et physiographiques (superficie, périmètre, Kc, L, altitude et pente médianes). Les deux variables canoniques physiographiques (V1 et V2) ont servi de base pour l’espace physiographique : c’est-à-dire que les valeurs V1 et V2 de chaque station déterminent ses coordonnées dans cet espace;
Analyse variographique : il s’agit de calculer le variogramme expérimental de la variable débit moyen interannuel dans l’espace physiographique, et ce, à l’aide des valeurs de cette variable observées aux 21 stations de jaugeage retenues et de leurs positions dans l’espace déterminé par leurs valeurs de V1 et V2. Un variogramme théorique est par la suite ajusté au variogramme expérimental;
Validation croisée : afin de vérifier la capacité du krigeage canonique à bien estimer le débit moyen interannuel, une série de validations croisées ont été conduites afin d’optimiser le choix des paramètres du variogramme théorique ainsi que la taille du voisinage (nombre de sites à inclure dans l’estimation et qui sont voisins du point pour lequel l’estimation est faite). La configuration conduisant à la meilleure performance est retenue et ses résultats sont rapportés dans le présent article. Comme pour la régression, les performances du krigeage sont mesurées au travers de R2, BMR et REQMR.
3.5 Résultats et discussion
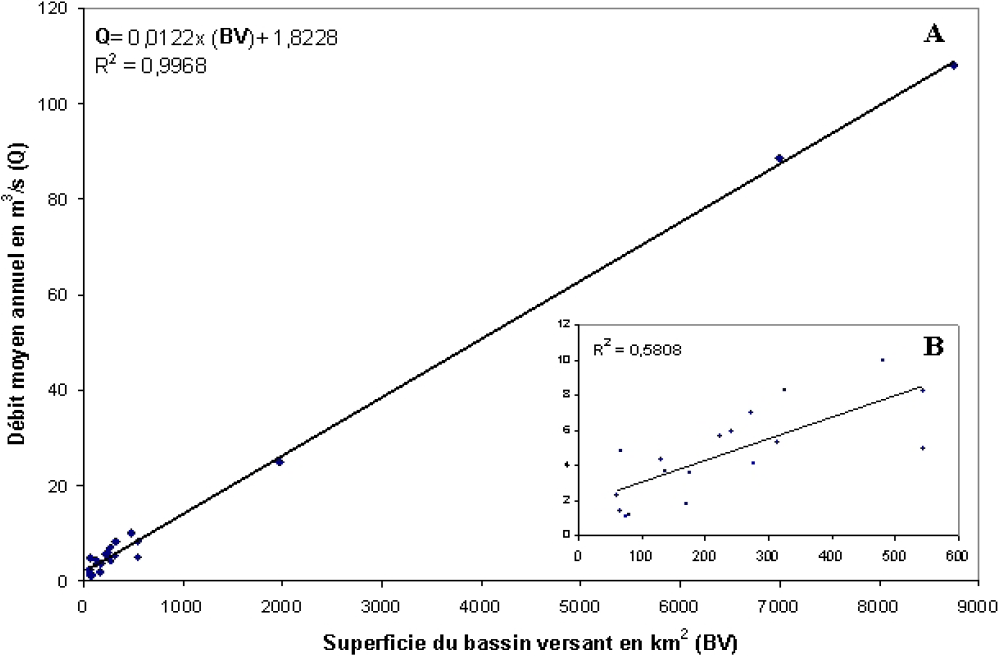
La figure 5A présente les résultats de calibration du modèle régressif. Il en ressort que ce modèle s’ajuste aux données des 21 stations de jaugeage avec un coefficient de détermination quasi parfait de l’ordre de 0,997, démontrant ainsi que la superficie du bassin versant pourrait expliquer la quasi-totalité de la variation observée dans le débit moyen interannuel. Toutefois, il paraît que cet ajustement parfait est dominé par le poids de trois points correspondant aux trois plus grands bassins versants du jeu de données, dont les superficies respectives sont de 1 970 km2, 6 998 km2 et 8 749 km2. En revanche, les 18 bassins versants restants affichent des superficies allant de 60 km2 à 544 km2. En effet, en excluant ces trois bassins, le coefficient de détermination de l’étalonnage du modèle régressif tombe à 0,58 (Figure 5B).
Figure 5
Régression entre le débit moyen interannuel et la superficie du bassin versant : A) toutes les stations de jaugeage, B) excluant les trois plus grands bassins versants.
Regression between the mean annual streamflow and catchment area: A) all gauging stations, B) without the three largest basins.
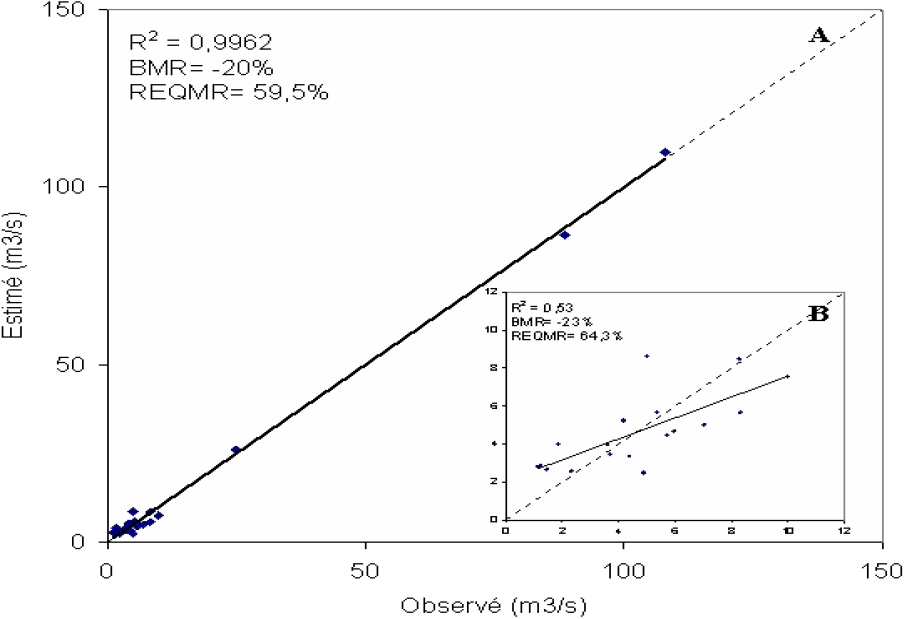
La figure 6 présente les résultats de la validation croisée du modèle régressif. En considérant la totalité des stations, le modèle produit un coefficient de détermination élevé de 0,99 avec un biais relatif moyen de ‑ 20 % (Figure 6 A). Ceci signifie que, en moyenne, le modèle régressif surestime la valeur du débit moyen interannuel d’environ 20 %. Malgré la valeur élevée du coefficient de détermination, l’erreur d’estimation est assez importante. Elle représente en moyenne 60 % de la valeur observée du débit moyen interannuel. En écartant du calcul les valeurs correspondant aux trois plus grands bassins versants, les valeurs de l’erreur et du biais de l’estimation sont plus importantes, et le coefficient de détermination passe de 0,99 à 0,53 (Figure 6 B). En étudiant la relation linéaire entre valeurs observées et valeurs estimées du groupe excluant les trois plus grands bassins, il s’avère que la pente et l’ordonnée à l’origine de cette relation sont significativement différentes de 1 et de 0. Ceci confirme la constatation évoquée plus haut quant au poids prépondérant des trois plus grands bassins versants. Ainsi, le modèle de régression aurait tendance à mieux s’ajuster au débit des grands bassins au détriment des plus petits. Par conséquent, l’ensemble des bassins ne serait pas hydrologiquement similaire et ne pourrait pas être considéré comme faisant partie de la même région hydrologique homogène. En d’autres termes, la relation entre le débit moyen interannuel et la superficie du bassin versant ne pourrait être décrite par un modèle unique. Toutefois, la taille limitée de l’échantillon de stations ne permettait pas de faire autrement.
Figure 6
Validation croisée du débit moyen interannuel estimé à l’aide de la régression simple : A) toutes les stations de jaugeage, B) excluant les trois plus grands bassins versants.
Cross validation of the mean annual streamflow estimated using simple regression: A) all gauging stations, B) without the three largest basins
Le débit moyen interannuel a été par la suite estimé sur l’ensemble des bassins versants non jaugés à l’aide du modèle régressif (Figure 7). Le débit est exprimé en lame d’eau. Il est à noter que le modèle de régression linéaire n’est pas adapté aux très petits bassins (taille inférieure à 10 km2). En effet, les valeurs estimées de la lame d’eau pour ces bassins sont erronées (trop élevées pour la superficie considérée). Ces bassins totalisent une superficie d’environ 2 762 km2 ce qui représente près de 10 % de la surface totale du territoire. La lame d’eau moyenne annuelle, estimée à l’aide de cette méthode, est donc d’environ 924 mm pour l’ensemble du territoire continental. Les îles adjacentes n’ont pas été considérées dans cette régionalisation puisque nous n’avons aucune donnée disponible et exploitable dans ces parties du territoire. Les zones correspondant aux trop petits bassins ainsi que les îles adjacentes apparaissent vides à la figure 7.
Figure 7
Lame d’eau ruisselée moyenne annuelle estimée par régression linéaire sur le territoire continental de Haïti.
Mean annual runoff depth (in mm) estimated by linear regression over continental Haïti.
En ce qui concerne le krigeage canonique, l’analyse variographique a été effectuée à travers l’espace physiographique sur une distance de 3,5 avec un intervalle de 0,40 (pas de distance utilisé pour le calcul de la semi-variance en fonction de la distance) (Figure 8). Le variogramme expérimental ainsi obtenu a été par la suite modélisé à l’aide d’un variogramme théorique de forme gaussienne. Ce dernier offrait la meilleure qualité d’ajustement au variogramme expérimental (un coefficient de détermination de 0,9962). Selon l’analyse variographique, le débit moyen interannuel affiche, à courte distance, une forte autocorrélation spatiale (faible semi-variance) dans l’espace physiographique. Celle-ci décroît par la suite rapidement (croissance rapide de la semi-variance) pour afficher une légère inflexion vers une distance de 3 sans atteindre pour autant un palier au-delà de cette distance. L’absence de palier dans le variogramme pourrait être expliquée par la non-stationnarité de la variable débit dans l’espace physiographique : c’est-à-dire que la valeur moyenne du débit (espérance mathématique) n’est pas constante dans l’espace physiographique, ce qui dénote l’existence d’une tendance dans la variable à travers l’espace. Par conséquent, le krigeage ordinaire serait moins approprié puisque l’hypothèse de stationnarité de second ordre ne serait pas vérifiée (une variable est stationnaire de second ordre quand l’espérance mathématique existe et ne dépend pas de la position dans l’espace, et que la covariance entre chaque paire d’observations existe et ne dépend que de la distance qui les sépare (ARNAUD et EMERY, 2000)). Toutefois, l’application du krigeage ordinaire pourrait être justifiée en se basant sur l’hypothèse intrinsèque qui est moins contraignante (une variable est dite intrinsèque quand ses accroissements sont stationnaires d’ordre deux). Cette hypothèse est compatible avec des variances a priori infinies (variogramme expérimental sans palier (ARNAUD et EMERY, 2000)).
Figure 8
Variogrammes expérimental (□) et théorique (–) du débit moyen interannuel à travers l’espace canonique physiographique.
Experimental (□) and theoretical (–) Variograms of the mean annual streamflow over the physiographical canonical space.
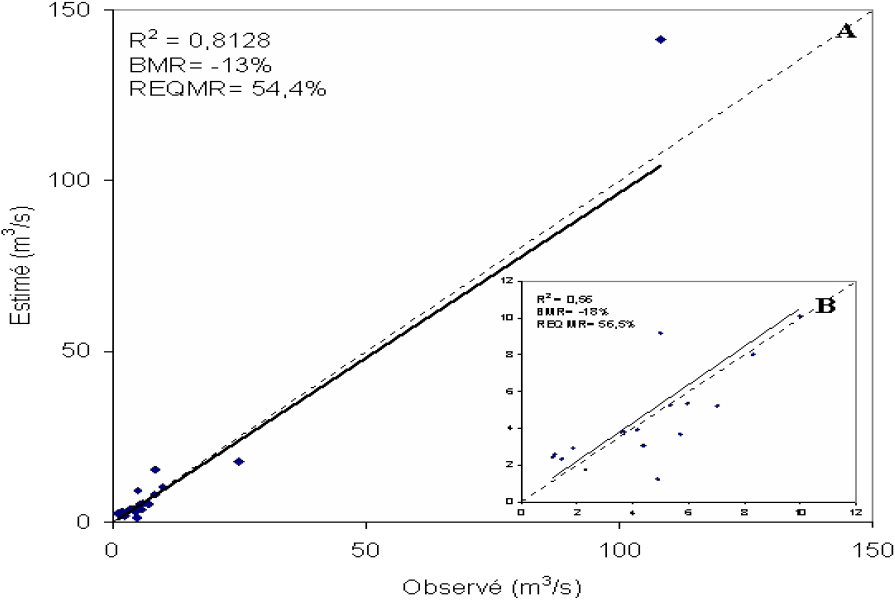
La méthode a été par la suite validée à l’aide de la validation croisée en utilisant une structure de voisinage incluant la totalité des sites disponibles pour l’interpolation (les 20 stations restantes, ce qui revient à une distance de recherche de voisins qui s’étend sur tout l’espace physiographique, c’est-à-dire une distance de 4). Les résultats sont illustrés à la figure 9A. À première vue, le krigeage canonique produit des résultats moins probants que la régression linéaire, surtout si on se fie au coefficient de détermination qui est de 0,8128. En effet, cette méthode a eu plus de difficulté à reproduire les valeurs de débit pour les plus grands bassins, et l’écart entre valeur observée et valeur estimée est d’autant plus grand que le débit est important. Toutefois, le krigeage permet d’estimer le débit moyen interannuel avec un biais moyen et une erreur quadratique plus faibles que le modèle régressif (‑ 13 % et 54,4 % respectivement). En écartant les trois plus grands bassins versants, il s’avère que les performances du krigeage sont meilleures que celles de la régression (Figure 6B, Figure 9B). En effet, les trois critères de performance sont plus favorables au krigeage. De plus, la pente et l’ordonnée à l’origine de la relation entre valeurs observées et valeurs estimées ne sont pas significativement différentes de 1 et de 0, respectivement, dénotant une bonne concordance entre valeurs observées et valeurs estimées (les intervalles de confiance à 95 % de la pente et de l’ordonnée à l’origine sont de, respectivement, (0,56; 1,52) et (-2,43; 2,71).
Figure 9
Validation croisée du débit moyen interannuel estimé à l’aide du krigeage canonique : A) toutes les stations de jaugeage, B) excluant les trois plus grands bassins versants.
Cross validation of the mean annual streamflow estimated using canonical kriging: A) all gauging stations, B) without the three largest basins.
La difficulté du krigeage à reproduire le débit des trois plus grands bassins versants confirme, d’une part, l’hypothèse avancée plus haut selon laquelle ces bassins ne font pas partie du même groupe hydrologique que le reste des bassins, et, d’autre part, l’existence d’une tendance dans le débit à travers l’espace physiographique. Par conséquent, la variation du débit dans l’espace physiographique pourrait être expliquée en partie par la position dans cet espace. Ainsi, il serait possible d’ajuster un modèle de régression spatiale entre le débit moyen interannuel des sites jaugés et leurs coordonnées dans l’espace physiographique, et appliquer le krigeage pour les résidus de la régression. Pour un site non jaugé, le débit sera estimé en additionnant la partie systématique de l’estimation, calculée à l’aide de la régression spatiale appliquée à ses coordonnées dans l’espace (V1, V2), et la partie aléatoire (les résidus) calculée à partir des résidus des sites jaugés voisins à l’aide du krigeage canonique.
Lors de l’application originale du krigeage canonique (sur un jeu de données de 151 stations de jaugeages), CHOKMANI et OUARDA (2004) ont trouvé que cette technique estime les quantiles de crues avec un coefficient de détermination allant de 0,68 à 0,77, une REQMR allant de 21 % à 27 % et un BMR inférieur à 1 %. Ces résultats, comparés à ceux obtenus dans le présent travail, démontrent que le krigeage canonique, surtout en se référant aux valeurs de l’erreur et du biais, ne s’est pas montré assez robuste. En effet, le débit moyen interannuel, en étant une valeur centrale de la fonction de distribution du débit, serait normalement plus aisé à estimer que des valeurs extrêmes telles les quantiles de crues. Cependant, vu la taille de l’échantillon et la nature des variables disponibles, les performances du krigeage canonique demeurent toutefois acceptables. Mis à part le coefficient de détermination dont la valeur est de 0,81 (et qui est dans l’absolu très satisfaisante), le krigeage canonique génère des valeurs de biais et d’erreur d’estimation meilleures que le modèle régressif. Il faut rappeler que les variables physiographiques utilisées ont été exclusivement de nature morphologique et elles ont été pour l’essentiel plus ou moins reliées à l’élévation du terrain. Or, comme il a été mentionné plus haut, le climat, le paysage et les types de couverture et d’occupation du sol affichent une grande variabilité spatiale à travers le territoire haïtien. Ne pas prendre en compte de telles caractéristiques du territoire limiterait la portée de n’importe quelle méthodologie d’étude du ruissellement. Il faut rappeler que le krigeage canonique, à travers la définition de l’espace physiographique, se base essentiellement sur la notion du voisinage hydrologique. Or, afin de bien définir cet espace, il est important de prendre en compte le maximum de paramètres physiographiques/climatiques influençant le régime hydrique.
Le krigeage a été également appliqué à l’ensemble des bassins non jaugés afin d’estimer le débit moyen interannuel à travers tout le territoire continental d’Haïti. Ainsi, le débit a été interpolé à l’emplacement des bassins non jaugés dans l’espace physiographique, en utilisant la même structure de voisinage employée lors de la validation croisée : c’est-à-dire un nombre maximum de 20 voisins inclus dans l’estimation et un rayon de recherche de 4. Les résultats sont illustrés dans la figure 10. Il est à noter que certains bassins non jaugés se sont trouvés en dehors du rayon maximal de recherche de voisins. Leurs positions dans l’espace physiographique ont été trop loin des sites jaugés en raison de leurs caractéristiques physiographiques très différentes de ces sites. Par conséquent, leurs débits n’ont pas pu être estimés par le krigeage canonique. Il s’agit pour l’essentiel de très petits bassins versants (Figure 10). La superficie totale des bassins qui n’ont pas pu être estimés par le krigeage a été légèrement inférieure à celle dont le débit calculé par le modèle régressif a été jugé erroné et a été écarté des résultats. Elle totalise 2 274 km2 ce qui représente environ 8,2 % de la surface totale du territoire. La lame d’eau moyenne annuelle estimée par le krigeage a été d’environ 1 056 mm, soit 132 mm de plus que la valeur estimée par la régression linéaire (924 mm). Cependant, rappelons que là aussi, seule la surface continentale a été considérée puisque aucune donnée exploitable n’est disponible pour les îles adjacentes. Par ailleurs, grâce à ces cartes, il est désormais possible d’apprécier la répartition spatiale de la ressource en eau de surface disponible à travers le territoire haïtien. Ceci constitue un premier pas vers la gestion efficace de cette ressource et une meilleure planification des projets d’aménagement et en particulier d’approvisionnement en eau potable.
Figure 10
Lame d’eau ruisselée moyenne annuelle (en mm) estimée par krigeage canonique.
Mean annual runoff depth (in mm) estimated by canonical kriging.
4. Conclusion
L’objectif de la présente étude a été de tester la généralité et la robustesse du krigeage canonique, une nouvelle approche d’estimation régionale hydrologique qui a été développée et appliquée pour l’estimation des quantiles de crues au Québec (Canada). L’évaluation de la robustesse a été réalisée dans le contexte de l’estimation du débit moyen interannuel sur le territoire continental de Haïti. Ainsi, le krigeage canonique a été appliqué sous un climat tropical caractérisé par une grande variabilité spatiale, surtout au niveau de la répartition des précipitations. Le krigeage a également été appliqué dans des conditions non optimales de qualité et de disponibilité de données. En effet, l’échantillon à l’étude se limitait à 21 stations hydrométriques dont la répartition spatiale n’est pas représentative de la variabilité des régimes hydriques du pays. Par ailleurs, les seules données physiographiques disponibles se limitaient au modèle numérique d’altitude, à partir duquel ont été calculées une série de variables dérivées qui ont servi à la définition de l’espace physiographique canonique; superficie du bassin de drainage, périmètre du bassin, coefficient de compacité, pente du terrain, etc. Les performances du krigeage canonique ont été par la suite vérifiées à l’aide de la validation croisée et, comparées à celles de la régression linéaire entre le débit moyen interannuel et la superficie du bassin versant, appliquée dans les mêmes conditions. La régression linéaire a été appliquée en considérant les 21 stations hydrométriques comme faisant partie de la même région hydrologique homogène.
Les deux approches d’estimation régionale ont éprouvé des difficultés pour l’estimation du débit moyen interannuel sous de telles conditions. Ceci apparaît particulièrement au niveau du biais et de l’erreur d’estimation, qui ont été supérieurs à, respectivement, 10 % et 50 %. Cependant, le krigeage canonique a affiché en général des performances légèrement supérieures. La régression linéaire a produit de meilleures estimations pour les plus grands bassins versants et ce, au détriment du groupe des moyens et petits bassins, ce qui remet en question la décision de considérer l’ensemble des stations jaugées comme une seule région hydrologiquement homogène. Le krigeage canonique, en revanche, a produit de meilleures estimations pour les moyens et petits bassins, tout en échouant à bien reproduire le débit des trois plus grands bassins. Ceci serait attribuable à la méthode d’interpolation utilisée (le krigeage ordinaire). Celle-ci ne serait probablement pas adaptée à la variable étudiée. En effet, l’analyse variographique et les résultats obtenus suggèrent l’existence d’une tendance dans le débit moyen interannuel à travers l’espace physiographique. Dans ce cas, une technique d’estimation tel que le krigeage universel (ISAAKS et SRIVISTAVA, 1989), qui est une combinaison entre régression spatiale et krigeage ordinaire, serait plus appropriée et produirait de meilleurs résultats.
Les résultats moins probants d’application du krigeage canonique obtenus dans la présente étude par comparaison aux résultats rapportés par CHOKMANI et OUARDA (2004) démontrent la complexité de l’estimation du débit moyen interannuel dans des conditions aussi défavorables. Ayant appliqué la méthode d’estimation, simultanément, sous un autre climat pour estimer une autre variable, en utilisant d’autres types de variables explicatives et dans des conditions imparfaites de qualité et de disponibilité de données, il est impossible d’attribuer la baisse observée dans les performances à une déficience dans la généralité de l’approche ou dans sa robustesse, ou encore à un effet conjugué des deux. Afin de juger de la généralité du krigeage canonique par exemple, il aurait été souhaitable de tester le modèle dans un autre climat ou pour estimer une autre variable tout en employant une base de données exhaustive et de bonne qualité. Malgré les conditions défavorables à toutes les méthodes d’estimation régionale, les résultats produits par le krigeage canonique demeurent acceptables. De plus, il y aurait encore place à l’amélioration en adaptant la technique d’interpolation et/ou en incluant des variables physiographiques/climatiques supplémentaires. Les données de télédétection du domaine publique représenteraient une source intéressante pour de telles informations.
Parties annexes
Remerciements
Les auteurs remercient le Programme canadien de bourses de la francophonie (PCBF), l’Agence canadienne de développement international (ACDI) et le conseil de recherche en sciences naturelles et en génie du Canada (CRSNG) pour le soutien financier ayant contribué à la réalisation de cette étude.
Références
- ARNAUD, M. et X. EMERY (2000). Estimation et interpolation spatiale. Méthodes déterministes et méthodes géostatistiques. Hermes Sciences Publications 8, Lavoisier (Éditeur), Paris, France, 221 p.
- BIRIKUNDAVYI, S., J. ROUSELLE, V.T.V. NGUYEN (1996). Estimation régionale des quantiles de crues par l’analyse des correspondances. Can. J. Civil Eng., 24, 438‑447
- CHOKMANI, K. et T.B.M.J. OUARDA (2004). Physiographical space-based kriging for regional flood frequency estimation at ungauged sites. Water Resour. Res., 40, W12514, doi : 10.1029/2003WR002983.
- COSANDEY, C et M ROBINSON (2000). Hydrologie Continentale. Armand Colin (Éditeurs), Paris, France, 368 p.
- DURRANS, S.R., S. TOMIC (1996). Regionalization of low-flow frequency estimates: an Alabama case study. Water Resour. Bull., 32, 23-37.
- EMMANUEL, E. et P. LINDSKOG (2000). Regards sur la situation des ressources en eau de la République d’Haïti, 25 p.
- GREHYS (GROUPE DE RECHERCHE EN HYDROLOGIE STATISTIQUE) (1996). Presentation and review of some methods for regional flood frequency analysis. J. Hydrol., 186, 63-84.
- HACHÉ, M, T.B.M.J. OUARDA, P. BRUNEAU, B. BOBÉE (2002). Estimation régionale par la méthode de l’analyse canonique des corrélations : comparaison des types de variables hydrologiques. Can. J. Civ. Eng., 29, 899-910.
- HAMZA, A., T.B.M.J. OUARDA, D. S. ROCKY, B. BOBÉE (2000). Développement de modèles de queues et d’invariance d’échelle pour l’estimation régionale des débits d’étiage. Can. J. Civil Eng., 28, 291-304
- ISAAKS, E.H. et R.M. SRIVISTAVA (1989). Applied geostatistics. Oxford University Press (Éditeurs), New York, E.U., 561 pp.
- JOSEPH, G. (2005). Étude du potentiel des eaux de surface à Haïti pour répondre aux problèmes de pénurie d’eau potable. Mémoire de maîtrise. Institut national de la recherche scientifique, Eau, Terre et Environnement, Université du Québec, Québec, Canada, 195 pp.
- KUNZEL, W. (1999). Modèle numérique de terrain d’Haiti et République Dominicaine. www.gdin.org/haitiDEMapr04.html, consulté en mars 2006.
- MDE (MINISTÈRE DE L’ENVIRONNEMENT) (1998). Programme de formulation de la politique de l’eau. Commission interministérielle sur l’environnement. Secrétariat du plan d’action pour l’environnement (PAE), Haiti, 29 p.
- MIQUEL, J. (2001). Hydrologie statistique. Introduction à l’étude des processus hydrométéorologiques. Application à la prédétermination des débits de crues. http://www.enpc.fr , 70, 8-12, consulté en mars 2006.
- MIC, R., G. GALÉA, P. JAVELLE (2002). Modélisation régionale des débits de crue du basin hydrographique du Cris : approche régionale classique et par modèles de référence, Rev. Sci. Eau, 15, 677-700.
- OUARDA, T.B.M.J., M. LANG, B. BOBÉE, J. BERNIER, P. BOIS (1999). Synthèse de modèles régionaux d’estimation de crue utilisés en France et au Québec. Rev. Sci. Eau, 12 , 155-182.
- OUARDA, T.B.M.J., F. ASHKAR (1998). Effect of trimming on LP III flood quantile estimates, J. Hydrol. Eng., 3-1, 33-42.
- OUARDA, T.B.M.J., M. HACHÉ, P. BRUNEAU, B. BOBÉE, (2000). Regional flood peak and volume estimation and northen Canadian basin. J. Cold Reg. Eng., 14, 176-190. J. Hydrol. Eng., 3, 33-42.
- OUARDA, T.B.M.J., C. GIRARD, G.S. CAVADIAS, B. BOBÉE (2001). Regional flood frequency estimation with canonical correlation analysis, J. Hydrol., 254, 157‑173.
- PANDEY, G.R. et V.-T.-V. NGUYEN (1999). A comparative study of regression based methods in regional flood frequency analysis. J. Hydrol., 225, 92-101.
Liste des figures
Figure 1
Région d’étude et Modèle Numérique d’Altitude (MNA) d’Haïti (KUNZEL, 1999).
Location of the area of study and Digital Elevation Model (DEM) of Haïti (KUNZEL, 1999).
Figure 2
Localisation des 21 stations hydrométriques retenues.
Location of the 21 hydrometric stations.
Figure 3
Nombre de stations en fonction du nombre d’années d’observation.
Number of stations as a function of the number of years of observation.
Figure 4
Carte de délimitation des bassins jaugés (en couleur) et des bassins non jaugés (en blanc) – les limites de Haïti sont en pointillé.
Delineation map of gauged (coloured) and ungauged (white) basins – the dashed line represents the Haitian boundary.
Figure 5
Régression entre le débit moyen interannuel et la superficie du bassin versant : A) toutes les stations de jaugeage, B) excluant les trois plus grands bassins versants.
Regression between the mean annual streamflow and catchment area: A) all gauging stations, B) without the three largest basins.
Figure 6
Validation croisée du débit moyen interannuel estimé à l’aide de la régression simple : A) toutes les stations de jaugeage, B) excluant les trois plus grands bassins versants.
Cross validation of the mean annual streamflow estimated using simple regression: A) all gauging stations, B) without the three largest basins
Figure 7
Lame d’eau ruisselée moyenne annuelle estimée par régression linéaire sur le territoire continental de Haïti.
Mean annual runoff depth (in mm) estimated by linear regression over continental Haïti.
Figure 8
Variogrammes expérimental (□) et théorique (–) du débit moyen interannuel à travers l’espace canonique physiographique.
Experimental (□) and theoretical (–) Variograms of the mean annual streamflow over the physiographical canonical space.
Figure 9
Validation croisée du débit moyen interannuel estimé à l’aide du krigeage canonique : A) toutes les stations de jaugeage, B) excluant les trois plus grands bassins versants.
Cross validation of the mean annual streamflow estimated using canonical kriging: A) all gauging stations, B) without the three largest basins.
Figure 10
Lame d’eau ruisselée moyenne annuelle (en mm) estimée par krigeage canonique.
Mean annual runoff depth (in mm) estimated by canonical kriging.