Résumés
Résumé
Dans cet article, nous présentons les résultats d’une recherche visant à explorer les raisonnements statistiques d’élèves à risque de la fin du primaire pendant la résolution de situations problèmes. Les démarches des élèves ont été analysées en mettant en relation leurs stratégies avec les caractéristiques des situations. Les élèves à risque ont proposé des stratégies originales et variées en mobilisant des savoirs pertinents. Quelques passages cruciaux dans l’évolution des raisonnements statistiques sont mis en évidence. Cet article permet également d’envisager le potentiel des situations et de discuter des conditions d’engagement d’élèves à risque dans une tâche de résolution de problèmes statistiques.
Mots clés:
- difficultés d’apprentissage,
- élèves à risque,
- raisonnement multiplicatif,
- situations problèmes,
- enseignement de la statistique
Summary
This article presents the results of a research to explore statistical reasoning of at-risk students at the end of primary school as they solve various problems. The processes used by the students were analyzed by relating their strategies with characteristics of each situation proposed. The at-risk students proposed various and original strategies while mobilizing pertinent knowledge. The authors describe some crucial passages that show the evolution of statistical thinking processes. The authors envisage the potential of situations presented and present a discussion of the conditions in which at-risk students engage in a task requiring the resolution of statistical problems.
Key words:
- learning difficulties,
- at-risk students,
- multiplication reasoning,
- problem situations,
- statistical teaching
Resumen
En este artículo, presentamos los resultados de una investigación que tiene por propósito explorar los razonamientos estadísticos de alumnos de riesgo de final de primaria durante la resolución de situaciones problemas. Las gestiones de aprendizaje de los alumnos fueron analizadas relacionando sus estrategias con las características de las situaciones. Los alumnos de riesgo propusieron estrategias originales y variadas movilizando saberes pertinentes. Se destacan algunos momentos cruciales en la evolución de los razonamientos estadísticos. Asimismo este artículo permite contemplar el potencial de las situaciones y discutir las condiciones de implicación de alumnos de riesgo en una tarea de resolución de problemas estadísticos.
Palabras claves:
- dificultades de aprendizaje,
- alumnos de riesgo,
- razonamiento multiplicativo,
- situaciones problemas,
- enseñanza de la estadística
Corps de l’article
Introduction
Les concepteurs du Programme de formation de l’école québécoise (ministère de l’Éducation du Québec – MÉQ, 2001) accordent une place centrale au développement de la compétence qui consiste à résoudre une situation problème mathématique dès le début du primaire. Cette orientation demande à l’enseignant de proposer aux élèves des situations mathématiques complexes qui nécessitent une réflexion approfondie et une véritable recherche de la démarche de résolution. La résolution d’une situation problème peut alors représenter un défi particulièrement important pour des élèves qui présentent un retard ou qui ont des difficultés d’apprentissage pouvant les mener à l’échec, élèves dits aussi à risque[1]. En effet, plusieurs auteurs mettent en évidence certaines caractéristiques de ces élèves qui peuvent rendre la résolution plus ardue. Ainsi, ils ont des stratégies moins développées lors de la résolution de problèmes (Pericola Case, Harris et Graham, 1992), ils ont plus de difficultés à se construire une représentation mentale du problème et à se servir de mesures de contrôle lors de la résolution, ils manquent d’autonomie (Focant, 2003 ; Perrin-Glorian, 1993) et ils ont de la difficulté à changer de point de vue, ce qui manifeste une certaine rigidité (Perrin-Glorian, 1993). Toutefois, certaines difficultés pourraient trouver leurs origines dans des effets liés au contrat didactique, ainsi que dans la perception qu’ont les élèves de leur rôle et du rôle de l’enseignant à l’école (Perrin-Glorian, 1993).
Dans les travaux en didactique des mathématiques qui se sont intéressés aux élèves faibles ou en difficulté, plusieurs auteurs (Cange et Favre, 2003 ; Conne, 1999, 2003 ; Lemoyne et Lessard, 2003) mettent en évidence les caractéristiques d’un enseignement souvent dispensé aux élèves en difficulté. On observe une tendance au ré-enseignement et au sur-enseignement, à l’enseignement de gestes, à la fragmentation des contenus, à l’allègement des tâches, à une insistance sur les préalables (par exemple, les tables de multiplication) qui maintient des élèves adolescents dans des contenus d’élèves de 7-8 ans. Ces phénomènes ne sont pas sans effets sur l’apprentissage des élèves et le rapport qu’ils entretiennent avec le savoir, l’enseignement des mathématiques et l’école, comme le suggère Perrin-Glorian (1993). Les élèves développent alors des attitudes nuisibles à des apprentissages mathématiques significatifs. De plus, le manque d’engagement cognitif des élèves dans les tâches mathématiques est une source de difficultés et celles-ci ne peuvent que s’aggraver avec le temps (Kamii, 1996 ; Mary, 2003).
Nous pensons dès lors qu’il est important de proposer aux élèves à risque des situations problèmes riches, problématiques par définition, qui permettent un engagement cognitif de leur part. Les situations de problèmes statistiques sont particulièrement intéressantes à cet égard. En effet, certaines recherches semblent suggérer que le contexte statistique est favorable aux élèves faibles, qui en bénéficieraient davantage que des élèves forts. Tout au moins, ces situations ne leur poseraient pas plus de problèmes qu’aux autres élèves (Galmacci et Scrucca, 2000 ; Van Reeuwijk, 1992). Les résultats de Van Reeuwijk (1992) suggèrent que l’analyse statistique de données réelles peut s’effectuer par les élèves à différents niveaux de formalisme et d’abstraction et qu’elle constitue une source de motivation et d’engagement pour les élèves. Le fait que plusieurs réponses soient possibles et que ces réponses soient discutables peut aussi expliquer l’intérêt que suscite le travail effectué par les élèves.
Notre étude cherche à la fois à connaître le potentiel de raisonnements d’élèves à risque scolarisés dans une classe spécialisée de fin primaire, et le potentiel des situations utilisées pour faire émerger ces raisonnements. Elle vise à proposer la résolution de problèmes statistiques à des élèves à risque, de manière à pouvoir envisager, par la suite, une séquence d’enseignement dans ce domaine encore peu exploré, à notre connaissance, pour des élèves à risque de niveau primaire[2].
Cadre théorique
Plusieurs recherches sur l’apprentissage et l’enseignement de la statistique ont déploré, chez les élèves du secondaire, du collégial ou les étudiants universitaires, un manque de compréhension des concepts simples et ce, même après avoir suivi une formation explicite sur le sujet (Cai, 1995 ; Gattuso et Mary, 1996 ; Mevarech, 1983). À la suite de ce constat d’échec et avec l’émergence de la perspective socioconstructiviste dans la recherche sur l’enseignement, les chercheurs intéressés à l’enseignement de la statistique ont tenté de rapprocher les activités de classe en statistique de l’activité du statisticien, de manière à donner du sens aux concepts à enseigner et à développer une véritable pensée statistique. Ainsi, plusieurs expérimentations ont placé l’élève en situation d’analyse des données réelles provenant de sondages ou d’expérimentations (Bakker, 2001 ; Cobb, 1999 ; Doerr et English, 2001 ; Lehrer et Romberg, 1996 ; Rigatti Luchini, Perelli D’Argenzio, Moncecchi et Giambalvo, 2000). Ces recherches ont montré que, placés dans des situations adéquates, les élèves arrivent à développer une première compréhension de concepts statistiques qui leur permettent de caractériser des ensembles de données. Ce point de vue rejoint celui de chercheurs préoccupés par les élèves en difficulté, qui proposent d’enrôler l’activité de l’élève dans des pratiques mathématiciennes (Conne, 1999) ou de problématiser les situations (Lemoyne et Lessard, 2003).
La volonté de rapprocher l’activité de l’élève de celle du statisticien ou du mathématicien, à l’origine de nombreuses recherches en didactique des mathématiques, a placé la résolution de problèmes au coeur de la classe. On parle ici de situations problèmes, où le problème n’est pas seulement vu comme permettant la manifestation de connaissances chez les élèves, mais aussi comme permettant d’en développer de nouvelles, à travers une réelle activité mathématique. La situation problème est alors conçue de manière à ce que l’élève puisse s’engager dans la résolution sans qu’il ait forcément tous les moyens pour y arriver de façon optimale (Astolfi, 1993). Dans ce contexte, les moyens de validation dont dispose l’élève jouent un rôle important dans la progression de la résolution. Souvent, cette validation est réalisée par l’intermédiaire d’une confrontation des stratégies ou d’un débat (Astolfi, 1993). Les situations problèmes, conçues ainsi pour développer le raisonnement mathématique, permettent aux élèves de raffiner ensemble les stratégies et de lever les obstacles d’ordre épistémologique ou cognitif, obstacles qui appartiennent au développement même des connaissances (Astolfi, 1993). Dans cet article, nous allons présenter des situations de problèmes statistiques qui ont un potentiel de situations problèmes comme nous les avons définies plus haut.
De nombreuses difficultés sont répertoriées dans les écrits sur l’apprentissage de la statistique. Cobb (1999) identifie deux passages nécessaires pour accéder à une pensée statistique : 1) le passage au concept de distribution (la collection de données n’est plus vue comme un ensemble d’informations particulières, mais comme une entité ayant ses propres caractéristiques), et 2) le passage à une pensée multiplicative (par opposition à une pensée additive consistant à comparer les sommes plutôt que les rapports). Avant la réalisation de ces passages, on peut observer des difficultés à considérer un ensemble de données comme un tout, une entité, et des difficultés à raisonner multiplicativement. Différents travaux sur le raisonnement proportionnel mettent bien en évidence ces difficultés (Levain, 1996). Les passages décrits sont à surveiller de façon particulière chez les élèves à risque pour lesquels les mêmes difficultés sont susceptibles d’être observées, mais de façon plus persistante (Perrin-Glorian, 1993). Les difficultés et les obstacles qui y sont liés ont guidé le choix de nos situations d’expérimentation qui nécessitent, comme nous le verrons ultérieurement, la comparaison de deux ensembles de données à effectif différent.
Objectif et type de recherche
Notre étude vise à décrire les raisonnements mobilisés lors de situations de problèmes statistiques par des élèves à risque de fin primaire, scolarisés en classe spécialisée, et à dégager comment ces raisonnements évoluent au fil des interactions. La recherche, de type exploratoire, mènera à des hypothèses ou des questions à investiguer quant au développement d’une pensée statistique, au potentiel des situations pour le développement de cette pensée et à la viabilité de ces situations avec des élèves en difficultés.
Méthodologie
Participants à l’étude
L’expérimentation a eu lieu dans deux classes primaires (nommées classe 1 et classe 2 dans cet article) d’une école de la grande région de Montréal qui accueille exclusivement des élèves présentant un retard sur le plan des apprentissages, sans toutefois être classés comme déficients intellectuels. Les sujets de l’expérimentation (N = 20) étaient âgés, pour la plupart, de 13 ans et en étaient à leur dernière année de fréquentation d’une institution primaire[3]. L’enseignement réalisé en mathématiques se situait aux niveaux de 4e, 5e et 6e année primaire. Sur le plan des apprentissages en statistique, les élèves avaient été initiés aux pictogrammes et diagrammes à bande dans les années précédentes. Avant l’expérimentation, indépendamment de celle-ci, les élèves avaient reçu un enseignement explicite sur la moyenne dans la classe 1 (N1 =12) et sur les diagrammes à lignes brisées dans la classe 2 (N2 = 8). Notons également que dans ces classes, selon les enseignantes, plusieurs élèves présentaient un déficit de l’attention avec hyperactivité ou étaient diagnostiqués dyslexiques, dysorthographiques ou dysphasiques, et ce, surtout dans la classe 2.
Description des outils
La proposition d’une situation problème apparaît particulièrement appropriée pour accéder aux connaissances des élèves et à leur raisonnement (Lemoyne et Lessard, 2003). Nous avons choisi des situations de comparaison de groupes à effectifs différents, car elles étaient susceptibles, a priori, de faire émerger des connaissances et des raisonnements qui sont cruciaux dans le développement d’une pensée statistique et numérique. Nous avons choisi de faire analyser aux élèves des données réelles pour rendre l’activité la plus significative possible.
Nous avons opté pour une situation de classe avec travail en petits groupes pour favoriser le partage et la confrontation des idées, ce qui permet de faire évoluer les stratégies de résolution. Les situations problèmes devaient alors offrir une certaine liberté et permettre l’émergence de stratégies de résolution différentes chez les élèves afin de rendre possibles des échanges significatifs. Nous avons effectué une analyse a priori des situations et des données analysées afin de nous assurer de la possibilité de l’émergence d’une bonne diversité de stratégies.
Dans le cadre de cette étude, la séquence d’activités proposée aux élèves comprend les étapes suivantes : 1) collecte de données ; 2) formulation de questions aux données compilées ; 3) production d’un moyen pour répondre à certaines des questions posées et 4) représentation graphique ou visuelle à des fins de communication.
La collecte de données a été réalisée par l’enseignante, la semaine précédant la première rencontre avec les élèves. Les élèves devaient répondre à un certain nombre de questions portant sur des caractéristiques personnelles (sexe, date de naissance, couleur des cheveux, port de lunettes, etc.) et certaines habitudes de vie (nombre d’heures de télévision par semaine, heure du lever, transport utilisé pour aller à l’école, etc.). Les variables du questionnaire ont été choisies par les chercheurs afin de permettre la formulation de questions variées avec, entre autres, la comparaison d’ensembles de données à effectif différents et la comparaison de données quantitatives et qualitatives. Les résultats de ce questionnaire ont été compilés par les chercheurs sous forme de tableau (Tableau 1), afin de permettre la réalisation de la suite des activités dans le temps alloué.
Tableau 1
Extrait du tableau de compilation des données présenté aux élèves
La suite des activités s’est réalisée sur quatre rencontres d’environ une heure. Lors de la première séance, les élèves devaient formuler des questions auxquelles il était possible de répondre grâce aux résultats compilés dans le tableau[4]. Les questions formulées par les élèves ont été présentées et discutées en grand groupe. Parmi ces questions, deux ont été retenues pour la suite de l’expérimentation[5] :
Est-ce que les enfants qui portent des lunettes écoutent plus la télévision que les autres[6] ? (Port de lunettes/nombre d’heures de télévision)
Est-ce que les garçons ont les cheveux plus foncés que les filles ? (Sexe/couleur des cheveux)
Ce sont les deux seules questions qui demandaient la comparaison de deux ensembles de données et pour lesquelles la réponse n’était pas immédiate. Ces questions permettaient également de placer les élèves dans les situations problématiques espérées. Les tâches sont analysées plus en détail dans la section Description des résultats.
Au cours des trois autres séances, les élèves devaient trouver, en équipe, un moyen pour répondre aux questions. Lorsqu’ils avaient trouvé une réponse satisfaisante à leurs yeux, ils devaient ensuite l’illustrer sur de grands cartons. Afin de donner du sens à l’activité de représentation, ils devaient, par la suite, l’expliquer au grand groupe. Pour ce faire, les élèves avaient à leur disposition des pictogrammes représentant les différentes catégories d’enfants concernés par les questions (personnages avec ou sans lunettes, garçons et filles). Finalement, chaque équipe a présenté et expliqué sa solution. Les autres élèves étaient appelés à questionner et à commenter ces solutions. Cette séance en grand groupe permettait alors de nouvelles confrontations d’idées. Dans cet article, nous présentons en détail les résultats concernant ces trois séances.
Les classes étaient divisées en sous-groupes de quatre à cinq élèves, animés chacun par l’enseignante de la classe ou un des chercheurs. Le rôle des animateurs consistait à donner les consignes, à donner la parole aux élèves, à s’assurer que les élèves s’écoutaient et qu’ils avaient entendu les arguments des autres, à demander des réactions, à relancer les questions posées par un élève et à favoriser l’argumentation entre les élèves. Leur objectif était d’investiguer le raisonnement des élèves dans les situations avec le moins d’interventions induisant une réponse, même si l’animation orientait forcément le déroulement[7]. Parfois, des questions étaient prévues pour vérifier la compréhension des élèves. Par exemple, dans le cas où les élèves auraient procédé à un calcul de moyenne, la question suivante, suggérée dans le document donné aux animateurs, visait à vérifier le sens qu’ils accordaient au résultat : Comment se fait-il que la moyenne soit plus grande dans ce groupe (celui avec lunettes), alors que c’est dans l’autre groupe (celui sans lunettes) que l’on retrouve la personne avec le plus grand nombre d’heures d’écoute (le maximum) ?
Méthode de compilation et d’analyse des résultats
Après chaque rencontre, les chercheurs faisaient un rapport écrit de leurs observations et préparaient la séance suivante. Toutes les rencontres ont été filmées et un transcrit en a été réalisé. Les productions finales des élèves sur grands cartons ont été récupérées. L’analyse a consisté à décrire le plus fidèlement possible les solutions ou amorces de solutions, les changements dans les stratégies et les difficultés rencontrées, en mettant en évidence les aspects cruciaux du raisonnement statistique, tel qu’il se présentait, tout en faisant le lien avec les caractéristiques des situations. Pour réaliser cette analyse des stratégies des élèves, nous avons étudié a priori les problèmes posés de manière à porter un regard averti sur les stratégies des élèves. Cette analyse a priori, qui sera présentée plus loin, permet, d’une part, de juger de la variété et de l’originalité des solutions des élèves lorsqu’elles se présentent et, d’autre part, de juger a posteriori du potentiel de la situation en fonction d’anticipations réalisées en analyse a priori (Artigue, 1996).
Description des résultats
Dans un premier temps, nous présenterons, pour chacune des questions, les caractéristiques des données que les élèves avaient à analyser au regard de la question posée. Par la suite, nous décrirons et analyserons les stratégies utilisées par les élèves pour répondre aux deux questions, avec les difficultés qui sont apparues. Toutefois, dans le cas de la deuxième question (sexe/couleur des cheveux), la description servira surtout à montrer l’obstacle qu’ont rencontré certains élèves.
1. Port de lunettes / nombre d’heures de télévision
a) Analyse du problème posé
Les différentes équipes de travail devaient trouver un moyen pour déterminer si, parmi les enfants interrogés, le groupe de ceux qui portent des lunettes écoute plus la télévision que le groupe de ceux qui n’en portent pas. Ces deux groupes ne comportent pas le même nombre d’individus : 16 personnes ne portent pas de lunettes et 4 en portent. La différence des effectifs dans les deux groupes a des répercussions importantes sur la résolution du problème, puisque la simple addition des heures de télévision de chacun des deux groupes ne permet pas de tirer des conclusions pertinentes. Les élèves doivent donc passer par la proportionnalité et faire preuve d’un raisonnement multiplicatif, passage crucial dans le développement d’une pensée statistique (Cobb, 1999). Les notions de pourcentage et de fractions équivalentes, auxquelles les élèves avaient déjà été initiés, pouvaient alors servir. La comparaison des rapports se trouve facilitée, étant donné que le nombre de personnes dans un groupe (16) est un multiple du nombre de personnes dans l’autre (4). De plus, la distribution des nombres d’heures présente une configuration particulière : chez les porteurs de lunettes, tous écoutent la télévision plus de 20 heures par semaine, tandis qu’une majorité (presque les deux tiers) des personnes qui ne portent pas de lunettes en écoutent moins de 20 heures. Par ailleurs, les trois quarts des porteurs de lunettes en écoutent plus de 21,60 heures (moyenne des deux groupes) contre le tiers dans l’autre groupe. Une telle analyse de la distribution pouvait être utilisée par les élèves pour répondre à la question posée.
D’autres moyens pouvaient être considérés. Ainsi, les porteurs de lunettes ont en moyenne 28 heures d’écoute de télévision à leur actif, tandis que chez ceux qui ne portent pas de lunettes, cette moyenne n’est que de 20 heures. Par ailleurs, la médiane pour le premier groupe est de 27, tandis que pour le deuxième, elle est de 17,50. Le recours à la moyenne pouvait être envisagé comme une stratégie probable pour les élèves d’une des classes, puisque l’enseignante venait d’aborder cette notion. Les élèves pouvaient aussi être tentés de comparer les valeurs extrêmes des distributions. Toutefois, celles-ci (52 heures comme valeur la plus élevée et 5 heures et demie comme valeur la moins élevée) se retrouvent toutes les deux dans le groupe des personnes qui ne portent pas de lunettes. La simple considération d’une des valeurs extrêmes ne permet donc pas de tirer de conclusion.
b) Analyse des stratégies d’élèves
Les réponses formulées par les élèves dans la première classe (classe 1)
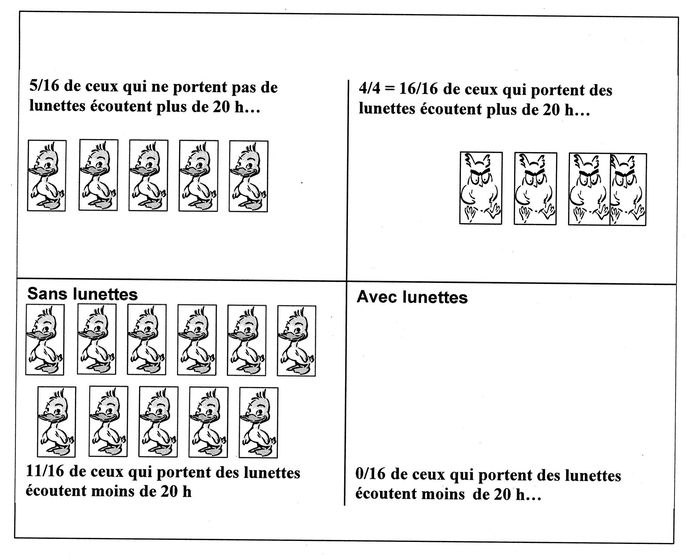
Les stratégies formulées par les trois équipes de la première classe sont très diversifiées. La première équipe de travail a analysé la distribution des nombres d’heures d’écoute de télévision chez les porteurs de lunettes et chez ceux qui n’en portent pas, en comparant les fractions du nombre de personnes dans chacun des deux groupes qui écoutent plus de 20 heures de télévision par semaine et de ceux qui affirment passer moins de 20 heures devant le téléviseur. Ils ont illustré leur stratégie dans un tableau en se servant des pictogrammes (Figure 1) et ont conclu que ce sont les personnes qui portent des lunettes qui écoutent plus la télévision.
Figure 1
Problème 1 : groupements et comparaison des effectifs relatifs
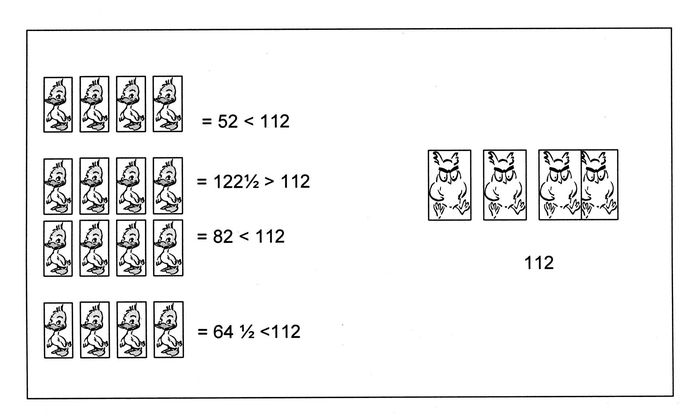
La deuxième équipe (Figure 2) a, pour sa part, comparé les sommes des heures d’écoute de groupes égaux. Constatant l’impossibilité d’utiliser simplement les sommes du groupe de porteurs de lunettes et de celui des personnes sans lunettes, les membres de cette équipe ont séparé les 16 personnes sans lunettes en quatre groupes de quatre, ce qui leur permettait de comparer chacun des quatre groupes à celui des porteurs de lunettes. Ils ont ensuite conclu que trois groupes de personnes sans lunettes écoutaient moins la télévision que le groupe des porteurs de lunettes et que, par conséquent, ce sont les porteurs de lunettes qui écoutent davantage la télévision.
Figure 2
Problème 1 : comparaison de groupes de même taille
Cependant, cette solution n’apparaissait pas idéale pour deux membres de l’équipe, puisque le résultat pouvait dépendre de la constitution des groupes. Un calcul de moyenne des heures d’écoute pour chacun des deux groupes a donc été ajouté à l’illustration.
La troisième équipe a eu directement recours au calcul de la moyenne et a conclu, comme les deux autres équipes, que ce sont les personnes qui portent des lunettes qui passent plus de temps devant le téléviseur. Notons que, dans cette classe, comme la moyenne avait été enseignée, chacune des équipes y a eu recours pendant la résolution. Cette connaissance a permis à plusieurs élèves d’entrer dans la résolution de façon assurée. D’autres avaient une vague idée de réaliser une approximation de l’ensemble des données par un nombre, sans toutefois recourir précisément à un calcul de moyenne.
Les réponses formulées par les élèves dans la deuxième classe (classe 2)
Dans la deuxième classe, la première équipe a tenté de produire un graphique à lignes brisées qui venait d’être vu en classe. Ils ont procédé en associant à chaque individu un point correspondant au nombre d’heures de télévision écoutée et en réunissant les points pour former une ligne brisée. Ce moyen n’a toutefois pas permis aux élèves de trouver une solution. Le graphique permettait de voir clairement les variations entre les individus, mais ne permettait pas directement de répondre à la question posée.
Dans l’autre équipe, deux moyens ont été envisagés, qui n’ont cependant pas fait consensus. Toutefois, dans les deux cas, il est apparu essentiel de comparer des populations égales, comme c’était le cas pour une équipe de l’autre classe (Figure 2). Rappelons que la prise en considération des effectifs différents et de la nécessité de comparer des populations égales sont des éléments déterminants dans le choix des stratégies. La première solution a consisté à choisir quatre personnes parmi les 16 ne portant pas de lunettes pour les comparer aux quatre porteurs de lunettes[8]. Cette solution a été envisagée par plusieurs élèves, dans différentes équipes. La deuxième solution a consisté à augmenter le nombre de personnes du groupe portant des lunettes à 16, de manière à ce qu’il soit égal au nombre de personnes sans lunettes, tout en conservant les propriétés de la population, comme en témoignent les extraits suivants provenant du même élève : Mais ceux qui ont des lunettes écoutent 23, 37, 31 et 21[heures]. […] Si tu mets le même nombre, […]le mettre égal ok ? Entre les deux groupes. / Puis là, tu estimes à quel temps ils font ceux-là et tu mets à peu près le même temps avec les autres. Cela va donner que les lunettes vont avoir plus de temps. / Ils sont 16 personnes qui ne portent pas de lunettes sur 20. Il y en a quatre qui portent des lunettes. Si tu en rajoutes, si tu en rajoutes 12, […] ceux qui portent des lunettes écoutent plus de télévision que ceux qui n’en portent pas.
Les difficultés rencontrées par les élèves
Si les résultats des réflexions des élèves sont fort intéressants et diversifiés, ceux-ci ont cependant été trouvés à la suite d’un processus parfois ardu, caractérisé par de nombreuses difficultés, dont celle de l’inférence des croyances relatives au résultat et celle du passage à un raisonnement sur les effectifs.
L’inférence des croyances relatives au résultat
Dans tous les groupes de travail, les élèves semblaient éprouver des difficultés importantes à se détacher de leurs croyances par rapport au résultat attendu. Ainsi, de nombreux élèves ont fait remarquer que, si quelqu’un porte des lunettes, ce n’est pas nécessairement parce qu’il a passé trop d’heures devant la télévision. Cet argument se manifestait de plusieurs manières. Un élève a avancé que, si on prend en considération le nombre d’heures passées devant la télévision, il faut également inclure les heures d’utilisation de l’ordinateur ou d’une console de jeux vidéo. Un autre a abordé plus directement la relation de cause à effet : Ce n’est pas parce qu’on écoute plus la télévision qu’on porte des lunettes. Les élèves qui ont avancé cet argument ont alors été dans l’impossibilité, du moins temporaire, de se centrer sur les données recueillies. Ces réflexions ont donc parfois été des obstacles dans l’avancée vers la solution. Toutefois, d’un autre point de vue, elles font partie de l’activité du statisticien. En effet, le statisticien qui s’interroge sur ses données doit se poser des questions comme celle-ci : est-ce que le critère choisi (écouter la télévision) est le meilleur critère à considérer pour étudier les causes du port de lunettes ? En fait, bien que la tâche ne visait pas à lier les deux critères dans une relation de dépendance (porter des lunettes / écouter la télévision), les élèves l’ont interprétée dans ce sens.
Le passage au raisonnement sur les effectifs
Un passage crucial dans la résolution du problème est sans doute la prise en considération des effectifs différents et de la non-pertinence de comparer les sommes totales, étant donné, justement, les effectifs différents. La comparaison des sommes totales, d’abord envisagée par certains, est vite contestée. Cela amène à envisager deux types de moyens pour résoudre le problème. Le premier consiste à comparer les sommes après égalisation des effectifs des groupes à comparer. Le deuxième consiste à comparer les distributions, soit à l’aide d’une mesure de tendance centrale, la moyenne, une notion qui a été vue en classe, soit en considérant les effectifs relatifs pour des sous-groupes d’individus. Peu ont envisagé cette deuxième voie. La conviction qu’il fallait comparer des populations à effectifs égaux a permis de faire évoluer le groupe, comme nous l’avons observé, mais pouvait aussi mener à une impasse. C’est ce que montre le comportement de certains élèves au problème 2 présenté à la section suivante.
2. Le sexe/la couleur des cheveux
a) Analyse du problème posé
Avec ce problème, les élèves devaient trouver un moyen pour déterminer si les garçons de la classe, pris globalement, ont les cheveux plus foncés que les filles. Les données représentant la couleur des cheveux étant de nature qualitative, il n’est plus possible de recourir à des mesures de tendance centrale telle la moyenne, ni à un calcul de sommes. Ici encore, les deux groupes à comparer, celui des garçons (16) et celui des filles (7), ne comportent pas le même nombre d’éléments[9]. Une solution inadéquate mais probable consistait en une comparaison des effectifs en absolu : par exemple, les garçons ont les cheveux plus foncés, car il y a quatre garçons qui ont les cheveux noirs et seulement une fille. Par contre, une illustration telle la Figure 1, présentée la semaine précédente, constituait un moyen pertinent de répondre à la nouvelle question posée[10]. Avec cette deuxième question, il était particulièrement intéressant d’observer comment se comporteraient les élèves qui avaient calculé la moyenne des heures d’écoute de télévision au problème précédent. Nous voulions notamment savoir dans quelle mesure ils allaient récupérer la stratégie de l’équipe qui comparait les effectifs relatifs au premier problème (Figure 1).
b) Analyse des stratégies d’élèves
Les réponses formulées par les élèves dans les deux classes
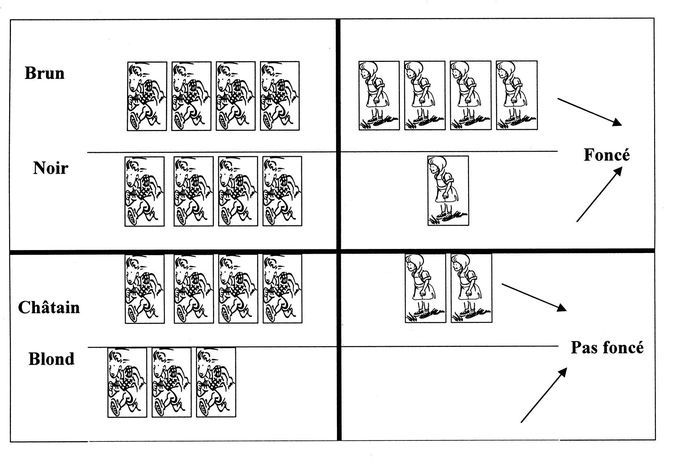
Presque tous ont utilisé une représentation semblable à la Figure 1 en comparant la portion de garçons aux cheveux foncés (noirs et bruns) à celle des filles aux cheveux foncés. Deux équipes y sont arrivées avec l’aide de l’animatrice qui, par son discours, a induit l’utilisation des rapports. Toutefois, quelques élèves n’ont pas produit cette solution. Parmi ceux-ci, se retrouvent ceux qui, au premier problème, avaient réalisé la Figure 2 (solution basée sur la comparaison de groupes de même taille). Les élèves ont dit explicitement qu’ils voulaient s’inspirer de la Figure 1, présentée la semaine précédente. Comme les autres, leur solution a consisté à grouper les élèves selon la couleur des cheveux en deux classes (foncés/clairs, Figure 3) sans toutefois qu’ils passent aux rapports : huit garçons ont les cheveux foncés contre seulement cinq filles, donc les garçons ont les cheveux plus foncés que les filles.
Figure 3
Problème 2 : groupement en classe
Ils n’envisageaient pas d’autres moyens malgré les objections des autres élèves. L’analyse des discussions montre bien la difficulté du passage d’une comparaison absolue des effectifs à une comparaison relative. Les élèves ont acquiescé au fait que les populations étaient de taille différente mais il fallait faire avec. Ils n’ont pas envisagé l’utilisation de rapports pour régler le problème d’effectifs différents. Notons que, dans cette équipe, les deux élèves qui avaient utilisé la moyenne au premier problème ont voulu ici comparer les rapports sans pouvoir y arriver, le dénominateur commun étant difficile à trouver.
Discussion
L’activité des statisticiens en herbe et la résolution de problèmes
Nous avons proposé aux élèves de réaliser le travail d’un statisticien (voir le cadre théorique) qui développe un moyen de répondre aux questions qu’il se pose à propos d’un corpus de données en l’illustrant. Nous montrerons que les élèves se sont engagés dans une telle activité en rapprochant l’activité de l’élève de l’activité du statisticien. Nous discuterons aussi des difficultés rencontrées.
Les élèves ont élaboré des moyens pour répondre à deux questions issues de leurs propres interrogations. La recherche de ces moyens a fait émerger des réflexions sur la pertinence des questions posées, sur la possibilité de comparer des populations à effectifs différents et sur les moyens qui pouvaient être envisagés pour le faire. Les moyens auxquels les élèves ont abouti se sont avérés riches. Dans le premier problème, devant la non-pertinence de comparer les sommes totales, les élèves ont envisagé de résumer ces données par une moyenne, notion préalablement vue en classe par certains, ou par des sommes (puisqu’il fallait déterminer lequel, parmi deux groupes, écoutait le plus la télévision). Comme le soulignent Doerr et English (2001), ainsi que Jones, Langrall, Thornton, Mooney, Wares, Jones, Perry, Putt et Nisbet (2001), cette opération de résumer appartient à la pensée statistique. L’absence de l’outil moyenne, dans le cas de la classe 2, a pu constituer un handicap pour les élèves confrontés au traitement inhabituel d’ensembles de données, surtout dans le cas où, comme ici, le recours à des sommes est inefficace. L’invention de cet outil ne paraît pas aller de soi, même si quelques indices nous laissent penser qu’un élève était sur la voie d’y arriver[11].
Par ailleurs, l’obstacle que présentait la comparaison de deux populations à effectifs différents a mené à envisager des moyens originaux pour permettre la comparaison. Plusieurs élèves ont cherché à égaliser les groupes en choisissant quatre individus parmi seize. Dans certaines équipes, le choix de ces quatre individus s’est raffiné au fil des discussions pour envisager un choix représentatif des données ou au hasard. Même si le procédé n’est pas au point, il contribue à la recherche d’une solution. Un élève a envisagé d’égaliser les groupes en élargissant le groupe de quatre individus à 16 en respectant les propriétés du groupe d’origine. Toutes ces solutions montrent une véritable activité statistique, dans la mesure où le statisticien se trouve constamment dans la situation de trouver le meilleur outil pour répondre aux questions qui lui sont posées. Nous pourrions y voir également des embryons de concepts statistiques tels que l’échantillon et la population parente. Quant à l’équipe qui a produit la figure 1, elle a groupé les données selon certaines caractéristiques : porter ou non des lunettes, écouter la télévision plus de 20 heures ou moins. Dans le problème 2, les élèves ont majoritairement regroupé les données en deux catégories : cheveux clairs et cheveux foncés. Cette opération de grouper, étrangère à l’arithmétique, est propre à la pensée statistique (Doerr et English, 2001 ; Jones et collab., 2001). L’établissement des classes (ou regroupements) doit se faire à partir de critères qui ne sont pas toujours évidents à déterminer. Soulignons aussi que la figure 1 constitue ce que les statisticiens appellent un tableau de contingence sur lequel il serait possible d’appliquer un test statistique, tel celui du Chi carré.
Parmi les illustrations utilisées par les élèves, nous ne retrouvons pas de diagrammes à pictogrammes ou à bandes, notions qui ont été abordées en classe dans les années antérieures. Cela est étonnant, puisque les images fournies aux élèves pouvaient les inciter à réaliser de tels diagrammes. Ou bien les élèves n’ont pas reconnu, dans les situations, les tâches habituellement associées à l’exécution de ces diagrammes, ou bien les élèves n’en avaient pas compris le rôle au moment où ils ont été enseignés. Outre ce constat, il faut noter qu’aucune équipe n’a eu tendance à ordonner les données dans le problème 1. Dans le problème 2, plusieurs ont ordonné de la couleur la plus claire à la plus foncée (blond, châtain, brun, noir), ou inversement, pour réaliser le groupement. Cette opération d’ordonner, aussi constitutive d’une pensée statistique (Doerr et English, 2001 ; Jones et collab., 2001), n’apparaît donc pas spontanément dans les problèmes à données quantitatives.
Le difficile passage à la comparaison relative des effectifs
Les travaux sur le développement de la pensée statistique soulignent l’importance du raisonnement multiplicatif. Notre étude, plus spécifiquement, illustre la difficulté à raisonner en termes de rapports.
En comparant le comportement des élèves aux deux problèmes, nous constatons que les élèves qui ont utilisé la moyenne comme production finale au premier problème passent à la comparaison des rapports au deuxième problème. Nous pouvons faire l’hypothèse qu’une compréhension de la moyenne comme rapport a permis ce passage. Nous constatons, cependant, que les élèves qui proposent une comparaison de groupes égaux (Figure 2) au premier problème ne passent pas d’emblée à la comparaison des effectifs relatifs au problème 2. Cela peut s’expliquer.
Dans le premier problème, les élèves pensent à comparer les données (le nombre d’heures d’écoute de la télévision), des sommes de données ou des moyennes (ce qui donne un résultat de même nature que les données – un nombre d’heures). De plus, ils réalisent rapidement que la comparaison des heures totales de télévision sans considérer l’effectif n’a pas de sens puisque l’effectif est différent. Plusieurs élèves envisagent alors de faire la moyenne ou de comparer des groupes à effectifs égaux ; peu passent à une comparaison relative des effectifs. Dans le problème 1, des voies alternatives à cette comparaison relative étaient donc possibles. Dans le problème 2, les seules données numériques connues sont des effectifs. Le raisonnement sur les effectifs devient nécessaire. Certains n’ont pas pu envisager cette possibilité, bien qu’ils aient vu la solution présentée à la figure 1 la semaine précédente. La considération des effectifs différents et la comparaison de ces effectifs de manière multiplicative apparaît donc particulièrement difficile pour certains élèves. Ces résultats rejoignent ceux connus quant aux difficultés associées au raisonnement proportionnel à l’âge de nos élèves (Levain, 1996).
Spécificités des élèves à risque
Pour les élèves à risque sujets de l’expérimentation, la présente recherche ne permet pas de pointer des difficultés sur le plan cognitif qui leur seraient spécifiques. Malgré tout, quelques idées ressortent de notre étude, qui méritent d’être soulignées et discutées.
Les élèves ont utilisé des stratégies variées qui montrent un génie mathématique. Même si les moyens envisagés pour résoudre ne sont pas toujours au point, leur utilisation s’appuie sur un raisonnement qui a du sens. De plus, les élèves ont utilisé des notions vues précédemment en classe, même si le moyen utilisé n’a pas toujours mené à une solution. Ces constats permettent de nuancer les résultats de recherches antérieures qui affirment que les élèves en difficulté présentent une certaine rigidité intellectuelle, que leurs stratégies sont peu développées et que la question posée n’est pas réellement prise en compte, phénomènes que Perrin-Glorian (1993) relie à leur difficulté à se représenter le problème. Lors de l’analyse des résultats, les tâches proposées aux élèves et l’approche utilisée sont à prendre en considération. Ainsi, les caractéristiques des situations problèmes que nous avons proposées (analyse de données réelles, recherche à partir de questions provenant des élèves, accent sur le moyen pour résoudre et non sur une réponse à trouver) peuvent avoir eu un effet bénéfique.
Par ailleurs, il faut bien souligner les difficultés rencontrées par les expérimentateurs. Dans certaines équipes, il est parfois apparu difficile de faire en sorte que les idées avancent. Les discussions stagnaient. Il arrivait qu’une idée soit oubliée aussitôt prononcée, même par l’élève qui l’avait émise. Toutefois, ce caractère volatile est aussi une caractéristique d’une intuition. Par moments, aussi, les élèves avaient de la difficulté à s’écouter. Dans certaines équipes, l’animateur a éprouvé de la difficulté à gérer la discussion. Les élèves étaient particulièrement indisciplinés et des préoccupations autres que celles visées par la tâche interféraient dans l’animation. La classe 2 était plus problématique à cet égard.
Les difficultés de la classe 2 peuvent s’expliquer par la présence importante d’élèves avec déficit d’attention et hyperactivité. L’absence de l’enseignante de la classe en début d’expérimentation peut également avoir contribué aux difficultés. Toutefois, il semble vraisemblable que le manque relatif de moyens des élèves de la classe 2, en comparaison avec la classe 1 (absence de l’outil moyenne, un raisonnement en termes de rapports vraisemblablement moins développé), ait également contribué à une certaine désorganisation de cette classe.
Par ailleurs, dans les situations proposées, le débat présentait certains aspects problématiques, du fait que la validation repose entièrement sur la confrontation des solutions. Pour juger de leurs résultats, les élèves ne disposaient ni de l’évidence que donnerait la validation d’un résultat de façon expérimentale, ni de celle que pourrait apporter une argumentation de nature déductive. Le rejet d’un moyen envisagé s’effectuait sur la base de sa vraisemblance ou de son invraisemblance : ça n’a pas de sens de comparer le nombre d’heures d’écoute en faisant la somme lorsque les groupes sont à effectif différent. La validation d’une réponse reposait sur l’assurance que leur donnait le moyen qu’ils utilisaient (le calcul de la moyenne, le calcul des sommes ou la comparaison des rapports) par rapport aux moyens rejetés.
Mais alors, comment décider qui a raison et comment faire bouger les élèves, convaincus de la légitimité de leur raisonnement ? Lorsqu’un élève en particulier a présenté sa solution devant la classe (comparaison des effectifs en absolu), ses camarades ont contesté. Devant cette contestation, l’élève s’est emporté et l’enseignante a dû contenir cet élève qui argumentait. Comme l’expérimentation se terminait, elle s’est permis de reprendre son rôle d’enseignante en faisant le lien entre la situation présentée et une situation de fractions vues en classe.
Pour comprendre le phénomène d’indiscipline dans ces classes, il importe de se questionner sur le rapport de ces élèves au savoir et d’analyser finement les interactions qui ont lieu au sujet de ce savoir, des comportements déviants pouvant en être le résultat. La situation décrite au paragraphe précédent aurait pu dégénérer. Les difficultés de compréhension entre les élèves peuvent être attribuées à un manque d’écoute ou à de l’indiscipline, mais elles peuvent aussi en être la cause. Une argumentation tenue en termes de rapports, incomprise par la plupart des élèves, peut s’expliquer par le saut conceptuel que nécessite à la fois le raisonnement sur les effectifs et le raisonnement multiplicatif. Les autres élèves peuvent décrocher parce qu’ils ne comprennent pas, ou celui qui avance le raisonnement peut décrocher parce que les autres ne l’entendent pas. Dans des classes multi-niveaux, il apparaît important de se pencher sur cette problématique lorsque le débat est utilisé à l’intérieur d’une situation problème. Notons que, si dans la classe 1[12], les élèves avaient cette culture de débattre de leurs solutions, ce n’était pas autant le cas dans la classe 2. Cette différence a pu également jouer un rôle déterminant pour l’engagement des élèves de la classe 2.
Implications sur le travail en classe
L’expérimentation montre clairement que des élèves de classes spécialisées peuvent produire des solutions riches et originales lors de situations problèmes statistiques. Plusieurs des solutions partent d’intuitions plus ou moins systématisées sur lesquelles il est possible de construire. Les méthodes utilisées par les élèves doivent être discutées, voire confrontées, avec celles de statisticiens d’expérience qui serviront à valider les stratégies des élèves. Les situations expérimentées pourraient avantageusement servir comme situations d’apprentissage pour le développement d’une pensée statistique, puisqu’elles incitent à mobiliser les notions de moyenne et de pourcentage, à faire des groupements, à raisonner multiplicativement. Il apparaît toutefois important de les inscrire dans une séquence d’activités à plus long terme. Nous pensons qu’à partir d’une connaissance approfondie des élèves et des moyens dont ils disposent pour aborder le problème, il serait souhaitable de greffer d’autres situations problèmes à celles proposées. Ainsi, nos situations auraient pu être précédées de situations demandant la comparaison de groupes à effectifs égaux, ce qui aurait sans doute été plus fécond dans la classe 2. Dans les situations expérimentées, les élèves de cette classe étaient confrontés au double problème de comparer des ensembles de données (ce qui n’est pas évident lorsque les comparaisons se sont faites jusqu’ici sur deux nombres seulement) et de tenir compte des effectifs différents, ce qui nécessite un raisonnement multiplicatif (un obstacle pour plusieurs élèves). La comparaison à effectifs égaux simplifie le problème, mais le moyen pour comparer les groupes reste à inventer.
Par ailleurs, nous avons vu que le problème de la couleur des cheveux a fait apparaître, de manière évidente, la difficulté à passer à une comparaison relative des effectifs. Certains élèves maintenaient une comparaison des effectifs de manière absolue, malgré la contestation des autres, prétextant qu’on est bien obligé de faire avec, qu’il faut répondre à la question, et qu’on ne peut pas inventer des individus. Cette difficulté avait été évitée dans le problème précédent, le calcul d’une moyenne ou la comparaison de sommes partielles étant possible. Il nous semble donc essentiel de soumettre aux élèves des problèmes très variés, pour que se développent une compréhension riche des situations statistiques et des moyens de résolution possibles. De plus, il apparaît aussi important que les élèves participent à l’élaboration des questions d’enquête, pour que l’activité d’enquête elle-même soit vue comme un moyen pour répondre à des questions que l’on se pose.
Sur un autre plan, les problèmes d’indiscipline et les difficultés d’animation notés par les chercheurs posent, d’une part, la question de l’encadrement à donner aux élèves en difficultés d’apprentissage lorsque sont mises en place des situations problèmes. Lors de l’expérimentation, une personne par équipe était chargée de l’animation ; dans la classe ordinaire gérée par un seul enseignant, l’encadrement des équipes de travail peut être problématique. D’autre part, nous pouvons nous interroger sur les conditions qui permettent l’engagement des élèves à l’intérieur des situations problèmes elles-mêmes. Les situations qui ont été proposées consistaient à inventer une méthode pour répondre à des questions, sorties du domaine réel, que se sont posées eux-mêmes les élèves ; d’où, sans doute, la variété et l’originalité des productions d’élèves. Les élèves sont entrés dans un processus de création. En même temps, ces situations fournissaient peu de moyens pour décider de la légitimité des façons de faire. L’animation dans chacune des équipes de travail devenait alors cruciale.
En lien avec la discussion plus haut, nous devons nous questionner sur la manière d’assurer une plus grande autonomie des élèves lors de la résolution de problème. Pour les situations expérimentées, nous n’avons pas de réponse précise, mais il semble primordial d’instaurer une culture de recherche et de débat dans la classe pour que de telles situations puissent fonctionner.
Implications sur la recherche
Les différences observées entre les élèves des deux classes expérimentales nous invitent à répéter l’expérience avec des élèves issus de classes aux caractéristiques différentes, dont des classes ordinaires du primaire. Le portrait des démarches des élèves permettrait éventuellement de préciser les différences entre les populations, d’étudier plus à fond les conditions d’engagement des élèves dans la tâche et d’étudier la place de l’élève à risque en classe ordinaire dans le processus de résolution de problème. Comme de plus en plus d’élèves en difficultés d’apprentissage sont intégrés à des classes ordinaires au Québec, on peut se demander quelle contribution ces élèves pourraient faire lors d’une activité similaire à l’intérieur d’une équipe hétérogène qui comporte des élèves beaucoup plus forts qu’eux. Dans le prolongement de l’étude présentée dans cet article, c’est l’objectif visé par une recherche en cours, qui propose une situation semblable à des élèves d’une classe ordinaire comportant certains élèves identifiés à risque par les enseignantes[13].
Par ailleurs, certains travaux réalisés antérieurement (Van Reeuwijk, 1992 ; Galmacci et Scrucca, 2000) et l’étude qui vient d’être rapportée montrant la richesse des productions des élèves nous laissent penser que le contexte statistique pourrait être utilisé de façon avantageuse pour le développement de compétences numériques chez les élèves en difficultés dans ce domaine. Des recherches sont à effectuer dans ce sens.
Conclusion
Dans le présent article, notre objectif était de décrire les stratégies d’élèves à risque de niveau fin primaire dans des situations de problèmes statistiques. Les résultats montrent que les équipes de travail ont été en mesure de développer des stratégies diversifiées, même si ce processus a parfois été ardu. Malgré le fait que certains comportements pouvaient être anticipés, compte tenu des caractéristiques des problèmes et des élèves, il n’y avait pas d’objectifs d’enseignement et nous n’avions pas d’attentes particulières quant à la solution à produire. Il nous apparaît important de donner aux élèves la possibilité de vivre de telles situations en les dégageant de toute attente spécifique sur le plan des notions mathématiques. Il nous paraît aussi essentiel que les situations soient assez inusitées et riches pour permettre le développement de raisonnements, en tenant compte des connaissances des élèves et de leurs caractéristiques. De plus, il se peut que le domaine de la statistique offre une occasion de travailler positivement avec les élèves à risque, dits en difficultés d’apprentissage. Le domaine statistique, encore nouveau dans la classe, pourrait porter, moins que les autres domaines mathématiques, le poids des connaissances et se retrouver alors moins connoté négativement par les élèves à risque.
Parties annexes
Notes
-
[1]
Le ministère de l’Éducation du Québec (2000, p. 5) identifie comme élèves à risque ceux qui, entre autres, présentent des retards d’apprentissage ou des difficultés pouvant mener à l’échec. C’est le sens que nous donnons à élève à risque dans cet article.
-
[2]
Quelques recherches se sont intéressées au raisonnement statistique d’élèves au primaire (citons, par exemple, Lehrer et Romberg, 1996, et Rigatti Luchini et collab., 2000), mais à notre connaissance, aucune ne porte spécifiquement sur les élèves à risque.
-
[3]
Au Québec, les élèves de 6e année ne présentant pas de retard ont entre 11 et 12 ans. À 13 ans, les élèves passent nécessairement dans un établissement secondaire.
-
[4]
Dans cet article, nous ne pouvons présenter une analyse détaillée de toutes les questions formulées par les élèves. En voici quelques exemples, parmi lesquels certains montrent des lacunes de formulation et d’autres posent des questions auxquelles le tableau ne donne pas de réponse : La moyenne d’âge selon les élèves ? Combien de personnes qui prennent le train ? Combien de personnes entre les deux classes ? Quelle est la différence de moyenne entre la classe de Céline (nom fictif) et la classe de Michèle (nom fictif) dans les heures de télévision ? Qui est le plus maniaque de télévision ? Combien de kilomètres parcourons-nous ensemble pour venir à l’école ? Pourquoi ça prend plus de temps àcertaines personnes pour se rendre à l’école si elles font moins de kilomètres ?
-
[5]
Si ces questions ne s’étaient pas présentées, nous en aurions proposées de semblables aux élèves.
-
[6]
Au Québec, écouter la télévision est utilisé au lieu de regarder la télévision.
-
[7]
Par exemple, le choix de donner la parole à une personne en premier peut déterminer la suite des événements.
-
[8]
Dans cette classe, un élève a d’abord choisi quatre individus parmi ceux qui ne portent pas de lunettes (les quatre derniers de la liste), afin de les comparer aux quatre individus qui portent des lunettes, pour finalement envisager un choix au hasard, à la suite de l’objection d’un coéquipier.
-
[9]
Pour ne pas obtenir les mêmes nombres qu’au problème précédent, nous avons demandé aux élèves d’ajouter aux données la couleur des cheveux des deux enseignantes et celle d’une nouvelle élève.
-
[10]
Précisons que, comme les élèves de la deuxième classe ont été moins productifs au premier problème que ceux de la première classe et qu’ils ont demandé à voir les affiches préparées par l’autre classe, nous les leur avons montrées. La figure 1 leur avait aussi été présentée la semaine précédente.
-
[11]
Un élève utilise le mot moyenne, en envisageant certaines compensations. Le discours est flou et loin d’être opérationnel, mais on y trouve une idée de ce qu’est la moyenne.
-
[12]
Plusieurs élèves de la classe 1 ont participé à des expérimentations avec débat les années précédentes, et l’enseignante de la classe privilégiait cette façon de faire dans son enseignement régulier.
-
[13]
Recherche subventionnée par le FQRSC, sous la responsabilité de Laurent Theis.
Références
- Artigue, M. (1996). Ingénierie didactique. Dans J. Brun (Dir.) : Didactique des mathématiques. Lausanne, Suisse : Delachaux et Niestlé.
- Astolfi, J.-P. (1993). Placer les élèves dans une situation problème ? Probio-Revue, 16(4), 311-321.
- Bakker, A. (2001). Symbolizing data into a « bump ». Proceedings of the 25th International Conference for the PME, 2, Utrecht, Netherlands : Utrecht University.
- Cai, J. (1995). Beyond the computational algorithm : students’understanding of the arithmetic average concept. Proceedings of the 19th International Conference for the PME. Pernambuco, Brasil : Universitad Federal de Pernambuco.
- Cange, C. et Favre, J.-M. (2003). L’enseignement des mathématiques dans l’enseignement spécialisé est-il pavé de bonnes analyses d’erreurs ? Éducation et francophonie, 21(2). [En ligne]. Disponible le 19 décembre 2007 : http://www.acelf.ca/c/revue/revuehtml/31-2/09-cange.html
- Cobb, P. (1999). Individual and collective mathematical development : the case of statistical data analysis. Mathematical Thinking and Learning,1(1), 5-43.
- Conne, F. (1999). Faire des maths, faire faire des maths et regarder ce que ça donne. Dans G. Lemoyne et F. Conne (Dir.) : Le cognitif en didactique des mathématiques. Montréal, Québec : Presses de l’Université de Montréal.
- Conne, F. (2003). Interactions de connaissances et investissement de savoir dans l’enseignement des mathématiques en institutions spécialisées. Éducation et francophonie, 31(2), 81-102.
- Doerr, H., and English, L. (2001). A modeling perspective on students’ learning through data analysis. Dans M. Van den Heuvel-Panhizen (Dir.) : Proceedings of the 25th International Conference for the PME, 2. Utrech, Netherlands : Utrech University.
- Focant, J. (2003). Impact des capacités d’autorégulation en résolution de problèmes cez les enfants de 10 ans. Éducation et francophonie, 31(2), 45-64
- Galmacci, G. et Scrucca, L. (2000). Strategie didattiche per l’insegnamento della statistica : alcuni risultati di una sperimentazione. Giornate di studio sull’insegnamento della statistica, Roma, dicembre 2000.
- Gattuso, L., and Mary, C. (1996). Development of concept of arithmetic average from high-school to university. Proceedings of the 20th International Conference for the PME. Valencia, España : Universidad de Valencia.
- Jones, G., Langrall, C., Thornton, C., Mooney, E., Wares, A., Jones, M., Perry, B., Putt, I., and Nisbet, S. (2001). Using student’s thinking to inform instruction. Journal of Mathematical Behavior,20(1), 109-144.
- Kamii, C. (1996). La théorie de Piaget et l’enseignement de l’arithmétique. Perspectives, 26(1), 105-118.
- Lehrer, R., and Romberg, L. (1996). Exploring children’s data modeling. Cognition and Instruction, 14(1), 69-108.
- Lemoyne, G. et Lessard, G. (2003). Les rencontres singulières entre les élèves présentant des difficultés d’apprentissage en mathématiques et leurs enseignants. Éducation et francophonie, 21(2). [En ligne]. Disponible le 19 décembre 2007 : http://www.acelf.ca/c/revue/revuehtml/31-2/01-lemoyne.html
- Levain, J.-P. (1996). Développement cognitif et apprentissage de la proportionnalité. Revue européenne de psychologie appliquée, 46(2e trimestre), 131-138.
- Mary, C. (2003). Interventions orthopédagogiques sous l’angle du contrat didactique. Éducation et francophonie, 31(2).
- Mevarech, Z. (1983). A deep structure model of students’ statistical misconceptions. Educational Studies in Mathematics, 14(4), 415-429.
- Ministère de l’Éducation du Québec (2000). Élèves handicapés ou élèves en difficultés d’adaptation ou d’apprentissage (EHDAA). Définitions. Québec, Québec : Gouvernement du Québec.
- Ministère de l’Éducation du Québec (2001). La formation à l’enseignement. Les orientations. Les compétences professionnelles. Québec, Québec : Gouvernement du Québec.
- Pericola Case, L., Harris, K. R., and Graham, S. (1992). Improving the mathematical problem-solving skills of students with learning disabilities : self-regulated strategy development. The Journal of Special Education, 26(1), 1-19.
- Perrin-Glorian, M.-J. (1993). Questions didactiques soulevées à partir de l’enseignement des mathématiques dans des classes « faibles ». Recherche en didactique des mathématiques, 13(1/2), 5-18.
- Rigatti Luchini, S., Perelli D’Argenzio, M. P., Moncecchi, G., and Giambalvo, O. (2000). Teaching statistics at primary and secondary school : an Italian research. Proceedings of the International Conference « Mathematics for living : The Mathematics Education Into The 21st Century Project ». Amman, Giordania.
- Van Reeuwijk, M. (1992). The standards applied : teaching data visualization. The Mathematics Teacher, 85(7), 513-518.
Liste des figures
Figure 1
Problème 1 : groupements et comparaison des effectifs relatifs
Figure 2
Problème 1 : comparaison de groupes de même taille
Figure 3
Problème 2 : groupement en classe
Liste des tableaux
Tableau 1
Extrait du tableau de compilation des données présenté aux élèves