Corps de l’article

Introduction

Les recherches classiques, menées en didactique des mathématiques, pour comprendre comment se construit la connaissance, ont motivé l’étude du rôle que jouent les représentations mentales. Pendant longtemps, les chercheurs se sont penchés sur le concept de schème, ce qui a provoqué l’étude approfondie du rôle des représentations mentales. Une des premières idées qui a surgi de cette étude est que la construction des concepts à travers les schèmes était une construction hiérarchisée. C’est, par exemple, le cas de Skemp (1971) qui s’est penché sur la construction des schèmes et sur le caractère hiérarchique des concepts, comme nous allons le voir plus loin. Malheureusement, l’insistance mise sur les représentations mentales a produit une diminution de l’intérêt des chercheurs pour les représentations sémiotiques.

Aujourd’hui, les nouvelles approches psychologiques nous montrent que les concepts ne définissent pas une hiérarchie, au sens strict (Richard, 1998, p. 54-56). Par ailleurs, une nouvelle approche sur les schèmes a donné lieu à la notion de schéma. Richard, en particulier, développe et raffine l’étude sur la construction de schémas et de réseaux sémantiques. À ce sujet, il donne (Ibid., p. 70-71) une caractérisation des schémas de connaissance qui sont : des blocs de connaissances, des objets complexes, des structures générales et abstraites, et des expressions de connaissances déclaratives. Nous reviendrons sur ce point plus tard.

On constate une évolution des aspects théoriques en général : les exemples utilisés pour expliquer les nouvelles approches ont été pris dans la vie quotidienne. Cela nous amène à nous demander si la construction des concepts mathématiques suit la même voie que la construction des concepts en connexion avec la vie quotidienne. Pour Duval (1993, 1995, 2002), la réponse est non, et c’est son point de vue sur la construction des concepts mathématiques que nous allons présenter.

En analysant les travaux de Duval (1993, 1995), nous avons constaté que l’emphase qu’il a mise sur la construction des concepts mathématiques à travers les représentations sémiotiques est très justifiée. Cependant, il nous semble que son approche se rattache « aux représentations officielles » (représentations sémiotiques qu’on trouve dans les manuels, ou que les enseignants utilisent dans leurs cours de mathématiques, etc.). De ce point de vue, nous pourrions dire que son approche utilise des représentations statiques.

Pour notre part, nous voulons prendre en considération le rôle des représentations mentales qui nous amènent à la production des représentations sémiotiques pour mieux comprendre un énoncé mathématique et, ainsi, faire un lien entre les différentes représentations en jeu lors de la résolution d’un problème. Pour ce faire, nous nous attarderons au rôle des représentations sémiotiques produites par une étudiante lors de la résolution d’un problème (représentations qui ne sont probablement pas des représentations officielles) et de leur caractère fonctionnel pour la compréhension. Afin d’analyser le rôle des représentations dans la construction des concepts mathématiques et dans la résolution de problèmes sous le même angle, nous nous inspirerons de quelques travaux de recherche traitant des aspects mentionnés ci-dessus. Nous commencerons notre analyse avec l’idée de schème.

La notion de schème et la construction de concepts

En premier lieu, nous présenterons la notion de schème développée par Skemp (1971) dans The psychology of learning mathematics. Skemp (Ibid.) a travaillé sur la construction de concepts en général et sur la construction de concepts mathématiques en particulier. Une partie de son développement est le suivant :

Nous considérons les concepts comme des adaptations aux structures conceptuelles appelées schèmes.

Abstraire et classifier – Nous classifions chaque fois que nous reconnaissons un objet.

Abstraire – Il s’agit d’activité au moyen de laquelle nous arrivons à être conscients des similitudes.

Classifier – C’est rassembler nos expériences sur les bases de ces similitudes.

Un concept a donc besoin pour sa formation d’un certain nombre d’expériences, lesquelles ont quelque chose en commun. Un concept est un objet purement mental.

p. 19-21

Toujours en lien avec l’idée de schème et de hiérarchie, Skemp (Ibid.) continue :

Chacun de ces concepts par nature est à l’intérieur d’une structure formée avec d’autres concepts. Chacun d’eux se dérive des antérieurs et contribue à la formation de nouveaux concepts, c’est-à-dire, ils font partie d’une hiérarchie […]. Comprendre quelque chose signifie l’assimiler dans un schème approprié.

p. 35-43

Nous pouvons observer qu’à l’époque, on concevait l’idée classique de hiérarchie comme étant la plus importante dans la construction des connaissances. En effet, comme Richard (1998, p. 54) le signale, il y a une relation qui privilégie les concepts les uns par rapport aux autres et cette relation, c’est celle d’emboîtement de classes. De ce point de vue, les classes sont homogènes et parfaitement délimitées. Il y a eu beaucoup de recherches pour montrer la non-homogénéité des classes. Un exemple bien connu du « phénomène de typicité » dans l’apprentissage de la probabilité est celui de Fischbein (1987).

Skemp (1962, 1971) donne deux types d’exemples quand il parle de sa théorie sur la construction des connaissances. Un des exemples qu’il utilise est celui du concept de « chaise » pour montrer que nous classifions chaque fois que nous reconnaissons certaines similitudes. Dans son article écrit en 1962, Skemp a voulu introduire dans le monde anglophone les idées de Piaget sur les schèmes. À cet effet, il a fait une expérimentation en utilisant des symboles pour désigner des personnes, des objets, des actions, etc., et il a essayé de construire un schème congruent avec ces symboles.

Dans son expérience, il a proposé le même type de symboles à deux groupes d’étudiants ; l’idée poursuivie étant de construire deux schèmes artificiels en suivant deux approches différentes. Skemp (1962) montre clairement la différence entre deux types d’apprentissage. Il affirme que le schème construit par les étudiants dans l’ambiance papier et crayon est plus stable que la construction des connaissances par coeur. Bien qu’ayant souligné l’importance des productions des étudiants en ambiance papier et crayon, nous devons prendre en considération que, dans son exemple, la construction de schèmes a suivi un chemin direct et qu’il a donné les symboles. La construction des concepts suit-elle un chemin similaire ? Même sans parler de la construction des concepts mathématiques, nous avons vu, précédemment, que Richard (1998) répondait par la négative à cette question. Il est alors naturel de penser que la construction des concepts mathématiques suit un chemin différent. Nous allons poursuivre notre argumentation dans ce sens, en essayant de montrer la complexité de la construction des concepts mathématiques, tout en revenant sur l’instabilité des connaissances.

La notion de schéma

Richard (1998) a fait évoluer l’idée de schème pour l’amener à une nouvelle notion qu’il a appelé schéma. Pour y arriver, il a utilisé la notion de réseau sémantique, une notion déjà connue. Un réseau sémantique est composé de noeuds et d’arcs ; les noeuds sont les concepts et les arcs sont les relations entre les concepts. Alors, en utilisant cet aspect théorique de réseau sémantique, Richard (Ibid.) donne une caractérisation des schémas de connaissance :

  • les connaissances sur les objets (les concepts) et leur organisation en réseau sémantique ;

  • les connaissances sur les situations et les événements exprimés par des schémas ;

  • les connaissances sur les actions et, plus généralement, les procédures (p. 53).

De ce point de vue, les concepts sont organisés à travers un réseau sémantique. Un point important dans le travail de Richard, c’est l’explication qu’il donne du processus qui mène à la compréhension. Pour lui, comprendre, c’est construire une structure conceptuelle.

Richard (Ibid., p. 97), en faisant un réseau propositionnel, montre à l’aide d’une représentation figurale les noeuds, les arcs et les concepts qui sont mentalement mis en jeu (construction d’une structure conceptuelle temporelle) pour comprendre ce texte. Ainsi, nous pouvons dire que l’approche de Richard est liée aux concepts quotidiens, à titre d’exemple, le concept « voyager ». Nous pouvons alors poser la question suivante : la construction des concepts mathématiques suit-elle un chemin similaire à celui montré par Richard pour la construction des concepts quotidiens ?

Cette question a été reprise par plusieurs chercheurs qui se questionnent sur la construction des concepts mathématiques, en prenant en compte des idées de réseau sémantique. Ces chercheurs se questionnent aussi sur la stabilité des connaissances (Hiebert et Carpenter, 1992). À partir de l’idée de schème, Vergnaud (1994) développe une nouvelle approche théorique :

En affinant progressivement la définition d’un schème, je dirai d’abord que c’est une totalité dynamique fonctionnelle, c’est-à-dire quelque chose qui fonctionne comme une unité ; en deuxième lieu, que c’est une organisation invariante de la conduite pour une classe de situations données (l’algorithme est un cas particulier de schème) ; et en troisième lieu, qu’un schème est composé de quatre catégories d’éléments :

  • des buts, intentions et anticipations ;

  • des règles d’action ;

  • des invariants opératoires ;

  • des possibilités d’inférence en situation.

p. 180-181

Dans le même sens, Brun (1994, p. 73) fait remarquer le caractère fonctionnel des représentations. La construction des concepts mathématiques, et en général celle des structures cognitives, a été reprise de façon à intégrer les résultats de la recherche sur la résolution de problèmes. Nous voulons faire émerger ce point de vue et, ainsi, nous rapprocher du problème de la construction des structures cognitives liées aux connaissances mathématiques.

Les structures cognitives

Du point de vue de Perkins et Simmons (1988), les erreurs que font les étudiants dans les activités mathématiques sont dues à une carence de structures cognitives. Cette carence ne permet pas à l’étudiant de réaliser les connexions nécessaires dans la résolution d’un problème ou d’aller plus loin dans un problème déjà résolu. Ces structures sont en relation directe avec la compréhension. Perkins et Simmons (Ibid.) distinguent quatre types de structures : la structure des connaissances du contenu, des connaissances en résolution de problèmes, inquisitoire et épistémique. Ils font aussi remarquer que l’enseignement des mathématiques se limite, en général, à la structure de contenu (enseigner un contenu mathématique), point de vue classique de l’enseignement, ou à celle de résolution de problèmes, nouvelle approche qui est déjà prise en compte dans le curriculum (par exemple, les Standards and principles du National Council of Teachers of Mathematics, 2000). Les structures inquisitoires (se questionner sur ce qu’on a fait et sur la généralisation du résultat) et les structures épistémiques sont, quant à elles, généralement délaissées. Au sujet de cette dernière structure, Perkins et Simmons (1988) écrivent à ce sujet que

[c]ette structure incorpore la maîtrise de normes spécifiques et générales, en plus de stratégies concernant la validation d’affirmations dans le domaine. À l’intérieur d’un domaine bien développé, les « faits spécifiques » dans la structure de contenu sont validés au moyen de normes établies dans la structure épistémique.

p. 305

Perkins et Simmons (Ibid.) soutiennent qu’une réelle compréhension des mathématiques dépend de ces quatre structures. Alors, pour éclaircir notre propos au sujet des structures de contenu et épistémique, nous allons donner l’exemple de la discussion qu’il y a eu dans une classe de mathématique entre un étudiant et une étudiante, spécifiquement, au sujet de la formule du carré du binôme.

Cet exemple montre avec clarté la différence entre la structure de contenu « tu sais la formule » et la structure épistémique « il y a plusieurs manières de réaliser ce calcul » dans le sens de Perkins et Simmons (Ibid.).

Par contre, il semble que leur approche sur les structures cognitives est très générale. Nous sommes partiellement d’accord sur le fait qu’il existe effectivement une structure épistémique, mais, de notre point de vue, elle est beaucoup plus complexe. Un point essentiel c’est de savoir comment construire cette structure épistémique.

Les différentes approches théoriques que nous avons analysées jusqu’ici, parlent des constructions mentales et presque tous les exemples qui y sont donnés sont liés aux situations quotidiennes (sauf le dernier qui est notre exemple), et ils ne tiennent pas compte, de façon primordiale, des représentations sémiotiques dans la construction des réseaux sémantiques et dans la construction des concepts mathématiques.

Depuis les travaux de Janvier (1987), les études sur les représentations ont été reprises sérieusement. Dans ce sens, l’approche théorique de Duval (1993, 1995) nous semble très importante, car il analyse en profondeur le rôle des représentations sémiotiques dans la construction de concepts mathématiques.

Les représentations sémiotiques dans la construction des concepts mathématiques

Nous savons que les objets mathématiques ne sont pas directement accessibles au moyen des sens, mais seulement à travers des représentations sémiotiques. C’est pourquoi il est important d’analyser le rôle que jouent celles-ci dans la construction de la connaissance mathématique. Les études expérimentales de Duval (1988, 1993, 1995), qui s’insèrent dans l’étude des difficultés d’utilisation des représentations dans un système mathématique de signes et sur les difficultés de conversion des représentations entre plusieurs systèmes en connexion à un même objet mathématique, ont généré une nouvelle notion qui est celle du registre de représentation, dont l’idée est totalement liée aux fonctions essentielles à toutes les activités cognitives. Duval (1993) caractérise un système sémiotique, un registre, comme un système de représentation, de la manière suivante :

Figure 1

Modèle de la représentation centrée sur la fonction d’objectivation

Modèle de la représentation centrée sur la fonction d’objectivation

Les flèches 1 et 2 correspondent aux transformations internes d’un registre. Les flèches 3 et 4 correspondent aux transformations externes, c’est-à-dire à des conversions par changement de registre. La flèche C correspond à ce que nous appellerons la compréhension intégrative d’une représentation : elle suppose une coordination de deux registres. Les flèches en pointillé correspondent à la distinction classique entre représentant et représenté. Naturellement, ce schéma, envisage le cas le plus simple de la coordination entre deux registres.

Duval, 1995, p. 67-68

-> Voir la liste des figures

Quand Duval (1993, p. 46) parle de la construction de concepts mathématiques, il établit qu’étant donné que chaque représentation est partielle dans ce qu’elle représente, nous devons considérer comme absolument nécessaire l’interaction entre différentes représentations de l’objet mathématique pour la formation du concept. Alors, les activités de traitement à l’intérieur des registres et les activités de conversion entre représentations d’un registre dans un autre registre, génèrent leur intégration et, par conséquent, ces activités aident à la construction des concepts. C’est-à-dire que l’importance que Duval (1993) accorde aux tâches de conversion, entre représentations pour la construction des concepts mathématiques, est un aspect essentiel de son travail. En conséquence, Duval n’accorde pas la primauté au système algébrique pour la construction desdits concepts comme le font d’autres chercheurs. En effet, il fait une analyse approfondie des problèmes cognitifs liés aux processus de transformations dans le même registre ainsi que des problèmes cognitifs créés par le passage d’une représentation à une autre.

L’une des conséquences importantes que l’on peut tirer des travaux de Duval (Ibid.) est que la construction d’un concept se fait lorsqu’il y a une coordination sans contradictions entre les différentes représentations de l’objet mathématique. Nous devons souligner que, vu sous cet angle, le concept est toujours en construction. Nous pouvons cependant faire quelques objections au travail de Duval. En premier lieu, nous pensons qu’une trop grande importance est donnée, implicitement, aux représentations officielles (celles qu’utilisent les enseignants et celles que nous trouvons dans les manuels) et que, par conséquent, les représentations sémiotiques des élèves lors de la résolution d’un problème et lors de la construction des concepts mathématiques n’ont pas, implicitement, l’importance qu’elles devraient avoir. En deuxième lieu, Duval met de côté les constructions intermédiaires et les conceptions qui jouent un rôle quelquefois d’aide et quelquefois d’obstacle pour la construction d’un concept mathématique (Hitt, 1998b, 2003).

Pour analyser de près les représentations sémiotiques produites par des élèves lors de la résolution de problèmes, nous voulons introduire les résultats d’une enquête qui montre le bien-fondé de lier l’approche théorique de Duval avec d’autres considérations théoriques.

Instabilité des structures liées à la résolution de problèmes du point de vue arithmétique et algébrique

Dans un projet sur l’instabilité des habiletés arithmétiques et algébriques (Hernàndez, 1999 ; Hitt, 2000), nous avons eu l’occasion de faire passer un questionnaire à deux très grandes populations. La première était composée de 3508 étudiants d’environ 14 ans (fin du 1er cycle de l’école secondaire au Mexique, 12-14 ans). La seconde était composée de 6 230 étudiants d’environ 17 ans ayant terminé le 2e cycle secondaire (le 2e cycle précède l’université, 15-17 ans). L’examen consistait en 70 questions sur des sujets divers (géographie, littérature, etc.), et 30 questions (voir annexe) d’arithmétique et d’algèbre que nous avions voulu tester en rapport avec notre recherche. Les deux populations ont eu exactement ces 30 questions en commun. Parmi les questions, on trouvait 10 problèmes qui pouvaient être résolus, soit par une approche arithmétique, soit par une approche algébrique.

Ce que nous voulions savoir à travers cette recherche, c’est si l’apprentissage usuel de l’algèbre comme « outil plus puissant que l’arithmétique » allait améliorer les performances des élèves. Plus précisément, les habiletés développées par les élèves lors de la résolution de problèmes algébriques allaient-elles améliorer les résultats des élèves plus âgés ? Notre hypothèse était que non. En effet, nous craignions qu’un apprentissage de l’algèbre qui ne mettrait pas en évidence une articulation entre les habiletés arithmétiques et algébriques provoquerait un apprentissage du type instrumental (Skemp, 1978), ce qui entraînerait, après quelques années, la diminution des habiletés arithmétiques. En résumé, nous pensions que la primauté de l’algèbre sur l’arithmétique dans l’enseignement secondaire allait faire diminuer les habiletés arithmétiques.

Selon ce point de vue, notre question de recherche était : les problèmes cognitifs, lors du passage de l’arithmétique à l’algèbre, ont-ils trop attiré notre attention et nous ont-ils empêchés de regarder attentivement les problèmes de construction d’une articulation entre les habiletés arithmétiques et les habiletés algébriques ?

Les 10 problèmes que nous avions choisis pouvaient être résolus, soit par une approche arithmétique, soit par une approche algébrique. En voici un exemple :

Nous avons isolé les étapes importantes de la résolution de chacun des problèmes, et nous avons créé des exercices d’arithmétique ainsi que des exercices d’algèbre en lien avec les contenus de chacun des problèmes. À titre d’exemple, pour le problème 3, nous avons demandé de résoudre les questions : « Calculer : forme: 012672aro002n.png ou « Trouver la valeur de x dans x – 0,15 x = 14,50 ». Les questions d’arithmétique (10), d’algèbre (10) et les problèmes (10) ont été placées à des endroits différents du questionnaire (voir les 30 questions en annexe).

Les exercices d’arithmétiques portaient sur l’addition, la soustraction, la multiplication et sur la division de nombres décimaux similaires à ceux utilisés dans les énoncés des problèmes. De la même manière, les questions de type algébrique étaient liées à la résolution d’équations, à une ou deux inconnues, et dont les coefficients étaient des nombres entiers ou décimaux. Les problèmes ont été choisis de manière à ce que la résolution puisse être faite, soit par l’arithmétique, soit par l’algèbre.

Les résultats globaux à ces 30 questions sont illustrés aux figures 2, 3 et 4. Dans la figure 2, nous avons représenté le pourcentage des élèves qui ont réussi aux 10 questions d’arithmétique. Dans la figure 3, le pourcentage des élèves qui ont réussi aux 10 questions d’algèbre et finalement, dans la figure 4, nous trouvons les résultats globaux aux 10 problèmes.

Figure 2

Réussite aux questions d’arithmétique

Réussite aux questions d’arithmétique

-> Voir la liste des figures

Nous pouvons observer qu’il n’y a pas de différence significative entre les deux populations en ce qui concerne les exercices d’arithmétique. Leurs connaissances des décimaux n’évoluent pas avec l’augmentation de la scolarité (3 ans).

Figure 3

Réussite aux questions d’algèbre

Réussite aux questions d’algèbre

-> Voir la liste des figures

En ce qui concerne les habiletés algébriques, nous pouvons noter une légère amélioration chez les élèves qui ont trois ans d’études de plus, mais elle n’est pas réellement significative. De plus, nous pouvons remarquer que cette amélioration porte uniquement sur la résolution d’équations qui nécessitent la manipulation de nombres entiers. Ce résultat n’a rien d’étonnant puisqu’on revient sur l’algèbre lors du premier cours du 2e cycle d’études secondaires. La question qu’on est cependant en droit de se poser est : l’enseignement de l’algèbre se fait-il majoritairement avec des nombres naturels ?

Figure 4

Réussite aux problèmes globaux

Réussite aux problèmes globaux

-> Voir la liste des figures

Si les résultats dans le cas de l’arithmétique et l’algèbre sont faibles, dans le cas des habiletés de résolution de problèmes, ils le sont encore davantage. Cette difficulté est probablement liée à ce qu’exprime Richard (1998) sur la compréhension des énoncés. « Comprendre, c’est construire une structure conceptuelle […] Il faut alors construire ces relations au fur et à mesure de la lecture du texte » (p. 96).

Il nous semble que, globalement, il n’y a pas eu de différence significative entre les résultats obtenus par les deux populations, bien que trois ans de scolarité les séparent. Devons-nous tirer la conclusion que les étudiants ont appris l’algèbre comme étant un outil plus puissant que l’arithmétique, mais que trois ans plus tard, ils ne sont pas réellement capables de s’en servir plus efficacement ?

Les étudiants des deux échantillons ont privilégié l’algèbre pour la résolution des problèmes. Cependant, il est étonnant de constater que, tout en privilégiant l’approche algébrique, les étudiants éprouvent des difficultés importantes lors des manipulations nécessaires à la résolution des problèmes et des exercices correspondants. Cela voudrait-il dire que les étudiants ont perdu leurs habiletés arithmétiques sans pour autant posséder de solides habiletés algébriques ? L’enseignement des mathématiques au secondaire met-il l’accent sur l’algèbre sans autant promouvoir une articulation entre les deux types d’habiletés ?

Il nous semble qu’il existe plusieurs difficultés qui empêchent d’améliorer la pratique scolaire. Les enseignants n’ont pas été éduqués dans une ambiance de résolution de problèmes ; c’est difficile de leur faire adopter un curriculum qui va dans ce sens (Standars, 2000). Peut-être est-ce plus facile d’instaurer un curriculum dans lequel on peut utiliser plusieurs représentations (verbale, graphique, numérique et algébrique) et des tâches de passage d’une représentation à une autre comme la théorie de Duval (1993, 1995). Mais, on a commencé à faire exactement cela dans l’enseignement depuis la moitié de la décennie des années 1990. Peut-être que l’approche adoptée ne tient-elle pas compte de certaines difficultés cognitives comme, à titre d’exemple, celles soulevées par Duval. On ne prend en compte que le côté facile qui consiste seulement à proposer des tâches mécaniques sur le passage d’une représentation à une autre.

À l’heure actuelle, nous croyons qu’il nous manque, spécifiquement, des résultats de recherche sur l’articulation entre l’arithmétique et l’algèbre. Plus précisément, nous nous interrogeons sur les recherches à faire pour préserver les habiletés arithmétiques tout en développant les habiletés algébriques. Si on pense que la théorie des représentations est importante pour l’enseignement des mathématiques, et nous croyons vraiment qu’elle l’est, nous devons approfondir le rôle des représentations sémiotiques dans la construction des connaissances.

Nous voulons reprendre l’idée de Perkins et Simmons (1988) sur les structures cognitives, mais d’un point de vue plus spécifique, avant de nous plonger dans une nouvelle approche sur l’étude des représentations sémiotiques pour la construction des concepts mathématiques et la résolution de problèmes.

La contradiction logique et la contradiction cognitive

Avant d’aborder le coeur de cette partie, nous insistons sur l’existence de schémas contradictoires chez un même individu. En effet, nous pouvons constater que, par exemple, dans la construction de procédures ou de concepts, il peut y avoir des schémas qui s’opposent à la construction adéquate de cette procédure ou de ce concept. Parfois, on peut construire un schéma alternatif (un enseignement adéquat pourrait permettre de mettre en place un schéma plus approprié), mais le premier ne disparaît pas pour autant. Dans certains cas, l’ancien schéma peut resurgir chez un individu, lorsqu’on lui présente une activité plus complexe, et provoquer la même erreur qu’auparavant, mais dans le cadre de cette nouvelle activité.

Les incohérences existant entre deux schémas provoquent des conflits internes que les étudiants devront résoudre peu à peu. En effet, la construction d’une nouvelle connaissance, qui va déplacer la connaissance plus ancienne qui ne fonctionne que dans certaines situations, et qui ne fonctionne plus dans une nouvelle situation, sera difficile à faire. En fait, ce que nous faisons régulièrement, c’est la construction de conceptions. S’il existe chez un individu deux conceptions contradictoires, nous avons besoin d’une activité qui puisse donner à l’étudiant la possibilité de se rendre compte de la contradiction où il est plongé (tableau 1).

Tableau 1

Résultats obtenus dans la résolution de l’inéquation

Résultats obtenus dans la résolution de l’inéquation

-> Voir la liste des tableaux

Dans ce contexte, et en lien avec les obstacles épistémologiques (dans le sens de Brousseau, 1983, 1997 et Duroux, 1983), le dépassement d’un obstacle de ce type est lié à une activité mathématique riche où l’individu est immergé dans un processus de questionnement sur la nature de ses conceptions et, où il réalisera lui-même une reconstruction, ou une nouvelle construction, d’un schéma qui jouera un rôle significatif dans des situations qu’auparavant il ne maîtrisait pas. La construction de ce nouveau schéma doit avoir une relation avec un réseau de connaissances plus ample qui déplace l’ancien schéma de telle sorte que cette nouvelle construction peut, grâce à l’amplitude du réseau auquel elle est reliée, être plus efficace. Cependant, il faut dire qu’il n’est pas facile de déceler quand une personne a construit un schéma adéquat. En effet, celui-ci peut se développer à travers des activités qui ne sont pas forcément reliées à des activités scolaires.

Voyons un exemple d’une recherche importante sur la contradiction cognitive. Dans une étude réalisée sur une population de 300 étudiants de 4e secondaire (Hitt, 1978), on a voulu observer la contradiction cognitive à travers des exercices semblables.

L’exercice a été conçu en prenant en considération la notion d’obstacle épistémologique dans le sens de Brousseau (1983, 1997). C’est-à-dire, que nous savions a priori que la multiplication dans les nombres naturels pouvait être un obstacle épistémologique pour la construction de la multiplication des décimaux compris entre zéro et un. Ainsi, nous nous attendions aux erreurs montrées dans la figure 5.

Figure 5

Erreurs et obstacles épistémologiques

Erreurs et obstacles épistémologiques

-> Voir la liste des figures

Il y a eu des procédures correctes et des procédures incorrectes dans la résolution de l’exercice. Voici quelques exemples de procédures suivies par les étudiants (figure 6).

Figure 6

Exemples de procédures suivies par les étudiants

Exemples de procédures suivies par les étudiants

-> Voir la liste des figures

Ci-dessous, nous analyserons la procédure développée par un étudiant qui, bien qu’il soit parmi les 13 des 229 étudiants qui n’ont pas résolu correctement l’exercice même après la perception d’une contradiction, nous semble intéressante (figure 7).

Figure 7

Procédures développées

Procédures développées

-> Voir la liste des figures

Nous voulons nous concentrer, dans une première partie, sur ce que l’étudiant a barré (figure 8 et tableau 2).

Figure 8

Éléments retranchés

Éléments retranchés

-> Voir la liste des figures

Tableau 2

Interprétation des procédures

Interprétation des procédures

-> Voir la liste des tableaux

Soulignons que l’étudiant a probablement décelé une contradiction. La procédure qu’il a utilisée nous permet de le placer dans une catégorie différente de celle des autres étudiants qui ont commis des erreurs et qui n’ont réalisé aucune réflexion sur leur procédure (peut-être ne se sont-ils pas rendu compte de la contradiction qui existait entre leurs réponses aux questions a et b. Lorsque cet étudiant a constaté une contradiction entre sa première réponse à la question a et le libellé de la question b, il s’est trouvé dans ce que nous appellerons une situation de « contradiction cognitive ». Nous pouvons aussi observer (partie b dans la figure 7) qu’il a commis plusieurs erreurs dans le traitement des décimaux, probablement qu’il a fait des erreurs après qu’il se soit rendu compte de la contradiction (0,2 × 15 = 0,30, 1,10 - 8 = -6,8 et 2,88 / 0,72 = 0,4). Il y a persistance de l’erreur dans la multiplication des décimaux, l’obstacle épistémologique ne peut pas être facilement effacé. Mais, ce qui est important chez cet étudiant, c’est le fait que ses réponses finales aux questions a et b l’ont satisfait (à ce moment, il n’y avait plus de contradiction cognitive), même s’il y avait une contradiction logique puisqu’il n’a pas donné la réponse correcte.

Les représentations dans une démarche heuristique

Dans cette partie, nous souhaitons analyser les représentations utilisées par deux étudiants lors d’une démarche heuristique de résolution d’un problème, et faire une comparaison entre les différentes approches théoriques présentées dans ce document. Notre comparaison s’appuiera sur les recherches faites par Skemp (1978) sur la compréhension instrumentale et relationnelle, Hiebert et Lefevre (1986) sur la connaissance conceptuelle et procédurale, et Duval (1988, 1993, 1995) sur les registres de représentation sémiotique.

Lorsque Hiebert et Lefevre (1986) parlent du rôle que jouent les représentations dans la résolution de problèmes, ils écrivent : « la connaissance conceptuelle est caractérisée clairement comme une connaissance riche en relations » (p. 3). En ce qui concerne la connaissance procédurale, ils nous indiquent qu’elle est construite en deux parties. L’une comprend le langage formel, c’est-à-dire le système de représentation symbolique des mathématiques. L’autre comprend les algorithmes et règles nécessaires pour compléter les tâches mathématiques. En résumé, la connaissance mathématique procédurale englobe deux types d’informations. La première information consiste à se familiariser avec les symboles isolés du système et avec les conventions syntaxiques pour la configuration acceptable des symboles. La seconde information consiste en règles ou procédures pour résoudre les problèmes mathématiques. L’approche théorique de Hiebert et Lefevre (Ibid.) et de Duval (1995) repose implicitement sur des systèmes sémiotiques de représentation nommées avant comme « officielles », mais ils ne parlent pas explicitement des productions des élèves, ce qui nous amène à dire que l’on peut envisager d’autres aspects que ceux mentionnés par ces auteurs. Si nous nous situons dans la perspective de la production des représentations sémiotiques lors de la résolution d’un problème mathématique, les représentations des étudiants sont de nature différente de celles envisagées par Duval (1995) et Hiebert et Lefevre (1986).

Nous voudrions signaler que les productions sémiotiques des élèves ne coïncident pas nécessairement avec celles que le professeur utilise dans son cours (ou que l’on trouve dans les manuels). En voici un exemple, tiré d’une étude colombienne, qui consiste à proposer à des élèves de différents niveaux les mêmes problèmes (Benitéz et Santos, 2000). Une élève de 11 ans, Soath, a développé la procédure illustrée à la figure 9 pour trouver la solution du problème suivant.

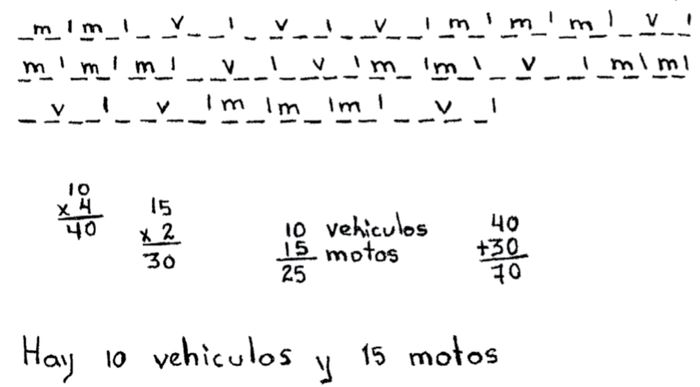
Figure 9

Passage du figural au numérique

Passage du figural au numérique

-> Voir la liste des figures

Dans cette première partie, on peut voir que Soath a fait des productions sémiotiques liées au problème proposé (« m » symbolise une motocyclette et « v » un véhicule, c’est-à-dire un taxi). Pour ce faire, elle a mobilisé différents types de représentations et on peut constater qu’il y a eu coordination entre elles. En effet, nous pouvons constater qu’elle a cherché à contrôler le nombre total de roues (70) et qu’elle a seulement compté après le nombre de motocyclettes et de taxis. Il a eu une coordination entre le passage de la représentation figurale à la représentation numérique qui prend en considérations les autres données du problème.

Soath a utilisé des représentations sémiotiques différentes de celles envisagées par Duval (1993, 1995) et Hiebert et Lefevre (1986). Nous ne pouvons ignorer que Soath a mobilisé une représentation sémiotique qui montre une continuité de pensée et ceci nous oblige à envisager un autre type d’explication théorique. Les productions sémiotiques des étudiants dans un processus heuristique ont un caractère fonctionnel, et ce sont leurs productions qui donnent un caractère continu à leur pensée face à la résolution d’un problème. Il faut aussi signaler que leur processus heuristique leur permet aussi de confronter leurs conceptions.

Nous pensons qu’il est important d’observer la mobilisation des représentations d’un point de vue fonctionnel et dynamique. Dans la démarche heuristique suivie par Soath, les représentations sémiotiques jouent un rôle temporaire et fonctionnel conduisant à la résolution du problème. À l’étape suivante, Soath produit la représentation illustrée à la figure 10.

Figure 10

Rôle des représentations sémiotiques

Rôle des représentations sémiotiques

-> Voir la liste des figures

La séquence ci-dessus laisse penser qu’elle avait 23 véhicules et que l’action d’en ajouter « deux » lui a fait penser à échanger un taxi contre deux motocyclettes. On peut penser que Soath est très attachée à ses représentations sémiotiques, et on peut attendre une généralisation, mais elle a peut-être besoin de ses représentations plus qu’on ne croit. On peut noter une abstraction quand elle refait sa représentation parce que, pour elle, peu importe l’ordre des voitures et des motos. Le fait qu’elle obtienne un taxi de plus, nous permet de penser qu’il s’agit de l’échange d’un taxi contre deux motos. Soath aurait pu échanger d’un seul coup deux taxis par quatre motocyclettes pour trouver le résultat. Pourquoi ne l’a-t-elle pas fait ? Ici, nous croyons pouvoir expliquer sa procédure comme une primauté de l’action positive (ajouter) sur la négative (soustraire) et un manque de coordination entre ces deux actions. Mais, le fait d’échanger un taxi contre deux motocyclettes et la mobilisation des représentations pour produire une autre représentation sémiotique montre que Soath a pleine confiance en ses représentations figurales pour contrôler la situation. Nous pouvons remarquer qu’une fois encore, sa représentation figurale est bien liée à sa représentation numérique. Ces représentations ont une caractéristique fonctionnelle et sont un élément essentiel pour donner une cohérence à sa production numérique pour atteindre le résultat. Pour terminer, Soath produit ce qu’illustre la figure 11.

Figure 11

Caractéristiques fonctionnelles

Caractéristiques fonctionnelles

-> Voir la liste des figures

Tout ceci laisse penser que la mobilisation des représentations mentales, à travers un réseau sémantique, a induit la production de représentations sémiotiques qui ont mené Soath à une solution juste à travers des manipulations arithmétiques correctes. Il semble que Soath a développé une structure particulière dans laquelle ses représentations mentales et sémiotiques ont une caractéristique fonctionnelle qui la conduitse vers la solution du problème.

Nous analyserons maintenant la procédure utilisée par un étudiant du secondaire (Benitéz et Santos, 2000) pour résoudre ce même problème (figure 12). Alvaro (14 ans) suivait un cours d’algèbre.

Figure 12

Rôles des inconnues

Rôles des inconnues

-> Voir la liste des figures

La représentation mentale qu’Alvaro s’est faite du problème l’a amené à utiliser des inconnues. En lisant attentivement la production d’Alvaro, nous pensons que, dans sa représentation mentale du problème, il a bien distingué le nombre de roues des motocyclettes et celui des taxis. Son erreur s’est probablement introduite lorsqu’il a assigné les inconnues 2x et 4x à ses représentations mentales. Nous pouvons constater que, pour lui, « l’inconnue » peut jouer des rôles différents. À titre d’exemple, Alvaro va échanger « x » et « 2x ». Peut-être, pour Alvaro, l’inconnue « x » représente-t-elle un nombre impair et l’inconnue « 2x », un nombre pair. Le terme véhicule, qui est utilisé dans l’énoncé pour désigner soit une motocyclette, soit un taxi, peut aussi être la cause de la confusion.

Pourquoi Alvaro a-t-il écrit 70 + 4x = 25 ? À quoi cet étudiant a-t-il pensé en écrivant cette équation ? On ne le sait pas vraiment ! Par la suite, il est arrivé à l’expression 4x = 25 - 70. L’obtention d’un nombre négatif a-t-il frappé son esprit ? Est-ce la raison pour laquelle il a recommencé ? Alvaro a alors écrit l’expression x + y = 70. Ici, « x » peut bien correspondre au « nombre de roues des motocyclettes » et « y » au « nombre de roues des taxis ». L’expression y = 70 - 2x, montre bien que, pour Alvaro, « x » et « 2x » sont interchangeables. Probablement que, en accord avec son idée initiale, l’expression « 70 - 2x » correspond au « nombre total de roues moins le nombre de roues des motocyclettes ». Il a obtenu alors y = 68x. Possiblement qu’il a eu une idée semblable pour le résultat x = 66y. À partir de l’expression 68x + 66y, il a fait la somme « 68 + 66 » pour laquelle il a obtenu « 134 ». Ce résultat était-il différent de ce à quoi il s’attendait puisque, pour lui, x + y = 70 ? Il est revenu sur cette expression, mais sa conception de l’« inconnue », qui joue plusieurs rôles dans ses représentations sémiotiques, l’a conduit à commettre des erreurs. Alvaro est resté dans une situation contradictoire, contradiction logique du point de vue mathématique, sans s’apercevoir de la contradiction. C’est-à-dire, Alvaro n’est pas arrivé à une contradiction cognitive parce qu’il n’a pas perçu de contradiction logique.

À l’entrevue, le chercheur lui ayant demandé s’il pouvait expliquer comment il avait fait pour obtenir un résultat final correct, il a répondu qu’il avait copié sur son camarade.

Pour mettre en relief les différences qu’occasionne le traitement d’un même problème à travers deux points de vue, d’abord celui de l’arithmétique, ensuite celui de l’algèbre, nous pourrions dire que, dans la résolution arithmétique de Soath, nous avons pu remarquer l’utilisation des représentations liées à « une mobilisation des représentations mentales avec des caractéristiques fonctionnelles dans une approche d’approximation arithmétique » et que, dans la résolution d’Alvaro, nous pourrions remarquer un manque de coordination entre ses représentations mentales et ses productions sémiotiques. Ce type d’analyse sur les démarches suivies par des étudiants nous semble très important pour mieux comprendre la construction des concepts qui sont liés à la résolution de problèmes.

Il y a beaucoup d’études sur les difficultés occasionnées par la transition de l’arithmétique vers l’algèbre, et nous voulons, ici, mettre l’accent sur l’importance de préserver les habiletés arithmétiques qui sont liées à leurs productions sémiotiques et de continuer à les développer chez les étudiants tout au long de leurs études. C’est-à-dire, que nous voulons penser à la possibilité de développer chez les étudiants une articulation entre les habiletés arithmétiques et les habiletés algébriques.

Conclusion

Nous avons analysé différentes approches portant sur la construction des concepts et nous avons pu constater que beaucoup d’entre elles font référence à des situations de la vie quotidienne. Comme nous voulions nous rapprocher de ce type de recherche sur les constructions des réseaux sémantiques et des concepts, nous nous sommes tournés vers l’approche de Duval qui, du point de vue de la construction des concepts mathématiques, nous permet une nouvelle orientation théorique basée sur l’importance des systèmes sémiotiques de représentation. Cela nous a amené à voir l’importance de l’articulation entre les registres de représentation pour la construction des concepts mathématiques en prenant en considération que les représentations des objets mathématiques sont partielles quant à ce qu’elles représentent.

Dès lors, il devient absolument nécessaire de proposer aux étudiants des activités de conversion entre les représentations d’un registre à un autre pour que les représentations en jeu, qui par nature sont complémentaires, donnent un support à la construction du concept en question. À titre d’exemple, dans le cas de la construction du concept de fonction entrent en jeu les registres de représentation de la langue naturelle, algébrique, tabulaire, graphique, etc., où l’articulation entre les registres est fondamentale (Janvier, 1987 ; Hitt, 1998a) pour la construction de ce concept.

En analysant en profondeur le rôle des représentations sémiotiques, nous avons pu constater qu’un changement a eu lieu pour donner un statut plus important aux représentations sémiotiques et nous croyons que ce statut a été restreint aux représentations officielles. Nous avons voulu montrer que la production des représentations par les étudiants dans une démarche heuristique est beaucoup plus importante que ce que nous avons cru par le passé. Le caractère fonctionnel et dynamique de ces représentations sémiotiques permet à l’étudiant d’avoir un contrôle sur la démarche qui le mène à la solution.

En ce qui concerne la stabilité des connaissances, nous avons pris des exemples dans l’arithmétique et dans l’algèbre afin de montrer l’insuffisance des structures cognitives pour résoudre des problèmes. Les structures cognitives que nous envisagions doivent inclure des caractéristiques générales comme, à titre d’exemple, la sensibilité à la contradiction. Pour finir, il nous semble que les représentations sémiotiques produites par les étudiants peuvent jouer un rôle important pour déceler une contradiction logique.