Apprentissage de logiciels de modélisation 3D et pratique de loisirs

Charles, Sophie

doi:https://doi.org/10.18162/ritpu-2024-v21n1-05

Introduction

Dans le cadre d’un programme d’investissement français e-FRAN, qui s’intéresse aux « effets, positifs et négatifs, de l’utilisation du numérique dans les pratiques d’enseignement et d’apprentissage » (Ministère de l’éducation nationale, de l’enseignement supérieur et de la recherche, Ministère de l’économie, de l’industrie et du numérique et Commissariat général à l’investissement, 2016, p. 3), notre recherche s’est portée sur les conditions d’utilisation de logiciels de modélisation volumique et leurs liens avec les habiletés spatiales d’étudiantes et étudiants ingénieurs en première année (Charles, 2023). En 2009, Wai et al. ont établi le lien entre les habiletés spatiales et la réussite dans les études en sciences, technologie, ingénierie et mathématiques (STIM). Des travaux spécifiques ont mis en évidence le caractère prédictif de la performance à des tests spatiaux dans la capacité à modéliser en trois dimensions (Branoff et Dobelis, 2012b; Steinhauer, 2012). Parmi les activités favorables au développement de ces compétences spatiales, d’autres recherches ont souligné l’importance de la pratique de loisirs spécifiques (Gold et al., 2018), de certaines activités sportives (Moreau et al., 2012) et de l’apprentissage de la modélisation volumique dans le cadre du cursus scolaire (Górska, 2005; Martín‐Dorta et al., 2008).

Notre étude vise à explorer de potentiels facteurs de développement de compétences de modélisation auprès d’un groupe d’étudiantes et étudiants en première année d’école d’ingénieurs française, en examinant à la fois les sphères éducative et personnelle, avant qu’ils n’entament leur cursus dans cette école. Elle ne vise pas à étudier ces liens en regard de l’impact d’un enseignement de conception assistée par ordinateur (CAO), souvent exploré dans la revue de littérature (Chester, 2007; Rynne et Gaughran, 2007). On cherche à étudier s’il existe un lien direct entre bagage technologique et performance en modélisation volumique, ou bien si la pratique de certains loisirs, qui contribue au développement des habiletés spatiales dont le caractère prédictif de la performance en modélisation a été établi, est une variable explicative de la performance à une tâche de modélisation volumique.

Pour ce faire, notre recueil de données a combiné des mesures de méthodes quantitatives, en soumettant des étudiantes et étudiants ingénieurs de première année à un exercice de modélisation volumique et à une batterie de cinq tests spatiaux (College Entrance Examination Board, 1939; Guay, 1976; Thurstone et Jeffrey, 1965; Vandenberg et Kuse, 1978; Yoon, 2011), et des méthodes qualitatives, en demandant à nos sujets de répondre à des questionnaires interrogeant leur pratique antérieure des modeleurs volumiques et de loisirs dans l’enfance et l’adolescence, puis à l’âge adulte. Notre étude cherche à explorer les influences possibles à la bonne maitrise de logiciels de modélisation 3D, aussi bien dans la sphère éducative ayant précédé le cursus en école d’ingénieurs française que dans la sphère personnelle. Un second objectif vise à vérifier le caractère prédictif des tests spatiaux de la performance en modélisation pour des étudiantes et étudiants ingénieurs français et, par extension, de leur capacité à repérer ceux qui sont en difficulté, destinataires de dispositifs de remédiation.

1. Revue de littérature

1.1 Apprentissage de la modélisation volumique

La caractéristique de l’apprentissage de la modélisation 3D dans les études d’ingénierie est qu’il est indissociable de l’apprentissage de l’utilisation de modeleurs volumiques (Ault et John, 2010, p. 13; Leopold, 2005, p. 40). Les modeleurs volumiques, ou modeleurs 3D, sont des logiciels de CAO. Selon Bhavnani et John (2000, p. 109), ces logiciels sont des systèmes informatiques complexes, c’est-à-dire qu’ils nécessitent l’apprentissage d’outils, de tâches à réaliser et de méthodes efficaces. En d’autres mots, il s’agit d’apprendre comment manipuler le logiciel, ce qu’il permet ou exige de faire et comment le faire efficacement. Dans le cas des logiciels de modélisation volumique, ceci concernerait l’apprentissage des commandes disponibles dans le modeleur, de la manière de les exécuter (Hamade et al., 2005, p. 307) et de stratégies efficaces pour tirer le meilleur parti des fonctionnalités offertes par le logiciel (Bertoline et al., 2009, p. 645). Lieu et Sorby (2009, p. 6-2) disent de ces logiciels qu’ils sont des outils permettant de créer des images exactes d’un objet, d’analyser ses fonctions, d’enregistrer son historique et de visualiser son apparence. Selon Bertoline et al. (2009, p. 640-641), ils permettent aux concepteurs de concevoir virtuellement des objets 3D en créant des esquisses, dans lesquelles ils définissent des spécificités géométriques et dimensionnelles, auxquelles ils attribuent des fonctions pour les transformer en volumes. L’historique des esquisses et des fonctions est visible dans l’arbre de construction. Les modeleurs volumiques paramétriques permettent de plus de créer des relations de dépendance entre des éléments, qui engendrent des mises à jour dynamiques de tous les éléments liés par un paramètre lors de la modification d’un élément auquel on peut accéder dans l’arbre de construction. Ces logiciels permettent aussi de visualiser l’objet au cours de sa création, notamment en le faisant pivoter pour l’observer à partir de différents points de vue (Lieu et Sorby, 2009, p. 6-10). Notre recherche (Charles, 2023) a porté sur la mobilisation d’étudiantes et étudiants de première année en école d’ingénieurs de l’ensemble de ces fonctionnalités, mais notre article est focalisé sur le produit de l’activité réalisée en manipulant les fonctionnalités précédemment citées : la performance en modélisation, évaluée au travers de la justesse des modèles produits à l’issue d’une tâche de modélisation.

1.1.1 Évaluation de la performance en modélisation

La caractérisation de la performance en modélisation d’étudiantes et étudiants en sciences de l’ingénieur est abordée au travers de critères de justesse, d’efficacité et de stratégie. La justesse peut être évaluée à partir des caractéristiques géométriques et dimensionnelles de l’objet à modéliser (Lang et al., 1991, p. 260; Steinhauer, 2012, p. 47) et du nombre d’erreurs relevé dans les réalisations (Lang et al., 1991, p. 260). L’efficacité peut être appréhendée en mesurant le temps de réalisation (Hamade et al., 2007, p. 645; Johnson et Diwakaran, 2011, p. 22.305.3) et en comptant le nombre de commandes utilisées (Lang et al., 1991, p. 260). Les stratégies de modélisation individuelles ont été caractérisées grâce à l’observation filmée de l’activité de modélisation : filmage de l’écran, du clavier et de la tablette pour Lang et al. (1991, p. 261) et enregistrement de l’activité à l’écran pour Chester (2007, p. 29). Ces observations ont permis de caractériser les stratégies de modélisation déployées dans cette activité en s’intéressant aux séquences de modélisation (Lang et al., 1991, p. 261), au dénombrement de stratégies désignées comme expertes (Chester, 2007, p. 30) ou encore à l’approche et à la structure adoptées par la personne apprenante (Steinhauer, 2012, p. 47). Alors que les critères de justesse ont été évalués en observant les réalisations finales des étudiantes et étudiants (Branoff et Dobelis, 2012b, p. 39) et certains critères de stratégie (approche et structure adoptées) grâce à l’arbre de construction (Steinhauer, 2012, p. 45), les séquences (Lang et al., 1991, p. 261) et le recours à des stratégies expertes (Chester, 2007, p. 30) ont été observés dans l’activité de modélisation.

1.1.2 Performance en modélisation 3D et sources de variance

Les études s’intéressant à la performance en modélisation et à ses possibles influences portent sur l’expérience antérieure de logiciels de CAO et des dessins d’ensemble (Rynne et Gaughran, 2007, p. 63), et sur la performance à des tests visant à mesurer les compétences visuospatiales (Branoff et Dobelis, 2012b, p. 38; Sorby, 1999, p. 4.465.3; Steinhauer, 2012, p. 44). Ces études font état d’une meilleure performance pour les étudiantes et étudiants ayant déjà manipulé des modeleurs volumiques et familiers des dessins techniques (Rynne et Gaughran, 2007, p. 64) et d’une différence de performance significative en faveur de ceux dont les scores de visualisation spatiale sont les plus élevés (Branoff et Dobelis, 2012b, p. 40; Sorby, 1999, p. 4.465.4; Steinhauer, 2012, p. 47).

1.2 Habileté spatiale

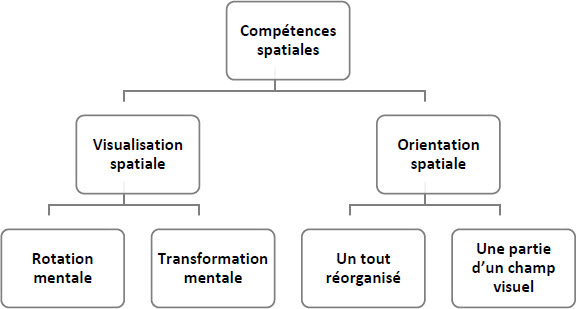
Selon Linn et Petersen (1985, p. 1482), l’habileté spatiale fait référence à « [a] skill in representing, transforming, generating and recalling symbolic, nonlinguistic information[1] ». D’après Tartre (1984, p. 7), cette habileté est composée de deux facteurs, la visualisation spatiale et l’orientation spatiale, euxmêmes divisés en quatre sousfacteurs. Cette classification est illustrée dans la figure 1.

Figure 1

***Classification simplifiée des compétences spatiales selon Tartre***

Selon la même auteure, la visualisation spatiale concerne la manipulation d’une image mentale (p. 27). Elle s’appuie sur la distinction de Kersh et Cook (1979, cités dans Tartre, 1984, p. 7) qui s’intéressent à la portion de l’objet concerné pour distinguer cette première compétence en deux sous-facteurs. Lorsque la manipulation concerne la totalité d’une image mentale, l’auteure parle de rotation mentale (p. 8), comme lorsque l’on s’imagine faire tourner un objet mentalement pour en voir toutes les faces. Lorsque la manipulation concerne une partie de l’objet, comme quand on s’imagine plier un patron pour former un cube, l’auteure considère qu’il s’agit de transformation mentale (p. 10).

Le second facteur, l’orientation spatiale, est décrit comme la capacité à comprendre une représentation visuelle ou un changement qui a eu lieu entre deux représentations (p. 6). Tartre divise cette compétence en deux sous-facteurs : d’une part, savoir organiser et comprendre la totalité d’un objet (p. 16), comme dans le cas du cube de Necker (1832) que l’on peut percevoir vu de dessus ou de dessous; d’autre part, avoir la capacité de comprendre la relation existant entre un élément et le tout dont il est issu (p. 19), comme lorsqu’il s’agit de placer une pièce dans un cassetête.

Dans le cas de la visualisation spatiale, il s’agit de manipuler mentalement des objets, alors que l’orientation spatiale concerne la compréhension d’un objet, quelle que soit la représentation qui en est donnée.

1.2.1 Outils de mesure de l’habileté spatiale

De nombreux tests ont été conçus pour évaluer les compétences spatiales (Eliot et Macfarlane Smith, 1983). Il existe des tests de performance, qui nécessitent la manipulation de matériel (American Psychological Association, 2018b), et des tests papier-crayon (Eliot et Macfarlane Smith, 1983, p. 2). Ces derniers sont les plus fréquemment utilisés dans les études portant sur la relation entre habileté spatiale et modélisation volumique (Agbanglanon, 2019, p. 70; Branoff et Dobelis, 2012b, p. 39; Steinhauer, 2012, p. 44). Nous présentons dans cet article cinq tests visant à mesurer les quatre facteurs spatiaux de la classification de Tartre, regroupés selon qu’ils relèvent de la visualisation spatiale ou de l’orientation spatiale. Nous verrons dans la méthodologie pourquoi nous avons utilisé cette sélection pour notre recherche.

Le Mental Rotation Test (MRT) (Vandenberg et Kuse, 1978) et le Revised Purdue Spatial Visualization Test: Rotations (R PSVT:R) (Yoon, 2011) visent à mesurer la rotation mentale. Le Mental Cutting Test (MCT) (College Entrance Examination Board, 1939) a pour objet d’évaluer la transformation mentale. Ces trois tests demandent à manipuler mentalement des objets, ils concernent la visualisation spatiale. Les compétences visuospatiales sont les habiletés spatiales les plus étudiées dans les recherches portant sur le lien entre ces habiletés et les études d’ingénierie (Ault et John, 2010, p. 13; Kelly, 2013, p. 6).

Le Purdue Spatial Visualization Test: Visualization of Views (PSVT:V) (Guay, 1976) vise la capacité à reconnaitre un objet à partir de plusieurs points de vue. Le Closure Flexibility Test (Concealed Figures) Form A (CFT) (Thurstone et Jeffrey, 1965) sollicite la capacité à dissocier un élément intriqué dans un motif complexe. Ces deux tests relèvent de l’orientation spatiale, c’estàdire de la capacité à reconnaître et à comprendre un objet.

1.2.2 Performances spatiales et sources de variance

Les travaux de Wai et al. (2009, p. 825), qui s’appuient sur 346 665 participants issus de la cohorte Project TALENT (Flanagan, 1962), montrent que la probabilité d’obtenir une qualification élevée en STIM est fonction de l’habileté spatiale mesurée à l’adolescence. Cette corrélation encourage de nombreux chercheurs et chercheuses à examiner de potentielles sources de variance (Eliot et Macfarlane Smith, 1983, p. 6). Parmi celles-ci, la pratique de loisirs, sources d’apprentissage informel, et celle d’apprentissages spécifiques, réalisés dans des dispositifs conçus pour développer les compétences spatiales (Uttal et al., 2013, p. 356).

La performance spatiale a été liée notamment à la pratique de loisirs dans des études portant sur les jeux vidéo (Feng et al., 2007, p. 853; Gold et al., 2018, p. 10), le sport (Moreau et al., 2012, p. 86), les jeux de construction (Gold et al., 2018, p. 10), les casse-têtes (Reilly et al., 2017, p. 22), les activités artistiques, tel le coloriage, et narratives, comme jouer à la marchande, pratiquées par de jeunes enfants (Caldera et al., 1999, p. 859).

Le lien entre performance spatiale et performance en STIM encourage de nombreux enseignants et enseignantes de l’éducation supérieure à concevoir des dispositifs pédagogiques de développement des compétences spatiales. Sorby, notamment, travaille depuis les années 1990 à repérer les étudiants et étudiantes de la Michigan Technological University en première année de sciences de l’ingénieur aux compétences spatiales les plus faibles grâce à des tests de visualisation spatiale, pour les inscrire à des cours de remise à niveau au début de l’année universitaire (Metz et al., 2016, p. 2) : les auteures constatent un effet positif de ce dispositif sur la performance scolaire et la rétention des étudiantes et étudiants ciblés. La malléabilité des habiletés spatiales a été établie dans la méta-analyse d’Uttal et al. (2013, p. 360), et parmi les dispositifs pédagogiques déployés, certains s’appuient sur la modélisation volumique avec succès (Górska, 2005, p. 203; Martín‐Dorta et al., 2008, p. 509). On remarque parallèlement à cet effet positif de la pratique des modeleurs volumiques sur la performance spatiale une dimension prédictive des scores de visualisation spatiale de la capacité à modéliser (Branoff et Dobelis, 2012b, p. 40; Steinhauer, 2012, p. 47). Steinhauer (2012, p. 48) explique la corrélation qu’elle observe entre les scores du MCT, qui vise à évaluer la transformation mentale, et son exercice de modélisation par le fait que ces deux tâches nécessitent d’identifier le profil en deux dimensions (2D) d’une forme à associer à un objet en 3D. De fait, les modeleurs volumiques sont des logiciels de simulation d’objets en 3D, dont la conception requiert de dessiner une esquisse 2D avant de lui appliquer des balayages qui transforment le profil en solide (Bertoline et al., 2009, p. 640).

2. Problématique

Notre recherche s’intéresse à déterminer de possibles facteurs de développement des capacités à modéliser un objet en trois dimensions à l’aide d’un logiciel spécialisé, auprès d’un groupe d’étudiantes et étudiants en première année d’école d’ingénieurs. Deux sphères d’acquisition sont examinées : celle de l’apprentissage formel, qui comprend le bagage technologique des étudiantes et étudiants et leur pratique des modeleurs volumiques, et celle de la sphère personnelle abordée au travers des habiletés spatiales, dont le caractère prédictif a été décrit dans la littérature, et de la pratique des loisirs, elle-même liée au développement des habiletés spatiales. Il n’existe pas à notre connaissance d’étude portant sur la relation entre performance en modélisation et pratique de loisirs. Pour étudier le lien entre compétences de modélisation 3D et pratique de loisirs, au centre de laquelle se trouvent les habiletés spatiales, nous construisons notre démarche sur une approche psychocognitive de la définition de ces compétences et de leur mesure à l’aide d’instruments de mesure normalisés.

3. Méthodologie

3.1 Personnes participantes

Les données sont issues d’un travail de thèse qui a porté sur 146 étudiantes et étudiants (Charles, 2023). Nous retenons pour cet article ceux qui étaient présents à l’ensemble des expérimentations qui y sont décrites. La population de notre échantillon est constituée de 127 étudiants ingénieurs en première année, âgés de 18 à 22 ans (M = 19,8). Elle est composée de N_F = 26 (20,5 %) femmes et N_H = 101 (79,5 %) hommes, provenant de classes préparatoires, de licence 2 ou 3, de sections de technicien supérieur et d’instituts universitaires de formation. Parmi ces personnes participantes, 71 (55,9 %) ont reçu des enseignements technologiques dans ces formations et 111 (87,5 %) ont déjà utilisé un modeleur volumique.

3.2 Recueil et traitements des données

Nous présentons ci-après la méthodologie adoptée pour recueillir et traiter les données. Elle comprend des mesures de la performance en modélisation volumique, évaluée au travers de critères géométriques, dimensionnels et fonctionnels et des compétences spatiales du modèle de Tartre (1984). À cela s’ajoute l’investigation des logiciels de modélisation pratiqués par les étudiants et étudiantes et de leurs loisirs. Elle inclut des traitements d’encodage des données issues des questionnaires portant sur les modeleurs et les loisirs ainsi que les traitements statistiques réalisés. Le consentement des étudiants et étudiantes a été sollicité au travers d’un formulaire explicitant les objectifs et modalités de la recherche. Conformément à la loi 2018493 du 20 juin 2018 (République française, 2018), les personnes répondantes ont été informées de leur droit d’accès aux données recueillies durant l’expérimentation. La conformité de notre protocole de recueil de données avec la réglementation relative à l’éthique a été validée par la déléguée à la protection des données de l’école. L’ensemble des données a été anonymisé.

3.2.1 Performance en modélisation volumique

Afin d’éviter un effet des enseignements sur les performances spatiales et de modélisation, nous avons décidé de positionner nos expérimentations à l’arrivée des étudiants et étudiantes à l’école. La plateforme de développement de produits Onshape (Hirschtick et al., 2014) a été choisie pour sa facilité de prise en main.

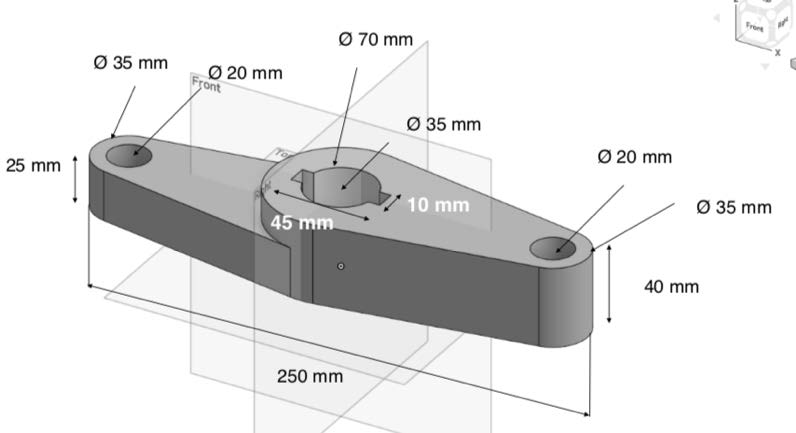
Le pas-à-pas de prise en main et la tâche de modélisation ont été conçus à partir de la formation en ligne de la plateforme. Il s’agissait de modéliser un objet à partir de trois vues, dont une cotée, illustrée dans la figure 2. Les vues projetées, traditionnellement utilisées en modélisation, ont été évitées, car leur interprétation nécessite un apprentissage spécifique (Rynne et Gaughran, 2007, p. 65). Le pas-à-pas de prise en main et la tâche de modélisation ont été validés auprès d’un échantillon de quatre étudiantes et étudiants ingénieurs volontaires.

Figure 2

***Vue cotée de la pièce à modéliser***

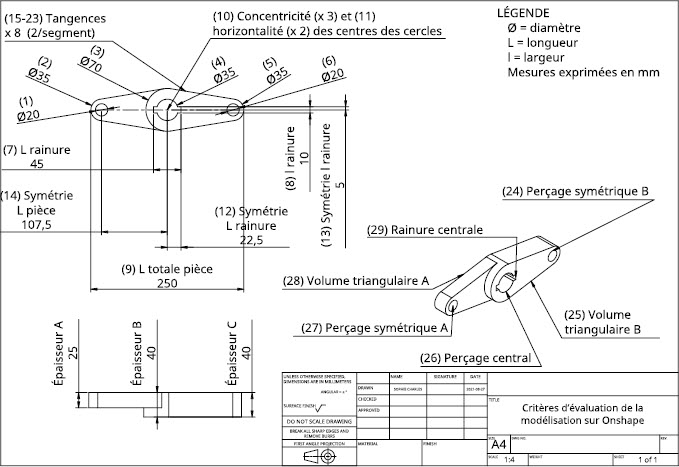
Parmi les critères d’évaluation de la performance en modélisation décrits dans la littérature au paragraphe 2.1.1, nous retenons celui de la justesse des réalisations pour cette étude. Nous menons actuellement d’autres recherches pour examiner les critères d’efficacité et de stratégie. L’évaluation de la justesse porte sur 16 critères géométriques (p. ex., symétrie de la pièce), 12 critères dimensionnels (p. ex., longueur totale de la pièce) et 7 critères fonctionnels (p. ex., rainure centrale) que les étudiants et étudiantes doivent inférer (p. ex., concentricité des cercles) ou extraire des vues présentées (p. ex., largeur de la rainure). Les critères fonctionnels ont été inclus pour évaluer si les étudiantes et étudiants produisaient bien les volumes fonctionnels attendus, c’est-à-dire s’ils réussissaient le passage à la troisième dimension, et s’ils le faisaient de manière rigoureuse. Le détail des éléments évalués se trouve dans le tableau 1 et est illustré dans la figure 3 selon un numérotage (129) et un nommage (AC) communs. Un point supplémentaire concerne le rognage des éléments superflus. Le total des points s’élève à 35.

Tableau 1

***Barème d’évaluation de la modélisation***

Figure 3

***Illustration graphique des critères géométriques, dimensionnels et fonctionnels d’évaluation de la tâche de modélisation***

Les réalisations des étudiantes et étudiants, esquisses ou modélisations complètes, ont été converties en dessins techniques, dont un exemple est illustré dans la figure 3, et complétées par la consultation des esquisses dans le modeleur quand un critère était difficile à évaluer dans le dessin technique (p. ex., doute sur la concentricité de deux cercles). Comme décrit dans la revue de littérature, la modélisation d’un objet 3D requiert la création d’une esquisse 2D à laquelle on applique un balayage pour la transformer en volume.

3.2.2 Performance spatiale

La méthodologie de relevé de la performance spatiale est issue d’un processus d’expérimentations et de résultats en deux phases. Lors de la première phase, les trois tests spatiaux les plus cités dans les études portant sur le lien entre habileté spatiale et études d’ingénierie ont été repérés et acquis (Ault et John, 2010, p. 13; Kelly, 2013, p. 6), soit les tests de visualisation spatiale MRT, MCT et Purdue Spatial Visualization Test: Visualization of Rotations (PSVT:R) (Guay, 1976). La version mise à jour du PSVT:R par Yoon (2011), le R PSVT:R, a été choisie en raison de la plus grande justesse des stimuli (Maeda et al., 2013, p. 766). En septembre 2018, 137 étudiants ingénieurs primo-arrivants, N_F = 37 (27,0 %) femmes et N_H = 100 (73 %) hommes, ont passé le MCT et le MRT et 131 étudiants, N_F = 36 (26,2 %) femmes et N_H = 95 (69,3 %) hommes, ont passé le R PSVT:R. Une analyse de variance a mis en évidence le caractère prédictif des scores spatiaux de la performance des étudiantes et étudiants dans des évaluations scolaires, dont une nécessitant de manipuler le modeleur CATIA (Dassault Systèmes, 2012) (Charles et al., 2019, p. 243). La deuxième phase a consisté à repérer, à acquérir et à expérimenter des tests d’orientation spatiale. Une description de ces expérimentations est accessible dans nos travaux de thèse (Charles, 2023, p. 56-61). Elles ont abouti à la sélection du PSVT:V, pour évaluer la capacité à changer de point de vue, et du CFT, pour mesurer la compétence de dissociation. Il est à noter que certains tests spatiaux sont difficiles à obtenir parce qu’ils ne sont pas commercialisés et/ou qu’il n’est plus possible d’en contacter les auteurs. Nous avons pu nous les procurer grâce au Spatial Intelligence Learning Center et à la solidarité des chercheuses et chercheurs que nous avons contactés après avoir repéré qu’ils les avaient utilisés dans leurs expérimentations. Le catalogue de tests spatiaux d’Eliot et Mcfarlane Smith (1983) permet de trouver leurs références bibliographiques.

Notre étude utilise le R PSVT:R, le MRT et le MCT, pour mesurer la visualisation spatiale, et le PSVT:V et le CFT, pour mesurer l’orientation spatiale. L’ensemble des tests a été traduit en français, à l’exception du MRT déjà accessible en français (Albaret et Aubert, 1996), afin de ne pas mesurer un effet du niveau d’anglais des sujets sur leur performance spatiale. La batterie de tests a été passée en une prise de performance auprès de l’ensemble des étudiants et étudiantes en respectant les instructions. De même, les scores ont été calculés selon les recommandations des auteurs.

En regard de nos intentions, nous notons les limites des tests spatiaux utilisés dans cette étude : de précédents travaux (Albaret et Aubert, 1996, p. 271; Hegarty, 2018, p. 1214) ont montré que des stratégies autres que celles visées par les tests étaient mises en oeuvre dans ces outils de mesure. Bien qu’ils visent des compétences spécifiques, il se peut que d’autres compétences y soient mobilisées. Ces limites ont été prises en considération dans nos travaux (Charles, 2023, p. 202-205).

3.2.3 Investigation des loisirs

Les loisirs relevés dans la revue de littérature, décrits en 1.2.2, ont été abondés en interrogeant les sujets qui ont participé à nos expérimentations des tests spatiaux, décrites en 3.2.2. Nous avons choisi deux temporalités, l’enfance et l’adolescence d’une part, et l’âge actuel d’autre part, de manière à dissocier l’effet des loisirs pratiqués plus jeune et potentiellement abandonnés à l’âge adulte de celui des loisirs récents. Les réponses ont été recueillies grâce à des questionnaires à choix multiples présentant une fréquence de pratique en cinq points : jamais, quelques fois par an, tous les mois, toutes les semaines, tous les jours. Cette échelle vise à prendre en compte l’influence de la fréquence de la pratique (Gold et al., 2018, p. 13).

Les loisirs ont été qualifiés selon cinq dimensions : dynamique, manipulatoire, limitée à la 2D, de construction 3D et artistique. Le détail de ces traitements est accessible dans nos travaux de thèse (Charles, 2023, p. 138-142) . Pour chaque dimension, le loisir est qualifié comme relevant de cette dimension ou pas, que ce soit de manière virtuelle ou réelle dans le cas des dimensions dynamique, manipulatoire et de construction 3D. Par exemple, l’athlétisme est qualifié sans 2D, sans construction 3D, manipulatoire, dynamique et pas artistique. Un indice est ensuite attribué à chaque dimension selon le nombre de loisirs choisis par l’étudiant ou l’étudiante, pratiqués régulièrement (c.àd. tous les jours, toutes les semaines, tous les mois) et qualifiés avec la même dimension. Par exemple, quand l’étudiante ou l’étudiant n’a choisi aucun loisir dynamique, il lui est attribué l’encodage sans loisir dynamique. Décrits succinctement, les indices décrivent un continuum d’une pratique nulle (0A) à une pratique élevée (2F). Nous obtenons pour chaque catégorie de loisirs un nombre de dimensions indicées possibles dont seules certaines sont actives. Ces dimensions sont nécessaires pour tester la relation entre pratique de loisirs et performance en modélisation. Un indice dimensionnel pour les cinq dimensions encodées est affecté aux étudiants et étudiantes.

Le questionnaire a été complété par une question portant sur la pratique de logiciels de modélisation : cinq choix ont été proposés, soit SolidWorks (SolidWorks, 1995), CATIA (Dassault Systèmes, 2012), SketchUp (Schell et Esch, 2000), autre et aucun. La pratique d’au moins un logiciel a été calculée.

3.2.4 Traitements statistiques

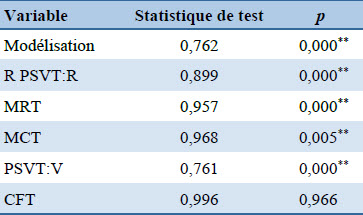
Les analyses statistiques ont été effectuées à l’aide du logiciel SPSS (version 28.0). La normalité de la distribution des scores de modélisation et des scores spatiaux a été vérifiée à l’aide du test de Shapiro-Wilk (Shapiro et Wilk, 1965). Seuls les scores du CFT respectent une distribution normale (tableau 2). Nous avons opté pour des tests non paramétriques pour la majorité des traitements statistiques :

Pour comparer la performance des groupes d’étudiants et étudiantes selon leur pratique de loisirs, le test de Kruskal-Wallis (Kruskal et Wallis, 1952) a été utilisé. Les résultats significatifs ont été complétés de boîtes à moustaches pour en vérifier la signification;
Pour comparer la performance des groupes d’étudiants et étudiantes selon leur pratique des modeleurs volumiques et leur bagage technologique, le test de Mann-Whitney (Mann et Whitney, 1947) a été utilisé. Les résultats significatifs ont été complétés de boîtes à moustaches pour en vérifier le sens;
Pour explorer le lien entre la performance en modélisation et la performance spatiale, des corrélations de Spearman ont été calculées. Elles ont été complétées par l’étude de nuages de points pour en vérifier la validité (Kinnear et Gray, 2015, p. 290).

Tableau 2

***Valeur du test de Shapiro-Wilk, et valeur de p de la performance en modélisation et des tests spatiaux (N = ddl = 127)***

4. Résultats

Nous présentons tout d’abord les résultats concernant le lien entre performance en modélisation et indicateurs relevant de la sphère éducative, c’est-à-dire le bagage technologique et la pratique antérieure de modeleurs volumiques. Nous soumettons ensuite ceux se rapportant à la sphère personnelle, soit la performance à des tests visant à mesurer les habiletés spatiales et la pratique de loisirs spécifiques.

4.1 Performance en modélisation et bagage technologique

La distribution des scores de l’exercice de modélisation, illustrée dans la figure 4, ne suit pas la loi normale. La performance élevée peut s’expliquer par le fait que 87,4 % (n = 111) des sujets de notre échantillon avaient déjà utilisé un modeleur volumique.

Figure 4

***Distribution des scores de modélisation***

La comparaison de la performance en modélisation des étudiants et étudiantes selon le contenu technologique des formations réalisées avant de rejoindre l’école produit un résultat significatif (U = 2402,50; p = 0,042). L’observation des distributions des scores de modélisation des étudiantes et étudiants selon leur bagage technologique antérieur illustrées dans la figure 5 décrit une performance supérieure et une distribution des scores plus resserrée pour ceux ayant reçu des enseignements technologiques (n = 71; 55,9 %).

Figure 5

***Distribution des scores de modélisation selon le contenu technologique du bagage scolaire***

4.2 Performance en modélisation et pratique antérieure de modeleurs volumiques

La comparaison de la performance en modélisation des étudiants et étudiantes selon la pratique antérieure d’un logiciel de modélisation produit un résultat très significatif (U = 1252,50; p = 0,007). L’observation des distributions des scores de modélisation des étudiantes et étudiants selon leur pratique antérieure des modeleurs volumiques illustrées dans la figure 6 décrit une performance supérieure pour ceux ayant pratiqué les modeleurs volumiques (n = 111; 87,4 %).

Figure 6

***Distribution des scores de modélisation selon la pratique antérieure de modeleurs volumiques***

4.3 Performance en modélisation et performance spatiale

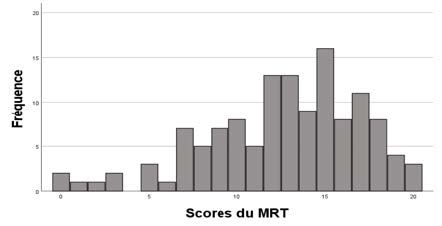
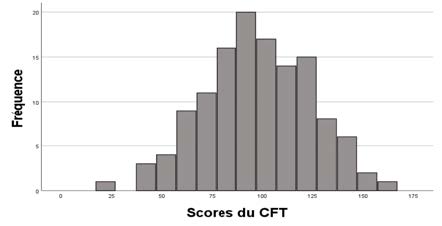
Les distributions des scores spatiaux illustrées dans la figure 7 ne suivent pas la loi normale, à l’exception du CFT : les scores sont majoritairement audelà des 60 % de réussite. Ceci peut s’expliquer par le fait que les étudiantes et étudiants sont spécialisés en STIM : il est probable que leurs compétences spatiales soient élevées (Wai et al., 2009). Cette remarque ne s’applique pas aux résultats du CFT, le test visant à mesurer la capacité à isoler un élément intriqué dans un motif complexe. Nous faisons l’hypothèse que les études suivies par notre échantillon n’ont pas mis en oeuvre des situations d’apprentissage favorables au développement de cette compétence, qui serait acquise dans les pratiques individuelles.

Figure 7

Distribution des scores du R PSVT:R (a), du MRT (b), du MCT (c), du PSVT:V (d) et du CFT (e)

-> Voir la liste des figures

Dans le tableau 3, on constate des corrélations de Spearman significatives entre la performance à l’exercice de modélisation et les scores spatiaux. Nous contrôlons ces résultats à l’aide de nuages de points pour confirmer la linéarité de cette association (Kinnear et Gray, 2015, p. 290).

Tableau 3

***Statistiques descriptives (M = moyenne; σ = écart type) et corrélations de Spearman pour les scores spatiaux et de modélisation volumique***

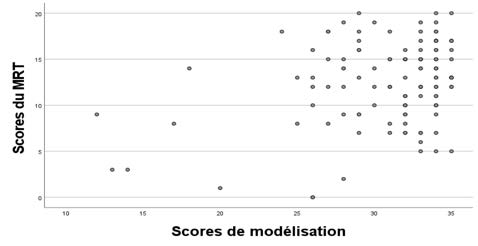
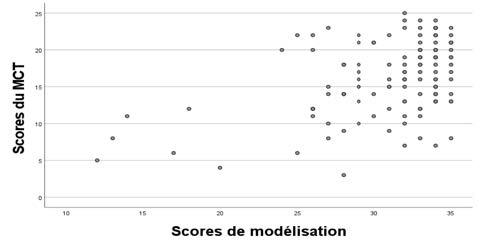
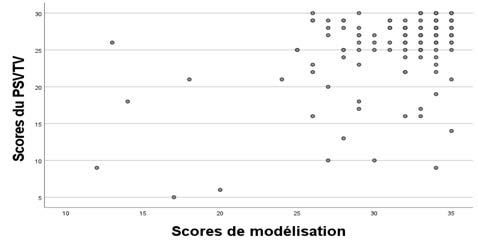
Les nuages de points, illustrés dans la Figure 8, montrent une concentration des valeurs autour de l’axe de corrélation pour les scores de modélisation à partir de 25, c’est-à-dire 94 % des étudiants et étudiantes. On remarque cependant un groupe de sujets, aux proportions variables selon les tests, obtenant des scores élevés en modélisation, mais faibles à modérés aux tests spatiaux. Cette dispersion au long de la progression explique que ces corrélations soient significatives mais faibles.

4.4 Performance en modélisation et pratique de loisirs

Parmi les dimensions indicées possibles que nous avons déterminées (voir 3.2.3), seules certaines sont mobilisées et pour quelques-unes d’entre elles, dans des proportions faibles. La mise en regard des scores de modélisation et des pratiques de loisirs ne produit pas de résultats significatifs, quelle que soit la temporalité. On observe cependant dans le tableau 4 des résultats proches de la significativité pour la catégorie manipulatoire (𝜒²(15) = 23,49; p = 0,074) et la catégorie construction 3D (𝜒²(5) = 10,95; p = 0,052) à l’âge adulte.

Valeur du 𝜒2, degrés de liberté (ddl) et valeur de p de la performance en modélisation volumique selon les loisirs — Tableau 4

***Valeur du 𝜒², degrés de liberté (ddl) et valeur de p de la performance en modélisation volumique selon les loisirs***

Figure 8

Dispersion des scores de modélisation selon le R PSVT:R (a), le MRT (b), le MCT (c), le PSVT:V (d) et le CFT (e)

-> Voir la liste des figures

5. Discussion

Nous observons que les étudiantes et étudiants ayant un bagage technologique obtiennent de meilleurs scores de modélisation que ceux qui ont reçu des enseignements qui en étaient dépourvus (figure 5). Il semblerait que les contenus technologiques, même s’ils n’ont pas mobilisé de modélisation volumique, aient permis de développer des compétences utiles pour la modélisation 3D.

Les étudiants et étudiantes ayant déjà utilisé des modeleurs volumiques performent significativement mieux à l’exercice de modélisation que les novices (figure 6). D’un certain point de vue, c’est un effet attendu d’une pratique antérieure des modeleurs que de contribuer à la performance à une tâche de modélisation. Cependant, seuls 23 (18,1 %) des sujets interrogés ont déclaré avoir utilisé un autre modeleur que ceux proposés dans notre questionnaire, soit SolidWorks, CATIA et SketchUp : il est donc peu probable que le nombre d’étudiants et étudiantes ayant déjà pratiqué Onshape, le modeleur retenu pour notre expérimentation, soit suffisamment élevé pour que l’on puisse lier ce résultat à la familiarité avec ce modeleur. Nous le rapprochons plutôt des études affirmant la transférabilité des stratégies de modélisation d’un logiciel de modélisation à un autre (Hamade et al., 2005, p. 306; Lang et al., 1991, p. 258) : les apprentissages de la modélisation 3D seraient effectifs quel que soit le logiciel utilisé. En d’autres mots, les enseignements reçus auraient permis l’acquisition de connaissances procédurales telles que la connaissance des stratégies pouvant être mobilisées pour réaliser une tâche de conception (Chester, 2007, p. 23; Hamade et al., 2005, p. 306; Lang et al., 1991, p. 258; Rynne et Gaughran, 2007, p. 59).

Nos résultats confirment le caractère prédictif des scores de tests visant la visualisation spatiale de la performance en modélisation décrit dans la littérature (Branoff et Dobelis, 2012b, p. 40; Steinhauer, 2012, p. 47) et l’étendent aux tests d’orientation spatiale. Les corrélations observées avec les scores du PSVT:V et du CFT sont par ailleurs plus élevées que dans le cas du MRT, un test de visualisation spatiale. Ce résultat invite à explorer davantage la pertinence de ces tests au travers notamment d’une analyse discriminante : les outils sélectionnés ainsi pourraient être utilisés pour repérer les étudiants et étudiantes les plus faibles en début d’année et leur proposer des dispositifs visant à développer un niveau de compétence spatiale suffisant pour effectuer des choix de spécialisations moins limités. Comme nous l’avons indiqué en 3.2.2, de précédents travaux (Albaret et Aubert, 1996, p. 271; Hegarty, 2018, p. 1214) ont montré que des stratégies autres que celles visées par les tests étaient mises en oeuvre dans ces outils de mesure. Bien que les tests soient conçus pour viser une compétence spécifique, il se peut que d’autres compétences y soient mobilisées. Une investigation des relations entre performance en modélisation et stratégies mises en oeuvre dans les tests est nécessaire pour repérer les compétences spatiales mises au travail dans les tests les plus pertinents pour la performance en modélisation 3D. Cette information serait utile à la conception de dispositifs pédagogiques visant à développer ces compétences.

De précédentes études liant la performance spatiale aux loisirs d’une part (Gold et al., 2018; Moreau et al., 2012), et à l’apprentissage de la modélisation volumique dans le cadre d’un apprentissage formel (Górska, 2005; Martín‐Dorta et al., 2008) d’autre part, nous voulions vérifier si ces relations pouvaient être étendues à la pratique de loisirs comme facteur favorisant de la performance en modélisation. Notre étude ne confirme pas ce lien pour les loisirs pratiqués dans l’enfance et produit des résultats faiblement significatifs (p < 0,1) concernant les loisirs manipulatoires et de construction 3D pratiqués à l’âge adulte (tableau 4), proches de ceux obtenus avec l’échantillon élargi (Charles, 2023, p. 211-213). Il est possible que cette pratique contemporaine à la prise de performance y contribue, ou que les étudiants et étudiantes pratiquant ces loisirs aient des compétences de modélisation élevées.

En résumé, notre étude met en évidence un lien significatif entre performance en modélisation et pratique antérieure de modeleurs volumiques d’une part, et performance en modélisation et bagage technologique, qui ne comprend pas toujours l’apprentissage des modeleurs 3D d’autre part. De plus, nous observons une relation significative entre performance en modélisation et performance spatiale. En revanche, cette étude fait ressortir l’absence d’une relation significative associant performance en modélisation et pratique de loisirs pour notre échantillon. Ceci suggère que les compétences de modélisation, à la différence des compétences spatiales, sont acquises grâce à des apprentissages particuliers, qui n’ont pas d’équivalent dans les pratiques de la vie courante et/ou dans les enseignements généraux. Cet apprentissage formel et spécifique permettrait de neutraliser les différences individuelles, développées au travers de la pratique de loisirs, manifestes dans les tests spatiaux.

6. Limites et autres dimensions investiguées

L’ordre des tests spatiaux a été le même pour l’ensemble des étudiants et étudiantes. De ce fait, il est possible que les performances observées dans les tests placés après le premier test aient été affectées par l’effet d’ordre (American Psychological Association, 2018a) : la pratique des tests placés en début de batterie a pu influencer la performance dans ceux placés à leur suite. D’autre part, la participation des étudiantes et étudiants étant volontaire, il se peut que ceux qui ont participé à l’ensemble des expérimentations soient animés d’une motivation particulière.

Les résultats significatifs observés pour les cinq tests spatiaux de notre batterie ne permettent pas de déterminer le test, ou la combinaison de tests, le plus pertinent pour caractériser la relation entre habiletés spatiales et performance en modélisation 3D. De nouvelles études statistiques sont nécessaires pour les définir et concevoir des outils de diagnostic des habiletés spatiales, en vue de repérer les étudiantes et étudiants en difficulté auxquels des dispositifs de remédiation pourraient être proposés.

De plus, notre corpus est composé d’étudiantes et étudiants très majoritairement issus de filières d’excellence et ayant choisi une école d’ingénieurs privilégiant la modélisation volumique. Cette spécialisation peut avoir un effet accélérateur mais aussi rébarbatif qui n’est pas neutre dans la recherche menée. Il serait donc intéressant de mener de nouvelles études auprès d’un public moins spécifique pour confirmer le caractère prédictif des scores spatiaux de la performance en modélisation 3D.

L’effet des enseignements du premier semestre, comprenant un cours consacré à l’apprentissage de la CAO et du modeleur volumique CATIA (Dassault Systèmes, 2012), sur les performances spatiales initiales des étudiants et étudiantes a été investigué (Charles, 2023, p. 255-256) : les habiletés spatiales ayant été mesurées à leur arrivée et à la fin du premier semestre, un test du signe (N = 92) a mis en évidence une progression significative (p < 0,05) des scores obtenus au R PSVT:R, une augmentation très significative (p < 0,001) des scores obtenus aux PSVT:V, MRT et MCT, alors qu’un test t pour échantillons appariés a permis de constater une progression très significative (p < 0,001) des scores obtenus au CFT.

Conclusion

Notre recherche ne portait pas sur l’impact d’enseignements de modélisation 3D à l’aide d’un logiciel spécialisé : elle cherchait à investiguer le lien potentiel entre performance en modélisation et facteurs de développement issus des sphères éducative et personnelle pour des étudiantes et étudiants ingénieurs français en première année, avant qu’ils ne reçoivent des enseignements de CAO. Les précédentes recherches (Branoff et Dobelis, 2012b; Chester, 2007; Rynne et Gaughran, 2007; Steinhauer, 2012) ont évalué les performances en modélisation à l’aide de modeleurs volumiques de leurs sujets apprenants pendant ou après qu’ils ont suivi des enseignements spécialisés. Un des indicateurs de la capacité de modélisation à l’aide d’un modeleur d’un sujet apprenant utilisé dans la littérature est la justesse du modèle réalisé (Branoff et Dobelis, 2012a, p. 25.548.6; Steinhauer, 2012, p. 47). Notre étude met en évidence un lien significatif entre performance en modélisation, évaluée au travers de la justesse et de la pratique antérieure des modeleurs volumiques, ainsi qu’un lien significatif avec le bagage technologique, sans qu’il ait forcément inclus des enseignements de modélisation. Notre investigation de la relation entre loisirs et performance en modélisation volumique a fait état d’une absence de résultat significatif. Les compétences de modélisation 3D seraient donc acquises grâce à des enseignements spécifiques, ne portant pas nécessairement sur la pratique des modeleurs 3D, qui ne trouvent pas leur égal dans les pratiques informelles, et qui contribueraient à réduire l’impact des différences individuelles sur la performance en études d’ingénierie. Ce résultat laisse apparaitre l’importance d’enseignements spécifiques d’apprentissage de la modélisation volumique au travers de logiciels de modélisation 3D dans l’acquisition de ces compétences. Nous avons corroboré la relation entre performance en modélisation 3D et compétences visuospatiales, et l’avons étendue aux compétences d’orientation spatiale, qui sont peu explorées dans la littérature (Agbanglanon, 2019; Kelly Jr, 2013; Sorby et al., 2013). Ces résultats ouvrent des perspectives de prise en compte de ces compétences déterminantes pour la réussite en STIM en général et celle en modélisation 3D en particulier. À l’instar de Sorby et de ses collègues (Sorby, 2005; Veurink et al., 2009), les habiletés spatiales des étudiantes et étudiants en ingénierie pourraient être mesurées en début de cursus pour proposer à ceux d’entre eux enregistrant les scores les plus faibles des dispositifs pédagogiques visant à développer ces compétences déterminantes, à favoriser leur apprentissage et leur réussite (Sorby, 2005, p. 11) et à leur donner accès à un plus large éventail de spécialisations.

Apprentissage de logiciels de modélisation 3D et pratique de loisirsImpact of Leisure Activities on Learning 3D Modeling Software

Résumé

Abstract

Introduction

1. Revue de littérature