Corps de l’article

Je poursuis ici le propos que j’ai abordé aux journées sur l’image scientifique tenues à Liège en mars 2007. L’objet de recherche de l’équipe que je coordonne dans le cadre d’un projet FRFC (Fonds de la recherche fondamentale collective) est la textualité du discours scientifique, autrement dit l’étude sémiotique de l’organisation interne des énoncés relevant de ce genre discursif. C’est ce qui explique que, dans ce qui va suivre, je parle de l’image telle qu’on la mobilise dans le discours scientifique d’exposition (article, traité, ouvrage de vulgarisation, page Web, etc.), lequel a ses spécificités rhétoriques, et non de l’image produite par les dispositifs d’observation scientifique (image obtenue par tomographie, RMN (résonance magnétique nucléaire), etc.)[1]. Un chapitre de cette recherche est celui où l’on envisage l’intégration des images aux textes verbaux. Ce que j’ai essayé de faire en proposant d’abord une esquisse de grammaire générale de l’interaction texte-image (Klinkenberg, à paraitre b) et en observant ensuite la manière dont le discours scientifique mobilise les potentialités de cette grammaire (Klinkenberg, à paraitre a). Dans ce qui suit, il s’agira de s’interroger sur l’apport global de l’image au discours scientifique : que peut-elle ?

Dernière précision : m’autorisant de Jacques Bertin (cité par Badir, 2005 : 50), qui définit l’image comme « la formesignificative perceptible dans l’instant minimum de vision » (Bertin, [1967] 1973 : 142), je traiterai ici du cas particulier des graphiques, des histogrammes, des diagrammes de dispersion, des schémas et des tableaux. Dans la plupart des cas, il s’agit de la catégorie globale de ce que Desnoyers (2005a, 2005b) appelle les « analogrammes », auxquels pourront venir s’adjoindre certaines autres espèces comme les organigrammes. Pour désigner tous ces types d’énoncés, j’emploierai le mot « schéma » ; celui-ci sera donc pris dans son sens générique, et non au sens restreint de la géométrie algébrique.

1. Écriture et spatialité

Je convoque ici l’écriture pour en souligner un trait essentiel, et tirer de celui-ci une conséquence qui va nous être utile dans l’étude du schéma.

Ils sont peu nombreux les théoriciens de l’écriture (en dehors de Harris, 1995 ; Cárdenas, 2001 ; Perri, 2001) à avoir pointé la caractéristique capitale de l’écriture – capitale, car elle est la source du caractère multidimensionnel de l’écriture – : que cette dernière fait passer la parole du canal oral sur le canal visuel.

Or, les sémiotiques qui transitent sur l’un et l’autre de ces canaux sont profondément affectées par les propriétés de ceux-ci, ce qui – soit dit en passant – justifie une prise en considération des canaux, qui était jusqu’à nos jours largement refusée par la sémiotique[2]. Il n’est évidemment pas question de ramener toute la question du sens à la nature du canal (comme le veut une position polémique que résume la formule bien connue de McLuhan « Le médium, c’est le message »), mais de prendre au sérieux l’idée que les aspects matériels de la communication font de plein droit partie du travail de signification et de référence.

Je précise que par canal, j’entends, d’une première part, l’ensemble des stimuli des signes qui dépendent du support matériel permettant leur transmission et, de seconde et troisième parts, les caractéristiques des appareils émetteurs et récepteurs, qui ont chacun leurs potentialités propres. C’est que la configuration des énoncés dépend de ces instances de transmission. Les appareils visés ne sont en effet sensibles qu’à une gamme spécifique de phénomènes physiques. Ainsi, le canal auditif ne permet pas de traiter à la fois autant d’informations que le canal visuel, beaucoup plus puissant. Ce dernier permet en effet de faire transiter 107 fois plus d’informations que le premier, dans le même laps de temps (voir Groupe µ, 1992). Cette différence de puissance a des répercussions non négligeables sur les modes d’organisation des unités sémiotiques dans un syntagme. On peut aisément constater que les sémiotiques s’appuyant principalement sur l’ouïe privilégient les chronosyntaxes, ou syntaxes linéaires (où les informations se présentent pour être traitées les unes après les autres), et que celles qui exploitent la vision font un usage de toposyntaxes, ou syntaxes tabulaires (un terme qui va être glosé ci-après), où l’on traite simultanément un certain nombre d’informations, cette simultanéité étant autorisée par la puissance du canal.

Lorsqu’une même sémiotique mobilise des signes fondés sur des stimuli différents – autrement dit lorsqu’elle exploite des canaux différents –, ceci entraine une conséquence importante : on ne peut avoir une équivalence parfaite entre la variante du code transitant par le canal a et celle qui transite par le canal b, puisqu’un canal particulier fait peser des contraintes spécifiques sur l’organisation de ces signes. On doit donc s’attendre à ce qu’en passant d’un canal à un autre, les messages performés à partir d’un code donné perdent une partie de leurs caractéristiques mais gagnent en échange d’autres caractéristiques. Ainsi, en passant par la modalité sensorielle qu’est la vision – en étant écrits –, les énoncés linguistiques conservent-ils leur caractère linéaire, tout en acquérant un caractère spatial.

Et c’est bien cette dimension spatiale qui est importante lorsqu’on définit l’écriture, et non son caractère visuel : celui-ci est tout au plus la source de ladite spatialité. On constate en effet que cette spatialité peut être exploitée sur d’autres canaux que le visuel. Par exemple les signes scripturaux peuvent faire l’objet d’une transposition tactile, comme « l’écriture Braille » : non visuels, ils se définissant eux aussi par une disposition spatiale.

Grâce à la spatialisation, l’énoncé écrit cesse donc de se déployer dans un espace à une dimension (induisant des relations exclusivement linéaires) mais investit un espace à deux dimensions au moins (induisant des relations tabulaires)[3]. Cet espace à deux ou à trois dimensions permet une aperception simultanée. Mais le champ de cette aperception est toutefois orienté (et animé) par des relations linéaires. La particularité de l’espace écrit réside dans cette dialectique : il est le champ où se déploient à la fois des relations tabulaires et des relations linéaires. L’énoncé langagier devient image, au sens de Bertin[4].

2. Le schéma scientifique et l’écriture

Le schéma scientifique est étroitement lié à l’écriture, et cela pour deux raisons.

De première part, il se présente toujours dans un environnement textuel visuellement perceptible, auquel il est non seulement intégré, mais subordonné.

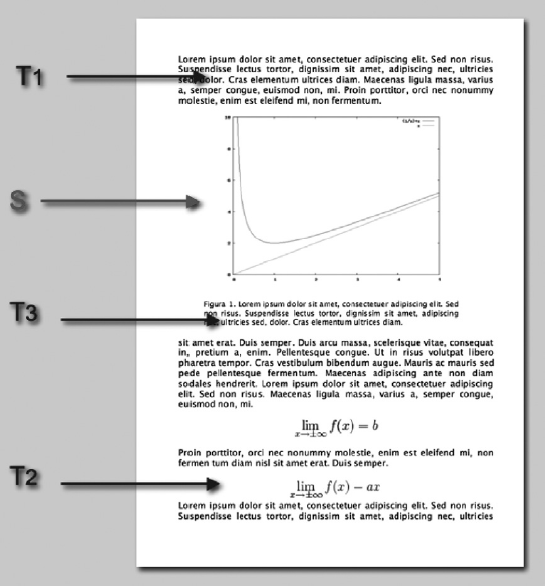
Même s’il contribue à l’organiser, le schéma est systématiquement intégré au texte : rapport, encyclopédie, manuel, article, page Web. Il forme avec ce texte un énoncé global. À l’intérieur de cet énoncé global, on peut certes distinguer au moins deux grands composants nettement individualisés : le texte verbal T, et le schéma proprement dit S ; et au sein du composant textuel T, on peut opérer de nouvelles décompositions : le texte suivi proprement dit T1 et les formules T2, par exemple (voir fig. 1).

Figure 1

Intégration du schéma et du texte : composant schématique et composants textuels.

Intégration du schéma et du texte : composant schématique et composants textuels.

-> Voir la liste des figures

Mais S + (T1 + T2) constitue indéniablement une unité. D’où provient cette unité ? De procédures indexicales assez générales. Pour rappel, l’index – qu’on se gardera de confondre avec l’indice – est un dispositif sémiotique ayant pour fonction de focaliser l’attention sur un objet déterminé, ou de donner un certain statut à cet objet (exemple : le doigt pointé, la flèche, l’étiquette, etc.). Ce type de signe ne fonctionne qu’en présence de l’objet désigné, de sorte que sa définition mobilise l’idée de contigüité. Si la nature des objets appelés à devenir des index peut être très variable (ils peuvent très bien être de nature linguistique : « ce type-là »), ils exploitent donc toujours l’espace, voire le temps (« le président actuel »). Ce sont de telles indications indexicales, culturellement variables, qui fournissent l’unité du dispositif global. Nous savons ce que c’est qu’une page, à quoi elle sert, comment elle se manipule, et sommes dressés à considérer tout ce qui figure dans l’espace délimité par sa bordure comme une unité de forme et de sens. Nous savons aussi ce qu’est un livre, et y postulons de la même manière une unité de forme et de sens.

Figure 2

Fonction indexicale de la page.

Fonction indexicale de la page.

-> Voir la liste des figures

Une certaine culture a ainsi formé ses membres à discrétiser le champ de l’expérience en plages distinctes et à postuler une homogénéité de ces plages.

Notons une autre sujétion du schéma au texte : ce schéma est le plus souvent légendé. La légende (T3) peut être considérée, historiquement, comme une excroissance du texte englobant T (T1 + T2), obtenue par la sélection de certains éléments de celui-ci, considérés comme devant entretenir une relation privilégiée avec le schéma. La légende a fini ainsi par devenir un intermédiaire entre S et T1 + T2, deux unités avec lesquelles il entretient une certaine relation de redondance (redondance partielle, on va le voir). La légende établit une autre relation indexicale très claire entre son contenu linguistique et le schéma, induisant une relation verbo-éidétique[5].

Tout ceci mène à un constat : le faible degré d’autonomie du schéma par rapport au texte. Mais alors, dira-t-on, quel est son apport ? et quelle spécificité a-t-il par comparaison à T ? Répondre à cette question est l’objectif de la présente contribution. Pour l’instant, contentons-nous de dire que, intégré au texte, le schéma subit la loi de ce texte. On comprend donc que les procédures de lecture d’un schéma soient affectées par les habitudes de lecture textuelle qui sont les nôtres. Par exemple, on observe une tendance à produire des schémas qui supposent une lecture allant de gauche à droite. On s’en persuade aisément en comparant les exemples 3a et 3b qui suivent : le second est manifestement agrammatical.

Figures 3a et 3b

La lecture orientée du schéma.

La lecture orientée du schéma.

-> Voir la liste des figures

Si le schéma est subordonné au texte, il comprend par ailleurs toujours des éléments textuels : mots isolés, données chiffrées, qui entrent dans le schéma à titre de formants, ou traits du langage du schéma. Ces formants textuels ont aussi pour conséquence d’intégrer la linéarité dans le dispositif spatial. Certes, ils sont souvent présents sous une forme minimaliste : celle de lettres ou de chiffres. Mais bien qu’il y ait des lettres symétriques[6], les formants littéraux comportent le plus souvent, et dans la plupart des écritures, une orientation.

Il y a donc une double intégration du langage et du schéma : subordonnante et superordonnante. Cette intégration confère donc à ce dernier la propriété canonique dialectique de l’espace scriptural : spatial, il est aussi linéaire et orienté.

Cette « orientationnalité »[7] que le schéma reçoit de l’écriture entre évidemment en redondance avec d’autres formants ayant le même signifié général d’orientationnalité. Ce sont, par exemple,

  • des signes comme la flèche, qui a plusieurs signifiés possibles dans le schéma : expression de l’orientationnalité (cas des flèches proches de sigma et e dans les exemples 4a et 4b), ou lien à fonction indexicale (reliant un énoncé linguistique et une portion d’énoncé d’une autre nature ; cas de la flèche proche du mot « seuil » en 4b) ;

  • des traits ou pointillés à la même fonction indexicale, où la portion d’énoncé distinct peut être iconique;

  • le comportement de certains tracés, encyclopédiquement conçus comme directionnels : dans la droite asymptotique, par exemple, la tangence constitue une indication de l’orientationnalité.

Figures 4a et 4b

Dispositifs à valeurs indexicales.

Dispositifs à valeurs indexicales.

-> Voir la liste des figures

Ce n’est donc pas seulement par l’intervention du linguistique que le schéma est linéairement orienté : il doit aussi ce trait à des formants non linguistiques. Mais il n’est pas exagéré de dire que le linguistique joue un rôle important dans cette vectorialisation. Pour l’instant, pointons surtout la double propriété de l’espace du schéma : à la fois spatial et linéaire[8].

3. Tabularité et analyse

Cette double dimension produit une tabularité. La tabularité est une notion que nous avons introduite dans notre Rhétorique de la poésie (Groupe µ, 1977). La tabularité caractérise la lecture de certains énoncés. Dans la lecture tabulaire, un élément de l’énoncé prend son sens grâce au rapport qu’il entretient avec d’autres éléments, sur au moins deux axes linéaires distincts. Dans la plupart des schémas, précise Badir,

[…] la tabularité s’exprime par l’utilisation de l’orthogonalité de l’espace. Cela est vrai des tableaux, où lignes et colonnes, établissant les paramètres à croiser, sont établis dans la très grande majorité des cas à l’horizontale et à la verticale […]. L’orthogonalité est également manifestée dans tous les diagrammes, y compris les camemberts qui sont des diagrammes employant les quatre quadrants (alors que, généralement, les diagrammes sont construits sur la base du seul quadrant des valeurs positives). L’orthogonalité est encore présente dans les organigrammes et les arborescences, où la verticalité renvoie à la hiérarchisation des éléments tandis que l’horizontalité renvoie à leur distribution au sein d’un même niveau. (2007 : 284-285)[9]

Mais, évidemment, ce schéma de base peut se voir complexifié : il peut y avoir plus de deux axes distincts, soit qu’un schéma mime la troisième dimension par des artifices adéquats, soit qu’on renonce à l’orthogonalité en multipliant les axes dans le même plan (comme dans le diagramme de Kiviat).

Par la multiplicité des axes, la tabularité privilégie les rapports établis en dehors de la ligne du temps (mais sans exclure ceux-ci, comme on va le voir).

La tabularité est aussi l’un des instruments privilégiés de l’analyse, si l’on entend par analyse la déclinaison d’un objet en plusieurs composantes expressément choisies, deux au moins. Suivons encore Badir :

Comme la tabularité conduit à attribuer un sens à un objet graphique en fonction de deux paramètres, comme la tabularité, plus précisément, est le moyen de diviser le sens de l’objet en fonction de deux composantes générales qui le catégorisent, il est clair qu’un énoncé graphique, quel qu’il soit et quel que soit son objet, présente une analyse. (2007 : 286)

Explicitant le choix des composantes, le schéma reflète donc, comme le voulait Tufte (1983), la logique de l’analyse menée. Indépendamment de son intégration au texte, il constitue donc un discours argumentatif, puisqu’il sélectionne et isole les paramètres d’un phénomène tout en proposant des hypothèses sur les relations (causales ou autres) entre ces paramètres.

Il est important de noter que les schémas ne sélectionnent jamais ces composantes au hasard. Une dimension au moins de l’analyse que mènent un bon nombre d’entre eux[10] fait obligatoirement intervenir la variation. Le tableau, l’histogramme, le diagramme ont en commun de présenter des valeurs variant. Or, la variation est un processus, et qui dit processus dit temporalité. La temporalité est donc toujours présente, à titre de référent, dans les schémas dont il est question ici. Il s’agit parfois d’une temporalité au sens strict (comme les différents moments d’une réaction physique, les années où les mois de prises de la mesure de la précipitation, ou les moments où l’on a établi la valeur de telle monnaie) ; un des paramètres du schéma est alors constitué par des unités de mesure du temps. Mais il peut aussi s’agir non de temps explicitement exprimé, mais de phénomènes référables à des procès, à titre de modalités ou de résultat. Ces phénomènes présupposent le procès dont ils dépendent, et donc le temps. On s’en persuade aisément si l’on remplace les substantifs des schémas – ces substantifs que privilégie le scientifique, tout à son désir d’exprimer une vision essentialiste de ses pratiques – par leur équivalent verbal : « offrir » et « demander » (à la place de « offre » et de « demande »), « varier selon le paramètre de la pression », « varier selon le paramètre de la température», etc. Le schéma s’adosse donc toujours à un récit.

C’est bien ce dynamisme que la propriété d’orientationnalité du schéma permet d’exprimer. Et il est juste de parler d’iconisme : il y a ici motivation, puisque l’orientationnalité du plan de l’expression correspond à une temporalité sur le plan du contenu.

4. Que fait le schéma ?

C’est ici qu’il faut poser la question annoncée : qu’ajoute le diagramme au texte ? Pour répondre à cette question, on ne peut se contenter de verbes passe-partout comme « illustrer », « rendre frappant », « expliquer ». Toutes ces expressions renvoient à des réponses simplistes, ou au moins incomplètes. Examinons deux de celles-ci.

Horn (1998) souligne la pertinence des éléments visuels dans une communication d’entreprise globale, et l’attribue au fait que l’intégration des éléments verbaux et visuels permet une meilleure compréhension et un gain de temps, ce qu’avait déjà souligné Bertin. Que l’interaction verbo-éidétique produise un effet de compacité et d’immédiateté qu’il doit aux caractéristiques du canal visuel et donc à la spatialité de ses messages, la chose n’est pas douteuse. Que cette compacité aide à la compréhension non plus. Mais, précisément, ce que cette réponse laisse dans l’ombre, c’est la spécificité de ce qui peut être compris grâce à cette intégration. Ne s’agit-il que d’une simple reprise de ce qui peut être compris par le langage seul ou par le graphique seul ?

Une telle idée est parente de celle de redondance. Celle-ci constitue une seconde réponse possible. En effet, un regard rapide sur le schéma permet de croire qu’il propose une redondance totale entre les éléments textuels et les éléments spatiaux. Ceux-ci entretiennent en effet une relation de co-référence, dont le corrélat sémantique est la redondance. Par exemple, un symbole (n, x, p, etc.) à côté d’un vecteur signifie que tout le vecteur est saturé par la donnée à laquelle renvoie ce symbole. Or, il est admis par beaucoup que la science est un ensemble d’énoncés axiomatiques (qui sont non pas indémontrables, mais acceptés sans démonstration, sous peine de circularité) ; et les systèmes axiomatiques sont ceux qui sont pleinement tautologiques.

Cette seconde réponse n’est pas beaucoup plus satisfaisante que la première. On peut en effet poser que si le diagramme est considéré comme nécessaire[11], c’est bien que le texte est insuffisant. Si le formalisme du texte – qu’il s’agisse de son hypostase verbale T1 ou de son hypostase formule T2 – était satisfaisant, le schéma S serait purement redondant.

De l’exigence générale du schéma, on peut donc inférer que le formalisme souhaité dans le discours scientifique n’est nullement établi par le langage. Ni le texte langagier ni la formule ne semblent permettre une appréhension satisfaisante des phénomènes étudiés. Ce qui semble ne pouvoir être atteint que par le binôme texte-schéma. La question se repose donc : qu’est-ce qu’on peut comprendre ? Quel formalisme spécifique ajoute le schéma ? Quelle est la spécificité de celui-ci dans l’attribution de sens ?

Ma réponse sera double : le schéma apporte un formalisme qui, en associant le spatial et le linéaire, permet de réconcilier le paradigme et le syntagme, et de réconcilier le général et le particulier. Dans ces deux cas, nous montrerons que ce que peut le schéma, il le doit à son statut double, à la fois spatial et vectoriel.

a. Réconciliation du syntagme et du paradigme

On sait ce qu’est un paradigme : un répertoire d’unités commutables dans un certain contexte. Ce répertoire est obtenu par une manoeuvre de catégorisation : un paradigme est en effet une classe d’éléments, par définition homogènes d’un certain point de vue. C’est bien ce que nous avons dans un schéma : celui-ci rend compte de toutes les occurrences présentant des caractéristiques comparables (par exemple comparables du point de vue de la pression ou de la température, ou de la valeur d’échange) dans un empan de variation considéré comme pertinent. Mais comment cette homogénéité est-elle établie ? On le sait, l’opération constitutive d’un paradigme est la commutation : l’homogénéité paradigmatique se définit par le fait que ces éléments peuvent apparaitre au même endroit d’un syntagme donné. La relation paradigmatique vise donc l’ensemble des liens que des unités non manifestées entretiennent entre elles, hors d’un énoncé particulier. Ces relations paradigmatiques opèrent sur l’axe de la sélection. Comme elles mettent en relation des éléments qui ne sont pas co-présents, on dira qu’elles opèrent in absentia, littéralement « en l’absence » (d’un ou de plusieurs éléments corrélés à un autre, présent). Les diverses valeurs que peuvent prendre une variable dans un schéma constituent bien, de ce point de vue, un paradigme : une seule des valeurs distinguées par l’analyse peut être actualisée à un moment donné, les autres restant virtuelles. Le temps est donc absent de la virtualité paradigmatique : le paradigme est par définition intemporel.

En ce qu’il produit une analyse, le schéma donne bien à lire le paradigme, et signifie cette intemporalité.

Mais le schéma a la particularité de constituer également un syntagme. On se rappellera que le syntagme est un modèle de relations entre unités, l’énoncé actualisant ce syntagme virtuel. Le schéma est un syntagme car il rend compte de l’actualisation des potentialités : de la totalité des actualisations possibles des termes dans l’empan de variation considéré pertinent, mais actualisation tout de même. Syntagmatique, le schéma l’est à un double titre : d’abord parce que toutes les actualisations possibles de la variation sont mises en relation les unes avec les autres (sous forme de nuages de points, ou sous forme linéaire), selon une règle déterminée ; ensuite, et toujours parce qu’il est un instrument d’analyse, le schéma institue des relations entre ces combinaisons d’actualisations, toujours selon une règle déterminée. Au total, le schéma est donc une mise en relation de relations. Or le temps est une caractéristique obligée du syntagme.

Dans l’espace du schéma, l’orientationnalité injecte le temps. L’intemporalité, qui est la propriété du paradigme, connait ainsi une mutation de nature : elle devient simultanéité.

b. Réconciliation du général et du particulier

L’ensemble du dispositif verbo-éidétique exprime la généralité. Comment en irait-il autrement dès lors qu’il sert le discours scientifique, et qu’il n’y a de science que du général ?

Mais allons au-delà de ce slogan, qui a le gout de la pétition de principe, pour constater que la mission d’exprimer la généralité est inégalement répartie au sein du dispositif global. Constatons ainsi que les formules (T2) se situent résolument du côté du général. Le texte T1, quant à lui, oscille entre les deux pôles. Tantôt il formule verbalement les propositions générales exprimées avec plus de compacité par la formule. Tantôt, il se réfère à des faits particuliers. Mais ceux-ci sont parfois convoqués comme illustration de la loi (c’est l’exemplum de l’ancienne rhétorique), parfois comme point de départ d’un processus intellectuel menant à la formulation d’une loi (« Soit n, un point quelconque… »).

Le schéma permet également une expression des deux pôles, mais ce n’est pas sous la forme d’un choix ou d’une oscillation : c’est sous la forme d’une conjonction. Une fois de plus, cette conjonction est rendue possible par la tabularité.

Le schéma particularise une première fois parce qu’il attribue des contenus aux lois.

Certes, selon les mathématiciens, un diagramme n’a pas besoin de contenu, puisqu’il énonce des relations de relations. Et il serait possible de construire un langage qui ne se définirait que par sa syntaxe. Pour Netz (1999), les expressions littérales des diagrammes anciens ne sont pas des signes revoyant à une réalité ; les lettres ne désignent pas un réel qui préexisterait, mais construisent celui-ci par la monstration (« quand montrer, c’est faire… ») : « cette ligne-là, j’en établis le statut en la nommant a-b »). On pourrait en conséquence ajouter qu’elles sont les déclencheurs d’une force illocutoire qu’elles reçoivent de leur fonction indexicale. Aux yeux d’un sémioticien toutefois, qui reconnait évidemment la force illocutoire de la monstration, il est contradictoire qu’à une expression ne puisse correspondre aucun contenu : que celui-ci ne puisse être thématisé avec précision et qu’il reste donc d’une grande généralité ne lui ôte rien à son statut de contenu.

Mais il n’est sans doute pas utile d’entrer dans cette discussion : de toute manière, même si un schéma n’avait pas besoin de contenu, cela ne signifierait pas qu’il ne puisse y en avoir. Le plus souvent, son sémantisme advient du fait qu’il fournit à la fois une loi et les objets auxquels s’applique cette loi. Et, ici encore, on constate une répartition des fonctions : montrer la loi est la tâche qu’assument ses formants spatiaux ; et désigner les contenus est celle qui est dévolue aux formants verbaux. Une fois de plus, cette intrication découle de la co-référence que rend possible l’indexicalité.

Dans l’hypothèse où l’on admettrait qu’il y ait des schémas sans contenu, cette première particularisation serait tout optionnelle. La seconde, elle, est en tout état de cause nécessaire et est une conséquence directe de la tabularité.

Cette tabularité permet d’observer un point particulier où s’applique la loi générale exprimée par la formule, de faire arrêt sur lui ou le mettre en évidence[12]. La co-référence permet en effet de faire ce que fait aussi le composant verbal du texte scientifique : donner le statut d’exemple particulier à un point ou à une donnée du schéma. Mais ces cas particuliers sont en grand nombre, voire en nombre infini lorsque les formants graphiques sont continus (comme avec la courbe). Le schéma permet donc de saisir les faits – des grandeurs, des phénomènes physiques, des phénomènes sociaux – dans le continu de leur réalisation ; il permet de parcourir toute la série des formes particulières qu’ils prennent. Il rend donc compte simultanément des particuliers – de la totalité des particuliers – et de la généralité qui engendre cette totalité ou qui en est l’expression.

Comme la formule, le schéma a une fonction d’analyse, mais si la formule exprime toutes les potentialités de cette analyse, elle le fait de manière intemporelle, et donc statique. Par son orientationnalité, qui permet de parcourir la totalité des actualisations, le schéma introduit dans l’analyse une dimension dynamique. Ici encore, intemporalité et processualité connaissent une dialectique dont le résultat est la simultanéité.

5. Spécificité pragmatique

La dialectique de la spatialité intemporelle et de la séquentialité dynamique n’est pas un monopole du schéma, mais constitue une propriété de tous les instruments d’intellection, même les plus élémentaires. Notre perception, en effet, est celle de phénomènes particuliers qui se présentent à nous de manière discontinue, et c’est nous qui y introduisons l’unité et la continuité[13]. Cette continuité nous l’obtenons par une stabilisation qui est une généralisation (voir Groupe µ, 1998 ; Klinkenberg, à paraitre c). Ainsi fonctionne la mémoire, qui emmagasine les résultats des perceptions successives pour les rendre simultanées dans le traitement qu’elle leur réserve. Ainsi, si les éléments fournis par la langue se présentent de manière linéaire au cours de la communication langagière, cela ne signifie nullement qu’elles font l’objet d’un traitement linéaire : leur simultanéité est en tout cas assurée par la mémoire.

Opérer ce type de synthèse n’est donc pas une propriété exclusive du schéma. La spécificité de ce dernier dans la manoeuvre est dès lors sans doute de nature pragmatique, ou sociologique.

Quand il a été question de la synthèse du paradigme et du syntagme, le lecteur n’a pas manqué de se souvenir de la définition de la fonction poétique jadis proposée par Jakobson (1960), car elle se présente elle aussi comme un accommodement du paradigme et du syntagme. La procédure assurant cette fonction consistait, on s’en souviendra, à projeter la logique d’équivalence et de susbstituabilité du paradigme sur la réalisation syntagmatique. Principe explicatif puissant, puisqu’il rend compte de phénomènes aussi différents que la rime ou la métaphore.

Mais on voit que, par-delà cette ressemblance, le schéma et la figure poétique divergent profondément quant aux objectifs qu’ils s’assignent. On doit donc s’attendre à ce qu’ils gèrent de manière très différenciée les modalités de la synthèse entre syntagme et paradigme, général et particulier.

La poésie, c’est bien connu, assume la co-présence des éléments du paradigme (Klinkenberg, 1996). Sa spécificité est d’admettre la coïncidence des actualisations du système, et ces actualisations sont sélectionnées de manière non explicite. Le schéma, quant à lui, a une double fonction d’analyse et d’argumentation, comme je l’ai rappelé. En tant qu’il argumente, il exprime explicitement le choix de ses points de vue. S’il vise à l’exhaustivité dans les actualisations de la potentialité, celles-ci sont toujours soumises au principe de non-contradiction. En tant que dispositif analytique, il distingue et individualise en effet toujours ces actualisations, même si c’est sous la forme de l’allocation d’une valeur à un point précis d’un continuum.

Pour le sémioticien, la puissance explicative du schéma provient donc du fait qu’il associe, dans une perception globale (voire immédiate) qu’il doit à sa tabularité, le général du paradigme avec la totalité des particuliers exprimée par sa structure syntagmatique. Cette puissance réside aussi dans les interpolations, les extrapolations et les hypothèses qu’il autorise sur des ensembles de données qui n’ont été obtenues que par un nombre restreint de mesures : c’est là l’un de ses principaux apports, en ce sens qu’il fournit une information inaccessible par les données brutes dont il est la représentation. Or, un tel apport n’est possible que grâce à la conjonction de la linéarité, qui permet l’ordonnancement des mesures, et de la tabularité, qui permet les extrapolations et les interpolations. Le schéma assure également une connaissance sensible et heuristique, voire empirique, des phénomènes qu’il décrit, connaissance impossible à dériver directement depuis les données ou les équations qui en sont la source. Pour Luciano Boi (à paraitre),

[...] seules les mathématiques permettent […] de réconcilier le mouvement et le changement incessants des phénomènes et de la réalité avec la permanence et la stabilité de certains êtres ou logoï physico-mathématiques ; autrement dit, la variabilité universelle avec l’identité générique, l’ubiquité transpatiale et translocale avec l’individuation ontologique d’êtres et d’organismes déterminés.

Sans doute seules les mathématiques permettent-elles d’élaborer cette réconciliation, mais seul le schéma permet de la faire percevoir – de la faire comprendre – dans l’instant.