Résumés
Résumé
La notion de vigilance didactique vise à rendre compte du rôle joué par la maîtrise de connaissances mathématiques et didactiques dans les pratiques enseignantes, et le développement de son exercice est un enjeu de formation. Un scénario basé sur un jeu de rôles, que nous avons conçu, mis en oeuvre et analysé dans nos travaux précédents, nous a semblé susceptible de participer à ce développement. Dans cette recherche, nous caractérisons les choix de mises en oeuvre de ce scénario de deux formatrices, au regard d’un développement potentiel de l’exercice de la vigilance didactique des personnes formées. Nos analyses mettent en évidence des dynamiques différentes dans des mises en lien de connaissances à mobiliser, de gestes professionnels à mettre en oeuvre et de finalités d’apprentissages pour les élèves.
Mots-clés :
- jeu de rôles,
- vigilance didactique,
- pratiques,
- formation,
- formateurs,
- formatrices
Abstract
The concept of didactic vigilance seeks to account for the role played by the mastery of mathematical and didactic knowledge in teaching practices, and developing this vigilance is an issue for training. A role-playing scenario, which we designed, implemented and analyzed in our previous research, appeared as a way to contribute to this development. In this study, we describe the choices made by two trainers when implementing this scenario, in connection with the potential development of didactic vigilance in trainees. Our analyses highlight the various dynamics involved in linking the knowledge to be applied, the professional acts to be implemented, and the learning aims for the students.
Keywords:
- role-playing,
- didactic vigilance,
- practices,
- training,
- trainers
Resumen
La noción de vigilancia didáctica busca dar cuenta del rol que juega el dominio de los conocimientos matemáticos y didácticos en las prácticas docentes, y el desarrollo de su ejercicio es un desafio formativo. Un escenario basado en un juego de roles, que hemos diseñado, implementado y analizado en nuestros trabajos anteriores, nos ha parecido susceptible de contribuir a este desarrollo. En esta investigación, caracterizamos las elecciones de implementación de este escenario por parte de dos formadoras, en relación con un desarrollo potencial del ejercicio de la vigilancia didáctica de las personas formadas. Nuestros análisis destacan dinámicas diferentes en la conexión de conocimientos a movilizar, gestos profesionales a implementar y finalidades de aprendizaje para los alumnos.
Palabras clave:
- juego de roles,
- vigilancia didáctica,
- prácticas,
- formación,
- formadores y formadoras
Corps de l’article
1. Introduction
Dans une recherche précédente, nous avons conçu, mis en oeuvre et analysé un scénario de formation basé sur un jeu de rôles (JdR) qui plonge les futurs professeures et professeurs des écoles (PE) (primaire) dans une situation d’aide à un élève rencontrant une difficulté dans une tâche portant sur les nombres décimaux (Lajoie et al., 2019). Ce travail a révélé des potentialités du dispositif pour faire émerger certaines connaissances et pratiques chez les PE en formation initiale, mais il a également révélé qu’un travail exigeant était nécessaire de la part des personnes formatrices pour développer des connaissances professionnelles. Nous avons prolongé l’étude en observant la mise en oeuvre du scénario en formation initiale (master 2 Métiers de l’enseignement, de l’éducation et de la formation) en France par deux formatrices n’ayant pas participé à sa conception. La manière dont elles exploitent les mises en avant effectives (les moments où le jeu a lieu devant la classe), les savoirs qu’elles dégagent lors des phases de discussion ont été au coeur de nos analyses (Guille-Biel Winder et al., 2022). Dans la continuité de ce qui précède nous cherchons à caractériser les choix des formatrices au regard d’un développement potentiel de l’exercice de la vigilance didactique des personnes formées.
La notion de vigilance didactique (VD), définie par Charles-Pézard (2010), vise à rendre compte du rôle joué par la maîtrise de connaissances mathématiques et didactiques (Houdement, 2013) dans les choix effectués par les PE. Développer l’exercice de la VD peut alors être considéré comme un enjeu de formation (Celi et al., 2019; Houdement et Masselot, 2019; Guille-Biel Winder et Mangiante-Orsola, 2023), en particulier dans le cadre d’un dispositif de formation de type JdR. Nous estimons que la notion de VD peut permettre de mieux caractériser ce qui guide prioritairement les choix des personnes formatrices dans la gestion de ces situations de formation même dans un contexte où le développement de l’exercice de la vigilance didactique n’est pas explicitement visé.
2. Points d’appui théoriques et questions de recherche
Nos travaux s’inscrivent dans la continuité des recherches sur les pratiques enseignantes en mathématiques à l’école primaire (par exemple Charles-Pézard et al., 2012). Celles-ci sont considérées comme à la fois complexes, stables et cohérentes, et le développement professionnel est envisagé en matière d’enrichissement des pratiques (Robert et Rogalski, 2002). Chez les personnes débutantes, la cohérence des pratiques est en germe, et il nous semble essentiel de favoriser un travail de mise en relation de connaissances mathématiques et didactiques dans une organisation des pratiques en construction à différents niveaux. Des travaux portant sur le développement professionnel enseignant, et notamment sur les effets de certains dispositifs de formation sur les pratiques, considèrent que les dispositifs de formation qui visent le niveau local des pratiques et qui s’appuient sur des observations de moments d’enseignement sont susceptibles d’enrichir les pratiques, c’est-à-dire d’amener à envisager différentes solutions alternatives et à «élargir la palette des possibles» (Robert, 2005; Charles-Pézard et al., 2012; Butlen et al., 2017; Abboud et al., 2022). Dans ces recherches les gestes professionnels sont définis comme des activités élémentaires, c’est-à-dire des manières pour la personne enseignante de réaliser des tâches élémentaires (par exemple, donner la consigne) (Charles-Pézard et al., 2012). Ces gestes se construisent avec l’expérience professionnelle. Ils ne sont jamais isolés mais organisés en vue de la réalisation d’une même tâche: nous parlons de composition de gestes (Guille-Biel Winder et Mangiante-Orsola, 2023).
Définie par Charles-Pézard (2010) comme «un ajustement didactique permanent de la part du professeur», s’exerçant «dans les trois niveaux global, local et micro[1]» (p. 210), «une “bonne” vigilance didactique assure un déroulement de classe piloté prioritairement par les mathématiques, “au plus près” des apprentissages visés» (p. 211). Son exercice se situe «à la fois du côté du savoir mathématique, des connaissances didactiques et de leur mise en fonctionnement dans l’acte d’enseigner» (p. 211). Notons que la VD s’exerce à différents moments de l’activité d’enseignement: dans le travail de préparation, durant la mise en oeuvre et après la classe. Nous prenons appui sur la modélisation des conditions d’exercice de la VD qui apparaît sous la forme du triplet: connaissances mathématiques et didactiques (CMD); gestes et compositions de gestes (cG); finalité d’apprentissages mathématiques (FAM) (Guille-Biel Winder et Mangiante-Orsola, 2023). En effet selon Charles-Pézard et ses collègues (2012), l’exercice d’une certaine VD nécessite de la part de la personne enseignante la maîtrise de connaissances mathématiques et didactiques (CMD), la mise en oeuvre de gestes et compositions de gestes (cG) au regard des apprentissages visés et la prépondérance d’une finalité quant aux apprentissages mathématiques (FAM) pour les élèves. Ces trois éléments sont intimement articulés et il est donc nécessaire de les considérer conjointement (Guille-Biel Winder et Mangiante-Orsola, 2023). Prenant appui sur cette modélisation, nous admettons l’hypothèse suivante: la mise en lien, par la personne formatrice, de CMD, de cG ainsi que de FAM est susceptible de favoriser le développement de l’exercice d’une certaine VD.
Le dispositif jeu de rôles (JdR) pour la formation développé au Québec (Lajoie et Pallascio, 2001; Lajoie, 2020) nous semble propice à une mise en lien des différents éléments du triplet (CMD, cG, FAM), susceptible de favoriser le développement de l’exercice d’une certaine VD chez les PE en formation. En effet, l’intérêt du JdR réside notamment dans la proposition de traitement d’une question professionnelle (au travers d’une «mise en situation»), qui amène à interroger à la fois les choix d’enseignement et leur mise en oeuvre au regard des apprentissages visés, et qui nécessite la mobilisation et/ou le développement de connaissances mathématiques et didactiques. Le JdR prend également en compte différents moments de l’activité enseignante mettant en jeu l’exercice d’une certaine VD: la préparation, la mise en oeuvre d’un moment d’enseignement (durant la phase de «mise en avant») et son analyse collective (dans une phase de discussion). Pendant la phase de discussion, l’explicitation et l’analyse des gestes professionnels observés lors de la mise en avant visent à questionner les apprentissages souhaités chez les élèves, en appui sur les connaissances mathématiques et/ou didactiques des PE.
Notre question de recherche est alors la suivante: les formatrices observées lors de la mise en oeuvre d’une situation de formation de type JdR participent-elles au travers de leurs choix à la mise en lien de certains éléments du triplet modélisant la VD? Dans l’éventualité d’une articulation entre différents éléments du triplet, est-il possible d’en repérer certaines spécificités?
3. Recueil de données et méthodologie d’analyse
Nous avons proposé un scénario de formation déjà étudié (Lajoie et al., 2019) auprès de deux formatrices, que nous nommerons Suzy et Zoé, ayant des profils différents du point de vue de leur formation et de leur expérience en formation, mais possédant toutes deux une expérience professionnelle d’enseignement en amont, en collège ou en lycée. Ces dernières exercent en formation initiale M2-MEEF[2] en France avec des étudiantes et étudiants de profils proches.
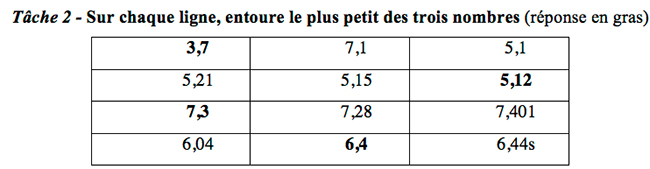
Une ressource présentant le «JdR sur les nombres décimaux» (annexe 3), constituée de tous les supports (questionnaire, synthèse sur les nombres décimaux, travaux d’élèves, matériel), d’une proposition de déroulement «clés en main», ainsi que de documents pouvant nourrir l’observation et donner des pistes sur les éléments à institutionnaliser (Guille-Biel Winder et al., 2022), a été mise à disposition des formatrices avec possibilité de nous demander des précisions. Celles-ci ont mis en oeuvre le JdR avec plusieurs groupes sur une ou deux séances pour une durée variant entre deux et trois heures. Les séances de formation ont été enregistrées (audio pour Zoé, vidéo pour Suzy) et transcrites. Puis des entretiens individuels semi-dirigés (à distance) avec chacune des formatrices ont permis de revenir sur la ou les séances et d’aborder différents aspects liés à la mise en oeuvre du JdR. Ces entretiens ont été enregistrés (audio) et transcrits. Dans cet article, nous faisons le choix de limiter notre étude au JdR portant sur la tâche mathématique suivante:
Figure 1
Notre intention est d’identifier les éléments du triplet (CMD, cG, FAM) mis en lien par chaque formatrice ainsi que la manière dont elle s’y prend. Notons que la question du développement de la VD n’a pas été abordée avec elles. Notre méthodologie consiste à mener une analyse a priori de la tâche d’enseignement «aider un élève dans la tâche mathématique», en appui sur des éléments déjà présentés dans Lajoie et al. (2019). Puis nous cherchons à cerner les potentialités de formation à l’exercice d’une certaine VD qu’offre à la formatrice le temps de mise en avant: cette analyse permet en effet de voir certains choix en ce qui a trait aux gestes professionnels (cG) faits par Ens[3], parmi lesquels certains semblent relever de l’exercice de la VD. S’il n’est pas possible de trancher (car nous ne connaissons pas les intentions réelles derrière les gestes observés), nous estimons néanmoins que ces choix pourraient faire l’objet de discussions collectives, ce qui pourrait contribuer à interroger, voire à enrichir, l’exercice de la VD. À partir de l’identification de cG réalisées par Ens, nous émettons des hypothèses à propos de CMD et de FAM pouvant être abordées par la formatrice, que nous considérons comme des potentialités de formation. Notons que Ens ne poursuit pas forcément les finalités que nous avons identifiées, voire peut ne pas être conscient de la possibilité de les poursuivre, ou avoir de bonnes raisons d’en poursuivre d’autres. L’analyse de la phase de discussion vise à repérer si des éléments de triplets sont abordés (implicitement) et s’ils sont mis en lien. Précisons que la formatrice peut aussi renoncer à les exploiter pour des raisons tout à fait légitimes, par exemple parce qu’elle estime le questionnement trop éloigné des pratiques en germe des personnes formées… Ainsi, il s’agit de repérer les interventions de la formatrice susceptibles de contribuer au développement de l’exercice d’une certaine VD chez les PE. Notre analyse est complétée par ce que les formatrices nous ont dit dans les entretiens.
4. Analyse de la mise en oeuvre de Zoé
Nous retenons d’une analyse a priori réalisée lors d’un précédent travail (Lajoie et al., 2019), qu’au regard de la consigne proposée pour le JdR et de la tâche mathématique, la FAM pourrait être la suivante: comprendre et maîtriser une procédure de comparaison des nombres décimaux. Il s’agit ici de la finalité que nous avons identifiée mais des FAM plus ou moins proches de celle-ci pourraient être visées par cette tâche. Dans ce qui suit, nous présentons une analyse de la mise en avant (annexe 1) au regard d’un possible exercice de la VD, suivie d’une analyse de la discussion au regard d’un possible développement de l’exercice de la VD.
4.1 Mise en avant
La mise en avant porte sur la troisième ligne du tableau (7,3; 7,28; 7,401). À la demande de Ens, El[4] explique que pour ordonner les trois nombres, elle a comparé le nombre de chiffres dans chacun. Ens propose de vérifier: elle choisit le tableau «avec la barre rouge», et demande de placer 7,3 en rappelant que la barre rouge «c’est comme si c’était la virgule». Ens invite El à nommer la position occupée par le 7 (les unités), puis à l’inscrire dans la colonne des unités. Elle fait la même chose pour le chiffre 3 (qu’elle invite à placer dans la colonne des dixièmes). Ens invite El à placer les autres nombres dans le tableau. El se trompe en inscrivant le 7: «Là tu as mis 7 dizaines. Et on a dit que 7 c’était les?» Ens poursuit en demandant à El de nommer la position occupée par chacun des chiffres à placer dans le tableau. Elle revient sur la procédure énoncée par El au début de la mise en avant: «Tu m’as dit tout à l’heure que tu avais mis que c’était 7 virgule 3 le plus petit parce qu’il n’en avait qu’un seul [chiffre après la virgule]. D’accord, mais on a 3 dixièmes, 3 dixièmes, c’est aussi combien de centièmes?» Mais El répond «0 centième». Ens sort alors les bandes pour «vérifier» avec El. La formatrice intervient pour compléter la présentation que Ens fait du matériel: elle précise que les dixièmes correspondent à une unité partagée en dix et les centièmes à un dixième partagé en cent. Pour comparer les trois nombres avec les bandes, Ens propose de ne pas s’occuper des unités car «on a 7 [unités] pour les trois». Elle amène donc El à représenter «3 dixièmes», puis «2 dixièmes et 8 centièmes», en précisant qu’«on commence toujours par la gauche», puis «4 dixièmes, 1 millième». Une fois les trois nombres représentés avec les bandes, Ens demande à El s’il pense toujours que le plus petit est 7,3. Elle avance alors qu’on «voit» bien que le plus grand est 7,401. Puis Ens se tourne vers le groupe et explique qu’elle donnerait les autres nombres du tableau et demanderait de comparer les unités, dixièmes. Elle ajoute que, puisque les trois nombres ont le chiffre 7 aux unités, il faut comparer les chiffres à la position des dixièmes (3, 2 et 4). Même si la comparaison aurait pu s’arrêter là, Ens affirme qu’il faut continuer: «J’ai encore des chiffres après. Donc là comme il n’y a rien je vais pouvoir mettre un 0 et ensuite on continue.» Une étudiante intervient d’ailleurs en disant «ça [comparer les dixièmes] suffit».
4.2 Potentialités offertes à Zoé
Nous faisons l’hypothèse que les cG liées au choix et à l’usage du tableau de numération en début d’aide ne sont pas pilotées par des connaissances didactiques, mais pourraient plutôt l’être par une volonté d’aider l’élève à réussir la tâche (aide procédurale), ou par le fait que cet outil est très souvent associé au travail sur la numération. Ce choix d’entrer par l’utilisation du tableau pourrait donc être interrogé par Zoé dans la discussion, en lien avec des finalités d’apprentissages mathématiques. Il en est de même pour le choix d’utiliser les bandes (cG). Si on fait l’hypothèse que Ens utilise les bandes parce que l’utilisation du tableau n’a pas abouti et qu’elle veut trouver un autre moyen de faire réussir la comparaison à El (visée de réussite immédiate), alors cet usage n’est toujours pas guidé par une volonté de faire comprendre le lien dixièmes/centièmes, ce qui constitue une potentialité pour la discussion. Par ailleurs, Ens laisse El utiliser une bande d’un centième en la mettant «debout» (c’est-à-dire dans une direction différente des dixièmes); elle fait comparer les longueurs des bandes mais pas le nombre de centièmes ou de dixièmes de chacun des nombres. De plus, elle n’exploite pas ce travail d’un point de vue mathématique (pas de décontextualisation). Ainsi l’usage que Ens fait des bandes ne semble pas être en lien avec une finalité de compréhension d’une procédure de comparaison (FAM). Il en est de même du lien manquant entre le tableau et les bandes: Ens se sert du travail sur les bandes pour invalider la comparaison initiale. Elle semble être encore ici sur la réussite de la tâche, ce qui offre des possibilités de travail sur des cG pour la discussion.
La mise en avant peut aussi laisser penser à certains moments à l’exercice d’une certaine VD de la part de Ens, sur lequel la formatrice pourrait aussi travailler dans la discussion. Ens demande par exemple à El de convertir 3 dixièmes en centièmes afin d’effectuer la comparaison. El répond 0 (et non 30 comme Ens l’attendait sûrement pour pouvoir comparer ensuite), ce qui amène Ens à changer de support (utilisation des bandes): si on fait l’hypothèse d’un ajustement à chaud de la part de Ens qui serait piloté par des connaissances mathématiques ou didactiques (ou simplement par la difficulté rencontrée par El), alors cela pourrait relever de l’exercice de la VD. En effet le tableau risquerait ici d’amener El vers des «trucs» d’ajouts de 0 qui ne permettraient pas de mettre en jeu la conversion demandée par Ens, alors que l’usage des bandes peut amener à revenir aux relations entre dixièmes et centièmes. Ens ne se contente pas de la comparaison des longueurs des bandes, elle cherche à revenir sur la tâche initiale de comparaison à partir des écritures décimales. Là encore cela pourrait relever de l’exercice d’une certaine VD (pilotée par la connaissance mathématique d’une technique de comparaison des décimaux): Ens utilise le détour par les bandes pour revenir ensuite sur la technique de comparaison qu’elle cherche à installer chez El (FAM).
4.3 Analyse de la discussion
Comme le révèle le synopsis de la dicussion (figure 2), Zoé aborde différents gestes professionnels les uns après les autres. Nous les reprenons dans ce qui suit.
Figure 2
4.3.1 Choisir un support d’aide
Zoé interroge la pertinence du choix du support (tableau de numération) fait par Ens lors de la mise en avant. Elle pointe un problème lié à ce choix: le tableau «c’est la position» (aspect positionnel de la numération), alors qu’avec les bandes on voit qu’on a affaire à des unités différentes, car «les longueurs ne sont pas les mêmes». Elle s’appuie donc sur des connaissances (CMD) pour pointer la spécificité de différents supports (tableau et bandes), en lien avec des finalités d’apprentissages concernant les unités de numération (FAM). Après un détour par des connaissances (CMD) à propos de la comparaison des décimaux, à savoir des erreurs fréquentes d’élèves (comparer les parties décimales comme des entiers, soit en les comparant directement ou en comparant le nombre de chiffres les composant), Zoé revient sur le choix du tableau (cG) dans la discussion. Elle explique alors que le tableau ne permet pas de «sortir de cette difficulté fondamentale» des élèves (celle à la source des erreurs mentionnées précédemment). Elle fait une analogie avec la monnaie pour expliquer l’importance de prendre en compte les unités. Des CMD (à propos de la comparaison des nombres décimaux), puis des FAM (les relations décimales à l’origine de certaines erreurs d’élèves), permettent donc de revenir sur la cG liée au choix de support. Zoé propose aussi une autre solution concernant le choix et l’utilisation du support, qui s’appuie sur des CMD et vise la même FAM: avant d’utiliser le tableau il faut travailler la signification des unités avec les bandes («La première remédiation ce serait de faire construire le nombre, avec le matériel, avec l’unité […] leur faire dire que 3 dixièmes c’est comme 30 centièmes et comme 300 millièmes»). Elle conclut alors par un apport de connaissances didactiques: le tableau est certes synthétique et pratique, mais insuffisant. Zoé cherche ainsi à montrer que l’usage du tableau doit intervenir dans un second temps, après un travail sur la signification.
4.3.2 Utiliser les bandes
Zoé revient sur le fait que Ens parle tout de suite de «dixièmes» à El, sans faire le lien avec l’unité. Elle cherche à montrer qu’il faut faire le lien entre «unité» et «dixième» pour comprendre ce qu’est un dixième (FAM). Et pour cela il faut voir la représentation de l’unité (pas seulement des dixièmes). Elle semble donc chercher à renforcer, par des connaissances mathématiques (les relations entre unités de numération), les gestes d’usage des bandes qui ont été observés tout en restant au plus près des apprentissages visés (comprendre ce qu’est un dixième). Zoé propose aussi une façon d’enrichir ces gestes en s’appuyant sur un exemple d’utilisation un peu différent: «Représente ce 3 là, qu’est ce qu’il veut dire? Représente-le avec le matériel.» Elle justifie sa proposition: «Il est vraiment indispensable d’avoir le modèle de l’unité» (CMD). Elle confirme que le matériel des bandes peut être un moyen de représenter chaque unité, mais souligne aussi que son usage nécessite la mise en évidence de l’unité, pour permettre aux élèves de comprendre les dixièmes et centièmes (FAM). En plus d’insister sur ce point, Zoé remarque, toujours en lien avec l’usage: «Quand vous avez dit mettez-les bout à bout, pourquoi? On n’est pas obligé […] [il faut] laisser [à l’élève] la liberté de représenter, […] il ne faut pas être trop rigide avec la consigne.» Nous identifions cette affirmation comme un apport visant à nourrir l’exercice d’une certaine VD mais à un niveau plus global, correspondant peut-être aux grands choix didactiques et pédagogiques (Butlen et al., 2017).
4.3.3 Faire verbaliser
Zoé aborde aussi la question de la verbalisation en lien avec l’usage des bandes en proposant un exemple: «Faire dire aux enfants c’est 3 dixièmes, c’est 28 centièmes, c’est là qu’il y en a plus/ puis leur faire dire que 3 dixièmes c’est comme 30 centièmes et comme 300 millièmes. Il y aura un temps important de verbalisation.» Elle propose un moyen d’enrichir des cG en lien avec l’usage des bandes, en les mettant en relation avec la FAM «donner du sens», et en s’appuyant sur des CMD liées aux unités (déjà citées pour l’usage du tableau de numération). Elle justifie aussi ce geste par rapport à ce qu’il va produire chez les élèves.
4.3.4 Mettre en lien plusieurs supports
Zoé soumet le problème suivant: comment faire le lien entre les bandes et le tableau? À la suite des difficultés rencontrées par Ens dans la mise en avant, elle semble ainsi chercher à discuter des cG permettant un usage articulé de ces supports.
4.3.5 Aider les élèves
Zoé revient sur l’erreur de l’élève: «L’erreur de Mélanie, c’est la longueur, l’erreur du nombre de chiffres. Des élèves font comme ça.» Elle pointe une connaissance didactique (l’erreur du nombre de chiffres). Elle indique alors que «c’est important de laisser l’enfant se coltiner à la difficulté», sans toutefois justifier ni argumenter ce propos, que l’on peut considérer ici encore comme un apport susceptible de nourrir les grands choix didactiques et pédagogiques des PE. Cela peut-il suffire à faire comprendre que l’aide était ici très guidée? La formatrice ne revient pas explicitement sur ce point. Toutefois, elle signale plus tard qu’il faut «qu’on puisse travailler sur ses représentations», ce qui vient compléter ces apports avec une recherche de généralisation. Lors des discussions sur l’usage des bandes, Zoé semble chercher à faire des apports plus généraux, que nous interprétons comme étant liés aux différences entre aide à visée productive et constructive (Chappet-Pariès, 2004; Vandebrouck, 2008): «Risque de la recette, ce n’est pas une aide, ça cache le sens profond.» Elle semble aussi chercher à généraliser au-delà de cette aide particulière: «À chaque fois que vous donnez une aide aux élèves, tout de suite dans votre tête, posez-vous la question: “Est-ce que je suis dans la recette? Pourquoi c’est comme ça, ça vient d’où?”.»
4.3.6 Synthèse
Nous relevons ainsi une certaine régularité dans la façon de Zoé de travailler autour d’une cG lorsque les gestes sont liés au choix et à l’usage d’un support. Elle relève en effet dans la mise en avant des cG qui posent problème, qui pourraient traduire un exercice insuffisant de VD. Elle expose le problème en s’appuyant sur des CMD qu’elle explicite, tout en rappelant les FAM (comparaison des nombres décimaux, liens entre unités de numération). Elle propose ensuite une cG alternative (travailler sur les unités de numération) en explicitant et en mettant en lien des CMD (sur les nombres décimaux) et des FAM (les liens entre les unités de numération). Elle conclut la réflexion par une synthèse (sur le choix du tableau, l’usage des bandes). Pour les cG relatives à l’aide à un élève, Zoé semble se situer à un niveau plus global des pratiques, correspondant peut-être aux grands choix didactiques et pédagogiques (Butlen et al., 2017), en formulant un conseil général mais sans apporter de justification en lien avec des CMD.
4.4 Compléments
L’entretien avec Zoé nous permet de mieux cerner ses intentions lors de la mise en oeuvre du JdR et ses choix à propos des gestes professionnels observés. Si Zoé identifie différents enjeux possibles, elle semble toutefois chercher à exploiter le dispositif pour développer principalement des CMD, ce qui, pour elle, correspond aux besoins principaux de ses étudiants et étudiantes. Elle est, par exemple, tout à fait consciente des potentialités de ce JdR pour travailler sur la façon d’aider un élève, qu’elle reconnaît aussi comme un besoin de ses étudiants et étudiantes qui «sont souvent dans la monstration», mais elle n’en fait pas un enjeu de formation prioritaire ici, ce qui peut expliquer qu’elle en reste à l’affirmation de certains grands choix à ce sujet. Lors de l’entretien, Zoé évoque principalement les cG relatives au choix et à l’usage des supports, qui lui permettent de travailler des CMD liées aux différents supports qu’elle cherche à renforcer, afin de faire dépasser certaines conceptions (par exemple «le tableau de numération, c’est avec ça qu’on va apprendre»), et de montrer des potentialités de ces supports pour les apprentissages des élèves (FAM sur la notion d’unité et les relations entre unités notamment).
5. Analyse de la mise en oeuvre de Suzy
Notre étude de la mise en oeuvre de Suzy s’effectue selon la même méthodologie. Nous nous appuyons sur la transcription de la mise en avant (annexe 2).
5.1 Mise en avant
Ens demande à El d’expliquer ce qu’il fallait faire dans l’exercice et de justifier les réponses données. À propos de la première ligne (3,7; 7,1; 5,1), El dit qu’il a entouré «3 virgule 7», «parce que 3 c’est plus petit que 7 et que 5 aussi». Ens complète la réponse en disant qu’il a donc regardé «le nombre entier» et qu’il a entouré «le plus petit». À propos de la deuxième ligne (5,21; 5,15; 5,12), Ens amène El à dire que regarder «le nombre entier» ne suffit pas. Celui-ci explique alors qu’il a comparé 12, 15 et 21 et Ens ajoute qu’il a regardé «la partie décimale». À propos de la troisième ligne (7,3; 7,28; 7,401), El explique qu’il a vu que «3 c’est plus petit que 28 et plus petit que 401», mais semble un peu hésitant puisqu’il précise que ces trois nombres n’ont pas le même nombre de chiffres dans la partie décimale. Ens l’invite alors à utiliser le tableau pour voir si «ça marche», puis le guide pas à pas. Elle lui suggère de mettre tous les nombres «sur la même unité de numération» et justifie sa proposition en disant que cela pourra l’aider. El ne comprenant pas, Ens lui demande ce qu’on peut mettre dans les cases vides. El joue le jeu: il remplit toutes les cases vides avec des zéros. Ens l’amène alors à comparer les écritures qu’elle pointe du doigt (300, 280 et 401). Elle essaie ensuite de formuler la règle à utiliser pour comparer les nombres décimaux, mais ne parvient pas à s’éloigner du contexte des nombres utilisés. Elle conclut en invitant à nouveau El à utiliser le tableau. Celui-ci réitère la mise au même format des nombres. Ens lui demande alors d’expliciter ce qu’il a retenu. Celui-ci répond: «Pour comparer, il faut que je regarde le nombre de chiffres après la virgule.» Tout le monde rit.
5.2 Potentialités offertes
Ens cherche à «faire expliciter la procédure» par El. Nous faisons l’hypothèse qu’elle peut alors être amenée à mobiliser certaines connaissances à propos des nombres décimaux et des procédures de comparaison possibles (CMD). Cependant les formulations qu’elle emploie pour parler des nombres décimaux laissent penser que ses connaissances mathématiques sont peu assurées. Lorsque Ens invite El à utiliser le tableau pour vérifier la pertinence de la procédure donnée à propos de la troisième ligne, on peut s’interroger sur la finalité visée par ce choix de support et par l’usage qui en est fait. Si Ens recourt au tableau, est-ce pour corriger la réponse donnée? Pour mettre en défaut la règle utilisée par El pour la troisième ligne, consistant à comparer les parties entières en les traitant comme des entiers? Pour une autre raison? Ainsi, la FAM en lien avec les cG mises en oeuvre pourrait être questionnée par la formatrice lors de la discussion.
Nous notons aussi que le guidage exercé par Ens lors de l’utilisation du tableau est important. Les cG mises en oeuvre mobilisent certaines connaissances portant sur le rôle joué par les unités de numération dans les procédures de comparaison. Constater l’équivalence d’écriture grâce à une technique consistant à remplir les cases vides par des zéros peut ne pas conduire vers la FAM que nous retenons (donner du sens à l’écriture décimale des nombres décimaux). De plus, la technique de comparaison par mise au même format n’est pas la mieux adaptée pour construire une procédure de comparaison des nombres décimaux reposant sur une compréhension des connaissances mathématiques en jeu. Ens cherche à «verbaliser et à faire verbaliser ce qui est à retenir», mais peine à formuler une généralisation de la règle utilisée, difficultés qui ne passent pas inaperçues dans le groupe de formation. Cela nous amène à nouveau à faire l’hypothèse de connaissances mathématiques peu utilisées. Ainsi, nous décelons plusieurs cG dans la mise en avant qui sont autant de potentialités dont la formatrice pourrait se saisir pour amener les personnes en formation à développer leur VD en les mettant en relation avec des FAM et des CMD.
5.3 Analyse de la discussion
Le synopsis de la discussion menée par Suzy est donné figure 3. Pour chacun des gestes sur lesquels elle revient, Suzy prend appui sur les propositions des formés et enchaîne les questions en les articulant les unes aux autres.
5.3.1 Choisir un support d’aide
Dès le départ, Suzy questionne le groupe à propos du choix du support utilisé (cG). Les personnes observatrices soulèvent de «bons points»: le tableau permet d’écrire tous les nombres avec le même nombre chiffres après la virgule; il est alors facile de comparer; «c’est rapide et efficace»; «on a juste à mettre des zéros». Suzy ne rebondit pas trop sur ces points positifs! Elle donne l’impression qu’elle veut entendre autre chose. Elle insiste néanmoins sur le fait que le tableau permet de comparer, et que c’est ce qui justifie le choix qui a été fait. Elle tente d’amener le groupe à s’interroger sur les avantages et les inconvénients du tableau, mais sans succès pour autant. Elle poursuit donc le questionnement: «Pour l’apprentissage d’autres tâches, est-ce que vous ne voyez pas? Qu’est-ce que vous me disiez par rapport au tableau de numération? Est-ce qu’on ne va pas induire à un moment un obstacle ou autre chose?» Plus tard elle demande comment «s’assurer que l’élève va pouvoir réutiliser ses connaissances dans un autre contexte?» (FAM). Afin de faire avancer la discussion, Suzy se réfère à un moment précis du jeu, celui où Ens a distingué partie entière et partie décimale, et insiste sur le fait que la comparaison se faisait séparément sur chacune des parties. Un observateur réagit alors en explicitant ce que la formatrice cherchait à mettre en évidence quant au désavantage: «Mais là il y a un problème qui peut se présenter en effet, c’est qu’au fond c’est comme si elle traitait deux nombres différents: d’un côté la partie décimale et de l’autre la partie entière.» Ainsi la formatrice parvient à réorienter les échanges au regard de la FAM. Elle invite le groupe à observer les cG mis en oeuvre (ici choisir un support), non pas au regard de la réussite de la tâche, mais à celui de la compréhension de l’écriture à virgule des nombres décimaux. L’adéquation des cG au regard des FAM est questionnée.
Figure 3
5.3.2 Accompagner les élèves dans l’usage du support
Lors de la discussion, les pricipaux inconvénients évoqués à propos du choix du tableau sont en lien avec son usage. En effet, les personnes formées estiment qu’il peut être difficile pour les élèves de placer les nombres décimaux dans le tableau et que cela peut amener à s’interroger sur le choix de ce support. Néanmoins, Suzy exploite peu ces remarques. Elle cherche avant tout à mettre en évidence le fait que «ajouter des zéros» constitue une technique vide de sens. En mettant en parallèle les formulations utilisées («ajouter des zéros» versus «convertir en unités de numération»), elle conduit la discussion de manière à mettre en évidence le fait que l’usage du tableau doit permettre de donner du sens à l’écriture des nombres décimaux. Ce faisant, elle met en lien des connaissances didactiques (convertir en unités de numération) et des cG consistant à accompagner les élèves dans l’usage du tableau. De plus, elle inscrit ces cG dans la perspective d’une FAM (privilégier un usage du tableau qui donne du sens aux unités de numérations).
5.3.3 Prendre en compte l’erreur de l’élève
Suzy amorce la discussion de manière à faire expliciter la démarche choisie par Ens. Celle-ci a en effet invité El à écrire les nombres dans le tableau, à les mettre au même format puis à les comparer (cG). Ens semble institutionnaliser comme règle: «mettre tous les nombres sur la même unité de numération». L’aide apportée consiste donc à donner une technique. La formatrice dit: «C’est le principe que vous avez choisi.» Elle acquiesce lorsque le groupe souligne que «c’est rapide». Néanmoins, tout au long des échanges, Suzy cherche implicitement à questionner le type d’aide: si l’aide apportée permet de trouver rapidement la réponse, est-ce qu’elle permet à El d’apprendre? Elle insiste surtout sur le fait que le travail mené doit aider El à exécuter d’autres tâches à venir. Ce faisant, elle inscrit l’aide dans une FAM à long ou moyen terme. Le triplet en jeu ici autour de l’aide à apporter aux élèves prend appui sur des CMD (comme la distinction entre aide procédurale et aide constructive), que la formatrice cherche à mettre en lien avec des FAM.
5.3.4 Synthèse
Ainsi, au regard de l’exercice de la VD, Suzy amène les personnes formées à préciser la FAM dans l’intention d’interroger le choix du support (cG). Tout se passe comme si elle cherchait à jouer sur la finalité visée (passer d’une finalité de réussite de la tâche à une finalité d’apprentissages mathématiques), pour remettre en question le choix du tableau. Ainsi, elle fait mettre en lien cG et FAM. Plus précisément, en prenant appui sur la FAM, elle cherche à remettre en question les cG. De plus les cG abordées (et listées ci-avant) sont mises en lien les unes avec les autres dans le fil de la discussion, Suzy gérant les échanges de manière à amener les personnes étudiantes à analyser leurs choix.
5.4 Compléments
Lors de son entretien, Suzy partage avec nous trois objectifs en lien avec cette séance (figure 4).
Figure 4
Le premier objectif ne ressort pas dans nos analyses parce qu’il est considéré, par Suzy, comme un préalable au JdR pour s’assurer d’un minimum de maîtrise de CMD: «Si eux-mêmes ne savent pas placer des centièmes sur la droite graduée, ils vont avoir quand même des soucis.» Suzy l’a alors travaillé en début de séance à l’occasion de la présentation des différents supports. Les deux objectifs suivants entrent en résonance avec nos analyses: ils témoignent de l’intention d’une mise en lien entre des cG et une FAM. Lors de l’entretien, Suzy confie qu’elle est assez satisfaite de ce qu’elle a pu faire en lien avec ses objectifs, mais aussi qu’elle devra revenir sur la séance car elle considère qu’elle n’a pas tout exploité, par manque de temps ou parce qu’elle ne voulait pas «se disperser».
6. Conclusion
Dans ce texte, notre intention était de poursuivre le questionnement sur les potentialités du dispositif JdR. Aborder l’analyse de l’activité de deux formatrices en prenant appui sur la notion de VD nous permet d’enrichir le travail amorcé dans Guille-Biel Winder et al. (2022). Nous nous sommes fondés sur l’hypothèse de travail selon laquelle le développement de l’exercice de la VD serait favorisé par la mise en lien de connaissances mathématiques et didactiques, de gestes et compositions de gestes ainsi que de finalités d’apprentissages mathématiques.
Nos analyses nous ont permis d’obtenir deux résultats. L’étude des données recueillies confirme l’existence dans les pratiques des deux formatrices de mises en lien au sein de triplets (CMD, cG, FAM), qui sont, d’après cette hypothèse, susceptibles de développer l’exercice d’une VD. De plus, notre travail d’identification de ces mises en lien a permis de mettre au jour des dynamiques spécifiques à chacune des deux formatrices, découlant de leurs choix. Ces dynamiques se caractérisent par des mises en lien différentes entre des éléments du triplet. En effet Zoé prend appui sur des cG observées dans la mise en avant qui lui semblent problématiques pour mieux expliciter certaines CMD qu’elle considère comme des prérequis nécessaires pour enseigner, tout en rappelant des FAM. Suzy, quant à elle, questionne le groupe à propos des apprentissages visés pour analyser certaines cG observées dans la mise en avant. Elle semble poursuivre un objectif principal (discuter de l’usage du tableau de numération). Ainsi Suzy s’interroge sur la FAM (visée ou pas), pour faire évoluer la réflexion sur le choix du support (cG). Notre travail met ainsi au jour un levier de formation utilisé par Suzy, que l’on pourrait résumer par: «enrichir l’analyse des apprentissages potentiels, pour questionner le choix du support» ou encore «amener les PE à identifier une FAM, afin de questionner la cG mise en oeuvre».
Notre étude confirme la place centrale des connaissances didactiques et mathématiques dans les pratiques de formation en appui sur le JdR mise en évidence par Marchand et al. (2022). Alors que ces chercheuses et chercheurs montrent une variété de postures mises en oeuvre par les personnes formatrices, notre travail met au jour des mises en lien différentes de ces connaissances avec des cG et des FAM.
Nos résultats tendent aussi à confirmer l’intérêt du dispositif JdR, comme favorisant la mise en lien d’éléments de triplets (CMD, cG, FAM) par les formatrices et à terme l’exercice de la VD durant la classe, ce qui rejoint des observations réalisées par Lajoie (2018) concernant le potentiel de ce dispositif pour le développement du «savoir remarquer sur le champ» (noticing-in-the-moment) et le «savoir intervenir sur le champ» (kwnowing-in-the-moment), des concepts empruntés à Mason et Davis (2013) et Mason et Spence (1999) respectivement.
Toutefois, notre travail présente certaines limites. Tout d’abord la restriction de nos analyses à un moment précis (le retour sur une seule mise en avant) d’un scénario donné basé sur un seul JdR ne permet pas d’accéder à des dynamiques qui se joueraient à un niveau plus large (sur l’ensemble de la séance ou sur d’autres JdR). Par ailleurs, les pratiques de formation étant variées, nous limiter à deux formatrices n’éclaire qu’une petite partie de la palette des possibles.
Dans ce projet, nous n’avons pas travaillé sur l’impact du JdR sur le développement de l’exercice de la VD des personnes formées ni sur les conceptions sur l’apprentissage qui pourraient y faire obstacle. À partir des données recueillies, il serait présomptueux d’émettre des hypothèses sur les différences possibles de développement de l’exercice de la VD des personnes formées dans ces deux classes, d’autant plus que ce développement pourrait dépendre d’autres facteurs que la seule mise en lien des éléments du triplet, comme les proximités entre le discours des formatrices et les activités des personnes formées au cours de la séance (Abboud et al., 2022). Ces questions liées aux effets sur les pratiques des PE en formation, complexes à traiter, constitue l’une de nos perspectives de recherche.
Parties annexes
Notes
-
[1]
«Le niveau “global” concerne les grands choix didactiques et pédagogiques des enseignants, les programmations, progressions et scénarios mis en oeuvre, les grandes modalités d’aides ou de gestion des interactions. Le niveau “local” concerne la séance ou une partie consistante de celle-ci ainsi que les routines (ensemble de gestes permettant au professeur de réaliser une tâche importante, par exemple institutionnaliser ou dévoluer). Le niveau “micro” concerne une unité de temps ou d’action plus petite comme la réalisation d’une tâche élémentaire (apporter une aide limitée, écrire au tableau, rappeler à l’ordre un élève, etc.) et les gestes qui le permettent» (Butlen et Masselot, 2018, p. 65).
-
[2]
Deuxième année de Master éducation enseignement et formation (MEEF) comportant pour certaines des personnes inscrites un stage en responsabilité à mi-temps.
-
[3]
Dans tout ce qui suit, Ens désigne le ou la formée qui joue le rôle de l’enseignant ou de l’enseignante.
-
[4]
Dans tout ce qui suit, El désigne le ou la formée qui joue le rôle de l’élève.
Bibliographie
- Abboud-Blanchard, M. et Robert, A. (2015). Former des formateurs d’enseignants de mathématiques du secondaire: un besoin, une expérience et une question d’actualité. Annales de didactique et de sciences cognitives, 20, 181‑206.
- Abboud-Blanchard, M., Robert, A. et Rogalski, J. (2022). Interroger les pratiques de formation des professeurs de mathématiques: orientations de recherche et perspectives (un agenda). Annales de didactique et de sciences cognitives, 1, 261‑285.
- Butlen, D., Mangiante-Orsola, C. et Masselot, P. (2017). Routines et gestes professionnels, un outil pour l’analyse des pratiques effectives et pour la formation des pratiques des professeurs des écoles en mathématiques. Recherches en didactiques, 24, 25‑40.
- Butlen, D. et Masselot, P. (2018). De la recherche à la formation: enrichir les pratiques des enseignants pour favoriser les apprentissages des élèves en mathématiques. Recherche et formation, 1, 61‑75.
- Celi, V., Masselot, P. et Tempier, F. (2019). L’évaluation en mathématiques des professeurs des écoles débutants: quelles alternatives face aux contraintes de la formation? Actes du colloque EMF2018 (p. 115‑123). IREM de Paris.
- Chappet-Pariès, M. (2004). Comparaison de pratiques d’enseignants de mathématiques. Recherches en didactique des mathématiques, 24(2-3), 251‑284.
- Charles-Pézard, M. (2010). Installer la paix scolaire, exercer une vigilance didactique. Recherches en didactique des mathématiques, 30(2), 197‑261.
- Charles-Pézard, M., Butlen, D. et Masselot, P. (2012). Professeurs des écoles débutants enseignant en ZEP: quelles pratiques? Quelle formation? La pensée sauvage.
- Guille-Biel Winder, C., Lajoie, C., Mangiante-Orsola, C., Masselot, P. et Tempier, F. (2022). Priorités et stratégies d’un formateur lors de la mise en oeuvre d’un jeu de rôles en mathématiques. Annales de didactique et de sciences cognitives, 1, 55‑89.
- Guille-Biel Winder, C. et Mangiante-Orsola, C. (2023). Contribution à l’étude de la vigilance didactique. Recherches en didactique des mathématiques, 43(2), 199‑240.
- Houdement, C. (2013). Au milieu du gué: entre formation des enseignants et recherche en didactique des mathématiques [note de synthèse]. Université Paris Diderot.
- Houdement, C. et Masselot, P. (2019). La vigilance didactique, un concept à interroger pour les formateurs d’enseignants [communication]. Colloque Réseau éducation et formation (REF 2019), Toulouse, France.
- Lajoie, C. (2010). Les jeux de rôles: une place de choix dans la formation des maîtres du primaire en mathématiques à l’UQAM. Dans J. Proulx et L. Gattuso (dir.), Formation des enseignants en mathématiques: tendances et perspectives actuelles (p. 101‑113). Éditions du CRP.
- Lajoie, C. (2018). Learning to act in-the-moment: Prospective elementary teachers’ roleplaying on numbers. Dans K. Hino et G. J. Stylianides (dir.), Research advances in the mathematical education of pre-service elementary teachers. An international perspective (p. 231‑244). Springer.
- Lajoie, C. (2020). Le jeu de rôles pour former à enseigner les mathématiques: potentialités et limites selon différents points de vue. Revue de mathématiques pour l’école, 233, 16‑27.
- Lajoie, C., Mangiante-Orsola, C., Masselot, P., Tempier, F. et Winder Guille-Biel, C. (2019). Former à aider un élève en mathématiques: une étude des potentialités d’un scénario de formation basé sur un jeu de rôles. Revue canadienne d’enseignement des sciences, des mathématiques et des technologies, 19(2), 168‑188.
- Lajoie, C. et Pallascio, R. (2001). Role-play by pre-service elementary teachers as a means to develop professional competencies in teaching mathematics. Proceedings of SEMT ‘01. Prague, Czech Republic.
- Lajoie, C. et Pallascio, R. (2001). Le jeu de rôles: une situation-problème en didactique des mathématiques pour le développement de compétences professionnelles. Dans Actes du colloque des didacticiens et des didacticiennes des mathématiques (p. 120‑132).
- Mangiante-Orsola, C. (2012). Une étude de la cohérence en germe dans les pratiques de professeurs des écoles en formation initiale puis débutants. Recherches en didactique des mathématiques, 32(3), 289‑331.
- Marchand, P., Martin, V., Thibault, M. et Bisson, C. (2022). Postures et gestes de personnes formatrices exploitant les jeux de rôles comme dispositif de formation à l’enseignement des mathématiques: analyse de récits de pratiques. Annales de didactique et de sciences cognitives, 1, 19‑53.
- Martinand, J.-L. (1994). La didactique des sciences et de la technologie et la formation des enseignants. Aster, 19, 61‑75.
- Mason, J. et Davis, B. (2013). The importance of teachers’ mathematical awareness for in-the-moment pedagogy. Canadian Journal of Science, Mathematics and Technology Education, 13(2), 182‑197.
- Mason, J. et Spence, M. (1999). Beyond mere knowledge of mathematics: The importance of knowing to act in the moment. Educational Studies in Mathematics, 38, 135‑161.
- Robert, A. (2005). De recherches sur les pratiques aux formations d’enseignants de mathématiques du second degré: un point de vue didactique. Annales de didactique et de sciences cognitives, 10, 209‑249.
- Robert, A. et Rogalski, J. (2002). Le système complexe et cohérent des pratiques des enseignants de mathématiques: une double approche. Revue canadienne de l’enseignement des sciences, des mathématiques et des technologies, 2(4), 505‑528.
- Vandebrouck, F. (2008). Résultats sur l’activité des élèves en classes de seconde. Dans F. Vandebrouck (dir.), La classe de mathématiques. Activités des élèves et pratiques des enseignants (p. 197‑225). Octarès.
Liste des figures
Figure 1
Figure 2
Figure 3
Figure 4