Corps de l’article

Répondre à de multiples questions au cours d’un même essai clinique est un problème bien connu des chercheurs qui s’investissent dans la recherche clinique. Or, si multiplier les analyses est une tentation légitime, le risque d’aboutir dans ce contexte à des conclusions faussement positives est réel et affecte la crédibilité des résultats. Le contrôle de ces erreurs s’effectue par un ajustement sur l’erreur de type I [1][1].

De nombreuses méthodes ont été développées dans cet objectif. Elles utilisent habituellement un «fractionnement» du risque d’erreur de type I appliqué à chacune des hypothèses testées. La méthode choisie doit être définie dans le protocole; à défaut, il sera demandé d’utiliser l’approche la plus conservative (procédure de Bonferroni, voir plus loin). Les procédures les plus couramment utilisées sont décrites ci-dessous; pour approfondir certaines techniques, le lecteur est invité à consulter des revues plus détaillées [2-5], ainsi que les références de chaque technique.

Pourquoi ajuster sur l’erreur de type I ?

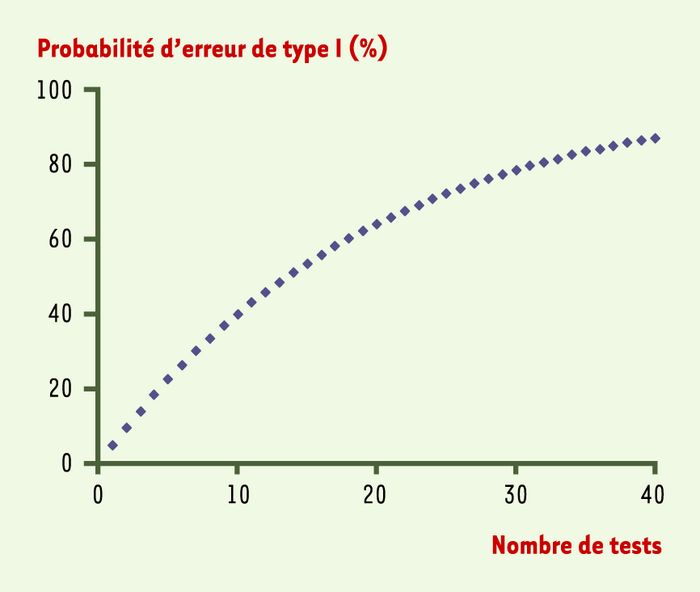
Supposons que n tests, correspondant à n critères de jugement, soient réalisés pour comparer un nouveau traitement à un traitement témoin, chaque test étant réalisé au niveau de signification α (en général, α = 5%)[2]. Même si les traitements administrés dans les deux groupes ont des effets identiques, c’est-à-dire que l’hypothèse nulle est vraie pour les n critères de jugement, il est possible que les données expérimentales mettent en évidence des variations dues au seul effet du hasard. Dans le cas des essais à comparaisons multiples, la probabilité de faire au moins une erreur de type I augmente en fonction du nombre de tests réalisés (Figure 1): ainsi, la probabilité d’obtenir au moins une différence faussement significative est de 40% en réalisant dix tests, de 64% avec vingt tests et de 87 % avec quarante tests (risque d’erreur= 1 – [1- α]n). Toutefois, ces probabilités sont calculées en supposant que les tests sont indépendants; or, les tests sont en général positivement corrélés, ce qui diminue le risque d’erreur de type I[3]. Néanmoins, le risque d’inflation du risque de type I est réel et doit être contrôlé: on fait alors appel à un ajustement.

Figure 1

Probabilité de conclure à tort à l’existence d’une différence significative en fonction du nombre de tests réalisés.

Probabilité de conclure à tort à l’existence d’une différence significative en fonction du nombre de tests réalisés.

Chaque test est effectué au niveau α = 5%.

-> Voir la liste des figures

Techniques d’ajustement

Ajustement de Bonferroni

L’une des méthodes les plus couramment utilisées pour contrôler l’erreur de type I est l’ajustement de Bonferroni. Cet ajustement consiste à identifier le nombre de tests n, puis à effectuer chacun des n tests non pas au niveau de signification α, mais au niveau α/n. De façon équivalente, cette méthode d’ajustement consiste à multiplier chaque valeur p[4] par n et à la comparer au niveau de signification α. On peut montrer que la probabilité de commettre au moins une erreur de type I est dans ce cas toujours inférieure à α.

Cette méthode soulève néanmoins un certain nombre de problèmes. Tout d’abord, le contrôle satisfaisant de l’erreur de type I a comme contrepartie une augmentation de l’erreur de type II[5], c’est-à-dire une diminution de la puissance de chaque test. Si le nombre de sujets est calculé de façon à obtenir une puissance non ajustée de 80 %, la puissance de chaque test (dans l’hypothèse où ces tests sont indépendants) est diminuée, comme le montre la Figure 2. Ainsi, en testant dix critères de jugement avec ajustement de Bonferroni, la puissance de chaque test n’est plus de 80%, mais de 50 %. Il est donc nécessaire d’augmenter considérablement le nombre de sujets si l’on souhaite obtenir une puissance de 80% pour chaque critère. La procédure de Bonferroni est par ailleurs la plus conservative: elle a tendance à conserver l’hypothèse nulle, et des résultats significatifs sont donc plus difficiles à mettre en évidence. Ne tenant pas compte du fait que les critères de jugement sont en général positivement corrélés, la procédure de Bonferroni souffre donc d’un manque de puissance, en particulier lorsque de nombreux critères sont évalués. De plus, lorsque plusieurs tests sont significatifs au niveau α, mais aucun au niveau α/n, il est impossible de conclure à la supériorité du traitement actif, quand bien même il existe de fortes présomptions en observant les n critères de jugement dans leur globalité.

Figure 2

Puissance de chaque test avec ajustement de Bonferroni, en fonction du nombre de tests réalisés.

Puissance de chaque test avec ajustement de Bonferroni, en fonction du nombre de tests réalisés.

Chaque test est effectué au niveau a = 0,05/n, le nombre de sujets étant fondé sur une puissance non ajustée de 80%.

-> Voir la liste des figures

Des extensions de la procédure de Bonferroni ont été proposées, notamment la procédure de Holm [6]. Toutefois, ces extensions ne répondent que partiellement à ces objections.

Hiérarchisation des tests

Une alternative à l’ajustement de Bonferroni consiste à hiérarchiser les tests, et donc à ordonner, du plus important au moins important, les critères de jugement ou les comparaisons entre les traitements. L’ordre des critères de jugement ou des comparaisons doit être spécifié dès l’étape du protocole et décrit dans le plan d’analyse [7]. La procédure consiste alors à tester le premier critère au niveau de signification α sans ajustement. Si ce test est significatif, il est possible de tester le second critère, toujours au niveau de signification α,∈et ainsi de suite. La procédure s’arrête au premier critère pour lequel aucune différence significative ne peut être démontrée. Il est alors impossible de revendiquer un bénéfice significatif pour un critère de rang inférieur au premier critère non significatif.

Le principal apport de cette méthode est que chaque test est réalisé au niveau de signification α, sans ajustement du risque d’erreur de type I. Cette procédure garantit néanmoins que le risque global d’erreur de type I n’excède pas α; par ailleurs, elle n’affecte pas la puissance du critère principal (à l’inverse de l’ajustement de Bonferroni) et présente un avantage certain en termes de simplicité (la hiérarchisation est en effet très facile à mettre en oeuvre).

En revanche, la puissance des critères secondaires, en supposant que les tests sont indépendants, diminue rapidement en fonction de leur rang dans la hiérarchie, comme l’illustre la Figure3. Dans la pratique, néanmoins, les tests sont généralement positivement corrélés, ce qui atténue la diminution de la puissance. Un autre problème inhérent à cette approche est qu’elle impose une hiérarchisation nécessairement subjective des critères ou des comparaisons. L’évaluateur peut par exemple ne pas approuver l’ordre établi par le promoteur de l’étude, ce qui nécessite une phase de dialogue préalable.

Figure 3

Puissance de chaque test, en fonction de son rang dans la hiérarchie.

Puissance de chaque test, en fonction de son rang dans la hiérarchie.

Les différents tests sont supposés indépendants, la puissance individuelle de chaque test étant de 80%.

-> Voir la liste des figures

Utilisation d’un test global

Certaines procédures permettent de tester simultanément l’ensemble des critères de jugement. On peut notamment citer le T2 de Hotelling ou la procédure de O’Brien [8]. L’hypothèse nulle testée est qu’il n’existe aucune différence pour aucun des critères de jugement; l’hypothèse alternative postule qu’une différence existe pour au moins un des critères de jugement.

Les avantages de ces procédures sont nombreux. Tout d’abord, un test unique permet de comparer les traitements sur l’ensemble des critères de jugement. Aucun ajustement du risque α n’est donc nécessaire. De plus, ces procédures tenant compte des corrélations entre les différents critères de jugement, la puissance du test global est d’autant plus grande que les critères sont corrélés. Enfin, ces procédures sont très puissantes si une tendance est observable sur la majorité ou la totalité des critères de jugement, même si cette tendance n’est pas significative en testant les critères un à un à l’aide d’un test univarié. En cela, ces techniques permettent de répondre aux critiques formulées à l’encontre de la procédure de Bonferroni.

Le principal défaut de ces procédures d’ajustement est de ne répondre que partiellement à la question posée. Même si l’hypothèse nulle globale est rejetée, la seule conclusion que l’on peut tirer des résultats est qu’il existe une différence pour au moins un critère de jugement, sans préciser lequel ou lesquels. En considérant les critères de jugement au même niveau, ces procédures n’utilisent pas la connaissance a priori de l’effet du traitement.

Procédure de tests fermés

Les tests fermés [9] apportent une solution à ce problème. Si un test global établit l’existence d’une différence entre les groupes de traitement, cette procédure peut permettre d’identifier le (ou les) critère(s) de jugement qui diffère(nt) significativement.

Dans la procédure de tests fermés, un test global est tout d’abord réalisé sur l’ensemble des n critères de jugement au niveau de signification α (sans ajustement). Si ce test est significatif, tous les tests globaux comprenant n-1 critères sont réalisés. À l’étape suivante, les tests comprenant n-2 critères sont réalisés uniquement si tous les tests comprenant les n-1 critères sont significatifs, et ainsi de suite jusqu’au niveau des tests univariés individuels.

Pour illustrer cette procédure, supposons que trois critères de jugement C1, C2 et C3 soient évalués pour comparer un traitement actif à un placebo. La première étape consiste à effectuer un test global concernant les trois critères. Si ce test global est significatif au niveau α, on effectue alors les trois tests globaux, sur les couples (C1,C2), (C1,C3) et (C2,C3). Les résultats de ces tests déterminent ensuite les tests individuels qui peuvent être effectués. Le critère C1, par exemple, ne peut être testé que si les tests (C1,C2) et (C1,C3) sont significatifs, comme cela est illustré sur la Figure 4.

Figure 4

Procédure de tests fermés pour trois critères de jugement.

Procédure de tests fermés pour trois critères de jugement.

-> Voir la liste des figures

Pour pouvoir conclure à l’existence d’une différence significative sur l’un des critères de jugement, une différence doit donc être détectée à tous les niveaux supérieurs: cette procédure garantit que la probabilité de conclure à tort sur au moins un critère de jugement n’excède pas le niveau α. La procédure de tests fermés est attractive, car elle autorise une approche automatique permettant de contrôler l’erreur de type I. Elle est également cohérente, car on ne peut tester une hypothèse simple que si toutes les hypothèses nulles de niveau plus élevé ont été rejetées.

En revanche, elle ne garantit pas qu’une fois l’hypothèse nulle globale rejetée, d’autres hypothèses nulles individuelles seront rejetées; il est donc possible de conclure à la différence globale des traitements sans pouvoir identifier au niveau de quels critères siège cette différence. Un autre problème avec ce type d’approche est qu’il est impossible de s’assurer que certains critères jugés importants seront effectivement testés. Dans ce cas, l’approche par hiérarchisation peut s’avérer préférable.

Interprétation des données issues de comparaisons multiples

Bien que disposant de solutions d’ajustement acceptables, l’évaluateur de l’essai se trouve souvent confronté, dans les essais à inférences multiples, à des problèmes d’interprétation clinique. C’est pour gérer cette situation que les autorités européennes d’évaluation du médicament ont rédigé, en 2002, un document technique [10] destiné à répondre aux questions les plus fréquemment rencontrées, en matière d’évaluation et d’interprétation des résultats des essais sur les médicaments, face à des problèmes de multiplicité. Les éléments essentiels de ces recommandations font l’objet de la suite de cet article qui traitera, d’une part, des recommandations générales sur la pratique des ajustements, d’autre part des situations particulières.

Les cas où il n’est pas nécessaire d’ajuster

  1. En théorie, seuls les essais cliniques à deux bras, avec critère de jugement unique, une seule hypothèse testée, et sans analyse intermédiaire, peuvent se prévaloir de ne pas nécessiter un ajustement sur l’erreur de type I.

  2. En pratique, la pertinence de l’interprétation clinique des résultats devant rester l’objectif majeur, aucun ajustement n’est requis dans les cas suivants:

    1. Plusieurs critères de jugement d’importance égale sont nécessaires pour décrire le bénéfice d’un traitement: les risques α, identiques pour chacune des hypothèses testées sur ces critères, sont fixés au niveau de risque admis pour l’erreur de type I globale. Cette procédure diminue la puissance globale de l’essai et par conséquent nécessite plus de sujets.

    2. Les critères de jugement sont hiérarchisés: il n’est pas nécessaire d’ajuster, mais un résultat statistiquement significatif ne peut être pris en compte que si les critères hiérarchiquement supérieurs sont également significatifs. Dans ce cas, la puissance de l’essai diminue d’autant plus que le critère est bas dans la hiérarchie.

    3. Plusieurs analyses de populations spécifiques sont prévues dans le protocole: si la population faisant l’objet de l’analyse principale a été clairement définie dans le protocole (en général population en intention de traiter), les analyses portant sur les autres populations sont considérées comme des analyses de sensibilité.

    4. Les comparaisons multiples portent sur les variables relatives à la tolérance des traitements et leurs résultats ont une valeur d’alerte. Les techniques d’ajustement multiple seraient ici contre-productives, dans la mesure où l’objectif n’est pas de contrôler le risque de première espèce, mais de détecter d’éventuels excès de risque.

    5. Il s’agit d’un plan expérimental à trois bras: nouveau traitement/traitement de référence/placebo. L’objectif de tels essais est triple:

      • prouver la supériorité du nouveau traitement par rapport au placebo (efficacité);

      • prouver la supériorité du traitement de référence par rapport au placebo (validation interne);

      • prouver la non-infériorité, l’équivalence ou la supériorité du nouveau traitement par rapport au traitement de référence.

      La signification statistique doit être atteinte pour chacune des comparaisons au risque d’erreur fixé, sans ajustement pour comparaisons multiples.

    6. Une association fixe de deux produits est testée: il faut conduire un essai à trois bras comparant chacun des composants seul à l’association des deux. Celle-ci ne sera jugée pertinente que si elle montre sa supériorité par rapport à chacun des deux composants. L’analyse globale n’est ici pas informative et il n’y a pas lieu d’ajuster le risque d’erreur de type I.

Quelques situations particulières

Résultats obtenus sur des critères secondaires

  1. Si l’hypothèse nulle n’a pas pu être rejetée pour le critère principal, les résultats obtenus sur les critères secondaires devront être considérés comme «exploratoires» et nécessiteront une étude de confirmation.

  2. Si l’hypothèse nulle a pu être rejetée pour le critère principal, les résultats sur les critères secondaires pourront être pris en compte en utilisant une procédure hiérarchisée.

Résultats obtenus sur des sous-groupes de patients

  1. Si l’analyse sur l’ensemble de la population n’atteint pas la significativité statistique, les résultats sur les sous-groupes ne peuvent être considérés qu’à visée exploratoire.

  2. Pour revendiquer un effet bénéfique dans un sous-groupe donné, il faut définir a priori l’hypothèse nulle correspondante et la stratégie d’analyse, sans oublier de prendre en compte au niveau du protocole les impacts sur la puissance et les modalités de randomisation.

  3. D’un point de vue réglementaire, un résultat statistiquement significatif sur l’ensemble de la population ne permet pas de revendiquer une indication pour tous les sous-groupes. Au contraire, si la définition de la population de l’étude n’est pas bien documentée, les autorités peuvent restreindre l’indication à un sous-groupe. Il existe en effet dans certains cas une hétérogénéité importante de l’effet positif ou des effets secondaires des traitements entre les groupes, et celle-ci peut conduire à exclure certaines populations des indications d’un produit.

Critères composites

  1. Les critères évoqués dans le document technique correspondent à ceux souvent utilisés dans les études de morbidité-mortalité analysées avec des modèles de survie. Ils résultent de la combinaison de plusieurs événements rattachés à une même entité pathologique; le délai de «survie» est ici calculé jusqu’à la survenue d’un de ces événements. Chacun des événements composant le critère ayant une faible incidence, cette combinaison augmente la puissance de l’étude. Les critères doivent être définis dans le protocole.

  2. La comparaison des résultats doit ici porter sur le critère tel que défini dans le protocole, dans sa globalité.

  3. La comparaison des résultats obtenus pour chacun des événements pris individuellement est possible, mais seulement à titre exploratoire, et ne nécessite pas d’ajustement si la comparaison est significative sur le critère principal.

  4. La construction d’un critère composite suppose un effet à peu près semblable du traitement sur chacun des événements. Dans le cas contraire, les conséquences varieront en fonction du type d’essai réalisé:

    1. perte de puissance pour les essais de supériorité;

    2. difficultés d’interprétation pour les essais d’équivalence ou de non-infériorité.

Conclusions

De nombreuses techniques statistiques peuvent être utilisées pour prendre en compte les inférences multiples et éviter l’interprétation erronée de différences statistiquement significatives. Cependant, toutes ces méthodes ont leurs limitations propres et peuvent ne pas apporter une réponse satisfaisante au regard des objectifs scientifiques d’un essai. Il en est ainsi pour de nombreuses études réalisées dans le cadre d’évaluations de médicaments, cadre ayant fait l’objet de recommandations spécifiques rédigées par les autorités réglementaires européennes. Ces recommandations ont le mérite et l’intérêt de recenser un grand nombre de situations d’inférences multiples et de proposer des stratégies d’analyse adéquates. Elles ne sont cependant pas exhaustives et pourraient être utilement complétées par des informations relatives aux analyses intermédiaires et aux analyses avec mesures répétées.