Résumés
Résumé
Cette étude examine l’impact des classes et des écoles sur les performances en mathématiques des élèves de 4e année du primaire dans deux villes de la République démocratique du Congo en recourant à l’analyse multiniveau. Elle révèle que 71 %, 16 % et 13 % de la variance totale se situent respectivement aux niveaux élève, classe et école. L’étude montre en outre qu’au-delà de l’effet des caractéristiques individuelles, les caractéristiques de la classe expliquent 2,9 % (niveau classe) et 3,4 % (niveau école) de la variance totale. Cependant, seules la moyenne de la classe au prétest et la taille de classe sont significativement associées aux performances des élèves. L’étude montre enfin que si les caractéristiques de l’école expliquent 1,5 % de la variance totale située au niveau de l’école, l’expérience du directeur est le seul prédicteur significatif des performances des élèves.
Mots-clés :
- effet-école,
- effet-classe,
- effet de composition,
- performances en mathématiques,
- analyse multiniveau,
- République démocratique du Congo
Abstract
Based on a multilevel analysis, this study explores the impact of classes and schools on the mathematics performance of 4th grade elementary students in two cities of the Democratic Republic of the Congo. It reveals that, out of the total variance, 71%, 16% and 13% are situated at student, classroom and school levels, respectively. The study further shows that beyond the effect of individual characteristics, class characteristics explain 2.9% of the variance situated at class level and 3.4% of the variance located at school level. However, only the pretest class average and class size are significantly associated with student performance. The study finally shows that if school characteristics explain 1.5% of the variance situated at school level, the principal’s experience stands for the unique significant predictor of students’ performance.
Keywords:
- school effect,
- class effect,
- composition effect,
- mathematics performance,
- multilevel analysis,
- Democratic Republic of the Congo
Resumo
Este estudo examina o impacto das turmas e das escolas no desempenho matemático de alunos do 4.º ano do ensino básico em duas cidades da República Democrática do Congo, recorrendo à análise multinível. Ele revela que 71%, 16% e 1 % da variação total estão localizados respectivamente ao nível do aluno, da turma e da escola. O estudo também mostra que, além do efeito das características individuais, as características da turma explicam 2,9% (nível classe) e 3,4% (nível escola) da variação total. No entanto, apenas a média da turma no pré-teste e o tamanho da turma estão significativamente associados aos desempenhos dos alunos. O estudo mostra finalmente que, se as características da escola explicam 1,5% da variação total localizada ao nível da escola, a experiência do diretor é o único preditor significativo dos desempenhos dos alunos.
Palavras chaves:
- efeito-escola,
- efeito-classe,
- efeito de composição,
- desempenhos em matemática,
- análise multinível,
- República Democrática do Congo
Corps de l’article
Introduction
Comme dans plusieurs autres systèmes éducatifs, les mathématiques constituent, avec la lecture et l’écriture, les branches principales dans le système éducatif de la République démocratique du Congo. Elles sont importantes non seulement car elles facilitent l’apprentissage d’autres disciplines scolaires, mais également parce qu’elles sont à la base de la réalisation de plusieurs activités de la vie courante (Díez-Palomar, Simic et Varley, 2006 ; Mosvold, 2005). En effet, nous appliquons inconsciemment les mathématiques dans chaque aspect de la vie (Salout, Behzadi, Shahvarani et Manuchehri, 2013).
Cependant, les préoccupations du milieu scolaire sur les difficultés d’apprentissage en mathématiques apparaissent de plus en plus grandissantes (Mary, Squalli, Theis et Deblois, 2014). Elles sont d’autant plus épineuses que le système éducatif de la République démocratique du Congo connaît une crise importante. Déclenchée en 1974 par la nationalisation des écoles, la crise du système éducatif congolais s’est accentuée avec le Programme d’ajustement structurel dans les années 1980 et, plus encore, avec les guerres que le pays a connues depuis la décennie 1990. En conséquence, le système éducatif enregistre un faible rendement quantitatif, marqué par une forte déperdition (Mokonzi, 2010 ; UNESCO et IIPE Pôle de Dakar, 2014), par un faible rendement qualitatif et par de faibles acquis des élèves (Banque mondiale, 2005 ; De Herdt, Marivoet et Muhigirwa, 2015).
D’après l’étude du Programme d’analyse des systèmes éducatifs de la CONFEMEN (PASEC, 2011), 26 % des élèves de 2e année et 51 % des élèves de 5e année du primaire en République démocratique du Congo présentent des difficultés d’apprentissage. Aussi, la proportion d’élèves ayant un score inférieur à 25 sur 100 est-elle de 10,8 % en français et de 14,3 % en mathématiques pour la 2e année et de 27,3 % en français et de 14,2 % en mathématiques pour la 5e année.
Dans un système éducatif caractérisé par un si faible niveau, les écoles et les classes se distinguent-elles encore dans leur effet sur les performances des élèves ? En s’intéressant à cette question, la présente étude analyse les performances des élèves de 4e année du primaire en mathématiques en recourant au modèle multiniveau dans le but de dégager à la fois l’effet de la fréquentation d’une classe et d’une école particulières.
Revue de la littérature
Quel effet l’école exerce-t-elle sur l’apprentissage des élèves ? Bien que vieille, cette question est devenue plus préoccupante vers la fin des années 1950 et a donné naissance, au cours de la décennie suivante, particulièrement à partir du rapport Coleman (Coleman et al., 1966), au courant de recherche dénommé input-output ou fonction de production.
Ce courant étudie fondamentalement l’effet des caractéristiques quantifiables, dont les ressources matérielles de l’école, sur l’apprentissage des élèves. Il s’intéresse moins aux processus mis en oeuvre à l’école qu’aux effets produits en matière d’acquisitions scolaires (outputs), après qu’on en a contrôlé les entrées (Bressoux, 1995). Pour les études axées sur ce courant, l’influence potentielle des caractéristiques scolaires est additionnelle par rapport au rôle joué par les caractéristiques des élèves (Van Damme et al., 2009).
En réaction à la fonction de production, des travaux relevant plutôt du courant de recherche « processus-produit » ont débuté aux États-Unis et en Grande-Bretagne vers les années 1970 et se sont étendus à d’autres pays du nord au cours des décennies 1980 et 1990. Ils ont mis en évidence un effet-école un peu plus important que celui rapporté par des travaux de type input-output (Bressoux, 1995).
Indépendamment des travaux sur l’effet-école, un autre courant de recherche basé sur les caractéristiques de l’enseignement s’est développé. Ce courant s’est initialement concentré sur l’étude des caractéristiques personnelles des enseignants, avant de s’intéresser aux relations entre les comportements observés des enseignants et les performances des élèves (Van Damme et al., 2009). Autrement dit, la recherche étudie dans quelle mesure la fréquentation de telle classe (maître) plutôt que de telle autre peut avoir des répercussions sur les acquisitions des élèves, et quelles sont les pratiques pédagogiques qui apparaissent les plus efficaces (Bressoux, 1995 ; Scheerens et Bosker, 1997 ; Teddlie et Reynolds, 2000).
Depuis la décennie 1990, de nombreux auteurs (Creemers, 1994 ; Creemers et Kyriakides, 2008 ; Palardy et Rumberger, 2008) se sont efforcés de synthétiser et de conceptualiser des résultats issus des travaux fondés sur la fonction de production, sur le processus-produit et sur l’efficacité de l’enseignement.
Modèle conceptuel
Comme nous l’avons déjà indiqué, depuis le milieu de la décennie 1990, des synthèses des recherches ont été établies, et des modèles conceptuels intégrant les résultats des études basées sur la fonction de production, sur le processus-produit et sur les caractéristiques de l’enseignement ont été développés. Au-delà de leurs spécificités, ces modèles prennent tous en considération le caractère hiérarchique des systèmes éducatifs dans lesquels les élèves subissent l’influence des classes (ou maîtres), qui sont elles-mêmes sous l’effet des écoles. Ces modèles admettent qu’à chacun de ces niveaux interviennent les ressources (inputs), les processus et leurs effets (outputs). Un de ces modèles est celui de Palardy et Rumberger (2008), auquel se réfèrent les données exploitées dans cette étude (voir Figure 1).
Figure 1
Modèle conceptuel général multiniveau pour l’étude d’effet-école
Pour faire ressortir l’effet-école et l’effet-classe, la recherche sur l’efficacité de l’enseignement privilégie essentiellement les études longitudinales (Gustafsson, 2010 ; Reynolds, Sammons, De Fraine, Townsend et Van Damme, 2011). De telles études, impliquant trois niveaux (élève, classe et école), sont rarement menées dans les pays en développement.
En Afrique, on peut citer l’étude de Kiwanuka, Van Damme, Van den Noortgate, Anumenden et Namusi (2015) menée en Uganda, pour laquelle 68,8 %, 14,2 % et 17,0 % de la variance totale des performances en mathématiques des élèves de 1re année du secondaire se situent respectivement aux niveaux de l’élève, de la classe et de l’école. Cette étude n’a pourtant procédé au suivi des élèves qu’au cours d’une année scolaire. Par contre, pour l’étude transversale menée par Thuku et Hungi (2013), 61,1 %, 5,1 % et 33,8 % de la variance des acquis en mathématiques des élèves kenyans de 6e année du primaire se situent respectivement aux niveaux de l’élève, de la classe et de l’école.
Variables de la classe
Suivant les résultats de la recherche sur l’efficacité de l’enseignement, l’effet-classe est plus important que l’effet-école. Il explique de 10 à 20 % de la variance des performances des élèves (Bianco et Bressoux, 2009 ; Bressoux, 1994), alors que l’effet-école n’en explique que 4 à 5 %. Pour Palardy et Rumberger (2008), parmi les variables de la classe qui affectent les performances des élèves, la recherche s’est intéressée notamment à sa taille, à la composition du groupe et à l’effet-maître.
La taille de la classe
La caractéristique morphologique de la classe la plus explorée est sans doute sa taille (Goldstein, Yang, Omar, Turner et Thompson, 2000). À ce propos, une première méta-analyse, basée sur 77 études menées pendant environ 7 décennies dans près de 12 pays, a été réalisée par Glass et Smith en 1979. En prenant en compte uniquement 14 de ces études considérées comme les mieux contrôlées, Glass et Smith ont conclu qu’il y avait des effets positifs des tailles de classe inférieures à 20 sur les performances des élèves. Ils ont également montré que la relation entre la taille de classe et les résultats des élèves est plus forte au secondaire qu’au primaire, et qu’elle ne diffère pas significativement suivant les matières scolaires, ni le quotient intellectuel des élèves. Les conclusions mises en évidence par Glass et Smith n’ont pas toujours été confirmées par les études ultérieures. Pour certains travaux (Angrist et Lavy, 1999 ; Nye, Hedges et Konstantopoulos, 2000), la réduction de la taille de classe permet d’améliorer les résultats scolaires. Pour d’autres (Akerhielm, 1995 ; Pong et Pallas, 1999), la taille de classe entretient une relation positive avec les performances des élèves. Pour d’autres encore (Goldstein et al., 2000 ; Hanushek, 2003), il n’y a pas de lien entre ces deux variables.
La composition du groupe
En plus de la taille de classe, la composition du groupe est l’une des variables sur lesquelles la recherche s’est également penchée (Dupriez, 2010). Elle est entendue comme l’effet des caractéristiques agrégées des élèves sur leurs performances, après avoir pris en compte l’effet des variables individuelles. Depuis le rapport Coleman en 1966, la plupart des études qui ont examiné cet effet (Bellin, Dunge et Gunzenhauser, 2006 ; Opdenakker et Van Damme, 2004, 2009) indiquent une association positive et significative entre la composition de classe et la réussite des élèves.
En étudiant la relation entre l’effet de composition et les pratiques de classe à partir d’un échantillon représentatif des écoles secondaires de la Flandre, en Belgique, Opdenakker et Van Damme (2004) ont montré que la composition du groupe influe sur les pratiques de la classe, en particulier sur l’environnement de l’apprentissage et sur le climat de classe. Par exemple, une classe au départ forte en mathématiques pourrait recevoir, au cours de l’année, plus d’occasions d’apprendre, avoir une meilleure relation avec l’enseignant et bénéficier d’un climat propice pour l’apprentissage, ce qui, au bout du compte, conduirait à de meilleures performances des élèves. Autrement dit, la composition de classe influe sur les performances des élèves par la médiation des pratiques enseignantes et du climat d’apprentissage.
L’effet-maître
Une bonne partie de l’effet-classe provient de l’effet-maître (Bressoux, 1994). Sur l’enseignant, la recherche a essentiellement modélisé trois groupes de variables : ses caractéristiques, ses pratiques enseignantes et ses attitudes (Palardy et Rumberger, 2008). Si, pour Hanushek (1997), une très faible proportion d’études a débouché sur des associations positives entre les caractéristiques des enseignants et l’apprentissage, telle n’est pas la conclusion de la revue de la littérature effectuée par Greenwald, Hedges et Laine (1996), laquelle a plutôt mis en évidence de fortes relations entre les caractéristiques des enseignants et la réussite scolaire.
L’expérience professionnelle et la formation
L’expérience professionnelle de l’enseignant (mesurée en années passées dans la profession) et sa formation sont parmi les variables explorées par la littérature sur l’effet-maître. Concernant l’impact de l’expérience, certaines études (Clotfelter, Ladd et Vidgor, 2007 ; Kane, Rockoff et Staiger, 2006) affirment que les enseignants moins expérimentés sont moins efficaces que les plus expérimentés. Pour d’autres études (Aaronson, Barrow et Sander, 2007 ; Betts, Zau et Rice, 2003), l’expérience des enseignants n’influence pas les performances des élèves. Selon Rice (2010), les jeunes enseignants améliorent rapidement leurs performances au cours des trois premières années de la carrière. Cette amélioration plafonne après cinq années, de sorte que les jeunes enseignants peuvent parfois avoir un meilleur impact sur le rendement des élèves que les enseignants les plus expérimentés (Harris et Sass, 2007). Cependant, l’effet de l’expérience professionnelle des enseignants dépend du contexte socioéconomique et du soutien pédagogique offert par le système éducatif (Ingersoll et Strong, 2011).
La formation initiale et la formation continue
Quant à la formation, la recherche s’est penchée sur l’impact de la formation initiale et de la formation continue de l’enseignant. À propos de la formation continue, certains travaux attestent son effet positif sur les performances des élèves (Damar, 1996, cité par Balta, Arslan et Duru, 2015 ; Naoreen, Aslam, Arshad et Nausheen, 2011), tandis que d’autres (Jacob et Lefgren, 2004) mettent en évidence soit un faible effet, soit l’absence de relation entre ces variables. Pour l’Afrique subsaharienne en particulier, Lauwerier et Akkari (2015) ont remarqué que la formation initiale et la formation continue ont un faible impact sur les pratiques en classe.
Selon une modélisation élaborée par Guskey (2000, cité par Djibo et Gauthier, 2017), cinq composantes essentielles permettent à la formation continue d’influer positivement sur la réussite scolaire : 1) les politiques d’enseignement valorisées lors des activités de formation ; 2) les pratiques d’enseignement étudiées au cours de ces activités ; 3) les stratégies d’organisation des activités, notamment le lieu et la durée de la formation ; 4) les connaissances et habiletés acquises par l’enseignant à la fin des activités de formation ; et 5) le soutien organisationnel apporté par l’administration et la communauté locale. Djibo et Gauthier (2017) ajoutent à cette modélisation une sixième composante, à savoir la participation des enseignants.
Les attitudes
Concernant les attitudes, la recherche a examiné les perceptions que les enseignants ont du climat de l’école et de la communauté (Raudenbush, Rowan et Cheong, 1992 ; Rowan, Raudenbush et Kang, 1991), leur satisfaction (Lee, Dedrick et Smith, 1991), leur efficacité (Hoya et Spero, 2005) ainsi que la relation entre ces variables et le rendement des élèves (Palardy et Rumberger, 2008).
Les pratiques enseignantes
Des études se sont également intéressées à l’effet des pratiques enseignantes (Bressoux, 2012 ; Nandwa, Wasi et Wanjala, 2015 ; Talbot, 2012). Elles ont globalement mis en évidence des effets significatifs de celles-ci sur les performances des élèves. En dépit de cette conclusion, les études basées sur les questionnaires n’établissent pas toujours des effets significatifs des pratiques enseignantes, contrairement aux travaux qui recourent aux observations (Thum, 2000).
L’occasion d’apprendre est l’une des pratiques enseignantes explorées par la recherche. Définie comme l’alignement entre les objectifs éducatifs, les curricula prévus et mis en oeuvre ainsi que les résultats scolaires, l’occasion d’apprendre est considérée comme une caractéristique d’une éducation efficace (Scheerens, 2017). Pourtant, les résultats des travaux qui ont étudié l’effet de cette variable sur les performances des élèves sont contradictoires. C’est ce que Carnoy et Arends (2012) ont trouvé dans une étude menée en Afrique du Sud et au Botswana. Alors que l’occasion d’apprendre a été positivement et significativement associée au gain d’apprentissage réalisé en mathématiques par les élèves sud-africains, tel n’a pas été le cas pour les élèves du Botswana. De même, un peu plus de 50 % des effets d’occasions d’apprendre examinés dans une méta-analyse effectuée par Lamain, Scheerens et Noort (2017) sont statistiquement significatifs et près d’une autre moitié d’effets sont non significatifs.
Selon Schmidt (2009), l’occasion d’apprendre est une variable multifacette dont la mesure, pour être valide, devrait prendre en compte au moins trois aspects différents : 1) le contenu du programme couvert par l’enseignement ; 2) le temps d’enseignement consacré à chaque sujet ; et 3) la difficulté d’apprentissage des notions enseignées.
Pour Palardy et Rumberger (2008), les pratiques enseignantes influent plus directement sur les performances des élèves que les caractéristiques et les attitudes des enseignants. Les effets de ces deux dernières catégories de variables sont plutôt médiés par les pratiques enseignantes.
Variables de l’école
Plusieurs variables de l’école ont fait l’objet de la recherche sur l’efficacité de l’enseignement, au-delà des ressources sur lesquelles s’est principalement penché le courant de recherche input-output (Bressoux, 1994, 1995 ; Duru-Bellat, 2001). Aussi, des listes des caractéristiques des écoles efficaces ont été élaborées (Edmonds, 1979 ; Marzano, 2000).
Le leadership de la direction d’école
Le leadership de la direction est l’une des variables de l’école prises en compte par la recherche. En matière d’influence exercée sur le rendement des élèves, le leadership de la direction se classe juste après l’enseignement en classe (NASSP et NAESP, 2013).
Des études portant sur le leadership de la direction montrent que plus les directeurs d’école sont expérimentés, plus ils affectent positivement les performances scolaires (Clark, Martorell et Rockoff, 2009). Ceux qui consacrent plus de temps à la gestion organisationnelle dirigent des écoles ayant de meilleures notes (Horng, Klasik et Loeb, 2009), et importent leurs politiques et pratiques d’une école à l’autre (Cannon, Figlio et Sass, 2013).
L’expérience du directeur d’école aurait plutôt un effet indirect sur les performances des élèves par la médiation des pratiques enseignantes. En effet, il est logique de penser qu’au fil des années, un directeur d’école développe une politique scolaire qui influe sur la qualité du processus enseignement-apprentissage (Creemers et Kyriakides, 2010). Pour la National Association of Secondary School Principals et la National Association of Elementary School Principals (2013), avec l’expérience, le directeur : 1) développe une vision du succès scolaire pour tous les élèves ; 2) crée un climat hospitalier à l’éducation pour que prévalent la sécurité, l’esprit coopératif et d’autres déterminants d’une interaction fructueuse ; 3) cultive le leadership chez d’autres membres de la communauté scolaire afin qu’ils assument leur part de responsabilité dans la réalisation de la vision de l’école ; 4) améliore les pratiques enseignantes ; et 5) gère les personnes, les ressources et les processus de manière à favoriser l’amélioration de l’école.
La formation continue des directeurs d’école est l’un des aspects du leadership de la direction qui, en général, affectent positivement l’efficacité des écoles (Pont, Nusche et Moorman, 2008 ; Walker, 1982). Pourtant, suivant la recherche menée par Goddard, Hoy et Hoy (2000), cette formation ne peut être efficace que si elle s’oriente vers l’amélioration de la culture et du climat de l’école, la gestion du changement et l’amélioration de l’apprentissage des élèves.
Toutefois, selon la synthèse de 37 recherches quantitatives réalisée par Witziers, Bosker et Kruger (2003), le leadership de la direction a un faible effet sur les performances des élèves, expliquant à peine 1 % de la variance totale.
La composition de l’école
Outre le leadership de la direction, la recherche a également analysé l’effet de composition de l’école sur les performances des élèves. Le rapport Coleman en 1966 est la première étude de grande envergure à s’intéresser à cet effet. Il a notamment montré que les résultats des élèves étaient plus fortement associés à la composition socioéconomique et ethnique de l’école que n’importe quelle autre caractéristique de l’école. Depuis, plusieurs travaux se sont intéressés à l’effet de composition de l’école en mettant l’accent sur certaines variables, notamment la capacité ou le niveau intellectuel des élèves, leur statut socioéconomique, l’appartenance ethnique et le genre (Boonen et al., 2014).
Concernant la capacité intellectuelle, pour la plupart des études (Danhier et Martin, 2014 ; Dumay et Dupriez, 2008 ; De Fraine, Van Damme, Van Landeghem, Opdenakker et Onghena, 2003 ; Opdenakker et Van Damme, 2001), le niveau de maîtrise des connaissances par le groupe au début de l’année est une importante source de variation des performances des élèves. Opdenakker et Van Damme (2001) ont trouvé un effet positif du niveau moyen de l’école sur les performances réalisées en mathématiques par les élèves des écoles secondaires de la Flandre. Cependant, même si la littérature sur l’effet de composition de l’école est abondante, aucun consensus clair n’a été obtenu sur la signification et l’ampleur de cet effet (Dumay et Dupriez, 2008).
La taille de l’école
La relation entre la taille d’école et les performances des élèves a également été examinée par la recherche sur l’effet-école. Pour certaines études (Gershenson et Langbein, 2015 ; Jones et Ezeife, 2011), la taille d’école n’influe pas sur les résultats des élèves. Par contre, d’autres études (Alspaugh et Gao, 2003 ; Wendling et Cohen, 1981) ont établi une relation négative entre ces deux variables ; autrement dit, plus grande est la taille d’école, moins bien réussissent les élèves. Dans une méta-analyse des travaux réalisés à partir de 1960, Greenwald et ses collègues (1996) ont trouvé que la réussite des élèves scolarisés dans une petite école est meilleure que celle des élèves fréquentant une grande école. Le même constat a été relevé, d’une part, par Alspaugh et Gao (2003) et Wendling et Cohen (1981) au primaire, et, d’autre part, par Lee, Smith et Croninger (1997) dans les écoles secondaires, particulièrement en mathématiques et en sciences. Cependant, pour certains chercheurs (Bickel, Howley, Williams et Glascock, 2001 ; Jones et Ezeife, 2011), la corrélation entre la taille d’école et les performances des élèves est influencée par d’autres variables, notamment le statut socioéconomique des élèves et leur année d’études. De même, comme le notent Egalite et Kisida (2016), une grande partie de la recherche sur la relation entre la taille d’école et les performances des élèves est de nature corrélationnelle ou a utilisé la régression multivariée avec des données transversales ; elle n’a pas abordé les questions de biais de sélection. Ces chercheurs estiment que les données longitudinales permettent de mieux appréhender l’effet de la taille d’école sur les performances des élèves. En effet, cette dernière approche permet de comparer les élèves à eux-mêmes à différents moments marqués par différentes tailles d’école.
Le secteur de l’école (privée/publique)
Le secteur auquel appartient une école est une variable à laquelle les études se sont également intéressées. À ce sujet, certains travaux (Frenette et Chan, 2015 ; Hahn, Kim et Seo, 2014 ; Kamba, 2018) ont montré que les élèves des écoles privées réussissent mieux que ceux des écoles publiques. D’autres travaux (Mahuteau et Mavromaras, 2014 ; Rong’uno, 2017 ; Thomson, De Bortoli et Buckley, 2013) ont révélé l’inexistence de différences entre ces deux types d’écoles. Pour Cobbold (2015), si la supériorité de la réussite des élèves des écoles privées se manifeste généralement dans les comparaisons brutes, les différences entre les résultats des écoles publiques et ceux des écoles privées disparaissent lorsque certaines caractéristiques des élèves et des écoles sont contrôlées dans les analyses, notamment le statut socioéconomique.
Questions
Cette étude vise à répondre aux questions suivantes :
-
Quelle part des différences des performances réalisées en mathématiques par les élèves de 4e année du primaire est attribuable aux classes et aux écoles ?
-
Quelles variables de la classe sont associées aux performances des élèves ?
-
Quelles variables de l’école affectent ces performances ?
Méthodologie
Échantillon d’étude
Les données exploitées pour cette publication proviennent d’une recherche longitudinale menée depuis 2010 par le Service de planification et d’évaluation en éducation de l’Université de Kisangani, en collaboration avec le Center for Educational Effectiveness and Evaluation de l’Université KU Leuven, dont font partie les auteurs de la présente étude. Appuyée par le Conseil interuniversitaire flamand, cette recherche vise à identifier les facteurs d’efficacité des écoles primaires et secondaires de la Province orientale en République démocratique du Congo.
Un échantillonnage stratifié pondéré d’écoles a été effectué dans les deux agglomérations les plus importantes de cette province sur le plan de la démographie et du nombre d’écoles, à savoir les villes de Kisangani et de Bunia. Le nombre d’écoles retenues dans l’échantillon a été fixé à 50, soit environ 18 % des écoles primaires, sur les 280 que comprenaient ces villes en 2010.
L’échantillonnage des écoles s’est basé sur la structure du système éducatif de la République démocratique du Congo. En effet, trois catégories d’écoles, connues sous le nom de « réseaux », sont organisées dans ce pays : des écoles publiques non conventionnées (EPUNC), des écoles publiques conventionnées (EPUC) et des écoles privées (EPR). Les EPUNC sont à la fois financées et gérées par l’État. Les EPUC sont, en principe, financées par l’État et gérées par l’Église, tandis que les EPR sont financées et gérées par leurs promoteurs, qui sont, de manière générale, des particuliers ou des associations.
Étant donné cette structure, la procédure d’échantillonnage a consisté, dans un premier temps, en la sélection aléatoire, dans chaque réseau, d’un nombre d’écoles proportionnel au nombre total d’écoles que compte le réseau dans les villes de Kisangani et de Bunia. Ensuite, dans une école disposant d’une ou de deux classes de 4e année, ces dernières ont d’office été retenues dans l’échantillon d’étude. Par contre, étant donné les effectifs pléthoriques des classes en République démocratique du Congo en général et dans la Province orientale en particulier, pour une école ayant plus de deux classes de 4e année, seulement deux classes ont été sélectionnées aléatoirement pour faire partie de l’échantillon. Enfin, tous les élèves des classes sélectionnées ont été retenus pour la recherche.
Cette procédure d’échantillonnage a conduit à la sélection de 50 écoles et de 82 classes de 4e année. Néanmoins, étant donné qu’au cours de la première étape de collecte des données, une école de Bunia n’a pas pris part à la recherche, l’échantillon sélectionné couvre 49 écoles, 80 classes et 4777 élèves de 4e année (voir Tableau 1).
Tableau 1
Échantillon de l’étude
Variables retenues
Variable dépendante
Les scores au test de mathématiques appliqué en avril 2012, appelé ici post-test, sont utilisés comme variable dépendante. De fidélité élevée (α = 0,87), ce test, composé de 40 questions, porte sur la numération, sur les fractions, sur les opérations et sur les mesures.
Variables indépendantes
Variables de niveau 1 (élève)
Outre le genre (codé 0 pour la fille et 1 pour le garçon) et l’âge (variant de 7 à 16 ans), 5 autres variables individuelles ont été incluses dans les analyses : 1) la langue la plus parlée à la maison ; 2) le statut socioéconomique (SSE) ; 3) le soutien parental (SOUTPAR) ; 4) le redoublement (REDBLT) ; et 5) le prétest.
La variable langue comprend 4 modalités : 0 pour le français, 1 pour le swahili, 2 pour le lingala et 3 pour les autres langues nationales (AUTRELAN)[1]. Le SSE est une variable composite, dérivée de l’application de l’analyse en composantes principales aux renseignements relatifs au niveau d’instruction des parents et à la possession des biens (électricité, livres, ordinateur, poste téléviseur, chaises et tables pour le devoir à domicile, jouets). Cette analyse a fait ressortir une structure à un facteur correspondant à 49 % de la variance totale. Le score du soutien parental est la somme des réponses fournies à trois questions visant à explorer si, pour la réalisation de ses devoirs à domicile, l’élève bénéficie de l’aide de sa mère, de son père et de ses frères et soeurs. L’échelle du soutien parental varie ainsi de 0 (si l’élève ne bénéficie d’aucun appui) à 3 (si l’élève bénéficie du soutien des trois catégories de membres de la famille). Le redoublement est une variable dichotomique codée 0 pour le non-redoublement et 1 pour le redoublement d’au moins une classe de la 1re à la 4e année. Enfin, le prétest est un test de mathématiques appliqué au début de l’année scolaire (septembre 2011) ; il comprend 36 questions couvrant les mêmes rubriques du programme que la variable dépendante. Sa fidélité est également satisfaisante (α = 0,88).
Variables de niveau 2 (classe)
Au niveau de la classe, nous nous sommes intéressés aussi bien aux variables de composition qu’aux caractéristiques de l’enseignant. Les premières se rapportent à la moyenne réalisée par les élèves au prétest et à la taille de la classe. Les valeurs de ces variables s’étendent respectivement de 4,42 à 32,41 pour la moyenne au prétest et de 13 à 117 pour la taille de classe.
Quant aux caractéristiques de l’enseignant, en plus du genre (codé 0 pour l’enseignante et 1 pour l’enseignant), 3 autres variables ont été considérées dans les analyses : sa formation, son expérience et l’occasion d’apprendre. D’abord, la formation a été explorée à travers la formation continue. Il s’est agi d’examiner si les enseignants avaient participé à au moins une séance de formation continue au cours des cinq dernières années. Cette variable est codée 0 pour la non-participation et 1 pour la participation à au moins une séance de formation continue. Ensuite, l’expérience est mesurée par le nombre d’années passées dans l’enseignement. Elle varie de 1 à 43 ans. Enfin, à partir d’un questionnaire soumis aux enseignants, l’occasion d’apprendre est simplement fournie par le pourcentage des questions du post-test couvertes par le contenu des enseignements assurés au cours de l’année. Elle varie de 41 % à 100 %.
Variables de niveau 3 (école)
Pour ce niveau, nous avons retenu dans un premier temps deux caractéristiques de composition de l’école, à savoir la moyenne au prétest et la taille d’école, représentée par l’effectif des élèves. La moyenne de l’école au prétest varie de 4,42 à 23,05, tandis que la taille d’école s’étend de 143 à 1327. Nous avons ensuite considéré le « réseau » auquel appartient l’école. En effet, les 49 écoles retenues dans l’échantillon se répartissent dans trois réseaux différents, soit 11 écoles publiques non conventionnées, 32 écoles publiques conventionnées et 6 écoles privées. Enfin, deux caractéristiques du directeur d’école ont été intégrées dans les analyses : son expérience professionnelle comme directeur d’école, exprimée par le nombre d’années (variant de 1 à 44 ans), et sa participation à des séances de formation continue au cours des cinq dernières années. Cette dernière variable est codée 0 si le directeur n’a pas participé à la formation continue et 1 s’il a pris part à au moins une séance de formation continue au cours des cinq dernières années.
Quelques considérations sur l’analyse des données
Données manquantes
Étant longitudinale, la recherche à laquelle se réfère cette étude fait face à des données manquantes. Celles-ci peuvent affecter les résultats d’une étude en fonction de la manière dont elles sont gérées (Tomarken et Waller, 2005), de leur proportion (Tabachnick et Fidell, 2007), du niveau structurel auquel elles se situent et si elles apparaissent aléatoirement ou plutôt de manière prévisible (Allison, 2002). Dans la recherche menée par le Service de planification et d’évaluation en éducation, le pourcentage de ces données varie de 0,3 % à 15 %, excepté le prétest, dont les données manquantes représentent 30 % de l’échantillon. Nous avons procédé à l’imputation multiple des données afin d’éviter d’obtenir des paramètres qui s’écartent trop de ceux de la population, auxquels peuvent conduire les méthodes classiques de traitement des données manquantes (Graham, 2009), notamment la suppression des sujets ayant des données manquantes, la substitution par la moyenne et l’imputation par la régression. Dans l’imputation multiple des données, chaque valeur manquante est remplacée par une liste de valeurs simulées (ensemble de valeurs plausibles). Comme principal avantage, l’imputation multiple n’impose aucune hypothèse quant à l’absence de données manquantes (Tabachnick et Fidell, 2007).
Il convient de noter que plus le nombre d’imputations est élevé, plus les résultats se rapprochent de ceux auxquels débouche l’imputation par le maximum de vraisemblance complète (Graham, Olchowski et Gilreath, 2007). Étant donné le pourcentage des données manquantes enregistrées au prétest (30 %), nous avons effectué 10 imputations au moyen du logiciel R (version 3.5.0) et du package Amelia (Honaker, King et Blackwell, 2011). L’analyse des caractéristiques statistiques du prétest indique qu’il n’y a pas d’importantes variations entre les différents ensembles des données issues de ces imputations (voir Annexe). C’est pourquoi les analyses effectuées dans cette étude ont porté uniquement sur l’un de ces ensembles des données, à savoir la deuxième imputation.
Analyse exploratoire
L’analyse exploratoire des données a consisté à calculer les corrélations de Bravais-Pearson ou de Spearman entre les variables retenues respectivement aux niveaux de l’élève, de la classe et de l’école.
Analyse multiniveau
Le traitement des données a été réalisé par la régression multiniveau au moyen du logiciel MLwiN (version 2.24 ; Rasbash, Charlton, Browne, Healy et Cameron, 2011). Pour estimer l’effet net des classes et des écoles, un modèle à trois niveaux a été utilisé : le niveau élève, le niveau classe et le niveau école. Au départ, un modèle vide sans variables explicatives a été calculé dans le but de décomposer la variance totale du critère en composantes de variance intraclasse, interclasse et interécole. Les caractéristiques de l’élève ont ensuite été intégrées dans l’analyse (Modèle 1) dans le but d’estimer les composantes de variance en retirant du critère l’effet prédictible des variables individuelles. La troisième étape d’analyse a consisté en l’introduction successive des variables de la classe, d’abord sans l’effet de composition par rapport aux connaissances initiales en mathématiques (Modèle 2), puis avec cet effet (Modèle 3). Dans la dernière étape, nous avons modélisé les caractéristiques de l’école sans la moyenne de l’école au prétest (Modèle 4), puis en intégrant cet effet dans le modèle (Modèle 5).
Pour faciliter la comparaison des effets, nous avons procédé à la standardisation de toutes les variables prédictrices continues.
Pour chaque modèle adopté, trois éléments ont été exploités dans les commentaires des résultats : 1) l’examen des effets aléatoires ou des variances des erreurs ; 2) l’interprétation des effets fixes ou des coefficients de régression ; et 3) l’analyse de l’ajustement du modèle aux données de l’étude.
L’examen des effets aléatoires dans le modèle vide a été effectué au moyen de la division de la variance des erreurs de chaque niveau par la variance totale dans le but de déterminer le pourcentage de la variance située aux niveaux de l’élève, de la classe et de l’école. Par contre, pour chacun des autres modèles (Modèle 1 au Modèle 5), nous avons comparé les composantes de variance à celles du modèle antérieur (moins complet).
L’analyse de la signification des effets fixes a nécessité, quant à elle, le calcul de la statistique Z fournie par le rapport entre chaque coefficient de régression et son erreur type.
L’appréciation de l’ajustement du modèle 1 aux données par rapport au modèle vide a été faite grâce à la statistique de la déviance (-2logV). Il en est de même de l’ajustement des modèles 2 à 5. Selon Bressoux (2010) :
La statistique de déviance est interprétable de manière relative, c’est-à-dire lorsqu’on la compare à une ou plusieurs autres valeurs -2logV sous certaines conditions précises : c’est-à-dire lorsque les variables explicatives d’un modèle considéré comme initial sont un sous-ensemble de celles d’un modèle considéré plus complet. On s’intéresse alors à la différence entre ces deux valeurs, c’est-à-dire à la décroissance de la déviance quand on passe d’un modèle initial à un modèle plus complet
p. 241
La décroissance suit une loi du chi2 à m degrés de liberté, m étant le nombre de paramètres supplémentaires à estimer quand on passe d’un modèle à un autre plus complet (Bressoux, 2010).
Afin de vérifier la pertinence de l’application de l’analyse multiniveau aux données de cette étude, nous avons examiné la distribution des résidus à chaque niveau du modèle adopté. En effet, les résidus doivent se distribuer normalement, ce qui implique une absence de valeurs aberrantes extrêmes. Pour Hox (2010) :
Cela s’applique aux résidus après avoir inclus toutes les variables explicatives importantes et les paramètres pertinents dans le modèle. Si nous analysons une séquence de modèles, nous avons une série de résidus différents pour chaque modèle, et les scruter tous à chaque étape n’est pas toujours pratique […]. Une approche raisonnable consiste à examiner les termes résiduels uniquement dans le modèle vide, afin de déterminer s’il y a des violations flagrantes des hypothèses du modèle
p. 25, trad. libre
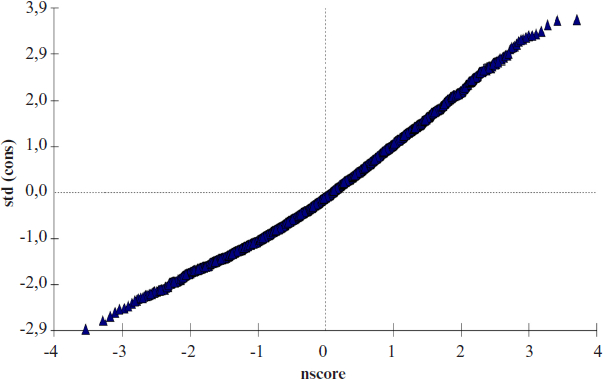
En suivant cette recommandation de Hox, nous avons examiné la normalité de la distribution des résidus aux niveaux élève, classe et école en nous basant uniquement sur le modèle vide. Ainsi que le montrent les figures 2, 3 et 4, les résidus se distribuent normalement à chaque niveau du modèle vide adopté dans cette étude.
Figure 2
Distribution des résidus de niveau 1 (élève)
Figure 3
Distribution des résidus de niveau 2 (classe)
Figure 4
Distribution des résidus de niveau 3 (école)
Résultats
Modèle vide
Les équations du modèle linéaire hiérarchique utilisées pour l’analyse du modèle vide sont les suivantes :
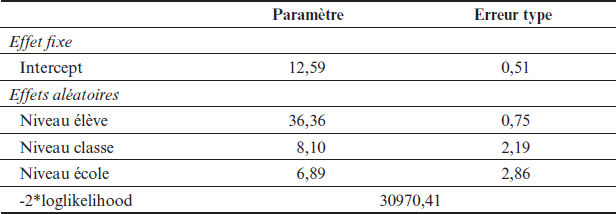
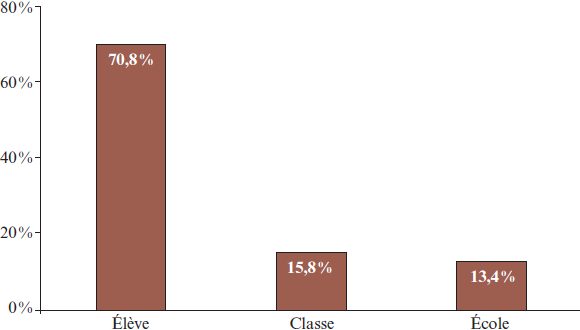
Partant de ces équations, l’analyse du modèle vide montre que 70,8 % de la variance des performances (soit 36,36/51,35×100) se situent au niveau de l’élève, 15,8 % (soit 8,10/51,35×100) au niveau de la classe et 13,4 % (soit 6,89/51,35×100) au niveau de l’école (voir Tableau 2 et Figure 5). Ainsi, bien que l’essentiel des différences se trouve au niveau des élèves au sein des classes, d’importantes différences existent également entre les classes dans les écoles et entre les écoles.
Tableau 2
Modèle vide
Figure 5
Composantes de variance pour le modèle vide
Effet des variables de l’élève (individuelles)
Les équations du modèle linéaire hiérarchique appliquées pour étudier l’effet des variables de l’élève sont les suivantes :
Dans cette équation, Yijk, π0jk et εijk ont les mêmes significations que dans le modèle vide ; π1jk…………. π9jk sont des coefficients de régression.
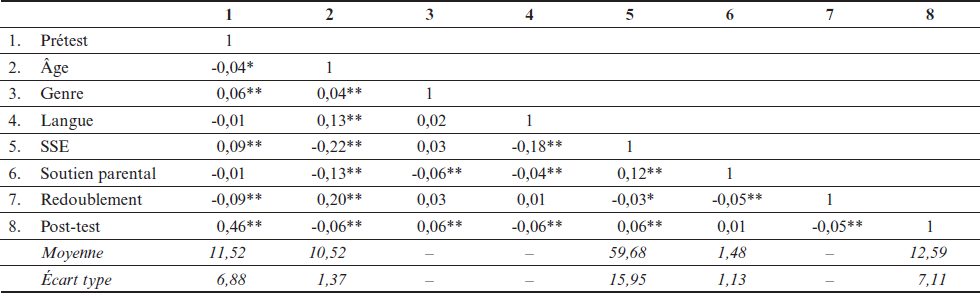
L’exploration des variables individuelles montre qu’excepté le soutien parental, tous les prédicteurs retenus sont significativement corrélés au post-test (voir Tableau 3). Cependant, en dehors de la relation entre le prétest et le post-test (r = 0,46), ces corrélations sont très faibles, variant de -0,06 à 0,06.
Comme le montrent le tableau 4 et la figure 6, l’ensemble des variables individuelles explique 20,6 % de la variance totale. Cette dernière est en effet passée de 51,35 pour le modèle vide à 40,77 pour le modèle 1. La variance expliquée par les caractéristiques individuelles équivaut à 6,9 %, 6,4 % et 7,3 % respectivement aux niveaux élève, classe et école (voir Figure 6). L’observation de chaque variable introduite dans le modèle 1 fait apparaître que le prétest est le meilleur prédicteur des performances en mathématiques (πPrétest = 2,33 ; p < 0,001). En plus du prétest, le genre a également un impact significatif sur les performances des élèves (πGenre = 0,45 ; p < 0,05). Par contre, l’âge, le statut socioéconomique, le soutien parental et le redoublement ne permettent pas de prédire les résultats des élèves. Pour la langue la plus parlée à la maison, la différence des acquis s’observe uniquement entre les élèves qui parlent français et ceux qui parlent le lingala (πLingala = -0,50 ; p < 0,05).
Le modèle 1 ajuste mieux les données que le modèle vide, la statistique chi2 étant hautement significative pour 9 degrés de liberté (χ2 = 528,60 ; dl = 9 ; p < 0,001).
Tableau 3
Corrélations, moyennes et déviation standard pour les prédicteurs du niveau élève (N = 4777)
Tableau 4
Effet des variables individuelles
Effet des variables de la classe
Les analyses effectuées pour estimer l’effet des variables de la classe l’ont été par les équations suivantes aux niveaux élève, classe et école :
– Modèle du niveau élève :
– Modèle du niveau classe :
Sans la moyenne de la classe au prétest (Modèle 2)
Avec la moyenne de la classe au prétest (Modèle 3)
L’exploration des corrélations bivariées montre que, de toutes les variables indépendantes modélisées au niveau de la classe, il n’y a que la moyenne au prétest qui est significativement liée aux performances des élèves (voir Tableau 5). En outre, seule la moyenne de la classe au prétest est un bon prédicteur de ces performances, soit βMoyPrét = 1,67 ; p < 0,001 (voir Tableau 6, Modèle 3). Après avoir pris en compte les caractéristiques de l’élève en comparant le modèle 3 au modèle 1, les caractéristiques de la classe expliquent 2,9 % de la variance totale située au niveau de la classe et 3,4 % de la variance totale située au niveau de l’école (voir Figure 7). En effet, du modèle 1 au modèle 3, la variance située au niveau de la classe est passée de 4,84 à 3,36, alors que celle située au niveau de l’école est passée de 3,12 à 1,40. En excluant la moyenne de la classe au prétest (voir Modèle 2), seule la taille de classe est négativement et significativement reliée aux performances des élèves (βTailleclasse = -0,71 ; p < 0,05).
Figure 6
Variance expliquée par les caractéristiques de l’élève
Tableau 5
Corrélations, moyennes et déviation standard pour les prédicteurs du niveau classe (N = 80)
Tableau 6
Effet des variables de la classe
La modélisation des caractéristiques de la classe (Modèle 3) ajuste mieux les données que la seule modélisation des caractéristiques individuelles (Modèle 1), la statistique chi2 étant largement significative (χ2 = 35,65 ; dl = 6 ; p < 0,001). Par contre, le modèle 2 n’ajuste pas mieux les données que le modèle 1 (χ2 = 9,9 ; dl = 5 ; p ˃ 0,05).
Figure 7
Variance expliquée par les caractéristiques de l’élève et de la classe
Effet des variables de l’école
Les équations exploitées pour l’estimation de l’effet des caractéristiques de l’école sont les suivantes :
– Modèle du niveau élève (Modèles 4 et 5) :
– Modèle du niveau classe (Modèles 4 et 5) :
– Modèle du niveau école :
Sans la moyenne de l’école au prétest (Modèle 4)
Avec la moyenne de l’école au prétest (Modèle 5)
L’analyse de l’effet des variables de l’école (Modèle 5) révèle que la composition de l’école par rapport aux connaissances initiales des élèves n’a pas d’impact sur les performances des élèves (γMoyPrét = -0,14 ; p ˃ 0,05). Il en est de même de la taille d’école (γTaillécole = -0,41 ; p ˃ 0,05). La formation continue du directeur d’école (γFormcontDir = -0,14 ; p ˃ 0,05) et le réseau d’appartenance de l’école (γEPUC = 0,36 ; p ˃ 0,05 et γEPR = 0,79 ; p ˃ 0,05) n’influent pas non plus sur la réussite des élèves. Seule l’expérience du directeur s’avère un prédicteur significatif des performances des élèves, même si son effet est faible (γExpérDir = 0,80 ; p < 0,05). L’exploration des statistiques descriptives (voir Tableau 7) montre que seule la moyenne de l’école au prétest est significativement associée à la variable dépendante (r = 0,79 ; p < 0,01).
Bien qu’elles n’influent pas toutes significativement sur les performances des élèves, les variables introduites dans le modèle 5 expliquent 1,5 % de la variance totale située au niveau de l’école (voir Figure 8). Tout en ajustant mieux les données que la modélisation des variables individuelles (χ2 = 42,44 ; dl = 12 ; p < 0,001), le modèle 5 n’est pas plus pertinent que le modèle 3 (χ2 = 6,79 ; dl = 12 ; p > 0,05). Si l’on exclut la moyenne de l’école au prétest (voir Tableau 8, Modèle 4), aucune caractéristique de l’école n’est significativement associée aux performances des élèves. En dépit de cette situation, le modèle 4 ajuste également mieux les données que le modèle 1 (χ2 = 42,38 ; dl = 11 ; p < 0,001) et que le modèle 2 (χ2 = 32,48 ; dl = 5 ; p < 0,001).
Figure 8
Variance expliquée par les caractéristiques de l’élève, de la classe et de l’école
Tableau 7
Corrélations, moyennes et déviation standard pour les prédicteurs du niveau école (N = 49)
Tableau 8
Effet des variables de l’école
Discussion
Cette étude met en évidence le fait que, même si un système éducatif est en crise et que les caractéristiques de l’enseignant (son expérience professionnelle, sa formation continue et l’occasion d’apprendre qu’il offre à la classe) n’ont pas d’impact sur l’apprentissage, les caractéristiques de la classe (notamment sa taille et le niveau intellectuel du groupe) influent sur les performances des élèves. Elle révèle également que l’expérience du directeur dans la gestion de l’école influe sur les performances des élèves.
Cependant, l’étude remet en question l’efficacité de la formation continue des enseignants et des directeurs d’école, de même que l’opinion largement répandue en République démocratique du Congo selon laquelle les écoles gérées par l’Église (écoles publiques conventionnées) et les écoles privées sont plus efficaces que les écoles gérées directement par l’État (écoles publiques non conventionnées).
De manière plus détaillée, comme les analyses effectuées l’ont révélé, 15,8 % et 13,4 % de la variance totale des performances réalisées en mathématiques par les élèves de 4e année du primaire de Kisangani et de Bunia se situent respectivement aux niveaux de la classe et de l’école. Ces résultats diffèrent de ceux de Thuku et Hungi (2013), selon lesquels 5,1 % et 33,8 % de la variance des acquis en mathématiques des élèves kenyans de 6e année du primaire sont aux niveaux de la classe et de l’école. Ils s’apparentent néanmoins aux résultats de l’étude de Kiwanuka et ses collègues (2015), suivant lesquels 31,2 % des différences des performances des élèves de 1re année du secondaire des écoles ougandaises se situent au niveau de la classe (14,2 %) et de l’école (17,0 %).
La divergence des résultats de cette étude avec ceux de Thuku et Hungi pourrait s’expliquer par le fait que le travail de ces deux chercheurs a porté sur un échantillon issu de l’ensemble du territoire de la République du Kenya (8 provinces), alors que la présente recherche a été menée uniquement dans deux villes d’une seule province de la République démocratique du Congo. Cette caractéristique de notre échantillon d’étude pourrait également expliquer le rapprochement de la répartition de la variance totale à celle obtenue par Kiwanuka et ses collaborateurs, dont la recherche a été menée uniquement dans la ville de Kampala et ses environs.
Variables de la classe
De la modélisation des variables de la classe, il ressort que la composition de classe, par rapport au prétest, est positivement associée aux performances des élèves. Ce résultat rejoint la conclusion de la plupart des études antérieures (Bellin et Gunzenhauser, 2006 ; Opdenakker et Van Damme, 2004, 2009). Il souligne le fait que l’effet de composition (cognitive) de classe ne dépend pas du contexte de l’apprentissage. Cet effet s’avère positif et significatif, même dans un environnement marqué par la crise comme celui de la République démocratique du Congo et même si les caractéristiques de l’enseignant (formation et expérience) et de l’enseignement (occasion d’apprendre) n’ont pas d’impact sur les performances des élèves.
Les analyses effectuées montrent également que la taille de classe influe négativement sur les performances des élèves lorsque la moyenne de la classe au prétest n’est pas introduite dans le modèle. Cela contredit, d’une part, les études pour lesquelles la taille de classe entretient une relation positive avec les acquis des élèves (Akerhielm, 1995 ; Pong et Pallas, 1999) et, d’autre part, les travaux n’ayant établi aucun lien entre la taille de classe et les performances des élèves (Goldstein et al., 2000 ; Hanushek, 2003). Cette conclusion s’apparente à celle des études d’Angrist et Lavy (1999) et Nye et Konstantopoulos (2000). La contradiction entre le résultat de cette étude et l’effet positif mis en évidence par des travaux intégrés dans la méta-analyse réalisée par Glass et Smith (1979) tient en partie au fait qu’au lieu de travailler uniquement avec les classes dont la taille est inférieure à 20, nous avons pris en compte tous les effectifs observés dans l’échantillon sélectionné ; ceux-ci varient de 13 à 117 élèves. C’est également de cette manière qu’ont procédé les travaux dont les résultats convergent avec ceux de cette étude. En outre, le fait d’avoir analysé l’effet de la taille de classe sur le rendement des élèves au post-test et non sur la progression réalisée par ceux-ci du début à la fin de l’année peut partiellement expliquer la divergence du résultat mis en évidence par cette étude et celui de certaines études antérieures.
De plus, contrairement à ce qu’ont révélé les travaux de Clotfelter et ses collègues (2007) et de Kane et ses collaborateurs (2006), l’expérience des enseignants n’influe pas, dans la présente étude, sur les performances des élèves. Cette divergence s’explique, d’une part, par le fait que l’échantillon de la présente étude est constitué à majorité (soit 66 %) d’enseignants ayant plus de cinq années d’expérience professionnelle. Or, l’impact de l’expérience est le plus fort au cours des trois premières années d’enseignement ; il diminue ensuite au point de plafonner après cinq années (Rice, 2010). D’autre part, l’impact de l’expérience des enseignants sur la réussite des élèves dépend du contexte socioéconomique et du programme de soutien pédagogique fourni par un système éducatif (Ingersoll et Strong, 2011). Ainsi, l’absence, dans le système éducatif congolais, de programmes de mentorat en faveur des jeunes enseignants et le contexte socioéconomique global du pays, marqué par la pauvreté, ne sont pas susceptibles d’avoir un impact positif sur l’expérience des enseignants et sur les performances des élèves.
Les analyses ont également mis en évidence le manque d’incidence de la formation continue des enseignants sur les performances des élèves. Ce résultat confirme le constat fait par Lauwerier et Akkari (2015), à savoir qu’en Afrique la formation initiale et la formation continue des enseignants influent faiblement sur les pratiques pédagogiques appliquées en classe. Pour cette étude et sur la base de la modélisation de Guskey (2000, cité par Djibo et Gauthier, 2017), telle que complétée par Djibo et Gauthier (2017), nous pouvons nous demander si les séances de formation auxquelles les enseignants ont pris part comportaient des composantes susceptibles de garantir leur influence sur la réussite des élèves. Ce constat remet ainsi en question : 1) la pertinence des politiques valorisées lors des activités de formation ; 2) l’efficacité des pratiques didactiques enseignées ; 3) l’adéquation des stratégies d’organisation des activités, notamment la durée de la formation ; 4) la validité des connaissances et des habiletés acquises à la fin de la formation ; 5) l’effectivité du soutien organisationnel ; et 6) le degré de participation des enseignants.
L’effet non significatif, bien que positif, de l’occasion d’apprendre sur les performances des élèves nous semble assez surprenant. Ce résultat induit pourtant le fait qu’il ne suffit pas qu’un contenu soit enseigné pour qu’il soit maîtrisé par les élèves. Autrement dit, au lieu d’être uniquement basée sur le contenu du programme, tel que cela a été fait au cours de la collecte des données exploitées dans la présente étude, la mesure de l’occasion d’apprendre devrait également intégrer le temps d’enseignement consacré à chaque sujet et la difficulté du contenu enseigné (Schmidt, 2009).
Variables de l’école
Au sujet de la modélisation des caractéristiques de l’école, cette étude a d’abord établi que la composition de l’école, par rapport au prétest, n’entretient pas de relation significative avec les performances des élèves, contredisant ainsi la conclusion des travaux de Danhier et Martin (2014), Dumay et Dupriez (2008), De Fraine et ses collègues (2003) ainsi que Opdenakker et Van Damme (2001). Ce résultat peut être dû au fait que, contrairement aux travaux antérieurs qui ont analysé la composition d’école à partir de l’ensemble des élèves des écoles sélectionnées, la présente étude a construit cette variable uniquement sur la base des résultats des élèves de quelques classes des écoles échantillonnées.
De même, la taille d’école n’est pas significativement associée aux performances des élèves. Cette observation confirme celle des études de Gershenson et Langbein (2015) et de Jones et Ezeife (2011). À l’instar de ces travaux, la présente étude s’est appuyée sur des données transversales et n’a pas pris en compte les relations indirectes entre la taille d’école et les performances des élèves. En effet, la relation entre la taille d’école et les performances des élèves est influencée par des variables telles que le statut socioéconomique des élèves et leur année d’études (Bickel, Howley, Williams et Glascock, 2001 ; Jones et Ezeife, 2011).
Le secteur (public ou privé) d’appartenance de l’école n’est pas non plus un bon prédicteur (direct) des performances des élèves. Ce constat est semblable au résultat mis en évidence par les études de Mahuteau et Mavromaras (2014) ainsi que Thomson et ses collègues (2013). Comme ces études, cette recherche n’a pas analysé la relation indirecte entre le secteur de l’école et les performances des élèves. Or, la qualité de l’école ne dépend pas directement du secteur auquel elle appartient (Mahuteau et Mavromaras, 2014). En République démocratique du Congo, les frontières entre les écoles publiques et les écoles privées sont devenues très floues depuis plus de deux décennies. Aussi bien sur le plan du financement, de la qualité des ressources matérielles (infrastructures et équipement) que des ressources humaines (enseignants), les écoles privées ne se démarquent pas des écoles publiques (Mokonzi, 2018). En ce qui concerne la prestation des services, il n’y a pas non plus une grande démarcation entre ces deux catégories d’écoles. Ainsi, contrairement à l’observation faite au Kenya par Rong’uno (2017), l’horaire journalier des écoles privées n’est pas plus important que celui des écoles publiques. L’ampleur de la supervision du travail des enseignants ne diffère pas non plus suivant le secteur auquel appartient l’école.
Par ailleurs, la formation continue des directeurs d’école n’influe pas significativement sur les performances des élèves. Contredisant l’observation relevée dans les études de Pont et ses collaborateurs (2008) et de Walker (1982), ce résultat interroge le contenu des séances de formation dont les directeurs d’école ont bénéficié au cours des cinq années précédant cette recherche. En effet, pour être efficace, la formation continue des directeurs d’école doit être axée sur l’amélioration de la culture et du climat de l’école, sur la gestion du changement et sur l’amélioration de l’apprentissage des élèves (Goddard et al., 2000).
Enfin, des variables de l’école modélisées dans cette étude, seule l’expérience du directeur est positivement associée aux performances des élèves. Ce constat concorde avec celui des études de Clark et ses collègues (2009) et de NASSP et NESP (2013). L’effet de l’expérience n’est pas ainsi fonction du contexte d’un système éducatif. Néanmoins, nous pensons que cette variable joue indirectement sur la réussite des élèves par la médiation d’une politique qui a un impact sur la qualité du processus enseignement-apprentissage (Creemers et Kyriakides, 2010).
Limites
En dépit des analyses effectuées, cette étude comporte quelques limites. La première tient au fait qu’elle n’a pas analysé systématiquement l’effet de composition de la classe par rapport au prétest, de sorte que nous ne savons pas si cet effet opère de manière homogène pour tous les élèves ou de façon plutôt différentielle. Nous ne savons pas non plus par la médiation de quels facteurs cette variable influe sur les performances des élèves.
Le fait de n’avoir pas non plus déterminé les variables de médiation de l’effet de l’expérience du directeur sur les performances des élèves constitue la deuxième limite de cette étude.
La troisième limite de l’étude provient du manque de modélisation de certaines variables de la classe pointées par la littérature comme étant les plus significatives pour la prédiction des performances des élèves. Pour Palardy et Rumberger (2008), ce sont les pratiques enseignantes qui sont le plus associées à ces performances. En plus du genre, cette étude a principalement modélisé la formation continue et l’expérience professionnelle de l’enseignant. Toutefois, ces variables influent indirectement sur l’apprentissage à travers leur association avec les pratiques enseignantes.
La variable relative aux pratiques enseignantes modélisée dans la présente étude, à savoir l’occasion d’apprendre, a uniquement été mesurée sur la base d’une dimension (soit le contenu du programme couvert par le test), sans prendre en compte la durée de l’enseignement et le degré de difficulté de chaque notion enseignée. L’occasion d’apprendre a, d’autre part, été appréhendée au moyen d’un questionnaire soumis aux enseignants. Or, des mesures des pratiques enseignantes issues des questionnaires tendent à être limitées et à ne pas être corrélées avec des mesures plus directes de ces pratiques (Palardy et Rumberger, 2008).
Comme quatrième limite, l’effet de la taille d’école a été étudié seulement en 4e année du primaire. Pourtant, l’impact de cette variable sur les performances des élèves dépend, entre autres, de l’année d’études considérée dans les analyses (Bickel et al., 2001 ; Jones et Ezeife, 2011). En d’autres termes, c’est au moyen des données longitudinales que l’effet de la taille d’école peut être adéquatement mis en évidence.
La taille de l’échantillon d’écoles (n = 49), soit le niveau le plus élevé du modèle exploité dans cette étude, constitue la cinquième limite. En effet, avec l’accroissement de la taille de l’échantillon à chaque niveau du modèle, les paramètres estimés et leurs erreurs types deviennent plus précis. Kreft (1996, cité par Hox, 2010) suggère la règle 30/30, selon laquelle les chercheurs devraient travailler avec un échantillon d’au moins 30 groupes comprenant chacun au moins 30 individus. Ce conseil de Kreft est valable si l’intérêt de la recherche porte sur les paramètres fixes, c’est-à-dire les coefficients de régression. Par contre, si l’intérêt de la recherche porte sur l’interaction entre les niveaux, le nombre de groupes devrait être plus élevé par l’adoption de la règle 50/20, soit au moins 50 groupes composés chacun d’au moins 20 individus. Enfin, si l’intérêt porte plutôt sur la partie aléatoire du modèle (les composantes de variance et de covariance), le nombre de groupes devrait être encore plus important, ce qui conduirait à la règle de 100/10, soit 100 groupes d’au moins 10 individus chacun (Hox, 2010). Puisque nous nous sommes intéressés aussi bien aux effets fixes qu’aux effets aléatoires, nous aurions dû travailler avec au moins 100 écoles pour assurer plus de précision aux analyses effectuées.
Le contrôle du prétest comme variable individuelle pour la détermination de l’effet net de l’école n’est pas adéquat puisque le prétest appréhendé au début de la 4e année est également influencé par l’école au cours des années antérieures. C’est donc dire que, comme sixième limite, cette étude n’a pas estimé de manière optimale l’effet-école.
Enfin, la septième limite de cette étude tient au fait qu’elle n’a pas analysé les relations indirectes et réciproques qu’entretiennent les variables de la classe (notamment la composition de la classe et les caractéristiques de l’enseignant) et de l’école (la composition de l’école, son réseau d’appartenance et les caractéristiques du directeur) avec les performances des élèves.
Conclusion
Le but de cette étude était d’analyser l’effet des classes et des écoles sur les performances en mathématiques d’élèves de 4e année du primaire. L’étude a été basée sur un échantillon de 4777 élèves répartis dans 80 classes et dans 49 écoles des villes de Kisangani et de Bunia en République démocratique du Congo.
L’étude montre que 15,8 % et 13,4 % de la variance des performances des élèves se situent respectivement aux niveaux de la classe et de l’école. En outre, de toutes les variables de la classe et de l’école modélisées dans cette étude, seules la taille de classe, la moyenne de la classe au prétest et l’expérience du directeur d’école se sont avérées de bons prédicteurs des performances des élèves. Contrairement aux deux dernières variables, qui sont positivement associées à la variable dépendante, la taille de classe entretient plutôt une relation négative avec les acquis des élèves.
Étant donné les limites de cette étude, résumées dans la section précédente, il serait intéressant d’analyser aussi bien des relations directes que des relations indirectes entre les prédicteurs et le critère. Il importerait également d’analyser systématiquement l’effet de composition de la classe par rapport au prétest et d’intégrer dans la modélisation des variables qui sont directement associées aux pratiques enseignantes. Il serait par ailleurs important d’approfondir l’analyse de l’effet de l’expérience du directeur d’école en identifiant les variables par la médiation desquelles cette caractéristique a un impact sur les performances des élèves.
Outre ces aspects, les recherches auraient beaucoup à gagner dans l’étude de l’effet des classes et des écoles en recourant à l’analyse multiniveau multivariée, par la prise en compte des composantes du programme sur lesquelles sont axés les tests de mathématiques de 4e année conçus par le Service de planification et d’évaluation en éducation de l’Université de Kisangani, à savoir la numération, les fractions, les opérations et les mesures.
Parties annexes
Annexe
Tableau 9
Quelques caractéristiques statistiques des imputations du prétest
Remerciements
Les auteurs remercient vivement le Conseil interuniversitaire flamand (VLIR-UOS) pour l’appui qu’il apporte au projet Contribution à l’amélioration de l’efficacité des écoles primaires et secondaires de la Province orientale en République démocratique du Congo et pour avoir permis à l’un d’entre eux de séjourner pendant trois mois auprès du Center for Educational Effectiveness and Evaluation de l’Université KU Leuven.
Note
-
[1]
Le swahili et le lingala font partie des langues nationales utilisées comme langues d’enseignement dans les deux premières années de l’école primaire.
Références
- Aaronson, D., Barrow, L., & Sander, W. (2007). Teachers and student achievement in the Chicago public high schools. Journal of Labor Economics, 25, 95-135. doi : 10.1086/508733
- Akerhielm, K. (1995). Does class size matter ? Economics of Education Review, 14(3), 229-241. doi : 10.1016/02727757(95)00004-4
- Allison, P. D. (2002). Missing data. Thousand Oaks, CA : SAGE.
- Alspaugh, J. & Gao, R. (2003). School size in elementary school achievement. Washington, DC : Education Resources Information Center.
- Angrist, J. D. & Lavy, V. (1999). Using Maimonides’ rule to estimate the effect of class size on scholastic achievement. The Quarterly Journal of Economics, 114(2), 533-575. doi : 10.1162/003355399556061
- Balta, N., Arslan, M., & Duru, H. (2015). The effect of in-service training courses on teacher achievement : A meta-analysis study. Journal of Education and Training Studies, 3(5), 254-263. doi : 10.11114/jets.v3i5.1037
- Banque mondiale. (2005). Le système éducatif de la République démocratique du Congo : priorités et alternatives. New York, NY : Banque mondiale.
- Bellin, N., Dunge, O., & Gunzenhauser, C. (2006). The importance of class composition for reading achievement : Migration background, social composition, and instructional practices. An analysis of the German 2006 PIRLS data. Retrieved from www.ierinstitute.org/fileadmin/Documents/IERI_Monograph/IERI_Monograph_Volume_03_Chapter_1.pdf
- Betts, J. R., Zau, A. C., & Rice, L. A. (2003). Determinants of student achievement : New evidence from San Diego. San Francisco, CA : Public Policy Institute of California.
- Bianco, M. et Bressoux, P. (2009). Effet-classe et effet-maître dans l’enseignement primaire : vers un enseignement efficace de la compréhension ? Dans X. Dumay et V. Dupriez (dir.), L’efficacité dans l’enseignement : promesses et zones d’ombre (pp. 35-54). Bruxelles : De Boeck.
- Bickel, R., Howley, C., Williams, T., & Glascock, C. (2001). High school size, achievement equity, and cost : Robust interaction effects and tentative results. Education Policy Analysis Archives, 9(40), 1-32.
- Boonen, T., Speybroeck, S., de Bilde, J., Lamote, C., Van Damme, J., & Onghena, P. (2014). Does it matter who your schoolmates are ? An investigation of the association between school composition, school processes and mathematics achievement in the early years of primary education. British Educational Research Journal, 40(3), 441-466. doi : 10.1002/berj.3090
- Bressoux, P. (1994). Les recherches sur les effets-écoles et les effets-maîtres. Revue française de pédagogie, 108, 91-137.
- Bressoux, P. (1995). Les effets du contexte scolaire sur les acquisitions des élèves : effet-école et effets-classes en lecture. Revue française de sociologie, 36(2), 273-294. doi : 10.2307/3322249
- Bressoux, P. (2010). Modélisation statistique appliquée aux sciences sociales. Bruxelles : De Boeck.
- Bressoux, P. (2012). L’influence des pratiques enseignantes sur les acquisitions scolaires des élèves. Regards croisés sur l’économie, 2(12), 208-217. doi : 10.3917/rce.012.0208
- Cannon, S., Figlio, D., & Sass, T. (2013). Principal quality and persistance of school policies. Unpublished document.
- Carnoy, M. & Arends, F. (2012). Explaining mathematics achievement gains in Botswana and South Africa. Prospects, 42(4), 453-468. doi : 10.1007/s11125-012-9246-6
- Clark, D., Martorell, P., & Rockoff, J. (2009). School principals and school performance. Working paper No. 38. Washington, DC : Calder.
- Clotfelter, C. T., Ladd, H. F., & Vigdor, J. L. (2007). How and why do teacher credentials matter for student achievement ? Working paper No. 12828. New York, NY : National Bureau of Economic Research. Retrieved from www.nber.org/papers/w12828
- Cobbold, T. (2015). A review of academic studies of public and private school outcomes in Australia. Australia : Save our Schools.
- Coleman, J. S., Campbell, E. Q, Hobson, C. F, McPartland, J., Mood, A. M, Weinfeld, F. D., & York, R. L. (1966). Equality of educational opportunity. Washington, DC : U.S. Government Printing Office.
- Creemers, B. P. M. (1994). The effective classroom. London : Cassell.
- Creemers, B. P. M. & Kyriakides, L. (2008). The dynamics of educational effectiveness : A contribution to policy, practice and theory in contemporary schools. New York, NY : Routledge.
- Creemers, B. P. M. & Kyriakides, L. (2010). Using the dynamic model to develop an evidence-based and theory-driven approach to school improvement. Irish Educational Studies, 29(1), 5-22. doi : 10.1080/03323310903522669
- Danhier, J. & Martin, E. (2014). Comparing composition effects in two educational systems : The case of the Belgian communities. British Journal of Educational Studies, 62(2), 171-188. doi : 10.1080/00071005.2014.930091
- De Fraine, B., Van Damme, J., Van Landeghem, G., Opdenakker, M.-C., & Onghena, P. (2003). The effect of schools and classes on language achievement. British Educational Research Journal, 29(6), 841-859. doi : 10.1080/0141192032000137330
- De Herdt, T., Marivoet, W. et Muhigirwa, F. (2015). Analyse de la situation des enfants et des femmes en République démocratique du Congo : vers la réalisation du droit à une éducation de qualité pour tous. Rapport final. Kinshasa, RDC : UNICEF.
- Díez-Palomar, J., Simic, K., & Varley, M. (2006). Math is everywhere : Connecting mathematics to students’ lives. Journal of Mathematics and Culture, 1(2), 20-36.
- Djibo, F. et Gauthier, C. (2017). L’efficacité de la formation continue des enseignants du primaire : le cas du Burkina Faso. Formation et profession, 25(2), 35-47. doi : 10318162/fp.2017.330
- Dumay, X. & Dupriez, V. (2008). Does the school composition effect matter ? Evidence from Belgian data. British Journal of Educational Studies, 56(4), 440-477. doi : 10.1111/j.1467-8527.2008.00418.x
- Dupriez, V. (2010). Séparer pour réussir ? Les modalités de groupement des élèves. Paris : UNESCO-IIPE.
- Duru-Bellat, M. (2001). Effets maîtres, effets établissements : quelle responsabilité pour l’école ? Revue suisse des sciences de l’éducation, 23(2), 321-335.
- Edmonds, R. R. (1979). A discussion of the literature and issues related to effective schooling. Cambridge, MA : Center of Urban Studies, Harvard Graduate School of Education.
- Egalite, A. J. & Kisida, B. (2016). School size and student achievement : A longitudinal analysis. School Effectiveness and School Improvement, 27(3), 406-417. doi : 10.1080/09243453.2016.1190385
- Frenette, M. & Chan, P. W. C. (2015). Academic outcomes of public and private high school students : What lies behind the differences ? Catalogue No. 11F0019M. Ottawa : Statistics Canada.
- Gershenson, S. & Langbein, L. (2015). The effect of primary school size on academic achievement. Educational Evaluation and Policy Analysis, 37(1S), 135S-155S. doi : 10.3102/0162373715576075
- Glass, G. V. & Smith, M. L. (1979). Meta-analysis of research on class size and achievement. Educational Evaluation and Policy Analysis, 1(1). 2-16. doi : 10.3102/01623737001001002
- Goddard, R. D., Hoy, W. K., & Hoy, A. W. (2000). Collective teacher efficacy : Its meaning, measure, and impact on student achievement. American Educational Research Journal, 37(2), 479-507. doi : 10.3102/0002831037002479
- Goldstein, H., Yang, M., Omar, R., Turner, R., & Thompson, S. (2000). Meta-analysis using multilevel models with an application to the study of class size. Applied Statistics, 49, 399-412. doi : 10.1111/1467-9876.00200
- Graham, J. W. (2009). Missing data analysis : Making it work in the real world. Annual Rewiew of Psychology, 60, 549-576. doi : 10.1146/annurev.psych.58.110405.085530
- Graham, J. W, Olchowski, A. E., & Gilreath, T. D. (2007). How many imputations are really needed ? Some practical clarifications of multiple imputation theory. Prevention Science, 8, 206-213. doi : 10.1007/s11121-007-0070-9
- Greenwald, R., Hedges, L. V., & Laine, R. D. (1996). The effect of school resources on student achievement. Review of Educational Research, 66(3), 361-396. doi : 10.2307/1170528
- Gustafsson, J. E. (2010). Longitudinal designs. In B. P. R. Creemers, L. Kyriakides & P. Sammons (Eds.), Methodological advances in educational effectiveness research (pp. 77-101). London/New York : Routledge.
- Hahn, S., Kim, T. H., & Seo, B. (2014). Effects of public and private schools on academic achievement. Seoul Journal of Economics, 27(2), 137-147.
- Hanushek, E. A. (1997). Assessing the effect of school resources on student performance : An update. Journal of Economics Literature, 19(2), 141-164. doi : 10.3102/01623737019002141
- Hanushek, E. A. (2003). The failure of input-based schooling policies. The Economic Journal, 113, F64-F98. doi : 10.1111/1468-0297.00099
- Harris, D. N. & Sass, T. R. (2007). Teacher training, teacher quality, and student achievement. Working paper No. 3. Washington, DC : Calder.
- Honaker, J., King, G., & Blackwell, M. (2011). Amelia II : A program for missing data. Journal of Statistical Software, 45(7), 1-47. doi : 10.18637/jss.v045.i07
- Horng, E. I., Klasik, D., & Loeb, S. (2009). Principals’ time-use and school effectiveness : School leadership research report. Stanford, CA : Institute for Research on Education Policy and Practice.
- Hox, J. (2010). Multilevel analysis : Techniques and applications. New York, NY : Routledge.
- Hoya, A. W. & Spero, R. B. (2005). Changes in teacher efficacy during the early years of teaching : A comparison of four measures. Teaching and Teacher Education, 21, 343-356. doi : 10.1016/j.tate.2005.01.007
- Ingersoll, R. M. & Strong, M. (2011). The impact of induction and monitoring for beginning teachers : A critical review of the research. Review of Educational Research, 8(2), 201-233. doi : 10.3102/0034654311403323
- Jacob, B. A. & Lefgren, L. (2004). The impact of teacher training on student achievement : Quasi-experimental evidence from school reform efforts in Chicago. The Journal of Human Resources, 39(1), 50-79. doi : 10.3386/w8916
- Jones, K. R. & Ezeife, A. N. (2011). School size as a factor in the academic achievement of elementary school students. Psychology, 2(8), 859-868. doi : 10.4236 :psych.2011.28131
- Kamba, A. (2018). Efficacité différenciée des écoles publiques et privées : situation des écoles primaires au Congo-Kinshasa. Sarrebruck, Allemagne : Éditions universitaires européennes.
- Kane, T. J., Rockoff, J. E., & Staiger, D. O. (2006). What does certification tell us about teacher effectiveness ? Evidence from New York City. Working paper No. 12155. Cambridge, MA : National Bureau of Economic Research.
- Kiwanuka, H. N., Van Damme, J., Van den Noortgate, W., Anumenden, D. N., & Namusi, S. (2015). Factors affecting mathematics achievement of first-year secondary school students in Central Uganda. South African Journal of Education, 35(3), 1-16. doi : 10.15700/saje.v35n3a1106
- Lamain, M., Scheerens, J., & Noort, P. (2017). Review and vote count analysis of OTL-effect studies. In J. Scheerens (Ed.), Opportunity to learn, instructional alignment and test preparation : A research review (pp. 61-95). Cham, Switzerland : Springer. doi : 10.1007/978-3-319-43110-9
- Lauwerier, T. et Akkari, A. (2015). Les enseignants et la qualité de l’éducation de base en Afrique subsaharienne. Paris : UNESCO.
- Lee, V. E., Dedrick, R. F., & Smith, J. B. (1991). The effect of the social organization of schools on teachers’ efficacy and satisfaction. Sociology of Education, 64, 190-208. doi : 10.2307/2112851
- Lee, V. E., Smith, J. B., & Croninger, R. G. (1997). How high school organization influences the equitable distribution of learning in mathematics and science. Sociology of Education, 70(2), 128-150. doi : 10.2307/2673160
- Mahuteau, S. & Mavromaras, K. (2014). Student scores in public and private schools : Evidence from PISA 2009. Working paper No. 8471. Bonn, Germany : Institute for the Study of Labor.
- Mary, C., Squalli, H., Theis, L. et Deblois, L. (2014). Recherches sur les difficultés d’enseignement et d’apprentissage des mathématiques : regard didactique. Québec, QC : Presses de l’Université du Québec.
- Marzano, R. J. (2000). A new era of school reform : Going where the research takes us. Aurora, CO : McREL Research for Education and Learning.
- Mokonzi, G. B. (2010). Diagnostic et perspectives de l’éducation pour tous en République démocratique du Congo. Repéré à http://fseg2.univ-tlemcen.dz/rev%2010%20en%20pdf/GRATIEN%20MOKONZI%20BAMBANOTA.pdf
- Mokonzi, G. B. (2018). Privatisation de l’éducation en République démocratique du Congo : cas de la ville de Kinshasa. Kinshasa, RDC : OSISA.
- Mosvold, R. (2005). Mathematics in everyday life : A study of beliefs and actions (Doctoral thesis, University of Bergen, Bergen, Norway). Retrieved from http://bora.uib.no/bitstream/handle/1956/1153/Thesis.pdf
- Nandwa, O. M., Wasi, D. W., & Wanjala, T. W. (2015). Influence of instructional practices on secondary school students’ achievement in mathematics. Journal of Education and Practice, 6(26), 28-36.
- Naoreen, B., Aslam, S., Arshad, M., & Nausheen, R. (2011, February). Impact of in-service teacher training on students’ learning achievement in mathematics. Paper presented at the International Conference on Social Science and Humanity, Singapore. Retrieved from https://pdfs.semanticscholar.org/6bac/fddba3cd16f6ae0311c3bbe4cc347a0ca030.pdf
- National Association of Secondary School Principals (NASSP) & National Association of Elementary School Principals (NAESP). (2013). Leadership matters : What the research says about the importance of principal leadership. Reston/Alexandria, VA : NASSP/NAESP. Retrieved from www.naesp.org/sites/default/files/LeadershipMatters.pdf
- Nye, B., Hedges L. V., & Konstantopoulos, S. (2000). The effects of small classes on academic achievement : The results of the Tennessee class size experiment. American Educational Research Journal, 37(3), 123-152. doi : 10.2307/1163474
- Opdenakker, M.-C. & Van Damme, J. (2001). Relationship between school composition and characteristics of school process and their effect on mathematics achievement. British Educational Research Journal, 27(4), 407-432. doi : 10.1080/01411920120071434
- Opdenakker, M.-C. & Van Damme, J. (2004). Are equal opportunities in our classes and schools ? An investigation of the relationship between class composition, indicators of the learning environment and class climate, effort, and mathematics achievement of classes. Unpublished manuscript. Leuven, Belgium : Center for Educational Effectiveness and Evaluation.
- Opdenakker, M.-C. et Van Damme, J. (2009). L’efficacité des classes dans l’enseignement secondaire. Dans X. Dumay et V. Dupriez (dir.), L’efficacité dans l’enseignement : promesses et zones d’ombre (pp. 55-72). Bruxelles : De Boeck.
- Palardy, G. & Rumberger, R. W. (2008). Teacher effectiveness in first grade : The importance of background qualifications, attitudes and practices for student learning. Educational Evaluation and Policy Analysis, 30(2), 111-140. doi : 10.3102/0162373708317680
- Pong, S. & Pallas, A. (1999). The impact of class size on eighth-grade math achievement. Working paper No. 99-11. Front Royal, VA : Population Research Institute.
- Pont, B., Nusche, D., & Moorman, H. (2008). Improving school leadership : Policy and practice (vol. 1). Paris : OECD. Retrieved from www.oecd.org/education/school/44374889.pdf
- Programme d’analyse des systèmes éducatifs de la CONFEMEN (PASEC). (2011). L’enseignement primaire en République démocratique du Congo : quels leviers pour l’amélioration du rendement du système éducatif ? Dakar, Sénégal : CONFEMEN.
- Rasbash, J., Charlton, C., Browne, W. J., Hearly, M., & Cameron, B. (2011). MLwiN (version 2.24) [Computer software]. Bristol, UK : Center for Multilevel Modelling.
- Raudenbush, S. W., Rowan, B., & Cheong, Y. F. (1992). Contextual effects on the self-perceived efficacy of high school teachers. Sociology of Education, 65(2), 150-167. doi : 10.2307/2112680
- Reynolds, D., Sammons, P., De Fraine, B., Townsend, T., & Van Damme, J. (2011, January). Educational effectiveness research (EER) : A state of the art review. Paper presented at the annual meeting of the 24th International Congress for School Effectiveness and School Improvement, Limassol, Cyprus. doi : 10.1080/09243453.2014.885450
- Rice, J. F. (2010). The impact of teacher experience : Examining the evidence and policy implications. Washington, DC : National Center for Analysis of Longitudinal Data in Education Research.
- Rong’uno, S. K. (2017). A comparison of academic performance between public and private secondary schools in Wareng district, Kenya. British Journal of Education, 5(11), 58-67.
- Rowan, B., Raudenbush, S. W., & Kang, S. J. (1991). Organizational design in high schools : A multilevel analysis. American Journal of Education, 99(2), 238-266.
- Salout, S. S., Behzadi, M. H., Shahvarani, A., & Manuchehri, M. (2013). Students’ conception about the relation of mathematics to real life. Mathematics Education Trends and Research, 1-7. doi : 10.5899/2013/metr-00009
- Scheerens, J. (2017). Opportunity to learn, instructional alignment and test preparation : A research review. Cham, Switzerland : Springer. doi : 10.1007.9787-3-319-43110-9
- Scheerens, J. & Bosker, R. J. (1997). The foundations of educational effectiveness. Oxford, UK : Pergamon.
- Schmidt, W. H. (2009). Exploring the relationship between content coverage and achievement : Unpacking meaning of tracking in eighth grade mathematics. Lansing, MI : Education Policy Center at Michigan State University.
- Tabachnick, B. G. & Fidell, L. S. (2007). Using multivariate statistics (5th ed.). Boston, MA : Pearson Education.
- Talbot, L. (2012). Les recherches sur les pratiques enseignantes efficaces : synthèse, limites et perspectives. Questions vives, 6(18), 129-140. doi : 10.4000/questionsvives.1234
- Teddlie, C. & Reynolds, D. (2000). The international handbook of school effectiveness research. London/New York : Falmer Press.
- Thomson, S., De Bortoli, L., & Buckley, S. (2013). PISA 2012 : How Australia measures up. Camberwell, Australia : Australian Council for Educational Research.
- Thuku, F. W. & Hungi, N. (2013). Explaining differences in mathematics and reading achievement among standard 6 pupils in Kenya : Emerging policy issues. Paper presented at the Conférence internationale sur la recherche des politiques éducatives, Paris, France. Retrieved from www.sacmeq.org/sites/default/files/sacmeq/research/Papers%20from%20the%202005%20International%20Invitational%20Educational%20Policy%20Research%20Conference/thuku.pdf
- Thum, Y. M. (2000). Measuring progress toward a goal : Estimating teacher productivity using a multivariate multilevel model for value-added analysis. Sociological Methods & Research, 32(2), 153-207. doi : 10.1177/0049124103257073
- Tomarken, A. J. & Waller, N. G. (2005). Structural equation modeling : Strengths, limitations, and misconceptions. Annual Review of Clinical Psychology, 1, 31-65. doi : 10.1146/annurev.clinpsy.1.102803.144239
- UNESCO et IIPE Pôle de Dakar (2014). République démocratique du Congo : rapport d’état du système éducatif. Pour une éducation au service de la croissance et de la paix. Dakar, Sénégal : UNICEF/UNESCO/IIPE Pôle de Dakar. Repéré à https://unesdoc.unesco.org/ark:/48223/pf0000232623
- Van Damme, J., Opdenakker, M.-C., Van Landeghem, G., De Fraine, B., Pustjens, H. et Van de Gaer, E. (2009). Fondements et principaux résultats de recherche sur l’efficacité dans l’enseignement. Dans X. Dumay et V. Dupriez (dir.), L’efficacité dans l’enseignement : promesses et zones d’ombre (pp. 19-34). Bruxelles : De Boeck.
- Walker, R. S. (1982). Effects of principal inservice training on teacher classroom behaviors and student academic motivation. Retrospective Theses and Dissertations. Ames, IO : Iowa State University. Retrieved from https://pdfs.semanticscholar.org/e5a4/563678f8e9e74f24dc2a78b88d95b74c20a1.pdf?_ga=2.182991590.1770728722.1580321909-62462466.1578169433
- Wendling, W. & Cohen, J. (1981). Education resources and student achievement : Good news for schools. Journal of Education Finance, 7(1), 44-63.
- Witziers, B., Bosker, R. J., & Kruger, M. L. (2003). Educational leadership and student achievement : The elusive search for an association. Educational Administration Quarterly, 39(3), 398-425. doi : 10.1177/0013161X03253411
Liste des figures
Figure 1
Modèle conceptuel général multiniveau pour l’étude d’effet-école
Figure 2
Distribution des résidus de niveau 1 (élève)
Figure 3
Distribution des résidus de niveau 2 (classe)
Figure 4
Distribution des résidus de niveau 3 (école)
Figure 5
Composantes de variance pour le modèle vide
Figure 6
Variance expliquée par les caractéristiques de l’élève
Figure 7
Variance expliquée par les caractéristiques de l’élève et de la classe
Figure 8
Variance expliquée par les caractéristiques de l’élève, de la classe et de l’école
Liste des tableaux
Tableau 1
Échantillon de l’étude
Tableau 2
Modèle vide
Tableau 3
Corrélations, moyennes et déviation standard pour les prédicteurs du niveau élève (N = 4777)
Tableau 4
Effet des variables individuelles
Tableau 5
Corrélations, moyennes et déviation standard pour les prédicteurs du niveau classe (N = 80)
Tableau 6
Effet des variables de la classe
Tableau 7
Corrélations, moyennes et déviation standard pour les prédicteurs du niveau école (N = 49)
Tableau 8
Effet des variables de l’école
Tableau 9
Quelques caractéristiques statistiques des imputations du prétest