La mobilité de la charge de fond des rivières torrentielles méditerranéennes

Liébault, Frédéric; Clément, Pierre

doi:https://doi.org/10.7202/029567ar

Introduction

La mobilité de la charge de fond des rivières graveleuses est un phénomène physique complexe, difficile à mesurer en conditions naturelles, d’une part parce que les lits fluviaux ne sont pas accessibles en période de crue et d’autre part, du fait de la forte variabilité spatio-temporelle du phénomène (Hoey, 1992 ; Powell et Ashworth, 1995). Celle-ci s’explique par la complexité des contraintes hydrauliques et de l’organisation spatiale des forces de résistance à l’entraînement, le fond granulaire étant caractérisé par une distribution granulométrique et des structures sédimentaires hétérogènes. Les observations de terrain sont donc peu nombreuses malgré leur caractère indispensable pour la validation des approches mécanistes théoriques, souvent calibrées avec des données obtenues en chenal artificiel et dont la transposition en conditions naturelles est souvent malaisée. Ceci est particulièrement vrai sur les petites rivières torrentielles à forte pente, où les incertitudes des formules de transport solide sont les plus grandes (Rickenmann, 2001). Une attention particulière doit être notamment portée sur les seuils de mise en mouvement et les distances de transport des particules, dont les applications en termes de connaissance de la dynamique sédimentaire et morphologique des lits fluviaux sont multiples.

L’étude des seuils de mise en mouvement permet d’appréhender la mobilité du substrat et la capacité de transport du cours d’eau sous certaines contraintes hydrauliques. Le problème se pose en termes de prédiction des forces nécessaires à l’entraînement des grains. L’application des formulations physiques de ces seuils reste délicate compte tenu de la diversité des approches de détermination et de la variabilité naturelle des paramètres qui permettent de les apprécier (le transport solide, la géométrie du lit et la granulométrie du substrat). La compilation synthétique des données de force tractrice critique adimensionnelle (t*_c), ou paramètre de Shields, critère communément employé pour déterminer les conditions critiques de mobilisation, montre des valeurs comprises entre 0,030 et 0,086 pour les rivières graveleuses (Buffington et Montgomery, 1997). Ceci souligne l’absence de valeur unique pour les écoulements turbulents, contrairement à ce que montre la courbe de Shields avec une valeur constante de 0,06 pour ce type d’écoulement, ce qui complique l’usage de t*_c dans les études de transport solide. Les observations de terrain sur la mobilité de la charge de fond sont ainsi primordiales pour obtenir des référentiels de t*_c et faciliter l’usage du concept de force tractrice critique. D’autres grandeurs peuvent également être employées pour caractériser les seuils de mise en mouvement : ce sont les débits et les puissances hydrauliques critiques (Ferguson, 1994 ; Petit et al., 2005). Leur détermination est très utile lorsque des mesures de débit sont disponibles. En revanche, sur les cours d’eau non jaugés, l’utilisation de la force tractrice pose moins de problèmes, un simple dispositif d’enregistrement des hauteurs d’eau permettant d’obtenir les variables hydrauliques de calcul (la pente de la ligne d’eau et le rayon hydraulique). Les seuils d’entraînement fondés sur les débits offrent l’avantage de pouvoir calculer la fréquence du charriage, à conditions de disposer de longues chroniques hydrologiques.

Une fois mises en mouvement, les particules vont se déplacer et parcourir une certaine distance, si bien que le charriage peut être formalisé comme un ensemble de déplacements granulaires par saltation et roulage sur le fond. La vitesse virtuelle de ces déplacements, définie comme le rapport de la distance totale de transport sur la durée du transport solide, peut être utilisée pour calculer le flux solide grossier (Hubbell et Sayre, 1964 ; Wilcock, 1997 ; Haschenburger et Church, 1998). D’autres auteurs proposent d’intégrer ces vitesses dans le temps et de déterminer ainsi le charriage événementiel total à partir des distances moyennes de transport (Laronne et al., 1992). Les distances de transport sont également utilisées pour la modélisation stochastique du routage des sédiments dans les bassins-versants (Benda et Dunne, 1997), l’interprétation des séquences de formes élémentaires de type pool-bar (Pyrce et Ashmore, 2003), très fréquentes dans les rivières graveleuses.

Un programme de suivi de la mobilité de la charge de fond a été mis en place entre 1997 et 2002 sur trois affluents torrentiels de la Drôme (Préalpes françaises du Sud), rivière de piémont fortement incisée (Landon et al., 1998), de façon à caractériser et à comparer la dynamique sédimentaire des têtes de bassin. Ces travaux s’inscrivent dans une démarche globale d’analyse de la recharge sédimentaire de la Drôme, dont les stocks sédimentaires s’épuisent sous l’effet cumulé du tarissement des entrées et des extractions de graviers conduites jusqu’au début des années 1990 (Liébault et al., 1999). L’objectif poursuivi dans cet article est de déterminer à partir de techniques simples et peu onéreuses la fréquence du charriage, les seuils de mise en mouvement et les distances de transport des sédiments grossiers d’affluents torrentiels caractérisés par la présence de stocks de graviers actifs bien préservés.

Sites d’étude

Les torrents de la Barnavette, de la Béoux et de l’Esconavette sont des affluents de rive gauche de la Drôme de taille représentative (tabl. I). Ils s’inscrivent dans une configuration morphostructurale identique : des reculées qui entaillent le flanc occidental de la combe anticlinale de Die, vaste dépression méridienne creusée dans des alternances de marnes, de calcaires marneux et de marno-calcaires du jurassique (fig. 1). Les sédiments grossiers sont produits essentiellement dans les dérochoirs (fig. 1), terme local qui désigne de grands amphithéâtres d’érosion associant du ravinement et des glissements de terrain sur les pentes basses et intermédiaires, sculptées dans des marno-calcaires, et des chutes de blocs dans les abrupts calcaires sommitaux. Les matériaux grossiers sont transmis vers l’aval via des chenaux torrentiels à forte pente (>20 %) où des dépôts de laves torrentielles sont observés. Les pluviographes installés dans les bassins de réception des trois torrents en décembre 1999 donnent des précipitations annuelles moyennes comprises entre 765 et 870 mm. Ces pluies se concentrent en automne et au printemps ; les saisons d’été et d’hiver sont moins arrosées. Les crues peuvent se produire à n’importe quelle période de l’année, bien qu’elles soient plus fréquentes en automne et au printemps. Les régimes hydrologiques sont de type méditerranéen de montagne. De violents orages surviennent parfois en été et peuvent être à l’origine de crues brutales. Il n’est pas rare d’observer une interruption de l’écoulement en été, notamment sur la Barnavette et l’Esconavette, dont les bassins sont de taille plus modeste. Ces cours d’eau ne disposent pas de stations de jaugeage permanentes. Les débits de la crue de fréquence 1,5 ans ont été estimés au moyen d’une analyse statistique régionale fondée sur les surfaces drainées (Liébault, 2003). Les valeurs obtenues sont de 2,0 m³/s pour la Barnavette, 3,7 m³/s pour la Béoux et 1,4 m³/s pour l’Esconavette.

Figure 1

Les bassins-versants de la Barnavette, de la Béoux et de l’Esconavette.

Drainage basins of the Barnavette, Béoux and Esconavette.

-> Voir la liste des figures

Un tronçon d’étude a été délimité sur chaque cours d’eau, en prenant comme zone de départ un stock alluvial actif remarquable (zone de formation d’atterrissements alluvionnaires majeurs) et comme terminaison aval l’exutoire du bassin. Un dispositif de suivi de la mobilité de la charge de fond a été installé au droit de chaque zone de départ ; les tronçons d’étude correspondent au linéaire de diffusion potentielle des matériaux mobilisés dans la zone de départ et sont de nature exclusivement alluviale (aucun affleurement rocheux n’est observé). Sur l’Esconavette, la zone de départ se situe à 270 m en amont de la confluence avec la Drôme. Le lit présente ici un style divagant (wandering pattern), avec un chenal principal qui sinue entre de grands bancs alternes (fig. 2A). Des accumulations de bois morts se forment par endroits, sur les bancs exondés. Ce type morphologique est observé sur l’ensemble du tronçon d’étude. La zone de départ de la Barnavette est localisée à 1 250 m de l’exutoire. Il s’agit d’un grand banc médian au droit d’une sinuosité (fig. 2B). Le tronçon d’étude présente un style morphologique à fond grossier de type plane bed (Montgomery et Buffington, 1997), ponctuellement interrompu par de courts tronçons à bancs exondés qui s’observent généralement dans les courbes. Sur la Béoux, la zone de départ située à 500 m de l’exutoire présente un style divagant avec des bancs de convexité bien développés (fig. 2C). Le tronçon d’étude montre une alternance de segments rectilignes à fond grossier de type plane bed et de segments élargis à bancs exondés.

Figure 2

Les sites équipés pour le suivi de la mobilité de la charge de fond (zones de départ).

Bedload mobility monitoring sites (sediment departure zones).

-> Voir la liste des figures

Matériel et méthodes

Suivi de la mobilité de la charge de fond

La mobilité de la charge de fond des zones de départ a été étudiée entre 1997 et 2002 au moyen d’un suivi topographique du lit sur des profils en travers bornés, d’une série de chaînes d’érosion installées à intervalles réguliers au droit des profils en travers et d’un traçage peinture des particules exposées sur les bancs de graviers.

Le suivi topographique des profils en travers a été effectué systématiquement après chaque crue mobilisatrice, de façon à caractériser la mobilité du lit sur une base événementielle. Une crue mobilisatrice a été définie comme un événement qui mobilise partiellement ou totalement les parcelles peintes (surface : 1 m²) situées sur les surfaces exondées en basses eaux. Plutôt que de définir la mobilisation sur la base d’une fraction granulométrique transportée, nous avons préféré le critère de mobilisation des bancs, plus facile à caractériser et plus significatif en termes de transport solide. La fréquence des crues survenues pendant la période de suivi n’a pu être déterminée selon les approches probabilistes classiques, car les rivières étudiées ne disposent pas de stations de jaugeage. La mesure altitudinale a été effectuée par nivellement (niveau Wild Heerbrugg NA20 et mire graduée). Les lectures de cotes ont été faites au demi centimètre. Les distances ont été mesurées avec un ruban d’arpentage gradué tous les centimètres, fixé sur les bornes permanentes des profils en travers. L’intervalle moyen entre les points de mesure positionnés dans la bande active est compris entre 0,41 et 0,54 m pour les différents sites. Le seuil de détection du changement altitudinal après une crue peut être considéré comme équivalent au D₉₀ de surface. Ce dernier donne une approximation de la rugosité maximale du fond dont les valeurs mesurées sur les trois sites d’étude sont comprises entre 40 et 100 mm (tabl. I).

La technique des chaînes d’érosion est utilisée en complément du suivi topographique, incapable de détecter une mise en mouvement lorsque les creusements et les dépôts se compensent lors d’un événement. Les chaînes permettent d’enregistrer ces fluctuations altitudinales et de diagnostiquer avec certitude une mobilisation des sédiments. Si le fond est mobilisé, la chaîne forme un coude qui permet de mesurer l’épaisseur des tranches érodées et déposées (Leopold et al., 1966 ; Laronne et al., 1994). La longueur de chaîne insérée verticalement dans le fond du lit a été fixée à 1 m. Nous avons utilisé des chaînes en acier galvanisé dont le diamètre de maille est équivalent au D₅₀ de surface (20 mm). La technique d’insertion, fondée sur l’utilisation d’une barre d’insertion amovible, présente l’avantage de ne pas perturber la structure sédimentaire lors de l’installation (Liébault et Laronne, 2008). Nous avons installé 20 chaînes au total sur quatre profils en travers (fig. 3) ; sept chaînes ont été installées sur le profil de l’Esconavette, dont la largeur du fond de lit (w_f) est de 18,6 m, cinq sur le profil de la Barnavette (w_f = 12,5 m) et huit sur les deux profils de la Béoux (w_f = 12,4 et 16,2 m). L’intervalle moyen entre les chaînes est de 3 m. Leur disposition spatiale permet de bien caractériser la mise en mouvement des bancs exondés (fig. 3).

La mesure des distances de transport a été réalisée à partir des parcelles peintes de 1 m² positionnées sur les bancs dans les zones de départ. Les relevés post-crues consistent à parcourir le tronçon situé en aval de la zone de départ et à mesurer le diamètre selon l’axe B et la distance parcourue pour chaque particule peinte retrouvée. Les parcelles ont été repeintes après chaque crue mobilisatrice en utilisant une couleur différente afin d’éviter les confusions entre les événements. Cette technique permet d’attribuer une distance moyenne de transport pour chaque événement. Le traçage peinture a été préféré au traçage magnétique ou radio pour différentes raisons. Les techniques de traçage actif présentent l’avantage de détecter les particules enterrées, ce qui augmente significativement le pourcentage de traceurs retrouvés (Hassan et Ergenzinger, 2003). Néanmoins, ces techniques ne permettent pas de suivre les particules dont le diamètre est trop petit pour permettre l’insertion d’un aimant ou d’un radio émetteur. Elles risquent donc de sous-estimer les distances moyennes de transport. Elles présentent aussi l’inconvénient de perturber les structures sédimentaires puisque les particules doivent être prélevées, perforées et repositionnées dans le lit. Il faut enfin souligner que ces approches impliquent des opérations post-crues qui sont longues et fastidieuses, nécessitant l’utilisation d’un détecteur magnétique ou d’une antenne radio pour localiser chaque particule. Compte tenu du caractère événementiel des mesures et du fait que les crues se produisent souvent à des intervalles de temps rapprochés, il était impératif de privilégier une approche facile à mettre en oeuvre et permettant des relevés rapides. L’utilisation de la peinture répondait mieux à ces objectifs.

Suivi hydrométrique et calculs hydrauliques

Nous avons installé des dispositifs hydrométriques identiques sur chacun des trois torrents. Ils ont été positionnés à proximité des zones de départ, sur des tronçons stables, rectilignes et homogènes, où les conditions d’écoulement sont proches de l’uniformité. Ces dispositifs se composent d’une échelle à maximum constituée d’un ruban adhésif coloré qui devient translucide au contact de l’eau. Ce système permet d’enregistrer la hauteur d’eau maximale atteinte durant un épisode de crue. Des mesures de vitesse d’écoulement en surface ont également été effectuées pour quelques crues afin d’estimer les débits. Ces mesures ont été réalisées à l’aide de flotteurs sur de longues distances (30 m) et elles ont été répétées cinq fois afin d’obtenir une moyenne. La marge d’erreur calculée d’après l’écart type est comprise entre 2 et 15 %.

Ce dispositif rudimentaire a permis d’estimer les contraintes hydrauliques des crues pour la caractérisation des seuils de mise en mouvement. Les forces tractrices critiques ont été calculées d’après la formule :

avec τ, la force tractrice en N/m², ρ, la masse volumique du fluide (1 000 kg/m³), g, l’accélération de la gravité (9,81 m/s²), R, le rayon hydraulique en m et s, la pente de la ligne d’énergie en m/m. Le rayon hydraulique de chaque événement a été calculé à partir de la géométrie hydraulique du pic de crue, fondée sur la topographie de la section issue de l’événement antérieur et de la hauteur d’eau enregistrée par l’échelle à maximum. Nous faisons l’hypothèse que le régime hydraulique est proche des conditions permanentes et uniformes, la géométrie transversale des tronçons étant homogène, ce qui nous permet d’approximer la pente de la ligne d’énergie à partir de la pente du lit. Cette procédure nous donne une approximation de la force tractrice moyenne sur la section pour chaque crue. Les forces tractrices critiques adimensionnelles ont été calculées à partir du D₅₀ des sites, à l’aide de la formule de Shields :

avec τ*_c, le critère adimensionnel de Shields, τ_c, la force tractrice critique en N/m², D, le diamètre de la particule considérée en m (ici le D₅₀) et ρ_s, la masse volumique du sédiment (estimée à 2 650 kg/m³). Le D₅₀ a été obtenu à partir d’un échantillonnage aléatoire de surface (Wolman, 1954) effectué sur une centaine de particules prélevées sur les bancs.

Les débits de pointe ont été estimés de manière indirecte à partir de la formule de Manning-Strickler (Benson et Dalrymple, 1967). Les coefficients de rugosité ont été déterminés à partir des mesures de vitesse d’écoulement en surface. Les reconstitutions indirectes des débits critiques de mise en mouvement ont été comparées avec les valeurs calculées à partir des deux formules les plus communément utilisées. Il s’agit de la formule de Schoklitsch (1962) :

avec Q_c, le débit critique unitaire en m³/s/m et D₄₀, le percentile 40 de la distribution granulométrique en m, et de la formule de Bathurst et al. (1987) :

avec D₁₆, le percentile 16 de la distribution granulométrique en m.

Les approximations des débits critiques ont permis également d’évaluer les puissances hydrauliques spécifiques critiques. La formule utilisée est la suivante :

avec ω_c, la puissance spécifique critique en W/m² et w, la largeur de la bande active en m.

Résultats

Fréquence du charriage

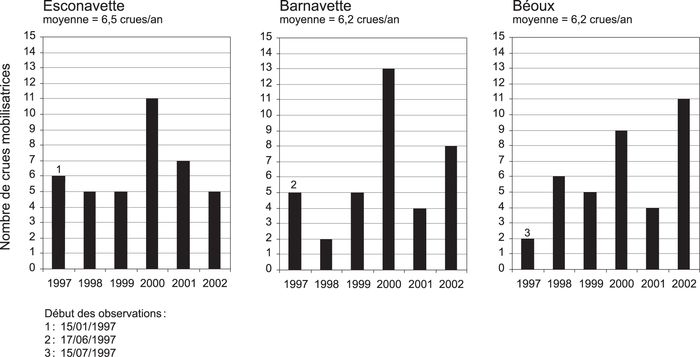
Le suivi des crues qui se sont produites entre 1997 et 2002 montre que les bancs sont mis en mouvement six à sept fois par an en moyenne sur les trois cours d’eau (fig. 4). De fortes disparités interannuelles sont observées, avec des fréquences extrêmes comprises entre deux et 13 crues mobilisatrices par an. Des différences importantes sont également visibles entre les cours d’eau. L’année 2002 montre 11 événements sur la Béoux et seulement cinq sur l’Esconavette. En 2001, on observe 13 crues mobilisatrices sur la Barnavette et seulement neuf sur la Béoux. Ainsi, sur un total de 57 jours de charriage, seulement 19 ont été actifs sur les trois cours d’eau, ce qui ne représente que 33 % des événements observés. La majorité de ces crues synchrones se sont produites à l’automne (47 %).

Les crues mobilisatrices se produisent principalement à l’automne (36 %) et secondairement au printemps (25 %) (tabl. II). La répartition saisonnière montre néanmoins que le transport solide peut se produire à tout moment dans l’année. Il est intéressant de noter l’occurrence de crues d’été sur ces cours d’eau tandis que de tels événements sont quasi inexistants sur la Drôme (Liébault, 2003). Ces crues sont générées par des cellules orageuses puissantes qui se manifestent sur de petites surfaces de drainage. Il faut également mentionner le nombre élevé de crues d’été observé sur la Béoux comparativement aux autres bassins. Ceci peut s’expliquer par sa position plus exposée aux circulations des cellules orageuses en provenance du sud.

Tableau II

**Répartition saisonnière des crues mobilisatrices observées entre 1997 et 2002 (les résultats sont exprimés en nombre de crues observées)**

Seuils de mise en mouvement

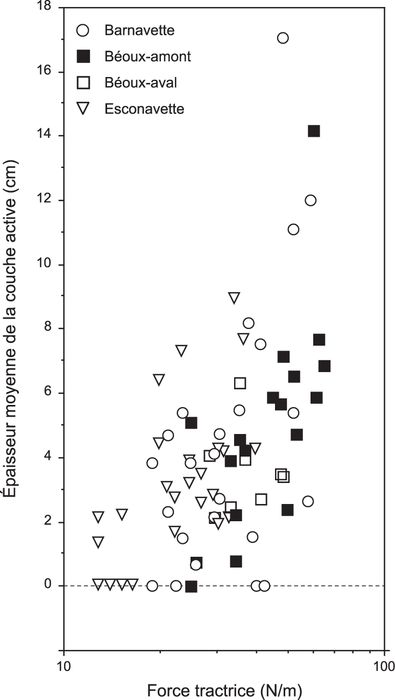
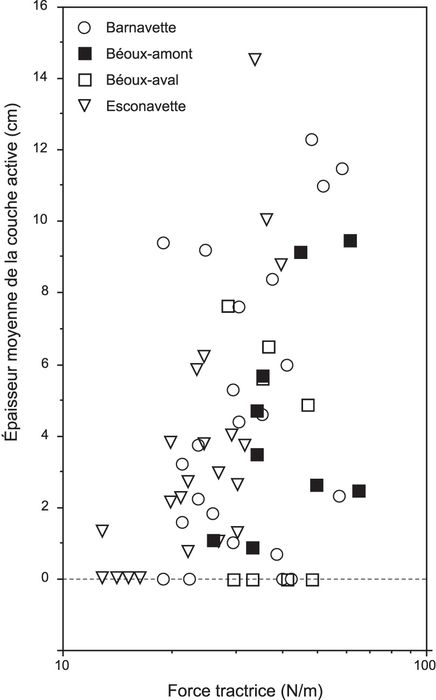
Les seuils de mise en mouvement de la charge de fond ont été déterminés par confrontation des observations géomorphologiques et hydrométriques. La relation entre l’épaisseur moyenne de la couche active obtenue par suivi topographique des profils en travers (moyenne des sections érodées et remblayées, pondérée par la largeur active) et la force tractrice moyenne sur la section, calculée avec la profondeur d’eau moyenne, montre que les forces tractrices critiques de mise en mouvement (τ_c) sont comprises entre 10 et 40 N/m² (fig. 5A). Pour l’Esconavette, ces valeurs s’échelonnent entre 10 et 20 N/m² ; elles sont comprises entre 15 et 40 N/m² pour la Barnavette et entre 20 et 40 N/m² pour la Béoux (station amont et station aval). Les calculs de τ*_c donnent des valeurs comprises entre 0,023 et 0,046 pour l’Esconavette, entre 0,048 et 0,127 pour la Barnavette, entre 0,034 et 0,068 pour la Béoux station amont et entre 0,020 et 0,041 pour la Béoux station aval. L’intervalle moyen des quatre sites est compris entre 0,031 et 0,071. Une approche équivalente a été conduite à partir des observations réalisées avec les chaînes d’érosion. L’épaisseur de la couche active a été calculée en faisant la moyenne des valeurs d’érosion et de dépôt de chaque événement. Cette variable a été mise en relation avec la force tractrice de la crue (fig. 5B). Les forces tractrices critiques sont comprises entre 10 et 45 N/m². Le calcul de τ*_c donne des valeurs comprises entre 0,023 et 0,058 pour l’Esconavette, entre 0,064 et 0,127 pour la Barnavette, entre 0,034 et 0,068 pour la Béoux station amont et entre 0,030 et 0,051 pour la Béoux station aval. L’intervalle moyen est compris entre 0,038 et 0,076. Ces valeurs sont très légèrement supérieures à celles qui sont obtenues à partir du suivi topographique.

Figure 5

Relations entre l’épaisseur moyenne de la couche active mesurée (A) par suivi topographique ou (B) avec les chaînes d’érosion et la force tractrice moyenne sur la section.

Relationship between mean active depths measured (A) by topographic resurveys or (B) by scour chains and the cross section mean shear stress.

-> Voir la liste des figures

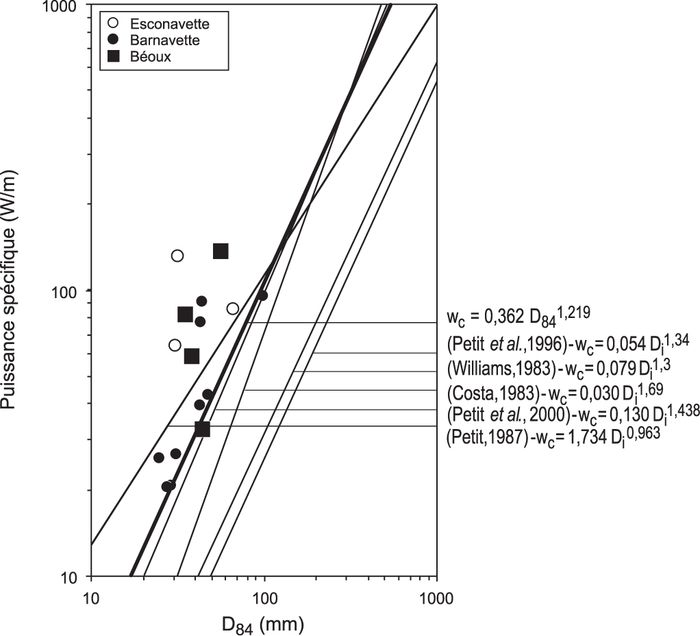
L’évaluation indirecte des débits critiques de mise en mouvement (Q_c) à partir des hauteurs moyennes critiques donne des valeurs comprises entre 1,6 et 9,0 m³/s (tabl. III). Les comparaisons montrent que nos débits critiques sont toujours situés entre les valeurs obtenues à partir des équations 3 et 4, tout en étant souvent plus proches des débits de la formule de Bathurst et al. (tabl. III). Les puissances spécifiques critiques calculées à partir des débits critiques et des largeurs de la bande active oscillent entre 15 et 87 W/m² (tabl. III). Nous avons mis en relation les puissances spécifiques avec la taille des particules mobilisées pendant les crues (fig. 6). Le D₅₀ et le D₈₄ ont été calculés à partir des traceurs mis en mouvement et retrouvés après chaque crue. Les droites de régression obtenues sont :

Nous pouvons également tracer des courbes enveloppes qui passent par les points bas des nuage de points ; les équations de ces courbes sont les suivantes :

Tableau III

**Débits et puissances hydrauliques critiques pour la mise en mouvement de la charge de fond**

Figure 6

Relation entre la puissance spécifique critique (w₀) et la taille des particules mobilisées : (A) D₅₀ et (B) D₈₄. Des modèles établis sur d’autres rivières sont indiqués à titre de comparaison.

Relationship between the critical stream power (w₀) and statistical grain sizes of tracers : (A) D₅₀ and (B) D₈₄. Empirical models obtained for different rivers are indicated for comparison.

-> Voir la liste des figures

Distances de transport

La qualité des données dépend du nombre de traceurs retrouvés après chaque événement. Celui-ci varie entre 10 et 2 189. Les taux de récupération n’ont pas été mesurés parce que la technique de marquage par parcelle se prête mal à ce type d’exercice. On peut néanmoins donner un ordre de grandeur à partir des synthèses effectuées sur le traçage peinture, où les taux de récupération sont généralement de l’ordre de 30 % (Hassan et Ergenzinger, 2003).

Les distances annuelles de transport ont été obtenues par cumul des distances événementielles mesurées sur la période 1997-2002. Nous obtenons ainsi des déplacements moyens compris entre 450 et 470 m/an (fig. 7). Ces valeurs représentent entre 20 et 30 fois la largeur à pleins bords des cours d’eau. La variabilité interannuelle des déplacements est forte ; les valeurs extrêmes sont de 105 et 1 269 m/an.

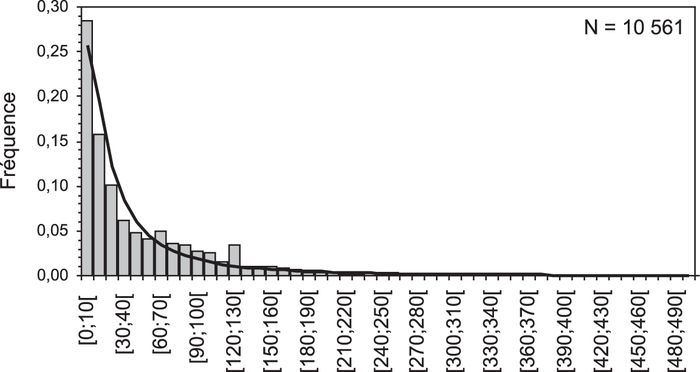
La distribution des distances de transport événementielles montre une configuration classique de type exponentiel (fig. 8A). L’inflexion des distributions se produit pour des distances comprises entre 30 et 40 m. On observe également que 95 % des particules mobiles se déplacent sur des distances inférieures ou égales à 125 m. Si nous comparons les résultats obtenus sur chaque cours d’eau, on observe des distributions légèrement différentes (fig. 8B). La Barnavette et la Béoux se caractérisent par des courbes dont l’inflexion se produit pour des distances plus courtes. En revanche, les particules les plus mobiles se sont déplacées sur de grandes distances. L’Esconavette montre une plus faible dispersion des traceurs vers l’aval. Le centile 90 prend alors les valeurs respectives suivantes pour l’Esconavette, la Barnavette et la Béoux : 102, 149 et 227 m. Ces différences ne peuvent être mises en relation avec les caractéristiques granulométriques des traceurs qui sont similaires entre les trois cours d’eau (fig. 9). En revanche, elles s’échelonnent conformément aux puissances spécifiques des tronçons d’étude, qui peuvent être évaluées grossièrement à partir de la pente globale du lit, de la largeur moyenne de la bande active et du débit de fréquence 1,5 ans, déterminé à partir des surfaces drainées. Les valeurs obtenues sont respectivement pour l’Esconavette, la Barnavette et la Béoux, de 13, 18 et 40 N/m². Les obstacles végétaux étant peu présents sur les tronçons de diffusion, nous pouvons admettre que leur influence sur les distances parcourues est faible.

Figure 8

Distributions des distances de transport événementielles intégrant la totalité des traceurs retrouvés à l’issue des crues mesurées entre 1997 et 2001. (A) Distribution globale. (B) Distributions regroupées par cours d’eau. (C) Courbes des fréquences cumulées, où N représente le nombre de particules. Les courbes en A et B correspondent aux distributions log-normales calculées à partir des moyennes et des écart types.

Distribution of event-based distances of transport for all the recovered tracers during the flow events that occurred between 1997 and 2001. (A) Global distribution. (B) Distributions stratified by streams. (C) Cumulative frequency curves, where N represents the number of recovered tracers. Curves plotted in A and B were calculated with mean and standard deviation.

-> Voir la liste des figures

Les distributions des distances parcourues en fonction des classes granulométriques montrent que la taille des traceurs n’exerce pas d’influence sur les distances de transport (fig. 10). Les distances des classes comprises entre 4 et 128 mm sont peu différentes. Il faut noter en revanche des distances de transport plus faibles pour les tailles extrêmes. Il est néanmoins difficile d’affirmer que la mobilité de ces granulométries est réduite, compte tenu du faible nombre de traceurs concernés (22 pour la classe 2-4 mm et 22 pour la classe 128-256 mm) et de la probabilité d’enfouissement et de décapage complet pour les petits diamètres.

Discussion

Nos observations montrent qu’il se produit en moyenne six à sept crues mobilisatrices par an sur les affluents de la Drôme. Ces fréquences sont proches de celles qui sont observées sur d’autres petites rivières de montagne. Le traçage peinture de la charge de fond des têtes de bassin ardennais a montré que les sédiments grossiers sont mis en mouvement entre huit et dix jours par an (Petit et al., 1996). Ces auteurs définissent la mobilité sur la base de l’entraînement partiel ou total de placettes peintes sur des dépôts représentatifs de la charge grossière en transit. Sur la rivière Lainbach (pente du lit : 2 %) dans les Alpes bavaroises, la fréquence de dépassement du seuil de mise en mouvement de traceurs magnétiques dont la gamme des tailles est comprise entre le D₃₀ et le D₇₀ des matériaux du lit, est comprise entre trois et quatre jours par an (Gintz et al., 1996). Les résultats obtenus dans la Drôme confirment le caractère très épisodique du charriage dans les petites rivières de montagne (exception faite des torrents à régime nival et glaciaire), comparativement aux grandes rivières à lits de graviers où les fréquences peuvent atteindre 20 à 40 jours par an, comme sur le Rhône par exemple (Tricart, 1961). De telles différences trouvent une explication dans la plus ou moins grande régularité des régimes hydrologiques : plus le régime est irrégulier, plus le transport solide se concentre sur une courte période (Leopold et al., 1964). Nous observons également le caractère asynchrone du charriage, car seulement 33 % des crues mobilisatrices se sont produites simultanément sur les trois torrents, d’où l’importance des cellules orageuses localisées dans la dynamique du transport solide des torrents. Ceci est particulièrement notable sous climat méditerranéen, la taille des cellules convectives et la synchronisation dans l’espace des précipitations de forte intensité étant d’autant plus réduites que le climat est plus aride (Wolman et Gerson, 1978).

Les seuils de mise en mouvement de la charge de fond ont été évalués à l’aide de plusieurs paramètres. Les forces tractrices adimensionnelles sont comprises entre 0,031 et 0,076. Ces valeurs sont conformes à celles communément admises sur les rivières graveleuses. Garcia et al. (2000) observent sur la Tordera, une petite rivière torrentielle méditerranéenne des chaînes côtières de Catalogne dont la taille et la morphologie sont comparables à celles des rivières étudiées, des valeurs comprises entre 0,048 et 0,096. Elles ont été obtenues au moyen de trappes à charge de fond automatiques, de type Birkbeck. L’utilisation de radio émetteurs pour le traçage des particules sur une rivière à forte pente (2,6 %) de l’Idaho a permis d’analyser finement les périodes de déplacement et de repos de la charge grossière et le couplage de ces informations avec les hydrogrammes de crues a montré des t*_c compris entre 0,027 et 0,063 (McNamara et Borden, 2004). Buffington et Montgomery (1997) proposent une gamme comprise entre 0,030 et 0,086 d’après la compilation de 80 années d’étude de transport solide dans les rivières à charge graveleuse. Notre évaluation morphologique des forces tractrices critiques, que ce soit à partir du suivi topographique ou des chaînes d’érosion, confirme la forte variabilité de t*_c et permet d’obtenir des valeurs dans la gamme des ordres de grandeurs obtenus avec des techniques sophistiquées. Les plus faibles valeurs de t*_c sont obtenues sur l’Esconavette. Ceci est à mettre en relation avec le style morphologique de cette rivière, caractérisé par un stock alluvial mobile plus abondant (fig. 2), ce qui suggère des structures sédimentaires moins efficaces en termes de résistance à l’entraînement. On peut également émettre l’hypothèse de crues plus brutales, occasionnant un charriage en vrac défavorable à la fabrication des structures. Les relations entre les forces tractrices et la profondeur moyenne de la couche active sur la section montrent une forte dispersion des nuages de points. Outre l’influence des facteurs de dispersion physiques communément admis (fluctuations de la fourniture sédimentaire, migration des micro- et méso-formes sédimentaires, influence morphosédimentaire des crues antérieures), il faut également voir ici l’effet de l’intégration sur la section en travers, qui donne des valeurs moyennes globales. On peut facilement imaginer des relations moins dispersées avec un dispositif de mesure permettant de connaître en tout point de la section les forces hydrauliques en présence et les tranches érodées et déposées.

La mise en relation de la granulométrie des éléments déplacés et des puissances spécifiques maximales donne des résultats comparables à ceux qui sont obtenus sur plusieurs rivières torrentielles ardennaises (Petit, 1987 ; Petit et al., 2000) (fig. 6). Il faut mentionner les similitudes morphologiques de ces rivières avec nos sites d’étude (pente, granulométrie et géométrie transversale équivalentes) et la prédominance des formations rocheuses imperméables dans la constitution géologique de tous ces bassins-versants. Ceci suggère des fréquences et intensités de crue du même ordre de grandeur. Il faut signaler que les puissances spécifiques critiques obtenues sont relativement fortes si on les compare à celles des modèles établis sur les grandes rivières (Williams, 1983 ; Petit et al., 1996). Ceci peut s’expliquer, comme le soulignent Petit et al. (2000), par l’importance relative de la résistance des formes dans les petites rivières torrentielles. Cette configuration engendre une déperdition d’énergie importante lors des crues et implique des puissances hydrauliques critiques supérieures pour des conditions granulométriques identiques.

Les distances de migration des particules peintes montrent des distributions événementielles asymétriques avec un pic marqué vers les faibles distances, ce qui se modélise souvent par des ajustements de type gamma (Hassan et al., 1991 ; Schmidt et Ergenzinger, 1992 ; Gintz et al., 1996). Nous observons également que les distances maximales parcourues lors d’une crue sont plus importantes sur la Barnavette et la Béoux que sur l’Esconavette. Ceci est à mettre en relation avec des puissances hydrauliques spécifiques plus fortes. Ces résultats sont fondés sur le décompte des particules qui sont restées en surface après le déplacement. Ils ne peuvent être généralisés que si on considère un comportement équivalent avec les particules enterrées à l’issue d’une crue. Cette hypothèse a été validée par Hassan (1990) qui observe des distances de transport événementielles similaires entre les particules enterrées et restées en surface, par traçage magnétique sur des rivières graveleuses semi-arides. Ceci doit être relativisé lorsque les déplacements granulaires sont appréhendés sur le long terme, car les phénomènes de mixage vertical et d’enfouissement des particules vont fortement influencer les distances de migration par le biais du stockage temporaire des grains sous la couche active (Ferguson et al., 2002).

Le cumul des parcours événementiels nous donne des distances annuelles de charriage comprises entre 450 et 470 m/an, ce qui représente entre 20 et 30 fois la largeur à pleins bords des torrents. Des résultats équivalents ont été obtenus par Beechie (2001) à partir de la compilation des vitesses de migration mesurées sur 16 rivières à charge graveleuse, qui montre des distances annuelles représentant en moyenne 20 fois la largeur à pleins bords. Ce type de relation empirique ne peut cependant être généralisée, dans la mesure où les vitesses annuelles de déplacement vont dépendre principalement de la fréquence du charriage (régime hydrologique) et de la transmissivité sédimentaire du cours d’eau, elle-même contrôlée par le style morphologique et la présence d’obstacles (débris végétaux grossiers).

Conclusion

Les observations sur la mobilité de la charge de fond conduites entre 1997 et 2002 sur trois affluents torrentiels de la Drôme montrent qu’il se produit en moyenne six à sept événements par an capables de mettre en mouvement les bancs. Les forces tractrices critiques adimensionnelles obtenues à partir de techniques morphologiques (suivi topographique et chaînes d’érosion) sont comprises entre 0,031 et 0,076. Le traçage peinture a permis d’évaluer les puissances hydrauliques critiques de mise en mouvement ainsi que les distances de transport des particules. Nous obtenons des déplacements annuels moyens compris entre 450 et 470 m. Ces valeurs représentent entre 20 et 30 fois la largeur à pleins bords des cours d’eau étudiés. La taille des particules n’exerce pas d’influence nette sur ces distances.

Ces résultats montrent que nous avons pu obtenir de nombreuses informations sur la dynamique de la charge de fond des affluents de la Drôme à partir d’un dispositif simple à mettre en oeuvre, fondé sur la mesure conjointe des fluctuations altitudinales du lit et des distances parcourues par les particules. Nos résultats confirment l’intérêt de ce type d’approche, encore relativement peu utilisé dans les études de transport solide. Les développements technologiques récents en matière de mesure topographique (GPS différentiel, télémétrie laser aéroportée) et de traçage sédimentaire (radio-traçage) devraient permettre une plus large diffusion de ces approches qui présentent un réel intérêt en matière de connaissance des seuils de mise en mouvement et des distances de transport des sédiments grossiers.

La mobilité de la charge de fond des rivières torrentielles méditerranéennesBedload mobility of Mediterranean mountain streams

Résumé

Abstract

Introduction

Sites d’étude

Matériel et méthodes

Suivi de la mobilité de la charge de fond

Suivi hydrométrique et calculs hydrauliques