Utilisation de contextes fantaisistes dans les problèmes écrits mathématiques au sein des cahiers d’apprentissage du primaire

Cette chronique présente le résumé d’un mémoire de maitrise portant sur l’utilisation des contextes fantaisistes dans les problèmes écrits mathématiques (Forest, 2021).

Problématique

Un consensus scientifique soutient que la résolution de problèmes doit être au coeur de l’enseignement des mathématiques (Kilpatrick et al., 2001 ; Lajoie et Bednarz, 2016). La résolution de problèmes, notamment sous forme écrite, occupe donc une place importante dans les programmes scolaires (MEES, 2019 ; NCTM, 2014). Les problèmes écrits proposés aux élèves du primaire présentent divers contextes, ceux-ci référant aux éléments non mathématiques contenus dans l’énoncé qui agissent comme mise en situation. Notre étude se concentre précisément sur ces contextes.

Comme le mentionnent Verschaffel et al. (2020), le problème écrit mathématique a fait l’objet de nombreuses études depuis les 50 dernières années. Différents aspects du problème écrit ont été analysés, dont les facteurs liés à l’énoncé pouvant influencer sa résolution. Parmi ces facteurs, le contexte semble avoir été peu étudié, notamment le contexte fantaisiste. Il s’agit d’un constat surprenant étant donné l’importance de la fantaisie dans la vie des enfants, qui est présente dans diverses sphères de leur quotidien (Woolley et Cornelius, 2013). Alors que la fantaisie détient une place considérablement importante pour les enfants, qu’en est-il de sa présence à l’école, plus précisément dans les problèmes écrits mathématiques ?

Soulignons ici que la nature des contextes des problèmes écrits mathématiques a grandement évolué depuis le siècle dernier, passant de problèmes à visée exclusivement pratique à des possibilités multiples, y compris les contextes fantaisistes. Bien que l’apparition des contextes fantaisistes dans les documents ministériels québécois permette d’augmenter le nombre de problèmes pouvant être envisagés dans la pratique, la justification derrière cet ajout n’est pas précisée (Lajoie et Bednarz, 2012). À notre connaissance, une seule étude touchant spécifiquement les contextes fantaisistes des problèmes écrits mathématiques a été réalisée (Wiest, 1996). Les résultats montrent que les élèves ont un intérêt envers les contextes fantaisistes et que leurs performances sont équivalentes entre les problèmes écrits ayant un contexte fantaisiste et ceux ayant un contexte réaliste.

Au regard des connaissances actuelles relatives aux contextes fantaisistes des problèmes écrits mathématiques, un double problème de recherche est soulevé : 1) la définition du contexte fantaisiste est imprécise en didactique des mathématiques et 2) nous manquons de connaissances empiriques sur l’utilisation des contextes fantaisistes, et ce, même si l’utilisation d’une variété de contextes est valorisée dans les problèmes mathématiques. Deux objectifs de recherche sont donc poursuivis : 1) élaborer une définition des concepts de fantaisie et de contexte fantaisiste et 2) brosser un portrait de l’utilisation des contextes fantaisistes dans les énoncés de problèmes écrits mathématiques des cahiers d’apprentissage du primaire. Puisque le premier objectif est préalable à la réalisation du deuxième, il a d’abord fallu préciser la nature des contextes fantaisistes. Le cadre conceptuel propose donc une typologie des contextes et un système d’attentes ontologiques[1] pour définir le contexte fantaisiste et distinguer divers types de fantaisie (Forest, 2021).

Cadre conceptuel

Il existe différentes façons de catégoriser les contextes d’histoires pour enfants. Par exemple, il est généralement admis qu’un crapaud se transformant en prince est magique, tandis qu’un enfant jouant avec un chien est réaliste. D’autres contextes, parfois qualifiés de fantaisistes, sont plutôt hors du commun, comme un alligator caché sous un lit. Toutefois, à notre connaissance, il n’existe pas de définitions consensuelles de ces termes ni de typologies complètes sur le sujet. Nous avons donc élaboré une typologie (fig. 1) basée sur des typologies partielles existantes (Goldstein et Alperson, 2020 ; Hopkins et Weisberg, 2017).

Figure 1

Typologie des contextes

Au premier niveau, un contexte est réel ou fictif. La réalité comprend tout ce qui est réel alors que la fiction est, à l’opposé, une création de l’imaginaire ayant des possibilités infinies. Un contexte est considéré comme réel s’il présente des éléments qui se déroulent ou qui se sont véritablement déroulés dans la réalité. En revanche, un contexte fictif ne vise pas à décrire la réalité, même s’il peut inclure des éléments véridiques.

Au deuxième niveau, la fiction est subdivisée selon son degré de plausibilité. La fiction réaliste présente des éléments qui pourraient se dérouler dans la réalité, même si ce n’est pas le cas. La fiction fantaisiste, quant à elle, comprend des éléments qui ont peu ou pas de chance de se produire dans la réalité.

Au troisième niveau, la fiction fantaisiste se précise en distinguant la fantaisiste improbable ou impossible. La fantaisie improbable comprend des éléments peu susceptibles de se produire dans la réalité, mais sans contrevenir aux attentes des individus par rapport au monde réel. En comparaison, la fantaisie impossible comprend des éléments dont on ne s’attend pas à ce qu’ils se produisent dans la réalité, contredisant une ou plusieurs lois de la nature telles que généralement conçues.

Cadre méthodologique

Afin d’atteindre notre deuxième objectif, un devis de recherche quantitatif descriptif a été mis en place au moyen d’une analyse de contenu (Leray et Bourgeois, 2016). Nous avons ainsi élaboré une grille d’analyse de contenu et un guide de codification, ce qui a permis d’analyser les contextes des énoncés de problèmes écrits (n = 2687) de 38 cahiers d’apprentissage du 1^er au 3^e cycle du primaire provenant de trois maisons d’édition. À partir des données recueillies, une analyse statistique descriptive a été réalisée.

Principaux résultats

Les résultats variés de cette étude brossent un portrait de l’utilisation des contextes fantaisistes dans les problèmes écrits des cahiers d’apprentissage du primaire. Les principaux résultats soutiennent que les contextes fantaisistes sont fréquemment utilisés, représentant environ un énoncé sur quatre dans l’échantillon. Un exemple est présenté à la figure 2 (pour d’autres exemples, voir Forest, 2021, figures 6 à 25). Pour les 1^er et 2^e cycles du primaire spécifiquement, c’est près de 35 % des énoncés qui présentent un contexte fantaisiste. En contrepartie, les contextes fantaisistes sont significativement moins utilisés au 3^e cycle du primaire, suggérant une évolution vers des contextes plus réalistes au fil de la scolarité.

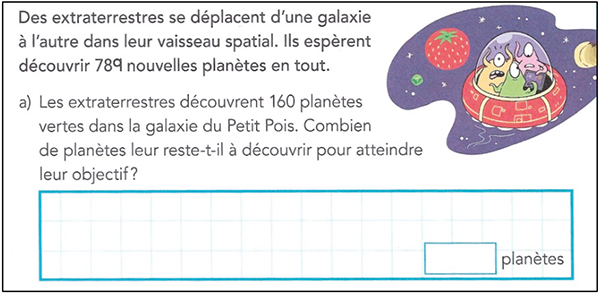
Figure 2

Exemple d’un problème écrit présentant un contexte fantaisiste (tiré de Borduas et al., 2019, p. 75)

Nos résultats révèlent également des variations dans l’utilisation des contextes fantaisistes selon les maisons d’édition. En effet, les auteurs de Chenelière Éducation utilisent davantage les contextes fantaisistes comparativement aux maisons d’édition Pearson ERPI et CEC, ce qui illustre que les choix des auteurs par rapport aux contextes fantaisistes diffèrent d’une maison d’édition à l’autre.

Un autre fait intéressant concerne la récurrence : les contextes fantaisistes sont statistiquement plus récurrents comparativement aux contextes réalistes. Autrement dit, les mêmes éléments fantaisistes reviennent d’un énoncé de problèmes à un autre dans une même collection, ce qui semble mettre en place un univers fantaisiste. Par exemple, plusieurs collections mettent en scène un personnage principal qui est en fait un animal agissant comme un humain, par exemple Matcha, un léopard qui parle, qui va à l’école, qui porte des vêtements, etc. (Borduas et al., 2019). Dans les énoncés de problèmes mettant en scène Matcha, il est considéré comme normal qu’un léopard agisse comme un humain : rien ne laisse entendre qu’il s’agit de quelque chose de surprenant ou d’inattendu. Ainsi, dans l’univers de Matcha, les élèves s’attendent à ce que les animaux parlent et portent des vêtements. Cette notion d’univers, présentant des similitudes avec la notion de monde imaginaire (Wolf, 2012), pourrait être liée à l’idée qu’un énoncé de problème représente un style littéraire en soi (Gerofsky, 1996). En considérant l’énoncé de problème comme un style de texte particulier, cela pourrait amener les auteurs à créer des univers plus élaborés plutôt qu’à simplement rédiger des énoncés indépendants.

Conclusion

Cette étude a contribué à produire des connaissances sur un sujet peu exploré en didactique des mathématiques. D’une part, le premier objectif a mené à une proposition conceptuelle originale afin de distinguer plus finement ce qui est entendu par fantaisie. Cette façon de définir la fantaisie, en plus d’être opérationnelle, ajoute des nuances importantes aux différentes façons de présenter la fantaisie à l’écrit. D’autre part, nos résultats aident à combler le manque de données scientifiques par rapport aux contextes fantaisistes des problèmes écrits : nous avons désormais un portrait de leur utilisation selon différentes variables. Alors qu’un tel portrait a été réalisé par rapport à la fantaisie dans les médias destinés aux enfants (Goldstein et Alperson, 2020), aucune étude n’avait jusqu’à présent analysé la fantaisie dans le matériel didactique.

Note

• [1] Dans la présente chronique, par souci de synthèse, seule la typologie des contextes est présentée.