Résumés
Résumé
À partir d’un regroupement en classes socioéconomiques homogènes quant au niveau de vie, l’étude montre qu’entre 1969 et 2008 les structures de consommation des ménages canadiens sont très différenciées selon les classes et que la hiérarchie de ces structures reproduit celle des statuts sociaux. Cependant, les comportements moyens des classes convergent depuis le début des années 1970, mais à l’intérieur de chaque classe les comportements sont de plus en plus hétérogènes. Au fil du temps les classes socioéconomiques sont donc devenues moins pertinentes pour expliquer les différences de comportement de consommation. Pour analyser cette différenciation, nous construisons un pseudo-panel long à partir de sept enquêtes canadiennes de budgets de ménages afin d’estimer des fonctions de demande sur une longue période. La différence entre les estimations en dimensions transversale et temporelle permet de révéler les contraintes non monétaires qui influent sur les comportements de consommation des ménages, et leur évolution. Nous trouvons des évolutions différenciées de ces contraintes selon les postes de consommation, qui semblent cohérentes avec une explication en termes de coût temporel de la consommation.
Abstract
Starting from a classification of homogenous socioeconomic classes, the study shows that between 1969 and 2008 the consumption structures of Canadian households are very differentiated across classes, and that the hierarchy of these structures mimics that of social statuses. Class means tend to converge since the beginning of the 1970s, but within classes the consumption structures have grown more heterogenous, thus making socioeconomic classes less pertinent to explain differences in consumption patterns. In order to analyze these differences, we build a pseudo-panel drawing from seven Canadian household expenditure surveys in order to estimate long-term demand functions. The differences in estimations between the cross-section and the time dimensions can be used to reveal the non-monetary constraints that influence households’ consumption behaviour. We find variegated evolutions of these constraints across consumption categories, that are coherent with an analysis in terms of time-cost of consumption.
Corps de l’article
Introduction
Une question majeure concernant l’évolution des structures de consommation des ménages est celle d’une convergence de ces comportements vers une norme sociale de consommation (comme le suppose par exemple la théorie de la régulation) ou au contraire d’une différenciation croissante de ces comportements. Comment a évolué dans le temps la différenciation sociale des structures de consommation? Quelles sont les tendances historiques d’évolution de chaque classe? Y a-t-il eu tendance au rapprochement entre classes ou, au contraire, éloignement? La disponibilité d’enquêtes canadiennes comparables sur une longue période offre un terrain privilégié pour une telle analyse. Une fois étudiée la convergence, nous évaluerons l’hypothèse selon laquelle les classes socioéconomiques deviennent moins discriminantes pour expliquer les différences de structure de consommation.
Nous proposons de répondre à cette question en premier lieu par une analyse classique de la structure de la consommation marchande des ménages canadiens dans le but de dégager des tendances de long terme qu’une analyse économétrique par systèmes de demande ne permettrait pas de cerner. Cette analyse sur 40 ans porte sur des populations homogènes quant au niveau de vie, étudiées de manière originale sous une forme de pseudo-panel. Cette statistique permet de considérer les inflexions conjoncturelles et de comparer le comportement de diverses sous-populations définies de manière homogène en utilisant en particulier une définition originale des classes socioéconomiques.
Une seconde analyse, de nature plus économétrique, trouve son origine dans les travaux de Theil et de ses collaborateurs (Theil, Suhm et Meisner, 1981; Theil et Clements, 1987; Selvanathan, 1993) sur les régularités internationales de la consommation des ménages, qui ont établi sur données agrégées par pays l’existence de lois de consommation stables et communes à tous les pays, ainsi que des résultats de convergence internationale des comportements de consommation. Le résultat de convergence des structures de consommation des classes de ménages canadiens depuis les années 1970, conforme à ceux de Theil, est étonnant lorsque l’on s’interroge sur ses causes, puisqu’au cours de cette période les revenus moyens par classe se sont écartés – du moins en termes absolus – l’écart relatif restant constant (voir Fortin et al., 2012; Fortin et Lemieux, 2015). Puisqu’en outre les prix s’imposent identiques à toutes les catégories sociales (c’est le propre d’une étude intra nationale, par opposition à une étude internationale dans laquelle les prix relatifs peuvent tendre à s’harmoniser entre pays), les facteurs économiques monétaires ne peuvent pas expliquer ce mouvement de rapprochement. Rappelons que les modèles économiques de la consommation n’expliquent qu’une partie assez faible de la variance des dépenses (de l’ordre de 10 % à 30 %), la partie résiduelle dépendant de variables latentes non observées que nous représenterons par le jeu de prix virtuels qui leur correspondent.
C’est pour cette raison que nous nous tournons vers l’étude des déterminants non monétaires de la convergence des structures de consommation. En particulier, la méthode originale que nous développons permet de révéler s’il existe des contraintes ou des ressources non monétaires corrélées au niveau de revenu. Les décisions économiques réelles sont en effet affectées par la multitude de contraintes ou de ressources non monétaires : temps disponible pour la consommation d’un bien ou service, facilité d’accès à l’offre d’un type de biens, acceptabilité sociale d’un type de consommation... Parmi ces contraintes, certaines ne sont pas différenciées selon le revenu; celles-là ne nous intéressent pas ici puisque, si elles sont distribuées uniformément à travers les catégories de revenus, elles ne sauraient avoir de rôle dans la convergence entre catégories. En revanche, les contraintes corrélées au revenu ont pu évoluer au cours de la période et ainsi influer sur le rapprochement des comportements de consommation. En effet, si les contraintes ou les ressources latentes non monétaires sont moins différenciées qu’auparavant selon le niveau de revenu, il semble normal, dans la mesure où les préférences restent identiques dans toute la population, que les comportements de consommation des catégories sociales (entre lesquelles les niveaux de revenu sont assez différenciés) se soient rapprochés.
L’article est organisé comme suit : la première section discute de la convergence sociale au Canada sur cette période, la deuxième section expose le modèle, la méthodologie économétrique et les données utilisés, la troisième section discute les résultats d’estimation.
1. Convergence sociale des consommations
1.1 Définition des classes et présentation des données
Nous étudions une série d’enquêtes de consommation sur une période de 40 ans, de 1969 à 2008. Par souci d’homogénéité, nous excluons les dernières enquêtes correspondant à la Grande Récession. Cette série permet de considérer les inflexions conjoncturelles et de comparer le comportement de diverses sous-populations, en utilisant en particulier une définition originale des niveaux de vie issue des travaux de François Gardes et Simon Langlois (Gardes et Langlois, 1995; Gardes, Gaubert et Langlois, 2000; Gardes, Langlois et Bibi, 2010). Entreprise sur une longue période, cette analyse couvre le cycle complet de la vie active des chefs de ménage qui ont eu 18 ans en 1969, ainsi que le cycle plus court des cohortes suivantes.
Le revenu des ménages et la profession exercée par les individus sont les indicateurs les plus couramment utilisés pour caractériser les classes socioéconomiques. Or, ces indicateurs unidimensionnels sont devenus insuffisants pour cerner ces classes de manière précise, et plus précisément pour étudier la différenciation des comportements de consommation. Ainsi, la pauvreté doit désormais être comprise comme un phénomène multidimensionnel, qui ne se laisse pas réduire à un simple seuil de revenu. Lollivier et Verger (1997) ont montré que seul 2 % environ des ménages français pouvaient être classés comme pauvres sur trois critères considérés simultanément (monétaire, conditions de vie, pauvreté subjective). Les groupements sociaux sont en effet de moins en moins homogènes, contrairement à la situation d’il y a 30 ou 40 ans, et, phénomène révélateur, les organismes de statistique européens travaillent depuis les années 2000 à la construction de nouveaux indicateurs sociaux de pauvreté (voir Caussat, Lelièvre et Nauze-Fichet, 2006).
Le présent travail s’appuie sur la construction d’un indice multidimensionnel de pauvreté-richesse (IMPR) prenant en compte trois critères ou dimensions du statut social : la privation, la marginalisation au sein d’une classe de référence et l’insuffisance de revenus. La dimension de privation caractérise la non-satisfaction des besoins de base et est fondée sur l’idée selon laquelle les ménages pauvres sont contraints d’allouer une part importante de leur budget à des dépenses de subsistance, dont la part du budget allouée à l’alimentation à domicile est un indicateur classique depuis les travaux de Engel[1]. Un ménage est défini comme étant pauvre sur cette dimension s’il présente un coefficient budgétaire pour l’alimentation à domicile d’un tiers supérieur à la moyenne de ce coefficient dans sa population de référence et comme riche si son coefficient est d’un quart inférieur à la moyenne. La population de référence est définie par le croisement de trois critères : l’âge du chef de ménage, son niveau d’éducation et la province de résidence, ce qui donne pour chaque enquête une partition en 150 sous-populations. La marginalisation au sein d’une classe de référence prend en compte, au-delà des besoins de subsistance, les besoins sociaux : sont considérés comme pauvres dans cette dimension les ménages ayant une dépense totale (par unité de consommation) inférieure à 67 % de la dépense totale moyenne de leur groupe de référence et comme riches ceux dont la dépense totale dépasse les 150 % de cette moyenne. La troisième dimension concerne l’insuffisance du revenu disponible du ménage (par unité de consommation) : on définit comme pauvres les ménages dont le revenu appartient au quartile inférieur de la distribution des revenus de l’ensemble de la population et riches les ménages dont le revenu appartient au quartile supérieur. On regroupe finalement les ménages en 7 classes (IMPR) de pauvreté-richesse, suivant le nombre de dimensions dans lesquelles le ménage est classé comme pauvre ou riche.
La répartition des ménages entre ces 7 classes socioéconomiques est relativement stable au fil des enquêtes. Les ménages pauvres représentent en moyenne 8 % de l’échantillon, les ménages quasi pauvres 12 %, la classe moyenne inférieure 16 %, la classe moyenne 27 %, la classe moyenne supérieure 21 %, les ménages quasi riches 10 %, les ménages riches 6 %. Comparée à un découpage par quantiles de revenu, la classification par IMPR présente l’avantage de définir des classes de comportement. On constate qu’elle explique pour toutes les enquêtes une part significativement supérieure de l’inertie des structures de consommation à celle expliquée par un découpage en classes de revenu disponible par unité de consommation effectué selon les mêmes quantiles de la population.
Les données analysées proviennent des microdonnées des enquêtes de dépenses des ménages de Statistique Canada, compilées et harmonisées par Simon Langlois à l’Université Laval (Québec) et sont disponibles auprès de ce dernier[2]. Pour les années 1969, 1978, 1982, 1986 et 1992 nous utilisons l’Enquête de dépenses des familles et, pour les années de 1996, 2004 et 2008, son successeur l’Enquête de dépense des ménages. L’Enquête de dépense des ménages a également été menée chaque année entre 1997 et 2003 et entre 2005 et 2008 mais nous choisissons de ne pas utiliser ces données; d’une part parce que les enquêtes de 1997 à 2003 ne comprennent pas la variable niveau d’éducation de la personne de référence, variable essentielle à la construction du pseudo-panel, d’autre part pour garder une périodicité relativement stable et ne pas accorder un poids plus important à la décennie 2000 dans les estimations. La construction du pseudo-panel nous a également obligés à retirer de l’échantillon les ménages dont la province de résidence n’est pas renseignée, soit un nombre marginal chaque année.
Afin d’éliminer les données aberrantes nous avons effectué un filtrage des ménages présentant une dépense totale négative ou des postes de dépense négatifs et ceux dont le centile de dépense nette s’éloigne de plus de 30 du centile de revenu. Ces opérations retirent pour chaque enquête moins de 10 % de l’échantillon. Il reste finalement 14 266 ménages en 1969, 8 786 en 1978, 10 010 en 1982, 9 467 en 1986, 8 624 en 1992, 9 219 en 1996, 12 999 en 2004 et 8 820 en 2008. Nous avons agrégé les données selon les 12 postes de la nomenclature fonctionnelle COICOP du Système de comptabilité nationale des Nations Unies (1993).
1.2 Analyse des structures de consommation
Tableau 1
Dépense totale moyenne des ménages (par unité de consommation) selon la typologie IMPR et l’année (en dollars canadiens courants)
La dépense totale moyenne[3] de chaque classe augmente d’année en année, multipliée par un même facteur sur la période (en supposant une évolution identique de l’indice de prix moyen pour toutes les classes socioéconomiques), d’où un fort accroissement des écarts absolus. Cependant les écarts relatifs restent presque parfaitement stables : les ménages de la classe riche dépensent en moyenne 5 fois plus que ceux de la classe pauvre, le rapport de la classe quasi riche à la classe pauvre étant quant à lui de 3,5. On obtient donc, en termes absolus, un résultat clair de divergence entre classes, résultat que l’on retrouve pour les dépenses absolues ventilées par poste. Cette divergence correspond au constat d’une augmentation générale des inégalités de revenus au Canada (voir Fortin et al., 2012). Ceci montre une grande diversité des comportements de consommation, tant dans la dimension transversale que dans la dimension temporelle.
Tableau 2
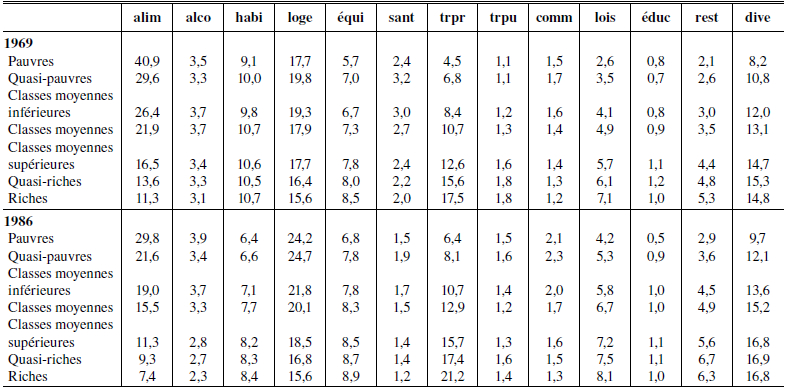
Coefficients budgétaires moyens par classe socioéconomique (typologie IMPR) et par année (en pourcentage)
Note : ALIM : dépense alimentaire à domicile; ALCO : alcool à domicile et tabac; HABI : habillement; LOGE : dépenses de logement (y compris loyer fictif); EQUI : équipement ménager; SANT : dépenses d’hygiène personnelle et santé; TRPR : transports privés; TRPU : transports publics; COMM : dépenses de communication; LOIS : loisirs; EDUC : éducation; REST : restaurants et hôtels; DIVE : autres dépenses.
En considérant les structures de consommation (tableau 2), définies comme l’ensemble des parts des postes de consommation dans la dépense totale, on observe une différenciation transversale supérieure à la différenciation temporelle : par exemple, le coefficient de l’alimentation à domicile se réduit de moitié pour toutes les classes entre 1969 et 2008, mais est chaque année quatre fois supérieur pour les ménages pauvres que pour les ménages riches. La différenciation transversale est dominée à chaque période par les différences des postes alimentation à domicile, transports privés et dépenses diverses et, dans une moindre mesure, par les postes équipement ménager, loisirs et dépenses de restaurants et d’hôtels. Ces postes créent pour chaque enquête une hiérarchie des ménages presque identique à celle définie par l’IMPR[4]. On note en outre l’existence de tendances historiques communes à l’ensemble des classes, au premier rang desquelles figurent la perte d’importance du poste alimentation à domicile et l’augmentation du poste logement. Ce dernier est, en fin de période, le premier poste de dépense pour toutes les classes socioéconomiques, ce qui n’était le cas que pour les trois classes les plus aisées en début de période.
On notera que, pour certains postes, l’évolution temporelle est conforme à la différenciation des dépenses entre classes socioéconomiques : ainsi, à chaque période une moindre part de l’alimentation à domicile est un marqueur clair d’élévation du niveau de vie. Or son poids diminue fortement pour toutes les catégories sociales sur l’ensemble de la période et l’évolution à la baisse est plus forte chez les ménages pauvres que chez les ménages riches[5]. Les dépenses de transports privés et de loisirs suivent une évolution similaire : leur part est positivement corrélée avec le niveau de vie à chaque période, et augmente pour toutes les classes au fil des décennies. Les dépenses d’habillement, positivement liées au statut social en début de période, tendent quant à elles à s’harmoniser entre les classes à mesure que leur poids baisse au cours du temps.
L’évolution des postes logement et communication suit une logique inverse : alors qu’ils sont, en transversal, négativement corrélés avec le niveau de richesse, leur poids augmente pour toutes les catégories au cours du temps, et les écarts interclasses tendent à se creuser. Les dépenses de transports publics suivent enfin une évolution singulière : positivement corrélées avec le statut social en début de période, elles sont quasiment égales de classe à classe en 1986, pour devenir à la fin de la décennie 2000 des dépenses de nécessité, négativement corrélées avec la richesse.
Tableau 3
Inertie des structures de consommation des ménages (totale, intra, inter et par classe, IMPR, × 1000)
La comparaison des moyennes par classes ne produit cependant qu’une image partielle des phénomènes de convergence, qu’il convient de compléter par l’observation de l’inertie[6] des structures de consommation et sa décomposition selon les classes socioéconomiques. Celle-ci donne lieu à trois résultats. Premièrement, la claire évolution à la baisse[7] de l’inertie interclasses confirme l’hypothèse de rapprochement entre les moyennes de classes et pose un constat de sigma-convergence[8]. Deuxièmement, l’inertie intraclasse augmente progressivement au cours de la période et son poids dans l’inertie totale augmente (83 % en 1969, 91 % en 2008) : l’appartenance à une classe socioéconomique est donc de moins en moins contraignante quant aux comportements de consommation et les frontières entre classes tendent à se brouiller. Troisièmement, l’inertie par classe est à chaque période positivement corrélée avec le niveau de vie et augmente systématiquement entre 1969, 1986 et 2008. Ce double constat peut être, comme précédemment, interprété en termes de rapprochement vers les comportements associés aux classes riches. Il rejoint par ailleurs la littérature sociologique sur les consommateurs omnivores, définis par Peterson et Kern (1996) dans un article de référence sur les goûts musicaux aux États-Unis. Les individus consomment plus qu’auparavant des produits culturels variés et traditionnellement réservés à d’autres classes – une consommation de plus en plus omnivore, particulièrement dans les classes supérieures (voir Coulangeon, 2004, pour une revue de littérature). Il y a une continuité conceptuelle avec notre étude : nous avons en effet observé que les comportements de consommation sont moins strictement dictés par l’appartenance de classe à mesure que l’on s’élève dans la hiérarchie sociale. Chaque classe socioéconomique devient plus omnivore au fil des enquêtes, dans la mesure où la dispersion intraclasse des comportements augmente régulièrement (pour une analyse plus détaillée, voir Boelaert, 2012). Cette interprétation rejoint par ailleurs la perspective microéconomique : tant en transversal qu’en temporel, l’augmentation du revenu disponible va de pair avec une moindre contrainte de la nécessité, une plus grande liberté de choix et, par conséquent, une plus grande diversité des comportements.
2. Modèle et données
Nous avons avancé l’hypothèse que les membres des différentes classes socioéconomiques ont un comportement de consommation de moins en moins prévisible par leur appartenance de classe. Ceci indique un phénomène de différentiation sociale intraclasse qui pourrait s’expliquer par l’apparition de nouvelles contraintes de choix différenciées selon les ménages, contraintes liées à la dimension non monétaire des consommations ou à leur partage du temps disponible après le travail marchand et les tâches indispensables à leur bien-être personnel. Par exemple, l’accroissement du chômage ou du travail à temps partiel lors de la récession des années 2008-2011 aux États-Unis a amené les ménages touchés par cette baisse d’activité marchande à compenser leur perte de revenu monétaire par une augmentation de leur temps de travail domestique (Aguiar, Hurst et Karabarbounis, 2013 ; Alpman et Gardes, 2015). Nous proposons dans cette section une analyse de ces contraintes, à partir d’un système de demande estimé en pseudo-panel.
2.1 Contraintes non monétaires et prix virtuels
Le coût véritable de la consommation d’un bien ou service ne se limite pas au prix monétaire, c’est-à-dire au prix de marché. À ce prix monétaire s’ajoute en effet une foule de coûts liés par exemple à la technologie de production domestique, à la valorisation du temps investi dans l’activité de consommation, à la structure familiale, aux contraintes de liquidité, aux normes sociales de consommation. L’analyse en coûts complets n’est pas nouvelle. L’exemple le plus commun est le modèle d’allocation du temps de Becker (1965) dans lequel le prix complet de la consommation d’un bien est la somme de son prix monétaire et de son coût en temps, le temps étant valorisé au taux de salaire de l’agent. Deux agents dont le taux de salaire diffère seront donc confrontés à des prix complets différents pour la consommation d’un même bien, à prix monétaire et temps de consommation constants.
On trouve un autre exemple de l’intérêt des analyses en prix complets intégrant la production domestique des ménages dans l’étude des effets de la structure démographique des ménages opérée par Barten (1964). Celui-ci montre que les effets de substitution entraînés par la modification du coût unitaire des diverses consommation selon leur degré de consommation publique – qui change avec la composition démographique du ménage (diminution par exemple du coût unitaire des transports privés avec la taille de la famille dans la mesure où elle continue à voyager avec une seule voiture) – modifient les prix relatifs des consommations (selon leur nature privative ou publique). Barten note par exemple qu’un litre de lait coûte relativement plus cher pour une famille nombreuse, ce qui en réduit la consommation relativement aux consommations publiques dont le coût total n’a pas changé pour le ménage. La structure démographique du ménage déterminera donc en partie le système de prix virtuels qui s’impose à lui et, en particulier, le système de prix complets dans la mesure où cette structure démographique modifie l’allocation du temps des différents membres du ménage.
La relation que nous établissons entre caractéristiques du ménage et coûts non monétaires s’inspire de l’analyse de Neary et Roberts (1980), qui montrent comment sous hypothèses de convexité, continuité et stricte monotonie des préférences, toute contrainte de rationnement d’un ménage peut se traduire par des prix virtuels pour les biens contraints (les prix virtuels étant définis comme les prix qui conduiraient un ménage non contraint à se comporter de la même manière que s’il était soumis à un vecteur de contraintes de rationnement). Les différentes contraintes qui s’imposent aux ménages au titre de leur structure familiale, de leur place dans l’échelle des revenus et de leur technologie de production domestique pose un problème dans l’analyse des fonctions de demande en ce qu’elles introduisent une grande hétérogénéité entre ménages, ce qui complique l’analyse de leur choix. La traduction des contraintes de rationnement en prix virtuels à la Neary-Roberts présente le grand avantage de résumer cette hétérogénéité de caractéristiques interménages à de simples différences de prix.
Gardes et al. (2005) montrent qu’il est possible de révéler les prix virtuels à partir de l’estimation d’un même modèle de demande dans deux dimensions, transversale et temporelle. En effet, en suivant Mundlak (1978), dans un modèle de panel linéaire à effets fixes, les paramètres estimés en dimension transversale sont biaisés en présence d’une corrélation entre l’effet fixe et la transformation between d’une partie des variables exogènes. Une telle corrélation peut provenir de l’existence de variables latentes permanentes (telles la génération, le milieu social d’origine, le niveau d’éducation) corrélées à la fois avec l’effet fixe et les moyennes individuelles (sur l’ensemble de ses observations temporelles) des variables exogènes. L’estimation du même modèle dans la dimension temporelle ne souffrira pas de ce biais. Formellement, Mundlak prend comme point de départ le modèle de panel linéaire à effets individuels :
où xht est un vecteur de variables explicatives pour l’individu h observé à l’instant t, β est le vecteur de paramètres d’intérêt, αh est un effet individuel inobservé, et εht est un terme d’erreur idiosyncratique iid. On suppose ensuite qu’αh est un effet fixe lié aux moyennes par individu des variables x par la spécification suivante :
où ν est un vecteur, ![]() et wh est un terme d’erreur iid. On note bw et bb respectivement les estimateurs within et between de β. Mundlak montre que si ν est différent du vecteur nul (c’est-à-dire si l’on se trouve bien en présence d’effets fixes), alors bw est BLUE, tandis que l’estimateur between est biaisé :
et wh est un terme d’erreur iid. On note bw et bb respectivement les estimateurs within et between de β. Mundlak montre que si ν est différent du vecteur nul (c’est-à-dire si l’on se trouve bien en présence d’effets fixes), alors bw est BLUE, tandis que l’estimateur between est biaisé :
et que la différence entre les deux estimateurs donne un estimateur BLUE de v :
L’originalité de l’argument de Gardes et al. réside dans l’interprétation de cette différence d’estimateurs en termes de prix virtuels dans le cadre d’une équation de demande. En effet, le vecteur v ci-dessus représente le lien entre les effets fixes individuels et les régresseurs K; il résume donc le lien entre les régresseurs et des variables latentes qui influent sur le comportement de consommation. Ces variables latentes sont composées de ressources non monétaires et de contraintes de rationnement des ménages, et peuvent être exprimées par des prix virtuels à la Neary-Roberts. La différence entre les estimations dans les dimensions temporelle et transversale permet alors de révéler les différences de prix virtuels[9] entre agents. Plus spécifiquement, si l’on considère pour le bien i, le ménage h à la période t le modèle de demande
où xiht est le coefficient budgétaire du bien i, h et t sont respectivement des indices de ménage et de période, z est un vecteur de variables explicatives, pj le prix logarithmique du bien j, et uiht un terme d’erreur qui se décompose en un terme spécifique individuel et un terme idiosyncratique (uiht = αih + εiht), alors en considérant uniquement l’effet sur le prix du bien i d’un sous-ensemble {z1, z2,…zK} des variables z, on obtient, pour un coefficient de prix γij fixé,
Ce raisonnement fournit une explication au constat empirique de différence entre élasticités transversales et temporelles de la consommation, constat établi sur des données de plusieurs pays. Par exemple, Gardes et al. (2005) et Cardoso et Gardes (1996b) trouvent, pour la France, les États-Unis et la Pologne, une différence significative pour les deux tiers des postes de consommation entre les élasticités-revenus estimées dans les dimensions transversale et temporelle. Ils trouvent en particulier que, pour chaque pays, les élasticités-revenu en dimension transversale sont affectées d’un biais négatif pour l’alimentation à domicile et d’un biais positif pour l’alimentation à l’extérieur. Ce qui, en liant les prix virtuels à une approche de production domestique à la Becker (intégrant le temps dans le coût d’une consommation), peut s’expliquer par une croissance de la composante temporelle du prix complet de la consommation alimentaire avec le revenu relatif du ménage.
L’estimation des prix virtuels par cette méthode présente un intérêt particulier pour l’étude de la convergence des comportements de consommation, puisqu’elle permet de rendre compte des variations de conditions de choix des ménages, poste par poste, pour chaque période considérée. On peut alors étudier l’évolution des contraintes au cours du temps, et observer dans quelle mesure les conditions de choix s’harmonisent entre classes sociales.
2.2 Prix virtuels dans un système QUAIDS linéarisé
Pour étudier les variations des prix virtuels au Canada, nous employons un système de demande QUAIDS (Banks Blundell et Lewbel, 1997), extension quadratique de l’Almost Ideal Demand System (Deaton et Muellbauer, 1980). Ce système présente l’avantage d’être quasi linéaire tout en permettant une modélisation relativement flexible des comportements de consommation, en particulier des courbes de Engel quadratiques. Dans le cadre de données de panel, pour un ménage h à l’époque t la part budgétaire wiht allouée à la consommation du bien i s’écrit :
avec
Ce modèle est habituellement estimé selon une procédure itérative, en exploitant le fait que le système est linéaire si a(p) et b(p) sont fixés. L’estimation within interdit cependant une telle procédure d’estimation : en effet, le calcul du déflateur ln a(p) en équation 3 fait intervenir les termes constants αi de l’équation 2 et la transformation within consiste précisément à faire disparaître ces termes constants. Nous optons donc pour une variante linéarisée du système QUAIDS, exposée par Christensen (2014), qui permet l’estimation correcte, en dimension temporelle, des effets-revenu :
Le déflateur Sht donné par l’équation 6 est l’indice de prix de Stone, qui remplace le déflateur paramétrique a(pht) de l’équation 3 et rend l’équation 5 linéaire en fonction des paramètres. Ce système linéarisé présente deux défauts par rapport au QUAIDS original : d’une part il n’est pas intégrable (il n’existe pas de fonction d’utilité dont la maximisation sous contrainte budgétaire linéaire donne ces fonctions de demande), d’autre part la linéarisation risque de biaiser l’estimation des paramètres de prix γij (de la même façon que pour l’estimation d’un AIDS linéarisé, voir Pashardes, 1993).
En appliquant l’équation 1 de révélation des prix virtuels au système de demande 5, en ne retenant que les variations de prix virtuels liées aux termes de revenu déflaté, on obtient :
où
où les indices (B) et (W) correspondent respectivement aux estimations en dimensions transversale (between) et temporelle (within). Dans le cas où les coefficients de prix γij ne sont pas correctement estimés[11], on peut décrire les variations de prix virtuels en étudiant uniquement les variations de φi. Dans ce cas, seules des comparaisons poste par poste sont possibles, puisque les variations des prix virtuels entre postes dépendent des grandeurs γii, qui vraisemblablement varient selon les postes. Notons que puisque φi est une fonction linéaire de la dépense totale logarithmique, les prix virtuels logarithmiques sont une fonction quadratique de la dépense totale logarithmique–particularité qui vient de l’expression quadratique de QUAIDS. En intégrant l’expression 9 en fonction de ![]() , on obtient :
, on obtient :
avec
où C est une constante d’intégration. En l’absence de paramètres γii, la représentation des Φi renseigne sur les variations de prix virtuels en fonction de la dépense totale des ménages. En revanche, puisque d’une part C est inconnu, et que d’autre part les prix virtuels sont le quotient de Φi et de paramètres γii (que l’on traite comme des inconnues), l’analyse des Φi ne porte pas sur leur valeur, mais uniquement sur leurs variations. Nous normaliserons les Φi pour faciliter la représentation graphique. Notons que, les paramètres de prix γii étant habituellement négatifs, nous prenons pour Φi l’opposé d’une primitive de φi, afin qu’ils représentent mieux les prix virtuels.
2.3 Pseudo-panel de données de consommation canadiennes
La méthode de révélation des prix virtuels présentée ci-dessus nécessite des données structurées en panel, puisqu’elle demande d’estimer des paramètres à la fois dans la dimension transversale (biaisée) et dans la dimension temporelle (non biaisée). Or nous ne disposons pour le Canada que de données d’enquêtes répétées (décrites ci-dessous) qui ne présentent pas a priori cette structure; le problème est résolu par la construction d’un pseudo-panel. La pseudo-panélisation, initiée par Deaton (1985), consiste à donner une structure de panel à des enquêtes successives en coupe transversale, en regroupant les individus de chaque enquête par cohortes (une cohorte est un groupe défini par des critères stables au cours du temps), à calculer pour toutes les variables des moyennes par cohorte, puis à traiter les cohortes obtenues comme des individus que l’on suit d’une enquête sur l’autre. L’intuition de la méthode de Deaton est simple : s’il existe dans la population une relation linéaire au niveau individuel, on retrouvera cette même relation au niveau des moyennes par cohorte, avec une réduction des biais liés aux aléas individuels.
L’estimation d’un modèle linéaire sur pseudo-panel n’est pas sans poser certains problèmes par rapport à un panel véritable, et nécessite généralement d’adapter légèrement la méthode d’estimation. Deaton (op. cit.) considère que les moyennes calculées par cohorte sont entachées d’erreurs de mesure en raison du nombre limité d’observations et propose un estimateur en conséquence. Verbeek et Nijman (1993) trouvent cependant que cet estimateur n’est pas convergent pour un nombre fini de périodes lorsque les effets spécifiques sont corrélés avec les variables explicatives et proposent un estimateur convergent (une généralisation de l’estimateur de Deaton). Verbeek et Nijman (1992) montrent par ailleurs que le problème des erreurs de mesure des moyennes de cohortes est négligeable si d’une part les cohortes contiennent chaque année un grand nombre d’observations (100 à 200) et si d’autre part les vraies moyennes par cohorte évoluent suffisamment au fil du temps. Dans ce cas les estimateurs standards de modèles à effets fixes (within ou différences premières) sont convergents, ce qui simplifie considérablement l’estimation. Enfin, Inoue (2008) développe un estimateur GMM efficace dans le cas où le nombre d’observations par cellule est grand relativement au nombre de cohortes et de périodes.
Nous construisons un pseudo-panel regroupant les enquêtes de 1978, 1982, 1986, 1992, 1996, 2004 et 2008. Les cohortes sont formées selon deux critères : l’année de naissance du chef de ménage[12] (par groupes de cinq années) et le niveau d’éducation du chef de ménages (5 niveaux d’éducation). Après regroupement des cohortes proches à trop faible effectif et élimination de certaines cohortes pour obtenir un pseudo-panel cylindré (nous ne retenons que les ménages dont la personne de référence est née entre 1925 et 1959, et n’exploitons pas l’enquête de 1969), nous obtenons 22 cohortes, soit 154 points. Les cellules (couples cohorte-année d’enquête) comptent entre 78 et 901 observations, pour une moyenne de 280 et un écart-type de 154; seules 7 cellules comptent moins de 100 observations. On se trouve donc dans le cas étudié par Verbeek et Nijman (1992) et Inoue (2008), dans lequel l’estimateur within est convergent. Le nombre total de cellules est relativement faible pour un travail de régression, mais n’est pas inhabituel dans la littérature empirique sur les pseudo-panels; Inoue cite plusieurs travaux employant des pseudo-panels à moins de 60 cellules. Pour chaque cellule, on calcule la moyenne des régresseurs de l’équation 5. Les prix sont tirés des données d’indices des prix à la consommation de Statistique Canada et les prix des différentes provinces sont harmonisés à l’aide des indices comparatifs des niveaux de prix à la consommation de 2008.
3. Résultats
3.1 Élasticités et prix virtuels
Nous estimons un modèle QUAIDS linéarisé (équation 5, tableaux 6 et 7) sur le pseudo-panel décrit en section 2.3, dans les deux dimensions transversale et temporelle. La pseudo-panélisation lève le problème habituel d’endogénéité de la dépense totale, puisqu’on ne considère que les moyennes par cohortes des coefficients budgétaires et de la dépense totale logarithmique; les termes de dépense totale logarithmique ne sont donc pas instrumentés. En outre puisque les régresseurs sont les mêmes dans toutes les équations du modèle, l’estimation est menée équation par équation (voir Zellner, 1962). Nous incluons trois variables de contrôle : le nombre d’unités de consommation du ménage, la proportion d’enfants dans le ménage, et une variable indicatrice pour le fait d’habiter en zone urbaine. L’estimation between revient à effectuer une régression sur les seules moyennes par cohorte, soit 22 observations; afin de gagner quelques degrés de liberté, nous excluons de l’équation 5 les termes de prix croisés[13]. Chaque coefficient budgétaire est donc exprimé en fonction des deux termes de dépense totale, de son propre prix et des trois variables de contrôle. Les résultats d’estimation sont présentés dans les tableaux 7 et 8 en annexe 4 et le tableau 3 donne les élasticités-revenu estimées en dimension temporelle (les estimations between ne donnent aucune élasticité-revenu significativement différente de 0).
Tableau 4
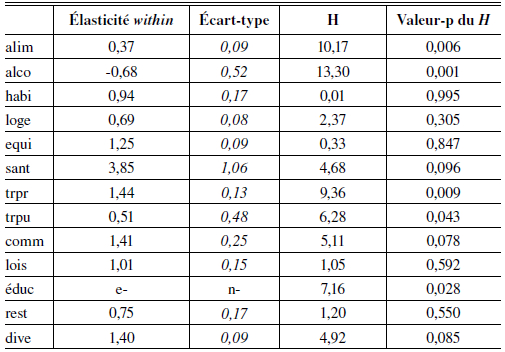
Élasticités-revenu estimées au point moyen en dimension temporelle et statistique de Hausman (H) pour les paramètres de dépense totale
Note : L’élasticité-revenu temporelle des dépenses d’éducation est omise car très élevée et non significative, ce qui peut s’expliquer par la mesure biaisée de ces dépenses dans les enquêtes (avec en particulier un nombre important de dépenses nulles) et par le financement différencié du financement public de l’éducation selon les provinces et son évolution.
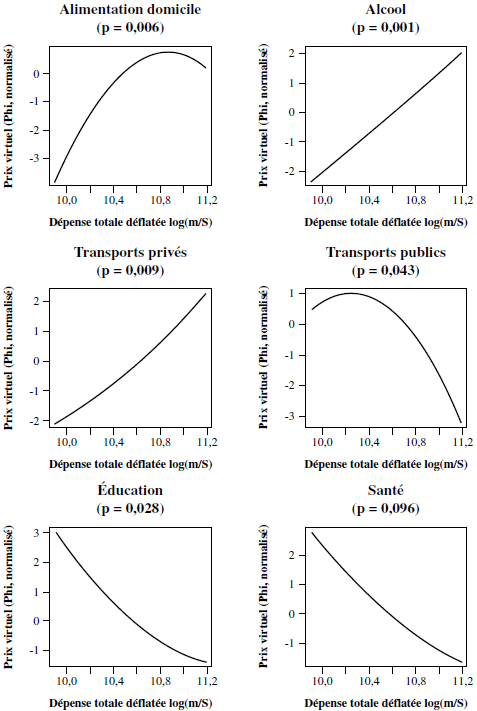
Nous effectuons des tests de Hausman afin de déterminer si les estimations en dimensions transversale et temporelle sont suffisamment différentes pour que l’on puisse détecter des variations de prix virtuels; la statistique est calculée par bootstrap[14]. Le tableau 4 donne pour chaque poste de dépense la statistique de Hausman calculée pour les termes de dépense totale (paramètres βi et λi dans l’équation 5). La différence des paramètres de dépense totale est significative au seuil de 5 % pour les postes alimentation à domicile, alcool et tabac, transports privés, transports publics, et éducation, et au seuil de 10 % pour les postes santé, communication et divers. Le graphique 1 en annexe 5 représente, pour ces postes, l’évolution des prix virtuels en fonction de la dépense totale. Les prix virtuels associés aux postes alimentation à domicile, alcool et tabac, et transports privés sont une fonction croissante de la dépense totale, et la relation n’est véritablement quadratique que dans le cas de l’alimentation, poste pour lequel le prix virtuel semble constant pour le quartile supérieur de la dépense totale. Autrement dit, la consommation de ces postes est plus coûteuse pour les ménages riches. A contrario, les prix virtuels associés aux transports publics et à l’éducation décroissent avec la dépense totale des ménages, de même que (si l’on retient un seuil de 10 %) pour les postes santé, communication et divers. Ces résultats sont conformes à ceux précédemment établis suivant la même méthode sur d’autres enquêtes, en particulier en ce qui concerne l’alimentation à domicile (voir Cardoso et Gardes, 1996a et Gardes et al., 2005).
Ces estimations montrent que les prix virtuels changent le long de la distribution des revenus. Dans la mesure où cette distribution des revenus entre les ménages tend à s’élargir au cours de cette période, comme le montrent les analyses économiques sur la polarisation des revenus relatifs des ménages canadiens, on peut s’attendre à une volatilité croissante des prix virtuels. En effet, l’élargissement de la distribution des revenus disponibles et la polarisation sont bien documentées à cause de la croissance des inégalités de revenu de marché et des changements dans les politiques de redistribution qui parviennent plus difficilement à contrer la hausse des inégalités des revenus du travail et de placement. Ce phénomène de polarisation est encore plus marqué dans les grandes villes canadiennes (voir Heisz, 2007). On observe effectivement une plus forte volatilité des prix virtuels après 1982, période de crise au Canada marquée par des modifications importantes des taux d’intérêt et d’autres déterminants économiques des choix des ménages. Cette volatilité croissante peut affecter les différences de prix virtuels entre classes socioéconomiques (c’est le comportement le plus probable) ou des différences intraclasses (donc dépendant d’autres caractéristiques des ménages que celles qui les définissent). Cette différenciation des prix virtuels traduit un effet plus prononcé des déterminants latents des choix des ménages, qui modifiera leur comportement d’une classe à l’autre ou à l’intérieur d’une même classe : ceci s’accompagnera donc d’une divergence interclasses ou intraclasse des structures de consommation que nous avons analysées dans la première partie de cet article.
Cette différenciation des prix virtuels entre les ménages entraînera, par les effets des changements de prix sur les dépenses, une différenciation des structures de consommation entre les classes socioéconomiques, dans la mesure où la dispersion des prix virtuels (donc des variables latentes que ces prix représentent) selon le niveau de vie s’applique à des classes définies en particulier par le niveau de vie des ménages. Cette différenciation des structures de consommation entre les ménages d’une même classe socioéconomique est apparue clairement dans les analyses présentées en section 1 : ceci tient possiblement au fait que la distribution des revenus et les contraintes liées à l’allocation du temps au sein du ménage (subissant les changements de leur offre de travail et la pression croissante des budgets-temps causée par la diversification des activités de loisirs) se serait différenciées en fin de période entre ménages d’une même classe. Le test de cette hypothèse pourrait se faire par une analyse précise de ces distributions. Elle nécessite une définition plus désagrégée des classes que la classification simplifiée que nous avons utilisée. Par ailleurs, les élasticités-prix diffèrent entre les ménages riches et les ménages pauvres, et cette différence s’accentue ou disparaît sur cette très longue période d’observation. Une analyse complète des effets des prix virtuels est donc complexe[15].
La classification des postes selon la croissance ou décroissance des prix virtuels associés à la dépense totale (tableau 5) est distincte de celle entre biens nécessaires et biens de luxe; ainsi l’alimentation et les transports publics sont, d’après les élasticités within du tableau 3, des biens de nécessité, alors qu’ils montrent des évolutions contraires de prix virtuels. On peut néanmoins rapprocher les variations de prix virtuels des évolutions transversales et temporelles observées en section 1.2 : alimentation à domicile et transports privés sont deux postes pour lesquels les écarts entre classes de richesse se sont estompés au cours du temps, alors que les inégalités se sont accentués pour les transports publics et la communication. Par ailleurs, les différences de prix virtuels sont interprétables en termes de coût temporel : l’alimentation à domicile, l’alcool à domicile et les transports privés sont des consommations particulièrement intenses en temps, ce qui explique pourquoi elles coûtent relativement plus chers aux ménages riches, qui ont un coût d’opportunité du temps supérieur. On notera que l’évolution des prix virtuels en fonction du revenu des ménages est parallèle pour toutes les enquêtes (avec un déplacement vers la droite de cette relation entraîné par l’augmentation du niveau de vie des ménages, ce qui montre bien que les prix virtuels dépendent du positionnement relatif des ménages dans l’échelle des revenus). L’analyse suivante approfondit cette interprétation temporelle, à partir d’une étude des dépenses temporelles des ménages.
Tableau 5
Variations des prix complets, estimés sur données monétaires et temporelles appariés
Note : * Filtrage de la population : élimination d’au plus 5 % de valeurs aberrantes.
** Écarts des élasticités-revenu des prix complets à leur moyenne pondérée (-0,5). Ces élasticités sont calculées comme les coefficients d’un ajustement double-logarithmique des prix complets (définis en fonction du coût d’opportunité estimé pour chaque ménage) par rapport au revenu par UC des ménages.
*** Prix complets définis par le taux de salaire net moyen du ménage et non par un coût d’opportunité estimé.
3.2 Prix virtuels, prix complets et revenu des ménages
Le graphique 1 en annexe 5 représente, pour ces postes, l’évolution des prix virtuels en fonction de la dépense totale[16]. Les prix virtuels associés aux postes alimentation à domicile, alcool et tabac, et transports privés sont une fonction croissante de la dépense totale, et la relation n’est véritablement quadratique que dans le cas de l’alimentation, poste pour lequel le prix virtuel semble constant pour le quartile supérieur de la dépense totale. Autrement dit, la consommation de ces postes est plus coûteuse pour les ménages riches. A contrario, les prix virtuels associés aux transports publics et à l’éducation décroissent avec la dépense totale des ménages, de même que (si l’on retient un seuil de 10 %) pour les postes santé, communication et divers. Ces résultats sont conformes à ceux précédemment établis suivant la même méthode sur d’autres enquêtes, en particulier en ce qui concerne l’alimentation à domicile (voir Cardoso et Gardes, 1996a et Gardes, Blundell et Lewbel, 2005).
Une des composantes possible des prix virtuels (donc de l’endogénéité liée ici aux variables latentes dépendant du revenu des ménages) tient à l’existence d’une contrainte de temps qui s’ajoute à la contrainte monétaire dans les choix de dépense des ménages. Becker a fourni un cadre à l’étude de cette contrainte dans son modèle d’allocation du temps qui ajoute à la dépense monétaire une valorisation du temps passé pour la consommation, la somme de ces deux éléments fournissant le coût complet de la consommation. On présente en annexe une méthode de définition des prix complets basée sur un appariement d’une enquête de budgets de famille avec une enquête de budgets-temps (Gardes, 2014, 2018) : la projection des temps passés à de grandes activités telles que l’alimentation ou le transport depuis les budgets-temps sur des ménages comparables observés dans les budgets de famille permet en effet, à partir d’une valorisation du temps (calibrée, par exemple par le taux de salaire moyen du ménage ou estimée), de mesurer la composante temporelle du prix complet de Becker. Ces proxies de prix complets sont calculés pour chaque ménage de l’enquête appariée (en utilisant un coût d’opportunité spécifique à chacun des ménages). L’évolution de ces proxies le long de la distribution des revenus est alors comparée à l’évolution parallèle des prix virtuels définis par la section précédente. On constate sur le tableau 6 que l’évolution relative des proxies des prix complets (par rapport à leur tendance générale à la décroissance) par rapport au revenu des ménages est comparable à celle qui a été observée pour les prix virtuels : ces deux prix augmentent le long de la distribution des revenus pour l’alimentation, les dépenses de logement et d’habillement, alors qu’ils diminuent ensemble pour les dépenses de transport (transports publics pour les prix virtuels). Dans le cas des dépenses de loisir, dont les prix complets tendent à diminuer, l’évolution des prix virtuels repérée dans nos analyses de la consommation canadienne est plutôt à la baisse en début de période mais croissante après 1990, ce qui est contraire à l’évolution des prix complets. La correspondance des évolutions des deux types de prix est observée pour cinq postes sur six. L’analyse de ces prix complets montre une concordance marquée avec les prix virtuels estimés précédemment.
On observe que les prix complets varient assez largement d’un ménage à l’autre, comme le montrent leurs écarts-types, en moyenne de 60 % des niveaux d’élasticités, ce qui, indiquant des différenciations sociales de contraintes et de ressources non monétaires, explique ainsi une partie des différences observées dans les choix de consommation des ménages. Par ailleurs, ces prix complets présentent une tendance générale à la diminution le long de la distribution des revenus, tendance qu’on a corrigée en calculant dans le tableau 6 l’écart des élasticités à leur moyenne. Les évolutions de ces élasticités normalisées par rapport au revenu des ménages recoupent assez largement les évolutions repérées pour les prix virtuels qui ont été estimés en section 3 : par exemple, le prix complet des dépenses alimentaires augmente avec le revenu (élasticité corrigée égale à +0,195) comme le prix virtuel de ces mêmes dépenses dont l’évolution croissante le long de la distribution des revenus est indiquée dans le graphique 1 de l’annexe B.
Enfin, on a montré par ailleurs dans Gardes (2014) que la prise en compte de ces prix complets dans une estimation des courbes de Engel permet d’expliquer 80 % de la différence des estimations d’élasticités-revenu en cross-section (sur une enquête, par comparaison de ménages aux revenus dissemblables) et en série temporelle (par l’analyse des changements de consommation et de revenu d’un même ménage au cours du temps), différence qui a servi, dans les analyses précédentes, à générer les prix virtuels liés à des variables latentes et permanentes corrélées au revenu dans la dimension transversale. Ceci montre de nouveau que les proxies de prix complets que nous avons définis mesurent également une partie importante des prix virtuels de variables latentes permanentes, qu’on a calculés dans la section précédente par la comparaison des estimations transversales et temporelles des effets-revenus. Cette évolution des prix complets en fonction du revenu permet donc de tenir compte assez largement des biais d’endogénéité des estimations en cross-section qui ont été analysés dans cet article.
L’appartenance à une classe socioéconomique implique l’existence de conditions de choix et de coût particuliers à cette classe, qui se traduiront dans notre modèle par un ensemble de prix virtuels différenciés par rapport au reste de la population. Une modification de ces conditions spécifiques (et donc des prix virtuels qui leur sont associés) changera les dépenses des ménages dans le sens d’une convergence vers les structures de dépenses des autres classes. La méthode permettant de révéler ces prix virtuels que nous avons développée dans cet article permet de mieux analyser les causes cachées des processus de convergence ou de divergence entre classes socioéconomiques que nos analyses descriptives ont révélés.
Conclusion
Notre étude de 40 années de données de consommation canadiennes (1969-2008) conduit à 3 conclusions principales. Premièrement, les structures de consommation des ménages sont très différenciées selon les classes socioéconomiques et la hiérarchie de ces structures reproduit celle des statuts sociaux. On constate en effet une évolution monotone, des pauvres aux riches, des parts budgétaires de la plupart des consommations. C’est par exemple nettement le cas des dépenses d’alimentation et de logement, dont on connaît le rôle structurant dans les choix budgétaires des ménages. Deuxièmement, les comportements moyens des classes convergent depuis le début des années 1970 et cette convergence est liée en particulier à la diminution de la part de l’alimentation, plus marquée au sein des classes pauvres. Troisièmement, à l’intérieur de chaque classe les comportements sont de plus en plus hétérogènes. Cette hétérogénéité intraclasse observée en fin de période mériterait une étude plus approfondie.
Ces constats nous ont amenés à analyser les différenciations sociales en termes de prix virtuels, qui correspondent à des contraintes ou des ressources non monétaires et permanentes des ménages. Ainsi, ce qui s’analyse habituellement comme des différences de comportements inexplicables se trouve traduit en termes de prix, et donc susceptible d’une analyse économique. La révélation de ces prix virtuels est opérée par une méthode originale et l’on montre qu’ils dépendent en particulier des temps utilisés pour les activités de consommation des ménages. Ceci révèle l’intérêt de lier la consommation marchande et la production domestique des ménages, dans le but d’expliquer les différenciations sociales de leurs choix.
Le calcul de prix virtuels à partir des enquêtes sur les dépenses des ménages révèle des coûts cachés correspondant à des contraintes ou des ressources non monétaires particulières à certains ménages. Ces coûts cachés sont souvent directement repérés par les services publics qui constatent par exemple que certains types de ménages (immigrés, pauvres ou personnes âgées) ne profitent pas de certaines réductions fiscales : il est ainsi connu que de nombreux Canadiens ne réclament pas tous les crédits d’impôt auxquels ils auraient droit dans leur déclaration de revenu. Ceci peut être dû à un manque d’information ou de temps disponible, tous éléments qui correspondent à des spécificités — contraintes ou ressources — non monétaires des individus. La puissance publique tentera généralement de réduire ces problèmes en mettant en oeuvre des politiques d’information ou des simplifications administratives qui, supprimant ces spécificités cachées, réduiront en même temps les prix virtuels qui leur sont associés. La réussite de cette politique publique pourrait donc être mesurée par la diminution des différences de prix virtuels entre individus que révéleraient des analyses statistiques ultérieures opérées selon notre méthode.
Parties annexes
Annexe
A. Résultats d’estimation QuAIDS sur pseudo-panel
Tableau 6
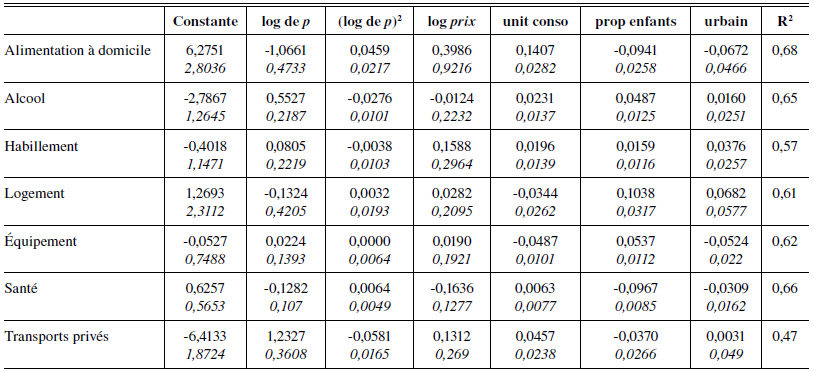
Résultats d’estimation within du modèle Quaids linéarisé, Écarts-types en italiques
Tableau 7
Résultats d’estimation between du modèle Quaids linéarisé, Écarts-types en italiques
B. Représentation des prix virtuels
Graphique 1
Représentation des Φi (approximation des prix virtuels liés au niveau de revenu, valeur-p de la statistique de Hausman entre parenthèses)
C. Estimation du coût d’opportunité du temps et des prix complets
C.3 Calcul de la valeur du temps
Un modèle de production domestique développé dans Gardes (2014) permet d’estimer le coût d’opportunité du temps localement, pour chaque ménage d’un échantillon, qui renseignerait à la fois les dépenses monétaires et le temps consacré à un ensemble d’activités, tels le travail marchand, l’alimentation, les transports, les loisirs… Un appariement d’enquêtes de budgets de famille avec des enquêtes de budgets-temps présenté plus loin fournit pour chaque ménage ce type de données.
On suppose que le ménage produit des biens finaux Qi en utilisant deux facteurs de production : une dépense monétaire mi et un temps ti soumis l’un et l’autre à des contraintes de revenu et de temps qu’on peut réunir, dans la tradition beckerienne, dans une contrainte de budget complet où le temps hors travail marchand est valorisé à un coût d’opportunité ω supposé différer du taux de salaire marchand moyen du ménage (net des taxes). L’utilité du ménage dépend directement de ces biens finaux. L’utilité comme les fonctions de production domestiques sont spécifiées comme des formes de Cobb-Douglas (dont les paramètres seront estimés pour chaque ménage et correspondront donc à des substitutions locales autour de l’équilibre du ménage, et non pas à la comparaison de ménages différents). Le programme d’optimisation du ménage s’écrit :
avec w le taux de salaire marchand net moyen du ménage, sous la contrainte de revenu complet :
Pour estimer le coût d’opportunité du temps, l’utilité peut s’écrire en fonction de moyennes géométriques des dépenses monétaires et temporelles :
La dérivation de l’utilité par rapport à ces dépenses moyennes permet de calculer ce coût d’opportunité comme le rapport des utilités marginales par rapport au revenu monétaire et au temps disponible :
Les substitutions entre les dépenses monétaires et temporelles utilisées pour une même activité, jointes aux partages de temps ou de monnaie entre deux activités, permettent de calculer les paramètres des fonctions de production et de l’utilité sous des contraintes d’absence d’économie d’échelle αi + βi = 1 et ![]() :
:
Cette dernière équation s’écrit encore sous la forme d’un système de (n-1) équations indépendantes qui permettra d’estimer ω :
C.4 Définition des prix complets
La dépense complète correspondant à une activité i s’écrit comme la somme de la dépense monétaire pi xih du ménage h et du temps passé à l’activité, que valorisera le coût d’opportunité du temps préalablement estimé : (pit + ωhtτih)xih. Cette dépense complète dépend des caractéristiques des ménages, qui déterminent sa participation totale à l’activité ti = τihxih en fonction du temps unitaire τih et de la quantité consommée xih. On suppose que la quantité de bien composite marchand x permet de mesurer également l’activité Q dans la mesure où la quantité du bien marchand est également supposée proportionnelle à la quantité d’activité (on généralise facilement au cas d’une activité nécessitant l’achat d’un vecteur de biens marchands). On suppose par ailleurs que le prix monétaire de l’unité d’activité, pi, est constant, c’est-à-dire identique pour l’ensemble des ménages. Un indicateur (proxy) des prix complets peut alors être défini par le rapport de la dépense complète et de sa composante monétaire :
Ce rapport, mesurable dès que sont connus dépense monétaire, temps imputé et coût d’opportunité du temps, contient en effet toute l’information sur le coût de l’activité provenant de l’usage de temps, défini par ωh et τih.
Deux hypothèses ont été faites pour cette mesure des prix complets : d’une part les fonctions de productions domestiques suivent une technologie de Leontief. Une autre définition des prix complets avec substituabilité des deux facteurs de production domestique donne des résultats d’estimation très proches (voir Gardes, 2014, 2018); d’autre part on suppose l’absence de production jointe (même laps de temps pour produire deux activités), ce qui est plus aisément admissible pour une définition étendue des activités telle que celle que nous adoptons.
C.5 Présentation des enquêtes et des méthodes d’appariement
Dans la méthode que nous proposons, notre objectif est d’obtenir, regroupés en un seul item, les dépenses monétaires et les dépenses en temps valorisées monétairement à partir des informations des enquêtes de budgets de famille et de budget-temps. Cet exercice relativement difficile et nouveau nécessite quelques hypothèses arbitraires concernant l’équivalence entre le temps passé sur diverses activités et les dépenses monétaires : nous supposons une parfaite substitution entre temps de travail domestique ou de loisir et temps de travail marchand et l’absence de production jointe liée à la production de plusieurs activités en même temps; par ailleurs, les temps d’activité domestique ou marchande sont valorisés par un coût d’opportunité du temps estimé.
L’Enquête sur les dépenses des ménages (Survey of Household Spending) de 1998 est appariée avec l’Enquête de budgets-temps contenue dans l’Enquête sociale générale (General Social Survey) de la même année. Ces deux enquêtes sont représentatives de la population canadienne. La taille du ménage et le nombre d’enfants n’étant pas renseignés de manière suffisamment précise pour une partie de l’échantillon du SHS, l’échantillon apparié est limité aux familles composées de deux adultes et au plus un enfant de moins de quatorze ans. L’appariement (opéré par Philip Merrigan) tient compte des problèmes de sélection lié aux faux zéros des dépenses monétaires ou temporelles par une estimation Tobit.
Remerciements
Ce travail a bénéficié du financement du contrat ANR MALDI 06-BLAN-0140, et du Conseil de Recherche en Sciences Humaines du Canada (CRSH). Nous remercions Philip Merrigan de nous avoir permis d’effectuer les calculs de la dernière section (3.2) à partir de l’appariement qu’il a réalisé entre les enquêtes canadiennes de 1998 sur les Dépenses des Ménages et leurs Budgets-Temps.
Notes
-
[1]
Le critère alimentaire devient de moins en moins pertinent dans les sociétés développées. Il est néanmoins malaisé de distinguer l’ensemble des biens nécessaires de leur complément, l’ensemble des consommations discrétionnaires, puisque celles-ci différent d’une classe socioéconomique à l’autre et entre les pays. On notera néanmoins que la dépense alimentaire était élevée au Canada en 1969 et que le temps de production domestique lié à l’alimentation reste élevé encore aujourd’hui. On note sur les graphiques du coefficient budgétaire de l’alimentation par rapport au revenu des ménages que la loi de Engel joue pour toutes les cohortes, mais de manière différente et par ailleurs amoindrie pour les plus jeunes. Une estimation de cette loi sur l’ensemble de la population est donc biaisée par cette disparité entre générations.
-
[2]
Communiquer avec simon.langlois@soc.ulaval.ca.
-
[3]
Toutes les statistiques calculées dans cette section sont pondérées par les poids d’échantillonnage de Statistique Canada, multipliés par le nombre d’unités de consommation du ménage, de sorte que l’unité d’analyse est l’individu.
-
[4]
Cette relation est partiellement due au fait que le poids de l’alimentation à domicile entre dans le calcul de l’IMPR, mais la hiérarchie est la même pour une partition en classes de la dépense totale.
-
[5]
Les différences transversales restent pourtant importantes, et les écarts relatifs entre classes sont relativement stables tout au long de la période (écart de 1 à 4 entre ménages pauvres et riches).
-
[6]
Nous entendons par inertie la généralisation de la variance à un nuage de points multidimensionnel, à savoir la somme des variances des différentes variables.
-
[7]
Les variances des estimateurs d’inertie, non reproduites ici, indiquent pour tous les types d’inertie des différences significatives au seuil de 5 % entre les enquêtes de 1969, 1986 et 2008.
-
[8]
On parle de sigma-convergence lorsque la dispersion des comportements diminue au cours du temps (voir Sala-i-Martin, 1996 dans le cadre de la convergence internationale des PIB).
-
[9]
La définition des prix virtuels dans Gardes et al. (2005) et ici n’est pas la même que celle de Neary-Roberts. Alors que chez ces derniers les prix virtuels correspondent aux prix complets, nous considérons que le prix virtuel est la partie non monétaire du prix complet, selon une spécification logarithmique
-
[10]
Pour un exposé plus détaillé, voir Gardes et al. (2005) ou Gardes (2011).
-
[11]
On peut citer au moins deux sources de mauvaise estimation des paramètres de prix : d’une part, comme noté plus haut, la linéarisation du système QUAIDS introduit un biais dans l’estimation, d’autre part les indices de prix par province que nous employons ci-dessous sont fortement corrélés entre les différents postes.
-
[12]
Un problème de pseudo-panélisation est posé par l’évolution de la définition du chef de ménage ou personne de référence au fil des enquêtes. La règle de stabilité de l’appartenance aux cohortes n’est pas strictement respectée.
-
[13]
L’estimation des effets de prix croisés serait par ailleurs rendue difficile par la forte corrélation des différents indices de prix.
-
[14]
Cette procédure est rendue nécessaire par le fait que, sous l’hypothèse nulle (corrélation nulle entre les effets fixes et les variables de dépense totale), aucun des deux estimateurs n’est efficace; la matrice de variance-covariance de la différence des estimateurs ne peut donc pas être estimée séparément par les variances des estimateurs.
-
[15]
Cette analyse nécessite une estimation des élasticités-prix par sous-population, puis une microsimulation de ces effets-prix entre les classes sociales et intraclasse.
-
[16]
On notera que les prix virtuels ont été générés ici par la seule dimension revenu des variables latentes.
Bibliographie
- Aguiar, M. A., E. Hurst et L. Karabarbounis (2013), « Time Use during the Great Recession », American Economic Review, 103(5) : 1664-96.
- Alpman, A. et F. Gardes (2015), « Time Use during the Great Recession–A Comment », Cahiers de recherche du CES, 2015.12.
- Banks, J., R. Blundell et A. Lewbel (1997), « Quadratic Engel Curves and Consumer Demand », Review of Economics and Statistics, 79(4) : 527-539.
- Barten, A. (1964), « Family Composition, Prices and Expenditure Patterns », in Hart, P., G. Mill et J. Whittaker (éds), Economic Analysis for National Income Planning, Butterworth.
- Becker, G. (1965), « A Theory of the Allocation of Time », The Economic Journal, 75(299) : 493-517.
- Boelaert, J. (2012), « La convergence internationale et intranationale des structures de consommation des ménages », Thèse de doctorat, Université Paris 1 Panthéon-Sorbonne, Centre d’économie de la Sorbonne.
- Cameron, A. C. et P. K. Trivedi (2005), Microeconometrics, Methods and Applications, Cambridge University Press.
- Cardoso, N. et F. Gardes (1996a), « Caractérisation et analyse des comportements de consommation des ménages pauvres sur données individuelles françaises », Revue économique, 47 : 687-698.
- Cardoso, N. et F. Gardes (1996b), « Estimation de lois de consommation sur un pseudo-panel d’enquêtes de l’Insee (1979, 1984, 1989) », Economie et Prévision, 5 : 111-125.
- Caussat, L., M. Lelièvre et E. Nauze-Fichet (2006), « Les travaux conduits au niveau européen sur les indicateurs sociaux de pauvreté », DREES, Communication au 11e colloque de l’Association de Comptabilité Nationale.
- Christensen, M. (2014), « Heterogeneity in Consumer Demands and the Income Effect : Evidence from Panel Data », The Scandinavian Journal of Economics, 116(2) : 335-355.
- Coulangeon, P. (2004), « Classes sociales, pratiques culturelles et styles de vie. Le modèle de la distinction est-il (vraiment) obsolète? », Sociologie et sociétés, 36(1) : 59-85.
- Deaton, A. (1985), « Panel Data from Time Series of Cross-sections », Journal of Econometrics, 30 : 109-126.
- Deaton, A. et J. Muellbauer (1980), « An Almost Ideal Demand System », The American Economic Review, 70(3) : 312-326.
- Division Statistique de l’ONU (1993), Système de Comptabilité Nationale 1993, ONU.
- Fortin, N., D. A. Green, T. Lemieux, K. Milligan et W. C. Riddell (2012), « Canadian Inequality : Recent Developments and Policy Options », Canadian Public Policy/Analyse de politiques (IRPP), 38(2) : 121-145.
- Fortin, N., et T. Lemieux (2015), « Change in Wage Inequalitiy in Canada : An Interprovincial Pespective », Canadian Journal of Economics, 48 (2) : 682-713.
- Gardes, F. (2011), « Différenciation sociale et dynamique des prix dans une économie walrassienne », inBaranzini, R., A. Legris et L. Ragni (éds): Léon Walras et l’équilibre économique général, Recherches récentes, Paris, Editions Economica, p. 291-307.
- Gardes, F. (2014), « Full Price Elasticities and the Value of Time. A Tribute to the Beckerian Model of the Allocation of Time », Cahiers de recherche du CES, 2014.14.
- Gardes, F. (2018), « The Estimation of Price Elasticities and the Value of Time in a Domestic Framework: An Application on French Micro-data », Annals of Economics and Statistics, forthcoming.
- Gardes, F., G. J. Duncan, P. Gaubert, M. Gurgand et C. Starzec (2005), « Panel and Pseudo-panel Estimation of Cross-sectional and Time Series Elasticities of Food Consumption : The Case of US and Polish Data », Journal of Business & Economic Statistics, 23(2) : 242-253.
- Gardes, F., P. Gaubert et S. Langlois (2000), « Pauvreté et convergence des consommations au Canada », Canadian Review of Sociology and Anthropology, numéro 1 : 1-27.
- Gardes, F. et S. Langlois (1995), « Une nouvelle mesure pour analyser la pauvreté au Québec : l’indice synthétique de pauvreté-richesse », Service Social, 44(3) : 29-53.
- Gardes, F., S. Langlois et S. Bibi (2010), « Pauvreté et convergence des comportements de consommation entre classes socioéconomiques au Québec », 1969-2006, Recherches sociographiques, 51(3) : 343-364.
- Heisz, A. (2007), « Inégalité et Redistribution du Revenu au Canada : 1976 à 2004 », Statistique Canada, Direction des études analytiques, document n° 298.
- Inoue, A. (2008), « Efficient Estimation and Inference in Linear Pseudo-panel Data Models », Journal of Econometrics, 142(1) : 449 - 466.
- Lollivier, S. et D. Verger (1997), « Pauvreté d’existence, monétaire ou subjective sont distinctes », Economie et Statistique, 308-309-3010 : 113-142.
- Mundlak, Y. (1978), « On the Pooling of Time Series and Cross-section Data ». Econometrica, 46(1) : 483-509.
- Neary, J. P. et K. W. S. Roberts (1980), « The Theory of Household Behaviour under Rationing », European Economic Review, 13(1) : 25-42.
- Pashardes, P. (1993), « Bias in Estimating the Almost Ideal Demand System with the Stone Index Approximation », The Economic Journal, 103(??) : 908-915.
- Peterson, R. A. et R. M. Kern (1996), « Changing Highbrow Taste : From Snob to Omnivore », American Sociological Review, 61 : 900-907.
- Sala-i-Martin, X. (1996), « The Classical Approach to Convergence Analysis ». The Economic Journal, 106(437) : 1019-1036.
- Selvanathan, S. (1993), A System-Wide Analysis of International Consumption Patterns, Kluwer Academic Publishers.
- Theil, H. et K. W. Clements (1987), Applied Demand Analysis : Results from System-Wide Approaches, Ballinger, Cambridge.
- Theil, H., F. E. Suhm et J. F. Meisner (1981). International Consumption Comparisons : A System-Wide Approach, Elsevier.
- Verbeek, M. et T. Nijman (1992), « Can Cohort Data be Treated as Genuine Panel Data? », Empirical Economics 17 : 9-23.
- Verbeek, M. et T. Nijman (1993), « Minimum MSE Estimation of a Regression Model with Fixed Effects from a Series of Cross-sections », Journal of Econometrics, 59 : 125-136.
- Zellner, A. (1962), « An Efficient Method of Estimating Seemingly Unrelated Regression Equations and Tests for Aggregation Bias », Journal of the American Statistical Association, 57 : 348-368.
Liste des figures
Graphique 1
Représentation des Φi (approximation des prix virtuels liés au niveau de revenu, valeur-p de la statistique de Hausman entre parenthèses)
Liste des tableaux
Tableau 1
Dépense totale moyenne des ménages (par unité de consommation) selon la typologie IMPR et l’année (en dollars canadiens courants)
Tableau 2
Coefficients budgétaires moyens par classe socioéconomique (typologie IMPR) et par année (en pourcentage)
Note : ALIM : dépense alimentaire à domicile; ALCO : alcool à domicile et tabac; HABI : habillement; LOGE : dépenses de logement (y compris loyer fictif); EQUI : équipement ménager; SANT : dépenses d’hygiène personnelle et santé; TRPR : transports privés; TRPU : transports publics; COMM : dépenses de communication; LOIS : loisirs; EDUC : éducation; REST : restaurants et hôtels; DIVE : autres dépenses.
Tableau 3
Inertie des structures de consommation des ménages (totale, intra, inter et par classe, IMPR, × 1000)
Tableau 4
Élasticités-revenu estimées au point moyen en dimension temporelle et statistique de Hausman (H) pour les paramètres de dépense totale
Note : L’élasticité-revenu temporelle des dépenses d’éducation est omise car très élevée et non significative, ce qui peut s’expliquer par la mesure biaisée de ces dépenses dans les enquêtes (avec en particulier un nombre important de dépenses nulles) et par le financement différencié du financement public de l’éducation selon les provinces et son évolution.
Tableau 5
Variations des prix complets, estimés sur données monétaires et temporelles appariés
Note : * Filtrage de la population : élimination d’au plus 5 % de valeurs aberrantes.
** Écarts des élasticités-revenu des prix complets à leur moyenne pondérée (-0,5). Ces élasticités sont calculées comme les coefficients d’un ajustement double-logarithmique des prix complets (définis en fonction du coût d’opportunité estimé pour chaque ménage) par rapport au revenu par UC des ménages.
*** Prix complets définis par le taux de salaire net moyen du ménage et non par un coût d’opportunité estimé.
Tableau 6
Résultats d’estimation within du modèle Quaids linéarisé, Écarts-types en italiques
Tableau 7
Résultats d’estimation between du modèle Quaids linéarisé, Écarts-types en italiques








 10.7202/009582ar
10.7202/009582ar