La rigidité comme paradigme socio-politique

Saint-Paul, Gilles

doi:https://doi.org/10.7202/1035109ar

Introduction

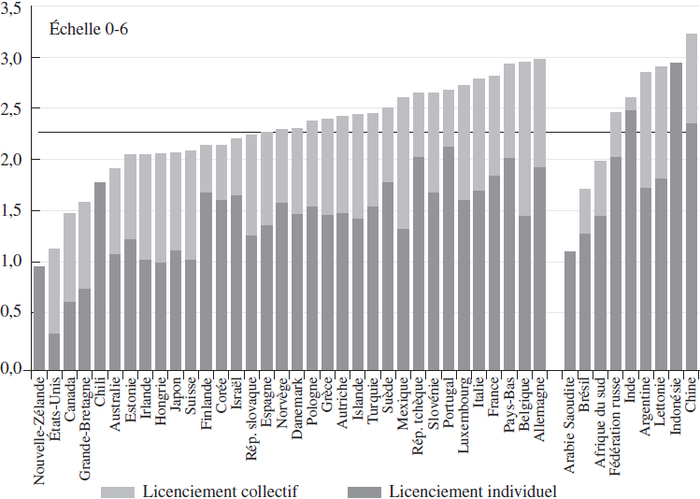
De nombreux analystes déplorent les rigidités de la société française. Cela signifie à la fois un fonctionnement économique sclérosé en régime courant, et qui se traduirait par des incitations faibles à investir, à embaucher, à innover, à se réorienter ou à accumuler du capital humain, et des blocages institutionnels, politiques et sociétaux lorsqu’il s’agit de mettre en place des réformes structurelles. On constate en général une réglementation excessive des marchés si on compare la France à d’autres pays avancés. Ces réglementations frappent de nombreux secteurs, et notamment ceux qui jouent un rôle majeur dans l’existence, comme le marché du travail ou celui du logement. Ces rigidités sont illustrées par de nombreuses décisions politiques. On peut mentionner l’interdiction du travail du dimanche, l’interdiction du travail à mi-temps, ou le plafond sur les loyers établi par la récente loi Duflot. Ces anecdotes corroborent les conclusions que l’on peut généralement tirer des comparaisons internationales de divers indicateurs de rigidité des marchés. Par exemple, la France est le quatrième pays de l’OCDE le plus rigide en ce qui concerne la législation de protection de l’emploi (graphique 1) et se caractérise également par un indicateur élevé de contrôle de l’État sur l’économie (graphique 2).

Graphique 1

**Indice de protection de l’emploi de l’OCDE**

Graphique 2

**Indicateur de contrôle étatique de l’OCDE, 2008**

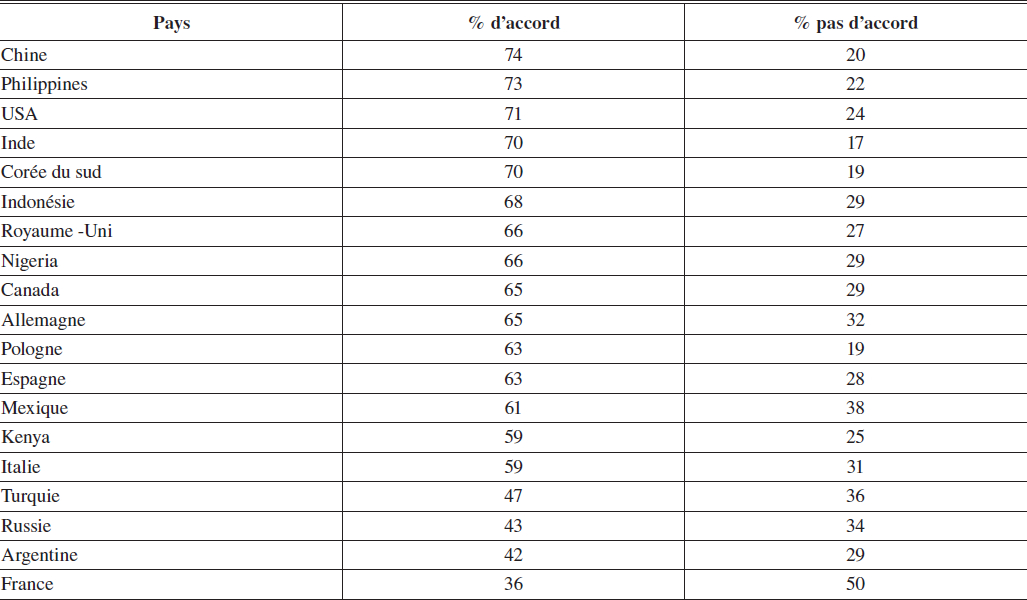
Mais ces rigidités ne se limitent pas à la sphère économique. S’il était généralement considéré qu’elles constituent des aberrations, un gouvernement démocratiquement élu abolirait purement et simplement une grande partie d’entre elles. Or, on constate que l’opinion publique n’est pas défavorable à ces interventions et plus généralement que l’attitude de la population envers l’économie de marché est particulièrement négative en France comparée à d’autres pays, comme en témoigne un sondage récent (tableau 1)[1].

Tableau 1

**Réponse à la question : « L’économie de marché est le meilleur système sur lequel fonder l’avenir du monde »**

Ces réponses corroborent les attitudes générales des Français face au rôle de l’État dans l’économie, telles que celles observées dans le WorldValueSurvey et résumées dans le tableau 2. On note en particulier une forte aversion à la concurrence en France comparé à ses homologues anglo-saxons, ainsi qu’une volonté plus forte d’égalisation des revenus.

Réponses au WorldValueSurvey en France, aux États-Unis, au Royaume-Uni et au Canada — Tableau 2

**Réponses au *WorldValueSurvey* en France, aux États-Unis, au Royaume-Uni et au Canada**

La rigidité économique est donc soutenue par un système de croyances[2]. Inversement, l’existence d’une société rigide économiquement peut renforcer des croyances négatives erronnées sur l’économie de marché (Saint-Paul, 2010, pour certains résultats allant dans ce sens).

Un autre facteur de persistance des rigidités est le fait que les agents vont s’organiser, en dehors des circuits habituels du marché, pour pallier ces rigidités. Ces activités se traduisent par l’accumulation d’un capital organisationnel, qui, s’il est inégalement réparti, peut conduire à l’émergence de lobbies opposés à la déréglementation des marchés. C’est ce type de phénomène que nous discutons ici.

Dans une économie où les marchés fonctionnent mal, d’autres structures sociales sont appelées à les remplacer. En particulier, les réseaux sociaux peuvent jouer le rôle d’un circuit au sein duquel les échanges sont conduits[3]. Le « capital social », c’est-à-dire, ici, la taille du réseau de connaissances auquel un individu peut accéder, joue alors un rôle important dans les ressources que cette personne peut obtenir. On peut en conclure que les dysfonctionnements économiques vont se traduire par un investissement plus élevé en capital social.

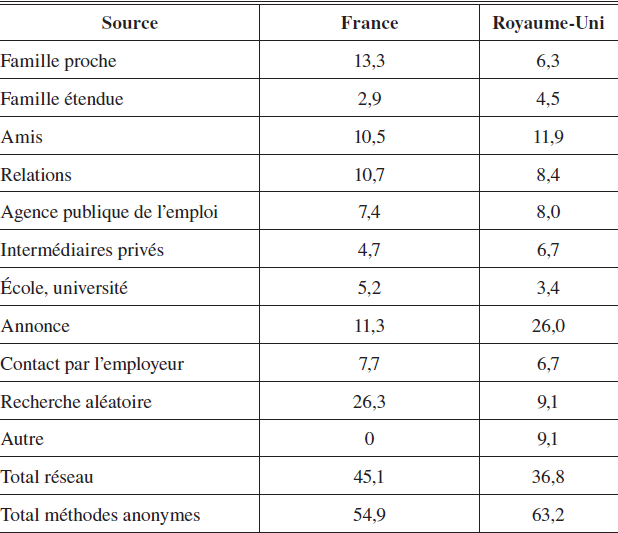
Cette hypothèse est-elle corroborée par les données? Le rôle des réseaux sociaux est assez bien documenté dans l’une des activités économiques : il s’agit de la recherche d’emploi[4]. On peut donc envisager de comparer les méthodes de recherche d’emploi entre un pays rigide et un pays flexible. Il serait naturel de choisir la France comme pays rigide et les États-Unis comme pays flexible. Mais il existe malheureusement d’importants effets fixes. Les enquêtes sociologiques semblent montrer que le lien social est particulièrement dégradé en France. Par exemple, d’après l’ISSP, 67 % des personnes interrogées admettent n’avoir aucun ami proche sur leur lieu de travail, contre seulement 22 % aux Etats-Unis. Pour cette raison, il est sans doute plus judicieux de comparer la France avec le Royaume-Uni. La vague 2001 du InternationalSocialSurveyProgramme (ISSP) demande aux participants leurs sources d’information sur les emplois disponibles. Ces données nous permettent d’établir le tableau 3.

Tableau 3

**Sources d’information pour la recherche d’emploi (%)**

On constate que les réseaux sociaux jouent un plus grand rôle dans la transmission d’information en France qu’au Royaume-Uni. On note au passage que les « weakties » (Granovetter, 1973) ne semblent pas plus utiles que les « strongties ». La famille proche et les amis jouent un rôle plus important que la famille éloignée et les relations.

Il n’est en revanche pas clair que la taille des réseaux sociaux soit plus élevée en France qu’au Royaume-Uni. Comme le montre le tableau 4, en ce qui concerne les amis, c’est l’inverse qui est le cas.

Cependant, ces mêmes données montrent que les Français s’investissent plus dans les relations familiales que les Britanniques. Ce sont d’ailleurs celles-ci qui expliquent l’essentiel de la différence entre les deux pays concernant les méthodes de recherche d’emploi. Le tableau 5 nous donne la fréquence des visites à différents membres de la famille (ainsi qu’aux amis) dans les deux pays.

Tableau 5

**Pourcentage des sondés qui rendent visite à la relation concernée plus d’une fois par mois**

Si ces données sont mitigées, elles ne sont donc pas incompatibles avec l’idée que les Français investissent plus dans les réseaux sociaux et que ceux-ci sont importants dans la capacité à conduire des transactions économiques. On pourrait même expliquer la moindre importance des amis en France comparé à la Grande-Bretagne par un effet de substitution favorable à la famille, qui serait dû au fait que celle-ci joue un rôle dans l’accès à certains biens, tandis que c’est moins le cas pour les amis. Cette interprétation est cohérente avec le tableau 5 ainsi qu’avec le modèle théorique qui sera exposé plus bas.

Il est difficile de trouver des études empiriques qui documenteraient le fait que des considérations économiques comme l’accès au marché joueraient un rôle important dans la formation des réseaux. On peut cependant mentionner l’étude de Comola (2007) sur la Tanzanie.

Une question intéressante que l’on peut se poser est la suivante : en quoi le développement des réseaux sociaux favoriserait-il la persistence des rigidités? On peut d’abord penser que le capital social d’un individu est une forme de rente, et que l’objectif de conserver cette rente rigidifie le comportement des individus. En effet, toute décision de mobilité géographique ou professionnelle implique, dans une certaine mesure, l’obsolescence du réseau social. Par exemple, si le contrôle des loyers rend difficile l’obtention d’un logement, mes connaissances me seront utiles pour en obtenir un; une décision de mobilité géographique est alors coûteuse, parce qu’elle est associée à la perte de mon réseau social, c’est-à-dire à une hausse du coût d’obtention d’un logement. En revanche, dans un système de marché, les conséquences de cette décision ne sont pas aussi graves car je sais que dans ma nouvelle résidence je pourrai obtenir un logement au prix de marché.

On voit donc qu’une société où les échanges reposent sur les réseaux sociaux est moins « fluide », plus sclérosée qu’une société où les échanges passent par le marché. C’est parce que le réseau social est une forme de capital dans lequel on a investi, et que sa portabilité n’est que partielle. En revanche, dans une économie de marché « pure », la capacité à effectuer des transactions sur le marché n’est pas une forme de capital, elle ne peut donc se déprecier et elle est garantie indépendamment des décisions faites par l’individu.

Il existe d’autres vecteurs de persistence d’une société rigide. Les mécanismes politiques sont particulièrement intéressants. On peut montrer que si le marché du travail est rigide, au sens où les travailleurs en place ont un bien-être strictement supérieur à celui de travailleurs de mêmes caractéristiques, mais qui se trouvent au chômage, alors sous certaines conditions on s’attend à une persistance élevée des choix politiques – en d’autres termes on voit apparaître des résistances aux réformes (Saint-Paul, 1996). Ces résistances sont dues au fait qu’une réforme se traduisant par des réallocations d’emploi, les travailleurs en place éprouvent une aversion envers celles-ci, à cause du fait qu’elles sont associées à des pertes d’emploi et donc de rente.

Le développement des réseaux sociaux peut créer des mécanismes politiques du même genre. Dans un marché qui fonctionne mal, et où les individus ont développé leurs réseaux sociaux afin de pallier ces dysfonctionnements, il existe des groupes d’intérêts en faveur du maintien de la rigidité du marché (dans la mesure, évidemment, où celle-ci comporte quelques avantages). Ce sont ceux qui s’en tirent bien dans la situation rigide, c’est-à-dire dont le capital social est relativement élevé, tandis que de par leur situation économique ils sont peu exposés aux pertes d’efficacité engendrées par l’imperfection du marché.

Le reste de cette étude développe une analyse théorique de ces mécanismes.

1. Imperfections de marché et réseaux sociaux : un modèle

Voyons comment les idées que nous venons d’énoncer peuvent être illustrées à l’aide d’un modèle simple.

Il existe un continuum de biens de masse totale égale à 1, ainsi qu’un bien générique utilisé comme numéraire. La consommation de chaque bien (autre que le numéraire) est indivisible et égale à 0 ou 1. Il y a N consommateurs, qui sont chacun dotés de R unités du numéraire. Soit j un consommateur et i un bien. Le consommateur j dérive une utilité égale à v_ij du fait de consommer une unité du bien i. Cette quantité diffère selon les consommateurs, et pour un consommateur donné elle est distribuée uniformément sur [0, v] ceci de façon non corrélée entre consommateurs. Comme les biens forment un continuum, ceux-ci peuvent être réindexés de telle sorte que le bien i donne une utilité vi (mais cette réindexation est spécifique au consommateur j). Enfin, la contribution du numéraire à l’utilité du consommateur est égale à la quantité consommée notée c. On peut donc écrire sa fonction d’utilité comme suit :

Le classement des biens diffère de façon aléatoire et uniforme entre consommateurs. Pour un consommateur donné, l’utilité dérivée d’un bien sélectionné au hasard est donc distribuée de faço uniforme sur [0, v], il en va de même pour l’utilité dérivée d’un bien donné par un consommateur sélectionné au hasard.

On suppose que tous les biens sont symétriques et que leur prix, exprimé en termes de numéraire, est égal à p. Donc, pour un consommateur donné, le bien i est consommé si et seulement si vi > p. Ce consommateur voudra donc consommer tous les biens tels que i > i* = p / v. Le nombre de biens consommés est donc égal à 1- p / v et l’utilité indirecte peut être également calculée, ce qui donne :

Pour un bien donné, la probabilité qu’un consommateur choisi au hasard en veuille est égale à P(v_i > p) = 1− p / v Cette quantité est aussi égale à la probabilité qu’un consommateur donné veuille d’un bien choisi au hasard.

L’offre totale d’un bien quelconque i est supposée inélastique et égale à X. De plus, on suppose que X < N, ce qui implique qu’à l’équilibre chaque consommateur ne peut pas consommer de tous les biens. Il est facile de voir que le prix d’équilibre d’un bien quelconque est celui qui satisfait à

Ce prix est donc égal à p* = v(1− X / N).

1.1 Le rôle du rationnement

Supposons maintenant que le gouvernement impose un plafond sur le prix de chaque bien égal à p̅ < p*. La demande pour chaque bien est supérieure à l’offre et il y a rationnement. On suppose ici que le rationnement se fait de façon purement aléatoire, selon le mécanisme suivant. Pour chaque bien, il existe Q consommateurs qui bénéficient d’un droit à consommer ce bien. La probabilité qu’un consommateur donné obtienne un tel permis est donc Q / N. Un consommateur titulaire d’un tel droit peut décider, s’il le veut, d’acquérir une unité du bien au prix officiel égal à p̅. La quantité de droits à consommer est ajustée de façon à ce que la totalité de l’offre soit absorbée. Comme la probabilité qu’un droit à consommer soit effectivement utilisé est égale à 1− p̅ / v, le nombre de droits est tel que

En utilisant la relation (1), on voit que l’on doit avoir

On voit que Q décroît lorsque p̅ baisse : la réduction du nombre de droits à consommer est la seule façon de conmpenser le fait que la demande pour chaque bien augmente. Par ailleurs, lorsque le prix régulé concide avec celui de l’équilibre Walrasien, c’est-à-dire p̅ = p*, alors Q = N, ce qui signifie que tous les consommateurs reçoivent des droits à consommer pour tous les biens.

1.2 Le rôle des réseaux sociaux

Dans ce qui précède, un consommateur j qui reçoit un droit à consommer un bien i tel que v_ij < p̅ ne s’en sert pas. Supposons maintenant que les droits inutilisés peuvent être échangés au sein d’un réseau social. Pour prendre en compte cette possibilité, on peut modifier le modèle de la manière suivante. Le processus de rationnement se fait en deux étapes. Lors de la première étape, Q consommateurs, choisis au hasard, reçoivent des droits, pour chacun des biens. Ils les utilisent si c’est optimal pour eux. Lors de la seconde étape, une fraction π des consommateurs sont appariés ensemble de façon aléatoire et échangent de l’information sur les droits qu’ils détiennent encore. Ce processus d’appariement définit donc un réseau social tel que chaque individu a une ou zéro connection, et π s’interprète comme la densité du réseau. Un consommateur j utilisera les droits de celui avec qui il est apparié pourvu que cela soit rentable, c’est-à-dire pourvu que les biens concernés satisfassent à la condition v_ij > p̅.

Voyons maintenant le niveau des échanges que permet ce processus. Un consommateur donné reçoit des droits à consommer une masse de biens égale à Q / N. Il utilise une fraction 1− p̅ / v de ces droits et le nombre de biens qu’il désire acquérir et pour lesquels il n’a pas de droit est égal à 1− p̅ / v − Q(1− p̅ / v) / N = (1− p̅ / v)(1− Q / N). Par ailleurs, il possède (Q / N)(p̅ / v) droits inutilisés qu’il échangera dans le réseau social.

Lorsque deux consommateurs sont appariés dans le réseau social, le premier offre donc au second (Q / N)(p̅ / v) droits à consommer inutilisés. La probabilité que le second veuille consommer l’un d’eux est égale à (1− p̅ / v)(1− Q / N). Chaque participant réalise donc une quantité totale :

d’achats additionnels lors de la participation au réseau social. Le nombre de droits émis par le gouvernment doit donc être tel que la quantité de chaque bien échangée est égale à X, soit

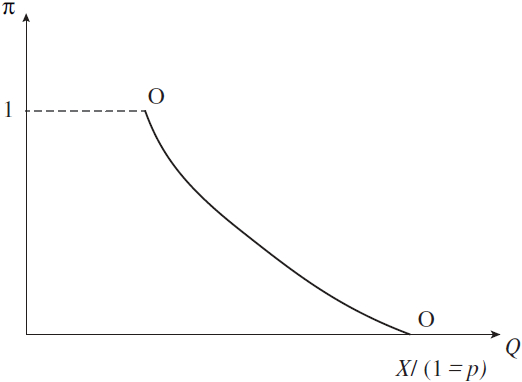
Cette formule détermine une relation décroissante entre Q, la quantité de droits émise, et π, l’intensité du réseau social. Elle reflète le fait que plus π est élevé, plus les agents vont utiliser leurs droits efficacement grâce au réseau social, et donc plus le nombre de droits émis doit être faible pour éviter que la demande de biens n’excède l’offre. Cette relation est représentée par la courbe OO sur le graphique 3 dans le plan (Q, π ). Une hausse du prix p̅ déplace la courbe OO vers le haut. En effet, une hausse de réduit la probabilité qu’un droit soit utilisé, et donc doit être compensée par une hausse du nombre de droits (cette propriété était également vraie en l’absence de réseaux sociaux). De plus, la pente de la courbe OO est plus grande, en valeur absolue, lorsque p̅ est plus élevé. Cela signifie que le nombre de droits émis est moins sensible à l’intensité du réseau social lorsque le rationnement est plus faible. Dans le cas limite où ce dernier disparaît, on a p̅ = p*, et Q = N, et la courbe devient verticale. Dans un marché en équilibre, le réseau social ne joue plus de rôle allocatif. Les agents consomment tous les biens qui peuvent augmenter leur utilité lors de la première étape du processus. Il ne reste aucun bien qu’ils désirent consommer au prix de marché lors de la deuxième étape.

Graphique 3

**L’effet du réseau sur le nombre de droits à consommer**

Le réseau social joue en quelque sorte le même rôle qu’un marché secondaire, mais pour simplifier on suppose que chaque membre transfère les droits de consommation à la personne avec laquelle il est apparié sans contrepartie monétaire (puisque la valeur résiduelle d’un droit est nulle pour celui qui le détient au départ, cela serait le cas si, dans la négociation bilatérale entre deux consommateurs appariés entre eux, chaque partie avait la totalité du pouvoir de marchandage sur les droits qu’elle acquiert, et inversement aucun pouvoir de marchandage sur les droits qu’elle vend).

On notera que contrairement à ce qui se passe chez Kranton et Minehart (2001), le réseau social est un vecteur d’échange alternatif au marché, et qui lui est inférieur. Chez ces auteurs, au contraire, le réseau constitue l’infrastructure incontournable au sein de laquelle les transactions du marché sont conduites.

1.3 L’investissement dans les réseaux sociaux

Je vais maintenant introduire l’autre partie importante du modèle, à savoir l’investissement endogène dans le réseau social.

On suppose que chaque individu peut investir dans sa propre probabilité d’appariement π à un coût c(π). Dans un équilibre symétrique, tous les agents choisiront la même valeur de π, et les calculs de la sous-section précédente restent valables. La quantité c(π) peut prendre en compte aussi bien le coût en termes de ressources de l’établissement d’un réseau, que le bénéfice en termes d’utilité d’avoir des connaissances. On supposera , , et , ce qui garantit un optimum intérieur pour π.

Calculons maintenant l’utilité d’un agent. Un individu consomme

s’il n’est pas apparié, et

s’il l’est. Le nombre de biens consommé par un individu avec une probabilité d’appariement égale à π est donc égal à

La valeur de ces biens pour l’individu est distribuée uniformément sur [p̅, v]. Cela permet de calculer l’utilité de l’agent, qui est égale à

On peut ensuite calculer la condition du premier ordre pour la valeur d’équilibre de π, et on obtient

Cette condition définit une relation non monotone entre Q et π, représentée sur le graphique 4 par la courbe PP (la valeur π₀ est telle que . Le membre de gauche est le coût marginal d’augmenter la probabilité de rencontre d’une unité. Le membre de droite est le bénéfice marginal. On peut le réécrire comme , soit le produit du nombre de transactions effectuées au sein du réseau social, fois le surplus moyen de ces transactions, égal à .

Graphique 4

**Détermination de la taille optimale du réseau social**

La courbe PP représente l’effet sur l’intensité du réseau social du nombre de droits à consommer. Un aspect intéressant est qu’elle n’est pas monotone. Si Q est proche de N, le rationnement est faible et la valeur du réseau en tant que vecteur d’échanges économiques est également faible; les individus ne recherchent pas de droits supplémentaires à consommer, car ils ont consommé presque tous les biens qu’ils désirent lors de la première étape du processus. L’intensité du réseau social est alors proche de π₀, qui est celle qu’on obtiendrait si la taille du réseau ne dépendait que de ses effets hédoniques. Si Q est très faible, les consommateurs sont très demandeurs de droits pendant la seconde étape, mais ils savent que la personne avec laquelle ils seront appariés en détient très peu. L’intérêt d’investir dans le réseau afin de consommer plus est à nouveau très faible et π est proche de π₀. Pour des valeurs intermédiaires de Q, la valeur du réseau social est nettement supérieure à sa valeur hédonique car il permet de réaliser des échanges supplémentaires. Son intensité sera donc significativement supérieure à π₀. On peut interpréter cela comme le fait que l’on socialise avec des gens « que l’on n’aime pas » afin de bénéficier de leurs droits à consommer inutilisés.

1.4 L’équilibre

L’équilibre de ce modèle est déterminé par l’intersection des courbes OO et PP. Dans ce qui suit, je supposerai que cet équilibre est unique et que, localement, PP est au-dessus de OO à gauche du point d’intersection (graphique 5). Cette situation correspond à une hypothèse de stabilité heuristique de l’équilibre. En effet, OO représente la détermination de Q comme fonction de π par les autorités, tandis que PP représente celle de π comme fonction de Q par les individus privés qui investissent dans les réseaux sociaux.

Graphique 5

**Détermination de l’équilibre**

Quel est l’effet du prix administré, p̅, sur l’intensité d’équilibre du réseau social? Les formules qui précèdent montrent que cet effet est complexe. Cependant on peut montrer qu’il est nécéssairement non monotone et qu’on a π = π₀ pour p̅ = 0 et pour p̅ = p*, ce qui implique un effet nécessairement positif au voisinage de p̅ = 0 et négatif au voisinage de p̅ = p*. En effet, le nombre de transactions sur le réseau ρ, vaut zéro dans chacun de ces deux cas. Si p̅ = 0, les consommateurs achètent tous les biens lors de la première étape et n’ont donc pas de droits à fournir lors de la seconde étape. Si p̅ = p*, Q = N et les consommateurs ont autant de droits que de biens disponibles lors de la première étape; ils ne sont donc pas demandeurs de droits supplémentaires lors de la seconde étape. Lorsque p̅ ∈ (0, p*) on a ρ > 0; le membre de droite de (6) est donc strictement positif, ce qui implique π > π₀. La dépendance de l’intensité du réseau social en fonction de p̅ est donc telle que représentée sur le graphique 6. Si le taux de rationnement est élevé parce que le prix est très faible, un accroissement du rationnement réduit la taille du réseau social. Si au contraire le prix est élevé, bien qu’inférieur au prix d’équilibre, un accroissement du rationnement augmente la taille du réseau social.

Graphique 6

**Effet du prix administré sur la taille du réseau**

1.5 Le bien-être

Il est intéressant de calculer le bien-être des agents dans ce modèle. Pour cela, il suffit de confronter la relation (4) avec (3) pour en déduire que

Dans ce modèle, le gouvernement ajuste parfaitement les droits qu’il émet pour s’assurer que le processus de rationnement permet d’épuiser exactement les ressources disponibles. Donc chaque individu consomme une masse de X/N biens différenciés. Si l’on reporte cette expression dans la fonction d’utilité (5) on obtient alors que

Cette expression fait apparaître clairement le fait que l’intensité optimale du réseau social est telle que , soit π = π₀. Les tentatives des agents individuels d’être servis plus souvent en utilisant les réseaux sont annulées par le fait que comme la quantité totale de biens est fixe, le gouvernment y répond en réduisant le nombre de permis à consommer qui sont émis. Nous avons donc affaire à une pure externalité de congestion. Cette conclusion serait remise en question s’il y avait des « pertes en ligne » dans le processus de rationnement et si le réseau social limitait ces pertes.

Au niveau agrégé, le revenu total (soit la somme des revenus R de tous les agents) est égal à la rente des détenteurs de la ressource X, égale à p̅X. L’utilité totale est donc égale à

Clairement, un planificateur social utilitariste choisira la valeur la plus élevée possible de p̅ soit p̅ = p*[5]. Comme on l’a vu plus haut, les agents privés choisiront alors π = π₀, ce qui est efficace.

1.6 Réseaux sociaux et économie politique du rationnement

L’analyse qui précède implique qu’une société économiquement « rigide », sera associée à un investissement excessif dans le réseau social. Bien que cela ne soit pas modélisé ici, on peut penser que l’existence de ces réseaux est elle-même un facteur de rigidité, dans la mesure où elle réduit la mobilité géographique et professionnelle, à cause de l’effet négatif de ces mobilités sur le capital social.

Dans cette section, on s’intéresse à une question connexe : dans quelle mesure le réseau social conduit-il à des choix politiques susceptibles de renforcer la rigidité? On va voir qu’un tel mécanisme existe dans le modèle que nous sommes en train d’analyser.

Dans le cas qui nous occupe, la notion de rigidité coïncide avec le degré de rationnement dans l’économie, c’est-à-dire en d’autres termes avec le prix p̅. Nous nous intéresserons donc aux choix collectifs concernant le niveau de ce prix. Nous venons de voir qu’un planificateur social utilitariste ne choisira pas de mettre en place un rationnement. Supposons maintenant que les individus diffèrent selon leur dotation en biens : l’individu j a une dotation en biens égale à θ_jX / N, avec donc E(θ_j) = 1. Son revenu est égal à R_j = p̅θ_jX / N et, d’après les formules de la section précédente, sa fonction d’utilité s’écrit :

Cette formule implique que l’individu j préfère l’absence de rationnement si θ_j > 1 / 2, et préfère la valeur la plus faible possible de p̅ (donc le rationnement maximum) si θ_j < 1 / 2. Par ailleurs, ces préférences sont totalement indépendantes du niveau du réseau social, puisque celui-ci n’a pas d’effet sur la quantité de bien effectivement consommée.

Considérons le déroulement suivant des événements : dans un premier temps, les agents investissent dans le réseau social, en choisissant leur valeur optimale de π. Comme celle-ci ne dépend pas de R_j, elle sera la même pour tout le monde, comme on l’a analysé plus haut. Puis, les agents votent sur p̅. Pour simplifier, on supposera qu’ils choisissent entre deux valeurs, p_L et p_H, avec p_L < p_H = p*. Enfin les transactions ont lieu selon le processus de rationnement décrit plus haut.

Il est évident que si le médian dans la distribution de θ est inférieur à 1/2, l’équilibre politique sera tel que p = p_L tandis que si ce médian est supérieur à 1/2, il n’y aura pas de rationnement. Le rationnement redistribue indirectement du revenu entre les riches, dont la dotation est élevée, et les pauvres, dont la dotation est faible. Cette méthode de redistribution est évidemment inefficace, mais l’on suppose ici qu’il n’en existe pas d’autre. On voit que la logique est la même que dans Meltzer et Richard (1981). De plus, le choix de p̅ en deuxième période est totalement indépendant du niveau de réseau social qui a été choisi. C’est donc seulement la distribution des revenus qui détermine le degré de rationnement.

Nous allons maintenant rendre ce modèle plus intéressant en supposant que les individus diffèrent aussi dans leur capacité d’acquérir un réseau social. Cela signifie que le coût du réseau social, dénoté c_j(π_j), est spécifique à l’individu j. Une fois l’investissement en réseau social réalisé, il en résulte une distribution {π_j} de l’intensité du réseau social. Il est facile de voir que l’équation qui détermine Q est alors remplacée par celle-ci :

où = E(π_j) est la valeur moyenne de π_j. Le nombre de biens consommé diffère maintenant selon les individus. Il est égal à , soit donc

avec, rappelons-le . La fonction d’utilité de l’individu j est donc

Cette formule fait apparaître que les individus dont le réseau social est meilleur ont un gain supérieur de réduire p̅. En effet, leur réseau social leur permet d’accéder à un plus grand nombre de biens que la moyenne. En d’autres termes, si les détenteurs de capital « financier » (ceux tels que θ_j est élevé) sont opposés au rationnement, les détenteurs de capital « social » (ceux pour qui π_j est élevé) sont favorables au rationnement.

Considérons un exemple numérique simple. On suppose v = 1 et p_L = 1 / 2. Il est toujours possible de s’arranger pour que la valeur de choisie par les agents dans le cas où p_L = 1 / 2 soit = 1 / 2. Supposons que X / N = 9 / 32 Le prix d’équilibre walrasien est alors égal à . Dans le cas où p̅ = p_L, l’équation (7) revient alors à

La seule solution telle que Q < N est Q = N / 2. Le nombre de transactions passant dans le réseau est donc, dans ce cas, . Il en résulte, d’après (₈) pour l’individu j une utilité égale à :

Dans le cas où p̅ = p*, on a ρ = 0 et l’on obtient

Les agents qui préfèrent l’économie rationnée sont donc ceux tels que

On voit donc qu’il s’agit des agents riches en capital social et pauvres en capital financier. Si la proportion d’agents dans cette situation est supérieure à 1/2, alors la société votera pour le rationnement. Cela est d’autant plus probable que la richesse financière est concentrée en peu de mains, tandis que les consommateurs peu connectés constituent une minorité.

De plus, la distribution des π_j est endogène et dépend des anticipations faites par les agents sur le degré de rigidité de l’économie qui sera choisie lors du vote. Supposons que les fonctions c_j() soient telles que . Alors, si les agents anticipent que la société flexible sera choisie, ils choisiront tous un niveau de réseau social identique et égal à π_j = π₀ = = 0. L’analyse du début de cette section s’applique et on a vu que les personnes qui votent en faveur de la rigidité sont celles telles que θ_j < 1 / 2[6]. Si les agents anticipent une société rigide, alors l’analyse qui précède s’applique et les partisans de la rigidité sont ceux qui satisfont à (9). Ces conditions sont représentées sur le graphique 7. Les quantités A,B,C,D représentent la masse totale d’agents se trouvant dans la zone correspondante. On voit que pour qu’une économie flexible soit une prédiction autoréalisatrice, il faut qu’on ait C+D>1/2, tandis qu’on doit avoir B+C>1/2 pour que la rigidité soit auto-réalisatrice. Il est possible que ces deux conditions soient simultanément satisfaites. Dans ce cas, la même société peut être rigide, avec un niveau élevé de réseaux sociaux et des marchés fortement réglementés, ou avec des marchés libéralisés et des réseaux sociaux moins développés.

Graphique 7

**Les différents groupes socio-économiques**

Le graphique 7 partitionne la société en quatre groupes socio-politiques :

Ceux dont l’accès au réseau est suffisamment élevé et/ou la richesse financière suffisamment faible, pour qu’ils soient partisans de la rigidité quelle que soit la distribution initiale de l’intensité des réseaux. Il s’agit du groupe B.
Ceux dont la richesse financière est relativement élevée, quoiqu’inférieure à ½, et l’accès aux réseaux relativement faible (de sorte que leur capital social est inférieur à la moyenne si la société anticipe qu’elle sera rigide). Ceux-ci votent pour une société rigide si l’on a anticipé qu’elle était flexible (en effet dans ce cas ils ne sont pas handicapés par leur manque de réseaux sociaux, mais bénéficient des effets redistributifs de la rigidité), mais ils votent pour une société flexible si l’on anticipait qu’elle serait rigide (leur handicap social dans l’accès aux biens ayant un effet plus fort que la baisse du prix de ceux-ci). Il s’agit du groupe A, dont le comportement électoral tend à invalider les anticipations.
Ceux dont la richesse financière est élevée et qui tendent à souffrir de la rigidité à cause de cela, mais dont le talent social est élevé. Ceux-là sont partisans de la flexibilité si on l’anticipait, et sont partisans de la rigidité si on l’anticipait. Ces agents tendent à valider les anticipations. Il s’agit du groupe C.
Enfin, les agents bien dotés en capital financier, et relativement handicapés socialement (groupe D). Ceux-là sont en faveur de la flexibilité dans tous les cas.

Il est facile de voir qu’une condition nécessaire pour qu’il y ait des équilibres multiples est A < C. c’est-à-dire que le groupe social qui tend à invalider les anticipations est moins nombreux que celui qui tend à valider les anticipations. C’est donc l’existence d’une classe moyenne relativement aisée et relativement privilégiée dans l’accès au réseau social, suffisamment nombreuse, qui crée cette possibilité d’équilibres multiples.

Conclusion

Dans un monde où les rigidités de marché créent du rationnement, les réseaux sociaux jouent un rôle important dans l’accès aux ressources. Il en résulte un investissement excessif des agents privés dans ces réseaux. Cet investissement excessif peut alors accroître le soutien politique en faveur des politiques rigides; si les individus sont plus ou moins « populaires » et ont plus ou moins de talent pour accroître la taille de leur réseau social, le fait de se trouver dans une société rigide peut donner naissance à un groupe social qui grâce à ses relations privilégiées profite de la rigidité, alors même que celle-ci lui serait néfaste si la société était originellement flexible. Il s’agit en quelque sorte d’une « classe moyenne inférieure » sur le plan économique, mais « supérieure » sur le plan sociologique. On a montré que si ce groupe d’intérêt est suffisamment nombreux, alors une société rigide s’auto-entretient, mais il en va de même pour une société flexible; en d’autres termes il existe des équilibres multiples.

Ce résultat n’est pas sans rappeler le débat français sur l’accès privilégié qu’auraient les enfants de professeurs (bourgeoisie relativement modeste financièrement mais ayant accès à une information privilégiée sur le système scolaire) aux filières d’excellence de l’éducation nationale (gratuites et d’autant plus rationnées qu’il est coûteux pour le gouvernement d’accroître le nombre de places en fonction de la démographie). Selon le journaliste Eric Le Boucher (2010), « Ne réussissent statistiquement en France que les élèves accompagnés le soir par leurs parents, qui refont les cours, qui aident, qui connaissent les filières, qui trouvent des appuis internes. L’Education nationale française, celle de l’égalité républicaine, la sélection par le mérite, est devenue pire que la Chine : elle ne sert plus qu’à promouvoir les fils du Parti, le parti scolaire. »

La rigidité comme paradigme socio-politique

Introduction