Corps de l’article

Introduction

Il existe aujourd’hui de fortes divergences entre la performance commerciale de la France et de l’Allemagne sur les marchés internationaux. En effet, depuis la fin des années quatre-vingt-dix, la part de marché française à l’exportation a fortement diminué, passant de 5,3 % en 1997 à 3,9 % en 2008[1]. À l’inverse, la part de marché allemande à l’exportation est restée stable (environ 9,5 %). L’Allemagne s’affirmait même depuis 2003 comme le premier exportateur mondial et seule l’intense concurrence chinoise a su remettre en cause cette suprématie. Le cas français n’est pas unique : les principales nations exportatrices perdent des parts de marché depuis de nombreuses années déjà. Comment expliquer un tel constat?

Si l’impact des spécialisations commerciales peut être écarté (Boulhol et Maillard, 2005; Felettigh et al., 2006; Madariaga, 2009), nombre d’études empiriques mettent en exergue le rôle fondamental joué par les différences de compétitivité entre nations (Kabundi et Nadal de Simone, 2009).

La compétitivité est traditionnellement décomposée en deux aspects distincts : la compétitivité prix et la compétitivité structurelle. Bien que les prix constituent un élément essentiel dans les échanges de produits, ils ne représentent en effet que partiellement la capacité d’un pays à imposer ses produits sur les marchés mondiaux (Junz et Rhomberg, 1973). Ainsi, les nouvelles théories du commerce international (Krugman, 1989; Grossman et Helpman, 1991), fondées sur les analyses en termes de concurrence imparfaite, insistent sur les déterminants hors prix de la compétitivité. Dans cette optique, deux biens différenciés peuvent supporter des prix différents. Dès lors, la compétitivité structurelle ou compétitivité « hors prix » indique la capacité d’une entité économique sur le moyen et long terme à se démarquer de la concurrence et ce par d’autres moyens que le prix. Elle s’effectue pour l’essentiel non seulement par la recherche d’une qualité accrue des biens et services produits, mais aussi par l’image et la réputation que le marché concoure à leur attribuer ou qui sont forgées par le marketing (Dejardin, 2006). Selon Morris (1985), c’est bien la compétitivité structurelle plus que la compétitivité prix qui détermine la performance à l’exportation d’une économie.

Bien que fondamentale, la compétitivité structurelle est délicate à appréhender statistiquement à un niveau relativement désagrégé (Erkel-Rousse, 1992) et alimente nombre de controverses. De l’image de marque d’une entreprise à la qualité des produits considérés, ses déterminants sont multiples et de nature hétérogène. En réalité, seules des enquêtes réalisées auprès d’importateurs peuvent permettre une mesure directe de la qualité des biens, comme celle menée par le Coe-Rexecode sur l’image des biens européens. Cependant, se référer à ces études n’est pas exempt de critiques puisque celles-ci sont par nature subjectives et portent seulement sur certains types de biens (consommation et équipement). Pour éviter non seulement cette subjectivité et la complexité de mise en oeuvre d’une enquête, les effets de la qualité et plus particulièrement de la compétitivité structurelle sont appréhendés dans la littérature empirique par l’utilisation de mesures indirectes ou proxys. Des biais subsistent néanmoins. Ces mesures assimilent en effet bien souvent la compétitivité structurelle à ce que Fagerberg et al. (2007) appelle « la compétitivité technologique », c’est-à-dire à la capacité d’une nation à différencier ses produits par la technologie. Le concept de compétitivité est cependant plus large et ne peut se réduire au seul facteur innovation (Crozet et Erkel-Rousse, 2004). Il importe donc d’utiliser des indicateurs élargis de compétitivité structurelle.

Répondant à ce besoin, ce présent travail utilise l’indice de compétitivité globale publié par l’Institute for Management Development (IMD) : le World Competitiveness Yearbook (WCY). Étant le plus ancien et le plus connu des benchmarks de la compétitivité des pays, cet indice englobe en effet plus de 300 critères et repose à la fois sur des enquêtes d’image mais aussi sur des variables quantitatives. À travers une étude en panel (Hervé, 2001) pour 11 pays[2] de la zone euro sur la période 1996-2008, nous cherchons à vérifier si l’utilisation d’un tel indice est pertinente pour mesurer la compétitivité structurelle. Deux résultats majeurs peuvent être tirés de notre étude. Nous montrons en premier lieu qu’il existe une corrélation forte entre notre indicateur et l’évolution des exportations des pays membres de la zone euro. En second lieu, nos résultats reposant sur une décomposition de l’indicateur révèlent que d’autres variables de compétitivité telle que le taux de taxation sur les entreprises ou encore l’accès au crédit ont fortement influencé les performances commerciales des pays de la zone euro sur la période récente.

La première section de l’article introduit une revue de la littérature sur la modélisation de la compétitivité structurelle dans les équations d’exportation. La deuxième section présente nos données ainsi que la spécification générale des modèles estimés. La section 3 résume les enseignements de notre analyse économétrique. La conclusion sera enfin exposée dans une quatrième section.

1. Revue de la littérature

Dans la littérature empirique, les modèles les plus répandus pour modéliser les volumes d’exportation sont des variantes du modèle à substituts imparfaits, dont les fondements théoriques remontent à Armington (1969). Conceptuellement, le modèle repose sur deux hypothèses. L’imparfaite substituabilité entre les produits qui suppose que les produits nationaux et importés sont discernables selon leur origine géographique et l’indépendance des choix entre catégories de biens qui implique que les préférences des consommateurs pour différents produits en concurrence sur un marché donné ne sont pas affectées par leurs achats sur les autres marchés.

Dès lors, les équations d’échange vont découler d’un programme de maximisation d’utilité du consommateur en deux étapes (« two stage budgeting »). À la première étape, un pays, considéré comme l’entité de décision, détermine la demande totale par produit nécessaire pour satisfaire la consommation du pays. À la deuxième étape, le pays alloue à chaque fournisseur individuel, sa part de production en cherchant à minimiser ses coûts. Dans le modèle d’Armington (1969) la fonction d’utilité maximisée par les consommateurs est à élasticité de substitution constante (CES).

Les fonctions de demande qui en découlent s’expliquent par le revenu global (ou d’une variable d’activité substitutive du pays importateur), par les prix étrangers de biens échangés et par leur équivalent en prix domestique. Par ailleurs, les consommateurs ne sont nullement soumis à l’illusion monétaire, ce qui conduit à l’homogénéité des fonctions de demande. Par conséquent, la fonction se modélise par l’équation suivante :

où X représente la demande d’exportation en volume, wd la demande du reste du monde adressée au pays concerné, px le prix du produit exporté et p* son prix à l’étranger. L’homogénéité de degré 1 permet de spécifier la fonction d’exportation en volume sous la forme suivante :

avec wdr représentant cette fois la demande mondiale réelle adressée au pays considéré et rprx le terme de compétitivité prix, c’est-à-dire l’indice de prix relatifs.

L’hypothèse des élasticités d’offre et de demande infinies permet d’estimer les relations. Le modèle des substituts imparfaits implique un lien multiplicatif de ce type (Goldstein et Khan, 1985) :

La log-linéarisation de cette relation permet d’obtenir l’équation d’exportation de long terme d’un pays qui relie directement le volume des exportations à la demande mondiale adressée et aux prix relatifs à l’exportation. L’équation est de la forme suivante :

où α et β représentent, respectivement, les élasticités-demande et prix des exportations. L’équation (4) représente l’équation des exportations traditionnelle dite « à la Armington » (Erkel-Rousse et Garnero, 2008), qui sera la base de nos futures estimations.

Ces modélisations ont cependant le défaut de réduire la compétitivité aux seuls prix, omettant ainsi ses aspects hors prix. De plus, Bessone et Heitz (2005), puis Deruennes (2005), à partir d’une estimation de cette relation sur le court terme par un modèle à correction d’erreur (MCE), signalent que les équations d’exportation traditionnelles ne peuvent expliquer les évolutions des parts de marché à l’exportation de la France et de l’Allemagne sur la période récente. Il est donc nécessaire d’inclure à ce modèle des variables captant la compétitivité structurelle.

Plusieurs approches ont été élaborées pour tenter de capter les effets de compétitivité hors prix sur l’évolution des exportations d’un pays. Murata et al. (2000) incluent une tendance non linéaire aux équations d’exportation pour appréhender l’influence des facteurs hors prix sur l’évolution des exportations des pays membres de l’OCDE. Ils estiment un modèle à correction d’erreur pour chaque pays de l’échantillon sur des données trimestrielles couvrant la période 1975 à 1999. Ils trouvent des résultats très hétérogènes selon les pays étudiés. Ainsi, pour certains pays comme la France et l’Allemagne, la tendance a un impact négatif alors que pour d’autres, tel l’Espagne, elle a un impact positif; pour d’autres encore, comme l’Italie, elle n’est pas significative. Rouabah (2005) estime un modèle similaire pour le Luxembourg et montre que la tendance a un impact significatif et positif sur ses exportations.

L’utilisation d’une tendance comme mesure des effets hors prix enrichit les équations d’exportation traditionnelles grâce à une meilleure modélisation de l’évolution des exportations dans le temps, mais ne permet pas de discriminer entre les différents facteurs d’offre. En effet, on ne peut rien en conclure quant à l’impact de la qualité sur les performances commerciales de la France; le modèle ne le permet pas. Consciente de la forte hétérogénéité des variables d’offres, telles que la qualité des produits, la variété proposée, les investissements directs, les investissements immatériels mais aussi d’autres facteurs comme l’entrée sur le marché des pays émergents, la littérature empirique a eu recours à l’utilisation de proxys pour capter les effets hors prix de la compétitivité sur les performances commerciales des pays.

Pour certains auteurs, c’est l’innovation, facteur de qualité et de compétitivité, qui va permettre d’expliquer les différences de performances commerciales des économies. Fagerberg (1988) calcule ainsi un indice de compétitivité technologique reposant sur les dépenses civiles de recherche et développement (R&D) et les brevets déposés et montre que plus un pays possède un indice technologique élevé, plus ses performances commerciales sont importantes. À la suite, Magnier et Toujas-Bernate (1994) utilisent un proxy basé sur les dépenses relatives de R&D pour indiquer qu’à long terme, l’augmentation de celles-ci a un impact positif sur l’évolution des parts de marché des pays. Pamiès-Sumner (2005), puis Blot et Cochard (2008) utilisent un modèle similaire en séries temporelles et en panel pour tenter d’expliquer les différences de performances commerciales entre la France et l’Allemagne. Ils trouvent des résultats analogues et affirment que les produits français sont moins innovants que les produits allemands, contribuant à expliquer ainsi une partie du décalage entre les deux pays. Hummels et Klenow (2002) utilisent également un indicateur de dépenses de R&D pour mesurer la variété des produits proposés par les pays.

D’autres auteurs (voir notamment Amable et Verspagen, 1995) utilisent les brevets déposés comme proxy de l’innovation. D’autres proxys de l’innovation sont utilisés dans la littérature empirique : la part des secteurs de haute et moyenne technologie dans la production totale du pays (Barrell et Pomerantz, 2007), le stock net de capital fixe dans le secteur manufacturier (Athanasoglou et Bardaka, 2010) ou encore l’effort d’investissement (Erkel-Rousse, 1992). Toutes ces mesures enrichissent les équations d’exportation traditionnelles mais ont le défaut de réduire la compétitivité hors prix à l’innovation. C’est pourquoi Erkel-Rousse et Le Gallo (2002), puis Crozet et Erkel-Rousse (2004) ont tenté de modéliser un indicateur de qualité calculé à partir de l’enquête annuelle sur l’image des biens des pays européens du Centre d’Observation Économique (COE).

Dans notre étude, les équations traditionnelles seront améliorées par le biais d’un benchmark de la compétitivité globale : le WCY.

2. Méthodologie des données et du modèle économétrique

2.1 La construction du World Competitiveness Yearbook (WCY)

Le WCY, publié chaque année depuis 1989, figure parmi les indicateurs de compétitivité les plus connus. Il analyse et classe les pays en fonction de leur capacité à créer et à maintenir un environnement qui permet aux entreprises d’être compétitives. Les nations doivent, en effet, fournir un environnement macroéconomique qui encourage la compétitivité des entreprises : cela passe par des infrastructures, des institutions et des politiques efficientes. L’indicateur repose sur plus de 300 critères en référence à la littérature économique, aux sources internationales, nationales et régionales et suivant les recommandations de la communauté financière et des agences gouvernementales.

La méthodologie de construction du WCY prévoit une division de l’environnement économique national en quatre principaux facteurs de compétitivité : performances économiques, efficacité du secteur public, efficacité des entreprises et infrastructures. Chacun de ces facteurs est divisé en cinq sous-facteurs qui représentent différents aspects de la compétitivité[3]. Ces sous-facteurs sont alors eux aussi divisés en catégories qui définissent la compétitivité plus explicitement. Cependant, chaque sous-facteur n’inclut pas nécessairement le même nombre de critères : par exemple, il y a plus de critères pour le sous-facteur éducation que pour le sous-facteur prix. Chaque facteur, et ce indépendamment du nombre de critères qu’il contient, a le même poids dans le résultat final à savoir 5 %.

Les 300 critères évalués par le WCY incluent des proxys de l’innovation testés traditionnellement dans les modèles empiriques comme le nombre de brevets déposés dans le pays, les dépenses de recherche et développement du pays considéré, la recherche scientifique, le nombre de Prix Nobel depuis 1950, le nombre d’articles scientifiques publiés, les exportations dans le secteur de la haute technologie, le nombre de connexions Internet du pays ou encore l’investissement dans les télécommunications.

Cependant, contrairement à ces proxys, le WCY évalue d’autres aspects de la compétitivité structurelle comme l’éducation (le nombre d’ingénieurs qualifiés ou encore les dépenses publiques dans l’éducation), la santé et l’environnement (les dépenses publiques dans la santé, les émissions de CO2, l’espérance de vie ou encore les énergies renouvelables), l’investissement (investissements directs à l’étranger, formation brute de capital fixe ou encore les investissements de portefeuille) et des variables d’efficacité du gouvernement (politique fiscale, flexibilité du marché du travail ou encore le nombre de créations de firmes). De plus, l’IMD mène une enquête d’opinion pour compléter ses statistiques internationales, nationales et régionales. Contrairement aux données quantitatives qui mesurent directement la compétitivité sur une période donnée, l’enquête d’opinion mesure la perception qu’ont les acteurs économiques de la compétitivité. Cette enquête sert à quantifier des variables qui sont difficilement mesurables comme par exemple les pratiques de management, les relations de travail, la corruption, les problèmes environnementaux ou encore la qualité de la vie.

Au final, l’indicateur WCY est composé de 245 critères dont 135 proviennent de données quantifiables et 110 proviennent de données qualitatives tirées de l’enquête d’opinion. En effet, seulement 245 critères sont utilisés pour la construction de l’indicateur WCY, les 84 autres sont uniquement présentés pour information. Pour le calcul du score final obtenu par chaque pays à la date t, l’IMD prend la moyenne des scores aux quatre facteurs et convertit ensuite le résultat en un indice où le pays le mieux noté obtient une valeur de 100.

Il faut cependant noter que bien qu’il soit très populaire dans les médias, sa construction n’en reste pas moins fortement critiquable notamment au niveau du choix des variables et des pondérations de chaque critère (Musson, 2010). En effet, les pondérations sont fixées par l’IMD de manière ad hoc, sans aucune justification théorique ou empirique ce qui rend l’interprétation des valeurs de l’indicateur difficile pour la conduite des politiques économiques (Debonneuil et Fontagné, 2003).

2.2 Les modèles estimés

Dans la lignée des travaux précédents sur les différences de performances commerciales des pays, nous évaluons l’évolution des exportations des pays membres de la zone euro en utilisant les équations d’échange traditionnelles augmentées. Nous nous focalisons sur la mesure de la compétitivité hors prix dans ces équations.

Dans un premier temps, nous estimons les équations d’exportation à la Armington que nous enrichissons progressivement avec des mesures traditionnelles de la compétitivité hors prix. Nous ajoutons ensuite à ce modèle un benchmark de la compétitivité reposant sur le World Competitiveness Yearbook (WCY). L’objectif est de montrer que la compétitivité structurelle ne peut être réduite au seul facteur innovation, comme c’est le cas dans la plupart des études empiriques.

L’équation globale obtenue est la suivante :

avec :

Xi,t, les exportations de biens et services du pays i à la date t;

WDi,t, la demande mondiale adressée au pays i à la date t;

rPri,t, la compétitivité prix du pays i à la date t, mesurée comme le ratio entre l’indice des prix à l’exportation du pays i et l’indice des prix à l’exportation de ses principaux concurrents pondéré par la méthode des doubles pondérations;

rDDi,t, la demande intérieure relative du pays i à la date t (Erkel-Rousse et Garnero, 2008);

WCYi,t, la variable indicatrice basée sur le WCY de l’Institute for Management Development (IMD);

rRDi,t, les dépenses relatives de R&D;

WOi,t, le taux d’ouverture mondiale (Blot et Cochard, 2008)[4].

Nos estimations portent sur des données de panel concernant 11 pays de la zone euro sur la période 1996-2008. En effet, les données de panel ont l’avantage de rendre compte simultanément de la dynamique des comportements et de leur éventuelle hétérogénéité, ce qui n’est pas possible avec les séries temporelles. Elles permettent également de réduire les risques de multicolinéarité du modèle, de capter des effets de court et long terme et de réduire le biais d’estimation des coefficients. Enfin, l’utilisation de données de panel permet d’identifier l’effet associé à chaque individu, c’est-à-dire un effet qui ne varie pas dans le temps, mais d’un individu à l’autre.

Pour chacune des spécifications économétriques, la présence d’effets individuels est approuvée par un test de Fisher. Il est cependant important de spécifier la nature de ces effets individuels. En effet, ceux-ci peuvent être « fixes » c’est-à-dire constants et spécifiques au groupe i dans la régression ou « aléatoires », qui peuvent se décomposer en un effet spécifique et un effet résiduel. D’un point de vue pratique, le modèle à effets fixes entraîne la perte de degrés de liberté. Cependant, l’utilisation d’un modèle à effets aléatoires implique l’absence de corrélation entre les effets individuels et les variables explicatives du modèle estimé. Si cette hypothèse n’est pas vérifiée, l’estimateur between est biaisé et non convergent et l’estimateur within est sans biais. Lorsque le modèle est un véritable modèle à effets aléatoires, sans corrélation des effets, la différence entre les deux estimateurs within et between est non significative, mais lorsqu’il y a corrélation cette différence est significative (Trognon, 2003). Le choix entre les deux types d’effets repose donc sur l’hypothèse d’exogénéité des effets par rapport aux variables explicatives (Mundlak, 1978). Hausman (1978) propose un test permettant de vérifier l’indépendance des effets par rapport aux variables explicatives. Nous effectuons ce test pour toutes nos estimations et acceptons l’hypothèse nulle de non-corrélation des effets avec les variables aléatoires. Les effets fixes individuels sont retenus dans deux estimations sur quatre (le modèle avec R&D et le modèle complet). Pour les autres spécifications, nous optons pour l’utilisation des effets aléatoires puisque l’estimateur des moindres carrés généralisés (MCG) est convergent.

Nous testons également l’absence d’hétéroscédasticité dans nos modèles en utilisant deux tests. Dans une première étape, nous utilisons le test du multiplicateur de Lagrange proposé par Breusch et al. (1979) puis Breusch et Pagan (1980) pour déterminer la constance de la variance dans nos modèles. Ayant conclu à la présence d’hétéroscédasticité dans chacune de nos spécifications, nous tentons de savoir par le biais d’un test de Wald modifié, quelle est la nature de cette hétéroscédasticité. Les résultats du test confirment la présence d’hétéroscédasticité interindividus pour chacune de nos régressions. L’estimateur des moindres carrés ordinaires (MCO) n’est donc plus efficace alors que celui des MCG reste efficace. Pour chacune des spécifications, nous testons, enfin, l’existence d’autocorrélation des erreurs. Nous optons pour la procédure proposée par Wooldridge (2002), qui teste l’hypothèse nulle d’absence d’autocorrélation des résidus. Nous concluons quant à l’existence d’autocorrélation dans nos différents modèles. Il faut noter également que nous concluons quant à l’exogénéité de l’indicateur WCY en utilisant la procédure proposée par Nakamura et Nakamura (1981).

Pour corriger les problèmes d’hétéroscédasticité et d’autocorrélation, nous optons pour la transformation proposée par Prais et Winsten (1954) qui améliore la procédure exposée par Cochrane et Orcutt (1949). En effet, Beck et Katz (1995) ont montré que sur un échantillon restreint, les MCG pouvaient produire des erreurs standards incorrectes. Ce biais provient du fait que la méthode des MCG estime un nombre excessif de paramètres dans la matrice de variance-covariance (Beck, 2001). Sur un petit échantillon comme le nôtre on préfèrera appliquer la transformation proposée par Prais et Winsten (1954) afin d’éliminer l’autocorrélation des perturbations.

3. Résultats

3.1 La compétitivité structurelle ne se limite pas à l’innovation

Les résultats de nos premières estimations concernant les mesures traditionnelles de la compétitivité structurelle sont résumés dans le tableau 1.

Tableau 1

Résultats des estimations avec un indicateur de compétitivité globale

Résultats des estimations avec un indicateur de compétitivité globale

Note : les valeurs entre parenthèses représentent les écarts-types estimés.

*,**,*** : significatif à 10 %, 5 %, 1 %

-> Voir la liste des tableaux

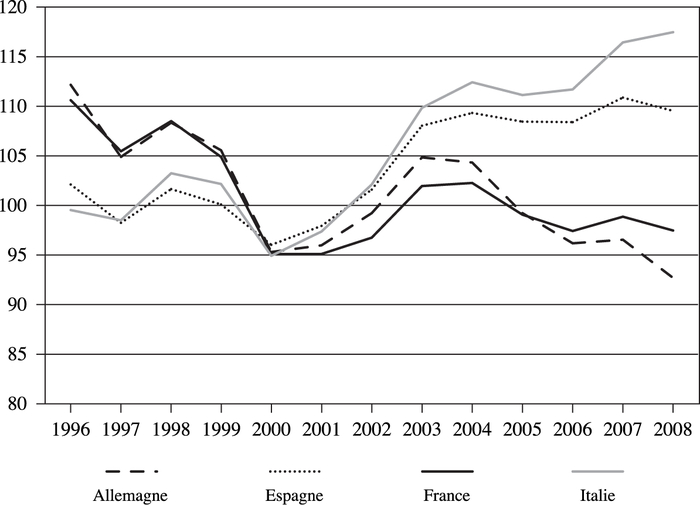
Les variables des différentes spécifications estimées sont toutes significatives. Conformément aux résultats des études précédentes, la demande mondiale adressée a un impact positif sur l’évolution des exportations des pays de l’échantillon. Ainsi, une hausse de la demande adressée au pays i lui permet d’accroître ses performances à l’exportation. Le signe associé à la variable de compétitivité prix est également conforme aux précédentes études empiriques. En effet, une hausse des prix à l’exportation du pays i relativement à ses principaux concurrents entraîne une contraction de ses exportations sur le marché mondial. Ces conclusions sont vraies quel que soit le modèle étudié. Cependant, comme l’ont montré Artus et Fontagné (2006), ces variables traditionnelles ne peuvent expliquer les différences de performances commerciales entre la France et l’Allemagne sur la période récente. En effet, si l’on regarde l’évolution de la compétitivité prix de la France et de l’Allemagne, on remarque une évolution similaire sur les dernières années (cf. graphique 1).

Graphique 1

Évolution de la compétitivité prix des biens et services de l’Allemagne, l’Espagne, la France et l’Italie

Évolution de la compétitivité prix des biens et services de l’Allemagne, l’Espagne, la France et l’Italie
Source : OCDE

-> Voir la liste des figures

En outre, les résultats concernant la demande intérieure relative sont contraires à nos attentes. En effet, elle a un impact positif sur l’évolution des exportations des pays de la zone euro. Ces pays n’ont donc pas de contrainte d’offre sur leur marché intérieur. Les différences d’intensité des demandes intérieures ne peuvent donc pas expliquer le décrochage récent des exportations françaises. Ces résultats sont semblables à ceux de Blot et Cochard (2008).

Enfin, les résultats de nos modèles révèlent que le coefficient associé au taux d’ouverture mondiale est positif, ce qui est contraire à nos attentes. Ce résultat peut s’expliquer par l’augmentation des importations mondiales et notamment des pays émergents. En effet, le taux d’ouverture mondiale capte à la fois l’augmentation des exportations des pays émergents mais aussi l’augmentation de leurs importations, qui est un facteur de croissance pour les exportations des pays partenaires.

Les résultats du modèle avec proxy de l’innovation confirment que l’inclusion d’une variable mesurant les effets hors prix est nécessaire pour améliorer les équations traditionnelles des échanges. L’inclusion d’un proxy lié à l’innovation et basé sur les dépenses relatives de R&D permet une meilleure compréhension de l’évolution des exportations de la zone euro. En effet, les résultats que nous obtenons indiquent que le coefficient associé à ce proxy est significatif et positif, avec une élasticité de 0,22. En conséquence, plus un pays investit dans la R&D et plus ses exportations seront dynamiques. Ces résultats sont dans la lignée des précédentes études empiriques (Fagerberg, 1988; Blot et Cochard, 2008). La faiblesse relative des dépenses de R&D est donc un frein aux performances commerciales françaises à l’exportation. En effet, si l’on analyse l’évolution de dépenses de R&D, on remarque qu’elles ont diminué sur la période 1996-2008, alors qu’au contraire, celles de l’Allemagne et de l’Espagne ont fortement augmenté[5].

Cependant, le modèle prenant en compte le WCY nous révèle que d’autres facteurs peuvent rentrer en jeu dans l’explication des performances commerciales des pays de la zone euro. Cette hypothèse est confirmée par l’estimation de l’équation globale. En effet, les résultats montrent qu’à la fois les dépenses relatives de R&D et l’indicateur global de compétitivité ont un effet sensible et positif sur les exportations des pays de l’échantillon. Le pouvoir explicatif du modèle, mesuré par le R2 ajusté, a très légèrement augmenté avec la prise en compte à la fois de l’innovation et de l’indicateur WCY. Ces résultats indiquent que d’autres facteurs de compétitivité hors prix inclus dans la construction de l’indicateur WCY ont pu influencer les performances commerciales des pays de la zone euro sur la période récente. La décomposition de cet indicateur en différentes variables de compétitivité hors prix permettrait, dès lors, une meilleure modélisation des exportations des pays de la zone euro.

3.2 D’autres facteurs sont à prendre en compte

Tout d’abord, pour mieux appréhender les évolutions de la compétitivité prix des pays de la zone euro, nous utiliserons dorénavant l’évolution de la compétitivité-coût. En effet, Blot et Cochard (2010) révèlent que l’analyse des prix à l’exportation peut cacher des différences de comportement de marge des entreprises. L’analyse de la compétitivité-coût rend donc bien compte de l’évolution des prix des exportations, et ce, indépendamment des comportements de contraction de marge des entreprises.

Ensuite, nos précédents résultats permettent de mettre en lumière d’autres facteurs de compétitivité structurelle par le biais de l’indicateur de compétitivité globale de l’IMD. Cet indicateur est divisé en quatre facteurs représentant la compétitivité des pays. Pour éviter les problèmes de multicolinéarité dans notre régression, nous ne sélectionnons que trois variables proxys au maximum par facteur. Nous suivons également la méthodologie proposée par la Banque mondiale pour le choix de nos variables. Ainsi, les éléments les plus importants pour les pays sont les infrastructures, le développement financier, le développement des entreprises et le niveau d’éducation. Notre choix se porte sur les variables suivantes :

Tableau 2

Répartition des variables choisies dans les facteurs du WCY

Répartition des variables choisies dans les facteurs du WCY

-> Voir la liste des tableaux

Nous estimons donc la relation suivante :

avec :

rCSUi,t, la compétitivité-coût du pays i à la date t exprimée comme le ratio entre les coûts salariaux unitaires du pays i et les coûts salariaux unitaires des 23 pays membres de l’OCDE pondérés par la méthode des doubles pondérations;

rFBCFi,t, la formation brute de capital fixe (FBCF) relative du pays i à la date t, calculée comme le ratio entre la FBCF du pays i et celle de ses principaux concurrents. Cette variable mesure les performances économiques du pays considéré en termes d’investissement;

rTi,t, le taux d’imposition sur les sociétés (IS) relatif du pays i à la date t. Le taux d’IS est mesuré comme la base légale appliquée aux entreprises par le gouvernement du pays i. Les données concernant cette variable sont tirées de la base de données de l’OCDE sur les taxes. Cela nous permet de mesurer la politique fiscale du pays considéré;

Cri,t, le montant des crédits octroyés au secteur privé du pays i à la date t en pourcentage du PIB. Il constitue un proxy du développement financier du pays considéré;

CAPi,t, la capitalisation boursière des entreprises cotées du pays i à la date t exprimée en pourcentage du PIB. Cette variable est également un proxy du développement financier des pays;

rPi,t, le nombre relatif de brevets déposés par le pays i à la date t. C’est un proxy de l’innovation;

ORDIi,t, le nombre d’ordinateurs détenus pour 100 personnes du pays i à la date t. Cette variable est un proxy des infrastructures de communication du pays considéré;

SUPi,t, la part de la population active du pays i ayant réalisé des études supérieures à la date t. C’est une mesure de l’éducation du pays considéré.

Notons que la variable de demande relative est exclue du modèle à cause de sa très forte corrélation avec la variable de FBCF relative[6]. Tout comme pour nos précédentes régressions, cette équation est estimée par la méthode de Prais et Winsten (1954) pour corriger le modèle des problèmes d’hétéroscédasticité et d’autocorrélation. Les résultats de cette estimation sont résumés dans le tableau 3. Les données concernant le nombre d’ordinateurs n’étant pas disponibles en 2008, l’estimation de l’équation (6) portera sur la période 1996-2007 et ne contiendra donc que 132 observations.

Tableau 3

Résultats de l’estimation avec décomposition de l’indicateur

Résultats de l’estimation avec décomposition de l’indicateur

Note : *,**,*** : significatif à 10 %, 5 %, 1 %

-> Voir la liste des tableaux

Les résultats de cette estimation révèlent que les facteurs expliquant les performances commerciales des économies ne se limitent pas seulement à la demande, aux prix et à l’innovation. De plus, l’introduction d’une mesure plus élargie de la compétitivité hors prix augmente le pouvoir explicatif des équations d’exportation (R2 ajusté supérieur : 0,92 contre 0,83 auparavant). La décomposition de l’indicateur WCY permet de mettre en avant de nouveaux facteurs de compétitivité et une meilleure compréhension des différences de performances commerciales au sein de la zone euro. Ainsi, on remarque que les caractéristiques de l’économie globale ainsi que celles des entreprises peuvent fortement influencer les performances commerciales d’un pays.

Tout d’abord, les résultats précédents concernant la compétitivité prix cachent une tout autre réalité concernant les coûts salariaux. En effet, si la France et l’Allemagne ont une compétitivité prix qui évolue de façon relativement similaire sur la période récente, le constat n’est pas le même concernant l’évolution de la compétitivité-coût. En outre, l’évolution des coûts salariaux relatifs a un impact négatif et significatif sur les performances commerciales des pays de l’échantillon. Or, la compétitivité-coût allemande s’est nettement améliorée depuis 2004, alors que celle de la France s’est détériorée depuis 2001[7]. La politique de modération salariale engagée en Allemagne depuis 2003 a permis aux entreprises domestiques d’augmenter leurs marges à l’exportation. Au contraire, les entreprises françaises, pour rester compétitives sur le marché mondial, ont été contraintes de réduire leurs marges à l’exportation : les différences de coûts expliquent alors en partie l’amélioration des exportations allemandes de biens et services. De même, le taux de taxation sur les profits des entreprises joue comme un frein aux exportations pour les pays de l’échantillon. En effet, plus le pays considéré applique une taxe importante aux entreprises résidentes, plus les coûts à l’exportation seront importants; une politique fiscale avantageuse favorise donc les transactions internationales du pays considéré. Si l’on regarde l’évolution du taux de taxation des entreprises au sein de la zone euro, on peut remarquer que le taux allemand s’est fortement réduit sur la période d’étude, passant de 48,4 % en 1996 à 15,8 % en 2008, soit une réduction d’environ 33 points de pourcentage (données OCDE). Au contraire, le taux de taxation des entreprises françaises n’a que faiblement diminué sur la même période (-7 points de pourcentage). La nouvelle « désinflation compétitive » allemande (Creel et Le Cacheux, 2006) caractérisée par une baisse des coûts salariaux et du taux d’imposition sur les sociétés a permis l’allègement des charges pour les entreprises domestiques et de meilleures performances sur le marché mondial.

Nos résultats indiquent également que les infrastructures du pays sont un facteur important de compétitivité. En effet, les coefficients associés aux variables ORDI et SUP sont significatifs et positifs. Ainsi, plus la main-d’oeuvre est qualifiée (ayant fait des études supérieures), plus la qualité des biens produits sera prononcée et donc plus les performances commerciales du pays seront élevées. De même, des infrastructures de communication efficientes et donc un acheminement des produits plus fluide, permettra à l’économie de gagner des parts de marché à l’exportation.

D’autre part, nos résultats mettent en lumière le rôle de l’accès au crédit dans les performances commerciales. On remarque que plus le nombre de crédits accordés au secteur privé est élevé, plus la performance domestique sur le marché mondial l’est également. Le constat est le suivant : plus les entreprises du pays considéré ont un accès facile au crédit plus elles vont pouvoir investir pour innover et faire face aux coûts fixes liés à l’exportation. Au sein de la zone euro, on peut remarquer qu’en moyenne entre 1996 et 2006, le montant des crédits octroyés au secteur privé allemand (en % du PIB) représentait 1,3 fois le montant des crédits français, même si cet écart tend à diminuer, notamment depuis 2007, en raison de la crise économique. Il est donc plus facile pour ces entreprises d’accéder au crédit; cela facilite leur accès au marché mondial. Cependant, on remarque que la capitalisation boursière des entreprises cotées n’a pas d’effet significatif sur les performances commerciales des pays à l’exportation.

On peut également noter que les variables traditionnelles telles que l’investissement (FBCF) et l’innovation (nombre relatif de brevets), ont toujours un impact significatif sur les performances à l’exportation des pays de la zone euro. Remarquons, enfin, que la variable d’ouverture mondiale (WO) n’est plus significative lorsque l’indicateur WCY est décomposé. Cette dernière a en effet permis d’identifier clairement des variables de compétitivité hors prix qui pouvaient être auparavant incluses dans le taux d’ouverture mondiale.

Conclusion

Conformément aux précédentes études empiriques sur le sujet, notre analyse justifie l’utilisation d’une mesure de la compétitivité structurelle dans les équations d’exportation. Cependant, nous montrons la nécessité de prendre en compte une mesure plus large qui ne se limite pas à la seule analyse de l’innovation. En effet, nos modèles révèlent que l’indicateur de compétitivité globale WCY, captant d’autres facteurs de compétitivité hors prix que la seule innovation, a un impact positif sur l’évolution des exportations de biens et services des pays de la zone euro. En outre, cette variable indicatrice de compétitivité hors prix enrichit les équations d’exportation traditionnelles. Il convient tout de même de nuancer cette conclusion à la lumière des critiques dont fait l’objet cet indicateur. Il est, en effet, remis en cause notamment au niveau de son mode de calcul et de son interprétation.

Toutefois, la décomposition de cet indicateur en quatre facteurs de compétitivité à l’aide de proxys nous permet de mettre en lumière d’autres variables dans l’explication des performances commerciales des pays de la zone euro sur la période récente. Ainsi, d’autres facteurs importants tels que le développement financier, le développement humain, les infrastructures et l’efficacité des entreprises peuvent expliquer les performances commerciales des économies. Ainsi, la surperformance allemande à l’exportation proviendrait d’une bonne compétitivité coût conjuguée à une innovation accrue de ses produits mais également d’une politique fiscale avantageuse et d’un meilleur accès au crédit pour les entreprises.

Le lien avec la théorie de l’hétérogénéité des firmes (Mélitz, 2003) demeure à établir. Une comparaison entre les entreprises françaises et allemandes, notamment en termes d’accès au crédit et de fiscalité est une piste pour de futures recherches sur le sujet. En effet, un accès plus facile au crédit et une politique fiscale avantageuse peuvent permettre aux entreprises de faire face aux coûts fixes liés à l’exportation et donc influencer leur probabilité d’entrée sur les marchés internationaux.