Résumés
Résumé
Cette revue quantitative de la littérature sur le paradoxe de Feldstein et Horioka (1980) adopte une méthodologie originale encore peu fréquente en économie internationale : la méta-analyse. Cette analyse systématique permet de construire un échantillon de 97 études qui ont été publiées entre 1980 et décembre 2007 et qui se concentrent sur l’évaluation de la corrélation entre le taux d’épargne et le taux d’investissement. Ainsi, 1 399 valeurs distinctes du coefficient de rétention de l’épargne sont exploitées. Cette méta-analyse montre une tendance de long terme en faveur d’une réduction de l’estimation du coefficient de rétention de l’épargne depuis 1850. Une fois les données statistiques, les échantillons de pays et le support de publication fixés, l’étude montre que les méthodologies économétriques conduisent à des valeurs du coefficient de rétention de l’épargne nettement différenciées. Il est donc nécessaire d’adopter différentes stratégies économétriques afin d’avoir un large aperçu du spectre des coefficients de rétention de l’épargne et de prendre en compte la diversité des résultats induite par le choix de la méthodologie économétrique. Cette étude quantitative montre enfin que les travaux sur le paradoxe de Feldstein et Horioka subissent un biais de publication.
Corps de l’article
Introduction
Dès le début des années soixante-dix, la forte mobilité des capitaux est apparue comme une hypothèse consensuelle en économie internationale. Elle permet de considérer que le déficit des comptes extérieurs peut être financé par de l’épargne étrangère puisque cette dernière peut circuler aisément entre les économies dès lors que l’épargne nationale est insuffisante par rapport à l’investissement domestique. Cette mobilité internationale du capital constitue le moyen de valider les déséquilibres des comptes extérieurs. Il devrait y avoir une séparation fondamentale entre l’épargne et l’investissement impliquant une corrélation faible, voire inexistante entre ces deux grandeurs. Feldstein et Horioka (1980) (dorénavant FH) dans leur tentative remarquée de validation empirique du lien entre l’investissement et l’épargne, qu’ils rapportent au PIB, ne sont pas en mesure de confirmer cette hypothèse d’intégration significative des marchés des capitaux. Les résultats de leurs régressions entre des moyennes quinquennales des taux d’investissement et des taux d’épargne sur un échantillon empilé de 16 pays de l’OCDE entre 1960 et 1974 montrent qu’en réalité les taux d’investissement sont très dépendants des taux d’épargne. Feldstein (2005 : 2-3) rappelle qu’à cette époque, les économistes considéraient que les marchés des capitaux étaient fortement intégrés, alors qu’ils apparaissaient en réalité très segmentés.
Depuis, l’analyse de la corrélation entre l’épargne et l’investissement a fait l’objet d’études récurrentes, y compris comme exemple d’application dans des manuels d’économétrie (Cadoret et al., 2004). Les résultats de cet important stock de travaux ne remettent pas en cause la robustesse des observations initiales, mais la différenciation des échantillons de pays, des périodes, des fréquences de données ainsi que des méthodologies économétriques rend délicates les comparaisons directes. Plusieurs revues de la littérature (Bordes, 1992; Frankel, 1992; Obstfeld, 1994; Moosa, 1997; Coakley et al., 1998; Apergis et Tsoumas, 2009) synthétisent l’information tant théorique qu’empirique. Néanmoins, il demeure difficile de définir une valeur du coefficient de rétention de l’épargne qui puisse permettre de dégager un consensus et de lever définitivement le voile sur ce paradoxe, qu’Obstfeld et Rogoff (2000) qualifient comme l’une des six grandes énigmes de la macroéconomie ouverte contemporaine.
Une synthèse plus rigoureuse de l’ensemble de la littérature existante peut s’effectuer en adoptant une technique statistique encore relativement récente en économie : la méta-analyse. Selon Stanley et al. (2008), la méta-analyse permet d’expliquer les différences de résultats obtenus lors de multiples recherches et la finalité de cette synthèse quantitative est, d’après Florax et al. (2002), d’obtenir des enseignements généraux à partir de la multiplicité des résultats de l’ensemble de la littérature qui a été publié sur un sujet précis. La méta-analyse favorise une meilleure compréhension des principales raisons de la diversité des résultats obtenus, puisqu’elle combine les résultats des autres études pour fournir un pouvoir explicatif plus grand que la simple revue de la littérature. C’est donc une « analyse d’analyses » selon Hunter et Schmidt (1990) cité par Florax et al. (2002 : 2) qui apparaît moins subjective qu’une revue narrative de la littérature. Weichselbaumer et Winter-Ebmer (2003 : 10) la qualifient même de « plus démocratique voire agnostique ».
La méta-analyse fait l’objet d’un usage particulièrement fréquent en médecine, psychologie et en sciences de l’éducation. En économie, les premières méta-analyses ont été appliquées à l’économie de l’environnement ou du travail[1], et le Journal of Economic Surveys (2005, 19(3) : 295-533) y a consacré un numéro spécial. Cette thématique suscite un vif intérêt, car parmi les études les plus récentes appliquées à l’économie internationale, certaines portent sur les firmes multinationales (Görg et Strobl, 2001), sur le taux de change réel d’équilibre des principaux pays d’Europe centrale et orientale ou sur la corrélation de leurs cycles (Egert et Halpern, 2006; Fidrmuc et Korhonen, 2006), sur le Renminbi chinois (Bineau, 2010) sur les effets d’une monnaie unique sur le commerce international ou sur le lien entre la distance et le commerce bilatéral (Rose 2004; Disdier et Head, 2008), sur la politique monétaire (De Grauwe et Costa Storti, 2004), sur l’analyse des effets des politiques budgétaires sur la croissance de long terme (Nijkamp et Poot, 2004), ou sur la croissance des exportations (Mookerjee, 2006).
À notre connaissance, l’application de la méta-analyse au test de corrélation de l’épargne et de l’investissement n’a jamais été réalisée. Une base de données composée de 97 articles et qui comprend 1 399 estimations du coefficient de rétention de l’épargne est construite. Près de 73 % des observations de cet échantillon concernent la période postérieure à 1973 qui consacra la suppression du régime de changes de Bretton-Woods. L’objectif est alors de synthétiser les informations puisque l’application de cette technique statistique permet de détecter l’influence systématique des caractéristiques des études, comme la composition des échantillons, les spécifications ou les méthodes économétriques, sur les valeurs estimées du coefficient de corrélation de l’épargne et l’investissement.
L’évaluation d’un coefficient de rétention de l’épargne qui puisse être consensuelle apparaît nécessaire pour au moins trois raisons. D’abord, évaluer la valeur du coefficient de rétention de l’épargne d’un pays est un moyen d’apprécier l’ampleur du déséquilibre entre l’épargne et l’investissement à moyen terme. Toute action qui modifie le PIB affecte le déséquilibre extérieur à court et moyen terme, même si la contrainte budgétaire intertemporelle est par ailleurs respectée. Si les coefficients de rétention de l’épargne des pays diffèrent de la valeur qui peut être déduite de façon consensuelle de la méta-analyse, alors l’accroissement de l’instabilité financière aura d’autant plus d’impact sur un pays donné que le coefficient de rétention de ce pays sera relativement plus proche du coefficient de rétention consensuel comparativement à ceux de ses partenaires économiques. Ensuite, l’estimation qualitative des sources de variabilité du coefficient de rétention de l’épargne constitue une voie pour des recherches ultérieures d’évaluation empirique des coefficients de rétention des pays concernés. Cette recherche pourrait enfin être utile pour réconcilier cette mesure de la mobilité internationale du capital avec les autres définitions usuellement mises en avant, notamment par Frankel (1992)[2], pour apprécier la mobilité internationale du capital.
La prochaine section présente le modèle initial de FH et procède à une revue sélective de cette littérature. La section 2 détaille la méthodologie adoptée pour la conduite de cette méta-analyse. Une analyse statistique des métavariables est effectuée dans la troisième section. L’analyse des résultats de la méta-analyse est menée dans la quatrième section. La section 5 vérifie si la littérature sur la corrélation entre l’épargne et l’investissement est soumise à un biais de publication. La dernière section conclut.
1. Le modèle linéaire de Feldstein et Horioka
Dans une petite économie totalement ouverte sur l’extérieur, l’investissement est conditionné par les rendements du capital et par les préférences des agents économiques, mais non par la demande domestique. Le montant de l’épargne reflète les différences structurelles entre les économies. Dans ce cas, le degré élevé de mobilité du capital et la forte intégration financière entre pays devraient se refléter dans une faible corrélation entre l’épargne et l’investissement. Partant de cette hypothèse de degré élevé d’intégration financière, FH tentent de montrer (1980 : 129-151), que cela devrait se caractériser par une déconnexion entre l’épargne et l’investissement. Leur relation linéaire qui reflète les comportements de long terme sans effets de rétroaction de court terme, s’écrit :
Les termes S, I et Y sont respectivement l’épargne brute nationale, l’investissement domestique et le PIB. Les deux premières grandeurs sont rapportées à la dernière afin de limiter l’incidence du cycle des affaires et favoriser la comparaison entre les pays. Le terme ε est un aléa (c.-à-d. avec (0, ![]() )). L’indice i exprime le pays. La mobilité internationale du capital s’interprète à partir de la valeur du coefficient de rétention de l’épargne[3] : β. Par construction 0 < β < 1. L’hypothèse nulle est celle où β = 0. Dans ce cas, la mobilité internationale du capital est forte, suggérant une importante intégration financière. Il n’y a pas de lien tangible entre le taux d’épargne et le taux d’investissement car dans une petite économie, ce dernier dépend du taux d’intérêt mondial et de la technologie, mais pas de l’épargne. L’hypothèse alternative implique une forte corrélation entre ces deux grandeurs, puisque l’épargne supplémentaire sert à financer l’investissement domestique. Les capitaux sont immobiles et l’intégration financière est réduite.
)). L’indice i exprime le pays. La mobilité internationale du capital s’interprète à partir de la valeur du coefficient de rétention de l’épargne[3] : β. Par construction 0 < β < 1. L’hypothèse nulle est celle où β = 0. Dans ce cas, la mobilité internationale du capital est forte, suggérant une importante intégration financière. Il n’y a pas de lien tangible entre le taux d’épargne et le taux d’investissement car dans une petite économie, ce dernier dépend du taux d’intérêt mondial et de la technologie, mais pas de l’épargne. L’hypothèse alternative implique une forte corrélation entre ces deux grandeurs, puisque l’épargne supplémentaire sert à financer l’investissement domestique. Les capitaux sont immobiles et l’intégration financière est réduite.
FH testent la relation (1) en régressant des moyennes des taux d’investissement sur celles des taux d’épargne sur un échantillon de 16 pays de l’OCDE entre 1960 et 1974. Leurs résultats initiaux montrent que la mobilité internationale du capital entre ces pays est réduite puisque le coefficient de rétention de l’épargne est de 0,889 et n’est pas significativement différent de l’unité. En moyenne, l’investissement domestique trouve son origine dans un financement via l’épargne domestique à hauteur de 89 %. FH en déduisent que la mobilité internationale des capitaux est faible. Ces résultats ainsi que des études ultérieures (Feldstein, 1983; Feldstein et Bacchetta, 1991) ont rapidement induit un développement substantiel de nouveaux travaux qui mobilisent divers arguments. L’ensemble des estimations empiriques de la corrélation entre l’épargne et l’investissement de ces études indiquent une réduction progressive du lien entre les taux d’épargne et d’investissement, même si les niveaux obtenus demeurent élevés. Deux orientations majeures de recherche sont clairement observables dans cette abondante littérature.
La première orientation de recherche se concentre essentiellement sur des arguments historiques, économiques voire géographiques pour tenter d’interpréter les résultats de FH. Plusieurs travaux d’histoire monétaire et financière (Flandreau et Rivière, 1999; Taylor, 2002; Obstfeld et Taylor, 2004) distinguent quatre grandes périodes d’intégration financière depuis le milieu du XIXe siècle, où l’inégale libéralisation financière mène à des mouvements différenciés de mobilité international du capital.
Obstfeld (1986), Murphy (1986) ainsi que Wong (1990) rappellent que si l’épargne et l’investissement disposent de déterminants communs, la mise en évidence d’un coefficient de rétention de l’épargne élevé n’est pas nécessairement le signe d’une faible mobilité internationale du capital. Tesar (1991) insiste sur le cycle de vie et confirme les principaux résultats d’une forte corrélation entre les taux d’épargne et d’investissement sur un échantillon de 23 pays de l’OCDE sur la période 1960-1986. Tobin (1983), Westphal (1983), Dooley et al. (1987) et Bayoumi (1990), pensent que les politiques d’équilibre des comptes courants rehaussent le coefficient de corrélation, alors qu’à plusieurs reprises, la taille des pays, voire des régions est évoquée, notamment par Harberger (1980), Wong (1990), Baxter et Crucini (1993), ainsi que par Bayoumi et Rose (1993). Dans un modèle où la taille cumulée des deux pays est donnée, ces derniers montrent qu’en modifiant la taille relative des pays, la corrélation entre l’épargne et l’investissement demeure élevée. Summers (1989) et Bayoumi (1990) insistent sur le caractère procyclique des taux d’épargne et d’investissement menant à une élévation de la corrélation à la suite de chocs persistants. Bordes (1988) émet l’hypothèse d’un biais domestique marqué des agents économiques, qui les conduit à orienter d’abord leurs projets d’investissement vers des actions localisées sur le territoire où ils exercent leurs activités. La plupart de ces travaux confirment la forte corrélation des taux d’épargne et d’investissement entre les pays. Mais au niveau régional, ces résultats ne sont pas confirmés puisque Sinn (1992), Bayoumi et Rose (1993) ainsi qu’Armstrong et al. (1996) constatent que le coefficient de rétention entre les régions est nettement plus faible qu’entre les pays, sans que les causes de ces valeurs puissent être appréciées avec pertinence.
La seconde orientation de ces recherches se concentre sur la méthodologie économétrique. En effet, parallèlement à l’accumulation de données statistiques sur de nombreux pays et à l’évolution de l’outil économétrique, l’essentiel des recherches récentes se concentre sur des interrogations méthodologiques en utilisant différentes techniques avec des régressions sur des données transversales, temporelles ou en panel et sur différentes périodes tant pour les pays industrialisés qu’en développement.
Krol (1996) est le premier à exploiter simultanément la dimension individuelle et la dimension temporelle des séries des taux d’épargne et d’investissement en utilisant des données en panel dans le cadre d’un modèle en panel à effets fixes. En s’appuyant sur la méthodologie de Krol (1996), Jansen (1996), Coiteux et Olivier (2000), et Corbin (2001), introduisent plus finement ces effets fixes et temporels. Ces derniers, mais aussi Tesar (1991) et Jansen (2000) considèrent alors que l’essentiel des différences dans les résultats tient aux pays inclus dans l’échantillon.
L’estimation du lien entre l’épargne et l’investissement appliquée aux séries chronologiques offre des réponses complémentaires aux précédentes. La première est de quantifier la corrélation de long terme de chaque pays en évitant la combinaison dans un même échantillon des nations ayant des degrés inégaux d’intégration financière. Sinn (1992) utilise des données annuelles plutôt que des séries en moyenne. Il conclut que la corrélation, qui varie considérablement à travers le temps est nettement plus faible. La seconde est de permettre d’adopter les tests de racine unitaire et de coïntégration puisque les séries d’épargne et d’investissement sont non stationnaires. Cependant, accepter l’hypothèse alternative de coïntégration entre ces deux séries non stationnaires ne permet que de conclure à la présence d’une tendance commune entre l’épargne et l’investissement, et du respect de l’équilibre extérieur intertemporel, indépendamment de la mobilité internationale du capital. C’est pourtant l’hypothèse fréquemment testée dans cette littérature issue des travaux d’Engle et Granger (1987), Johansen (1988) et Johansen et Juselius (1990). Les valeurs élevées de β que celle-ci rapporte ne font que refléter l’absence d’évolution explosive de la dette extérieure, donc le respect de l’équilibre extérieur intertemporel et de la solvabilité de long terme[4]. L’acceptation de l’hypothèse de coïntégration implique qu’un pays respecte sa contrainte budgétaire intertemporelle, sans que soient prises en compte ses relations avec le reste du monde. Le biais vers l’unité que présentent ces séries, lorsque la contrainte budgétaire intertemporelle est respectée, implique que les coefficients de corrélation obtenus à partir de données transversales donnent des valeurs proches de l’unité, puisqu’il s’agit des moyennes pondérées des valeurs annuelles (Sinn, 1992; Coakley et al., 1996). Les déséquilibres des uns peuvent correspondre aux déséquilibres des autres et les comportements consolidés peuvent impliquer que la solvabilité intertemporelle est respectée pour un ensemble donné de nations. Toutefois, les déséquilibres des pays qui respectent individuellement leur solvabilité intertemporelle peuvent aussi invalider l’équilibre intertemporel de la zone. Autrement dit, cela n’informe que très marginalement sur la mobilité internationale du capital, d’autant que l’hypothèse d’une stabilité du processus générateur de ces grandeurs temporelles demeure, alors qu’il peut en réalité se modifier sous l’effet de chocs surtout si la durée retenue de l’estimation est importante[5].
L’essentiel des tests sur séries temporelles hormis quelques travaux pour lesquels les ruptures dans les séries ne sont pas systématiquement prises en considération, porte sur des échantillons de quelques dizaines d’observations[6]. Or, de telles procédures de tests de racine unitaire et de coïntégration sur ces échantillons réduits disposant d’une dynamique fortement persistante favorisent trop fréquemment l’hypothèse nulle de racine unitaire, alors que l’augmentation de la fréquence ne permet pas d’améliorer la pertinence de ces résultats. Il convient alors de pallier la faiblesse de ces tests sur des séries individuelles non stationnaires en appliquant aux données en panel non stationnaires, ces tests de racine unitaire[7] et de coïntégration[8]. C’est pourquoi Ho (2002), Banerjee et Zanghieri (2003), Kim et al. (2005) ainsi que Pelgrin et Schich (2008) tentent de réconcilier l’approche sur des séries temporelles avec l’approche en panel non stationnaire afin d’apprécier plus finement l’hétérogénéité des comportements des pays.
Le nombre significatif d’articles qui a été publié conduit à un stock particulièrement important d’estimations du coefficient de rétention de l’épargne et d’une grande diversité de valeurs. En raison des périodes retenues, des tests employés et des fréquences de données qui varient, le spectre des résultats par pays est large. En l’absence de réel consensus empirique sur ce que devrait être la valeur du coefficient de corrélation entre l’épargne et l’investissement, la comparaison demeure délicate à mener. Genberg et Swoboda, (1992) insistent sur l’absence de fondements théoriques rigoureux à partir desquels la relation serait obtenue. Il n’est pas aisé de conclure sur l’état exact de l’intégration financière en se fondant sur la seule valeur de β. La méta-analyse apparaît comme un instrument pertinent de synthèse de cette diversité d’informations afin de déduire une valeur de référence de ce coefficient.
2. Méthodologie de la méta-analyse
Stanley (2001) décrit trois étapes pour conduire une méta-analyse. La base de données est d’abord constituée pour déboucher sur la définition de la méta-équation qui fera l’objet de l’estimation. La codification des données est effectuée lors de la troisième étape.
La première étape est la constitution de la base de données qui regroupe le maximum d’études théoriques et empiriques sur le sujet traité. Trois principales sources sont mobilisées. D’abord, des bases de données en ligne[9] ont fait l’objet de plusieurs requêtes en décembre 2007[10]. Un stock d’articles publiés dans les revues académiques est ainsi réuni. Cette collecte initiale reflète la synthèse des résultats publiés, plutôt que la synthèse de la réalité. Elle est complétée par un dépouillement des références bibliographiques afin d’obtenir des données supplémentaires extraites de chapitres d’ouvrages ou de documents de travail. C’est pourquoi une dernière requête est effectuée sur les annuaires internet standards et sur les sites internet d’universités ou d’instituts de recherche connus pour travailler sur ces thématiques comme le CEPII, CEPR, FMI et NBER. Cela permet de prendre en compte le maximum d’études.
L’étape suivante concerne la définition de l’équation méta-économétrique afin de synthétiser les résultats. L’expression de la métarégression est identique à celle proposée par Stanley et Jarrell (1989) :
Le terme βj est l’estimation du coefficient de rétention de l’épargne incluse dans l’étude j (j = 1, 2,…, N). La constante β0 de cette métarégression reflète l’effet réel observé sur tout l’échantillon. Les variables de modération sont les termes Zjk (k = 1, 2, …, K), qui décrivent une caractéristique particulière de l’étude pour laquelle le paramètre est obtenu et permettent d’expliquer la variation des βj entre les études. Elles décrivent la méthode, les périodes et les données qu’utilisent les différentes études. Le symbole γk estime l’impact de chaque caractéristique sur l’estimation du coefficient de rétention de l’épargne. Le terme d’erreur est exprimée par uj.
La dernière étape suppose la définition des variables et la codification des variables explicatives à la suite du dépouillement de tous les articles retenus. Cette codification s’effectue en utilisant des variables dichotomiques qui prennent la valeur 1 ou 0 lorsque le paramètre βj comprend, ou non, la caractéristique correspondante. L’application de la statistique I2 développée par Higgins et al. (2003)[11] qui vaut 99,50 % montre une hétérogénéité élevée des coefficients βj. Cette hétérogénéité qui résulte essentiellement des choix méthodologiques effectués pour réaliser chaque étude, justifie la méta-analyse et sera appréciée par l’intermédiaire d’un nombre élevé de métavariables. Il est donc nécessaire de distinguer différents critères qui apparaissent importants. Le dépouillement attentif des articles conduit à définir quatre grandes catégories de métavariables explicatives Zjk qui sont susceptibles d’expliquer les variations de βj entre les études. Le tableau 1 reprend le codage des variables utilisées.
Tableau 1
Codage des variables utilisées
La première catégorie de méta-analyse porte sur les données et concerne la chronologie, la fréquence et la structure des données qui sont exploitées. En effet, l’analyse porte sur des travaux dont certains exploitent des observations qui débutent en 1850 alors que d’autres utilisent des données qui s’achèvent en 2003. En accord avec les récents travaux d’histoire monétaire et financière (Flandreau et Rivière, 1999; Obstfeld et Taylor, 2004), quatre périodes sont clairement distinguées : 1850-1914; 1918-1944; 1945-1973 et 1974 à nos jours, notées respectivement P1, P2, P3 et P4. L’année centrale de chaque échantillon ayant servie à l’estimation de βj constitue alors le critère d’affectation dans l’une des catégories. Puis, une métavariable porte sur les données annuelles (F_A) et trimestrielles (F_T). Une autre métavariable détaille la structure des données : données transversales (D_CS); séries temporelles (D_ST) et données de panel (D_DP).
Le second groupe précise la composition de l’échantillon de pays. Six métavariables sont mises en évidence : groupe de pays de l’OCDE (OCDE); groupe de pays en voie de développement (PVD)[12]; un seul pays de l’OCDE (OCDE_1) ou de PVD (PVD_1); groupes de régions de l’OCDE (OCDE_R) ou la combinaison des pays de l’OCDE et de PVD (PVD_OCDE).
Puis, la troisième catégorie de métavariables décrit la qualité de la publication. Deux variables dichotomiques, qui se réfèrent au support de diffusion des résultats (revues académiques, documents de travail, chapitres d’ouvrages, actes de colloques et de conférences, …) sont créées à partir du classement de Kalaitzidakis et al. (2003). Ce dernier, qui a été exploité par Nijkamp et Poot (2004) ainsi que Knell et Stix (2005), porte sur 159 revues académiques. Une variable dichotomique (Q1) considère les revues qui sont incluses dans le classement de Kalaitzidakis et al. (2003). Les autres revues, les documents de travail, les extraits de livres ainsi que les actes de colloques et de conférences sont repris dans la seconde (Q2).
Le dernier ensemble détaille la méthode économétrique. Initialement, plus de 20 différentes techniques économétriques sont recensées. Six techniques sont finalement retenues afin d’avoir un nombre significatif d’observations dans chaque catégorie mais aussi parce que certaines d’entre elles sont proches ou asymptotiquement semblables pour de larges échantillons. Les techniques retenues sont liées à la méthode des moindres carrés ordinaires, (MCO), à la méthode des MCO dynamiques (DOLS) ou du maximum de vraisemblance (FMOLS) et aux variables instrumentales (IV). Les techniques de coïntégration sur séries chronologiques (CI_ST) et sur des données transversales (CI_P) sont prises en compte.
3. Les métadonnées
3.1 L’échantillon
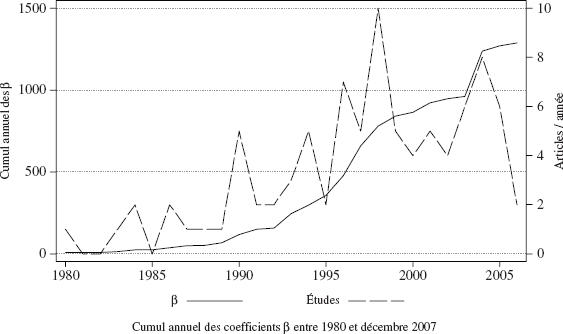
Le graphique 1 indique que le stock de coefficients disponibles augmente régulièrement entre juin 1980 et décembre 2007 alors que la quantité annuelle d’articles publiés est fluctuante. La collecte met en évidence 1 688 estimations βj de 114 articles.
Graphique 1
Articles publiés sur le thème de « Feldstein et Horioka »
Certains articles sont écartés car les informations sont initialement extraites de présentations effectuées dans d’autres articles, comme cela peut fréquemment s’observer dans les revues de la littérature. Il s’agit aussi de valeurs des coefficients issues de modèles associant des données simulées (Obstfeld, 1986; Alexakis et Apergis, 1994) ou qui introduisent des effets de seuil conduisant à estimer plusieurs valeurs du coefficient de rétention de l’épargne au sein de la même relation (Ho et Chiu, 2001; Ho, 2003). D’autres études font l’objet de publications multiples (Sarno et Taylor, 1998a, 1998b). Certaines adoptent des méthodes économétriques qui estiment des coefficients de rétention à partir des variations des taux d’épargne et d’investissement (Corbin, 2001; Narayan, 2005) alors que la spécification retenue porte sur des niveaux. Dix-sept études associant 284 coefficients de rétention sont éliminées car les spécifications utilisées ne permettent pas une comparaison directe avec le modèle linéaire. L’échantillon comprend 1 404 valeurs du coefficient de rétention de l’épargne.
Les valeurs du coefficient de rétention de l’épargne évoluent à l’intérieur de l’intervalle [-1,7; 4,5]. Cette étendue suggère l’existence de valeurs atypiques qui peuvent affecter la qualité des résultats. Le test de détection de points atypiques de Grubbs est adopté. Récemment utilisé par Disdier et Head (2008), ce test calcule l’existence d’observations atypiques en initialisant la procédure à la suite de l’exclusion d’une nouvelle valeur atypique. Cinq observations sont éliminées[13] conduisant à un échantillon de 1 399 observations au sein de 97 articles.
3.2 Métastatistiques descriptives
Le graphique 2 qui associe tous les coefficients de corrélation de l’épargne avec l’année centrale de chaque échantillon confirme l’hypothèse de l’accentuation de l’intégration financière et de la mobilité internationale des capitaux depuis le milieu du XIXe siècle. La première année observée est 1850 (Hoffman, 2004) et concerne la Grande-Bretagne. Si on effectue une régression entre chaque β et l’année centrale observée pour l’estimation de ce dernier, corrigée de l’année la plus ancienne, alors la constante de cette régression linéaire s’interprète comme le coefficient de rétention théorique de l’épargne en 1850[14], c’est-à-dire l’état initial de la corrélation entre l’épargne et l’investissement. La pente décrit la vitesse de modification de la mobilité internationale du capital. L’hypothèse implicite est que si la mobilité internationale du capital s’intensifie depuis 1850, en dépit des phases de libéralisation intense et de celles de restriction de la mobilité internationale du capital[15], le signe de cette pente devrait être négatif. Les résultats sont les suivants :
Graphique 2
Coefficients de rétention de l’épargne à long terme
Les chiffres entre les parenthèses indiquent les écart-types de l’estimateur. La constante est significative au seuil de 1 %. La mise en oeuvre d’un test de restriction où l’hypothèse nulle est que la constante de la régression est unitaire indique que χ2(1) = 7,334 (probabilité = 0,006). Cela n’est pas significatif au seuil de 5 % et la constante n’est pas différente de l’unité. Le taux d’épargne et le taux d’investissement sont globalement similaires en début de période. Le coefficient de la pente est significativement négatif au seuil de 1 %.
Il y a bien une tendance de long terme en faveur d’une réduction de l’estimation du coefficient de rétention de l’épargne depuis 1850. Malgré une statistique de Fisher significative, la faible valeur du coefficient R2 rappelle que la baisse des estimations du coefficient ne peut pas s’expliquer uniquement par la période d’estimation et que d’autres facteurs pourraient être pris en considération afin d’expliquer la variabilité du coefficient β.
L’hypothèse de linéarité apparaît forte puisque l’on suppose implicitement que l’accroissement des mouvements de capitaux s’est produit selon des modalités identiques pour tous les pays et pour toutes les périodes. L’application d’une courbe lissée sur les données suggère une intégration financière inégale depuis 1850 et renforce l’hypothèse des principales périodes d’intégration financière.
Selon le tableau 2, la moyenne et la médiane de toutes les périodes et toutes les publications confondues de l’échantillon complet sont respectivement de 0,61 et de 0,66. Ainsi, le taux d’investissement n’est pas indépendant du taux d’épargne, puisqu’une variation de 10 % de ce dernier est susceptible d’induire une variation moindre du taux d’investissement avec toutefois de fortes différences selon les périodes, puisque les nations financent en moyenne de 54 % à 75 % de leur investissement par de l’épargne domestique. La moyenne du coefficient de rétention sur la période 1974-2003 est nettement plus faible que celle observée pour les trois autres périodes. Cela suggère que le degré d’intégration financière des économies a atteint un niveau inégalé, malgré la récurrence des crises financières et bancaires des années quatre-vingt-dix, y compris au regard de la période de l’étalon-or. Les estimations postérieures à la Seconde Guerre mondiale sont majoritaires puisque cela concerne 73,77 % des estimations et que peu d’estimations sont disponibles pour les périodes antérieures au régime de Bretton-Woods. Le nombre relativement restreint de données explique la faible quantité d’estimations sur les années 1850 à 1944. En pratique, 13 travaux[16] utilisent des données antérieures à 1945, mais ils multiplient les estimations du coefficient β en générant plusieurs sous-périodes voire en utilisant différentes méthodes économétriques.
Tableau 2
Métastatistiques descriptives de β : échantillon complet
Note : Les moyennes sur les quatre périodes sont issues d’une régression de βj sur des variables dichotomiques des quatre périodes, sans constante. R² = 0,719; Fisher F = 932,81; N = 1399.
* Significatif au seuil de 1 %.
Le tableau 3 présente la distribution de notre échantillon au cours du temps en fonction des métavariables et de leur fréquence moyenne sur l’intégralité de l’échantillon. La quasi-totalité des estimations du coefficient de rétention a été réalisée avec des données annuelles, car les données trimestrielles ne représentent que 5,93 % de l’ensemble et ne portent que sur les périodes postérieures à 1945. Les publications dans des journaux académiques de la liste de Kalaitzidakis et al. (2003) sont relativement plus fréquentes représentant 54,32 % du total, mais la moyenne de b est sensiblement plus faible que celle des articles dans la catégorie Q2.
Tableau 3
Caractéristiques du coefficient de rétention par sous-périodes
Note : Se rapporter au tableau 1 pour le détail des acronymes
Pourcentage d’observations de chaque rubrique au regard du nombre total d’observations (N=1399).
Les données transversales (D_CS) ne représentent que 25,45 % des observations et les études avec des données de panel concernent 9,29 % des observations. Les données qui ont toujours fait l’objet d’une forte utilisation, 65,26 % des estimations, concernent les données chronologiques (D_ST). Près de 67,99 % des estimations portent sur au moins un pays membre de l’OCDE (OCDE, OCDE_1 et OCDE_R) avec une nette préférence pour les travaux sur un seul pays (OCDE_1 : 41,03 %), plutôt que sur des groupes de pays (OCDE : 24,23 %) alors que les travaux ayant pour objet des régions de l’OCDE sont réduits, au regard de la taille de l’échantillon (OCDE_R : 2,72 %). Les travaux sur un groupe ou un seul PVD (PVD, PVD_1) portent sur 30,02 % des estimations, et ceux combinant des pays de l’OCDE et des PVD sont peu nombreux (PVD_OCDE : 2,00 %).
La majorité des estimations du coefficient de rétention a été effectuée avec la méthode des MCO (MCO). Cela représente près d’une estimation sur deux dans le cas des données empilées et près du quart des estimations utilisant des séries temporelles. Le nombre d’articles adoptant la méthode des variables instrumentales (IV) est particulièrement faible. Sur la période récente et en lien avec le développement des séries chronologiques puis en panel, le nombre de coefficients de rétention estimé à l’aide des méthodes de coïntégration (CI_ST, CI_P) et d’estimations dynamiques (DOLS, FMOLS) augmente sensiblement.
L’utilisation de ces nombreuses variables dichotomiques lors de cette métarégression permet de considérer l’hétérogénéité des données et d’expliquer l’évolution différenciée de la corrélation entre l’épargne et l’investissement.
4. Interprétation des métarégressions
Lorsque toutes les variables muettes sont reprises dans l’estimation de la relation (2), la relation linéaire entre les variables est parfaite. Il devient impossible d’estimer les coefficients de la relation, puisqu’il s’agit du piège des variables muettes. C’est pourquoi une variable dichotomique incluse dans chacune des catégories est exclue des régressions. Ces variables omises qui se retrouveront dans la constante de la régression, sont celles dont la fréquence est la plus importante dans chacune de leur catégorie. L’interprétation d’une variable dichotomique s’effectue relativement à ces six variables absentes : F_A, D_ST, OCDE_1, P4, Q1 ainsi que MCO.
Les erreurs de la relation (2) ne respectent pas nécessairement les hypothèses standards. Les articles répètent fréquemment les estimations des coefficients de rétention avec des données, des pays, des périodes, des fréquences semblables et des méthodes économétriques distinctes ou non. Il y a donc une forte redondance des sources statistiques utilisées puisqu’il s’agit fréquemment du FMI, voire de l’ONU. Les estimations se reproduisent au sein de la même étude[17] et l’indépendance des observations ne peut pas être admise. La méthode des moindres carrés ordinaires produit des estimateurs qui n’ont plus la propriété de variance minimale. Le risque d’hétéroscédasticité des erreurs de la métarégression apparaît non négligeable. En raison de sa robustesse, la méthode de correction des termes de la matrice de variance-covariance de White (1980) est adoptée lorsque la technique économétrique utilisée est la méthode des MCO.
La méthode des moindres carrés pondérés suppose, quant à elle, la présence d’une variable de pondération. Les 1 399 observations des 97 articles ne donnent pas systématiquement la valeur de l’écart-type de l’estimateur et lorsque c’est le cas, il n’est pas toujours assuré que l’écart-type de l’estimateur soit robuste. Dans certains cas, il est reconstitué à partir de la statistique de Student disponible. L’information disponible est réduite car il ne reste plus que 89 articles qui produisent 1 259 valeurs différentes de l’écart-type de l’estimateur β. C’est pourquoi, la pondération adoptée correspond à l’année centrale observée pour l’estimation de chaque coefficient de rétention de l’épargne.
Le tableau 2 et le graphique 2 montrent que l’essentiel des observations est concentré sur les années 1974-2003 qui correspondent à une période de réformes du système monétaire international, de restructurations importantes des réseaux de financement des économies et d’intégration financière croissante. C’est pourquoi, un nouvel échantillon ne prenant en compte que des valeurs du b portant sur les années 1974-2003 est créé. Cela permet de prendre en considération l’important et récent progrès technique en économétrie. Il comprend alors 1 032 observations. Le tableau 4 présente les résultats des estimations selon ces deux échantillons.
Tableau 4
Métarégressions du coefficient de rétention de l’épargne
Note : Se rapporter au tableau 1 pour le détail des acronymes. MCO : méthode des moindres carrés ordinaires MCP : méthode des moindres carrés pondérés. Pondération : année moyenne de l’échantillon. Les écart-types lorsque la méthode MCO est adoptée sont corrigés en adoptant la méthode de correction des erreurs de White (1980). Ces écart-types sont entre les parenthèses
N : nombre d’observations F : Statistique de Fisher ***, ** et * signifient respectivement significatif au seuil de 1 %, 5 % et 10 %.
Le modèle explique à peine 20 % des variations du coefficient de rétention de l’épargne selon les variables incluses dans les régressions. Toutefois, la forte correspondance des signes des paramètres entre les différentes régressions et la significativité des statistiques de Fisher renforcent la pertinence des méthodes empiriques d’estimation et du choix des métavariables retenues.
La constante de la régression correspond au cas où l’article dont est extraite l’observation i) applique la méthode des MCO (MCO), ii) adopte des séries temporelles annuelles (F_A) sur un seul pays de l’OCDE (OCDE_1), iii) couvre la période 1974-2003 (P4), iv) a été publié dans la liste de Kalaitzidakis et al. (2003). Les estimations des constantes des régressions sont toutes significatives et varient de 0,620 à 0,627 pour l’échantillon complet et de 0,593 à 0,599 pour l’échantillon restreint aux années postérieures à 1973. Ces estimations sont inférieures à la moyenne calculée des colonnes (2-1) et (2-5). La corrélation de l’épargne avec l’investissement durant la période 1850-1918 (P1) est en moyenne plus faible que celle en vigueur durant la période 1974-2003 (P4) puisque la valeur du coefficient de rétention de l’épargne associée à la période est significativement négative. Si on retrouve bien la réduction régulière du coefficient de rétention de l’épargne de 1945 (P3), il apparaît que la période 1919-1945 (P2) n’a pas d’impact systématique sur l’estimation de β. Par conséquent, sur la période récente, l’épargne domestique devient de moins en moins importante pour financer l’investissement et les économies font de plus en plus souvent appel à de l’épargne étrangère pour financer les projets d’investissements. Le choix de la période a une forte influence sur les résultats car les paramètres estimés associés à la constante de la métarégression permettent de retrouver le cycle de l’intégration financière sur longue période. La hiérarchie des phases de l’intégration financière se constate à nouveau.
Les paramètres des métavariables D_CS et D_DP indiquent que l’utilisation de données empilées ou en panel a une incidence systématiquement positive sur l’estimation de β. Toutefois, leurs paramètres au sein de chaque régression sont proches. Il ne devrait pas y avoir de différences importantes lorsque l’estimation du coefficient β est effectuée avec des données de panel ou avec des données empilées. Dans ces conditions, le choix des données utilisées devrait essentiellement dépendre des contraintes liées à leur disponibilité. Puis, le choix de la fréquence n’exerce pas d’influence systématique sur les estimations de β car les paramètres n’apparaissent pas statistiquement significatifs. L’utilisation de données trimestrielles (F_T) tant pour l’échantillon complet que pour l’échantillon 1974-2003 ne devrait pas générer des valeurs du coefficient β différentes du cadre standard puisque les coefficients ne sont pas significatifs. Ces résultats apparaissent ambigus puisque si le choix de la fréquence n’affecte pas significativement les résultats, cela est différent pour le choix de la période. Il s’avère toutefois préférable d’adopter des données annuelles plutôt que trimestrielles. En effet, ces dernières sont peu nombreuses pour les périodes antérieures à 1945 et le tableau 3 indique que 94 % des études utilisent des données annuelles. Ces dernières sont généralement disponibles pour de plus larges éventails de pays et couvrent des périodes qui sont parfois relativement longues.
Le support de publication a une influence systématique sur la valeur du coefficient β puisque le coefficient de la variable dichotomique Q2 est significativement positif. Les coefficients varient de 0,058 à 0,060 pour l’échantillon complet et de 0,075 à 0,076 pour les échantillons qui se concentrent sur la période 1973-2003. Les auteurs qui publient leur recherche sur des supports qui ne sont pas repris dans la liste Q1 auront des estimations du coefficient de corrélation de l’épargne à l’investissement systématiquement plus importantes. La stratégie initiale d’accumulation d’observations en provenance de documents de travail, actes de colloques et autres supports de publications, donc incluses dans la catégorie Q2 et qui n’ont pas encore transité par les filtres qualitatifs des revues académiques, a conduit à modifier l’effet induit par l’usage d’observations issues de la catégorie Q1. Ce résultat suggère qu’un biais de publication est susceptible d’exister surtout si les travaux portent sur la période postérieure à 1973.
L’impact des variables décrivant la composition de l’échantillon ne doit pas être sous-estimé, car la mobilité internationale se détermine par rapport à un pays ou un groupe de pays, plus que par rapport aux caractéristiques des données et du support de publication. D’où l’importance de ces métavariables dans l’interprétation des résultats. Les paramètres de ces métarégressions montrent une influence systématique de la composition de l’échantillon sur la valeur de β. Lorsqu’une étude porte sur un groupe de pays de l’OCDE (OCDE, OCDE_R,) ou des PVD (PVD, PVD_1 et PVD_OCDE), les coefficients sont tous négatifs et significatifs. Cela conduit systématiquement à diminuer la valeur du coefficient β, même si l’effet final est inégal selon les métavariables.
Les coefficients des données régionales, (OCDE_R) sont tous plus importants que la constante de la régression correspondante puisqu’ils varient de -0,827 à -0,824 (resp. -0,785, -0,783) dans le cas de l’échantillon complet (resp. l’échantillon 1973-2003). Une nation étant l’agrégation de régions, supposées former une zone monétaire optimale, chaque région est plus intensément spécialisée que ne l’est la nation en moyenne. L’épargne apparaît nettement plus mobile entre des régions d’un même pays qu’entre différents pays, même si le niveau de vie apparaît relativement homogène. Afin de faire face aux déviations de la production relativement à celles du revenu, ces entités géographiques où les parités sont fixes s’ouvrent plus aisément au marché financier. L’absence d’anticipations de dépréciation des changes repousse les frontières de la solvabilité. L’incitation des autorités domestiques à intervenir se réduit puisqu’elles n’ont plus à se préoccuper des déséquilibres financiers régionaux, d’autant que les derniers peuvent être affectés par les transferts nets des administrations centrales auprès des instances régionales. Ces transferts intrarégionaux constituent alors le moyen d’assurer la solvabilité financière et justifient la faible corrélation entre l’épargne et l’investissement. La mobilité du capital apparaît forte et la corrélation entre l’épargne et l’investissement est réduite, voire négative, car les régions semblent former un ensemble relativement intégré, alors que les nations apparaissent relativement cloisonnées. L’Union européenne est susceptible de s’assimiler de plus en plus à un ensemble de régions où la mobilité intrarégionale du capital s’accroît alors même que la mise en place d’une zone de parités fixes, puis de la monnaie unique, accentue la mobilité du capital (Bhandari et Mayer, 1990). En contrepartie, la sensibilité du β à l’évolution de la conjoncture s’accroît (Armstrong et al., 1996). Ces résultats sur les données régionales, qui sont robustes à la méthodologie de calcul de l’épargne, sont en accord avec les conclusions des articles où des résultats de corrélation faibles et négatives sont mis en évidence, tant pour 11 régions britanniques, (Bayoumi et Rose, 1993), que pour des régions italiennes (Decressin et Disyatat, 2000), canadiennes (Helliwell et McKitrick, 1999; Decressin et Disyatat, 2000), japonaises (Yamori, 1995; Dekle, 1996) ainsi que nord-américaines (Sinn, 1992).
Les paramètres des trois métavariables qui se rapportent aux pays en voie de développement (PVD, PVD_1 et PVD_OCDE) sont tous significativement négatifs. L’illusion d’une substantielle mobilité internationale des capitaux entre ces pays est forte. Très rapidement, des travaux comme ceux de Wong (1990) et Dooley et al. (1987), avaient mis l’accent sur des coefficients de rétention de l’épargne relativement moins favorables que pour les pays de l’OCDE alors que des contrôles sur la mobilité des capitaux persistent encore dans de nombreux pays en voie de développement. Ces pays sont ouverts sur le reste du monde afin d’assurer leur développement et sont implicitement plus favorables à l’endettement extérieur, donc à une importation de capitaux, sans que cela reflète une intégration financière poussée.
Une interprétation possible de la faiblesse de cette corrélation entre l’épargne et l’investissement réside dans les défaillances qui peuvent apparaître dans les réseaux de collecte de l’information statistique au sein de ces pays. Également, il n’est pas certain que les méthodes économétriques mises en oeuvre pour les pays de l’OCDE soient aisément utilisables dans les pays en voie de développement en raison des difficultés qui peuvent exister pour obtenir des données fiables sur des périodes relativement significatives. La sous-déclaration statistique liée aux imperfections dans cette collecte peut induire des opérations d’arbitrages internationaux qui donnent lieu à des mouvements internationaux de capitaux. Ces derniers ne sont qu’imparfaitement, voire pas du tout, repris dans les statistiques nationales. Le coefficient de corrélation entre l’épargne et l’investissement est sous-évalué, sans que cela soit le résultat d’une forte mobilité des capitaux. De surcroît, les lacunes persistantes de certains réseaux financiers et bancaires dans la collecte de l’épargne peuvent sous-estimer la valeur effective de l’épargne nationale. Devant les faibles performances du système bancaire en matière de collecte de l’épargne et de financement de l’investissement, des réseaux parallèles, donc peu recensés, se mettent en place. Puis, l’aide étrangère au développement pour le financement des déséquilibres des balances des paiements peut exercer une large influence. En effet, une part substantielle de l’importation nette d’épargne provient de l’aide au développement versée par des organismes financiers publics ou privés. L’aide au développement qui est un flux non marchand ne reflète pas exactement l’état de l’intégration financière, selon une réponse endogène au marché, puisqu’elle passe préalablement par le filtre rigoureux de ces organismes financiers. Elle s’apparente dans ce cas à un supplément de consommation nationale, dont l’objectif est d’aider au développement économique par l’intermédiaire de l’accumulation du capital. L’écart entre l’épargne et l’investissement domestiques est modifié sans que la mobilité du capital en soit la cause initiale.
Implicitement, la significativité du coefficient sur la variable PVD_OCDE incite à revenir sur l’argument développé initialement par Harberger (1980), Murphy (1984) puis par Wong (1990) sur la taille des pays. Cette dernière peut conduire à conclure à une mobilité internationale du capital différente de celle qui existe dans la réalité. Par effet de taille, bien que la distinction n’apparaisse pas clairement dans la littérature, il est possible de distinguer d’une part, l’effet de taille à proprement parler, de l’effet lié aux niveaux inégaux de développement entre pays, souvent regardés comme petits au regard des élasticités prix, d’autre part. La taille d’un pays affecte d’abord les résultats en raison de ses structures productives, puis de son poids dans l’économie mondiale. Harberger (1980) avec Tobin (1983) montrent que la mobilité des capitaux est plus importante dans les petits pays que dans les pays de grande taille. Ces derniers bénéficient d’une structure productive plus diversifiée, où le nombre plus important de secteurs manufacturiers en excédent d’épargne permet de satisfaire les besoins des secteurs en déficit d’épargne. Cela permet de financer une fraction croissante de l’investissement domestique, sans que cela nécessite un financement extérieur important. Une estimation de la corrélation entre l’épargne et l’investissement pour de grands pays devrait donner des résultats plus élevés que pour de petits pays. D’ailleurs Murphy (1984), avec un échantillon de 17 pays de l’OCDE entre 1960 et 1980, montre que la corrélation entre les taux d’investissement et d’épargne s’améliore lorsqu’on exclut les petits pays ayant une faible part dans l’épargne totale.
Ces résultats infirment l’hypothèse selon laquelle les marchés financiers de grands pays comme les USA, la Grande-Bretagne ou le Japon sont relativement plus intégrés que ceux d’autres pays industrialisés. Que faut-il conclure sur le plan de la mobilité internationale du capital si le coefficient de rétention de l’épargne se réduit à la suite de l’exclusion de grands pays? Baisse-t-il parce que le grand pays est mieux intégré financièrement que les autres pays, ou bien parce que les pays restants n’ont qu’une influence réciproque réduite sur les tendances respectives de l’épargne et de l’investissement, ou bien parce qu’il existe des déterminants communs? Auquel cas, ce n’est pas la taille absolue qui importe, mais la taille relative entre les pays de l’échantillon. Une telle conclusion semble sortir de l’étude de Tesar (1991). Celle-ci, dans un échantillon de 24 pays de l’OCDE, tout en gardant les grands pays, exclut le Luxembourg en raison de son caractère atypique. La taille du Luxembourg et la structure de sa balance des paiements, liée à sa spécialisation internationale affecte la qualité des résultats. Les coefficients présentés se modifient significativement lorsque l’échantillon exclut le Luxembourg[18]. Si la corrélation était véritablement le signe d’une mobilité internationale forte du capital, l’exclusion de n’importe quel pays ne devrait pas affecter significativement les valeurs successives des coefficients de corrélation.
La technique économétrique adoptée exerce une grande influence sur la valeur de β. Cependant, le choix de la technique économétrique est simultanément conditionné par les données que le chercheur utilise et soumis au progrès technique inhérent à l’utilisation de l’économétrie elle-même. D’autres techniques plus récentes comme celles liées à la coïntégration sur des séries temporelles et sur des données en panel font actuellement l’objet d’une utilisation significative.
Le tableau 4 montre que la méthode des variables instrumentales (IV) n’a pas d’effet significatif sur l’estimation du coefficient β. Cependant, que l’équation linéaire 1 soit testée par la méthode des MCO, qui est la méthode économétrique la plus fréquemment utilisée, ou avec des méthodes alternatives, la forme statique de cette relation persiste, sans distinction possible entre la tendance de long terme liant le niveau du taux d’épargne et d’investissement et les ajustements de court terme, en supposant que le lien entre l’épargne et l’investissement soit constant et identique entre tous les pays. L’évaluation de la mobilité internationale du capital sous cette forme ne différencie pas les évolutions tendancielles de long terme de leurs évolutions cycliques, autrement qu’en réduisant la période totale en diverses sous-périodes, puis en comparant les valeurs des coefficients estimés entre eux et la dépendance des uns à l’égard des autres (Turner, 1986; Sinn, 1992).
Les modifications structurelles sont supposées inexistantes quand la moyenne sur les données est réalisée sur de longues périodes ou alors elles sont estimées par des moyennes sur de plus petites périodes. Comme le souligne Frankel (1989), les modifications structurelles, si elles existent, se réalisent selon une parfaite homogénéité pour tous les pays, puisque les données disponibles subissent le même traitement. Or cela est peu vraisemblable. Il est raisonnablement concevable que l’intégration financière ne se soit pas réalisée à un rythme identique pour tous les pays, car les niveaux de revenus ne sont pas nécessairement homogènes et conduisent à des relâchements significatifs et inégaux des valeurs des coefficients de corrélation. C’est pourquoi, les nombreuses études adoptant des séries temporelles nuancent ces résultats. Coakley et al. (1996), Jansen (1996, 1997), Jansen et Schulze (1996) pour la Norvège, Ballabriga et al. (1991), Argimon et Roldan (1994) pour certains pays de l’Union européenne[19], en s’appuyant sur la théorie de la coïntégration, remettent en cause l’interprétation initiale de la relation 1, lui préférant la représentation sous forme de correction d’erreur qui favorise la distinction entre la dynamique de court terme de celle de long terme. Dès lors, une estimation de β élevée n’est plus le reflet d’une faible mobilité internationale du capital mais le signe du respect de la contrainte budgétaire intertemporelle d’une économie ouverte puisque l’on recherche implicitement un vecteur de coïntégration (1, – ![]() ) = (1,-1). L’utilisation d’une méthode de coïntégration a systématiquement pour effet de majorer le coefficient β au regard du cadre de référence. L’influence d’une telle technique est plus importante sur l’échantillon 1973-2003 que sur l’échantillon complet puisque les coefficients varient de 0,137 à 0,144 dans le premier cas et 0,065 à 0,066 dans le second cas.
) = (1,-1). L’utilisation d’une méthode de coïntégration a systématiquement pour effet de majorer le coefficient β au regard du cadre de référence. L’influence d’une telle technique est plus importante sur l’échantillon 1973-2003 que sur l’échantillon complet puisque les coefficients varient de 0,137 à 0,144 dans le premier cas et 0,065 à 0,066 dans le second cas.
Pour autant, lorsque les études exploitent des séries temporelles, le coefficient β ne fait que décrire le lien au sein de chaque nation entre le comportement d’investissement et celui d’épargne, sans tenir compte des moyens qui sont mis en oeuvre pour subvenir à court et moyen termes au déséquilibre que reflète un β différent de l’unité et sans considérer simultanément l’incidence des autres économies et leurs éventuelles complémentarités sur le financement des déséquilibres. La multiplication des estimations du coefficient de rétention pour les mêmes nations conduit finalement à une multiplicité de résultats dont l’originalité réside dans la spécificité économétrique adoptée. Cependant, ni les travaux sur données empilées, ni ceux sur séries temporelles ne permettent de montrer les effets fixes liés à la localisation (pays, régions) et au temps, alors qu’ils peuvent jouer un rôle non négligeable dans la détermination du coefficient de rétention de l’épargne. Plutôt que de se concentrer sur chaque pays, il semble préférable de considérer les relations simultanément au sein d’un panel de pays afin de mieux incorporer l’hétérogénéité entre les pays et entre les périodes de temps. Krol (1996), Jansen (2000), Corbin (2001) ainsi que Coakley et al. (2004) soulèvent le problème lié à l’hétérogénéité des données lorsque l’on adopte des données de panel. Ces auteurs obtiennent des valeurs du coefficient de rétention de l’épargne nettement différentes de celles déduites par FH en utilisant des données en panel. Le signe du paramètre décrivant l’utilisation des techniques de la coïntégration appliquées aux données en panel (CI_P) est significatif et élevé au regard des autres coefficients (Kim et al. 2005; Eng et Habibullah, 2006; Pelgrin et Schich, 2008) dans les deux échantillons. La méthode DOLS mène aussi à des valeurs significatives du coefficient de rétention. Ces deux méthodes indiquent dans tous les cas une majoration systématique du coefficient de rétention de l’épargne comparé à celui que l’on peut déduire de l’utilisation de la méthode des MCO. L’utilisation de la méthode DOLS a le plus d’impact sur l’évaluation du coefficient de rétention de l’épargne puisque les coefficients associés à cette méta-variable sont de l’ordre de 0,23 ou 0,25 selon l’échantillon alors que les coefficients associés à la métavariable CI_P sont moindres. La méthode FMOLS n’exerce, quant à elle aucun impact systématique sur l’estimation de β.
Une fois que le choix est effectué sur les statistiques utilisées ainsi que leur fréquence, les échantillons de pays adoptés et le support de publication, on constate aisément que la méthodologie économétrique conduit à des valeurs du coefficient de rétention de l’épargne nettement différenciées. Il est donc nécessaire d’adopter différentes stratégies économétriques afin d’avoir un large aperçu du spectre du coefficient de rétention de l’épargne. Cette stratégie semble peu fréquemment mise en oeuvre puisqu’elle ne concerne qu’un tiers des articles.
5. Le biais de publication
Les éditeurs des journaux académiques ont fréquemment tendance à rejeter les propositions d’articles qui n’apportent pas de réelle valeur ajoutée à la littérature existante. Ces mêmes éditeurs ne sont pas nécessairement sensibles aux travaux dont les résultats ne sont pas significatifs au sens où l’hypothèse nulle est trop fortement acceptée, puisque les articles publiés sont ceux qui démontrent leur originalité, leur qualité technique et le caractère probant de l’hypothèse testée. Dès lors, il convient de vérifier la présence d’un biais de publication.
L’étude de la présence d’un biais de publication s’effectue d’abord visuellement à l’aide d’un « funnel graph » que complète une régression supplémentaire à partir d’un nouvel échantillon qui ne porte que sur les observations incluses dans la catégorie Q1. Des tests spécifiques qui suivent les enseignements de Stanley (2005 : 321) ainsi que Stanley et al. (2008) complètent cette analyse.
L’analyse du graphique (graphique 3) en entonnoir permet de visualiser l’existence d’un biais de publication. Ce graphique associe le coefficient de rétention de l’épargne sur l’axe horizontal avec l’inverse de l’écart-type de chaque β sur l’axe vertical. En l’absence de biais de publication, il devrait y avoir une répartition symétrique et aléatoire autour de l’effet réel. La base du graphique devrait être plus large car les estimations fondées sur de petits échantillons sont généralement moins précises et sont généralement moins proches de l’effet empirique réel. Le graphique 3 montre une plus forte concentration des coefficients de rétention de l’épargne à droite de la moyenne, représentée par la verticale, alors que la distribution des observations apparaît plus étendue à gauche de cette moyenne. Cette conclusion visuelle renforce l’hypothèse d’un biais de publication mais doit faire l’objet d’une validation empirique.
Graphique 3
Graphique en entonnoir des coefficients de rétention de l’épargne
Un échantillon restreint est élaboré à partir de la base de données initiale. Il comprend l’ensemble des coefficients de corrélation de l’épargne qui se trouvent dans des études classées dans la catégorie Q1. Cet échantillon contient 760 observations. Les résultats sont repris dans les colonnes (5-1) à (5-4) du tableau 5. Les statistiques de Fisher demeurent significatives mais le pouvoir explicatif du modèle demeure faible puisque les R2 varient de 21,5 % à 23,3 %. Les constantes des régressions (5-1) à (5-4) évoluent entre 0,570 à 0,592. La prise en compte de certaines variables de modération affecte donc significativement et systématiquement l’estimation du coefficient β. En effet, la fréquence des données, mais surtout la structure, n’ont plus l’effet systématique et significatif qui avait été précédemment observé. Cette catégorie Q1 semble privilégier des articles qui obtiennent des valeurs du coefficient β relativement plus faibles sur la période P1 comparé à la période P4, confirmant l’hypothèse communément défendue selon laquelle la période de l’étalon-or était une période de très forte intégration financière et de mobilité du capital. L’influence systématique sur l’estimation de β de la période retenue demeure mais quelques nuances doivent être apportées en ce qui concerne la composition de l’échantillon et la méthode économétrique. La composition de l’échantillon continue à exercer une influence persistante sur l’estimation de b, bien que les coefficients diffèrent fortement. Les colonnes (5-1) à (5-4) montrent que l’effet est toujours systématiquement négatif pour les métavariables PVD et PVD1 et OCDE_R. Par contre, l’impact systématique n’est plus retrouvé lorsqu’il s’agit d’un échantillon de pays de l’OCDE ou qui associe simultanément des pays de l’OCDE et des PVD. Les méthodes DOLS et de coïntégration sur séries temporelles (CI_ST) affectent toujours systématiquement les résultats, ce qui n’est plus le cas de la méthode en données de panel (CI_P).
Tableau 5
Métarégressions du coefficient de rétention de l’épargne : échantillon Q1
Note : Se rapporter au tableau 1 pour le détail des acronymes. MCO : méthode des moindres carrés ordinaires. MCP : méthode des moindres carrés pondérés. Pondération : année moyenne de l’échantillon. Les écart-types lorsque la méthode MCO est adoptée sont corrigés en adoptant la méthode de correction des erreurs de White (1980). Ces écart-types sont entre les parenthèses.
N : nombre d’observations. F : Statistique de Fisher. ***, ** et * signifient respectivement significatif au seuil de 1 %, 5 % et 10 %.
Enfin, un moyen de réduire la possibilité d’occurrence de ce biais de publication a été de considérer le maximum d’observations de β en provenance de sources différentes, en particulier des actes de colloques, des documents de travail ainsi que des chapitres de thèse. Cette littérature de recherche peut s’avérer difficilement accessible, notamment parce que leurs auteurs ne souhaitent pas qu’elle soit publiée en l’état, parce qu’elle a fait l’objet de refus de publication ou bien parce que les auteurs ne communiquent pas leurs travaux en cours de soumission. Card et Krueger (1995), Doucouliagos (2005) ainsi que Disdier et Head (2008) suggèrent de ne retenir qu’une seule observation par article. Ce choix d’une seule observation par article permet de renforcer l’hypothèse d’indépendance des observations. En effet, on ne prend en compte qu’un seul auteur simultanément et l’on suppose ainsi que les articles qui sont publiés l’ont été sur la base d’une méthodologie économétrique, de données statistiques et d’un échantillon de pays originaux. Cependant, l’utilisation d’un échantillon restreint n’est pas aisé dans la mesure où les auteurs ne fournissent pas nécessairement leur « spécification linéaire préférée […] dans leur étude » (Card et Krueger, 1995 : 240) et que cela ne favorise par nécessairement la reproductibilité de l’étude. Le choix d’une seule variable a alors d’autant moins de sens, qu’il n’est pas possible d’en extraire une valeur unique qui soit la mieux mise en avant par les auteurs (Stanley et Jarrell, 2005). C’est pourquoi l’utilisation du maximum d’observations constitue un moyen pertinent d’appréciation de l’existence du biais de publication. Les observations qui proviennent d’échantillons, de techniques économétriques, de fréquences de données qui sont différents et qui apparaissent directement exploitables pour l’analyse sont toutes retenues et sont considérées comme différentes, même si elles procèdent de travaux d’un même auteur. La discrimination du coefficient de rétention s’effectue par l’intermédiaire de la codification et des métavariables, d’autant que cela permet de mieux contrôler l’hétérogénéité de l’échantillon.
Les travaux initiaux des sciences médicales et de l’éducation (Egger et al. 1997; Sutton et al. 2000) réalisent fréquemment une régression entre l’effet estimé βj et son écart-type Sej dans le but d’apprécier le biais de sélection :
avec ςj et Zjk (k = 1, 2, …, K) qui correspondent respectivement à un terme d’erreur et aux variables de modération. Le symbole γk estime l’impact de chaque caractéristique sur la valeur du β. L’accent est mis sur le paramètre η0, plutôt que sur le paramètre η1. Ce dernier décrit l’effet réel de l’intégration financière sur la période, corrigé du biais de publication. En l’absence de biais de publication, il ne devrait pas y avoir de relation entre l’effet estimé βj et l’écart type associé Sej. L’effet estimé devrait évoluer de façon aléatoire autour de sa « vraie » valeur, indépendamment de l’écart-type associé. En présence de biais de publication, les actions sur les spécifications, les modèles, les échantillons voire sur les techniques économétriques permettent d’associer des effets estimés plus importants afin de compenser l’imprécision de la mesure induite par des écart-types plus élevés, lorsqu’il s’agit de petits échantillons.
Stanley (2005) montre que le test de détection de biais de sélection, qui porte sur le terme η0 est particulièrement robuste. Toutefois, le risque d’hétéroscédasticité étant important dans les méta-analyses, Stanley (2005 : 321), et Stanley et al. (2008) suggèrent qu’un moyen alternatif d’évaluation du biais de publication est d’effectuer une méta-regression de chaque statistique de Student![]() sur la précision de l’estimation respective (1/Sej). La relation, que l’on estime alors par la méthode des MCO, est de la forme suivante :
sur la précision de l’estimation respective (1/Sej). La relation, que l’on estime alors par la méthode des MCO, est de la forme suivante :
Le symbole vj est un terme d’erreur. L’évaluation du biais de publication dans cette littérature s’effectue en utilisant un test de significativité de la constante η0. Le biais de publication est détecté dès lors que la constante est significative. La précision de l’estimation 1/Sej devient alors la variable clef de cette relation.
Les tests de biais de publication sont présentés dans le tableau 6. Les colonnes (6-1) et (6-4) présentent l’estimation de la relation (4) sans variable de modération. Dans le cas où N=1259, la régression montre que la constante η0 = 7,127 est significative au seuil de 1 %. Ensuite, la pente de cette métarégression est positive et significative avec une estimation de η1 = 0,138. En présence d’un échantillon restreint, les paramètres correspondants qui sont aussi significatifs sont respectivement η0 = 6,681 et η1 = 0,013 et confirment l’hypothèse de biais de publication.
Tableau 6
Biais de publication
Note : Se rapporter au tableau 1 pour le détail des acronymes. t : statistique t de Student. Estimation par la méthode des MCO. Les écart-types sont corrigés en adoptant la méthode de correction des erreurs de White (1980). Ces écart-types sont entre parenthèses.
N : nombre d’observations. F : Statistique de Fisher. White : Test d’hétéroscédasticité de White. ***, ** et * signifient respectivement significatif au seuil de 1 %, 5 % et 10 %.
C’est pourquoi l’inclusion des métavariables de modération dans la relation constitue un moyen de confirmer ou d’infirmer ces premiers enseignements. Les résultats sont donnés dans les colonnes (6-2) et (6-5) qui présentent la relation (4) lorsque les variables de modération sont toutes incluses dans l’estimation alors que les colonnes (6-3) et (6-6) détaillent les résultats des régressions lorsque les variables de modération, dont la statistique de Student n’est pas significative, sont écartées. Les constantes des régressions (6-2) et (6-5), dont les estimations sont respectivement 0,737 et 0,965, sont significatives. L’effet réel de la corrélation entre l’épargne et l’investissement corrigé de l’effet de publication, décrit par la colonne (6-2), demeure significativement positif avec un coefficient η1 = 0,501. Toutefois, il semble que ces premiers résultats incitent à la prudence puisque les coefficients R2 sont particulièrement faibles (R2 < 0,07 dans les colonnes (6-1) et (6-4)), même si le test global selon Fisher donne des valeurs significatives. Les colonnes (6-3) et (6-6) confirment l’hypothèse de biais de publication puisque les paramètres η1 et η0 demeurent significativement positifs lorsque les variables non significatives sont exclues des estimations.
Ce résultat renforce le choix effectué initialement lors de la construction de la base de données d’une collecte aussi large que possible. Il faut inclure à la fois les articles ayant fait la preuve de leur qualité via la publication dans des revues de la liste de Kalaitzidakis et al. (2003) que des articles exclus de la première liste. L’hypothèse d’un biais de publication dans cette littérature est retenue. Cela permet de penser que les écarts obtenus dans les valeurs estimées du coefficient b, selon que les publications s’inscrivent dans la liste Q1 ou Q2, sont essentiellement le résultat de contraintes de publication et de choix méthodologiques plutôt que le fruit d’écarts qualitatifs entre les articles.
Conclusion
Cet article est une revue quantitative de la littérature sur la corrélation entre l’épargne et l’investissement. À la suite de l’article novateur de Feldstein et Horioka (1980), de nombreux travaux ont été publiés. La faiblesse des fondements théoriques rigoureux sur lesquels se base leur relation et les résultats initiaux qui infirment les hypothèses avancées conduisent à un développement substantiel de travaux empiriques et à l’apparition d’importantes controverses fondées sur la dissemblance des échantillons de pays, des périodes retenues, des données d’origines diverses, ainsi que sur la qualité des résultats obtenus, qui est affectée par les méthodologies économétriques qui sont adoptées. Le stock d’estimations du coefficient de rétention de l’épargne actuellement disponible dans la littérature est important et particulièrement hétérogène.
En l’absence de réel consensus sur ce que pourrait être la « vraie » valeur de ce coefficient, l’article adopte la méthodologie de la méta-analyse pour effectuer une revue quantitative de la littérature. La méta-analyse présente l’avantage d’une moindre subjectivité puisqu’elle se concentre, dans un cadre unifié, sur les modèles adoptés, sur les méthodes d’estimations et sur les données utilisées. Une base de données est construite qui comprend 1 399 valeurs du coefficient de rétention de l’épargne et 97 articles relevant de cette problématique.
Lorsqu’une étude est menée, le chercheur doit d’abord se préoccuper du traitement des données car l’utilisation de données empilées ou en panel affectera l’estimation du coefficient de rétention de l’épargne. Par contre, il n’est pas possible de considérer que l’usage de données trimestrielles apportera des résultats plus pertinents. Ensuite, les pays pris en considération exercent une forte influence puisque lorsque l’on adopte des données régionales des pays de l’OCDE, le résultat conduira à des valeurs du coefficient de rétention de l’épargne nettement plus faible que s’il s’agissait de données par pays ou par groupes de pays. Le type de support de publication est susceptible d’affecter systématiquement la valeur du coefficient de rétention de l’épargne. Mais une fois fixée les données statistiques, les échantillons de pays et le type de publication, les nombreuses méthodologies économétriques conduisent à des valeurs du coefficient de rétention de l’épargne nettement différenciées. Ainsi, lorsque l’étude mobilise des techniques liées à la théorie de la coïntégration sur des séries temporelles, l’estimation du coefficient de rétention de l’épargne sera en général plus importante que s’il s’agissait de la méthode des MCO, mais systématiquement plus faible que si l’étude adoptait des techniques DOLS. Les techniques plus récentes de coïntégration sur des données en panel apportent des résultats intermédiaires. Dès lors, il peut être préférable d’adopter une stratégie économétrique associant différentes méthodologies afin d’avoir un large aperçu du spectre des coefficients de rétention de l’épargne. Cette conduite de prudence apparaît peu fréquente puisqu’elle ne concerne qu’un tiers du total des articles recensés.
Cette étude démontre qu’il existe un biais de publication dans la littérature à la Feldstein et Horioka (1980) ce qui peut avoir pour conséquence de majorer la valeur estimée du coefficient de rétention de l’épargne. Dans des travaux ultérieurs, il conviendra de revenir sur ce biais de publication pour apprécier plus finement son impact sur chacun des éléments contribuant à l’estimation de β afin d’en corriger son estimation.
Parties annexes
Remerciements
L’auteur remercie Christian Calmès, deux rapporteurs anonymes de la revue, Hubert Jayet, Alain Ayong Le Kama, ainsi que les participants de la conférence franco-roumaine de Iasi (Roumanie, octobre 2007) pour leurs remarques.
Notes
-
[1]
Stanley (2001), et Florax (2002) pour une présentation et une liste de récents travaux ainsi que Dalhuisen et al. (2003), Jarrell et Jarrell (2004), Abreu et al. (2005), Longhi et al. (2005).
-
[2]
Frankel (1992) distingue : i) la mesure macroéconomique de FH; ii) la parité des taux d’intérêt réels; iii) la parité des taux d’intérêt non couverte et iv) la parité des taux d’intérêt couverte.
-
[3]
Afin d’éviter d’inutiles répétitions, les termes « β », « coefficient de corrélation entre l’épargne et l’investissement » seront utilisés au lieu de « coefficient de rétention de l’épargne ».
-
[4]
Tesar (1991), Coakley et al. (1996), Jansen (1996) et Jansen et Schulze (1996) défendent ce point de vue.
-
[5]
Ainsi De Haan et Siermann (1994) utilisent des données annuelles de 1900 à 1988; Jansen (1997) associe des données de 27 pays sur 40 ans. Coakley et Kulasi (1997) utilisent des données historiques et ne prennent pas clairement en compte la possible rupture dans le comportement de ces séries chronologiques.
-
[6]
Dans la majorité des cas, il s’agit d’un échantillon de 20 à 30 observations annuelles.
-
[7]
Ces tests sont développés par Maddala et Wu (1999), Hadri (2000), Levin et al. (2002) et Im et al. (2003).
-
[8]
Voir Kao (1999), Pesaran et al. (2001), ainsi que Nelson et Sul (2003), Pesaran (2003) et Bai et Ng (2004).
-
[9]
Les sites ayant fait l’objet d’interrogations approfondies sont ceux d’Ebsco, EconLit, JSTOR, SSRN, ainsi que les sites d’éditeurs comme Basic-Blackwell, Elsevier, Sage et Wiley.
-
[10]
Les requêtes sont : Capital Mobility, Correlation.Puzzle, Feldstein and Horioka, Saving-investment, Saving retention coefficient.
-
[11]
La statistique I2 est une correction apportée au test standard d’hétérogénéité de Cochran, Q, en raison de la puissance excessive de ce test lorsque le nombre d’étude est important (Higgins et al., 2003). Ce test est conduit sur 1 259 observations à cause de l’absence dans les autres cas de l’écart type de l’estimateur.
-
[12]
Un pays est dit PVD s’il ne fait pas partie de l’OCDE le 31 décembre 2007. Cette définition, bien qu’arbitraire, permet d’éviter de créer des sous-catégories selon que le pays est issu du continent asiatique, africain ou latino-américain. L’objectif est d’éviter un nombre important de métavariables qui incorporeraient une quantité parfois réduite d’observations.
-
[13]
Les observations sont +4,7; +2,44; -1,7; -1,34; -0,99 avec un seuil de significativité de 10 %.
-
[14]
Certains des travaux recensés portent sur des périodes débutant en 1850 (Bayoumi, 1990; Corbin, 2004; Hoffman, 2004 et Obsfeld et Taylor, 2004) pour s’achever en 2003 (Nell et Santos, 2007). Afin de situer précisément chaque étude dans l’une des périodes, puisque certaines sont susceptibles d’en couvrir plusieurs simultanément, le choix d’affectation s’effectue en fonction de la valeur prise par l’année qui se trouve au centre de la période totale d’estimation.
-
[15]
Voir à ce sujet le graphique p.28 dans Obstfeld et Taylor (2004).
-
[16]
Frankel (1989), Bayoumi (1990), De Haan et Siermann (1994), Taylor (1996, 1998), Pomfret (1997), Hogendorn (1998), Flandreau et Rivière (1999), Levy (2000), Corbin (2001, 2004), Hoffman (2004) ainsi que Obsfeld et Taylor (2004).
-
[17]
Cinq articles seulement sur les 97 de la base de données ne donnent qu’une seule estimation de β. Les cinq articles où une seule observation β est retenue sont ceux de Jansen et Schulze (1996), Pelagidis et Mastroyiannis (2003), Rossini et Zanghieri (2003), Narayan (2005) et Payne (2005).
-
[18]
L’exclusion du Luxembourg pour son « caractère atypique » est une constante de la littérature sur la corrélation entre l’épargne et l’investissement.
-
[19]
On peut notamment se reporter à Miller (1988), Girardin et Marimoutou (1991), Gulley (1992), Wickens et Uctum (1992) pour les USA et Montiel (1994) pour les PVD.
Bibliographie
- Abreu, M., H. De Groot et R. Florax (2005), « A Meta-analysis of Beta-convergence: The Legendary Two-percent », Journal of Economic Surveys, 19(3) : 389-420.
- Alexakis, P. et H. Apergis (1994), « The Feldstein-Horioka Puzzle and Exchange Rate Regimes: Evidence from Cointegration Tests », Journal of Policy Modeling, 16(5) : 459-472.
- Apergis N. et C. Tsoumis (2009), « A Survey of the Feldstein-Horioka Puzzle: What has been Done and Where do we Stand », Research in Economics, 63 : 64-76.
- Argimon, I. et J. Roldan (1994), « Saving, Investment and International Capital Mobility in EC Countries », European Economic Review, 38(1) : 59-68.
- Armstrong, H., V. Balasubramanyam et M. Salisu (1996), « Domestic Savings, Intra-national and Intra-European Capital Flows, 1971-1991 », European Economic Review, 40, 1229-1235.
- Ballabriga, F. J. Dolado et J. Vinals (1991), « Investigating Public and Private Saving-investment Gaps », CEPR Working Paper, 607.
- Bai, J. et S. Ng (2004), « A PANIC Attack on Unit Roots and Cointegration », Econometrica, 72(4) : 1127-1177.
- Banerjee, A. et P. Zanghieri (2003), « A New Look at the Feldstein-Horioka Puzzle Using an Integrated Panel », CEPII Working Papers, 2003-22.
- Bayoumi, T. (1990), « Saving-investment Correlations: Immobile Capital, Government Policy, or Endogenous Behaviour », IMF Staff Papers, 37(2) : 360-387.
- Bayoumi, T. et A. Rose (1993), « Domestic Savings and Intra-national Capital Flows », European Economic Review, 37(6) : 1197-1202.
- Baxter, M. et M. Crucini (1993), « Explaining Saving-investment Correlations », American Economic Review, 83(3) : 416-436.
- Bhandari, J. et T. Mayer (1990), « A Note on Saving-investment Correlations in the EMS », IMF Working Paper, 97.
- Bineau, Y. (2010), « Renminbi Misalignment: A Meta-analysis », Economic Systems, 34(3) : 259–269.
- Bordes, C. (1988), « Interprétation théorique du mouvement d’intégration des marchés des capitaux », Cahiers économiques et monétaires de la Banque de France, 31 : 5-47.
- Bordes, C. (1992), « Feldstein-Horioka 1980, Dix ans après ou l’intégration internationale des marchés des capitaux dans les années quatre-vingt », in H. Bourguinat et J.-C. Milleron (éds), Finance internationale : l’état actuel de la théorie, Economica, Paris, p.81-102.
- Cadoret, I., C. Benjamin, F. Martin, H. Herrard et S. Tanguy (2004), Econométrie appliquée, Coll. Ouvertures économiques, De Boeck, Bruxelles.
- Card, D. et A. Krueger (1995), « Time-series Minimum-wage Studies: A Meta-analysis », American Economic Review, 85(2) : 238-243.
- Coakley, J., A.-M. Fuentes et F. Spagnolo (2004), « Is the Feldstein-Horioka Puzzle History? », Manchester School, 72(5) : 569-590.
- Coakley, J. et F. Kulasi (1997), « Cointegration of Long Span Saving and Investment », Economics Letters, 54(1) : 1-6.
- Coakley, J., F. Kulasi et R. Smith (1998), « The Feldstein-Horioka Puzzle and Capital Mobility: A Review », International Journal of Finance and Economics, 3 : 169-188.
- Coiteux, M. et S. Olivier (2000), « The Saving Retention Coefficient in the Long Run and in the Short Run: Evidence from Panel Data », Journal of International Money and Finance, 19(4) : 535-548.
- Corbin, A. (2001), « Country Specific Effect in the Feldstein-Horioka Paradox: A Panel Data Analysis », Economics Letters, 72 : 297-302.
- Corbin, A. (2004), « Capital Mobility and Adjustment of the Current Account Imbalances: A Bound Testing Approach to Cointegration in 12 Countries 1880-2001 », International Journal of Finance and Economics, 9 : 256-276.
- De Grauwe, P. et C. Costa Storti (2004), « The Effects of Monetary Policy », CESIFO, Working Papers, 1224.
- De Haan, J. et C. Siermann (1994), « Saving, Investment, and Capital Mobility: A Comment on Leachman », Open Economies Review, 5 : 5-17.
- Dalhuisen, J., R. Florax, H. De Groot et P. Nijkamp (2003), « Price and Income Elasticities of Residential Water Demand: A Meta-analysis », Land Economics, 79(2) : 292-308.
- Decressin, J. et P. Disyatat (2000), « Capital Markets and External Current Accounts: What to Expect from the Euro », IMF Working Papers, 154.
- Dekle, R. (1996), « Saving-investment Associations and Capital Mobility: On the Evidence from Japanese Regional Data », Journal of International Economics, 41 ; 53-73.
- Disdier, A.-C. et K. Head (2008), « The Puzzling Persistence of the Distance Effect on Bilateral Trade », Review of Economics Studies, 90(1) : 37-48.
- Dooley, M., J. Frankel et D. Mathieson (1987), « International Capital Mobility: What Do Saving-Investment Correlations Tell-Us? », IMF Staff Papers, 34(3) : 503-550.
- Doucouliagos, C. (2005), « Publication Bias in the Economic Freedom and Economic Growth Literature », Journal of Economic Surveys, 19(3) : 367-387.
- Egert, B. et L. Halpern (2006), « Equilibrium Exchange Rate in Central and Eastern Europe: A Meta-regression Analysis », Journal of Banking & Finance, 30(5) : 1359-1374.
- Egger, M., G. Smith et A. Phillips (1997), « Meta-analysis: Principles and Procedures », British Medical Journal, 315, 1533-1537.
- Eng, Y.-E. et M. Habibullah (2006), « Assessing International Capital Mobility in East Asian Economies: A Panel Error-Correction Approach », Journal of the Asia Pacific Economy, 11(4) : 411-423.
- Engle, R. et C. Granger (1987), « Cointegration and Error-correction: Representation, Estimation and Testing », Econometrica, 55 : 251-276.
- Feldstein, M. (1983), « Domestic Saving and International Capital Movements in the Long Run and the Short Run », European Economic Review, 21(1-2) : 129-151.
- Feldstein, M. (2005), « Monetary Policy in a Changing International Environment: The Role of Capital Flows », NBER Working Papers, 11856.
- Feldstein, M. et P. Bacchetta (1991), « Domestic Saving and International Investment », in Bernheim, D. et J.B. Shoven (éds), National Saving and Economic Performance, University of Chicago Press, Chicago.
- Feldstein, M. et C. Horioka (1980), « Domestic Saving and International Capital Flows », Economic Journal, 90 : 314-329.
- Fidrmuc, J. et I. Korhonen (2006), « Meta-analysis of the Business Cycle Correlations between Euro Area and CEECs », Journal of Comparative Economics, 34(3) : 518-537.
- Flandreau, M. et C. Riviere (1999), « La grande ‘retransformation’ ? Contrôles des capitaux et intégration financière internationale, 1880-1996 », Économie Internationale, 78 : 11-58.
- Florax, R., H. De Groot et R. De Mooij (2002), « Meta-analysis », Tinbergen Institute Discussion Paper, 41/3.
- Frankel, J. (1989), « Quantifying International Capital Mobility in the 1980s », NBER Working Papers, 2856.
- Frankel, J. (1992), « Measuring International Capital Mobility: A Review », American Economic Review, 82(2) : 197-201.
- Genberg, H., A. Swoboda (1992), « Saving, Investment and the Current Account », Scandinavian Journal of Economics, 92(2) : 347-366.
- Girardin, E. et V. Marimoutou (1991), « Cycles d’épargne et cycles de balance des paiements : applications de techniques récentes aux cas américain et japonais », Economies et Sociétés, MO, 8 : 109-154.
- Görg, H. et E. Strobl (2001), « Multinational Companies and Productivity Spillovers: A Meta-analysis », Economic Journal, 111 : F723-F739.
- Gulley, O. (1992), « Are Saving and Investment Cointegrated: Another Look at the Data? », Economics Letters, 39 : 55-58.
- Hadri, K. (2000), « Testing for Stationarity in Heterogeneous Panel Data », Econometrics Journal, 3(2) : 148-161.
- Harberger, A. (1980), « Vignettes on the World Capital Market », American Economic Review, 70(2) : 331-337.
- Helliwell, J. et R. Mckitrick (1999), « Comparing Capital Mobility across Provincial and National Borders », Canadian Journal of Economics, 32(5) : 1164-1173.
- Higgins, J., S. Tompson, J. Deeks et D. Altman (2003), « Measuring Inconsistency In Meta-analysis », British Medical Journal, 327 : 557-560.
- Ho, T.-W. (2002), « A Panel Cointegration Approach to the Investment-saving Correlation », Empirical Economics, 27(1) : 91-100.
- Ho, T.-W. (2003), « The Saving-retention Coefficient and Country Size: The Feldstein-Horioka Puzzle Reconsidered », Journal of Macroeconomics, 25 :387-396.
- Ho, T.-W. et R.-L. Chiu (2001), « Country Size and Investment-saving Correlation: A Panel Threshold Error Correction Model », Eastern Economic Journal, 27(4) : 481-490.
- Hoffman, M. (2004), « International Capital Mobility in the Long Run and the Short Run: Can We still Learn from Saving-investment Data? », Journal of International Money and Finance, 23 : 113-131.
- Hogendorn, C. (1998), « Capital Mobility in Historical Perspective », Journal of Policy Modeling, 20(2) : 141-161.
- Hunter, J. et F. Schmidt (1990), Methods of Meta-analysis: Correcting Error and Bias in Research Findings, Sage, Newbury Park.
- Im, K. S., H. Pesaran et Y. Shin (2003), « Testing for Unit Roots in Heterogeneous Panels », Journal of Econometrics, 115 : 53-74.
- Jansen, W. (1996), « Estimating Saving-investment Correlations: Evidence for OECD Countries Based on an Error Correction Model », Journal of International Money and Finance, 15(5) : 749-781.
- Jansen, W. (1997), « Can the Intertemporal Budget Constraint Explain the Feldstein-Horioka Puzzle?», Economics Letters, 56 : 77-83.
- Jansen, W. (2000) « International Capital Mobility: Evidence from Panel Data », Journal of International Money and Finance, 19 : 507-511.
- Jansen, W. et G. Schulze (1996), « Theory-Based Measurement of the Saving Investment Correlation with an Application to Norway », Economic Inquiry, 34(1) : 116-132.
- Jarrell, S. et T. Jarrell (2004), « Declining Bias and Gender Wage Discrimination? A Meta-regression Analysis », Journal of Human Resources, 39(3) : 827-838.
- Johansen, S. (1988), « Statistical Analysis of Cointegration Vectors », Journal of Economic Dynamics and Control, 12 : 231-254.
- Johansen, S. et K. Juselius (1990), « Maximum Likelihood Estimation and Inference on Cointegration With Applications to the Demand for Money », Oxford Bulletin of Economics and Statistics, 52(2).
- Kalaitzidakis, P., T. Mamuneas et T. Stengos (2003), « Rankings of Academic Journals and Institutions in Economics », Journal of the European Economic Association, 1(6) : 1346-1366.
- Kao, C. (1999), « Spurious Regression and Residual-Based Tests for Cointegration in Panel Data », Journal of Econometrics, 90 : 1-44.
- Kim, H., K.-Y. Oh et C.-W. Jeong (2005), « Panel Cointegration Results on International Capital Mobility in Asian Countries », Journal of International Money and Finance, 24 : 71-82.
- Knell, M. et H. Stix (2005), « The Income Elasticity of Money Demand: A Meta-analysis of Empirical Results », Journal of Economic Surveys, 19(3) : 513-533.
- Krol, R. (1996), « International Capital Mobility: Evidence From Panel Data », Journal of International Money and Finance, 15(3) : 467-474.
- Levin, A. C.-F. Lin et C.-S. J. Chu (2002), « Unit Root Tests in Panel Data: Asymptotic and Finite-sample Properties », Journal of Econometrics, 108 : 1–24.
- Levy, D. (2000), « Investment-saving Comovement and Capital Mobility: Evidence from Century Long U.S. Times Series, Review of Economic Dynamics, 3(1) : 100-137.
- Longhi, S., P. Nijkamp et J. Poot (2005), « A Meta-analytic Assessment of the Effect of Immigration of Wages, Journal of Economic Surveys, 19(3) : 451-477.
- Maddala, G. S. et S. Wu (1999), « A Comparative Study of Unit Root Tests with Panel Data and New Simple Test », Oxford Bulletin of Economics and Statistics, 61 : 631-652.
- Miller, S. (1988), « Are Saving and Investment Co-Integrated? », Economics Letters, 27 : 31-34.
- Montiel, P. (1994), « Capital Mobility in Developing Countries; Some Measurement Issues and Empirical Estimates », The World Bank Economic Review, 8(3) : 311-350.
- Mookerjee, R. (2006), « A Meta-analysis of the Export Growth Hypothesis », Economics Letters, 105 : 395-401.
- Moosa, I. (1997), « Resolving the Feldstein-Horioka puzzle », Economia Internazionale, 60 :437-457.
- Murphy, R. (1984), « Capital Mobility and Relationship Between Saving and Investment Rates in OECD Countries », Journal of International Money and Finance, 3 : 327-342.
- Murphy, R. (1986), « Productivity Shocks, Non Traded Goods and Optimal Accumulation », European Economic Review, 30 : 1081-1095.
- Narayan, P. (2005), « The Saving and Investment Nexus for China: Evidence from Cointegration Tests », Applied Economics, 37 : 1979-1990.
- Nell, K. et L. Santos (2007), « The Feldstein–Horioka Hypothesis versus the Long-run Solvency Constraint Model: A Critical Assessment », Economics Letters, 98(1) : 66-70.
- Nelson, M. et D. D Sul (2003) « Cointegration Vector Estimation by Panel DOLS and Long-run Money Demand », Oxford Bulletin of Economics and Statistics, 65(5) : 655-680.
- Nijkamp, P. et J. Poot (2004), « Meta-analysis of the Effect of Fiscal Policies on Long-run Growth, European Journal of Political Economy, 20(1) : 91-124.
- Obstfeld, M. (1986), « Capital Mobility in the World Economy: Theory and Measurement, Carnegie-Rochester Series on Public Policy, 24 : 55-104.
- Obstfeld, M. (1994), « International Capital Mobility in the 1990’s », CEPR Working Paper, 902.
- Obstfeld, M. et K. Rogoff (2000), « The Six Major Puzzles in International Macroeconomics: Is there a Common Cause », NBER Macroeconomics Annual 2000, 15 : 339-412.
- Obstfeld, M. et A. Taylor (2004), Global Capital Markets: integration, Crisis and Growth, Cambridge University Press, Cambridge.
- Payne, J. (2005), « Saving-investment Dynamics in Mexico », Journal of Policy Modeling, 27 : 525-534.
- Pelagidis, T. et T. Mastroyiannis (2003), « The Saving-investment Correlation in Greece, 1960-1997: Implications for Capital Mobility », Journal of Policy Modeling, 25 : 609-616.
- Pelgrin, F. et S. Schich (2008), « International Capital -mobility: What do National Saving-investment Dynamics Tell Us », Journal of International Money and Finance, 27(3) : 331-344.
- Pesaran, M., Y. Shin et R. Smith (2001), « Bounds Testing Approaches to the Analysis of Level Relationships », Journal of Applied Econometrics, 16 : 289-326.
- Pesaran, M. (2003), « Estimation and Inference in Large Heterogeneous Panels with Cross Section Dependence », Cambridge Working Papers in Economics, 0305.
- Pomfret, R. (1997), « International Capital Mobility and the Feldstein-Horioka Paradox: Evidence from Settler Economies in the Gold Standard Era », CIES Working Paper, 06.
- Rose, A. (2004), « A Meta-analysis of the Effect of Common Currency on International Trade », NBER Working Papers, 10373.
- Rossini, G. et P. Zanghieri (2003), « A Simple Test of the Role of Foreign Direct Investment in the Feldstein-Horioka Puzzle », Applied Economics Letters, 10 : 39-41.
- Sarno, L. et M. Taylor (1998a), « Exchange Controls, International Capital Flows and Saving-investment Correlations in the UK: An Empirical Investigation », Weltwirtschaftliches archiv, 134(1) : 69-98.
- Sarno, L. et M. Taylor (1998b), « Saving-investment Correlations: Transitory Versus Permanent », Manchester School Supplement, 17-38.
- Sinn, S. (1992) « Saving-investment Correlations and Capital Mobility: on the Evidence from Annual Data », Economic Journal, 102 : 1162-1170.
- Stanley, T. (2001), « Wheat from Chaff: Meta-analysis as Quantitative Literature Survey », Journal of Economic Perspective, 15(3) : 131-150.
- Stanley, T. (2005), « Beyond Publication Bias », Journal of Economic Surveys, 19(3) : 309-345.
- Stanley, T., C. Doucouliagos et S. Jarrell (2008), « Meta-regression Analysis as the Socio-economics of Economics Research », Journal of Socio-Economics, 37 : 276-292.
- Stanley, T. et S. Jarrell (2005), « Meta-regression Analysis: A Quantitative Method of Literature Surveys », Journal of Economic Surveys, 3(2) : 161-170.
- Summers, L. (1989), « Tax Policy and International Competitiveness », NBER Working Papers, 2007.
- Sutton, A., S. Duval, R. Tweedie, K. Abrams et D. Jones (2000), « Empirical Assessment of Publication Bias on Meta-analysis », British Medical Journal, 320 : 1574-1577.
- Taylor, A. (1996), « International Capital Mobility in History: The Saving-investment Relationship », NBER Working Papers, 5743.
- Taylor, A. (1998), « Argentina and the World Capital Markets: Savings, Investment and International Capital Mobility in the Twentieth Century », Journal of Development Economics, 57 : 147-184.
- Taylor, A. (2002), « A Century of Current Account Dynamics », Journal of International Money and Finance, 21(6) : 725-748.
- Tesar, L. (1991), « Savings, Investment and International Capital Flows », Journal of International Economics, 31(1/2) : 55-78.
- Tobin, J. (1983), « Comment on: ‘Domestic Saving and International Capital Movements in the Long Run and the Short Run’ By M. Feldstein », European Economic Review, 21 : 153-156.
- Turner, P. (1986), « Savings, Investment and the Current Account: an Empirical Study of Seven Major Countries 1965-84 », Monetary and Economic Studies, 4(2) : 1-58.
- Weichselbaumer, D. et R. Winter-Ebmer (2003), « A Meta-analysis of the International Gender Wage Gap », Journal of Economic Surveys, 19(3) : 479-511.
- Wesphal, V. (1983), « Comment on ‘Domestic Saving and International Capital Movements in the Long Run and the Short Run’ by M. Feldstein », European Economic Review, 21 : 157-159.
- Wickens, M. et M. Uctum (1990), « National Insolvency: A Test of the Us Intertemporal Budget Constraint », CEPR Discussion Paper, 437.
- White, H. (1980), « A Heteroscedasticity-consistent Covariance Matrix Estimator and a Direct Test for Heteroscedasticity », Econometrica, 48 : 817-838.
- Wong, D. (1990), « What Do Saving-Investment Relationships Tell Us About Capital Mobility? », Journal of International Money and Finance, 9 : 60-74.
- Yamori, N. (1995), « The Relationships between Domestic Savings and Investment: The Feldstein-Horioka Test Using Regional Data », Economics Letters, 48 : 361-366.
Liste des figures
Graphique 1
Articles publiés sur le thème de « Feldstein et Horioka »
Graphique 2
Coefficients de rétention de l’épargne à long terme
Graphique 3
Graphique en entonnoir des coefficients de rétention de l’épargne
Liste des tableaux
Tableau 1
Codage des variables utilisées
Tableau 2
Métastatistiques descriptives de β : échantillon complet
Tableau 3
Caractéristiques du coefficient de rétention par sous-périodes
Tableau 4
Métarégressions du coefficient de rétention de l’épargne
Note : Se rapporter au tableau 1 pour le détail des acronymes. MCO : méthode des moindres carrés ordinaires MCP : méthode des moindres carrés pondérés. Pondération : année moyenne de l’échantillon. Les écart-types lorsque la méthode MCO est adoptée sont corrigés en adoptant la méthode de correction des erreurs de White (1980). Ces écart-types sont entre les parenthèses
N : nombre d’observations F : Statistique de Fisher ***, ** et * signifient respectivement significatif au seuil de 1 %, 5 % et 10 %.
Tableau 5
Métarégressions du coefficient de rétention de l’épargne : échantillon Q1
Note : Se rapporter au tableau 1 pour le détail des acronymes. MCO : méthode des moindres carrés ordinaires. MCP : méthode des moindres carrés pondérés. Pondération : année moyenne de l’échantillon. Les écart-types lorsque la méthode MCO est adoptée sont corrigés en adoptant la méthode de correction des erreurs de White (1980). Ces écart-types sont entre les parenthèses.
N : nombre d’observations. F : Statistique de Fisher. ***, ** et * signifient respectivement significatif au seuil de 1 %, 5 % et 10 %.
Tableau 6
Biais de publication
Note : Se rapporter au tableau 1 pour le détail des acronymes. t : statistique t de Student. Estimation par la méthode des MCO. Les écart-types sont corrigés en adoptant la méthode de correction des erreurs de White (1980). Ces écart-types sont entre parenthèses.
N : nombre d’observations. F : Statistique de Fisher. White : Test d’hétéroscédasticité de White. ***, ** et * signifient respectivement significatif au seuil de 1 %, 5 % et 10 %.