Que pouvons-nous apprendre des profils de pauvreté canadiens?

Makdissi, Paul; Groleau, Yves

doi:https://doi.org/10.7202/007253ar

Introduction

Il existe dans la littérature économique des méthodes permettant de tester la robustesse des comparaisons de bien-être. La littérature dans ce domaine s’est tout d’abord intéressée aux comparaisons d’inégalité. Les travaux de Kolm (1969), Atkinson (1970) et Dasgupta, Sen et Starret (1973) insistent sur la désirabilité d’identifier les classements ordinaux d’inégalité qui sont robustes à une modification du choix d’indicateur. Ces travaux proposent d’utiliser des courbes de Lorenz afin d’identifier ces classements robustes. Afin d’augmenter le pouvoir de classement, Shorrocks (1983) introduit les comparaisons de courbes de Lorenz généralisées afin d’identifier les comparaisons de bien-être qui sont robustes. Finalement, Atkinson (1987) et Foster et Shorrocks (1988a, b) développent des critères similaires pour identifier les classements de pauvreté robustes à un changement d’indice ou de seuil de pauvreté.

D’un autre côté, des profils de la pauvreté au Canada ont été effectués par plusieurs organismes et auteurs (voir Conseil du bien-être social du Canada, 1999; Ross, Scott et Smith, 2000; Osberg, 2000a et b, et Osberg et Xu, 1999). Ces études semblent indiquer que le problème de la pauvreté persiste et s’amplifie même au Canada et identifient les régions et les groupes démographiques les plus à risque d’être touchés par la pauvreté.

L’objectif de cet article est d’identifier les classements de pauvreté au Canada qui sont robustes à un changement d’indicateur et de seuil de pauvreté, et ceux qui sont contingents à un choix méthodologique particulier. Pour ce faire, nous effectuons dans un premier temps, un profil de pauvreté en adoptant comme mesure la classe d’indices de pauvreté proposée par Foster, Greer et Thorbecke (1984) tout en prenant en compte les différences du coût de la vie à travers les régions canadiennes. Nous utilisons en plus deux seuils de pauvreté différents : le seuil de faible revenu après impôt de Statistique Canada et le seuil de pauvreté de l’Institut Fraser. Tel que suggéré par Ravallion (1994), il est normalement avantageux d’utiliser deux seuils de pauvreté différents afin de vérifier rapidement quels résultats sont dépendants du seuil de pauvreté sélectionné. Par la suite, pour les résultats qui semblent robustes, nous testons pour un ensemble de mesures de pauvreté et de seuils de pauvreté en utilisant des tests de dominance stochastique. Nos résultats sont en accord avec les principaux classements de groupes démographiques au niveau de la pauvreté ainsi que de l’évolution de celle-ci au courant des années quatre-vingt-dix. Par contre, le classement des régions au niveau de la pauvreté est différent de ce qu’on a l’habitude de lire. Ceci etant dû au fait que nous ajustons pour les différences dans le coût de la vie entre les provinces. Nous testons aussi la robustesse de ces résultats par rapport à un changement dans les indices de prix régionaux.

Le reste de l’article s’articule de la façon suivante : la prochaine section présente les définitions et les méthodologies utilisées, la deuxième section présente les différents résultats de l’étude empirique. Finalement, la dernière section présente les conclusions à tirer de cette étude.

1. La pauvreté : concepts et méthodologies

La théorie de la mesure de la pauvreté nous enseigne qu’un analyste désirant effectuer des comparaisons de pauvreté fait normalement face à quatre problèmes majeurs : un problème de définition, un problème d’identification, un problème d’agrégation et un problème de comparaison. Dans cette section, nous décrivons la méthodologie employée pour faire face à ces problèmes.

1.1 Problème de définition

Souvent, dans les profils de pauvreté, la définition de la pauvreté s’arrête à la détermination du seuil de pauvreté. Ceci est assez surprenant puisque le concept est beaucoup plus complexe que la simple détermination de ce seuil.

Le concept de pauvreté réfère à une situation où une personne ou un groupe de personnes fait face à un manque ou une insuffisance quelconque par rapport à un standard minimum du niveau de vie. Il faut donc dans un premier temps définir ce qui constitue un indicateur de niveau de vie. Cette question relève essentiellement de la philosophie politique et dépasse largement le cadre de cet article. Par contre, un bref survol de ces concepts peut permettre une meilleure compréhension du problème de définition.

Comme le souligne Ravallion (1994), les économistes qui s’intéressent au concept de niveau de vie font traditionnellement référence à l’« utilité » ou au niveau de plaisir qu’une personne peut atteindre à l’aide d’un certain panier de biens de consommation. Ce niveau d’utilité est déterminé par les préférences du consommateur. Cette façon de voir le problème est en lien direct avec la pensée de la philosophie utilitariste développée par Bentham et Mill aux dix-huitième et dix-neuvième siècles. Mais les préférences d’un individu ne sont pas déterminées dès la naissance. Le caractère de celles-ci est en partie cognitif car elles se développent à partir du cadre socio-économique dans lequel l’individu évolue. Une personne qui est née dans un milieu défavorisé apprend à se satisfaire de moins. Une personne qui est née dans un milieu beaucoup plus favorisé exigera beaucoup plus pour se considérer comme heureuse. Par contre, il est opportun de se demander si cette différence dans les préférences individuelles est pertinente au niveau de l’évaluation de la justice sociale et distributive. Pour certaines personnes, la réponse est non. Pour cette raison, Rawls (1971) propose d’évaluer la distribution à l’aide des « biens premiers » disponibles aux individus plutôt que selon les niveaux d’utilité. Ces biens premiers sont définis comme étant tout ce qu’une personne normale peut désirer. Rawls cite à titre d’exemples le revenu, la richesse et les bases sociales du respect de soi. Ce faisant, Rawls élimine les différences entre les individus dans la procédure d’évaluation de la justice sociale. Plusieurs travaux ont par la suite proposé différentes façons d’évaluer la distribution des revenus et de la qualité de vie. Parmi ces travaux, Sen (1992) propose une méthode d’évaluation basée sur ce qu’il nomme les « capabilités »[1]. Ces capabilités sont définies comme étant la capacité qu’a un individu de bien fonctionner socialement et de saisir les opportunités socio-économiques qui s’offrent à lui. Sen argumente que, bien que Rawls ait de bonnes raisons de rejeter l’utilitarisme, celui-ci va trop loin dans son élimination des différences entre les individus. Sen est en accord avec le fait que la société ne doit pas tenir compte des différences dans les préférences entre les individus dans ses jugements de justice sociale. Par contre, elle doit tout de même tenir compte d’autres différences. Par exemple, une personne handicapée aura besoin de plus de ressources pour se déplacer qu’une personne non handicapée. Ce surplus de ressources ne permet tout de même pas à cette personne de réaliser plus de modes de fonctionnement qu’une autre mais ne lui permet que de se déplacer, tout comme la personne non handicapée. C’est pourquoi Sen propose plutôt d’évaluer la justice distributive et la qualité de vie sur les capabilités qui peuvent être vues comme les ensembles de modes de fonctionnement parmi lesquels la personne peut choisir. Sen illustre le concept à l’aide d’une bicyclette. La bicyclette est un bien de consommation qui, de par ses caractéristiques, permet à la personne de se déplacer d’une certaine façon. La caractéristique de transport de la bicyclette permet de réaliser la capabilité « se déplacer d’une certaine façon » et c’est cette capabilité qui procure à la personne de l’utilité ou du plaisir. Sen considère que c’est cette capabilité, et non pas l’utilité qu’elle procure, qui s’approche le plus du concept de niveau de vie. La société n’est pas responsable du niveau de bonheur ou de plaisir atteint par l’individu. C’est la responsabilité individuelle qui intervient à ce niveau. Par contre, il est facile de constater que, pour la personne handicapée, la réalisation de la même capabilité exigera plus de ressources. Il lui faudra acheter, par exemple, un fauteuil roulant électrique. Lorsqu’on fait une analyse des standards de vie par l’approche des capabilités, il faut donc tenir compte des éléments qui permettent aux individus de pouvoir fonctionner à l’intérieur de la société. Pour un portrait des niveaux de vie de l’ensemble d’une société, il est commun de considérer, en plus du revenu, des variables telles l’espérance de vie et la scolarisation puisque la combinaison de ces variables permet à l’individu de fonctionner à l’intérieur d’une société. C’est d’ailleurs cette conception qui est à la base de la mise en place de l’Indice de développement humain de l’ONU qui évalue le développement économique en considérant à la fois, le PIB per capita, l’espérance de vie et le niveau d’alphabétisation.

Dans cet article, nous n’allons considérer que le revenu comme indicateur de niveau de vie, même si celui-ci n’est pas un indicateur complet de prime abord. Mais, vu l’importance de la fourniture de services publics au Canada en éducation et en santé entres autres, nous pensons que le revenu peut-être un indicateur acceptable des capabilités accessibles aux individus. Par contre, le fait de nous restreindre au revenu comme indicateur ne nous permettra pas d’aborder séparément la pauvreté de deux groupes : les personnes handicapées et les enfants. Pour les personnes handicapées, une étude sur la pauvreté devrait inclure des informations sur les services adaptés disponibles à ces personnes (transport adapté, édifices adaptés, etc.). Pour les enfants, le problème est différent. Comme le souligne Phipps (1999), étant donné que la plupart des activités sociales des enfants se font en dehors de la sphère des échanges de marché, on peut facilement penser que le revenu, bien qu’important, devient un moins bon indicateur de la pauvreté et du bien-être de ceux-ci. Le capital social, concept qui inclut entre autres les réseaux d’amis et la sécurité de l’environnement social, est alors un facteur qui prend plus d’importance et qu’on ne peut mettre de côté. De plus, certains chercheurs en éducation considèrent que le niveau de scolarité des parents et en particulier celui de la mère est un meilleur indicateur du milieu socio-économique de l’enfant quand vient le temps d’évaluer les facteurs de succès scolaire[2]. C’est pourquoi, dans cette étude, nous ne considérerons la pauvreté chez les enfants qu’à travers les types de famille auxquels ils appartiennent.

1.2 Problème d’identification

Pour identifier les personnes ou les ménages pauvres, l’analyste utilise normalement un seuil de pauvreté z. Un ménage ayant un revenu inférieur à ce seuil sera considéré comme pauvre alors qu’un ménage ayant un revenu au-dessus du seuil sera considéré comme non pauvre. Par contre, il existe plusieurs seuils de pauvreté proposés au Canada. L’utilisation de seuils de pauvreté différents entraînera, bien sûr, des résultats différents. La plupart des débats publics sur la validité des comparaisons de pauvreté portent normalement sur l’identification de ce seuil de pauvreté. Dans cette étude nous allons considérer dans un premier temps deux seuils : le seuil de faible revenu (SFR) après impôt de Statistique Canada et le seuil de pauvreté de l’Institut Fraser (proposé par Sarlo, 1996). Le seuil de faible revenu de Statistique Canada représente un estimé du revenu à partir duquel une famille consacre plus de 54,7 % de son revenu pour les dépenses de première nécessité (nourriture, logement, vêtement). Pour 1997, ce seuil est de 27 346 $ pour un couple avec deux enfants vivant dans une région urbaine de plus de 500 000 habitants. Le seuil de pauvreté de l’Institut Fraser représente, quant à lui, un estimé du revenu nécessaire afin de maintenir une condition physique acceptable à long terme. Pour un couple avec deux enfants vivant en Ontario, ce seuil de pauvreté est de 17 621 $.

Une personne qui préconise une approche par les capabilités se surprendra que l’on puisse considérer le seuil de l’Institut Fraser comme étant un seuil acceptable de pauvreté car celle-ci ne peut se définir simplement par la capacité qu’a une personne de maintenir son état physique. La question est beaucoup plus complexe si on adopte une approche par les capabilités. On peut facilement penser qu’un seuil de pauvreté établi selon le revenu doit varier avec le niveau de richesse moyen d’une société puisque certains modes de fonctionnement comme « la base sociale du respect de soi » peuvent exiger des revenus différents d’une société à l’autre selon les revenus moyens de celles-ci. Dans un tel cadre, un seuil de pauvreté peut être relatif dans l’espace des revenus tout en correspondant à un concept qui est absolu dans l’espace des capabilités. Par exemple, une personne vivant dans une grande ville canadienne a certainement besoin d’un téléphone afin de fonctionner socialement. Par contre, une personne vivant dans la coopérative Bernardino Diaz Ochoa au Nicaragua peut très bien fonctionner socialement sans avoir de téléphone, puisque la plupart des résidents de celle-ci n’en ont pas. La même personne vivant à Toronto aura aussi besoin d’une plus grande garde-robe que le villageois nicaraguayen afin de pouvoir assurer les bases sociales du respect de soi. On peut faire le même raisonnement pour d’autres biens. La personne vivant à Toronto aura donc besoin de plus de ressources pour bien fonctionner socialement. Cela justifierait alors un seuil de pauvreté plus élevé pour Toronto que pour cette communauté du Nicaragua et ceci, même si on tient compte des différences dans le coût de la vie. D’ailleurs, l’idée que le seuil de pauvreté est contingent à une société et une époque remonte aussi loin qu’au dix-huitième siècle alors qu’Adam Smith argumentait déjà que la pauvreté était un concept qui variait d’une société à l’autre et d’une époque à l’autre[3]. De toute façon, étant donné que nous allons effectuer des tests de dominance stochastique afin de vérifier la robustesse de nos conclusions à un changement dans le seuil de pauvreté, l’identification d’un seuil est beaucoup moins importante. À ce propos, nous montrons, à la prochaine section, comment il est possible de s’entendre sur certains résultats même s’il y a divergence d’opinion quant au choix du seuil de pauvreté.

1.3 Problème d’agrégation

Un autre problème auquel l’analyste fait face est celui d’agrégation. Il doit utiliser les statistiques sur la pauvreté au niveau individuel pour établir un portrait de la pauvreté pour l’ensemble de la société ou d’un sous-groupe de la popula-tion qui l’intéresse. Pour ce faire, l’analyste doit choisir un indice de pauvreté. L’indice le plus fréquemment utilisé est l’indice numérique de pauvreté :

où q représente le nombre de ménages pauvres et N, le nombre de ménages dans l’économie. L’indice numérique de pauvreté nous donne tout simplement la proportion de ménages pauvres dans la population. Sa simplicité d’interprétation est probablement la meilleure explication de la popularité de cet indice. Par contre, comme le souligne Sen (1976), l’utilisation de celui-ci comporte deux problèmes majeurs : il est insensible à la profondeur de la pauvreté et à l’inégalité entre les pauvres. Pour illustrer le premier problème, prenons un exemple. Considérons une société composée de 10 individus dont les revenus sont respectivement de 7 000 $, 8 000 $, 11 000 $, 13 000 $, 14 000 $, 15 000 $, 16 000 $, 17 000 $, 18 000 $ et 20 000 $. Imaginons que dans cette société, 10 000 $ serait un seuil de pauvreté acceptable. Si on calcule l’indice numérique de pauvreté, on obtient un résultat de 20 % (soit 2 personnes ayant un revenu de moins de 10 000 $ divisé par 10 personnes). Imaginons maintenant qu’un changement économique provoque une chute des revenus des deux personnes pauvres soit de 7 000 $ à 5 000 $ pour l’une et de 8 000 $ à 6 000 $ pour l’autre. On aimerait considérer cette perturbation comme entraînant une augmentation de la pauvreté. Toutefois l’indice numérique de pauvreté demeure inchangé. Les deux situations sont considérées comme étant équivalentes.

Afin de tenir compte de la profondeur de la pauvreté on peut utiliser un autre indice, l’indice de déficit normalisé de pauvreté. Si nous considérons une situation dans laquelle les revenus sont classé en ordre croissants, cet indice est alors

où y_i est le revenu équivalent du ménage i. Il est possible de réécrire cet indice sous la forme :

où

avec μ^z représentant la moyenne de revenu des ménages pauvres. L’indice I représente alors l’écart moyen au seuil parmi les pauvres. L’équation (3) indique alors que l’indice PG correspond à l’écart moyen entre le revenu des pauvres et le seuil (I) pondéré par le poids des pauvres dans la population (H).

Dans le cadre de notre exemple, nous aurions eu dans la situation initiale

Si on répète l’exercice, pour la situation suivant la perturbation économique, on obtient

L’indice indique donc une augmentation de la pauvreté. Cette augmentation est due, non pas à l’augmentation de la proportion de pauvres qui reste constante à 20 %, mais à l’augmentation de l’écart moyen de 0,25 à 0,45 reflétant ainsi l’effort supplémentaire nécessaire pour éliminer complètement la pauvreté. Par contre, cet indice comporte aussi un problème si on considère que le fait d’enlever des ressources à un pauvre est un problème qui devient de plus en plus grave au fur et à mesure qu’on s’éloigne du seuil de pauvreté. On dit alors qu’on veut tenir compte de l’inégalité dans la distribution de l’écart de pauvreté. Afin de comprendre ce problème, reprenons la situation initiale de notre exemple dans laquelle un des pauvres a un revenu de 7 000 $ tandis que l’autre a un revenu de 8 000 $. Imaginons maintenant deux situations différentes. Soit la situation A où on enlève 500 $ à celui qui a 7 000 $ et la situation B où on enlève 500 $ à celui qui a 8 000 $. Si on considère que le fait d’enlever des ressources à un pauvre est un problème qui devient de plus en plus grave au fur et à mesure qu’on s’éloigne du seuil de pauvreté, on aimerait avoir un indice qui indique que la situation A est pire que la situation B. Malheureusement, en ne prenant en compte que le déficit moyen, l’indice PG va considérer ces deux situations comme équivalentes. Nous avons donc besoin d’un autre indice pour pouvoir tenir compte de ce facteur, c’est-à-dire un indice qui tient compte de l’inégalité dans la distribution de l’écart de pauvreté. Une classe d’indices qui permet de prendre en compte cette dimension de la pauvreté est la classe d’indices P_α de Foster, Greer et Thorbecke (1984). Si nous considérons une situation dans laquelle les revenus sont classés en ordre croissants, ces indices sont donnés par

Si α > 1, l’indice P_α est alors sensible à l’inégalité. Dans cet article nous utilisons l’indice P₂. Cet indice tient compte de la répartition du déficit de pauvreté en plus de tenir compte de son ampleur moyenne. Alors, dans ces conditions, une augmentation de P₂ indiquera une détérioration des conditions des plus pauvres. Pour établir notre profil de pauvreté, nous allons donc utiliser les trois indices que nous avons décrits : l’indice numérique de pauvreté, H, l’indice de déficit normalisé de pauvreté, PG, et l’indice P₂ de Foster, Greer et Thorbecke.

Notons ici qu’il existe dans la littérature d’autres types d’indices tels l’indice de Sen (1976), l’indice de Watts (1968), l’indice de Thon (1979) et l’indice de Shorrocks (1995) pour n’en citer que quelques-uns. Bien sûr, l’utilisation d’indices différents entraîne des résultats qui peuvent différer quant à l’établissement d’un profil de pauvreté. On n’a qu’à repenser aux exemples simples décrits plus haut pour s’en convaincre. Il est donc important de vérifier si les conclusions tirées dans un profil de pauvreté sont robustes à un changement d’indice de pauvreté. Nous allons donc tester cette robustesse pour les situations où le classement de la pauvreté entre deux régions, deux groupes démographiques ou deux années demeure le même pour nos trois indices et nos deux seuils. Pour ce faire, nous utiliserons des tests de dominance stochastique. Ces tests permettent de déterminer si les conclusions établies sur la pauvreté sont robustes à un changement de seuil et à un changement d’indice et ceci, en ne comparant que les distributions de revenu. Afin de décrire ces tests, considérons deux fonctions de distribution cumulative de revenu F₁ et F₂. Si nous considérons que les indices de pauvreté sont additifs, l’indice de pauvreté correspondant à la distribution F_i (i = 1 ou 2) est alors

où

La fonction p(y,z) mesure l’apport d’un revenu y à la pauvreté totale. Les indices P_α sont un exemple particulier de mesure de pauvreté additive où p(y, z) = (1 – y/z)^α. D’autres exemples sont l’indice de Chakravarty (1983) et celui de Watts (1968), qui est défini comme

Cet indice est à son tour un cas particulier de la deuxième classe d’indices de pauvreté de Clark, Hemming et Ulph (1981). Si on est incertain quant au choix méthodologique sur l’indice de pauvreté et sur le seuil de pauvreté, il est tout de même possible de tirer certaines conclusions dans ce contexte. Si on peut affirmer avec confiance que le seuil de pauvreté ne peut excéder une certaine valeur z⁺, Atkinson (1987) montre les résultats suivants :

Tests de dominance stochastique du premier degré : La pauvreté diminue lorsqu’on passe de la distribution F₁ à la distribution F₂ pour tout seuil de pauvreté z ≤ z⁺et pour tout indice de pauvreté additif tel que ∂p(y, z) / ∂y ≤ 0 si et seulement si

Tests de dominance stochastique du deuxième degré : La pauvreté diminue lorsqu’on passe de la distribution F₁ à la distribution F₂ pour tout seuil de pauvreté z ≤z⁺et pour tout indice de pauvreté additif tel que ∂p(y, z) / ∂y ≤0 et ∂²p(y, z) / ∂y² ≥0 si et seulement si

Les tests de dominance du premier degré, permettent d’identifier les situations pour lesquelles les conclusions demeurent inchangées quel que soit le seuil de pauvreté utilisé et quel que soit l’indice de pauvreté utilisé. Pour effectuer ces tests, il suffit donc de vérifier si la distribution cumulative dans une situation est en tout point inférieure à celle de l’autre situation jusqu’au seuil de pauvreté maximal considéré. Nous allons considérer toute valeur comprise entre 0 $ et 20 000 $ (dollars de 1997) comme seuil de pauvreté potentiel pour un célibataire. Le second type de tests, les tests de dominance du deuxième degré, permet d’identifier les situations pour lesquelles les conclusions demeureraient inchangées quel que soit le seuil de pauvreté utilisé et quel que soit l’indice de pauvreté utilisé à condition que cet indice soit sensible faiblement à l’inégalité[4]. Pour effectuer ces tests, il suffit donc de vérifier si l’aire sous la courbe de distribution cumulative dans une situation est en tout point inférieure à celle de l’autre situation jusqu’au seuil de pauvreté maximal considéré. Pour les situations où il y aurait croisement entre les courbes (ou l’aire sous la courbe), nous suivrons la méthode suggérée par Davidson et Duclos (2000) qui consiste à estimer le premier point de croisement entre les courbes.

1.4 Problème de comparaison

Finalement, il existe aussi un problème de comparaison. L’analyste doit trouver une façon de comparer des ménages de différentes tailles (nombre d’adultes, d’enfants dans le ménage) vivant dans des endroits différents et faisant potentiellement face à des prix différents. Pour ce faire, celui-ci utilise une échelle d’équivalence qui transforme le revenu du ménage en un revenu équivalent pour un ménage de référence. Dans un premier temps, il faut ajuster les revenus pour les différences dans le coût de la vie entre les régions. Comme le souligne Deaton et Muellbauer (1980), si les préférences ne sont pas homothétiques, il est important que l’indice utilisé tienne compte de la composition du panier de consommation du ménage qui nous intéresse. Afin d’être le plus près possible de cet indice idéal, nous avons calculé les indices implicites aux différents seuils de pauvreté basés sur les prix d’un panier de bien (MBML pour Market Basket Measure Lines) proposés par le Federal / Provincial / Territorial Working Group[5]. Pour calculer ces MBML, les analystes ont évalué les besoins d’un couple à faible revenu avec deux enfants. Pour la nourriture, le panier de biens nutritionnels d’Agriculture Canada pour lequel des prix sont disponibles pour 18 centres urbains au Canada a été choisi. Le prix de ce panier sera donc calculé pour le plus grand centre urbain de la province. Pour les coûts des vêtements, on a utilisé les prix de Toronto en 1991 ajustés pour l’inflation. Ce coût sera le même sur l’ensemble du Canada. Pour le logement, le loyer d’un appartement de trois chambres à coucher a été retenu. C’est pour cette dépense que l’information au niveau régional est la plus abondante. Le loyer médian pour ce type d’appartement est intégré à l’évaluation du coût du panier de bien. Pour les zones rurales, ce prix est estimé. Pour d’autres biens tels les soins personnels, les loisirs, le téléphone, les transports publics, etc., des guides budgétaires développés par des agences de services sociaux de différentes villes ont été utilisés. Nous considérons ce choix comme intéressant puisque les niveaux de prix sont calculés à partir d’un panier de consommation type pour une personne à faible revenu. Pour 1997, nous avons calculé des indices implicites à ces MBML en utilisant les rapports des niveaux de prix dans les différentes régions. Nous utilisons comme région de référence les agglomérations urbaines de plus de 500 000 habitants en Ontario. L’indice pour cette région est donc égal à 1,0000. Pour les autres régions, les indices sont calculés en divisant la valeur du MBML pour cette région par celle des agglomérations urbaines de plus de 500 000 habitants en Ontario. Pour 1989, nous avons reconstruit ces indices en utilisant les différentiels d’inflation entre les provinces sur la période 1989-1997. Les valeurs de ces indices pour l’année 1997 sont données au tableau 1. Si on prend à titre d’exemple une personne vivant au Québec dans une agglomération urbaine de plus de 500 000 habitants, cette personne pourrait atteindre le même niveau de vie en ne dépensant que 79,2 % du montant dépensé par l’Ontarien.

Tableau 1

**Indice implicite du revenu pour les différentes régions en 1997**

Après avoir ajusté les revenus pour les différences de prix entre les régions, on doit aussi faire un ajustement pour la taille de la famille. Afin de faire cet ajustement, nous utilisons la classe d’échelle d’équivalence paramétrique de Buhmann, Rainwater, Schmaus et Smeeding (1987) :

où ε est l’élasticité de l’échelle par rapport à la taille du ménage. Théoriquement, la valeur de ε est comprise entre 0 et 1 mais Buhmann et al. (1987) soulignent que les échelles les plus fréquemment utilisées par les analystes nous donnent des valeurs de ε comprises entre 0,23 et 0,84. Il existe donc une diversité d’opinions sur l’échelle d’équivalence tout comme il existe une diversité d’opinions sur le seuil de pauvreté. Tel que suggéré dans plusieurs études de l’OCDE, nous utiliserons une valeur de 0,5 pour ε (voir Föster, 2000).

2. La pauvreté au Canada

Afin d’établir un profil de pauvreté pour le Canada, nous avons utilisé les Enquêtes sur les finances des consommateurs – Familles économiques de 1990 et de 1998[6]. Celles-ci portent sur les revenus de 1989 et 1997 respectivement. Cette enquête a été abolie en 1998. Pour les revenus de 1998 et pour les années subséquentes, les analystes devront utiliser l’Enquête sur la dynamique du travail et du revenu. Nous avons donc choisi l’année 1997 afin que les comparaisons soient faites dans le cadre d’une même méthodologie d’enquête. Dans cette section, nous étudions l’évolution de la situation de la pauvreté entre 1989 et 1997 pour le Canada. Par la suite, nous établissons un profil de la pauvreté au Canada et décrivons l’évolution de la pauvreté pour les différents groupes démographiques et les différentes régions du pays. Pour les tests de dominance, nous considérerons toute valeur comprise entre 0 et 20 000 $ (prix de 1997) comme étant des seuils potentiels de pauvreté pour notre ménage de référence qui est le célibataire. Cet intervalle est assez large compte tenu que le seuil de faible revenu après impôt et transferts de Statistique Canada est de 14 227 $ pour un célibataire et que celui de l’Institut Fraser est de 7 715 $. Les revenus des autres types de ménages sont ajustés à l’aide de notre échelle d’équivalence pour pouvoir être comparés avec les revenus des célibataires. Nous montrons entre autres que la pauvreté a augmenté au courant des années quatre-vingt-dix au Canada et ainsi que pour la plupart des régions et groupes démographiques et que cette conclusion est vraie quel que soit le seuil de pauvreté utilisé et quel que soit l’indice de pauvreté utilisé. Cette constatation vient confirmer ce que les études déjà existantes affirment déjà. Par contre, nous montrons qu’en utilisant un ajustement pour les différences de prix entre les provinces, le classement des provinces en terme de pauvreté est différent de ce qu’on a l’habitude de lire dans les études déjà existantes (voir entres autres Conseil du bien-être social du Canada, 1999).

2.1 Une vue d’ensemble

Dans un premier temps, nous avons utilisé l’indice numérique de pauvreté, H, pour établir l’incidence de la pauvreté au Canada. Dans le tableau 2, on retrouve les valeurs de l’indice numérique de pauvreté pour 1989 et 1997 pour le seuil de faible revenu après impôt et transferts et le seuil de l’Institut Fraser. On remarque que l’incidence de la pauvreté s’est accrue entre 1989 et 1997 pour l’ensemble du Canada et pour les deux seuils de pauvreté utilisés. Si on considère le seuil de faible revenu, la proportion de pauvres dans la population passe de 13,9 % à 17,9 % pour une augmentation de 28,8 % de l’incidence de la pauvreté. Pour le seuil de l’Institut Fraser, la proportion de pauvres passe de 3,1 % à 5,7 % pour une augmentation de 83,9 % de l’incidence de la pauvreté.

Tableau 2

**Indice numérique de pauvreté – Canada**

Tournons-nous maintenant vers l’indice de déficit normalisé PG afin de dépeindre la profondeur de la pauvreté. Dans le tableau 2, on retrouve les valeurs de l’indice de déficit normalisé de pauvreté pour 1989 et 1997 pour le seuil de faible revenu après impôt et transferts et pour le seuil de l’Institut Fraser. On constate que la pauvreté encore un fois augmente pour les deux seuils entre 1989 et 1997. Si on considère le seuil de faible revenu, l’indice passe de 0,0421 à 0,0577 pour une augmentation de 37,1 %. Pour le seuil de l’Institut Fraser, il passe de 0,0129 à 0,0199 pour une augmentation de 54,3 %. Comme l’indice de déficit normalisé est composé de l’indice numérique de pauvreté multiplié par le déficit moyen de pauvreté, il est intéressant d’évaluer si cette augmentation est due seulement à l’augmentation du nombre de personnes pauvres. Pour le seuil de faible revenu, l’augmentation de l’incidence de la pauvreté aurait fait augmenter l’indice à 0,0542 si le déficit moyen de pauvreté était demeuré constant. Étant donné que l’augmentation observée est plus élevée, on peut conclure que le déficit moyen s’est lui aussi accru. Pour le seuil de l’Institut Fraser, la conclusion est renversée. L’augmentation de l’incidence de la pauvreté aurait fait augmenter l’indice à 0,0237 si le déficit de pauvreté était demeuré constant. Il y a donc eu une diminution du déficit moyen. Par contre, ceci ne veut pas nécessairement dire que la situation des gens qui étaient pauvres en 1989 s’est améliorée. Cette diminution peut être due au fait que les nouveaux pauvres ont un déficit qui, en moyenne, est moins important, faisant ainsi diminuer la moyenne de l’ensemble. C’est d’ailleurs pourquoi les analystes considèrent le déficit moyen de pauvreté, I, comme n’étant pas un bon indice de pauvreté, s’il est utilisé seul, et utilisent plutôt l’indice PG qui est égal à H ⋅ I.

Finalement, afin de voir l’effet de l’inégalité entre les pauvres, nous utilisons l’indice P₂. Le tableau 2 donne les valeurs de l’indice P₂ pour 1989 et 1997 pour le seuil de faible revenu après impôt et transferts et pour le seuil de l’Institut Fraser. On constate que la pauvreté encore un fois augmente pour les deux seuils entre 1989 et 1997. Si on considère le seuil de faible revenu, l’indice passe de 0,0212 à 0,0312 pour une augmentation de 47,2 %. Pour le seuil de l’Institut Fraser, il passe de 0,0086 à 0,0137 pour une augmentation de 59,3 %. Ces résultats indiquent une augmentation de l’extrême pauvreté puisque l’indice P₂ accorde plus de poids aux personnes ayant un revenu plus faible.

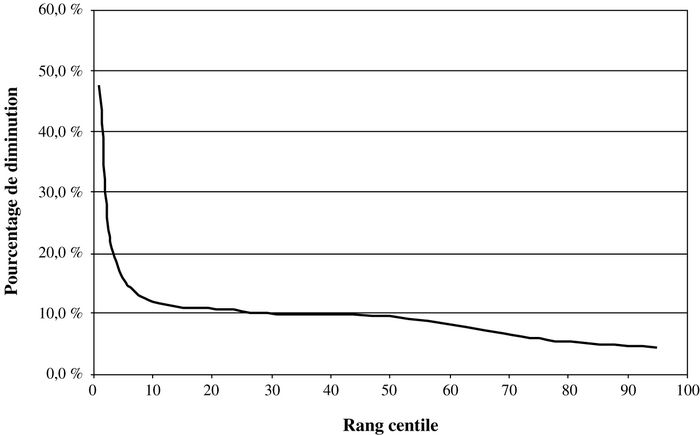
Tous ces résultats semblent indiquer une augmentation de la pauvreté. Mais comment expliquer ce phénomène? Étudions dans un premier temps l’évolution du revenu net moyen des ménages sur cette période. Celui-ci était de 37 299 $ en 1997 alors qu’il était de 40 035 $ en 1989 (en dollars de 1997). Le revenu moyen disponible a donc diminué de 6,8 % sur cette période de 8 ans. Ceci explique en partie l’augmentation de la pauvreté. Tournons-nous maintenant vers la distribution de cette baisse du revenu net. Si on calcule la diminution du revenu net pour différents rangs centiles, on s’aperçoit que cette diminution a touché plus durement les personnes ayant un revenu plus faible. Le graphique 1 montre comment cette baisse de revenu est répartie à travers les classes de revenus. Nous voyons facilement que les rangs centiles les plus bas ont été plus durement touchés par cette baisse du revenu net. Nous pouvons donc penser que l’augmentation de la pauvreté est un résultat relativement robuste. En effet, si nous effectuons un test de dominance stochastique du premier degré, nous constatons que la pauvreté a augmenté de 1989 à 1997 et que cette conclusion demeure valide quel que soit le seuil de pauvreté utilisé et quel que soit l’indice de pauvreté utilisé. Comme il y a dominance du premier degré, il n’est pas nécessaire d’effectuer un test de dominance du second degré puisque la dominance du premier degré implique nécessairement la dominance du deuxième degré.

Graphique 1

**Baisse du revenu réel net**

2.2 Décomposition démographique

Il est intéressant de savoir comment la pauvreté affecte les différents sous-groupes démographiques. Pour ce faire, nous divisons la population en neuf sous-groupes démographiques. Pour les familles dont le chef est âgé de moins de 65 ans, nous avons : les hommes célibataires, les femmes célibataires, les familles monoparentales dont le chef est une femme, les familles monoparentales dont le chef est un homme, les couples sans enfants et les couples avec enfants. Pour les familles dont le chef est âgé de plus de 65 ans, nous avons : les hommes célibataires, les femmes célibataires et les autres types de familles. Le graphique 2 nous donne, pour les années 1989 et 1997, la valeur de l’indice numérique de pauvreté, H, pour chacun des groupes démographiques, pour le seuil de faible revenu et le seuil de l’Institut Fraser. On remarque assez facilement que les groupes pour lesquels l’incidence de la pauvreté est la plus importante sont les mères monoparentales et les célibataires de moins de 65 ans. Suivent les pères seuls et les célibataires de plus de 65 ans. Il est surprenant de constater que les personnes âgées de plus de 65 ans ont une incidence de la pauvreté moins élevée que ceux de moins de 65 ans pour chaque type de ménages. On remarque aussi que l’incidence de la pauvreté a augmenté chez tous les groupes démographiques de 1989 à 1997 sauf chez les personnes et les familles âgées de plus de 65 ans si l’on considère le seuil de faible revenu après impôt et transferts de Statistique Canada.

Graphique 2

**Incidence de la pauvreté pour les différents groupes démographiques**

Le groupe qui semble le plus à risque d’être pauvre est tout de même celui des familles monoparentales dirigées par une femme. Il est donc intéressant de décomposer ce groupe par tranche d’âge. Le graphique 3 nous donne cette décomposition. L’incidence de la pauvreté semble diminuer chez les mères monoparentales lorsqu’elles sont plus âgées. Par contre, cette incidence demeure encore plus importante chez les mères monoparentales de plus de 45 ans que chez la plupart des autres groupes démographiques.

Graphique 3

**Incidence de la pauvreté chez les mères monoparentales**

Il est maintenant intéressant de se tourner vers l’indice de déficit normalisé de pauvreté, PG, afin d’avoir un portrait de la gravité de la pauvreté selon les groupes. Le graphique 4 nous présente, pour les années 1989 et 1997, les valeurs de cet indice pour chacun des groupes démographiques, pour le seuil de faible revenu et le seuil de l’Institut Fraser. On remarque ici que les familles monoparentales dirigées par des femmes sont encore le groupe le plus touché par la pauvreté si on considère le seuil de faible revenu. Par contre, les célibataires (hommes ou femmes) ont un niveau de pauvreté plus important si on considère le seuil de l’Institut Fraser. Le classement de ces deux groupes dépend donc du seuil de pauvreté utilisé. Il est intéressant encore une fois de se pencher sur la situation des mères monoparentales par tranches d’âges. Le graphique 5 donne les valeurs du déficit normalisé de pauvreté pour ces groupes d’âges. On remarque encore une fois que les mères seules de moins de 25 ans sont beaucoup plus touchées par la pauvreté. Leur situation est même pire que celle des célibataires pour le seuil de l’Institut Fraser alors que les mères monoparentales dans leur ensemble s’en tiraient mieux pour ce seuil de pauvreté.

Graphique 4

**Indice de déficit normalisé de pauvreté pour les différents groupes démographiques**

Graphique 5

**Indice de déficit normalisé de pauvreté chez les mères monoparentales**

Finalement, nous utilisons l’indice P₂ afin d’avoir un portrait de la façon dont le déficit de pauvreté est distribué à travers les pauvres. Le graphique 6 donne les valeurs de P₂ pour les années 1989 et 1997, pour les différents groupes démographiques pour le seuil de faible revenu et le seuil de l’Institut Fraser. Les groupes les plus touchés par la pauvreté sont encore les mêmes. Par contre, les célibataires de moins de 65 ans ont un niveau de pauvreté plus important que les mères seules (en 1997 pour les deux seuils de pauvreté sous considération). Étant donné que ce classement entre en contradiction avec le classement selon l’indice numérique de pauvreté et en partie avec l’indice de déficit normalisé de pauvreté, cela indique que plus de célibataires vivent dans une pauvreté extrême. Il est encore tout de même intéressant de décomposer par tranches d’âges pour les mères monoparentales, surtout pour voir ce qu’il advient de celles âgées de moins de 25 ans. Le graphique 7 donne les valeurs de P₂ pour ces groupes. Encore une fois, on remarque que les mères seules de moins de 25 ans s’en tirent moins bien que les célibataires dans leur ensemble et ceci, malgré le fait que les mères monoparentales dans leur ensemble s’en tirent mieux. Ce fait qui semble se répéter quel que soit l’indice de pauvreté utilisé est très inquiétant. En effet, on sait que P₂, en mesurant l’inégalité entre les pauvres, est plus sensible à l’extrême pauvreté. Alors, un indice P₂ plus élevé signifie qu’il y a des enfants en bas âge dont la mère a beaucoup de difficultés à subvenir aux besoins du ménage. Ce problème est extrêmement préoccupant. On peut penser qu’un manque important de ressources financières serait un facteur important de stress. Ceci augmenterait la probabilité que la mère ait de la difficulté à développer la zone d’intersubjectivité avec son enfant. Cette zone d’intersubjectivité comprend, entre autres, le mode de communication entre la mère et l’enfant en bas âge que les personnes hors de la famille ont de la difficulté à comprendre. Ce problème au niveau de la qualité de la zone d’intersubjectivité peut être par la suite à la source de problèmes de développement au niveau cognitif et langagier[7]. Tout ceci viendra alors limiter les capabilités accessibles à cet enfant notamment au niveau du développement de son capital humain.

Graphique 6

**Indice P2 pour les différents groupes démographiques**

Graphique 7

**Indice P2 pour les mères monoparentales**

Avant de terminer cette section, il est important de tester la robustesse des conclusions de la décomposition démographique à un changement de seuil ou d’indice de pauvreté en effectuant un test de dominance stochastique. Pour ce faire, nous avons utilisé une décomposition démographique en trois groupes : les mères monoparentales de moins de 65 ans, les ménages dont le chef est âgé de plus de 65 ans et les autres ménages. Si on commence par comparer les mères monoparentales avec les deux autres groupes, on peut affirmer que la pauvreté chez les familles monoparentales est plus élevée que pour les autres groupes démographiques et ceci, quel que soit l’indice de pauvreté et quel que soit le seuil de pauvreté. Si on compare les ménages dont le chef a plus de 65 ans avec les autres types de ménages, on constate que la pauvreté chez les ménages dont le chef a plus de 65 ans est moins élevée que pour les autres types de ménages et ceci, quel que soit l’indice de pauvreté et quel que soit le seuil de pauvreté, à condition que ce seuil soit inférieur à 16 300 $ pour une personne seule. Comme le seuil de faible revenu après impôt pour une personne seule est de 14 227 $, cette conclusion semble donc relativement robuste. Si on ne veut pas restreindre le seuil de pauvreté sous 20 000 $, on peut restreindre les indices de pauvreté que l’on considère à ceux qui sont sensibles à l’inégalité dans la distribution de la pauvreté et effectuer un test de dominance stochastique du deuxième degré. Ce test nous indique que la pauvreté chez les ménages dont le chef a plus de 65 ans est moins élevée que pour les autres types de ménages et ceci, quel que soit le seuil de pauvreté utilisé et quel que soit l’indice de pauvreté utilisé à condition que cet indice soit sensible à l’inégalité chez les pauvres. Il semblerait donc que les mesures publiques visant à lutter contre la pauvreté chez les personnes âgées soient relativement efficaces. En plus, l’observation des différents indices de pauvreté que nous avons calculés montre que, contrairement à tous les autres groupes démographiques, leur situation s’est améliorée pendant les années quatre-vingt-dix. Comme l’affirme Phipps (1999), cette constation semble indiquer qu’il y a une possibilité de lutter contre la pauvreté lorsqu’il y a une véritable volonté politique à ce niveau. Il faut noter aussi que ces personnes âgées, en ayant droit aux pensions de vieillesses, reçoivent en quelque sorte un « revenu minimum garanti » . Cette portion des programmes de sécurité de vieillesse est en effet versée à tous de façon inconditionnelle. On ne peut affirmer que le succès de la lutte à la pauvreté chez les personnes âgées est seulement dû à ce programme mais il serait certainement intéressant d’étudier l’effet de celui-ci puisque de plus en plus de personnes provenant d’horizons politiques extrêmement diversifiés réclament la mise en place d’un tel revenu pour l’ensemble de la population.

2.3 Décomposition géographique

Étant donné qu’une partie des transferts fédéraux visent à améliorer le sort des régions les plus pauvres, il est intéressant de faire une décomposition géographique de la pauvreté afin de savoir comment celle-ci affecte les différentes régions. Nous divisons le Canada en cinq régions, soit l’Atlantique, le Québec, l’Ontario, les Prairies et la Colombie-Britannique. L’objectif de cet exercice est d’illustrer comment l’ajustement pour tenir compte du coût de la vie peut changer la façon dont plusieurs études classent ces régions. Le graphique 8 nous donne, pour les années 1989 et 1997, la valeur de l’indice numérique de pauvreté, H, pour chacune des régions, pour le seuil de faible revenu et le seuil de l’Institut Fraser. On remarque que la région la plus touchée par l’incidence de la pauvreté est l’Atlantique. Cette région est aussi celle où l’augmentation de l’incidence est la plus marquée sur cette période. On remarque aussi que l’incidence de la pauvreté a augmenté entre 1989 et 1997 pour toutes les régions sauf pour les Prairies si on considère le seuil de l’Institut Fraser. Un résultat intéressant est que l’incidence de la pauvreté au Québec est moins importante qu’en Ontario en 1997 et qu’en Colombie-Britannique pour 1989 et 1997. Ce résultat semble contredire les résultats obtenus par le Conseil du bien-être social du Canada (1999). La raison principale pouvant expliquer cette différence est que nous avons tenu compte des différences de prix entre les régions alors que dans cette étude, cette différence n’est pas prise en compte. Par contre, nous tenons à préciser que, tout comme eux, nous obtenons une incidence de pauvreté à la hausse pour l’ensemble des régions.

Graphique 8

**Incidence de la pauvreté par région**

Il est intéressant d’étudier la façon dont la profondeur de la pauvreté affecte les différentes régions en calculant l’indice de déficit normalisé de pauvreté PG pour chacune des régions. Le graphique 9 nous donne, pour les années 1989 et 1997, la valeur de cet indice (PG) pour chacune des régions, pour le seuil de faible revenu et le seuil de l’Institut Fraser. Une première constatation émerge à la lecture de ce graphique. La région Atlantique, bien qu’étant la plus touchée par l’incidence de la pauvreté, s’en tire mieux que la Colombie-Britannique et l’Ontario au niveau du déficit normalisé de pauvreté. Les pauvres y sont plus nombreux, mais ils sont moins pauvres en moyenne. On remarque aussi que les régions les plus touchées par l’augmentation de la pauvreté telle que mesurée par PG sont la Colombie-Britannique, l’Ontario et le Québec.

Graphique 9

**Indice de déficit normalisé de pauvreté par région**

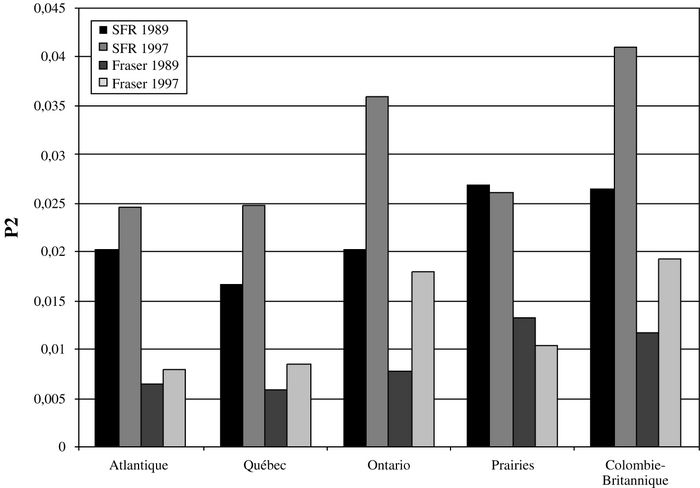
Finalement, afin de voir l’effet de l’inégalité entre les pauvres dans ces régions, nous utilisons l’indice P₂ de Foster, Greer et Thorbecke. Le graphique 10 nous donne, pour les années 1989 et 1997, la valeur de cet indice (P₂) pour chacune des régions, pour le seuil de faible revenu et le seuil de l’Institut Fraser. Les résultats de ce graphique sont assez révélateurs. L’indice P₂ est moins élevé pour l’Atlantique et le Québec que pour toutes les autres régions en 1997. Cela signifie que ces régions sont moins affectées par l’extrême pauvreté. On remarque aussi que, pour cet indice, la pauvreté a diminué dans les Prairies de 1989 à 1997 et ceci, pour les deux seuils de pauvreté considérés. Par contre, pour les autres régions, on note toujours cette augmentation de la pauvreté. Les régions les plus touchées par cette augmentation sont la Colombie-Britannique et l’Ontario.

À la lumière des différents résultats, il est intéressant de se demander si les conclusions tirées dans cette section sont robustes à un changement de méthodologie. Pour ce faire, nous avons effectué dans un premier temps des tests de dominance stochastique. Pour ce qui est de l’évolution de la pauvreté entre 1989 et 1997, on peut affirmer que la pauvreté a augmenté au Québec, en Ontario et en Colombie-Britannique pour tout seuil de pauvreté et tout indice de pauvreté. Pour les Prairies, la pauvreté a diminué pour tout seuil de pauvreté inférieur à 6 800 $ et tout indice de pauvreté. Comme le seuil de 6 800 $ est relativement faible, nous effectuons un test de dominance stochastique du deuxième degré et pouvons affirmer que la pauvreté a diminué pour tout seuil de pauvreté inférieur à 11 500 $ et pour tout indice de pauvreté sensible à l’inégalité. Pour les comparaisons entre les régions nous concluons qu’il y a moins de pauvreté au Québec qu’en Ontario et qu’en Colombie-Britannique et ceci, quel que soit l’indice de pauvreté utilisé et quel que soit le seuil de pauvreté. Nous pouvons aussi affirmer qu’il y a moins de pauvreté dans les Prairies qu’en Ontario et qu’en Colombie-Britannique et ceci, quel que soit l’indice de pauvreté utilisé et quel que soit le seuil de pauvreté. Les autres comparaisons ne sont pas robustes.

Comme le souligne Pendakur (1998), le choix d’un indice du niveau des prix entre les régions peut influencer les résultats obtenus au niveau des comparaisons de bien-être. Le résultat le plus surprenant que nous obtenons est la dominance du Québec sur l’Ontario et la Colombie-Britannique. Il convient à ce point de se demander si le résultat n’est pas contingent au choix de notre indice. Afin de tester la robustesse de nos conclusions, nous avons dans un premier temps effectué des tests de dominance stochastique en égalisant le niveau de prix entre les provinces. Pour le test du premier degré, nous ne pouvons conclure qu’il y a moins de pauvreté au Québec qu’en Ontario et qu’en Colombie-Britannique que pour des seuils de pauvreté inférieur à 6 100 $, ce qui est très faible comme seuil. Par contre, nous pouvons utiliser un résultat établi par Davidson et Duclos (2000) afin de tirer une conclusion de cette observation. Davidson et Duclos montrent que s’il y a dominance initiale d’une distribution sur une autre, alors il existe une classe de mesure de pauvreté avec une aversion à l’inégalité assez élevée telle qu’il y aura dominance totale pour les indices de cette classe[8]. Ce résultat nous permet donc d’affirmer que pour des indices de pauvreté qui seront assez averses à l’inégalité, il y aura moins de pauvreté au Québec qu’en Ontario et qu’en Colombie-Britannique. Dans cet ordre d’idée, nous avons effectué des tests de dominance du deuxième degré. Le premier test indique qu’il y a moins de pauvreté au Québec qu’en Ontario pour tout seuil inférieur à 9 200 $ et pour tout indice de pauvreté sensible à l’inégalité. Le second test indique qu’il y a moins de pauvreté au Québec qu’en Colombie-Britannique pour tout seuil inférieur à 11 000 $ et pour tout indice de pauvreté sensible à l’inégalité.

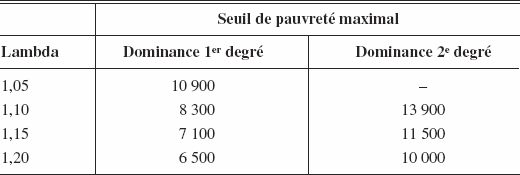
Dans un deuxième temps, nous avons aussi voulu tester la robustesse de nos conclusions pour un large choix d’indice. Pour ce faire, nous avons multiplié les prix au Québec par λ > 1 afin de vérifier comment nos conclusions se modifient lorsque le différentiel de prix diminue entre le Québec d’une part et l’Ontario et la Colombie-Britannique d’autre part. Le tableau 3 présente les seuils de pauvreté maximaux pour lesquels le Québec domine l’Ontario pour des tests de dominance stochastique du premier degré et du deuxième degré et pour différentes valeurs de λ. On remarque que si on augmente les prix de 5 % au Québec, il y a encore dominance du deuxième degré pour tout seuil de pauvreté. Pour la dominance du premier degré, le seuil de pauvreté maximum est alors de 10 900 $, une valeur se situant entre le seuil de l’Institut Fraser et le seuil de faible revenu de Statistique Canada. On remarque aussi que pour des augmentations plus élevées des prix, ces seuils deviennent de plus en plus faibles. Le tableau 4 présente les mêmes résultats pour le Québec et la Colombie-Britannique. On remarque que si on augmente les prix de 5 % au Québec, il y a encore dominance du premier degré pour tout seuil de pauvreté. Pour une augmentation de 10 %, il y a encore dominance du deuxième degré pour tout seuil de pauvreté. Il y a aussi dominance du premier degré pour tout seuil de pauvreté inférieur à 19 100 $, ce qui est très élevé. Pour une augmentation de 15 %, il y a encore dominance du deuxième degré pour tout seuil de pauvreté inférieur à 18 600 $, ce qui est, encore une fois, très élevé.

Tableau 3

**Dominance Québec/Ontario pour différents indices**

Tableau 4

**Dominance Québec/Colombie-Britannique pour différents indices**

Ces résultats sont très importants parce qu’ils mettent en lumière que les résultats obtenus sur la position relative du Québec au niveau de la pauvreté dans des études antérieures sont liés à une méthodologie très particulière. Entre autres, le Conseil du bien-être social du Canada (1999) ne tient pas compte des différences du coût de la vie entre les provinces dans ses profils de pauvreté. Une étude plus récente de Mayer et Morin (2000) indiquait que la différence entre le Québec et l’Ontario était moins élevée (le Québec étant toujours plus pauvre) que ce que présentait le Conseil du bien-être social du Canada (1999), si on utilise les revenus après taxes et transferts et si on corrige les différences de coût de la vie. Par contre, l’indice numérique de pauvreté, bien que facile à interpréter et à expliquer, comporte des propriétés qui peuvent être jugées non désirables par plusieurs personnes. Entre autres, il est insensible à la profondeur du déficit de pauvreté et à l’inégalité entre les pauvres. Ici, nous montrons que si nous utilisons des indicateurs qui prennent en compte ces dimensions de la pauvreté, nous inversons le classement entre les provinces.

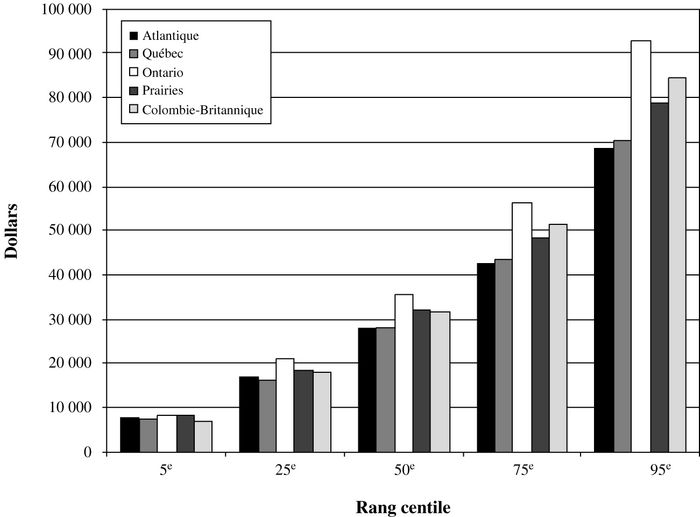
Mais, qu’est ce qui explique la mauvaise performance au niveau de la pauvreté de la Colombie-Britannique et de l’Ontario qui sont pourtant les provinces les plus riches du Canada? Si on se réfère au graphique 11, on constate en effet que le revenu net moyen des ménages dans ces deux provinces est plus élevé que pour les autres régions. Afin de comprendre le phénomène, nous devons nous demander comment ce surplus de revenu est distribué. Le graphique 12 nous donne les revenus nets pour quelques rangs centiles de la distribution. On y constate que cette différence dans le revenu net moyen est surtout provoquée par des différences au niveau des rangs centiles supérieurs. Ce plus grand revenu disponible a probablement pour effet de faire augmenter la demande de plusieurs biens entraînant ainsi des prix plus élevés. Les ménages des quantiles inférieurs font alors face à des niveaux prix supérieurs sans avoir pour autant un revenu net beaucoup plus grand.

Graphique 11

**Revenu moyen par région**

Graphique 12

**Revenu par différents rang centiles**

Conclusion

Dans cet article, nous avons dans un premier temps énoncé les difficultés conceptuelles sous-jacentes à toute comparaison de pauvreté. Par la suite, nous avons étudié la pauvreté au Canada. Quelques conclusions importantes ressortent de cet article. Premièrement, la pauvreté a augmenté au Canada entre 1989 et 1997 et ce résultat est robuste à un changement de méthode de calcul. Cette conclusion est alarmante en soi et doit être prise au sérieux par les décideurs publics. Quel facteur pourrait expliquer ce résultat? Bien sûr, la diminution du revenu net réel des familles explique en partie ce résultat. Outre ceci, une augmentation de l’inégalité dans les revenus nets serait aussi responsable d’une bonne partie de la performance du Canada.

Atkinson (1999) offre une explication potentielle de ce phénomène. Durant les années quatre-vingt, un changement s’est opéré au niveau des normes sociales de fixation des salaires partout en Occident. Nous avons passé d’une norme favorisant des salaires plus égaux au sein d’une entreprise à des salaires basés sur la performance et, par le fait même, beaucoup plus inégaux. Ce même changement de norme a entraîné un changement dans l’attitude politique face à la fiscalité distributive. La volonté politique de lutter contre l’inégalité et la pauvreté a ainsi diminué. Pire, au Canada, nous n’avons pas qu’assisté à la baisse des transferts envers les personnes les plus démunies mais aussi à un changement d’attitude de la population et des autorités politiques envers ces personnes. Par exemple, au Québec, on a instauré des enquêteurs spéciaux de la sécurité du revenu avec droit de perquisition sans mandat (boubou-macoutes). En Ontario, le gouvernement a instauré une « ligne d’urgence de fraude d’aide sociale » et songe à déposer un projet de loi visant à rendre obligatoire des prises de sang pour toute personne prestataire d’aide sociale. Ces prises de sang auront pour objectif de détecter la présence de drogue. Dans un tel contexte, il y a augmentation de la stigmatisation des prestataires de la sécurité du revenu. La base sociale du respect de soi de ces individus s’en trouve ainsi diminuée venant ainsi exacerber le problème de la pauvreté. Par contre, comme le souligne Atkinson, cet état de fait n’est pas une donnée irréversible et un leadership politique pourrait induire un nouveau changement de norme sociale.

Nous avons aussi montré comment la pauvreté affecte les différents groupes démographiques. Les mères monoparentales sont plus pauvres que le reste de la population et ont vu leur situation se détériorer pendant les années quatre-vingt-dix. Par contre, les personnes âgées de plus de 65 ans sont moins pauvres qu’en 1989 et se retrouvent maintenant moins pauvres que tous les autres groupes démographiques. Tout comme Phipps (1999) le souligne, ceci nous indique qu’il y a possibilité de lutter contre la pauvreté lorsqu’il existe une véritable volonté politique.

Finalement, nous avons montré comment la pauvreté affecte les différentes régions du Canada. Nous avons des résultats sensiblement différents des études antérieures. Entre autres, il semble y avoir moins de pauvreté au Québec qu’en Ontario et qu’en Colombie-Britannique. Nous avons montré que ce résultat, bien que lié à une méthodologie particulière, semble plus robuste que ceux obtenus par le Conseil du bien-être social du Canada (1999). Ceci s’explique par le fait que nous avons pris en compte les différences dans les coûts de la vie des différentes régions et que nous avons considéré une classe plus importante de mesures de pauvreté.

Que pouvons-nous apprendre des profils de pauvreté canadiens?

Résumé

Abstract

Introduction