Article body

Des limaces et des tempêtes

Le matin, sur le dallage devant notre maison, et plus particulièrement après la pluie, je trouve souvent un tracé complexe de traînées entrelacées, comme si quelqu’un avait griffonné partout dessus à l’aide d’un crayon à bave. En réalité, elles sont faites par des limaces qui sortent à la nuit tombée faire leurs incursions dans la végétation, seulement pour re-disparaître à l’aube dans les profondeurs mystérieuses d’où elles sont venues. Par temps frais et humide, les limaces peuvent braver la lumière du jour sans craindre la déshydratation, et nous pouvons les regarder se déplacer. Elles posent leur arrière-train sur le sol, et poussent leur devant en avant, contre cette résistance postérieure. Puis, une fois l’avant déposé à son tour, elles tirent leur arrière-train, répétant le cycle encore et encore dans un mouvement lent et gracieux. Ce cycle rythmique de pousser-tirer me semble être fondamental à la vie de la plupart, sinon de toutes les créatures animées, nous autres humains y compris.

À l’instar des limaces, nous devons nous mouvoir si nous souhaitons avancer. Nous inspirons et expirons, nous mettons un pied devant l’autre. Ainsi, notre mouvement n’est pas, comme nous pourrions le supposer, le déplacement d’un être déjà accompli d’un point à un autre, comme le « déplacement » d’une pièce d’échecs en jeu, ou de petits soldats de plomb sur un champ de bataille imaginaire. Si cela était le cas, alors les chemins pourraient être décrits comme des orbites ou des trajectoires, calculables à partir de conditions initiales et modifiables uniquement par le biais d’une intervention extérieure. De la même manière, les pauses ou les moments de repos seraient inscrits comme des états de stabilité, déterminés par l’équilibre de forces extérieures. Retirez votre main d’une pièce d’échecs ou d’un soldat de plomb et ceux-ci peuvent rester là indéfiniment. Mais nous en sommes incapables. En tant qu’êtres vivants et qui respirent, il nous est très difficile de rester parfaitement immobiles. Comme si l’on essayait de retenir sa respiration, on crée alors une tension intérieure qui devient de plus en plus intense au fur et à mesure qu’elle dure. Ainsi, nous avons le sentiment que lorsque nous bougeons, nous « avançons notre corps » le long du chemin de notre propre mouvement : un chemin qui est celui de la croissance et du devenir.

Pensez aux mouvements d’une tornade ou d’une tempête. Nous pourrions dire qu’elle frappe d’abord à un endroit, puis à un autre, et le météorologue pourrait essayer de déterminer sa trajectoire. Mais la tempête n’est pas une entité cohérente et autonome qui se déplace d’un point à l’autre dans le ciel. Il s’agit plutôt d’un mouvement en lui-même, d’un « enroulement » qui crée un point d’immobilité en son œil. Tandis qu’il s’enroule sur son front avant, il se déroule sur son front arrière. Mais est-ce différent de ce que fait la limace ? Dans son Évolution créatrice de 1911, le philosophe Henri Bergson affirme que chaque organisme est jeté comme un tourbillon dans le courant de la vie (1907). Comme si, au cours de son développement, il passait par « un processus circulaire ». L’être vivant qui a alors tourné sur lui-même présente seulement la ressemblance d’un objet délimité par sa perception extérieure. Cependant, dès que nous prenons conscience que sa forme extérieure n’est que l’enveloppe d’un mouvement, la tempête et la limace commencent à remarquablement se ressembler. De même que la tempête s’enroule et se déroule, laissant une traînée – de destruction, si elle est violente – sur la surface de la terre, la limace aussi pousse et se tracte alternativement, laissant ses traînées de bave sur le sol. Elles opèrent peut-être à des échelles très différentes, mais le principe reste le même.

Le maillage

Cette magnifique traînée de bave sur les dalles constitue ce que j’appelle un maillage (2011, 63‑94). Par ceci, j’entends un enchevêtrement de lignes entrelacées. Ces lignes peuvent créer une boucle ou s’enrouler autour d’autres, ou slalomer les unes autour des autres. Mais plus important encore, elles ne se connectent pas. Cette particularité est ce qui distingue le maillage du réseau. Les lignes du réseau sont des connecteurs : chaque ligne est présentée comme la relation entre des points, indépendamment et avant tout mouvement de l’un vers l’autre. Par conséquent, ces lignes sont privées de temporalité : le réseau est une construction purement spatiale. Les lignes du maillage, en revanche, sont celles du mouvement ou de la croissance. Ce sont les lignes le long desquelles les choses prennent forme. Chaque être animé, en se frayant un chemin à travers et parmi les chemins de tous les autres, doit nécessairement s’improviser un passage et, ce faisant, il trace une autre ligne. Nous pouvons en faire de même. De loin, le maillage peut ressembler à une surface emmêlée. Cependant, de près, comme si nos yeux étaient à côté des ongles de nos mains ou de nos orteils, nous nous trouvons enchevêtrés dans un « système de sympathies et de désirs, sans aucun point, seulement des lignes, toutes incurvées, qui entrent et sortent de stations de nœuds composées de toutes sortes d’art textile : tresses, nœuds de tous types, boucles, croisements et entrelacements » (Spuybroek 2011, 321).

Ces mots sont tirés d’un nouveau livre remarquable du théoricien de l’architecture et du design Lars Spuybroek. Comme il le laisse entendre ici, là où le réseau comporte des attaches, le maillage comporte des nœuds. Les nœuds sont des endroits où de nombreuses lignes en devenir sont étroitement liées les unes aux autres. Pourtant, chaque ligne dépasse le nœud dans lequel elle est nouée. Son extrémité est toujours libre, quelque part au-delà du nœud, où elle tâtonne vers un enchevêtrement avec d’autres lignes, dans d’autres nœuds. En effet, qu’est-ce que la vie, sinon une prolifération d’extrémités libres ! Elle ne peut être réalisée que dans un monde qui n’est pas entièrement connecté. Ainsi, la continuité même de la vie – sa durabilité, dans le jargon actuel – dépend du fait que rien ne s’emboîte jamais tout à fait. Le monde n’est pas construit comme un puzzle dans lequel chaque « bloc de construction » s’emboîte parfaitement dans une totalité déjà prédéfinie. En effet, de nos jours, on nous répète sans cesse que le monde dans lequel nous vivons est construit à partir de blocs : ainsi, les biologistes parlent de blocs de construction des organismes cellulaires, les psychologues, de blocs de construction de la pensée, les physiciens, de blocs de construction de l’univers en lui-même. Mais un monde construit à partir de blocs parfaitement emboîtables ne pourrait pas abriter la moindre vie. La réalité s’apparente davantage à un édredon où des éléments mal assemblés sont cousus ensemble le long de bords irréguliers pour former une couverture qui reste toujours provisoire, puisque des éléments peuvent à tout moment y être ajoutés ou retirés.

Le philosophe Gilles Deleuze et le psychanalyste Félix Guattari reprennent l’histoire de l’édredon pour développer leur idée d’une topologie lisse plutôt que striée, en montrant comment les premiers tissus brodés ont ouvert la voie à une technique de patchwork où des chutes de tissus ou des morceaux récupérés sur des vêtements usés étaient cousus ensemble. Avec ses intersections régulières et rectilignes de la trame et de la chaîne, le tissu – pour Deleuze et Guattari – est l’incarnation du strié. Mais dans le patchwork, « c’est une collection amorphe de morceaux juxtaposés, dont le raccordement peut se faire d’une infinité de manières », le principe de striation est subordonné à celui du lisse. Or aucun matériau n’illustre mieux le principe du lisse que le feutre. Composé d’un mélange de fibres de laine enchevêtrées, sans direction cohérente, et s’étendant sans limite et dans toutes les directions, le feutre – disent Deleuze et Guattari – est tout ce que le tissu n’est pas. C’est un anti-tissu (1980, 594). Ne pourrait-on pas en dire autant du maillage ? Les traces laissées par les limaces dans leurs méandres nocturnes ne sont-elles pas comparables aux fibres du feutre, qui à leur tour rappellent les traces laissées dans le sol, lors de leurs pérégrinations pastorales, par les moutons sur le dos desquels la laine a poussé ? Voilà en effet ce que Deleuze et Guattari voudraient nous faire croire. Pourtant, les lignes constitutives du lisse, disent-ils, sont abstraites, à la différence des lignes qui sont soit géométriques, soit organiques. Afin de mieux saisir où ils veulent en venir, nous devons examiner ces trois types de lignes plus en détail.

Les lignes géométriques et organiques

Commençons par la ligne géométrique, autrement dit la droite euclidienne, définie par le lien entre deux points. Comme son nom l’indique, la ligne géométrique est issue des méthodes des géomètres de l’Égypte ancienne pour mesurer la terre après les crues annuelles du Nil : ils tendaient une corde sur deux pieux enfoncés dans le sol. Comme nous le rappelle le philosophe Michel Serres, c’est de là que vient la notion légale de contrat : une « corde qui nous tire ou tracte ensemble » (1990). Or la corde, le fil ou la ficelle tendue garde un côté tactile : on peut sentir la tension ; pincez-la et elle vibrera. Comme l’explique l’artiste textile Victoria Mitchell, un fil tendu est une sorte de « tournant » entre la sensation et la forme, entre la kinésie corporelle et la raison spéculative (2006, 345). Mais alors que la géométrie entre dans les domaines des arts et des sciences de l’optique, et que la corde du géomètre se voit rejointe par les instruments optiques de navigateurs, le fil anciennement tangible et tendu prend une autre forme et devient un spectre intangible et immatériel : le rayon de soleil.

Pendant longtemps, le fil et le rayon de soleil, la ligne matérielle et son double spectral, apparaissent conjointement, comme une chose et son ombre. Leon Battista Alberti, dans son traité De la peinture, expose les principes de la perspective à l’aube de la Renaissance, et considère les lignes de vue comme des fils, pareils à ceux d’un voile tendu entre l’œil et la chose que l’on voie, mais si mince que jamais on ne pourra les fendre (1869, 98). Mais en tant que vecteur de projection, la ligne géométrique a fini par être dénuée de toute sa matérialité. Quand il s’agit de créer des connexions et de poser des limites, cette ligne est au centre de la loi, de la raison et de la pensée analytique. Elle est laconique et va toujours droit au but. Les lignes organiques, au contraire, tracent le réceptacle ou le pourtour des choses comme si ces dernières étaient contenues en leur centre : ce sont des contours. Elles sont également des séparateurs qui divisent les surfaces sur lesquelles elles sont dessinées en un côté de la ligne et en un autre : en ce sens, elles sont analogues aux coupes.

Cependant, ces lignes ne sont pas visibles sur ou dans les choses en elles-mêmes. Je pourrais dessiner le contour d’un œuf par un ovale, le tronc d’un arbre par deux lignes parallèles ou le ciel par un arc de cercle, mais je chercherais en vain leurs homologues sur un œuf, un tronc ou dans les cieux. Je pourrais essayer de dessiner un nuage avec des lignes courbées et aériennes, mais aucune ligne de ce genre ne se cache dans le nuage, attendant de piéger un avion insouciant. Je pourrais vouloir dessiner une pomme ou la limite entre une prairie et un champ labouré, mais comme le fait remarquer le philosophe Maurice Merleau-Ponty dans son essai L’Œil et l’Esprit (1964), il me serait insensé de croire que le contour de la pomme ou que la limite du champ existent réellement, ce sont des pointillés « tenus pour présents dans le monde, […] sur lesquels le crayon ou le pinceau n’auraient plus qu’à passer » (1964, 73). Car en regardant, nous ne voyons aucune ligne.

Cette remarque, ainsi que d’autres observations, ont mené de nombreuses figures à conclure qu’il n’existe aucune ligne dans la nature, et que les lignes que l’on dessine n’ont donc qu’un lien symbolique avec leur référent, basé sur un artifice ou une convention plutôt que par empirisme. Le philosophe Patrick Maynard a catalogué plusieurs affirmations dans ce sens (2005, 99). « Des lignes ? Je ne vois aucune ligne ! » s’exclamait le grand Goya, lui-même dessinateur industriel de renom. L’esprit impose parfois des choses à notre réalité, pense-t-il, qui n’existent pas dans ce que l’on voit. Enfin, dans son dernier panorama magistral des histoires et des théories des pratiques du dessin, l’artiste et curatrice Deanna Petherbridge s’entend à ce sujet. « La ligne en elle-même, précise-t-elle, n’existe pas dans le monde observable. La ligne est une convention figurative. » (2010, 90)

La ligne abstraite

En résumé, si la ligne géométrique est la marque de la raison, alors le contour s’apparente plus à une construction culturelle : l’expression visible d’un processus par lequel l’esprit, selon un paradigme anthropologique éculé, divise de manière plus ou moins arbitraire le continuum de la nature en des objets distincts qui peuvent être identifiés et nommés. Les lignes de ces puzzles pour enfants bien connus, dont le but est de relier des points, parviennent à être à la fois géométriques et organiques, car en même temps qu’ils relient des points, ils dessinent le contour d’objets. Si les géomètres ne sont pas des enfants qui relient des points, eux dessinent des cartes et, ainsi, le contour des rives et des côtes. Or les lignes de ce maillage, comme les traînées de bave des limaces ou encore la trajectoire des tempêtes, ne sont ni des contours, ni des connecteurs d’un point à un autre. À mes yeux, elles semblent pourtant bien réelles et toutes naturelles. Si nous acceptons que la marque d’un crayon à papier forme une ligne, alors pourquoi ne pouvons-nous pas accepter la même chose de la traînée d’une limace sur une dalle ? Il existe forcément des lignes dans le monde observable, car elles sont de toute évidence bien là. Pour quelles raisons concevables pouvons-nous donc dire qu’elles sont abstraites ?

Une réponse possible peut se trouver dans les travaux du grand pionnier de l’art abstrait moderne, Wassily Kandinsky. Dans son essai Du Spirituel dans l’art, Kandinsky insiste sur le fait que l’abstraction ne signifie pas vider une œuvre de tout son contenu afin de n’y laisser qu’un contour vide ou qu’une forme purement géométrique. Au contraire, cela signifie retirer tous ces éléments figuratifs qui se réfèrent uniquement au côté externe des choses (donc leur apparence physique) afin de révéler ce qu’il nomme « la nécessité intérieure » (2006). Il entend par là la force vitale qui les anime et qui, puisqu’elle nous anime nous aussi, nous permet de ne faire qu’un et de ressentir de l’intérieur leurs affects et leurs pulsations.

Dans un charmant croquis de 1935, Kandinsky nous demande d’envisager les similarités et les différences entre une ligne et un poisson (2006). Ils ont en effet certaines choses en commun : tous deux sont animés par des forces intérieures qui s’expriment par la qualité linéaire de leur mouvement. Un poisson nageant à toute allure peut être une ligne. Pourtant, le poisson demeure une créature du monde extérieur – un monde d’organismes et de leurs environnements – et son existence dépend de ce monde. La ligne, à l’inverse, n’en dépend pas. La ligne n’est pas plus, pas moins, que la vie elle-même. C’est pour cela, explique Kandinsky, qu’il préfère la ligne au poisson, du moins dans son tableau. Et c’est également pour cela que Deleuze et Guattari, dans la continuité de Kandinsky, peuvent dire d’une ligne « qu’elle ne délimite rien, qu’elle ne cerne plus aucun contour, qu’elle ne va plus d’un point à un autre, mais passe entre les points, […] sans dehors ni dedans, sans forme ni fond, sans commencement ni fin, aussi vivante qu’une variation continue », qu’elle est abstraite (Deleuze et Guattari 1980, p .621).

Telle est la ligne du courant de la rivière, ou celle des flux et reflux de la marée, aussi distincte des rives et des côtes reportées sur les plans d’un cartographe. Avec des paroles attribuées à Leonard de Vinci, Merleau-Ponty écrit que le secret pour dessiner tout ce que l’on veut est de découvrir « la manière particulière dont se dirige à travers toute son étendue […] une certaine ligne flexueuse qui est comme son axe générateur ». Une telle ligne, continue-t-il, n’est ni ici ou là, ni à cet endroit ou à un autre, mais « toujours entre ou derrière ce que l’on fixe » (1964, 74). On pourrait presque considérer ligne comme un verbe, et dire que lorsqu’une chose grandit – lorsqu’elle se met en avant, lorsqu’elle veut se montrer, comme le dirait le peintre Paul Klee– elle ligne (Klee 1961, 76).

Les lignes disgracieuses

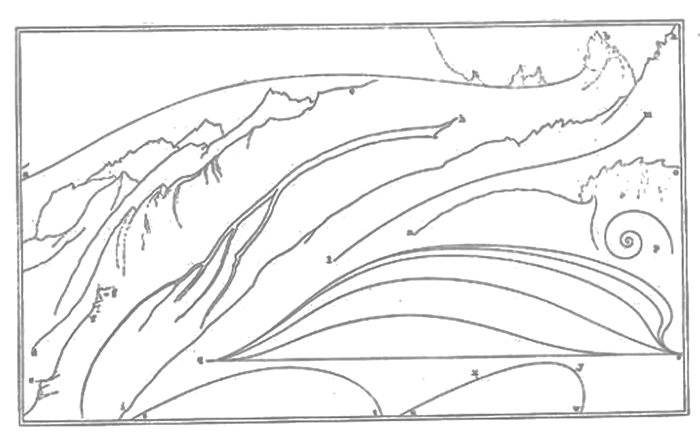
Cette idée serait certainement en accord avec l’opinion du critique du XIXe siècle John Ruskin. Dans son imposant recueil Les pierres de Venise, divisé en trois volumes (1851-53), Ruskin réunit une collection de ce qu’il appelle « lignes abstraites » en un unique dessin, où il combine ses observations des choses grandes et petites, d’un glacier et d’une crête de montagne, en passant par une branche d’épinette, jusqu’à une feuille de saule et une coquille de nautilus. Dans tous les cas, affirme-t-il, la ligne « exprime une action ou une force quelconque » (1903, 268). Ces lignes d’action et de force, comme il l’explique ensuite dans son traité de 1857, The Elements of Drawing, se discernent « chez l’animal dans son mouvement, l’arbre dans sa croissance, le nuage dans son cours, la montagne dans son usure ». Il conseille donc le novice : « chaque fois que vous regardez une forme, essayez toujours de voir en elle les lignes qui ont eu du pouvoir sur son destin passé et qui auront le pouvoir sur son avenir. Ce sont ses lignes disgracieuses ; veillez à bien les repérer, qu’importe que vous manquiez le reste. » (1904, 91)

Figure 1

Les lignes abstraites de Ruskin, planche 7, The Stones of Venice

-> See the list of figures

Selon Ruskin, la sagesse consiste à saisir non seulement la façon dont les choses sont, mais aussi la façon dont elles évoluent, ce qui signifie qu’il faut se concentrer non pas sur les contours de la forme, mais sur les lignes médianes de la force. Il s’agit des lignes disgracieuses. Si elles s’abstraient du réel, ce n’est pas par réduction, mais par l’enregistrement précis de sa variation. Le pouvoir impressionnant de ces lignes réside précisément dans leur capacité à briser les chaînes qui retiennent les choses prisonnières de leur enveloppe, et ainsi à les libérer pour qu’elles atteignent la plénitude de leur être. Telles sont les lignes qui composent le maillage et qui, pour Deleuze et Guattari, constituent la topologie du lisse. Selon eux, il s’agit d’une topologie qui repose non pas sur des points qui pourraient être reliés géométriquement, ni sur des objets qui pourraient être délimités organiquement, mais sur les qualités tactiles et sonores d’un monde de vent et de conditions météorologiques, où aucune ligne n’y sépare la terre et le ciel ; il n’y a pas de distance intermédiaire, de perspective ni de contour (Deleuze et Guattari 1980, 474).

Tel est le monde des limaces et des tempêtes, des sentiers sinueux et des vents tourbillonnants, de la terre et du ciel. Il ne s’agit pas d’un paysage, dans lequel tout est disposé sur le sol comme les accessoires et les décors sur une scène, prêts et dans l’attente du début de la représentation. Dans le paysage, la ligne géométrique définit la disposition des éléments, et la ligne organique délimite la représentation de leurs formes. Dans un tel monde, les lignes ne sont ni imposées par une convention de représentation, ni tracées entre des points. Plutôt, elles s’inscrivent dans le mouvement. Observez la nature, en tant que paysage, et vous n’y verrez aucune ligne. Elles n’existent que dans ses représentations graphiques. Mais observez avec elle, à l’image du ciel et de la terre, joignez-vous aux mouvements de sa formation, et les lignes sont partout. Ce sont les lignes mêmes le long desquelles, nous et les autres organismes, vivons.