Étude cinétique de l’adsorption du rouge de Congo sur une bentonite

Guiza, Sami; Bagane, Mohamed

doi:https://doi.org/10.7202/1014918ar

1. Introduction

L’utilisation des additifs, et plus particulièrement des colorants de synthèse, dans l’industrie alimentaire, pharmaceutique, cosmétique, textiles, papeterie, teinturerie, plastique, etc. ne cesse de croître depuis le début du siècle favorisant ainsi l’éclosion de nombreuses manifestations cliniques. De nombreux travaux ont montré la responsabilité de certains colorants dans plusieurs maladies (AHMED et HAMEED, 2010; GIRARD, 1981; KRIFA et al., 1990; UDDIN et al., 2009; VIMONSES et al., 2009a; ZOHRE et al., 2010). La décoloration des rejets de l´industrie textile, en particulier, est souvent difficile car les colorants organiques ne sont pas dégradés par les traitements conventionnels. En effet, ces produits sont stables aux agents oxydants, aux rayonnements et résistent fortement à la digestion aérobie. En conséquence, les industries qui rejettent des eaux colorées doivent les épurer avant de les évacuer. Pour cela, plusieurs types de traitement ont été proposés par l´osmose inverse, la précipitation/coagulation des matières colorantes, l’adsorption sur charbon actif, et se sont révélés efficaces mais, dans la plupart des cas, très onéreux (BALLAY et BLAIS, 1998; NEVINE, 2008; RODRIGUEZ et al., 2009). Plusieurs auteurs ont étudié l'adsorption de colorants sur divers matériaux naturels tels que les argiles (ALIAN et al., 2010; ALKAN et al., 2007; BAGANE et GUIZA, 2000; BAGANE et GUIZA 2002; BULUT et al., 2008; CHI et EGGLETON, 1999; ÖZDEMIR et al., 2006; GHOSH et BHATTACHAYYA, 2002; GUIZA et BAGANE 2004; GUIZA et al., 2004; LIAN et al., 2009; REYAD et TUTUNJI, 2003; SCHOONHEYDT et JOHNSTON, 2006; VIMONSES et al., 2009b), les matières agricoles : bagasse (MALL et al., 2006), épis de maïs, coquille de noix, etc., et certains rejets industriels : déchets de laine (PERINEAU et al., 1983), cendres volantes, (BHATNAGAR et MINICHA, 2006; EL GEUNDI, 1990) boues de haut fourneaux (ALLEN et KOUMANOVA, 2005) en raison de leurs disponibilités et leurs faibles coûts par rapport au charbon actif.

Le but du présent travail est l´étude de la cinétique d’adsorption d’un colorant acide, le rouge de Congo, sur une argile naturelle, et voir l´effet de la vitesse d´agitation de la solution, la masse d’argile, la concentration initiale en colorant et la granulométrie des particules du solide sur la vitesse de transfert de la matière, puis la recherche d’un modèle mathématique simple, approprié, permettant de mieux comprendre les phénomènes physiques mis en jeu pour mieux concevoir, faire fonctionner, optimiser et contrôler le processus de séparation industrielle. Les modèles simplifiés de diffusion externe sont testés pour décrire le processus d’adsorption, et le coefficient de diffusion externe, k_f, est déterminé au moyen de différents modèles puis corrélé aux variables expérimentales.

2. Théorie

Le mécanisme d’adsorption d’un soluté sur la surface d’un solide peut être décomposé en plusieurs étapes élémentaires successives, chacune d’elles pouvant contrôler le phénomène global dans des conditions données. L’adsorption d’un colorant nécessite (i) son transport du sein de la phase liquide jusqu’au voisinage immédiat de la surface externe du solide : Transport externe; (ii) son transfert à l’intérieur de la particule poreuse : Transport interne, et puis (iii) son adsorption sur les sites. Cette dernière étape est considérée très rapide par rapport au deux premières et, par la suite, sa contribution à la résistance globale au processus d’adsorption est souvent négligée. En conséquence, l'étape limitante du processus peut être soit du type externe, interne ou les deux à la fois.

Les modèles à deux résistances sont très complexes car les équations de transfert sont couplées et la résolution du système d’équations nécessite des méthodes de résolutions numériques.

Il est très difficile de prédire, sans faire des expériences d’adsorption, si l’une ou/et l’autre des résistances (externe ou interne) limite le processus global.

Plusieurs chercheurs ont étudié le problème du transport externe afin de définir les conditions dans lesquelles les hypothèses de ce type de transfert et, par la suite, la méthode du calcul du coefficient dans le film externe, k_f, sont valides (COONEY, 1991; FURUSAWA et SMITH, 1973; GORDON et al., 1980; CHOY et al., 2004; MATHEWS et WEBER, 1976; RADCLFFE et THOMAS, 1982). Dans toutes ces méthodes de calcul de k_f, la résistance dans le film externe est l’étape limitante au début d’adsorption.

Dans le présent travail, pour le calcul de k_f et afin de retenir le modèle qui décrit le mieux la réalité physique du processus d'adsorption, nous avons confronté le problème suivant : Quelle est la meilleure méthode pour le calcul de k_f? Pour cela, cinq méthodes prises de la bibliographie ont été testées, à savoir : a) Les méthodes des pentes initiales (I) (FURUSAWA et SMITH, 1973); b) Mathews et Weber (1976) (II) (CHOY et al., 2004); c) Furusawa pour une isotherme linéaire (III) (FURUSAWA et SMITH, 1973); d) Furusawa et Smith pour une isotherme non linéaire (IV) (FURUSAWA et SMITH, 1973), et e) L’analyse adimensionnelle de Harriott (V) (TIEN, 1994). Notons que les quatre premières méthodes sont basées sur les données expérimentales d’adsorption alors que le dernier est complètement empirique.

2.1 Modèle des pentes initiales

Ce modèle a été utilisé au début dans l’adsorption du benzène sur du charbon actif (FURUSAWA et SMITH, 1973). Dans un adsorbeur parfaitement agité, la concentration du soluté, C_t, à l´instant t, ainsi que celle du solide, m_s, sont supposées uniformes à l´intérieur de la phase liquide. m_s peut être calculée par l´équation suivante :

dans laquelle m et V désignent respectivement la masse du solide et le volume de la phase liquide traités dans l´adsorbeur.

Pour des particules sphériques de diamètre moyen, d_p, de masse volumique apparente, ρ_p, l'aire d´échange externe peut être obtenue comme suit :

La variation, en fonction du temps de la concentration du soluté en phase liquide, est reliée avec le coefficient de transfert externe, k_f (m•s^‑1), par la relation :

C_s est la concentration du soluté en phase liquide à la surface externe des particules. Au début du processus d´adsorption, les concentrations C_s et C_t tendent respectivement vers 0 et C₀ et, par la suite, en négligeant la diffusion interne du soluté, l'équation 3 devient alors :

Donc k_f peut être simplement déterminé à partir de la pente initiale de la courbe C_t/C₀ en fonction du temps. Ensuite, les valeurs de k_f sont corrélées à chaque variable (concentration, vitesse d’agitation, etc.), X, par une équation générale du type (GORDON et EL GEUNDI, 1988) :

B et p sont deux constantes à déterminer à partir des données expérimentales.

2.2 Équation de Mathews et Weber (M & W)

L'intégration de l'équation 3 quand t et C_s tendent vers zéro conduit à :

Dans ces conditions, k_f peut être calculé rapidement à partir de la pente de la droite ln (C_t/C₀) en fonction du temps t.

2.3 Modèle linéaire de Furusawa et Smith

Dans le cas où l’équilibre entre le soluté et le solide est du type linéaire (qe = K_L C_e), l’équation du modèle sera (FURUSAWA et SMITH, 1973) :

À partir de l’ordonnée à l’origine et de la pente droite, m_s K_L/(1 + m_s K_L), et la pente, -((1 + m_s K_L)/m_s K_L) K_f A_p, de la droite ln(C_t/C₀ – 1/(1 + m_s+ K_L)) en fonction du temps, on déduit k_f.

2.4 Modèle non linéaire de Furusawa et Smith

Pour un isotherme d’adsorption du type Langmuir, l’équation de bilan de matière sur une particule solide s’écrit comme suit (FURUSAWA et SMITH, 1973) :

b et K_L sont les paramètres de l’équation de l’isotherme de Langmuir.

Il est évident que le recours aux méthodes numériques appropriées de résolution des équations différentielles est inévitable si on veut déterminer k_f à partir de l’équation 8.

Pour cela, un programme Matlab 7.0 (KHARAB et UENTHER, 2006) de résolution des équations différentielles d'ordre 1 combiné à un programme d'optimisation des coefficients sont mis à profit pour déterminer k_f.

2.5 Analyse adimensionnelle : Méthode de Harriot

Selon Harriot, le coefficient de transfert de matière entre le liquide et une particule suspendue dans une cuve agitée, k_f peut être calculé à partir de la relation de Tien (TIEN, 1994) :

k_f* est le coefficient de transfert de matière des particules se déplaçant avec leurs vitesses terminales, u_t (m/s), au sein du liquide.

Pour estimer k_f*, Harriot propose l’utilisation de la corrélation de Ranz-Marshall (RANZ et MARSHALL, 1952) ci-après :

Le coefficient de diffusion moléculaire du soluté en phase liquide, D_m, est donné par la relation de Wilk-Chang (TREYBAL, 1981) :

avec ϕ : Facteur d’association solvant-colorant (pour l’eau ϕ = 2,26). (GEANKOPLIS, 2003).

3. Matériel et méthodes

3.1 Adsorbant

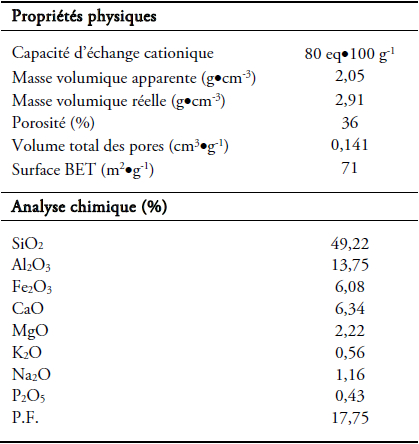
Dans cette étude, l’adsorbant utilisé est un matériau argileux naturel de couleur grisâtre (sans prétraitement physique ou chimique préalable) provenant d’une région d’El Hicha du sud tunisien (gouvernorat de Gabès), Tunisie. Les propriétés physico-chimiques du matériau sont rassemblées dans le tableau 1.

Tableau 1

**Propriétés physico-chimiques du matériau argileux.**

**Physicochemical properties of the clay.**

3.2 Colorant

Le colorant d'étude est le rouge de Congo (RC), un colorant anionique (acide) faisant partie de la classe des azoïques, de formule brute chimique C₃₂H₂₂N₆O₆S₂Na₂, de masse molaire 696,7 g•mol^‑1. La formule structurale de la molécule est portée dans la figure 1. Son utilisation dans l’industrie chimique est multiple. Une étude de son spectre UV visible à des longueurs d’ondes comprises entre 200 et 750 nm, réalisée à l’aide d’un spectrophotomètre type UV-1700 phamaspec Shimadzu, a permis de déterminer la longueur d’onde qui correspond au maximum d’absorbance, λ_max = 500 nm.

Figure 1

**Structure de la molécule de rouge de Congo.**

**Chemical structure of Congo red.**

3.3 Mode opératoire

L'étude est menée à l'échelle de laboratoire en phase liquide dans une cuve agitée « adsorbeur » fonctionnant en batch. Il s'agit d'un réacteur à double enveloppe de volume de 2 litres maintenu à température constante et muni d’un agitateur à pales. Une étude préalable de la stabilité du colorant en fonction du pH a montré qu’il est sous sa forme basique pour un pH de 8,5 et que la capacité d’adsorption de l’argile à cette valeur est maximale (170 mg•g^‑1).

Nous introduisons un litre d’une solution de rouge de Congo à des concentrations allant de 5 à 30 mg•L^‑1, pour différentes masses d’argile variant de 0,02 à 0,15 g et pour des granulométries variant de 0,45 à 1,75 mm.

Les prélèvements effectués au cours du temps permettent de suivre l’évolution de la concentration du colorant restant en solution. Des échantillons de 5 mL sont prélevés puis centrifugés pendant un temps minimum à une vitesse de 2 000 tr•min^‑1. La concentration résiduelle de la solution en rouge de Congo est déterminée à partir d’une courbe d’étalonnage préalable. Nous suivons pour une masse d’argile sèche de 0,1 g par litre de solution, une concentration initiale en colorant de 30 mg•L^‑1, une vitesse d’agitation variable et une granulométrie moyenne de 0,45 mm, l’évolution de la concentration réduite : C_t/C₀ en fonction du temps.

4. Résultats et discussion

4.1 Effet de la vitesse d’agitation

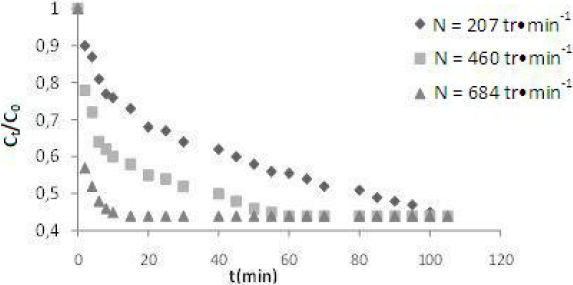
De la figure 2, nous observons que la vitesse d'adsorption dépend de la vitesse d'agitation, N. D’autre part, elle est rapide pour t < 20 min, puis elle se ralentit. Ce phénomène peut être dû à l’augmentation de la vitesse d’agitation qui affecte la résistance au transfert de matière à l’extérieur de la particule argileuse (GORDON et al., 1986; GORDON et al., 1996).

Effet de la vitesse d’agitation sur la cinétique d’adsorption du (RC) C0 = 30 mg•L‑1; m = 0,1 g•L‑1; pH = 8,5; T = 20 °C; N = 460 tr•min‑1. — Figure 2

**Effet de la vitesse d’agitation sur la cinétique d’adsorption du (RC) C₀ = 30 mg•L^‑1; m = 0,1 g•L^‑1; pH = 8,5; T = 20 °C; N = 460 tr•min^‑1.**

**Effect of agitation on the kinetics of (CR) dye adsorption C₀ = 30 mg•L^‑1; m = 0.1 g•L^‑1; pH = 8.5; T = 20°C; N = 460 rpm.**

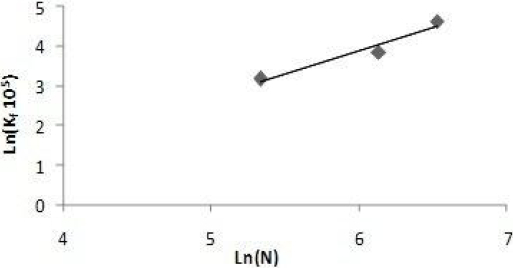
Dans ce qui suit, pour le calcul de k_f, nous allons détailler la méthode des pentes initiales pour sa simplicité et sa rapidité. La figure 3 montre la variation de Log k_f en fonction de Log N, et à partir de laquelle nous avons trouvé la corrélation suivante entre k_f et N : k_f = 1,26 10^‑9 N¹,⁸¹.

Ln (105 kf) en fonction de Ln(N). — Figure 3

**Ln (10⁵ k_f) en fonction de Ln(N).**

**Ln (10⁵ k_f) versus Ln(N).**

4.2 Effet de la masse d’argile

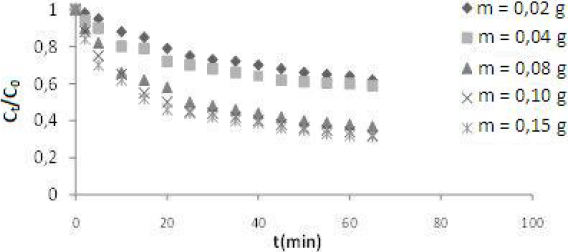
La figure 4 illustre que pour un temps de contact de 20 min, la cinétique d'adsorption devient de plus en plus rapide en augmentant la masse d'argile jusqu'à une masse de 0,1 g puis, au-delà de 60 min, la vitesse de transfert de matière tend vers zéro.

Effet de la masse d’argile sur la cinétique d’adsorption du (RC) C0 = 30 mg•L‑1; pH = 8,5; T = 20 °C; N = 461 tr•min‑1. — Figure 4

**Effet de la masse d’argile sur la cinétique d’adsorption du (RC) C₀ = 30 mg•L^‑1; pH = 8,5; T = 20 °C; N = 461 tr•min^‑1.**

**Effect of clay mass on the kinetics of (CR) dye adsorption C₀ = 30 mg•L^‑1; pH = 8.5; T = 20°C; N = 461 rpm.**

À partir de la figure 5, la corrélation entre k_f et m est : k_f = 26 10^‑5 m⁰,⁸⁸.

Ln (105 kf) en fonction de Ln(m). — Figure 5

**Ln (10⁵ k_f) en fonction de Ln(m).**

**Ln (10⁵ k_f) versus Ln(m).**

Ce résultat indique que le transport du soluté du colorant dans le film externe est contrôlé aussi par la masse d’argile en solution. L’augmentation de la masse d’argile en solution contribue à accroître le coefficient de transfert dans le film liquide.

4.3 Effet de la concentration initiale

La figure 6 montre que l'adsorption est plus rapide à son début qu'à sa fin. En effet, après 45 min, l'adsorption est ralentie : phénomène dû probablement à la résistance au transfert de matière à l'intérieur des particules argileuses. Vers les hautes concentrations, l'écart devient serré et la fraction adsorbée est petite. De plus, le temps nécessaire pour atteindre l’équilibre varie avec la concentration initiale en colorant.

Effet de la concentration initiale en (RC) sur la cinétique d’adsorption m = 0,1 g•L‑1; pH = 8,5; T = 20 °C; N = 461 tr•min‑1. — Figure 6

**Effet de la concentration initiale en (RC) sur la cinétique d’adsorption m = 0,1 g•L^‑1; pH = 8,5; T = 20 °C; N = 461 tr•min^‑1.**

**Effect of initial dye concentration on the kinetics adsorption m = 0.1 g•L^‑1; pH = 8.5; T = 20°C; N = 461 rpm.**

À partir de la figure 7, la corrélation entre k_f et C₀ est : k_f = 17,1 10^‑5 C₀^‑0,66.

Ln (kf•105) versus Ln(C0). — Figure 7

**Ln (k_f•10⁵) *versus* Ln(C₀).**

**Ln (10⁵ k_f) versus Ln(C₀).**

La valeur négative de p indique, pour le couple colorant/argile étudié, que le coefficient de transfert dans le film externe diminue avec la concentration initiale en colorant : en accord avec les observations de GORDON (GORDON et al., 1987; GORDON et EL GEUNDI,1988).

4.4 Effet de la granulométrie de l’argile

La figure 8 montre qu’une augmentation du diamètre du grain de la particule entraîne une diminution de la vitesse de transfert de matière (CHOY et al., 2004).

Effet de la granulométrie de la particule sur la cinétique d’adsorption du (RC) C0 = 30 mg•L‑1; pH = 8,5; T = 20 °C; m = 0,1 g•L‑1; N = 461 tr•min‑1. — Figure 8

**Effet de la granulométrie de la particule sur la cinétique d’adsorption du (RC) C₀ = 30 mg•L^‑1; pH = 8,5; T = 20 °C; m = 0,1 g•L^‑1; N = 461 tr•min^‑1.**

**Effect of particle size on the kinetics of (CR) dye adsorption C₀ = 30 mg•L^‑1; pH = 8.5; T = 20°C; m = 0.1 g•L^‑1; N = 461 rpm.**

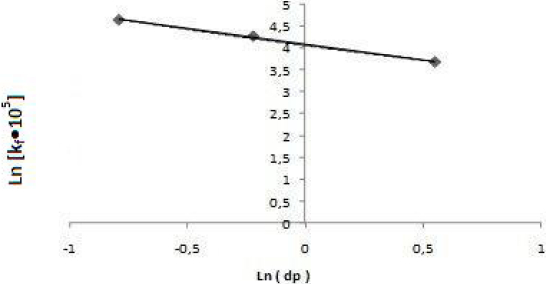
À partir de la figure 9, la corrélation entre k_f et dp est : k_f = 57,9 10^‑5 dp^‑0.0.71.

Ln (kf•105) en fonction de Ln (dp). — Figure 9

**Ln (k_f•10⁵) en fonction de Ln (dp).**

**Ln (10⁵ k_f) en fonction de Ln (dp).**

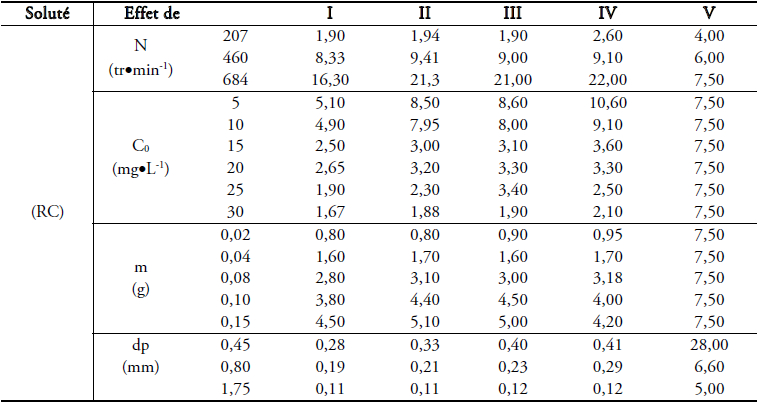
Le résultat définitif et complet du calcul, par les différents modèles de k_f en fonction des paramètres opératoires testés, est porté dans le tableau 2.

Résultats de calcul de kf par les différents modèles (x10‑5 m•s‑1). — Tableau 2

**Résultats de calcul de k_f par les différents modèles (x10^‑5 m•s^‑1).**

**Results of calculation of k_f by the different models (x10^‑5 m•s^‑1).**

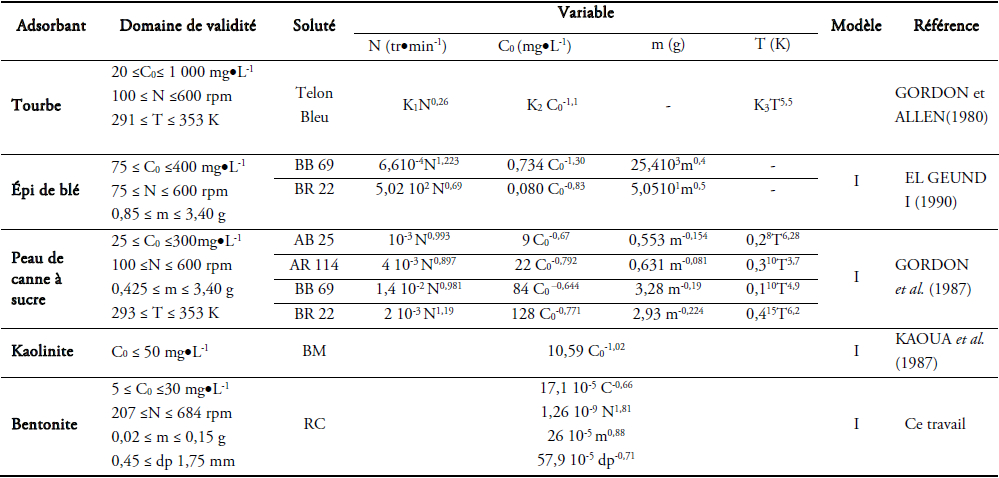
D'autre part, dans le tableau 3, nous avons porté une comparaison entre nos résultats et ceux trouvés dans la bibliographie.

Coefficient de transfert externe (kf 10‑5 m•s‑1) : Comparaison avec la bibliograhie. — Tableau 3

**Coefficient de transfert externe (k_f10^‑5 m•s^‑1) : Comparaison avec la bibliograhie.**

**External mass coefficient (k_f 10^‑5 m•s^‑1): Comparison with the literature.**

Il en ressort les remarques suivantes :

Malgré la diversité des couples étudiés, l'ordre de grandeur de k_f se trouve dans la gamme de 10^‑5 à 10^‑4 m•s^‑1;
Pour certains couples colorant/adsorbant, une variation croissante de k_f avec m et, pour d'autres, une variation plutôt contraire, c'est-à-dire décroissante;
L'effet de la concentration initiale en colorant est négatif : effet contraire à celui de la vitesse d'agitation;
Le calcul de k_f par la méthode d'analyse adimensionnelle ne prévoit pas la variation de ce coefficient avec la concentration initiale et la masse d'adsorbant en solution. D'autre part, les lois de la théorie de la couche limite stipulent que k_f est proportionnel au coefficient de diffusion du soluté dans le milieu environnant et des conditions d'écoulement autour des particules solides. Nous rendons cette variation avec C₀ et m au gradient de concentration établi au début du processus d'adsorption. Malgré ce handicap par cette méthode, l'ordre de grandeur de k_f se trouve toujours dans la marge citée auparavant;
La différence entre les valeurs de k_f calculées par les modèles I et II est très infime. Nous rendons ce résultat au terme m_s*K_L/(1 + m_s*K_L) qui est quasiment égal à 1 dans le cas du couple d’étude;
On peut suggérer l’utilisation du modèle I pour la détermination expérimentale de k_f, et ce, pour sa simplicité et sa rapidité.

5. Conclusion

Dans le présent travail, nous avons étudié la cinétique d'adsorption du rouge de Congo sur une argile naturelle en vue de concevoir un adsorbeur industriel. Il a été démontré en premier volet que le temps d’adsorption optimal est de 30 min. pour une concentration d'argile en solution de 0,25 g•L^‑1, une vitesse d'agitation minimale de 700 tr•min^‑1 et un diamètre moyen des particules de 0,45 mm. Dans ces conditions, le taux d'élimination de la matière polluante est supérieur à 90 %.

Le coefficient de transfert dans la couche limite externe a été déterminé. Ce coefficient varie avec la vitesse d'agitation, la concentration initiale en colorant, la masse d'adsorbant et la granulométrie. Malgré la diversité des couples étudiés, l'ordre de grandeur de k_f se trouve dans la gamme de 10^‑5 à 10^‑4 m•s^‑1.

Nomenclature

A_P	Aire d’échange (m²•m^‑3)
B	Constante
b	Constante de Langmuir (g•L^‑1)
C_r	Concentration du soluté à l’intérieur de la particule (mg•L^‑1)
C₀	Concentration initiale du soluté (mg•L^‑1)
C_e	Concentration à l’équilibre (mg•L^‑1)
C_s	Concentration du soluté à la surface externe du grain (mg•L^‑1)
C_t	Concentration instantanée (mg•L^‑1)
D_m	Coefficient de diffusion moléculaire (m²•s^‑1)
d_p	Diamètre moyen des particules (m)
K_L	Constante de Langmuir (L•g^‑1)
k_f	Coefficient de transfert de matière externe (m•s^‑1)
k_f*	Coefficient de transfert de matière externe à l’équilibre (m•s^‑1)
m	Masse de l’adsorbant (g)
M	Masse molaire moléculaire du solvant (g•mol^‑1)
m_s	Masse d’adsorbant en solution (g•L^‑1)
N	Vitesse d’agitation (tr•min^‑1)
P	Constante
q_t	Quantité adsorbée à l’instant t (mg•g^‑1)
q_e	Quantité adsorbée à l’équilibre (mg•g^‑1)
r	Rayon à l’intérieur des particules (m)
T	Température (K)
t	Temps (s)
u_t	Vitesse terminale (m•s^‑1)
V	Volume de la solution (L)
V_m	Volume molaire (m³•mol^‑1)
ϕ	Facteur d’association solvant-colorant (pour l’eau ϕ = 2,26)
µ	Viscosité dynamique du fluide (kg•m^‑1•s^‑1)
υ	Viscosité cinématique (m²•s^‑1)
ρ_p	Masse volumique de la particule (kg•m^‑3)
ρ	Masse volumique du fluide (kg•m^‑3)

Étude cinétique de l’adsorption du rouge de Congo sur une bentoniteKinetics study of Congo red dye adsorption from aqueous solutions onto bentonite

Résumé

Abstract

1. Introduction