Modélisation du régime de crue en Débit – durée – Fréquence du bassin de l’oued Mekerra dans l’ouest Algérien

Yahiaoui, Abdelhalim; Touaïbia, Bénina; Bouvier, Christophe; Dechemi, Noureddine

doi:https://doi.org/10.7202/1006105ar

1. Introduction

Les inondations constituent l’un des risques naturels les plus importants et affectent quasiment toutes les régions du monde. En Algérie, les inondations sont caractérisées par des montées brutales des oueds, caractéristiques des régions semi-arides. En avril 2007, le débordement de l’oued Mekerra a conduit à un bilan de six morts et six blessés et plus de 300 familles sinistrées.

L’étude des crues qui engendrent des inondations catastrophiques a fait l’objet de nombreuses recherches. Lorsque les données sont disponibles pour un grand nombre d’années, l’analyse fréquentielle des débits (YAHIAOUI, 1997) et les méthodes hydrométéorologiques (GUILLOT et DUBAND, 1967; MARGOUM, 1992) telles que le GRADEX et AGREGEE sont des approches privilégiées pour étudier les régimes de crue et obtenir une prédétermination des crues rares et extrêmes. Cependant, l’analyse fréquentielle ne caractérise en général que les débits de pointe ou débit maximal des crues, et doit être complétée par des traitements visant à déterminer les dépassements de seuils de débits pour différents intervalles de temps jugés critiques au regard de la vulnérabilité du milieu. La prise en compte de ces dépassements de seuils est une information indispensable dans une analyse probabiliste des crues (GILARD, 1998). Lors de l’étude des régimes de crues des bassins versants, il est nécessaire, pour la compréhension des développements ultérieurs, de prêter une attention particulière à la notion de la « durée » qui intervient dans un bon nombre de concepts hydrologiques, la caractérisation de l’écoulement d’un bassin versant, la demande sociale en matière de besoins, de risques de dégâts, etc., toutes choses étroitement liées aux événements hydrologiques temporels (GALÉA et PRUDHOMME, 1997).

Les recherches menées au Cemagref autour de la modélisation régionale ont permis d’aboutir à la mise au point de modèles dits QdF (Débit – durée – Fréquence) des principaux régimes hydrologiques de crue. La modélisation QdF, de plus, s’intéresse aux débits maximums instantanés et aussi à l’analyse des caractéristiques relatives à différentes durées d pour affecter à un débit moyen (volume) maximal VCXd une fréquence. Cette représentation a été initiée par l’Institut d’Hydrologie de Wallingford (NERC, 1975) pour les crues. Cette méthodologie a connu des développements multiples au Cemagref : l’approche QdF de type bassin de référence en crue (GALÉA et PRUDHOMME, 1997) et en étiage (GALÉA et al., 1997), et récemment le modèle QdF convergent (GALEA et al., 2000, JAVELLE, 2001 et JAVELLE et al., 2002). Les courbes QdF peuvent être exploitées pour construire des hydrogrammes de projet (SAUQUET et al., 2004) qui présentent des caractéristiques en débit homogènes en fréquence.

Les notions de base et concepts à l’origine de la modélisation QdF ont été présentés par OBERLIN et al., (1989). L’application de cette modélisation à trois bassins versants : Vandenesse, Soyans et Florac choisis, d’une part, pour leur diversité hydro-climatologique et, d’autre part, pour la disponibilité de l’information hydrologique, permet de définir une typologie régionale des régimes d’écoulement, ce qui lui confère une large représentativité spatiale (GALÉA et PRUDHOMME, 1997). Il a ainsi été montré que les régimes de crue pouvaient être convenablement décrits à l’aide des trois modèles régionaux de Vandenesse, Soyans et de Florac, les noms des bassins représentatifs retenus pour chacune des régions en question. D’autres études ont cherché à généraliser la modélisation QdF, soit d’un point de vue conceptuel (JAVELLE, 2001), soit d’un point de vue géographique, en testant la méthode dans d’autres régions (MEUNIER, 2001).

L’objectif de cet article est de déterminer le modèle QdF de type bassin de référence aux crues du bassin versant de l’oued Mekerra dans l’Ouest algérien en zone semi-aride. On cherchera tout d’abord à évaluer l’adéquation de ces caractéristiques à différents modèles régionaux, notamment à ceux établis en zone méditerranéenne, afin de fournir un outil exploitable dans l’étude de l’aléa et de la vulnérabilité sur d’autres sites algériens.

On déterminera les courbes QdF locales à partir d’ajustements statistiques adéquats réalisés sur les séries de débits moyens (volumes) caractéristiques VCXd de durée d. On comparera les résultats obtenus en matière de quantiles aux quantiles issus des différents modèles QdF de type bassin de référence établis suivant les caractéristiques locales des écoulements et des modèles régionaux définis en France. On conclura sur l’appartenance du bassin versant de l’oued Mekerra à un bassin de référence pour telle ou telle période de retour.

2. La zone d'étude et les données disponibles

2.1 Le bassin versant de l’oued Mekerra

La wilaya de Sidi-Bel-Abbès subit fréquemment des précipitations torrentielles qui se traduisent par des inondations catastrophiques et meurtrières. Les inondations du 2 octobre 1994 et juillet 2000 qui ont touché la ville de Sidi-Bel-Abbès et celle d’avril 2007 à Moulay Slissen (44 km au sud du chef-lieu de la wilaya) sont des exemples où il y a eu des pertes humaines et des dégâts matériels très importants.

Le bassin versant de l’oued Mekerra fait partie du grand bassin versant de la Mecta dans le Nord-Ouest Algérien (Figure 1). Il se trouve à environ 400 km à l’ouest d’Alger, entre 0° 30’ et 1° de longitude O et entre 34° 20’ et 35° 15’ de latitude N. Il couvre une superficie de 3 000 km² environ, qui développe un talweg d’une longueur de 115 km, qui prend sa source dans les hauts-plateaux à Ras El Ma, jusqu’à la ville de Sidi-Bel-Abbès, en traversant une agglomération assez encaissée en amont dans les terrasses fluviales où les débordements des écoulements ne causent aucun dégât considérable. Le cours d’eau débouche en aval dans la plaine alluviale dont la pente ne dépasse que rarement les 0,2 % engendrant des vitesses d’écoulement relativement faibles, causant ainsi des dépôts qui obturent pratiquement le lit du cours d’eau.

Le bassin versant de l’oued Mekerra est soumis à un climat semi-aride caractérisé par des précipitations très irrégulières occasionnant d’importantes crues dont les effets se font ressentir dans l’agglomération de Sidi-Bel-Abbès. La précipitation maximale annuelle décennale à la station pluviométrique de Sidi-Bel-Abbès est de 141 mm.

2.2 Acquisition des données

Pour étudier le régime de crue du bassin versant de l’oued Mekerra, les données hydrométriques disponibles relatives à la station hydrométrique de Sidi-Bel-Abbès (code 110301) qui existe à l’exutoire du bassin (Figure 1), sont les crues observées sous forme d’hydrogramme à pas de temps horaires, et les débits instantanés maxima annuels QIXA, pour une période d’observation couvrant les années hydrologiques de 1947-48 à 1960-61, de 1968-69 à 1970-71 et de 1974-75 à 1999-2000, soit 46 ans. Ces données ont été fournies par l’Agence Nationale des Ressources Hydrauliques (ANRH) d’Alger.

La série des QIXA possède une moyenne arithmétique de 46,7 m³•s^-1 et un écart-type de 48,4 m³•s^-1, et suivant les tests relatifs à l’échantillonnage de GRUBBS et BECK (1972), MANN et WHITNEY (1947) et de WALD et WOLFOWITZ (1943), la série des QIXA est indépendante, homogène, et ne présente aucune singularité dans ses éléments.

3. Indices et débits caractéristiques

Le concept de la modélisation QdF (Débit – durée – Fréquence) a été établi sur des bases objectives (GALEA et PRUDHOMME, 1993, 1997) et son extension à des bassins versants non jaugés fournit une description fréquentielle théorique multi-durée des quantiles de crue. Elle s’intéresse essentiellement à deux variables hydrologiques représentatives du régime de crue d’un bassin extraites de la chronique annuelle des débits Q(t). En plus des variables hydrologiques, deux indices du régime de crue du bassin versant sont essentiels à déterminer, à savoir le débit instantané maximal annuel décennal QIXA10 et la durée caractéristique de crue du bassin versant D.

3.1 Estimation du QIXA10

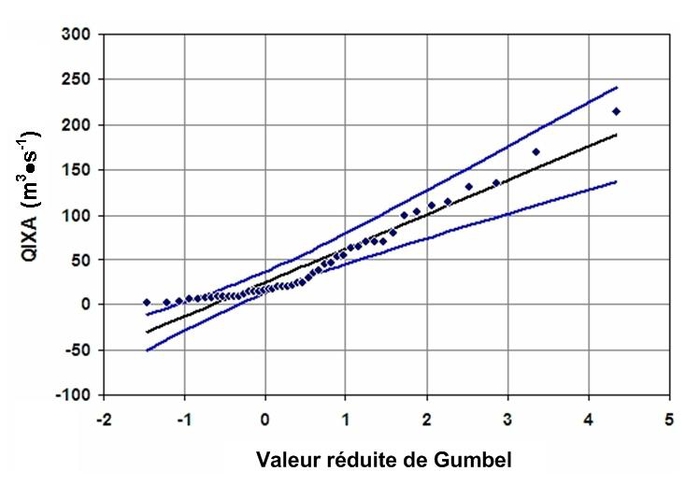
L’ajustement statistique de la série des débits instantanés maximums annuels QIXA à la loi de Gumbel (Figure 2) est adéquat selon les tests d’adéquations (PPC, KS et RMSD). QIXA10 n’est autre qu’une estimation suivant cet ajustement du quantile de débit pour la période de retour décennale, qui vaut dans le cas de l’oued Mekerra 110 m³•s^-1.

3.2 Détermination de la durée caractéristique de crue du bassin versant D

Nous retiendrons comme définition de la durée caractéristique d’une crue d_s la durée pendant laquelle la moitié du débit de pointe Q_s est continument dépassée.

Pour chaque crue observée et enregistrée au niveau de la station hydrométrique de Sidi-Bel-Abbès, sa durée caractéristique d_s et son débit de pointe Q_s ont été déterminés. Dans un plan (Q_s,d_s), la durée caractéristique de crue du bassin versant D au sens de la méthode de SOCOSE (CTGREF et al., 1980-1982) est définie comme étant la valeur de la médiane conditionnelle des d_s pour la valeur du débit instantané maximal annuel décennal QIXA10 correspondant (Figure 3). Pour le cas du bassin versant de l’oued Mekerra, la durée caractéristique de la crue est estimée à dix heures.

Si, dans la méthode du Gradex, une seule durée est utilisée voisine de 2D, des études ultérieures (JIN et GALEA, 1990) ont montré une certaine souplesse sur le choix de la durée d de l’intervalle [D/2 , 5 à 6D]. Par conséquent, la valeur de la durée d est choisie dans l’intervalle [5; 50] heures.

À partir de l’hydrogramme continu Q(t) de la chronique annuelle, et pour un intervalle de temps [t₀, t₀+ d], le débit moyen (Volume) caractéristique sur une durée d VCd correspondant au volume d’eau V écoulé pendant la durée d est :

Pour la même durée d, un débit seuil caractéristique dépassé QCd peut être défini, c’est-à-dire :

Le balayage de tout l’hydrogramme Q(t) permet de déterminer, pour chaque durée d incrémentée d’un pas de temps d’une heure, une séquence de débits moyens (Volume) VCd.

Le choix des plus forts débits caractéristiques VCd, qui correspondent aux épisodes de crues de chaque chronique annuelle, permet de former une série des débits moyens (Volumes) caractéristiques sur une durée continue d, maXimal (VCXd) (GILARD, 1998).

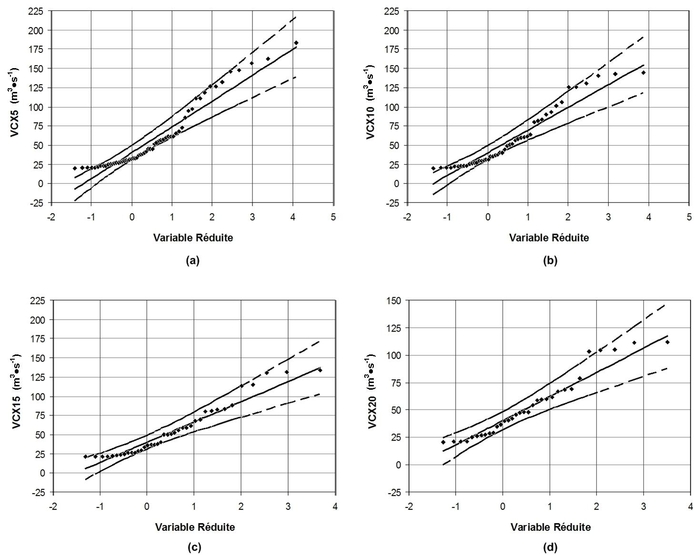
Selon cet échantillonnage, les séries VCXd de l’oued Mekerra (Figure 4) sont indépendantes homogènes, stationnaires et ne présentent pas de singularité, suivant les tests relatifs à l’échantillonnage de GRUBBS et BECK (1972), MANN et WHITNEY (1947) et de WALD et WOLFOWITZ (1943). L’ajustement des séries VCXd selon la loi du Gumbel (Figure 5) est satisfaisante. Les tests d’adéquation : coefficient de corrélation PPC (Probability Plot Correlation) (FILLIBEN, 1975; VOGEL, 1986), de Kolmogorov – Smirnov KS et de la Racine de l’Écart Quadratique Moyen (RMSD), montrent que les séries VCXd proviennent d’une population de Gumbel.

Les quantiles VCXdT de débits moyens (volume) maxima, pour une durée d et de période de retour T, peuvent être facilement calculés. Ils traduisent le Débit – durée – Fréquence (QdF) local issu de l’ajustement statistique à la loi de Gumbel.

Figure 2

**Ajustement et intervalles de confiance (95 %) de la série des débits instantanés maxima annuels QIXA (Débit (Q) Instantané maXima Annuel)**

**Fitting and 95% confidence limits of the annual instantaneous maxima flow sample (QIXA)**

Figure 3

**Estimation de la durée caractéristique de crue du bassin versant de l’oued Mekerra**

**Estimation of the characteristic flood duration of the oued Mekerra catchment**

Figure 4

**Caractéristiques principales des séries des débits moyens (Volume) maxima VCXd (Débit moyen (Volume) Cractéristique maXimal de durée d) de l’oued Mekerra**

**Principal characteristics of the maxima mean flow samples (VCXd) of oued Mekerra**

Figure 5

**Ajustement de la loi de Gumbel aux séries des débits moyens maxima VCXd (Débit moyen (Volume) Cractéristique maXimal de durée d) de durées d = 5, 10, 15 et 20 h.**

**Fitting of the Gumbel distribution to the maxima mean flow samples (VCXd) with d =5, 10, 15 & 20 h.**

4. Application des modèles QdF de type bassin de référence

Un modèle QdF de type bassin de référence permet de traduire sous une forme synthétique opérationnelle la grande variabilité spatio-temporelle des débits VCXd d’un bassin versant, observés ou non (GALEA et PRUDHOMME, 1994). La représentation formelle des modèles QdF en VCX ( est :

Pour 0,5 ≤ T(an) ≤ 20 : généralisation d’une loi exponentielle à deux paramètres adaptée aux valeurs extrêmes, en fonction de d/D et QIXA10 :

Pour 20 < T(an) ≤ 1 000 : généralisation de la forme d’extrapolation du gradex esthétique par le gradex des pluies maximales (MICHEL, 1982) en fonction de d/D et QIXA10 :

Avec, VCX10d, le quantile décennal du débit volume est obtenu à partir de l’équation 3.

A_q, B et A_p sont respectivement le gradex des débits, le paramètre de position de la loi exponentielle et le gradex des pluies; ils sont explicités en fonction de d/D par :

Pour déterminer x₁, x₂,…,x₉, trois bassins versants ont été choisis comportant une longue série de données de qualité à pas de temps variables et représentant des régimes constatés. Ces bassins permettent d’aborder une typologie des régimes de crue. Il s’agit de GILARD (1998) :

station de la Dragne à Vandenesse, région Bourgogne;
station du Roubion à Soyans, région Rhône-Alpes;
station de la Mimente à Florac, région Languedoc-Roussillon.

Ces stations ont été choisies par le Cemagref (GILARD, 1998) pour la qualité et la fiabilité de leurs données, et en raison du contexte hydrométéorologique auquel elles appartiennent. Le modèle de Vandenesse est représenté par une station placée largement sous influence océanique. Le modèle de Soyans s’appuie sur une station située un peu à l’écart du sillon rhodanien et il prend en compte des influences plus continentales. Quant au modèle de Florac, il s’appuie sur une station placée sous influence méditerranéenne.

Suivant la disponibilité des données hydro-pluviométriques au niveau des trois bassins versants (Vandenesse, Soyans et Florac), les paramètres x₁,x₂,x₃,…,x₉ ont été définis pour chaque modèle QdF en VCX (Tableau 1).

Entre les quantiles VCXdT estimés localement par la distribution de Gumbel et les VCXdT issus du modèle QdF de type bassin de référence, l’illustration graphique pour comparer ces quantiles (Figure 6) permet dans un premier lieu de localiser le bassin versant de l’oued Mekerra pour telle ou telle période de retour par rapport aux bassins versants (Vandenesse, Soyans et Florac).

5. Choix du modèle QdF de type bassin de référence

Vu l’indisponibilité des gradex des pluies pour différentes durées, les performances de l’un des modèles QdF de type bassin de référence sont évaluées dans un cadre utilisant le calage-validation. Deux critères ont été utilisés pour telle ou telle période de retour :

- Critère de Nash (Figure 7) (NASH et SUTCLIFFE, 1970). Le critère de Nash peut varier de ∞ à 1. La valeur optimale est 1 (calage parfait). Une valeur supérieure à 0,7 est habituellement considérée comme satisfaisante. Ce critère est exprimé par :

où :

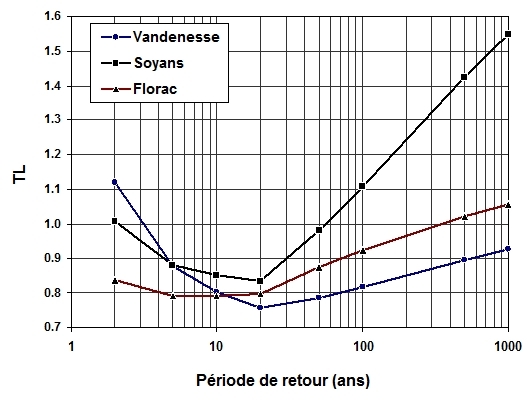
- Critère de la tangente du droit linéaire (Figure 8), c’est-à-dire, si les éléments du modèle QdF de type bassin de référence et leurs homologues dans le QdF issu de l’ajustement statistique appartient à la première bissectrice, si cette tangente tend vers 1, le modèle QdF de référence est accepté. Ce critère est exprimé par :

Les résultats de ces deux critères (Figures 7 et 8) montrent que le modèle QdF Soyans est meilleur dans le domaine des fréquences observables (0,5 ≤ T(an) ≤ 100), alors que dans le domaine des fréquences rares (T(an) > 100 ans), le modèle QdF de Florac est meilleur que le Soyans, et entre les deux modèles et suivant ces deux critères, il y a une légère différence dans le domaine des fréquences observables. En plus de ces critères, il y a aussi le contexte hydroclimatologique qui se trouve le bassin versant de l’oued Mekerra et la situation géographique de la station de Sidi-Bel-Abbès qui se trouve sous l’influence d’un climat méditerranéen, ce qui nous ramène à dire que le modèle QdF de référence de Florac est le modèle le plus adapté pour la prédétermination des crues de l’oued Mekerra.

Paramètres xi des trois modèles QdF de référence en débits moyens maxima VCX (Débit moyen (Volume) Caractéristique maXimal). — Tableau 1

**Paramètres x_i des trois modèles QdF de référence en débits moyens maxima VCX (Débit moyen (Volume) Caractéristique maXimal).**

**Parameters x_i of the three reference QdF models of maxima mean flow (VCX).**

Figure 6

**Comparaison entre les courbes QdF de référence et locales en débits moyens maxima VCXd (Débit moyen (Volume) Cractéristique maXimal de durée d) de l’oued Mekerra**

**Comparison between reference QdF curves and the local QdF for oued Mekerra**

Figure 7

**Coefficient de Nash entre les VCX (Débit moyen (Volume) Caractéristique maXimal ) estimés localement et les VCX estimés par un modèle QdF de référence**

**Nash coefficient between local VCX calculated by a statistical method and VCX calculated by the QdF model**

Figure 8

**Critère de la tangente de la droite linéaire**

**Tangent criterion**

6. Modèle QdF en débits seuils

Les modèles QdF en débits seuils (QCX) répondent directement aux besoins hydrologiques d’une modélisation hydraulique intégrée du bassin versant. En effet, pour répondre à la demande sociale, notamment en matière de lutte contre les inondations, il est nécessaire de considérer les notions classiques de fréquence, mais aussi de durée de submersion ou de hauteur maximale. Toutes ces notions doivent être comparées entre elles pour que l’on puisse définir des objectifs de protection clairs et concevoir des aménagements capables de prendre en compte l’ensemble de ces demandes (GILARD et al., 1993).

Les modèles QdF en débits seuils rendent possible une telle comparaison, puisqu’ils permettent de transformer toutes ces demandes en une variable comparable, correspondant à la période de retour d’une crue de durée nulle, autrement dit la période de retour du débit de pointe correspondant à l’objectif de protection. Par ailleurs, les entrées des modèles hydrauliques transitoires nécessitent des hydrogrammes de crue. Par cohérence avec le traitement des objectifs de protection, il est nécessaire d’établir, pour la modélisation hydraulique des aléas, des Hydrogrammes Synthétiques Mono-Fréquences (HSMF) qui répondent à cette attente.

D’après GALEA et PRUDHOMME (1993), l’élaboration des modèles QdF en débits seuils suit la même démarche que celle mise en ouvre pour les débits moyens (volumes) VCXd, mais il est clair que les modèles QdF en VCX et en QCX sont définis pour le même bassin versant de référence, car les volumes qu’ils définissent sont cohérents avec les débits seuils. On admettra que l’on peut utiliser le modèle QdF en VCX, dans les mêmes conditions, pour le modèle QdF en QCX.

Le modèle QdF en QCX est identique au modèle QdF en VCX, c’est-à-dire que les équations 3 et 4 sont les mêmes, sauf que VCXdT est remplacé par QCXdT et les paramètres x_i (i = 1,…9) prennent les valeurs suivant le tableau 2, ce qui permet d’avoir l’expression du quantile QCXdT comme suit :

Pour 0,5 ≤ T(an) ≤ 20 :

Pour 20 < T(an) ≤ 1 000 :

Avec QCXd10, le quantile décennal du débit seuil est obtenu à partir de l’équation 8.

Les courbes QdF en QCX peuvent être tracées à partir des expressions 8 et 9 de QCXdT (Figure 9).

Paramètres xi du modèle QdF de référence de Florac en débits seuil QCX (Débit (Q) seuil Caractéristique maXimal) — Tableau 2

**Paramètres x_i du modèle QdF de référence de Florac en débits seuil QCX (Débit (Q) seuil Caractéristique maXimal)**

**Parameters x_i of the reference QdF Florac of the QCX**

Figure 9

**Courbes QdF en débits seuils QCX (Débit (Q) seuil Caractéristique maXimal) du bassin versant de l’oued Mekerra**

**QdF curves of QCX for the oued Mekerra catchment**

7. Conclusion

En vue d’étudier les inondations de l’oued Mekerra, la modélisation QdF du régime de crue a été établie suivant les quantiles de débits volumes issus d’un ajustement statistique qui sont comparés, en tenant compte des caractéristiques du régime de crue du bassin versant (QIXA10 et D), aux différents quantiles homologues issus des modèles QdF de type bassin de référence de Vandenesse Florac et de Soyans développés au Cemagref.

Les séries VCXd obtenues par un échantillonnage qui tient compte des épisodes de crues observées sur l’ensemble des chroniques annuelles ont permis un ajustement satisfaisant de la loi exponentielle à deux paramètres. Pour l’application de modèles QdF régionaux de type bassin de référence (Vandenesse, Soyans et Florac), les deux paramètres locaux essentiels, le débit instantané maximal annuel décennal QIXA10 et la durée caractéristique de crue du bassin versant D, ont pu être estimés à partir des données locales.

Suivant les critères de Nash et de la tangente de la droite linéaire, d’une part, et le contexte hydroclimatologique, d’autre part, le modèle QdF de Florac est plus adapté, ce qui permet de synthétiser et consolider les connaissances issues tant des observations hydrométriques que des simulations par des modèles conceptuels.

On pourra utiliser ces résultats pour déterminer le régime de crue sur le bassin versant de l’oued Mekerra et aux bassins versants et sous-bassins avoisinants, dans le cas où il y a une insuffisance de mesures, ou des courbes de tarages (GALEA et al., 1997). Cependant, il est nécessaire d’élargir cette étude à d’autres bassins pour lesquels on dispose de longues chroniques de débits, afin de construire un modèle régional plus précis et adapté au contexte algérien.

La détermination du modèle QdF du bassin versant de l’oued Mekerra sur la base de l’étude des VCX et, par conséquent, la détermination du modèle QdF en QCX qui permet de calculer les Hydrogrammes Synthétiques Mono – Fréquences, fournit un outil très important pour l’étude et la prédétermination de l’aléa et la vulnérabilité qui sont les facteurs essentiels du risque des inondations.

Modélisation du régime de crue en Débit – durée – Fréquence du bassin de l’oued Mekerra dans l’ouest AlgérienWatershed flood regime modelling with the Flow-duration-Frequency approach as applied to the oued Mekerra catchment in western Algeria

Résumé

Abstract

1. Introduction