Article body

1. Introduction

La caractérisation des conditions d’écoulement des eaux souterraines et de transport de soluté dans les réseaux de fractures a fait l’objet de nombreuses études depuis les années 80, à partir de différentes approches théoriques, numériques ou mêmes expérimentales (ANDERSSON et THUNVI, 1986; DAVY et al., 1990; DE MARSILY, 1985; PONTLEVOY et al., 2004).

Dans les pays occidentaux, l’intérêt porté à la modélisation des milieux fracturés, au cours de ces dernières années, a été le plus souvent orienté vers la recherche de sites de stockage de déchets radioactifs. Les nombreux travaux conduits sur les sites de Stripa en Suède (DERSHOWITZ et al., 1991; NERETNIEKS, 1993), de Fanay-Augères en France (CACAS et al., 1990), de Mirror Lake (HSIEH et al., 1993) et de Yucca Mountain (WITHERSPOON, 2000) aux États-unis ont contribué à améliorer la connaissance et la compréhension du fonctionnement de ces milieux.

Le sous-sol de l’Afrique de l’Ouest est composé quasi exclusivement de roches de socle qui présentent une perméabilité de fractures. L’étude de ces systèmes aquifères est donc fondamentale, notamment pour le captage des eaux souterraines (BIÉMI, 1992; BOUKARI et GUIRAUD, 1985; JOURDA, 2005; KOUAMÉ, 1999; SAVADOGO, 1984; SAVANÉ, 1997), leur gestion (BASSOLÉ et al., 2001; DEWANDEL et al., 2006; MARÉCHAL et al., 2006) ainsi que leur protection.

Les roches des socles cristallin et cristallophyllien sont intrinsèquement très peu perméables. Les fractures qui les affectent sont à l’origine de la quasi-intégralité de leurs propriétés de perméabilité (perméabilité de fractures). Suivant leur densité, leur taille, leur arrangement dans le milieu et leurs propriétés physiques, les fractures modifient considérablement les propriétés hydrauliques des roches de socle (DARCEL, 2002; DE DREUZY, 2000). En effet, les roches cristallines et cristallophylliennes sont dotées d’une porosité interstitielle très faible; donc, la formation des aquifères n’est possible que par l’action du couple fracturation-altération (DEWANDEL et al., 2006 ). Sur les terrains granitiques, la couche altérée la plus superficielle (saprolite) présente une porosité significative et une faible perméabilité. Lorsqu’elle est saturée en eau, elle forme un réservoir capacitif (MARÉCHAL et al., 2004). Le niveau fracturé-altéré sous-jacent, qui résulte lui aussi des processus d’altération, est un milieu anisotrope et hétérogène. Il est caractérisé par une fracturation horizontale dense dans les premiers mètres et une décroissance de la densité des fractures subhorizontales et subverticales en fonction de la profondeur. Ses propriétés hydrodynamiques sont contrôlées par les processus d’altération (DEWANDEL et al., 2006; MARÉCHAL et al., 2004). Cet horizon fracturé-altéré joue un rôle transmissif. Lorsqu’il est capté par forage, il permet en général de disposer de ressources en eau en toute saison (BIÉMI, 1992). Les discontinuités préexistantes du socle (filons, anciennes fractures, etc.) sont en général marquées par un approfondissement et une verticalisation de cet horizon fracturé-altéré. Il ressort donc que la fracturation, tant ancienne (filons, fractures, etc.) que plus récente (profils d’altération), constitue l’un des principaux paramètres de caractérisation des systèmes hydrogéologiques en milieu de socle.

La structure des réseaux de fractures et leurs caractéristiques hydrodynamiques, sont les principaux éléments qui sont susceptibles d’expliquer le fonctionnement hydraulique des milieux fracturés (BOUR, 1997; DAVY et al., 1990). L’hétérogénéité et l’anisotropie qui les caractérisent ne permettent pas toujours d’utiliser une approche de type milieu continu pour la modélisation des écoulements d’eau souterraine (SNOW, 1969). Dans ce cas, l’approche discrète peut être appropriée. Se pose alors le problème de la connaissance et de la description détaillée de la structure du réseau de fractures, limite à laquelle se heurte l’approche déterministe, car les réseaux de fractures ne peuvent être décrits, dans la plupart des cas, que de façon partielle. Pour pallier à ce manque de connaissance, une représentation statistique des propriétés du milieu s’avère nécessaire (de MARSILY, 1985). La géométrie des réseaux est alors décrite par les distributions statistiques des paramètres géométriques des fractures et les propriétés hydrauliques sont estimées à partir du comportement moyen calculé sur de multiples réalisations (DE DREUZY, 2000).

L’objectif du présent travail est l’exploitation des données issues de la télédétection dans un modèle hydrogéologique à fractures discrètes pour déterminer les propriétés hydrogéologiques du socle archéen de Touba (Côte d’Ivoire). À partir d’images satellitaires Landsat-TM et d’investigations géologiques de terrain, la carte du réseau de fractures est établie. Le traitement de ces données, à partir d’outils statistiques, permet d’obtenir une description paramétrique du réseau de fractures (distribution des longueurs, densité, position) et de définir le régime de connectivité. L’analyse de la connectivité permet de calculer les propriétés hydrauliques (perméabilité). Une modélisation mathématique est ensuite effectuée au moyen d’un modèle à fractures discrètes. Enfin, les résultats sont comparés aux données hydrogéologiques de terrain.

2. Présentation de la zone d’étude

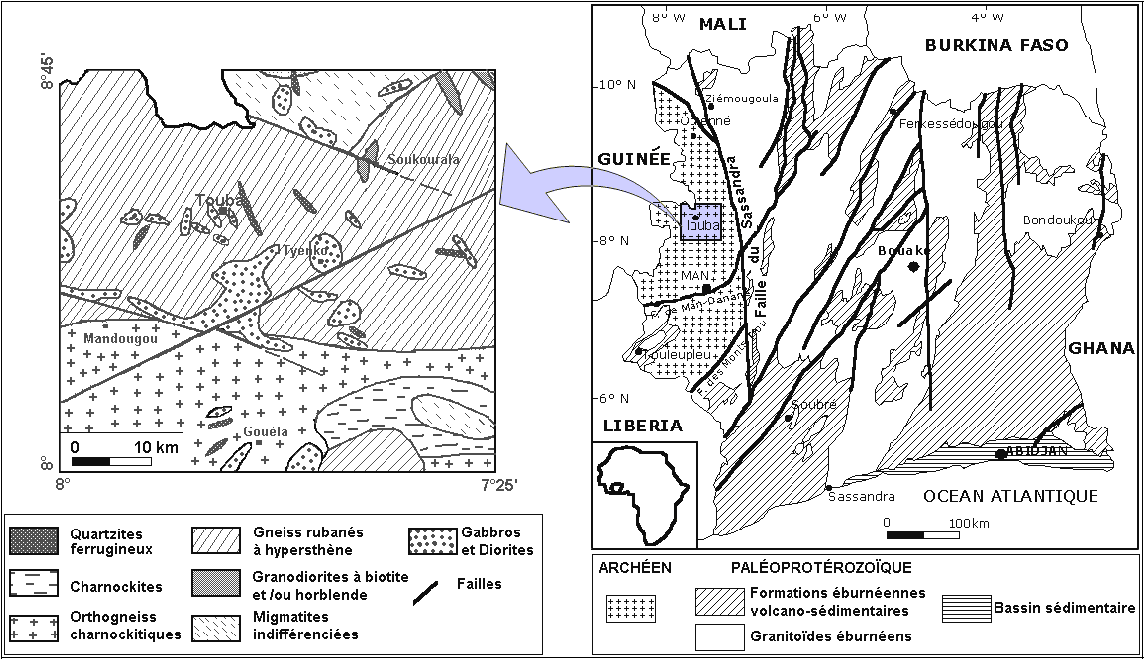
La région d’étude est située au nord-ouest de la Côte d’Ivoire (Figure 1). Elle est soumise à un climat tropical de transition, caractérisé par une pluviométrie moyenne de 1 500 mm•an‑1. Le relief est formé de plateaux, d’altitude moyenne égale à 550 m. Quelques monts isolés culminent entre 600 et 750 m et présentent des modelés aux formes massives, à sommets convexes et aux flancs raides. Le réseau hydrographique est très varié (types parallèle, dendritique et en treillis). Il souligne le plus souvent un contrôle structural. Cette région appartient au domaine archéen de la dorsale de Man (CAMIL, 1984; KOUAMÉLAN, 1996) où les formations géologiques (gneiss para et ortho-dérivés, charnockites, migmatites, quartzites) ont subi les influences des mégacycles orogéniques Léonien (3500‑2900 Ma.) et Libérien (2900‑2500 Ma.). Au plan tectonique, la faille du Sassandra, d’orientation N-S, qui sépare le domaine archéen (Ouest) du domaine paléoprotérozoïque (Est), est la structure la plus importante de l’ouest ivoirien (Figure 1). Cette faille, qui s’étend sur plus de 250 km de long, a une zone de déformation large de plus de 10 km. Au cours de son histoire, cette faille a été en activité à plusieurs reprises, soit de manière dextre, soit de façon senestre (DJRO, 1998; KONÉ et al., 1996). Ces contraintes tectoniques variées ont abouti à la mise en place d’un schéma structural complexe.

Figure 1

Carte géologique de la région de Touba.

Geological map of the Touba region.

Carte géologique de la région de Touba.

-> See the list of figures

La description des systèmes aquifères à partir des sondages hydrogéologiques révèle un aquifère constitué de deux principaux niveaux. Le premier niveau, en surface, est constitué par les altérites (10-15 m d’épaisseur), à fonction essentiellement capacitive, et le second, immédiatement sous-jacent, est constitué par le réseau fracturé-altéré (25-30 m d’épaisseur) à fonction conductrice. Les venues d’eau les plus importantes se situent au sein de la partie la plus superficielle de ce dernier horizon, qu’il est nécessaire d’atteindre lors de l’exécution des ouvrages de captage (BIÉMI, 1992).

En milieu rural, des débits instantanés de l’ordre de 2 m3•h‑1 par forage sont acceptables pour l’approvisionnement en eau potable. Pour les agglomérations de plus grande taille, comme Touba, des débits dépassant les 5 m3•h‑1 sont recherchés.

3. Méthodologie et résultats

3.1 Données utilisées

La base de données géoscientifiques utilisée comporte des images satellitaires Landsat-TM (scène 198-56 acquise le 28/12/1990, en saison sèche), une carte topographique de TOUBA à 1/200 000, une carte géologique à 1/200 000 (DIRECTION DE LA GÉOLOGIE, 1996), des données descriptives des caractéristiques géologiques et hydrauliques des forages (GÉOMINES, 1982) ainsi que des mesures structurales obtenues à partir d’investigations de terrain.

Le traitement numérique des images a été réalisé au Centre Universitaire de Recherche et d’Application en Télédétection (CURAT, Université de Cocody) à l’aide du logiciel ENVI. La modélisation discrète du réseau de fractures est réalisée grâce aux outils développés à l’Université de Rennes 1 (BOUR, 1997; DARCEL, 2002; DAVY et al., 1990; DE DREUZY, 2000).

3.2 Cartographie du réseau de fractures

La cartographie du réseau de fractures du socle archéen de Touba a été réalisée en deux phases : premièrement, le traitement des images Landsat-TM pour l’identification et l’extraction des linéaments, et deuxièmement, la validation structurale grâce aux données géoscientifiques complémentaires. Le terme « linéament » utilisé dans cette étude décrit toute structure ayant un tracé rectiligne ou curviligne (HOBBS, 1904; O’LEARY et al., 1976) et dont l’interprétation a une signification géologique.

Les images Landsat-TM ont été acquises en saison sèche, en l’absence de couverture nuageuse. Elles sont nettes et claires et présentent une radiométrie satisfaisante, facilitant les analyses géologique et structurale.

Après leur correction géométrique, diverses opérations de traitements numériques sont réalisées afin d’identifier et d’extraire les linéaments. Les exemples de travaux réalisés dans l’anti-atlas au Maroc (HIMYARI et al., 2002; MAHMOUD, 1996), dans le socle précambrien en Côte d’Ivoire (BIÉMI, 1992; KOUAMÉ et al., 1999; SAVANÉ, 1997), dans le Bouclier canadien (DESJARDIN et al., 2000), etc. montrent que l’application des filtres (spatiaux et directionnels) facilite l’accentuation des discontinuités litho-structurales assimilables aux linéaments. Les filtres directionnels de matrice 7 x 7 de type Sobel, testés avec succès par KOUAMÉ et al. (1999) pour la cartographie structurale du secteur Man-Danané, situé au sud de Touba, ont été appliqués dans les directions N-S, E-W, NW-SE et NE-SW. Le tableau 1 présente les matrices appliquées dans les directions N-S et E-W.

Tableau 1

Matrice 7 x 7 du filtre de Sobel (directions N-S et E-W).

Seven by seven matrix of Sobel filter (North-South and East-West orientations).

Direction Nord-Sud

Direction Est-Ouest

1

1

1

2

1

1

1

‑1

‑1

‑1

0

1

1

1

1

1

2

3

2

1

1

‑1

‑1

‑2

0

2

1

1

1

2

3

4

3

2

1

‑1

‑2

‑3

0

3

2

1

0

0

0

0

0

0

0

‑2

‑3

‑4

0

4

3

2

‑1

‑2

‑3

‑4

‑3

‑2

‑1

‑1

‑2

‑3

0

3

2

1

‑1

‑1

‑2

‑3

‑2

‑1

‑1

‑1

‑1

‑2

0

2

1

1

‑1

‑1

‑1

‑2

‑1

‑1

‑1

‑1

‑1

‑1

0

1

1

1

-> See the list of tables

Le relevé des linéaments est effectué par interprétation visuelle des bandes TM 3, 4, 5 et 7 rehaussées, des néo-canaux issus des filtrages spatiaux et des images obtenues après l’analyse en composantes principales (Figure 2a). Les différents traitements numériques mettent en évidence les structures géologiques (failles, contacts lithologiques, filons, etc.) de la région de Touba. Sur les images filtrées (Figure 2b), les discontinuités images sont très bien rehaussées et soulignées par les variations brusques de tonalité. L’interprétation visuelle permet d’identifier les linéaments et d’établir la carte détaillée du bâti structural (Figure 3) qui représente les linéaments considérés comme d’origine tectonique.

Figure 2

Images Landsat de la région de Touba : a) deuxième composante de l’Analyse en Composantes Principales; b) discontinuités-images rehaussées par le filtrage NE-SW de Sobel (fenêtre encadrée).

Landsat imagery of the Touba region: a) Second component of Principal Component Analysis; b) Image discontinuities enhanced by Sobel NE-SW filtering (window outline).

Images Landsat de la région de Touba : a) deuxième composante de l’Analyse en Composantes Principales; b) discontinuités-images rehaussées par le filtrage NE-SW de Sobel (fenêtre encadrée).

-> See the list of figures

Figure 3

Carte de linéaments du socle archéen de Touba et rosace directionnelle.

Lineament map of the Touba Achaean basement and directional rosette diagram.

Carte de linéaments du socle archéen de Touba et rosace directionnelle.

-> See the list of figures

La deuxième phase de la cartographie structurale est la validation de la nature structurale des linéaments issus de l’interprétation des images satellitaires. Dans un premier temps, les tracés rectilignes relatifs aux activités anthropiques (routes, pistes, lignes de transport d’énergie) ont été éliminés par un croisement avec les cartes disponibles dans la base de données. Ensuite, les investigations géologiques, réalisées aux cours des travaux antérieurs de cartographie géologique (CAMIL, 1984; DIRECTION DE LA GÉOLOGIE, 1996; KONÉ et al., 1996), ont été utilisées pour être confrontées aux résultats obtenus.

Sur la carte obtenue (Figure 3), les pics directionnels relevés (N 80‑110°, N 60‑70° et N 10‑20°) concordent avec les grandes directions tectoniques relevées dans le domaine archéen de la Côte d’Ivoire (CAMIL, 1984; DJRO, 1998; KONÉ et al., 1996; KOUAMÉ, 1999; LASM, 2000). Les linéaments N 80‑100° (E-W) ont une répartition statistique prépondérante dans la région de Touba, tout comme dans le secteur de la chaîne des Toura (CAMIL, 1984; KOUAMÉ et al., 2006). Ces accidents structuraux sont d’extension kilométrique et sont le plus souvent observés sur les formations charnockitiques et gneissiques. Les observations réalisées à l’affleurement montrent des systèmes de fractures sub-verticales (pendages supérieurs à 80°) dans 80 % des cas et des figures de cisaillements (crochons, queues de recristallisation) exprimant des mouvements dextres ou senestres. La faille E-W, située au sud de la ville de Touba, est un exemple de ce type d’accident.

Les travaux de KONÉ et al. (1996) ont mis en évidence un couloir de transpression de direction N-S, limité par les failles du Sassandra à l’est et de Booko à l’ouest. La déformation transpressive post-archéenne N-S s’est faite par aplatissement et cisaillement et a affecté le socle cristallin de Touba qui présente de nombreux témoins de cette déformation (direction N 10‑20°). Les accidents tectoniques majeurs du Sassandra (DJRO, 1998), de Booko et Kouroumassa (KONÉ et al., 1996) sont orientés dans cette direction.

Les fractures N 60‑70° (NE-SW) marquent l’influence de l’orogenèse éburnéenne (KOUAMÉLAN, 1996). Dans l’ouest de la Côte d’Ivoire, la direction NE-SW, qui est aussi celle des plis isoclinaux affectant les gneiss migmatitiques et les quartzites à magnétite, est l’une des directions considérées comme les plus productives du point de vue hydrogéologique. Les forages captant ces fractures ont des débits forts à très forts (SALEY, 2003).

La densité de fracturation de la région de Touba, et plus globalement du socle archéen de l’ouest de la Côte d’Ivoire, prouve que les effets des événements tectono-métamorphiques des orogenèses léonienne et libérienne sont très importants. En conséquence, le socle a une architecture très fracturée, mise en évidence aussi bien à l’affleurement qu’en imagerie satellitaire, comme c’est le cas à Man-Danané au sud de Touba (KOUAMÉ, 1999) et dans le bassin versant de la Marahoué (BIÉMI, 1992) situé à l’est.

3.3 Caractérisation de la géométrie du réseau de fractures

La détermination des paramètres géométriques du réseau de fractures extrait des images Landsat-TM est basée sur les théories développées par DAVY et al. (1990) qui sont fondées sur des observations de la déformation à l’échelle continentale et sur des expériences analogiques de déformation. Elles interprètent les caractéristiques des réseaux de fractures comme étant fractales et proposent un modèle statistique basé sur une double loi puissance (Équation 1).

où n (l, L) est le nombre de fractures de longueur l dans un sous-système de taille L. L’exposant a caractérise la distribution en loi puissance des longueurs l de fractures dans l’intervalle [lmin, lmax] et l’exposant b est la dimension fractale des barycentres des fractures qui fixe la dépendance d’échelle du nombre de fractures. Le 3e paramètre α est la densité de fractures (nombre de centres de fractures par unité de surface fractale).

L’étude des lois d’échelles dans le réseau de fractures est réalisée par l’analyse de la distribution statistique des longueurs de fractures. L’étude de la distribution des centres de fractures est réalisée par approche fractale.

L’étude de la distribution des longueurs de fractures peut se faire à l’aide de la distribution des fréquences, des fréquences cumulées et de la densité de fréquence. Dans le présent travail, la courbe de densité de fréquence des fractures relevées dans la région de Touba est ajustée à la loi puissance sur un diagramme bi-logarithmique afin de déterminer le paramètre « a », l’exposant de la loi puissance. Une telle loi permet de mieux caractériser la distribution statistique d’un phénomène tel que la fracturation qui se déploie sur des échelles s’étendant sur plusieurs ordres de grandeur (du local au régional).

Concernant le deuxième paramètre caractéristique des lois d’échelle, soit la dimension fractale « D » du réseau de fractures en 2D, deux approches sont le plus souvent utilisées : la méthode de comptage de boîtes ou « Box counting method » (WALSH et WATTERSON, 1993) et la méthode de la répartition spatiale de masses. La première méthode est très sensible aux effets de bords et est mal adaptée aux réseaux de fractures (OUILLON et SORNETTE, 1996). La deuxième méthode a été appliquée dans ce travail. La démarche consiste à assimiler chaque fracture à son centre et à calculer le nombre N(r) de centres de fractures contenus dans des cercles de rayons r réduits progressivement et centrés aléatoirement sur les centres de fractures considérés (BOUR et DAVY, 1997). Cette méthode permet de conserver la notion de fracture discrète en mesurant la dimension fractale sur l’ensemble des barycentres des fractures.

Les travaux de BOUR (1997) montrent que la corrélation spatiale entre les centres de fractures d’un réseau naturel est mieux estimée par la méthode de la fonction de corrélation C2(r) définie par l’équation 2 (HENTSCHEL et PROCACCIA, 1983) :

où 2Np(r) représente le nombre de paires de points dont la distance est inférieure à r et N le nombre total de points du système. La dimension fractale D est déterminée par la pente de la courbe représentative de la fonction de corrélation C2(r), dont les points s’alignent suivant une droite dans un diagramme bi-logarithmique.

Le calcul de la dimension fractale D du réseau permet de déterminer b comme suit : D = b si a > 2, et D = b+2 ‑ a  si a < 2. L’avantage du modèle présenté à l’équation 1 tient au fait qu’il permet de dériver le terme de densité de fracture α, qui fixe le nombre moyen de fractures par unité d’aire « fractale » (DAVY et al., 1990). Ce paramètre, indépendant de l’échelle du système, apparaît robuste et représentatif de la loi d’échelle, car il est maintenu constant quelle que soit la taille du domaine étudié.

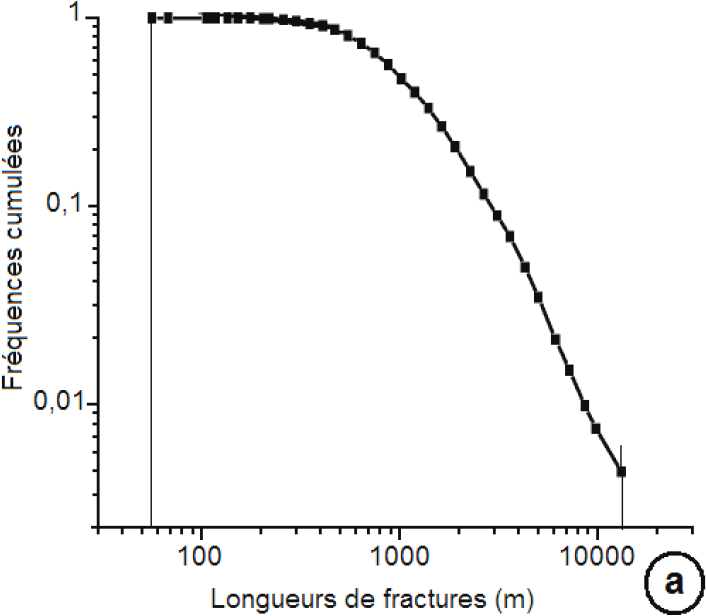
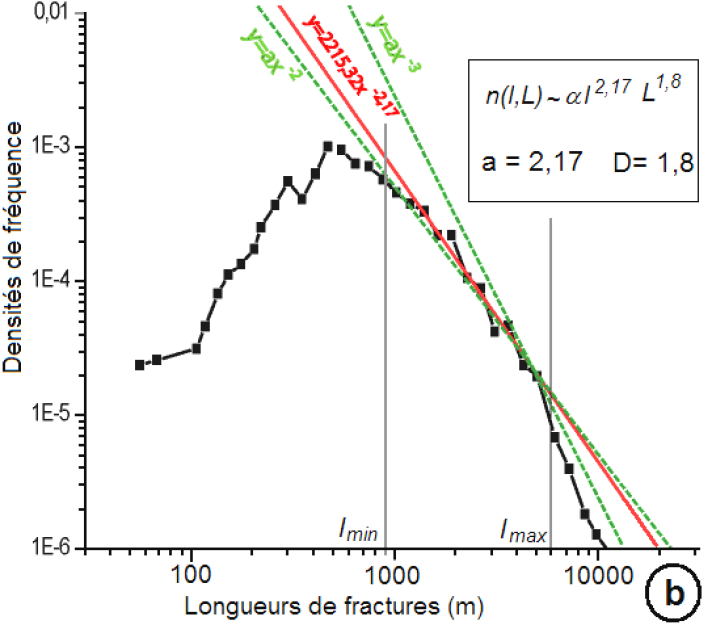
Le réseau de fractures de la région de Touba comporte des fractures de tailles variant de 45 m à 10 000 m, s’échelonnant donc sur deux ordres de grandeurs (Figure 4a). La distribution des densités de fréquence des longueurs de fractures dans un diagramme bi-logarithmique montre une loi puissance sur deux décades. Entre 900 m et 6 000 m, les données expérimentales sont proches de la droite théorique de la loi puissance (Figure 4b) avec un coefficient de corrélation R2 = 0,97. Aux deux extrémités de la distribution, les valeurs expérimentales s’écartent de la loi puissance, en raison des effets liés au sous-échantillonnage des petites fractures (< 900 m) sur les images satellitaires (résolution spatiale, filtrage spatial) et à l’altération de la distribution des grandes fractures (> 6 000 m). Ces dernières sont tronquées à cause de la taille du domaine étudié. La fracture la plus longue est de 10 000 m alors que la droite théorique extrapolée donne des valeurs de l’ordre de 20 000 m. Selon ODLING (1997), la meilleure façon de caractériser la distribution des longueurs d’un réseau de fractures serait donc de faire un échantillonnage à différentes échelles (micro, méso et macro) et de recaler les données pour obtenir une seule distribution.

Figure 4

Distribution des longueurs de fractures : a) distribution cumulée; b) densité de fréquence ajustée à la loi puissance.

Distribution of fracture lengths: a) cumulative distribution; b) frequency density graph fit by the power law.

a

b

-> See the list of figures

La loi puissance apparaît comme un bon modèle pour représenter les distributions de longueurs d’un grand nombre de réseaux de fractures (BONNET et al., 2001; BOUR, 1997; DARCEL, 2002; DAVY et al., 1990; DE DREUZY, 2000). Elle présente l’avantage de n’avoir pas de longueur caractéristique en dehors des limites physiques du domaine.

L’exposant a de la loi puissance est égal à 2,17. Cette valeur indique la proportion de petites fractures par rapport aux grandes. La synthèse des exposants réalisée par BONNET et al. (2001) indique des valeurs allant de 1,7 à 2,75 avec un maximum autour de 2. La valeur obtenue est donc en accord avec les travaux déjà réalisés et concorde avec les valeurs d’un réseau de failles, généralement comprises entre 1 et 3 (BODIN et RAZACK, 1999; DE DREUZY, 2000). Dans le domaine très accidenté de Man, situé au sud de Touba, LASM (2000) a obtenu une valeur de 2,9. Selon DE DREUZY (2000), la distribution des longueurs de fractures suivant la loi puissance indique que le réseau de fractures étudié aurait atteint un stade de développement très avancé. En effet, le stade final de développement, c’est-à-dire le stade de maturité des réseaux de fractures, correspondrait à la loi puissance. Ce résultat est en accord avec les données géologiques et structurales (CAMIL, 1984; DJRO, 1998) du domaine archéen de la Côte d’Ivoire. L’histoire de la tectonique polyphasée (DJRO, 1998; KONÉ et al., 1996) a conduit à une géométrie complexe du réseau de fractures de Touba. En effet, ce domaine a été structuré grâce aux différents épisodes tectoniques et métamorphiques des mégacycles orogéniques léonien et libérien.

L’étude de la fonction de corrélation a permis de caractériser la distribution spatiale des centres des fractures. La dimension fractale D calculée est égale à 1,8 (si a > 2, alors D = b). D est très proche de 2, ce qui permet de dire que la distribution des positions de fractures est quasi homogène. La valeur obtenue est inférieure à celle déterminée par LASM (2000) pour la région de Man, qui est de 1,9. VIGNES-ADLER et al. (1991) ont analysé à différentes échelles (1/5 000 000 à 1/15 000), les propriétés fractales des failles interprétées à partir d’images Landsat, de photo aériennes et de photographies prises sur le terrain ainsi que des réseaux de drainage issus des cartes topographiques de deux zones tests en Afrique de l’Ouest et Centrale. Ils ont utilisé trois méthodes d’analyse fractale (comptage de boites, répartition des masses, approche multifractale) et trouvé des dimensions fractales variant de 1,4 à 1,6 (approche multifractale). Ces auteurs soulignent que le site test des plateaux d’Assaba et de Tagant (sud de la Mauritanie, Afrique de l’Ouest) possède des dimensions fractales plus élevées que celles des sites d’Afrique Centrale (Cameroun, Congo, Centrafrique). Cela est en relation avec le nombre et les mécanismes de mise en place des systèmes de fracturation de ces différentes zones. Le présent travail réalisé à Touba corrobore les résultats de VIGNES-ADLER et al. (1991) en ce sens qu’il montre que le socle archéen ivoirien est très fracturé (dimension fractale proche de 2).

Le modèle géométrique du réseau de fractures de Touba peut donc être décrit comme suit :

Ce réseau de fractures est caractérisé par une distribution des longueurs de fractures en loi puissance (réseau mature) dans l’intervalle [900 m – 6 000 m]. La distribution de la position des fractures est quasi homogène (fractale). Les caractéristiques géométriques déterminées sont utilisées pour décrire le réseau et permettent de définir le régime de connectivité, facteur pouvant contrôler les modalités d’écoulement des eaux souterraines au sein du système de fractures de la région d’étude.

3.4 Étude de la connectivité du réseau de fractures

Dans le modèle de DAVY et al. (1990), chaque fracture est définie par ses paramètres propres (forme, longueur) et par sa localisation par rapport au reste du domaine (densité, position, corrélation). L’évolution de la densité de fracturation à travers les échelles est fractale et la distribution des longueurs est en loi puissance. Ainsi, le réseau de fractures est un ensemble de fractures discrètes et individualisées qui peut être représenté par les propriétés géométriques d’ensemble des fractures. Deux types de propriétés sont considérés : la structure du réseau et la perméabilité de chaque fracture.

Dans le présent travail, la matrice rocheuse est considérée comme imperméable, seules les fractures étant supposées perméables. Ces dernières sont considérées comme verticales, ce qui permet de travailler en plan (X, Y), et sont supposées perméables sur toute leur extension (selon X et Y), quels que soient leur origine génétique (altération, fracturation tectonique), leur âge et leur orientation. En outre, il est considéré que les fractures présentent toute la même perméabilité (Kf = 1 m•s‑1).

Ces hypothèses fortes, une fois formulées, le transfert de flux et la perméabilité en grand du réseau de fractures dépendent en premier lieu de son état de connectivité (ODLING et al., 1999). À partir du réseau de fractures, il importe de déterminer un domaine dont la taille dépasse significativement la fracture la plus longue. LONG et al. (1982) suggèrent qu’un réseau de fractures de taille « L » soit généré dans un système de taille « k L » (k = rapport de proportionnalité; k > 1) afin de limiter les effets de bord. En effet, dans le cas des distributions de longueurs de fractures en loi puissance, les effets de bord peuvent être non négligeables. La probabilité de connexion et la perméabilité augmentent quand le rapport entre la taille du réseau et la taille du domaine augmente.

Nous avons extrait un réseau de taille L = 40 km dans un domaine de taille 1,5 L (60 km) en considérant les intersections entre bords du domaine et fractures, d’une part, et entre fractures, d’autre part. Les fractures connectées forment des groupements appelés amas. Parmi les amas, certains peuvent être connectés aux bords du domaine : ce sont les amas infinis qui fournissent les chemins possibles que peut emprunter un fluide à travers le réseau s’il se déplace d’un bord du domaine à l’autre. Les règles de définition des amas infinis par connexion de deux ou quatre bords sont dénommés R2 et R4 (REYNOLDS et al., 1980).

Dans la présente étude, la règle de connexion R2 a été retenue, malgré la probabilité non nulle d’obtenir plusieurs amas infinis. Un réseau qui connecte les bords non imperméables du domaine aura une perméabilité non nulle (DE DREUZY, 2000).

Lorsqu’un amas relie les quatre bords, ou les deux bords non imperméables opposés du système, il est dit percolant. Pour identifier un amas percolant encore appelé « backbone », il importe de déterminer l’amas le plus grand du réseau et d’étudier ses connexions avec les bordures du domaine. Ensuite, il faut déterminer si la taille de cet amas, normalisée par rapport à la taille du réseau, est supérieure à 0,5; c’est-à-dire que l’amas occupe plus de la moitié de la surface du réseau.

La connectivité est la condition nécessaire à l’observation d’un écoulement à travers un réseau de fractures. L’étude de la connectivité des réseaux a été abordée dans de nombreux travaux, avec des réseaux ayant une distribution de longueurs en loi puissance (BOUR et DAVY, 1997; DE DREUZY et al., 2001), ainsi qu’avec des réseaux de fractures corrélés (distribution de longueurs en loi de puissance et réseau fractal) par DARCEL (2002). Pour un réseau 2D, ayant une distribution en loi puissance des longueurs de fractures, BOUR et DAVY (1997) proposent l’équation 4 comme l’expression qui permet une meilleure détermination du paramètre de percolation :

où L est la taille du domaine, n (l,L) est la distribution donnée par l’équation 1, lmin et lmax sont respectivement les minima et maxima de l’intervalle de distribution des longueurs de fractures.

Le premier terme de l’équation 4 correspond au concept classique de volume exclu (BALBERG, 1984), qui quantifie le nombre moyen d’intersections par fracture dans un système continu, et le deuxième terme comptabilise le nombre de fractures de taille plus grande que le système, qui assurent la connectivité du système par elles-mêmes.

Lorsqu’on s’intéresse à un réseau de fractures de géométrie atypique (large distribution de longueur, par exemple), la principale difficulté est de rechercher un paramètre de percolation qui représente une mesure fiable et pertinente de la connectivité du réseau, c’est-à-dire qui ne dépend pas de l’échelle au seuil de connectivité.

Pour les systèmes de taille infinie, il existe une valeur critique du paramètre de percolation appelé seuil de percolation (pc). Pour un réseau de fractures donné, si p dépasse pc, alors le réseau est connecté et sa perméabilité est non nulle; si p est en dessous de pc, le réseau est non connecté.

Lorsque les règles de connectivité sont établies, il devient possible de calculer des flux et la perméabilité équivalente du réseau de fractures. Les flux ont été déterminés en considérant un domaine d’étude carré au sein duquel deux côtés opposés sont considérés comme imperméables et aux deux autres est affecté un gradient de charge hydraulique (Figure 5).

Figure 5

Illustration du calcul des flux et des conditions aux limites utilisées pour le calcul de la perméabilité équivalente.

Illustration of flow modelling and boundary conditions used for the determination of equivalent permeability.

Illustration du calcul des flux et des conditions aux limites utilisées pour le calcul de la perméabilité équivalente.

-> See the list of figures

Dans ces conditions retenues pour son étude, le réseau de fractures de Touba apparaît comme bien connecté (Figure 6a), excepté le coin sud-est dont l’amas n’est pas connecté (Figure 6b) à l’amas principal. Formé majoritairement de fractures de petites tailles, l’amas principal est connecté aux quatre bords du domaine (amas percolant). Le niveau de connectivité est caractérisé par le paramètre de percolation p estimé à 5,78. Cette valeur traduit une connexion au seuil. Selon DE DREUZY (2000), le paramètre p au seuil varie très peu en fonction de la taille du réseau et tend vers une moyenne de 5,6. La connectivité des réseaux de fractures conditionne énormément les étapes de calcul des flux et de détermination de la perméabilité dans les milieux fracturés. Les travaux de BOUR (1997), DARCEL (2002) et DE DREUZY (2000) ont permis d’élucider les régimes de connectivité des réseaux en fonction de leurs paramètres géométriques. Selon DARCEL (2002), les valeurs relatives des exposants D (dimension fractale) et a (distribution des longueurs) permettent de distinguer différents régimes de connectivité. Lorsque a < D + 1, la connectivité à l’échelle du système est entièrement dominée par l’exposant a de la distribution des longueurs de fractures. Ce cas est celui du réseau de fractures de la région de Touba (a = 2,17 < 2,8). La connectivité est alors largement contrôlée par les fractures dont la taille est équivalente à la taille du domaine choisi; les fractures de petites tailles jouant un rôle secondaire (a = 2,17, est proche de 2). Il en découle que la connectivité du réseau croît avec l’échelle d’observation, donc avec la taille du domaine d’étude choisi a priori.

Figure 6

Connectivité et flux simulés : a) amas connecté; b) amas déconnecté; c) flux simulé dans le réseau de fractures (les teintes foncées sont les chemins où le flux est maximum).

Connectivity and simulated flow: a) connected group; b) disconnected group; c) simulated flow in the fracture network (dark colours represent pathways with maximal flow).

a

b

c

-> See the list of figures

3.5 Calcul des flux et de la perméabilité

Le calcul des flux dans le réseau ainsi établi et pour le gradient hydraulique (valeur absolue, direction et sens) choisi permet de définir les axes d’écoulement de l’eau souterraine et de déterminer la perméabilité du réseau de fractures du socle archéen de Touba, pour les hypothèses choisies et décrites ci-dessus. La recherche des flux en régime permanent dans l’amas infini est réalisée selon la loi de Darcy dans les conditions aux limites de type gradient avec une différence de charge hydraulique imposée de 1 bar. On fait l’hypothèse d’un écoulement idéal au niveau de chaque segment de fracture et le flux total Q est proportionnel au gradient de charge conformément à la loi de Darcy (Équation 5) :

où L est la taille du domaine, h1 et h0 sont les charges hydrauliques locales, K est la perméabilité.

Le calcul de la perméabilité est réalisé sur une grille irrégulière dont les noeuds sont formés par l’intersection des fractures dans le réseau ou par l’intersection entre une fracture et les limites du système. La discrétisation conduit à un système d’équations de dimension égale au nombre de points du réseau dont la solution est la perméabilité du réseau de fractures. La méthode de résolution utilisée est la décomposition LU (DE DREUZY et ERHEL, 2003). La perméabilité est calculée sur le réseau complet où toutes les fractures de l’amas infini participent à l’écoulement, ainsi que sur le réseau tronqué où les fractures inférieures à 900 m sont supprimées.

La modélisation des flux permet d’observer des écoulements concentrés dans les grandes fractures (Figure 6c). Selon DE DREUZY (2000), la distribution en loi puissance des longueurs de fractures induit des écoulements fortement chenalisés. Il apparaît une chenalisation du cheminement de l’eau et les axes préférentiels épousent une direction générale NE-SW. Sur la figure 6c, la teinte des chemins indique l’intensité du flux. Les axes de teinte plus foncée correspondent aux chemins où le flux est maximum. Les transferts s’effectuent selon l’axe de drainage N-S dans les secteurs nord et ouest de la zone étudiée. L’axe de drainage de direction E-W au sud de Touba connecte un nombre important d’accidents structuraux. Le coin sud‑est n’est pas connecté à l’amas principal dans la fenêtre d’étude.

3.6 Comparaison de la carte des flux et des débits des forages

La carte des débits des forages est surimposée à celle des flux pour rechercher d’éventuelles concordances entre les axes de drainage calculés à partir du modèle hydrogéologique et les zones à bonne potentialité hydrogéologique (Figure 7). C’est une approche indirecte de validation des résultats théoriques produits par le modèle hydrogéologique. À cet effet, sont utilisés les débits en fin de foration qui caractérisent la transmissivité locale des aquifères captés. Plus de la moitié des forages a été implantée sur la base de critères géomorphologiques (bas de versant, proximité d’un cours d’eau, alignements structuraux, etc.) ou sociologiques (proximité du logement des autorités coutumières, dans le village, à l’école, etc.), la photo aérienne et la géophysique n’intervenant que pour les cas d’échecs répétés (GÉOMINES, 1982). Les forages à débits moyens (2,5 à 5 m3•h‑1) et forts (5 à 7,5 m3•h‑1) semblent se superposer aux flux simulés par le modèle hydrogéologique. Dans le centre et à l’ouest, les résultats sont satisfaisants. Les secteurs à débits forts (> 7,5 m3•h‑1) sont recherchés pour l’implantation de forages d’Hydraulique Villageoise Améliorée (HVA) destinés à l’approvisionnement en eau des grandes agglomérations comme Touba.

Figure 7

Relations entre les flux simulés dans le réseau de fractures et les débits des forages.

Relationship between simulated flow in the fracture network and well discharge.

Relations entre les flux simulés dans le réseau de fractures et les débits des forages.

-> See the list of figures

Dans les coins NW et SE, où les fractures ne sont pas connectées à l’amas percolant, des forages à débit élevé (10,7 et 12 m3•h‑1) sont néanmoins observés. Le calcul des flux étant effectué sur l’amas infini principal détecté, il n’y a pas de flux modélisé dans ces secteurs.

L’examen des coupes géologiques des deux forages à fort débit des secteurs NW (10,7 m3•h‑1) et SE (12 m3•h‑1) montre respectivement cinq et quatre arrivées d’eau. Les observations de terrain montrent que ces forages sont situés dans des couloirs de cisaillements. De plus, les fractures horizontales et subhorizontales observées sur le terrain ne sont pas intégrées dans le modèle alors qu’elles induisent une connectivité horizontale améliorant la productivité des forages.

La concordance partielle entre les deux sources de données (modèle hydrogéologique, mesures de débits in situ) au niveau des zones à productivités moyenne et forte constitue un résultat intéressant dans la perspective de la recherche des sites d’implantation de forages à gros débits.

3.7 Caractéristiques hydrauliques dérivées du modèle géométrique du réseau

Les flux simulés à partir de l’amas principal infini ont été utilisés pour l’estimation de la perméabilité équivalente globale. On fait l’hypothèse que toutes les fractures ont la même ouverture et, par conséquent, la même perméabilité (Kf = 1 m•s‑1). Pour le réseau naturel complet, la perméabilité équivalente KRn est égale à 0,037 m•s‑1, alors que pour le réseau tronqué, dans lequel les fractures de tailles inférieures à 900 m ont été filtrées, KRt est égale à 0,024 m•s‑1. Ce paramètre hydraulique est lié au modèle géométrique de réseau choisi. Or, le réseau de fractures se heurte au problème de sous-échantillonnage des fractures de petite taille (< 900 m) et à la troncature des fractures dont la taille est plus grande que le domaine. Ces biais dans les données ont une incidence sur les perméabilités calculées, comme l’expriment les résultats différents obtenus pour les réseaux naturel et tronqué.

Les valeurs de perméabilités équivalentes sont normalisées en prenant en compte les caractéristiques hydrauliques in situ, comme la conductivité hydraulique moyenne (Khm) qui est considérée constante. MOURZENKO et al. (2004) ont montré que la perméabilité d’un réseau de fractures en loi puissance avec une conductivité uniforme est proportionnelle à la densité des surfaces des fractures. En utilisant la valeur de Khm = 3,5 10‑5 m•s‑1, déterminée par BIÉMI (1992) sur plus de quatre-vingt forages dans le bassin versant de la Marahoué, situé à l’est de la région de Touba, la perméabilité du réseau naturel complet KRn est égale à 1,3 10‑6 m•s‑1. Cette valeur est comparable et cohérente avec les valeurs de perméabilités induites par les fractures calculées par la méthode de FRANCISS (1970), obtenues dans le bassin de la Marahoué (BIÉMI, 1992), à Man-Danané (KOUAMÉ, 1999) et à Korhogo (JOURDA, 2005) qui oscillent entre 10‑8 et 10‑4 m•s‑1. Dans la région d’Odienné (bassin du Bani-Niger) et au Burkina Faso (bassin de la Sissili), SAVANÉ (1997) et SAVADOGO (1984) ont quant à eux obtenu des valeurs plus faibles et inférieures à 10‑8 m•s‑1.

Les estimations de la perméabilité équivalente à partir du modèle hydrogéologique testé sont cohérentes avec les mesures in situ réalisées dans le socle fracturé d’Afrique de l’Ouest. Ceci est une indication de la robustesse et de la performance de ce modèle à fractures discrètes, appliqué pour la première fois en Côte d’Ivoire.

4. Discussion

Les caractéristiques géométriques (distribution des longueurs de fractures en loi puissance) et fractales (auto-similaire) montrent que le réseau de fractures de Touba peut être décrit par le modèle mathématique développé par DAVY et al. (1990). L’architecture du réseau de fractures est fortement tributaire du support de caractérisation de la fracturation ainsi que de l’expérience du photo-interprète. Les images satellitaires Landsat-TM, utilisées dans le cadre de cette étude, possèdent une limite de résolution spatiale qui est à la base du sous-échantillonnage des petites fractures et, par conséquent, engendre des biais dans la cartographie du réseau. Afin de réaliser une description plus fine du réseau de fractures et de prendre en compte différentes échelles spatiales de mesure, il serait souhaitable d’utiliser d’autres images de résolution spatiale plus fine telles que les images IKONOS, QUICKBIRD et SPOT‑5 que l’on devra aussi coupler aux investigations de terrain pour une meilleure caractérisation des systèmes géométriques de Touba. Comme le suggère ODLING (1997), cela permettra de faire un échantillonnage à différentes échelles et de recaler les données pour que les lois d’échelles définies aboutissent à des distributions représentatives des caractéristiques géométriques du réseau étudié.

Dans le réseau de fractures de Touba, l’hétérogénéité de la distribution des flux est l’un des résultats les plus frappants. Elle se manifeste, pour les hypothèses théoriques d’écoulement choisies, par la chenalisation extrême du flux dans les grandes fractures. La modélisation hydrogéologique d’un tel réseau peut prendre en compte les grandes structures de façon déterministe et les fractures de petite taille de façon stochastique (LEE et al., 2001). Le couplage de ces deux approches peut donner un modèle efficace. Toutefois, selon HSIEH (1998), la question fondamentale dans la modélisation n’est pas tant le choix entre une approche continue où discrète que dans la détermination du niveau d’hétérogénéité ou de détail à inclure dans le modèle. En effet, l’approche continue et l’approche discrète deviennent équivalentes si, pour l’approche continue, la maille élémentaire d’homogénéisation est inférieure ou de l’ordre de la taille des plus petites fractures du système.

L’un des défis, pour que les modèles mathématiques soient opérationnels et applicables, est la validation des résultats des simulations (HOFFMANN et SANDER, 2007). Les résultats issus du modèle présenté au sein de cet article sont théoriques et restent tributaires des hypothèses simplificatrices formulées (toutes les fractures sont perméables, les fractures ont la même ouverture, les fractures sont perméables sur toute leur étendue, le domaine d’étude a été choisi arbitrairement, il a une forme carrée, indépendante de la topographie, etc.). L’un des avantages de l’approche discrète réside dans l’utilisation des données à la fois géométriques et hydrauliques pour construire des modèles de propriétés hydrauliques simples et cohérents. Le modèle hydrogéologique utilisé dans cette étude a été validé par BOUR et al. (2002) dans le bassin de Hornelen en Norvège où le réseau de fractures a été cartographié à des échelles allant du mètre au kilomètre. L’originalité de cette approche réside dans l’exploitation des informations géométriques pour analyser les propriétés hydrauliques afin de définir les modèles d’écoulement typiques associés. Les études numériques menées avec ce modèle ont mis en évidence une forte influence des paramètres géométriques de distribution de longueur et d’ouverture sur les caractéristiques de l’écoulement (BOUR, 1997; DARCEL, 2002; DE DREUZY, 2000). Il convient alors de tester diverses autres hypothèses de distribution statistique et de corrélation entre les paramètres (recherche des modèles les plus pertinents), d’une part, et de confronter les propriétés hydrauliques globales obtenues par le modèle aux observations et mesures de terrain, d’autre part.

Le recours aux caractéristiques du système hydrogéologique naturel pour la calibration et la validation du modèle géométrique ainsi que du modèle hydraulique qui en découle s’avère indispensable pour tester la performance du modèle. Ce test a été réalisé à l’aide des données de débits de forages. La concordance est partielle entre les zones d’écoulement du modèle et les forages à débits moyens et forts. Pour conforter la validité des flux simulés et évaluer les interrelations entre les écoulements et la ressource en eau, les débits d’étiages des cours d’eau pourraient aussi être analysés et être confrontés à un modèle qui prendrait en compte l’influence de la topographie sur les écoulements naturels. Dans ce contexte granito-gneissique, soumis à un climat tropical (1 200‑1 700 mm•an‑1), les débits d’étiages pourraient en effet traduire le drainage des aquifères, donc les propriétés de ces derniers, de manière plus intégrée que les données ponctuelles issues de forages.

Le choix d’étudier en priorité des modèles de réseaux 2D a été motivé, d’une part, par le manque de données tridimensionnelles complètes et, d’autre part, par les limites de capacité numérique. Il est à noter qu’un ensemble d’observations 2D ne conduit à des informations tridimensionnelles que si les plans d’observation sont corrélés, ce qui n’est pas le cas en général (DE DREUZY, 2000). L’extrapolation des données 2D et 3D nécessite l’utilisation d’une hypothèse sur la structure du réseau, une sorte d’hypothèse d’ergodicité qui permet de fixer les propriétés 3D du réseau grâce à des observations 2D.

5. Conclusion

La télédétection satellitaire est couplée aux travaux de géologie structurale pour la cartographie du réseau de fractures de la région de Touba. Les paramètres géométriques (lois d’échelles) indiquent que le réseau a atteint un stade de développement très avancé (distribution des longueurs de fractures en loi puissance) et est fractal (auto-similaire). Ces caractéristiques géométriques sont utilisées pour décrire le réseau. Elles permettent de définir le régime de connectivité qui conditionne les modalités de détermination de la perméabilité équivalente.

Les flux simulés dans le réseau montrent, pour les hypothèses théoriques retenues, une chenalisation qui épouse une direction générale NE-SW. Le transfert de flux s’effectue au droit des fractures de tailles régionales qui contrôlent la connectivité du réseau. La concordance partielle entre les axes souterrains définis par le modèle à fractures discrètes et les forages à débits moyens et forts constitue un résultat encourageant pour la prospection des eaux souterraines dans le socle fracturé de Touba.