Article body

1. Introduction

L’analyse probabiliste des risques liés à l’occurrence des pluies fortes s’effectue généralement à partir d’un échantillon constitué de la plus forte valeur mesurée chaque année, notée XA. Plusieurs variantes ont été proposées pour optimiser l’exploitation de l’information disponible. Une première approche consiste à retenir l’ensemble des valeurs XS supérieures à un seuil S, ce qui permet d’étoffer l’échantillon d’analyse, qui n’est plus limité à une seule valeur par année. Le risque annuel de non‑dépassement est obtenu en composant la distribution des valeurs XS supérieures à un seuil avec la distribution du nombre k de valeurs observées chaque année (Shane et Lynn, 1964) en supposant l’indépendance des deux distributions) :

Une seconde approche consiste à raisonner sur l’ensemble des valeurs de la série, ce qui augmente considérablement la taille de l’échantillon. Lorsque les valeurs successives de la variable X sont supposées indépendantes, la distribution des valeurs maximales annuelles s’obtient directement :

où N est le nombre de valeurs successives dans une année (par ex. N = 365 pour la pluie journalière). Dans un graphique de Gumbel, avec un changement d’échelle sur les probabilités (variable réduite de Gumbel), les distributions des variables XA et X sont parallèles et espacées de LnN. Dans le cas des pluies journalières successives, il existe une autocorrélation mais qui reste faible (variable selon les saisons et les régions, de l’ordre de 0,1 à 0,5 d’après Duband, dans CFGB, 1994). L’autocorrélation des valeurs successives conduit à réduire l’écart entre la distribution de toutes les valeurs successives et la distribution des valeurs maximales annuelles, sans remettre en cause leur parallélisme :

Ce principe est d’ailleurs celui retenu par Reedet al. (1999), dans le cadre d’une analyse régionale des pluies, où un échantillon global est constitué à partir de l’agglomération de l’ensemble des valeurs réduites aux différents postes.

L’objectif de ce travail est lié à une méthode d’extrapolation de la distribution des crues, la méthode du Gradex (Guillot et Duband, 1967), utilisée en France depuis une trentaine d’années pour le dimensionnement des évacuateurs de crue des grands barrages. Cette méthode repose sur l’emploi de lois à décroissance exponentielle pour la distribution des pluies, dont la loi de Gumbel constitue l’exemple le plus connu. Nous nous proposons d’effectuer une analyse de sensibilité sur l’estimation du gradex des pluies, égal dans le cas d’une loi de Gumbel ou une loi exponentielle au paramètre d’échelle de la loi des pluies, en testant différents modes d’échantillonnage, par valeurs maximales annuelles, valeurs supérieures à un seuil, ou valeurs cumulées successives. Après un rappel des différentes distributions utilisées pour chacun de ces modes d’échantillonnage, nous présentons le jeu de données pluviométriques disponible sur une soixantaine de bassins de la Moselle et une dizaine de bassins du Rhône. Après avoir constitué des séries chronologiques de pluie de bassin, nous analysons les variations saisonnières des gradex, ainsi que le coefficient d’abattement spatial sur le gradex. Nous comparons ensuite les différentes estimations du gradex des pluies de bassin, pour les différents modes d’échantillonnage testés.

2. Les différentes distributions utilisées par mode d’échantillonnage

2.1 Rappels sur la théorie des valeurs extrêmes

La théorie des valeurs extrêmes propose un cadre théorique pour caractériser le comportement asymptotique des queues de distribution (Bacro, 2006; Coles, 2001). Lorsque les valeurs de l’échantillon à analyser sont indépendantes et identiquement distribuées (i.i.d), on peut montrer (Fisher et Tippet, 1928; Gnedenko, 1943; Jenkinson, 1955) que la variable XA suit une loi généralisée des valeurs extrêmes, définie par :

Lorsque l’on raisonne sur les dépassements XS au-dessus d’un seuil S (supposés i.i.d), la distribution asymptotique est une loi de Pareto généralisée (Davison et Smith, 1990; Pickands, 1975) :

La liaison entre les deux distributions FA(x) et GS(x) s’obtient facilement lorsque le nombre annuel k de dépassement XS suit une loi de Poisson :

avec µ̑ = (Nb valeurs XS)/Nb années. La combinaison des relations 1 et 6 donne alors :

2.2 Estimation du gradex des pluies à partir d’échantillons de valeurs maximales

Dans le cas d’une loi de Gumbel (Éq. 4, avec k = 0), le gradex des pluies est estimé par la méthode des moments par la relation :

à partir de l’écart-type s de l’échantillon des valeurs maximales annuelles XA. Le gradex correspond à la pente de la distribution sur un graphique à échelle de Gumbel, avec une relation linéaire entre le quantile xp et la variable réduite de Gumbel yp = ‑Ln (‑Ln p) :

avec Prob [XA < xp] = p

Dans le cas d’une loi exponentielle (Éq. 5, avec k = 0), le gradex des pluies est estimé par la méthode du maximum de vraisemblance par la relation (Miquel, 1984) :

à partir de la moyenne m de l’échantillon des valeurs XS supérieures au seuil S. La combinaison des relations 5 et 7 montre que le gradex correspond également à la pente de la distribution sur un graphique à échelle de Gumbel :

L’indépendance des valeurs XS de l’échantillon est obtenue en imposant une durée minimale entre deux valeurs (10 jours) et un coefficient de redescente de la pluie entre deux épisodes (valeur inférieure à 90 % du maximum sélectionné). Le choix du seuil S a été obtenu en vérifiant que le processus d’occurrence des valeurs extraites pouvait bien être modélisé suivant une loi de Poisson, basée sur les hypothèses d’indépendance, stationnarité et homogénéité des valeurs. Deux tests ont été appliqués, le premier (Cunnane, 1979) sur l’indice de dispersion I du nombre k d’événements par année (ou saison) : I = Var(k)/E(k); le second (Langet al., 1999) sur la date d’occurrence des événements, en reportant sur un graphique le nombre cumulé d’événements en fonction de la date. Un exemple d’illustration de ces deux tests sera présenté en section 4.2.

2.3 Estimation du gradex des pluies à partir de l’ensemble des valeurs successives

Le parallélisme asymptotique entre la distribution des valeurs successives X et la distribution des valeurs maximales annuelles XA (Éq. 3) permet d’estimer le gradex des pluies à partir de la pente de la distribution, dans un graphique à échelle de Gumbel. Le gradex correspond au paramètre d’échelle de chacune des distributions testées : mélange d’exponentielles, max (a, b); loi gamma tronquée, ρ; loi exponentielle simple, a.

2.3.1 Loi somme de deux exponentielles

Les paramètres α, β, a et b de la loi somme de deux exponentielles :

avec α + β = θ = 1 - F(0), fréquence des jours avec précipitation non nulle, peuvent être estimés de façon analytique lorsqu’une hypothèse forte est imposée sur le coefficient de pondération α :

La méthode des moments conduit aux deux estimateurs suivants :

avec  K = (m2 + s2)/2.

Gouy (1994) a précisé le domaine d’application de cette loi :

2.3.2 Loi Gamma tronquée

Cette loi est utilisée en alternative à la loi somme de deux exponentielles, lorsque la condition (15) n’est pas vérifiée, en particulier lorsque le coefficient de variation CV est inférieur à 1. Les paramètres λ et ρ de la loi gamma tronquée :

sont estimés par la méthode des moments :

La correspondance entre la loi gamma ajustée sur les valeurs non nulles et la distribution F(x) de l’ensemble des valeurs est la suivante :

2.3.3 Loi exponentielle simple à un paramètre

Cette loi est un cas particulier de la loi Gamma (λ = 1), lorsque la fréquence des valeurs nulles est égale à zéro. Le paramètre a de la loi exponentielle à un paramètre :

est estimé par :

La loi exponentielle simple n’est pas adaptée aux séries dont le coefficient de variation Cv est très différent de 1.

3. Première analyse d’un jeu de données pluviométriques

3.1 Constitution d’un jeu de pluies de bassin

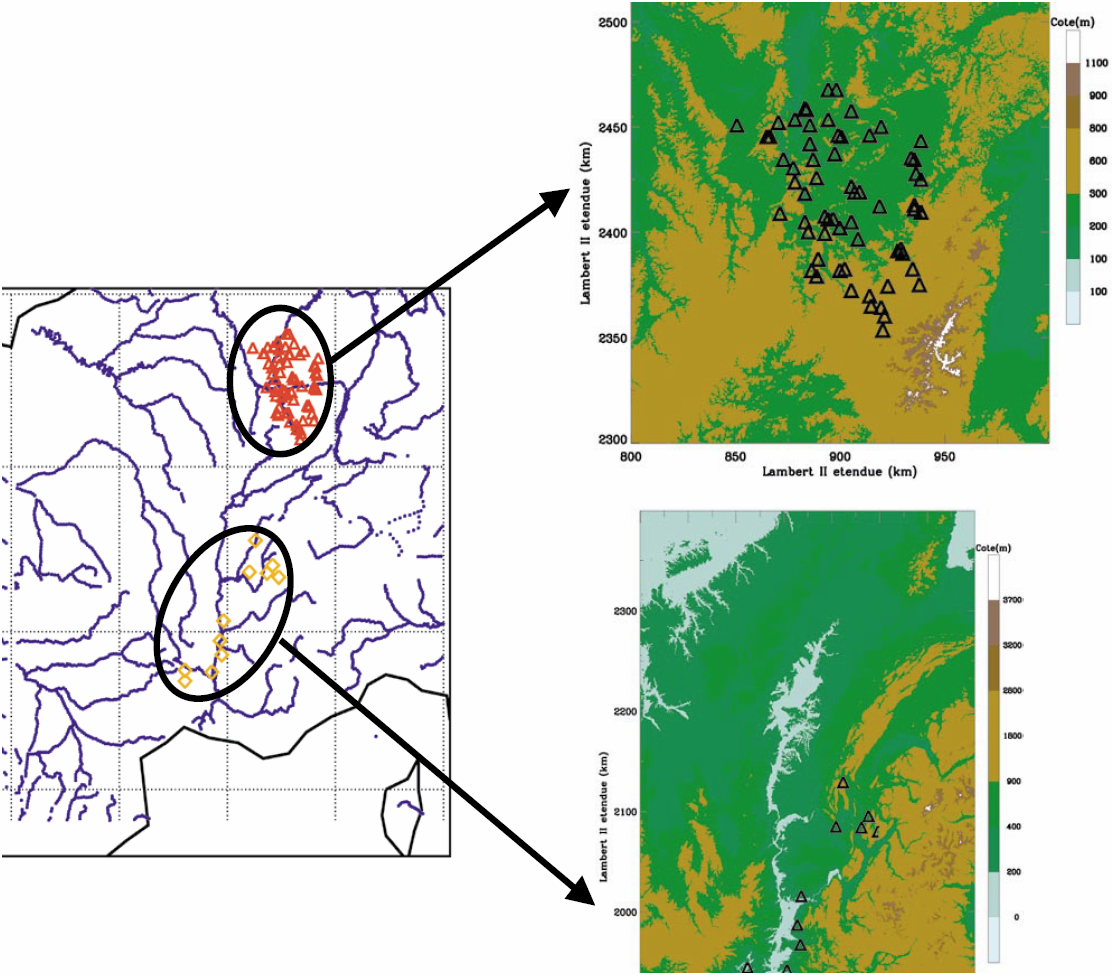
Nous avons utilisé deux jeux de données pluviométriques, constitués respectivement de 192 et 213 stations sur la Moselle et le Rhône. La critique et la correction des données ont été réalisées sur la Moselle par Javelle (2001), dans le cadre du projet PACTE (Galéa et Blum, 2005), et sur le Rhône par Safege (2000) et les différents organismes impliqués dans l’étude globale des crues du Rhône. Le calcul de la lame d’eau a été effectué sur 63 bassins de la Moselle, pour lesquels ont été retenues 100 stations, et sur 11 bassins du Rhône à partir de 112 stations (Figure 1).

Le nombre de postes sélectionnés a été défini d’après la taille de chaque bassin versant et la relation établie par Lebel (1984), qui relie la portée p (en km) (ou distance de décorrélation, au-delà de laquelle deux stations sont considérées comme indépendantes) d’une station pluviométrique avec le pas de temps t (en h) considéré :

Des chroniques de lame d’eau spatiale journalière ont ainsi été calculées par moyenne arithmétique des pluies ponctuelles de chacun des postes des bassins versants, sur la période 1968-1998 (30 ans) pour la Moselle, et 1950-1998 (49 ans) pour le Rhône. On dispose en moyenne de 1 à 56 pluviomètres par bassin sur la Moselle, et de 5 à 42 postes pour le Rhône (Figure 2).

Afin de bien prendre en compte la variabilité spatiale de la pluie, nous avons retenu un nombre plus important de postes dans le calcul de la lame spatiale, en considérant que chacun des postes n’était représentatif que sur le tiers de la portée définie précédemment.

L’échantillonnage des chroniques a ensuite été réalisé en travaillant sur plusieurs pas de temps : 1, 2, 3, 4, 5 , 6 et 7 jours pour les 11 bassins du Rhône, et 1, 3, 6, 15 et 20 jours pour les 63 bassins de la Moselle. Les pas de temps retenus sont compatibles avec le temps de concentration de chaque bassin, fonction de la dynamique des crues et de la taille des bassins. Celle-ci varie de 16 km2 (Elvon à Bazancourt) à 10 770 km2 (Moselle à Uckange) sur la Moselle, et de 854 km2 (Eyrieux) à 29 908 km2 (Saône) sur le Rhône.

Figure 1

Localisation des sous-bassins versants étudiés sur la Moselle et le Rhône.

Location of the studied sub-basins of the Moselle and Rhone rivers.

Localisation des sous-bassins versants étudiés sur la Moselle et le Rhône.

-> See the list of figures

Figure 2

Distribution des surfaces des sous-bassins et du nombre de pluviomètres utilisés pour le calcul de la lame d’eau (bassins de (a) la Moselle et (b) du Rhône).

Distribution of the catchment areas and the number of raingauges used for areal rainfall computation ((a) Moselle and (b) Rhone catchments).

(a)

(b)

-> See the list of figures

3.2 Analyse du régime saisonnier

Le traitement probabiliste des pluies fortes s’effectue généralement en supposant vérifiées plusieurs hypothèses de base sur les valeurs de l’échantillon : caractère aléatoire, stationnarité, indépendance et homogénéité. Le dernier point est mis en défaut dans le cas d’un régime pluviométrique à plusieurs saisons, où l’échantillon des plus fortes valeurs est issu d’un mélange de populations. Lang et Desurosne (1994) ont testé l’apport de la saisonnalisation sur l’estimation du gradex des pluies d’une vingtaine de postes pluviométriques du Sud-Est de la France. Ils ont mis en évidence une sous-estimation variant de 10 à 40 %, suivant la durée des pluies étudiées (de 1 h à 30 j), lorsque le gradex ponctuel est calculé à partir de l’ensemble des valeurs de l’année plutôt que sur la saison à plus fort risque.

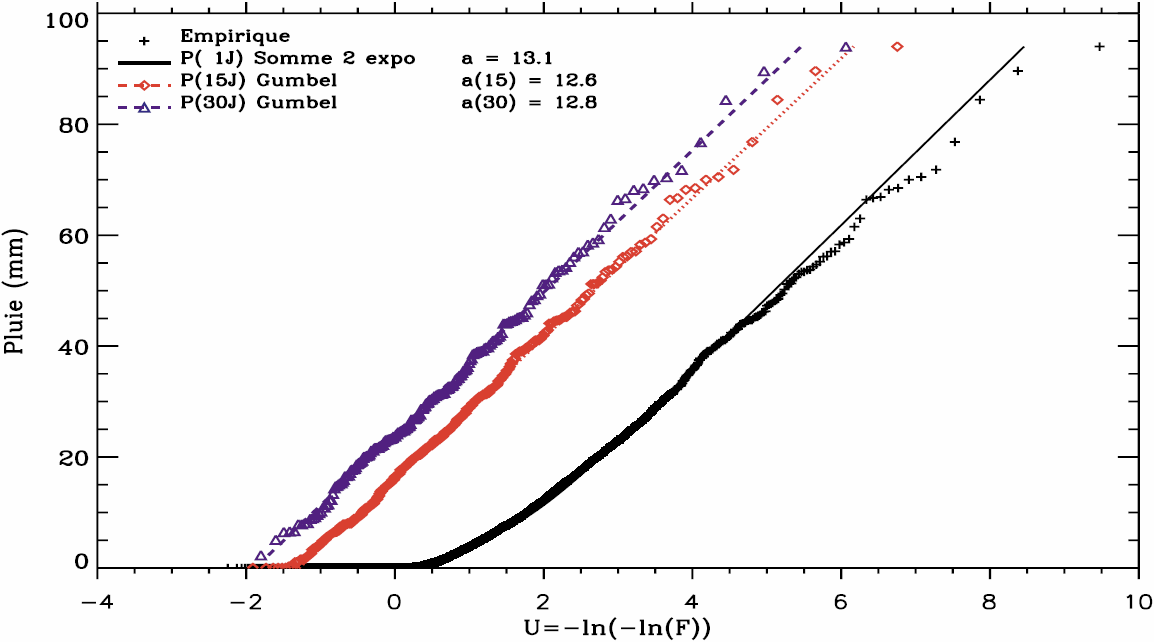
La détermination de la saison à plus fort risque sur les bassins de la Moselle et du Rhône a été réalisée à partir de l’estimation du gradex de la lame d’eau spatiale, calculée sur les valeurs de chacun des douze mois de l’année. La figure 3 présente la distribution des pluies maximales journalières du bassin de l’Ardèche à Saint-Martin-d’Ardèche pour le mois de septembre (NA années), en considérant trois modes d’échantillonnage (de gauche à droite) : maximum de chaque mois de septembre (NA valeurs), maximum de chacune des deux quinzaines du mois de septembre (2 NA valeurs), valeurs successives journalières en septembre (30 NA valeurs). L’estimation du gradex mensuel est réalisée à partir du troisième échantillon, en considérant une loi somme de deux exponentielles et une loi gamma. Un contrôle de cohérence permet de vérifier que le gradex obtenu est compatible avec celui estimé à partir des deux autres échantillons (parallélisme des trois ajustements).

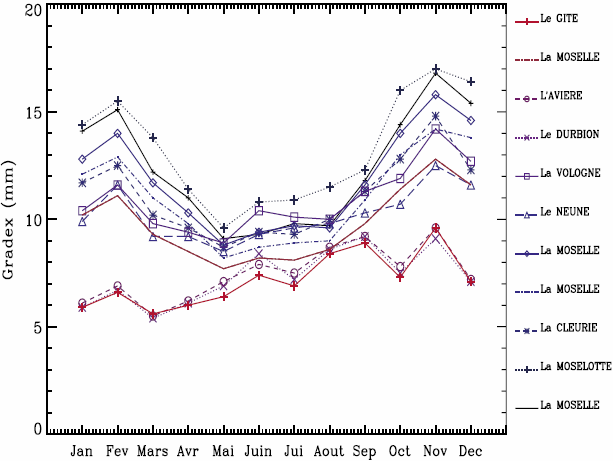
La figure 4 présente les variations mensuelles du gradex des pluies spatiales cumulées de 11 bassins versants de la Moselle (pluie cumulée de 3 jours) et de 11 bassins du Rhône (pluie cumulée de 1 jour). Sur la Moselle, la saison à plus fort risque court de septembre à mars (7 mois), avec une saison à risque secondaire d’avril à août (5 mois). Les bassins du Rhône ont un régime pluviométrique plus contrasté, avec une saison à risque d’août à décembre. Compte tenu du fait que certains bassins du Rhône n’ont pas de fortes valeurs de gradex en août ou décembre, nous avons finalement retenu l’automne (septembre à novembre : 3 mois) comme la saison à plus fort risque.

À titre de vérification, nous avons comparé les résultats obtenus sur la Moselle avec ceux de Laborde (1984), sur neuf postes pluviographiques de la Lorraine. Le découpage saisonnier était légèrement différent du nôtre, avec deux saisons de six mois chacune (mai-octobre et novembre-avril), et l’échantillonnage était relatif aux valeurs maximales des mois successifs de la saison étudiée. Les valeurs de gradex obtenues par chacun des deux découpages saisonniers sont pratiquement identiques sur la saison à plus fort risque (hiver) et diffèrent de moins de 5 % sur la saison secondaire (été). Par la suite, nous présenterons les résultats obtenus sur la saison à plus fort risque, l’hiver (septembre-mars) pour les bassins de la Moselle, et l’automne (septembre-novembre) pour les bassins du Rhône.

3.3 Exemple d’ajustements avec les différents modes d’échantillonnage

Nous présentons un exemple d’ajustement des pluies maximales d’hiver sur l’Esch à Jezainville. On observe sur la figure 5 un basculement de la pente de la distribution des valeurs XS, du fait de la sélection de valeurs supplémentaires en seconde ou troisième position dans l’année. D’une façon générale, on observe sur l’ensemble des bassins testés une meilleure homogénéité des valeurs issues d’un échantillonnage des précipitations supérieures à un seuil, par rapport à un maximum annuel ou saisonnier. La figure 6 compare (de gauche à droite) sur le bassin de Rupt-sur-Moselle la distribution des valeurs maximales journalières, obtenues par sélection de la valeur maximale de chaque mois de la saison (Nr NA valeurs) ou sélection de la valeur maximale de chaque quinzaine de la saison (2Nr NA valeurs), avec celle des valeurs successives de la saison à risque (˜ 30Nr NA valeurs). On constate que la faible auto-corrélation des données journalières successives n’influe pas sur le parallélisme des différentes distributions échantillonnées. La sélection de l’ensemble des valeurs journalières successives permet ainsi de disposer d’un échantillon plus fourni et d’avoir une estimation du gradex moins sensible à la distribution d’échantillonnage que celle obtenue avec la seule valeur maximale de la saison.

3.4 Estimation du coefficient spatial d’abattement

Le coefficient spatial d’abattement traduit la décroissance du risque de pluie forte au fur et à mesure que l’on s’intéresse à une superficie de plus en plus étendue. Dans le domaine du risque d’inondation, l’analyse probabiliste des pluies doit prendre en compte l’extension spatiale du phénomène et pas simplement la variabilité spatiale d’une intensité de pluie mesurée ponctuellement. Une première approche consiste à choisir le poste pluviométrique supposé être représentatif de la pluie de bassin, à partir d’une analyse cartographique de la variabilité spatiale des gradex ponctuels de pluie. Une approche plus complète doit permettre d’intégrer les phénomènes de concomitance et de structuration spatiale de la pluie.

Figure 3

Distribution des pluies journalières spatiales du mois de septembre pour le bassin de St-Martin-d’Ardèche (S = 2 430 km2, Rhône).

Gumbel plot of 1 day maximum areal precipitation in September for two St-Martin-d’Ardèche catchments (S=2430 km2, Rhône).

Distribution des pluies journalières spatiales du mois de septembre pour le bassin de St-Martin-d’Ardèche (S = 2 430 km2, Rhône).

-> See the list of figures

Figure 4

Variations mensuelles du gradex des pluies spatiales de (a) 11 sous-bassins de la Moselle (pas de temps 3 jours) et (b) 11 sous-bassins du Rhône (pas de temps 1 jour).

Monthly areal rainfall gradex values of (a) 11 sub-catchments of the Moselle River (time step 3 d) and of (b) 11 sub-catchments of the Rhône Rivers (time step 1 d).

(a)

(b)

-> See the list of figures

Figure 5

Exemple d’ajustement des pluies journalières : comparaison de deux modes d’échantillonnage (max hiver, sup-seuil hiver) sur l’Esch à Jezainville.

Example of a Gumbel plot of maximum daily precipitation: comparison between two kinds of sampling methods (maximum winter values and winter peak-over-threshold (POT) values).

Exemple d’ajustement des pluies journalières : comparaison de deux modes d’échantillonnage (max hiver, sup-seuil hiver) sur l’Esch à Jezainville.

-> See the list of figures

Figure 6

Exemple d’ajustement des pluies journalières saisonnières : comparaison de deux modes d’échantillonnage par maximum (mois, quinzaine) avec l’ensemble des valeurs successives.

Example of a Gumbel plot of seasonal maximum daily precipitation: comparison between two kinds of sampling methods (monthly and bi-monthly) including all successive values.lues.

Exemple d’ajustement des pluies journalières saisonnières : comparaison de deux modes d’échantillonnage par maximum (mois, quinzaine) avec l’ensemble des valeurs successives.

-> See the list of figures

Nous pouvons comparer la moyenne des gradex ponctuels des stations appartenant à un bassin donné avec le gradex de la lame d’eau de ce bassin, et déterminer un coefficient d’abattement empirique fonction de l’intercorrélation entre les stations. En effet, prendre pour gradex spatial la moyenne des gradex, revient à dire que toutes les corrélations spatiales entre postes sont égales à un, et amène donc à une surestimation. La figure 7 montre que l’estimation du gradex du bassin par la moyenne des gradex ponctuels entraîne une surestimation par rapport au gradex des pluies de bassin, qui prend implicitement en compte la corrélation spatiale des précipitations (cf. section 3.1, avec un calcul de lame d’eau spatiale journalière). Le coefficient d’abattement des pluies d’hiver sur la Moselle varie de 12 % à 6 % (respectivement cumuls journaliers et de trois jours). Les valeurs obtenues pour l’été sont un peu plus fortes, et peuvent atteindre 15 %.

Ces pourcentages fournissent un ordre de grandeur de l’abattement spatial des pluies sur la Moselle, pour une première estimation du risque de pluie forte. La climatologie des pluies étant variable d’un bassin à un autre, il est préférable, dans la mesure du possible, de raisonner sur le gradex de la lame d’eau spatiale, à partir d’une chronique de pluie spatiale, qui intègre de fait les interrelations entre les stations.

4. Estimation du gradex des pluies suivant le mode d’échantillonnage

4.1 Comparaison du gradex issu de la distribution des valeurs maximales annuelles et supérieures à un seuil

La figure 8 présente une comparaison du gradex obtenu avec un échantillonnage par valeurs maximales annuelles (indice x) et par valeurs supérieures à un seuil (indice s), pour les 63 bassins de la Moselle et les 11 bassins du Rhône. Les deux courbes du haut correspondent au ratio µs / µx de la moyenne des gradex sur l’ensemble des bassins traités; les deux courbes du bas correspondent au coefficient de corrélation r de la régression linéaire obtenue à partie de l’équation 21.

D’une façon générale, la corrélation r entre les deux gradex est meilleure lorsque l’on utilise un découpage saisonnier qui produit des valeurs plus homogènes, et on note une sous-estimation du gradex par la méthode classique (max annuel) de 10 à 20 % par rapport à l’échantillonnage par valeurs supérieures à un seuil (rapport µs / µx).

Figure 7

Comparaison entre (a) le gradex (1 et 3 jours) de la pluie moyenne du bassin et (b) le gradex moyen du bassin (63 sous-bassins de la Moselle).

Comparison between (a) the 1 and 3 day gradex values of the areal rainfall and (b) the average spatial gradex values (63 sub-catchments of the Moselle River).

(a)

(b)

-> See the list of figures

Figure 8

Comparaison du gradex obtenu à partir de valeurs maximales annuelles ou supérieures à un seuil. (a) Bassin de la Moselle (63 bassins); (b) bassin du Rhône (11 bassins).

Comparison of gradex estimates from annual maximum values or peak-over-threshold (POT) values. (a) Moselle catchment (63 catchments); (b) Rhône catchment (11 catchments).

(a)

(b)

-> See the list of figures

4.2 Comparaison du gradex issu de la distribution des valeurs supérieures à un seuil et des valeurs successives

4.2.1. Distribution des valeurs cumulées successives

À l’issue du traitement des données, nous avons constaté que la loi somme de deux exponentielles ne pouvait être appliquée sur des cumuls de plus de six jours. Lorsque le pas d’étude devient important, la fréquence des valeurs nulles est proche de zéro et le coefficient de variation est souvent inférieur à l’unité. Ainsi, on utilise généralement plutôt la loi gamma ou la loi normale pour l’étude de la distribution des pluies mensuelles. Dans le cadre de cette étude, nous avons distingué deux cas de figure, suivant la fréquence F(0) des valeurs nulles :

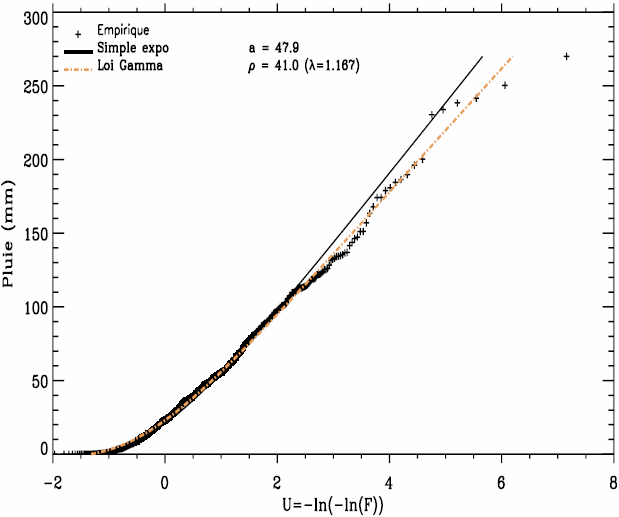
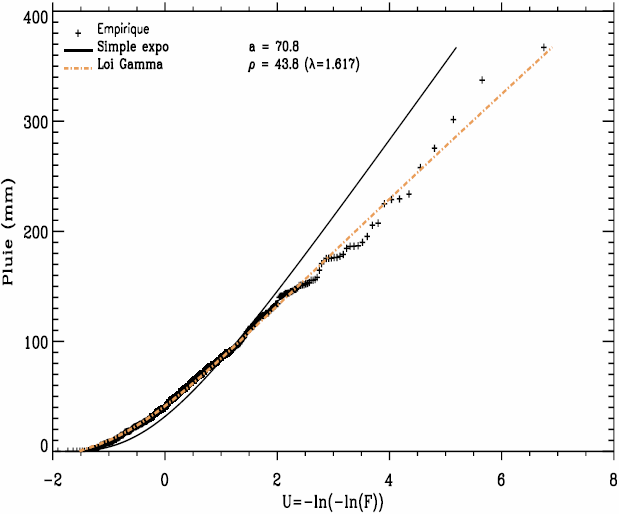
  • quand F(0) ≈ 0, la loi exponentielle simple à un paramètre s’ajuste bien avec les précipitations, même lorsque le coefficient de variation est inférieur à l’unité (cf. Figure 9 : CV = 0,71, F(0) = 0). Le gradex estimé est comparable à celui obtenu avec la loi gamma.

  • quand F(0) > 0, la loi exponentielle simple à deux paramètres s’ajuste bien si le coefficient de variation est proche de l’unité. Dans le cas contraire, nous avons retenu l’estimation du gradex obtenue à l’aide d’une loi gamma. La figure 10 donne l’exemple du bassin de Rupt-sur-Moselle, où la loi exponentielle s’ajuste bien aux pluies journalières cumulées de 10 jours (CV = 0,93, F(0) = 0,024). Elle conduit par contre à surestimer la distribution des pluies cumulées de 15 jours, pour des valeurs de CV inférieur à 1 (CV = 0,79; F(0) = 0,011).

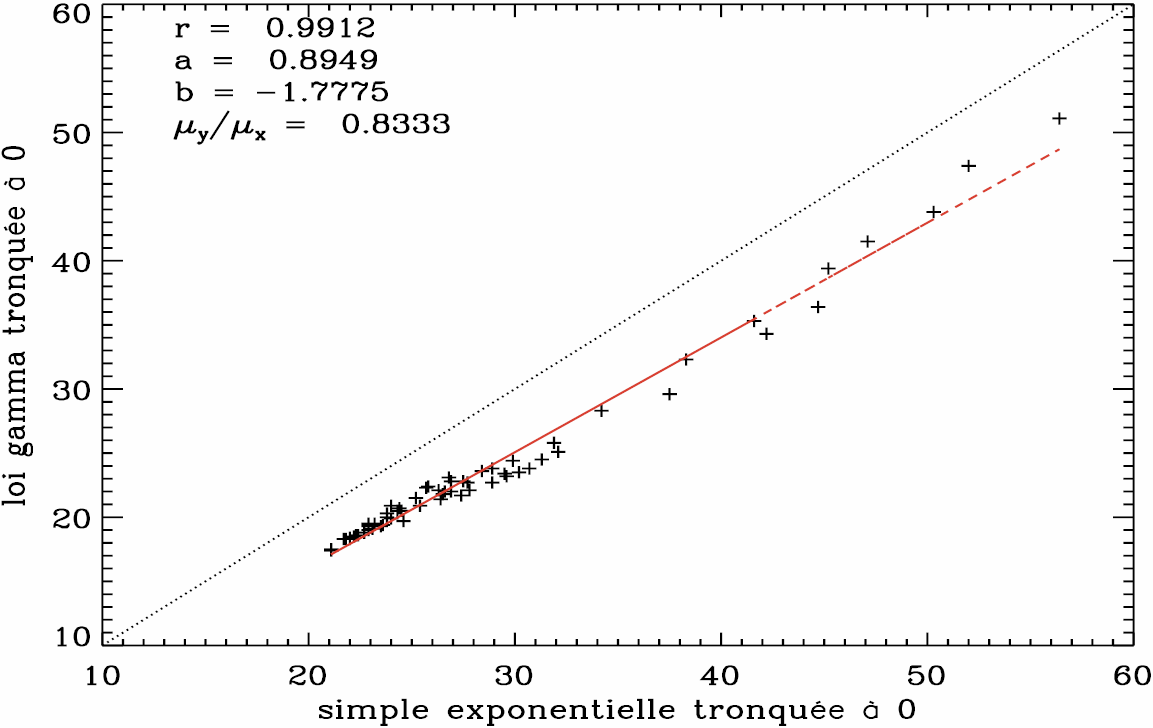
La figure 11 montre qu’en moyenne, sur les 63 sous-bassins de la Moselle, la loi exponentielle appliquée aux pluies cumulées de 20 jours surestime le gradex d’environ 20 %, en comparaison avec une loi gamma tronquée (rapport µy/µx = 0,83). Cette dernière distribution est donc à recommander pour l’étude des cumuls pluviométriques de plus de sept jours.

4.2.2. Comparaison avec la distribution des valeurs supérieures à un seuil

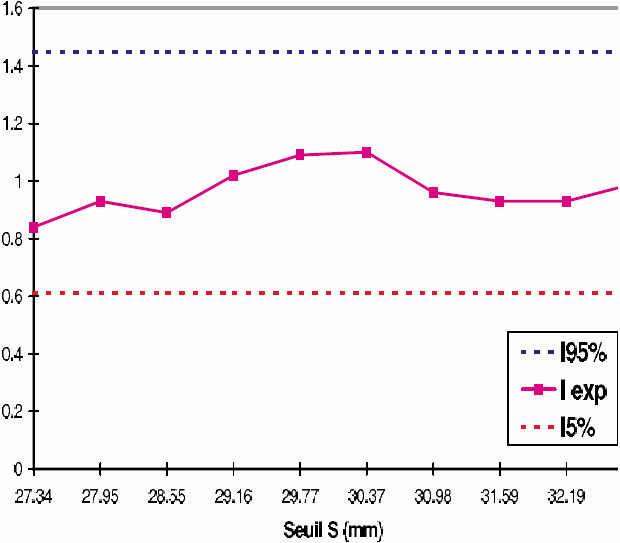
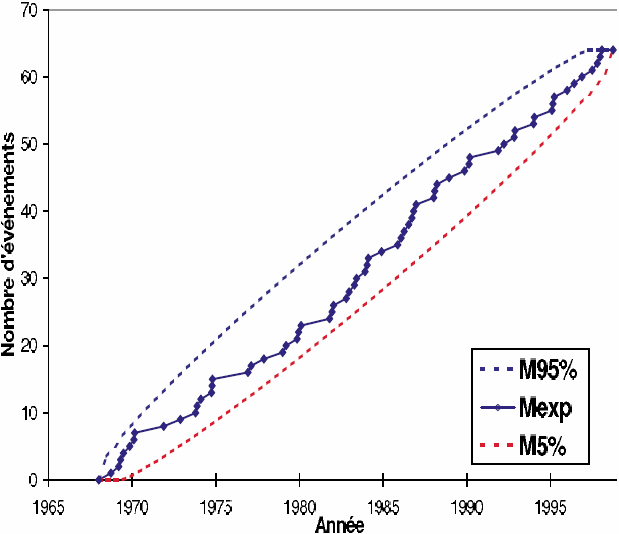
La figure 12 permet de vérifier le respect des hypothèses de stationnarité et d’indépendance sur les valeurs de pluie cumulée de trois jours du bassin de Rupt-sur-Moselle. Quel que soit le seuil retenu (de 27 à 33 mm), l’indice de dispersion expérimental I, théoriquement égal à un pour la loi de Poisson, est situé à l’intérieur de l’intervalle de confiance à 90 %. Ceci conduit à valider le choix de la loi de Poisson et les critères d’espacement utilisés pour éliminer des épisodes trop rapprochés. Pour le seuil de 28 mm, qui correspond à un nombre moyen annuel de deux épisodes, le processus est stationnaire (cf. test sur les dates d’occurrence), à un risque d’erreur près de 10 %.

La figure 13 présente une comparaison du gradex obtenu avec un échantillonnage par valeurs successives (sans indice) et par valeurs supérieures à un seuil (indice s), pour les 63 bassins de la Moselle et les 11 bassins du Rhône. Les deux courbes du haut correspondent au ratio µs/µ de la moyenne des gradex sur l’ensemble des bassins traités, en raisonnant sur l’année ou la saison à risque; les deux courbes du bas correspondent au coefficient de corrélation r de la régression linéaire.

Figure 9

Exemple d’ajustement des pluies cumulées de 20 jours en hiver (Rupt-sur-Moselle).

Example of a Gumbel plot of 20 day rainfall in winter (Rupt-sur-Moselle).

Exemple d’ajustement des pluies cumulées de 20 jours en hiver (Rupt-sur-Moselle).

-> See the list of figures

Figure 10

Exemple d’ajustement des pluies cumulées de (a) 10 jours et (b) 15 jours en hiver (Rupt-sur-Moselle).

Example of a Gumbel plot of (a) 10 and (b) 15 day rainfall in the winter (Rupt-sur-Moselle).

(a)

(b)

-> See the list of figures

Figure 11

Comparaison du gradex des pluies cumulées de 20 jours en hiver, estimé d’après une loi gamma ou une loi exponentielle (63 sous-bassins de la Moselle).

Comparison of gradex estimates of 20 day rainfall in the winter, with a Gamma or an exponential distribution (63 sub-catchments of the Moselle River).

Comparaison du gradex des pluies cumulées de 20 jours en hiver, estimé d’après une loi gamma ou une loi exponentielle (63 sous-bassins de la Moselle).

-> See the list of figures

Figure 12

Vérification des hypothèses de (a) stationnarité et (b) d’indépendance. Application aux pluies cumulées de 3 jours, supérieures à un seuil (bassin de Rupt‑sur‑Moselle).

Test of (a) stationarity and (b) independance. Application to POT values of 3‑day precipitations (Rupt‑sur‑ Moselle catchment).

(a)

(b)

-> See the list of figures

Figure 13

Comparaison du gradex obtenu à partir de valeurs cumulées successives ou supérieures à un seuil. (a) Bassin de la Moselle; (b) Bassin du Rhône.

Comparison of gradex estimates from successive cumulated values or peak-over-threshold (POT) values. (a) Moselle catchment; (b) Rhône catchment.

(a)

(b)

-> See the list of figures

Les résultats obtenus sont sensiblement différents entre les deux jeux de données. Sur la Moselle, les estimations du gradex restent voisines pour les durées de 1 à 6 jours et divergent au-delà, du fait d’une mauvaise adéquation de la loi exponentielle simple à la distribution des pluies cumulées sur de longues durées. Comme indiqué au paragraphe 2.3, une bonne alternative consiste à utiliser une loi Gamma, mieux adaptée à ce type d’échantillon (cf. Figure 10b).

Sur le Rhône, la différence entre les estimations du gradex est de l’ordre de ± 5 à 15 %, ce qui n’excède pas l’écart-type théorique du gradex. On peut noter par ailleurs que l’écart d’estimation est plus marqué avec un échantillonnage sur l’année, plutôt qu’avec un échantillonnage sur la saison.

La disparité des résultats entre le Rhône et la Moselle peut s’expliquer par le fait que certains des bassins étudiés sur la Moselle sont de taille réduite, pour lesquels on ne disposait pas d’un nombre suffisant de postes à l’intérieur du bassin considéré. Dans ce cas de figure, le calcul de la lame spatiale est forcément moins robuste que sur des grands bassins avec un plus grand nombre de pluviomètres.

5. Conclusion

L’objet de ce travail était d’évaluer l’effet du mode d’échantillonnage sur l’estimation du paramètre d’échelle de la distribution des pluies maximales. Un premier résultat est la nécessité d’étudier au préalable le comportement saisonnier du régime des pluies et de raisonner sur la saison à plus fort risque. Cette étape permet d’obtenir des valeurs d’échantillons plus homogènes et des ajustements de bien meilleure qualité qu’avec simplement des valeurs maximales sélectionnées sur l’année complète. Dans le cas contraire, la sous-estimation du paramètre d’échelle est de l’ordre de 10 à 20 % pour les pluies de bassin et de 10 à 40 % pour des pluies ponctuelles.

Il est par ailleurs indispensable de bien appréhender le phénomène d’abattement spatial des précipitations, qui traduit le fait que le risque d’une pluie forte diminue en fonction de l’extension spatiale considérée. Le calcul simplifié consistant à faire une analyse ponctuelle des pluies et à calculer une valeur moyenne spatiale du gradex conduit à surestimer le paramètre d’échelle des pluies de 10 à 15 %, suivant la saison considérée. Il est préférable d’estimer les paramètres de la distribution de la lame d’eau de bassin. La combinaison de ces deux erreurs (sous-estimation liée au caractère saisonnier et surestimation liée à la dépendance spatiale) se neutralise seulement en moyenne, sachant que dans certains cas l’erreur finale peut être de l’ordre de ± 40 %.

En alternative à l’échantillonnage classique par valeurs maximales annuelles ou par saison, on peut préconiser : a) l’emploi d’un échantillonnage par valeurs supérieures à un seuil, ou b) l’étude de la distribution des pluies journalières successives. L’intérêt est de disposer d’un échantillon plus fourni et d’obtenir une estimation plus robuste de la distribution des pluies. La contrepartie est, dans le cas a), d’effectuer une étude de sensibilité sur le choix du seuil et, dans le cas b), d’utiliser une loi adaptée à la présence de valeurs nulles. Ce dernier point a été abordé par Djerboua et al. (2004). Les résultats obtenus par les deux approches sont globalement cohérents et peuvent être recommandés pour l’étude de la distribution des pluies fortes.

La question du comportement asymptotique de la distribution des pluies fortes reste déterminante, notamment pour déterminer si l’hypothèse exponentielle est acceptable ou pas. Muller (2006) a réalisé une analyse sur 22 longues séries pluviométriques en France avec plus de 100 années de mesure. Si l’hypothèse k > 0 est acceptée pour près d’un poste sur deux, il reste difficile de rejeter par une analyse locale la loi de Gumbel au profit de la loi généralisée des valeurs extrêmes, du fait de la forte variabilité de l’estimateur de k.