Article body

1. Introduction

La chloration optimale de l’eau potable vise la protection des consommateurs contre les maladies d’origines hydriques tout en réduisant la formation des composés organiques chlorés. Ces derniers, regroupés sous l’appellation « sous‑produits de la désinfection par le chlore », sont soupçonnés être responsables d’autres maladies chez l’Homme (SADIC et RODRIGUEZ, 2004; WIGLE, 2001). À l’intérieur des réseaux d’alimentation en eau potable (AEP), la réduction du chlore libre obéit à des lois de réaction et de transport, imposées par la nature des conduites, la qualité de l’eau et les régimes hydrauliques (VASCONCELOS et al., 1997). Pour des réseaux caractérisés par des chemins hydrauliques longs, des baisses considérables des taux de chlore libre sont généralement observées entre les points d’application et les extrémités (BREMOND et al., 1998). Afin de pallier cette contrainte, les stations d’appoint sur les réseaux d’eau potable peuvent constituer une solution et permettre d’améliorer l’homogénéité du taux de chlore libre. D’autres problèmes se présentent alors : où positionner les stations d’appoint? quelles consignes imposer au niveau des sources et au niveau des stations d’appoint sur le réseau? Le nombre et les emplacements des stations d’appoint dépendent essentiellement de la structure du réseau (longueurs et interconnections des conduites). Ils relèvent de la gestion à moyen et à longs termes des réseaux. Cependant, les consignes de la chloration sont généralement déterminées pour des points d’application connus et une modulation horaire de la demande caractéristique de chaque journée. C’est la gestion à court terme de la chloration.

L’optimisation de la gestion des réseaux d’eau potable a été largement analysée par les méthodes conventionnelles. BRION et MAYS (1991) et LANSEY (1994) ont utilisé la programmation dynamique pour optimiser le fonctionnement d’une station de pompage. D’autres auteurs ont choisi de simplifier les problèmes étudiés pour utiliser la programmation linéaire (BOCCELLI et al., 1998; GUHL, 1999; TRYBY et al, 2002). BISCOS et al. (2003) et YU et al. (1994) ont utilisé la programmation non linéaire pour optimiser les mêmes types de problème. Toutes ces méthodes étaient peu efficientes et fortement pénalisées par la taille des problèmes étudiés. Dans ce cadre, BOULOS et al. (2002) ont souligné que la réussite de ces techniques est très limitée car celles‑ci mettent en jeux des modèles mathématiques complexes, elles dépendent du nombre de variables et des contraintes, elles exigent de fortes simplifications et elles sont facilement piégées dans des optimums locaux. Contrairement à ces méthodes, les Algorithmes Génétiques (AG) conviennent parfaitement pour résoudre les problèmes d’optimisation combinatoires (HRSTKA et KUCEROVA, 2004). De nombreuses applications pour la gestion des réseaux d’eau potable ont été proposées dans la littérature. REIS et al. (1997) ont développé un AG pour l’optimisation du choix des vannes de contrôle pour la réduction des fuites. SAVIC et WALTER (1997), VAN VUUREN (2002) et LIONG et ATIQUZZAMAN (2004) ont développé des AG efficients pour l’optimisation du choix des diamètres des conduites. MEIER et BARKDOLL (1999) ont réalisé le calage des réseaux hydrauliques sous pression par AG. SCHAETZEN et al. (2000) ont utilisé un AG pour le choix optimal des points de calage des réseaux. MORLEY et al. (2001) ont présenté un outil d’optimisation des extensions. BOULOS et al. (2002) se sont intéressés à l’optimisation du fonctionnement des stations de pompages par AG. MUNAVALLI et KUMAR (2003) et ROUHIAINEN et TADE (2003) ont présenté des AG pour l’optimisation des consignes de chlore pour des stations d’appoint connues sur les réseaux. OSTFELD et SALOMONS (2004) ont également utilisé les AG pour la minimisation du coût de fonctionnement des stations de pompage et des stations d’appoint. Tous les auteurs ont souligné la réussite des AG dans la recherche des solutions optimales.

Le présent travail vise le développement d’un AG pour le choix optimal des emplacements des stations d’appoint du chlore sur les réseaux de distribution. Après un bref aperçu sur cette technique, la méthodologie d’optimisation choisie ainsi que les principales étapes de calcul seront exposées. Un réseau de distribution caractérisé initialement par une chloration déséquilibrée a été utilisé pour tester le modèle.

2. Rappels sur les algorithmes génétiques

2.1 Principe

Par similitude à la théorie de l’évolution de Darwin, les AG font évoluer les individus d’une population, choisie initialement au hasard, par le biais des opérateurs génétiques : sélection, croisement et mutation (BACK et al., 2000; GOLDBERG, 1991). Une stratégie d’évolution est généralement associée à ces opérateurs pour permettre le passage d’une génération à une autre. Ce processus itératif est arrêté en cas de stagnation de l’évolution ou lorsque le nombre maximum de générations est atteint (DREO et al., 2003).

2.2 Les opérateurs génétiques

2.2.1 La sélection

À chaque génération, des individus se reproduisent, survivent ou disparaissent de la population sous l’action de deux opérateurs de sélection : (1) la sélection pour la reproduction, et (2) la sélection pour le remplacement (BACK et al., 2000; DREO et al., 2003). De nombreuses techniques de sélection peuvent être citées : (1) la sélection proportionnelle, essentiellement celle par roulette de casino conçue à l’origine par J. Holland pour les algorithmes génétiques, (2) la sélection selon le rang de l’individu et (3) la sélection par tournoi. Ces techniques engendrent des pressions de sélection très différentes. Une pression de sélection élevée conduit l’algorithme à converger prématurément vers un optimum local. Une faible pression empêche l’algorithme de converger (DREO et al., 2003).

2.2.2. Le croisement

Les techniques de croisement citées dans la littérature diffèrent par le nombre de points de croisement entre les parents et le mode d’échange du matériel génétique. Le nombre de parents et le nombre d’individus produits constituent des variantes de chaque technique. Le mécanisme de croisement est généralement appliqué selon une probabilité qui varie entre 0,5 et 0,8 (BACK et al., 2000; DREO et al., 2003; PELIKAN et al., 2003).

2.2.3. La mutation

Ce mécanisme introduit dans la population une variabilité aléatoire, selon une probabilité entre 0,01 et 0,1. La mutation aléatoire déterministe, la mutation « bit-flip » et la mutation gaussienne auto-adaptative sont les plus citées dans la littérature (BACK et al., 2000; DREO et al., 2003; PELIKAN et al., 2003).

2.2.4. Les stratégies d’évolution

Une stratégie d’évolution définit les mécanismes qui permettent de passer d’une génération d’individus à une autre. Le nombre maximal de générations est un paramètre de la stratégie d’évolution qui arrête le processus itératif en cas de non‑convergence de l’algorithme (BACK et al., 2000; DREO et al., 2003; PELIKAN et al., 2003).

3. Formulation du problème

La performance de la chloration sur un réseau d’AEP peut être évaluée par l’homogénéité du taux de désinfectant dans l’espace et dans le temps (PROPATO, 2003). L’importance des frais d’investissement et de gestion, engagés pour appliquer la chloration, entrent également dans l’évaluation de la performance. Ainsi, nous fixons comme objectifs (1) assurer aux consommateurs une chloration tolérable et homogène et (2) minimiser le nombre de stations d’appoint utilisées.

3.1 Fonctions objectifs

L’objectif (1) peut être exprimé par la minimisation de la somme des carrés des écarts entre les taux du chlore libre calculés, au niveau des noeuds de consommation, et la moyenne de l’intervalle des valeurs admissibles. La fonction objectif de l’homogénéité s’écrit alors :

où E(NN, T) est la somme des carrés des écarts à tous les noeuds n et à tous les pas de temps t, c(n, t), la concentration en chlore libre du noeud n au pas de temps t, εmin et εmax, les limites respectivement minimale et maximale de l’intervalle admissible du taux de chlore libre, NN, le nombre total des noeuds sur le réseau et T, la période de simulation.

L’objectif (2) est assuré par la minimisation du nombre de stations d’appoint de chlore sur le réseau. La fonction objectif s’écrit :

où Nstation(R) est le nombre de stations d’appoint de chlore sur le réseau R.

3.2 Conditions aux limites

Les conditions aux limites pour ce problème d’optimisation fixent les valeurs du taux de chlore libre au niveau des sources d’eau C(sources), au niveau des stations d’appoints C(appoint) et au niveau des noeuds de consommation c(n, t) :

Au niveau des sources d’eau (Réservoirs et stations de pompage), on impose :

Au niveau des stations d’appoint de chlore sur le réseau de distribution, on impose :

Au niveau des noeuds de consommation sur le réseau de distribution, on impose :

4. Méthodologie

Une solution au problème étudié est une disposition adéquate de stations d’appoints sur le réseau de distribution. La modélisation hydraulique et la propagation du chlore libre dans le réseau sont réalisées par le logiciel EPANET2 (ROSSMAN, 2000), utilisant une loi de réaction-transport unidimensionnelle. De plus, nous considérons que la réaction du chlore libre à travers les réseaux de distribution est de premier ordre (VASCONCELOS et al., 1997). Après la simulation de chaque solution au problème, l’AG utilise les taux de chlore libre calculés en chaque noeud, et à tout pas de temps, pour évaluer la performance de la solution. Partant d’un ensemble de solutions choisies au hasard, l’algorithme fait évoluer les individus et améliore la performance maximale de la population. Ce processus est arrêté par la stagnation de l’évolution de la population (DREO et al., 2003).

5. Algorithme d’optimisation

L’AG proposé crée au hasard un ensemble de solutions réalisables : population initiale. Une stratégie d’élitisme associée aux opérateurs génétiques : sélection par tournoi, croisement en deux points et mutation aléatoire se chargent ensuite de prospecter l’espace des solutions à la recherche de l’individu optimal.

5.1 Algorithme

5.1.1. Création de la population initiale

Un individu de la population aura la configuration présentée au tableau 1.

Tableau 1

Structure d’une solution au problème étudié.

Solution structure of the studied problem.

Structure d’une solution au problème étudié.

-> See the list of tables

Dans ce tableau, NN désigne le nombre total de noeuds du réseau, ns = 1 indique qu’une station d’appoint se trouve au noeud ns alors que ns = 0 indique qu’il n’y a pas de station d’appoint au noeud ns . Le nombre de solutions créées détermine la taille de la population, constante pour toutes les générations.

5.1.2. Évaluation des individus de la population initiale

La solution optimale au problème doit minimiser la somme des carrés des écarts ainsi que le nombre de stations utilisées. La transformation de ce problème de minimisation en un problème de maximisation de la performance d’une solution j permet de définir les fonctions suivantes :

La fonction homogénéité Fh(j) :

La fonction de réduction du nombre de stations sur le réseau Fsmin(j) :

où NombreStation(j) est le nombre de stations d’appoint pour la solution j.

La fonction d’évaluation globale d’une solution j sera :

où p1 et p2 sont les poids de pondération des fonctions d’évaluation. Le choix de ces paramètres fixe le compromis entre l’homogénéité et le nombre de stations utilisées.

5.1.3. Évolution

Afin de garantir une pression de sélection acceptable, la technique de sélection par tournoi a été adoptée. DREO et al. (2003) recommandent d’ajuster sa pression par le choix de deux participants dans chaque tournoi. Le présent AG utilise le croisement entre deux parents en deux points pour produire deux enfants. Les points de croisement sont choisis par des tirages au hasard. La mutation adoptée est le changement de la valeur d’un bit, choisi au hasard, de 0 à 1 ou de 1 à 0. Pour disposer d’une garantie contre la convergence prématurée, DREO et al. (2003) recommandent d’associer une stratégie d’élitisme à la technique de sélection par tournoi.

6. Exemple étudié

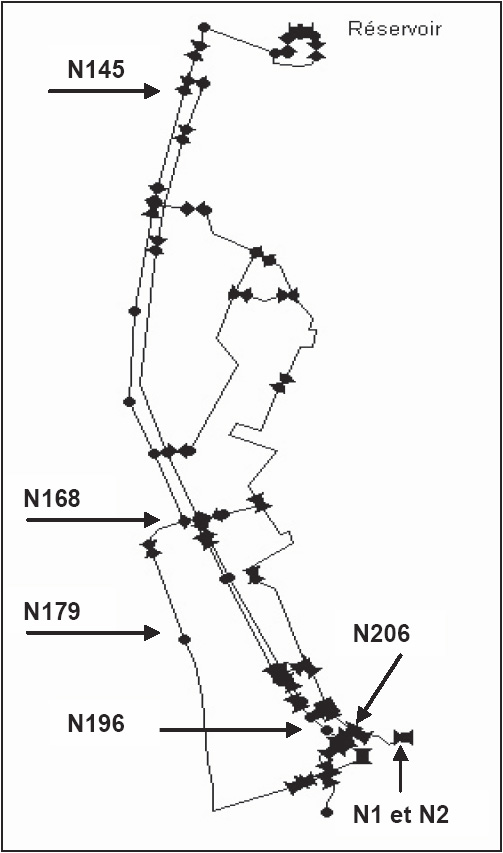
La structure du réseau retenue pour la modélisation est formée d’un réservoir et de 20 km de conduites. La forme allongée du réseau a imposé des temps de séjour importants et a toujours provoqué des déséquilibres du taux de chlore libre. Afin d’évaluer la chloration, trois noeuds de contrôle ont été choisis : N145 (premier noeud de consommation), N168 (milieu du réseau) et N206 (extrémité du réseau) (Figure 1).

Le taux de chlore libre optimum sur les réseaux est fixé à 0,3 mg/L (KOOIJ, 2003). À cette valeur le réseau est protégé contre les risques de maladies d’origine hydrique et ceux liés à la formation des sous‑produits de la chloration. De plus, les goûts et les odeurs, en présence du chlore libre, sont généralement détectés pour des taux supérieurs à 0,24 mg/L (TURGEON et al., 2004). Cependant, divers choix de l’intervalle admissible ont été présentés dans la littérature. CONSTANS (1999) a proposé l’intervalle [0,1-0,5] mg/L, ROUHIAINEN et TADE (2003) ont adopté l’intervalle [0,1-0,6] mg/l alors que PROPATO (2003) a considéré l’intervalle [0,2-0,4] mg/L. Pour la présente application, nous adoptons l’intervalle [0,1-0,5] mg/L, dont la moyenne correspond au taux optimum estimé à 0,3 mg/l. D’autre part, le coefficient de réaction du chlore libre avec l’eau Kb a été considéré égal à – 0,2 h-1 (NOUIRI et al., 2003). Le coefficient de réaction avec les parois des conduites, Kw, est défini en fonction de la nature et de l’âge de la conduite.

Figure 1

Schéma du réseau test.

Test network map.

Schéma du réseau test.

-> See the list of figures

6.1 Condition actuelle de chloration

Actuellement, le gestionnaire du réseau étudié impose une consigne constante du taux de chlore libre à la sortie du réservoir. Le logiciel EPANET 2 a permis de calculer les sommes des carrés des écarts E(NN,T) pour les consignes 0,4; 0,5; 0,6; 0,7 et 0,8 mg/L. L’examen de la figure 2 permet de constater que la consigne 0,5 mg/L assure les sommes des carrés des écarts les plus faibles durant la majorité des pas de temps. Au cours de la troisième journée de simulation (48 à 71 heures), cette consigne assure la meilleure homogénéité spatio-temporelle de la chloration, avec la somme des carrés des écarts la plus faible égale à 65,9 mg2/L2.

Figure 2

Somme des carrés des écarts pour différentes consignes de chloration.

Sum square deviation for different chlorination scheduling.

Somme des carrés des écarts pour différentes consignes de chloration.

-> See the list of figures

L’examen de la figure 3 révèle qu’à l’extrémité aval du réseau (N206) le taux de chlore libre simulé est toujours inférieur à la limite minimale de l’intervalle admissible.

D’autre part, la distribution spatiale du taux de chlore libre après 60 heures de simulation montre que 27 % des noeuds présentent des taux inférieurs à 0,1 mg/L. Avec ce mode de gestion (chloration constante à la sortie du réservoir), la seule possibilité de corriger le déficit de chloration est d’augmenter la consigne à la sortie du réservoir. La simulation d’une consigne égale à 0,8 mg/L a conduit à une augmentation à des taux inacceptables aux premiers noeuds de consommation (0,73 mg/L). En plus, ce scénario soumet 26 % des noeuds à des taux supérieurs à 0,5 mg/L et 10 % d’entre eux à des taux inférieurs à 0,1 mg/L. Ainsi, pour toutes les consignes de chloration simulées une partie importante des noeuds de consommation reste soumise à des taux en dehors de l’intervalle admissible. La gestion actuelle de la chloration sur le réseau test peut être jugée non satisfaisante.

Figure 3

Taux de chlore libre au niveau des noeuds de contrôle.

Free chlorine rates in control nodes.

Taux de chlore libre au niveau des noeuds de contrôle.

-> See the list of figures

6.2 Application du modèle d’optimisation

Avant son utilisation, l’AG a nécessité la définition de la probabilité des croisements (0,9), celle des mutations (0,05), la taille de la population (100) et le nombre maximal de générations (300). De plus, lors de la présente application, il est donné la même importance à l’homogénéité de la chloration et à la réduction du nombre de stations d’appoint (p1 = p2 = 0,5). D’autre part, les consignes de tous les points d’application du chlore sont considérées constantes égales à 0,5 mg/L.

L’application du modèle d’optimisation sur le réseau test a révélé trois phases d’évolution de la performance maximale de la population. Une première phase d’évolution rapide se situe entre les générations 1 et 40. Un ralentissement de l’évolution est enregistré entre les générations 41 et 100. Au cours de la troisième phase, on assiste à une stagnation de la performance maximale de la population pendant 50 générations. L’AG arrête alors la recherche au bout de 150 générations. (Figure 4).

Figure 4

Évolution des performances des populations.

Evolution of the population fitness functions.

Évolution des performances des populations.

-> See the list of figures

La solution optimale déterminée par le modèle d’optimisation consiste en la création de deux points d’application de chlore au niveau des noeuds N179 et N196 (Figure 1). La simulation de cette configuration optimale a permis d’améliorer considérablement l’état de la chloration sur le réseau de distribution par :

  1. La réduction de la somme des carrés des écarts pour la même journée de simulation qui est passée de 65,9 mg2/L2, avec la chloration unique à partir du réservoir, à 38,8 mg2/L2 en présence des deux stations d’appoint. Les répartitions horaires des sommes des carrés des écarts pour la chloration initiale et pour le scénario optimal sont présentées à la figure 5.

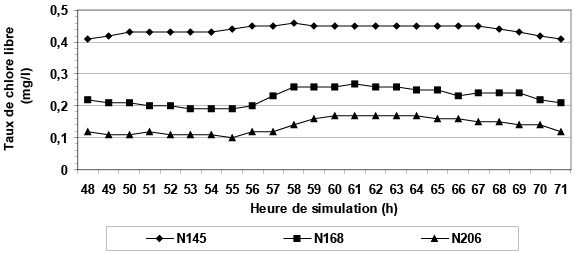
  2. Au niveau des trois noeuds de contrôle, les taux de chlore libre sont toujours compris dans l’intervalle admissible (Figure 6).

  3. Le pourcentage des noeuds soumis à des taux de chlore libre en dehors de l’intervalle [0,1 – 0,5] mg/L est de moins de 2 %. Seuls les noeuds N1 et N2, caractérisés par des temps de séjour qui ont atteint 19,2 h, présentent des taux de chlore libre inférieurs à 0,1 mg/L (Figure 1).

Figure 5

Somme des carrées des écarts pour les deux scénarios de chloration.

Sum square deviation of the two chlorination. approaches.

Somme des carrées des écarts pour les deux scénarios de chloration.

-> See the list of figures

Figure 6

Taux de chlore libre au niveau des points de contrôle avec les stations d’appoints.

Free chlorine concentrations at control nodes with booster stations.

Taux de chlore libre au niveau des points de contrôle avec les stations d’appoints.

-> See the list of figures

7. Conclusion

Cet article a présenté un AG pour la détermination des emplacements optimums des stations d’appoints de chlore sur les réseaux d’eau potable. Deux objectifs ont été considérés : (1) l’amélioration de l’homogénéité de la chloration et (2) la réduction du nombre de stations d’appoint de chlore sur le réseau. Le modèle a été testé sur un réseau de distribution où l’injection de chlore est initialement assurée au niveau d’un réservoir. Le gestionnaire y maintient un taux de chloration constant de 0,5 mg/L. Ce mode de gestion a été caractérisé par une somme des carrés des écarts égale à 65,9 mg2/L2, avec 27 % des noeuds soumis à des taux inférieurs à 0,1 mg/L. De plus, il a été démontré que l’adoption d’une consigne plus élevée (0,8 mg/L) ne permet pas d’améliorer la situation. L’application du modèle d’optimisation a permis de déterminer les emplacements de deux stations d’appoint de chlore, avec des consignes constantes (0,5 mg/L). La simulation de la solution optimale a révélé la réduction de la somme des carrés des écarts à 38,8 mg2/L2 et a assuré au niveau de plus de 98 % des noeuds des taux de chlore libre compris dans l’intervalle [0,1 – 0,5] mg/L.

L’AG proposé a montré son efficacité pour l’identification des emplacements optimums des stations d’appoint de chlore sur les réseaux de distribution. Ce modèle constitue une première étape de l’optimisation de l’homogénéité de la chloration, essentiellement sur les réseaux caractérisés par des inhomogénéités importantes des taux de chlore libre. L’utilisation de cet outil nécessite la modélisation hydraulique du réseau, la simulation du comportement du chlore libre et la définition des coefficients de réaction du chlore et les paramètres de l’AG. L’optimisation des consignes des points d’application du chlore est une étape ultérieure au présent travail. Cette opération est réalisée en fonction de la modulation de la demande ou suite à des modifications importantes des régimes hydrauliques. Lorsqu’il s’agit d’une gestion en temps réel de la chloration, l’optimisation des consignes peut être actualisée même à des pas de temps horaires.