Abstracts
Résumé
Cet article relate les étapes d’une recherche de développement didactique ayant mené à la création d’un outil informatique que nous avons nommé AnDIE, soit l’acronyme d’Analyse Didactique des Items avec Excel. Dans le cadre de cet article, nous montrons les différentes étapes qui nous ont permis de créer cet outil, basées sur le modèle de développement d’objet pédagogique de Van der Maren (1999). AnDIE vise à aider les apprenants à mieux comprendre les concepts et les techniques d’analyse de la théorie classique des tests. Dans cet article, il sera donc question de rendre compte de la démarche de conception de l’outil et de l’apport pédagogique et didactique de ce dernier dans un cours axé sur la mesure des apprentissages.
Mots-clés :
- Théorie classique de tests,
- didactique,
- application informatique,
- Excel,
- mesure
Abstract
This article describes the different steps of a didactic development research that led to the creation of a computer tool that we named AnDIE which is the acronym for Analyse Didactique des Items avec Excel. In this article, we show the different steps that allowed us to create this tool, based on the pedagogical object development model of Van der Maren (1999). AnDIE aims to help learners better understand the concepts and techniques of classical test theory. In this article, we will explain how we built the tool and how it can facilitate learning of classical test theory.
Keywords:
- Classical test theory,
- didactic,
- computer application,
- Excel,
- measurement
Article body
1. Contexte
Au Canada, seuls les programmes de maîtrise et de doctorat en mesure et évaluation permettent aux étudiants[1] de développer une expertise pointue en mesure dans un contexte éducatif. Il n’existe pas, comme dans d’autres disciplines, un programme de baccalauréat qui leur permet d’apprendre les concepts, les méthodes et les théories associés à la mesure. À titre d’exemple, aucun programme de formation des maîtres au Canada n’offre un cours en mesure des apprentissages. Comme le souligne Blais (2003), il y a plusieurs acceptions[2] associées à la mesure, que ce soit dans le cadre du courant de l’axiomatisation de la quantité, du mouvement du mental testing, ou encore de la théorie de la mesure conjointe additive. Dans le cadre de cet article, nous nous appuierons sur la proposition de Wilson (2005, p. 5) qui la définit comme :
… un processus visant à fournir des informations raisonnables et cohérentes sur la façon dont les réponses des sujets, qui peuvent exprimer des résultats scolaires, des attitudes ou tout autre construit humain, peuvent être traitées avec différents instruments comme des sondages, des questionnaires, des tests ou des échelles de mesure [traduction libre des auteurs][3].
L’apprentissage des théories et des modèles de la mesure[4] pose de nombreux défis. Malheureusement, peu d’études présentent de façon systématique ces défis et les pistes de solution pour les relever (Dahlman, 2014). Les seules recherches récentes sur lesquelles on peut s’appuyer, afin de dresser un parallèle, se sont principalement déroulées dans le contexte de l’enseignement des méthodes quantitatives (Buchler, 2009; Burton, 2003; Leavy, Hannigan et Fitzmaurice, 2013). Au regard des conclusions de ces chercheurs, on peut remarquer que plusieurs d’entre elles pourraient expliquer ce que nous observons dans le cadre de l’apprentissage de la mesure : dans la majorité des universités canadiennes, le nombre peu élevé d’étudiants dans les programmes de mesure et évaluation, offerts dans les facultés d’éducation, rendent les choix de cours souvent problématiques; ceux dans lesquels il est possible d’aborder les concepts avancés en mesure sont souvent très rares. Les spécialistes du domaine qui exercent sur le terrain ont, eux aussi, accès à des offres de formation limitées, voire inexistantes. Qui plus est, le berceau des théories de la mesure se trouve aux États-Unis, comme en témoignent la vaste majorité des écrits des formations (parfois offertes en ligne) en anglais recensés.
Pour certains francophones, cela représente un obstacle supplémentaire pour l’apprentissage des théories de la mesure. Un autre frein important est, à notre avis, la connaissance souvent parcellaire ou carrément déficiente des préalables mathématiques. L’étude des théories de la mesure exige un niveau minimal[5] en mathématiques afin de comprendre adéquatement les démonstrations qui accompagnent l’explication des concepts, les techniques ou encore les méthodes. Chez plusieurs personnes (étudiants, praticiens, etc.) qui oeuvrent ou désirent oeuvrer en évaluation, ces lacunes apparaissent souvent comme étant insurmontables dans la compréhension des théories ou des modèles de la mesure. Ce constat est, à de maintes reprises, mentionné dans les études qui s’intéressent à l’apprentissage des méthodes quantitatives (Lunsford et Poplin, 2011).
Enfin, notons que la discipline mesure et évaluation telle qu’on la connaît aujourd’hui est une jeune discipline qui est née au détour des années 1960. Au Québec, comme dans d’autres juridictions, un schisme est alors survenu, car la création des facultés d’éducation a entraîné un besoin d’experts en évaluation des apprentissages. En effet, il fallait former les futurs enseignants du primaire et du secondaire non seulement à enseigner, mais aussi à évaluer. À cette époque, les experts de cette discipline étaient des psychométriciens, premiers professeurs à la formation initiale des maîtres qui offraient les cours en évaluation des apprentissages. Quelques décennies ont passé et la mesure et l’évaluation sont devenues une discipline à part entière dans chaque faculté d’éducation. De nos jours, quasi chacune d’entre elles au Canada possède au moins un expert en mesure et évaluation des apprentissages. Paradoxalement, pendant que l’expertise en évaluation des apprentissages se développait dans les institutions académiques, celle de la mesure (édumétrie) déclinait. Aujourd’hui, il devient parfois difficile de trouver un seul de ces experts dans les facultés d’éducation. Pourtant, les besoins concernant l’étude des propriétés des instruments sont loin de se tarir et cela n’est pas récent (Lambert, 1991).
2. Origine du projet
Ce projet de recherche et de développement a émergé à partir de travaux contractuels que nous menions avec un ministère de l’Éducation d’une province canadienne. Dans le cadre de ces travaux, nous avions la tâche d’étudier les propriétés métriques des items à un test administré à tous les élèves de la province en question. Au début de l’étude, nous avons tôt fait de nous rendre compte que le responsable et son équipe possédaient des connaissances limitées en théorie de la mesure. Nous avions alors le mandat de non seulement produire des analyses pertinentes, mais aussi de les présenter de façon compréhensible à un lecteur non pas expert, mais novice[6] en la matière. Il était impératif pour nous de trouver une façon de rendre accessibles autant les éléments théoriques et méthodologiques que les résultats. En effet, nous voulions que les personnes du ministère comprennent les résultats et soient en mesure d’y jeter un regard critique. En définitive, nous souhaitions surtout qu’elles les utilisent pour bonifier les épreuves produites lors des années subséquentes. C’est dans ce contexte que le projet de développement d’AnDIE – Analyse Didactique des Items avec Excel – s’est amorcé. Après avoir élaboré un canevas de présentation des résultats à caractère pédagogique, nous avons décidé de l’automatiser à l’aide d’Excel.
Ce texte vise à exposer la démarche de conception et son résultat, à savoir l’application AnDIE qui sera aussi présentée. La section suivante décrit les étapes qui nous ont guidés pour la conception de cet outil. Cet article vise, également, à démontrer l’utilité de recourir à un modèle de développement quand des pédagogues souhaitent innover en créant un nouvel objet pédagogique.
3. Étapes du développement de l’objet pédagogique
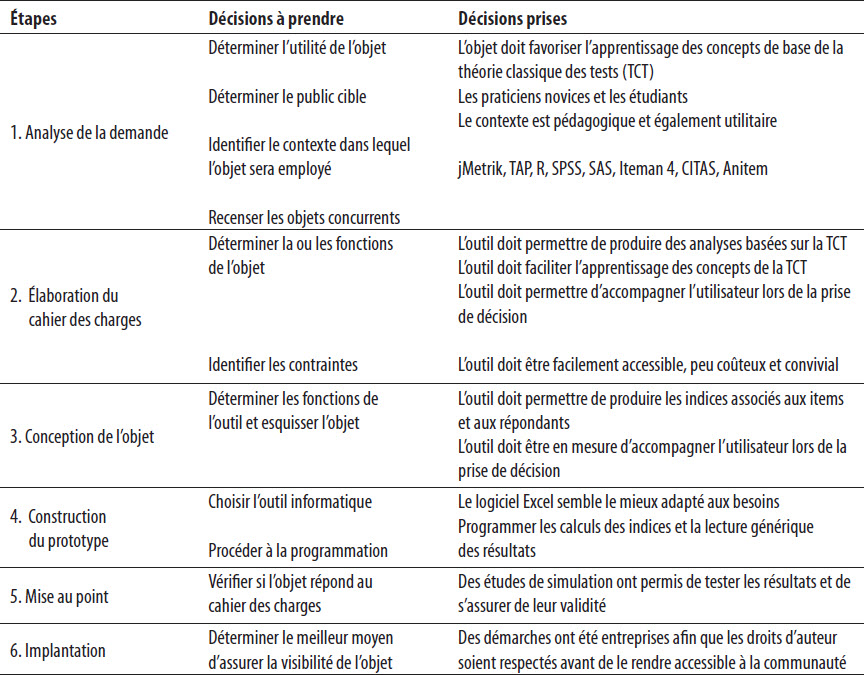
À partir du moment où l’idée de concevoir un outil pour favoriser l’apprentissage de la mesure a pris naissance, il fallait alors se doter d’une méthode de travail reconnue empiriquement. Nous avons choisi le modèle de développement d’objet pédagogique proposé par Van der Maren (1999) pour des raisons de parcimonie; en effet, il s’agit d’un modèle à la fois simple et complet que nous exposerons maintenant. Ce dernier propose une méthode en six étapes : 1) analyse de la demande, 2) élaboration du cahier des charges, 3) conception de l’objet, 4) construction du prototype, 5) mise au point et 6) implantation. Le tableau 1 brosse un portrait sommaire des éléments qui seront maintenant discutés. La première colonne présente les étapes du modèle de Van der Maren (1999), la seconde expose les décisions à prendre et la troisième affiche les décisions effectivement prises dans le cadre de ce projet de conception d’objet pédagogique. Dans le cadre de cet article, l’accent sera mis davantage sur les cinq premières étapes puisque la sixième, comme le souligne Van der Maren, échappe le plus souvent aux concepteurs. Pour éviter la redite, nous avons également choisi de regrouper les étapes 3 et 4 ainsi que les étapes 5 et 6.
Tableau 1
Étapes ayant mené à la création d’AnDIE
3.1 Analyse de la demande
La première étape du modèle proposé par Van der Maren (1999) consiste à identifier le(s) besoin(s), déterminer à qui s’adressera l’objet, identifier le contexte dans lequel l’objet sera utilisé et, finalement, recenser les concurrents qui répondent déjà complètement ou partiellement au(x) besoin(s). Dans le cas qui nous occupe, nous souhaitions concevoir un outil permettant de favoriser l’apprentissage de la théorie classique des tests (TCT) chez des apprenants novices en la matière. L’outil devait pouvoir être utilisé dans le cadre de cours sur la mesure des apprentissages en contexte universitaire ou de formations en contextes variés, comme la formation continue ou en entreprise. Dans tous les cas, l’accent devait être résolument didactique[7] pour offrir aux apprenants un outil guidant et favorisant les apprentissages.
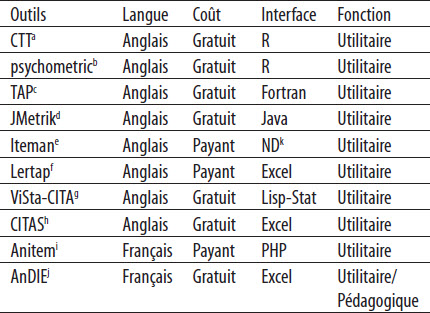
Avant d’entreprendre la démarche de conception, nous avons réalisé une recension des écrits pour recenser les logiciels qui permettent de réaliser des analyses se basant sur la TCT. Nous avons, entre autres, consulté la base de données entretenue par le National Council on Measurement in Education (n.d.), fait une recherche autant dans les bases de données ERIC[8] que dans PUBMED et, plus généralement, sur Internet afin de trouver les outils commerciaux consacrés aux tâches qui nous intéressaient. Nous avons ensuite analysé chacun des logiciels pour déterminer leurs forces et leurs limites, particulièrement sous l’angle de l’apprentissage de la TCT. Ainsi avons-nous, entre autres, examiné la facilité à : 1) saisir ou importer les données, 2) produire les analyses, 3) interpréter les résultats et 4) exporter les résultats vers un logiciel de traitement (ex. Excel, Word, PowerPoint, etc.). Le tableau 2 présente les principaux outils que nous avons répertoriés. On y présente également la langue d’usage, les coûts du logiciel, l’interface ainsi que la fonction principale telle que mentionnée par les auteurs de chacun d’entre eux.
Tableau 2
Principaux logiciels consacrés à l’analyse d’items en se basant sur la théorie classique des tests
a.Willse (2018). b. Fletcher (2010). c. Brooks (2016). d. Meyer (2016). e. Berk et Griesemer (1976). f. Nelson (2001). g. Ledesman et Molina (2009). h. Thompson (n.d.). i. Auger (2013). j. Dionne et Grondin (2018). k. Non disponible.
Comme on peut le constater, la grande majorité des outils sont accessibles en anglais seulement. Seuls les logiciels Anitem et AnDIE proposent des solutions en français. On constate également que la plupart (7/10) des logiciels sont gratuits (freeware). Seuls les logiciels Iteman 4, Lertap et Anitem sont payants. En ce qui concerne l’interface et la base de programmation, les codes de deux d’entre eux (CTT et Psychometric) sont accessibles dans les bibliothèques du logiciel libre R. C’est ce langage de programmation qui est donc à la base des outils proposés. Le logiciel Excel est mis à profit pour trois outils (Lertap, CITAS, AnDIE) alors que TAP est codé en Fortran, jMetrik en Java, Anitem en PHP et ViSta-CITA avec Lisp-Stat. On remarque donc une variété importante de langages de programmation utilisés. Tous les outils fonctionnent sous Windows et la moitié sont compatibles avec Mac OS. Enfin, la majorité (9/10) des logiciels sont à vocation utilitaire, c’est-à-dire qu’ils servent principalement pour la production d’analyses d’items. Le seul outil qui vise également à répondre à des considérations pédagogiques est AnDIE. Nous entendons par « pédagogiques » des outils pour lesquels on indique clairement qu’ils peuvent servir dans un contexte d’enseignement ou encore qui s’adressent à des usagers novices.
Cette recension nous a permis de constater que le besoin que nous avions subodoré était bien réel et qu’il y avait place pour un outil dont la vocation principale serait pédagogique. En effet, ceux qui sont disponibles ont pour rôle premier de produire des indices psychométriques sans se soucier de rendre l’ergonomie attrayante pour l’usager. Les résultats sont, dans la plupart des cas, présentés sous la forme de tableaux de données n’offrant aucun indice sur la façon de les interpréter. L’usager est ainsi laissé à lui-même pour prendre des décisions comme soustraire un item des analyses afin de vérifier si cette action entraîne un gain au regard de la qualité de la mesure. Devant la paucité des outils existants, il nous semblait pertinent d’en proposer un qui répondrait à des impératifs résolument didactiques.
3.2 Élaboration du cahier des charges
À la seconde étape, il s’agissait alors d’identifier précisément les fonctions de l’outil et les contraintes qu’il faut prendre en compte. En ce qui concerne les fonctions spécifiques, elles étaient de deux ordres : 1) produire des indices précis et scientifiquement valides basés sur la TCT, 2) favoriser les apprentissages des apprenants en leur offrant, de façon automatique, une première interprétation des indices.
3.2.1 Les indices
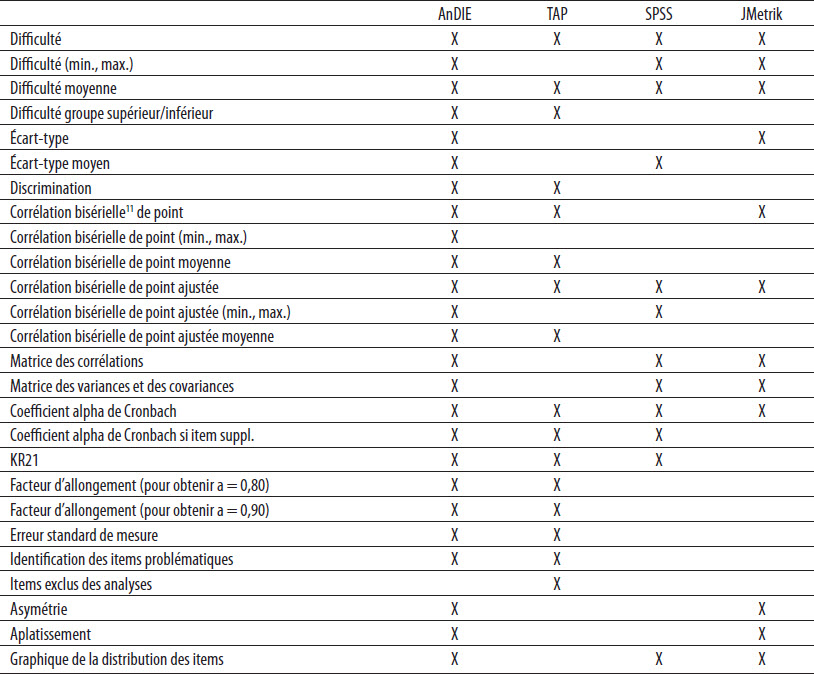
Dans le cadre de l’élaboration de cet objet didactique, nous avons intégré différents indices édumétriques relatifs autant aux items[9] qu’aux sujets. Les tableaux 3 et 4 présentent les indices retenus. Chaque « X » signifie que l’indice est directement fourni par le logiciel en question. La nuance est ici importante, car notre intention était de développer un outil favorisant l’apprentissage de la théorie classique des tests par un usager novice. Or, ce dernier aurait possiblement de la difficulté à assimiler les notions s’il devait, en plus, réaliser une série de manipulations compliquées avant d’obtenir le résultat souhaité. Par exemple, il est possible avec SPSS de calculer l’écart-type des scores des sujets. De fait, SPSS permet de calculer à peu près tous les indices présentés dans les deux tableaux qui suivent en utilisant les menus ou encore en programmant les sorties (fonction syntaxe). Par contre, il faut que l’usager réalise un certain nombre de manipulations avec ce dernier avant d’obtenir cette information. Les éléments de programmation ne faisant généralement pas partie du coffre à outils de l’analyste débutant, nous avons coché uniquement les résultats que SPSS permettait d’obtenir simplement avec les menus déroulants. Le lecteur est invité à prendre connaissance des tableaux 3 et 4 en ayant cette nuance à l’esprit. On retrouve également des informations comparatives avec deux autres outils, à savoir TAP et jMetrik. Nous avons choisi de comparer la présence des indices avec ces outils en raison de leur accessibilité (TAP et jMetrik sont gratuits). Nous avons aussi retenu SPSS, car il s’agit, encore aujourd’hui, de l’un des logiciels le plus souvent employés pour produire des analyses statistiques en sciences sociales.
Dans les paragraphes qui suivent, nous présenterons sommairement ces indices[10] édumétriques. Ajoutons que l’outil que nous avons développé ne prend en compte, dans cette première version d’AnDIE, que les données dichotomiques (les scores peuvent prendre deux valeurs, par exemple 0 ou 1 comme c’est souvent le cas dans le cadre de la correction d’items à choix multiples).
Tableau 3
Indices comparés des items avec les outils AnDIE, TAP, SPSS et JMetrik
En ce qui concerne les items, les principaux indices employés sont : 1) l’indice de difficulté (p), 2) l’indice de discrimination (D), 3) les corrélations item-total (bisérielle[11] de point et bisérielle de point ajustée), 4) la variance, 5) l’indice alpha de Cronbach, 6) l’indice alpha de Cronbach en cas de suppression de l’item, 7) l’indice Kuder-Richardson (KR-21), 8) le nombre d’items à ajouter pour améliorer l’indice alpha de Cronbach (formule de prédiction de Spearman-Brown), 9) la distribution des scores sous la forme d’un graphique, et 10) les caractéristiques de la distribution des scores des items (asymétrie et aplatissement). Quand cela est approprié, AnDIE présente également les valeurs minimum, maximum et moyenne et l’écart-type de la distribution. À titre de comparaison, on constate qu’AnDIE propose 25 des 26 indices comparés. Les trois autres outils en présentent beaucoup moins puisque TAP en offre 16, jMetrik en propose seulement 12 et SPSS n’en fournit, quant à lui, que 12 au moyen des menus déroulants. Dans ce dernier cas, il est possible de calculer les 14 autres indices que donne AnDIE, mais au prix de manipulations relativement compliquées pour des novices. Par exemple, pour calculer l’indice de discrimination (D), l’analyste doit ordonner les scores à une épreuve (du plus élevé au plus faible) afin de pouvoir identifier le groupe dit supérieur (27 % des scores les plus élevés) et le groupe inférieur (27 % des scores les plus faibles). Cette identification se fait manuellement puisqu’il faut calculer soi-même le nombre de sujets appartenant à chacun des groupes (27 %). Une fois les deux groupes identifiés, il faut utiliser le menu pour obtenir un tableau croisé à partir duquel le taux de réussite (difficulté moyenne) de chacun des groupes pourra être extrait. Enfin, l’indice de discrimination pourra être calculé en soustrayant la difficulté moyenne du groupe inférieur de celle du groupe supérieur. Comme on peut le constater, il s’agit de manipulations plutôt compliquées pour des novices.
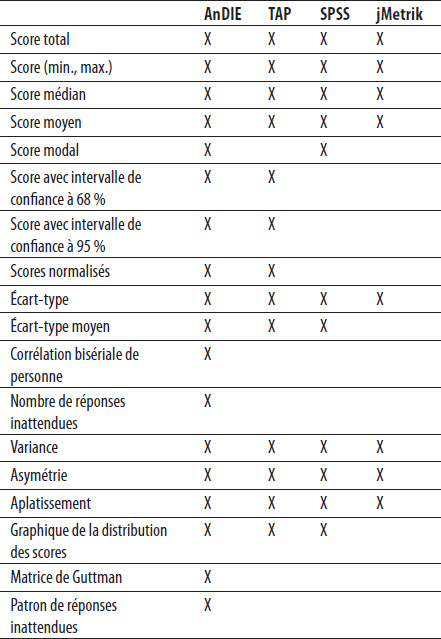
Le tableau 4 présente les indices associés aux sujets. Les indices généraux fournis par AnDIE sont : 1) le score du sujet, 2) l’écart-type de la distribution des scores des sujets, 3) la corrélation bisériale (aussi appelée bisérielle) de personne, 4) le nombre de réponses inattendues, 5) l’allure de la distribution (variance, asymétrie et aplatissement, graphique), 6) la matrice de Guttman et 7) les patrons de réponses inattendues. En comparant les informations fournies par AnDIE avec les trois autres outils, on constate qu’AnDIE en présente 18, TAP en propose 13 et SPSS n’en fournit que 11 alors que jMetrik, quant à lui, en offre 8.
Tableau 4
Indices comparés des sujets avec les outils AnDIE, TAP, SPSS et jMetrik
Dans le cahier des charges que nous avons rédigé, nous comptions donc 43 indices édumétriques (25 indices associés aux items et 18 associés aux sujets) que nous souhaitions intégrer à l’outil développé.
AnDIE a été conçu avec le logiciel Microsoft Excel (version 11.5612.5606). Plusieurs raisons nous ont incités à utiliser ce logiciel grand public plutôt, par exemple, qu’un langage de programmation comme C++. Premièrement, nous voulions une interface connue par la plus grande proportion d’apprenants possible et qui leur est familière. Les produits Microsoft sont certainement les outils informatiques les plus diffusés sur la planète et nous étions sûrs que les utilisateurs d’AnDIE seraient plus à l’aise avec une interface comme celle qui est offerte sur Excel. Deuxièmement, nous désirions offrir un outil gratuit et facilement accessible. AnDIE n’est pas, en un sens, totalement gratuit, car l’utilisateur doit déjà avoir Excel sur son poste de travail pour pouvoir l’utiliser. Cependant, nous sommes sûrs que les usagers qui souhaitent analyser leurs données avec une théorie de la mesure ont déjà Excel, ce qui, du coup, rend AnDIE très accessible. Troisièmement, ce projet a été réalisé sans aucun financement externe. Nous devions alors développer un prototype, mais avec des moyens limités. Le logiciel Excel étant offert à prix abordable dans le milieu académique, il s’est donc avéré une solution idéale pour notre contexte. Quatrièmement, il était important pour nous de développer un outil fonctionnel afin de tester l’intérêt de ce dernier auprès du public cible; un tel outil pourrait aussi nous aider à mieux expliquer, éventuellement, à des programmeurs ce que nous souhaitons intégrer comme nouvelle fonctionnalité dans une prochaine version de l’application. Enfin, mentionnons que puisque nos intentions étaient pédagogiques et didactiques, nous avons décidé de limiter les analyses à 100 sujets et à 30 items. Ces valeurs nous apparaissent raisonnables autant dans un contexte édumétrique que dans un contexte pédagogico-didactique. Ces tailles d’échantillon sont suffisantes pour produire des analyses basées sur la TCT tout en permettant à Excel de générer rapidement les résultats. Les tests nous ont montré qu’une taille d’échantillon plus élevée pouvait ralentir les calculs et augmenter ainsi le temps de génération des résultats par Excel.
3.2.2 Favoriser l’apprentissage
La production d’indices édumétriques valides et fiables est une condition essentielle lors de la création d’un outil pédagogique, mais non suffisante. Dans le cahier des charges que nous avons rédigé, la fonction pédagogique était au coeur du développement et représentait le besoin auquel nous souhaitions répondre. Il fallait donc concevoir un dispositif permettant d’accompagner les apprenants dans l’interprétation de ces indices. En effet, les étudiants sont parfois totalement désemparés, car ils arrivent à générer des indices statistiques en suivant une séquence (un mode d’emploi), mais ils n’arrivent pas, par la suite, à les interpréter pour prendre les décisions qui s’imposent (ex. éliminer un item problématique dont la discrimination est négative).
De plus, la plupart des logiciels présentent les résultats sous la forme de tableaux ou de graphiques, mais ces derniers ne donnent aucun indice pour identifier quelles sont les informations importantes pour prendre des décisions éclairées. Pour y arriver, nous avons mis en place deux stratégies complémentaires : 1) l’utilisation d’un code de couleur et 2) un paragraphe généré automatiquement sur l’interprétation des indices. L’idée de mettre à profit ces deux stratégies nous est venue en analysant les sorties du logiciel SPSS. En effet, les dernières versions de ce logiciel offrent des indices (ex. identification des statistiques significatives à p 0,05) permettant de guider l’utilisateur. Partant de cette idée, nous avons adapté et étendu AnDIE afin de tirer profit de ces deux stratégies. Les deux caractéristiques, précédemment mentionnées, distinguent AnDIE des autres logiciels ou outils qui sont à la disposition des professeurs ou des formateurs. Dans la section suivante, nous expliquons comment nous avons intégré ces caractéristiques à l’objet développé.
3.3 Conception de l’objet et construction du prototype
La troisième étape du modèle de Van der Maren (1999) consiste à concevoir l’objet. Il faut ainsi esquisser le plan qui permet à la fois de répondre au besoin et de tenir compte des contraintes. Dans le cas qui nous occupe, il fallait donc réfléchir à un outil qui permettait de générer les indices édumétriques de la TCT, dans un environnement pédagogique favorisant les apprentissages, et qui était familier aux apprenants. Notre choix s’est rapidement arrêté sur Excel, comme nous l’avons déjà souligné, un logiciel qui permet de réaliser des calculs et qui intègre déjà des fonctions statistiques utiles dans le cadre de la TCT. Une rapide analyse nous a permis de constater qu’il était réaliste de produire les calculs nécessaires à la production des 43 indices que nous souhaitions fournir.
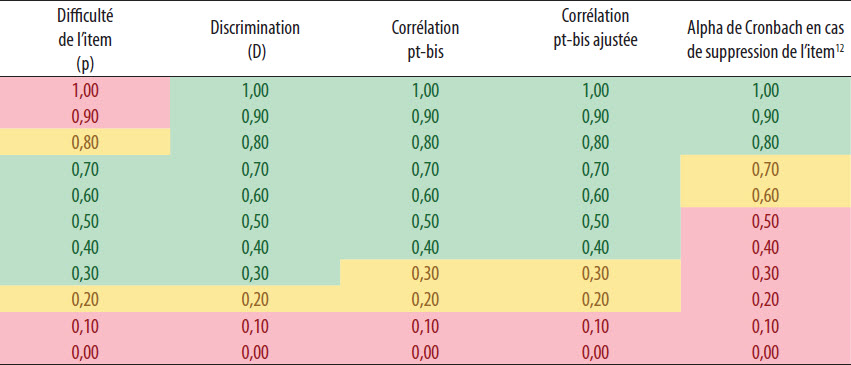
Rappelons qu’AnDIE permet non seulement de calculer les indices de la TCT, mais également de générer automatiquement leur interprétation. Pour y arriver, nous avons dû identifier les balises habituellement recommandées pour chacun des indices. Le tableau 5 présente un exemple pour illustrer ces intervalles. Les cellules colorées en rouge indiquent des valeurs qui se retrouvent à l’extérieur des balises jugées adéquates pour la statistique en question. Les cellules en jaune représentent des valeurs susceptibles d’être problématiques et méritent ainsi l’attention de l’analyste. Ce sont ces items dont il faudrait discuter avant de prendre une décision finale comme conserver l’item, le modifier ou l’éliminer. Enfin, les cellules colorées en vert représentent des valeurs situées à l’intérieur des balises que l’on retrouve dans les écrits scientifiques. Cela ne signifie pas qu’il ne faille pas vérifier ces items, mais plutôt qu’a priori, il ne semble pas y avoir de problèmes importants.
Tableau 5
Exemple d’intervalles permettant de baliser le jugement au regard de la difficulté, de la discrimination, de la corrélation bisérielle de point ajustée et de la valeur de l’alpha de Cronbach en cas de suppression de l’item[12]
Bien que ces balises s’appuient sur des recommandations contenues dans les écrits scientifiques (les balises présentées dans le tableau 5 s’appuient, par exemple, sur les propositions d’Ebel, 1965), nous étions conscients des limites d’une proposition unique. En effet, ces intervalles sont discutables et peuvent varier, par exemple, selon le contexte de testing. Ainsi avons-nous ajouté une contrainte dans le cahier des charges voulant que ces intervalles puissent être modifiables selon les besoins des apprenants. La figure 1 ci-dessous présente l’onglet 8 qui permet de paramétrer les balises des différents indices.
Figure 1
Onglet 8 permettant de paramétrer les balises pour chacun des indices
En nous basant sur ces intervalles, nous avons ensuite généré des phrases types correspondant aux interprétations adéquates à l’égard de chacun des indices. Ce sont donc les balises et les codes de couleur qui ont généré automatiquement les paragraphes permettant une première analyse des indices. La figure 2 qui suit présente un exemple des indices, codes de couleur et interprétations que fournit AnDIE.
Figure 2
Un exemple des informations fournies par AnDIE
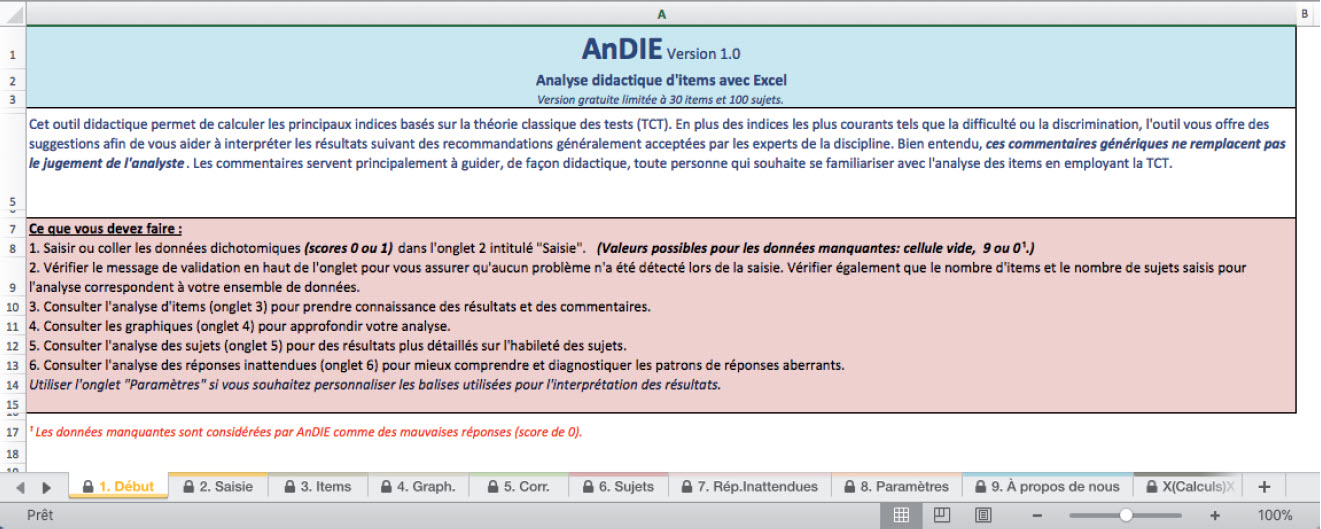
La figure 3 présente la fenêtre qui accueille les apprenants à l’ouverture d’AnDIE. Ces derniers n’ont qu’à ouvrir l’application et à ensuite naviguer dans l’un ou l’autre des neuf onglets.
Figure 3
Une vue d’ensemble d’AnDIE
Dans le cadre de cet article, nous présenterons principalement les onglets 3 et 6 qui affichent, respectivement, les informations sur les items et sur les sujets. La figure 4 présente une illustration de ce qui est présenté aux apprenants quand ils prennent connaissance des informations relatives aux items.
Figure 4
L’onglet présentant les résultats pour chacun des items
Les 10 premières colonnes indiquent respectivement le numéro de l’item, le score à l’item, l’indice de difficulté, la proportion de réussite pour les sujets du groupe supérieur, la proportion de réussite dans le groupe inférieur, l’indice de discrimination, la valeur de la corrélation bisérielle de point, la valeur de la corrélation bisérielle de point ajustée, la valeur du coefficient alpha de Cronbach si l’on élimine ledit item et la valeur de la variance des scores à l’item. Ces différents indices ou ces différentes valeurs faisaient partie du cahier des charges. Notons que nous avons décidé de conserver la proportion de réussite pour les sujets du groupe inférieur ou supérieur pour des raisons clairement pédagogiques. En effet, ces valeurs n’ajoutent que peu d’information dans la mesure où l’on présente déjà l’indice de discrimination et la valeur de la corrélation ajustée point-bisériale. Par contre, elles permettent aux apprenants de mieux comprendre le principe de l’indice de discrimination : les sujets les plus compétents devraient réussir dans une grande proportion les items les plus difficiles et les sujets les moins compétents ne devraient pas réussir facilement autant les items difficiles que les items faciles.
Toujours en se référant à la figure 4, on peut voir l’utilité des codes de couleur qui permettent de rapidement constater que l’indice de difficulté, l’indice de discrimination et la valeur du coefficient alpha de Cronbach en cas de suppression de l’item semblent adéquats (en vert). Quant à elles, les valeurs corrélationnelles sont à surveiller (en jaune). Enfin, la valeur de la variance serait, dans ce cas-ci, à surveiller (en rouge).
La onzième colonne présente le paragraphe synthèse qui permet de guider l’analyse de l’item étudié. Le court texte reprend chacun des indices en présentant une première tentative d’analyse des résultats. Bien entendu, l’étudiant ou l’utilisateur novice devra, par la suite, poursuivre le travail d’analyse en établissant les liens qui s’imposent. La visée de cette lecture générique est de guider l’utilisateur afin de lui permettre d’amorcer une réflexion sur les données analysées.
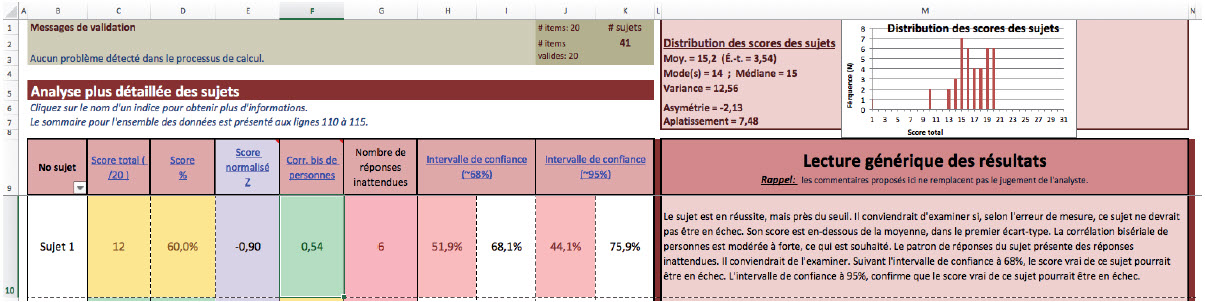
De la même manière que pour les items, la figure 5 présente les résultats pour les sujets. Les 10 premières colonnes présentent respectivement : le numéro du sujet, le score total, le score total en pourcentage, le score normalisé, la valeur de la corrélation bisérielle de personne, le nombre de réponses inattendues, l’intervalle de confiance à 68 % du score total et l’intervalle de confiance à 95 % du score total.
Figure 5
L’onglet présentant les résultats pour chacun des sujets
Les codes de couleur précédemment présentés sont utilisés de la même façon pour les indices relatifs aux sujets. Dans l’exemple de la figure 5, on constate que le score du sujet 1 est à surveiller, car il se situe près du seuil fixé (par l’utilisateur) à 12/20 (60 %) (en jaune). La corrélation bisérielle de personne est jugée adéquate (en vert). Le vecteur-réponse du sujet 1 présente des valeurs inattendues qui ne respectent pas l’ordre de Guttman (en rouge). On remarque également que les scores minima dans chacun des intervalles de confiance se situent en deçà du seuil fixé à 60 (en rouge). Ce faisant, l’analyste devrait porter attention à ce résultat puisqu’il existe une probabilité non nulle que le score du sujet se situe en deçà du seuil de passation.
La onzième colonne présente le paragraphe synthèse qui permet de guider l’analyse des scores pour le sujet 1. Le court texte reprend chacun des indices en présentant une première tentative d’analyse des résultats de façon analogue à ce qui a déjà été présenté dans le cadre de l’analyse de l’item 1. L’étudiant ou l’utilisateur novice peut alors se référer aux informations sur la distribution des scores des sujets qui sont aussi présentées dans cet onglet.
3.4 Mise au point et implantation
Les différentes versions de l’outil ont été testées de façon itérative au fur et à mesure qu’elles étaient disponibles. Lorsque l’outil nous a semblé suffisamment peaufiné, nous avons simulé des données pour ensuite comparer les résultats obtenus à partir d’AnDIE avec d’autres logiciels qui ont pour vocation de fournir des résultats d’analyse semblables. En effet, nous devions nous assurer que l’outil développé produise des résultats à la fois justes et précis. Le paragraphe qui suit présente l’information sur cette étape du processus de validation de l’outil que nous avons créé.
Nous avons simulé six ensembles de données à l’aide du logiciel Test Analysis Program (TAP) développé par Brooks (2016) à l’Université de l’Ohio. Les ensembles de données (100 sujets et 30 items) ont été simulés afin d’obtenir un éventail de scores moyens de 40 %, 50 %, 60 %, 70 %, 80 %, 90 % et 95 %, ce que ne permettraient pas facilement des données réelles. Nous avons donc examiné les résultats au regard de ces sept ensembles de données simulées; il s’agissait de simuler un test très difficile à un test très facile. Après avoir simulé ces données, nous les avons d’abord utilisées avec TAP pour ensuite les importer dans les logiciels JMetrik (Meyer, 2016) et IBM SPSS Statistics for Windows (version 24.0).
Les tableaux 6 et 7 présentent les résultats comparatifs des indices associés aux items et aux indices associés aux sujets pour les quatre logiciels qui ont servi à analyser les résultats. En examinant le tableau 6, on peut constater que les valeurs associées aux différents indices sont exactement les mêmes pour les quatre logiciels, sauf pour l’indice de discrimination. Il y a des différences négligeables entre les valeurs produites par AnDIE, TAP et jMetrik. Nous n’avons pas accès au code des logiciels et il est difficile de donner une raison scientifiquement fondée pour expliquer ces nuances[13].
Tableau 6
Comparaison de la plupart des résultats communs obtenus avec AnDIE, TAP, SPSS et JMetrik pour les paramètres des items
Le tableau 7 permet d’examiner les résultats pour les indices associés aux sujets. On peut constater qu’il n’existe aucune différence dans l’estimation des indices en lien avec les scores. En ce qui concerne les paramètres des distributions, on note des différences négligeables certainement en raison des méthodes d’arrondissement des logiciels.
Tableau 7
Comparaison des résultats communs obtenus avec AnDIE, TAP, SPSS et jMetrik pour les paramètres des sujets
Les différentes simulations montrent que l’outil que nous avons développé donne des résultats similaires à ceux des autres logiciels communément utilisés en édumétrie. Les objectifs d’AnDIE n’étant pas uniquement de produire avec précision les différents indices habituellement utilisés lors d’une analyse d’items à l’aide de la TCT, nous avons également réalisé une validation auprès d’experts qui ont accepté d’examiner AnDIE. À ce point-ci, deux experts ont pu remplir notre questionnaire de rétroaction. Ainsi, au regard des objectifs pédagogiques et didactiques d’AnDIE, tous deux indiquent qu’AnDIE est, aux niveaux pédagogique et ergonomique, facile à utiliser et aide à apprendre l’analyse des propriétés métriques des items. De plus, les commentaires génériques formulés par AnDIE sont justes et pertinents pour permettre une première analyse des résultats. Pour l’un des experts, les commentaires sont suffisamment adaptés à des apprenants novices; pour l’autre, ils ne le sont pas suffisamment. Pour compléter cette réponse, l’expert suggère de faire une synthèse des commentaires afin de fournir un verdict à l’utilisateur, à savoir, par exemple, s’il convient « d’éliminer l’item », de le « travailler » ou de le « conserver ».
Rappelons que notre objectif n’est pas de suggérer une conclusion à l’analyste, mais plutôt de faciliter son apprentissage des concepts de la TCT en l’accompagnant dans sa prise de décision. Nous croyons que suggérer un verdict ne répondrait pas à ces objectifs puisque les décisions de l’analyste doivent prendre en compte les objectifs et les contraintes liés à l’opération de mesure, des informations qu’AnDIE ne peut pas traiter. Enfin, les experts indiquent qu’AnDIE présente suffisamment de données édumétriques pour effectuer une analyse d’items adéquate. En conséquence, les experts sont d’avis qu’AnDIE pourrait être utilisé dans le cadre d’un cours de niveau maîtrise qui aborde les notions de mesure.
Conclusion
Cet article visait à présenter un nouvel outil que les professeurs ou formateurs en édumétrie peuvent utiliser dans le cadre de leurs cours ou de leurs formations. Il cherchait également à montrer la pertinence de s’appuyer sur un modèle théorique lors de la conception d’un objet pédagogique, dans ce cas-ci le modèle développé par Van der Maren (1999). Les résultats montrent que l’outil permet de générer des informations valides au regard des différents indices édumétriques. L’étude est cependant loin d’être complétée, car il reste à mesurer les effets d’un tel outil sur les apprentissages des étudiants. Nous souhaitons également élargir l’étendue des données analysables en permettant le traitement des scores polytomiques ainsi que l’analyse des leurres. Enfin, nous examinerons la possibilité de traiter des échantillons plus grands autant à l’égard des items que des sujets.
Appendices
Notes
-
[1]
Le masculin est utilisé dans ce texte dans le seul but d’en alléger la lecture.
-
[2]
Le lecteur intéressé peut se référer à cet auteur pour un regard panoramique de ces dernières.
-
[3]
Wilson (2005, p. 5) : « The central purpose of measurement, as interpreted here, is to provide a reasonable and consistent way to summarize the responses that people make to express their achievements, attitudes, or personal points of view through instruments such as attitude scales, achievement tests, questionnaires, surveys, and psychological scales. »
-
[4]
La psychométrie consiste à recourir à des modèles de mesure pour rendre compte des construits psychologiques alors que la mesure (aussi appelée édumétrie) consiste à recourir à des modèles de mesure afin de circonscrire les apprentissages.
-
[5]
Nous entendons par niveau minimal la connaissance, par exemple, des concepts de base en statistique (ex. variance, moyenne, etc.).
-
[6]
Nous qualifions de « novice » une personne qui n’a pas suivi de cours en mesure.
-
[7]
Dans le cadre de cet article, nous retenons la définition proposée par Thouin (2014, p. 8) concernant le terme didactique : « La didactique est l’étude des questions d’ordre cognitif posées par l’enseignement et l’apprentissage des différentes matières scolaires. »
-
[8]
Nous avons employé les mots-clés suivants ainsi que leur équivalent en français : test theory, classical test theory, software, item analysis, difficulty, discrimination, et tool (théorie des tests, théorie classique des tests, logiciel, analyse d’item, difficulté, discrimination, outil).
-
[9]
Les items correspondent à des énoncés ou à des questions servant de stimulus alors que les sujets correspondent aux individus qui répondent aux stimuli (Osterlind, 1998).
-
[10]
Puisque ces derniers sont standardisés, nous ne les présenterons pas de façon détaillée et renverrons plutôt le lecteur intéressé aux ouvrages de référence sur lesquels nous nous sommes nous-mêmes appuyés (Crocker et Algina, 2008; Cronbach, 1951; Ebel, 1965; Guilford, 1965).
-
[11]
Nous tenons à rappeler au lecteur que les termes : corrélation bisérielle et point bisérial ont la valeur sémantique.
-
[12]
Les écrits scientifiques ne sont pas toujours très clairs sur les balises à utiliser pour interpréter certains indices et c’est le cas pour l’interprétation de la valeur de l’alpha de Cronbach en cas de suppression de l’item. Nous avons choisi de fournir des balises basées sur la comparaison entre l’alpha général et l’alpha en cas de suppression de l’item.
-
[13]
On utilise généralement 27 % des données du groupe inférieur et 27 % des données du groupe supérieur, mais certains chercheurs divisent les groupes en proportion égale (33 %), ce qui explique peut-être, en partie, les nuances. Aussi, certains logiciels (ex. jMetrik) utilisent la valeur de la corrélation ajustée point-bisériale pour la discrimination, ce qui peut aussi expliquer les différences.
Références
- Auger, R. (2013). Anitem (version 2 Web) [logiciel]. Récupéré du site OgDDASt : http://oddas.ca
- Berk, R. A. et Griesemer, H. A. (1976). Iteman: An item analysis program for tests, questionnaires, and scales. Educational and Psychological Measurement, 36(1), 189-191. doi:10.1177/001316447603600122
- Blais, J.-G. (2003). Synthèse sur les fondements de la mesure et sur la contribution de la modélisation moderne. Dans J.-G. Blais et G. Raîche (dir.), Regards sur la modélisation de la mesure en éducation et en sciences sociales (p. 9-32). Québec, Canada : Presses de l’Université Laval.
- Brooks, G. (2016). TAP: Test analysis program (version 12.9.23) [logiciel]. Récupéré du site de l’auteur : http://ohiouniversityfaculty.com/brooksg
- Buchler, J. (2009). Teaching quantitative methodology to the math averse. Political Science and Politics, 42(3), 527-530. doi:10.1017/S1049096509090842
- Burton, S. (2003). Not another stats course! A problem‐based quantitative methods course for (reluctant) doctoral students. Decision Sciences Journal of Innovative Education, 1(1), 151-154. doi:10.1111/1540-5915.00013
- Crocker, L. M. et Algina, J. (2008). Introduction to classical and modern test theory. Mason, OH : Cengage Learning.
- Cronbach, L. (1951). Coefficient alpha and the internal structure of tests. Psychometrika, 16, 297-334. doi:10.1007/BF02310555
- Dahlman, K. A. (2014). Survey on the prevalence of measurement in undergraduate psychology curricula across the United States (thèse de doctorat, University of Nebraska-Lincoln, États-Unis). Récupéré du répertoire de l’Université : http://digitalcommons.unl.edu
- Dionne, E. et Grondin, J. (2018). AnDIE. Analyse didactique des items avec Excel [feuille de calcul]. Récupéré du site de la Faculté de médecine de l’université d’ottawa : http://med.uottawa.ca
- Ebel, R. L. (1965). Measuring educational achievement. Englewood Cliffs, NJ : Prentice-Hall.
- Fletcher, T. D. (2010). psychometric: Applied psychometric theory (R package version 2.2) [logiciel]. Récupéré de l’archive CRAN : http://cran.r-project.org
- Guilford, J. P. (1965). Fundamental statistics in psychology and education (4e éd.). Mahwah, NJ : Lawrence Erlbaum Associates.
- Lambert, N. M. (1991). The crisis in measurement literacy in psychology and education. Educational Psychologist, 26(1), 23-35. doi:10.1207/s15326985ep2601_2
- Leavy, A. M., Hannigan, A. et Fitzmaurice, O. (2013). If you’re doubting yourself then, what’s the fun in that? An exploration of why prospective secondary mathematics teachers perceive statistics as difficult. Journal of Statistics Education, 21(3). https://doi.org/10.1080/10691898.2013.11889684
- Ledesman, R. et Molina, J. G. (2009). Classical item and test analysis with graphics: The ViSta-CITA program. Behavior Research Methods, 41(4), 1161-1168. https://doi.org/10.3758/BRM.41.4.1161
- Lunsford, M. L. et Poplin, P. (2011). From research to practice: Basic mathematics skills and success in introductory statistics. Journal of Statistics Education, 19(1). https://doi.org/10.1080/10691898.2011.11889604
- Meyer, P. J. (2016). jMetrik (version 4.0.3) [logiciel]. Récupéré du site Psychomeasurement Systems : http://itemanalysis.com
- National Council on Measurement in Education. (n.d.). Psychometric software database. Récupéré du site de l’organisation : http://ncme.org
- Nelson, L. R. (2001). Item analysis for tests and surveys using Lertap 5. Récupéré du site de l’auteur : http://larrynelsonstuff.com
- Osterlind, S. J. (1998). Constructing test items: Multiple-choice, constructed-response, performance and other formats. Hingham, MA : Kluwer Academic.
- Thompson, N. (n.d.). CITAS: Classical item and test analysis spreadsheet [feuille de calcul]. Récupéré du site Assessment Systems for Good Measure : http://assess.com
- Thouin, M. (2014). Réaliser une recherche en didactique. Montréal, Canada : MultiMondes.
- Van der Maren, J.-M. (1999). La recherche appliquée en pédagogie : des modèles pour l’enseignement. Bruxelles, Belgique : De Boeck Université.
- Willse, J. T. (2018). CTT: Classical test theory functions (R package version 2.3.2) [logiciel]. Récupéré de l’archive CRAN : http://cran.r-project.org
- Wilson, M. (2005). Constructing measures: An item response modeling approach. Mahwah, NJ : Lawrence Erlbaum Associates.
List of figures
Figure 1
Onglet 8 permettant de paramétrer les balises pour chacun des indices
Figure 2
Un exemple des informations fournies par AnDIE
Figure 3
Une vue d’ensemble d’AnDIE
Figure 4
L’onglet présentant les résultats pour chacun des items
Figure 5
L’onglet présentant les résultats pour chacun des sujets
List of tables
Tableau 1
Étapes ayant mené à la création d’AnDIE
Tableau 2
Principaux logiciels consacrés à l’analyse d’items en se basant sur la théorie classique des tests
Tableau 3
Indices comparés des items avec les outils AnDIE, TAP, SPSS et JMetrik
Tableau 4
Indices comparés des sujets avec les outils AnDIE, TAP, SPSS et jMetrik
Tableau 5
Exemple d’intervalles permettant de baliser le jugement au regard de la difficulté, de la discrimination, de la corrélation bisérielle de point ajustée et de la valeur de l’alpha de Cronbach en cas de suppression de l’item[12]
Tableau 6
Comparaison de la plupart des résultats communs obtenus avec AnDIE, TAP, SPSS et JMetrik pour les paramètres des items
Tableau 7
Comparaison des résultats communs obtenus avec AnDIE, TAP, SPSS et jMetrik pour les paramètres des sujets